Diffusion MR of Hyperpolarized ¹³C Molecules in Solution

Abstract

We combined the high MR signal enhancement achieved using dissolution dynamic nuclear polarization (DNP) with a pulsed gradient double spin echo diffusion MR sequence to rapidly and accurately measure the diffusion coefficients of various hyperpolarized ¹³C molecules in solution. Furthermore, with a diffusion-weighted imaging sequence we generate diffusion coefficient maps of multiple hyperpolarized metabolites simultaneously. While hyperpolarized experiments can measure rapid, non-equilibrium processes by avoiding signal averaging, continuous signal loss due to longitudinal relaxation (T₁) complicates quantitation. By correcting for this signal loss, we demonstrate the feasibility of using hyperpolarized ¹³C diffusion weighted MR to accurately measure real-time (seconds) molecular transport phenomena. Potential applications include rapidly measuring molecular binding, cellular membrane transport, in vivo metabolite distribution and establishing a magnetic field independent hyperpolarized parameter.

Diffusion MR has a variety of applications in solution, and is central to modern biomedical imaging. Many variations of the pulsed gradient spin echo experiment originally developed by Stejskal and Tanner¹ have been used to measure diffusion coefficients², compartment size³, as well as molecular transport⁴ and molecular exchange⁵. Diffusion measurements often suffer from low sensitivity and require time-intensive signal averaging to obtain a sufficient signal to noise ratio (SNR) for reliable measurements. Long experimental times also require samples to be at steady state, since any signal perturbations other than molecular motion can skew measured diffusion constants. Since sensitivity has traditionally been limiting for diffusion MR experiments, ¹H has been used more frequently than other spin-1/2 nuclei (e.g, ¹³C, ¹⁵N, ³¹P) that have low gyromagnetic ratios and natural abundance. Hyperpolarized gasses, most notably ³He and ¹²⁹Xe, circumvent this low signal problem and allow for rapid diffusion measurements^6,7. Unfortunately, these inert gasses are not typically involved in chemical reactions or metabolic pathways of interest.

In this paper, we combine diffusion MR with dissolution dynamic nuclear polarization (DNP)⁸ hyperpolarized ¹³C and thereby lay the foundation for making real-time, non-equilibrium diffusion measurements. The signal gain provided by hyperpolarization and the chemical shift sensitivity of ¹³C will allow for diffusion studies to be carried-out on the time scale of chemical reactions⁹ or metabolic processes¹⁰. Since both diffusion MR and hyperpolarized experiments are characterized by a time-decay constant, the experimental setup for diffusion measurements of hyperpolarized molecules must allow for the quantitative separation of these two factors.

Dissolution DNP is typically used to polarize ¹³C nuclei with long spin-lattice (T₁) relaxation times (tens of seconds) and, upon dissolution, a solution of hyperpolarized spins is obtained. A conventional NMR spectrum of this solution can exhibit a signal enhancement of greater than 10,000-fold⁸ when compared to a spectrum of a similar solution at its thermal equilibrium polarization in a typical magnetic field of an NMR at ambient temperature. Hyperpolarized [1-¹³C] pyruvate has been used most extensively to study various cancers by monitoring [1-¹³C] lactate generation^11,12. Additionally, numerous other molecules have also been polarized to monitor other reactions and metabolic processes^13,14,15,16, either as single agents or in combination¹⁷. The challenge in combining hyperpolarization with diffusion MR lies in the non-renewable nature of the hyperpolarized spin state and its fast decay, where small imperfections in data acquisition can lead to large NMR signal modulations and thereby increase diffusion measurement error. When correctly implemented, the merging of these two techniques will provide significant advances in numerous fields, including molecular biding, cellular transport studies and in vivo diffusion weighted MRI.

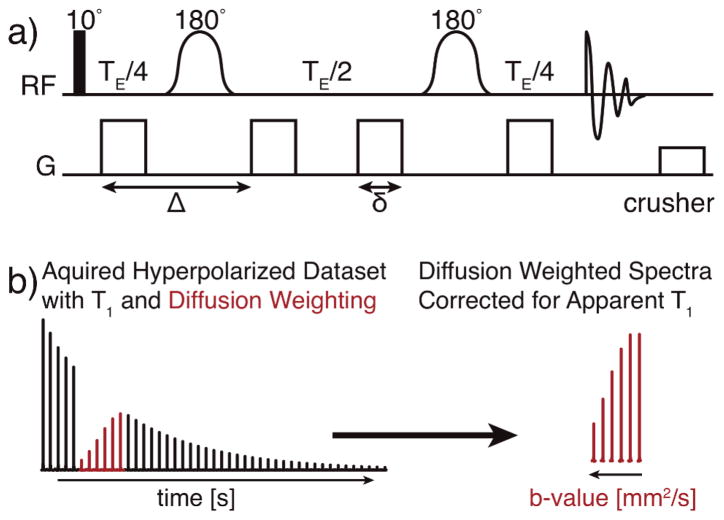
To perform diffusion MR of hyperpolarized ¹³C molecules, we used a pulsed gradient double spin echo sequence (Fig. 1a). The 10° excitation pulse allows for continuous sampling of the non-renewable hyperpolarized signal and enables precise quantitation. The pair of adiabatic 180° refocusing pulses are evenly spaced within the sequence’s echo time (TE), the time from the excitation pulse to maximum signal at the echo. Given the high SNR typical of hyperpolarized experiments, no signal averaging was necessary.

Fig. 1.

(a) The pulsed gradient double spin echo pulse sequence used for hyperpolarized diffusion experiments, with a 10° excitation pulse and adiabatic 180° pulses. (b) Representative spectra for which the apparent T₁ (black) and hyperpolarized diffusion measurements (red) are interleaved. Correcting the hyperpolarized diffusion weighted spectra for the T₁ enables an accurate calculation of diffusion coefficient for the hyperpolarized molecules.

All experiments were done on a Varian 600 MHz 1H/150 MHz ¹³C micro-imaging system at 27°C. For more detailed methods, see electronic supplementary information.

Hyperpolarized experiments consisted of interleaved acquisitions to measure both the hyperpolarized molecule’s apparent T₁ and its diffusion coefficient. Diffusion acquisitions with increasing gradient strengths (Fig. 1b, red lines) were interspersed with T₁ acquisitions with small crusher gradients (Fig. 1b, black lines). Diffusion coefficients were calculated by fitting the diffusion spectra with the following equation:

$$S=S_{o}exp(-bD)exp(-t/T_1)exp(-T_E/T_2){cos}^n(\theta )$$

where D is the diffusion coefficient (mm²/s) and b, commonly referred to as the b-value, is the diffusion weighting defined by 2γ²G²δ²(Δ−δ/3). Gradient (G) durations (δ) were 5 ms, gradient separations (Δ) were 20 ms, and γ is the gyromagnetic ratio for ¹³C. The cosine term corrects the data for multiple excitations (n) of the hyperpolarized magnetization with a flip angle θ. Individual spectra are corrected for T₁-dependent signal loss based on a per-time basis (t). Since the T_E (50 ms) for all experiments was kept constant, any T₂-weighting was a constant across all spectra and datasets and therefore was not needed to calculate the reported diffusion coefficients.

This approach for measuring diffusion coefficients relies on correcting for the effects of T₁ relaxation since hyperpolarized experiments are characterized by a T₁-dependant signal loss. While determining the T₁ of a hyperpolarized molecule in solution is trivial, accurate T₁ measurements become more difficult in complex environments, such as with molecular binding or in tissue.

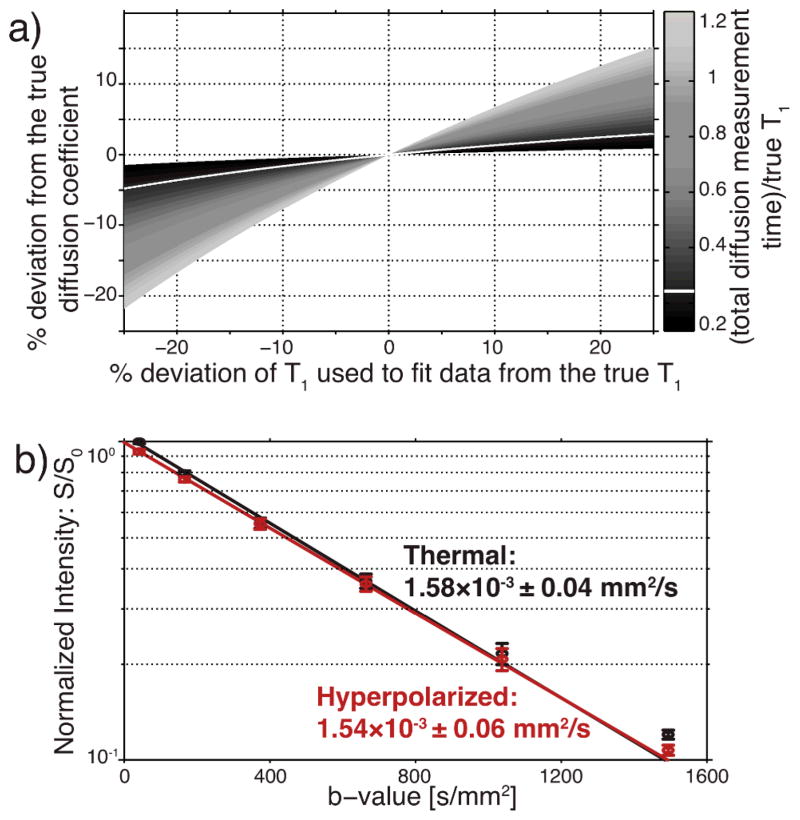
The simulation presented in Fig. 2a illustrates the dependence of the calculated diffusion coefficient on both the apparent T₁ of the hyperpolarized spin used to correct the dataset and the total diffusion measurement time required for the experiment. As the ratio of the total diffusion measurement time to the true relaxation time decreases (i.e., darker regions in Fig. 2a), the calculated diffusion coefficient becomes less sensitive to errors in the apparent T₁ used to correct the hyperpolarized diffusion dataset. Since long T₁ carbon species are typically used in hyperpolarized experiments (on the order of 30–60s), the diffusion measurement time can be significantly shorter than signal loss due to relaxation. The acquisition is also further accelerated due to the increased signal intensity afforded by hyperpolarization of the molecule of interest. Furthermore, while the decay nature of hyperpolarized signal complicates these experiments, within experimental tolerances, this can be addressed to generate reliable diffusion measurements.

Fig. 2.

(a) A simulation for hyperpolarized ¹³C urea shows how a short total diffusion measurement time relative to the T₁ makes calculations of the diffusion coefficient less sensitive to the apparent T₁ accuracy. The white line represents the (total diffusion measurement time)/true T₁ ratio used in our hyperpolarized ¹³C urea experiments, where errors of up to 25% in apparent T₁ only result in less than 5% errors in the diffusion coefficient. (b) Diffusion coefficients of ¹³C urea at 27°C, measured using thermal equilibrium polarization and hyperpolarization. b-value is a measure of the degree of diffusion weighting.

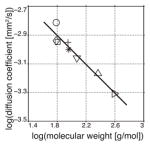
To confirm our ability to accurately measure the diffusion coefficient of a hyperpolarized molecule, we compared measurements of ¹³C urea both at its thermal equilibrium polarization and hyperpolarized, polarized to 8.4% ± 0.6. As seen in Fig. 2b the diffusion coefficients of thermally polarized and hyperpolarized ¹³C urea were 1.58×10⁻³ ± 0.04 and 1.54×10⁻³ ± 0.06 mm²/s, respectively, and not statistically different. In a similar fashion, we measured the diffusion coefficients of ¹³C pyruvate and ¹³C lactate (Table 1), polarized to 18.5% ± 0.7 and 2.9% ± 0.5, respectively.

Table 1.

Diffusion Coefficients (D) and relaxation times (T₁) of hyperpolarized ¹³C molecules measured in aqueous solution.

Molecule	MW [g/mol]	T1 [s]a	D [10−3 mm2/s]b	Literature D [10−3 mm2/s]c
13C urea (○)	61.05	35.3±2.6	1.54±0.06	1.4518
[1-13C] acetate (⋄)	61.04	46.2±0.7	1.15±0.03	1.1519
[1-13C,d3] acetate (□)	64.04	49.9±1.7	1.13±0.02	—
[1-13C] pyruvate (+)	89.05	43.8±3.3	1.12±0.04	—
[1-13C] lactate (✳)	91.07	32.3±0.7	1.00±0.01	1.1220
N-[acetyl-1-13C] glycine (▽)	118.10	16.9±0.8	0.87±0.07	1.11*,21
N-[acetyl-1-13C,d3] triglycine (△)	232.20	9.9±0.7	0.68±0.04	0.70*,21
N-[acetyl-1-13C,d3] RGD (▷)	391.37	5.4±0.8	0.49±0.03d	—

^aT₁ relaxation times are at 14.1 T/150 MHz for ¹³C.

^bMeasurements at 27°C.

^cLiterature references cite diffusion coefficients of either exactly the compound or a similar compound (marked with *), e.g., the diffusion coefficient for triglycine as compared to N-acetyl-triglycine. All literature values were adjusted for temperature using the Stokes-Einstein equation.

^dA 12 hr diffusion acquisition of thermally polarized N-acetyl-RGD (0.47×10⁻³ mm²/s) corresponds with this diffusion coefficient. Mean ± SD, n = 3.

We extended the technique developed here to measuring diffusion coefficients of larger molecules. Utilizing secondary hyperpolarization⁹, we generated hyperpolarized amino acids and peptides, achieving signal enhancements similar to those previously reported. The technique reacts hyperpolarized [1,1-¹³C] acetic anhydride (polarized to 2.4% ± 0.2) with nucleophilic amine termini. In this manner, we measured the diffusion coefficients of ¹³C acetate and ¹³C N-acetyl-glycine at 27°C in aqueous solution (Table 1). To lengthen the T₁ of larger secondarily hyperpolarized peptides, we polarized perdeuterated [1,1-¹³C,d₆] acetic anhydride (polarized to 2.9% ± 0.5), which avoids cross-relaxation between the carbonyl carbon and methyl protons. Reacting this with triglycine, we measured the diffusion coefficients of perdeuterated ¹³C acetate and ¹³C N-acetyl-triglycine (Table 1). Finally, we reacted the cell integrin adhesion peptide arginine-glycine-aspartic acid peptide (RGD) with perdueterated ¹³C acetic anhydride to measure the diffusion coefficient of ¹³C N-acetyl-RGD (Table 1). This experiment shows the feasibility of using hyperpolarized diffusion measurements to studying the translational motion and interaction of biologically relevant small peptides.

To demonstrate the feasibility of using diffusion MR of hyperpolarized metabolites in the clinical setting, we added a concentric echo planar imaging readout to the pulsed gradient double spin echo to generate diffusion coefficient maps (Fig. 3). Here, the diffusion coefficient maps of hyperpolarized ¹³C urea (1.55×10⁻³ ± 0.07 mm²/s), ¹³C pyruvate (1.12×10⁻³ ± 0.06 mm²/s) and ¹³C lactate (0.98×10⁻³ ± 0.04 mm²/s), measured simultaneously with frequency specific excitation pulses, match values acquired with hyperpolarized diffusion NMR.

Fig. 3.

Diffusion weighted MRI of three hyperpolarized metabolites, acquired simultaneously. (a) Representative T₁ corrected diffusion weighted images with increasing diffusion weighting (b-values 1.7, 173, 693 and 1560 s/mm²) used to simultaneously generate diffusion coefficient maps (b) of ¹³C urea, ¹³C pyruvate and ¹³C lactate.

Hyperpolarized diffusion NMR can allow for rapid measurements of real-time, non-equilibrium chemical process. For example, molecular binding can be measured using a pulsed gradient spin echo approach²². These experiments require time intensive signal averaging and today commonly utilize signal enhancement via the nuclear Overhauser effect (NOE)²³. Conversely, hyperpolarized diffusion NMR would greatly reduce the measurement times of these experiments, would not be complicated by NOE polarization transfers²⁴ when using ¹³C and would allow for the simultaneous observation of any changes in chemical shifts.

Like non-steady state chemical kinetics, assessment of metabolic flux requires rapid measurement, since metabolism occurs on the order of seconds. Closely associated with a metabolic pathway’s activity is the cellular membrane transport of these metabolites. Prior diffusion NMR studies took advantage of differences in metabolite diffusivity in the intra- and extracellular environments to measure intracellular metabolite concentrations²⁵. This approach used diffusion NMR as a filter, but because of the need for signal averaging, it could solely measure steady state metabolites. The hyperpolarized diffusion NMR technique developed here can be extended for use as a diffusion filter to measure real-time membrane transport of various hyperpolarized metabolites. For example, the intra-versus extracellular localization of the hyperpolarized ¹³C lactate produced in cancer cells could help elucidate aggressiveness and metastatic potential²⁶. Of course, hyperpolarized diffusion filters could be used to measure cellular transport from a variety of metabolites, especially when applying these studies to bioreactors²⁷.

While diffusion-weighted MRI has become a standard clinical tool for assessing anatomy, combining it with hyperpolarized substrates has the potential to inform on metabolism localization in the cellular microenvironment. Larson et al. recently developed a super stimulated echo sequence to suppress vascular hyperpolarized ¹³C signal²⁸. By only imaging hyperpolarized ¹³C lactate in the tissue, this technique improved the delineation of primary tumors in vivo. Extending this technique to create a diffusion filter could allow for measurement of both the generation of hyperpolarized metabolites and their tissue distribution, similar to how cell studies would elucidate membrane transport kinetics. Furthermore, hyperpolarized ¹³C diffusion MRI could measure apparent diffusion coefficient (ADC) maps for hyperpolarized metabolites. Noteworthy is that such ADC maps are magnetic field independent, a particular benefit since hyperpolarized ¹³C signal intensities change according to initial polarization levels and magnetic field dependent T₁ relaxation.

In summary, we present the foundations for carrying out fast diffusion studies with dissolution DNP hyperpolarized ¹³C molecules. The SNR gain provided by hyperpolarization and the chemical shift sensitivity of ¹³C allows for diffusion studies to be carried-out on the time scale of chemical reactions or metabolic processes, where both products and reactants can be measured simultaneously. Our technique demonstrates how to robustly sample dynamic hyperpolarized magnetization in order to obtain quantitatively accurate diffusion measurements. Given this, hyperpolarized ¹³C diffusion MR has far reaching applicability in areas such as binding studies, metabolomics, clinical diagnoses and many more.