Stochastic dynamics of cancer initiation

Abstract

Most human cancer types result from the accumulation of multiple genetic and epigenetic alterations in a single cell. Once the first change (or changes) have arisen, tumorigenesis is initiated and the subsequent emergence of additional alterations drives progression to more aggressive and ultimately invasive phenotypes. Elucidation of the dynamics of cancer initiation is of importance for an understanding of tumor evolution and cancer incidence data. In this paper, we develop a novel mathematical framework to study the processes of cancer initiation. Cells at risk of accumulating oncogenic mutations are organized into small compartments of cells and proliferate according to a stochastic process. During each cell division, an (epi)genetic alteration may arise which leads to a random fitness change, drawn from a probability distribution. Cancer is initiated when a cell gains a fitness sufficiently high to escape from the homeostatic mechanisms of the cell compartment. To investigate cancer initiation during a human lifetime, a ‘race’ between this fitness process and the aging process of the patient is considered; the latter is modeled as a second stochastic Markov process in an aging dimension. This model allows us to investigate the dynamics of cancer initiation and its dependence on the mutational fitness distribution. Our framework also provides a methodology to assess the effects of different life expectancy distributions on lifetime cancer incidence. We apply this methodology to colorectal tumorigenesis while considering life expectancy data of the US population to inform the dynamics of the aging process. We study how the probability of cancer initiation prior to death, the time until cancer initiation, and the mutational profile of the cancer-initiating cell depends on the shape of the mutational fitness distribution and life expectancy of the population.

1. Introduction

Tissues of multi-cellular organisms are organized into morphologically stable compartments or niches [1, 2]. Such compartments are made up of separate clones of cells, which proliferate to fulfill their organ-specific tasks [3, 4]. In healthy tissues, compartment sizes are stabilized by homeostatic mechanisms which induce compensatory regulatory responses via cellular signaling, apoptosis, and other processes [5]. During each cellular replication, a genetic or epigenetic alteration may arise. Many of those changes do not alter the reproductive fitness of the cell and are selectively neutral [6]. Some alterations, however, provide the cell with a fitness advantage due to increased proliferation capabilities, decreased death, enhanced migration and invasion, or the ability to induce angiogenesis [7]. Once a cell has evolved a sufficiently aggressive phenotype, it can escape from homeostatic control mechanisms and initiate tumorigenesis [8, 9, 10, 11, 12, 13, 14]. During the expansion of this initiated clone, additional genetic and/or epigenetic changes are accumulated that drive cancer progression and lead to more malignant and ultimately invasive phenotypes [7].

While tumorigenesis has classically been defined as a disease resulting from the accumulation of genetic alterations [15], it is becoming increasingly apparent that epigenetic modifications are similarly important for the initiation and progression of human cancer [16]. Patterns of DNA methylation and chromatin structure are significantly altered in cancer cells and include genome-wide losses of, and regional gains in, DNA methylation. Aberrant promoter methylation, for instance, is associated with the loss of gene function that can provide a selective advantage to tumor cells, as do genetic alterations. For example, the von Hippel-Lindau (VHL) gene, which causes familial renal cancer if mutated in the germ line, is often epigenetically silenced in the sporadic form of this tumor type [17]. Similarly, the breast cancer 1, early onset (BRCA1) and serine/threonine kinase 11 (STK11) genes are often epigenetically inactivated in sporadic cases of breast and colon cancer, respectively, while they predispose to these cancer types in carriers of a germ line mutation [18, 19]. In addition to gene silencing events that are associated with methylation changes, methylation patterns can also influence tumorigenesis by other mechanisms; cytosine methylation, for instance, can cause spontaneous hydrolytic deamination of cytosine and lead to C to T transitions [20]. This enhanced mutagenesis might lead to many gene alterations observed in tumors – as many as 50% of inactivating point mutations in the coding region of the human TP53 tumor suppressor gene in somatic cells occur at methylated cytosines [21]. Epigenetic alterations therefore cannot be neglected in the study of cancer.

Due to its importance for an understanding of tumorigenesis, the dynamics of cancer initiation have been the subject of several mathematical investigations. These studies considered cancer initiation to occur when a single cell has accumulated n specific alterations [22, 23, 24, 25, 26, 27]. The fitness effects of these alterations were assumed to be either neutral or advantageous; the latter was realized as an additive jump in the growth rate of the mutated cell. Several authors studied the situation in which the accumulation of two alterations is sufficient to initiate tumorigenesis [22, 23, 24, 25]; cells were considered to proliferate according to the Moran model in a population of fixed size [28]. Later on, scenarios in which n ≥ 2 mutations are necessary for cancer initiation were investigated [26, 27]. These contributions are part of a literature of mathematical approaches to cancer initiation and progression [29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51].

In this paper, we propose a novel mathematical model of cancer intiation. Unlike earlier efforts, we do not consider the situation in which cancer is initiated once a specified number of genetic alterations has been accumulated; rather, cancer initiation occurs as soon as the fitness of a cell passes a threshold value. Once this threshold is reached, the cell can escape from homeostatic control and initiates clonal expansion. In particular, we model a mechanism for the breakdown of homeostasis in a normally fixed-size compartment of cells via the accumulation of random mutational fitness changes emerging during cell replication. The fitness changes conferred by (epi)genetic alterations are modeled as random variates selected from a mutational fitness landscape. The fitness threshold necessary for cancer initiation can then be reached via a large number of mutations each conferring small fitness changes, a few mutations each conferring large fitness effects, or a mixture of large and small effects. We then investigate the dynamics of cancer initiation conditioned on the event that initiation occurs prior to death of the patient due to causes other than the cancer type of interest. This conditioning is addressed by adding a second dimension representing an aging process to the model. This framework is used to determine the probability of cancer initiation prior to death as well as the expected waiting time until cancer initiation. Furthermore, we investigate the expected number of neutral and non-neutral mutations that are present in the cancer-initiating clone. This quantity is of clinical interest since it provides insight into the genotype of the cancer-initiating cell and thus the genotypic composition and potentially the drug sensitivity of the resulting tumor. Our mathematical framework sheds light onto the effects of the shape and characteristics of the mutational fitness landscape on the dynamics of cancer initiation, and provides a methodology to assess the consequences of different life expectancy distributions on lifetime cancer incidence and the mutational composition of cancer-initiating cells.

2. The Model

Consider a compartment of N cells that proliferate according to a stochastic Moran process (see the Appendix for a discussion of this process) [28, 52]. This compartment consists of those cells that are at risk of accumulating the mutations leading to cancer initiation. If only tissue-specific stem cells live long enough to accumulate the necessary changes, then the population is made up of stem cells [53]; alternatively, the compartment additionally contains progenitor cells [50, 54]. Since healthy tissues are subdivided into small compartments of cells [1, 2], N is small. Initially, all cells are unmutated and have relative fitness 1. The time intervals between reproduction events are independent, identically distributed exponential random variables with mean 1/N. During each reproduction event, one cell is chosen at random to die, and one cell is chosen to reproduce according to its relative fitness. The population size is strictly constant. The probability of a specific cell being chosen for reproduction during an event is determined by the contribution of its fitness to the total fitness of the population; if there is a single cell of fitness s in a population of N − 1 cells of fitness 1, then the cell with fitness s is chosen to reproduce with probability s/[s + (N − 1)]. Here fitness is defined as the relative reproductive success of cells.

Mutational fitness distribution f_ψ

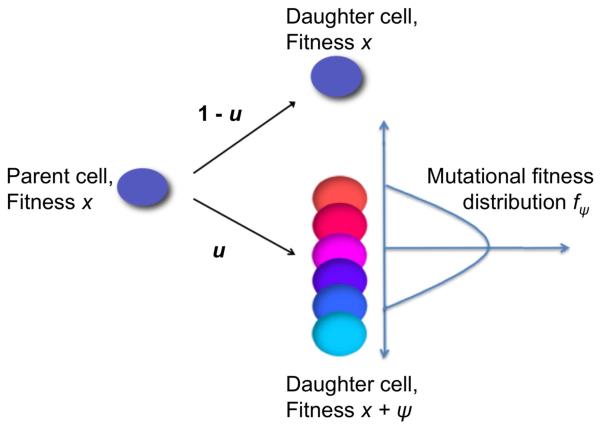
During each cell division event, an (epi)genetic alteration may occur with probability u ≪ 1; thus alterations arise in the compartment of cells at rate Nu. The fitness effects of individual alterations are random variates drawn from a probability distribution, f_ψ, which represents a mutational fitness landscape. This distribution f_ψ may be state-dependent and thus vary according to the fitness of the parent cell (e.g. $f_{\psi }^x$ is dependent on the fitness x of the parent cell). Figure 1 shows a schematic of this process for a state-independent distribution f_ψ. This flexible framework allows us to study the effects of mutational fitness landscapes on the dynamics of cancer initiation.

Figure 1. A schematic representation of the stochastic process governing cellular fitness.

We consider a population of N cells residing in a compartment or niche of fixed size. These cells replicate according to a stochastic Moran process. During each elementary time step of the process, a cell is chosen at random proportional to fitness to divide and its offspring replaces another randomly chosen cell. During each cell division, a genetic or epigenetic alteration arises with probability u. Each alteration may confer a random additive fitness change to the cell. The parent cell, on the left, thus gives rise to a daughter cell with the same fitness, x, with probability 1 − u (upper right). With probability u, the parent cell produces a mutated offspring with fitness x + ψ, where ψ is a random additive fitness change selected according to the mutational fitness distribution f_ψ (lower right). If a cell within the compartment gains a sufficiently large fitness value, then tumorigenesis is initiated.

Dynamics in fitness space

Suppose the population consists of two types of cells at time t = 0: N − 1 normal cells and one cell carrying a single mutation. Define the waiting time until a cell in this population accumulates a second mutation as T_mut and the time until homogenization (i.e., until the cell carrying the mutation reaches zero or one hundred percent frequency in the population) as T_hom. Then we have

$$P(T_{\mathit{mut}}\le T_{\mathit{hom}})\le 3\mathit{Nu}(\log N+\gamma ),$$ (1)

where γ is the Euler-Mascheroni constant. In other words, if 3Nu(log N + γ) ≈ 0, a cell harboring a mutation is far more likely to reach fixation in the compartment or die out before a second mutation arises. See the Appendix for the proof of equation (1). Therefore, when u ≪ 1/N², the periods of time during which the compartment is not homogeneous comprise a negligible amount of time. As the population size and/or the mutation rate increase during tumor progression, more complex dynamics emerge [55]; this scenario, however, is likely not applicable to situations of cancer initiation since in healthy tissues, compartment sizes and mutation rates are small. For the parameter ranges of interest for the study of cancer initiation, a cell compartment is almost always homogeneous.

Based on these considerations, the process describing the evolution of fitness values in a compartment of cells is approximated by a Markov process Z(·), where Z(t) represents the fitness of the homogeneous compartment at time t. The process Z jumps whenever a cell harboring a novel non-neutral mutation reaches fixation in the compartment, and takes values in the space of all possible fitness values dictated by the fitness landscape. By equation (1), this process closely approximates the behavior of cellular fitness values in a small compartment for the vast majority of time. Note that by focusing on the times when the process is homogenous, the state space of the system is significantly reduced, thus allowing for more feasible computational analysis.

Consider the fitness values a and b, for some 0 ≤ a < b, such that a compartment of cells remains in a homeostatic state for fitnesses within the range [a, b]; thus Z(t) ∈ [a, b] for all times t. Once a cell in the compartment gains a fitness greater than the threshold b, it escapes from homeostasis and cancer is initiated. The fitness value a is defined as a reflecting boundary for Z; any cell with fitness below a is immediately replaced by a cell with fitness a. For computational purposes, we consider the process Z living on a discretized state space on the range [a, b]. Since we consider a homeostatic cell compartment before initiation of tumorigenesis, a natural choice for the parameters is a = 1 − 1/N and b = 1 + 1/N since these values signify the boundaries for neutral evolution [56].

Let us now consider in detail the dynamics of Z in fitness space. We introduce the mutation kernel M(·, ·), where M(x, y) represents the probability that a cell with fitness x produces a daughter cell with fitness y (i.e. $M(x,y)=f_{\psi }^x(y-x)$). If y > x, then the fitness of the daughter cell is advantageous as compared to the fitness of its parent cell; if y < x, it is disadvantageous, and if y = x, it is neutral. Since neutral mutations are allowed to occur, M(x, x) can be non-zero. If a single cell of fitness y arises in a population of N − 1 cells of fitness x, the probability that the cell with fitness y reaches fixation in the population is given by

$${\rho }_{x,y}=\frac{1-x∕y}{1-{(x∕y)}^N}.$$ (2)

This expression is called the fixation probability and can easily be found by first step analysis. By symmetry, we have ρ_x,x = 1/N. The intensity matrix for the Markov process Z is then defined as

$$Q(x,y)=Nu{\rho }_{x,y}M(x,y),$$

for y < b. This expression becomes Q(x, y) = NuM(x, y) when y ≥ b. The reflecting behavior at the lower boundary is realized through the mutation kernel M. By definition, we have

$$Q(x,x)=\sum _{y\ne x}Q(x,y).$$

Since the process stops as soon as one cell gains a fitness value greater than b, the states x ≥ b are absorbing, so Q(x, y) = 0 for all y and x ≥ b. The summation is over all y in the discrete fitness space.

Modeling the lifetime of a patient

The Moran model dynamics described by the coarse-grained process Z represent the change in the fitness values of cells in the compartment over time. In order to model the dynamics of cancer initiation during a human lifetime, a ‘race’ between this fitness process Z and the aging process of the patient is considered. To this end, we introduce a second stochastic process, L(t), which is a continuous-time Markov chain with an absorbing state representing death of the patient. Thus this process, L, hits the absorbing state with probability one and the first passage time of this event represents the age of the patient at death. The transition probabilities of this Markov chain can be tuned to match mortality data for the population of interest. We fit the dynamics of the process L to qualitatively describe the current life expectancy in the United States [57].

To address a similar problem, Liu and Lin [58] utilized a Coxian phase-type distribution to construct an aging process to fit life expectancy data. We follow a simplified version of this approach, and define L to be a Coxian process with d states. In particular, the process L(t) is initialized at state 1 and takes values in the state space {1,…,d}. If L(t) = ℓ < d, it jumps monodirectionally to state ℓ + 1 at rate 1, and the final state d is an absorbing state. The time for the process to hit the absorbing state is described by a Gamma(d − 1, 1) distribution. The transition intensity matrix for this process is (S)_i,j = S_i,j, which satisfies S_i,i = −S_i,i+1 and is constant along the diagonal. Let us denote this value along the main diagonal by S instead of unity, since changing the diagonal allows for flexibility in the choice of time scales with respect to the replication rate of cells in the compartment. Figure 2 shows that death of a patient occurs when the process L makes d − 1 upward steps; note that the time between each step is an exponential random variable with mean 1. The Gamma distribution provides a good qualitative approximation for the lifetime distribution of a population. When modeling the fraction of people that survive longer than x years via P(G > x), where G is a Gamma(81,1) random variable, then this tail probability stays relatively flat until around 68 years, at which point it begins a sharp decay towards zero.

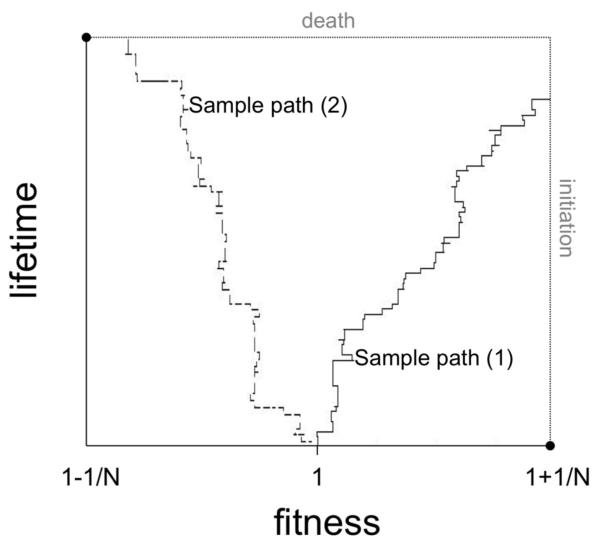
Figure 2. Sample path simulations of the two-dimensional stochastic process.

We consider a stochastic process governing the evolution of fitness values of cells within the compartment (see Fig. 1) coupled with a stochastic process representing aging and death of the patient. The figure shows two sample path simulations of this two-dimensional process. The fitness of cells within the compartment is shown on the horizontal axis, and the lifetime of the patient is displayed on the vertical axis. If the trajectory hits the right boundary before reaching the upper border, then cancer initiation occurs before death of the patient (sample path (1)); if the trajectory hits the top boundary before reaching the right border, then death occurs before cancer initiation (sample path (2)). The fitness values bounding the area of interest are dictated by the cutoffs for neutral evolution [56].

In summary, we have designed a model of cancer initiation during a human lifetime using atwo-dimensional Markov process. The first dimension of this process, Z, represents the fitness of cells at risk of accumulating the mutations initiating tumorigenesis; these cells are organized into small compartments or niches of a constant size. The second dimension L represents the aging process of a patient. The state of the process Z is governed by the more detailed dynamics of a Moran process at the cellular level, and the process L is chosen so that its absorption time, which has a phase-type distribution ϕ, matches mortality data. This model has several parameters: the mutation rate u, the lifetime distribution ϕ(t), the number of cells in the compartment N, and the mutational fitness distribution f_ψ. This model is then used to determine the dynamics of the event that cancer initiation occurs prior to death, i.e. that the right boundary of Z is reached (corresponding to one cell reaching a fitness value greater than or equal to the boundary value a) prior to absorption in the L-direction. Figure 2 shows a diagram of this process and two possible sample paths. All paths initiate at (Z = 1, L = 1) and sample path (1) demonstrates a trajectory in which cancer initiation occurs prior to death; such paths, however, comprise only a fraction of all possible outcomes. Sample path (2) visualizes a trajectory in which death occurs prior to cancer initiation. Note that cancer initiation is not equivalent to diagnosis of the disease, so that the initiation statistics cannot be compared to cancer incidence data.

3. Analysis

The stochastic model outlined above is used to determine several quantities: (i) the probability of cancer initiation prior to the time of death; (ii) the waiting time until cancer initiation prior to death, and (iii) the expected number of neutral and non-neutral mutations present in the cancer-initiating cell, conditional to cancer initiation occurring before death. The estimates for these quantities are obtained in the form of the solution to simple linear systems in order to keep the analysis applicable to general mutation kernels M. These estimates are later used to study the effect of the mutation kernel and of lifetime distributions on the dynamics of cancer initiation.

3.1. The probability of cancer initiation prior to death

For a given state in the two dimensional space (x, r), let I(x, r) denote the probability of Z(t) reaching a fitness value above b (i.e. initiating cancer) before L(t) reaches the absorbing state d (i.e. death), starting from the initial condition Z(0) = x, L(0) = r. For the process Z, there can be a transition of the form x → y and for the process L(t), there can be a transition of the form r → s. Thus when the current state of the two processes is (x, r), then conditional on a jump occurring, the jump v has the following probability distribution:

$$\begin{array}{cc}\hfill & \mathbb{P}(v=(y-x,0\left)\right)=\frac{Nu{\rho }_{x,y}M(x,y)}{-Q(x,x)-S}\doteq P_Z(x,y\mid r),\hfill \\ \hfill & \mathbb{P}(v=(0,s-r\left)\right)=\frac{S}{-Q(x,x)-S}\doteq P_L(r,s\mid x),\hfill \end{array}$$

for any y ≠ x in the fitness space and any s ∈ {1,…,d}, s ≠ r.

By first step analysis, we obtain a linear system that the probabilities I(x, r) satisfy:

$$I(x,r)=\sum _{y}I(y,r)P_Z(x,y\mid r)+\sum _{s}I(x,s)P_L(r,s\mid x).$$ (3)

We also have the boundary conditions I(x, d) = 0 for all x ∈ [a, b] and I(b, r) = 1 for r ∈ [0, d). This linear system can easily be solved to obtain I(x, r). Cancer initiation is then defined as the event that the fitness of one cell reaches a = 1+1/N before death of the patient; the probability of initiation prior to death is p_i ≡ I(1, 1). The transition probabilities for the compound process (Z,L) conditioned upon initiation prior to death are given by

$${\tilde{P}}_Z(x,y\mid r)\doteq P_Z(x,y\mid r)\frac{I(y,r)}{I(x,r)}$$ (4)

and

$${\tilde{P}}_L(r,s\mid x)\doteq P_L(r,s\mid x)\frac{I(x,s)}{I(x,r)}.$$ (5)

3.2. The waiting time until cancer initiation

Let τ represent the time of cancer initiation, and σ the time at which the process L is absorbed, i.e. the patient dies. Denote the time until the first jump of the process (Z, L) by T₁. Then we have

$$\mathbb{E}\left[{\theta }^{T_1}\right]=\mathbb{E}\left[{\theta }^{T_1}\mid \tau <\sigma \right]=\frac{-S-Q(x,x)}{\log \theta -S-Q(x,x)}.$$

This result is important because of the following:

$$\mathbb{E}\left[{\theta }^{\tau }\mid \left(Z\right(T_1),L(T_1\left)\right)=(y,r)\right]=\mathbb{E}\left[{\theta }^{T_1}\right]{\mathbb{E}}_{(y,r)}\left[{\theta }^{\tau }\right].$$

This expression results from the independence of the duration of the first jump time and all subsequent jump times. The generating function for the conditioned initiation time starting from state (x, r) is defined as

$$G(x,r,\theta )={\mathbb{E}}_{(x,r)}\left[{\theta }^{\tau }\mid \tau <\sigma \right].$$ (6)

Then, performing first step analysis, we obtain the linear system:

$$\begin{array}{cc}\hfill & G(x,r,\theta )\hfill \\ \hfill & =\frac{-S-Q(x,x)}{\log \theta -S-Q(x,x)}\left(\sum _y{\tilde{P}}_Z(x,y\mid r)G(y,r,\theta )+\sum _s{\tilde{P}}_L(r,s\mid x)G(x,s,\theta )\right).\hfill \end{array}$$

The boundary condition is G(b, r, θ) = 1.

We perform a simpler calculation to determine the mean waiting time until cancer initiation. Define w(x, r) to be the expected time until initiation starting from the state (x, r), conditioned on initiation prior to death: $w(x,r)={\mathbb{E}}_{x,r}[\tau \mid \tau <\sigma ]$. Then we have

$$w(x,r)=\sum _y{\tilde{P}}_Z(x,y\mid r)w(r,y)+\sum _s{\tilde{P}}_L(r,s\mid x)w(x,s)+\frac{1}{-Q(x,x)-S}$$ (7)

with boundary condition w(b, r) = 0.

3.3. The number of neutral mutations in the cancer-initiating cell

An accurate understanding of the genomic composition of the cell that leads to clonal expansion and cancer initiation may aid in the identification of drug targets. Furthermore, it helps to elucidate the distribution of advantageous and passenger (selectively neutral) mutations in cancer. Let us first consider the number of neutral mutations that have been accumulated in the compartment before cancer is initiated. Denote the number of neutral mutations present in the compartment at time t by m(t). Next we compute the function

$$\mu (x,r)={\mathbb{E}}_{(x,r)}\left[m\right(\tau )\mid \tau <\sigma ].$$ (8)

Thus, μ represents the number of neutral mutations accumulated in the cancer-initiating cell conditional to cancer initiation occuring before death of the patient.

Between jumps of the two-dimensional process (Z, L), a random number of neutral mutations can reach fixation within the compartment of cells. Let T_j and T_j+1 be the jump times of (Z, L), and for simplicity denote (Z(T_j), L(T_j)) = X_j. During the transition from X_j to X_j+1, the compartment can accumulate Y_j (X_j) neutral mutations. Define

$$\eta (x,r)=\frac{uM(x,x)}{uM(x,x)-Q(x,x)-S}.$$

The top of the fraction represents the rate at which neutral mutations which eventually reach fixation arise within the compartment, and the bottom of the fraction represents the total rate at which fixating mutations arrive and the time process changes. With this definition, Y_j(x, r) is distributed like a geometric random variable with

$$\mathbb{P}\left(Y_j\right(x,r)=n)=\eta {(x,r)}^n(1-\eta (x,r\left)\right),$$

which gives

$$\mathbb{E}\left[Y_j(x,r)\right]=\frac{\eta (x,r)}{1-\eta (x,r)}.$$

By conditioning on the first step, we obtain that μ(·, ·) satisfies the following linear system for each possible fitness x in [a, b]:

$$\mu (x,r)=\frac{\eta (x,r)}{(1-\eta (x,r\left)\right)}+\sum _y{\tilde{P}}_Z(x,y\mid r)\mu (y,r)+\sum _s{\tilde{P}}_L(r,s\mid x)\mu (x,s).$$

Note that μ(x, r) = 0 for those fitnesses that lie outside of [a, b]. Therefore μ(·, ·) can be determined by solving the linear system above.

3.4. The number of non-neutral mutations in the cancer-initiating cell

Let us next determine the mean number of advantageous and disadvantageous mutations in the intiating cell. Let n(t) be the number of non-neutral mutations present in the compartment of cells at time t. Then, the number of non-neutral mutations at initiation is given by

$$\nu (x,r)={\mathbb{E}}_{(x,r)}\left[n\left(\tau \right)\mid \tau <\sigma \right],$$

where ν(x, r) satisfies the system

$$\nu (x,r)=\sum _{y\ne x}{\tilde{P}}_Z(x,y\mid r)\left(\nu \right(y,r)+1)+\sum _s{\tilde{P}}_L(r,s\mid x)\nu (x,s)$$

with boundary condition ν(b, r) = 0. The expected number of advantageous or disadvantageous mutations present can be obtained in a similar fashion. For example, by defining n_a(t) to be the number of advantageous mutations present at time t, the number of advantageous mutations present at initiation is given by

$${\nu }_a(x,r)=\mathbb{E}(x,r)\left[n_a\left(\tau \right)\mid \tau <\sigma \right]$$

and ν_a(x, r) satisfies the linear system

$$\begin{array}{cc}\hfill {\nu }_a(x,r)=& \sum _{y>x}{\tilde{P}}_Z(x,y\mid r)\left({\nu }_a\right(y,r)+1)+\sum _{y<x}{\tilde{P}}_Z(x,y\mid r){\nu }_a(y,r)\hfill \\ \hfill & +\sum _s{\tilde{P}}_L(r,s\mid x){\nu }_a(x,s),\hfill \end{array}$$ (9)

where the boundary condition is again ν_a(b, r) = 0.

4. Application of the model to colorectal cancer initiation

Let us now apply this mathematical framework to colorectal cancer as a specific example. Colorectal tumors progress through four distinct clinical stages: dysplastic crypts, small benign tumors, malignant tumors invading surrounding tissues, and finally metastatic cancer [11]. This progression is driven by the accumulation of several genetic changes [59]. Mutations of the adenomatous polyposis coli (APC) gene are considered the earliest and most prevalent genetic changes in colorectal tumorigenesis [11]; other important contributors are mutations in the KRAS and TP53 genes [11]. Colonic tumors arise from the rapidly proliferating epithelium of the colon. This epithelium is organized into N_crypts = 10⁷ compartments of cells called crypts [60]. Each crypt contains about 1000 - 4000 cells. Approximately 4 - 10 of those cells are stem cells, residing at the base of each crypt [4, 61]. The progeny of stem cells migrate up the crypt, continuing to divide until they reach its mid-portion. Then they stop dividing and differentiate into mature cells. When the cells reach the top of the crypt, they undergo apoptosis and are engulfed by stromal cells or shed into the gut lumen. The cell migration from the base to the top of the crypt takes about 3 - 6 days [62].

To study the probability of cancer initiation from any crypt, we estimate the probability of initiation from a single crypt prior to death, p_i. Then the number of crypts containing cancer-initiating cells is binomially distributed with parameters N_crypts and p_i. Taking a Poisson approximation, the probability of cancer initiation prior to death from any crypt becomes approximately 1 − exp[−p_iN_crypts], and the average number of crypts containing cancer-initiating cells emerging prior to death is N_crypts × p_i. Note that if p_i is of order 10⁻⁶ or greater, the probability of having at least one cancer-initiated crypt before death is 1. If p_i is on the order of 10⁻⁸ or less, the probability of having at least one such crypt before death is much less than 1. Unfortunately no data is available on the frequency of cancer-initiated crypts in the population since these crypts are generally too small to be detected by routine colonoscopies, but slightly larger growths – adenomatous polyps – are observed in approximately 50% of people above age 70 [63, 64, 65]. These statistics can be used to guide parameter choices for the mutational fitness distribution.

For the purpose of our mathematical model, we consider a compartment size of N = 10 colonic stem cells and a stem cell division frequency of approximately once per week [66, 67]. The overall mutation rate – giving rise to neutral, advantageous or deleterious mutations – is about u = 0.001 per cell division, since there are 3 · 10⁹ base pairs in the human genome and the per base pair mutation rate is about 10⁻¹¹ to 10⁻¹² [68]. There are no estimates for the shape of the mutational fitness distribution for human colonic epithelial cells. Therefore, to investigate the dependence of the dynamics of cancer initiation on the mutational fitness distribution f_ψ, we construct a general family of fitness distributions with a mode at zero. For simplicity, assume that the mutational fitness distribution is state independent: $f_{\psi }=f_{\psi }^x$. The general form of the mutational distribution is then given by

$$P(\psi =k\Delta )=c{\alpha }^k,k\in \mathbb{N},$$

and

$$P(\psi =-k\Delta )=c{\beta }^k,k\in \mathbb{N},$$

where c is a normalization constant. In practice, we use a truncated approximation of this unbounded distribution. The point mass at the origin represents neutral mutations, such as alterations in non-coding DNA. The parameter Δ represents the fitness space discretization, which is set as Δ = 0.004. This distribution thus has two key shape parameters: α, which controls the decay rate on the right (i.e. advantageous mutations), and β, which controls the decay rate on the left (i.e. deleterious mutations). When α and β are set to 1, the distribution is uniform. Note that a larger probability of neutral mutations can be added by considering a mixture of this distribution with a point mass at 0. Figure 3 illustrates this family of distributions. An increase in the shape parameter β while holding α constant results in a more slowly decaying deleterious tail of the distribution; this leads to a higher percentage of disadvantageous mutations with more negative fitness jumps possible. Similarly, an increase in α while holding β constant results in a higher percentage of advantageous mutations with larger positive fitness jumps possible (distribution not shown). This general form of fitness distributions is next used to determine the consequences of changing the distribution on the dynamics of cancer initiation.

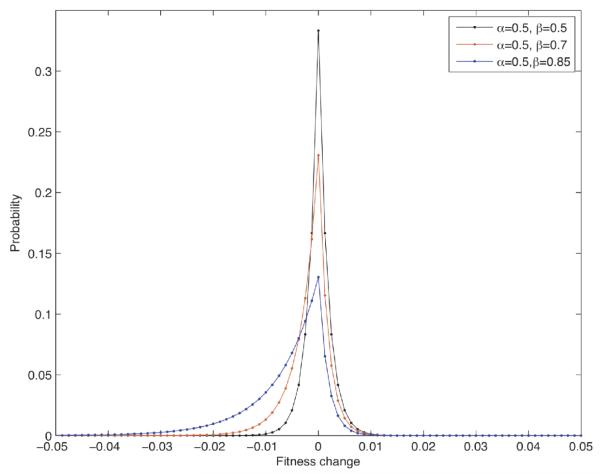
Figure 3. The mutational fitness distribution.

The stochastic process governing the evolution of fitness values of cells within a compartment depends on the shape of the fitness distribution conferred by mutations. For simplicity, we consider a general family of fitness distributions determined by the shape parameters α and β, which govern the decay of advantageous and deleterious mutations, respectively. This flexible setup allows us to study the effects of varying the mutational fitness distribution on the dynamics of cancer initiation. As specific examples, the figure displays the probability density function of f_ψ for α = 0.5 and β = 0.4, 0.5, 0.6.

4.1. Effects of varying the mutational fitness distribution, f_ψ

Let us now investigate the results of modifying the shape parameters of the mutational fitness distribution on the dynamics of cancer initiation from a single compartment of cells. Throughout this section, we consider an aging process L whose properties are qualitatively fitted to the US mortality data [57], with d = 82 states.

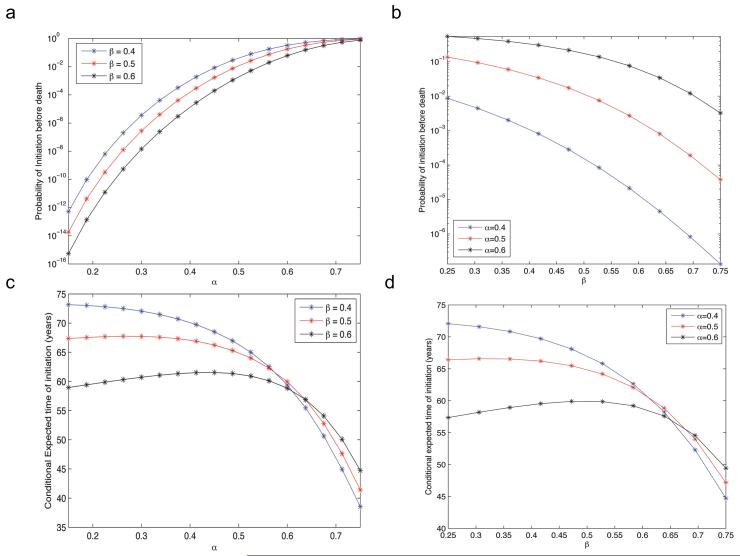
We first study the consequences of varying the decay rates, α and β, of the positive and negative tails of the mutational fitness distribution f_ψ on the probability of cancer initiation. Figure 4a and b displays the probability of initiation before death, p_i, as the shape parameters α and β are varied; here p_i is determined by solving equation (3) for I(1, 1). Fig. 4a shows the probability of cancer initiation as a function of α, for different values of β; note that as α increases, the probability of initiation is enhanced since the frequency and fitness advantages of beneficial mutations increase. Similarly, as β increases (Fig. 4b), the probability of cancer initiation decreases. The incidence of human tumors provides some clues as to the relative magnitude of α and β. Based on the frequency of adenomatous polyps in the US population (≈ 50%) [63, 64, 65], the probability of harboring a cancer-initiated crypt before death is estimated between 50 – 90%. Thus it is unlikely that p_i ≫ 10⁻⁷, since this choice would result in an unrealistically high probability of cancer initiation. Therefore, it is unlikely that α ≫ β, corresponding to a vast majority of mutations being advantageous, because the probability of cancer initiation would also be unrealistically high for this regime.

Figure 4. The probability of and time until cancer initiation prior to death.

(a) and (b) The panels display the probability of cancer initiation from a single compartment of cells, p_i, before death of the patient due to causes other than the cancer type of interest. The panels are plotted on a semilogarithmic plane for clarity. The probability of cancer initiation increases with α and decreases with β. (c) and (d) The panels display the expected time of cancer initiation, conditioned on initiation occurring before death of the patient. (a) and (c) We vary the shape parameter α, which governs the decay rate on the right of the distribution (i.e. advantageous mutations). (b) and (d) We vary the shape parameter β, which governs the decay rate on the left of the distribution (i.e. deleterious mutations). The aging process L is fit to US life expectancy data [57] and parameters are u = 0.001 and N = 10.

Let us now investigate the expected time until cancer initiation conditional upon initiation occurring prior to death. This quantity is found by solving for w(1, 1) in equation (7), and corresponds to the age of a patient at the time of cancer initiation. Note again that this quantity is not synonymous to the age of a patient at diagnosis with a tumor. Figure 4c and d shows the conditional expected time of cancer initiation as a function of varying α (Fig. 4c) and β (Fig. 4d). The dynamics of this system display complex nonlinear behaviors; when α is large, the initiation time declines sharply, since a mutational fitness distribution placing more mass on advantageous mutations results in faster cancer initiation. In this regime, increasing β results in a larger conditional initiation time since increasing mass is placed on disadvantageous mutations, and therefore more time is required for cancer initiation. However, for small values of α, alarger β results in exactly the opposite behavior – shorter average conditional initiation times. This observation is counterintuitive, since distributions with large β (and hence mostly disadvantageous mutations) are expected to result in a longer initiation time as in the case of large α. Similar dynamics can be observed in Fig. 4d, where the initiation time, τ_init, is shown as a function of varying β for several values of α. When β is small, the probability of initiation is high and increasing α results in smaller initiation times; when β is large, increasing α results in the opposite effect.

Figures 4c and d demonstrate that these interesting dynamics occur in regimes that coincide with small cancer initiation probabilities (see Figures 4a and b), suggesting that the decrease in the conditional initiation time is caused by a selection effect on the sample paths due to the conditioning event. This regime includes the biologically relevant range in which the probability of initiation is realistically small (e.g., approximately 10⁻⁷) for asingle compartment of cells. Thus we hypothesize that in the regime in which the probability of initiation, p_i, is small, the sample paths that result in initiation are the relatively rare paths in which the average advantageous mutational fitness jump is high, resulting in a low initiation time. As β increases, the probability of initiation decreases so this selection effect is enhanced. In other words, paths reaching cancer initiation in this low p_i regime experience fewer, but more beneficial, advantageous mutations as the mutational fitness distribution is skewed more to the left (i.e. as β increases).

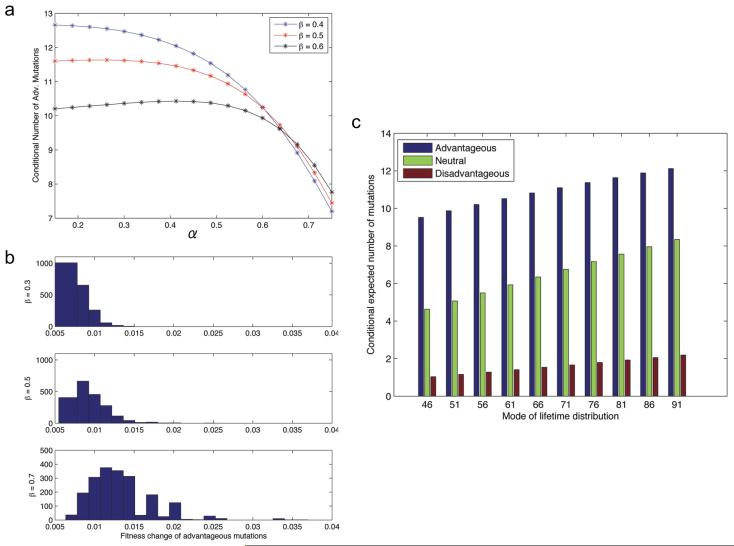
To investigate this behavior in greater detail, let us next examine the conditional average number of advantageous and disadvantageous mutations that reach 100% frequency in the population prior to cancer initiation. This quantity is given by equation (9). Figure 5a shows the conditional average number of advantageous mutations as a function of increasing α (Fig. 5a). At high values of α (corresponding to a high p_i regime), increasing β results in more advantageous mutations, whereas at low values of α (corresponding to a low p_i regime), increasing β results in fewer advantageous mutations. This observation agrees with our hypothesis that the rare sample paths that reach initiation in the low p_i regime experience fewer but stronger advantageous mutations as β increases. To test this hypothesis, we performed Monte Carlo simulations of the two dimensional process (Z, L) conditioned upon initiation to evaluate the average fitness advantage of beneficial mutations. We investigated low p_i regimes and observed that as β increases, the distribution of average fitness changes of advantageous mutations shifts to the right (Fig. 5b). For parameters in the high p_i regime (i.e., high α), this phenomenon does not occur (data not shown). This observation, together with the analysis of the expected number of advantageous mutations in the initiating cell, independently confirm the hypothesis that in the regime of low p_i, conditioning on initiation prior to death results in the selection of rare sample paths with fewer, and more beneficial, advantageous mutations as β increases.

Figure 5. Advantageous mutations in the cancer-initiating cell.

(a) The panel displays the expected number of advantageous mutations in the cell that reaches the fitness threshold 1 + 1/N and initiates tumorigenesis; these numbers of mutations are conditioned on cancer initiation occurring before death of the patient due to causes other than the cancer type of interest. We vary α, for β = 0.4, 0.5, 0.6, and display the expected number of advantageous mutations in the cancer initiating cell. The aging process L is fit to US life expectancy data [57] and parameters are u = 0.001 and N = 10. (b) The panel shows the empirical density (histogram) of the average fitness change of advantageous mutations that reach fixation in the compartment of cells prior to cancer initiation, conditioned on initiation occurring before death. Parameter values are α = 0.15 and β = 0.3(top), α = 0.15 and β = 0.5(middle), and α = 0.15 and β = 0.7(bottom). The otherparameters are as in (a). (c) The panel showsthe conditional expected number of advantageous, neutral and disadvantageous mutations that have reached fixation in the compartment prior to cancer initiation. The mode of the lifetime distribution ϕ_mode is varied. Parameters are u = 0.001, α = 0.25, β = 0.5 and N = 10.

In summary, in the biologically relevant regime with a relatively small probability of cancer initiation before death (approximately 10⁻⁷ per compartment), the dynamics of initiation display interesting dependencies on the shape parameters of the mutational fitness distribution f_ψ. As the parameter β increases and the distribution is skewed towards deleterious mutations, the average number of advantageous mutations and the average time until initiation both decrease, somewhat counterintuitively. This behavior occurs due to the strong selection effect of conditioning on cancer initiation prior to death; very few sample paths reach the event of cancer initiation, and these paths have selectively fewer, but effectively stronger, advantageous mutations. Therefore, an explicit consideration of the temporal axis (and conditioning on initiation occurring prior to death) reveals counterintuitive, qualitatively different dynamics that would not be observed in models without this essential feature. Determining the shape characteristics of the mutational fitness distribution would elucidate key properties of the dynamics of emergence and genotype of colorectal cancer-initiating cells. Towards this end, our analyses suggest that it is unlikely that α ≫ β (i.e. many more advantageous than disadvantageous mutations) in the mutational fitness distribution of stem cells in the colonic crypt, since this regime would lead to unrealistically high cancer initiation probabilities. Additionally, in the parameter space in which the probability of initiation is plausibly small, we expect approximately O(10) advantageous mutations in the initiating cell (Figure 5a); recall, however, that the scenario studied is bounded by the fitness values of neutral evolution and therefore, advantageous mutations confer a higher fitness to the cell but are not considered true ‘driver’ mutations.

4.2. Effects of varying the mode of the lifetime distribution

Let us now investigate the sensitivity of the dynamics of colon cancer initiation to the life expectancy distribution. Since lifetime distributions vary between different countries, socioeconomic classes and races, this methodology can provide insight into the differing cancer incidence rates among these populations. To investigate this dependency, we retain the same phase-type Gamma distribution structure for the lifetime distribution, but vary the mode, ϕ_mode, and consider the effects of longer and shorter overall life expectancies on the probability of cancer initiation. Table 1 displays the probability of cancer initiation prior to death for a range of values of ϕ_mode. The data in Table 1 is shown for three mutational fitness distributions where α < β (corresponding to more disadvantageous mutations), α = β (corresponding to a symmetric distribution), and α > β (corresponding to more advantageous mutations). The mode of the data fitting current US life expectancy data is ϕ_mode = 80. As the life expectancy increases, the probability of cancer initiation before death increases subexponentially. Furthermore, the ratio of α to β significantly impacts the initiation probability; when β > α, disadvantageous mutations are more frequent than advantageous mutations, and the probability of a cell accumulating fitness 1 + 1/N (i.e. cancer initiation) is low. When β < α, advantageous mutations are more frequent and thus the probability of initiation is increased. These results suggest that the probability of cancer initiation is highly sensitive to the mutational fitness distribution, and in particular to the ratio of beneficial to deleterious mutations.

Table 1. The effects of the life expectancy distribution on cancer initiation.

The table displays the probability of cancer initiation prior to death of the patient for a varying mode of the lifetime distribution, ϕ_mode. Three mutational fitness distributions are considered: α < β, α = β, and α > β. As the life expectancy increases, the probability of cancer initiation before death also increases. Furthermore, the ratio of α to β significantly impacts the initiation probability; when β > α, disadvantageous mutations are more frequent than advantageous mutations, and the probability of a cell accumulating fitness 1 + 1/N (i.e. cancer initiation) is low. When β < α, advantageous mutations are more frequent and thus the probability of initiation is enhanced. The mode of the data fitting current US life expectancy data is ϕ_mode = 80. Parameters used are u = 0.001 and N = 10.

ϕ mode	α = 0.25, β = 0.5	α = 0.3, β = 0.3	α = 0.5, β = 0.25
45	4.0450e-10	1.0608e-06	1.5979e-02
50	6.3142e-10	1.9604e-06	2.4384e-02
55	9.3832e-10	3.4264e-06	3.5433e-02
60	1.3372e-09	5.7100e-06	4.9395e-02
65	1.8381e-09	9.1313e-06	6.6441e-02
70	2 4486e-09	1 4086e-05	8.6642e-02
75	3.1736e-09	2.1050e-05	1 0996e-01
80	4.0147e-09	3.0584e-05	1 3627e-01
85	4.9705e-09	4.3330e-05	1.6533e-01
90	6.0369e-09	6.0017e-05	1.9686e-01

We also determined the conditional expected number of neutral and non-neutral mutations that reached fixation in the population prior to cancer initiation. Figure 5c shows the conditional expected number of advantageous, neutral, and disadvantageous mutants in the initiating cell. As the mode of the lifetime distribution increases, the average number of each type of mutation increases linearly. In addition, the ratio of the conditional expected number of neutral to conditional expected number of advantageous/disadvantageous mutations appears invariant to ϕ_mode. Note that the number of disadvantageous, neutral, and advantageous mutations in the initiating cell does not correspond to the frequencies of these mutations in the mutational fitness distribution f_ψ. For example, Figure 5c demonstrates that the frequency of neutral mutations in the total mutation incidence is approximately 30 – 35%; however, the mutational fitness distribution, f_ψ, used in this example places approximately 40% of its mass on neutral mutations. This difference is once again an effect of conditioning; sample paths in the set in which cancer initiation occurs prior to death exhibit a different mutational fitness distribution than the original distribution. This observation also demonstrates the necessity of explicitly considering a temporal process and conditioning on cancer initiation prior to death, since this difference would not be observed in models without this feature. We conclude that colon cancer incidence is predicted to be lower in patient populations with lower life expectancies; in those cases in which tumorigenesis is initiated, fewer passenger mutations are present in the cancer-initiating cell as compared to cases in populations with larger life expectancies.

4.3. Sensitivity to the mutation rate

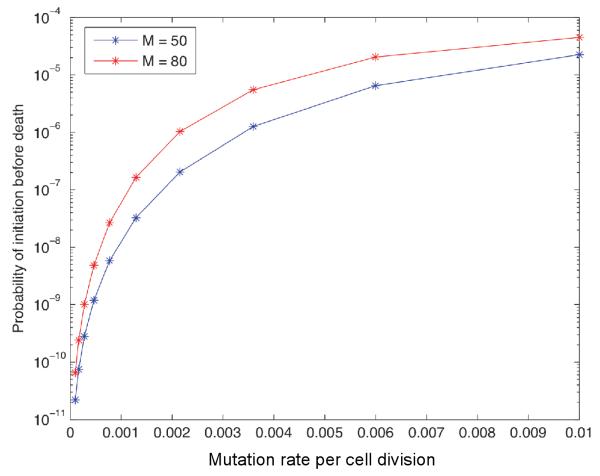
Finally, let us investigate the sensitivity of the probability of colon cancer initiation prior to death to the mutation rate u. Figure 6 shows the probability of initiation as a function of the mutation rate in the setting β > α. The probability of cancer initiation decreases super-exponentially as the mutation rate decreases. This functional dependence is studied for two different values of ϕ_mode; the super-exponential decay is similar in both scenarios, but the curves are shifted by a constant. Thus we expect that patient populations with higher mutation rates accordingly have a higher colon cancer incidence; this observation is consistent with increased cancer incidence after exposure to radiation and other carcinogens.

Figure 6. The effects of the mutation rate on cancer initiation.

The figure shows the probability of cancer initiation prior to death of the patient for varying mutation rate u. Two values for the mode of the lifetime distribution are shown: ϕ_mode = 50, 80. Parameters are α = 0.4, β = 0.6 and N = 10.

5. Discussion

In this paper, we have introduced a novel stochastic model to investigate the dynamics of cancer initiation prior to the death of the patient. In the context of this model, cancer initiation occurs when a single cell within a small fixed-size compartment of cells acquires the characteristics necessary to initiate clonal expansion of cells. We have introduced several novel features with this model:

1. Genetic and epigenetic alterations confer random fitness changes to the cell.

2. Cancer initiation is a fitness-dependent event – once a cell gains a sufficiently large fitness, clonal expansion ensues.

3. The stochastic process governing the evolution of cellular fitness is coupled with a temporal aging process to determine the dynamics of cancer initiation prior to death of the individual.

These features are unlike earlier models of cancer initiation [22, 23, 24, 25, 26, 27]; in these models, cancer initiation was assumed to occur as soon as a single cell has accumulated a specific number and type of mutations, which were considered to confer fixed fitness effects on cells. Furthermore, these earlier models did not couple the dynamics of mutations arising in populations of cells with the processes of aging and death of individuals. Without considering the latter dynamics, however, the consideration of cancer initiation is incomplete.

We have considered a Moran process describing a compartment of cells in which genetic and epigenetic alterations confer random fitness changes which are variates drawn from a mutational fitness distribution. This approach allows for the inclusion of all possible (epi)genetic alterations arising in proliferating cells rather than a single class of mutations. We considered a spectrum of mutational fitness effects, from mutations which are positively selected during tumorigenesis, to passenger mutations which are selectively neutral, and deleterious alterations which confer a fitness cost to the cell. The consideration of non-advantageous mutations is important because most alterations have the potential to affect the evolutionary dynamics of cancer initiation, even though they may not play a direct and causative role in carcinogenesis. For instance, the accumulation of mutations can alter the fitness of a cell and thus affect the likelihood and timing of cancer initiation. We have introduced a second dimension to the process of cancer initiation to ensure that the dynamics are dictated by tumors that initiate within a human lifetime. This goal is achieved by modeling the lifetime of a patient as the first passage time of a simple continuous-time Markov chain in an aging dimension, and investigating the conditioned dynamics on the set for which cancer initiation occurs before patient death. The explicit consideration of the temporal axis and conditioning on cancer initiation occurring prior to death reveals counterintuitive, qualitatively different dynamics that would not be observed in models without this essential feature.

We then examined the dynamics of colon cancer initiation as a specific example. We utilized parameter values dictated by the geometry of colonic crypts, the number of colonic stem cells, and the mutation rate estimated for human cells. Furthermore, we considered the life expectancy data of the US population to inform the dynamics of the aging process. Since no estimates of the shape of the mutational fitness distribution are available, we chose a specific parametric family of distributions representing a broad class of distributions that includes exponential decay and uniform distributions. We then studied how the probability of cancer initiation prior to death, the time until cancer initiation, and the mutational profile of the cancer-initiating cell depends on the shape of the mutational fitness distribution, the life expectancy distribution, and the mutation rate. We observed qualitatively different dynamics in parameter regimes where the probability of cancer initiation is low as compared to those biologically unrealistic scenarios in which tumorigenesis is initiated often and quickly. In particular, we observed that tumors that are initiated in the regime of low initiation probabilities experience fewer, but more beneficial, advantageous mutations as the mutational fitness distribution is skewed more towards disadvantageous alterations. This behavior arises due to the strong selection effect of conditioning on cancer initiation prior to death; very few evolutionary trajectories lead to initiation before the death of the patient, and these trajectories accumulate fewer but selectively stronger advantageous mutations. Furthermore, this analysis demonstrated that human populations with shorter average life expectancies have fewer cases of cancer initiation; in those cases in which tumorigenesis is initiated, fewer passenger mutations are present in the cancer-initiating cell. Note that passenger mutations are defined as those that do not confer any fitness change to the cell; the number of passenger mutations in the cancer-initiating cell we determine using this model might differ from that identified by cancer genome screens since the latter analyses might identify all neutral and near-neutral mutations as ‘passengers’. This number might then represent an overestimation of the number of true (strictly neutral) passenger mutations. Note also that the mutational distribution of the cancer-initiating cell is substantially different from the originating distribution of mutational fitness effects, exhibiting another differential result of conditioning on cancer initiation prior to death. This analysis could be extended to comparatively study the dynamics of cancer initiation in populations with varying life expectancy distributions, such as different countries, ethnic groups or socio-economic classes. To perform such analyses, it is necessary to consider differential dynamics in Z as well as the aging process L. In particular, certain populations may have higher mutation rates due to behavior, diet and other environmental factors which are in turn linked to life expectancy.

This mathematical framework represents only one out of many possibilities of modeling the processes leading to cancer. For simplicity, we have neglected spatial effects that could lead to different dynamics in separate areas of the same compartment or tissue. We have therefore considered colonic crypts to be independent from one another. However, crypt division and replacement by neighboring crypts may induce a complex local dependence between cellular compartments; these issues will be explored in future work. Furthermore, we have not considered interactions of normal and mutated cells with the immune system; such interactions may modulate the dynamics of cancer initiation since certain cell types may be inhibited by immune system cells. Also, we have not investigated the effects of temporally or spatially varying fitness values of cells which could result from their interactions with the microenvironment or other cell types. Our work can further be extended to consider a dependency between the dynamics of the fitness process Z and the aging process L. Specifically, as a patient ages, DNA repair mechanisms deteriorate, thus resulting in higher mutation rates; consideration of such scenarios will be the topic of future work. For an accurate understanding of the dynamics of tumorigenesis in human populations, the elucidation of mutational fitness distributions as well as cell type-specific mutation rates is essential. The determination of these parameters in experimental systems is an important goal of the field and would contribute to the investigation of the evolutionary dynamics of human cancer.

6. Appendix

6.1. Standard Moran Process

The Moran process [28] is a standard tool for studying populations that maintain a constant size N (see e.g., [24, 69]). In the traditional setting, two types of cells are considered – cell types a and A – whichhave respective fitness values (i.e. growth rates) f and 1. Reproduction events arrive according to a Poisson process with rate N. If the number of type A cells is j, then the probability that a type A cell will reproduce during the next birth is given by j/[j + f(N − j)]. In addition, after each birth event a cell is randomly chosen to die. The Moran process is the Markov process that tracks the number of type A (or a cells) cells over time.

6.2. Multi-Type Moran Process

As a departure from the Moran process described in the previous subsection, we consider afixed-size population of cells containing greater than two types of cells. Each cell may have a fitness in the set $\mathbb{F}=\{f_1,\dots ,f_K\}$. The state of the system at time t is described by $Z_t=(Z_t^1,\dots ,Z_t^K)$, where $Z_t^K$ represents the number of cells with fitness f_k at time t. Reproduction events occur at the arrival times of a Poisson process with rate N; these times are denoted by {T_i}_i≥1. Given that the current state of system is z = (z¹,…,z^K), during the next reproduction event a cell of fitness f_k will be chosen to reproduce with probability

$$\frac{z^k{f}_k}{{\sum }_{j=1}^K{z}^j{f}_j},$$

and a cell is chosen at random to die. During each cell division event, there is a probability u of producing a daughter cell with a new fitness value which is chosen from amutational fitness distribution. Equation (1) states that this process can be replaced with a simpler process which jumps between homogeneous states (i.e., all cells in the compartment have the same fitness). To investigate the accuracy of this approximation, let us consider a system that starts in state z₀, where N − 1 cells have fitness f and one cell has fitness $\widehat{f}$. We will use the following notation: $P_z(\cdot )\doteq P(\cdot \mid Z_0=z)$. Then we have

Lemma 1

P_z0(T_mut < T_hom) ≤ 3Nu(log N + γ).

Proof of Lemma 1

Define N(t) to be the number of replication events by time t, and let m(n) = 1 if a mutation occurs at replication event n. Then note that

$$\begin{array}{cc}\hfill P_{z_0}(T_{\mathit{mut}}<T_{\mathit{hom}})=& \sum _{n=1}^{\infty }{P}_{z_0}\left(N\right(T_{\mathit{mut}})=n,N(T_{\mathit{hom}})>n)\hfill \\ \hfill \le & \sum _{n=1}^{\infty }{P}_{z_0}\left(N\right(T_{\mathit{mut}})=n,N(T_{\mathit{hom}})>n-1)\hfill \\ \hfill \le & \sum _{n=1}^{\infty }{P}_{z_0}\left(m\right(n)=1,N(T_{\mathit{mut}})>n-1,N(T_{\mathit{hom}})>n-1)\hfill \\ \hfill =& u\sum _{n=1}^{\infty }{P}_{z_0}\left(N\right(T_{\mathit{mut}})>n-1,N(T_{\mathit{hom}})>n-1)\hfill \\ \hfill \le & u\sum _{n=1}^{\infty }{P}_{z_0}\left(N\right(T_{\mathit{hom}})>n-1\mid N(T_{\mathit{mut}})>n-1).\hfill \end{array}$$

Then a conditioning argument shows that

$$P_{z_0}(Z_{T_1}=z_1\mid N(T_{\mathit{mut}})>n-1)=\frac{1}{1-u}P(Z_{T_1}=z_1\mid Z_0=z_0)$$

for all z₁ such that $\{1\le k\le K:z_1^k>0\}\subset \{1\le k\le K:z_0^k>0\}$. For all other z₁ we have that

$$P_{z_0}(Z_{T_1}=z_1\mid N(T_{\mathit{mut}})>n-1)=0.$$

Let $\tilde{P}(\cdot )$ denote the probability measure associated with a Moran process with only two types of cells and no further mutation allowed. Then it follows that

$$P_{z_0}\left(N\right(T_{\mathit{hom}})>n-1\mid N(T_{\mathit{mut}})>n-1)={\tilde{P}}_{z_0}\left(N\right(T_{\mathit{hom}})>n-1).$$

Thus it remains to bound ${\tilde{E}}_{z_0}\left(N\right(T_{\mathit{hom}}\left)\right)$. This will be done by following a similar approach as the proof of Thm 6.3 of [69]. First let $r=\widehat{f}∕f$, then for each 1 ≤ y ≤ N − 1 define N_y to be the number of visits of the Moran process to the state y. During each visit of the process to the site y, B_y birth events occur, where B_y is a geometric random variable with success probability

$${\rho }_y=\frac{y(N-y)(\tilde{f}+f)}{N\left(\widehat{f}j+f(N-j)\right)},$$

It follows that

$${\tilde{E}}_{z_0}\left(N\right(T_{\mathit{hom}}\left)\right)=\frac{1}{{\rho }_y}\sum _{y=1}^{N-1}{E}_{z_0}{N}_y.$$

Using formula for E_z0N_y from the proof of Thm. 6.3 of [69], we arrive at

$${\tilde{E}}_{z_0}\left(N\right(T_{\mathit{hom}}\left)\right)=N\sum _{y=1}^{N-1}\left(\frac{r^{N-y}-1}{r^N-1}\right)\left(\frac{1}{N-y}+\frac{r}{y}\right).$$

Note that for all r ≥ 0, we have

$$\frac{r^{N-y}-1}{r^N-1}\le 1.$$

It then follows that

$$\tilde{E}\left(N\right(T_{\mathit{hom}}\left)\right)\le N\sum _{y=1}^{N-1}\left(\frac{1}{N-y}+\frac{r}{y}\right)\approx (1+f_K)N(\log N+\gamma )$$

where γ is the Euler-Mascheroni constant and we used the approximation

$$\sum _{j=1}^N\frac{1}{j}\approx \log N+\gamma .$$

The result follows by recalling that f_K ≤ 2.