Does a basic deficit in force control underlie cerebellar ataxia?

Abstract

Because damage to the cerebellum results in characteristic movement incoordination known as “ataxia,” it has been hypothesized that it is involved in estimation of limb dynamics that occur during movement. However, cerebellar function may extend beyond movement to force control in general, with or without movement. Here we tested whether the cerebellum is involved in controlling force separate from estimating limb dynamics and whether ataxia could result from a deficit in force control. We studied patients with cerebellar ataxia controlling their arm force isometrically; in this condition arm dynamics are absent and there is no need for (or effect from an impairment in) estimations of limb dynamics. Subjects were required to control their force magnitude, direction, or both. Cerebellar patients were able to match force magnitude or direction similarly to control subjects. Furthermore, when controlling force magnitude, they intuitively chose directions (not specified) that required minimal effort at the joint level—this ability was also similar to control subjects. In contrast, cerebellar patients performed significantly worse than control subjects when asked to match both force magnitude and direction. This was surprising, since they did not exhibit significant impairment in doing either in isolation. These results show that cerebellum-dependent computations are not limited to estimations of body dynamics needed for active movement. Deficits occur even in isometric conditions, but apparently only when multiple degrees of freedom must be controlled simultaneously. Thus a fundamental cerebellar operation may be combining/coordinating degrees of freedom across many kinds of movements and behaviors.

people with cerebellar damage have difficulty making smooth, accurate movements. One popular hypothesis is that the cerebellum is involved in estimating the often complex forces required to move in a coordinated manner (Miall 1998; Wolpert et al. 1998). Damage to the cerebellum could disrupt this control (Bastian 2006; Bastian et al. 1996; Kawato 1999; Schweighofer et al. 1998; Shadmehr and Krakauer 2008) via an inaccurate estimate of the forces required to produce desired movement or an inaccurate prediction of the movement from planned forces.

However, cerebellar function may extend beyond movement to force control in general. In other words, the role of the cerebellum may be to control muscle force independent of any computation of limb dynamics. Because proper movement requires appropriate force control, impairment in force control could lead to abnormal movement. Here we asked whether cerebellar ataxia extends to force control in the absence of movement.

Even in isometric conditions (i.e., in the absence of movement), controlling force requires that the neuromuscular system compensate for many complexities of the neuromusculoskeletal system. For example, neural signals to muscles must account for the nonlinear and history-dependent properties of muscle force and for position-dependent moment arms generating joint torque. Furthermore, while isometric conditions do not involve interaction torques (torque at one joint caused by movement in other joint; Bastian et al. 1996; Hollerbach and Flash 1982), they do require coordination across degrees of freedom (DOF) to account for configuration-dependent transformations between joint torque and hand force when interacting with the environment. In addition, because limbs have more muscles than DOF, the computation of the muscle activation required to produce a joint torque or hand force is not a simple one-to-one mapping. Thus, even when the forces required to make a movement are known, the implementation of those forces is a nontrivial problem.

Here we asked whether the cerebellum is involved in controlling force separate from estimating limb dynamics and whether ataxia could result from a deficit in force control. To separate force control from the estimation of limb dynamics, we studied subjects controlling their arm force isometrically, which removes limb dynamics. Any impairment in the estimation of limb dynamics should not affect performance in an isometric force task. In patients with ataxia, normal performance in an isometric force control task would indicate that cerebellar function includes movement-related computations but does not extend to force control in general. Impaired performance would indicate that the cerebellum is involved in controlling force independent of any computation of limb dynamics. However, impaired performance could not be used as evidence against cerebellar estimation of limb dynamics since the cerebellum could be involved in limb dynamics modeling and force control.

We found that cerebellar patients' ability to simultaneously control force magnitude and direction was significantly impaired, indicating that cerebellum-dependent computations are not limited to body dynamics needed for active movement—deficits occur even in isometric conditions. The gap in performance between cerebellar patients and control subjects was present from the beginning but widened with time as control subjects learned to improve their performance with practice, while patients did not. Interestingly, patients did not show significant impairment in controlling force magnitude or direction individually, indicating that a fundamental cerebellar operation may be combining/coordinating DOF across many kinds of movements and behaviors.

MATERIALS AND METHODS

Subjects

Twelve patients with cerebellar damage and twelve control subjects participated in this study. The control subjects were matched for age, sex, and handedness (Table 1). All subjects gave informed written consent before participating. The protocols were approved by the Johns Hopkins Institutional Review Board.

Table 1.

Cerebellar patients

Patient ID	Age, yr	Sex	Hand	Fmax, N	Diagnosis	ICARS Total	ICARS Kinetic
CBL1	59	M	R	183	SCA6	28	11
CBL2	57	F	R	89	SCA6	33	12
CBL3	58	M	R	103	Auto Dom	3	1
CBL4	61	F	R	67	Auto Dom	38	15
CBL5	41	F	R	85	SCA6	58	28
CBL6	57	F	R	62	SCA6	60	26
CBL7	55	F	R	71	Idiopathic	61	25
CBL8	75	M	R	85	PICA	17	11
CBL9	56	M	R	218	SCA6	63	20
CBL10	50	F	R	143	PAPT	36	19
CBL11	38	M	L	187	SCA8	43	19
CBL12	68	F	R	111	SCA6	13	4
Patients	56 ± 10	5 M, 7 F	11 R, 1 L	117 ± 53		38 ± 20	16 ± 9
Control subjects	55 ± 10	5 M, 7 F	11 R, 1 L	107 ± 31

Group values are means ± SD. F_max, maximum force; ICARS, International Cooperative Ataxia Rating Scale; SCA, spinocerebellar ataxia; Auto Dom, autosomal dominant; PICA, posterior inferior cerebellar artery stroke; PAPT, progressive ataxia and palatal tremor.

Experimental Procedure

Prior to the experiment, all patients were rated on the International Cooperative Ataxia Rating Scale (ICARS; Trouillas et al. 1997). Table 1 gives patients' total score as well as their subscore for kinetic function (mainly a rating of upper limb movement). Higher scores indicate more impairment. All subjects also underwent a neurological exam to ensure that they had no proprioceptive or somatosensory deficits, no signs of corticospinal tract damage, no abnormalities of muscle tone, and no weakness or muscle atrophy.

The forces required in this study were calculated as a percentage of each subject's maximum force, F_max (Table 1). To determine F_max for each subject, we used a handheld dynamometer to estimate how much endpoint force each subject could produce in horizontal shoulder adduction and abduction and elbow flexion and extension. To ensure that subjects could produce the required forces in all directions, we defined F_max as the lowest force produced by these actions.

The main experiment in this study required subjects to control the magnitude and direction of force at the same time. Before participating in this experiment, subjects underwent either one or two pretests. The pretests were designed to verify that patients and control subjects could learn the mapping from their actual isometric force to a visual display of their force. Seven patients (CBL1–CBL7) participated in pretest 1, while five patients (CBL8–CBL12) participated in both pretests 1 and 2 (in random order). Control subjects underwent the exact same series of tests and experiments as the patients they matched.

All testing was done with subjects sitting in a chair with their dominant arm and forearm supported in the horizontal plane by a robotic exoskeleton (KINARM; BKIN Technologies, Kingston, ON, Canada). The shoulder and elbow were in 45° and 90° of flexion, respectively (Fig. 1). Each subject's dominant forearm was placed in a wrist brace that was rigidly attached (at the wrist) to a force sensor (Mini-45; ATI Industrial Automation, Apex, NC). The force sensor measured the force applied by the subjects in the horizontal plane (termed “actual force”) and did not allow any arm movement. Subjects viewed a graphical display (part of the KINARM setup), which showed a target force and visual feedback of the magnitude and/or direction of the actual force (depending on the task), in the plane of their arm.

Fig. 1.

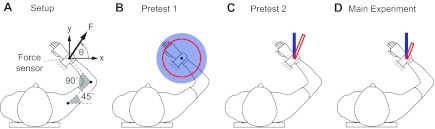
Experimental setup. A: features common to pretest 1, pretest 2, and the main experiment. B–D: the visual feedback for each test, where the red circle or rectangle represents the actual force and the blue circle or rectangle represents the target force.

Pretest 1.

The purpose of pretest 1 was to assess whether cerebellar patients could learn the mapping between the magnitude of their force and its representation in the visual display. Subjects were given visual feedback of the magnitude (but not direction) of the actual force in the form of a red circle with radius proportional to the magnitude of the actual force (Fig. 1). Also displayed was a target force in the form of a blue disk, and subjects were asked to change the magnitude of the actual force so that the red circle matched the size of the blue disk. The time allotted to match the target force (the “matching period”) was 3 s for the first seven patients (CBL1–CBL7) and 2 s for the last five patients (CBL8–CBL12). The 2-s constraint was given on the last five patients to ensure that they could perform the magnitude-only task within a shorter time span. No instruction or visual feedback was given regarding the direction of force production. Subjects practiced force matching over eight trials (2 times at magnitudes of 3%, 6%, 12%, 15% of F_max). They were then assessed as they performed three trials (all at 9% of F_max).

Pretest 2.

The purpose of pretest 2 was to verify that cerebellar patients could learn the mapping between the direction of their force and its representation in the visual display. Subjects were given visual feedback of the direction (but not magnitude) of the actual force in the form of a red rectangle whose direction matched that of the actual force (Fig. 1). The rectangle appeared when subjects' force was above 6% of F_max, and the length of the rectangle, L, was constant regardless of the magnitude of the actual force. A target direction was displayed in the form of a blue rectangle of length L. Subjects were asked to change the direction of the actual force to match the direction of the blue rectangle. The duration of the matching period was 2 s. As in pretest 1, subjects practiced force matching over eight trials (2 times in each of the following directions: 58.5°, 130.5°, 274.5°, and 346°) and were then assessed in a new direction (at 202.5°; all force angles were defined counterclockwise from the positive x-axis as shown in Fig. 1A).

Main experiment.

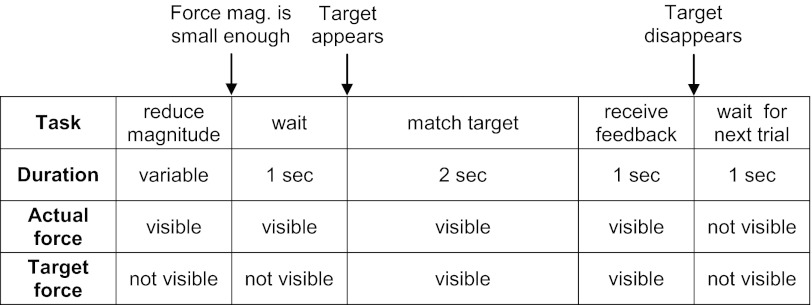
The purpose of the main experiment was to assess patients' ability to control an isometric arm force in both magnitude and direction. Subjects were given visual feedback of the magnitude and direction of the actual force in the form of a red rectangle (a vector) with length proportional to the magnitude of the actual force and direction equal to the direction of the actual force (Fig. 1). A target force was displayed in the form of a blue rectangle. Subjects were asked to change the magnitude and direction of the actual force to match that of the target force. Each trial consisted of the following five periods (Fig. 2): 1) At the beginning of each trial, subjects were required to relax their arm and let the magnitude of their force become small. 2) As soon as subjects decreased their force magnitude below 1% of F_max, we initiated a 1-s waiting period, after which a target force appeared. 3) Subjects were given 2 s (the “matching period”) to modify the actual force to match the target force. 4) Immediately after the matching period, subjects received feedback of their performance on that trial. If the actual force was close enough to the target force (if the magnitude of the vector difference was <10% of the length of the target vector), the red rectangle representing the actual force turned green; otherwise it turned white. 5) The feedback period was followed by a 1-s break before the start of the next trial.

Fig. 2.

Series of events during the main experiment.

Sixteen different target vectors (5% and 10% of F_max in 8 directions) were repeated in 11 blocks for a total of 176 trials. The target forces were presented in order in the first block (90°, 45°, 0, 315°, …, 135° at 5% of F_max, then repeated at 10% of F_max) and in pseudorandom order for blocks 2–11. There was a 5- to 10-min break between blocks 6 and 7.

Immediately before each pretest and the experiment, subjects were given a brief practice period (up to a few minutes) to ensure that they understood the task requirements. During this practice period, subjects were allowed to exert force and see the visual display of their force (the red circle or rectangle) in the absence of the blue target.

Task demands.

Matching the magnitude and/or direction of the actual force produced at the hand to a target force required subjects to coordinate their shoulder and elbow torques (Fig. 3, A and B). The relationship between the force produced at the hand and the shoulder and elbow torques required to produce that force is given by the Jacobian matrix. For the limb posture maintained in our experiments (Fig. 1A), this relationship was

$$\left[\begin{array}{c}{T}_s\\ T_e\end{array}\right]=J^T\left[\begin{array}{c}{\text{F}}_x\\ {\text{F}}_y\end{array}\right]=\frac{-1}{\sqrt{2}}\left[\begin{array}{cc}{L}_1+L_2& -L_1+L_2\\ L_2& L_2\end{array}\right]\left[\begin{array}{c}{\text{F}}_x\\ {\text{F}}_y\end{array}\right]=\frac{-\text{F}}{\sqrt{2}}\left[\begin{array}{cc}{L}_1+L_2& -L_1+L_2\\ L_2& L_2\end{array}\right]\left[\begin{array}{c}\cos \phi \\ \sin \phi \end{array}\right]$$

where T_s is the torque produced at the shoulder, T_e is the torque produced at the elbow, J is the Jacobian matrix, T is the transpose operator, L₁ is the length of the upper arm, L₂ is the distance from the elbow to the attachment to the force transducer, and the force at the hand has been represented in terms of x- and y-components (F_x and F_y) and in terms of magnitude and direction (F and ϕ; see Fig. 1A). While L₂ was the same for each subject (0.24 m), L₁ differed between subjects (mean ± SD = 0.29 ± 0.019 m, range = 0.25–0.33 m), so the Jacobian was subject dependent. Nevertheless, matching the target force required all subjects to coordinate shoulder and elbow torques; in general, both the magnitude and direction of the force produced at the hand depended on both shoulder and elbow torques.

Fig. 3.

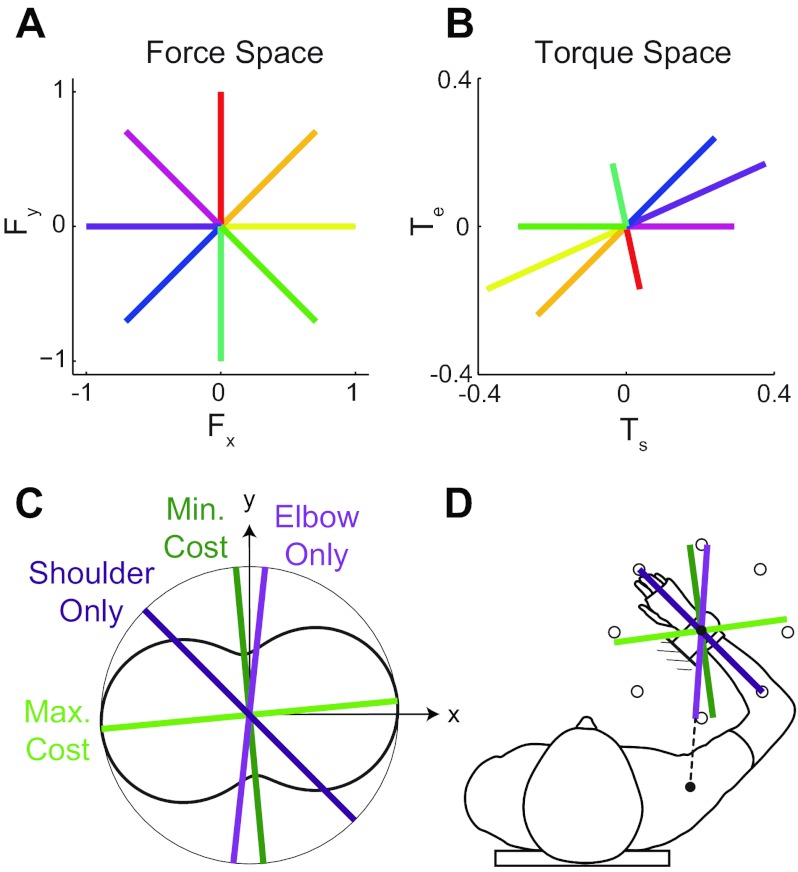
Task demands. A and B: producing isotropic force at the hand (A) requires anisotropic torque at the shoulder and elbow joints (B). C: the torque magnitude and number of degrees of freedom (DOF) required to produce force in a given direction are costs associated with that direction. The curved black trace is a polar plot of the cost in torque magnitude (square root of sum of squares of shoulder and elbow torques) associated with producing force in different directions. Directions of minimum- and maximum-torque magnitude, and directions that only require a single DOF, are also shown. D: same as C but set in the context of the subject and force target directions.

The relationship between hand force and joint torque is fully determined, so matching both the magnitude and direction of the target force requires a unique combination of shoulder and elbow torques (Fig. 3, A and B). In contrast, matching only the magnitude or direction of the target force can be achieved through many combinations of shoulder and elbow torques. An important part of motor control is the ability to choose from among the infinite variety of possible muscle combinations those that are close to optimal in the sense that they minimize the cost of control (which may involve force/torque, energy, variability, attention, and many other factors). In pretest 1, subjects were free to choose the direction of the actual force. Generating force is more difficult in some directions of our task than others (see below), and we were particularly interested in whether cerebellar subjects would choose “easy directions” as well as control subjects. In the main experiment, subjects were not free to choose the direction of the actual force, but we predicted that control subjects' performance would be better in the “easy directions,” and we were interested in whether the same was true for cerebellar patients.

There are two reasons why applying force in some directions is easier than in others. First, even though the magnitude of the target force (the square root of the sum of the squares of the target force in x and y) was the same in all directions (either 5% or 10% of F_max in each of 8 directions), the magnitude of the joint torque (the square root of the sum of the squares of the joint torques at the shoulder and elbow) required to produce a target force was not the same in all directions (Fig. 3, A and B). In other words, because the Jacobian of the arm is anisotropic, hand forces of isotropic magnitude require joint torques of anisotropic magnitude. We calculated the Jacobian for each subject (taking into account differences in subjects' arm lengths) and determined the magnitude of the joint torque required to produce force in different directions (Fig. 3C). The force direction that required the least torque magnitude was 95.8 ± 2.3° (mean ± SD, range 91.4–100.5°) from the x-axis. The force direction that required the most torque magnitude is perpendicular to this direction (Fig. 3, C and D).

Second, there are differences in the number of DOF required to produce force in different directions. While producing force in most directions requires torque about both the shoulder and elbow joints, there are two directions that only require torque about a single joint (Fig. 3, C and D). The force direction that only requires shoulder torque is parallel to the forearm. The direction that only requires elbow torque is along the line that connects the shoulder joint and the point of attachment of the forearm to the force sensor. The orientation of this line, which depends on each subject's arm length, was 84.3° ± 1.6° (mean ± SD, range 81.2–87.7°) from the x-axis. To produce force in all other directions requires a combination of torques at both joints.

The magnitude of the torque and the number of DOF required to produce force in a given direction affect the effort and complexity associated with that direction and can therefore be considered as costs for that direction. While there are many other possible costs, we focused our attention in this study on these two costs: the torque magnitude (the square root of the sum of the squares of shoulder and elbow torque) and the number of DOF (in this case 1 or 2) required to produce force in a given direction. In pretest 1, subjects were free to choose the direction of the actual force. We expected subjects to choose a direction associated with a low cost—a direction associated with either a single DOF or minimum torque magnitude. In the main experiment, where subjects were required to match force in all eight directions, we expected subjects to perform better in directions associated with lower cost.

Analysis

Measures.

Pretest 1 required subjects to match a force magnitude. We defined subjects' performance in terms of the magnitude error EM, which is defined as the absolute value of the difference between the magnitudes of the target force vector and the actual force vector at the end of the matching period:

$$\text{EM}=\text{abs}\left(\Vert {\stackrel{\rightharpoonup }{F}}_{\text{T}}\Vert -\Vert {\stackrel{\rightharpoonup }{F}}_{\text{A}}\Vert \right)$$

We also analyzed the direction in which subjects chose to exert force (direction was not specified) in the following steps. First, we transformed the left-handed subjects' directions into a right-handed coordinate frame. Second, since the cost is the same for directions separated by 180° (e.g., at 95° or 275°, as shown in Fig. 3C), we reflected all forces to lie between 0 and 180° to simplify the analysis. Third, for each subject we then computed the mean angle (over the 3 test trials at 9% of F_max) between the direction of the actual force and the minimum-torque direction for that subject. Fourth, we also determined subjects' precision, defined here as the standard deviation of their directions (on the 3 test trials). Control subjects C5 and C12 had much higher variability in their force directions than the other subjects (2.4 and 3.6 SDs from the mean, respectively) and were excluded from the analysis.

Pretest 2 required subjects to match a force direction. We defined subjects' performance in terms of the direction error ED, which is defined as the angle between the target force vector and the actual force vector at the end of the matching period:

$$\text{ED}={\cos }^{-1}\left(\frac{{\stackrel{\rightharpoonup }{F}}_{\text{T}}·{\stackrel{\rightharpoonup }{F}}_{\text{A}}}{\Vert {\stackrel{\rightharpoonup }{F}}_{\text{T}}\Vert \Vert {\stackrel{\rightharpoonup }{F}}_{\text{A}}\Vert }\right)$$

where denotes the dot product. By this definition, 0 ≤ ED ≤ 180°. We also investigated the amount of force subjects chose to exert on their three test trials (force magnitude was not specified other than that it had to be >6% of F_max). Patient CBL11 was excluded because his final force magnitude was below 6% during the three test trials.

The main experiment required subjects to match a force vector, so we defined subjects' performance in the experiment in terms of the vector error EV, defined as the magnitude of the difference between the target force vector and the actual force vector at the end of the matching period:

$$\text{EV}=\Vert {\stackrel{\rightharpoonup }{F}}_{\text{T}}-{\stackrel{\rightharpoonup }{F}}_{\text{A}}\Vert$$

By this definition, EV ≥ EM (EV = EM only when ED = 0). To determine whether patients' impairment in controlling EV, if any, was due to an underlying impairment in controlling EM, ED, or both, we also computed EM and ED for each trial of the main experiment. EV was also used to determine whether subjects performed best (and whether there was any difference between groups) in directions of lowest cost. Secondarily, we were interested in understanding how subjects' force vector, magnitude, and distance progressed over time (and not just at the end of the matching period), so we also computed EV, EM, and ED as functions of time over the entire matching period. Finally, we asked whether subjects performed better in the experiment in the direction they had chosen in pretest 1. We determined for each subject the force target direction (0°, 45°, …, 315°) that was closest to his/her mean direction in pretest 1 and computed the average EV value in that direction.

Statistical analysis.

To compare performance in pretest 1 between groups (cerebellar or control), we performed a t-test of EM (average of each subject's 3 test trials at 9% of F_max) between groups. Differences in the chosen force direction between groups were also evaluated by t-test. Likewise, for pretest 2 we ran a t-test of ED (average of each subject's 3 test trials at 202.5°) between groups.

Performance in the main experiment was analyzed by repeated-measures ANOVA with factors group (cerebellar or control), magnitude (5% or 10% of F_max), and direction (0°, 45°, …, 315°). Separate ANOVAs were run for EV, EM, and ED. Because directions of low cost vary for right- and left-handed subjects, we transformed left-handed subjects' measures into a right-handed coordinate frame prior to statistical analysis. We evaluated by t-test whether there was any difference between groups in how well they performed in the main experiment, looking specifically in the direction they had chosen in pretest 1.

Last, to test for differences in learning between groups, we also compared EV on the first block (first 16 trials) and on the last block (trials 161–176). To determine whether subjects improved their performance over the course of the experiment, we compared the first and last blocks to each other by running a repeated-measures ANOVA of EV with factors period (first or last block), magnitude, and direction (separately for each group). Patient CBL1 only participated in a subset of the main experiment and was therefore excluded from this portion of the analysis.

RESULTS

We found no difference in maximum force, F_max (Table 1), between cerebellar and control groups (P = 0.56).

Pretest 1

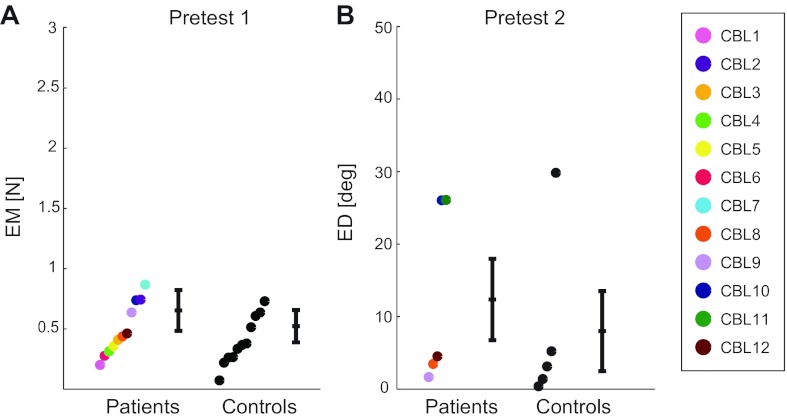
As described in materials and methods, the time allotted to match the target force was 3 s for the first seven patients and 2 s for the last five patients. However, when the 3-s and 2-s groups were compared at the end of 2 s, there was no significant difference in EM between patients in the 3-s and 2-s groups (P = 0.17) or between control subjects in the 3-s and 2-s groups (P = 0.33). Therefore, we evaluated the performance of all subjects at the end of 2 s and combined the 3-s and 2-s groups for the statistical analysis (resulting in 12 patients and 12 control subjects). We found that cerebellar subjects performed as well as control subjects (P = 0.29; see Fig. 4A; CBL11 and a control subject were excluded from the comparison because they were at 2.97 and 2.90 SDs from their group mean, respectively). Figure 5 shows the directions that each subject chose on each trial of the force-matching task. There were no differences in the chosen direction between subjects tested in the 3-s or 2-s versions of this task, so all subjects were grouped together. All subjects chose directions closer to their minimum-torque direction than to their maximum-torque direction. There was no significant difference between cerebellar patients and control subjects in how close force directions were to the minimum-torque direction (P = 0.60). Patients missed their minimum-torque direction by 24 ± 12° (mean ± SD) and control subjects by 22 ± 8°. Both cerebellar patients and control subjects were very consistent in their choice of force direction (or possibly 180° removed) in the various trials of pretest 1. The standard deviation among subjects' chosen direction (taken over the 3 test trials) was 2.6 ± 2.4° for patients (mean ± SD) and 2.5 ± 1.5° for control subjects, with no significant difference between groups (P = 0.97).

Fig. 4.

Results of the pretests. Shown are errors in magnitude (EM) in pretest 1 (A) and errors in direction (ED) in pretest 2 (B). Dots represent individual subjects, coded by color and ranked by EM (A) or ED (B) to allow for easier comparison between groups. Also shown is the mean ± SE for each group.

Fig. 5.

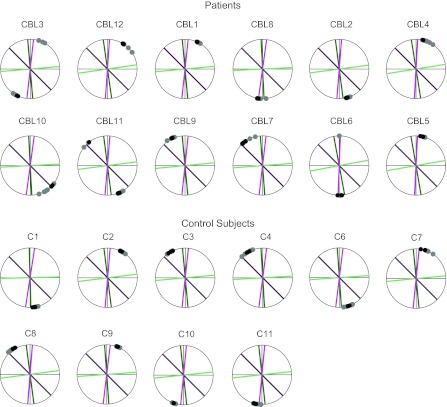
Force directions chosen in pretest 1. Directions chosen in the 8 training trials and 3 test trials are shown as gray and black filled circles, respectively. For comparison, the minimum- and maximum-torque magnitude directions and the single-DOF directions are also shown (same color code as in Fig. 3, C and D). Thin lines show the horizontal and vertical directions for reference. Cerebellar subjects are ordered from least impaired (CBL3) to most impaired (CBL5) according to their International Cooperative Ataxia Rating Scale (ICARS) kinetic subscore (see Table 1). Control subjects are simply listed in numerical order. Two control subjects (C5 and C12) were excluded from the analysis (see materials and methods).

Pretest 2

Cerebellar patients and control subjects performed direction matching in pretest 2 equally well, producing comparable errors (P = 0.59, Fig. 4B). To compare the results of pretest 2 (which only included 5 subjects per group) to pretest 1 and to the main experiment (which included 12 subjects per group) on an equal basis, we performed a power analysis and found that increasing the number of subjects in pretest 2 to 12 would still not result in a significant difference between groups (the significance level would decrease from 0.59 to 0.40). In this pretest, subjects were free to choose how much force they wanted to exert as long as it was above 6% of F_max. Patients chose to exert 16 ± 9.1% of F_max (mean ± SD) and control subjects 10 ± 4.0% of F_max. There was no significant difference between groups (P = 0.24).

Main Experiment

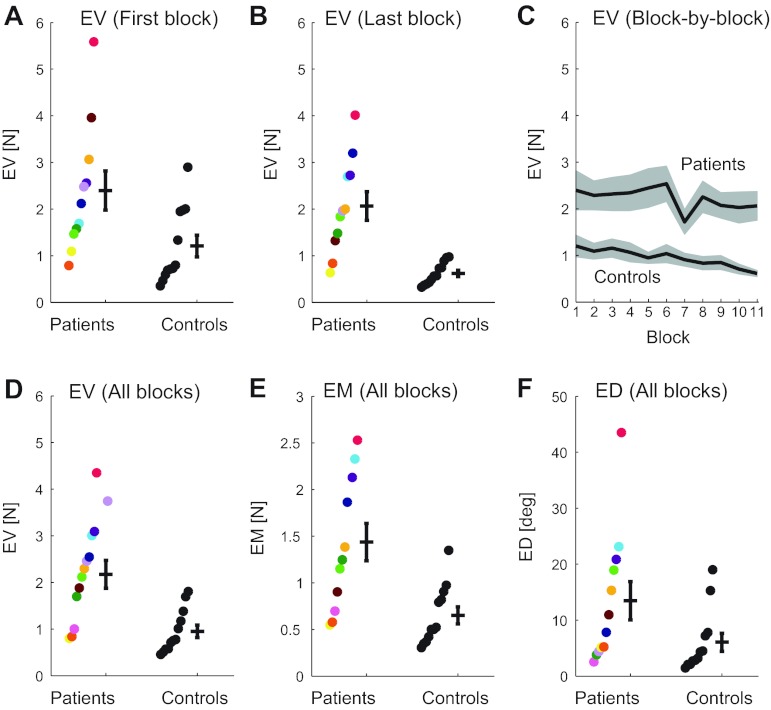
In the main experiment, cerebellar patients performed significantly worse than control subjects (P = 0.001; Fig. 6, A–D). This impairment was present in the first block (P = 0.015; Fig. 6A) and remained in the last block (P < 0.001; Fig. 6B). Furthermore, patients did not exhibit significant improvement from the first to the last block (P = 0.36), while control subjects did (P = 0.017; Fig. 6C).

Fig. 6.

Results of the main experiment. A, B, and D: vector error (EV) in the first block (first 16 trials), last block, and all blocks. C: block-by-block view of EV for patients and control subjects. Patients' dip in EV between blocks 6 and 7 is likely due to the 5- to 10-min break subjects received between blocks 1–6 and 7–11. E and F: EM and ED across all blocks. Dots represent individual subjects, coded by color (key in Fig. 4) and ranked by EV (A, B, D), EM (E), or ED (F) to allow for easier comparison between groups. Error bars in each subplot indicate 1 SE. Patient CBL1 is not included in A and B (see materials and methods).

Patients' impairment in the experiment could result from an underlying impairment in controlling magnitude, direction, or both. Compared with control subjects, patients had more error in magnitude (Fig. 6E; EM, P = 0.002) and a strong trend for direction (Fig. 6F; ED, P = 0.063) in the context of the main experiment. The difference in EM between groups is most robust and closely mirrors the difference in EV between groups. Cerebellar impairments in magnitude and direction are evident not only at the end of the matching period but also during the trial. Figure 7 shows that both control subjects and cerebellar patients reduced their error over the duration of a single trial, but control subjects did so more quickly than cerebellar patients.

Fig. 7.

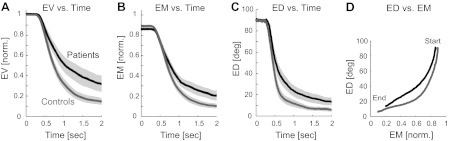
Progression of error during the course of a trial. A–C: patients are slower at reducing all errors (EV, EM, and ED, averaged over all trials in main experiment). Gray bands indicate ±1 SE across each group. EV and EM were normalized by the target force prior to averaging so we could average trials at 5% and 10% of F_max together. D: patients and control subjects reduce their ED more quickly than their EM, and control subjects more so than patients. Graphs in D progress in time from top right (much error) to bottom left (little error).

During each trial, subjects could choose to reduce their EM first and then their ED, or vice versa, or both at the same time, and we were interested in whether patients and control subjects chose different strategies. We determined patients' and control subjects' strategy from the shape of their ED vs. EM trajectories, as shown in Fig. 7 (note that while the slope of the trajectories depends on the units of ED and EM, the shape of the trajectories—concave or convex—does not). Patients and control subjects reduced their ED more quickly than their EM (the concave shape denotes this), but control subjects did so more than patients.

Performance generally deteriorated with increasing target force magnitude, and more so for patients than for control subjects. Patients had significantly more EV and EM on trials that required 10% of F_max than those that required 5% of F_max (P < 0.05), while control subjects showed a similar but nonsignificant trend.

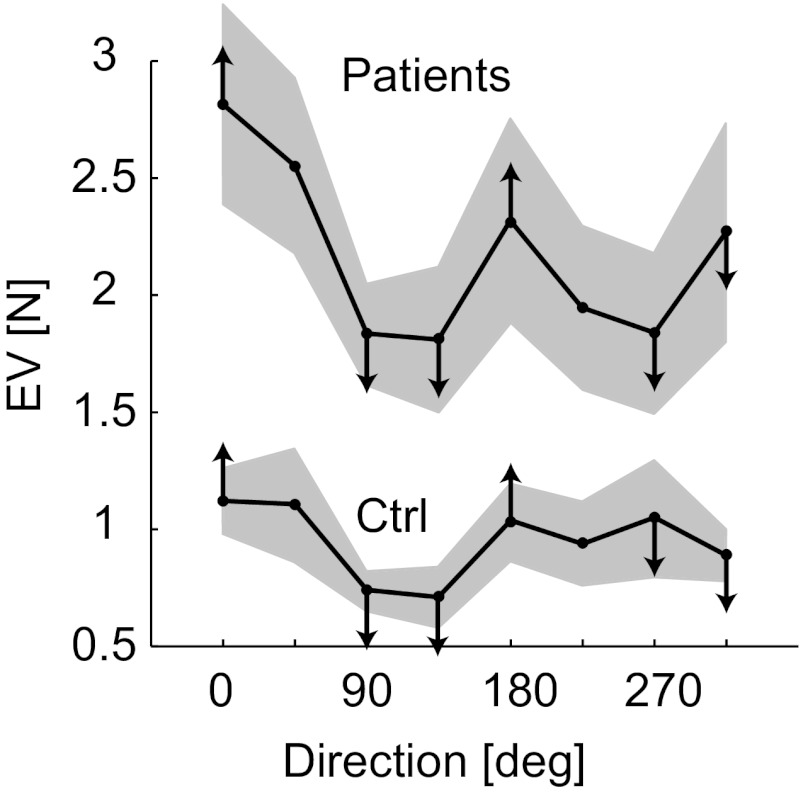
In general, performance varied with direction as predicted (compare Fig. 3D and Fig. 8). The differences between directions were more pronounced at higher force magnitudes than at lower force magnitudes. In the 10% trials, subjects performed significantly worse at 0° than in all other directions except 45° and 180° (and worse at 45° than in all other directions except 0°, 180°, and 315°; all P < 0.05), while there were no significant differences between directions in the 5% trials.

Fig. 8.

Performance varied with direction as predicted. Performance in the main experiment (EV averaged across all force magnitudes and blocks) is plotted as a function of target direction for patients and control subjects (θ in Fig. 2A). Gray bands represent ±1 SE across each group. Arrows indicate predicted error trends: arrows at 0 and 180° point toward high errors because those directions are associated with the highest cost in torque magnitude, while the other arrows point toward low errors because those directions are associated with low torque magnitude and/or single DOF (see Fig. 3, C and D).

Overall, there were no significant differences between patients and control subjects in terms of how their performance varied with direction. Interestingly, however, by the end of the main experiment (by the last block of trials), control subjects had eliminated differences in performance between directions, while differences still persisted for patients (even in the last block, patients performed significantly worse at 0° than in all other directions except 45°; P < 0.05).

Because cerebellar patients performed as well as control subjects in pretest 1 (Fig. 4A) in a direction of their choice (Fig. 5), we were interested in whether cerebellar subjects maintained that high level of performance in the main experiment in that same direction, so we looked at performance (in the main experiment) in the target closest to their direction chosen in pretest 1. We found that all subjects' performance in the main experiment was generally better in the direction they chose in pretest 1 than their mean performance over all directions. However, it was not generally their best direction, and patients' performance in their chosen direction (in the experiment) was still significantly worse than control subjects' performance in their chosen direction (P = 0.033).

Finally, we tested whether patients' performance in the main experiment correlated with their ICARS score. We found that patients' mean EV (averaged over all trials of the main experiment) was not correlated with their ICARS score (Pearson correlation coefficients of 0.35 and 0.25 for the total ICARS score and for the kinetic function subscore, respectively).

DISCUSSION

The main finding of this study is that patients with cerebellar ataxia are impaired at controlling arm force, even when there is no movement of the arm. This is significant because it suggests that the role of the cerebellum in limb control, which is generally hypothesized to involve movement, may be more general than previously thought and may include force production, with or without movement. We also found that while patients with cerebellar ataxia were impaired at controlling the amount and direction of their force simultaneously, they did not exhibit significant impairment at controlling the amount or direction separately, indicating that the cerebellum may generally play a role in combining or organizing the various aspects needed for coordinated motor control. Mai and colleagues also found that cerebellar patients exhibited clear deficits in controlling isometric force in a 1-DOF pinch task (Mai et al. 1988). In their experiment patients were required to produce prehensile force (between thumb and index finger) to match a target magnitude, and they found that patients exhibited clear deficits in maintaining a constant force output, performing fast repetitive force changes, and tracking a time-varying force target. Even though the tasks in their experiment tested the control of only 1 DOF of force (magnitude), they required coordination of multiple aspects of force control (finger and thumb, changing force fast and repetitively, or tracking a time-varying target). This coordination requirement was greater than in our pretests and may explain why deficits were observed even in a 1-DOF task.

Given that cerebellar patients have difficulty adapting to novel environments (Martin et al. 1996; Maschke et al. 2004; Smith and Shadmehr 2005), a deficit in cerebellar performance in our main experiment might be due to an inability to understand the mapping between force and the visual display of force instead of an inability to control force. The two pretests were intended to test patients' ability to control the two aspects of this mapping (magnitude and direction). The fact that patients performed as well as control subjects in the pretests indicates that there was no difficulty in learning the mapping. Thus patients' subnormal performance in the first block of the main experiment (Fig. 6A) was not likely due to an inability to understand and work within the novel environment. The fact that patients performed as well as control subjects in the pretests also indicates that patients' impaired performance in the main experiment (which required similar force magnitudes) was not due to an inability to generate sufficient force or to generate force quickly enough. The initial gap between patients and control subjects widened during the main experiment, as control subjects exhibited significant improvement in their performance with practice (P = 0.017) while patients did not (P = 0.36; Fig. 6C).

Why was there a significant difference between groups in controlling magnitude and direction together, but not separately? Furthermore, given that there was no significant difference between groups in controlling force magnitude in a chosen direction in pretest 1, why was there a significant difference in controlling force magnitude in eight prescribed directions in the main experiment? The observation that patients exhibited significant impairment in controlling force magnitude and direction together, but not separately, is similar to other observations of cerebellar ataxia in the literature, such as patients' ability to control movement of a single DOF but not multiple DOF (Bastian et al. 1996, 2000) and the finding that patients' impairments in separate eye and hand tasks are accentuated during combined eye-hand tasks (Vandonkelaar and Lee 1994). Thus it appears that the cerebellum may play an essential role in combining or coordinating multiple aspects of motor control (Thach et al. 1992). Other parts of the brain may only be able to compensate for cerebellar loss during simple (e.g., single DOF) problems.

It has been suggested that the architecture of the cerebellum could enable it to link large combinations of appropriate stimulus responses through a trial-and-error learning process (Thach 1998). Thach proposed that, because a single parallel fiber contacts many Purkinje cells, it could provide a linking mechanism for coordination across parts of the body, or across muscles (Thach 1998). Climbing-fiber firing would presumably decrease the strength of the synapse between the parallel fiber and Purkinje cell in response to error, leaving only appropriate stimulus-response connections after learning (Thach 1998). This hypothesis would explain why our cerebellar patients were impaired at combining multiple elements and improving their performance with practice. Motor control may rely on a number of internal models, and many researchers have found evidence indicating that “at least some internal models are acquired and stored in the cerebellar cortex” (Kawato 1999). While we do not know how these internal models are divided or represented in a cellular network, coordinated movement requires that the internal models (together) transform between movement and force in an external space and muscle activation in an internal space. A possible division of internal models (inside or outside of the cerebellum) is diagramed in Fig. 9A, together with the physical execution of the internal model plan (Fig. 9B). The top path in Fig. 9A could be viewed as the process by which the brain estimates the muscle activation u⇀ required to produce a desired hand trajectory x⇀_des. The bottom path in Fig. 9A represents this process for isometric force application, which computes the muscle activation u⇀ required to produce a desired force F⇀_des at the hand. Following a desired trajectory x⇀_des and simultaneously applying a desired force F⇀_des requires both paths (e.g., for movements like pushing a door open). The model relating joint displacement to joint torque and muscle force to muscle activation is dynamic (i.e., the input-output relationship depends on past states and involves time derivatives of inputs and/or outputs), while the model relating hand force to joint torque and joint torque to muscle force is static (depending only on the current configuration of the limb). Coordinated movement involves both dynamic and static relationships (Katayama and Kawato 1993), so the lack of coordination in cerebellar ataxia indicates that cerebellum-dependent computations may a priori include dynamic and/or static internal models. However, the role of the cerebellum in limb control is generally hypothesized to involve dynamics. Furthermore, because most past investigations of internal models in the cerebellum have involved movement (top path in Fig. 9A), it has not been possible to determine whether a motor deficit was caused by a deficit in dynamic, static, or both types of internal models.^… The isometric (bottom path in Fig. 9A) tasks in this experiment do not require an internal model of limb dynamics, nor should a defective model of limb dynamics affect performance. The fact that patients' performance in the main experiment was impaired argues that the cerebellum is involved in controlling forces independent of any computation of limb dynamics, and that hypotheses of cerebellar function should be expanded to include internal models needed for force control, with or without movement (i.e., the internal models in the bottom path in Fig. 9A). Interestingly, because controlling hand force in a single dimension (either magnitude or direction) requires control of multiple dimensions of joint torque, muscle force, and muscle activation, the finding that patients with cerebellar ataxia did not exhibit significant impairment in controlling force magnitude or direction separately suggests that the internal models downstream of joint torque are not significantly impaired, and that the impairment in controlling force magnitude and direction together (which requires control over more dimensions in hand force but not in joint torque, muscle force, or muscle activation) may be caused by an impairment in the static model relating hand force to joint torque.

Fig. 9.

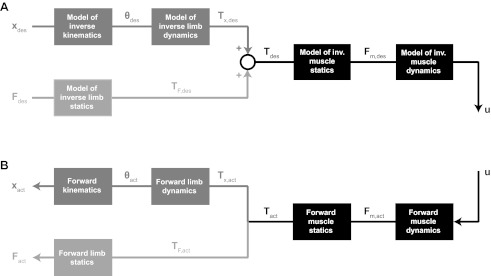
A possible internal model scheme for planning a hand trajectory and force (A), together with the physical execution of the plan (B). A: this internal model scheme computes the muscle activation u⇀ required to achieve a desired hand trajectory x⇀_des and/or hand force F⇀_des. The intermediate variables θ⇀_des, T⇀_x,des, T⇀_F,des, T⇀_des, and F⇀_m,des represent the joint trajectory and torque required to achieve the desired hand trajectory, the joint torque required to produce the desired hand force, and the total torque and muscle force required to produce the desired trajectory and force at the hand. B: applying the muscle activation u⇀ produces actual muscle force, joint torques, and eventually hand trajectory and force.

Patients' subnormal performance does not, however, argue against internal models of limb dynamics in the cerebellum because it is possible that the cerebellum is involved in estimating limb dynamics as well. Thus the cerebellum may store multiple types of internal models capable of explaining the deficits observed in cerebellar ataxia. Finally, force control deficits may also result from impairment in the perception of force. A recent study showed that cerebellar patients are impaired at correctly perceiving self-generated forces associated with movement (Bhanpuri et al. 2012). Through feedback, such a deficit in perception could produce inappropriate force output, although we would expect to see it in the pretests as well.

In summary, the results in this report clearly indicate that cerebellar involvement in motor control is not limited to an internal model of limb dynamics. Deficits in initial and learned performance occur even in isometric conditions, but significant impairment was only found in the simultaneous control of multiple DOF. Thus the cerebellum may play a fundamental role in combining or organizing various elements required for coordinated movement.

GRANTS

This research was supported by National Institutes of Health R21 Grant 5R21NS-061189 and R01 Grant HD-040289.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.K.C., A.M.O., and A.J.B. conception and design of research; S.K.C. performed experiments; S.K.C. analyzed data; S.K.C., A.M.O., and A.J.B. interpreted results of experiments; S.K.C. prepared figures; S.K.C. drafted manuscript; S.K.C., A.M.O., and A.J.B. edited and revised manuscript; S.K.C., A.M.O., and A.J.B. approved final version of manuscript.