Directed functional connectivity matures with motor learning in a cortical pattern generator

Abstract

Sequential motor skills may be encoded by feedforward networks that consist of groups of neurons that fire in sequence (Abeles 1991; Long et al. 2010). However, there has been no evidence of an anatomic map of activation sequence in motor control circuits, which would be potentially detectable as directed functional connectivity of coactive neuron groups. The proposed pattern generator for birdsong, the HVC (Long and Fee 2008; Vu et al. 1994), contains axons that are preferentially oriented in the rostrocaudal axis (Nottebohm et al. 1982; Stauffer et al. 2012). We used four-tetrode recordings to assess the activity of ensembles of single neurons along the rostrocaudal HVC axis in anesthetized zebra finches. We found an axial, polarized neural network in which sequential activity is directionally organized along the rostrocaudal axis in adult males, who produce a stereotyped song. Principal neurons fired in rostrocaudal order and with interneurons that were rostral to them, suggesting that groups of excitatory neurons fire at the leading edge of travelling waves of inhibition. Consistent with the synchronization of neurons by caudally travelling waves of inhibition, the activity of interneurons was more coherent in the orthogonal mediolateral axis than in the rostrocaudal axis. If directed functional connectivity within the HVC is important for stereotyped, learned song, then it may be lacking in juveniles, which sing a highly variable song. Indeed, we found little evidence for network directionality in juveniles. These data indicate that a functionally directed network within the HVC matures during sensorimotor learning and may underlie vocal patterning.

how neural circuits encode complex, learned motor skills is poorly understood. Accumulating evidence suggests that learned motor sequences and sensory information may be encoded by feedforward networks (Abeles 1991; Amari 1972; Drew and Abbott 2003; Isaacson and Scanziani 2011; Long et al. 2010). Mechanisms underlying at least a subset of feedforward architectures have been described: inhibitory interneurons form sequentially active groups that dynamically synchronize subsets of principal (projection) neurons, enabling coordinated activation of coincidence detectors in the next target group (Bonifazi et al. 2009; Buzsaki and Chrobak 1995). For example, sensory stimulation drives the sequential activation of physically distributed interneuron groups (Assisi et al. 2011).

Topographic maps are key features of neural systems. Recovery after injury is linked to cortical remapping, and the appearance of somatotopic maps coincides with the capacity for skilled movement (Monfils et al. 2005; Wittenberg 2010). Maps are used for senses as diverse as somatosensation, vision, audition, olfaction, and echolocation (e.g., Penfield and Boldrey 1937). Notably, topographic maps encode temporal aspects of sensory stimuli and behaviors. For example, the acoustic delay between the ears is mapped in the nucleus laminaris of barn owls (Konishi 2003). Studies in zebrafish have reported maps of swim rhythms in the spinal cord (McLean et al. 2007) and firing persistence in the brainstem, velocity-to-position neural integrator for eye movements (Miri et al. 2011). However, a topographic map of motor activation sequence (i.e., a map of the temporal order of spiking that drives a behavior) has not been reported.

Song in the zebra finch is a stereotyped, sequential behavior. We hypothesized that the song pattern generator would contain a topographic map of sequence, detectable as network directionality, with anatomic regions of the network firing together in a dynamic, stereotyped pattern. Evidence indicates that the cortical birdsong nucleus, the high vocal center (HVC) (Reiner et al. 2004), forms a motor pattern generator (Aronov et al. 2008; Ashmore et al. 2005; Long and Fee 2008; Nottebohm et al. 1976; Simpson and Vicario 1990; Solis and Perkel 2005; Vu et al. 1994) that is shaped by vocal learning (Crandall et al. 2007a, 2007b; Day et al. 2009), which suggests that it may contain the neural architecture for song sequence. Sleep replay of sequential song activity patterns in the HVC and its synaptic target, the robust nucleus of the arcopallium (RA), closely approximates motor activity during singing (Dave and Margoliash 2000) and occurs under anesthesia (Schmidt and Konishi 1998). Both types of HVC principal neurons, corticocortical and cortico-basal ganglia, fire action potentials during activity bursts under anesthesia (Day et al. 2011). The similarity of the activity sequence during singing and replay enables analysis of sequential premotor activity in anesthetized finches, which facilitates simultaneous recording of many HVC neurons.

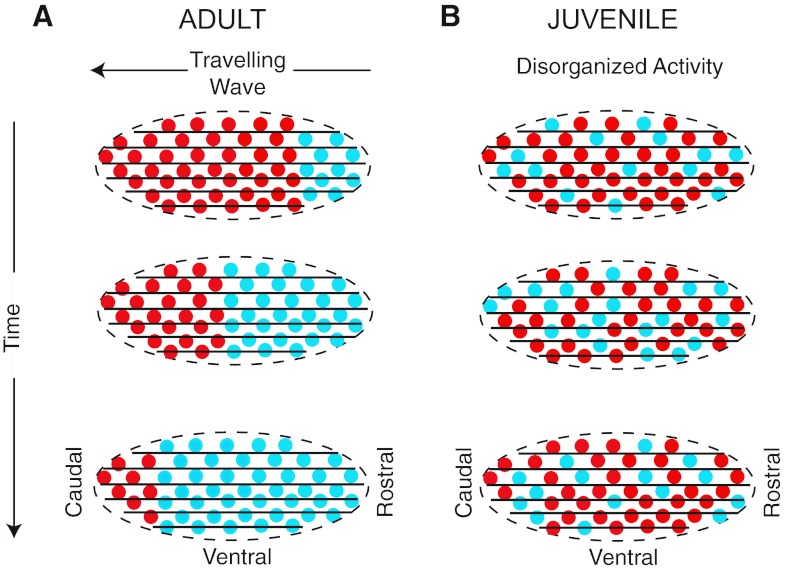
Zebra finch song crystallizes, becoming resistant to change, at the end of a developmental sensorimotor phase, not unlike that of human babbling speech (Bolhuis et al. 2010; Marler 1970). We tested the hypothesis that a topographic map of activation sequence was important for learned song by comparing the spatial relationships of network activity in plastic juveniles versus crystallized adults (Fig. 1). In adults, we tested the hypotheses that principal neurons fire with neurons that are in front or behind them in the rostrocaudal axis and that principal neurons fire in a rostrocaudal sequence. We also tested the hypothesis that network functional connectivity reflects motor sequence learning and, thus, that juveniles would have no detectable network directionality.

Fig. 1.

Simplified schematics of the hypothesis that the adult HVC song nucleus contains an asymmetric network that supports travelling waves, whereas the juvenile HVC does not. Parasagittal sections of the HVC (ovoid shapes) are shown. Neuronal cell bodies are represented by circles, with spiking activity indicated by cyan and quiescence by red. Rostrocaudally oriented axons are indicated by black lines. A: in adults, three snapshots in time reveal the asymmetrical activation of the HVC as an activity wave travels in the rostrocaudal axis. B: in contrast, the asymmetrical activation of the juvenile HVC would not be detectable, according to the hypotheses that dynamic network structure is important for the production of learned song and that juveniles lack this structure.

MATERIALS AND METHODS

Animals and surgical procedures.

Juvenile and adult zebra finches (Taeniopygia guttata) were reared in our laboratory. Birds were housed under a 14:10-h light:dark cycle and were given food and water ad libitum. The Institutional Animal Care and Use Committee of The University of Minnesota approved all procedures. Surgical and recording methods were as previously described (Day et al. 2011). Tetrode recordings were obtained from 25 male zebra finches: juveniles were 45–66 days old (n = 9 finches, 12 recording sessions), adults used in the rostrocaudal experiments were >138 days old (n = 12 finches, 18 sessions), and adults used in the mediolateral experiments were >100 days old (n = 4 finches, 7 sessions).

All animals were deprived of food and water for a minimum of 1 h before an initial intramuscular injection of 20% urethane (5 μl/g). Two additional subdoses (not exceeding 30 μl/dose) were given at 30- to 45-min intervals. The bird was placed in a stereotaxic apparatus (Herb Adams Engineering), and lidocaine (1% Xylocaine) was injected under the scalp. After resection of the scalp, craniotomies were made over the following regions: the HVC, area X, and the RA.

Bipolar stimulating electrodes were constructed from 200-μm Teflon-coated tungsten rods (A-M Systems, Sequim, WA) and cemented into place with dental acrylic within area X at a depth of 3.7–4.2 mm. A reference electrode (125-μm bare silver wire) was cemented in place ∼3.5 mm anterior and 4 mm lateral of the lambda arterial sinus. A threaded headpost was cemented to the bird's skull. After this preparatory surgery, the animal was moved into a sound-attenuating chamber (Industrial Acoustics) on an air table (TMC, Peabody, MA). Once the animal was secured by the headpost, a bipolar stimulating electrode (FHC, Bowdoin, ME) (300- to 500-kΩ impedance) was inserted into the RA, except in the case of the adult mediolateral experiments, in which technical limitations precluded the insertion of the RA-stimulating electrode.

Voltage recording and electrical stimulation.

Ensembles of single units in the HVC were recorded extracellularly in 10- to 15-min recording sessions with a 4-tetrode array (A4x1, Neuronexus Technologies, Ann Arbor, MI), which was amplified by a 16-channel headstage preamplifier (10×) that connected to a model 3600 16-channel alternating current amplifier (A-M Systems). Tetrodes were linearly distributed within the HVC and positioned relative to the midsagittal sinus in the rostral-caudal (parallel to the sinus) or medial-lateral (perpendicular) plane with a spacing of 150 μm. Tetrodes with a recording site area of 312 μm² were used (0.5- to 2.0-MΩ impedance). Signals were amplified (1,000×), filtered (1 or 300–10,000 Hz), and acquired at 22.05 kHz (PCI 6251, National Instruments, Austin, TX) under the control of custom written Matlab (Mathworks, Natick, MA) software. Activity in the HVC was collected on 15 channels; the fourth recording site on one tetrode (tetrode 4) was not recorded to enable the collection of chamber sound events on our analog-to-digital PCI card, which was limited to 16 channels.

Current stimulation (20–400 μA) was delivered by a stimulus isolation unit triggered by a Master 8 (AMPI, Jerusalem, Israel) to the efferent targets of the HVC: area X and the RA. Only one target was stimulated at a time. Single, monophasic pulses of 200-μs duration were delivered at a rate of 0.5 Hz. Stimulation intensity was gradually increased until reliable antidromic spikes with few failures were observed in the HVC.

Antidromic collision tests were executed in a subset of experiments to further confirm the antidromicity of the stimulation and to rule out the possibility of intervening synapses. For spike collisions, a two-window discriminator (FHC) was used to identify specific spontaneous spikes and selectively trigger stimulation within 1.5 ms.

Spike feature clustering.

Spikes from multiple units on the same tetrode were sorted using automatic clustering of waveform features in 9–12 dimensions, depending on the number of recorded channels (tetrode 4 had only three channels due to use of the fourth channel for sound), followed by manual checking of each cluster; 22-point (∼1-ms) spike waveforms and their corresponding timestamp were used for clustering if they crossed a relatively low, predetermined threshold (median + 4 SD, calculated independently on each channel for each recording session). Our conservative threshold included numerous “noise” events and clusters, which were subsequently rejected during cluster checking. Having a low threshold decreases the possibility of excluding part of a cluster. For each channel, features of thresholded waveforms were calculated (MClust, A. D. Redish) and subjected to unsupervised clustering with a Gaussian mixture model with unconstrained covariance matrixes (KlustaKwik, K. Harris, Rutgers, http://klustakwik.sourceforge.net) to obtain a maximum of 30 initial “preclusters” using a classification expectation-maximization algorithm. KlustaKwik allows for a variable number of clusters, penalized by the Akaike information criterion. The initial preclusters identified by KlustaKwik were manually checked and occasionally combined or split using MClust 3.5 (A. D. Redish, http://redishlab.neuroscience.umn.edu/MClust/MClust.html) in the Matlab environment. Clustering was performed on either a Dell PC or a blade server with a 64-bit processor.

Cluster quality was assessed using four criteria to ensure that sorted spikes accurately reflected single units. Clusters that did not pass all criteria were discarded. The four criteria for cluster quality were as follows: 1) L ratio score < 0.1, 2) isolation distance > 16, 3) <1% violations of a 1-ms refractory period, and 4) visual separation of the cluster from “noise” and other clusters on at least two (of 12) dimensions. The L ratio is a measure of the compactness of a cluster, whereas isolation distance quantifies how well a cluster separates from other clusters (Harris et al. 2000; Jackson et al. 2006; Schmitzer-Torbert et al. 2005). For spike waveform display and spike width analysis, a matrix of 64-point waveforms was created with the same indexes as the 22-point waveform matrix that was used for clustering.

Identification of clustered antidromic single units.

All clusters used for further analysis, including those identified by antidromic stimulation, met the four criteria described above. Axons of principal units innervate target areas outside of the HVC. Stimulation of these target areas thus leads to the activation of recorded somata of principal units within the HVC. Action potential collisions are a strict test of antidromicity, since they occur only in cells whose axons are stimulated shortly after their own spontaneous spikes (Lipski 1981; Ranck 1975). Collisions do not occur in neurons that synaptically activate the principal neuron. Antidromic spikes coclustered with a subset of spontaneous spikes. Spontaneous spikes that triggered spike collisions also coclustered with antidromic spikes. The coclustering of spontaneous spikes with antidromic and/or collided spikes enabled the identification of spontaneous events as those of a principal neuron. Precise spike times relative to stimulation enabled the identification of fixed latency spikes and the determination of antidromic latency and its variability. To exclude driving effects of stimulation as a mechanism of increased coherency, all spikes that were collected during and 100 ms after stimulation were excluded from analyses of waveform properties and network interactions. Antidromic latency was defined as the mean time from stimulation to the peak of the action potential for at least 10 stimuli. Latency variability was defined as the SD of the latencies. The latency variability cutoff for the identification of a unit as a principal neuron was set at <125 μs.

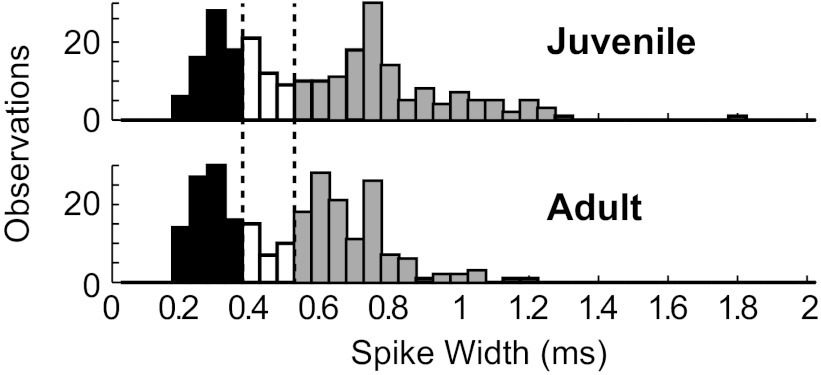
For a detailed study of the spatial pattern of functional connectivity relative to the principal neurons that we report below, we sought to expand our sample of principal neurons. We tested a variety of waveform parameters and found that a measure of the positive peak width at 25% maximum >0.5 ms correctly identified >81% of both antidromically identified principal neuron types while selecting only 30% of all HVC neurons in both juveniles and adults. This measure has been previously described for the classification of HVC neurons (Rauske et al. 2003). As in other systems (e.g., Nick and Ribera 2000), the action potential duration of HVC neurons may change with development. If so, the classification of neurons based on spike width may result in differential contamination of principal and interneuron groups in juveniles relative to adults. Histograms of the spike width of juvenile and adult neurons both indicated a dip at 0.35–0.50 ms (Fig. 2). Collectively, these findings led us to classify neurons with spike widths of <0.35 ms as putative “interneurons” and those with spike widths of >0.50 ms as putative “principal neurons.” Neurons from this latter group are referred to below as “spike width-defined principal neurons” to distinguish them from the more rigorously tested but overlapping set of antidromically defined principal neurons.

Fig. 2.

Histograms of HVC neuronal spike widths reveal a dip in the distribution between 0.35 and 0.50 ms (marked by dotted lines and open bars) in juveniles (top) and adults (bottom). Putative interneurons had spike widths of <0.35 ms (solid bars), whereas putative principal neurons had spike widths of >0.50 ms (shaded bars). n = 250 neurons for juveniles and 246 neurons for adults.

Analyses of functional interactions and statistics.

To investigate the spatial distribution of spike train relationships, the correlated activity of neuron pairs within and between tetrodes (spanning 150–450 μm) was quantified using coherency (Kimpo et al. 2003). True cross-correlation and cross-covariance are less optimal for these experiments due to sensitivities to firing rate and oscillations. The entire recording between antidromic stimulation epochs (excluding a 100-ms poststimulus buffer) was used for coherency calculations. Coherency was calculated as previously described (Kimpo et al. 2003; Rosenberg et al. 1989) with custom-written Matlab code. Coherency is the cross-covariance of the two spike trains normalized by the autocovariances of both (Rosenberg et al. 1989; Kimpo et al. 2003). Coherency [γ_A-B(ω)] was computed in the frequency domain as follows:

$${\gamma }_{\text{A}-\text{B}}\left(\omega \right)=\frac{C_{\text{A}-\text{B}}\left(\omega \right)}{\sqrt{C_{\text{A}-\text{A}}\left(\omega \right)\times C_{\text{B}-\text{B}}\left(\omega \right)}}$$

where C_A-B(ω) is the cross-covariance of the two spike trains in the frequency domain and C_A-A(ω) and C_B-B(ω) are autocovariances. For further analysis and plotting, γ_A-B(ω) was transformed into the time domain (Kimpo et al. 2003). Coherency reflects the relative probability of one neuron firing, given that the other has fired at time (t) = 0. Coherency values are unitless and range between −1 and 1. A large coherency value at t = −5 ms, for example, would indicate that every time one unit fired, the other was highly likely to fire 5 ms earlier. All group coherencies shown in bar graphs are medians calculated at t = −5 to −1 ms. Same tetrode data are contaminated by overlapping waveforms only at t = 0 ms. In all figures except for Fig. 7G, this time range (−5 to −1 ms) can be interpreted as a measure of the activity of the principal neuron within 5 ms before the firing of the other neuron. Jackknife SD was computed according to established methods (Beran 1984): variance was estimated by repeated resampling and recalculation of the coherency, with each run leaving out one sample.

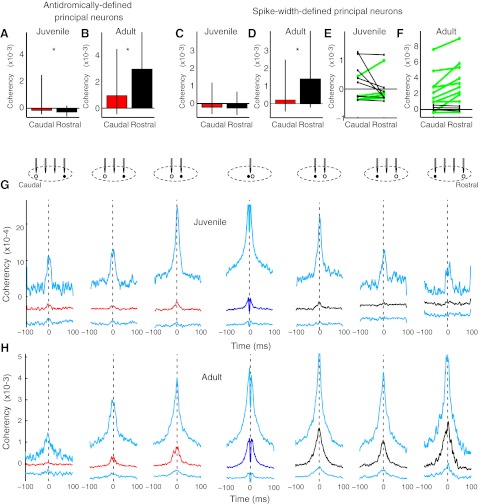
Fig. 7.

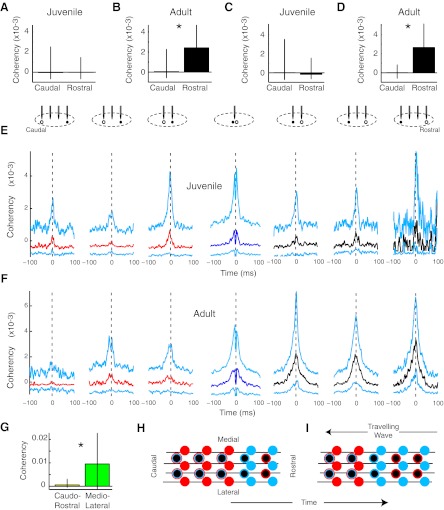
Principal neuron-interneuron functional connectivity was rostrocaudally skewed in adults but not in juveniles. A: the coherency of juvenile principal neurons with putative interneurons was not spatially distinct (n = 286 and 155 pairs). B: in contrast, adult principal neurons fired preferentially with rostral rather than caudal interneurons (n = 236 and 328 pairs, *P < 2e⁻⁶). C and D: a more restrictive definition of putative interneurons (<0.25-ms spike width for C and D only) yielded the same pattern of results in juveniles (n = 62 and 27 pairs) and adults (n = 35 and 221 pairs). E: in juveniles, no consistent pattern was observed in the spatial distribution of coherencies between principal neurons and putative interneurons. Median (caudal, red; same tetrode, dark blue; rostral, black) and IQR (cyan) coherencies are shown for juveniles. n = 37, 112, 137, 143, 107, 44, and 4 pairs. F: adult principal neurons were more functionally coactive with rostral interneurons than with those that were caudal to them. n = 31, 81, 124, 146, 148, 127, and 53 pairs. G: adult interneurons were more synchronized in the mediolateral axis than in the rostrocaudal axis. n = 105 and 12 pairs, *P < 0.038. H and I: one simple model that can explain the results posits a rostral-to-caudal travelling wave or advancing front of inhibition. In these images, the wave would travel right to left. The solid circles indicate inhibitory neurons. Principal neurons have a black center. Spiking activity is indicated by cyan and quiescence by red. Rostrocaudally oriented axons are indicated by black lines. Before the wave arrives, interneurons are relatively quiescent (red), whereas principal neurons may or may not be active (as indicated by red and cyan outlines). At the leading edge of the wave, all neurons are active. In the trailing wave, interneurons, but not principal neurons, are active.

All measures of central tendency and dispersal are shown as medians with interquartile ranges (IQR). The nonparametric Wilcoxon rank-sum test was used to compare unmatched data, whereas the Wilcoxon signed-rank test was used to compare matched data. The nonparametric Kruskal-Wallis test was used for multiple comparisons. Significance was defined as α = 0.05.

RESULTS

A linear array of tetrodes enables the study of neuron-neuron interactions in a reproducible relationship.

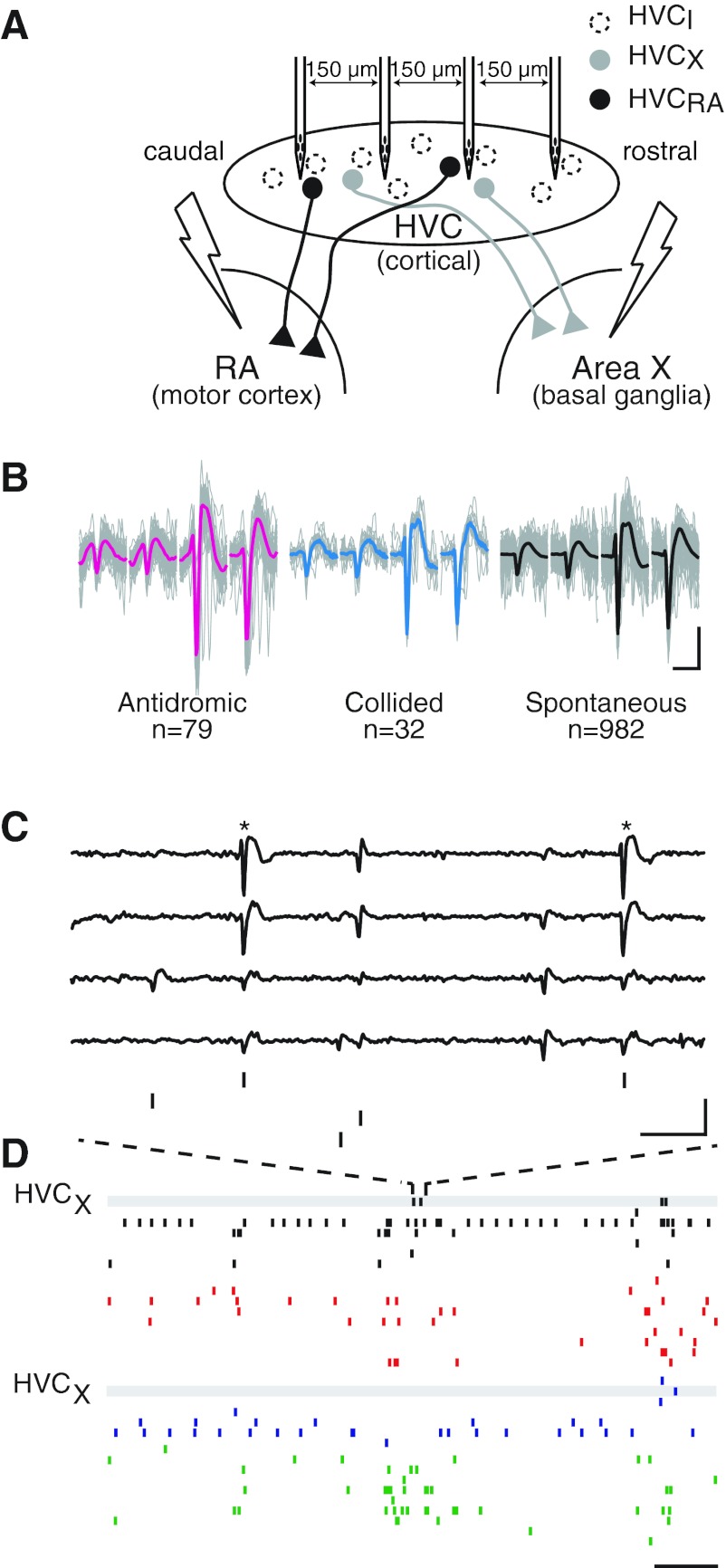
Spatial gradients of HVC activity were investigated with four-tetrode array recording combined with the antidromic identification of principal units (Fig. 3A) (Day et al. 2011). This technique allows the study of identified single units in the context of a network. HVC units that projected either to the cortical nuclues, the RA (HVC_RAs), or to the song basal ganglia, area X (HVC_Xs) (Farries and Perkel 2002; Reiner et al. 2004), were driven by antidromic stimulation. Single units recorded on the same tetrode were separated through spike feature clustering. Spontaneous action potentials that coclustered with antidromic and/or antidromically collided spikes were classed as those of a principal neuron (Fig. 3B) (Day et al. 2011). Principal neurons were then studied in the context of HVC population activity, which exhibited characteristic replay bursts (McCasland and Konishi 1981; Nick and Konishi 2001; Schmidt and Konishi 1998) that occurred in the absence of stimulation in anesthetized zebra finches (Fig. 3, C and D).

Fig. 3.

The recording configuration enabled the monitoring of multiple units across the HVC. A: diagram of the recording and stimulation configuration showing the linear four-tetrode array within the HVC. Bipolar stimulating electrodes were placed in the following song nuclei: robust nucleus of the arcopallium (RA) and area X. HVC_X, HVC unit that projects to area X; HVC_RA, HVC unit that projects to the RA. B: waveforms of spikes from an area X-projecting neuron were identified with spike sorting methods. Each image shows overlaid traces of clustered spikes of a single unit recorded on each of four electrodes (gray, with their means in color) that are shown separately based on whether they were driven by antidromic stimulation, occurred spontaneously and resulted in a collision with an antidromically driven spike, or occurred spontaneously during the period with no stimulation. Antidromic spikes (left; mean in red), spontaneous spikes that resulted in collisions (middle; mean in blue), and spontaneous spikes that occurred in the absence of stimulation (right; mean in black) were similar enough to cocluster with each other based on established methods (Day et al. 2011). The number of waveforms from each group are listed below each image. Scale bar = 1 ms, 250 μV. C: raw voltage traces from the four channels of one of four tetrodes are aligned with the spike times of four clustered units. Here, the unit that was identified as area X projecting in B (*) fired twice, along with three other clustered neurons. Scale bar = 3 ms, 400 μv. D: raster plots of spike times for the units shown in D on a longer timescale are temporally aligned with the activities of units on three other tetrodes. The tetrodes are ordered caudal to rostral, with different colors indicating different tetrodes. The activities of HVC_X units are highlighted with gray bars. Scale bar = 15 ms.

To investigate the spatial distribution of spike train relationships, the correlated activity of neuron pairs within and between tetrodes (spanning 150–450 μm) was quantified using coherency. Coherency is the cross-covariance of the two spike trains normalized by the autocovariances of both. Example coherencies of juvenile and adult single unit pairs that each contained an HVC_X are shown in Fig. 4. We found that the average spike train coherency of all HVC neuron pairs, regardless of cellular identity, increased with development [coherency (×10⁻⁴): n = 5,300 pairs for juveniles (median: −1.19; IQR: −6.68 to 18.11); n = 4,214 pairs for adults (median: 8.21; IQR: −4.22 to 35.53), P < 3 × 10⁻⁵⁵]. These data indicate that pairs of adult units consistently fire in more reliable temporal relationships than those of juveniles.

Fig. 4.

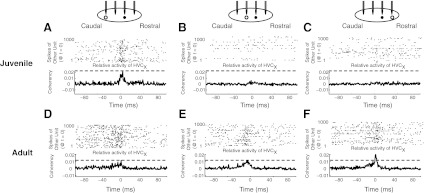
Coherency analysis reveals spike train relationships of single neurons in the HVC. Examples are shown from a juvenile (A–C) and an adult (D–F). In A–F, examples of coherency relationships between a HVC_X and another neuron are plotted below schematics that show the rostrocaudal relationship of the HVC_X (●) and its partner neuron (○) and dot rasters that show the first 1,000 spike times of the HVC_X relative to the partner that spiked at time (t) = 0. For aid in visual alignment, gray dashed lines indicate the peak coherency in the left graph. The bin size for the dot rasters and coherency calculation was 1 ms. A–C: spiking activity and coherency of a juvenile HVC_X single unit relative to other single units that were 300 μm caudal, 150 μm caudal, or 150 μm rostral, respectively. D–F: activity and coherency of an adult HVC_X single unit relative to single units that were 300 μm caudal, 150 μm caudal, or 150 μm rostral, respectively.

Principal neurons are coactive with the single units that are rostral to them.

We were able to identify a small group of single principal units in the context of the broader network using antidromic stimulation, as previously described (Day et al. 2011). Principal neurons fire sparsely compared with local interneurons (Hahnloser et al. 2002; Mooney 2000) and interact with the surrounding HVC network (Mooney and Prather 2005). We took functional snapshots of HVC circuit activity by calculating the coherency of spike trains of principal neurons relative to those of other neurons. These snapshots of HVC circuit activity taken at relatively sparse principal neuronal spike times were used to construct a probabilistic model of the network and determine the gross dynamic architecture. We hypothesized that principal neurons would preferentially fire with groups of neurons in front or behind them in the rostrocaudal axis, revealing functional network polarization.

In adults, but not juveniles, antidromically defined principal neurons were more co-active with rostral than with caudal neighbors (Fig. 5, A and B). In adults, the trend in both HVC_RAs (n = 6) and HVC_Xs (n = 16) was for these principal neurons to be more strongly functionally activated with partners that were rostral than those that were caudal. The trend was significant when the two principal neuron types were combined (Fig. 5B). In contrast, juvenile principal neurons were not more coherent with rostral partners (HVC_RA = 6 pairs and HVC_X = 13 pairs). The opposite pattern was observed: coherence was significantly less negative with the firing of caudal compared with rostral neighbors (Fig. 5A), indicating that juvenile projection neurons were typically less active when rostral neurons fired.

Fig. 5.

A decreasing rostral-to-caudal gradient of functional connectivity was found in adults but not in juveniles. A: antidromically identified principal neurons in juveniles had less negative spike correlations with caudal than rostral neighbors, giving a small reversed connectivity gradient (n = 160, 133 pairs, *P < 0.004 by Wilcoxon rank-sum test). Median coherencies of −5 to −1 ms were compared in A–F and in Figs. 6 and 7. Medians with interquartile ranges (IQRs; 25th and 75th percentiles) are shown. B: in contrast, adult antidromically defined neurons had stronger positive functional connections with rostral than caudal neighbors (n = 96, 137 pairs). C and D: similar to antidromically identified principal neurons, putative principal neurons that were identified based on spike width had slightly negative interactions with other neurons in juveniles and positive, rostrocaudally skewed interactions in adults. E: examination of individual juvenile recording sessions revealed no consistent axis of functional connectivity of principal neurons (n = 12 sessions, P = 0.47 by Wilcoxon signed-rank test). The green lines indicate sessions in which median rostral coherencies were greater than caudal coherencies. F: in contrast, adult recording sessions consistently indicated that principal neurons have stronger functional connections with rostral than caudal neighbors (n = 13 sessions, P < 0.014). G, top: the rostrocaudal relationships of neuron pairs are indicated by the schematics. The principal neuron (●) and partner (○) are shown below the tetrodes that recorded them. There was 150 μm between tetrodes. Bottom, corresponding coherency medians (caudal, red; same tetrode, dark blue; rostral, black) and IQRs (cyan) of principal neurons with partner neurons for all spatial relationships. Juveniles did not have detectable rostrocaudal patterns in functional connectivity of principal neurons with other neurons. n = 191, 433, 632, 724, 548, 312, and 110 pairs. H: in contrast, adult principal neurons had stronger functional relationships with rostral partners that were visible as higher peaks in the median and 75th percentile coherency. Note the change in the y-axis. n: 97, 277, 434, 511, 439, 299, and 112 pairs. The coherency deflection at t = 0 for same-tetrode measurements is due to the inability to identify synchronous spikes due to overlapping waveforms.

To study the spatial mapping of principal neuron functional connectivity in detail, we expanded our sample of principal neurons by using a spike width measure. We defined principal neurons as those with spike widths of >0.5 ms, which is more conservative than in a previous report [>0.35 ms (Rauske et al. 2003)]. Thresholds of 0.4 and 0.6 ms yielded findings similar to those described below. However, it is still possible that some interneurons were inadvertently included in this group. The spatial patterns of activity coherency were similar to those of antidromically defined principal neurons in juveniles (Fig. 5C) and adults (Fig. 5D), respectively. All data below are from putative principal neurons that were identified based on spike width.

To rule out the possibility that the observed spatial effects were due to the compounding of differences among the relative locations of principal neurons and variation in functional connectivity across recording sessions, we compared data from each session in which principal neurons had both caudal and rostral neighbors. No reliable pattern was observed in juveniles (Fig. 5E). In contrast, in adults, rostral coherencies were stronger than caudal coherencies in 10 of 13 sessions, and the effect was significant (Fig. 5F). The shapes of coherency relationships are shown by plots of the median and IQRs of spike train coherency based on the relative recording location of neuronal pairs (Fig. 5, G and H). Note the width of the coherency relationships, which is at least partially due to the tendency of HVC neurons to burst and thus have increased correlated activity during a broader timeframe than if they fired single spikes. In adults, in addition to the rostrocaudal skew, there was also a tendency for tighter functional coupling of neurons on adjacent tetrodes [coherency ± 150 μm distant (n = 804 pairs), median: 0.0010, IQR: −0.0003 to 0.0037; coherency ± 450 μm distant (n = 181 pairs), mediam: 0.0003, IQR: −0.0002 to 0.0023, P < 0.05]. Juveniles also showed this trend, but it was not significant.

Principal neuron pairs do not account for the network directionality in coherency magnitude.

HVC principal neurons synaptically activate other principal neurons (Mooney and Prather 2005). Principal-principal neuron coherencies were thus compared according to spatial location. Because we compared each pair in both relative spatial orientations, the coherency plots were necessarily spatially symmetrical (Fig. 6, E and F). However, it was possible that rostral might lead caudal neurons and have a coherency peak before t = 0 in one orientation and a peak after t = 0 in the other. However, in terms of coherency magnitude (measured t = −5 to −1 ms), there was no significant rostrocaudal gradient in juveniles or adults (Fig. 6, A and B).

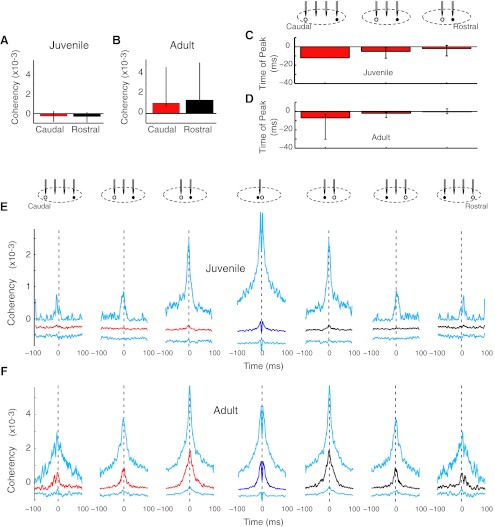
Fig. 6.

Principal neuron pairs did not show pronounced directionality in the strength of functional connectivity. A and B: neither juvenile nor adult principal neuron pairs had spatial differences in the magnitude of coherency. C and D: principal neuron pairs had rostrocaudal asymmetries in the time of peak coherency. In adults (D), this rostrocaudal pattern was significant. n = 1, 12, and 24 pairs for juvenilles (P = 0.43 by Kruskal-Wallis test); n = 3, 11, and 28 pairs for adults (*P < 0.05). E: median (caudal, red; same tetrode, dark blue; rostral, black) and IQR (cyan) coherencies are shown for juveniles. The caudal and rostral data are mirror images because coherency was computed for each principal neuron in the pair. n = 86, 194, 321, 410, 321, 194, and 86 pairs. F: in adults, principal neuron pairs did not show the strong rostrocaudal skew in magnitude characteristic of principal neurons versus the entire population of HVC neurons (see Fig. 4H). n = 32, 125, 184, 278, 184, 125, and 32 pairs.

In contrast, there were small, but significant, shifts in the time of peak coherency. Time of peak coherency is a more sensitive measure of spike timing differences than coherency magnitude at the specific time window of t = −5 to −1 ms. To further enhance sensitivity to timing differences, we only considered principal neuron pairs that had a significant positive coherency, defined as greater than three times the jackknife error. We compared the time of peak coherency across relative tetrode locations using Kruskal-Wallis one-way nonparametric ANOVA. In juveniles, the rostral principal neuron trended to fire earlier than its caudal partner (Fig. 6C). In adults, the pattern was significant: principal neurons fired in a spatially skewed rostral-to-caudal sequence (P < 0.038; Fig. 6D). The further the distance apart, the earlier the rostral neuron fired. These data indicate that the principal neurons fire in a rostral-to-caudal order, consistent with a rostrocaudal map of sequential activation. A rough estimate of the speed of these travelling waves of activity can be obtained by examining the difference in times of peak coherency relative to distance between tetrodes. For adults, this measure is ∼300 μm/3 ms, or ∼100 μm/ms (Fig. 6D).

In adults, principal neuron pairs on adjacent tetrodes were more functionally coupled than more distant pairs [coherency ± 150 μm distant (n = 407 pairs), median: 0.0011, IQR: −0.0003 to 0.0041; coherency ± 450 μm distant (n = 81 pairs), median: −0.00002, IQR: −0.0002 to 0.0015, P < 0.008]. Juveniles also had this trend, but it was not significant.

Because we sorted based on spike width, there is the possibility that either or both groups of principal neurons and interneurons were contaminated with members of the other group. However, the fact that we report differentiable patterns in adults with regard to principal-principal neuron versus principal neuron-interneuron functional interactions (see below) indicates that the groups are distinct.

Interneurons are coactive with the principal neurons that are caudal to them.

In addition to principal neurons, HVC contains local inhibitory interneurons that do not project out of the nucleus and that can be putatively identified based on their more narrow waveforms (< 0.35 ms at 25% positive peak) (Rauske et al. 2003). Principal neurons activate interneurons, which, in turn, inhibit principal neurons (Mooney and Prather 2005). In a further attempt to identify the partners of the principal neurons that were dominant in the overall directional pattern (Fig. 5), we examined principal neuron-interneuron functional interactions. As with the general population (Fig. 5), the spatial pattern of functional connectivity of spike width-defined principal neurons with putative interneurons was skewed in adults but not in juveniles (Fig. 7). More severe restriction of waveform duration (< 0.25 ms at 25% positive peak), which further increased the probability of selecting a pure population of interneurons, yielded similar results (Fig. 7, C and D).

Interneurons are more synchronized in the mediolateral axis than in the rostrocaudal axis.

The rostrocaudal polarization of principal-interneuron pairs supports a model in which a progressive wave of inhibition moves across HVC from rostral-to-caudal (Fig. 1). If true, then putative inhibitory neuron pairs should be more strongly correlated in the mediolateral axis than in the rostrocaudal axis. To test this hypothesis, we executed a separate set of recordings in adults in which the tetrode array was oriented in the mediolateral axis rather than in the rostrocaudal axis. Tetrode spike sorting and coherency analysis were identical to those with a rostrocaudal array. Consistent with the model, we found that the coherency of interneuron pairs was stronger in the mediolateral than rostrocaudal axis (Fig. 7G).

DISCUSSION

Directed functional connectivity matures with vocal learning.

Like human speech (Marler 1970), zebra finch song is a learned sequential motor skill. This report indicates that directed functional connectivity arises during vocal learning and may serve to codify motor sequence in a functional topographic map.

The data presented here are consistent with a model in which a wave of inhibition spreads across the HVC from rostral to caudal, with principal neurons firing at the leading edge (Fig. 7, H and I). According to this model, principal neurons spike at the forefront of the wave and then decrease or cease their firing, possibly due to continuing inhibition from the travelling wave and/or long-term inhibitory mechanisms that have been previously described (Dutar et al. 2000; Schmidt and Perkel 1998).

Mechanisms that may regulate HVC network directionality.

Other than the insertion of new neurons and synaptic plasticity, additional potential developmental changes that may help to explain the maturation of directed functional connectivity include changes in extrinsic inputs, increases in intrinsic excitability, and the maturation of a broad inhibitory network that could orchestrate population activity. Understanding the factors involved in the development of the functional directionality may illuminate the mechanisms of sensorimotor song learning and, perhaps, of motor sequence learning, in general. The correlation between developmental timelines for song learning and functional connectivity does not indicate causation, and more work is needed to link the two.

Does the HVC network directionality reveal an anatomic feedforward network?

Computational models of sequential neural activity often rely on feedforward models, which consist of layered neural networks within which different groups of neurons fire in sequence (Abeles 1991; Amari 1972; Drew and Abbott 2003; Isaacson and Scanziani 2011; Long et al. 2010). If a functionally layered HVC network produces song, there has been no evidence until now that structural layering underlies this functionality. Because HVC neurons have axons that ramify and form synapses within the HVC (Fortune and Margoliash 1995; Katz and Gurney 1981; Mooney and Prather 2005), there was no a priori requirement for functional physical mapping. Although topographic mapping of both major downstream targets of the HVC has been described (Luo et al. 2001; Wild 1993), no organized topography of HVC neurons or their projections has been reported (Bottjer et al. 1989; Foster and Bottjer 1998; Luo et al. 2001; Sutter and Margoliash 1994), although an axial structure exists (Nottebohm et al. 1982; Stauffer et al. 2012). This would be expected if the topography of the HVC were a map of activation sequence, as our data now suggest.

As in other systems (Assisi et al. 2011; Bonifazi et al. 2009; Buzsaki and Chrobak 1995), the role of inhibition may be to organize principal neuron activity and sharpen the timing of the network and corresponding behavior. Consistent with more precise timing with song development, we have previously found that bursts of HVC activity during singing are shorter duration and higher rate in adults compared with juveniles and that HVC bursts in the same animal shorten with song development (Crandall et al. 2007b; Day et al. 2009).

Possible functions of network directionality.

We hypothesize that the primary role of interneurons is to constrain and orchestrate the activity of the principal neurons, which include HVC_RAs and HVC_Xs. The interneurons may serve to organize the sequence of song or of shorter-duration song elements, such that the role of the functional directionality is the sequential playback of song. On the other hand, inhibition may regulate the synchrony of principal neuron groups, such that song is more or less variable. In this case, the role of the directed functional connectivity is regulation of variability. Finally, waves of inhibition in the HVC may function similarly to what has been proposed in the hippocampus (Lubenov and Siapas 2009): activity waves may serve in pathfinding to enable representation of a segment instead of a point in time. These hypotheses, which are not necessarily mutually exclusive, are discussed below.

The temporal sequence of song may be represented in the sequential firing pattern of principal neurons that is shaped by or reflected in a polarized network. This model is consistent with a previous report showing that the HVC contains a synaptic chain in which HVC_RAs depolarize abruptly instead of ramping to threshold (Long et al. 2010). HVC_RAs may either drive the network in sequential order or be driven by HVC_Xs, whose activity is shaped by inhibition (Mooney 2000; Mooney and Prather 2005). The speed of the travelling waves (∼100 μm/ms; Fig. 6D) is too fast to enable encoding of the entire song motif (∼1 s) with one pass through the HVC (∼1 mm in the rostrocaudal axis). The present data were collected in anesthetized animals, so one explanation is that the wave travels much faster under anesthesia than during singing. However, previous results have suggested that the rhythm of song activity patterns is similar across states (Dave and Margoliash 2000). Another song sequence hypothesis would propose that the HVC encodes short duration (tens of milliseconds) song elements along its rostrocaudal length and that these patterns are overlapping. This would require that the HVC or an afferent area keep track of the coarser time point in song or syllables such that the correct element would be played. Consistent with this hypothesis, evidence suggests that the song system codes song at multiple temporal levels: finer vocal structures crystallize later in song learning than coarser, syllable-level structures (Ravbar et al. 2012).

On the other hand, the observed network directionality may reflect the activity of a dynamically synchronizing and desynchronizing circuit (Battaglia et al. 2012). Song variability is necessary for trial-and-error learning during vocal plasticity (Fee and Scharff 2010). In the present study, we found that principal neurons fire with rostral interneurons. It may be that desynchronization of the circuit is achieved by a travelling wave of inhibition that is not related to song sequence. Instead, the primary role of the observed inhibition may be to generate jitter in the timing of premotor command and/or efference copy. If so, then why don't juveniles, which have variable song, have directed functional connectivity? We measured HVC functional connectivity relative to principal neurons. It is possible that there is already an inhibitory functional directionality in juveniles that we have not detected because of our methods. Alternatively, the proposed jitter generator may only function in adults to serve in the maintenance of song.

Finally, rhythmic oscillations, which are measured in local field potential recordings, shape the firing of principal neurons (Burgess and O'Keefe 2011). A recent study found that the phases of theta waves are topographically organized in the hippocampus (Lubenov and Siapas 2009). The authors proposed that the waves may function to enable hippocampal output at any moment to reflect a segment of space rather than a point. At a given instant, cells that represent the animal's current point in space fire with those that represent adjacent points in space. This would presumably aid in pathfinding. Likewise, waves in the HVC may enable “vocal pathfinding,” with neurons firing during the part(s) of song they encode as well as during adjacent song segments. If so, one may expect to see a ramping up of activity in at least some HVC neurons. While this has not been observed in recordings of corticocortical HVC_RAs (Long et al. 2010), voltage recordings in the cell bodies of HVC_RAs may not accurately reflect synaptic potentials in the dendrites. Furthermore, this question has not been examined in corticobasal ganglia HVC_Xs, which have inhibitory postsynaptic potentials and drive HVC_RAs (Mooney 2000; Mooney and Prather 2005). We observed graded changes in the coherency of neuron pairs containing HVC_Xs (Fig. 4, D–F), indicating that the probability of HVC_X firing ramps up relative to the firing of other HVC neurons. More investigation of the HVC network and its developmental modulation is necessary to test these hypotheses and clarify key mechanisms of motor sequence learning.

GRANTS

This work was supported by National Science Foundation Grant IOS/BIO-1025825 (to T. A. Nick) and CAREER Grant DMS-0847749 (to D. Q. Nykamp), National Institutes of Health Grants K02-DC-008521l (to T. A. Nick) and NI5-T32-GM-008471-15, the John Merck Scholars Program (to T. A. Nick), and a University of Minnesota Dissertation Fellowship (to N. F. Day).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: N.F.D. and K.L.T. performed experiments; N.F.D., K.L.T., D.Q.N., and T.A.N. analyzed data; N.F.D. and T.A.N. prepared figures; N.F.D., K.L.T., D.Q.N., and T.A.N. approved final version of manuscript; T.A.N. edited and revised manuscript; T.A.N. conception and design of research; T.A.N. interpreted results of experiments; T.A.N. drafted manuscript.