Control of position and movement is simplified by combined muscle spindle and Golgi tendon organ feedback

Abstract

Whereas muscle spindles play a prominent role in current theories of human motor control, Golgi tendon organs (GTO) and their associated tendons are often neglected. This is surprising since there is ample evidence that both tendons and GTOs contribute importantly to neuromusculoskeletal dynamics. Using detailed musculoskeletal models, we provide evidence that simple feedback using muscle spindles alone results in very poor control of joint position and movement since muscle spindles cannot sense changes in tendon length that occur with changes in muscle force. We propose that a combination of spindle and GTO afferents can provide an estimate of muscle-tendon complex length, which can be effectively used for low-level feedback during both postural and movement tasks. The feasibility of the proposed scheme was tested using detailed musculoskeletal models of the human arm. Responses to transient and static perturbations were simulated using a 1-degree-of-freedom (DOF) model of the arm and showed that the combined feedback enabled the system to respond faster, reach steady state faster, and achieve smaller static position errors. Finally, we incorporated the proposed scheme in an optimally controlled 2-DOF model of the arm for fast point-to-point shoulder and elbow movements. Simulations showed that the proposed feedback could be easily incorporated in the optimal control framework without complicating the computation of the optimal control solution, yet greatly enhancing the system's response to perturbations. The theoretical analyses in this study might furthermore provide insight about the strong physiological couplings found between muscle spindle and GTO afferents in the human nervous system.

in this article, we provide evidence that simple low-level spinal feedback using muscle spindles alone results in very poor control of joint position and movement. In short, this is because muscle spindles cannot detect the changes in muscle-tendon complex (MTC) length that occur as a consequence of tendon stretch. We propose that afferent signals from Golgi tendon organs (GTOs) can be seen as a proxy for tendon length and that, in combination with muscle spindles, they can be effectively used for low-level feedback during both postural and movement tasks. Before describing in more detail the specific aims of this study, we first provide an overview of the current view on the role of muscle spindles and GTOs relevant to this article.

In recent years several theories have been postulated about how the central nervous system (CNS) controls position and movement. These theories all share the common premise that to control movements, the CNS must have information about the current state of the musculoskeletal system. Some of this information is provided by the many sensory afferent signals available to the CNS. Furthermore, most theories of motor control postulate that the CNS has knowledge about static properties of the musculoskeletal system, like the force-length relationship of muscles and their moment arm-angle relationships or torque-angle relationships (e.g., Bizzi and Abend 1983; Feldman 1986). In addition, some theories also propose that the CNS contains internal models of the dynamics of the musculoskeletal system and therefore also requires knowledge about, for example, inertia of limb segments and force-velocity relationships of muscles (e.g., Kawato et al. 1987; Miall et al. 1993; Todorov 2004). Although it is currently unclear how posture and movement are controlled, given the complexity of the musculoskeletal system, it is clear that a vast amount of knowledge about the neuromusculoskeletal system needs to be “represented,” “stored,” or “coded” within the CNS.

In the field of human movement control, muscle spindles take a prominent role. Muscle spindles provide information related to the length and contraction velocity of muscle fibers (e.g., Crowe and Matthews 1964; Edin and Vallbo 1990; Prochazka 1981; Prochazka and Gorassini 1998b). It has been shown that direct negative feedback of spindle afferents enhances the dynamic stiffness and damping of muscle and as such helps to stabilize posture and movement (e.g., Hogan 1985; Nichols and Houk 1976). Furthermore, several theories of motor control propose that muscle spindle information is used by the CNS to generate muscle activation patterns in a predictive manner (e.g., Kawato 1999; Wolpert et al. 1995, 1998).

Another sensor found in the MTC, the GTO, provides a signal related to the tension of tendons (e.g., Appenteng and Prochazka 1984; Prochazka 1981; Prochazka and Gorassini 1998a; Prochazka and Wand 1980) but is often neglected in theories of movement control. GTOs are commonly found in MTCs examined across a wide variety of animals. For example, feline studies show GTO-to-spindle count ratios ranging from ∼1 for hindlimb and tail muscles to ∼0.2 for jaw muscles (see for review Jami 1992). There are few reports in the literature of GTO counts in human muscles. One study examining human m. palmaris longus and m. plantaris reported GTOs in all 40 investigated myotendinous junctions (Jozsa et al. 1993), and another study reported GTOs in all 10 hand flexor tendons investigated (Zimny et al. 1989).

Presumably, GTOs play a less prominent role in current theories of movement control because their function is less understood. For example, it is even disputed whether the feedback of GTOs is positive or negative (e.g., Cleland et al. 1982; Duysens and Pearson 1980; Prochazka et al. 1997a, 1997b). Recent research provides evidence that the feedback of GTOs results in a positive force feedback (Donelan and Pearson 2004; Parkinson and McDonagh 2006; Pratt 1995; Van Doornik et al. 2011). Another possible reason why GTOs receive less attention in movement control theories is that tendons, in which GTOs are situated, are often ignored altogether in associated mathematical models of the musculoskeletal system (e.g., Gribble and Ostry 2000; Katayama and Kawato 1993; Liu and Todorov 2007; Shadmehr and Mussa-Ivaldi 1994; Uno et al. 1989).

Evidence is provided in the literature that both tendons and GTO information play an important role in the dynamics of the musculoskeletal system. For example, it has been shown that tendons play a major role in the behavior of a muscle because they beneficially influence the dynamic reaction of a muscle to external perturbations (Brown and Loeb 1997; Houk 1979; Kistemaker and Rozendaal 2011; van Soest and Bobbert 1993). Albeit task-dependent, tendons greatly enhance the mechanical efficiency of movements by storing and releasing energy (e.g., Alexander 1984; Alexander and Bennet-Clark 1977). A clear example is the hopping of kangaroos (Bennett and Taylor 1995; McGowan et al. 2008b; Morgan et al. 1978) and wallabies (Biewener and Baudinette 1995; McGowan et al. 2005, 2008a), which would not be possible without the presence of elastic tendons storing and releasing energy. Estimates based on experimental data indicate a 50% reduction in energy requirements in steady-state hopping in both red kangaroos (Cavagna and Citterio 1974) and tammar wallabies (Biewener and Baudinette 1995). Also, without tendons, the maximal shortening speed of the total muscle (from now on referred to as the MTC) would be limited by the maximal shortening velocity of the muscle fibers. With tendons, the maximal shortening velocity of the MTC can well exceed that of the muscle fibers and as such allow mechanical work even at high velocities, for example, when kicking or throwing a ball (e.g., Joris et al. 1985). Tendons also play a role in very fast muscle stretches (e.g., Alexander 2002; Cook and McDonagh 1996; Hof 1998; Kistemaker and Rozendaal 2011; Rack and Westbury 1984) that occur, for example, when landing from a height. Without tendons, muscle stretch would be completely determined by the (very high) angular velocity during impact, and even a small drop would lead to severe muscle damage.

Direct spinal force feedback based on GTO information has been proposed as a mechanism to enhance dynamic muscle stiffness (e.g., Houk 1979; Nichols and Houk 1976; van Soest and Rozendaal 2008). It has also been suggested that GTO feedback plays a role in linearizing muscle stiffness by compensating for nonlinear muscle properties (Nichols and Houk 1976; Windhorst 2007). Positive GTO feedback has indeed been observed experimentally in some postural tasks (Dietz et al. 1992; Pratt 1995) and has been shown to contribute to the placing reaction (Prochazka et al. 1997a, 1997b). Furthermore, it has been suggested that (positive) GTO feedback may play a role in central pattern generators (e.g., Patrick 1996). These results suggest that it is important to include both tendons and GTO feedback in motor control models.

The presence of compliant tendons enhances the dynamic behavior of the musculoskeletal plant but, in general, will also complicate its control (Scott and Loeb 1994). In “traditional” position (servo) control, muscle spindle information is used in a feedback loop operating on the difference between measured muscle length (and velocity) and the muscle length at a desired joint position. In such a situation, spindles are thought to code effectively for the length/velocity of the MTC. However, in the presence of compliant tendons, such simple control is unlikely to be effective. A tendon in the musculoskeletal system stretches as a consequence of the contractile and skeletal forces exerted on it. Therefore, there is no one-to-one relationship between muscle contractile element length (l_CE) and muscle-tendon complex length (l_MTC). In other words, any given l_MTC can arise from an infinite set of combinations of l_CE and tendon length [l_SE; from now on we use the term series elastic element (SE) as shorthand for all the tendinous tissue that is in series with the contractile element (CE)]. Therefore, muscle spindles by themselves cannot code for joint position.

In this study we propose that GTOs, in combination with muscle spindles, may be used by the CNS for low-level spinal feedback that stabilizes both posture and movement. As stated before, GTOs are generally seen as force sensors. However, since the tendon behavior is largely elastic (tendon length is related to tendon force), signals from GTOs also provide information about tendon length. As such, when used in a feedback loop, GTOs can be used to signal the muscle force-dependent stretch of the tendon. In particular, in this article we propose that the information provided by the muscle spindle combined with that of the GTO can effectively be used to provide information about the l_MTC and hence can be used to signal joint position. Interestingly, recent human physiological data obtained during grasping provided evidence that (change in) l_MTC is poorly correlated with muscle spindle discharge but well correlated with combined spindle and GTO discharge (Dimitriou and Edin 2008).

The main purpose of this study was to explore the feasibility of combined spindle and GTO information for low-level spinal feedback in the control of posture and movement of the musculoskeletal system. It should be noted that we are not simply evaluating the merits of feedback vs. no feedback (obviously, the merits of feedback have been documented widely) or simply adding more feedback variables. In this study we specifically assess whether GTO feedback can be used in a novel way, namely, as a proxy for tendon length, to compensate for the errors that would arise from failing to take account of muscle force-dependent changes in tendon length.

First, we carried out a simple mathematical analysis to assess the static error that arises from controlling angular position of a limb on the basis of muscle spindle information only while ignoring tendon stretch. We then used a musculoskeletal model of the arm, shown previously to adequately describe the static and dynamic behavior of the real system (Kistemaker et al. 2005, 2006, 2007a), to assess the response quality when feeding back either muscle spindle afferents alone (while ignoring tendon compliance) or a combination of spindle and GTO afferents. We assessed the dynamical response of the model to 1) a position perturbation, 2) a sudden change in cocontraction of antagonistic muscles, and 3) an external constant torque perturbation. Finally, we incorporated the proposed feedback scheme in an optimally controlled 2-DOF model of the arm capable of simulating fast shoulder and elbow movements. The feasibility of the feedback was assessed by comparing simulated movements with those observed experimentally and assessing the dynamical responses to transient torque perturbations.

METHODS

Ethics Statement

All subjects reported no history of visual, neurological, or musculoskeletal disorder. Written informed consent was obtained from each subject before participation. All procedures were approved by the University of Western Ontario Research Ethics Board.

Experimental Setup

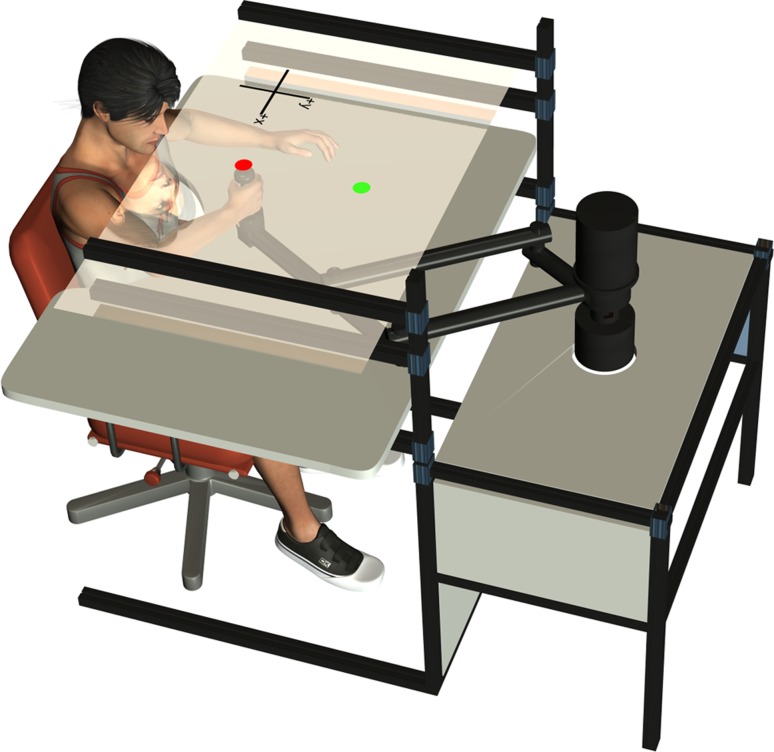
The experimental setup was similar to that used in a previous study (Kistemaker et al. 2010; see Fig. 1). In short, subjects made movements while grasping the handle of an InMotion robotic manipulandum (Interactive Motion Technologies, Cambridge, MA). The right arm was supported by a custom-made air sled, which expelled compressed air beneath the sled to minimize surface friction. The subject's arm and the manipulandum were beneath a semi-silvered mirror, which reflected visual targets projected by a computer-controlled liquid crystal display (LCD) screen. Visual targets were projected that appeared to lie in the same plane as the hand. Eight right-handed male subjects performed 100 center-out movements to a visual target that was 30 cm away from the start position (see Fig. 1). A small dot representing their hand position was plotted during the experiment. When the target circle (2-cm diameter) was reached, the target changed color to provide feedback indicating that the movement was well-timed (between 300 and 500 ms), too slow, or too fast. Positional and force data were sampled at 600 Hz and were filtered afterward using a fourth-order bidirectional Butterworth filter with a cutoff frequency of 15 Hz.

Fig. 1.

Experimental set up. Visual targets (red = start and green = final) were projected on a semi-silvered mirror with the use of a liquid crystal display (LCD) monitor placed 15 cm above the mirror (monitor not shown).

Musculoskeletal Models of the Arm

Overview.

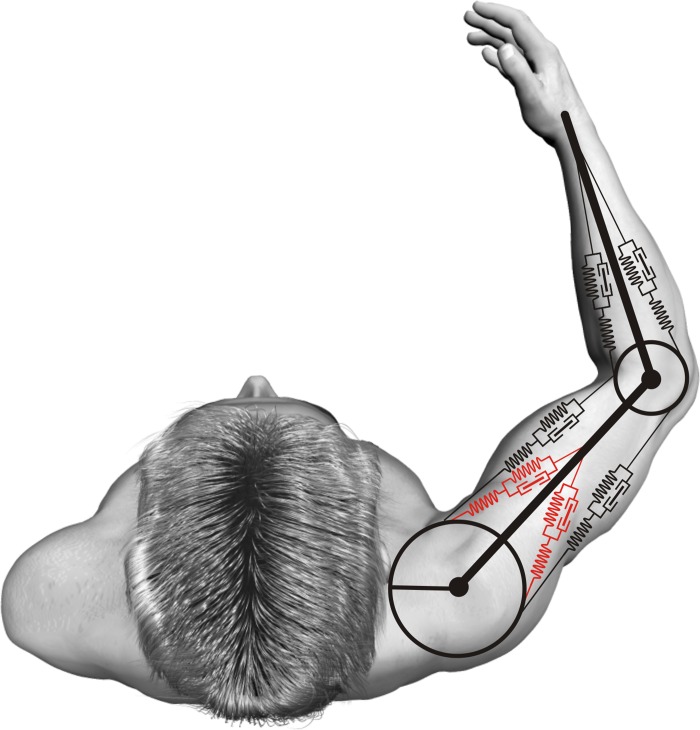
The 1-DOF and 2-DOF musculoskeletal models of the arm used in this study (Fig. 2) have been described in full detail elsewhere (Kistemaker et al. 2006, 2007b, 2010; see also van Soest and Bobbert 1993). In short, the 1-DOF model consisted of two rigid segments (representing forearm and upper arm) interconnected by two hinge joints (representing glenohumeral joint and elbow joint) and driven by four lumped muscle models. The 1-DOF model was restricted to move in a horizontal plane at shoulder height while the upper arm was fixed at a position of 45°, identical to the musculoskeletal model described previously (Kistemaker et al. 2006, 2007b).

Fig. 2.

Schematic overview of the musculoskeletal models used. The 1-degree-of-freedom (1-DOF) model was driven by four Hill-type muscle-tendon models. The shoulder joint was fixed at 45° from the positive x-axis, and 0° elbow position was defined as fully stretched. For the simulations with the optimally controlled arm with combined spindle and Golgi tendon organ (GTO) feedback, the model was expanded to have 2 DOF (shoulder and elbow rotations) and 2 monoarticular shoulder muscles (depicted in red).

The muscles modeled were a monoarticular elbow flexor (representing m. brachioradialis, m. brachialis, m. pronator teres, and m. extensor carpi radialis), a monoarticular elbow extensor (representing m. triceps brachii caput laterale, m. triceps brachii caput mediale, m. anconeus, and m. extensor carpi ulnaris), a biarticular elbow flexor (representing m. biceps brachii caput longum and caput breve) and a biarticular elbow extensor (representing m. triceps brachii caput longum). The 2-DOF musculoskeletal model was also allowed to rotate in the shoulder and was extended to also include two monoarticular shoulder muscles: a monoarticular shoulder flexor (representing m. pectoralis major pars clavicularis and sternocostalis and the ventral part of m. deltoideus) and a monoarticular shoulder extensor (representing m. infraspinatus, m. teres minor, and the dorsal part of m. deltoideus).

Activation and contraction dynamics.

The modeled muscle units consisted of a model of activation dynamics and contraction dynamics and are described briefly below. Activation dynamics describing the relation between neural input to the muscle (STIM) and active state (q), here defined as the relative amount of Ca²⁺ bound to troponin C (Ebashi and Endo 1968), were modeled according to Hatze (1984; see also Kistemaker et al. 2005). This model of activation dynamics first describes how γ̇_rel changes as a function of γ_rel, the relative amount of intracellular Ca²⁺; STIM, the normalized α-motoneuron firing frequency; and rate constant m:

$${\dot{\gamma }}_{rel}=m·\left(STIM-{\gamma }_{rel}\right).$$

The model secondly nonlinearly relates active state q to γ_rel and l_CE:

$$q=f\left({\gamma }_{rel},l_{CE}\right).$$

This last step accounts for the CE length-dependent [Ca²⁺] sensitivity that has been shown to adequately predict the shifts in optimum muscle length as a function of activation level (Kistemaker et al. 2005).

Contraction dynamics describe how the muscle delivers force depending on q, l_CE, and the CE contraction velocity (v_CE) and were modeled in two steps. First, the isometric force of the CE was calculated on the basis of changes in the actin myosin overlap function and was modeled as an inverted parabola:

$$F\left(l_{CE}\right)=-a·l_{CE\_rel}^2=2a·l_{CE\_rel}-a+1,$$

where a = 1/width², the width of the force-length relationship. This force is multiplied by q and thus together with the activation dynamics describes the muscle activation-dependent optimum CE lengths.

Second, the force is made nonlinearly dependent on v_CE. The eccentric force only depends on v_CE and was modeled using a hyperbola. For the concentric part, a classical Hill equation is used for which, on the basis of physiological data, maximal shortening speed is made dependent on q and l_CE:

$$F\left(v_{CE}\right)=f\left(v_{CE},l_{CE,}q\right).$$

The muscle-specific parameters are shown in Table 1. For a detailed overview of all modeled steps and all non-muscle-specific parameters, please refer to our previous papers (Kistemaker et al. 2006, 2007a, 2010).

Table 1.

Muscle-specific parameters

Muscle	Fmax, N	lCE_opt, m	lSE_0, m	lPE_0, m	a0, m	a1e, m	a1s, m	a2e, m
MEF	1,422	0.092	0.172	0.129	0.286	−0.014	0	−3.96E−3
MEE	1,549	0.093	0.187	0.130	0.236	0.025	0	−2.16E−3
BEF	414	0.137	0.204	0.192	0.333	−0.016	−0.030	−5.73E−3
BEE	603	0.127	0.217	0.178	0.299	0.030	0.030	−3.18E−3
MSF	838	0.134	0.039	0.187	0.151	0	0.03	0
MSE	1,207	0.140	0.066	0.196	0.232	0	−0.03	0

F_max, maximal isometric contractile element (CE) force; l_{CE_opt}, optimum CE length for maximal isometric force at maximal activation; l_{SE_0}, series elastic element slack length; l_{PE_0}, parallel elastic element slack length; a₀, a_1e, a_1s, and a_2e, parameters describing muscle-tendon complex length as a function of joint angle; MEF, monoarticular elbow flexor; MEE, monoarticular elbow extensor; BEF, biarticular elbow flexor; BEE, biarticular elbow extensor; MSF, monoarticular shoulder flexor; MSE, monoarticular shoulder extensor.

Tendon behavior.

The length of the tendon only depends on the force exerted on it: it typically behaves like a nonlinear (quadratic) spring (Gerus et al. 2011; Lieber et al. 1991; Maganaris and Paul 1999; Zajac 1989) and was modeled as such. The tendon is at slack length (l_{SE_0}) when the muscle is not delivering any force and is assumed to be stretched to 4–6% (5% was used in our model) when the muscle delivers its maximal isometric force (e.g., Maganaris and Paul 1999; Zajac 1989). The tendon force (F_SE) was modeled as half a parabola to ensure that the tendon is only delivering force when stretched:

$$F_{SE}=k_{SE}·{\left[\max \left(0,l_{SE}-l_{SE\_0}\right)\right]}^2,$$ (1)

where f = max(0, x) means that for values of x less than 0, f = 0, and for values of x greater than 0, f = (x). The value of k_SE was chosen such that it is 105% of l_{SE_0} at maximal isometric force.

MTC length.

The MTC lengths (l_MTC) were modeled as second-order polynomials depending on elbow (φ_e) and shoulder position (φ_s):

$$l_{MTC}\left({\varphi }_e,{\varphi }_s\right)=a_0+a_{1e}{\varphi }_e+a_{2e}{\varphi }_e^2+a_{1s}{\varphi }_s,$$ (2)

where a_1e, a_2e, and a_1s per muscle were based on cadaver data literature (Murray et al. 1995, 2000; Nijhof and Kouwenhoven 2000) obtained using the tendon displacement method (see Grieve et al. 1978). Values for a₀, representing l_MTC at φ_e = φ_s = 0, were chosen such that the optimum angle for maximal isometric moment (also dependent on the force-length relationship) was consistent with the literature (Kistemaker et al. 2007a).

Relation Between Changes in MTC Length and Joint Position

By using the fact that the work done by a muscle can be expressed in terms of either muscle force or muscle torque, the relation between the change in MTC length and the change in joint position (φ) can be found (see also An et al. 1984; Shadmehr and Wise 2005):

$${\displaystyle \int d{l}_{MTC}}={\displaystyle \int arm·d\varphi }.$$ (3)

This relation is used later to investigate the static errors that arise when using spindle feedback only while neglecting tendon compliance.

Incorporating Feedback in the Musculoskeletal Model

The muscle model described above was used to test the feasibility of feedback of spindles alone and in combination with GTOs. We used the controlled model to simulate responses to transient position and static torque perturbations. Below we describe in detail how the feedback is incorporated in the control of the model.

Muscle spindle feedback.

In this study we assumed that muscle spindles provide accurate information about the length and contraction velocity of the CE (see discussion). This is used to essentially feedback negatively the difference between the reference and actual (time delayed) CE lengths plus feedback of CE contraction velocities. The only input to the muscles are the muscle activations, STIM(t):

$$STIM\left(t\right)=sti{m}_{open}\left(t\right)+k_p\left[l_{CEref}\left(t\right)-l_{CE}\left(\Delta t\right)\right]+k_d\left[-V_{CE}\left(\Delta t\right)\right],$$ (4)

where stim_open represents the open-loop muscle activations, k_p and k_d are two optimized feedback gains (see below), l_{CE_ref} are the reference CE lengths of the muscles involved, and Δt is the time minus time delay (25 ms). By cocontracting muscles, as defined by stim_open, the CNS can influence the low-frequency stiffness and damping of a joint (see below).

As stated in the Introduction, due to tendon compliance there is no one-to-one mapping between CE length and joint position: the CE length depends on the joint position and the forces generated by the muscle. To investigate the result of simply neglecting tendon compliance, we have chosen to set the reference CE lengths to l_{CE_opt} (see results and discussion).

Combined muscle spindle and GTO feedback.

It has been shown that the (ensemble of) afferent firing activity of GTOs is proportional to the (total muscle) force in the tendon (e.g., Appenteng and Prochazka 1984; Prochazka 1981; Prochazka and Gorassini 1998a; Prochazka and Wand 1980). Because tendons are passive structures, this also means that the information provided by the GTOs is, albeit nonlinearly, one-to-one related to the length of the tendon, and for the proposed controller it is assumed that this relationship between GTO firing rate and l_SE is known (see discussion). Furthermore, it is assumed that CNS has knowledge about the one-to-one mapping from (desired) joint position to l_MTC, in this case the relationship formulated in Eq. 2. Again, the only input to the muscles was STIM:

$$STIM\left(t\right)=sti{m}_{open}\left(t\right)+k_p\left[l_{MTC\_ref}\left(t\right)-l_{CE}\left(\Delta t\right)-l_{SE}\left(\Delta t\right)\right]+k_d\left[-V_{CE}\left(\Delta t\right)\right].$$ (5)

Alternatively, assuming that a tendon behaves as a quadratic spring (see Tendon behavior), this can be rewritten in terms of muscle force:

$$STIM\left(t\right)=sti{m}_{open}\left(t\right)+k_p\left[l_{MTC\_ref}\left(t\right)-l_{CE}\left(\Delta t\right)-\sqrt{\frac{F_{SE}}{k_{SE}}}\left(\Delta t\right)\right]+k_d\left[-V_{CE}\left(\Delta t\right)\right].$$ (5a)

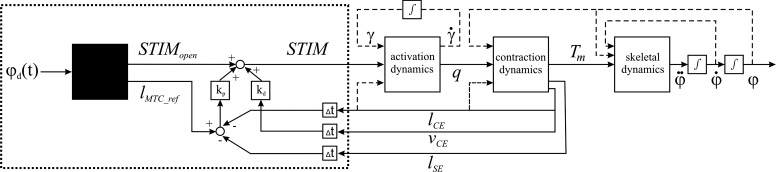
Figure 3 shows a flow chart of the controlled musculoskeletal model.

Fig. 3.

Flow chart of the controlled musculoskeletal model. The area within the dotted box refers to the modeled parts of the peripheral and central nervous system, and the rest to the musculoskeletal system. The solid lines refer to muscle inputs and feedback loops. The dashed lines refer to the muscle states influencing the activation contraction and skeletal dynamics. See text for definitions.

Optimal Control

It has been suggested in the literature that feedforward controllers, such as optimal controllers, suffer from the “posture-movement problem” or “Von Holst paradox,” which refers to the question of how movements from an initial position to a new position are produced without triggering resistance from postural reflexes and posture-stabilizing structures (Ostry and Feldman 2003; see discussion). We tested whether the suggested feedback of spindles and GTOs can be incorporated in optimal control (OC) such that 1) the controller does not suffer from the posture-movement problem, 2) it increases the resistance to perturbations like “normal” negative feedback does, and 3) it does not increase the computational demands of finding an open-loop OC muscle activation pattern.

Optimal activations (stim_OC) were found for the six muscle-tendon units of the 2-DOF musculoskeletal model for a fast “center-out” movement of the hand over 30 cm in 400 ms, similar to task of the 8 subjects. The musculoskeletal model was identical to that described before, apart from one single parameter that defined the difference in concentric and eccentric slope of the force-velocity relationship at zero CE contraction velocity. This was originally set such that the slope of the eccentric part was twice that of the concentric part (see also van Soest et al. 1993). Such discontinuity in the derivative of the force-velocity relationship was found to be problematic for the OC solver and was set such that the slopes were equal. (Forward simulations with both slope factors for the movements investigated here showed only very subtle differences.)

The OC solver identified the optimal muscle activations minimizing control effort. Such a criterion minimizes the sum of the time integral of the squared muscle stimulations, which minimizes movement variability in the presence of signal-dependent noise (Diedrichsen et al. 2010) and has been used successfully to reproduce various human movements (e.g., Diedrichsen 2007; Nagengast et al. 2009).

$$J={\displaystyle \sum _{n=1}^6{\displaystyle {\int }_0^{T}sti{m}_{OC\_n}\left(t\right)·sti{m}_{OC\_n}\left(t\right)\prime dt,}}$$ (6)

where stim_{OC_n}(t) is the activation of muscle n and T is the total movement time. Boundary constraints were the start positions of the shoulder and elbow joints (35° and 172°), desired end positions (64° and 127°), stim_OC(t = 0) = 0, and all state derivatives equal to zero at the start and end of the movement (T = 0.4 s).

The OC problem for the cost function J(stim_OC) was transformed into a discrete parameter optimization using 1) the boundary constraints mentioned above, 2) the temporal discretization of the dynamical constraints, and 3) temporal discretization of stim_OC(t). The dynamical constraints for each of the 50 time points (collocation points) are equality constraints representing the differential equations on the one side and a Euler approximation of the state derivatives on the other: the Euler discretization scheme (Betts 2001). As an example of the general approach, we consider the dynamic constraint for the activation dynamics of the nth collocation point, t_n. The Euler approximation for γ̇_rel is

$${\dot{\gamma }}_{rel}\left(t_n\right)=\frac{{\gamma }_{rel}\left(t_{n+1}\right)-{\gamma }_{rel}\left(t_n\right)}{\Delta t}.$$

This approximation of γ̇_rel should satisfy the differential equation describing the activation dynamics (see above), yielding the following constraint equation:

$$\frac{{\gamma }_{rel}\left(t_{n+1}\right)-{\gamma }_{rel}\left(t_n\right)}{\Delta t}=m·\left[STIM-{\gamma }_{rel}\left(t_n\right)\right].$$

The resulting nonlinear programming problem containing all 50 collocation points and all dynamical equations was solved using a sparse nonlinear optimal controller embedded in MATLAB (SNOPT; TOMLAB Optimization, Pullman, WA). SNOPT is a sequential quadratic programming algorithm for solving large-scale sparse nonlinear programming problems (Gill et al. 2002). The OC optimization was checked by running forward simulations using the identified stim_OC, yielding only very small differences between the states of the musculoskeletal model at the 50 collocation points and the states at the same time points obtained from the forward simulations (see also Ackermann and van den Bogert 2010).

The identified OC activation pattern was subsequently used in forward simulations that incorporated both the stim_OC and feedback from spindles and GTOs. Note that the feedback loops were not an integral part of the musculoskeletal model while identifying the stim_OC. The optimization explained above only dealt with the open-loop part of the musculoskeletal model. During the forward simulations, the total muscle activation equaled the stim_OC plus the feedback components:

$$STIM\left(t\right)=STI{M}_{OC}\left(t\right)+k_p\left[l_{MTC\_ref}\left(t\right)-l_{CE}\left(\Delta t\right)-l_{SE}\left(\Delta t\right)\right]+k_d\left[-V_{CE}\left(\Delta t\right)\right].$$ (7)

This scheme is identical to that described by Eqs. 5 and 5a and depicted in Fig. 3; only stim_open was replaced by stim_OC. Reference MTC lengths (l_{MTC_ref}) were the MTC lengths accompanying a minimal jerk trajectory (joint based) from the start positions to the target positions. We computed the minimal jerk trajectories of the shoulder and elbow joints, and for each time point l_MTC was calculated using Eq. 2.

Importantly, we deliberately chose not to use the actual optimized movement trajectory as the reference trajectory to reveal if a similar (but not exactly the same) movement could be adequately used as reference trajectory. Accurately predicting a movement on the basis of open-loop muscle commands in a feedforward manner may computationally be hard. Therefore, if the suggested controller would be able to accurately control movements with the use of a closely resembling, but not identical, reference joint position trajectory, it would further minimize computational demands and enhance the robustness of the suggested feedback. Obviously, using the feedforward computed actual movement as a reference movement would make the results better, or identical at worst.

The onset of the minimal jerk trajectory was chosen such that it best fitted the simulated movement in the absence of feedback. Simulations were carried out with and without torque perturbations. The perturbations were half-period sinusoids with an amplitude of either 10 or −10 N·m and a half-period of 0.015 s. Note that stim_OC will be the same for all simulated movements and thus independent of the type of feedback and the presence or absence of perturbations.

To summarize the key steps of the controller: 1) find the stim_OC that minimizes the cost function (Eq. 6) for moving the arm from the start to the end position; 2) use minimal jerk trajectories for shoulder and elbow joint movements from start to end position and convert them to l_{MTC_ref}; and 3) send out stim_OC to the muscles and add the feedback based on reference MTC lengths, time-delayed SE length, CE length, and CE velocity.

Cocontraction Level

An important facet of motor control that has been recently examined in the literature is the neural control of limb stiffness through cocontraction (e.g., Franklin et al. 2007; Gribble et al. 2003; Milner 2002; Osu and Gomi 1999). The challenges posed by the presence of a series elastic element (tendon) described here not only apply to the control of movement but pose an equal challenge to the control of limb stiffness through cocontraction. To examine this issue, we also performed simulations in which the desired position of the limb remains constant but cocontraction levels are increased from a low (near zero) level to a high level representing maximal low-frequency stiffness (16 N·m/rad). Cocontraction was modulated by changing stim_open such that the net torque in the desired position remained zero while the low-frequency stiffness was maximized.

Position and Torque Perturbations

The 1-DOF model was used to predict the responses of the model without any feedback, with only spindle feedback, and with spindle plus GTO feedback to positional and torque perturbations. For the positional perturbation we applied a sudden step in joint position. During the whole response, open-loop stimulation was kept constant with a cocontraction level leading to a low-frequency stiffness level of 16 N·m/rad.

The response of the 1-DOF model to static torque perturbation also was simulated using a cocontraction level leading to a low-frequency stiffness of 16 N·m/rad with a constant perturbing torque, starting at t = 0, of either −3 or 5 N·m. The 2-DOF torque perturbations were applied to the shoulder joint 0.2 s after perturbation onset. The transient torque perturbation was a half-sinusoid with an amplitude of either −10 or +10 N·m and a half-period of 0.015 s (thus the total duration of the perturbation was 0.015 s). The stim_OC as a function of time was identical for all simulated 2-DOF movements.

The simulations depicted in Fig. 9 are similar to those in Fig. 8 (see results), but in this case after 0.20 s of the onset of the movement, a transient torque perturbation was applied to the shoulder joint (note again that stim_OC was identical for all simulated movements). This perturbation consisted of a half-sinusoid with an amplitude of −10 N·m and a half-period of 0.015 s.

Fig. 9.

Simulated responses to torque perturbations during fast point-to-point movements. Simulations of musculoskeletal model with the OC muscle activation pattern (gray area) are shown. This unperturbed movement is identical to that depicted in blue in Fig. 8 and was plotted as a reference. The blue line represents the same system (i.e., without feedback) but was perturbed with a 15-ms half-sinusoid torque 0.2 s after movement onset (depicted by the vertical line). The movement does not arrive at the target. Yet, with feedback of spindle and GTO information, movement is restored to the desired end point. Note that simulations with spindle feedback only were omitted because the model was not able to arrive at the target location without any perturbations (see Fig. 8).

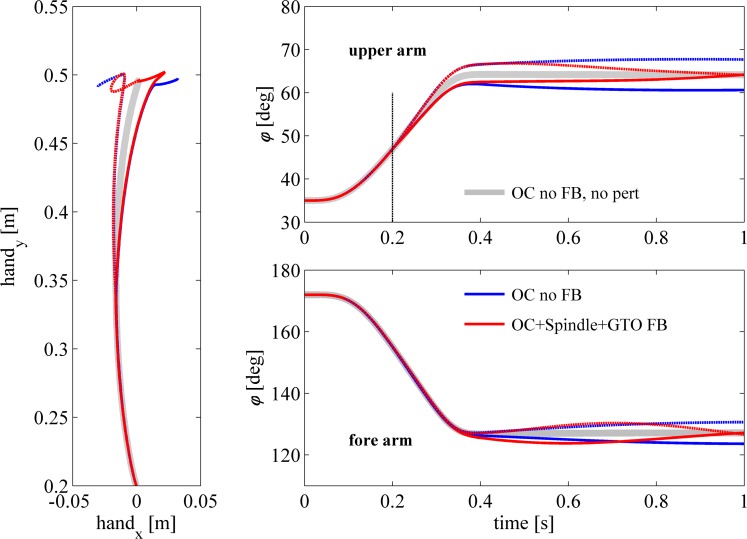
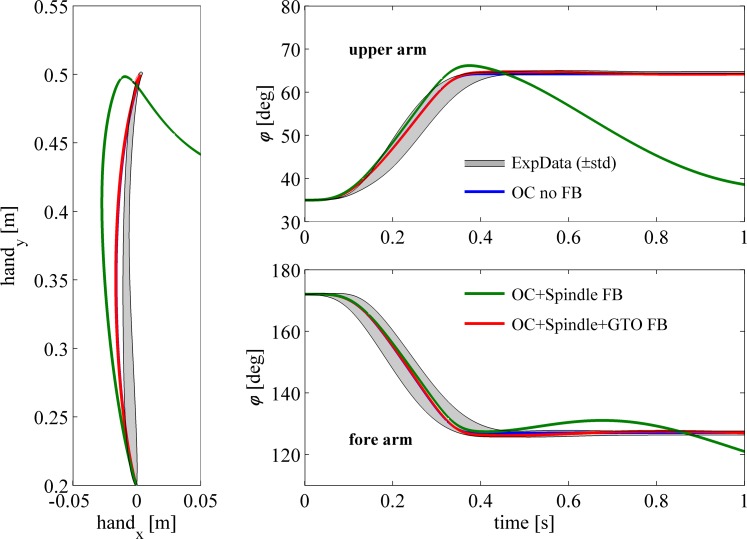
Fig. 8.

Experimental data and model simulations of fast point-to-point movements. Experimental data (gray area; mean ± SD) and simulated data of fast 2-DOF arm movements are shown for the hand path (left), the shoulder position (top right), and the elbow position (bottom right). Simulations of the musculoskeletal model with the optimal control (OC) muscle activation pattern (blue lines) show good resemblance with the movement observed experimentally (note that because of overlap, the blue line is hardly visible). Adding feedback of only muscle spindles caused the movement to deviate from the optimal path from the onset of the movement and caused the model to not arrive close to the target location. When GTO information was used in combination with muscle spindles, movement was very similar to the model without feedback and the experimental data.

Optimization of Feedback Gains

We chose to be very conservative with respect to the optimization of the feedback gains. This was done to test the robustness of the suggested feedback without introducing (many) feedback gains optimized specifically for a certain type of perturbation. We 1) chose the feedback gains for k_p and k_d to be identical for all muscles, 2) only modeled homonymous feedback (i.e., feedback of a muscle only influences the activation of that same muscle), 3) kept feedback gains constant during the simulations, and 4) only optimized k_p and k_d for one response and left them unchanged in all other simulated responses.

For the 1-DOF model, the feedback gains k_p and k_d (see Eq. 5) were optimized only for the sudden change in cocontraction level (k_p = −5.50 and k_d = −0.04). In particular, the gains were selected such that the time integral of the squared deviation of the joint angle from the desired joint angle (60°) was minimal.

For the 2-DOF model, after the OC open-loop muscle activations were identified, feedback gains for the center-out task were optimized by minimizing the time from onset to reaching the shoulder and elbow joint positions within 0.02 rad (≈1°) of the target positions with angular velocities <0.2 rad/s. To get an impression of the sensitivity of the feedback gains set, the gains were only optimized for a positive torque perturbation described before (k_p = −2.08 and k_d = −0.003), and thus not to both perturbations.

Computations

All simulations and optimizations were run under MATLAB. The optimal values for the feedback gains were identified using a Nelder-Mead simplex search method (Lagarias et al. 1998), and the stim_open defining the cocontraction level maximizing maximal low-frequency elbow stiffness was identified using a sequential dynamic programming algorithm. Optimal control muscle activations were computed using a large-scale sparse linear and nonlinear programming solver (SNOPT, TOMLAB).

RESULTS

Static Errors Under Spindle Feedback Control

As mentioned in methods, tendons typically stretch about 5% at maximal isometric force. This means that, for example, the tendon of a biceps with a slack length of ∼20 cm (see Table 1) can stretch about 1 cm. Thus, at a given fixed CE length, the MTC length of a biceps muscle can change up to 1 cm due to stretches in the tendon, depending on the forces exerted on it. Changes in tendon length at a fixed CE length, and consequent changes in joint position, are not sensed by the muscle spindles since the CE length remains unchanged.

To investigate the importance of this 1-cm change in MTC length, we used Eq. 3 to calculate the range of elbow positions at a constant CE length (i.e., CE optimum length) with a tendon that ranges from its slack length (muscle delivers no force) to being maximally stretched (muscle delivers its maximal isometric force). These changes in joint position, shown in Fig. 4, are the smallest static errors that one can expect when the position of the joint is controlled by feedback on the basis of muscle spindle only while ignoring the tendon stretch. If a position against gravity is to be maintained through any kind of positional feedback, there will be an additional static error depending on the feedback gain set. The actual angle at which the arm stays put is that angle for which the desired minus actual muscle length multiplied by the feedback gain leads to a muscle torque that exactly counteracts the gravitational torque. This difference in actual state and desired state gets smaller for higher feedback gains (and is zero for an infinitely high gain). In the real system, feedback gains have an upper limit due to time delays and thus would lead to an additional static error to be added to those shown in Fig. 4.

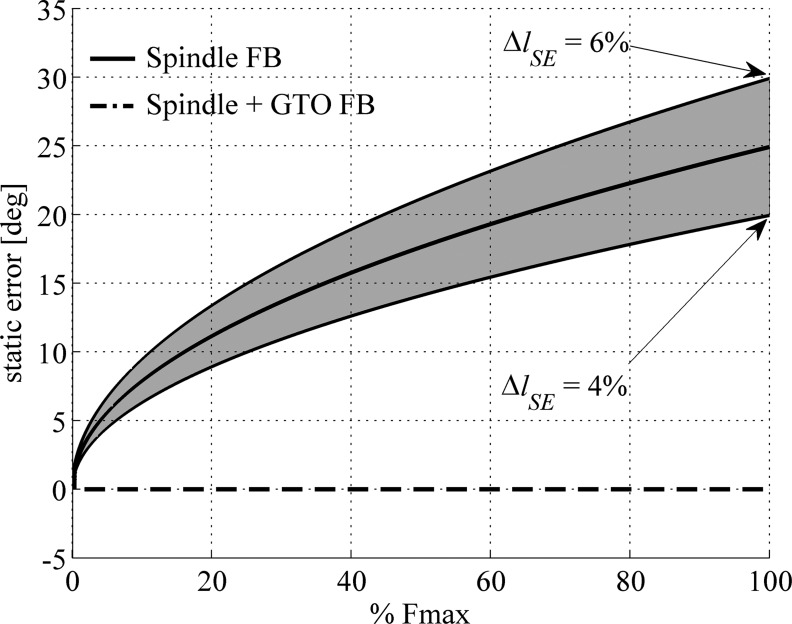
Fig. 4.

Static error with spindle feedback only. Graph shows expected minimal static error in elbow joint position with the use of feedback control based on muscle spindles only. Data are based on contractile element (CE) length feedback of the biceps muscle only. Reference positions were 45° shoulder position and 90° elbow position. When not activated, at these positions the biarticular biceps muscle is at optimum length and has an estimated moment arm at the elbow of 0.023 m. The muscle parameter values were identical to those in Kistemaker et al. (2006): maximal isometric force (F_max) = 414 N, optimum length (l_CE) = 0.137 m, slack length (l_SE) = 0.204 m. Force of the series elastic element (SE) was modeled as a quadratric spring with 4% (bottom line), 5% (middle line), or 6% (top line) SE stretch (Δl_SE) at F_max. FB, feedback.

When looking at Fig. 4, two important observations can be made. First, even though the tendon is only stretched over 1 cm at maximal isometric force (thus maximally activated), the static error is about 25°. This surprisingly large error can be readily understood from Eq. 3, because the change in joint position equals the change in MTC length divided by the moment arm of the muscle, and moment arms are in general small (about 0.023 m in this case). Second, due to the nonlinear characteristics (tendon stiffness is low at low muscle forces; Maganaris and Paul 1999; Zajac 1989), the error in elbow positions is substantial even at low-to-moderate muscle forces that, for example, occur when small weights are held against gravity. This result implies that due to tendon compliance, simple low-level spinal control of angular position (and hence movement) of a realistic musculoskeletal system with the use of spindle feedback alone is not feasible.

Responses to Position Perturbation

To assess the feedback of either muscle spindles alone or the combination of spindles and GTOs, we simulated model responses to transient positional perturbations. Figure 5 shows the simulated responses to a fast transient position perturbation from an elbow position of 60° to a position of 30°. The blue line represents the perturbation response without any feedback and thus reflects only the muscle viscoelastic properties. With feedback from only the muscle spindles (green lines), the model responds much faster yet introduces large static errors depending on the feedback gain that was set: the higher the gain, the higher the error. Only when the gain was set to zero was static error zero. The error was additionally dependent on the forces applied by the muscles and, more importantly, the reference CE lengths set (in this case l_{CE_opt}; see methods and discussion). These errors were qualitatively the same for all other perturbations and are not shown for the other 1-DOF perturbations.

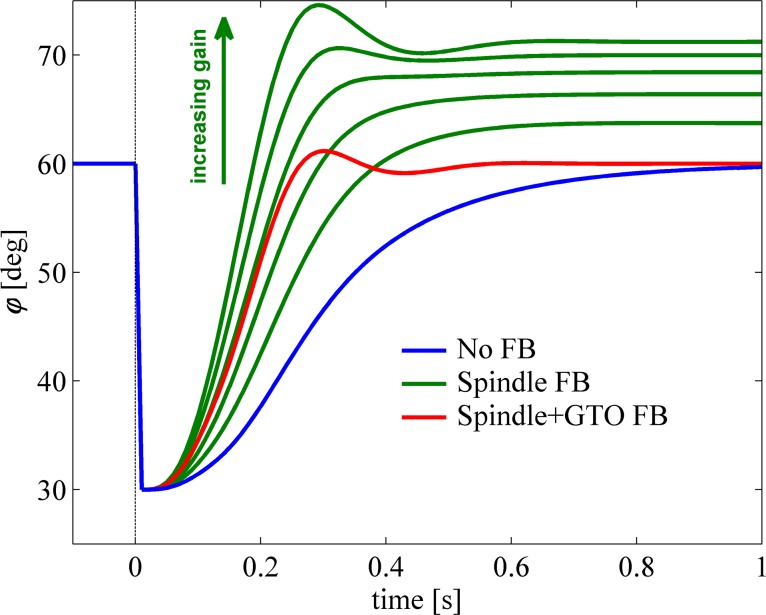
Fig. 5.

Response to position perturbation. Adding feedback of only muscle spindles led to substantial end-point errors. The error depended on the gain that was set and the reference CE length that was set (see also discussion). With combined feedback of muscle spindles and GTOs, responses did not show end-point error and took >50% less time to arrive at the end point with zero velocity than without feedback. φ, Joint position.

When spindle afferents were combined with signals from the GTOs, no end-point error occurred and the responses were much faster: without feedback it took the arm 1.33 s to reach the set point again, and with feedback, 0.61 s.

Response to Sudden Changes in Stiffness Level

The level of cocontraction influences limb stiffness by changing the forces produced by muscles, consequently leading to a change in tendon stretch. Here we examine the feasibility of spindle and GTO feedback by looking at the response to a sudden change in cocontraction level that leads to a maximal stiffness level, without changing the desired joint position.

Figure 6A shows the simulated response of the musculoskeletal model for an abrupt change in cocontraction level while the elbow position set point is kept at 60°. Mechanically, that means that for both open-loop muscle activation levels (thus, that for the low and that for a high cocontraction level), the sum of all steady-state muscle torques equals zero at exactly 60°. During the transition, however, the sudden change in muscle activation level caused the muscles to build up force unevenly, leading to a transient movement away from the set point. Without feedback (blue trace), the elbow position initially moved rapidly away from and subsequently slowly recovered toward the set point. Figure 6B shows the change in CE length of only the biceps during the transition (note, however, that the model for these simulations contained 4 MTCs). Clearly, the CE length changed during the transition, and this was caused by changes in muscle force and movement of the arm. Figure 6C shows the stretch of the biceps tendon, caused by the rise in muscle CE force during the transition. From Fig. 6, it is clear that neither the time histories of the CE nor that of the SE is simply related to that of the joint position; only the change in the combined CE and SE length is related (Fig. 6D).

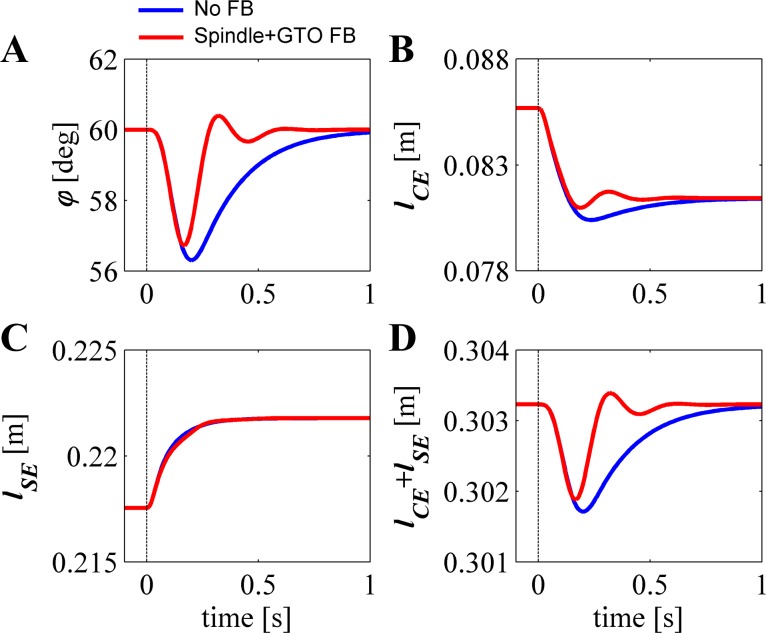
Fig. 6.

Response to sudden change in cocontraction. Graphs show responses of the musculoskeletal system to a step in cocontraction level leading to maximal stiffness while keeping the equilibrium position unchanged. A: joint position; blue line is response without feedback, and red line is response with combined feedback from spindles and GTOs. B: l_CE during the transition from a low to a high activation level. C: stretch of the tendon (l_SE). D: summary graph of the CE and SE lengths, equaling the MTC length, which is one-to-one related to joint position.

Red traces in Fig. 6, A–D, show the response to the same abrupt change in cocontraction level, but with feedback of the combined signal of CE and SE length (see methods). With feedback, the maximal deviation was reduced only slightly (by about 12%; 3.70° vs. 3.28°). This reduction is small because feedback contribution lags due to the neural time delay, muscle activation dynamics (it takes time to change the amount of actin-myosin binding places), and contraction dynamics (it takes time to change muscle force/length). Yet, the total response with feedback was greatly improved. The time taken to return to the reference position (within 0.001 rad and velocity within 0.01 rad/s) was reduced almost 50% from 1.06 to 0.56 s when spindle and GTO feedback were included.

Figure 6D shows that MTC length (note again that MTC length is the sum of CE and SE length) is independent of the forces produced by the muscle and hence the commanded (change in) cocontraction level. Thus, to use low-level positional feedback, the CNS only needs to know the static mapping between joint positions and MTC lengths. For example, in this case the desired joint position of 60° corresponded to an MTC length of the biceps of 0.3032 cm. In contrast, the CE length of the biceps in equilibrium at the desired joint angle changed substantially from 0.0858 cm at a low cocontraction level to 0.0817 cm at a high cocontraction level. Note that we just used the biceps muscle as an example; in reality the reference lengths of all muscles involved must be set.

Response to External Torque Perturbations

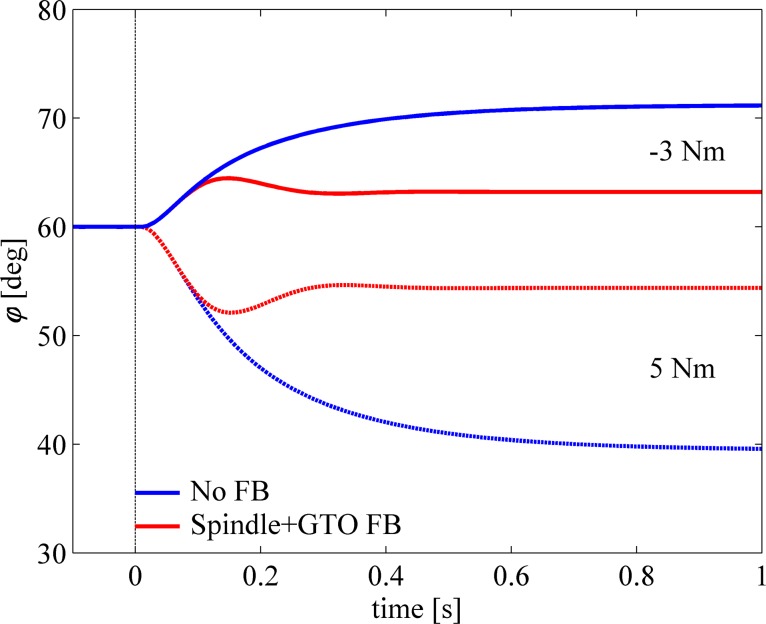
To test the robustness of the spindle and GTO feedback to static perturbations, we simulated the responses to constant torques. Figure 7 shows the responses for the same musculoskeletal model to a constant external torque of either −3 N·m (solid lines) or +5 N·m (dashed lines) at the same elbow position and open-loop activation as in Fig. 5. The blue lines depict the responses without, and the red lines with, spindle and GTO feedback. Not surprisingly, the model performed much better with feedback from spindles and GTOs than without. Note again that we have omitted simulations with spindle feedback only because errors become very large, as explained in the text and as shown in Fig. 5. The static error, the steady-state deviation from the set point, was about 11.1° and −20.4° without feedback and 3.1° and −5.4° with feedback, respectively (over 70% reduction in static error). Not only was the static error much smaller with feedback, but also the time to reach steady state (here defined as absolute angular velocity < 0.01 rad/s) was greatly diminished: from 0.88 and 1.03 s to 0.32 and 0.33 s, respectively (about 65% reduction). Again, reference MTC length was the same throughout the perturbation.

Fig. 7.

Response to torque perturbation. Graph shows responses of the model to a constant external torque perturbation. Without feedback (blue traces), steady-state errors were larger and responses were slower than when feedback from both muscle spindles and GTOs was used (red traces).

Spindle and GTO Feedback in Optimal Control

One potential concern is that the suggested feedback loop might be (computationally) hard to implement in forward controllers. Here we show that spindle plus GTO feedback can be readily incorporated in OC without the need to incorporate the time-delayed feedback loops in the system to be optimized by the CNS, and with the benefits of low-level spinal feedback.

Figure 8 depicts experimental data and corresponding simulations of the musculoskeletal model with and without feedback. Figure 8 shows the path of the hand in Cartesian coordinates (left), the shoulder joint trajectory (top right), and the elbow joint trajectory (bottom right). The gray-shaded area represents the average last 10 movements of 8 subjects plus and minus 1 standard deviation (mean ± SD). The blue line represents the simulated movement with optimal muscle activation patterns without feedback. The simulated movements in the shoulder and elbow joints were very similar to those observed experimentally; they stayed well within the gray area depicting the mean ± SD. The movement of the hand, however, was slightly more curved than movements observed in our subjects. The green line represents the optimally controlled arm plus feedback of muscle spindles with l_{CE_opt} used as the reference CE length. During the first 400 ms, the movement was dominated by the open-loop muscle commands. As such, during this period feedback played a minor role, and hence the distorting effect of neglecting tendon compliance was minimal. However, near the end of the movement, feedback became more dominant and, as with the 1-DOF position perturbation, movement control was seriously distorted. When GTO information was also incorporated (red lines), movement was identical to that without feedback. Note that the optimal open-loop muscle activations were not recalculated when feedback was used: they were identical for all simulations. Movements with feedback were affected by the feedback loop even when there was no perturbation, because the “desired” (in this case, minimal jerk; see methods) trajectory was not identical to that of the optimal muscle activation only. More importantly, even if the actual trajectory of the optimally controlled model were used, there would still be an influence of the damping due to feedback of CE contraction velocity (see Eq. 7). However, this effect of damping was compensated by the feedback of CE length, resulting in movements that were very close to those obtained without feedback. This result indicates that 1) the suggested feedback loop can be easily implemented within the OC framework without the need for reoptimization or incorporation of the feedback loop within the optimized system and that 2) the reference trajectory does not need to be known exactly beforehand.

The simulations depicted in Fig. 9 are similar to those shown in Fig. 8, but in this case after 0.20 s of the onset of the movement, a transient torque perturbation was applied to the shoulder joint (note again that stim_OC was identical for all simulated movements). This perturbation consisted of a half-sinusoid with an amplitude of −10 N·m and a half-period of 0.015 s. The blue line is the movement obtained without feedback, and the red line represents the movement when feedback was active. Without feedback, the end position was not restored within the simulated time window. As mentioned previously, the difference between the model with and without the proposed feedback was apparent only after 400 ms (i.e., 200 ms after perturbation onset), the end time of the unperturbed movement. This is because up to that moment, the total muscle activation was dominated by the open-loop optimal muscle activation. Feedback contribution (i.e., feedback gains) both in simulations and in the real system were necessarily limited to ensure stability due to feedback delays and activation dynamics. Together with Fig. 8, these results show that once a suitable open-loop muscle activation pattern is found, the suggested feedback scheme can be readily added without adding substantial computational demands for the CNS.

DISCUSSION

Even though GTO afferent signals are abundantly available to the CNS, the information provided by GTOs plays a minor role in current theories of human sensorimotor control, especially compared with muscle spindles. We suggested in the Introduction that this might be because the role of GTOs for the control of movement is less clear and also because the tendons in which they are situated are often ignored altogether. Yet, as also mentioned in the Introduction, there is ample evidence that both tendons and GTOs play a crucial role in neuromusculoskeletal dynamics, for example, as shown in the control of human standing (e.g., Loram and Lakie 2002; Loram et al. 2005, 2007; van Soest et al. 2003) and feline walking (e.g., Appenteng and Prochazka 1984; Prochazka and Gorassini 1998a). In this report we argue that GTOs may play an important role in movement control because they can be used in low-level positional feedback to account for muscle force-dependent changes in tendon length.

In this study, we have shown, first, that for a realistic musculoskeletal system with tendons, simple feedback of muscle spindle information to adequately control joint position is infeasible. In short this is because spindles sense only information about the CE. Simulated perturbations during both 1-DOF positioning tasks and 2-DOF fast point-to-point movements further support these findings by showing large steady-state errors that increased with increasing feedback gains and depended on the reference CE length chosen (see below). This result implies that tendon compliance needs to be taken into account to adequately sense and control muscle-tendon length or joint position (see also Scott and Loeb 1994). We have shown that a combination of muscle spindle and GTO information can be used for low-level positional feedback during both postural and movement tasks. The responses to static and transient perturbations were quicker and reached steady state faster (Figs. 5–7) in both 1-DOF postural (Fig. 5) and 2-DOF movement tasks (Fig. 9) and showed smaller static errors (Fig. 7).

Note that in the current study we applied stringent limitations on the optimization of feedback gains (for details see methods). These limitations are unlikely to be present in the real system, and thus it is to be expected that the dynamical behavior of the neuromusculoskeletal system including spindle and GTO feedback can be even more beneficial than presented in this study. Furthermore, direct feedback about CE contraction velocity was used (see Eqs. 5 and 7), rather than feedback with respect to a reference/desired velocity, which also has been shown to improve neuromusculoskeletal dynamics substantially (Kistemaker et al. 2006).

We want to stress here that our goal was not to show the advantages of negative position-velocity feedback, per se, as opposed to having no feedback at all. Rather, it was to provide supporting evidence for our hypothesis that combined information from muscle spindles and GTOs can be effectively used in low-level spinal feedback to overcome the problem introduced by the presence of series elastic elements (e.g., tendons, aponeurosis, etc.).

Incorporating GTO Feedback in Existing Models

Figure 3 shows the open- and closed-loop parts of the suggested control scheme. The inputs of the total scheme are the desired joint positions. The outputs of the “black box” are the open-loop muscle activations and the reference MTC lengths. The suggested feedback loop does not depend on how the open-loop activations are calculated and what they “represent.” For example, such an open loop could be a series of muscle activations defining stable equilibrium points, as done previously by Kistemaker et al. (2006, 2007b). It could also be open-loop muscle activations produced by (a combination of) forward and inverse neural models (e.g., Kawato 1999; Kawato and Wolpert 1998; Todorov 2004). In particular, we incorporated the proposed scheme in an optimally controlled 2-DOF model of the arm for fast point-to-point shoulder and elbow movements, without further complicating the computation of the OC solution yet greatly enhancing the system's response to perturbations.

It has been suggested that controllers using forward and inverse neural models suffer from the so-called posture-movement problem (also referred to as the Von Holst paradox; see Ostry and Feldman 2003). This problem has described how intentional movements from an initial position to a new position are produced without triggering resistance from postural reflexes and posture-stabilizing structures that generate electromyographic signals and forces to resist perturbations from the initial position. In this study we used feedback as an additional “layer” on top of the OC signals, which did not suffer from this problem; in fact, feedback helped to resist perturbations both during the movement and in the final position.

There is an alternative way to use spinal spindle feedback in a system having compliant tendons without making use of GTOs, yet this would turn out to be much more complex. Typically, it would entail subtracting sensed CE lengths from reference CE lengths set by the CNS. This is very different from using MTC lengths, because CE (reference) lengths depend on the forces produced by the muscles and MTC length does not (see results, Response to Changes in Stiffness Level). To calculate CE reference lengths, the CNS would have to have full knowledge about the statics and dynamics of muscle contraction, for example, in the form of a “forward internal model” (e.g., Kawato 1999; Kawato and Wolpert 1998; Todorov and Jordan 2002; Wolpert et al. 1995), and calculate the CE reference lengths from the open-loop muscle activations. This is unequivocally not a simple task, because such a calculation in a real system would require knowledge about, among other things, motor neuron pool dynamics [such as the size principle (Henneman et al. 1965) and rate coding (Monster and Chan 1977)], contraction dynamics (the force-length-velocity relationship), (history dependent) muscle activation dynamics, skeletal dynamics, and dynamics of the environment. Furthermore, these forward calculations would need to be very accurate, because even small differences in (reference) CE lengths can give rise to large angular errors due to the small moment arms of muscles (see Fig. 4). Nevertheless, it has been suggested that the cerebellum might be involved in feedforward computations of muscle dynamics (e.g., Desmurget and Grafton 2000; Kawato et al. 2003; Miall et al. 1993), and it cannot be ruled out that such mechanisms might be able to calculate CE reference lengths adequately. Be that as it may, using a combination of spindle and GTO information might greatly simplifying this issue; only a simple mapping from joint position to MTC length is required.

In Vivo CE Length vs. MTC Length

There is ample experimental evidence that during normal day-to-day contractions, CE length is indeed not well correlated with MTC length, as for example shown by in vivo measurements of both human (Lichtwark et al. 2007) and feline walking (Maas et al. 2009). Throughout the midstance period the CE of the feline medial gastrocnemius contracts mostly isometrically (i.e., CE length is constant) while the MTC lengthens, and during the early stance phase CE is consistently shortening while the MTC is lengthening (Maas et al. 2009). In humans, such “paradoxical muscle movement” was also observed with the use of dynamic ultra sound imaging during standing (Lichtwark and Wilson 2006; Loram et al. 2004), walking, and running (Lichtwark et al. 2007). Furthermore, as mentioned before, an electrophysiological study that examined human grasping showed that spindle output is poorly related to MTC length (Dimitriou and Edin 2008).

Positive Force Feedback vs. Negative Length Feedback

An interesting insight arises from the idea that a combination of spindle and GTOs might be used to effectively feedback MTC length during the control of posture and movement. In the literature, it has been suggested that force feedback from GTOs enhances the stabilization of posture (e.g., Dietz et al. 1992, 1993; van Soest and Rozendaal 2008). It has been theorized that GTO feedback needs to be positive (for an overview see Prochazka et al. 1997a) and indeed seems to be supported experimentally (e.g., Dietz et al. 1993; Pratt 1995; Prochazka et al. 1997a, 1997b). In the proposed scheme of low-level position control, spindle and GTO afferents are combined to sense muscle-tendon complex length, which is subtracted from a reference MTC length and fed back to the α-motoneuron. Perhaps counterintuitively, because only one negative feedback gain was used for MTC length (see Fig. 3 and Eqs. 5 and 7), this scheme also implies positive tendon force feedback. This is because an increase in tendon length (i.e., tendon or muscle force) increases α-motoneuron activity, which increases muscle force. In other words, an increase in tendon length/muscle force will lead to an increase of muscle force due to feedback and thus an increase of tendon length. Similarly, a decrease in tendon length/muscle force will lead to a decrease in muscle force and hence a decrease in tendon length.

Fusimotor Control

Typically, muscle spindles are included in computational models of motor control as simple muscle length and contraction velocity sensors that are used for low-level feedback control of (joint) position and velocity (e.g., de Vlugt et al. 2002; Feldman 2009; Gribble et al. 1998; Houk and Rymer 2011; Inbar 1972; Kandel et al. 2000; McIntyre and Bizzi 1993). In the simulations described in this study, we adopt a similar approach. We have shown that using spindle feedback alone results in systematic errors in posture and movement control due to the force-dependent stretch of the tendon.

The true nature of spindle afferents is much more complicated than currently assumed in typical models of motor control. There is a body of neurophysiological data about spindle behavior collected primarily from passive preparations (Crowe and Matthews 1964; Edin and Vallbo 1990), chronic recordings of locomotion (Prochazka and Gorassini 1998a, 1998b), and active movements in humans (Dimitriou and Edin 2008a, 2008b), all of which have attempted to relate spindle signals to some kinematic component of muscle state (length, contraction velocity, and acceleration). However, the exact nature of signals during movements remains unknown. Current empirical techniques are not able to relate afferent signals to the complete set of inputs and states of extra- and intrafusal muscles. Further studies may clarify the role of gamma drive and spindle afferents during active movement.

In this study we showed that a control scheme using only spindle afferents to feedback l_CE and v_CE is ineffective in a realistic system due to the stretch of the tendon. This limitation exists irrespective of the precise nature of the relationship between fusimotor drive, spindle afferents, and muscle states. It is important to note that no signal originating from spindles alone will be able to correct for the force-dependent stretch of the tendon.

Physiological Plausibility of Combined Spindle and GTO Feedback

Having provided theoretical evidence that the combined information from spindles and GTOs for low-level spinal feedback is both useful and feasible, the question becomes: are there (neuro)physiological data that make the suggested combined feedback physiologically plausible? For the feedback loop to work, the GTOs need to signal tendon length. As stated before, GTOs are classically seen and empirically proven to signal tendon force. We argue simply that because tendon length is dependent on tendon force, GTOs can just as well be seen (and proven) to signal tendon length. As such, spindle and GTO together should be able to sense MTC length. Indeed, recent human physiological data have shown that MTC length is well predicted by a combination of spindle and GTO output (Dimitriou and Edin 2008). Interestingly, spindle and GTOs are frequently found in line with and attached to each other to form “tendon organ-spindle dyads” (e.g., Marchand et al. 1971; Richmond and Abrahams 1975; Scott and Young 1987). Another requirement is that GTOs need to be sufficiently present in the tendons to ensure adequate estimation of all muscles involved. Human data on GTO numbers are not readily available, but monkey and feline studies show that GTOs are present in all muscles investigated and may have ratios of GTO to spindle count up to 1 (see Windhorst 2007). Furthermore, GTOs and spindles should have common afferent spinal pathways that feedback onto α-motoneurons. Early physiological data of intracellular recording in the spinal cord (laminae V and VI) show that Ia spindle and Ib GTO afferents in general work “in concert” as they coexcite interneurons that are directly connected to α-motoneurons (e.g., Czarkowska et al. 1981; Jankowska et al. 1981; Lundberg 1979). Recent neurophysiological feline data suggest that all spindle (Ia and II) and GTO afferents monosynaptically excite interneurons that directly excite α-motoneurons (Bannatyne et al. 2009), and it is proposed to rename these interneurons “group I/II interneurons” (Jankowska and Edgley 2010). Last, the CNS must have some neural mapping between joint position and MTC length and should be able to influence the feedback. The relationship between joint position and MTC length is simple because it is a static one-to-one relationship and thus is not dependent on any neuromusculoskeletal or environmental dynamics. Reticulospinal neurons from the caudal brain stem directly act on the group I/II interneurons (e.g., Cabaj et al. 2006) and as such might be able to send a centrally generated reference MTC length for the feedback loop. In summary, experimental data on both the sensors and interneurons in the spinal cord provide grounds, but do not prove in any way, that the suggested combined feedback from muscle spindles and GTOs is physiologically plausible. In turn, the theoretical analyses of this study might shed light on the reasons why such strong physiological couplings between spindles and GTOs are present, namely, because of the result of the mechanical interaction between the contractile element and tendon in the musculoskeletal system.

GRANTS

D. A. Kistemaker is supported by European Community Seventh Framework Programme CORDIS FP7-PEOPLE-2011-CIG-303849. J. D. Wong is supported by Canadian Institutes of Health Research (CIHR). P. L. Gribble is supported by CIHR and the National Institutes of Health.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

D.A.K., A.K.J.V.S., J.D.W., I.L.K., and P.L.G. conception and design of research; D.A.K. and J.D.W. performed experiments; D.A.K. analyzed data; D.A.K., A.K.J.V.S., J.D.W., I.L.K., and P.L.G. interpreted results of experiments; D.A.K. prepared figures; D.A.K., J.D.W., and P.L.G. drafted manuscript; D.A.K., A.K.J.V.S., J.D.W., I.L.K., and P.L.G. edited and revised manuscript; D.A.K., A.K.J.V.S., J.D.W., I.L.K., and P.L.G. approved final version of manuscript.