Ventricular beat detection in single channel electrocardiograms

Abstract

Background

Detection of QRS complexes and other types of ventricular beats is a basic component of ECG analysis. Many algorithms have been proposed and used because of the waves' shape diversity. Detection in a single channel ECG is important for several applications, such as in defibrillators and specialized monitors.

Methods

The developed heuristic algorithm for ventricular beat detection includes two main criteria. The first of them is based on steep edges and sharp peaks evaluation and classifies normal QRS complexes in real time. The second criterion identifies ectopic beats by occurrence of biphasic wave. It is modified to work with a delay of one RR interval in case of long RR intervals. Other algorithm branches classify already detected QRS complexes as ectopic beats if a set of wave parameters is encountered or the ratio of latest two RR intervals RR_i-1/RR_i is less than 1:2.5.

Results

The algorithm was tested with the AHA and MIT-BIH databases. A sensitivity of 99.04% and a specificity of 99.62% were obtained in detection of 542014 beats.

Conclusion

The algorithm copes successfully with different complicated cases of single channel ventricular beat detection. It is aimed to simulate to some extent the experience of the cardiologist, rather than to rely on mathematical approaches adopted from the theory of signal analysis. The algorithm is open to improvement, especially in the part concerning the discrimination between normal QRS complexes and ectopic beats.

Background

Ventricular beat (VB) detection is one of the most frequently addressed tasks in ECG signal processing and analysis. A number of methods, electronic circuits, algorithms and programs have been developed for real time and off-line implementation. Various mathematical and heuristic approaches have been used [1-13].

Some VB detectors operate on two ECG leads simultaneously. At first glance, such an attempt offers direct advantages. Actually, it is bound to two non-evident choices:

• addition or subtraction, or other procedure to be applied on the lead signals, having in mind possible changes of the dominant beat polarities;

• conjunction or disjunction of detected beats not coinciding in time.

Real time algorithm for beat detection in single channel ECG signal is suitable especially for stand-alone monitors, telemetry devices of limited bandwidth, event recorders for home use, defibrillators, pacemakers etc.

Friesen et al. [14] compared nine QRS detection algorithms with respect to noise immunity. Unfortunately, the authors did not publish the threshold rules used for beat candidates selection. We applied some of the reported algorithms on signals with drift, electrode disconnection and other artifacts without application of adaptive threshold and obtained unsatisfactory results.

Dotsinsky [15] has proposed a criterion for VB candidates, taking into consideration: i) high amplitudes, ii) steep rising and trailing edges and iii) sharp peaks. Good separation of ventricular beats from high and sometimes sharp T waves was shown as an advantage. Similar concept has been proposed by Zong et al. [16].

Bakardjian [17] applied Menard's derivative on a quasi-orthogonal ECG lead. Ventricular beats (VBs) were detected by conventional threshold law [6] and classified using fractal number data. However, in our opinion some of the classes have too small differences to be physiologically distinguishable.

Trahanias [18] has proposed mathematical morphology transform for clipping and analyzing wave peaks, thus giving priority to QRS complexes. Morphological classification has been reported also by Maier et al. [11].

Suppappola and Sun [19] have used non-linear transform. Poli et al. [8] have optimized QRS detectors by genetic algorithm. Afonso et al. [10] have proposed filter banks for ECG signal decomposition in separate frequency bands, where several features were independently computed and combined in a decision rule.

The existence of many algorithms for QRS and/or VB detection shows implicitly that despite the usually reported high sensitivity and specificity, not all waveform diversities offered by nature have been adequately identified. Therefore, a continuous tendency can be observed for development of newer and improvement of existing QRS and VB detection methods.

The first step of a rhythm analysis needs discrimination between normal QRS complexes and ectopic (supraventricular or ventricular) beats. Some authors consider that it must be done at a second detection step, when T waves have been eliminated and wave onsets and offsets have been identified [20,21,9].

The efficiency of VB detection algorithms has usually been assessed using ECG signals from the internationally recognized databases of the American Heart Association (AHA) and the Massachusetts Institute of Technology (MIT). Because of the enormous data array, correspondence between annotated and detected beats had to be checked and counted automatically. The marks (locations) of the annotated beats have varying positions in time (e.g. in the AHA database the marks are mostly near to the onset of the R wave). Suppappola and Sun [19] determined a valid detection interval, within which marks of the tested algorithm were considered true positive (TP) with respect to the annotations. The interval borders included the onset and offset of the QRS complex. They may be set by the user. Otherwise, the authors proposed default values for the AHA database: 10 ms before and 140 ms after the annotated locations. Any additional marks in the valid interval are treated as false positive (FP). Detection marks out of the intervals were classified as false negative (FN). The sensitivity Se and specificity Sp are normally computed by [10]:

Published values for Se and Sp by many authors have been quite high, usually above 95%. Afonso et al. [10] reported Se = 99.59% and Sp = 99.56%, obtained with the MIT-BIH Arrhythmia Database. With the same database, Poli et al. [8] showed 99.60% and 99.51%, respectively. However, they did present neither the formulae nor the number of TP beats used for Se and Sp computation.

Millet et al. [9] have proposed algorithms for discrimination between normal QRS complexes and ectopic beats (EBs) by means of the following parameters: highest positive and negative peaks, sums of the signed and unsigned amplitudes, number of samples with amplitude exceeding 70% of the unsigned highest peak, distance between this peak and the averaged position of the other peaks. The authors designated Se as a quotient between correctly detected normal beats and the total beats number. Sp was defined similarly for the EBs. The values obtained for two algorithms are: Se = 94.6% and 98%; Sp = 97.3% and 98%. The valid detection interval of the first algorithm encloses the annotated beats by samples with slope change higher than 180°. In the second algorithm, the left and the right interval borders are located at 60 ms and 80 ms before and after the R wave peak, respectively. However, the reported values for Se and Sp are obtained by seven files only, taken from the MIT-BIH Arrhythmia Database and consequently they hardly represent a high confidence estimation of the algorithm efficiency.

Method

The algorithm for ventricular beat detection in single-lead ECG improves previously developed method for QRS detection, based on steep edges and sharp peaks evaluation [15]. It includes branches for separate detection of ectopic beats (EBs). Parameters and thresholds used below have been evaluated by means of ECG databases in order to obtain better Se and Sp.

Two filters are used for eliminating power-line interference and suppressing baseline drift. The first is a comb filter with first zero at 50 Hz (60 Hz for certain countries). The second one is high-pass filter with a cut-off frequency f_c = 1 Hz, given by the recursive formula

Y_n = k₁Y_n-1 + k₂(X_n - X_n-1)     (3)

Here Y_n is the current sample to be filtered, Y_n-1 is the previously filtered sample and X_n and X_n-1 are unfiltered samples. The coefficients k₁ and k₂ are defined by

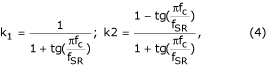
where f_SR is the sampling frequency.

A very simplified flow chart of the algorithm is shown in Fig. 1. It presents the main considerations only and is used to depict the heuristic principles implemented.

Figure 1.

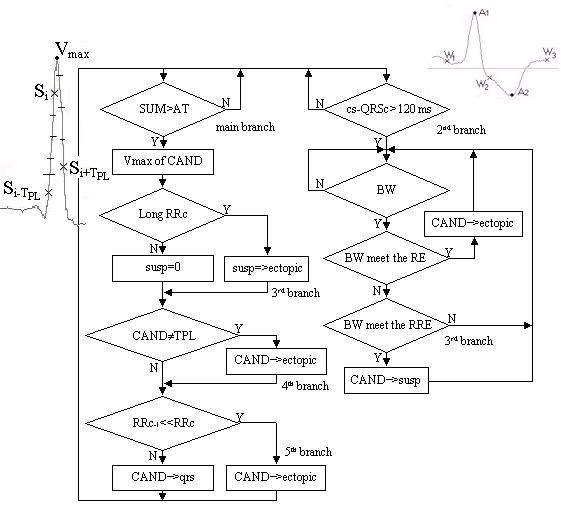
Simplified flow-chart: cs – current sample; CAND – VB candidate; Vmax – max value of CAND; RR_c – current RR interval; RR_c-1 – last but one RR interval; qrs – QRS buffer; ectopic – EB buffer; susp – buffer for subsequent analysis; TPL – normal QRS template; BW – biphasic wave; RE – requirement to BW ectopic beat; RRE – reduced RE.

The main branch calculates the SUM of absolute amplitude differences between the ongoing sample S_i and two surrounding it samples S_i-TPL and S_i+TPL, where T_PL is the period of the power-line frequency. Additional requirement is the equal sign of the two differences, i.e. SUM = abs(2S_i - S_i-TPL - S_i+TPL) if sign(S_i - S_i-TPL) = sign(S_i - S_i+TPL). Then SUM is compared to an adaptive threshold AT. Its initial value AT₀ (starting the algorithm) is AT₀ = 0.2 mV. A QRS complex candidate is marked each time when SUM > AT. After that, the threshold has the following time-course:

• AT = 0.7 SUM, except for the occurrence of peak amplitude <400 μV together with SUM > 0.3 mV (amplitude values are referred to the amplifier input) when AT becomes equal to 0.6 SUM.

• The threshold does not change for 200 ms (to avoid high-amplitude T-waves).

• Further, AT decreases linearly to reach 0.2 of its initial value at the end of the first second.

• Then the slope of the linear function becomes twice lower until the threshold drops down to a level of 0.2 mV, where it remains constant in order to avoid errors due to noise and low-amplitude signal.

It seems that the T_PL coincidence with the intervals for SUM calculation makes the preliminary interference cancellation superfluous. Really, maximum SUM may be obtained by shorter than T_PL intervals in case of narrow Q, R or S wave that has to be checked on free of interference signal.

A true beat candidate is expected to appear after a delay DIST following the latest detected beat. DIST is related to the expected QT interval duration of the ongoing RR interval. Initially DIST = 200 ms. It is updated further using a version of the empirical formula for the QT interval:

Here mRR represents a combination of the averaged latest four intervals RR_mean with the shortest one of them RR_min in a ratio of 7:1.

(7RR_mean + RR_min)/8

The enhanced participation of RR_min was introduced after heuristic assessment of its influence, according to our previous experience in arrhythmia analysis [22]. DIST is limited to 350 ms maximum, corresponding approximately to QT segment duration for heart rate HR = 55 beat/min. Lower HR detection may be erroneous if one QRS complex is missed or burst of EBs is encountered.

When the beat candidate is located nearer than DIST to the latest detected QRS complex, the candidate is ignored if its SUM is less than the SUM of the latest detected complex. Otherwise, the latest valid detected beat is discarded assuming it is a lower amplitude component of the same QRS complex.

Further, the maximum value V_max in an interval of 120 ms around the candidate is found. The V_max address is entered in the buffer qrs to mark the position of VB if two requirements are met: V_max > 80 μV and the number of zero crossings N < 8. The first threshold allows the detection of low-amplitude QRS complexes. The second condition is aimed at suppression of electromyogram artifacts and other high frequency disturbances.

The second algorithm branch, which is for EB (ectopic beat) detection is activated 120 ms after each detected QRS complex. Its basic criterion is the presence of biphasic wave. Intervals delineated by three consecutive crossing of thresholds with alternative polarity W₁÷W₃ are checked in sequence. The first threshold is the minimum of 200 μV or 0,25V_max. This measure improves EB detection in case of low amplitude QRS complexes. The corresponding values of the second threshold are 300 μV or 0,25V_max. The level of 200 μV for the first threshold is set lower (with respect to 300 μV) because the previous detected QRS complex might be really a large EB with sharp peak, which remains for a long time-interval above or below the zero line. The third threshold is of 100 μV and is set low again to block erroneous end of long-trailing EB.

The two waves delineated by the thresholds are classified as parts of EB if:

• The distance between their peaks A₁ and A₂ are longer than 30 ms (in order to avoid higher frequency noise) and shorter than 300 ms (to reject zero line shift provoked by large artefacts).

• The distance between W₁ and W₃ do not exceed either 700 ms in case of |A₁| > 0.8 V_max or 400 ms otherwise.

• The sum |A₁| + |A₂| is higher than the threshold LEV, which is equal to 0.6 V_max if V_max > 400 μV. Otherwise LEV = 600 μV.

• A₁ and A₂ do not differ by more than 25%.

• The time interval from the latest VB to one of the peaks A₁ and A₂ is longer than DIST. By default the peak used is A = A₁, except for the case A₂ > 2A₁ when A takes the address and amplitude of A₂.

If the above-mentioned requirements are not met, W₁ is discarded, while W₂ and W₃ are marked as W₁ and W₂. They compose the next two waves together with a new crossing of the third threshold W₃. This cycle is repeated until EB or QRS is detected.

The address of A is entered in the buffer ectopic, marking the EB position, and in the buffer susp for additional analysis by the third algorithm branch for EB detection.

Two consecutive VBs may occur at distance shorter than DIST in case of long RR intervals, which include burst of EBs or an EB followed by compensatory pause. Therefore, DIST is multiplied by 0.7 in the third algorithm branch for EB detection. A criterion that does not need the approximate equality of A₁ and A₂ is added. Instead, EB must have steep rising or trailing edge, tested as absolute amplitude difference between A and one of the samples located at 50 ms before or after A. If the difference exceeds 0.7 LEV, EB candidates are conditionally saved in the buffer susp waiting for confirmation with the appearance of the next beat detection. Long RR intervals are assumed if they extend above 1.3 s or 1.5 mINT.

The candidates in susp are substituted for EBs that are detected and saved in ectopic during long RR interval if:

• only one candidate is present (susp = ectopic + 1).

• the candidates are more than one (susp >ectopic) and the amplitude of the first of them is higher than 60% of the second one.

If susp >ectopic but the above amplitude requirement is not met, the first candidate is not saved in ectopic, as it is assumed to be a high T wave. The latest saved candidate is examined for non-corresponding proximity to the latest detected QRS complex. The checking for long RR interval ends with setting the susp pointer at the ectopic pointer value.

The forth algorithm branch for EB detection compares the parameters of the currently detected QRS complexes with the corresponding parameters of a template QRSe chosen initially as normal QRS. The parameters are: the maximum positive and negative amplitudes A_p and A_n, the corresponding peak-to-peak amplitude A_PP = A_p - A_m, the number of samples N_p exceeding the highest of the thresholds 0.4 V_max or +400 μV in intervals of 50 ms around V_max, as well as the number of samples N_n below the lowest of the thresholds -0.4 V_max or -400 μV in the same intervals. The following differences are formed:

ΔA_p = abs(A_p - A_pe), ΔA_m = abs(A_m - A_me), ΔA_PP = abs(A_PP - A_PPe), ΔN_p = abs(N_P - N_Pe) and ΔN_m = abs(N_m - N_me).

The template parameters are marked by index e. The latest detected VB is classified as EB if

(ΔA_PP > 0.4A_Ppe) | (ΔN_p > 0.2N_pe) | (ΔN_m > 0.2N_me) | ((ΔA_PP > 0.2A_Ppe) &

((ΔN_p > 0.4N_pe) | (ΔN_m > 0.4N_me)) & signQRS ≠ signQRSe),     (6)

where & and | are the symbols for conjunction and disjunction, respectively. The set of criteria (6) includes the following cases of detected VBs with relatively steep edges and/or sharp peak that may be rather classified as EBs:

• deviation of the maximum QRS peak-to-peak amplitude A_PP above the limits due to respiration and change in the patient body position.

• deviation in the QRS complex width either at positive (0.4 V_max or +400 μV) or negative (-0.4 V_max or -400 μV) level.

• deviation in A_PP and change in the positive or negative amplitude, the higher of them with different sign compared to the highest template amplitude.

The program implementing the algorithm selects a QRSe among QRS complexes with predominant polarity in a learning period after starting the detection. This is a very rapid and simple criterion but sometimes it may indicate EB as normal beat that will change the annotation marks used. Therefore, a sophisticated criterion is suitable for the future algorithm improvement. In case of long term cardiac monitoring, user intervention would be also convenient.

The QRS parameters are measured after candidates' confirmation. If the conditions presented in (6) are met, the QRS address is transferred from the qrs buffer to the ectopic buffer. The template parameters are updated with 0.1% participation of the latest confirmed normal QRS complex.

In a fifth algorithm branch for EB detection the latest two RR intervals RR_i and RR_i-1 are analyzed. The latest but one QRS complex is classified as EB and its address is moved from qrs into ectopic if RR_i > 1.6 s and RR_i-1 < 0.3(RR_i + RR_i-1).

Results and discussion

ECG signals taken from the AHA and MIT-BIH databases and processed by the program, written in MATLAB environment and implementing the described algorithm are presented in the following figures.

Fig. 2 shows correctly identified normal QRS complexes and EBs marked by * and o, respectively. The epochs shown include both leads d1 and d2 of the designated file and database (AHA 6002 d1 and d2). The used unfiltered lead is colored in blue. The VB symbols are set on the filtered signal shown in black. The green signal is the unused lead, which offers an auxiliary point of view in case of uncertainty, e.g. about the EBs marked before the 1303^rd and the 1308^th s in d1.

Figure 2.

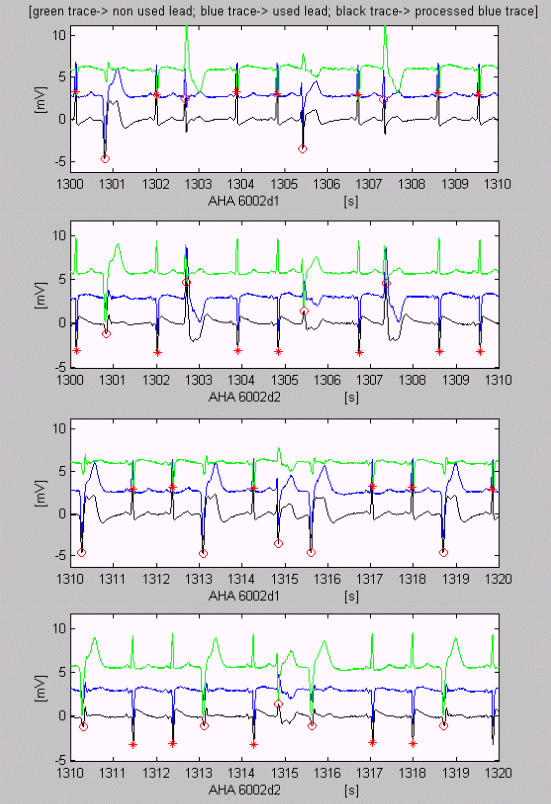
Examples of VB detection. Correctly identified normal QRS complexes and EBs marked by * and o respectively. Here, as well as in Fig. 3,4,5,6,7, the used unfiltered lead is colored blue. The VB symbols are set on the filtered black signal. The green signal is the unused lead.

A QRS complex early detected as EB because of muscle disturbances may be observed between the 768^th and 769^th s of AHA 6003d2 in fig. 3. The EBs marked after 22^nd and 28^th s in AHA 2008d1 are normal QRS complexes indeed. Difficult EBs with compensatory pause are detected in AHA 5001d1, except for the low amplitude EB after the 258^th s.

Figure 3.

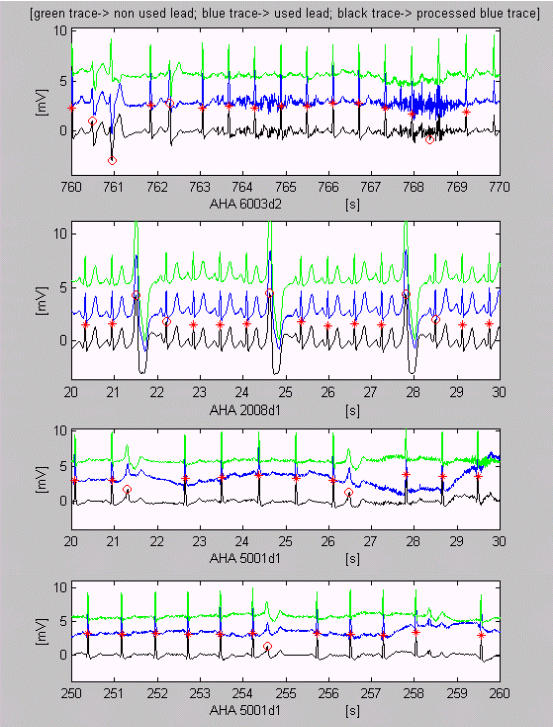
Correct VB detection with some exceptions. A QRS complex is early detected as EB because of muscle disturbances between the 768^th and 769^th s of AHA 6003d2. Normal QRS complexes after 22^nd and 28^th s in AHA 2008d1 are marked erroneously as EBs. Difficult EBs with compensatory pause are detected in AHA 5001d1, except for the low amplitude EB after the 258^th s.

Some high and sharp P waves accompanied by muscle disturbances are erroneously marked as EBs in AHA 1010d1 (Fig. 4). QRS complexes with amplitudes about 100 μV in an epoch of MIT-BIH 101d2 are correctly detected, with small exceptions. The recording MIT-BIH 212d2 shows transition between two types of heart activity. According to the algorithm, the latter is an EB sequence.

Figure 4.

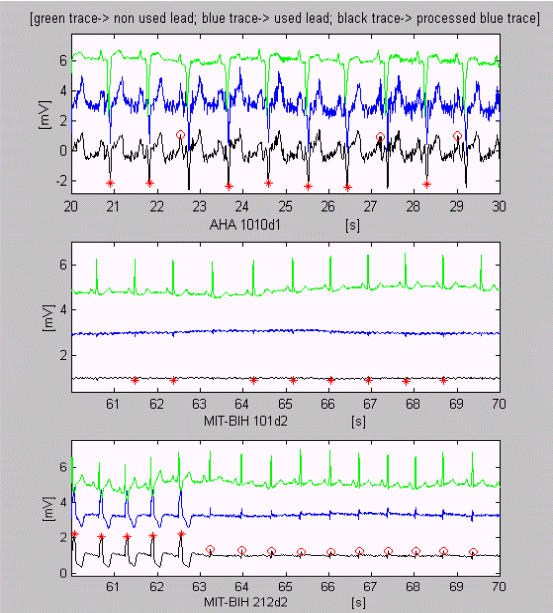
Examples of VB detection. Some high and sharp P waves accompanied by muscle disturbances are erroneously marked as EBs in AHA 1010d1. QRS complexes with very low amplitudes about 100 μV in an epoch of MIT-BIH 101d2 are correctly detected, with small exceptions. The recording MIT-BIH 212d2 shows transition between two types of heart activity.

The next three epochs of MIT-BIH 203 are examples of difficult for VB detection signals (Fig. 5). However, except for some contradictory classifications of EBs, only one error can be seen at the 49^th s, where non-existing VB is marked.

Figure 5.

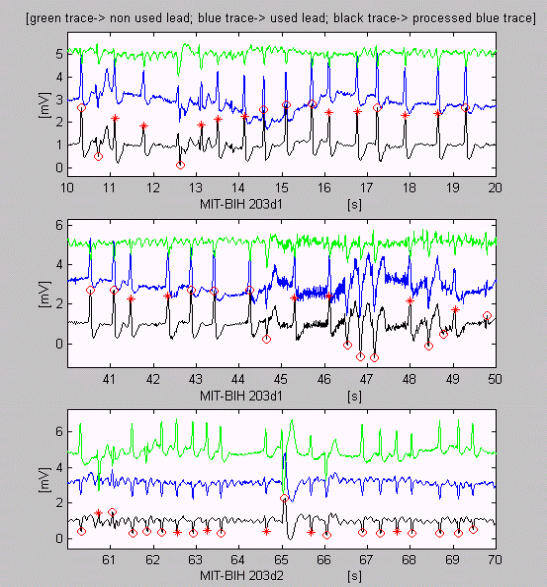
Difficult for detection epochs of ECG recordings. Except for some contradictory classifications of EBs, only one error can be seen at the 49^th s, where non-existing VB is marked.

Accurate detection with small exceptions may be observed in epochs of MIT-BIH 208d2 (Fig. 6).

Figure 6.

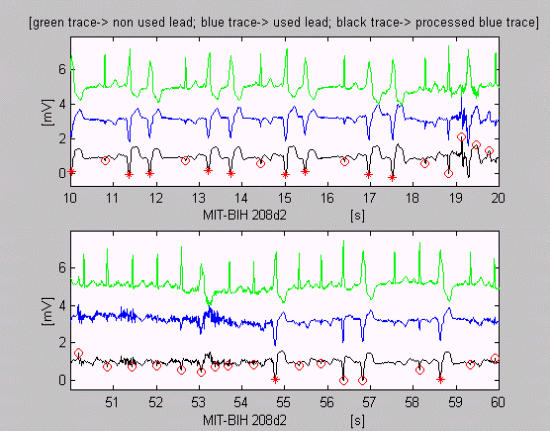
Precise (with small exceptions) VB detection with changed annotation marks for normal QRS complex and EB, because of the simple but rapid criterion used for normal QRS template selection. The erroneous discrimination of the beats before the 55 and 57 s is due to the assessment of their different widths.

A test program for automatic efficiency assessment of the algorithm was written in C++. It counts true positive TP, false positive FP, false negative FN and shifted SH beats. The algorithm marks the peaks of the complexes, while the annotated database locations most often designate the rising edges. Therefore, in opening a file we defined windows surrounding the annotated normal QRS complexes and EBs, if any. TPs are the detected beats within the window. Missed beats in the window are classified as FN. Detected beats outside the window are taken as FP. We introduced the category of SH beat, representing a single fault, assigned to a couple of adjacent erroneously detected FP and FN, if they are preceded and followed by TP beats. As SH beats are in fact non-existing, like the FN beats, both are summed for the computation of Se. We used formula (7) as an extension of the original formula (1).

Sp is calculated by eqn. (2). The values of Se and Sp obtained by applying the algorithm on recordings of AHA and MIT-BIH databases are given in the Table 1.

Table 1.

Sensitivity and Specificity

database	annotated beats N	true TP	false negative FN	false positive FP	shifted SH
AHA	328471	324739	1411	1376	945
	Se = 99.28 %		Sp = 99.58%
MIT-BIH	213543	210080	1570	648	1245
	Se = 98.68 %		Sp = 99.69%
AHA&MIT-BIH	542014	534819	2981	2024	2190
	Se = 99.04 %		Sp = 99.62%

The first and the last error of each recording are disregarded if they are within 1 s of the beginning or the end. The analyzed files from the first seven AHA sections (1xxx–7xxx) are 139. One file, AHA 5003d2, was excluded. Fig. 7 shows that QRS complexes cannot be detected even by experienced cardiologists without the use of the other lead AHA 5003d1. If the annotated beat number 2373 is added to the amount of FN, i.e. no beat was detected, Se of AHA database will drop down to 98.56%. Two recordings, MIT-BIH 101d2 (Fig. 4) and MIT-BIH 200d2, are also excluded from the 96 recordings of MIT-BIH arrhythmia database because of very low amplitudes in these single leads.

Figure 7.

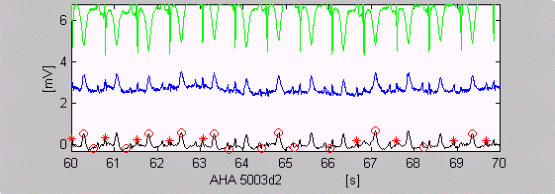
QRS complexes, which cannot be detected without using the other lead (green trace).

Many epochs with strong disturbances and practically zero amplitude because of low electrode contact are present in the recordings. Two of them are illustrated in Fig. 8, using the test program. In spite of the low amplitudes, the algorithm errors were accounted as wrong detections. The vertical red dashes show annotated normal QRS complexes. The blue small ellipses are for detected EB. The black rectangles delineate the window wherein the algorithm has missed VB. Time-marks are inserted into the signals.

Figure 8.

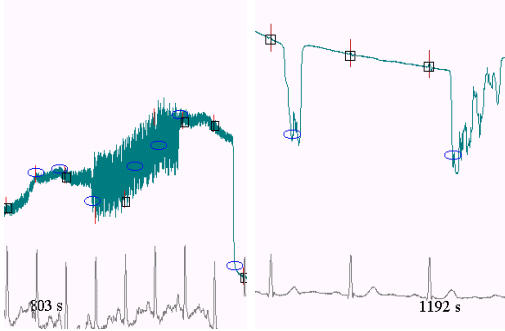
Automatic efficiency assessment of the algorithm. The vertical red dashes show annotated normal QRS complexes. The blue small ellipses are for detected EB. The black rectangles delineate the window wherein the algorithm has missed VB. Time-marks are inserted into the signals.

Conclusions

The results of applying the algorithm for one channel ventricular beat detection in real ECG signals taken from internationally accepted databases show high sensitivity and specificity. The algorithm can be categorized as a real-time algorithm since it has minimal beat detection latency. It is based on heuristic rules aimed to simulate to some extent the experience of the cardiologist, rather than to rely on mathematical approaches adopted from the theory of signal analysis. The algorithm is open to improvement, especially the branches concerning discrimination between normal QRS complexes and ectopic beats.

Authors' contributions

The authors contributed equally to this work.