A Simplified Confinement Method (SCM) for Calculating Absolute Free Energies and Free Energy and Entropy Differences

Abstract

A simple and robust formulation of the path-independent confinement method for the calculation of free energies is presented. The simplified confinement method (SCM) does not require matrix diagonalization or switching off the molecular force field, and has a simple convergence criterion. The method can be readily implemented in molecular dynamics programs with minimal or no code modifications. Because the confinement method is a special case of thermodynamic integration, it is trivially parallel over the integration variable. The accuracy of the method is demonstrated using a model diatomic molecule, for which exact results can be computed analytically. The method is then applied to the alanine dipeptide in vacuum, and to the α-helix ↔ β-sheet transition in a sixteen-residue peptide modeled in implicit solvent. The SCM requires less effort for the calculation of free energy differences than previous formulations because it does not require computing normal modes. The SCM has a diminished advantage for determining absolute free energy values, because it requires decreasing the MD integration step to obtain accurate results. An approximate confinement procedure is introduced, which can be used to estimate directly the configurational entropy difference between two macrostates, without the need for additional computation of the difference in the free energy or enthalpy. The approximation has similar convergence properties as the standard confinement method for the calculation of free energies. The use of the approximation requires about five times less wall-clock simulation time than that needed to compute enthalpy differences to similar precision from an MD trajectory. For the biomolecular systems considered in this study, the errors in the entropy approximation are under 10%. The approximation will therefore be most useful for cases in which the dominant source of error is insufficient sampling in the estimation of enthalpies, as arises in simulations of large biomolecules. Practical applications of the methods to proteins are currently limited to implicit solvent simulations.

1 Introduction

Quantitative understanding of biomolecular reactions requires knowledge of the relative free energies corresponding to the states of the system under consideration.¹ Complex biomolecular systems such as proteins are often described by a rugged potential energy surface, on which configurational transitions between local minima are rare events. For such systems, direct calculations of conformational free energy differences from equilibrium molecular dynamics simulations are impractical. Because conformational transitions underlie many processes of biological significance (e.g. protein conformational changes in response to the binding of a ligand) and are relevant for finding the most stable configurations of a molecular system (e.g. structure refinement), algorithms to calculate conformational free energy differences in an accessible time using computer simulations continue to be the focus of intense research (see e.g. Ref. 2 for an introduction).

Path-based methods for conformational free energy calculation^3–9 require the user to specify a reaction coordinate and/or a physical transition path that connects different conformations. For cases in which suitable reaction coordinates or transition paths are unknown, it is important to be able to calculate free energy differences by a path-independent method. Path-independent methods can also be used to provide estimates of the free energy to validate other methods.¹⁰

In this study we focus on confinement analysis,^11–13 a simple path-independent method that is related to Einstein’s early work on crystals (see e.g. Ref. 14, Ch. 5) and later studies,^15–17 in which internal motions were approximated as a superposition of harmonic oscillations. When the harmonic approximation is accurate, it can also be used to compute the entropy.^18,19 An application is the approximate calculation of the entropy difference between a folded and a denatured protein presented by Karplus et al. ²⁰. More generally, using molecular simulation tools, one can reversibly transform many types of biomolecules in silico to “ideal” crystals, whose thermodynamic properties can be determined analytically.^15,16 Reference states other than independent harmonic oscillators (HOs) have also been used²¹ with success. The HO state has the practical advantage that harmonic restraints have been implemented in the majority of molecular dynamics (MD) programs, so that the confinement approach generally does not require significant code modifications.

Frenkel and Ladd¹⁶ presented a method to compute the free energy of solids based on a reversible transformation of the solid to a system of interacting HOs. The free energy of the interacting HO system was then computed by Monte Carlo simulation. Tyka et al. ¹² described a similar method to compute side-chain entropies given fixed configurations of the protein backbone, an approach that is useful in protein structure prediction. Using reversible application of harmonic positional restraints of increasing stiffness, protein side-chains were transformed into weakly-interacting HOs, whose free energy (FE) was subsequently computed by Normal Mode Analysis (NMA). A key insight made in Ref. 12 was that the FE of transformation from the original state to the reference HO state could be computed accurately using thermodynamic integration (TI) in logarithmic space, based on the observation that the restraint force exhibits power-law behavior as the restraint stiffness is increased.¹² Cecchini et al. ¹³ extended the confinement analysis to a translation/rotation-invariant formulation, which facilitates the convergence of the confinement procedure for biopolymers without fixed atoms. The method of Ref. 13 also relies on NMA to compute the reference FE, although principal component analysis (PCA) of the dynamics of the restrained system could be used as well.¹³ If vibrational frequencies of the HO reference state are obtained from NMA or PCA by matrix diagonalization (as in the above two methods), the confinement analysis is inefficient for large systems (e.g. proteins composed of 10⁴ atoms or larger). Hensen et al. ²² and Park et al. ²³ avoided this problem by gradually turning off the contribution from the classical molecular force field used in the confinement procedure. This modification implies that the HO frequencies are known a priori (as evident from the Methods below) and, therefore, expensive diagonalization is not required. However, the requirement of turning off the force field makes the resulting method not readily usable in standard MD codes.

We describe a simplified confinement method (SCM) that does not require performing NMA, PCA, or turning off the molecular force field, and that is best suited for cases in which accurate free energy differences, rather than absolute free energies are desired. Using a test system for which the FE is known analytically (a homonuclear diatomic model), we demonstrate the convergence of the method. Convergence criteria are presented for systems in which the FE is unknown a priori.

Starting from the confinement formalism, we develop an approximation to compute directly the entropy difference between two states by a modified confinement procedure. The approximation requires simulating two replicas of the system interacting via a restraint potential, and uses an estimate of the difference in the exponential averages of the potential energy. In the simplest approximation, the exponential average is replaced by the conventional average. With this choice, the error between the approximate and the true entropy difference is found to be around 8% for two biomolecular systems. For large systems, in which the use of a truncated cumulant expansion of the exponential average is justified, the method can be used to compute the absolute entropy, but requires a precise estimate of the variance of the potential energy.

The present confinement approach is described in Methods. The method is validated using a model diatomic molecule for which the free energy can be obtained analytically. Applications to the alanine dipeptide and a β-hairpin polypeptide are described in Results. The utility and the limitations of the approach, as well as a comparison between SCM and the previous approaches are presented in the Concluding Discussion.

2 Methods

2.1 Simplified confinement analysis

The essential idea of confinement analysis is to relate the free energy of a system of interest with 3N degrees of freedom to the free energy of 3N harmonic oscillators (HOs), which is known analytically. Given a single Cartesian configuration X₀ of a system of N atoms (e.g. the Cartesian coordinates of an xray crystal structure of a protein) that belongs to a macrostate²⁴ Ω (alternatively, wide microstate²⁵ or conformational substate²⁶) in the canonical ensemble at a temperature T with partition function Z_Ω, the free energy of Ω can be written as

$$\begin{array}{l}-(1/\beta )log{Z}_{\mathrm{\Omega }}=G_{\mathrm{\Omega }}=G_{{HO}_{E^0}^{\nu }}-\mathrm{\Delta }{G}_{\mathrm{\Omega }\to {HO}_{E_0}^{\nu }}\\ =E^0+G_{{HO}^{\nu }}-\mathrm{\Delta }{G}_{\mathrm{\Omega }\to {HO}_{E^0}^{\nu }}\\ =E^0+\frac{3N}{\beta }log\beta h\nu -\mathrm{\Delta }{G}_{\mathrm{\Omega }\to {HO}_{E^0}^{\nu }},\end{array}$$ (1)

in which E⁰ = E(X₀) is the potential energy at X₀, G_HO^ν = (3N/β) logβhν is the free energy of 3N identical classical HOs with frequency ν,¹⁴ $G_{{HO}_{E^0}^{\nu }}$ is the free energy of the HOs with E⁰ as the energy at zero temperature, β = 1/(k_BT), and k_B and h are the Boltzmann and Planck’s constants, respectively. $\mathrm{\Delta }{G}_{\mathrm{\Omega }\to {HO}_{E^0}^{\nu }}$ corresponds to the free energy change of transforming (confining) the macrostate Ω to the HO state.^11–13 This term can be readily evaluated by MD sampling as follows. For reasons that will become clear below, we choose ν so large that the condition

$${(2\pi \nu )}^2\gg \mid {\nabla }^{2}E(X_0)M^{-1}\mid$$ (2)

is satisfied, in which |∇²E(X₀)M⁻¹| is largest eigenvalue of the mass-weighted Hessian computed at X₀.¹ Such values of ν clearly exist for any X₀ that can be used to start a MD calculation (a reasonable, though not unique choice is an energy-minimized structure¹³). A practical criterion for choosing ν is discussed below. With ν as in Eq. (2), the partition function for the ${HO}_{E^0}^{\nu }$ state can be written as

$$\begin{array}{l}{Z}_{{HO}_{E^0}^{\nu }}=C{\int }_{\mathrm{\Omega }}exp(-\beta (\sum _{i=1}^{N}2{(\pi \nu )}^2{m}_i{\left|\right|x^i-x_0^i\left|\right|}^2+E^0))\\ =C{\int }_{\mathrm{\Omega }}exp(-\beta (\sum _{i=1}^{N}2{(\pi \nu )}^2{m}_i{\left|\right|x^i-x_0^i\left|\right|}^2+E(X))),\end{array}$$ (3)

in which m_i are the particle masses, x_i are coordinate triplets, ||·|| is the Euclidean norm, and C contains the integral over the particle momenta (P) and Planck’s constant. The second equality in Eq. (3)) follows from Laplace’s saddle point method for the evaluation of exponential integrals, ²⁷ or from the representation of the Dirac delta function as the limit (ν → ∞) of a sequence of Gaussians. Heuristically, for a very large ν, the quadratic terms restrict the domain X for which the integrand is non-negligible to an infinitesimal neighborhood of X₀, so that E(X) tends to E⁰. Defining the Hamiltonian $H_{\lambda }(X;\lambda )=E(X)+P^T{M}^{-1}P/2+\lambda ({\sum }_i^N{(2\pi \nu )}^2{m}_i{\left|\right|x^i-x_0^i\left|\right|}^2/2)$, which for λ = 0 and λ = 1 corresponds to the Ω and the ${HO}_{E_0}^{\nu }$ states, respectively, $\mathrm{\Delta }{G}_{\mathrm{\Omega }\to {HO}_{E^0}^{\nu }}$ can be computed using thermodynamic integration (TI)²⁸

$$\begin{array}{l}\mathrm{\Delta }{G}_{\mathrm{\Omega }\to {HO}_{E^0}^{\nu }}=-(1/\beta )log(Z_{{HO}_{E^0}^{\nu }}/Z_{\mathrm{\Omega }})\\ ={\int }_0^1{\langle \partial H(X;\lambda )/\partial \lambda \rangle }_{H_{\lambda }(\lambda )}d\lambda \\ ={\int }_0^1\sum _{i=1}^{N}2{(\pi \nu )}^2{m}_i{\langle {\left|\right|x^i-x_0^i\left|\right|}^2\rangle }_{H_{\lambda }(\lambda )}d\lambda \\ =2{\pi }^2{\nu }^2\mathcal{M}{\int }_0^1{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }(\lambda )}d\lambda ,\end{array}$$ (4)

in which ℳ is the total mass of the system, and ρ_m(X, X₀) is the mass-weighted root-mean-square (RMS) distance between the coordinates X and X₀. Because the reference HOs are non-interacting, $\mathrm{\Omega }\supset {HO}_{E^0}^{\nu }$ for any Ω and ν as in Eq. (2), and the λ-averages in Eq. (4) generally converge rapidly.^12,13 Combining Eqs. (4) and (1) we obtain the expression for the free energy of the macrostate Ω

$$\begin{array}{l}{G}_{\mathrm{\Omega }}=E^0+\frac{3N}{\beta }log\beta h\nu \\ -2{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }(\lambda )}d\lambda .\end{array}$$ (5)

(A similar expression was also given by Frenkel and Ladd¹⁶.) The reference HO frequency ν may be estimated using a priori knowledge of the system, e.g. the highest bond vibration frequency obtained from the force field, or the high-frequency portion of the IR spectrum of alkanes (≃3000 cm⁻¹ or ≃90ps⁻¹). Although this estimate turns out to be reasonable in the examples below, physical insight may not be sufficient for all systems. Generally, ν can be estimated ‘on-the-fly’ using Eq. (5) as follows. With the change of the integration variable ζ = λν², Eq. (5) becomes

$$\begin{array}{l}{G}_{\mathrm{\Omega }}=E^0+\frac{3N}{\beta }log\beta h\nu \\ -2{\pi }^2\mathcal{M}{\int }_0^{{\nu }^2}{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\zeta }(\zeta )}d\zeta \end{array}$$ (6)

where H_ζ (X; ζ) = H_λ (X; ζ/ν²). Given a sufficiently large ν^* according to Eq. (2), for any ν >ν^*, ∂G_Ω/∂ (ν²) = (1/2ν)∂G_Ω/∂ν ≃ 0. Differentiating Eq. (6) and rearranging gives the relation

$${\nu }^2{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\zeta }({\nu }^2)}=\frac{3N}{{(2\pi )}^2\beta \mathcal{M}}.$$ (7)

To make use of the above convergence criterion, simulations are carried out according to H_ζ (ν²), starting with ν = 0 (which corresponds to regular MD). Additional simulations are performed with progressively larger values of ν until Eq. (7) holds. G_Ω is then computed from Eq. (5). Equations (5) and (6) are general, and will hold for any system, provided that the condition in Eq. (2) is satisfied. Since the Hamiltonian H_ζ (or H_λ) involves simple harmonic positional restraints with respect to a fixed structure X₀, the expectations in Eq. (6) are easily computed in standard MD programs. However, under certain circumstances, the expectation values will converge very slowly. In the case of pairwise-additive force fields, such as those currently employed in MD simulations of proteins, the system is invariant with respect to rigid-body motions. A naïve application of Eq. (5) would correctly result in infinite $\langle {\rho }_m^2(X,X_0)\rangle$ for λ = 0, since the simulated system can translate freely in any direction. For λ > 0, convergence of $\langle {\rho }_m^2(X,X_0)\rangle$ will be slow because of the mixing of the contributions to $\langle {\rho }_m^2(X,X_0)\rangle$ from the translational, rotational, and non-rigid-body motions. To remedy this problem, we employ a modified HO reference state, which is invariant with respect to rigid body motions.¹³ In this case, the reference state includes N three-dimensional HO located at X₀, as well as at all possible rotations and translations of X₀. This construction implies that the RMS distance $\langle {\rho }_m^2(X,X_0)\rangle$ now measures the distance between X and a mass-weighted best-fit alignment of X₀ onto X,^29–31 which is also generally available in standard MD codes.^32–34 The rotational invariance of the reference state implies that the total number of DOF is 3N less five or six rigid-body DOF, and the free energy G_Ω now excludes contributions from translation and rotation (which can be included separately if desired¹⁴). More generally, if the number of DOF in the reference system is reduced by the use of other constraints, such as SHAKE,³⁵ Eqs. (5)–(7) are modified to reflect the total number of unconstrained DOF. Numerical tests of Eqs. (5)–(7) are presented in Results.

2.2 Calculation of entropy differences

Equation (5) can be used as a starting point for deriving expressions for the entropy difference of two conformations of a molecule from confinement simulations. The simplest approach to compute the entropy difference using Eq. (5) is to obtain also an estimate of the enthalpy difference between the two conformations, which can be computed from unbiased MD simulations. However, because enthalpy estimates obtained by the ‘brute force’ method usually converge slowly (see Refs. 36–38, and also Tab. 4 in Results), it is useful to seek methods that avoid explicit enthalpy computation.

Table 4.

Free energy and entropy results for the 16-residue peptide in units of kcal/mol. The reference HO frequency is ν = 86ps⁻¹.

	α-helix	β-sheet	Δβ→α
G	−75.9±0.3†	−82.6±0.3†	6.7±0.4
Ē	−332.6±0.5	−346.2±0.5	13.6±0.7
TS	−37.6±0.6†	−44.5±0.6†	6.9±0.8
TS‡			7.4±0.5
TS§			4.2±0.6

^† The values for the absolute free energy and entropy are approximate because the convergence requirement (Eq. (7)) cannot be satisfied with the 1 fs time step (see text).

^‡ Computed with Eq. (15). The differences between the corresponding are accurate because of error cancellations (see text, Fig. 3c, and Ref. 13).

^§ Computed with Eq. (15) using the simulation of the α-helix in the presence of backbone dihedral restraints in the N-terminal domain (see text).

Since the only condition on X₀ in Eq. (5) is that X₀ ∈ Ω, a possible approach is to Boltzmann-average Eq. (5) over the macrostate to obtain

$$\begin{array}{l}{G}_{\mathrm{\Omega }}=\overline{E}+\frac{3N}{\beta }log\beta h\nu \\ -2{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\overline{\langle {\rho }_m^2(X,X_0)\rangle }}_{H_{\lambda }(\lambda )}d\lambda ,\end{array}$$ (8)

where $\overline{(·)}$ represents a Boltzmann average over Ω, and Ē is the average potential energy of the macrostate. ² Adding and subtracting the average kinetic energy K = 3N/(2β), and using U for the total energy E + K, Eq. (8) becomes

$$\begin{array}{l}{G}_{\mathrm{\Omega }}=\overline{U}+\frac{3N}{\beta }\left[log\beta h\nu -\frac{1}{2}\right]\\ -2{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\overline{\langle {\rho }_m^2(X,X_0)\rangle }}_{H_{\lambda }(\lambda )}d\lambda ,\end{array}$$ (9)

The last two terms on the right hand side represent the entropy (−TS_Ω). Equation (9) quantifies the intuitive relationship between RMS fluctuations observed in an MD simulation and the system entropy: a high value of the RMS distance between e.g. an xray structure and simulation structures (i.e. ${\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }(0)}$) is likely to correlate with a larger value for the entropy. To obtain the actual entropy (i) the integrand $\langle {\rho }_m^2\rangle$ in Eq. (9) is averaged over all possible reference configurations X₀ ∈ Ω, and (ii) one must include the reversible work of confining the system to a small neighborhood of each structure in X₀. We wish to construct dynamics according to a Hamiltonian that combines the averaging operations $\overline{(·)}$ and 〈·〉 of Eq. (9) into a single operation. Being able to do so would allow one to perform only one MD simulation for each λ to obtain S_Ω via Eq. (9). A possible choice for such a Hamiltonian (that is also relatively easy to define in standard MD programs) is

$$H_{\lambda }^2(X,X_0;\lambda )=E(X)+E(X_0)+P^T{M}^{-1}P/2+P_0^T{M}^{-1}{P}_0/2+\lambda (2{(\pi \nu )}^2\mathcal{M}{\rho }_m^2(X,X_0))$$ (10)

Evidently, $H_{\lambda }^2(X,X_0;\lambda )$ represents two identical systems (specified by X and X₀) that interact via λ-dependent harmonic restraint potentials. Unfortunately, the averages ${\overline{\langle ·\rangle }}_{H_{\lambda }(\lambda )}$ and ${\langle ·\rangle }_{H_{\lambda }^2(\lambda )}$ are not the same; a straightforward derivation (see the Appendix) shows that, in the limit ν → ∞ (which is implied by the use of Eq. (5)),

$$\begin{array}{l}2{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\overline{\langle {\rho }_m^2(X,X_0)\rangle }}_{H_{\lambda }(\lambda )}d\lambda \\ -2{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }^2(\lambda )}d\lambda \\ =\overline{E}+\frac{1}{\beta }log(\overline{exp(-\beta E)}),\end{array}$$ (11)

which gives the following expression for the entropy

$$\begin{array}{l}T{S}_{\mathrm{\Omega }}=2{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }^2(\lambda )}d\lambda \\ -\frac{3N}{\beta }\left[log\beta h\nu -\frac{1}{2}\right]+\overline{E}+\frac{1}{\beta }log(\overline{exp(-\beta E)}).\end{array}$$ (12)

For practical purposes, the formal requirement that ν → ∞, can be enforced by choosing ν sufficiently large, e.g. so that the convergence criterion of Eq. (7) holds, as was done for Eq. (5) (note that in this case the expectation is computed with respect to $H_{\lambda }^2$). A numerical test of Eq. (12) is shown in Fig. 1b. The utility of the dynamics based on $H_{\lambda }^2(X,X_0;\lambda )$ for evaluating the entropy therefore depends on the magnitude of the last term in Eq. (12), and on the accuracy with which it can be evaluated. Since the direct evaluation of exponential averages is known to suffer from poor convergence,^39,40 we approximate the last term in Eq. (12) using the cumulant expansion:

$$\overline{E}+\frac{1}{\beta }log(\overline{exp(-\beta E)})=\frac{\beta }{2!}\overline{{(E-\overline{E})}^2}-\frac{{\beta }^2}{3!}\overline{{(E-\overline{E})}^3}\dots ,$$ (13)

with the higher order terms omitted. For progressively large biomolecules, the distribution of the energy approaches a Gaussian, in view of the central limit theorem, as noted before⁴¹ (see also Fig. 4 in Results). In the Supporting Information, we apply the Lilliefors-Kolmogorov-Smirnov (LKS) test⁴² to the distributions of the potential energy corresponding to two larger proteins. For a globular protein with ~12K atoms (Myosin VI), the LKS test cannot distinguish between the sampled energy histogram and a Gaussian. In the case of a Gaussian distribution, only the first term of the expansion in Eq. (13) is nonzero,⁴³ and the following expression for the entropy of the macrostate becomes exact

Figure 1.

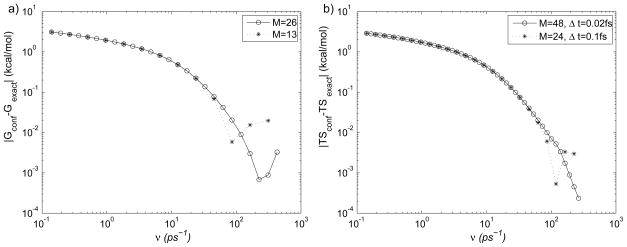
(a) Absolute error |G_conf−G_exact| in the free energy of the diatomic molecule computed using Eq. (6) and the exact analytical values below. M (13 and 26) corresponds to the number of integration points. For M = 13, the frequencies correspond to ν_i, i = 1,3, …,25 in Tab. 1. (b) Absolute error |TS_conf −TS_exact| in the entropy computed using Eq. (12). The exact (classical) free energy, average energy, and entropy values at T = 300K, are G ≃0.83085, Ē = 1/β = 0.59618, and TS = −0.23467, respectively (units of kcal/mol). For M = 48, the frequencies are computed as in Tab. 1, but with Δ = 0.25 The oscillatory behavior of the error for large frequencies is caused by using an integration step size that is too large (see text).

Figure 4.

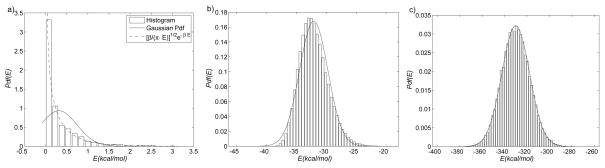
Normalized histograms of the potential energy for (a) diatomic molecule, (b) alanine dipeptide in the Ω_c7eq state, (c) β-hairpin in the helical conformation. The solid lines are Gaussian probability densities with the mean and variance computed from the corresponding histograms. The dashed line (a only) is the exact probability density, obtainable analytically for the classical harmonic oscillator as (β/[πE])^1/2 exp(−βE).

$$\begin{array}{l}T{S}_{\mathrm{\Omega }}=2{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }^2(\lambda )}d\lambda \\ -\frac{3N}{\beta }\left[log\beta h\nu -\frac{1}{2}\right]+\frac{\beta }{2}{\sigma }_{\mathrm{\Omega }}^2(E),\end{array}$$ (14)

in which we have defined σ_Ω(E) as the standard deviation of the internal energy distribution computed over the macrostate Ω. For systems in which the distribution of the energy deviates from a Gaussian, Eq. (14) will not give an accurate approximation to the entropy. We found that it still gives a good estimate of the entropy difference between the c7eq and c7ax conformations of the alanine dipeptide (see Results), despite the fact that the corresponding potential energy histograms are positively skewed (see Fig. 4). Equation 14 provides an interesting particular decomposition of the entropy in terms of the heat capacity (see below), confinement work, and a (HO) correction that depends only on the number of particles and the temperature. It does not, per se, offer an immediate computational advantage over the standard confinement procedure in Eq. (5), which involves H_λ (X;λ), since it requires calculating σ(E) (rather than Ē) to obtain the entropy.

To make Eq. (14) more useful for computations of entropy differences between conformational macrostates Ω¹ and Ω² of a molecule, we make the approximation that σ_Ω¹ (E) ≃ σ_Ω² (E). In view of the relationship between the canonical heat capacity of the system and fluctuations in the total energy, $\overline{\partial U/\partial T}=k_B{\beta }^2{\sigma }^2(U)$, this approximation amounts to assuming that the different macrostates of a large system have equal heat capacities at temperature T. The approximation is tested on two conformational states of the alanine dipeptide in Results. For this simple system, the difference in the last term of Eq. (14), $\beta {\sigma }_{\mathrm{\Omega }}^2(E)/2$, is found to be ≃ 0.1 kcal/mol, relative to the mean absolute value of ≃4.75 kcal/mol (see Tab. 3). In some cases, such as those involving protein-protein association, the energy fluctuations σ(E) will differ significantly for different states,⁴⁴ and the approximation is inaccurate. The assumption of equal heat capacities results in the following expression for the entropy difference

Table 3.

Comparison of the approximations to $\overline{E}+log\overline{e^{-\beta E}}/\beta$ for the alanine dipeptide (units of kcal/mol).

	Ωc7eq	Ωc7ax	ΔΩc7ax→Ωc7eq
Exact	2.34	2.27	0.07
Direct	2.96	2.97	−0.01
Cumulant	4.80	4.72	0.08

$$T\mathrm{\Delta }{S}_{{\mathrm{\Omega }}^1\to {\mathrm{\Omega }}^2}=2{(\pi \nu )}^2\mathcal{M}\times {\int }_0^1\left[{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }^2(\lambda ;{\mathrm{\Omega }}^2)}-{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }^2(\lambda ;{\mathrm{\Omega }}^1)}\right]d\lambda .$$ (15)

If the energy distributions cannot be represented by Gaussians (see e.g. Fig. 4b), Eq. (15) can be obtained by approximating the exponential average of the potential energy by a standard average, up to a system-dependent constant. An alternative derivation of Eq. (15) that does not explicitly involve the exponential average is provided in the Appendix.

Equation 15 is applied to transitions of the alanine dipeptide and of the β-hairpin (see Results). It is found that the use of Eq. (15) for these systems results in errors less than 10%. The efficiency of the direct entropy confinement approach is compared to that of the standard free-energy confinement method in Concluding discussion.

The Hamiltonians $H_{\lambda }^2(\lambda ;{\mathrm{\Omega }}^i)$ in Eq. (15) correspond to $H_{\lambda }^2$ with additional restraint terms to ensure that X, X₀ remain within Ωⁱ during MD simulations. For cases in which the mean transition time between macrostates Ωⁱ is much larger than the computationally affordable sampling time,²⁶ no such additional restraints will be necessary (see Results). Since most conformational transitions in large biomolecules occur on timescales that are far beyond those accessible to MD simulation (milli- vs. nano-seconds), restraint terms will usually not be required to confine the system to a given macrostate. However, restraint terms can also be added to limit the volume of a macrostate to improve convergence of the expectations in Eqs. (5) and (15). A potential problem with such restraints is that the resulting ‘restrained’ macrostates exclude important configurations that would otherwise contribute the the free energy. The dependence of the free energies on the definition of macrostate restraints is discussed further in Ref. 13

$H_{\lambda }^2$ (Eq. (10)) can be defined easily and without any codemodifications in the programCHARMM,³² which we use for calculations, as follows. First, the system topology and structure are duplicated to yield two identical systems (i.e. X and X₀). Nonbonded interactions between the two systems are then switched off using CHARMM’s BLOCK module. The λ-dependent part of the Hamiltonian can be added in the form of best-fit positional restraints. An alternative way of decoupling the systems X and X₀ is to specify a nonbonded exclusion list in the structure file, which should allow the use of other CHARMM-compatible MD programs, such as NAMD.³³

To carry out the TI in Eqs. (6) and (15), we use linear interpolation in logarithmic space.^12,13 For a function x(α) evaluated at the discrete points {a = α₁, α₂, … α_M+1 = b},

$$\begin{array}{l}{\int }_{{\alpha }_i}^{{\alpha }_{i+1}}x(\alpha )\simeq I_i[{\alpha }_i,{\alpha }_{i+1},x_i,x_{i+1}]\\ \equiv \frac{log({\alpha }_{i+1}/{\alpha }_i)\times ({\alpha }_{i+1}{x}_{i+1}-{\alpha }_i{x}_i)}{log({\alpha }_{i+1}{x}_{i+1})-log({\alpha }_i{x}_i)},\end{array}$$ (16)

and the integral is evaluated as

$${\int }_a^{b}x(\alpha )=\sum _{i=1}^M{I}_i$$ (17)

Uncertainty is propagated according to σ(I_i) = |∂I_i/∂x_i| × σ[x_i] + |∂I_i/∂x_i+1| × σ[x_i+1]. The accuracy of the above integration scheme was tested on a system of ideal gas particles by Tyka et al. ⁴⁵, who found that the transformation to double-logarithmic space produced integration errors of <1%. In contrast, the errors obtained with the trapezoidal rule in linear space were 6%–9%.⁴⁵ To determine whether the use of a higher-order interpolant would significantly change the free energy values reported in this study, we computed the integrals in Eqs. (5) and (15) for the alanine dipeptide transition described in Results using fourth order spline interpolation in logarithmic space. The difference from the values computed using the linear interpolation above were slightly less than 1%, which is smaller than the uncertainty due to limited sampling.

3 Results

3.1 Validation of methodology

In this subsection, we compute the classical free energy and entropy of a diatomic molecule using SCM, and compare them with the corresponding analytical result. The chosen molecule most closely corresponds to ethane represented using the polar hydrogen force field,⁴⁶ although the focus of the analysis is on the validation of the methods and not on the accuracy of the representation. The force field consists of a single harmonic bond potential U(r(X)) = K_b(r−r₀)²/2 with K_b = 450 kcal/mol/Ų and r₀ = 1.54Å. The mass of each extended carbon atom is 15.035 a.m.u., so that the system corresponds to a single HO with frequency ν ≃ 25.188ps⁻¹ (840.18cm⁻¹).

To compute the free energy using Eq. (6), MD simulations were preformed using $H_{\zeta }({\nu }_i^2)$ (see Methods) with frequencies ν_i listed in Tab. 1. The integration step was set to 0.1 fs and all simulations were 10ns in duration (the effect of the integration step size is discussed below). To maintain the temperature at 300K, a Langevin thermostat was used,⁴⁷ with the friction coefficient (γ) of 10ps⁻¹. X₀ corresponds to an equilibrium geometry with r(X₀) = r₀.

Table 1.

Frequencies used in confinement simulations ( ${\lambda }_i={\nu }_i^2/{\nu }_{26}^2$ in Eq. (5) or Eq. (12), and ${\zeta }_i={\nu }_i^2$ in Eq. (6)). They are computed in AKMA units (kcal/mol/a.m.u./Ų) used in CHARMM⁶⁷ according to the formula ν_i = 0.001×1.9^(i+5)Δ with Δ = 0.5. The conversion factor to inverse picoseconds is ≃20.45483. The frequencies are equispaced in logarithmic space, consistently with the TI protocol.¹²

i	νi(ps−1)×10−2
1	0.001402996671785
2	0.001933897452291
3	0.002665693676392
4	0.003674405159352
5	0.005064817985144
6	0.006981369802769
7	0.009623154171774
8	0.013264602625261
9	0.018283992926370
10	0.025202744987996
11	0.034739586560104
12	0.047885215477193
13	0.066005214464197
14	0.090981909406666
15	0.125409907481974
16	0.172865627872665
17	0.238278824215750
18	0.328444692958063
19	0.452729766009925
20	0.624044916620321
21	0.860186555418858
22	1.185685341578609
23	1.634354455295830
24	2.252802148999357
25	3.105273465062076
26	4.280324083098780

To show the convergence of Eqs. (5) and (12), we plot the absolute error in the free energy (G) and entropy (TS) in Fig. 1. The effect of resolution in the numerical integration is illustrated by using every other frequency value in Tab. 1 for the TI in Fig. 1a, and by doubling the resolution in Fig. 1b.

For ν ≲ 100ps⁻¹, the error in G and TS decreases as the frequency is increased, as expected (see the discussion of Eqs. (3) and (11) in Methods). The smallest errors computed from Eqs. (5) and (12) are 6.8×10⁻⁴ and 5.3×10⁻⁴, respectively (units of kcal/mol). The error cannot be made smaller by using higher frequencies because the simulation step (0.1fs) is too large to integrate the dynamical equations accurately. Instead, as the frequency is increased beyond ≃ 100ps⁻¹, the error curves exhibit small random oscillations. Assuming that accurate integration of the equations of motion using the second order Brünger-Brooks-Karplus (BBK) integrator⁴⁷ (in CHARMM) requires about 100 discrete steps per period, the largest oscillation that can be integrated at 0.1fs is ≃10fs, which corresponds to ν =100ps⁻¹, in rough correspondence with the results in Fig. 1. Because in most all-atom biomolecular simulations the integration step is ≃1 fs, computing absolute free energy values from Eq. (5) with high accuracy requires reducing the integration step by at least an order of magnitude. This requirement is clearly undesirable, as it would require increasing the simulation time to maintain uniform sampling. In principle, one could avoid the need to reduce the timestep below 1fs by choosing as a reference state a harmonic oscillator system with a lower frequency. For such a frequency (ν⁻) Eq. (3) does not hold, and the confined system corresponds to a system of interacting harmonic oscillators, because the effects of the force field are non-negligible. In that case, the free energy expression Eq. (5) would require a correction corresponding to the transformation of the interacting HO system into the noninteracting HO system (possibly of the same frequency ν⁻), which can be done with Monte-Carlo or MD sampling.^16,22 We show in the next subsection that if the free energy differences, rather than the absolute values, are desired, the need to compute the corrections does not arise, due to cancellations in systematic errors, as has been suggested previously.¹³ This feature of SCM makes it particularly useful in the calculation of free energy and entropy differences in classical MD simulations, since, for biomolecules at room temperature, quantum corrections to the free energy and entropy differences tend to be small, which is not the case for the corresponding absolute values. For example, the use of the present classical approach yields negative values for the absolute entropies (see below).

3.2 Calculation of Free Energy and Entropy Differences

Alanine dipeptide

The alanine dipeptide (AD) in vacuum is one of the simplest models for understanding the conformational space of the protein backbone,⁴⁸ and remains a standard model system for testing free energy computation methods. We use the SCM to compute the FE and entropy differences between the c7eq and c7ax conformations of AD and compare with a previously published result.¹³ We use the polar hydrogen force field in CHARMM⁴⁶ to represent AD, and perform MD calculations at 300K using the Langevin thermostat with the friction γ = 1ps⁻¹. The integration step ranges from 0.025fs to 1fs, as described below. The simulation time is 20ns. The frequencies used in the confinement simulations are computed in AKMA units according to the formula ν_i = 0.001×1.9ⁱ, i = {1,2, …,17}. This prescription is very similar to the one used for the diatomic molecule test case (see Tab. 1) that corresponds to the lower-resolution case in Fig. 1a.

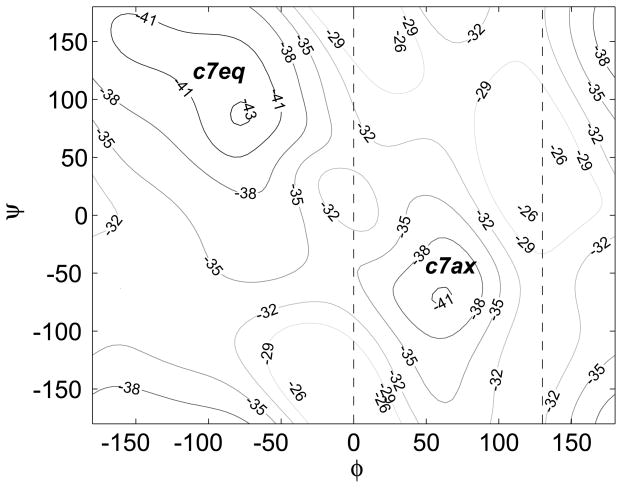
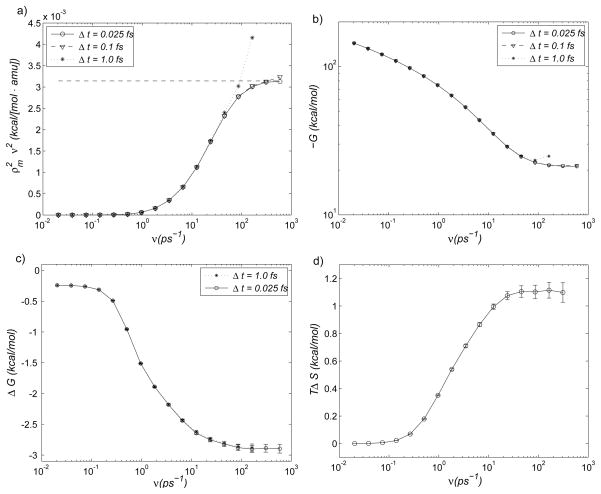
The adiabatic energy landscape of AD in vacuum in the (φ, ψ) dihedral variables is shown in Fig. 2. The two lowest-energy conformations of AD (c7eq and c7ax) correspond to the backbone dihedral coordinates (φ, ψ) = (−77,87) and (60,−70) in degrees (°). Following Cecchini et al. ¹³, we use a simple and somewhat arbitrary criterion to subdivide the conformational space into two states: Ω_c7ax = {X ∈ ℝ^3N: 130° ≥ φ (X) ≥ 0°}, and Ω_c7eq = ℝ^3N\Ω_c7ax. Because the macrostates Ω_c7eq and Ω_c7ax are separated by a relatively low energy barrier (≃7kcal/mol in Fig. 2), spontaneous transitions between them will occur for low values of the λ (or ζ) parameter in the Hamiltonian. To restrictMD sampling to one of the states, we employ ‘flat-bottom’ dihedral restraint potentials: ⁴⁹ U(X) = K_φ × max(0, |φ(X) − φ₀| − Δφ)²/2 with K_φ = 10 kcal/mol/rad²×(π/180 [rad/°])², and φ₀ = 65° and φ₀ = −115° for Ω_c7ax and Ω_c7eq, respectively, with the corresponding widths Δφ = 65° and Δφ = 115°. (In the equation for U(X), the range of the dihedral angle difference is taken to be (−π … π]). In the direct entropy confinement simulations, identical restraint potentials are added to each system. The results of the confinement calculations discussed below are summarized in Tab. 2. Unlike the previous case of the diatomic molecule, the free energies of the AD states Ω_c7ax and Ω_c7eq are not obtainable analytically. As discussed in Methods, Eq. (7) can be used to check convergence of the simulation. Figure 3a shows the two terms in Eq. (7) for Ω_c7ax (the results for Ω_c7eq are omitted, as they are similar), demonstrating convergence as ν → ∞. In analogy with the results in the previous section, the use of higher frequencies in the Hamiltonian requires decreasing the integration step: Δt < 1fs for ν ≳ 50ps⁻¹ and Δt < 0.1fs for ν ≳ 500ps⁻¹. If the integration step is too large for a given frequency, the value of ${\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }}$ overshoots the asymptotic limit. This phenomenon is expected, because the reference HO system becomes progressively less stable as ν increases for a fixed Δt, resulting in increased oscillations. This observation suggests that, heuristically, the most accurate estimate of G for a given Δt corresponds to the largest frequency for which the left-hand side of Eq. (7) is smaller than the right-hand side. Figure 3b shows free energy G_Ωc7ax computed using Δt = 1.0fs, 0.1fs and 0.025fs. In accord with Fig. 3a, G_Ωc7ax is converged for ν ≥ 200ps⁻¹, which requires the integration step Δt ≃ 0.1fs.

Figure 2.

Adiabatic energy surface in degrees for alanine dipeptide in vacuum calculated with the polar hydrogen representation. The locations and the energies of the two significant minima are: (φ_c7eq,ψ_c7eq) = (−77°,87°), E_c7eq = −43.30 kcal/mol; (φ_c7ax,ψ_c7ax) = (60°,−70°), E_c7ax = −41.31 kcal/mol. The area between the dashed lines defines the macrostate Ω_c7ax (see text).

Table 2.

Free energy and entropy results for the alanine dipeptide in units of kcal/mol. The uncertainty corresponds to the standard error of the mean. Entropies ere computed using TS_Ωi = Ē_Ωi+K-G_Ωi with K = [3N − 6]/[2β] = 15/β.

	Ωc7eq	Ωc7ax	ΔΩc7ax→Ωc7eq
G	−24.11±0.04	−21.21±0.03	−2.90±0.05
G†	−24.19±0.05	−21.34±0.045	−2.85±0.07
Ē	−33.81±0.02	−32.12±0.02	−1.69±0.03
TS	−0.76±0.05	−1.96±0.04	1.20±0.06
TS‡	−1.43	−1.98	0.55
TS§			1.10±0.03

^†Computed by switching off the force field after system was restrained at ν = 12.5ps⁻¹ (see text).

^‡ Computed from Normal Mode Analysis.

^§ Computed from the approximation in Eq. (15).

Figure 3.

Results of the confinement analysis for the alanine dipeptide (see text). a) Convergence criterion of Eq. (7) for different integration steps; symbols denote the left-hand side, and the horizontal dashed line denotes the constant right-hand side. b) Calculation of the absolute free energy for macrostate Ω_c7ax using different integration steps. c) Calculation of the free energy difference using two integration steps. d) Direct approximation of the entropy difference using Eq. (15) with an integration step of 1 fs.

In Fig. 3c we plot the free energy difference ΔG = G_Ωc7eq − G_Ωc7ax as a function of reference HO frequency. The most interesting feature of Fig. 3c is that ΔG is converged for ν ≃86ps⁻¹, even though the absolute free energy G (shown in Fig. 3b) is not converged (by ≃2 kcal/mol). This frequency is sufficiently low that stable MD can be achieved with Δt = 1fs, without the need to reduce the integration step. The present estimate of ΔG is −2.90±0.05 kcal/mol, in agreement with the previous result of −2.90±0.02 kcal/mol.¹³

For comparison, we also computed the free energies G_Ωc7eq and G_Ωc7ax using a confinement procedure that includes switching off the force field (annihilation).^22,23 The computational effort required to obtain absolute free energies in this procedure is similar to that of SCM, but is significantly greater than that of SCM if only free energy differences are desired (see Concluding Discussion). The corresponding free energy values are included in Tab. 2, and the technical details of the simulations are provided in the Supporting Information.

The average internal energies of the macrostates, Ē_Ωc7ax and Ē_Ωc7eq, were computed from 200ns of unbiased MD simulation of AD in each macrostate (flat-bottom dihedral restraints were used to restrict sampling to a given state). The long simulation times were required to obtain standard errors of ≃0.02 kcal/mol (see Tab. 2). Entropies were computed using TS_Ωi = Ē_Ωi+K − G_Ωc7eq (with K = [3N − 6]/[2β]), giving the values TS_Ωc7eq = −0.76±0.07 and TS_Ωc7ax = −1.96±0.04 (units of kcal/mol). These values are to be compared with the vibrational entropies computed from Normal Mode Analysis (NMA)⁵⁰ using the classical HO formula, which are $T{S}_{{\mathrm{\Omega }}_{c7eq}}^{\mathit{NMA}}=-1.43$ and $T{S}_{{\mathrm{\Omega }}_{c7ax}}^{\mathit{NMA}}=-1.98$. (We recall that classical entropies, i.e., those computed from continuous distributions, need not be positive because they are not invariant under variable transformations.^51,52) The agreement for Ω_c7ax suggests that this macrostate has an approximately harmonic energy landscape. For Ω_c7eq, the entropy estimate from NMA underpredicts the confinement result by ≃0.67 kcal/mol, indicating the presence of anharmonicities in the macrostate. This difference is evident in a qualitative sense from the contours corresponding to Ω_c7eq and Ω_c7ax in Fig. 2.

The entropy difference between the two states obtained from confinement analysis TΔS = TS_Ωc7eq − TS_Ωc7ax is 1.20±0.06 kcal/mol. We use this estimate, rather than the estimate obtained from confinement method with annihilation, because of the smaller uncertainty in the free energy difference (using the latter estimate would give an entropy difference of 1.15±0.08 kcal/mol). For the purpose of assessing the accuracy of approximation Eq. (15), in the following we consider this to be an unbiased estimate. The expectations in Eq. (12) were computed as described in Methods. The frequencies were specified as before (ν_i = 0.001×1.9ⁱ, i = {1,2, …,16}, ν₀ = 0), with ${\lambda }_i={\nu }_i^2/{\nu }_{16}^2$. The direct entropy simulations were integrated for 20ns using a time step of 1 fs, and Langevin friction of 1ps⁻¹. The direct entropy difference estimate of Eq. (15) is plotted as a function of the reference HO frequency in Fig. 3d. The estimates for ν₁₄ ≃163ps⁻¹ and ν₁₅ ≃310ps⁻¹ are TΔS = 1.105±0.05 and 1.115±0.06, respectively. Because the uncertainties in the unbiased entropy difference and in the entropy difference approximation are very similar, the simulation times associated with the two values can be compared directly to obtain a measure of the relative numerical efficiencies of the approaches. The exact entropy estimate involves explicit computation of the enthalpy difference, which required 200ns of MD simulation. On the other hand, the entropy approximation requires doubling the number of atoms, since the simulation system is composed of two identical replicas. The wall clock time associated with the entropy approximation is therefore approximately five times lower than that for the exact entropy evaluation (see also Concluding discussion). To reduce the uncertainty in the approximate entropy difference, we extended the entropy confinement simulations to 60ns per window (only for windows 1–14), which resulted in the estimate TΔS = 1.10±0.03. The difference in the mean values between the unbiased estimate and the approximate result is ≃8%. (We note that, even if the contribution to the uncertainties from the confinement integration were zero, the uncertainty in the unbiased TΔS would still be ≃0.03kcal/mol, due to the uncertainty in the average energies) The greater increase in the uncertainty with increasing frequency in Fig. 3d (compared with Fig. 3c) is caused by the lowering of the effective sampling temperature at high restraint energies, as discussed in the Appendix.

The above entropy values can be used with the time series of the internal energy computed from MD simulations to test the accuracy of the cumulant expansion (Eq. (13)). Figure 4b shows the normalized histogram of the internal energy obtained from a 200ns unbiased MD trajectory of AD in the Ω_c7eq state (the histogram for the Ω_c7ax is omitted, as it is similar). Qualitatively, the histogram is similar to the Gaussian distribution with the same mean and variance, even though the AD energy function involves only 12 atoms.⁴⁶ (The behavior can be contrasted with Fig. 4a, which shows the histogram for the diatomic molecule, discussed in the previous subsection.) To make a quantitative comparison, we evaluate both sides of Eq. (11) and compare to the cumulant expansion (Eq. (13)) to first order in β in Tab. 3. The energy histogram in Fig. 4a is clearly skewed toward positive values, which, in view of Eq. (13), suggests that truncating the cumulant expansion after the variance will overestimate the quantity $\overline{E}+log\overline{e^{-\beta E}}/\beta$ (Eq. (11)). In Tab. 3 we compare three different evaluations of this quantity. “Exact” values correspond to the left-hand side of Eq. (11), “direct” values are computed by using directly the instantaneous internal energy values obtained from unbiased MD in the exponential and arithmetic averages, and “cumulant” values correspond to βσ²(E)/2 obtained from unbiased MD. The uncertainty in the absolute values is ≃0.05 kcal/mol. Table 3 shows that the cumulant expansion overestimates the exact value by ≃2.5 kcal/mol. A direct calculation of the exponential average results in a smaller overestimate of ≃0.6 kcal/mol. The difference between the values corresponding to Ω_c7eq and Ω_c7ax is much smaller (≤0.08), and consistent with the entropy differences shown in Tab. 2. It is also noteworthy that for this test case Eq. (15) provides a reasonable approximation to the entropy difference even if the cumulant expansion of the exponential average is not very accurate.

β-hairpin from protein G

Investigations of β-sheets and α-helices, which are fundamental building blocks of protein structures, provide information about protein thermodynamics and dynamics, and can be useful for understanding the initial steps in the folding reaction.^53–56 A 16-residue β-hairpin fragment of streptococcal protein G⁵⁷ has been used as a realistic test system for the application of enhanced sampling methods to biomolecules.^13,58,59 We apply SCM to calculate the free energy and entropy differences between the β-sheet and α-helical conformations of this peptide. The difference between the two folded conformations is larger than that investigated in previous studies.

Spontaneous transitions to the α form have been observed in previous MD simulations in implicit solvent starting from the β form, and metastable states with significant helical content have been found in explicit solvent simulations (see Ref. 60 for a review). Whether the α-helical conformation of the β-hairpin peptide actually plays physical role is uncertain because solution experiments have not found evidence for appreciable α-helical content.⁶¹ Also, different force-fields overpredict either the α-helical (e.g. CHARMM27,⁶² but see the CHARMM36 force field⁶³) or β-sheet (e.g. AMBER⁶⁴) propensity in small peptides relative to experimental studies.^65,66 The primary focus of the present calculations is on the application of the confinement methodology to a realistic system, rather than on the biological significance of the result. It is found in the present analysis that the β form is more stable than the α form by ≃7 kcal/mol.

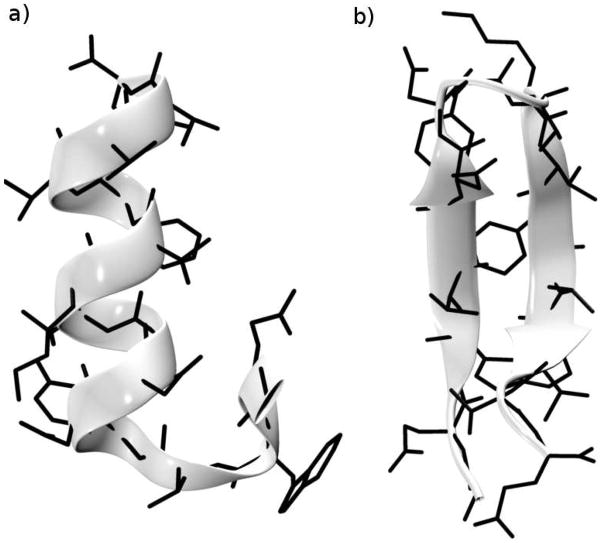
The β conformation was taken from the coordinates of protein G,⁵⁷ and subjected to 2000 steps of ABNR minimization in CHARMM.⁶⁷ The all atom force-field with the CMAP correction⁶² was used to represent the polypeptide, and the updated FACTS (Generalized Born) solvation model⁶⁸ (from CHARMM version c37) was used to approximate the effects of solvent in the minimization and in the subsequent dynamics simulations. The α-helical conformation was generated from the default internal coordinate entries in CHARMM,⁶² with the backbone dihedral φ and ψ angles fixed at −57° and −47°, respectively. The system was minimized for 2000 steps in the presence of harmonic restraints on the backbone φ and ψ dihedrals (K_φ = 1000 kcal/mol/rad²). The minimized α and β structures were then equilibrated at 300K in a 1ns MD simulation with harmonic restraints on the backbone atom positions (K_HARM = 10 kcal/mol/Ų) using the Langevin thermostat with γ = 1ps⁻¹. An additional equilibration for 30 ns is performed without restraints. The α and β conformations after equilibration are shown in Fig. 5. The N-terminal turn of the α-helix conformation unwinds (Fig. 5a), but the rest of the helix is stable for 30 ns of MD simulation, indicating that, with the CHARMM parameters and the FACTS solvation model, the α-helical conformation corresponds to a macrostate on this time scale.

Figure 5.

Equilibrated structures of the 16-residue peptide from protein G in (a) α-helical conformation, (b) β-sheet conformation. Details of the equilibration are given in the text. The N-terminal domain in panel a is at the bottom.

The confinement calculations were performed using the same frequencies as described for the alanine dipeptide. The integration step was 1 fs, and the duration of the simulations was 100ns for each frequency value, which corresponds to 210 hours on a Pentium Xeon X5650 2.67GHz CPU. The duration of the entropy confinement calculations was 20ns for each frequency value, which was sufficient to obtain an error of 0.5 kcal/mol for the entropy difference (see Tab. 4). Statistics of the internal energy were calculated from a 100ns unrestrained equilibration MD simulation. The results discussed below are summarized in Tab. 4. First, we note that the simulation time step of 1 fs is too large to achieve convergence according to Eq. (7). In the case of AD, convergence required a time step of at most 0.1 fs. For the polypeptide calculation, 10ns at 0.1fs per step would take ≃200 hours. We therefore did not perform simulations at frequencies above 86ps⁻¹ (which would require the 0.1fs step). The absolute free energy and entropy values in Tab. 4 should be considered approximate (the FE values are probably underestimated by ≃10%, in accordance with the results of the AD simulations in Fig. 3b) with the expectation that their differences are accurate, as described for AD.

The free energy difference between the α and β form is 6.7±0.4 kcal/mol in favor of the β form. The α-helical form is disfavored enthalpically by 13.6 kcal/mol, but favored entropically by 6.9 kcal/mol. The higher entropy of the α form is consistent with the unwinding of the N-terminal helical turn (Fig. 5a), which fluctuates in the MD simulation. Fluctuations are also observed in the C-terminal helical turn, but they are smaller, and do not result in unwinding. The direct entropy difference formula (Eq. (15)) predicts a value of 7.4 kcal/mol, overestimating the standard confinement result by 0.5 kcal/mol (≃8%). For large systems, the error of the entropy difference approximation can be difficult to obtain because the reference entropy values are computed by subtracting the free energy from the enthalpy, which is known to converge very slowly.³⁶ In principle, if the distributions of the internal energy of the two states are Gaussian, the cumulant expansion (Eq. (13)) can be truncated beyond the variance, and the entropy confinement results can be corrected by the difference in the variances (see Eq. (14)). Figure 4c shows that, visually, the energy histogram for the α-helix is indistinguishable from a Gaussian (although it is distinguishable by the Lilliefors Kolmogorov-Smirnov test;^42,69 see Supporting Information). The standard deviations computed from the time series are ≃12±1 kcal/mol, but the uncertainties are too high for the corrections to be useful for this case. The high uncertainty of the standard deviation estimate is due to the slow convergence properties of direct enthalpy calculations,³⁶ which was the main motivation behind developing the confinement entropy approximation.

To quantify the effect of the unwinding of the α-helix N-terminus on the entropy difference, we performed an additional entropy confinement simulation of the α-helical state, but with added restraint potentials applied to the φ and ψ dihedral angles involving residues 1–5 (which correspond to residue numbers 41–45 in the PDB file⁵⁷). The force constants in the restraint potentials were estimated from equilibrium fluctuations of residues 6–12 in the center of the α-helix by fitting to a Gaussian distribution according to k_φ = 1/(βσ²). The standard deviation of the dihedral angle fluctuations was σ ≃ 7° for both angles, corresponding to k_φ ≃40kcal/mol/rad². The restraints were sufficient to maintain the α-helical conformation of the N-terminus. The direct formula (Eq. (15)) predicts a reduced entropy difference of 4.2 kcal/mol between the restrained α-helix and the β-sheet relative to 7.4 kcal/mol obtained using the unrestrained α-helix (see Tab. 4). The difference corresponds to a decrease in the entropy of the restrained α-helix by 3.2 kcal/mol, relative to the unrestrained α-helix. The entropy difference per residue, 3.2 kcal/mol/5 res. = 0.64 kcal/mol/res. is considerably smaller than per-residue estimates of the entropy of protein unfolding, which are in the range 1.2–1.8 kcal/mol.^20,70 However, the N-terminus of the unrestrained α-helical state (Fig. 5a) is probably not sufficiently disordered or fluctuating to be considered unfolded, predominantly due to interactions with the rest of the α-helix, so the estimate of 0.64 kcal/mol/res. is reasonable.

4 Concluding Discussion

We have described a simplified confinement method (SCM) that does not require matrix diagonalization or switching off the molecular force field, and can be readily implemented in standard MD software, in some cases without writing a single line of new code. Simple convergence criteria are also presented and tested. The main difference between SCM and the standard confinement methods used in Refs. 12,13,45 is that SCM (Eq. (5)) involves a single reference frequency ν. Provided the frequency is sufficiently high, the thermodynamic integral represents the work required to transform the original system into a set of noninteracting HOs. The standard confinement methods^12,13,45 transform a system into a set of interacting HOs, which can be achieved with a lower frequency, but requires an additional transformation to a noninteracting HO state, e.g. using Normal Mode Analysis(NMA),^12,13 or umbrella sampling.¹⁶ In addition, SCM has a simple convergence criterion, which indicates whether the chosen frequency ν is sufficiently high. The present confinement formulation is well suited for the calculation of free energy differences between molecular conformations. The determination of such FE differences by classical MD simulations is of great interest because the corresponding quantum corrections are small in many applications (e.g. proteins at physiological temperature⁷¹).

SCM is less efficient for the calculation of absolute free energy values than the standard method, because it requires the reference HO frequency to be high, and necessitates decreasing the simulation time-step by an order of magnitude to reach convergence. If absolute free energies are desired, SCM is expected to be more efficient than the standard confinement for proteins with 10⁴ atoms or more, for which a single NormalMode calculation can take days, and requires several gigabytes of random-access memory. For smaller systems, the standard confinement procedure of Refs.^12,13 will be the faster method for obtaining absolute free energies because a high reference HO frequency is not required, and NMA takes between hours and minutes (the cost of diagonalization in NMA scales cubically with the number of atoms N, and also depends on the basis set used to represent the normal modes.⁵⁰).

To evaluate the efficiency and accuracy of the SCM relative to the confinement method with force field annihilation,^22,23 the free energies G_Ωc7eq and G_Ωc7ax for the alanine dipeptide were computed with both methods. The values obtained with the two methods are consistent, and the uncertainties are comparable (they are slightly smaller for the SCM, as can be seen from Tab. 2). Obtaining the absolute free energies for each macrostate required 840 ns of total simulation time for the confinement method with annihilation, and 1080 ns for the SCM. The major expense of the SCM was due to the calculations performed with the reduced time step Δt = 0.1fs. Since uncertainty in the free energy dfference obtained by SCM is slightly smaller than that from confinement with annihilation (0.05 kcal/mol vs. 0.07 kcal/mol, respectively), the efficiencies of the two methods appear to be comparable. However, if only the free energy differences are desired, the high-frequency calculations in the SCM are not required, and the corresponding computation cost drops to 560ns. The SCM therefore appears to be more efficient for the calculation of free energy differences. We also believe that the simplicity of implementation is an advantage of the SCM. In some MD programs, switching off the force field will require modification of the integrator, of the force calculation routines, and/or of the parameter or structure files (e.g. to scale down atomic charges, or force constants for bond or angle terms). These steps require the user to perform additional programming. Further details on the comparison are provided in the Supporting Information.

We also expect that the SCM will be well-suited for computing the free energies of ligand-protein binding, as well as those involved in protein-protein interaction. In such cases, the unbound state would require one independent confinement simulation for each ligand or protein molecule, and the bound state would require a single confinement simulation. The free energy penalty due to the loss of translational freedom is related to the standard concentration,^72,73 and that due to the loss of rotational freedom by the ligand(s) can be approximated by the rigid rotator expression involving the moments of inertia of the ligands.^14,74 In addition, if the ligand molecules have symmetry and can bind in n ways, the orientational free energy penalty is reduced by log(n)/β.⁷³ Such corrections to the free energy difference can easily be added in a postprocessing step.

Starting from the expression for the confinement free energy, we derived an approximation to the entropy difference between two states of a system that does not require computing either the free energy or the enthalpy. The approximation underestimates the unbiased entropy difference by ≃8% for the c7eq to c7ax transition in the alanine dipeptide (1.11 kcal/mol vs. 1.20 kcal/mol), and overestimates it by ≃7% for the helix-to-hairpin transition in a 16-residue peptide (7.4 kcal/mol vs. 6.9 kcal/mol). Generally, the approximation is expected to be most accurate for biomolecular conformational transitions that are not too large, e.g., those that do not involve significant changes to the secondary structure, but instead involve rearrangements of secondary structure elements such as α-helices and β-sheets. Heuristically, for such transitions, the differences in the entropies of the macrostates should be dominated by the differences in the anharmonicity of the microstates that comprise the macrostate. These differences are captured by the confinement procedure of Eq. (15) because the high restraint strengths of the reference state result in a lower anharmonicity due to a decrease in the effective sampling temperature (see Appendix). In contrast, for transitions which involve large secondary structure change, such as protein denaturation studied by Karplus et al. ²⁰, differences in the number of microstates corresponding to the given macrostate can make a large contribution to the entropy difference (e.g. a denatured state will have more microstates than a folded state). The β-hairpin transition test case studied here belongs to the class of large transitions, as it involves the breaking of all the hydrogen bonds and a complete change of secondary structure, which may explain the ≃7% error in the entropy difference. The significance of the error will clearly depend on the contribution that the entropy difference makes to the overall free energy difference for the particular problem under study.

The computational advantage of using Eq. (15) is that a separate calculation of the enthalpy is not required, and that the thermodynamic averages in Eq. (15) converge as quickly as those in Eq. (5) (albeit to an approximate result). Equation Eq. (15) is thus expected to be useful for cases in which the dominant source of error is insufficient sampling in the estimation of enthalpies, which can be true even for relatively small biomolecular systems (see Tab. 4). For the alanine dipeptide, obtaining the enthalpy with similar accuracy as the free energy required 200 ns of simulation, compared with 20 ns per replica for the free energy calculation (see Results). Although the total confinement simulation time was relatively large (2 macrostates × 20 ns × 14 replicas = 560 ns), simulations corresponding to different values of the integration parameter λ are independent and were therefore run simultaneously resulting in the same user time as that of a single 20ns simulation. Because the entropy approximation (Eq. (15)) requires simulating two identical MD systems concurrently, the computational cost associated with its use is approximately twice that of the conventional confinement approach (Eq. (5)). For the β-hairpin, enthalpies were calculated from 100 ns MD simulations. The standard error of the enthalpy difference was about 2^1/2 larger than the standard error in Eq. (15), which was computed from 20 ns restrained simulations. Therefore, about 200 ns of simulation would be needed to compute the enthalpy difference with the same precision as the approximate entropy difference. Thus, using a parallel computer for the calculation of the averages in Eqs. (5) and (15), the estimation of the entropy difference via Eq. (15) is about five times faster than an exact calculation via Eq. (5) (the difference is larger if the number of CPUs associated with the duplicated system is also doubled). Since the main disadvantage of the exact approach comes from the enthalpy calculation, any method that improves the convergence of the enthalpy will improve the performance of the exact method. One possiblilty is to perform several shorter unbiased MD calculations, starting from slightly different initial configurations within the same macrostate, and/or to use different random seeds for the thermostat (in the case that the thermostat is stochastic). The efficiency of such an approach will vary with the specific system under study, because it depends on the rate of divergence of trajectories started from similar configurations. In principle, the enthalpy could also be sampled during the free energy confinement simulations, followed by a reweighting procedure. However, only the very low-frequency windows of the confinement calculation would be well-suited for this purpose, because in the higher-frequency windows the sampling is effectively restricted to a small neighborhood of the reference structure.

The confinement method described here is ideally suited to the calculation of free energy and entropy differences of biomolecules in implicit solvent. Applications to explicitly solvated systems are more involved, for several reasons. First, the reference state for the solvent is invariant with respect to pairwise exchanges of solvent molecules. This degeneracy results in contributions to the free energy that depends on the number of solvent molecules, and would require (grand-canonical) corrections if the numbers of solvent molecules in different configurations are not the same. In addition, if the volumes of the explicitly-solvated configurations are not equal, a comparison of corresponding free energy values would require estimating the pressure-volume work difference between the different reference states. Furthermore, for simulations in the canonical ensemble using periodic boundary conditions with treatments of long-range electrostatics, any difference in the sizes of the periodic cells is likely to introduce additional errors. Finally, from a technical standpoint, the degeneracy of the reference state also introduces ambiguities into the definition of restraint potentials at low restraint strengths.⁴⁵ These challenges are the subject of ongoing work.

5 Appendix

To verify Eq. (11), we first perform the integration of the second term using the definition of $H_{\lambda }^2(X,X_0)$ (in analogy with Eq. (4)):

$$2{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }^2(\lambda )}d\lambda =-\frac{1}{\beta }log\left[\frac{C^2{\int }_{{\mathrm{\Omega }}^2}exp(-\beta ({\sum }_{i=1}^{N}2{(\pi \nu )}^2{m}_i{\left|\right|x^i-x_0^i\left|\right|}^2+E(X)+E(X_0)))}{C^2{\int }_{{\mathrm{\Omega }}^2}exp(-\beta (E(X)+E(X_0)))}\right],$$ (A1)

in which the constant C² contains the integral over the momenta of the two systems and Planck’s constant. In the limit ν → ∞, E(X₀) → E(X) by the continuity of the force field, and Eq. (A1) becomes

$$-\frac{1}{\beta }log\left[\frac{{\int }_{\mathrm{\Omega }}exp(-2\beta E(X))\{{\int }_{\mathrm{\Omega }}exp(-\beta ({\sum }_{i=1}^{N}2{(\pi \nu )}^2{m}_i{\left|\right|x^i-x_0^i\left|\right|}^2))\}}{{\int }_{\mathrm{\Omega }}exp(-\beta (E(X))){\int }_{\mathrm{\Omega }}exp(-\beta (E(X_0)))}\right]=-\frac{1}{\beta }log(\overline{exp(-\beta (E(X)))})+\frac{3N}{\beta }log\beta h\nu -G_{\mathrm{\Omega }}.$$ (A2)

Combining the last expression with Eq. (8) gives Eq. (11).

As noted in Methods, approximation Eq. (15) can be derived by an alternative argument. First, we note that the exponential average in Eqs. (11) and (A2) can be written as a difference of the free energies corresponding to the inverse temperatures β and 2β:

$$\frac{1}{\beta }log(\overline{exp(-\beta (E(X)))})=G_{\beta }-2G_{2\beta }+\frac{3Nlog2}{2\beta }$$ (A3)

(where the last term is the logarithm of the difference in the momentum integrals at the two temperatures). Combining Eqs. (A3) and (A2) gives

$$\begin{array}{l}{G}_{\beta }-G_{2\beta }=\frac{3N}{2\beta }log\left[(\beta h\nu )/(\sqrt{2})\right]\\ -{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }^2(\lambda )}d\lambda .\end{array}$$ (A4)

Making use of the thermodynamic identity ∂G/∂T = −S, we have

$$\begin{array}{l}T{S}^{\ast }\equiv 2{\int }_{T/2}^T\mathit{SdT}=2{(\pi \nu )}^2\mathcal{M}{\int }_0^1{\langle {\rho }_m^2(X,X_0)\rangle }_{H_{\lambda }^2(\lambda )}d\lambda \\ -\frac{3N}{\beta }log\left[(\beta h\nu )/(\sqrt{2})\right],\end{array}$$ (A5)

where we have defined S^* as the average entropy in the temperature window [T/2, T]. The approximation in Eq. (15) follows by writing the difference in the above expression for the two macrostates Ω² and Ω¹, and assuming $\mathrm{\Delta }{S}_{\beta ,{\mathrm{\Omega }}^1\to {\mathrm{\Omega }}^2}=\mathrm{\Delta }{S}_{{\mathrm{\Omega }}^1\to {\mathrm{\Omega }}^2}^{\ast }$. Furthermore, assuming that S_β = S^* is equivalent to using a finite difference (FD) approximation in the identity ∂G/∂T = −S with ΔT = T/2. Although, in principle, a smaller ΔT can be used in the FD estimate, the uncertainty in the entropy contribution TS diverges for ΔT →0 as $\sigma (TS)=\sigma (G)\sqrt{2}T/\mathrm{\Delta }T$. In view of the modest errors in the entropy approximation found in this study (less than 10%), the choice ΔT = T/2 apparently corresponds to a reasonable compromise between precision and accuracy for the calculation of entropy differences.

It was noted in Results that the uncertainty in the entropy difference estimated from Eq. (15) increases for very large frequencies. We show below that, as the frequency ν → ∞, the effective sampling temperature is lowered by a factor of two, which decreases the convergence rate of expectation values. (We recall that this limitation does not pose a significant drawback for estimating entropy differences, which do not require frequencies above ≃100ps⁻¹.) For simplicity, we sketch the proof for the motion of one-dimensional particles. The generalization to higher dimensions is straightforward. Using the Hamiltonian $H_{\lambda }^2(x,x_0;\lambda )$, a Langevin thermostat with friction γ and temperature T, and defining k = λ(2πν)², the equations of motion are

$$\begin{array}{l}m\ddot{x}=-\gamma \stackrel{.}{x}-\nabla E(x)-k(x-x_0)+\sqrt{2\gamma k_{B}T}\xi (t),\\ m{\ddot{x}}_0=-\gamma {\stackrel{.}{x}}_0-\nabla E(x_0)+k(x-x_0)+\sqrt{2\gamma k_{B}T}{\xi }_0(t),\end{array}$$ (A6)

where ξ (t) and ξ₀(t) are identically distributed white-noise stochastic processes with unit variance and zero mean. Defining x_a = (x+x₀)/2 and averaging the above equations, we have

$$m{\ddot{x}}_a=-\gamma {\stackrel{.}{x}}_a-({\nabla }_{x}E(x)+{\nabla }_{x_0}E(x_0))/2+\sqrt{2\gamma k_{B}T}{\xi }_a(t),$$ (A7)

where ξ_a(t) ≡ (ξ (t)+ξ₀(t))/2 is a white noise process distributed identically to ξ (t), but with variance 1/2. Normalizing ξ_a to unit variance, i.e. using $\eta (t)\equiv \sqrt{2}{\xi }_a(t)$, Eq. (A7) can be written as

$$m{\ddot{x}}_a=-\gamma {\stackrel{.}{x}}_a-({\nabla }_{x}E(x)+{\nabla }_{x_0}E(x_0))/2+\sqrt{2\gamma k_{B}T/2}\eta (t).$$ (A8)

Assuming that the force field is continuously differentiable, and letting k → ∞ implies that x → x₀, and that ∇_xE(x) → ∇_x0E(x₀). In this limit, Eq. (A8) describes the motion of a single unrestrained particle identical to x (with λ = 0) but moving in a thermal bath of temperature T/2. Since both x and x₀ tend to x_a, this completes the argument.