Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Feb 12;3:1264. doi: 10.1038/srep01264

Synthesis and Quantum Transport Properties of Bi2Se3 Topological Insulator Nanostructures

Yuan Yan 1, Zhi-Min Liao 1,a, Yang-Bo Zhou 1, Han-Chun Wu 2, Ya-Qing Bie 1, Jing-Jing Chen 1, Jie Meng 1, Xiao-Song Wu 1, Da-Peng Yu 1
PMCID: PMC3569629  PMID: 23405278

Abstract

Bi2Se3 nanocrystals with various morphologies, including nanotower, nanoplate, nanoflake, nanobeam and nanowire, have been synthesized. Well-distinguished Shubnikov-de Haas (SdH) oscillations were observed in Bi2Se3 nanoplates and nanobeams. Careful analysis of the SdH oscillations suggests the existence of Berry's phase π, which confirms the quantum transport of the surface Dirac fermions in both Bi2Se3 nanoplates and nanobeams without intended doping. The observation of the singular quantum transport of the topological surface states implies that the high-quality Bi2Se3 nanostructures have superiorities for investigating the novel physical properties and developing the potential applications.

Topological insulators (TIs) are new emerging quantum materials with an insulating bulk and gapless surface states1,2,3,4,5,6,7,8,9,10. Owing to the strong spin-orbit interaction, the conducting surface states are spin-polarized. The surface states are also immune to scattering by nonmagnetic impurities because of the preservation of time reversal symmetry and spin-momentum helical locking. These unique properties make TIs promising applications in spintronic devices. Recently, particular attention has been paid to three dimensional TIs such as Bi2Te3 and Bi2Se3, which have a single massless Dirac cone for the surface state6,7,8,9,10,11,12,13,14,15,16. Due to large surface-to-volume ratio of nanomaterials and enhanced surface contribution to conductivity, Bi2Se3 nanostructures have more advantages for both fundamental investigations of the exotic surface states and potential applications in spintronics17,18,19,20. Consequently, synthesis of high-quality Bi2Se3 nanostructures is highly desirable. Various methods have been developed to fabricate Bi2Se3 nanostructures, including mechanical exfoliation6,10, molecular beam epitaxial (MBE)11,12,13, sonochemical methods21, solvothermal synthesis20,22, metal-organic chemical vapor deposition23, and chemical vapor deposition (CVD)17,18,19. Nevertheless, synthesis of Bi2Se3 nanostructures with a variety of morphologies is still a challenge.

On the other hand, magneto-transport properties of Bi2Se3 nanostructures are very important for the potential applications in spintronic devices. The Aharonov-Bohm oscillations17, two-dimensional transport19, and Shubnikov-de Haas (SdH) oscillations24 related to the surface conduction of Bi2Se3 nanoribbons are reported. The surface Dirac fermions can be detected via transport measurement of SdH oscillations, which demonstrate a Berry's phase π24. However, plotting the Landau level fan diagram using the resistance minima or maxima of the SdH oscillations to identify the index field BN will give opposite results. Therefore, the accurate determination of the index field BN is important to obtain the correct conclusion especially for the condition of existence of bulk conduction.

In this work, we have synthesized various Bi2Se3 nanocrystals with various morphologies, including nanotower, nanoplate, nanoflake, nanobeam and nanowire, using a simple CVD method. To the best of our knowledge, our work reports the self-organized Bi2Se3 nanostructures with the most abundant shapes. The bulk-quantity growth of Bi2Se3 nanostructures is important for productive efficiency. These nanostructures were found to have high quality through systematical characterizations by scanning electron microscope (SEM), energy dispersive X-ray spectroscopy (EDS), atomic force microscopy (AFM), transmission electron microscopy (TEM), and selected area electron diffraction (SAED). The quantum transport properties of Bi2Se3 nanoplates and nanobeams were studied at 1.5 K with magnetic field up to 14 T. Well-distinguished Shubnikov-de Haas (SdH) oscillations were observed. We found that the determination of the index field BN using the SdH oscillations in resistance Rxx of the Bi2Se3 nanoplates and nanobeams was different, that is, the BN was identified with minima in Rxx for nanoplates, while with maxima in Rxx for nanobeams. Careful analysis of the SdH oscillations suggests the existence of Berry's phase π, which ambiguously demonstrates the quantum transport of the surface Dirac fermions.

Results

The Bi2Se3 nanostructures were synthesized via a CVD method in a horizontal tube furnace using powder Bi2Se3 as evaporation source. Details of the growth were described in the Method section and Supporting Information Figure S1. Si substrates covered with a thin gold layer were placed downstream of the source to collect the products. The morphologies of the acquired Bi2Se3 nanostructures are shown by the SEM images in Figure 1. We find that the Bi2Se3 nanostructures with different morphologies can be obtained by changing the distance between the source and the Si substrate. When the Si substrate was placed close to the source (≤5 cm), there were prismoids (Figure 1(a)) with gold particle on the head (confirmed by EDS) formed on the Si substrate. The size and density of the prismoids also depend on the pressure inside the tube. Under nearly atmospheric pressure, only few isolated structures formed (Figure 1(a)). On the other side, under a low vacuum, the source is easier to be evaporated at the same temperature. Abundant source vapors quickly deposited and nucleated, resulting in denser and smaller structures (Figure 1(b)). The layered character of the as-grown Bi2Se3 nanostructures can be clearly seen in Figures 1(a, b). On the top of most structures there were obviously metal particles, indicating that the growth mechanism is dominant by the vapor-liquid-solid (VLS) mechanism along the c axis [0001].

Figure 1. SEM image of the Bi2Se3 nanostructures.

Figure 1

Open in a new tab

(a-h) SEM images of the synthesized Bi2Se3 nanostructures with different morphologies by collecting the productions at the places downstream away from the source with different distances.

When the Si substrate is 6~7 cm away from the source, the most visible resultants were chunk of nanoplates or nanoflakes with regular morphologies, as shown in the Figures 1(c–f). Under this condition, the temperature is lower and the self-catalytic mechanism may play an important role during the two-dimensional nucleation growth. The layered properties of the synthesized 2-D Bi2Se3 islands were further characterized by SEM and AFM measurements, as shown in the Supporting Information Figure S2. The formation of spirals was observed in the AFM images in Figures S2(b,c). From the AFM line profile analysis shown in Figure S2(d), the typical step height (h) is ~1 nm, which is well consistent with the thickness of one quintuple-layer of Bi2Se3. The typical terrace width (λ) is ~ 800 nm. The small nanoplate slope 1/800 (p = h/λ) guarantees the two-dimensional growth mode. Recently, similar spirals were also observed during MBE epitaxy of Bi2Se3 on graphene/SiC25.

When the substrate is about 9~10 cm away from the source, we generally get nanobelts, nanobeams, or nanowires (Figures 1(g, h)). The nanobelts range from tens of to one hundred micrometers in length, several micrometers in width, and hundred nanometers in thickness. The difference between the nanobelts and nanobeams is the width size, which is about hundreds of nanometers for the latter (Figure 1(g)). The nanowires are about one hundred nanometers in diameter and rang from tens of to one hundred micrometers in length (Figure 1(h)). The cross-section shapes of the nanobelts and nanowires were further examined, and the SEM images are shown in Figure S3. The SEM characterization indicates that the cross-section shape of the nanobelts is rectangle. While for the so-called nanowire, the cross-section shape is not rectangle, as shown in Figure S3(e,f).

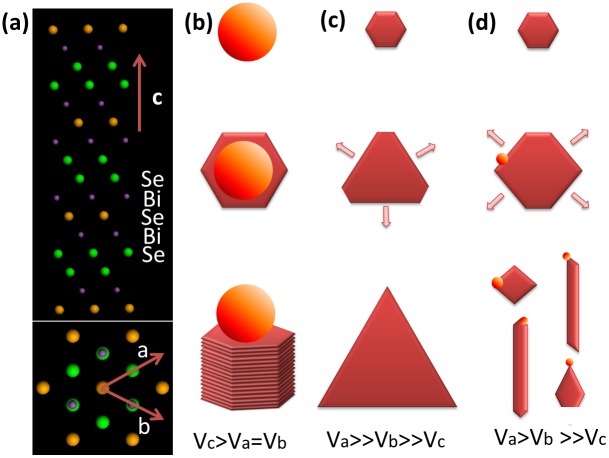
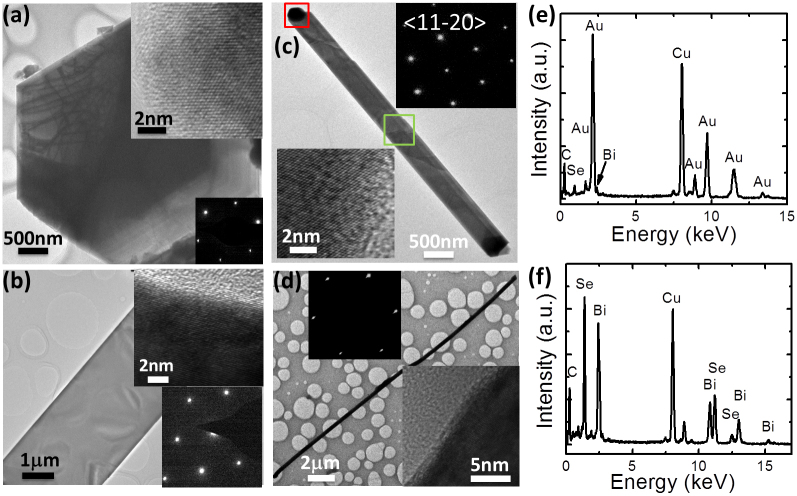
The detailed growth mechanisms were presented in Figure 2. Bi2Se3 was layered rhombohedral crystal structure along c axis, as illustrated in Figure 2(a). Here, the c axis [0001] of the hexagonal cell corresponds to Bi2Se3 [111] of the approximately cubic closest-packed layer crystal structure, where five atomic layers in sequence of –Se-Bi-Se-Bi-Se- form a basic unit, i.e. quintuple layer (QL). The interaction within the QLs is strong, but the adjacent QLs are coupled by relatively weak van der Waals interaction. The binding energies are different for different surfaces, which suggests different growth rate along different directions. The catalyst particles serve as nucleation sites for the growth of Bi2Se3 nanostructures. Via slow pumping, the evaporated molecules can be transported by the carrier gas and the dynamic balance during the growth process can also be largely maintained. Under high temperatures, the source vapors have high energy that can overcome the binding energy of [0001] surface, resulting in the growth along c axis with growth rate Vc > Va = Vb (Va, Vb, Vc are the growth rates along a, b, c axis, respectively), as seen the products in Figures 1(a, b) and the sketch in Figure 2(b). Under lower temperatures, the energy of the vapors may be insufficient to overcome the binding energy of [0001] surface. The growth along [10-10] or [01-10] directions becomes dominant and results in the polygon morphologies as shown the products in Figures 1(c–f) and the sketch in Figure 2(c), which are commonly present in epitaxial growth of Bi2Se3 nanoplates4,12. Under much lower temperatures, the growth induced by catalyst along [11-20] direction breaks the crystal intrinsic symmetry and results in the one-dimensional preferential growth as presented in Figures 1(g, h) and Figure 2(d), respectively. Therefore, different kinds of morphologies of Bi2Se3 nanostructures can be synthesized through changing the distance between the source and the Si substrate which changes the temperature of the collection substrates and energy of the source vapor. Morphologies and good crystallinity of the synthesized samples have been verified by the TEM images, high resolution TEM (HRTEM) images, and SAED patterns, as shown in Figure 3. Furthermore, EDS spectrums (Figures 3(e, f)) collected from the head and the body of one nanobeam (Figure 3(c)) show the Au catalyst particle on the head and the compositions of Bi and Se in the body, which obviously verify the VLS growth mechanism.

Figure 2. Schematic diagram of the growth mechanisms.

Figure 2

Open in a new tab

(a) The crystal structures of Bi2Se3 from side-view (top panel) and top-view (bottom panel). (b) The vapor-liquid-solid growth along [0001] direction. (c) The dominant growth along [10-10] or [01-10] directions. (d) The growth along [11-20] direction and the formation of quasi-one dimensional structure.

Figure 3. Microstructures and component analysis of the Bi2Se3 nanostructures.

Figure 3

Open in a new tab

(a-d) TEM images of different Bi2Se3 nanostructures. The insets show the corresponding HRTEM images and selected area electron diffraction patterns. (e, f) EDS spectra collected from the head and body of the Bi2Se3 nanoribbon in panel (c), respectively.

Electrical transport properties of the synthesized Bi2Se3 nanostructures were also studied. The as-grown Bi2Se3 nanostructures were transferred onto an insulator substrate. Micro-Hall devices based on the nanoplates and four-probe devices based on the nanobeams were fabricated via the processes including electron beam lithography, metal deposition, and lift-off. Typical SEM images of the devices are shown in Figures 4(a, e). As shown in Figure S4, the SEM image of a nanobeam device viewed using a 52° tilted sample stage indicates the nanobeam with a rectangle cross-section and a flat top surface. The temperature dependences of resistance for Bi2Se3 nanobeam and nanoplate are shown in Figure S5. The resistances for both samples decrease with decreasing temperature from 300 K to 20 K, showing a metallic behavior. Below 20 K, the resistance tends to saturate, which may result from the surface conduction and the bulk residual conduction.

Figure 4. Quantum transport properties of Bi2Se3 nanoplate and nanobeam.

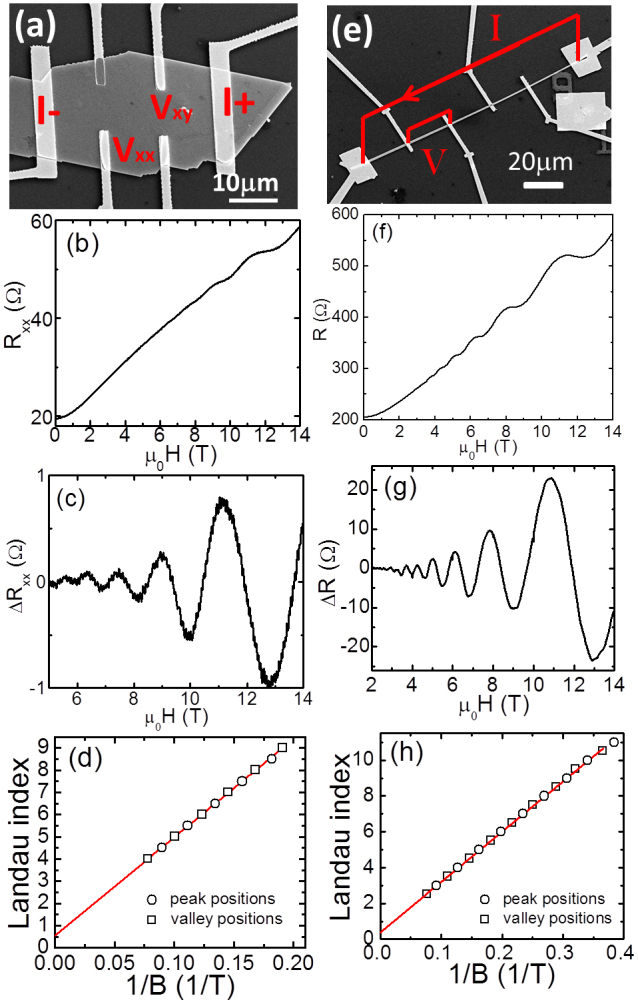
Figure 4

Open in a new tab

(a-d) are related to the Bi2Se3 nanoplates: (a) the SEM image of an individual Bi2Se3 nanoplate with Hall bar electrodes, (b) the magnetoresistance measured at 1.5 K, (c) the SdH oscillations observed after subtracting the magnetoresistance background, (d) Landau index vs 1/B, the peaks and valleys of the resistance oscillations correspond to N + 1/2 and N and are denoted by the circle and square symbols, respectively; (e-h) are related to the Bi2Se3 nanobeams: (e) the SEM image of an individual Bi2Se3 nanobeam with multi-terminal electrodes, (f) the resistance as a function of magnetic field measured at 1.5 K, (g) the resistance oscillations after subtracting the positive magnetoresistance background, (h) Landau index vs 1/B, the peaks and valleys of the resistance oscillations correspond to N and N + 1/2 and are denoted by the circle and square symbols, respectively.

The magnetoresistance (MR) of the nanoplate and nanobeam devices measured at 1.5 K are shown in Figures 4(b, f), respectively. A large positive MR of ~200% with no evidence of saturation was found at 14 T. Interestingly, there are also oscillations superposed on the linear MR at high magnetic field. Figures 4(c, g) show the SdH oscillations obtained by subtracting the positive MR background for the nanoplate and nanobeam, respectively. The well-resolved SdH oscillations indicate the high-quality of the samples and also offer a platform to study the special quantum properties of the topological insulators. To confirm the observed phenomenon, more than ten devices were measured and similar results were obtained.

We analyzed the SdH oscillations by plotting the Landau index versus the inverse of the magnetic field (1/B). Under a perpendicular magnetic field, the energy spectrum of the surface states are formed as Landau levels (LLs). As B is changed, the energy spacing between LLs and the degeneracy of each LL will change accordingly. When the Fermi energy is located between two LLs, the carriers are localized which results in the minima in conductance. Therefore, the value of BN can be indexed by the Landau index N (In the quantum Hall regime, it corresponds to the Hall platform). Due to the tensor relation, the conductance is expressed as Gxx = Rxx/[Rxx2 + Rxy2], where the Hall resistance Rxy = −B/(n·e·d), n is the carrier concentration, e is the charge element, and d is the sample thickness.

For the Bi2Se3 nanoplate devices, the Hall resistance (Rxy) was measured using the Hall bar structure. The Hall resistances of the nanoplate under various temperatures are shown in Figure S6(a). The sign of the Hall slope indicates the n-type carrier transport in the as-grown Bi2Se3 nanoplates. By fitting the Rxy-B curves in the low magnetic field region, the Hall carrier concentration and Hall mobility were calculated. As shown in Figure S6(b), the Hall carrier concentration is about ~1018 cm−3, and slightly increases with increasing temperature. The Hall mobility is ~6000 cm2/(V s) at 1.4 K and changes little below 30 K. The conductance Gxx was calculated and the Gxx-B curve is presented Figure S7(a). Via subtracting the background, the oscillations in Gxx at high magnetic field were clearly observed. To compare with the oscillations of Rxx, we plotted the ΔGxx and ΔRxx as a function of B in one figure, as shown in Figure S7(b). It is interesting to note that the minima in Gxx are well consistent with the minima in Rxx, suggesting that the Bi2Se3 nanoplates are of high quality and the surface conductance GxxS is dominant for the Bi2Se3 nanoplate device at low temperatures. Therefore, we plotted the 1/BN (where the minima in Rxx appear) against N for the Bi2Se3 nanoplate devices, as shown in Figure 4d. The linear fitting gives an intercept of 1/2, indicating the SdH oscillations are originated from the surface states with Dirac fermions. From the fitted slope F of 44.3, the carrier concentration n ~1.07 × 1012 cm−2 is also obtained.

For the Bi2Se3 nanobeams, it is very hard to determine the BN using the minima or maxima in Rxx without Hall data. We are aware that recently Fang et al. assigned the maxima in Rxx SdH oscillations to the Landau level index N (although the authors of Ref. 24 did not directly mention this point), which demonstrated the π-Berry phase of the surface states in Bi2Se3 nanoribbons24. Here, the Bi2Se3 nanobeams have similar morphology of nanoribbons. Under a perpendicular magnetic field, the surface states on the top/bottom surfaces contribute to the SdH oscillations, while the surface states on the side surfaces do not contribute to the SdH oscillations. Because Gxx is contributed from bulk conductance GxxB, side surface conductance GxxSide-S, and top/bottom surface conductance GxxTop/bottom-S parallel connection, the GxxTop/bottom-S to Gxx ratio may be low and the variation trends of Rxx are consistent with 1/Gxx in the Bi2Se3 nanobeams. We plotted Landau index N as a function of 1/BN (where the maxima in Rxx appear) in Figure 4(h). A good linear fitting is achieved. The fitting gives the intercept of 1/2 and the slope F of 28.06. The observation of the intercept of 1/2 implies the existence of Berry's phase π, which ambiguously indicates the SdH oscillations originate from the 2D surface Dirac electrons. According to the Onsager relation F = (h/4π2e)SF, we obtain the surface carrier concentration n = kF2/4π = 6.8 × 1011 cm−2, where h is the Planck's constant, SF ~ 2.7 × 1017 m−2 is the Fermi surface cross-section area, and kF~ 0.29 nm−1 is the Fermi wave-vector.

Discussion

The dimensionality of the SdH oscillations can be further checked by tilted magnetic field measurements. The magnetoresistance measured at temperature of 1.5 K with different angles between the normal direction of the substrate plane and the direction of the magnetic field was shown in Figure S8. The SdH oscillations in resistance are only related to the vertical component of the magnetic field, indicating two-dimensional transport properties26. We noticed that the 2D-like magneto-transport in highly doped Bi2Se3 from bulk carriers was recently reported27. In Ref. 27, the Rxx minima of the SdH oscillations were labeled with N, because the Gxx was all from the bulk carriers and the surface conduction can be neglected in such highly doped system. The authors of Ref. 27 thus obtained a zero intercept in the Landau level fan diagram. However, in our low doped Bi2Se3 nanoplates, surface conduction dominates the transport at low temperatures, which is the reason why we also assigned the valley positions in resistance to N in Figure 4(d).

In conclusion, Bi2Se3 nanostructures with different morphologies have been synthesized and characterized through the methods including SEM, EDS, AFM, TEM and SAED. The as-grown Bi2Se3 samples are n-type doped and display metallic behaviors, which are attributed to the existence of intrinsic selenium vacancies. Transport properties of two typical Bi2Se3 nanostructures (nanoplates and nanobeams) were studied. The topological surface states behave as Dirac fermions due to the existence of a Berry's phase π of the surface states deduced from the analysis of the SdH oscillations. The observation of the singular quantum transport of the topological surface states implies that the high-quality Bi2Se3 nanostructures have superiorities for investigating the novel physical properties and developing the potential applications.

Methods

Synthesis

The Bi2Se3 nanostructures have been synthesized by a simple chemical vapor deposition method in a horizontal tube furnace. Commercial grade Bi2Se3 powders (Alfa Aesar, 99.999% purity) were placed in the center of the tube and used as source materials. Single-crystalline silicon substrates with electron beam evaporated gold thin layer, which acted as catalyst, were placed downstream of the source in order to collect the products. At first, the system was purged by a mechanical roughing pump and flushed by Argon more than three times to get rid of the oxygen. Then the system temperature was elevated to 700°C at a rate of 20°C min−1. After stabilizing the temperature, argon carrier gas was introduced into the system at a flow rate of 30 sccm, not only to transport the sublimated vapors to cooler regions of the furnace, but also to control the proper environmental pressure for growth. The system was held at those conditions for about 0.5 hour and then cooled naturally to room temperature. In order to gather more source vapors, the substrates were placed in the tube furnace with an angle of 30 degrees to the horizontal.

Device fabrication and measurements

Bi2Se3 nanostructures were transferred to a Si substrate with 300 nm SiO2 layer. Using a standard e-beam lithography technique, six-terminal Hall bar structure was patterned on individual Bi2Se3 nanoplates and multi-terminal electrodes were patterned on individual Bi2Se3 nanobeams. Via e-beam evaporation of Cr/Au (50/100 nm) and lift-off processes, the fabricated devices allowed us to measure the transport properties via four-probe method or Hall bar configuration. Transport measurements were performed in an Oxford Instrument with variable temperature insert (VTI). The electrical signals were measured using low-frequency lock-in techniques. The magnetic field up to 14 T was applied perpendicular to the substrate plane.

Author Contributions

Z.M.L. conceived and designed the study. Y.Y. performed the experiments. Y.B.Z., Y.Q.B., J.J.C., J.M. helped to do the experiments. D.P.Y. and X.S.W. gave scientific advice. Z.M.L. wrote the manuscript. H.C.W. commented on the manuscript. All authors contributed to discussion and reviewed the manuscript.

Supplementary Material

Supplementary Information

Supporting Information

srep01264-s1.pdf (1.1MB, pdf)

Acknowledgments

This work was supported by MOST (Nos. 2013CB934600, 2012CB933401, 2009CB623703), NSFC (Nos. 11274014, 11234001), and the Program for New Century Excellent Talents in University of China.

References

  1. Bernevig B. A. & Zhang S. C. Quantum spin Hall effect. Phys. Rev. Lett. 96, 106802 (2006). [DOI] [PubMed] [Google Scholar]
  2. Fu L., Kane C. L. & Mele E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007). [DOI] [PubMed] [Google Scholar]
  3. Qi X. L., Hughes T. L. & Zhang S. C. Topological Field Theory of Time-Reversal Invariant Insulators. Phys. Rev. B 78, 195424 (2008). [Google Scholar]
  4. Hasan M. Z. & Kane C. L. Colloquium: Topological Insulators. Rev. Mod. Phys. 82, 3045 (2010). [Google Scholar]
  5. Qi X. L. & Zhang S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011). [Google Scholar]
  6. Checkelsky J. G. et al. Quantum interference in maroscopic cystals of nonmetallic Bi2Se3. Phys. Rev. Lett. 103, 246601 (2009). [DOI] [PubMed] [Google Scholar]
  7. Zhang H. J. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438 (2009). [Google Scholar]
  8. Xia Y. et al. Observation of a large-gap topological insulator class with a single dirac cone on the surface. Nat. Phys. 5, 398 (2009). [Google Scholar]
  9. Chen Y. L. et al. Experimental realization of a Three-Dimensional topological insulator, Bi2Te3. Science 325, 178 (2009). [DOI] [PubMed] [Google Scholar]
  10. Hsie D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101 (2009). [DOI] [PubMed] [Google Scholar]
  11. Zhang G. et al. Growth of Topological Insulator Bi2Se3 Thin Films on SrTiO3 with Large Tunability in Chemical Potential. Adv. Funct. Mater. 21, 2351 (2011). [Google Scholar]
  12. Wang M.-X. et al. The Coexistence of Superconductivity and Topological Order in the Bi2Se3 Thin Films. Science 336, 52 (2012). [DOI] [PubMed] [Google Scholar]
  13. Zhang Y. et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 6, 584 (2010). [Google Scholar]
  14. Zhang H. B. et al. Magnetoresistance Switch Effect of a Sn-Doped Bi2Te3 Topological Insulator. Adv. Mater. 24, 132 (2012). [DOI] [PubMed] [Google Scholar]
  15. Li H. et al. Controlled Synthesis of Topological Insulator Nanoplate Arrays on Mica. J. Am. Chem. Soc. 134, 6132 (2012). [DOI] [PubMed] [Google Scholar]
  16. Scanlon D. O. et al. Controlling bulk conductivity in topological insulators: key role of anti-site defects. Adv. Mater. 24, 2154 (2012). [DOI] [PubMed] [Google Scholar]
  17. Peng H. et al. Aharonov-Bohm Interference in Topological Insulator Nanoribbons. Nat. Mater. 9, 225 (2010). [DOI] [PubMed] [Google Scholar]
  18. Kong D. S. et al. Topological Insulator Nanowires and Nanoribbons. Nano Lett. 10, 329 (2009). [DOI] [PubMed] [Google Scholar]
  19. Tang H., Liang D., Qiu R. L. J. & Gao X. P. A. Two-Dimensional Transport-Induced Linear Magneto-Resistance in Topological Insulator Bi2Se3 Nanoribbons. ACS Nano 5, 7510 (2011). [DOI] [PubMed] [Google Scholar]
  20. Xiu F. X. et al. Manipulating Surface States in Topological Insulator Nanoribbons. Nat. Nanotech. 6, 216 (2011). [DOI] [PubMed] [Google Scholar]
  21. Cui H. M. et al. Sonochemical synthesis of bismuth selenide nanobelts at room temperature. J. Cryst. Growth 271, 456 (2004). [Google Scholar]
  22. Wang D. et al. Preparation and characterization of wire-like Sb2Se3 and flake-like Bi2Se3 nanocrystals. J. Cryst. Growth 253, 445 (2003). [Google Scholar]
  23. Lin Y.-F. et al. Preparation, Characterization, and Electrophysical Properties of Nanostructured BiPO4 and Bi2Se3 Derived from a Structurally Characterized, Single-Source Precursor Bi[Se2P(OiPr)2]3. J. Phys. Chem. C 111, 18538 (2007). [Google Scholar]
  24. Fang L. et al. Catalyst-Free Growth of Millimeter-Long Topological Insulator Bi2Se3 Nanoribbons and the Observation of the π-Berry Phase. Nano Lett. 12, 6164 (2012). [DOI] [PubMed] [Google Scholar]
  25. Liu Y., Weinert M. & Li L. Spiral Growth without Dislocations: Molecular Beam Epitaxy of the Topological Insulator Bi2Se3 on Epitaxial Graphene/SiC(0001). Phys. Rev. Lett. 108, 115501 (2012). [DOI] [PubMed] [Google Scholar]
  26. Qu D.-X. et al. Quantum Oscillations and Hall Anomaly of Surface States in the Topological Insulator Bi2Te3. Science 329, 821 (2010). [DOI] [PubMed] [Google Scholar]
  27. Cao H. et al. Quantized Hall Effect and Shubnikov–de Haas Oscillations in Highly Doped Bi2Se3: Evidence for Layered Transport of Bulk Carriers. Phys. Rev. Lett. 108, 216803 (2012). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supporting Information

srep01264-s1.pdf (1.1MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES