Comparison of dual-echo DSC-MRI- and DCE-MRI-derived contrast agent kinetic parameters

Abstract

The application of dynamic susceptibility contrast (DSC) MRI methods to assess brain tumors is often confounded by the extravasation of contrast agent (CA). Disruption of the blood–brain barrier allows CA to leak out of the vasculature leading to additional T₁, T₂ and ${\text{T}}_2^{\ast }$ relaxation effects in the extravascular space, thereby affecting the signal intensity time course in a complex manner. The goal of this study is to validate a dual-echo DSC-MRI approach that separates and quantifies the T₁ and ${\text{T}}_2^{\ast }$ contributions to the acquired signal and enables the estimation of the volume transfer constant, K^trans, and the volume fraction of the extravascular extracellular space, ν_e. To test the validity of this approach, DSC-MRI- and dynamic contrast enhanced (DCE) MRI-derived K^trans and ν_e estimates were spatially compared in both 9L and C6 rat brain tumor models. A high degree of correlation (concordance correlation coefficients >0.83, Pearson's r>0.84) and agreement was found between the DSC-MRI- and DCE-MRI-derived measurements. These results indicate that dual-echo DSC-MRI can be used to simultaneously extract reliable DCE-MRI kinetic parameters in brain tumors in addition to conventional blood volume and blood flow metrics.

1. Introduction

Contrast enhanced magnetic resonance imaging (MRI) methods, both relaxivity (T₁)- and susceptibility (T₂ and ${\text{T}}_2^{\ast }$)-based approaches, have demonstrated the potential to measure important characteristics of tumor vasculature in both preclinical and clinical applications. Studies that assess changes in tissue T₁ following the injection of a contrast agent (CA) are commonly termed dynamic contrast-enhanced MRI (DCE-MRI; reviewed in, e.g., Ref. [1]), whereas those relying on T₂ and ${\text{T}}_2^{\ast }$ changes are referred to as dynamic susceptibility contrast MRI (DSC-MRI; reviewed in, e.g., Ref. [2]). As the CA traverses through blood vessels and into the extravascular space, it alters the T₁, T₂ and ${\text{T}}_2^{\ast }$ relaxation rates of tissue water and therefore the measured MR signal intensity. The resultant signal intensity time courses can be related to changes in tissue CA concentration, and, by fitting the DCE- or DSC-MRI data to an appropriate pharmacokinetic model, physiological parameters can then be extracted. The analysis of DCE-MRI yields parameters that relate to tissue perfusion and permeability (denoted by the parameter K^trans) and the extravascular extracellular volume fraction (denoted by ν_e), both of which have been shown to be sensitive to tumor growth and treatment response (see, e.g., Refs. [3–5]). When the CA remains intravascular, blood volume, blood flow, and mean transit time can be extracted from DSC-MRI data and such parameters have been used to assess brain, breast and prostate tumor hemodynamics [6–9]. DSC-MR-derived brain tumor blood volume and blood flow data have demonstrated a correlation with tumor grade [7,10–12] and treatment response [13–15].

A central assumption in DSC-MRI studies is that the CA remains compartmentalized within the blood vessels such that a susceptibility gradient can be induced between the intravascular and extravascular space. Tumor vessels often have increased permeability, so the small molecular-weight Gadolinium-based agents that are widely used in the clinic readily extravasate, resulting in additional relaxation effects in the extravascular space, modulation of the effective transverse relaxivity and, ultimately, alteration of the measured signal intensity time course. The most commonly reported relaxation effect is a decrease in the T₁ of extravascular water which occurs during and following the first pass of the CA through the vasculature and results in a substantial increase of the MRI signal above the pre-contrast baseline [10,16,17]. Conversely, as a consequence of the use of pulse sequences with intentionally reduced T₁ sensitivity (e.g., low flip angle, longer echo times or dual-echo pulse sequences), an increasing number of studies are describing enhanced T₂ and/or ${\text{T}}_2^{\ast }$ effects that result in a substantial and prolonged (minutes after the first pass of the CA bolus) decrease of the MRI signal [18,19]. With commonly used DSC-MRI acquisition and analysis methods, CA leakage has been shown to lead to unreliable estimates of tumor blood volume and blood flow [10,16,17]. However, numerous techniques have been proposed to reduce or eliminate leakage effects including loading doses of CA prior to the bolus injection, low flip angles, longer echo times, dual-echo pulse sequences, baseline subtraction and model-based permeability compensation methods [17,18,20–23].

The correction of CA leakage effects using postprocessing methods or the more complex kinetic models of DSC-MRI signals in tumor tissue typically yield estimates of a parameter related to the CA extravasation rate and/or K^trans [17,18,20–25]. For application to tumors, the simultaneous measurement of blood flow, blood volume, mean transit time and K^trans using DSC-MRI could be a particularly useful and efficient means for grading tumors and assessing treatment response. It would also eliminate the need for multiple injections of contrast agent during a combined DCE/DSC-MRI study. However, estimating permeability or K^trans using DSC-MRI is confounded by competing T₁, T₂ and ${\text{T}}_2^{\ast }$ relaxation effects and the dependency of these interactions on pulse sequence parameters and the underlying physical and physiological properties of the tissue.

For accurate K^trans measurements, the relationship between the MRI signal intensity time courses and the CA concentration is required. While the relative importance of including exchange effects when converting DCE-MRI signals to CA concentrations is still debated, the formalism for such methods has been worked out and various groups are working to validate the models [26,27]. In contrast, the relationship between signal intensity and CA concentration in DSC-MRI, typically termed the susceptibility calibration factor, is unresolved and relies on the (unknown) heterogeneous spatial distribution of the CA within the vascular and extravascular extracellular space (EES) [28]. While this complex relationship may potentially prove to be a useful contrast mechanism, enabling the extraction of features of the EES (e.g. tumor cellular density and/or spacing [28,29]), it likely hinders the reliable measurement of tumor K^trans.

The separation of T₁- and ${\text{T}}_2^{\ast }$-induced signal changes using dual-echo pulse sequences has been shown to be a potential method to simultaneously estimate blood flow, blood volume (from the ${\text{T}}_2^{\ast }$ time series) and parameters related to the extravasation kinetics (from the T₁ time series) in human brain tumors [30–33]. Using similar multi-echo gradient-echo pulse sequences, Kim et al. [34] and Sourbron et al. [24] proposed methods to simultaneously derive the transverse and longitudinal relaxation rates and demonstrated their utility in phantoms and a subcutaneous mouse model of human colorectal cancer, respectively. However, to our knowledge, no study has directly compared DSC- and DCE-MRI-derived T₁ time series and their corresponding kinetic parameters in vivo. Such comparisons are essential if the dual-echo approach is to be seriously considered as a clinically viable alternative to sequentially acquired DCE-MRI and DSC-MRI data. In this report, the validity of the dual-echo-based DSC-MRI approach is evaluated by comparison to DCE-MRI in two rat glioma models with different vascular and CA kinetic properties.

2. Methods

2.1. Animal Studies

Dual-echo DSC-MRI- and DCE-MRI-derived measures of K^trans and ν_e were compared in two rat brain tumor models, the 9L gliosarcoma and the C6 glioblastoma. Animals were immobilized in a stereotactic head holder for all surgical and imaging procedures. Anesthesia was induced via a 5%:95% isoflurane/oxygen mixture and maintained via a 2%:95% isoflurane/oxygen mixture. Ten male Wistar rats (Harlan, Indianapolis, IN, USA) were inoculated with 1×10⁵ C6 gliosarcoma cells (American Type Culture Collection, Manassas, VA, USA) using a 10-μl gastight syringe (Hamilton, Reno, NV, USA). The site of the inoculation was 1 mm anterior and 3 mm lateral to the bregma on the right side of the head, at a depth of 4 mm relative to the dural surface. An identical procedure was used to inoculate 10 male Fischer rats (Harlan) with 1×10⁵ 9L glioma cells (American Type Culture Collection).

MRI experiments were performed on a Varian 4.7-T scanner equipped with a 63-mm quadrature birdcage coil 14–16 days after tumor inoculation. During the imaging experiment, a warm flow of air over the animal maintained the body temperature at 37°C. The respiratory rate was monitored throughout the experiment and maintained at 40–60 breaths per minute. A variable flip angle gradient-echo approach was employed to produce a T₁₀ map, with the following parameters: TR=200 ms, TE =3.1 ms, FOV=(40 mm)², slice thickness=2.0 mm, matrix= 64², four excitations and five flip angles (ranging from 12° to 60°). For the DCE-MRI study, a gradient-echo pulse sequence [TR=15.625 ms, TE=1.9 ms, FOV = (40 mm)², slice thickness=2.0 mm, flip angle=9°, matrix = 64², and one excitation, resulting in a temporal resolution of 1 image s⁻¹] was used to obtain 999 serial images of a single slice in ∼16 minutes of imaging. A bolus of 0.2 mmol kg⁻¹ per body weight of gadopentate dimeglumine (Gd-DTPA, Biophysics Assay Laboratory, Worcester, MA, USA), was manually delivered within 5 s via a jugular catheter after the acquisition of 60 baseline images.

After five Gd-DTPA blood-clearance half-lives (∼2.5 h) were allowed to elapse (without moving the animal within the magnet), the DSC-MRI studies were initiated. Prior to the DSC-MRI study, a second set of variable flip angle gradient- echo images, for T₁₀ mapping, was acquired to ensure complete washout of the CA from the first injection. The DSC-MRI protocol employed a gradient-echo pulse sequence [TR= 15.625 ms, TE1/TE2=5.0/10 ms, FOV=(40 mm)², slice thickness=2.0 mm, flip angle=9°, matrix =64² and one excitation, resulting in a temporal resolution of 1 image per second for 999 images]. Although this pulse sequence is not a traditional echo planar DSC-MRI sequence, we routinely use it for preclinical DSC-MRI studies at 4.7 T due to its lack of susceptibility-related artifacts and favorable signal-to-noise ratio. A similar sequence was previously used to acquire dual-echo DSC-MRI data in human brain tumors [32]. During the course of the image acquisition, a bolus of 0.2 mmol kg⁻¹ per body weight of Gd-DTPA was manually delivered via the same jugular catheter after the acquisition of 60 baseline images. All studies adhered to our institution's animal care and use committee policies.

2.2. Data Analysis

Although animals did not move significantly during the experiment, for each rat we first coregistered all images to the first precontrast image using a rigid-body algorithm. The multiple flip angle data were fit to the following equation to construct T₁₀ maps:

$$S=S_0\left[\text{sin}\alpha \left(1-\mathit{\text{exp}}\left(-\text{TR}/{\text{T}}_{10}\right)\right)/\left(1-\mathit{\text{exp}}\left(-\text{TR}/{\text{T}}_{10}\right)\cdot \text{cos}\alpha \right)\right],$$ (1)

where S₀ is a constant describing the scanner gain and proton density and it is assumed that map was then used to estimate $\text{TE}={\text{T}}_2^{\ast }$. The T₁₀ map was then used to estimate DCE R₁ time courses for each voxel from the raw signal intensity time courses in the manner of Landis et al. [35]. The dual-echo DSC-derived T₁-weighted signal time courses were computed through extrapolation of the dual-echo signal back to TE=0, at each time point, and then combined with the T₁₀ maps to compute the DSC R₁ time courses as previously described [32].

A reference region (RR) model was used to estimate the contrast agent pharmacokinetics from the DCE and DSC R₁ time courses. This model enables the computation of the contrast agent kinetic parameters without the need to measure an arterial input function. Given that a manual injection could introduce variability in the rate and total contrast agent dose administered, the reference region approach was considered preferable to assuming an arbitrary arterial input function as such differences would, in principle, be reflected in the measured reference region time series. Details of the RR theory are described elsewhere [36]. Briefly, a tissue of interest (TOI) R₁ time course, ${\mathit{\text{R}}}_1^{\text{TOI}}$, can be modeled as the following:

$$\begin{array}{l}{R}_1^{\text{TOI}}\left(T\right)=R\cdot (R_1^{\text{RR}}\left(T\right)-R_{10}^{\text{RR}})+R\cdot [\left(K^{\text{trans},\text{RR}}/{\nu }_{e,\text{RR}}\right)-(K^{\text{trans},\text{TOI}}/{\nu }_{e,\text{TOI}})].\\ \underset{0}{\overset{T}{\int }}(R_1^{\text{RR}}\left(t\right)-R_{10}^{\text{RR}})\cdot \mathit{\text{exp}}((-K^{\text{trans},\text{TOI}}/{\nu }_{e,\text{TOI}})\cdot \left(T-t\right))\text{d}t+R_{10}^{\text{TOI}},\end{array}$$ (2)

where ${\mathit{\text{R}}}_1^{\text{RR}}$ and ${\mathit{\text{R}}}_1^{\text{TOI}}$ are the longitudinal relaxation rate constants in the RR and TOI, respectively; K^trans,RR and K^trans,TOI are the contrast agent extravasation rate constants for the RR and the TOI, respectively; ν_e,RR and ν_e,TOI are the EES volume fractions for the RR and the TOI, respectively; ν_e,RR and R≡K^trans,TOI/K^trans,RR. Eq. (2) was used with a nonlinear least squares curve fitting routine to extract K^trans,TOI and ν_e,TOI from the DSC and DCE R₁ time courses for each voxel within the brain tumors. The RR time series was selected from a region of interest in muscle tissue. All imaging analysis was performed in AFNI [37].

2.3. Statistical Analysis

To compare the DSC- and DCE- derived maps of K^trans and ν_e, we performed both region-of-interest (ROI) and voxel-wise analyses. The ROI analysis focused on the correlation between mean tumor parameter values across animals, whereas the voxel-wise analysis focused on the spatial correlation between the DCE- and DSC-derived parameters within each animal. For ROI analysis, we first computed the ROI means of K^trans and ν_e for each animal and for each method. We then computed the following to assess the agreement between DCE and DSC ROI means: (1) the concordance correlation coefficient (CCC), (2) the Pearson correlation coefficient, and (3) the slope of the regression line using DSC as the dependent variable and DCE as the independent variable. For the voxel-wise analysis, we calculated the CCC, the Pearson's correlation and the slope for the regression line separately for each animal.

3. Results

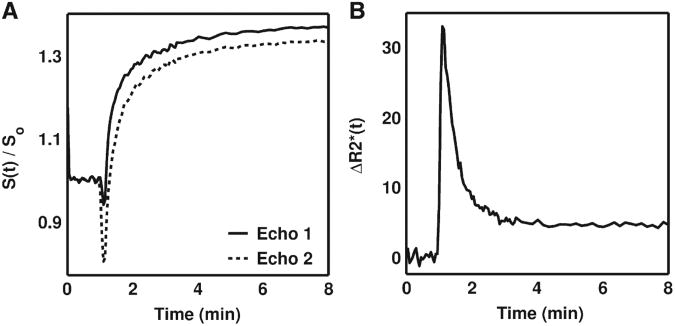
Fig. 1 illustrates examples of dual-echo DSC-MRI signals acquired in the rat C6 brain tumor. Compared to the longer echo time (‘Echo 2’), the shorter echo time (‘Echo 1’) had a higher sensitivity to T₁ leakage effects as evidenced by a smaller signal drop during the first pass of the agent and a higher signal enhancement following the first pass (Fig. 1A). As previous studies have shown, using these two signals to compute the $\Delta {\mathit{\text{R}}}_2^{\ast }$ time course (Fig. 1B) appears to have removed the T₁ leakage effects. Such curves have previously been used to compute measures of tumor blood flow and blood volume [21,31,34].

Fig. 1.

(A) Example C6 tumor MRI signals acquired with dual-echo DSC-MRI and (B) the resulting $\Delta {\mathit{\text{R}}}_2^{\ast }$ time course. As compared to the signal acquired at a longer echo time (Echo 2), the shorter echo time signal (Echo 1) had a lower signal drop during the first pass of the CA and a higher signal enhancement following the first pass, owing to its enhanced sensitivity to T₁ effects. The computed dual echo $\Delta {\mathit{\text{R}}}_2^{\ast }$ time course is free of T₁ leakage effects, which typically appear as negative $\Delta {\mathit{\text{R}}}_2^{\ast }$ values.

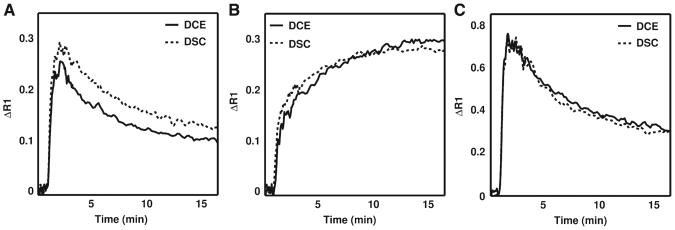
Example DSC- and DCE-derived ΔR₁ time curves for muscle, C6 glioma and 9L gliosarcoma ROIs are interest are illustrated in Fig. 2A–2C, respectively. For the example shown, the DSC-derived ΔR₁ time curve for muscle tissue (Fig. 2A) is 16% higher at peak value as compared to that measured with DCE-MRI. As the injections were manual, some differences in contrast agent dose and rate are expected. The DSC- and DCE-derived ΔR₁ time curves in C6 and 9L tumors, shown in Fig. 2B and C, respectively, are very similar in magnitude and shape. Note the marked difference between the kinetics of the two brain tumor models. This enabled a comparison of the DCE- and DSC-derived kinetic parameters in two tumor models with dissimilar hemodynamic characteristics.

Fig. 2.

Example DSC-MRI-and DCE-MRI-derived ΔR₁ time curves for (A) muscle, (B) C6 glioma and (C) 9L gliosarcoma regions of interest. Despite the use of manual contrast agent injections, the DSC-MRI and DCE-MRI methods yielded ΔR₁ time curves across all the datasets that were generally similar in both shape and magnitude. The ΔR₁ time curves in 9L and C6 whole-tumor regions of interest were markedly different, indicating that the underlying CA kinetics and hemodynamic characteristics of these tumors are dissimilar.

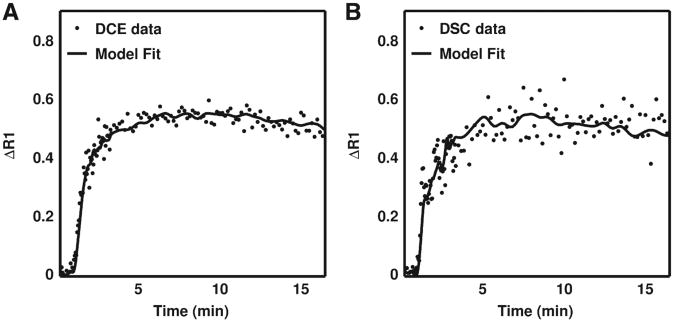
Fig. 3A and B display DSC- and DCE-derived ΔR₁ time curves for a nine-voxel ROIs in a C6 tumor, respectively, and the corresponding kinetic model fit. The filled circles represent the data and the solid lines are the best-fit lines obtained from Eq. (2). Similar to the results shown in Fig. 2, the tumor curves are qualitatively similar in shape and magnitude. Given the influence of noise on the reliability of nonlinear fitting algorithms, we computed each tumor's mean temporal signal-to-noise ratio (TSNR) for the DSC-MRI- and DCE-MRI-derived ΔR₁ time curves. No significant difference was found between the mean DSC and DCE TSNR values (P=.13). Furthermore, with the DSC and DCE methods used herein, we would expect, with 95% confidence, that the difference in TSNR between the two methods will be smaller than 5.6 (confidence interval=−5.6 to 0.77). To assess the goodness of the fit, we compared R² values for the reference region model fits of the DSC- and DCE-derived ΔR₁ time curves. The median DSC and DCE R² values in the 9L group were 0.95 and 0.97, respectively, and 0.96 and 0.98, respectively, in the C6 group.

Fig. 3.

Example (A) DCE-MRI- and (B) DSC-MRI-derived ΔR₁ time curves for a region of interest in a C6 tumor and the corresponding reference region model fit. For this dataset, the DCE-MRI- and DSC-MRI-derived K^trans values were 0.016 and 0.014 min⁻¹ and the ν_e values were 0.09 and 0.1, respectively. Across all animals no statistically significant difference was found between DSC-MRI and DCE-MRI temporal signal-to-noise ratios (P=.13).

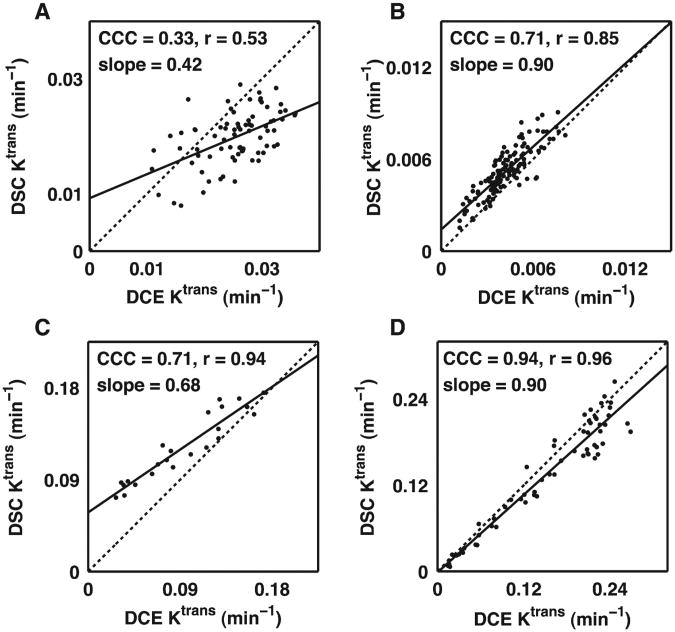
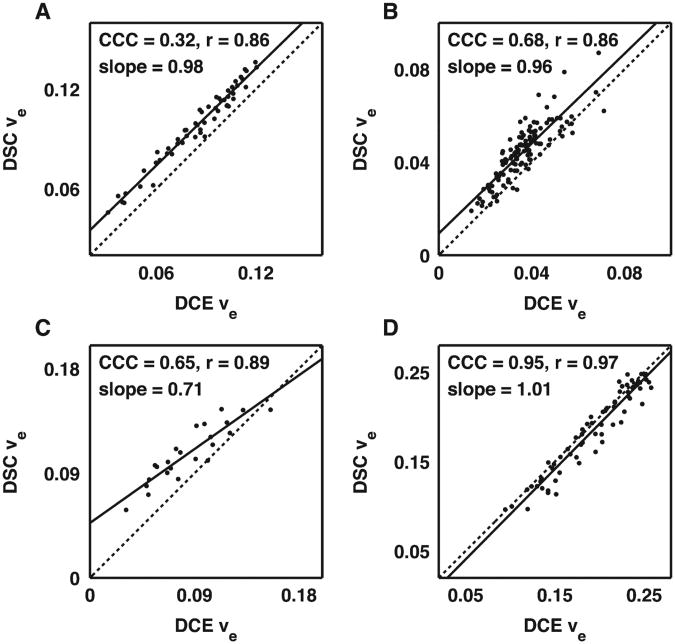
A voxel-by-voxel comparison of DSC- vs. DCE-derived K^trans and ν_e values from four brain tumor-bearing rats are shown in Figs. 4 and 5, respectively. To illustrate the range of the results, scatterplots are presented illustrating the lowest measured CCC (Figs. 4A and 5A) over all the 9L and C6 data, the CCCs closest to the median value for C6 (Figs. 4B and 5B) and 9L (Figs. 4C and 5C) data, and the highest CCC (Figs. 4D and 5D) over all the 9L and C6 data. For K^trans and ν_e, the median CCC, r and slope across all 9L and C6 tumors were 0.71, 0.88 and 0.83, and 0.67, 0.88 and 0.83, respectively.

Fig. 4.

Voxel-by-voxel comparison of DSC-MRI- and DCE-MRI-derived K^trans values representing the (A) lowest CCC for all C6 and 9L datasets, (B) median CCC dataset for C6 tumors, (C) median CCC dataset for 9L tumors and (D) the highest CCC dataset for all C6 and 9L datasets. Overall, there was a reasonable correlation and agreement between the DSC-MRI- and DCE-MRI-derived K^trans values in a given rat with a median CCC, r and slope across all 9L and C6 tumors of 0.71, 0.88 and 0.83, respectively.

Fig. 5.

Voxel-by-voxel comparison of DSC-MRI- and DCE-MRI-derived ν_e values representing the (A) lowest CCC for all C6 and 9L datasets, (B) median CCC dataset for C6 tumors, (C) median CCC dataset for 9L tumors and (D) the highest CCC dataset for all C6 and 9L datasets. There was a reasonable correlation between the DSC-MRI- and DCE-MRI-derived ν_e values in a given rat with a median CCC, r and slope across all 9L and C6 tumors of 0.71, 0.88 and 0.83, respectively.

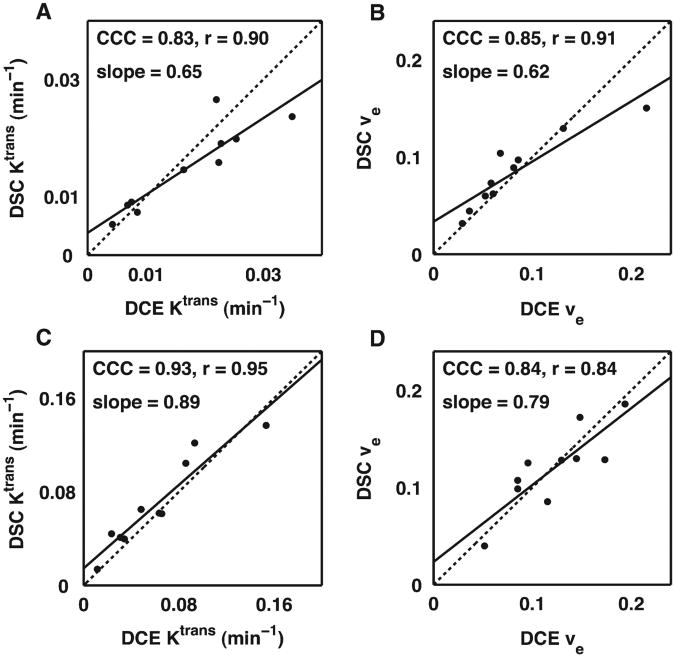
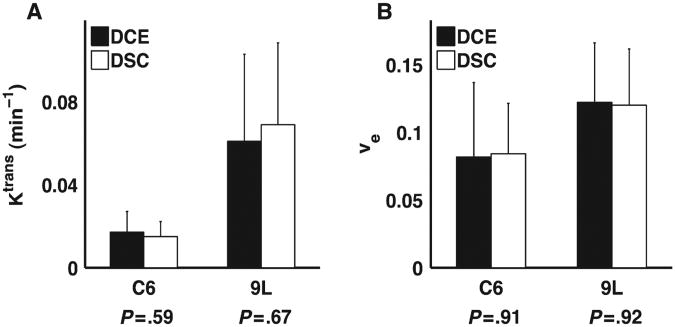
The grouped ROI comparison of DSC- vs. DCE-derived K^trans and ν_e values for the C6 and 9L tumors are illustrated in Figs. 6 and 7, respectively, and summarized in Table 1. As shown in Fig. 6 and Table 1, we found a strong correlation (all CCC and r values >0.83) between DSC and DCE estimates of K^trans and ν_e in both C6 and 9L tumors despite the differences in their underlying pathophysiology and associated CA kinetic characteristics. For all parameters, the slope of the DSC vs. DCE parameter Regression line was less than unity (ranging from 0.62 to 0.89). No significant difference (P>.5) was found between the mean DSC- and DCE-derived K^trans and ν_e values as shown in Fig. 7.

Fig.6.

Grouped region of interest correlation analysis of DSC-MRI- and DCE-MRI-derived K^trans (A and C) and ν_e values (B and D) for the C6 (top) and 9L tumors (bottom). The DSC and DCE estimates of K^trans and ν_e in both C6 and 9L tumors were strongly correlated (the CCC and r values >.83) despite the differences in their underlying CA kinetic characteristics.

Fig. 7.

Grouped region of interest analysis of mean DSC-MRI- and DCE-MRI-derived K^trans (A) and ν_e values (B) in the C6 and 9L tumors. There was no significant difference between the DSC-MRI and DCE-MRI kinetic parameters in either tumor model.

Table 1. ROI Correlation analysis of DSC and DCE kinetic parameters.

Parameter	CCC (95% CI)	r (95% CI)	Slope
Ktrans (C6)	0.83 (0.55−0.94)	0.90 (0.62−0.98)	0.65
νe (C6)	0.85 (0.63−0.94)	0.91 (0.67−0.98)	0.62
Ktrans (9L)	0.93 (0.74−0.98)	0.95 (0.62−0.98)	0.89
νe (9L)	0.84 (0.48−0.96)	0.84 (0.44−0.96)	0.79

CI: Confidence interval.

4. Discussion

In this report, we have described a direct comparison of dual-echo DSC-MRI- and DCE-MRI-derived estimates of K^trans and ν_e in the 9L and C6 rat brain tumor models. We found a high degree of correlation between the DSC-MRI- and DCE-MRI-derived parameters within tumors and across the two tumor types. In this case, a high correlation indicates that the DSC-MRI approach is sensitive to the same physiological range of K^trans and ν_e parameters as is measured with DCE-MRI. The mean tumor K^trans and ν_e parameters for each method were also in good agreement as no significant differences were found in either the C6 or 9L tumor models. This finding suggests that quantitative DSC-MRI measures of K^trans and ν_e should be comparable to those found using conventional DCE-MRI.

Ideally, the regression lines between the DSC- and DCE-derived parameters, such as those illustrated in Figs. 4–6, would have unity slope. For the group-based analysis, the slopes found for each tumor type was less than unity for K^trans and ν_e. In a previous DCE-MRI repeatability study, which used an almost identical study design, we found a slope of 0.77 between the K^trans values derived from the second and first injections of the contrast agent [38]. Such differences potentially result from variations in vessel perfusion expected in animals under anesthesia for extended durations (5 h in this study) or actual changes in tumor physiology over the course of the experiment. Although every effort was made to maintain constant body temperature and respiratory rates during the experiment, the animals' physiological status almost certainly changes under these circumstances and this could have altered the measurements. Imaging the animals on consecutive days could have reduced the animals' exposure to anesthesia during each day's experiment, but the tumor physiology would have likely changed during this period and it would have made it more difficult to compare the same section of tumor tissue. Alternatively, we could have reversed the order of the DCE and DSC studies in half of the animals to remove any bias that is introduced from performing the DSC study after hours of exposure to anesthesia. Furthermore, while the reference region kinetic model should account for any differences in the rate of contrast agent injection, the use of a power injector could have ensured more uniform injections between the DCE and DSC scans.

Given the sensitivity of pharmacokinetic modeling to signal noise, we anticipated that differences in the temporal SNR levels between the DSC-MRI- and DCE-MRI-derived R₁ time series could introduce uncertainty in the extracted parameters. Interestingly, we found no practical difference between TSNR levels or the goodness-of-fit measures between the DSC and DCE data. This indicates that the noise characteristics of the DSC-MRI data do not limit its reliability for DCE-MRI pharmacokinetic modeling.

As indicated earlier, an advantage of the dual-echo DSC-MRI approach for estimating K^trans and ν_e is its reliance on T₁ rather than on T₂ or ${\text{T}}_2^{\ast }$-based changes in the DSC-MRI signal. The estimation of these parameters using T₂ or ${\text{T}}_2^{\ast }$ is confounded by the complicated relationship between the signal intensity and CA concentration, which relies on the spatial distribution of the CA within the EES, the vascular architecture and the interaction of the susceptibility gradients generated by CA within the intra- and extravascular compartments. Even without CA extravasation this relationship is confounded because the vascular susceptibility calibration factor, which is the scaling constant between relaxation rate change and CA concentration, is known to vary across tissues with differing vascular geometries and architecture [39,40]. In tumor tissue, where vascular integrity and architecture are known to be highly heterogeneous, the estimation of CA concentration and the corresponding kinetic parameters from T₂ and/or ${\text{T}}_2^{\ast }$-based signal changes alone is likely to be less reliable than that measured from T₁-based methods.

Another potential advantage of the dual-echo signal acquisition is that it could improve the reliability of the K^trans and ν_e measures. Single-echo-based DCE-MRI signals can be confounded by ${\text{T}}_2^{\ast }$ effects originating from high levels of CA compartmentalized within the vasculature, particularly during its first pass. Similarly, the measurement of an arterial input function (AIF) can be challenging due to such ${\text{T}}_2^{\ast }$ effects. The dual-echo approach enables the quantification of ΔR₁ by removing these ${\text{T}}_2^{\ast }$ contributions so the derived measures of CA concentration, as well as the derived kinetic parameters, should be more reliable. To test this notion we will compare DSC-MRI- and DCE-MRI-derived kinetic parameters to those derived from gold standard methods (e.g. quantitative autoradiography).

Future studies will also focus on how the selection of the echo times, the number of echoes and the difference between them, influence the reliability of the computed ΔR₁ time series. With the goal of simultaneously assessing CA-induced T₁ and ${\text{T}}_2^{\ast }$ changes, it seems reasonable to minimize the shorter echo time for optimal T₁ contrast. The second echo time could be selected to optimize the quality of the AIF and the contrast-to-noise ratio. The dual-echo gradient-echo spiral -out sequence recently applied in a DSC-MRI study of human brain tumors could potentially satisfy both conditions [41]. While the use of additional echoes may increase the reliability of the derived T₁ and ${\text{T}}_2^{\ast }$ time series, it is likely at the expense of temporal resolution and/or tissue coverage.

It is increasingly apparent that T₁ and ${\text{T}}_2^{\ast }$ extravasation effects confound and reduce the reliability of DSC-MRI-derived measures of blood flow and blood volume. While the T₁ effects are easily removed using multiple-echo acquisitions, such as the dual-echo approach used herein, accounting for the ${\text{T}}_2^{\ast }$ effects remains an active area of investigation. As mentioned above, the influence of ${\text{T}}_2^{\ast }$ leakage effects on the acquired DSC-MRI signals will greatly depend on the geometrical compartmentalization of CA within the EES. The geometry of the CA within the EES is most likely determined by the cell density and the spatial distribution of cells around blood vessels. This will introduce an additional and unknown susceptibility calibration factor relating the measured ${\text{T}}_2^{\ast }$ change to the EES CA concentration. These ${\text{T}}_2^{\ast }$ effects can be substantial at time points past the first pass of the CA, where the vascular CA concentration is low. Indeed, DSC-MRI sequences employing heavily ${\text{T}}_2^{\ast }$-weighted acquisition methods often exhibit tumor $\Delta R_2^{\ast }$ time curves that do not return to the baseline over the duration of a typical DSC-MRI study and are higher in magnitude than would be observed for typical recirculation effects. Since the dual-echo approach provides a measure of the EES CA concentration, it may be possible to estimate this previously unknown calibration factor. This EES susceptibility calibration factor could provide a new contrast mechanism for characterizing tumor tissue as it potentially reflects features of tumor cellularity such as cell density. Furthermore, it may be possible to utilize the EES CA concentration time curves and the derived calibration factor to remove the contributions of the T₁ and ${\text{T}}_2^{\ast }$ extravasation effects on DSC-MRI signals and ultimately improve the reliability of the blood flow and blood volume measurements. With these improved acquisition schemes and signal characterization steps, DSC-MRI may become a robust tool for the characterization of cerebral and non-cerebral tumor tissues. However, systematic validation of the derived kinetic parameters with gold standard metrics is still critical for the widespread acceptance of DSC-MRI methodology.

With conventional DSC-MRI it is well recognized that measures of tumor blood flow, blood volume and mean transit time can be assessed. We demonstrate that a dual-echo DSC-MRI experiment, when combined with a pre-contrast T₁ map, enables the reliable determination of the K^trans and ν_e parameters typically acquired in a quantitative DCE-MRI study. Given the experimental and clinical success of the DSC- and DCE-derived parameters to interrogate tumor vascular status, tumor grade and treatment response, the simultaneous approach described herein could serve as an important clinical tool for the management of patients with brain tumors.