Abstract
It is well established that non-uniform sampling (NUS) allows acquisition of multi-dimensional NMR spectra at a resolution that cannot be obtained with traditional uniform acquisition through the indirect dimensions. However, the impact of NUS on the signal-to-noise ratio (SNR) and sensitivity are less well documented. SNR and sensitivity are essential aspects of NMR experiments as they define the quality and extent of data that can be obtained. This is particularly important for spectroscopy with low concentration samples of biological macromolecules. There are different ways of defining the SNR depending on how to measure the noise, and the distinction between SNR and sensitivity is often not clear. While there are defined procedures for measuring sensitivity with high concentration NMR standards, such as sucrose, there is no clear or generally accepted definition of sensitivity when comparing different acquisition and processing methods for spectra of biological macromolecules with many weak signals close to the level of noise. Here we propose tools for estimating the SNR and sensitivity of NUS spectra with respect to sampling schedule and reconstruction method. We compare uniformly acquired spectra with NUS spectra obtained in the same total measuring time. The time saving obtained when only 1/k of the Nyquist grid points are sampled is used to measure k-fold more scans per increment. We show that judiciously chosen NUS schedules together with suitable reconstruction methods can yield a significant increase of the SNR within the same total measurement time. Furthermore, we propose to define the sensitivity as the probability to detect weak peaks and show that time-equivalent NUS can significantly increase this detection sensitivity. The sensitivity gain increases with the number of NUS indirect dimensions. Thus, well-chosen NUS schedules and reconstruction methods can significantly increase the information content of multidimensional NMR spectra of challenging biological macromolecules.
Keywords: nuclear magnetic resonance, Non-uniform sampling, sparse sampling, signal-to-noise ratio, sensitivity, iterative soft threasholding, hmsIST
Introduction
Non-uniform sampling (NUS) has first been proposed twenty five years ago (Barna et al. 1987; Hoch 1989), and numerous procedures for designing sampling schedules, and reconstruction methods have been proposed (Hoch and Stern 1996, 2001). It has clearly been shown that the spectral resolution of multi-dimensional NMR spectra can be dramatically enhanced with NUS. However, its impact on signal-to-noise and sensitivity has not yet satisfactorily been explored and/or has been controversial. Thus, NUS has still not become mainstream perhaps because standard procedures for creating sampling schedules are still missing, and there are different procedures for spectra reconstruction that cannot easily be applied for routine NMR users or biochemists who are primarily concerned with biological or structural questions rather than signal processing. Off-the-shelf software packages for creating sampling schedules and processing NUS data are still not easily available. More importantly, the benefits of NUS in terms of gain in resolution, signal-to-noise ration (SNR) have not become obvious to the general NMR community. Here we show that NUS and suitable reconstruction methods can enhance both SNR and sensitivity in multidimensional NMR spectra of proteins, which opens new avenues for studies of larger and more challenging systems.
A crucial aspect for NUS is to develop optimal sampling schedules. Initially, it was proposed to use exponentially weighted random sampling (Barna et al. 1987) or uniformly random sampling (Mobli et al. 2006; Kazimierczuk et al. 2008; Rovnyak et al. 2004a). Different approaches of radial or concentric sampling have also been proposed (Kupce and Freeman 2003; Coggins and Zhou 2008). Recently, it was suggested to select the gaps of skipped sampling grid points according to a Poisson distribution (Hyberts et al. 2010; Hyberts et al. 2011) or arranging sampling points picked using Poisson discs (Kazimierczuk et al. 2008). For the comparisons described here we use Poisson-Gap sampling (Hyberts et al. 2010; Hyberts et al. 2011) although similar results might be obtained with other sampling schedules.
Initially, NUS data sets were reconstructed with different versions of Maximum Entropy principles (Barna et al. 1987; Hoch 1989), however several other methods have also been recently developed. Examples include various applications of the CLEAN procedure (Coggins and Zhou 2008; Högbom 1974; Kupce and Freeman 2005; Wen et al. 2011), or the multi-dimensional decomposition method (MDD)(Tugarinov et al. 2005; Hiller et al. 2009; Denk et al. 1986). We have developed the Forward Maximum entropy (FM) method (Hyberts et al. 2007) and could show experimentally that sensitivity can be gained compared to time-equivalent uniform sampling (Hyberts et al. 2010). While the FM approach provides excellent reconstructions of spectra non-uniformly sampled in one or two indirect dimensions (Hyberts et al. 2011; Hyberts et al. 2009) it is computationally expensive for 3D and 4D NMR spectra. A related variant of compressed sensing was shown using an iterative re-weighted least squares approach (Kazimierczuk and Orekhov 2011). The SIFT approach is another technique for reconstruction of NUS spectra (Matsuki et al. 2009). Kozminski and coworkers have developed a procedure termed SSA (Signal Separation Algorithm) (Stanek and Kozminski 2010; Stanek et al. 2011), which is a hybrid approach that combines the concepts of CLEAN (Högbom 1974) and manual artifact removal (Kazimierczuk et al. 2007). We recently developed a procedure based on the principle of iterative soft thresholding (IST) as outlined by Drori who used wavelet transforms (Drori 2007). Our implementation, hmsIST, uses the fast Fourier transform (FFT) and its inverse (FFT−1) as the most time consuming steps during reconstruction (Hyberts et al. 2012b). It is very fast and can readily reconstruct large high-resolution spectra up to 4 dimensions. Thus, we have used hmsIST for analyzing SNR and sensitivity of NUS spectra although similar results could be obtained with other reconstruction methods. Indeed, Nietlispach and coworkers recently described a related approach (Holland et al. 2011; Bostock et al. 2012) but used a minimization of the l1 norm of spectra to reconstruct NUS time domain data.
“Sensitivity” is a commonly debated concept in NMR, especially since NMR itself is considered an “insensitive” technique. Even though often used, it is nearly always confused with signal-to-noise ratio (SNR). While SNR is defined and measured relatively easy, the concept of sensitivity is more elusive. Whereas there is a relationship between the concepts of SNR and sensitivity, and a reasonable intuitive one when dealing with traditional uniformly sampled NMR spectra, the relationship becomes less intuitive when applied to reconstructed NUS spectra. Hence, we find it important to underscore the difference between “sensitivity” and SNR, and to develop a technique in which it is possible to comprehend the sensitivity issue for NUS NMR spectroscopy.
Signal-to-noise ratio (SNR) is a common concept throughout signal processing theory. In traditional signal theory, the SNR is measured in terms of the square root of the fraction between the power of the signal intensity and the power of the noise intensity. This is easily treated mathematically. In the NMR community, however, SNR is defined as the peak height over the root-mean-square value of the noise. Whereas the noise is treated similarly in the two methods of measuring SNR, the NMR way of measuring the signal strength is different. It is more intuitive, more obvious to measure and actually somewhat more sensitive to acquisition specifics than traditional handling in signal theory. The spectrometer-vendors are very well aware of the latter and have to specify sweep widths, carrier position, acquisition length and possible use of apodization, in addition to shimming and tuning of the probe, to receive reproducible values.
In this paper we describe different ways of measuring the SNR and show that NUS can significantly enhance the SNR compared to time-equivalent uniformly recorded multidimensional NMR spectra. In addition, we propose a technique for estimating the sensitivity, defined as the probability of detecting weak peaks, of NUS spectra as compared with time-equivalent uniformly sampled spectra. We show that judiciously planned sampling schedules and optimized reconstruction methods can dramatically enhance SNR and sensitivity. In addition, the enhancement is larger with higher dimensionality of the spectra. The results are based on spectral simulations and comparisons of time-equivalent US and NUS 2D HSQC spectra and 3D 15N-dispersed NOESY experiments. Obviously, there is always a trade off between resolution and sensitivity. The point of this paper is to analyze the effect of NUS on sensitivity at a given resolution determined by the length of the evolution time.
Materials and Methods
Simulations
For our simulations we have utilized several Linux based computer setups, namely (a) an Intel® Core™2 Quad CPU based at 2.40GHz, equipped with a solid-state disk drive for faster file transfer, (b) an 16 core Intel® Xeon® based at 2.67GHz, equipped with 4 optional NVIDIA C2050 Tesla GPU boards, and (c) a 128 core 32 node Intel® Xeon® based cluster at 3.00GHz. The first mentioned was typically used for 1D simulations, the other two options for 2D simulations. Reconstruction of GB1 spectra were performed on the 128-core cluster.
C-shell programming was used extensively for executing and controlling the simulations. Standard UNIX/Linux features as od (octal dump) and sort (sorting) was used on the data sets and several NMRPipe programs, such as addNMR, addNoise, nmrDraw and nmrPipe, constructed the data sets. For producing, reconstructing and converting the simulated data from US to NUS etc., in-house produced programs such as pipe2phf, reduce, phfReduce, istHMS and phf2pipe were used. Standard NMRpipe protocols were used for processing the simulated data.
For the purpose of this paper focused on sensitivity, the signal position was chosen in such a manner that the sinc functions are zero at every point in the frequency domain. This was done to eliminate bias of particular peak max position and keeping the signals symmetrical. In other words, the entire energy of the signals are concentrated in a particular location and not spread over the whole spectral width. This yields the maximum height of a particular signal. Effectively, this eliminates the need for peak fitting.
The procedure for creating sampling schedules with Poisson Gap sampling was described in detail before (Hyberts et al. 2010). We use three weighting approaches, which are identified with the ssw (sinusoidal weighting) parameter. Here ssw=0 indicates uniform random weighting over the whole time domain; ssw=1 stands for sinusoidal weighting using one half of a sinus period with dense sampling at the beginning and the end of the evolution time. Dense sampling at the beginning with weighting according to a quarter of a sinus period is obtained with ssw=2.
All simulations used 1024 complex time domain data points and a sweep width of 7507.50 Hz at 500.132 MHz. The dwell time 1/SW is hence 133.2 μs, and the length of the free induction decay is 137.4 ms. This corresponds to 1.2 T2 where T2 is 113 ms. The data are transformed by using one zero fill to 2048 real frequency domain data points. The final digital resolution is 3.666 Hz/point.
Sample Preparation
For recording the 2D HSQC spectra and the 3D 15N-dispersed NOESY experiments a 2 mM sample of 15N labeled GB1 was prepared as described previously (Gronenborn et al. 1991; Zhou et al. 2001).
Results
Comparison of time-equivalent US and NUS NMR spectra
An estimation of potential gains in SNR or sensitivity due to NUS needs to compare uniformly sampled and NUS NMR spectra acquired at the same overall measurement time. We call these time-equivalent spectra. When only 1/k points of the total Nyquist grid points are sampled, k times more scans per increment are recorded in time-equivalent NUS data. For example, when 8 scans per increment are recorded in the US spectrum, a NUS spectrum with 1% sampling records 800 scans per increment for the same total measuring time. All comparisons presented here are for such time-equivalent spectra.
Recording multidimensional NMR spectra to 1.2 T2 in the indirect dimensions
There is no generally accepted practice of how far out in the indirect dimensions NMR spectra should be sampled. We claim that optimal sampling should extend to around 1.2 T2 of the active coherence in each indirect dimension. This is based on the consideration that up to this evolution time measuring the signal increases the SNR while recoding data beyond this point decreases the SNR. This has been described in detail by Rovnyak (Rovnyak et al. 2004b). Thus, recording data up to 1.2 T2 would provide high resolution at a good SNR. Obviously, spectra of small proteins do not usually suffer from resolution problems and can efficiently be recorded at lower resolution and would not necessarily need high-field instruments. Experimental procedures for such simpler systems are well established. The goal of this study, however, is to optimize spectroscopy for large and challenging proteins that are limited by spectral crowding and sensitivity, and need to utilize the resolution of the highest field instruments.
All simulation and experiments described here are with the goal in mind to sample up to around 1.2 T2 in the indirect dimensions to make use of the resolution power of modern high field instruments while optimizing SNR and the sensitivity to detect as many weak peaks as possible. Indeed, we use the term “detection sensitivity” as the ability to observe weak peaks that are close to the noise level. This is in contrast to the “hardware sensitivity” usually reported by spectrometer companies, which is essentially the SNR for given standard compounds, and is usually much larger than one. This hardware sensitivity is well defined with regard to parameters, such as spectral width, processing, recycling delays, or noise measurement.
Non-uniform sampling can enhance the SNR depending on the sampling schedules used
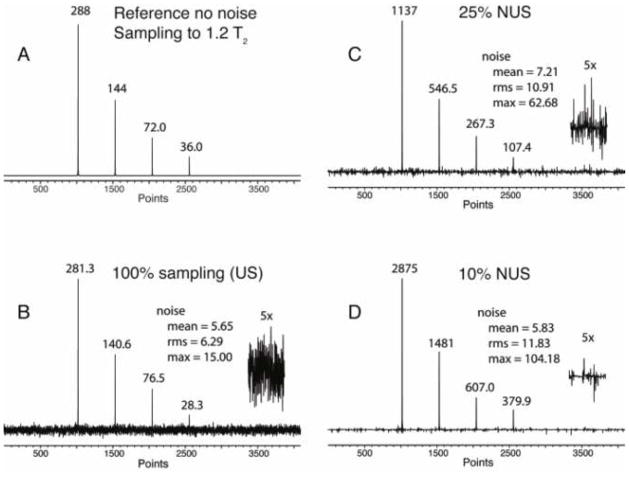
To test whether NUS can enhance the SNR we simulated a 1D spectrum as an example of an indirect dimension (1024 complex points, 7507.50 Hz), with four signals of relative intensities 1, 0.5, 0.25 and 0.125 (Fig. 1A and Table 1). RMS Gaussian noise was added to simulate real spectra with a final noise level of 2.2% rms of the tallest signal. The time domain signal was sampled out to 1.2 T2 (0.113 sec, 1024 complex points) either uniformly (Fig. 1B), or non-uniformly with sampling densities of 25% and 10%, using Poisson-Gap sampling as described previously (Hyberts et al. 2010) and using a sinusoidal weighting parameter (ssw=2), which weighs the gap lengths according to the first quarter of a sine function. This means dense sampling at the beginning and larger gaps at the end of the acquisition time. To compare time-equivalent spectra acquisition, in the 25% NUS spectrum, the signal intensities were increased by a factor of four, and the noise was increased by a factor of two. Similarly, in the 10% NUS spectrum, the signal intensities were increased by a factor of 10, and the noise was increased by a factor of . The NUS spectra were reconstructed with the hmsIST program (Hyberts et al. 2012b), and the time domain date of the US and the two reconstructed NUS FIDs were Fourier transformed with the same processing parameters.
Fig. 1.
Simulation of the effect of NUS on the signal to noise ratio (SNR) in time-equivalent spectra. A. Spectrum simulated with an array of four Lorentzian signals of different height without simulated noise. The time-domain signal is sampled to 1.2 T2. The FID contains 2k complex points. B. Same but noise was added, the time domain data we transformed with FFT. C. NUS (25% density, SS=2, 4 x NS) D. NUS (10% density, SS=2, 10 x NS). The NUS time domains were reconstructed with hmsIST. In all cases the final time domain signals were zero filled and Fourier transformed without apodization. The generated peak heights are marked in the figure.
Table 1.
Comparison of intensities and SNR of a simulated four-line spectrum with 2.2% rms white Gaussian noise relative to the tallest signal, sampled uniformly and non uniformly with 25% and 10% sampling densities (see Fig. 1).
| line | intensity absolute | Intensity relative | SNR mean | SNR rms | SNR max | |
|---|---|---|---|---|---|---|
| no noise | 1 | 288 | 1 | |||
| 2 | 144 | 0.5 | ||||
| 3 | 72 | 0.25 | ||||
| 4 | 36 | 0.125 | ||||
| US with noise | 1 | 281.3 | 1 | 49.8 | 45 | 18.8 |
| 2 | 140.6 | 0.499 | 24.9 | 22 | 9.4 | |
| 3 | 76.5 | 0.272 | 13.5 | 12 | 5.1 | |
| 4 | 28.3 | 0.101 | 5 | 4.5 | 1.89 | |
| 25% NUS | 1 | 1137 | 1 | 157 | 104 | 18.1 |
| 2 | 546.5 | 0.48 | 75 | 50 | 8.7 | |
| 3 | 267.3 | 0.235 | 37.1 | 25 | 4.2 | |
| 4 | 107.4 | 0.094 | 14.9 | 8.8 | 1.7 | |
| 10% NUS | 1 | 2875 | 1 | 483.1 | 244 | 27.6 |
| 2 | 1481 | 0.515 | 254 | 125 | 14.21 | |
| 3 | 607 | 0.211 | 104 | 51 | 5.83 | |
| 4 | 379.9 | 0.132 | 65 | 32 | 3.65 |
The peak heights obtained are annotated in the four panels of Fig. 1 and listed in Table 1. As can be seen the relative peak heights are essentially the same within the scope of the original noise added. The noise was measured using three different procedures: mean, rms and max. These are defined as following:
where |vi| is the absolute value of a data point only containing noise. A representative section of noise is plotted with a five-fold expansion and the values of measured noise are listed in the text boxes. The signal-to-noise ratios obtained for the three procedures of noise measurement are listed in Table 1. It is clear, when using mean or rms noise, the SNR is dramatically enhanced in time-equivalent NUS spectra. On the other hand, when using the maximum noise, or peak-noise the gain is more moderate. However, there are no points with larger value of noise than observed in the US spectra. If there were, such elements of noise could be taken as false positives.
It should be noted that the SNR as discussed above does not relate to the accuracy of measuring peak heights. To investigate this we used the same simulated spectrum as in Fig. 1, added 100 sets of random noise with different seed numbers and measured the peak heights. We find that the standard deviation of peak heights in time-equivalent US and NUS spectra is approximately the same (Supplementary Table 1). The hmsIST procedure iteratively transfers the top sections of the peaks to a second file location at stages when the spectrum is still very noisy due to artifacts and real noise. Thus, the accuracy of peak height measurement does not improve with NUS and IST reconstruction of the data. Mathematically speaking, the noise is not only non-Gaussian but also non-uniformly distributed. The IST reconstruction procedure suppresses apparent noise in spectral regions that do not contain signals because those regions are transferred to the other file location at late stages of the reconstruction. We measured the standard deviation of the noise in Figs. 1 B, C and D, which remains the same for these-equivalent US and NUS spectra (see noise measures in Fig. 1) but the noise is distributed differently as measured by the kurtosis and shown in Supplemental Fig. S1. On the other hand, the signal strengths are increased due to the NUS and IST reconstruction. The absolute peak heights are listed in Fig. 1 on top of the peaks. This causes the spectral appearances in Fig. 1 with an apparent increase of SNR, which facilitates analysis of the spectra and enhances the ability to detect weak peaks as described below.
Experimental comparison of SNR in US and time-equivalent NUS spectra
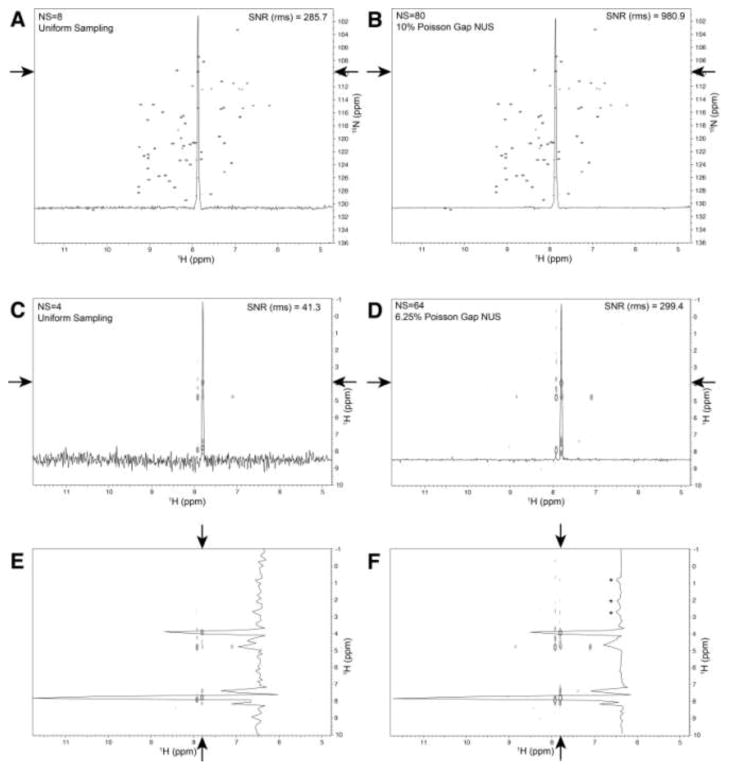
Next we asked whether the SNR gain in NUS spectra indicated by the simulations described above might also be observed experimentally. We measured two 1H-15N HSQC spectra of a 2 mM sample of the GB1 domain of staphylococcal protein G (GB1). The first spectrum (Fig. 2A) was recorded uniformly with 8 scans per increment; the second spectrum (Fig. 2B) was recorded non-uniformly with 10% Poisson Gap sampling, ssw=2, and 80 scans per increment. A representative cross section is shown in both spectra, and the SNR (rms) was calculated. The noise for this calculation was taken from the data between 7 and 6 ppm. Indeed, the SNR in the time-equivalent NUS spectrum has increased by a factor of ~3.5. This confirms the results of the simulations shown above. To confirm that this result can be extended to 3-dimensional spectra, we collected a low resolution 3D 15N edited NOESY (64 15N x 128 1H increments, 4 scans per increment, 500 MHz instrument, RT probe) on the above GB1 sample using both uniform sampling and non-uniform sampling of 1/16th of the data, with 16 times more scans per increment. Fig. 2C (uniform) and Fig. 2D (non-uniform) show the same 15N plane of the NOESY with a cross section in the direct 1H dimension running through a single peak. Noise measurements of the data between 10.5ppm and 8.5ppm where used to estimate the SNR. In this case, the SNR was improved ~7.2 times on the non-uniform sampled spectrum. Fig. 2E and Fig. 2F correspond to the same data as shown in Fig. 2C and Fig. 2D, respectively, however, a vertical cross-section is plotted; these are cross peaks from the diagonal backbone amide proton at ~ 7.8 ppm. The higher SNR apparent in Fig. 2D and hence Fig. 2F appears to make clearer several NOE cross peaks between 3ppm and 0.5 ppm (indicated by asterisks) that are within the noise in Fig. 2E. To test whether these peaks are real and not the result or reconstruction artifacts, we recorded a high resolution US spectrum on our sample with 64 15N x 1200 1H increments on a 900 MHz instrument with cryoprobe. A comparison of the vertical cross-sections through this system for the US, NUS and high resolution US spectra is shown in supplemental Fig. S2. It is clear the signals identified in the NUS cross-section with asterisks are real.
Fig. 2.
Experimental comparison of the SNR in time-equivalent US and NUS 2D 1H-15N HSQC spectra (A, B) and 3D 15N-dispersed NOESY experiments (C–F). The spectra were recorded on an Agilent 500 spectrometer with a RT probe. A) A 2D 1H-15N HSQC of GB1 was recorded uniformly with 8 scans per increment, or B) non-uniformly measuring 10% of the Nyquist points and 80 scans per increment. A single horizontal cross section through a peak (indicated by arrows) is plotted on both spectra. The SNR using the rms measure of noise was improved by a factor of 3.4. C) US (4 scans) and D) NUS (64 scans, 6.25% sparsity) versions of a 3D 15N dispersed NOESY experiment. In each case a single 15N plane is plotted and a horizontal 1D cross section is plotted through a single cross peak (C and D, indicated with arrows). The SNR using an rms measure indicates an improvement by a factor of ~ 7.2. Panels E and F correspond to panels C and D above, however a vertical cross section is drawn through one system of data (indicated by arrows). The SNR improvement can be qualitatively seen by the apparent appearance of extra NOE cross peaks for the NUS data, indicated by asterisks. Whether these are real peaks was tested with a longer uniformly sampled spectrum recorded on a 900 MHz instrument with a cryogenic probe. The comparison is shown in supplemental Fig. S2, which validates the labeled signals as real peaks.
Spectral sensitivity as the ability to observe a weak peak
The important aspect of sensitivity in multidimensional NMR experiments is the ability to detect weak peaks that are close to the noise level. Strong peaks will always be detectable with any sampling/reconstruction technique while very weak peaks will never be detected above the noise, irrespective of the sampling and processing method. Whether sensitivity is improved by specialized sampling/reconstruction has to focus on detectability of weak peaks with heights around the noise level. Thus, we asked whether time-equivalent NUS is more reliable than US for detecting weak peaks that are around or barely above the noise level.
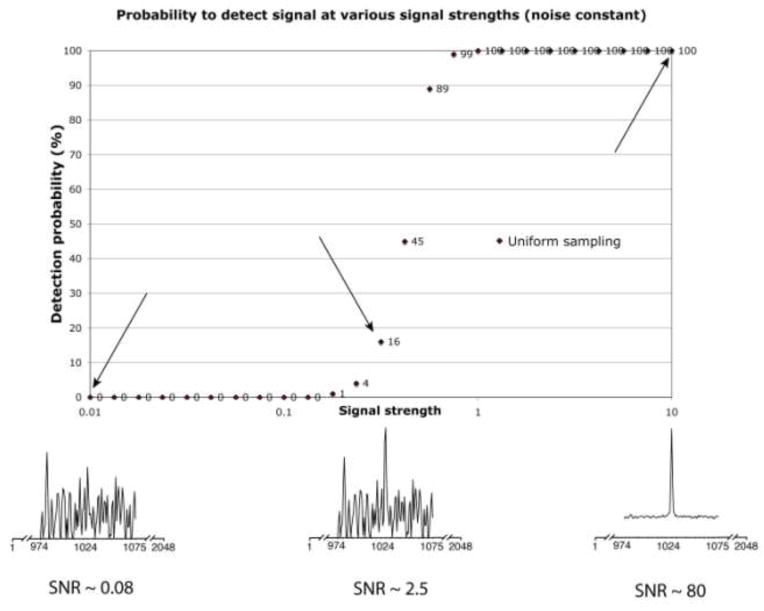
To address this question we performed a series of simulations. In each simulation, a single signal of defined intensity (signal strength) and line width is simulated, random noise is added, and an automated peak picker is used to see whether the signal can be detected unambiguously (see below). This procedure is repeated 100 times with different sets of noise generated randomly where the seed value varies from set to set, but the rms parameter of the noise is kept constant. The number of times the automated peak picker identifies the correct peak out of the 100 simulations is given as the probability of identification of the peak in percent. The results are summarized in Fig. 3 for signal strength from 0.01 to 10, plotted on a logarithmic scale. The intensity setting of 10 was later found to represent a SNR of approximately 80.
Fig. 3.
Procedure for estimating the detection sensitivity of NMR spectra. The method is applicable to US as well as NUS obtained data. For visualization, Figure 3 demonstrates the procedure on a one dimensional US spectrum. A signal is generated synthetically in the time domain, here using 1k complex data points. The frequency position is well known and documented, the simulated relaxation set to be exponentially declining to 1/(1.2*e) emulating an FID obtained to 1.2*T2. Various sets of white Gaussian noise, in this case 100 sets, were added with rms values set constant. This was the repeated for different signal strengths as indicated on the horizontal axis. The absolute signal strength of 10 was later found to represent a SNR of around 80. Each simulated spectrum is then zero-filled and Fourier transformed. A routine is developed that identifies if the signal is detected successfully (see text), and the fraction of correct identifications is plotted in percent versus the signal strength. Three examples of signal strength are further identified, when the signal cannot be detected, when the signal can be detected occasionally and when it is expected that the signal should be detected with no problem. Out of the curve it is then possible to identify various statistical measure, e.g., 10%, 50% and 90% likelihood measures.
For processing, each time-domain signal is zero-filled. The peak location of the simulated signals is known to be exactly in the center at 1024 of 2048 points. If the pixel with the greatest value is 1024 and at least a factor of , or 1.414 times greater than the next largest pixel value it is counted as a success. Three representative simulations with relative signal strengths of 0.01, 0.316 and 10 are plotted with the noise. The SNR for the three cases is 0.08, 2.5 and 80. The resulting probability of detecting the signals correctly is 0%, 16% and 100%, respectively. The probability (as a percentage) of finding the correct peak is plotted in Fig. 3. Below we use this procedure to compare the spectral sensitivity between different time-equivalent US and NUS spectra.
Comparison of the detection sensitivity of time-equivalent US and NUS spectra
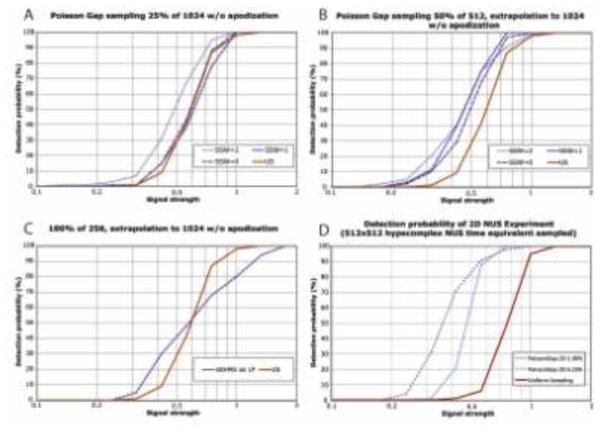
To test whether NUS can enhance the detection sensitivity we produced the sensitivity curve as described in Fig. 3 for different sampling schedules. Results are shown in Fig. 4. In Fig. 4A we compare the detection sensitivity of US (red) with three time-equivalent 25% NUS data generated with the Poisson-Gap Sampling procedure (Hyberts et al. 2010) corresponding to one indirect dimension. SSW=0 is a sampling schedule where the sampling gap parameter for the Poisson-Gap Sampling is uniform over the whole evolution time. Thus, the 25% sampled points do not have any preference to what part of the FID they are sampled more densely. The plot of SSW=0 compared to US shows that there is no sensitivity gain. SSW=1 represents a Poisson-Gap sampling schedule weighted with dense sampling at the beginning and the end of the indirect dimension, and the gap length parameter follows one half of a sine period. Again this does not provide a sensitivity gain. However, if we weigh the gap length parameter according to a quarter of the sine period (SSW=2) we obtain a significant gain of spectral sensitivity. For example, for a signal strength of 0.5, we have a 30% chance of detecting the signal with US and NUS using SSW=0 or 1, however with SSW=2, we have a 52% chance of observing the peak. Thus, we gain detection sensitivity when sampling densely where the signal is strongest.
Fig. 4.
Comparison of the detection sensitivity between US (red) and NUS spectra using different sampling schedules for one (A,B,C) and two (D) indirect dimensions. The procedure outlined in Fig. 3 is applied to various situations of NUS sampling (A,B,C) as well as multiple dimensions (D). The findings are discussed in the text. Note that the calibration of signal strength is dependent on the number of dimensions and other factors. Conclusions should only be drawn within a particular subfigure, not between subfigures. A: The spectral sensitivity for one indirect dimension is compared between US (solid red) and three NUS indirect dimensions with SSW=0, 1 or 2. Only SSW=2 yields a gain in spectral sensitivity as it samples densely at the beginning where the signal is strongest. B: The first half of the time domain was sampled with 50% sparsity. The missing points and the second half of the time domain were reconstructed with hmsIST. Here all three NUS schedules provide an improved spectral sensitivity. C. The first quarter of the FID was sampled uniformly, and the subsequent three quarters were reconstructed with hmsIST. Although there is a higher probability of detecting weak peaks it is less reliable for detecting stronger peaks. D: Simulation for two indirect dimensions indicates an even stronger enhancement of the spectral sensitivity.
In Fig. 4B we compare US sampling with 25% NUS time-equivalent spectrum where the first half of the time domain was NUS at half the Nyquist grid points selected with Poisson Gap sampling at SSW=0, 1, or 2, and the second half was not sampled at all but reconstructed with hmsIST. We find now that all NUS schedules provide a sensitivity gain. Here for a signal strength of 0.5 with a 30% chance of detection with US, the uniformly weighted NUS (SSW=0) yields a 50% chance of detection, and the two sinusoidal weighted sampling schedules exhibit a 60% chance of detection.
This result let us to ask the question whether it would be beneficial to just sample the first 25% of the time domain data uniformly and predict the subsequent 75% of the time domain data points with hmsIST. This is essentially an attempt to use hmsIST instead of linear prediction and would avoid the need of setting up NUS schedules in the spectrometers. The results of the simulations are shown in Fig. 4C. As can be seen this approach is not advisable. Although there is an enhanced probability of detecting weaker peaks the reliable detection of stronger peaks is significantly reduced.
Next we asked whether NUS in two indirect dimensions of 3D NMR experiments would result in the same or even more enhancement of detection sensitivity. Time-equivalent US and NUS spectra with two indirect dimensions of 512 x 512 hyper-complex points were simulated using the same procedure as described for one indirect dimension. The results are shown in Fig. 4D and indicate that enhancement of detection sensitivity is significantly larger than with only one indirect dimension. Here we compare a US spectrum with the time-equivalent NUS where 6.25% of the Nyquist points were sampled with 16 times more scans per increment. A signal with strength 0.5 is detected with 4% probability with US but with 88% probability when using NUS. When sampling only 1% of the Nyquist grid and recording 100 times more scans per increment the detection-probability curve is shifted even more toward weaker peaks. We expect that the gain in detection sensitivity will be even larger in 4D spectra. However, to perform the analysis as shown in Fig. 4 with simulating hundreds of NUS data sets in three indirect dimensions is extremely time consuming and cannot be done currently with our computing resources. An experimental comparison of US and time-equivalent NUS high-resolution 4D NMR experiments is not feasible since high-resolution 4D US spectra cannot be recorded within a reasonable amount of time. It has been shown however, that high-quality 4D NOESY spectra can be obtained with NUS and suitable reconstruction mehods (Hyberts et al. 2012b; Coggins et al. 2012).
Fidelity of peak positions and line widths in time-equivalent US and NUS spectra
To test whether NUS affects peak positions and line widths, and whether this depends on peak maxima place on or off the Nyquist grid we performed another set of simulations (100 sets of noise per case), which are summarized in Table 2. We compare US with three versions of NUS as described in Fig. 4. The peaks simulated were placed on and off the Nyquist grid. In the Table 2, on and off grid is identified by freq + 0.000, freq + 1.428 and 1.833, respectively. The latter puts the signal exactly between two grid points, the former about 39% away from a grid point. Furthermore, the peaks are simulated with the signal strength of 10.0 and 1.0, respectively. The weak peaks are notoriously difficult to pick, especially if there is only statistical probability of less than 1 to identify the peak at all. The peaks are picked with the NMRPipe peak peaking routine. Hence in this analysis, the peak fitting found in NMRDraw was used.
Table 2.
Effect of sampling schedule and on/off-grid sampling on peak positions and line widths for two representative signal strengths of 10 and 1. We compare uniform sampling (a) with NUS where 256 of 1024 points were selected with Poisson Gap Sampling (b), NUS of 256 out of the first 512 points and IST prediction of the subsequent 512 points (c), and uniform sampling of the first 256 points with IST prediction of the subsequent 768 points (d). Sinusoidal weighting schedules SSW = 0, 1 and 2 (see Methods section) are compared. Peak maxima placed on or off Nyquist grid are compared. Here “freq + 0.000”, “freq + 1.426” and “freq + 1.833” places the peak maximum on the Nyquist grid, at 1/3 off, and at ½ off the grid points. Peaks are fitted with nmrDraw and the resulting maxima (freq) and line width (line) are reported. The simulated data consist of 1024 complex time domain data points (136 ms) resulting in a spectral width after zero filling of 7507.50 Hz.
| digital resolution 3.666 Hz/point | On grid | 1/3 point off | 1/2 point off | On grid | 1/3 point off | 1/2 point off |
|---|---|---|---|---|---|---|
| freq + 0.000, strength = 10 | freq + 1.426, strength = 10 | freq + 1.833, strength = 10 | freq + 0.000, strength = 1 | freq + 1.426, strength = 1 | freq + 1.833, strength = 1 | |
| (a) Uniformly Sampled | freq: 2377.63 | freq: 2378.83 | freq: 2379.46 | freq: 2377.62 | freq: 2378.86 | freq: 2379.45 |
| +/− 0.020 | +/− 0.035 | +/− 0.052 | +/− 0.208 | +/− 0.370 | +/− 0.446 | |
| line: 7.03 | line: 7.83 | line: 8.53 | line: 7.06 | line: 7.89 | line: 8.16 | |
| +/− 0.030 | +/− 0.049 | +/− 0.054 | +/− 0.316 | +/− 0.515 | +/− 0.4704 | |
|
| ||||||
| (b) NUS 256/1024 | freq: 2377.63 | freq: 2378.84 | freq: 2379.46 | freq: 2377.67 | freq: 2378.93 | freq: 2379.52 |
| +/− 0.024 | +/− 0.037 | +/− 0.052 | +/− 0.211 | +/− 0.368 | +/− 0.432 | |
| line: 6.96 | line: 7.75 | line: 8.44 | line: 6.56 | line: 7.36 | line: 7.62 | |
| SSW=0 | +/− 0.028 | +/− 0.047 | +/− 0.053 | +/− 0.209 | +/− 0.419 | +/− 0.334 |
| freq: 2377.62 | freq: 2378.83 | freq: 2379.46 | freq: 2377.55 | freq: 2378.87 | freq: 2379.47 | |
| +/− 0.028 | +/− 0.044 | +/− 0.062 | +/− 0.289 | +/− 0.421 | +/− 0.471 | |
| line: 7.02 | line: 7.82 | line: 8.51 | line: 6.81 | line: 7.63 | line: 7.89 | |
| SSW=1 | +/− 0.032 | +/− 0.054 | +/− 0.062 | +/− 0.300 | +/− 0.525 | +/− 0.441 |
| freq: 2377.62 | freq: 2378.83 | freq: 2379.46 | freq: 2377.57 | freq: 2378.88 | freq: 2379.46 | |
| +/− 0.029 | +/− 0.048 | +/− 0.069 | +/− 0.284 | +/− 0.503 | +/− 0.575 | |
| line: 7.03 +/− | line: 7.83 | line: 8.51 | line: 7.00818 | line: 7.85131 | line: 7.97442 | |
| SSW=2 | 0.035 | +/− 0.062 | +/− 0.070 | +/− 0.349 | +/− 0.628 | +/− 0.585 |
|
| ||||||
| (c) NUS 256/512 + 512 | freq: 2377.65 | freq: 2378.8 | freq: 2379.51 | freq: 2377.67 | freq: 2378.94 | freq: 2379.54 |
| +/− 0.047 | +/− 0.116 | +/− 0.168 | +/− 0.231 | +/− 0.554 | +/− 0.607 | |
| line: 6.64 | line: 7.75 | line: 8.38 | line: 6.49 | line: 7.39 | line: 7.47 | |
| SSW=0 | +/− 0.063 | +/− 0.192 | +/− 0.195 | +/− 0.292 | +/− 0.591 | +/− 0.548 |
| freq: 2377.64 | freq: 2378.79 | freq: 2379.47 | freq: 2377.68 | freq: 2379 | freq: 2379.62 | |
| +/− 0.045 | +/− 0.111 | +/− 0.174 | +/− 0.186 | +/− 0.509 | +/− 0.560 | |
| line: 6.71 | line: 7.80 | line: 8.42 | line: 6.58 | line: 7.56 | line: 7.62 | |
| SSW=1 | +/− 0.064 | +/− 0.190 | +/− 0.214 | +/− 0.375 | +/− 0.541 | +/− 0.451 |
| freq: 2377.63 | freq: 2378.75 | freq: 2379.44 | freq: 2377.59 | freq: 2378.83 | freq: 2379.41 | |
| +/− 0.045 | +/− 0.090 | +/− 0.152 | +/− 0.281 | +/− 0.629 | +/− 0.721 | |
| line: 6.63 | line: 7.73 | line: 8.51 | line: 6.69 | line: 7.51 | line: 7.66 | |
| SSW=2 | +/− 0.061 | +/− 0.172 | +/− 0.205 | +/− 0.467 | +/− 0.859 | +/− 0.765 |
|
| ||||||
| (d) NUS 256/256 + 768 | freq: 2377.62 | freq: 2378.67 | freq: 2379.41 | freq: 2377.43 | freq: 2378.76 | freq: 2379.24 |
| +/− 0.032 | +/− 0.126 | +/− 0.209 | +/− 0.806 | +/− 1.012 | +/− 1.104 | |
| line: 6.15 | line: 7.26 | line: 8.06 | line: 6.82 | line: 7.00 | line: 7.09 | |
| +/− 0.026 | +/− 0.172 | +/− 0.195 | +/− 0.643 | +/− 0.629 | +/− 0.660 | |
From Table 2 it can be seen that both the frequency and the line width measures of NUS reconstruction are practically identical to that of the uniformly sampled data, considering the digital resolution of 3.666; except possibly when using IST to extrapolate rather than interpolate Table 2c and 2d. If there is any recognizable trend, the values are more in an agreement using SSW=2 rather than using SSW = 0 or 1.
The peak positions may depend on whether two or more signals are close to each other. Here a one-signal system was used in order to eliminate the issue of sensitivity enhancement due to interference between signals, and the main point of this paper is on sensitivity. However, we have treated the question of closely spaced peak positions in a recent publication (Hyberts et al. 2012b), which deals with the situation of nearly overlapping peaks but evaluated by FM reconstruction and SSW=2. In our experience there is no particular issue using SSW=2 over SSW=0,1 and IST reconstruction. When analyzing these issues for multiple small signals, the evaluation would not be so simple as to analyze peak maxima, and peak fitting would be appropriate.
The data discussed above show that IST reconstruction works better when interpolation is used rather than extrapolation. This is documented with Table 2 and above. It is inline with our earlier observations that resulted in the Poisson Gap Sampling method (Hyberts et al. 2010), which stated that (1) big gaps of the sampling schedule are generally unfavorable and (2) gaps at the beginning or end of the sampling are worse than in the middle. Indeed, Table 2 indicates an increasing although minor uncertainty of peak positions for the situation in Fig. 4C, especially at the lower intensities. The peak height may not be diminishing, but the ability to pick the maximum value at correct pixels is diminished. Fig. 4C also shows that the issue of sensitivity is not simply that of the initial energy of the sampled data points, but more complex in that the peak height (which essentially is used as a measure of ability to identify the signal) and the peak position also depends on later sampled data. In order to gain maximum sensitivity, a proper mixture of earlier and later sampled data points are observably required. Thus, we do not recommend the sampling schedule examined in Fig. 4C.
Discussion
This manuscript addresses a long-standing question whether NUS can enhance SNR and sensitivity. This is important for large and challenging systems that are at the limit of what can be handled with solution NMR. These are systems for which strongest magnetic fields are required providing the best resolution and hardware sensitivity to enable resonance assignments, structure determination and interaction studies. Uniform sampling in 3D and 4D experiments is not able to cover the resolution in the indirect dimensions that would be possible and desirable based on the spectrometer hardware. On the other hand, many smaller systems often studied with NMR spectroscopy do not require the highest resolution and sensitivity. They can be studied with US, and they do not typically require the highest field instruments. The study presented here is of interest for those systems that are at the limit of what can be done with NMR.
Here we introduce the term “detection sensitivity” and define it as the probabilistic ability to detect weak peaks. This is in contrast to the hardware sensitivity, which is part of the specifications of instruments and measured on concentrated standard samples where the SNR of the test signals are much larger than one. While the hardware sensitivity is clearly related to the detection sensitivity the latter depends on many parameters including the length of the evolution time relative to the relaxation times of the evolving coherences and the sampling schedules. Obviously, it also depends on a reconstruction procedure that doesn’t produce artifacts. The hmsIST program presented recently (Hyberts et al. 2012b) is an example of such software, and it can efficiently reconstruct high-resolution NUS spectra up to 4 dimensions. Other reconstruction procedures (Coggins et al. 2012; Hiller et al. 2009; Jaravine et al. 2006; Bostock et al. 2012) may do this as well but a comparison is outside the scope of this paper and should be performed by a third party.
As described above, the detection sensitivity depends strongly on the sampling schedule. The NUS approach allows sampling where there is most signal while maintaining resolution by sampling more sparsely at time points with lower signal (see Figs. 4A and 4B). Here we simulated and measured data with essentially exponentially decaying coherences. Thus, sampling densely at the beginning and less densely towards the end provides the highest detection sensitivity. The Poisson-Gap sampling makes sure to avoid large gaps and introduces randomization to avoid folding bias. The strategy to sample densely at the beginning and more sparse towards the end has some relation to the well-known multiplication of FIDs with a decaying exponential function. However, this is fundamentally different since multiplication with an exponential downscales measured time domain data points. Furthermore, it requires sampling of the entire Nyquist grid. Here we examined three versions of Poisson Gap sampling (ssw=0, ssw=1 and ssw=2), and also extending a NUS time domain data set into a time range not sampled and reconstructed using hmsIST. The sampling procedures described here are unlikely to present a final strategy of designing sampling schedules. Better schedules may be found, such as for signals with beats due to large uniform coupling constants or constant time evolution periods. This is an important topic for future research.
It is important to mention that the apparent noise produced by reconstructing NUS data is not white as in US spectra. Often the noise is assumed to be Gaussian distributed and white colored. By color of noise, a distribution with equal probabilities of all frequencies is considered “white” when low frequencies are predominant the noise is said to be red; blue noise indicate predominantly high frequency components. The assumption of Gaussian white noise is reasonable for proper use of the NMR electronics, and when no apodization, zero-filling or non-uniform sampling/reconstruction is applied. Apodization typically red-shifts the colors of noise as apodizations typically produce higher amplitudes at the beginning of the FID and smaller towards the end. Zero-filling bring in zero values for the blue components, hence also effectively red-shifts the noise. Non-uniform sampling brings a more complicated distribution of the noise, especially after reconstruction. Whereas the character of uniformly sampled noise after apodization and/or zero-filling is approximately Gaussian, this is far from the case for non-uniformly sampled NMR data. This has been noticed before (Stern et al. 2007; Candes et al. 2008; Hyberts et al. 2012a; Hyberts et al. 2012b; Hyberts et al. 2010). Hence we have suggested monitoring the maximum value of a noise pixel, “peak-noise”, or more mathematically expressed, L∞ noise. This approach has shown to be fruitful since small-intensity signals are often compared with the maximum height noise, and that the calculations have shown to be more fair and stable than L1 or L2 treatment when comparing SNR of uniform sampled data vs. reconstructed non-uniformly sampled data. However, the approach presented here enhances the ability to observe weak peaks that would be lost with traditional US and FFT processing. Our approach of spectra reconstruction also reconstructs noise. It appears to de-emphasizes weak noise points and maintains stronger noise points (see Fig. 1). Strong noise points may appear as false positives. However, they have typically spike-like line shapes and are not larger than the original noise, even for equal time. In heteronuclear 3D and 4D spectra they tend not to connect between assigned resonances. Thus, they do not represent a serious problem.
Conclusion
We have shown that NUS can enhance the SNR and the detection sensitivity of multidimensional NMR experiments when suitable sampling schedules are used. It is important to sample more where the signal is strong and less where it is weak. It is important to maintain much random character in the sampling schedules to avoid folding artifacts. This is achieved with the Poisson-Gap sampling schedules that guarantee randomness and avoid large gaps. The gain in detection sensitivity is more pronounced with higher dimensional data but also significant in spectra with only one indirect dimension. Thus, high-resolution spectra can be recorded at high detection sensitivity.
Supplementary Material
Acknowledgments
This research was supported by the National Institutes of Health (Grants GM047467, GM094608 and EB002026), and the Agilent Foundation.
Abbreviations
- NMR
nuclear magnetic resonance
- hmsIST
Harvard Medical School implementation of the iterative soft thresholding approach
- FFT
fast Fourier transformation
Footnotes
Contribution from Harvard Medical School, Boston, MA 02115, USA
Availability
The programs for generating Poisson Gap Sampling schedule and for reconstruction of NUS spectra are available upon request.
References
- Barna JCJ, Laue ED, Mayger MR, Skilling J, Worrall SJP. Exponential sampling, an alternative method for sampling in two-dimensional NMR experiments. J Magn Reson. 1987;73:69–77. [Google Scholar]
- Bostock MJ, Holland DJ, Nietlispach D. Compressed sensing reconstruction of undersampled 3D NOESY spectra: application to large membrane proteins. Journal of biomolecular NMR. 2012;54(1):15–32. doi: 10.1007/s10858-012-9643-4. [DOI] [PubMed] [Google Scholar]
- Candes EJ, Wakin MB, Boyd SP. Enhancing sparsity by reweighted l1 minimization. Fourier Anal Appl. 2008;14:877–905. [Google Scholar]
- Coggins BE, Werner-Allen JW, Yan AK, Zhou P. Rapid Protein Global Fold Determination Using Ultrasparse Sampling, High-Dynamic Range Artifact Suppression, and Time-Shared NOESY. Journal of the American Chemical Society. 2012 doi: 10.1021/ja307445y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coggins BE, Zhou P. High resolution 4-D spectroscopy with sparse concentric shell sampling and FFT-CLEAN. J Biomol NMR. 2008;42(4):225–239. doi: 10.1007/s10858-008-9275-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denk W, Baumann R, Wagner G. Quantitative evaluation of cross peak intensities by projection of two-dimensional NOE spectra on a linear space spanned by a set of reference resonance lines. J Magn Reson. 1986;67:386–390. [Google Scholar]
- Drori I. Fast l1 Minimization by Iterative Thresholding for Multidimensional NMR Spectroscopy. Eurasip Journal on Advances Signal Processing. 2007;2007:1–10. [Google Scholar]
- Gronenborn AM, Filpula DR, Essig NZ, Achari A, Whitlow M, Wingfield PT, Clore GM. A novel, highly stable fold of the immunoglobulin binding domain of streptococcal protein G. Science. 1991;253 (5020):657–661. doi: 10.1126/science.1871600. [DOI] [PubMed] [Google Scholar]
- Hiller S, Ibraghimov I, Wagner G, Orekhov VY. Coupled decomposition of four-dimensional NOESY spectra. J Am Chem Soc. 2009;131(36):12970–12978. doi: 10.1021/ja902012x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoch JC. Modern spectrum analysis in nuclear magnetic resonance: alternatives to the Fourier transform. Methods Enzymol. 1989;176:216–241. doi: 10.1016/0076-6879(89)76014-6. [DOI] [PubMed] [Google Scholar]
- Hoch JC, Stern AS. NMR data processing. Wiley-Liss; New York, NY: 1996. [Google Scholar]
- Hoch JC, Stern AS. Maximum entropy reconstruction, spectrum analysis and deconvolution in multidimensional nuclear magnetic resonance. Methods Enzymol. 2001;338:159–178. doi: 10.1016/s0076-6879(02)38219-3. [DOI] [PubMed] [Google Scholar]
- Högbom Aperture synthesis with a non-regular distribution of interferometer baselines. Astron Astrophys Suppl. 1974;15:417–426. [Google Scholar]
- Holland DJ, Bostock MJ, Gladden LF, Nietlispach D. Fast multidimensional NMR spectroscopy using compressed sensing. Angewandte Chemie. 2011;50(29):6548–6551. doi: 10.1002/anie.201100440. [DOI] [PubMed] [Google Scholar]
- Hyberts SG, Arthanari H, Wagner G. Applications of Non-Uniform Sampling and Processing. Top Curr Chem. 2011 doi: 10.1007/128_2011_187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyberts SG, Arthanari H, Wagner G. Applications of non-uniform sampling and processing. Top Curr Chem. 2012a;316:125–148. doi: 10.1007/128_2011_187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyberts SG, Frueh DP, Arthanari H, Wagner G. FM reconstruction of non-uniformly sampled protein NMR data at higher dimensions and optimization by distillation. J Biomol NMR. 2009;45(3):283–294. doi: 10.1007/s10858-009-9368-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyberts SG, Heffron GJ, Tarragona NG, Solanky K, Edmonds KA, Luithardt H, Fejzo J, Chorev M, Aktas H, Colson K, Falchuk KH, Halperin JA, Wagner G. Ultrahigh-Resolution (1)H-(13)C HSQC Spectra of Metabolite Mixtures Using Nonlinear Sampling and Forward Maximum Entropy Reconstruction. J Am Chem Soc. 2007;129 (16):5108–5116. doi: 10.1021/ja068541x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyberts SG, Milbradt AG, Wagner AB, Arthanari H, Wagner G. Application of iterative soft thresholding for fast reconstruction of NMR data non-uniformly sampled with multidimensional Poisson Gap scheduling. Journal of biomolecular NMR. 2012b;52(4):315–327. doi: 10.1007/s10858-012-9611-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyberts SG, Takeuchi K, Wagner G. Poisson-gap sampling and forward maximum entropy reconstruction for enhancing the resolution and sensitivity of protein NMR data. J Am Chem Soc. 2010;132(7):2145–2147. doi: 10.1021/ja908004w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaravine V, Ibraghimov I, Orekhov VY. Removal of a time barrier for high-resolution multidimensional NMR spectroscopy. Nature methods. 2006;3(8):605–607. doi: 10.1038/nmeth900. [DOI] [PubMed] [Google Scholar]
- Kazimierczuk K, Orekhov VY. Accelerated NMR spectroscopy by using compressed sensing. Angewandte Chemie. 2011;50(24):5556–5559. doi: 10.1002/anie.201100370. [DOI] [PubMed] [Google Scholar]
- Kazimierczuk K, Zawadzka A, Kozminski W. Optimization of random time domain sampling in multidimensional NMR. J Magn Reson. 2008;192(1):123–130. doi: 10.1016/j.jmr.2008.02.003. S1090-7807(08)00053-0 [pii] [DOI] [PubMed] [Google Scholar]
- Kazimierczuk K, Zawadzka A, Kozminski W, Zhukov I. Lineshapes and artifacts in Multidimensional Fourier Transform of arbitrary sampled NMR data sets. J Magn Reson. 2007;188(2):344–356. doi: 10.1016/j.jmr.2007.08.005. S1090-7807(07)00241-8 [pii] [DOI] [PubMed] [Google Scholar]
- Kupce E, Freeman R. Projection-reconstruction of three-dimensional NMR spectra. J Am Chem Soc. 2003;125 (46):13958–13959. doi: 10.1021/ja038297z. [DOI] [PubMed] [Google Scholar]
- Kupce E, Freeman R. Fast multidimensional NMR: radial sampling of evolution space. Journal of magnetic resonance. 2005;173(2):317–321. doi: 10.1016/j.jmr.2004.12.004. [DOI] [PubMed] [Google Scholar]
- Matsuki Y, Eddy MT, Herzfeld J. Spectroscopy by integration of frequency and time domain information for fast acquisition of high-resolution dark spectra. Journal of the American Chemical Society. 2009;131(13):4648–4656. doi: 10.1021/ja807893k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobli M, Stern AS, Hoch JC. Spectral reconstruction methods in fast NMR: reduced dimensionality, random sampling and maximum entropy. J Magn Reson. 2006;182(1):96–105. doi: 10.1016/j.jmr.2006.06.007. S1090-7807(06)00156-X [pii] [DOI] [PubMed] [Google Scholar]
- Rovnyak D, Frueh DP, Sastry M, Sun ZY, Stern AS, Hoch JC, Wagner G. Accelerated acquisition of high resolution triple-resonance spectra using non-uniform sampling and maximum entropy reconstruction. J Magn Reson. 2004a;170 (1):15–21. doi: 10.1016/j.jmr.2004.05.016. [DOI] [PubMed] [Google Scholar]
- Rovnyak D, Hoch JC, Stern AS, Wagner G. Resolution and sensitivity of high field nuclear magnetic resonance spectroscopy. J Biomol NMR. 2004b;30 (1):1–10. doi: 10.1023/B:JNMR.0000042946.04002.19. [DOI] [PubMed] [Google Scholar]
- Stanek J, Augustyniak R, Kozminski W. Suppression of sampling artefacts in high-resolution four-dimensional NMR spectra using signal separation algorithm. Journal of magnetic resonance. 2011 doi: 10.1016/j.jmr.2011.10.009. [DOI] [PubMed] [Google Scholar]
- Stanek J, Kozminski W. Iterative algorithm of discrete Fourier transform for processing randomly sampled NMR data sets. Journal of biomolecular NMR. 2010;47(1):65–77. doi: 10.1007/s10858-010-9411-2. [DOI] [PubMed] [Google Scholar]
- Stern AS, Donoho DL, Hoch JC. NMR data processing using iterative thresholding and minimum l(1)-norm reconstruction. J Magn Reson. 2007;188(2):295–300. doi: 10.1016/j.jmr.2007.07.008. S1090-7807(07)00211-X [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tugarinov V, Kay LE, Ibraghimov I, Orekhov VY. High-resolution four-dimensional 1H-13C NOE spectroscopy using methyl-TROSY, sparse data acquisition, and multidimensional decomposition. J Am Chem Soc. 2005;127 (8):2767–2775. doi: 10.1021/ja044032o. [DOI] [PubMed] [Google Scholar]
- Wen J, Wu J, Zhou P. Sparsely sampled high-resolution 4-D experiments for efficient backbone resonance assignment of disordered proteins. Journal of magnetic resonance. 2011;209(1):94–100. doi: 10.1016/j.jmr.2010.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou P, Lugovskoy AA, Wagner G. A solubility-enhancement tag (SET) for NMR studies of poorly behaving proteins. J Biomol NMR. 2001;20 (1):11–14. doi: 10.1023/a:1011258906244. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.