Abstract
Neurophysiogists want to place the tip of an electrode in a specific area of the brain. The coordinates of this area can be obtained from standard stereotaxic atlases. However, individual brains may not align with the atlas exactly. Additionally, for chronic recordings, electrodes are placed through a chamber attached to the animal's skull. Thus, the user wants to know where the area of interest is in chamber coordinates, not stereotaxic coordinates. After the chamber has been attached an MRI is often made. This assists in electrode placement, as the location of a target relative to the chamber can be determined based on the atlas. However, doing this in practice requires rough estimation or cumbersome calculations. pyElectrode provides a graphical display and performs calculations necessary to convert between stereotaxic and chamber coordinates, thus facilitating MR-based targeting from an implanted chamber. It also allows the experimenter to visualize recording or stimulation sites during experiments. Finally, it can display and output those sites on an MRI slice background in a format suitable for publication.
Keywords: brain, atlas, stereotaxic, 3D, slice
1. Introduction
In vivo visualization of the brain achieved through magnetic resonance imaging (MRI) technology has broadly impacted the fields of neurological diagnosis, interventional neurosurgery, and neuroscience research. MRI guidance was used as early as the 1980s for the stereotaxic placement of electrodes and radiosurgery probes (Olivier et al., 1983, 1987). In contrast to X-ray, this emerging method allowed the visualization of soft tissue landmarks, such as the anterior and posterior commissures, for surgical planning and execution (Villemure et al., 1987) (for a review, see (Peters, 2006)). Stereotaxic MRI guidance is now used routinely in the placement of deep brain stimulating electrodes in Parkinson's disease (Lozano et al., 2002; Volkmann, 2004) and neuropsychiatric disorders (Holtzheimer and Mayberg, 2011) (for recent reviews, see (Shah et al., 2010; Tierney et al., 2011)). In patients, MRI scanning has also played an important role in visualizing the ultimate position of surgically implanted electrodes, which can be done with little difficulty as long as the electrodes and associated connectors are nonferrous. Early studies recognized that MRI was superior to CT in this regard, allowing for the detailed 3-D visualization of the electrode within surrounding brain tissue (Pillay et al., 1992).
This revolution in brain imaging has not only had an enormous clinical impact, but has also changed the standards for electrophysiological research in nonhuman primates. Researchers with access to an MRI scanner are now able to target and verify the precise position of their electrodes used, for example, for single-unit recordings. In parallel with the early developments for clinical neurosurgery described above, the stereotaxic targeting of deep brain structures based on MRI was also developed for the nonhuman primate, typically the macaque monkey (Rebert et al., 1991). More recently, targeting of deep structures with submillimeter precision has been achieved with the use of natural anatomical landmarks (Asahi et al., 2003; Walbridge et al., 2006) or artificially implanted fiducial markers (Frey et al., 2004). Other efforts aimed to visualize electrodes in situ during (Cox et al., 2008) or after (Nahm et al., 1994) experiments by using X-ray methods coregistered to MRI scans. For more than a decade, MRI scans have been included in research publications to visualize, or in some cases verify, recording sites (Liu and Richmond, 2000; Paton et al., 2006; Matsui et al., 2006; Jing et al., 2010; Yamamoto et al., 2012; Monosov and Hikosaka, 2012), resulting in the gradual decline of postmortem histology as the basis of documenting the positions of recording sites. Most recently, functional magnetic resonance imaging (fMRI) (Logothetis et al., 2001) has made it possible to target electrode recording sites in the brain based on functional signals, which are overlaid on the anatomical MRI from the same animal (Tsao et al., 2006).
Electrophysiological recording in the behaving macaque typically involves the daily insertion of an electrode into the brain through a surgically implanted recording chamber (Evarts, 1968). As this chamber is often implanted at an angle relative to the stereotaxic coordinate system, an experimenter usually logs the position of the recording site with respect to the coordinates established within the angled chamber. A particularly convenient and widely used system for this involves the insertion of a grid system within the chronic recording chamber (Crist et al., 1988; Talbot et al., 2011). Alternatively, one commercial system uses artificial fiducial markers to plan chamber placement surgery and design chamber shape (Brainsight 2, Rogue Research Inc., Montreal, Canada). Chamber grids typically consist of a 2-D array of holes drilled through a 1cm piece of metal or plastic to form parallel columns. The hole spacing and diameter are variable, but are usually on the order of 1mm and 0.5mm, respectively. The selected hole within this 2-D grid (x,y), combined with the distance the electrode is advanced into the brain (z) provides a means to localize the electrode tip, or recording site, in three dimensional space.
It is possible to visualize the columns within the grid using high resolution MRI scans. This is typically done by filling a grid made of plastic with water, sometimes doped with gadolinium, providing a contrast between the visible column of fluid and the invisible surrounding plastic matrix (Paton et al., 2006; Tsao et al., 2006; Kalwani et al., 2009; Ohayon and Tsao, 2011). Based on the orientation of these columns on a given MRI slice, it is possible to determine the best grid hole to reach a given site, and to approximate the desired penetration depth.
Following such a scan, it is possible to determine the position of each chamber-based (x,y,z) position in the brain by extrapolating the trajectory of a given column. This approach requires that the columns be aligned in the same plane as the MRI slice. However, since the chamber, and by extension the grid holes, are often not in the MRI acquisition plane, achieving this alignment requires to rotate the 3D data set using one of many MRI visualization software, compute the electrode positions and finally manually place each computed position on the appropriate slice.
As there is, in principle, a simple transformation between the coordinates of the chamber and a given position in the MRI scan, the above process can be simplified. The present methodological report describes a straightforward means to achieve this transformation in order to allow for a quick visualization of past and prospective recording sites in the brain, along with the corresponding chamber coordinates. The algorithm is described here and is implemented in the form of source code written in Python, also available as executable files that operate on Linux, Windows and MacOs platforms.
The program's primary function is to convert an array of chamber-based coordinates, corresponding to recording sites collected from known depths within known grid holes, into brain coordinates. These sites are then plotted onto a brain slice underneath the recording chamber. In addition to this primary function, the program has the capacity to (1) compute the desired chamber hole and location for a site that is manually specified on the MRI, (2) visualize the orthogonal “chamber projection” onto cross sections at different depths perpendicular to an electrode penetration, (3) visualize the coronal section corresponding to the electrode tip1, and (4) save images in vector graphics format.
It is anticipated that this resource will be of particular use to electrophysiologists who acquire structural MRI images of their subjects following chamber implantation surgery. However, it may also be of interest for those performing targeted pharmacological injections, electrical or optogenetic stimulation, or excitotoxic lesions.
2. Materials and methods
2.1. Problem statement
Currently, reconstruction of an electrode's position is done in two steps. First, the user draws a grid on an MRI slice aligned with a recording plane of the chamber. Then she/he places a marker on the image for each electrode position on this recording plane. Because all the electrode recording positions are not usually located in the same plane, this procedure must be repeated several times and can become long and cumbersome. Given that the mathematical transformations between the chamber and the MRI volume are straightforward, a software solution to this problem would be of significant value. Such a solution must take several practical factors into account. First, it must allow the user to, as easily and accurately as possible, establish the chamber coordinate system. The success of this registration procedure will determine the precision of subsequent steps. Second, it must allow the user to visualize the brain from angles other than the native MRI acquisition angle. This is important because the acquisition, based on a configurable slice package on the scanner, may not be ideal for display, for example because it does not match the coronal section in a standard atlas. Third, the software must be able to fluidly and accurately transform points between the MRI, chamber, and user-visualization coordinates systems (see Section 2.5). Fourth, there must be a straightforward interface allowing the user to quickly register the anatomical MRI scans with the chamber coordinate system. Ideally, the program would additionally provide good visualization and output of the recording sites on the user-rotated MRI slices.
2.2. Data requirements
To work correctly, pyElectrode needs data complying with some requirements. First, pyElectrode can only read MR images saved under the DICOM format. Second, the method requires that the user aligns the chamber in the MRI. Thus, he/she needs visible landmarks to ensure that the chamber's origin and its orientation can be determined accurately. This second point is critical because the whole method is based on the correct localization and orientation of the chamber coordinate system. The procedure we used to obtain adequate landmarks will be described in section 2.8.1. Finally, special care must be taken to avoid distortions in the MR volume because it will affect the accuracy of the method.
2.3. Resampling and interpolation of the MRI volume
Anatomical MRI images are often anisotropic, that is, the resolutions in the three acquisition dimensions are often unequal. To simplify the computations, we resampled voxels in all dimensions using trilinear interpolation to make them isotropic. We used the provided information in the header of the MRI images files to compute the pixel size (Gp [mm/pix]). This gain is used to convert the chamber coordinates into voxel coordinates.
2.4. Coordinate systems
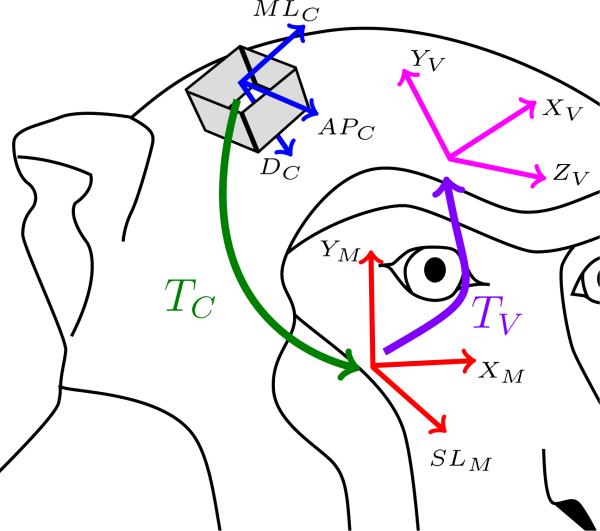
Figure 1 represents the three coordinate systems that will be used throughout the document. The first coordinate system corresponds to the raw MRI images (red lines in Fig. 1) with an origin OM. Two axes (XM and YM) represent the planar position of a voxel in a slice and the third axis (SLM) represents the slice position. The second coordinate system corresponds to the chamber coordinates (blue lines in Fig. 1) with an origin OC. Two axes (MLC and APC) represent the position of the electrode on the grid attached to the chamber and the third axis represents the depth (DC) of the electrode tip. The last reference frame (pink lines in Fig. 1) corresponds to the viewing reference frame, which can be defined arbitrarily by the user, with an origin OV. Because this coordinate system has no specific orientation (e.g. stereotaxic coordinates), the only constraint on three axes (XV, YV and ZV) is that they must define an orthonormal reference frame.
Figure 1.
Coordinate systems and transformations. Three coordinate systems are defined. The MRI axes (M subscripts and red lines), the chamber axes (C subscript and blue lines) and the user view axes (V subscript and pink lines). Two transformations between the coordinate systems are also defined. TC represents the transformation from the chamber coordinates to the MRI coordinates (green arrow) while TV represents the transformation between the MRI reference frame and the user view coordinate system (purple arrow).
The user establishes the chamber coordinate by identifying the center and orientation of the chamber on the MRI images. Ideally, this step only needs to be done once. The user-defined coordinate system can change according to the user's viewing or output preference.
Throughout the text, subscript V will be used to express the position of a point in the user-defined coordinate system, subscript M for the MRI coordinate system and subscript C for the chamber coordinate system.
2.5. Transformations between coordinate systems
Two transformations are used in the paper and represented in Fig. 1. The first one, TC (green arrow Fig. 1), defines the transformation from the chamber coordinate system into the MRI coordinate system. The second, TV (purple arrow in Fig. 1), defines the transformation from the MRI coordinate system into the user-defined reference frame.
Linear algebra and 4-D homogeneous coordinates were used to define these transformations (Foley and Van Dam, 1982):
| (1) |
| (2) |
With ΔCM and ΔMV representing the translations between the origins represented in the MRI coordinate systems:
| (3) |
| (4) |
and RCM, RMV representing the rotations between the coordinate systems. For TC, the rotations are defined to match DC with SLM and APC with YM. RCM is defined as:
| (5) |
with:
| (6) |
| (7) |
| (8) |
For TV, the rotations are defined to match SLM with ZV and YM with YV. RMV is defined as:
| (9) |
with:
| (10) |
| (11) |
| (12) |
2.6. Electrode coordinates in the user-defined view
Using eq. (3) and (5)-(8), one can transform the known positions of the electrode with respect to the chamber into the MRI coordinate system using:
| (13) |
| (14) |
| (15) |
Then, a similar operation can be done to project the position of the electrode into the user-defined reference frame:
| (16) |
| (17) |
| (18) |
2.7. Extract electrode coordinates from a user-defined target
The inverse operation of section 2.6 can be applied to guide electrophysiologists by predicting the coordinates in the chamber reference frame that must be used to hit a brain region. In this case, the user defines a target point (ET) in the user-defined coordinate system. Then, the corresponding chamber coordinates are computed using:
| (19) |
| (20) |
| (21) |
2.8. Software
A graphical user interface has been developed with python to implement the computations presented above. The sources as well as compiled executables for Windows, Linux and MacOs platforms are freely available under U.S. Government copyright from ftp://lsr-ftp.nei.nih.gov/lsr/pyElectrode.
2.8.1. Initial alignment of chamber coordinate system
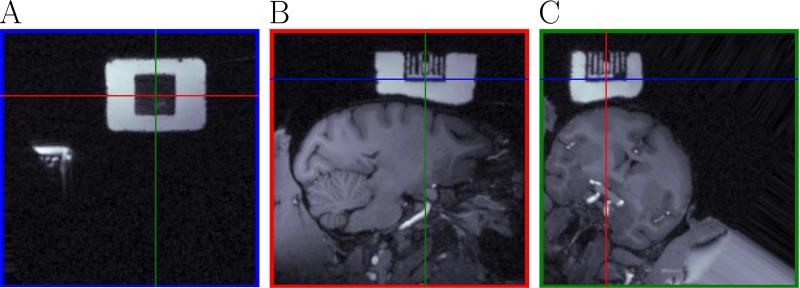
Figure 2 presents four preliminary steps needed to load the scan and align the chamber. These steps establish the chamber coordinate system based on the information in the scan. First, the user loads MRI images saved in DICOM format, then the software plots three orthogonal planes of the MRI with the native orientation, defined during the acquisition (Fig. 2A.1). Second, the user uses 90 deg rotations to create a canonical view in the three windows, showing the transverse plane in the first view, the sagittal plane in the second view and the coronal plane in the third view (Fig. 2A.2). The original MRI can be clipped to remove irrelevant parts of the original images. The MRI coordinate system is defined at this stage. Third, the user aligns the three views on the chamber center. This entails navigating through the MRI using translations to match the origin of the chamber coordinate system (corresponding to the (0,0,0) of the electrode tip) with the intersection of the three viewing planes (Fig. 2B.1). Fourth, the user rotates the MRI around the origin of the chamber coordinate system to align the axes of the chamber coordinate system with the axes of the three viewing planes (Fig. 2B.2). The anterior-posterior axis of the chamber must be aligned with the red line in the left upper view of Fig. 2B.2 (positive direction to the right). The medio-lateral axis of the chamber coordinate system must be aligned with green line in the left upper view in Fig. 2B.2 (positive direction down). Once the origin and the orientation are correctly set, the chamber coordinate system is defined in the program.
Figure 2.
pyElectrode: four steps to load DICOM MRI files and align the chamber coordinate system.
It is important to mention that there are certain assumptions and caveats that affect the accuracy of pyElectrode, or any other method that attempts to establish recording site coordinates on an MRI image. First, we assume that the electrode does not bend during its penetration. However, due to the small diameter of the electrode (in our case 200 μm), the deeper it goes, the more likely it is that the electrode will bend because the slenderness ratio (length over diameter) increases. Second, the method will be more accurate with a recently acquired MRI, because the method supposes that the brain does not move within the skull over time. Third, the method relies on the accuracy of the alignment of the chamber coordinate system.
Therefore, to maximize the utility of this method, it is critical to align MR images on the orientation of the recording chamber. Because every computation is based on the correct alignment of the chamber by the user, an error will be propagated to the position of the electrode in the MRI. For example, an error of 1 deg in the orientation of the chamber can affect the precision of the estimate of the electrode position by ≈0.35 mm for a 20 mm deep penetration. To prevent this type of error, we recommend the following two steps. First, a reference grid is placed inside the chamber. Second, the MR images are aligned on individual grid holes. This can be done by observing the grid hole images while rapidly translating through the MRI. Even a slight tilt will cause the images of the holes to move up and down.
2.9. Experimental procedure
One adult male rhesus monkey (Macaca mulatta) was used in this study. All procedures for animal care and experimentation were approved by the Animal Care and Use Committee of the National Eye Institute and complied with the Public Health Service Policy on the humane care and use of laboratory animals.
During the initial surgery, a plastic head holder and a plastic recording chamber were fixed to the skull under general anesthesia and sterile surgical conditions. The chamber was tilted laterally by 35 deg, and aimed at the ventromedial prefrontal cortex and the anterior portion of the caudate nucleus. The head holder and the recording chamber were embedded in dental acrylic that covered the top of the skull, and were connected to the skull using ceramic screws. (The monkey also had a posterior chamber on the back of its head; this chamber was not used for this report and so is not described.)
During anatomical MRI scanning, the monkey was anesthetized with Ketamine (10 mg/kg) and Diazepam (0.2 mg/kg) intramuscularly, before subsequently being positioned upright and immobilized in a customized chair, designed to be raised into a 4.7 T vertical bore magnetic resonance scanner (Bruker Corp.). Prior to being placed in the scanner, the recording chamber was filled with the magnetic resonance contrast-agent Magnevist (Bayer HealthCare Pharmaceuticals; 1:1200 in 0.9% saline) to visualize the chamber. In addition, a square reference grid (28 mm × 28 mm) was placed within the recording chamber. This reference grid was parallel with the edges of the square recording chamber. The center of the reference grid matched the center of the recording chamber and served as a reference point. The reference grid contained 49 holes (7×7), the centers of which were spaced 2 mm apart. The holes were filled with a saline-gadolinium solution to facilitate MR-based visualization. The reference grid was used specifically for MRI scanning and was different from the grid used for single neuron recording, which had smaller grid holes spaced 1 mm apart. A custom fabricated 12 cm volume transceiver RF coil was secured around the monkey's head. With the monkey sedated and the RF coil in place, the animal was raised into position and a 0.5 mm resolution isotropic MDEFT scan was obtained.
Electrode recordings were carried out in separate sessions while the monkey was awake. Single-neuron and multi-unit activity recording was performed using tungsten electrodes (Frederick Haer) that were inserted through a stainless steel guide tube and advanced by an oil-driven micro-manipulator (MO-97A, Narishige).
3. Results
Here we describe the application of the pyElectrode program in experiments in one monkey, where accurate targeting of medial frontal structures was required. The following sections describe the step-by-step application of the pyElectrode program to a geometrically challenging, but otherwise typical, electrophysiological recording experiment.
3.1. Chamber orientation
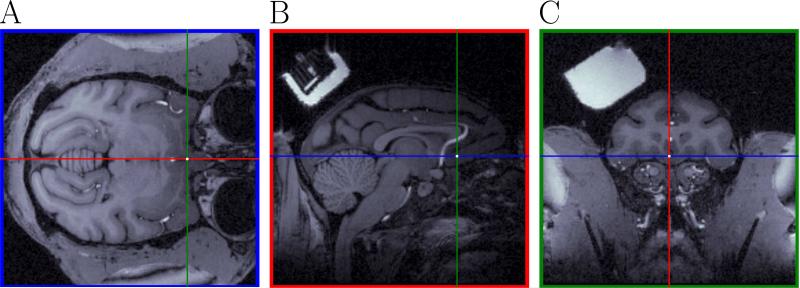
As described in section 2.8.1, the first step is to set the chamber's coordinate system. A correctly oriented chamber is represented in Fig. 3. First, we defined the center of the chamber by translating the three views (panels A-C in Fig. 3) until the intersection of each pair of lines in each panel corresponded to the origin of the chamber. The center was at (-56,-46,19) pixels (blue, red and green MRI coordinates). Once the center was set, we rotated the images to make the axes of the chamber coordinate system horizontal and vertical. According to our experience, the best way to achieve the correct orientation is to align the MR images on individual grid holes, or tubes. This can be done by observing motion of the white lines as you rapidly click the translation spinbox arrows. Even a slight tilt can be detected as vertical movement of the white lines in this “movie”. The goal is to fine-tune the tilt angle until vertical motion is no longer detected and each grid tube is visible uniformly along its entire length.
Figure 3.
Definition of the chamber coordinate system. This figure shows the MRI aligned with the chamber coordinate system defined by the user. Panel A represents a cut in the MRI corresponding to the blue lines in panels B and C. Panel B represents a cut in the MRI corresponding to the red lines in panels A and C. Panel C represents a cut in the MRI corresponding to the green lines in panels A and B. The intersection of each pair of lines in each panel represents the origin of the chamber coordinate system. Panel A shows part of the posterior recording chamber (also visible in Panel B of Fig. 4) not used for the experiment in this paper. The white block is the fluid filling the chamber. The square black block (A) is the reference grid. White columns (B, C) are the filled grid holes.
In this case the needed rotations were (3,4,-34) degrees (rotation around a normal to the plane of Fig. 3A, rotation around a normal to the plane of Fig. 3B and rotation around a normal to the plane of Fig. 3C). Once the chamber was correctly oriented, the last step was to determine a depth correction term to define zero depth for the electrode (because the origin chosen for the chamber coordinates in this case did not correspond to where we defined zero for the electrode). For our experiments, the depth correction term was equal to 16 mm, which corresponds to the distance between the bottom of the grid plug and the exit from the guide tube.
3.2. Hitting a neural region: calculation of electrode coordinates
The targeted neural area in our experiments was the ventromedial prefrontal cortex (vmPFC). White dots in Fig. 4A-C show the location of the targeted neural area. The corresponding MRI coordinates of the target were (2,0,42) pixels (blue, red and green coordinates). Panel C in Fig 4 corresponds to the +31 mm coronal section in the Saleem and Logothetis (2006) atlas.
Figure 4.
Prediction of the chamber coordinates to hit a desired neural area from the MRI. This figure shows the targeted neural structure for recordings in the MRI. Same color convention as in Fig. 3. A white dot at the intersection of the pairs of lines in each plot corresponds to the position of the targeted neural area (Panel B shows a posterior recording chamber (partially visible in Panel A of Fig. 3) not used for the experiment in this paper). Panel C shows the recording chamber used for the experiments in the paper.
Using eq. (19)-(21) from section 2.7, the pyElectrode program calculated the coordinates of the electrode in the chamber coordinate system that must be used to reach the targeted area in vmPFC. The computations give (3.07,9.13,20.777) mm (medio-lateral and anterio-posterior in the chamber, depth of the electrode). Because the spacing between the grid holes was equal to 1 mm for our setup, the computed values were rounded to the closest integer: (3,9,20.777) mm.
3.3. Online tracking of electrode position during recording
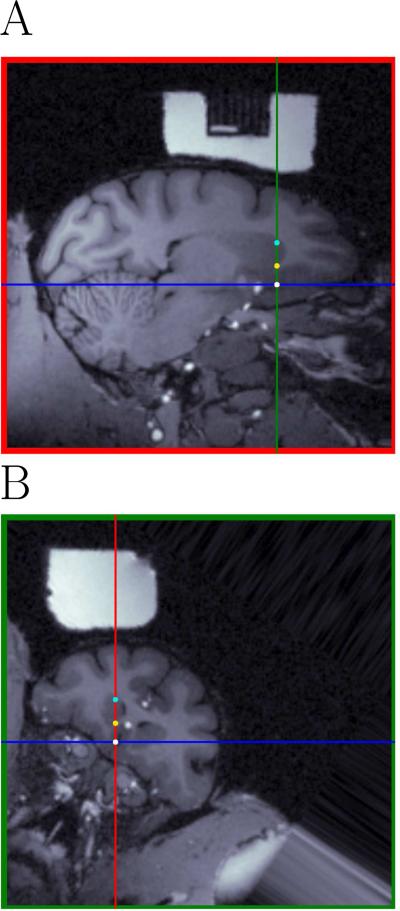
Judging from an MRI and an atlas at which depth a particular structure will be traversed during recording can be difficult, because the orientation of the MRI and the orientation of the chamber are not necessarily aligned, as previously mentioned. The pyElectrode program can be used to follow the electrode by comparing the neural activity during the recording with the computed position of the electrode tip on the MRI. Figure 5 shows views aligned with the chamber coordinate system and centered at the electrode tip (panels A-B). Comparing the size and the shape of the different neural areas in Fig. 5B and Fig. 4C with the +31 mm coronal section in Saleem and Logothetis (2006), one can see that the caudate is larger in Fig. 5B than in the atlas view or in the coronal view of the MRI. The intersection between red green and blue lines in Fig. 5A-B represents the vmPFC target, turquoise dots represents the first encountered neuron recorded in the caudate and yellow dots represent the position at which the experimenter decided, based on the pattern of neurophysiological responses, that the electrode was outside of the caudate for the first time. Finally, the green line in Fig. 5A and the red line in Fig. 5B represents the ideal straight electrode trajectory (see discussion). To find these electrode positions, one of the authors (PMD) used the software and recorded, online, the positions of the electrode given by a second author (IM) who could not see the screen and who indicated in which structure he thought the electrode was based on neural activity. As can be seen in Fig. 5, the dots are closely aligned with the corresponding anatomical features.
Figure 5.
Chamber-oriented views centered at the electrode tip (panels A-B). The intersection between the green and the blue lines in panel A and the blue and the red lines in panel B represents the position of the targeted neural area (vmPFC). Turquoise dots represent the location of the first recorded unit in the caudate (depth: 9.85 mm) and yellow dots represent the position at which the experimenter decided, based on the pattern of neurophysiological responses, that the electrode was outside the caudate (depth: 15mm). The white dot represents a unit recorded in vmPFC. The MRI reference grid appears as the dark rectangle in A. The recording chamber appears as the white material surrounding the reference grid in A, and as the white block in B. Note that this electrode track is outside the MRI reference grid, because the reference grid was smaller than the single neuron recording grid.
3.4. Reconstruction of electrode position in MRI
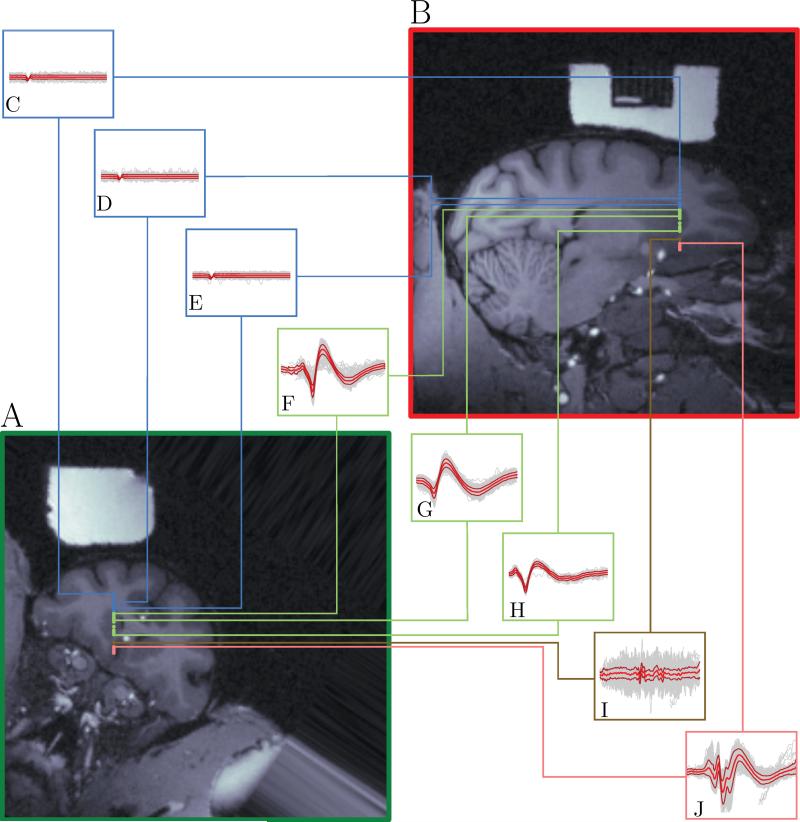
pyElectrode facilitates the placement of recording sites on a user-defined slice of the brain, which can be saved in a publication-ready vectorized format. Figure 6 shows all the recording sites we used in this paper, and demonstrates how pyElectrode can be used to map results from a single penetration onto MRI slices. Panels A and B are aligned with the chamber coordinate system. Panels C-J show the recorded waveforms at the depths corresponding to the linked dots. Blue boxes represent no activity. Green boxes represent waveforms recorded while isolating caudate neurons. Brown box represents some axonal activity recorded between the caudate and vmPFC. Finally, pink box represents the waveforms of vmPFC neuron. The accuracy of this approach depends on many factors besides the transformation calculations, such as bending of the electrode or movement of the brain. A study of accuracy within a given setting would require repeated penetrations to small targets, and is beyond the scope of this presentation.
Figure 6.
Demonstration of recordings at different depths mapped onto the MRI. Panels A and B are aligned with the chamber coordinate system. Blue dots represent depths at which only background activity was observed (no neurons). Green dots represent depths at which caudate neurons were recorded. Brown dots represent the depth at which axonal activity was recorded. Pink dots represents depths at which vmPFC neurons were recorded. Panels C-J represent the activity at the depth corresponding to the linked colored dot. Gray lines represent single activity traces, magenta lines the mean activity and red lines the standard deviation around the mean. Depths. C: 5.00 mm. D: 7.00 mm. E: 9.00 mm. F: 9.85 mm. G: 11.5 mm. H: 15.00 mm. I: 17.00 mm. J: 19.00 mm. All traces had the same threshold and the same height (4 mV). Boxes A-H have a width of 2.5 ms, box I has a width of 5.625 ms and box J has a width of 4.5 ms.
4. Discussion
Irrespective of how the chamber is positioned, through stereotaxic surgery or fiducial markers (Brainsight), our software addresses the subsequent steps of calculating target location in chamber coordinates, track the progress of an electrode during a penetration and finally producing publication-quality figures of recording sites on a slice with an user-defined orientation. This paper presents equations for the coordinate transformations needed to view arbitrary slices through the brain represented in a 3-D MRI data set.
The present article presents a solution for reconciling the coordinate systems mismatches associated with combining multiple brain measurement techniques. We demonstrate that the new software pyElectrode can fluidly overcome the challenges in registering the position of electrophysiological recordings with structural MRI scans. This approach can be helpful in planning, performing, and reporting the position of targets not only for electrophysiological measurements but for a range of invasive procedures that can benefit from MRI guidance.
Highlights.
 Compute electrode position in chamber coordinates to hit a neural region.
Compute electrode position in chamber coordinates to hit a neural region.
 Help to see which structures are encountered during electrode penetration.
Help to see which structures are encountered during electrode penetration.
 Plot electrode positions given in chamber coordinates in an MRI.
Plot electrode positions given in chamber coordinates in an MRI.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
And thus link it to atlas views.
References
- Asahi T, Tamura R, Eifuku S, Hayashi N, Endo S, Nishijo H, Ono T. A method for accurate determination of stereotaxic coordinates in single-unit recording studies in monkeys by high-resolution three-dimensional magnetic resonance imaging. Neuroscience research. 2003;47(2):255–260. doi: 10.1016/s0168-0102(03)00202-5. [DOI] [PubMed] [Google Scholar]
- Cox D, Papanastassiou A, Oreper D, Andken B, DiCarlo J. High-resolution three-dimensional microelectrode brain mapping using stereo microfocal x-ray imaging. Journal of neurophysiology. 2008;100(5):2966–2976. doi: 10.1152/jn.90672.2008. [DOI] [PubMed] [Google Scholar]
- Crist C, Yamasaki D, Komatsu H, Wurtz R. A grid system and a microsyringe for single cell recording. Journal of neuroscience methods. 1988;26(2):117–122. doi: 10.1016/0165-0270(88)90160-4. [DOI] [PubMed] [Google Scholar]
- Evarts E. A technique for recording activity of subcortical neurons in moving animals. Electroencephalography and clinical neurophysiology. 1968;24(1):83–86. doi: 10.1016/0013-4694(68)90070-9. [DOI] [PubMed] [Google Scholar]
- Foley J, Van Dam A. Fundamentals of interactive computer graphics. Vol. 1. Addison-Wesley; Mass: 1982. Addison-Wesley Systems Programming Series, Reading 1982. [Google Scholar]
- Frey S, Comeau R, Hynes B, Mackey S, Petrides M. Frameless stereotaxy in the nonhuman primate. Neuroimage. 2004;23(3):1226–1234. doi: 10.1016/j.neuroimage.2004.07.001. [DOI] [PubMed] [Google Scholar]
- Holtzheimer P, Mayberg H. Deep brain stimulation for psychiatric disorders. Annual Review of Neuroscience. 2011;34:289–307. doi: 10.1146/annurev-neuro-061010-113638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jing W, Wenchao W, Lin L, Li L, Guimei W, Heng T, Huihui J. A new mri approach for accurately implanting microelectrodes into deep brain structures of the rhesus monkey (macaca mulatta). Journal of neuroscience methods. 2010;193(2):203–209. doi: 10.1016/j.jneumeth.2010.07.039. [DOI] [PubMed] [Google Scholar]
- Kalwani R, Bloy L, Elliott M, Gold J. A method for localizing microelectrode trajectories in the macaque brain using mri. Journal of neuroscience methods. 2009;176(2):104–111. doi: 10.1016/j.jneumeth.2008.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Richmond B. Response differences in monkey te and perirhinal cortex: stimulus association related to reward schedules. Journal of Neurophysiology. 2000;83(3):1677–1692. doi: 10.1152/jn.2000.83.3.1677. [DOI] [PubMed] [Google Scholar]
- Logothetis N, Pauls J, Augath M, Trinath T, Oeltermann A, et al. Neurophysiological investigation of the basis of the fmri signal. Nature. 2001;412(6843):150–157. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
- Lozano A, Dostrovsky J, Chen R, Ashby P. Deep brain stimulation for parkinson's disease: disrupting the disruption. The Lancet Neurology. 2002;1(4):225–231. doi: 10.1016/s1474-4422(02)00101-1. [DOI] [PubMed] [Google Scholar]
- Matsui T, Koyano K, Koyama M, Nakahara K, Takeda M, Ohashi Y, Naya Y, Miyashita Y. Mri-based localization of electrophysiological recording sites within the cerebral cortex at single-voxel accuracy. Nature methods. 2006;4(2):161–168. doi: 10.1038/nmeth987. [DOI] [PubMed] [Google Scholar]
- Monosov I, Hikosaka O. Regionally Distinct Processing of Rewards and Punishments by the Primate Ventromedial Prefrontal Cortex. The Journal of Neuroscience. 2012;32(30):10318–10330. doi: 10.1523/JNEUROSCI.1801-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nahm F, Dale A, Albright T, Amaral D. In vivo microelectrode localization in the brain of the alert monkey: a combined radiographic and magnetic resonance imaging approach. Experimental brain research. 1994;98(3):401–411. doi: 10.1007/BF00233978. [DOI] [PubMed] [Google Scholar]
- Ohayon S, Tsao D. Mr-guided stereotactic navigation. Journal of Neuroscience Methods. 2011 doi: 10.1016/j.jneumeth.2011.11.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olivier A, Bertrand G, Peters T. Stereotactic systems and procedures for depth electrode placement: technical aspects. Stereotactic and Functional Neurosurgery. 1983;46(1-4):37–40. doi: 10.1159/000101239. [DOI] [PubMed] [Google Scholar]
- Olivier A, De Lotbiniere A, Peters T, Pike B, Ethier R, Melanson D, Bertrand G, Podgorsak E. Combined use of digital subtraction angiography and mri for radiosurgery and stereoencephalography. Stereotactic and Functional Neurosurgery. 1987;50(1-6):92–99. doi: 10.1159/000100691. [DOI] [PubMed] [Google Scholar]
- Paton J, Belova M, Morrison S, Salzman C. The primate amygdala represents the positive and negative value of visual stimuli during learning. Nature. 2006;439(7078):865–870. doi: 10.1038/nature04490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters T. Image-guidance for surgical procedures. Physics in medicine and biology. 2006;51:R505. doi: 10.1088/0031-9155/51/14/R01. [DOI] [PubMed] [Google Scholar]
- Pillay P, Barnett G, Awad I. Mri-guided stereotactic placement of depth electrodes in temporal lobe epilepsy. British journal of neurosurgery. 1992;6(1):47–53. doi: 10.3109/02688699209002901. [DOI] [PubMed] [Google Scholar]
- Rebert C, Hurd R, Matteucci M, De LaPaz R, Enzmann D. A procedure for using proton magnetic resonance imaging to determine stereotaxic coordinates of the monkey's brain. Journal of neuroscience methods. 1991;39(2):109–113. doi: 10.1016/0165-0270(91)90076-c. [DOI] [PubMed] [Google Scholar]
- Saleem K, Logothetis N. A combined MRI and histology atlas of the rhesus monkey brain in stereotaxic coordinates. Academic Pr. 2006 [Google Scholar]
- Shah R, Chang S, Min H, Cho Z, Blaha C, Lee K. Deep brain stimulation: technology at the cutting edge. Journal of clinical neurology (Seoul, Korea) 2010;6(4):167. doi: 10.3988/jcn.2010.6.4.167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talbot T, Ide D, Liu N, Turchi J. A novel, variable angle guide grid for neuronal activity studies. Frontiers in Integrative Neuroscience. 2011:6. doi: 10.3389/fnint.2012.00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tierney T, Sankar T, Lozano A. 6 deep brain stimulation: Emerging indications. Progress in Brain Research. 2011;194:83. doi: 10.1016/B978-0-444-53815-4.00015-7. [DOI] [PubMed] [Google Scholar]
- Tsao D, Freiwald W, Tootell R, Livingstone M. A cortical region consisting entirely of face-selective cells. Science. 2006;311(5761):670–674. doi: 10.1126/science.1119983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villemure J, Marchand E, Peters T, Leroux G, Olivier A. Magnetic resonance imaging stereotaxy: Recognition and utilization of the commissures. Stereotactic and Functional Neurosurgery. 1987;50(1-6):57–62. doi: 10.1159/000100685. [DOI] [PubMed] [Google Scholar]
- Volkmann J. Deep brain stimulation for the treatment of parkinson's disease. Journal of clinical neurophysiology. 2004;21(1):6. doi: 10.1097/00004691-200401000-00003. [DOI] [PubMed] [Google Scholar]
- Walbridge S, Murad G, Heiss J, Oldfield E, Lonser R. Technique for enhanced accuracy and reliability in non-human primate stereotaxy. Journal of neuroscience methods. 2006;156(1):310–313. doi: 10.1016/j.jneumeth.2006.01.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamamoto S, Monosov I, Yasuda M, Hikosaka O. What and Where Information in the Caudate Tail Guides Saccades to Visual Objects. The Journal of Neuroscience. 2012;32(32):11005–11016. doi: 10.1523/JNEUROSCI.0828-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]