Comprehensive Joint Feedback Control for Standing by Functional Neuromuscular Stimulation – a Simulation Study

Abstract

Previous investigations of feedback control of standing after spinal cord injury (SCI) using functional neuromuscular stimulation (FNS) have primarily targeted individual joints. This study assesses the potential efficacy of comprehensive (trunk, hips, knees, and ankles) joint-feedback control against postural disturbances using a bipedal, three-dimensional computer model of SCI stance. Proportional-derivative feedback drove an artificial neural network trained to produce muscle excitation patterns consistent with maximal joint stiffness values achievable about neutral stance given typical SCI muscle properties. Feedback gains were optimized to minimize upper extremity (UE) loading required to stabilize against disturbances. Compared to the baseline case of maximum constant muscle excitations used clinically, the controller reduced UE loading by 55% in resisting external force perturbations and by 84% during simulated one-arm functional tasks. Performance was most sensitive to inaccurate measurements of ankle plantar/dorsiflexion position and hip ab/adduction velocity feedback. In conclusion, comprehensive joint-feedback demonstrates potential to markedly improve FNS standing function. However, alternative control structures capable of effective performance with fewer sensor-based feedback parameters may better facilitate clinical usage.

I. Introduction

The goal of this study was to develop and assess the potential of a control system employing joint-feedback from the ankles, knees, hips, and trunk to continuously adjust stimulation to muscles following spinal cord injury (SCI) and reduce the upper-extremity (UE) loading required to maintain stable standing against postural perturbations. Neuroprostheses employing functional neuromuscular stimulation (FNS) have been proven clinically effective for restoring basic standing function following SCI [1]. Preprogrammed patterns of stimulation can produce effective sit-to-stand maneuvers while continuous stimulation at constant levels typically maintains upright posture. Under constant stimulation, the user is required to maintain balance against postural perturbation with UE loading on a support structure (e.g., walker, countertop). Sustained UE loading compromises the utility of standing with FNS by limiting the functional use of the hands and arms and reducing standing time due to rapid upper body fatigue. Feedback control of stimulation is necessary to provide automatic postural adjustments and reduce the onus of UE stabilization for balance.

Functional movements involve joint kinematics and multi-articulate muscle actions acting in three dimensions [2]. Consequently, any comprehensive control system for functional standing balance should consider individual muscle effects across the entire system and control trunk, hip, knee, and ankle joints simultaneously. Numerous groups have attempted to introduce servo-type joint-feedback control for standing with FNS in isolation at individual joints including the knees [3,4], hips [5,6], and ankles [7]. They restricted control actions to a single joint or anatomical plane (either sagittal or coronal), omitted FNS feedback control at the trunk, and held joints not under direct feedback control in extension by constant stimulation or mechanical bracing. These limitations were justifiable given the initial challenges of implementing these control systems on live SCI participants. However, these studies produced only moderate improvements in disturbance response or applied clinically unviable constraints. Consequently, current standing systems used clinically still do not employ feedback control of FNS. The next step towards clinically accepted closed-loop FNS standing include development of a feedback control system that simultaneously coordinates actions at multiple joints to balance posture in three dimensions.

This simulation study developed a FNS control system using joint-feedback and investigated its potential to comprehensively maintain standing posture against disturbances. The control system was created and tested using a three-dimensional computer model of human bipedal stance that includes realistic SCI musculature targeted for FNS control. A model-based approach was employed to introduce optimal patterns of muscle excitation into the solution process and thoroughly evaluate controller performance prior to online testing with SCI subjects. Given the limitations in strength of paralyzed muscles and the importance of considering volitional upper-body interactions during FNS standing [8], a model formulation for UE loading was created to interact with the bipedal standing model and simulate the stabilization forces that a user may exert. The complete model system included both UE loading and a muscle-based control system that represents the joint-feedback FNS controller. FNS controller performance was assessed according to the reduction in UE loading required to stabilize against disturbances compared to constant muscle excitation.

The joint-feedback control system was designed for proportional-derivative (PD) feedback to drive an artificial neural network (ANN) trained to relate changes in joint positions (ANN inputs) to changes in muscle excitations (ANN outputs) across the lower extremities and trunk. Previous studies have examined the performance of proportional-integral-derivative (PID) control for FNS applications [9, 10, 11]. Results have been limited due to classical PID control [12] being applied to highly nonlinear musculoskeletal systems [13]. Because of their capability of identifying complicated, nonlinear relationships, ANNs are desirable for neuroprosthetic control systems [14]. Blana et al. [15] have proposed a neuro-PID controller for feedback error rejection. The PID controller determined the linear dynamic response but the nonlinear, biomechanical system interactions between muscles and joints were characterized by the black-box formulation of an ANN. The control system proposed for bipedal standing in this study is a similarly structured neuro-controller composed of PD joint-feedback driving an ANN trained according to static stiffness objectives.

The role of stiffness has been implicated in both quiet [16] and perturbed [17] standing. A simple static stiffness model was able to characterize standing responses in both cases. Stiffness has been targeted previously for automatic control of paralyzed ankles during standing [18]. Actively-controlled ankle stiffness in conjunction with volitional upper body activity was sufficient to maintain paraplegic standing and reject select disturbances. However, this investigation restricted disturbances and control action to only the ankles while rigidly bracing the knees and lower torso. While such reductionist approaches to focus on function at an isolated joint or single anatomical plane are important for exploring preliminary control concepts, they rely on bracing or continuous stimulation to artificially constrain the system. To provide more natural, unencumbered and functional standing to individuals with SCI, clinically deployable systems need to be extended to encompass a more comprehensive approach.

This simulation study investigates the feasibility of full (three-dimensional, un-braced, no muscles held at constant stimulation) joint-feedback control of FNS standing. Using a bipedal computer model of typical SCI standing, the potential of an ANN-PD controller trained according to a static joint stiffness paradigm was explored. The model control system was tuned using a global-search optimization to minimize upper-body loading required to resist postural perturbations. Test performance was assessed by the reduction in upper-body loading observed with the controller active compared to constant muscle excitations across a variety of disturbances. These disturbances included force-pulse perturbations analogous to discrete external disturbances used for balance assessment [19,20] and sinusoidal loadings simulating internal disturbances occurring with functional one-arm reaching [21].

II. Methods

The overall model system (Figure 1) included two parallel controllers (FNS muscle control, UE loading) acting on a three-dimensional model of SCI bipedal standing. The FNS controller utilizes PD joint-feedback to drive an ANN trained on synergistic muscle excitation (ME) patterns. These patterns were optimized to minimize muscle stress while attaining specified static joint stiffness values about an erect setpoint posture. This posture is a single set of reference joint positions that the controller was designed to maintain. The most erect (i.e., highest vertical COM position) posture located above the center of the BOS was selected as the desired setpoint posture. An extensive set of static standing postures were created about the setpoint to provide a rich space over which the controller was expected to perform. An iterative regression scheme then determined a set of maximal joint stiffness values that can be achieved across this space using typical SCI-affected muscles targeted by FNS (Table I). The muscle excitation levels corresponding to the maximal stiffness values were the outputs and the joint errors (angle magnitudes away from setpoint posture) were the inputs for training an ANN. The trained ANN represented a synergy that provided a static mapping between patterns of joint errors and muscle excitations. The same ANN was then driven for dynamic performance using an optimally tuned PD controller for standing balance. As with standard PD feedback [22], joint angle (proportional) and angular velocity (derivative) errors were weighted according to feedback gains and subsequently summed as the net joint input to the static ANN. Gain values were determined that optimize dynamic performance in resisting postural disturbances with the objective of minimizing UE loading required for stabilization. Volitional UE loading was represented by PID control of shoulder position. The objective of both the FNS and UE control systems was to maintain the standing model at the setpoint posture. The FNS controller was evaluated according to the reduction in shoulder position controller output (i.e., reduction in UE loading) under various postural disturbances.

Figure 1.

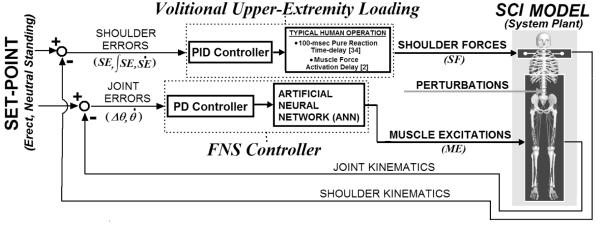
Overall model system. Two parallel controllers acting to maintain three-dimensional model of bipedal SCI stance at setpoint position against postural perturbations: (1) FNS controller modulates trunk, lower-extremity muscle excitations according to joint-feedback driving an ANN trained to output muscle excitations consistent with producing specified joint stiffness values, (2) Upper-extremity (UE) controller, representing user volitional loading, produces three-dimensional point forces at shoulders according to shoulder position errors relative to the set-point posture. Joint (angular) errors are defined with respect to the anatomical reference frame local to each joint. Shoulder positional errors are expressed in globally-fixed Cartesian coordinates (3-dimensions: anterior-posterior, medial-lateral, inferior-superior). The gains for UE control are determined according to Ziegler-Nichols tuning rules [22]. FNS controller gains are optimized using global-search algorithm [36] to minimize UE controller output (“loading”) against perturbations.

TABLE I.

STIMULATED MUSCLES AND CORRESPONDING SCI SCALING FACTORS AND BASELINE EXCITATION LEVELS

Muscle Group (stimulated by single channel)	Select Joint Articulation(s)	SCI Joint Moment (N-m) from [28]	SCI Scaling Factor	Optimal, Maximal Excitation Level
Soleus, Gastrocnemius	Ankle Plantarflexion	55	0.37	0.049, 0.262
Tibialis Anterior	Ankle Dorsiflexion	15	0.70	0.000, 1.000
Vastii (Medialis, Intermedius, Lateralis)	Knee Extension	80	0.29	0.960, 1.000
Adductor Magnus	Hip Extension, Hip Adduction	63, 30	0.34, 0.84 → 0.59*	0.767, 1.000
Gluteus Maximus	Hip Extension	63	0.34	1.000, 1.000
Gluteus Medius	Hip Abduction	44	0.78	0.281, 1.000
Semimembranosus	Hip Extension, Hip Adduction	63, 30	0.34, 84 → 0.59*	0.467, 1.000
Erector Spinae	Trunk Extension	70	0.53	0.645, 1.000

^*Note:. Scaling factor for muscle group taken to be average across two major joint articulations

A. Three-Dimensional Model of SCI Stance

A three-dimensional computer model of human bipedal stance was adapted from a previously described representation of the lower extremities (LE) [23] and trunk [24]. This model consisted of nine segments (two feet, two thighs, two shanks, pelvis-lumbar component, and head-arm-trunk complex) with 15 anatomical degrees of freedom (DOFs) representing bilateral motions of ankle plantar/dorsiflexion (PF/DF), ankle inversion/eversion (Inv/Ev), knee flexion/extension (F/E) , hip F/E internal/external rotation (Int/Ext), and hip ab/adduction (Ab/Ad). Passive moment properties [25] due to SCI were included at these DOFs. Both feet were in constant contact with the ground, defining a closed-chain which effectively reduced the number of independent DOFs to six. The LEs were in series with a single three-DOF (fore-aft pitch, roll, yaw) trunk joint at the lumbrosacral (L5-S1) region. The muscle groups actively controlled in the model were consistent with those targeted by an existing 16-channel implanted system [26]. Thus, joint-feedback was employed for all DOFs except ankle Inv/Ev, hip Int/Ext, and trunk roll and yaw due to an insufficient number of stimulus channels. Elements within each muscle group were constrained to act synchronously at the same level of excitation as if co-activated by a single stimulus output. Excitation is a normalized (0 to 1) command input to a muscle group that is analogous to stimulation level. Muscles were represented as Hill-type actuators with nonlinear force dynamics that includes excitation-activation coupling and conventional length-tension and force-velocity properties [27]. The peak force parameter for each muscle group (Table I) was scaled from normative values to produce the maximum isometric joint moments generated by individuals with complete thoracic-level SCI in response to electrical stimulation [28].

B. Creating Posture Space

The computer model facilitated creation of a broad posture space over which the ANN learned to produce the desired input-output behavior. A posture was defined by a set of joint positions (θ) that satisfied foot position constraints according to a closed-chain solver in the model dynamic equations. Each posture served as an individual data point for subsequent ANN training, testing, or validation. Relative to the desired setpoint posture defining the reference joint positions (θ_R), the position errors (Δθ_R = θ_R - θ) for each posture at the nine joint DOFs targeted for feedback (trunk pitch, bilateral ankle PF/DF, knee F/E, hip F/E, hip Ab/Ad) served as the ANN inputs. The optimal muscle excitation levels needed to statically produce joint moments consistent with stiffness objectives (section II.C) served as the ANN outputs. To encompass a training space pertinent to stable standing [29], postures were created by incrementally adjusting the joint angle DOFs within specified limits (Table II) and in combinations that ensured system center of mass (COM) remained over the base of support (BOS) and above 90% of its nominal height at erect standing. The magnitude of increment at each joint was minimized while allowing ANN training to converge with mean squared error (MSE) < 0.001 within 1000 epochs. A total of 4672 postures were created about the reference positions defined by the setpoint posture for subsequent determination of maximal joint stiffness values and ANN training. The resultant COM space of the postures spans 19, 29, and 7 cm in the anterior-posterior, medio-lateral, and inferior-superior directions, respectively.

TABLE II.

Joint DOF Angle Limits for Posture Space

Joint DOF	Angle Limits (deg)
Ankle PF/DF	4PF to 8DF
Knee F/E	30F to 0E
Hip Ab/Adduction	8Ab to 8Ad
Hip F/E	40F to 0E
Trunk F/E	50F to 0E

C. Determining Maximal Joint Stiffness Values

Given the limitations in SCI muscle strength, a nested optimization scheme (Figure 2) was employed to determine a set of maximal joint stiffness values, in Newtonmeters/degree (N-m/deg), that were concurrently achievable about the setpoint for all feedback joint DOFs across the specified posture space. A static optimization routine [30] determined the optimal muscle excitation levels that meet joint moment constraints for each posture. An outer loop adjusted the joint stiffness and bias values defining the moment (M) constraint at each joint DOF i with error in direction j (e.g., flexion or extension) relative to setpoint position as follows:

$$M(i,j)=K(i,j)\times \Delta \theta \left(i\right)+B\left(i\right)$$ (1)

K is the stiffness value that multiplies the joint angle error magnitude, Δθ, away from the desired setpoint position. K was determined in both directions (e.g., flexion and extension) for each joint DOF to insure that agonists and antagonists were equally represented in the analysis. B is a bias joint moment providing nominal basal support throughout the posture space, but necessarily at the setpoint position where error equals zero. For each posture serving as a single point for ANN training, the Δθ(ı) serve as the ANN inputs, and the optimal muscle excitation levels necessary to meet all M(i) serve as the ANN outputs. If the joint moment required to hold the posture statically against gravity was greater than the stiffness moment (equation 1), then the optimizer must satisfy this “gravity” moment instead. This condition insures the outer loop produces sufficient bias moment across the entire posture space to maintain neutral (i.e., no joint error) joint positions and still resist the effects of gravity and errors at other joints. Optimizer convergence upon a ‘feasible’ solution for a posture was defined as every joint moment constraint being satisfied within a tolerance of 0.001N-m. The set of muscle excitations (X) were optimized according to minimization of the following objective criterion developed for locomotion [31]:

$$\mathit{Func}\left(X\right)=\min \left(\underset{k=\mathit{MuscleIndex}}{\overset{\#\mathit{Muscles}}{\Sigma }}{\sigma }_k^2\right),{\sigma }_k=\frac{{\mathit{Force}}_k}{{\mathit{Area}}_k}$$ (2)

where σ = muscle stress, Force = muscle force, Area = muscle cross-sectional area.

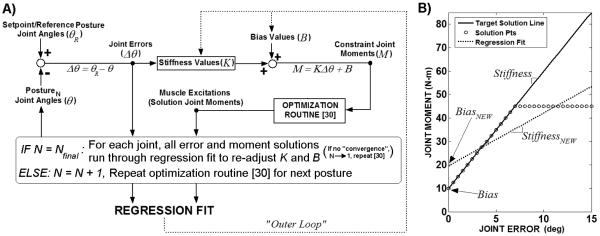
Figure 2.

A: Diagram of iterative regression scheme to determine maximal stiffness (K) and corresponding bias (B) moment values for each joint. For given set of K and B values for all joints, optimization routine [30] applied to all postures. Due to limitation in SCI muscle strength, all constraint moments, defined according to K and B, unlikely to be met by optimizer solutions. Linear regression applied to entire moment versus error solution space to re-adjust K and B (“outer loop”) according to fit for each joint DOF and in each direction. Note: For a bi-directional (e.g., flexion and extension) joint DOF, B_net = mean(B_flexion, B_extension). Optimization routine [30] re-applied to all postures to determine solutions for new constraint moment targets. Iteration scheme continues until convergence (mean ∣ΔK∣ < 0.005N/m-deg). The joint errors and muscle excitation solutions corresponding to the final K, B values serve as the ANN inputs and outputs, respectively. B: Example of linear regression applied to solution space for single joint DOF in one error direction. Optimizer produces either feasible solution points adhering to target solution line, representing constraint joint moments for given iteration, or infeasible solutions points deviating from target solution line. Linear regression applied to entire solution (feasible and infeasible) space to re-adjust K, B for next iteration.

The outer loop (Figure 2A) iteratively varied the stiffness and bias values at each joint so that the optimizer could converge upon feasible solutions for a maximum number of postures. The optimizer calculated muscle excitation solutions for all postures according to the joint moment constraints (target solutions) defined by the stiffness and bias values assigned on a given iteration. If constraints could not be satisfied within tolerance due to limitations in muscle strength, then the optimizer produced infeasible joint moment solutions that saturated and deviated from the target solution line (Figure 2B). The stiffness and bias values were modified for the following iteration of the outer loop according to a linear regression applied to the entire solution space (feasible plus infeasible solutions) in each joint DOF direction. The new stiffness and bias values were the slopes and intercepts of the regressions, respectively. A linear regression is consistent with a static stiffness model for standing maintenance [17], resulting in a single stiffness and bias value for each joint. For bi-directional control of a DOF, a regression was done in each direction with the net bias moment simply taken as the average of the two intercepts. The outer loop was repeated until convergence where the mean of the absolute value of change in K across all joint directions was < 0.005N-m/deg. The initial stiffness and bias values were 20N-m/deg and 0N-m for all DOFs. The initial stiffness value was preselected as a higher value than could be achieved by any joint at its largest deviation from the setpoint. The joint stiffness values were then incrementally reduced to increase the number of feasible solutions. The ‘zero’ initial bias moment was selected to allow for non-zero bias moments to emerge naturally from the linear regression algorithm fitting the gravitational requirements near the neural setpoint posture. The optimal muscle excitations corresponding to the joint moment constraints defined by the final stiffness and bias values served as the outputs for ANN training.

D. Training ANN on Optimization Data

For each posture, the position joint errors away from the neutral posture were the inputs and the corresponding optimal muscle excitation levels were the outputs for a single ANN training point. Only feasible posture solutions of the optimization procedure were retained and then randomly assigned for training (70%), testing (20%), and validation (10%) of the ANN. The ANN was constructed with the Neural Network Toolbox in MATLAB (Mathworks®, Natick, MA). The ANN had 16 OUTPUTS corresponding to the optimal excitation levels of the 16 targeted muscle groups. The ANN had nine INPUTS consisting of bilateral ankle PF/DF, bilateral knee F/E, bilateral hip F/E, bilateral hip Ab/Ad, and trunk fore-aft pitch joint position errors. A three-layer (input, hidden, output layers), feedforward ANN structure was employed for its universal mapping capability of nonlinear functions [32]. The number of hidden layer neurons was determined to be 22 by heuristically finding the number of neurons providing the lowest MSE after 1000 training epochs. All input and output data were normalized over [−1, +1] prior to training. The training function was the Levenberg-Marquardt algorithm [33]. A maximum of 10000 epochs were specified for training in lieu of an early-stopping criterion specified as 250 consecutive epochs of increasing fitting error to the validation set. To ensure the ANN was sufficiently general and not restricted to predicting synergies along the planes of increment for the created posture space, a “random posture” set was created for additional testing. It consisted of 500 postures within the same joint angle and COM limits for the posture space, but was created using a random number generator to initially specify joint DOF positions prior to application of the closed-chain solver.

E. Upper Extremity Controller

To approximate UE loading that a standing neuroprosthesis user may need to exert on an assistive support to resist postural perturbations, three-dimensional stabilization forces were applied to each shoulder position. PID controller output defined the shoulder force (SF) in each dimension ‘j’ (anterior-posterior, medial-lateral, or inferior-superior defined in globally fixed reference frame) according to input shoulder position errors (SE) relative to the reference positions at the setpoint posture as follows:

$${\mathit{SF}}_j=K_{p,j}\times {\mathit{SE}}_j+K_{i,j}\times \int {\mathit{SE}}_j+K_{D,j}\times {\mathit{SE}}_j$$ (3)

UE controller output was in accordance with shoulder position since the current model does not explicitly include dynamic representations of the arms, which would otherwise produce reaction loads at the shoulders. The three PID gains (K’s) were determined according to Ziegler-Nichols 2^nd method tuning rules [22] against a 100 N, 200 msec forward test pulse at the thorax COM. The same PID gains were used for all three dimensions since only a single Ziegler-Nichols ultimate gain was observed for the single test perturbation. This test pulse induced a model trunk acceleration of ~2.5 m/sec² which is less than that induced by “middle level” perturbations [19]. To approximate typical human operator response, 100 msec pure time-delays [34] and muscle force activation delays [2] were applied to the shoulder force outputs. To simulate one-arm support conditions, as required to functionally reach on the contralateral side, only support-side shoulder position controller forces were active.

F. Determining Optimal and Maximal Sets of Constant Excitation Levels for Baseline Performance

To provide a comparative baseline for controller performance across a range of sufficient but constant excitation levels for stable standing, the “optimal” and “maximal” excitation sets (Table I) were determined for the desired setpoint posture using the optimizer from [30]. The, “optimal” excitation levels represent the minimum constant excitation levels sufficient to support stable standing, while the “maximal” excitation levels represent the largest constant excitation levels supporting the same posture. The “optimal” hip (36.2N-m) and knee (11.5N-m) extension moment constraints were selected as those minimally necessary to support stable erect standing in energy-efficient postures without joint contractures as reported in [35]. Joint moment constraints at the trunk (20.2N-m, E) and ankles (2.9N-m, PF) were subsequently selected such that the static UE loading was zero when the model was at the setpoint shoulder positions. For comparison to clinically relevant systems applying supramaximal stimulation, the “maximal” set of constant excitations were specified as all muscles fully excited (excitation = 1.0) except the ankle plantarflexors, which were adjusted to 0.262 to again minimize static UE loading at the setpoint. The “maximal” set does drive the knees, hips, and trunk slightly (< 5deg) into hyper-extension, i.e., past the setpoint position defining full extension. Clinically, this is desired and commonly observed.

G. Perturbation Simulations

In all, 978 perturbation simulations were specified to optimally tune and evaluate the controller with respect to total UE loading. Total UE loading was the sum (left plus right sides) of the “net” force applied at each shoulder position. For each simulation, the computer model started at the desired erect setpoint, and UE loading was tracked during the application of a perturbation and following recovery period (500 msec). This recovery period was sufficient to sustain effective stabilization, defined as UE loading within 1% body-weight (BW) of its final steady-state value, across all simulations. Each perturbation simulation included a single pulse-force disturbance applied at a single point. The location, direction, magnitude, and duration of the perturbation were varied with each simulation. Perturbations were applied at the COM location of the thorax, pelvis, femur, or shank segment in the forward, backward, left, or right directions relative to a globally fixed reference frame. These force disturbances ranged from 5% to 15% BW in magnitude and 50 to 500 msec in duration. Perturbations were also repeated at the system COM, expressed in global three-dimensional coordinates.

H. Tuning Joint-Feedback Controller

For dynamic controller action, each of the nine joint inputs (‘i’) to the ANN was the sum of the joint angle position and velocity errors (θ’s) multiplied by proportional (K_P) and derivative (K_D) gains, respectively. This standard formulation for PD control to the ANN was as follows:

$$\mathit{ANN}{\mathit{Input}}_i=K_{p,i}\times {\theta }_i+K_{D,i}\times {\stackrel{.}{\theta }}_i$$ (4)

Integral control was omitted for joint-feedback since it was assumed that system windup errors [22] would be sufficiently eliminated by UE integral control. The ANN was originally trained statically (i.e., each joint input was equal to Δθ, the unweighted position error from setpoint position). However, optimal dynamic control was executed with inclusion of derivative joint-feedback to drive angular velocities to zero and optimizing both proportional and derivative feedback gains. Gains were optimized to minimize the objective function criterion of the total two-arm UE loading necessary for stabilization during perturbation and recovery over all 978 simulations. The gains for every joint input were optimally tuned using an asynchronous parallel pattern set global search algorithm implemented in the APPSPACK [36] software package running on a FUSION A8 multi-processor computer (Western Scientific, Inc., San Diego CA). Algorithm parameters were determined such that solutions were found within 100 hours of computational time. These parameters include gains bounded between 0 and 20, initial step size equal to 1, step tolerance equal to 0.01, and step contraction factor equal to 0.985. The initial gain values were based on manual tuning. This process included stepwise incrementing of the proportional gain then derivative gain of each joint to minimize UE loading while holding feedback gains at all other joints to zero. The test perturbation for manual tuning was again a100N, 200 msec force pulse at the thorax.

I. Testing Controller Performance

EEEExternal Force Pulse PerturbationsU

All 978 perturbation simulations were repeated with the feedback controller active and with constant baseline (optimal or maximal) excitation levels under two-arm and one-arm support conditions. The level of significance of any reduction in UE loading with the controller active compared to baseline was determined across perturbation direction, location, and magnitude by multiple analysis of variance (MANOVA).

UFunctional Task Performance (FTP)

functional implications of the controller were assessed in simulation with application of sinusoidal force loads at one shoulder to mimic postural disturbances due to weighted, voluntary single arm movements [21]. Three-dimensional, sinusoidal force loading was applied at the left shoulder while UE control was applied only at the right shoulder (i.e., one-arm support). The applied sinusoid forces were as follows: Anterior / Posterior: 1 Hz, 10 N amplitude, 0 N offset; Right / Left: 1 Hz, 20 N amplitude, 0 N offset; Superior/Inferior: 0.5 Hz, 20 N amplitude, −50 N offset. These amplitude and frequency specifications were consistent with those observed in loaded (2.27kg) single arm voluntary movements described in [21].

Controller Sensitivity

The ANN output sensitivity was calculated as the mean slope for ANN output excitation across all the muscles versus the joint error input at neutral stance. Feedback performance sensitivity was assessed by adding random position or velocity error to only one joint-feedback at a time and repeating perturbation simulations and tracking of UE loading. The relative contribution to degradation in controller performance of either position or velocity error at a specific joint was defined as the increase in mean UE loading relative to the sum of increases in mean UE loading across all joints.

III. Results

A. Stiffness Optimization Results

Only 14 iterations of the outer loop applying the regression in batch to the specified posture space were required to converge upon the final stiffness and bias moment values (Table III). Despite using only 16 muscle groups adjusted to generate typical forces following SCI, feasible solutions were found for over 95% of the posture space that comprehensively spans the BOS. The sagittal-plane bias moments at the trunk, hips and knees were all directed towards extension, which is consistent with clinical objectives in applying stimulation for standing following SCI [1]. However, the bias moment magnitudes were all considerably less than the reported maximums (Table I) since they have been adjusted according to gravitational requirements about the setpoint posture. This allowed greater joint-moment capacity (i.e., higher stiffness values) to be available for active joint-error corrections. The maximal joint stiffness value is also a byproduct of joint moment capacity (Table I) relative to the specified range of motion (Table II). The largest maximal stiffness values was at the ankles (> 6N-m/deg), which were only varied over 12 deg.

TABLE III.

CONTROLLER DEVELOPMENT RESULTS FOR EACH JOINT-FEEDBACK INPUT

Joint-feedback Input	Flexion Stiffness (N-m/deg)	Extension Stiffness (N-m/deg)	Bias Moment (N-m)	KP (unitless)	KD (sec)	Mean ANN Output Sensitivity	Position Error Performance Sensitivity	Velocity Error Performance Sensitivity
Ankle PF/DF	6.41	6.35	5.55 PF	6.49	0.52	0.031	53%	21%
Knee F/E	1.57	0.00	9.53 E	0.00	0.00	0.050	0%	0%
Hip Ab/Adduction	2.76	3.30	0.09 Ab	2.22	1.71	0.040	23%	71%
Hip F/E	1.18	0.00	8.52 E	0.00	1.08	0.017	0%	6%
Trunk F/E	0.94	0.00	29.95 E	7.78	13.64	0.016	24%	2%

B. Artificial Neural Network Training Results

The correlation fits between target and prediction for the training, validation, and testing data sets were all exceptionally high (> 0.98, Table IV) indicating good accuracy in predicting changes in muscle excitation levels with corresponding changes in posture. High correlation across the “random” postures further suggests strong universal prediction capability. The error in predicting de-normalized excitation outputs was consistently small (~0.03) compared to the typical mean prediction values (~0.4) across all data sets. The standard deviations in error were higher than the mean error in all cases. However, these values were still small relative to the mean prediction values themselves.

TABLE IV.

ARTIFICIAL NEURAL NETWORK RESULTS

Data Set	Mean Output	Mean Error ± S.D.	Correlation
Training	0.40	0.03 ± 0.04	0.991
Validation	0.41	0.03 ± 0.05	0.987
Testing	0.42	0.04 ± 0.05	0.985
Random	0.31	0.03 ± 0.05	0.984

C. Controller Gain Tuning

The final PID gains determined for the UE controller were 327N/m, 37N/m-sec, and 719N-sec/m. During forward simulations, these gains resulted in a maximum model UE loading of 25.4% BW during the test perturbations, which is similar to typical arm support (3 to 55%, 17% average) as reported in [37] for recipients of implanted FNS standing systems. The global-search optimization determined a set of gains (Table III) for the ANN-PD controller within the specified bounds that minimized the objective function of total UE loading across all simulations by 55% compared to the initial, manually tuned gains. The relatively high K_P at the ankles and trunk indicate their significant contributions to sagittal-plane system position in reducing UE loading relative to F/E at the hips or knees. K_D at the trunk is the highest, further indicating the importance of tracking dynamic changes at the trunk for minimizing UE loading. While only hip Ab/Ad provides significant medio-lateral stabilization, the intermediately low proportional K_P and K_D are explained by strong medio-lateral stabilization from the upper extremities and wider base of support in that direction.

Since K_P and K_D for joint-feedback inputs from the knee and K_P for hip F/E were driven to zero, these measured changes were U inconsequential for reducing UE loading against disturbances. Their effects were either small or redundantly compensated by measurements at other DOFs. Across all simulations, the knees remained effectively locked (deviations < 2 deg) in extension with near maximal (>90%) stimulation of the vastii muscles. This outcome results from knees typically remaining extended during perturbed standing [17] and gravitational requirements to do so being met using SCI-affected vastii. For UE stabilization in the sagittal plane, feedback gains for position measurements at the ankles and trunk were much higher and obviated those at hip F/E. But hip F/E control remains viable dynamically given non-zero K_D.

D. Controller Performance, Sensitivity Results

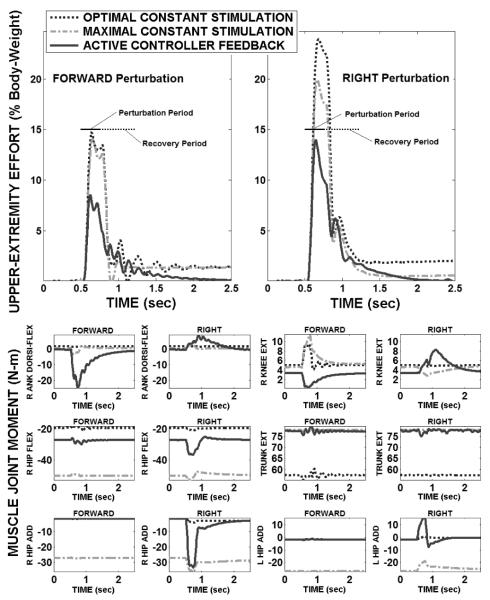
Typical two-arm UE loading and muscle-induced joint moments for baseline (optimal and maximal) and controller-active conditions are shown in Figure 3, where force pulses (15% BW, 250 msec) were either anteriorly or laterally (right) directed at the model COM. Across both directions, total UE loading was reduced during the perturbation plus recovery period by 46% and 36% by the controller compared to optimal and maximal baseline, respectively. The controller provided robust return to the setpoint posture with near-zero final UE loading. The joint moments produced by the controller during steady-state before and after the perturbation were similar (within 10N-m or 30% of maximum) to optimal baseline and lower than maximal baseline across all joints. Consistent with anatomical function, ankle plantar-flexion and hip extension were prominent in resisting a forward disturbance. Correspondingly, right hip abduction and left hip adduction were strongly activated to reject the rightward disturbance. Trunk extension was small even against a forward disturbance since it was applied at the system COM, which is too low to produce significant trunk flexion. Knee extension moments were small in all cases despite high vastii excitation because the knees were generally held in hyper-extension where vastii length-tension properties limited force output. The largest (>10N-m) controller mediated changes in joint moments occurred at the ankles and hips, further validating ankle and hip strategies [20] for stable standing.

Figure 3.

Two-arm UE loading and muscle-induced joint moments to stabilize against perturbation pulse (15% body-weight, 250 msec) applied at model COM in either forward or side (i.e., right) direction.

Composite simulation results for one-arm and two-arm resistance to perturbations are shown in Table V. Maximal constant excitation always resulted in lower UE loading than optimal, but inclusion of the joint controller universally improved performance over either baseline case. The conditions where the controller resulted in the smallest improvement in relative performance were backward and thorax perturbations (only 23, 35% reductions in UE loading versus maximal baseline). These results are likely due to a lack of available flexion musculature to be activated at the hips and trunk to effectively counter these disturbance types. UE loading also increased as perturbations were applied to more superiorly located segments. Perturbations applied to lower segments were more attenuated by muscle and inertial effects before greater UE stabilization was required.

TABLE V.

UPPER EXTREMITY (UE) LOADING FOR STABILIZATION AGAINST POSTURAL DISTURBANCES

Disturbance Condition	Mean Baseline UE Loading (N)		Mean Controller UE Loading (N)	%Reduction w/Controller
UDirection	Optimal	Maximal
Forward	131	94	38	60
Backward	64	44	34	23
Side (Left or Right)	102	71	33	54
Segment Location
Thorax	121	95	62	35
Pelvis	115	81	43	47
Thigh (Left or Right)	103	70	32	54
Shank (Left or Right)	77	43	12	72
Support Conditions
Two-Arm Support	64	56	38	32
One-Arm Support	146	88	32	64
One-Arm FTP	126	108	17	84

When comparing one-arm and two-arm support conditions, UE loading is significantly greater (i.e., standing is more unstable) during one-arm support under optimal or maximal baseline stimulation. Optimal baseline stimulation was further ineffective in one-arm support as the model COM occasionally failed to return to within 0.1m of its original position following disturbances. With the ANN controller active, similar UE loading was expended in resisting perturbations with either one-arm (32N) or two-arm (38N) support, demonstrating the consistency and value of controller feedback. The mean reduction in UE loading with the controller active compared to maximal baseline across all force pulse perturbations over both one-arm and two-arm conditions was 55%. Additionally, MANOVA indicated significant reduction in UE loading with rejection of the null hypothesis of equal means at p = 0.05 across all perturbation variables (direction, location, amplitude) using the controller compared to baseline. During one-arm FTP, the controller kept the model erect and reduced UE loading by 84% compared to maximal baseline excitation.

Feedback error analyses for individual joints (Table III) suggest rise in UE loading was most sensitive to position error at ankle PF/DF (53%) and velocity error at hip Ab/Ad (71%). Sensitivity of ANN excitation output to the same joint inputs was correspondingly high. While excitation output sensitivities about erect stance were desirably low (< 0.1) indicating stable performance, ankle PF/DF and hip Ab/Ad sensitivities were notably higher than those at the trunk or hip F/E. Modulation of knee F/E elicits the greatest mean change across all excitation outputs. This was due to knee extension being critical to preventing outright collapse and the ANN being trained on a space including knee-flexed postures. But during dynamic forward simulations, knee position and velocity changes were inconsequential to UE stabilization and resulted in optimal feedback gains of K_P = K_D = 0 at the knees. Accordingly, the reduction in controller performance due to feedback error at the knees was also zero.

IV. Discussion

Previous studies [3-7] have demonstrated measurable benefit using joint-feedback control for FNS standing, but under limited conditions (e.g., ankles only, knees only, hips only, sagittal-plane only). Our simulation results demonstrate that a neuroprosthesis concurrently regulating ankles, knees, hips, and trunk in three dimensions may also be realizable. These results suggest potentially substantial benefit despite limitations in the number of SCI-atrophied muscles targeted for stimulation in current clinical FNS standing systems [1]. Specifically, an ANN-PD controller employing joint error feedback from the lower extremities and trunk to drive ANN output of muscle excitation levels improved postural disturbance response compared to constant excitation levels typically used clinically. Using reduction in UE loading as the metric, the controller performed better than both optimal and maximal baseline cases for constant excitation. The controller exhibited universal improvement for both two-arm and one-arm support conditions when resisting perturbations from either force pulses or simulated voluntary arm movements.

Muscle synergies consistent with static joint stiffness values provided viable data for training an ANN employed to provide joint-feedback control about an erect setpoint posture. Applying active stiffness by FNS has been previously investigated [7, 18] and minimal ankle stiffness levels have been suggested for improved standing balance. This simulation study demonstrated that concurrently maximizing stiffness at all joints subject to typical SCI-adjusted musculature can produce a mapping for comprehensive joint-feedback to improve standing performance. The static objective of maximizing stiffness values and the dynamic objective of driving the stiffness mapping to reduce UE loading were successfully handled independently. This approach to determine maximal stiffness values relied on regression fits across an entire static posture space to incrementally adjust stiffness and bias values and allow the optimizer to produce solutions for a maximum number of postures. Since the stiffness values themselves were only incrementally reduced from high initial values and not varied according to strict optimization, the final set of stiffness values may not necessarily be a global maximum. However, this procedure intuitively determined stiffness and bias values from a static model of joint stiffness [17] while not requiring large computational time in globally searching for stiffness values in addition to optimizing muscle excitation solutions for 4000+ postures. Overall, the iterative regression procedure produced a set of stiffness values that met moment constraints according to the strength of musculature available and the posture space explored about the selected setpoint posture.

Higher stiffness values could be produced with either stronger muscle responses or a reduced posture space that is more pertinent to FNS standing whereby smaller ranges of motion or simplified (e.g., ankle-hip [20]) strategies may be observed. However, even with the comprehensive space investigated, significant UE loading reductions could be achieved. Variation in musculoskeletal parameters or selection of a different setpoint posture would also change achievable stiffness values. While stiffness values were adjusted regardless of which joints are most affected, this paradigm could be modified to accentuate higher stiffness at particular joints if it improves dynamic standing performance.

A conventional PD feedback control law was successful in reducing UE loading by driving an ANN that represents the nonlinear biomechanics of the system [14]. Only a feedforward ANN structure was necessary given inclusion of derivative control and optimal gain tuning. Derivative feedback to drive the ANN suggests a damping level response in addition to stiffness is beneficial for standing performance. Optimal tuning of the PD feedback parameters effectively compensated for muscle activation delays by substantially minimizing UE loading from initial, manually-tuned gain values. The gain optimization procedure employed a global search algorithm to produce a solution that synergistically considers multiple joints and found a set of gains within the specified bounds. The solution search is presumed sufficiently rigorous since the step tolerance (0.01) for termination was small relative to the search space (0 to 20). The search was not repeated at other initial set values since the manual tuning-procedure was intuitive in producing an initial set. Ultimately, the search algorithm determined optimal gains that further reduced UE loading using the fixed ANN structure.

A dynamic (time-delayed) ANN structure [14, 15] was not required for this FNS application since it has no dynamic open-loop element, such as commanded trajectory control. Although a dynamic ANN could be employed, tuning a PD controller to drive a static ANN is more desirable for clinical implementation. First, the static ANN can produce a unique solution at every static posture included or interpolated in its training space. A dynamic ANN employs time-based data which then requires consideration of trajectory characteristics (e.g., speed, path) for training. Second, while a dynamic ANN can be created to adapt to time-dependent data observed online, it would require varying of not only the 18 feedback gains but all ANN parameters (588 weights and biases in this study). Our formulation relies on a fixed-parameter ANN structure only to provide a black-box representation of the nonlinear biomechanical system and resolve basic anatomical constraints. These include closed-chain dependencies, mass-inertia properties, and musculoskeletal parameters determining the maximal stiffness values. This facilitates intuitive clinical tuning of gains at individual joints to improve performance.

Primary challenges to clinical implementation of a model-based control system include employing user-specific parameters. The anatomical model can be scaled readily to user length and mass parameters. Translating force generating characteristics of stimulated muscles to model parameters is not direct, but a similar scaling procedure as the one presented here could be performed for a specific user. Using a dynamometer, isometric joint moments are measured at the ankles, knees, hips, and trunk in response to a range (e.g., threshold to maximal) of pulse-width modulated stimulation. To correspond to model excitation levels, the stimulation range is normalized (0 to 1), and recruitment nonlinearities are represented as an added transfer function in the muscle model.

Characterizing a user-specific UE control structure is also important for initial model-based controller development. Integrating volitional control into LE FNS feedback systems has been identified as an important consideration for future developments in FNS standing [8, 38]. In this study, ANN training was independent of UE control since the static formulation intrinsically assumed hand-free maintenance of unperturbed standing. Subsequent reduction in UE loading primarily relied upon system tuning. In this model-based study, optimal tuning of FNS controller gains was contingent on the specific UE control structure itself since gains were varied to reduce UE output. The UE controller presented in this study was defined by only four parameters (one time-delay and three controller gains) and can potentially be optimized to represent the behavior of a specific user. User UE loading performance data can be collected using a walker with instrumented handles and a perturbation system (e.g., mounted linear actuators) capable of systematically applying loads upon a standing subject. Optimization techniques can then be applied to determine the UE model parameters that replicate this performance loading in simulation for the same loading conditions. This user-specific structure would be vital in constructing the best first-approximation of a model-based controller for clinical deployment. However, a systematic procedure for tuning an FNS controller online according to live user performance is still necessary since the user may adapt their volitional responses accordingly. In the future, it may be beneficial to investigate system tuning according to additional performance metrics (e.g., minimizing COM, joint-angle excursions). But if upper-body loading is required for stabilization, it is the primary SCI standing performance criterion to improve manual function and ease of system use.

Although this simulation study demonstrates potential benefit for comprehensive joint-feedback of FNS standing, a fundamental trade-off in clinical deployment must be considered. Closed-loop control of FNS standing requires sufficient, high-fidelity sensor measurements, but to facilitate clinical acceptance it is important to minimize the amount of worn instrumentation. Without bracing to restrain any DOFs, an inertial sensor must be placed on at least eight segments to attain the 18 position and velocity measurements proposed, which would be clinically unviable. However, this study suggests that accurate feedback measurements from certain joint DOFs (ankle PF/DF, hip Ab/Ad) are especially critical to standing performance and should be carefully considered for sensor placement and redundancy. The sensitivity to ankle position and hip Ab/Ad velocity is likely a result of both natural system biomechanics and the musculoskeletal parameters used in our analysis. In the coronal plane, the primary muscles available to make corrections are the hip ab/adductors. In the sagittal plane, small changes in ankle angle result in significant shifts in system COM when standing approximates an inverted pendulum [16]. Our results also indicate certain joint feedback signals may not be as critical. Knee feedback was typically negligible with sufficient vastii strength to damp knee buckling and facilitate ankle, hip, and trunk strategies. Furthermore, interactions at the trunk and hip may be sufficiently coupled to describe both joints with a reduced sensor set. Kim et al. [39] has suggested reduction of DOFs for FNS feedback control given the closed-chain nature of bipedal standing. However, even with systematic reduction of required feedback, further study is necessary to assess clinical viability of joint-based feedback control including performance assessment in the presence of typical sources of feedback error (e.g., sensor measurement and placement accuracy, insecure mounting on compliant tissue). The presented model system serves as an appropriate test-bed for future study to systematically introduce feedback error and quantitatively track performance degradation.

Upright maintenance of COM within the BOS is a fundamental goal of standing [29], and comprehensive joint-feedback by nature controls COM. But reducing joint-feedback signals can contaminate that representation of COM. Consequently, alternative feedback parameters should also be explored to reduce the sensors required for effective neuroprosthetic standing control. Desirable characteristics include being robust, faster acting than joint-feedback, and focally sensitive to COM dynamics. Thus, control structures utilizing parameters such as trunk acceleration, which is easily measured with a torso-mounted accelerometer and can be used to characterize balance control [40], may be valuable. An acceleration-based controller in isolation or in conjunction with minimal joint feedback may then extend functionality and facilitate clinical acceptance of automatic FNS control systems for regulating standing posture and balance.

While muscle fatigue is an important issue since it limits prolonged standing time with FNS [8, 38], it was not directly addressed in this study. If sufficient musculature were accessible to FNS for system redundancy, then similar ANN control structures could be devised for distinct muscle sets. This would facilitate controller development that both coordinates synergistic control action and reduces stimulation duty cycle to offset effects of fatigue.

V. Conclusions

Simulation results indicate that comprehensive three-dimensional joint-feedback control can markedly improve performance of a FNS standing system against postural disturbances over constant muscle excitation. The ANN approach presented in this study successfully produced a control solution that synergistically distributes muscle excitations while considering musculature that is multi-articulate, redundant, three-dimensional, and affected by SCI. Upper extremity loading during either external perturbations or one-arm task performance was reduced using the controller. While classic joint-feedback offers a potentially effective mode of comprehensive FNS standing control, alternative feedback signals that require fewer sensors and are focally sensitive to center of mass dynamics should be investigated.