Compaction and Tensile Forces Determine the Accuracy of Folding Landscape Parameters from Single Molecule Pulling Experiments

Abstract

We establish a framework for assessing whether the transition state location of a biopolymer, which can be inferred from single molecule pulling experiments, corresponds to the ensemble of structures that have equal probability of reaching either the folded or unfolded states (P_fold = 0.5). Using results for the forced unfolding of a RNA hairpin, an exactly soluble model, and an analytic theory, we show that P_fold is solely determined by s, an experimentally measurable molecular tensegrity parameter, which is a ratio of the tensile force and a compaction force that stabilizes the folded state. Applications to folding landscapes of DNA hairpins and a leucine zipper with two barriers provide a structural interpretation of single molecule experimental data. Our theory can be used to assess whether molecular extension is a good reaction coordinate using measured free energy profiles.

The response of biopolymers to mechanical force (f), at the single molecule level, has produced direct estimates of many features of their folding landscapes, which in turn has given a deeper understanding of how proteins and RNA fold. In particular, single molecule pulling experiments directly measure the distribution of forces needed to rupture biomolecules, roughness, and shapes of folding landscapes [1–4]. Such measurements have made it possible to decipher the molecular origin of elasticity and mechanical stability of the building blocks of life, which is the first step in describing how they interact to function in the cellular context. The major challenge is to provide a firm theoretical basis for interpreting the physical meaning and reliability of the folding landscape parameters that are extracted from trajectories that project dynamics in multidimensional space onto a one-dimensional molecular extension, which is conjugate to f.

The key characteristics of the folding landscape of biomolecules that can be extracted from single molecule force spectroscopy measurements are the f-dependent position of the transition state (TS), the distance (Δx^‡ = x_TS − x_N) from the ensemble of conformations that define the basin of attraction corresponding to the native states (NBA), and the free energy barrier (ΔF^‡). The assumption in the analysis of the single molecule force spectroscopy data is that the molecular extension is a good reaction coordinate for RNA and proteins, which implies that a single degree of freedom accurately describes the behavior of the multiple degrees of freedom explored by the biomolecule. The structural meaning of Δx^‡, a parameter that is unique to single molecule force spectroscopy, has never been made clear. Despite many subtleties in determining Δx^‡ from measurements [5–7], x_TS is most easily identified as a local maximum of the free energy profile at the transition midforce f_m, F(R|f_m), which can be constructed by measuring the statistics of end-to-end distance P(R) at f = f_m [1–4,8,9]. This method has been experimentally used to obtain sequence-dependent folding landscapes of DNA hairpins [2] and, more recently, proteins [3]. In order to render physical meaning to Δx^‡ we address two questions here: (i) Does Δx^‡ represent the structures in the transition state ensemble (TSE)? The TSE is a subset of structures that have equal probability of reaching the NBA or unfolded basin of attraction (UBA). (ii) Can a molecular tensegrity (short for tensional integrity) parameter [10] s = f_c/f_m, expressing balance between the internal compaction force f_m = ΔF_UF/Δx_UF and the tensile force f_c = ΔF^‡(f_m)/Δx^‡(f_m), describe the adequacy of Δx^‡(f_m) in describing the TSE structures?

We use simulations of a RNA hairpin and an exactly soluble model, both of which are apparent two-state folders as indicated by F(R|f), to answer the two questions posed above. The TS is a surface in the multidimensional folding landscape (stochastic separatrix [11]) across which the flux to the NBA and the UBA is identical. This implies that the fraction of folding trajectories corresponding to Δx^‡ that start from the TS should have equal probability (P_fold ≈ 0.5 [12]) of reaching the NBA and the UBA [12,13]. At f = f_m, the mean dwell times in the NBA and the basin of attraction corresponding to unfolded conformations (UBA) are identical, so that ${\int }_0^{x_{\text{TS}}}\mathit{dRP}(R)={\int }_{x_{\text{TS}}}^{\infty }\mathit{dRP}(R)=0.5$. However, it is unclear whether or not the barrier top position is consistent with the requirement P_fold ≈ 0.5 in force experiments.

To directly ascertain whether the barrier top position denotes the TSE (requiring P_fold ≈ 0.5 in force experiments), we study folding of P5GA, a RNA hairpin, for which the NBA and UBA are equally populated at f_m = 14.7 pN [8,9]. Both free energy profiles and the kinetics predicted by Kramers’ theory show excellent agreement with the simulation results [9] and formally establish that extension R is a good reaction coordinate for describing hopping kinetics at f ≈ f_m. In practice, experimental time traces that have a number of transitions such as the one in Fig. 1(a) can be used to estimate P_fold. With absorbing boundary conditions imposed at R_N = 2 nm and R_U = 7.5 nm [Fig. 1(c)], we directly count the number of molecules from 47 points belonging to the TS region (R = (4.1 – 4.2) nm [Fig. 1(c)]) that reach R < R_N (folded) and R > R_U (unfolded). Although the R distribution of the 47 points is uniform [Fig. 1(a)], we obtained P_fold ≈ 0.74. To determine P_fold by using the ensemble method, we launched 100 trajectories from each of the 47 structures and monitored their evolution [Fig. 1(b)] by using Brownian dynamics simulations [14] with the multidimensional energy function for the hairpin [8]. We find that P_fold = 0.65 [Fig. 1(c)], which is similar to the value obtained by analyzing the folding trajectory. An examination of the individual trajectories reveals that many molecules, initially with a gradient toward the UBA, recross the transition barrier to reach the NBA [blue trajectories in Fig. 1(b)]. Conversely, most of the molecules directly reach R = R_N if they initially fall into the NBA, showing few recrossing events. Although the precise percentage of molecules reaching the UBA or NBA depends on the particular value of the boundary (R_N and R_U), our simulations emphasize the importance of the recrossing dynamics, which is known to cause significant deviations from the transition state theory.

FIG. 1.

(color online). Relaxation dynamics of the ensemble of P5GA hairpins from the barrier top of F(R|f_m). (a) R(t) at f = f_m. TSE in the range R = (4.1–4.2) nm are shown in the green box with a uniform R distribution. (b) Starting from the TSE of hairpins from (a), 35% of the trajectories (red) reach UBA and 65% of the trajectories (blue) reach NBA. (c) Free energy profile at f = f_m. (d) TSE of P5GA has a broad distribution in the number of base pairs (N_bp).

Deviation from P_fold ≈ 0.50 suggests that the global coordinate R alone is not sufficient to rigorously describe the hopping kinetics of P5GA. At least one other auxiliary coordinate is needed, and for structural reasons we take it to be the number N_bp of base pairs [2]. The broad asymmetric distribution of N_bp within the narrow TS region [R = (4.1–4.2)] implied by F(R|f_m) [Fig. 1(d)] shows that hopping kinetics at f_m should be described by a multi-dimensional (at least two) folding landscape even though the f-dependent rates of hopping between the NBA and the UBA can be reliably predicted by using F(R|f_m) [9].

To further illustrate if the R coordinate alone is sufficient to determine the TSE structures, we consider an analytically solvable generalized Rouse model (GRM) [9] that has a single bond in the interior of the chain whose presence corresponds to the NBA. The GRM Hamiltonian [15]

$$\beta \mathcal{H}=\frac{3}{2a^2}{\int }_0^{N}ds\stackrel{.}{\mathbf{r}}(s)-\beta \mathbf{f}{\int }_0^{N}ds\stackrel{.}{\mathbf{r}}(s)+\beta V_c[\mathbf{r}(s_1)-\mathbf{r}(s_2)],$$ (1)

where V_c[x] = k(x² − c²)/2 for x ≤ c and V_c[x] = 0 for x > c, describes a simple Gaussian chain under tension with an additional cutoff harmonic interaction at the interior points s₁ and s₂. The distribution of R for the GRM, with Δs = |s₂ − s₁|, is

$$P(R;\mathrm{\Delta }s)\propto Rsinh(\beta fR)e^{-3R^2/2(N-\mathrm{\Delta }s)a^2}{\int }_0^{\infty }\mathit{dxx}sinh\left[\frac{3Rx}{(N-\mathrm{\Delta }s)a^2}\right]e^{-3x^{2}N/2\mathrm{\Delta }s(N-\mathrm{\Delta }s)a^2-\beta V_c[x]}.$$ (2)

To obtain P_fold we set N = 22 for the number of bonds, a = 0.545 nm for their spacing, β = 1/k_BT, βk = 1.65 nm⁻², c = 4 nm for the strength and cutoff distance of the interior bond interaction, respectively, and Δs = 18. For this set of parameters, the transition midforce [where P(x < c) = P(x > c)] is f_m ≈ 16.8 pN. The two minima and the position of the barrier top of the free energy βF(R|f_m) = −log[P(R)] are easily determined as R_N ≈ 3.91 nm, R_U ≈ 9.39 nm, and R_TS = 6.00 nm, respectively [Fig. 2(a)].

FIG. 2.

(color online). Relaxation dynamics of GRM chains from the barrier top of βF(R|f_m). (a) βF(R|f_m) for the GRM with interior interaction. Parameters are listed in the text. Red symbols are from the simulation result sampled by using the chain with the Hamiltonian of Eq. (1). The solid line is the theoretical fit. The arrow shows the position of the barrier top. (b) The distribution of interior distance at R = R_TS. The black line is the theoretical prediction. (c) The initial distribution of R prior to the relaxation dynamics, which is very tight around R ≈ R_TS = 6 nm. (d) The probability of being folded as a function of R. Open circles show the exact numerical solution for the sharp potential [Eq. (1)]. The filled circles are from simulations. The solid black line shows the approximate solution using the smoothed potential [Eq. (3)].

To calculate P_fold, we prepared 5000 GRM chains with R = R_TS = 6 nm that corresponds to the maximum in F(R|f_m) [Fig. 2(a)] and allowed the system to relax to either of the two basins of attraction, ending the simulation when the chain extension attains the value R_N or R_U. These simulations are performed by using the Hamiltonian in Eq. (1) and not on the simple one-dimensional profile βF(R) = −log[P(R)]. We find 60% (40%) of the initial chains from R_TS reach R = R_N (R = R_U), which implies P_fold = 0.6. Similar to the P5GA, the GRM dynamics projected onto the R coordinate using both sets of parameters exhibit a number of recrossing events.

To understand the relation between x (the structural coordinate which specifies the NBA and UBA in the GRM) and chain extension R (pulling coordinate that is conjugate to f), we approximate the sharp interaction in Eq. (1) by a smoothed potential:

$$\beta V_c[x]\approx \beta V_S[x]=-log(e^{-\beta k(x^2-c^2)/2}+1),$$ (3)

by taking advantage of the clear separation between the UBA and the NBA [Fig. 2(a)]. Defining 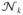= 〈e^{−βk(x2−c2)/2}δ(|R|−R)〉₀, with 〈…〉₀ denoting an average over the Gaussian backbone, we can compute approximately $P_R(x<c)={\int }_0^{c}dx\langle \delta (\mid \mathbf{R}\mid -R)\rangle \approx {\mathcal{N}}_k/({\mathcal{N}}_{k=0}+{\mathcal{N}}_k)$, with 〈…〉 representing an average over the GRM potential in Eq. (3). The probability of bond formation satisfies

$$P_R(x<c)\approx {\left[1+{\lambda }^{3/2}exp\left(\frac{3R^2\kappa {\sigma }^2}{2{Na}^2\lambda }-\frac{\beta k{c}^2}{2}\right)\right]}^{-1},$$ (4)

where κ = Na²βk/3, σ = Δs/N, and λ=1+σ(1−σ)κ. At R = 6 nm, Eq. (4) gives P_R(x < c) ≈ 0.402 ≠ 0.5. Thus, when the dynamics is initiated from the top of the apparent free energy barrier using the R variable, their internal coordinate (x) is populated primarily with unfolded conformations [Fig. 2(b)]. Despite the fact that the UBA is primarily populated at R = R_TS, we find that P_fold ≈ 0.6, so that the NBA will be predominantly populated as the trajectories progress. The midpoint of transition [P_R(x < c) = 0.5] occurs at R_mid = [(Na²λ/3κσ²)(βkc² − 3 logλ)]^1/2 = 5.91 nm, which deviates slightly from R_TS = 6.00 nm. The results from V_S[x], which are in excellent agreement with the simulations as well as the numerical results using V_c[x] (Fig. 2), also suggest that hopping kinetics in the GRM involves coupling between x and R. Thus, even in this simple system, accurate location of the TSE should consider two-dimensional free energy profiles (see [6,16]).

To answer the second question, we introduce a molecular tensegrity parameter, which is a ratio of tensile force and a force that determines the stability of the biopolymer. The limit of mechanical stability of the NBA is determined by the critical unbinding force f_c = ΔF^‡(f_m)/Δx^‡(f_m). At the midpoint force f = f_m, the tensegrity parameter s = f_c/f_m determines whether the applied external tension is sufficient to overcome the stability of the NBA. Models, which approximate the free energy profiles using a cubic or cusp potential [7], could alter f_c or f_m from the form suggested above. However, because s involves the ratio of the two forces, the precise numerical factors are not relevant. Barrier crossings between the NBA over the TS are governed by the competition between f_c and the applied force f = f_m. For f_c ≫ f_m, barrier recrossing from the NBA to the TS will be extremely rare, while if f_c ≪ f_m, barrier crossing events will be common. We would therefore expect as the ratio s = f_c/f_m increases, barrier recrossings from within the NBA to the TS will decrease, and the probability of reaching R = R_N will increase. Thus, P_fold, the structural link to Δx^‡, should be determined by the experimentally measurable tensegrity parameter s.

To confirm this expectation, we ran 20 different sets of GRM parameters (1000 runs each), with f_m ranging between 5 and 25 pN, βk ranging from 0.1 to 600 nm⁻², c between 0.26 and 6 nm, and Δs between N/2 and N. Figure 3 shows that P_unfold = 1 − P_fold decreases monotonically with s = f_c/f_m. The dependence of P_unfold on s (Fig. 3) can be derived by considering diffusion in a 1D version of the GRM potential in Eq. (1): $U(x)=-fx+\frac{1}{2}{k}_u{x}^2+V_c(x)$, with k_u being the curvature in the bottom of the UBA. Assuming constant diffusivity, $P_{\text{unfold}}={\int }_{x_N}^c{dx}^{\prime }{e}^{\beta U(x^{\prime })}/{\int }_{x_N}^{x_U}{dx}^{\prime }{e}^{\beta U(x^{\prime })}$ [17], where the positions of the transition barrier, native, and unfolded wells are given by c, x_N, and x_U, respectively. For s ≫ 1, we obtain P_unfold = (1 + s)⁻¹/2, with the entire dependence on the energy landscape encoded in s. The analytical result, plotted as a solid curve in Fig. 3, captures the overall trend of the GRM and P5GA simulations.

FIG. 3.

(color online). P_unfold as a function of s = ΔF^‡/f_mΔx^‡ for a variety of GRM parameters (colored circles). Red corresponds to small βk ~ (0.1–1) nm⁻², purple to intermediate βk ~ (1–50) nm⁻², and blue to high βk ~ (50–500) nm⁻². The point sizes indicate the magnitude of the midpoint force, with the smallest points at f_m = 5 pN and the largest at f_m = 25 pN. The large square indicates the results of the P5GA simulations with P_unfold = 0.35. The gray line is the theoretical prediction P_unfold(s) = (1 + s)⁻¹/2 for s≫1. The solid line in the inset shows the predicted P_unfold(s) for s ≪ 1 [Eq. (5)] using the DNA hairpin free energy profiles (not deconvolved) in Ref. [2]. The dashed line is for the leucine zipper, which has two barriers, using data from Ref. [3]. As explained in Ref. [18], numbers 1 and 2 are for NBA → I and I → UBA transitions, respectively. Because of different k_U values [Eq. (5)], dashed and solid lines do not coincide.

For s ≪ 1, P_unfold can be approximated as

$$P_{\text{unfold}}=\frac{1}{2}{\left[\frac{\mathrm{\Phi }}{1+\mathrm{\Phi }}+\frac{32f_m^2(\mathrm{\Phi }-1)}{\pi k_U{(\mathrm{\Phi }+1)}^3}s\right]}^{-1},$$ (5)

where $\mathrm{\Phi }=4f_m/\sqrt{2\pi k_B{Tk}_U}$ and k_U = ∂²U=∂x² at x = x_U. This relation can be used to predict the degree to which the extension is a good reaction coordinate for DNA hairpins. We calculated s from the measured energy landscapes in Ref. [2] and obtained P_unfold by using Eq. (5). We took f_m ≈ 12.5 pN and βk_U ≈ 0.2 nm⁻². The predicted P_fold inset in Fig. 3 varies between 0.54 and 0.61 for the DNA hairpin sequences A–D, close to the ideal value of 1/2, indicating that extension is a reasonable coordinate except possibly for sequence C, which has a T:T base pair (bp) mismatch 7 bp from the stem. The limitation of extension as a reaction coordinate for this sequence is consistent with the observation that folding of sequence C has an intermediate as indicated by the three minima in F(R|f_m) [2].

To illustrate that the theory is applicable when there are multiple barriers [4], we analyze the data for a leucine zipper which unfolds by populating an intermediate. In this case there are two tensegrity parameters: s₁(= 0.05) and s₂(= 0.15) (see [18]). The predicted P_unfold values show that the extension is a good reaction coordinate for the NBA → I transition but is less for the I → UBA transition. (Figure 3).

Our results can be confirmed by analyzing long time folding trajectories R(t) as long as multiple hopping events occur. Because Δx^‡ is f-dependent, it follows that tensegrity can be altered by changing f. Thus, the extension may be a good reaction coordinate over a certain range of f but may not remain so under all loading conditions.