Bayesian Meta-Experimental Design: Evaluating Cardiovascular Risk in New Antidiabetic Therapies to Treat Type 2 Diabetes

Summary

Recent guidance from the Food and Drug Administration for the evaluation of new therapies in the treatment of type 2 diabetes (T2DM) calls for a program-wide meta-analysis of cardiovascular (CV) outcomes. In this context, we develop a new Bayesian meta-analysis approach using survival regression models to assess whether the size of a clinical development program is adequate to evaluate a particular safety endpoint. We propose a Bayesian sample size determination methodology for meta-analysis clinical trial design with a focus on controlling the type I error and power. We also propose the partial borrowing power prior to incorporate the historical survival meta data into the statistical design. Various properties of the proposed methodology are examined and an efficient Markov chain Monte Carlo sampling algorithm is developed to sample from the posterior distributions. In addition, we develop a simulation-based algorithm for computing various quantities, such as the power and the type I error in the Bayesian meta-analysis trial design. The proposed methodology is applied to the design of a phase 2/3 development program including a noninferiority clinical trial for CV risk assessment in T2DM studies.

1. Introduction

The recent guidance document from the Food and Drug Administration (FDA) for the evaluation of new therapies in the treatment of type 2 diabetes (T2DM) (www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/ucm071627.pdf), calls for a program-wide meta-analysis of cardiovascular (CV) outcomes. This guidance requires that before submission of a new drug application, one must show that the upper bound of the two-sided 95% confidence interval (CI) for the estimated risk ratio for comparing the incidence of important CV events occurring in the investigational agent to that of the control group is less than 1.8. This can be demonstrated either by performing a meta-analysis of the randomized phase 2 and phase 3 studies or by conducting an additional single, large postmarketing safety trial. If the premarketing application contains clinical data from completed studies showing that the upper bound of the 95% CI for the estimated risk ratio is between 1.3 and 1.8 and the overall risk-benefit profile supports approval, a postmarketing trial generally will be necessary to definitively show that the upper bound of the 95% CI is less than 1.3. On the other hand, if the premarketing clinical data show that the upper bound of the 95% CI is less than 1.3, then a postmarketing CV trial generally may not be necessary. This requirement will most likely necessitate the performance of a specific CV outcomes study for any new therapy, but would also almost certainly include integrating data across randomized phase 2 and phase 3 studies. This particular guidance document establishes, for the first time, that the FDA accepts prospectively designed, formal meta-analysis in the regulatory approval path.

In 2009, the Safety Planning, Evaluation and Reporting Team (Crowe et al., 2009), formed in 2006 by the Pharmaceutical Research and Manufacturers of America with FDA participation, gave detailed recommendations for a well-planned and systematic approach to proactively plan for meta-analysis of the program-level safety data. In particular, Safety Planning, Evaluation and Reporting Team recommended that when it is not feasible at the individual study level, power for a particular safety outcome should be considered at the program level using the integrated safety database across clinical trials for a particular product.

A typical drug development program may consist of multiple clinical studies with different study objectives, endpoints, and possibly different patient populations. Recent literature for single trial Bayesian sample size determination includes Wang and Gelfand (2002), Spiegelhalter, Abrams, and Myles (2004), Inoue, Berry, and Parmigiani (2005), De Santis (2007), M’Lan, Joseph, and Wolfson (2008), and Chen et al. (2011). However, there has been no published work for sample size determination and power at a drug development program level by taking into account between-study heterogeneity within a meta-analysis framework. Sutton et al. (2007) proposed a hybrid frequentist-Bayesian approach for sample size determination for a future randomized clinical trial using the results of meta-analyses reported in the literature. Sutton et al. (2007) suggested that the power can be highly dependent on the statistical model used for meta-analysis and even very large studies may have little impact on a meta-analysis when there is considerable between-study heterogeneity. This raises a critical issue regarding how to account for between-study heterogeneity appropriately in the statistical model for meta-analysis.

In this article, we develop a new Bayesian meta-analysis approach using survival models to assess whether the size of a clinical development program is adequate to evaluate a particular safety endpoint. We extend the fitting and sampling priors of Wang and Gelfand (2002) to Bayesian meta-analysis clinical trial design with a focus on controlling the type I error and power. The historical survival data are incorporated via the power priors of Ibrahim and Chen (2000). Various properties of the proposed methodology are examined and an efficient Markov chain Monte Carlo sampling algorithm is developed to sample from the posterior distributions. In addition, we develop a novel simulation-based algorithm for computing various quantities, such as the power and the type I error, involved in the Bayesian meta-analysis trial design. The proposed methodology is applied to the design of a phase 2/3 development program, including a noninferiority clinical trial for CV risk assessment in T2DM studies.

The rest of the article is organized as follows. Section 2 describes a motivating example for designing a phase 2/3 development program of a new T2DM therapy and historical data used in formulating priors for the background rate. In Section 3, we present both log-linear random effects and fixed effects regression models for meta-survival data. In Section 4, we propose a general Bayesian methodology for the meta-analysis clinical trial design. Section 5 provides a detailed development of the incorporation of historical meta-survival data through the partial borrowing power prior formulation. The posterior computation and simulation-based computational algorithm for computing the type I error and power are developed in Section 6. In Section 7, we apply the proposed methodology to the design of meta-studies for evaluating the CV risk discussed in Section 2 and the results from our simulation studies are reported and discussed. We conclude the article with some discussion and extensions of the proposed method in Section 8.

2. Motivating Example

We assume there is a desire to develop an experimental drug that has different formulations and dosing frequencies for either mono or add-on therapy in treating T2DM. Based on the FDA guideline mentioned previously, one could consider various product development plans containing multiple phase 2 and 3 studies. In this article, we assume a development plan with an objective of using phase 2 and 3 studies to evaluate if the upper bound of 95% CI of the hazard ratio (HR) of the experimental drug to the control group is below 1.3. A composite endpoint is considered: time to CV deaths, stroke, or myocardial infarction (MI), whichever occurs first. Under this setting, the power is the probability that the upper 95% CI of the HR < 1.3, when the true HR = 1. Following Spiegelhalter et al. (2004), we first consider empirically pooling sample sizes from all studies and calculate the power by using the following theory:

$$\text{log}(\widehat{\text{HR}})~N(\text{log}(\text{HR}),4/\text{total number of endpoints observed from pooled studies}).$$ (1)

Assuming the development plan will contain studies in two categories, Table 1 summarizes the initial power calculations.

Table 1.

A design of meta studies with two categories for evaluating the CV risk.

	Control group	Experimental drug	Total
Category 1: randomized efficacy superiority studies
Individual study
Phase 2a—4 weeks (five doses, placebo)	25	125	150
Phase 2b—24 weeks (three doses, active control, placebo)	140	210	350
Phase 3—24 weeks (three doses, placebo)	100	300	400
Phase 3—24 weeks (four doses, placebo)	75	300	375
Phase 3 add on therapy—24 weeks (three doses, placebo)	185	555	740
Phase 3 add on therapy—24 weeks (two doses, placebo)	250	500	750
Phase 3 add on therapy—24 weeks (two doses, placebo)	188	376	564
Aggregated level
Total sample size of the above seven studies	963	2366	3329
Assumed annualized event rate of death/MI/stroke	1.2%	1.2%	1.2%
Expected endpoints	5	12	17
Probability of upper 95% CI on HR < 1.3		7.8%
Category 2: Randomized CV outcome study (2 year equal enrollment, minimal of 2 years follow-up)
Sample size	5000	5000	10,000
Assumed annualized event rate of death/MI/stroke	1.5%	1.5%	1.5%
Expected endpoints	226	226	452
Probability of upper 95% CI on HR < 1.3		79.6%
Combined categories 1 and 2
Expected endpoints	231	238	469
Probability of upper 95% CI on HR < 1.3		81.1%

Category 1: Traditional diabetes HbA1c superiority studies to demonstrate efficacy

We assumed there are seven phase 2 and 3 studies in this category. Those studies are randomized controlled studies with the primary efficacy endpoint defined as the change from baseline of HbA1c at 6 months. These studies include multiple dose groups for experimental drug and either active control or placebo as comparator(s). For the analysis of evaluating CV risk, the placebo and active controls are combined into one “control group,” and all active dose arms are combined as the “experimental drug.” Thus, the sample sizes are not same between the control group and the experimental drug group. The enrolled subjects in those studies are generally at low or moderate CV risk. Assuming the annualized event rate is 1.2%, this category is expected to have a total of 17 endpoints with a power of 7.8%. Such low power implies that a large scale CV outcome study is needed.

Category 2: CV outcome in noninferiority studies

In this category, we consider a large scale CV outcome study that has the primary objective of evaluating the CV risk of the experimental drug. This randomized controlled study has two treatment arms (experimental drug and control group) with 5000 subjects in each arm. The study is assumed to have steady enrollment for 2 years and the last patient enrolled has a minimum of 2 years of follow-up. The target population includes subjects with high CV risk. Thus, an annualized event rate of 1.5% is assumed (The Action to Control Cardiovascular Risk in Diabetes (ACCORD) Study Group, 2008; The ADVANCE Collaborative Group, 2008; Home et al., 2009). As a result, this category is expected to have a total of 452 endpoints with power of 79.6%.

By combining categories 1 and 2, it is expected to have a total of 469 endpoints with power of 81.1%. These power calculations are based on pooling sample sizes across studies using (1), but they do not account for the between-study variability in the meta-analytic framework, and do not allow for different baseline event rates and therefore are susceptible to issues related to the Simpson/Yule paradox. Moreover, certain historical information from other similar drugs for underlying CV risk is not incorporated. This motivates the idea of using a Bayesian meta-analysis design approach in this article. Under the Bayesian framework, the prior information for the underlying risk in the control population is based on the briefing documents from the FDA advisory meetings for Saxagliptin and Liraglutide in April 2009. The available historical data are summarized in Table 2. In Table 2, for Saxagliptin and Liraglutide, the events are the major adverse cardiac events defined in the FDA briefing document; for ACCORD, the events are CV death, nonfatal MI, or stroke, and the total patient years is approximated by the authors based on Table 4 in the original publication; and for ADVANCE, the total patient years is approximated as N times the median follow-up (5 years). In Section 5, we develop a novel method to elicit the priors using these five historical datasets.

Table 2.

Long duration historical meta data for the control arm.

Study (year of publication)	Group	N	Events	Total patient year	Annualized event rate
Saxagliptin (2009)	Total control	1251	17	1289	1.31%
Liraglutide (2009)	placebo	907	4	449	0.89%
	Active control	1474	13	1038	1.24%
ACCORD (2008)	Standard therapy	5123	371	16000	2.29%
ADVANCE (2008)	Standard therapy	5569	590	27845	2.10%

Table 4.

Powers and type I errors for the meta-design in Table 1

		n18 = n28 = 4000		n18 = n28 = 4500		n18 = n28 = 5000
Model	a0	Power	Type I error	Power	Type I error	Power	Type I error
Random effects	0	0.765	0.043	0.811	0.040	0.850	0.038
	0.00625	0.787	0.047	0.831	0.045	0.866	0.042
	0.0125	0.801	0.050	0.843	0.047	0.874	0.044
	0.015	0.805	0.051	0.846	0.048	0.876	0.045
	0.025	0.814	0.054	0.855	0.050	0.883	0.047
	0.0375	0.819	0.055	0.860	0.052	0.887	0.049
	0.05	0.821	0.057	0.862	0.053	0.889	0.051
	0.075	0.826	0.058	0.865	0.055	0.892	0.052
	0.1	0.829	0.059	0.867	0.056	0.893	0.053
	0.15	0.831	0.060	0.870	0.057	0.894	0.054
	0.2	0.833	0.060	0.871	0.058	0.895	0.055
Fixed effects	0	0.768	0.044	0.817	0.042	0.853	0.039
	0.1	0.787	0.045	0.831	0.044	0.864	0.040
	0.15	0.799	0.049	0.842	0.047	0.872	0.044
	0.2	0.809	0.052	0.853	0.050	0.878	0.046
	0.25	0.819	0.054	0.858	0.053	0.884	0.050
	0.3	0.826	0.057	0.865	0.055	0.888	0.051
	0.35	0.834	0.059	0.871	0.057	0.894	0.053
	0.4	0.840	0.061	0.876	0.059	0.896	0.055

3. The Meta-survival Data and Meta-analysis Models

Suppose we consider K randomized trials where each trial has two treatment arms (“Control” or “Inv Drug”). Let y_ijk denote the subject level time to event (failure time) and let ν_ijk denote the censoring indicator such that ν_ijk = 1 if y_ijk is a failure time and ν_ijk = 0 if y_ijk is right censored for the ith subject in the jth treatment arm and the kth trial for i = 1, …, n_jk, j = 1, 2, and k = 1, …, K. We write $y_{\mathit{\text{jk}}}={\displaystyle {\sum }_{i=1}^{n_{\mathit{\text{jk}}}}}{y}_{\mathit{\text{ijk}}}$, which denotes the total subject year duration, and ${\nu }_{\mathit{\text{jk}}}={\displaystyle {\sum }_{i=1}^{n_{\mathit{\text{jk}}}}}{\nu }_{\mathit{\text{ijk}}}$, which denotes the total number of events, for j = 1, 2 and k = 1, …, K. We also let x_jk denote a binary covariate, where x_jk = 1 if the kth trial recruits subjects with low or moderate CV risk for the jth treatment and x_jk = 0 if the kth trial recruits subjects with high CV risk for the jth treatment. In addition, let trt_jk = 1 if j = 2 (treatment) and 0 if j = 1 (control/placebo). Write D_K = {(y_ijk, ν_ijk, trt_jk, x_jk), i = 1, …, n_jk, j = 1, 2, k = 1, …, K}.

Assume the individual level failure time follows the exponential distribution, y_ijk ~ Exp(λ_jk), where λ_jk > 0 is the hazard rate. We consider both random effects and fixed effects models for λ_jk. The log-linear random effects model for λ_jk assumes

$$\text{log }{\lambda }_{\mathit{\text{jk}}}={\gamma }_0+{\gamma }_1{\text{trt}}_{\mathit{\text{jk}}}+\theta x_{\mathit{\text{jk}}}+{\xi }_k,{\xi }_k~N(0,{\sigma }^2),$$ (2)

where trt_jk = 1 if j = 2 (treatment) and 0 if j = 1 (control/placebo) for k = 1, …, K. In (2), σ² captures the between-trial variability and ξ_k also captures the trial dependence between y_1k and y_2k. Note that under the exponential model, the design parameter exp (γ₁) is precisely the HR of the treatment, and θ quantifies the CV risk effect (low or moderate CV risk versus high CV risk). Let ξ = (ξ₁, …, ξ_K)′ and γ = (γ₀, γ₁)′. Then, under the random effects model, the complete data likelihood function based on the meta-survival data D_K is given by

$$L_R(\mathit{\gamma },\theta ,\mathit{\xi },{\sigma }^2|D_K)={\displaystyle \prod _{k=1}^K}{\displaystyle \prod _{j=1}^2}(\text{exp}\{{\nu }_{\mathit{\text{jk}}}({\gamma }_0+{\gamma }_1{\text{trt}}_{\mathit{\text{jk}}}+\theta x_{\mathit{\text{jk}}}+{\xi }_k)\}\times \text{exp}[-\text{exp}\{{\gamma }_0+{\gamma }_1{\text{trt}}_{\mathit{\text{jk}}}+\theta x_{\mathit{\text{jk}}}+{\xi }_k\}{y}_{\mathit{\text{jk}}}])\times \frac{1}{\sqrt{2\pi }\sigma }\text{exp}\{-\frac{{\xi }_k^2}{2{\sigma }^2}\}.$$ (3)

We see from (3) that under the exponential model, the likelihood function based on the individual level meta-survival data D_K reduces to the likelihood function based on the treatment-level meta-survival data {(y_jk, ν_jk, trt_jk, x_jk), j = 1, 2, k = 1, …, K}. The log-linear fixed effects model for λ_jk assumes

$$\text{log }{\lambda }_{\mathit{\text{jk}}}={\gamma }_0+{\gamma }_1{\text{trt}}_{\mathit{\text{jk}}}+{\theta }_k,$$ (4)

for k = 1, 2, …, K. To ensure identifiability in (4), we assume that ${\displaystyle {\sum }_{k=1}^K}{\theta }_k=0$. For simplicity, we take ${\theta }_K=-{\displaystyle {\sum }_{k=1}^{K-1}}{\theta }_k$. Unlike the random effects model, the θ_k’s in (4) capture the differences among the trials. Because the θ_k’s are unknown, a necessary condition for existence of the maximum likelihood estimates of the θ_k’s is that there is at least one event, i.e., ν_1k + ν_2k ≥ 1, for each trial. Let θ = (θ₁, …, θ_K)′. Then, similar to (3), under the fixed effects model, the likelihood function based on the meta-survival data D_K is given by

$$L_F(\mathit{\gamma },\mathit{\theta }|D_K)={\displaystyle \prod _{k=1}^K}{\displaystyle \prod _{j=1}^2}\text{exp}\{{\nu }_{\mathit{\text{jk}}}({\gamma }_0+{\gamma }_1{\text{trt}}_{\mathit{\text{jk}}}+{\theta }_k)\}\times \text{exp}[-\text{exp}\{{\gamma }_0+{\gamma }_1{\text{trt}}_{\mathit{\text{jk}}}+{\theta }_k\}{y}_{\mathit{\text{jk}}}].$$ (5)

4. Bayesian Meta-design

In this section, we present a novel general methodology for Bayesian meta-design only for the log-linear random effects regression model. The method for the fixed effects model is very similar and therefore omitted here for brevity. We assume that the hypotheses for “noninferiority” testing can be formulated as follows:

$$H_0:\text{ exp}({\gamma }_1)\ge \delta \text{ versus }{H}_1:\text{ exp}({\gamma }_1)<\delta .$$ (6)

The meta-trials are successful if H₁ is accepted. Following Wang and Gelfand (2002), let π^(s)(γ, θ, σ²) denote the sampling prior, which captures a certain specified portion of the parameter space in achieving a certain level of performance in the Bayesian meta-design, and also let π^(f)(γ, θ, σ²) denote the fitting prior, which is used to fit the model once the data are obtained. Under the fitting prior, the posterior of γ, θ, and σ² given the data D_K takes the form ${\pi }^{(f)}(\mathit{\gamma },\theta ,{\sigma }^2|D_K)\propto \{{\displaystyle {\prod }_{k=1}^K}{\displaystyle \int }[{\displaystyle {\prod }_{j=1}^2}\text{exp}\{{\nu }_{\mathit{\text{jk}}}({\gamma }_0+{\gamma }_1{\text{trt}}_{\mathit{\text{jk}}}+\theta x_{\mathit{\text{jk}}}+{\xi }_k)\}\times \text{exp}\{-\text{exp}({\gamma }_0+{\gamma }_1{\text{trt}}_{\mathit{\text{jk}}}+\theta x_{\mathit{\text{jk}}}+{\xi }_k)y_{\mathit{\text{jk}}}\}][\frac{1}{\sigma }\text{exp}\{-\frac{1}{2{\sigma }^2}{\xi }_k^2\}]d{\xi }_k\}{\pi }^{(f)}(\mathit{\gamma },\theta ,{\sigma }^2)$. We note that π^(f)(γ, θ, σ²) may be improper as long as the resulting posterior, π^(f)(γ, θ, σ² | D_K), is proper.

We use the sampling prior, π^(s)(γ, θ, σ²), to generate the predictive data D_K. In other words, we view the distribution of D_K as the prior predictive marginal distribution of the data. The prior predictive data-generation algorithm is given as follows. For i = 1, …, n_jk, j = 1, 2, and k = 1, …, K, (i) set n_jk and x_jk; (ii) generate (γ, θ, σ²) ~ π^(s)(γ, θ, σ²); (iii) generate ξ_k ~ N(0, σ²) independently; (iv) compute λ_jk = exp{γ₀ + γ₁trt_jk + θx_jk + ξ_k}; (v) generate $y_{\mathit{\text{ijk}}}^{*}~\text{Exp}({\lambda }_{\mathit{\text{jk}}})$ independently; (vi) specify the censoring time C_ijk or generate C_ijk ~ g_jk (c_ijk) independently, where g_jk (c_ijk) is a prespecified distribution for the censored random variable; and (vii) compute $y_{\mathit{\text{ijk}}}=\text{min }\{y_{\mathit{\text{ijk}}}^{*},C_{\mathit{\text{ijk}}}\}\text{ and }{\nu }_{\mathit{\text{ijk}}}=1\{y_{\mathit{\text{ijk}}}^{*}\le C_{\mathit{\text{ijk}}}\}$, where the indicator function 1{A} is 1 if A is true and 0 otherwise.

From the above algorithm, it is easy to see that we do need to specify a proper sampling prior π^(s)(θ). To make the design using the meta-analysis models more feasible, we assume n_jk = ϕ_jk n_k for j = 1, …, q and n_k = κ_k n for k = 1, …, K, where both ϕ_jk and κ_k are prespecified nonnegative constants such that ${\displaystyle {\sum }_{j=1}^2}{\varphi }_{\mathit{\text{jk}}}=1\text{ and }{\displaystyle {\sum }_{k=1}^K}{\kappa }_k=1$. Under this setting, the total sample size based on the entire meta-analytic model is n. This sample size allocation is quite general and flexible, which allows ϕ_jk = 0 for certain treatment arms, which allows an unbalanced design for certain trials. In practice, the n_jk’s are often determined by the design analyst based on certain constraints in the studies/trials. An example of such a meta-design is shown in Table 1.

To complete the Bayesian meta-analytic design, we need to specify two sampling priors, denoted by, ${\pi }_0^{(s)}(\mathit{\gamma },\theta ,{\sigma }^2)\text{ and }{\pi }_1^{(s)}(\mathit{\gamma },\theta ,{\sigma }^2),\text{ where }{\pi }_0^{(s)}(\mathit{\gamma },\theta ,{\sigma }^2)\text{ and }{\pi }_1^{(s)}(\mathit{\gamma },\theta ,{\sigma }^2)$ are two proper priors, which are defined on the subsets of the parameter spaces induced by hypotheses H₀ and H₁. Following Chen et al. (2011), we define the key quantity

$${\beta }_{s\ell }^{(n)}=E_{s\ell }[1\{P(\text{exp}({\gamma }_1)<\delta |D_K,{\pi }^{(f)})\ge {\tau }_0\}],$$ (7)

where the posterior probability P(exp (γ₁) < δ| D_K, π^(f)) is computed with respect to the posterior distribution of γ₁ given the data D_K under the fitting prior π^(f)(γ, θ, σ²), and the expectation E_sl is taken with respect to the predictive marginal distribution of D_K under the sampling prior ${\pi }_{\ell }^{(s)}(\mathit{\gamma },\theta ,{\sigma }^2)$ for ℓ = 0, 1.

For given α₀ > 0 and α₁ > 0, we compute

$$n_{{\alpha }_0}=\text{min}\{n:{\beta }_{s0}^{(n)}\le {\alpha }_0\}\text{ and }{n}_{{\alpha }_1}=\text{min}\{n:{\beta }_{s1}^{(n)}\ge 1-{\alpha }_1\},$$ (8)

where ${\beta }_{s0}^{(n)}\text{ and }{\beta }_{s1}^{(n)}$ are given in (7). Then, the Bayesian meta-analysis sample size is given by n_B = max{n_α0, n_α1}. We note that the quantities ${\beta }_{s0}^{(n)}\text{ and }{\beta }_{s1}^{(n)}$ in (8) correspond to the Bayesian Type I error and power, respectively. Common choices of α₀ and α₁ are α₀ = 0.05 and α₁ = 0.20. We choose τ₀ to be sufficiently large, say τ₀ > 0.95, so that the Bayesian meta-analysis sample size n_B ensures that the type I error rate is at most α₀ = 0.05 and the power is at least 1 − α₁ = 0.80.

5. Specification of the Fitting and Sampling Priors using Historical Data

Suppose that the historical data are available only for the control arm from K₀ previous datasets. Let $y_{0k}={\displaystyle {\sum }_{i=1}^{n_{0k}}}{y}_{0\mathit{\text{ik}}}$ denote the total subject year duration and also let ${\nu }_{0k}={\displaystyle {\sum }_{i=1}^{n_{0k}}}{\nu }_{0\mathit{\text{ik}}}$ denote the total number of events for k = 1, …, K₀. In addition, we let x_0k denote a binary covariate, where x_0k = 1 if the subjects had a low or moderate CV risk and x_0k = 0 if the subjects had a high CV risk in the kth historical dataset. Suppose that only the trial-level data D_0K0 = {(y_0k, ν_0k, x_0k), k = 1, …, K₀} are available from the K₀ previous datasets. Assume the individual level failure time follows an exponential distribution, y_0ik ~ Exp(λ_0k), where λ_0k > 0 is the hazard rate. Under the random effects model, we assume the following log-linear model for λ_0k:

$$\text{log }{\lambda }_{0k}={\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k},{\xi }_{0k}~N(0,{\sigma }^2),$$ (9)

for k = 1, 2, …, K₀. Let ξ₀ = (ξ₀₁, ξ₀₂, …, ξ_0K0)′. Then, the complete data likelihood function based on the meta-survival data D_0K0 is given by

$$L_R({\gamma }_0,{\theta }_0,{\sigma }^2,{\mathit{\xi }}_0|D_{0K_0})={\displaystyle \prod _{k=1}^{K_0}}[\text{exp}\{{\nu }_{0k}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})\}\times \text{exp}\{-\text{exp}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})y_{0k}\}\times \left(\frac{1}{\sqrt{2\pi {\sigma }^2}}\right)\text{ exp }\{-\frac{1}{2{\sigma }^2}{\xi }_{0k}^2\}].$$ (10)

Under the fixed effects model, we assume

$$\text{log }{\lambda }_{0k}={\gamma }_0+{\theta }_{0k},$$ (11)

for k = 1, 2, …, K₀, where ${\displaystyle {\sum }_{k=1}^{K_0}}{\theta }_{0k}=0$. Again, for simplicity, we assume ${\theta }_{0K_0}=-{\displaystyle {\sum }_{k=1}^{K_0-1}}{\theta }_{0k}$. Let θ₀ = (θ₀₁, …, θ_0K0)′. Then, the likelihood function based on the meta-survival data D_0K0 is given by

$$L_F({\gamma }_0,{\mathit{\theta }}_0|D_{0K_0})={\displaystyle \prod _{k=1}^{K_0}}\text{exp}\{{\nu }_{0k}({\gamma }_0+{\theta }_{0k})\}\text{exp}\{-\text{exp}({\gamma }_0+{\theta }_{0k})y_{0k}\}.$$ (12)

Under the random effects model, comparing (9) to (2), we see that the models for the historical data and the current data share the common parameters γ₀ and σ². However, the CV risk effect parameters θ and θ₀ are different in these two models. Thus, the historical data are borrowed through common parameters γ₀ and σ² and having different parameters θ and θ₀ provides us with greater flexibility in accommodating different CV risk effects in the current and historical data. For example, from Table 1, the design value of θ is log{ − log (1 − 1.2%)} − log{ − log (1 − 1.5%)} = −0.225. Based on the historical data given in Table 2, an estimated value of θ₀, namely, E[θ₀ | D_0K0], is −0.641. This difference in CV risk effects can be automatically accounted for by our proposed models. Thus, the proposed models help us to maximize the similarity between the current data and the historical data, thereby allowing us to borrow more information from the historical data for the analysis of the current data. Under the fixed effects model, comparing (11) to (4), the models for the historical data and the current data share only one common parameter, namely, γ₀.

We now discuss how to specify the sampling prior and the fitting prior. Under the random effects model, for the sampling prior, ${\pi }_{\ell }^{(s)}(\mathit{\gamma },\theta ,{\sigma }^2)$, ℓ = 0, 1, we take ${\pi }_{\ell }^{(s)}(\mathit{\gamma },\theta ,{\sigma }^2)\propto {\pi }^{(s)}({\gamma }_0){\pi }^{(s)}(\theta ){\pi }^{(s)}({\sigma }^2){\pi }_{\ell }^{(s)}({\gamma }_1)$. In the sampling prior, we first specify a point mass prior for ${\pi }_{\ell }^{(s)}({\gamma }_1)\text{ with }{\pi }_{\ell }^{(s)}({\gamma }_1)={\mathrm{\Delta }}_{\{{\gamma }_1=\text{log}(\delta )\}}$ for ℓ = 0 and Δ_{{γ1= 0}} for ℓ = 1, where Δ_{{γ1 =γ10}} denotes a degenerate distribution at γ₁ = γ₁₀, i.e., P(γ₁ = γ₁₀) = 1. We then specify a point mass prior π^(s)(γ₀) at the design value of γ₀. For example, for the meta-design given in Table 1, we take Δ_{{γ0=log[−log(1−1.5%)]}}. In addition, we specify a point mass prior for each of π^(s)(θ) and π^(s)(σ²). For the meta-design given in Table 1, we take π^(s)(θ) = Δ_{{θ=−0.225}} and π^(s)(σ²) = Δ_{{σ²=σ̃²}}, where σ̃² is an estimate of σ² from the historical data. Under the fixed effects model, for the sampling prior, ${\pi }_{\ell }^{(s)}(\mathit{\gamma },\mathit{\theta })$, we assume ${\pi }_{\ell }^{(s)}(\mathit{\gamma },\mathit{\theta })={\pi }_{\ell }^{(s)}(\mathit{\gamma }){\pi }^{(s)}(\mathit{\theta })$. We take a similar sampling prior as the one for the random effects model for ${\pi }_{\ell }^{(s)}(\mathit{\gamma })$. Again, we specify a point mass sampling prior for π^(s)(θ). For the meta-design given in Table 1, we take π^(s)(γ₀) = Δ_{{γ0=−4.389}}, π^(s)(θ_k) = Δ_{{θk =−0.028}} for k = 1, …, K − 1, and π^(s)(θ_k) = Δ_{{θK =0.197}}.

For the fitting prior, using (10), we extend the power prior of Ibrahim and Chen (2000) to propose the following fitting prior for (γ, θ, σ²) under the random effects model:

$${\pi }_R^{(f)}(\mathit{\gamma },\theta ,{\sigma }^2|D_{0K_0},a_0)\propto {\displaystyle \int }\{{\displaystyle \int }{\displaystyle \prod _{k=1}^{K_0}}{[\text{exp}\{{\nu }_{0k}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})\}\times \text{exp}\{-\text{exp}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})y_{0k}\}]}^{a_0}\times \left[{\displaystyle \prod _{k=1}^{K_0}}\right(\frac{1}{\sigma }\left)\text{ exp }\right(-\frac{1}{2{\sigma }^2}{\xi }_{0k}^2\left)\right]d{\mathit{\xi }}_0\}{\pi }_0^{(f)}({\theta }_0)d{\theta }_0{\pi }_0^{(f)}\times ({\gamma }_0,{\sigma }^2,{\gamma }_1,\theta ),$$ (13)

where 0 ≤ a₀ ≤ 1, ${\pi }_0^{(f)}({\theta }_0)\text{ and }{\pi }_0^{(f)}({\gamma }_0,{\sigma }^2,{\gamma }_1,\theta )$ are initial priors. In (13), we further specify independent initial priors for (γ₀, γ₁, θ, θ₀, σ²) as follows: (a) a normal prior $N(0,{\sigma }_{0f}^2)$ is assumed for each of γ₀, γ₁, θ, and θ₀, where ${\sigma }_{0f}^2>0$ is a prespecified hyperparameter; and (b) we specify an inverse gamma prior for σ², which is given by ${\pi }_0^{(f)}({\sigma }^2)\propto [1/{({\sigma }^2)}^{d_{0f1}+1}]\text{ exp}\{-\frac{d_{0f2}}{{\sigma }^2}\}$, where d_0f1 > 0 and d_0f2 > 0 are prespecified hyperparameters. Under the fixed effects model, we propose the following fitting prior for (γ, θ):

$${\pi }_F^{(f)}(\mathit{\gamma },\mathit{\theta }|D_{0K_0},a_0)\propto {\displaystyle \int }{\displaystyle \prod _{k=1}^{K_0}}{[\text{exp}\{{\nu }_{0k}({\gamma }_0+{\theta }_{0k})\}\text{exp}\{-\text{exp}({\gamma }_0+{\theta }_{0k})y_{0k}\}]}^{a_0}\times {\pi }_0^{(f)}({\mathit{\theta }}_0)d{\mathit{\theta }}_0{\pi }_0^{(f)}(\mathit{\gamma },\mathit{\theta }),$$ (14)

where 0 ≤ a₀ ≤ 1, ${\pi }_0^{(f)}({\mathit{\theta }}_0)\text{ and }{\pi }_0^{(f)}({\mathit{\gamma }}_0,\mathit{\theta })$ are initial priors. In (14), independent initial normal priors, $N(0,{\sigma }_{0f}^2)$, are assumed for γ₀, γ₁, θ_k, and θ_0k.

In our informative prior specification, we consider a fixed a₀. When a₀ is fixed, we know exactly how much historical meta data are incorporated in the new-meta trial, and also how the type I error and power are related to a₀. As shown in our simulation study in Section 7, a fixed a₀ provides us additional flexibility in controlling the type I error. In addition, our informative prior specification only allows us to borrow historical meta data for the control arm. Thus, the historical meta data have the most influence on γ₀ but not on γ₁. However, the historical meta data does have certain influence on the new treatment through σ² under the random effects model, but not under the fixed effects model. Under both types of meta log-linear regression models, when analyzing the current data, the historical data can be borrowed only through the common parameters, namely (γ₀, σ²) or γ₀. For this reason, the power priors given in (13) and (14) are called partial borrowing power priors. Other additional properties of the informative prior specification are discussed in details in the Web Appendix.

6. Computational Development

We discuss how to compute type I error and power under the random effects model. The computation of the type I error and power for the fixed effects model is quite similar and even more straightforward. Let ξ = (ξ₁, …, ξ_K)′. Using (3) and (13), the posterior distribution of (γ, θ, σ², ξ, θ₀, ξ₀) is given by ${\pi }_R^{(f)}(\mathit{\gamma },\theta ,{\sigma }^2,\mathit{\xi },{\theta }_0,{\mathit{\xi }}_0|D_K,D_{0K_0},a_0)\propto L_R(\mathit{\gamma },\theta ,\mathit{\xi },{\sigma }^2|D_K)[{\displaystyle {\prod }_{k=1}^{K_0}}{(\text{exp}\{{\nu }_{0k}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})\}\text{exp}\{-\text{exp}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})y_{0k}\})}^{a_0}\times (\frac{1}{\sigma })\text{exp}\{-\frac{1}{2{\sigma }^2}{\xi }_{0k}^2\}]\times {\pi }_0^{(f)}({\theta }_0){\pi }_0^{(f)}({\gamma }_0,{\sigma }^2,{\gamma }_1,\theta )$. We use the Gibbs sampling algorithm to sample (γ, θ, σ², ξ, θ₀, ξ₀) from the above posterior distribution. The Gibbs sampling algorithm requires sampling from the following conditional posterior distributions in turn: (i) [γ | θ, ξ, θ₀, ξ₀, D_K, D_0K0]; (ii) [θ | γ, ξ, D_K]; (iii) [ξ | γ, θ, σ², D_K]; (iv) [θ₀ | γ₀, σ², D_0K0]; (v) [ξ₀ | γ₀, θ₀, σ², D_0K0]; and (vi) [σ² | ξ, ξ₀]. It can be shown that the conditional posterior distributions in (i) to (v) are log-concave in each of these parameters and [σ² | ξ, ξ₀] is an inverse gamma distribution. Thus, sampling (γ, θ, σ², ξ, θ₀, ξ₀) is straightforward.

Let $\{{\gamma }_1^{(m)},m=1,\dots ,M\}$ denote a Gibbs sample of γ₁ from the posterior distribution π^(f)(γ, θ, σ², ξ, θ₀, ξ₀ | D_K, D_0K0, a₀). Using this Gibbs sample, a Monte Carlo estimate of P(exp(γ₁) < δ | D_K, D_0K0, π^(f)) is given by ${\mathrm{P̂}}_f=\frac{1}{M}{\displaystyle {\sum }_{m=1}^M}1\{\text{exp}({\gamma }_1^{(m)})<\delta \}$. To compute ${\beta }_{s\ell }^{(n)}$ in (7), we propose the following computational algorithm: (i) Set n_jk, x_jk, τ₀, and N; (ii) Generate $(\mathit{\gamma },\theta ,{\sigma }^2)~{\pi }_{\ell }^{(s)}(\mathit{\gamma },\theta ,{\sigma }^2)$; (iii) Generate D_K via the predictive data-generation algorithm in Section 4; (iv) Run the Gibbs sampler to generate a Gibbs sample $\{{\gamma }_1^{(m)},m=1,\dots ,M\}$ of size M from the fitting posterior distribution ${\pi }_R^{(f)}$; (v) Compute P̂_f; (vi) Repeat Steps 1–5 N times; and (vii) Compute the proportion of {P̂_f ≥ τ₀} in these N runs, which gives an estimate of ${\beta }_{s\ell }^{(n)}$.

7. Applications to a Design of Meta-studies for Evaluating the CV Risk

We consider a meta-design discussed in Section 2. From Table 1, we have K = 8. Using the historical data shown in Table 2, we have K₀ = 5. The noninferiority margin was set to δ = 1.3. To ensure that the type I error is controlled under 5%, we chose τ₀ = 0.96. The choice of τ₀ = 0.96 was discussed in Chen et al. (2011) and recommended in the FDA Guidance, “Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials,” released on February 5, 2010 (www.fda.gov/MedicalDevices/DeviceRegulationandGuidance/GuidanceDocuments/ucm071072.htm). In the fitting prior (13), we chose an initial prior N(0, 10) for each of γ₀, γ₁, θ, and θ₀ and d_{0f 1} = 2.001 and d_{0f 2} = 0.1 for the initial prior for σ² under the random effects model. Note that this choice of (d_{0f 1}, d_{0f 2}) leads to a prior variance of 9.98 (about 10) for σ². Similarly, in the fitting prior (14), we chose an initial prior N(0, 10) for each of γ₀, γ₁, θ_k, and θ_0k under the fixed effects model. Thus, we specify relatively vague initial priors for all the parameters. Under this setting, the prior estimates, including prior standard deviations (SDs) and 95% highest prior density intervals of γ₀, θ₀, and σ² under the random effects model as well as γ₀ and θ₀ = (θ₀₁, …, θ₀₄)′ for the fixed effects model are given in Table 3 based on 20,000 Gibbs iterations.

Table 3.

Prior estimates of parameters based on the meta historical data in Table 2

Model	Parameter	prior estimate	Prior SD	95% Highest Prior density interval
Random effects	γ0	−3.799	0.153	(−4.106, −3.500)
	θ0	−0.641	0.269	(−1.182, −0.112)
	σ2	0.054	0.048	(0.009, 0.131)
Fixed effects	γ0	−4.241	0.128	(−4.492, −3.994)
	θ01	−0.133	0.231	(−0.596, 0.311)
	θ02	−0.544	0.420	(−1.398, 0.236)
	θ03	−0.186	0.250	(−0.684, 0.305)
	θ04	0.477	0.134	(0.222, 0.745)

We generated the data under the random effects model using the predictive data-generation algorithm presented in Section 3. We specified the point mass sampling priors at the design values for (γ₀, γ₁, θ) and a point mass sampling prior at the estimate of σ² from the historical data. From Table 1, we take γ₀ = log[− log (1 − 1.5%)] = −4.192 and θ = −0.225 under the random effects model. The estimate of σ² from the prior data was 0.054. The above point mass sampling priors implicitly imply that the “equivalent” design values of γ₀ and θ under the fixed effects model are γ₀ = −4.389 and θ_k = −0.028 for k = 1, 2, …, 7. From Table 3, we see that the prior mean of γ₀ is more similar to the design value of γ₀ under the fixed effects model than the random effects model. In addition to n₁₈ = n₂₈ = 5000 in Table 1, we also consider several other values of n₁₈ = n₂₈. Our design strategy is to find a minimum size of n₁₈ = n₂₈ and a value of a₀ so that the power is at least 80% and the type I error is controlled at 5% when the n_jk for j = 1, 2 and k = 1, 2, …, 7 are fixed in Table 1. The powers and type I errors for various values of a₀ and n₁₈ = n₂₈ are shown in Table 4 and plotted in Figure 1. In all computations of the type I errors and powers, N = 10,000 simulations and M = 10, 000 with 1000 burn-in iterations within each simulation were used.

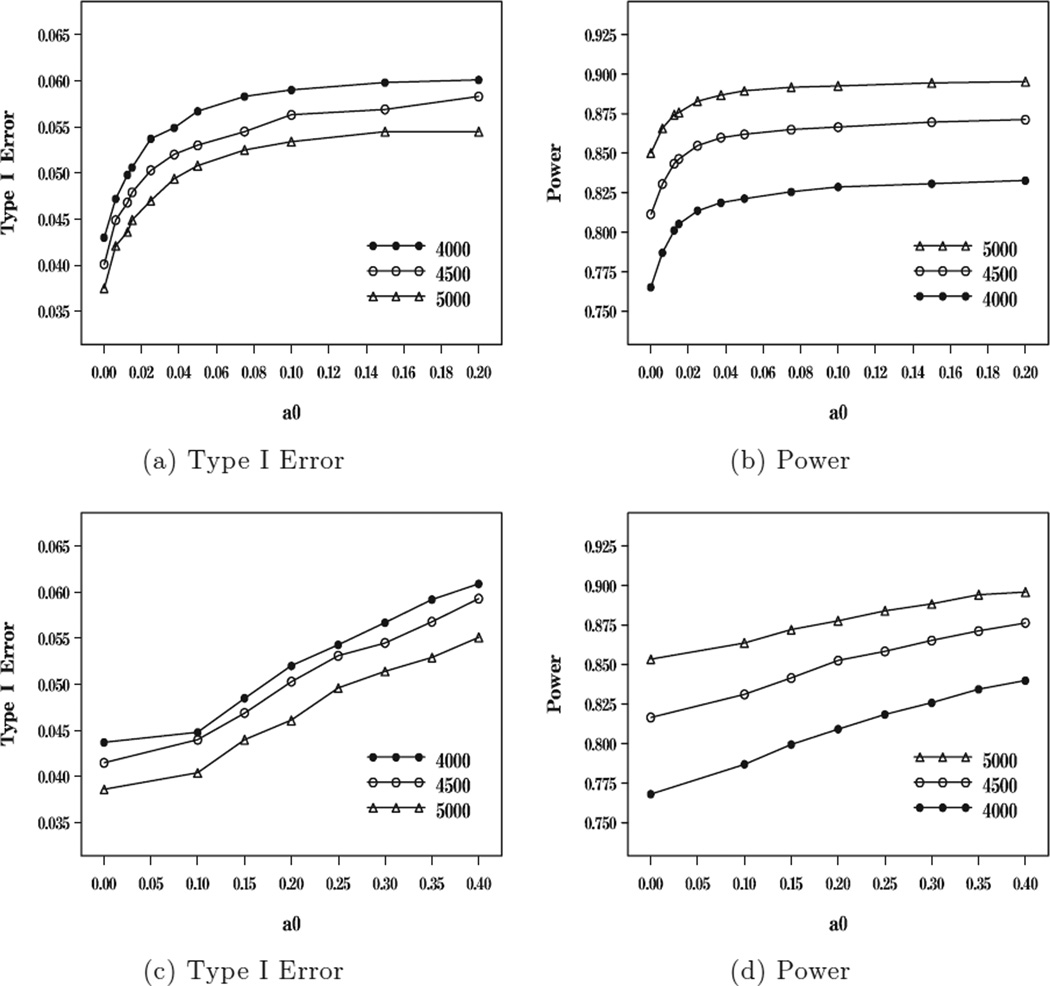
Figure 1.

Plots of type I error and power versus a₀ for n₁₈ = n₂₈ = 4000, 4500, 5000 under the random effects model ((a) and (b)) and under the fixed effects model ((c) and (d)).

From Table 4, we see that the type I errors and powers with no incorporation of historical meta-survival data are 0.043 and 0.765 when n₁₈ = n₂₈ = 4000, 0.040 and 0.811 when n₁₈ = n₂₈ = 4500, and 0.038 and 0.850 when n₁₈ = n₂₈ = 5000 under the random effects model. Similarly, without incorporation of historical meta-survival data, the type I errors and powers are 0.044 and 0.768 when n₁₈ = n₂₈ = 4000, 0.042 and 0.817 when n₁₈ = n₂₈ = 4500, and 0.039 and 0.853 when n₁₈ = n₂₈ = 5000 under the fixed effects model. Thus, without incorporation of historical meta-survival data, the 80% power is obtained when n₁₈ = n₂₈ = 4500. However, the sample size n₁₈ = n₂₈ = 4000 is not large enough to yield 80% power. With incorporation of historical meta-survival data and controlling the 5% type I error rate, the powers are 0.801 when a₀ = 0.0125 and n₁₈ = n₂₈ = 4000, 0.855 when a₀ = 0.025 and n₁₈ = n₂₈ = 4500, and 0.887 when a₀ = 0.0375 and n₁₈ = n₂₈ = 4500 under the random effects model; and these powers become 0.799 when a₀ = 0.15 and n₁₈ = n₂₈ = 4000, 0.853 when a₀ = 0.15 and n₁₈ = n₂₈ = 4500, and 0.884 when a₀ = 0.25 and n₁₈ = n₂₈ = 4500 under the fixed effects model. These results imply that (i) the gain in power is about 3.6% to 4.4% with incorporation of 1.25%, 2.5%, and 2.5% of the historical data for n₁₈ = n₂₈ = 4000, 4500, and 5000 under the random effects model and the gain in power is about 3.1% to 3.6% with incorporation of 15%, 20%, and 25% of the historical data for n₁₈ = n₂₈ = 4000, 4500, and 5000 under the fixed effect model. Thus, under both random and fixed effects models, the sample size n₁₈ = n₂₈ = 4000 is sufficient to yield 80% power. As discussed earlier, the historical meta data can be partially borrowed through the two common parameters γ₀ and σ² under the random effects model but through only one common parameter γ₀ for the fixed effects model. This implies that under the same value of a₀, i.e., the same amount of incorporation of the historical meta data, the power is higher under the random effects model than under the fixed effects model. On the other hand, the design value of γ₀ in the current meta-studies is more comparable to the value of γ₀ in the historical meta data under the fixed effects model than under the random effects model, which explains why more historical meta data can be allowed to be borrowed under the fixed effects model than the random effects model. From Figure 1, it is interesting to see that (i) both the power and type I error increase in a₀; (ii) the power and type I error are roughly quadratic in a₀ under the random effects model and roughly linear in a₀ under the fixed effects model; and (iii) the powers increase in n₁₈ = n₂₈ as expected.

Although not reported in Table 4, we also computed the powers and the type I errors for various values of a₀ for n₁₈ = n₂₈ = 3500. We obtained that without incorporation of the historical meta-survival data, the powers and type I errors are 0.720 and 0.036 under the random effects model and 0.726 and 0.039 under the fixed effects model. The powers and type I errors are 0.797 and 0.056 when a₀ = 0.10 under the random effects model and 0.796 and 0.052 when a₀ = 0.3 under the fixed effects model. Thus, the sample size of n₁₈ = n₂₈ = 3500 is too small to achieve 80% power under a 5% type I error. In simulation studies, we have also examined the power and type I error rates when τ₀ = 0.95. When n₁₈ = n₂₈ = 5000, with no incorporation of the historical meta data, the power and type I error are 0.871 and 0.047, respectively, under the random effects model and 0.873 and 0.049 under the fixed effects model. However, when n₁₈ = n₂₈ = 4000, with no incorporation of the historical meta data, the power and type I error are 0.796 and 0.053 under the random effects model and 0.798 and 0.054 under the fixed effects model. Thus, when τ₀ = 0.95, the type I error is not always controlled at 5% even without incorporation of historical meta data. Finally, we mention that we further examined the powers and the type I errors when the data were generated from the fixed effects model using the design values of the model parameters γ₀ and θ specified in Table 1. When n₁₈ = n₂₈ = 5000, the powers and type I errors are 0.853 and 0.037 when a₀ = 0 and 0.896 and 0.052 when a₀ = 0.1 under the random effects model; and 0.855 and 0.038 when a₀ = 0 and 0.883 and 0.045 when a₀ = 0.20 under the fixed effects model. These results are very similar to those given in Table 4 with slightly higher powers than those when the data were generated from the random effects model.

8. Discussion

In this article, we have extended the Bayesian sample size determination methods of Wang and Gelfand (2002) and Chen et al. (2011) to develop a new Bayesian method for the design of meta noninferiority clinical trials for survival data. The proposed Bayesian method not only allows for planning sample size for a phase 2/3 development program in the meta-analytic framework by accounting for between-study heterogeneity, but also allows for incorporating prior information for the underlying risk in the control population. We have also proposed the partial borrowing power prior with the fixed a₀ to incorporate the historical meta-survival data. The fixed a₀ approach greatly eases the computational implementation and also provides greater flexibility in controlling the type I error rates as empirically shown in Section 7.

Although “pure” Bayesian approaches do not necessarily emphasize on the notion of controlling type I error and power as traditional frequentist approaches, there have been some literature proposing that Bayesian methods should be “calibrated” to have good frequentist properties due to the inherent flexibility in the Bayesian design (Box, 1980; Rubin, 1984). Moreover, from the regulatory standpoint in medical product development, it is prudent in the design stage to understand the risk of erroneously approving an unsafe or ineffective product (type 1 error rate) and the probability of appropriately approving a safe and effective product (power). Therefore, as the current regulatory practice, the FDA in its guidance to medical device industry (www.fda.gov/MedicalDevices/DeviceRegulationandGuidance/GuidanceDocuments/ucm071072.htm) recommends that sponsors assess the operating characteristics (in terms of type 1 error and power) of a Bayesian design via simulations.

To account for heterogeneity among meta-studies, we have considered the log-linear random effects and fixed effects regression models. As empirically shown in our simulation studies, both types of regression models yield similar sample sizes of meta-studies to achieve a prespecified power (80%) under a prespecified type I error (5%). A natural practical question to ask is which model to use in the Bayesian meta-design: fixed or random effects models. There are advantages and disadvantages to each one and one model is not uniformly better than the other. The advantages of the random effects model is that it provides much greater flexibility for borrowing historical data than the fixed effects model and it has more parameters that control the borrowing over the fixed effects model. As a result, the random effects model requires a smaller a₀ than the fixed effects model for achieving a desired power and type I error. One of the minor disadvantages of the random effects model is that it is slightly more computationally intensive than the fixed effects model. Overall, we feel that the random effects model is a bit more natural and general to use in this setting, and thus if we were to recommend an approach, it would be the random effects model. In our simulation studies, we have observed zero events for several small trials. Thus, under the fixed effects regression model, the frequentist approach for the sample size calculation does not work when there are zero events for small trials. In the Bayesian approach that we adopt here, we use a proper prior for θ_k or θ_0k to get around this zero event problem, yielding reasonable sample sizes.

In this article, we considered the exponential regression model. One of the nice features of the exponential model is that the individual patient level survival data easily reduces to the study level survival data in the modeling development so that one does not need any individual level historical data for the Bayesian meta-design. Our proposed methodology can be extended to other survival regression models such as Weibull regression models and cure rate regression models (Ibrahim, Chen, and Sinha, 2001). However, under these regression models, the proposed method requires individual patient level survival data. In Section 5, we have proposed the partial borrowing power priors in (13) and (14). In our formulation, we did not discount each historical dataset by a power parameter a₀ because the meta-survival historical data have been accounted for by the random effects ξ_0k under the random effects model and the fixed effects θ_0k under the fixed effects model. The model becomes nonidentifiable if we do discount each historical dataset in this formulation. However, instead of (13) and (14), other forms of partial borrowing power priors can be considered. For example, under the fixed effects model, instead of (14), the following fitting prior for (γ, θ) can be considered: ${\pi }_F^{(f)}(\mathit{\gamma },\mathit{\theta }|D_{0K_0},a_0)\propto {[{\displaystyle \int }{L}_F({\mathit{\gamma }}_0,{\mathit{\theta }}_0|D_{0K_0}){\pi }_0^{(f)}({\mathit{\theta }}_0)d{\mathit{\theta }}_0]}^{a_0}{\pi }_0^{(f)}(\mathit{\gamma },\mathit{\theta })$. This version of the partial borrowing power is computationally less attractive than (14); however, it does have different theoretical properties than (14). The computational development and theoretical properties of this type of power prior along with the extensions to other survival regression models for Bayesian design of meta-survival trials are currently under investigation. We have implemented our methodology using the FORTRAN 95 software and our programs are available upon request.