Likelihood Ratio Test for Detecting Gene (G)-Environment (E) Interactions Under an Additive Risk Model Exploiting G-E Independence for Case-Control Data

Abstract

There has been a long-standing controversy in epidemiology with regard to an appropriate risk scale for testing interactions between genes (G) and environmental exposure (E ). Although interaction tests based on the logistic model—which approximates the multiplicative risk for rare diseases—have been more widely applied because of its convenience in statistical modeling, interactions under additive risk models have been regarded as closer to true biologic interactions and more useful in intervention-related decision-making processes in public health. It has been well known that exploiting a natural assumption of G-E independence for the underlying population can dramatically increase statistical power for detecting multiplicative interactions in case-control studies. However, the implication of the independence assumption for tests for additive interaction has not been previously investigated. In this article, the authors develop a likelihood ratio test for detecting additive interactions for case-control studies that incorporates the G-E independence assumption. Numerical investigation of power suggests that incorporation of the independence assumption can enhance the efficiency of the test for additive interaction by 2- to 2.5-fold. The authors illustrate their method by applying it to data from a bladder cancer study.

Testing for gene-environment (G-E ) and gene-gene (G-G) interactions has been of great interest in epidemiology. Despite recent success in genome-wide association studies for identification of susceptibility single nucleotide polymorphism (SNPs) for complex traits, very few G-E or G-G interactions have been reported so far. Interaction has diverse meanings in the epidemiologic literature (1), and there has been a long-standing controversy concerning its definition and the selection of proper scales for measuring the presence of interactions (2–4). Logistic regression models are widely used for analyses of case-control data with qualitative disease traits; a test for interaction under the traditional logistic model corresponds to a test for interaction on the odds ratio scale. For rare diseases—since odds ratios approximate relative risks— a test for interaction using a logistic model corresponds to a test for nonmultiplicative effects of underlying risk factors for a disease.

In spite of the popularity of the tests for multiplicative interaction, it is believed that methods for testing for the presence of additive interaction may be more relevant for a number of scientific objectives. A number of researchers have shown that conceptual models for biologic interactions translate to the presence of interaction on the additive scale and not necessarily on the multiplicative scale (1). Moreover, for evaluating certain public health decisions, such as whether it is beneficial to target individuals for intervention for an exposure based on genetic susceptibility, evaluation of risk differences and additive interactions is directly relevant (5, 6). Unfortunately, in spite of such relevance, methods for testing for additive interaction have received less attention.

In this report, we investigate the potential for improving the statistical power of the test for additive interaction in case-control studies exploiting the G-E independence assumption, which has been previously shown to lead to major gains in efficiency for tests for multiplicative interaction. We formulate the test using a generalized logistic regression model that embeds the additive model for disease risk by imposing certain constraints on parameters. We then develop a likelihood ratio test (LRT) applying the framework proposed by Chatterjee and Carroll (7) that permits the incorporation of the G-E independence assumption for case-control studies under such a generalized logistic model. We conduct a simulation study to compare the performance of the proposed method with a method for testing additive interaction that does not take into account the independence information. We illustrate our method by applying it to a test of interaction between smoking and a recently discovered susceptibility SNP in the etiology of bladder cancer. User-friendly software implemented in the R language (R Foundation for Statistical Computing, Vienna, Austria) is made available for general use.

MATERIALS AND METHODS

Models, a retrospective likelihood, and an LRT

We first describe a model for testing additive interaction between 2 categorical covariates, say G and E, that have J + 1 and K + 1 levels, respectively. Typically, for genetic association studies, G will denote SNP genotype data coded as 0, 1, or 2 depending on the number of minor alleles that a subject carries on a pair of homologous chromosomes. Sometimes, G may be coded as a binary variable assuming a dominant or recessive effect of the SNP allele.

Let G_i, E_i, and D_i be the genetic factor, the environmental exposure, and the disease indicator for the ith individual, respectively, in a case-control study of N subjects. Let r_i = Pr(D_i = 1|G_i, E_i) be disease risk in the underlying population, and consider a saturated parameterization of joint effects of G_i and E_i for disease risk on the additive scale:

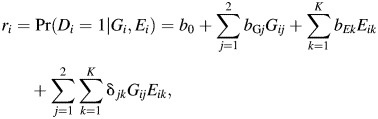(1)

where G_ij is a dummy variable for indicating whether G_i takes a value j and E_ik is a dummy variable for indicating whether E_i takes a value k. Alternatively, the saturated model for r_i = Pr(D_i = 1|G_i, E_i) can be specified using a traditional logistic regression of the form

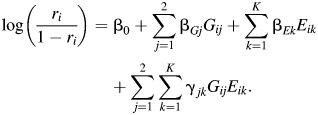(2)

Under equation 1, the null hypothesis for no additive interaction is given by H₀: δ_jk = 0 for j = 1, 2 and k = 1, 2, … , K.

In the Appendix, we show that if we assume a rare disease—so that relative risks can be approximated by odds ratios—the null hypothesis of no additive interaction corresponds to a set of constraints on the parameters of the logistic model in equation 2 of the form

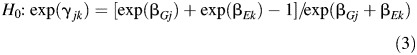(3)

for j = 1, 2 and k = 1, 2, …, K. Now, since the saturated model for disease risk is the same under logistic and additive parameterization, the test for no additive interaction against the alternative of the saturated model for joint risk can be performed within the logistic regression framework, by comparing the null hypothesis given by equation 3 against the alternative of the saturated model shown in equation 2.

We consider LRTs for testing H₀ as specified by equation 3 against the general alternative given in equation 2. A standard LRT for interaction is typically based on a “prospective likelihood” for case-control data that ignores the retrospective nature of the sampling design. Although such prospective treatment of case-control data is known to be efficient (8) when no assumption is made about the distribution of covariates, it is now well known that more efficient inference is possible if an assumption of G-E independence is invoked in the underlying population. In particular, an approach using the case-only design has been proposed for testing for multiplicative interaction under the independence constraint (9). The case-only approach, however, allows inference only on the interaction parameter of a logistic model and is not suitable for the test for additive interaction, since the null hypothesis has constraints involving both main effects and interaction parameters, as shown in equation 3. Umbach and Weinberg (10) and Chatterjee and Carroll (7) have defined alternative methods for analyses of case-control data that can exploit the assumption of G-E independence, utilizing both cases and controls for efficient inference on all of the parameters of a logistic regression model.

In this report, we use the profile-likelihood approach developed by Chatterjee and Carroll (7) to develop a retrospective LRT for additive interaction. The profile-likelihood method has been extended to take into account G-G or G-E dependence due to population stratification, by conditioning the likelihood on appropriate variables (S) such as self-reported ethnicity and/or principal components of population stratification markers (11). The profile-likelihood derived by Chatterjee and Carroll under the model (equation 2) is given by

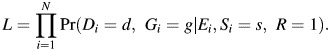R indicates the selection mechanism for the case-control design, and S_i is a stratifying variable. Under G-E independence, the likelihood L can be derived as

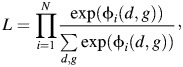(4)

where

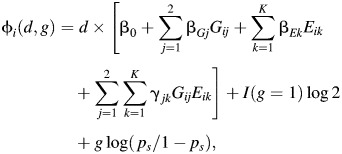and p_s is the minor allele frequency of SNP G_i; that is, Pr(G_i = 0|S_i = s) = (1 − p_s)², Pr(G_i = 1|S_i = s) = 2p_s(1 − p_s), and 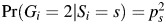in stratum s under Hardy-Weinberg equilibrium. For continuous S, such as principal components, Pr(G_i|S_i) can be modeled in terms of a polytomous regression model (12). In addition, under the above formulation, it is easy to incorporate additional covariates, such as age, that typically need to be adjusted for in the disease risk model (equation 2). Under the saturated model shown in equation 2 for joint risk of the disease, the profile likelihood (equation 4) can be maximized using freely available CGEN software (http://dceg.cancer.gov/bb/tools/genetanalcasecontdata), which currently allows fitting of the standard logistic regression model. For fitting of the model under the null hypothesis, we expressed the interaction parameters of the logistic model in terms of the main effects as specified by equation 3 and then maximized the likelihood only with respect to the reduced set of parameters under the given constraints. The corresponding LRT would asymptotically follow a chi-square distribution with 2K degrees of freedom.

Bladder cancer data

As an illustrative application, we analyze case-control data on bladder cancer to explore possible interactions between a recently discovered susceptibility SNP (rs2294008) for the disease in the prostate stem cell antigen gene (PSCA) (13, 14) and smoking status (never, former, or current smoker), a known risk factor for bladder cancer. We use data from a National Cancer Institute-led genome-wide association study that included 3,577 cases and 5,280 controls from 5 different study centers. More details about the study can be found elsewhere (14). We conduct tests for additive and multiplicative interactions under a dominant model for the minor allele of rs2294008 (CC/CT + TT) and smoking status, categorized as “never” versus “ever.” We also perform these tests allowing for 3 nominal levels for the SNP (CC/CT/TT) and smoking status (never/former/current). For each test, we apply both prospective and retrospective LRTs under a logistic model that adjusts for study center, age, sex, and DNA source (blood or buccal cells). In the retrospective likelihood, the SNP and all other covariates, including smoking status, are assumed to be independent, conditional on study. That is, a stratifying variable S in equation 4 in this case is the study variable.

Simulation methods

To evaluate the efficiency gain for the test of additive interaction using the retrospective likelihood (LRT_R) as compared with the prospective likelihood (LRT_P), we conduct several sets of simulations. For simplicity, we use a model where both G and E are binary with 2 levels of 0 and 1. We assume that these 2 factors are independently distributed in the underlying population and the prevalences are given by Pr(E = 1) = 0.2 and Pr(G = 1) = 0.5, respectively. We assume the disease is rare, so that disease-free subjects approximately represent the underlying population.

In our simulation setting, the saturated models for disease risk under the additive and multiplicative interaction scales are given by

and

(5)

respectively. We fix the marginal odds ratio (MOR) for G (MOR(G)); that is, the disease odds ratio for G if E is ignored in the analysis is fixed at 1.2, reflecting the modest strength of genetic association that is typically observed in genome-wide association studies. Simulation using a larger genetic effect with MOR(G) = 1.5 is also conducted and is shown in Web Figure 1 and Web Table 1, which are available on the Journal's website (http://aje.oxfordjournals.org/). We fix the MOR for E (MOR(E)) at 2.5 or 3.5. For each fixed value of the MOR parameters, we vary the magnitude of additive interactions by assigning 4 distinct values for the relative excess risk due to interaction (RERI) (15) of 0.5, 1, 1.5, and 2, where RERI is defined as

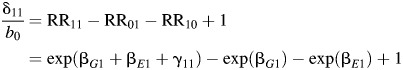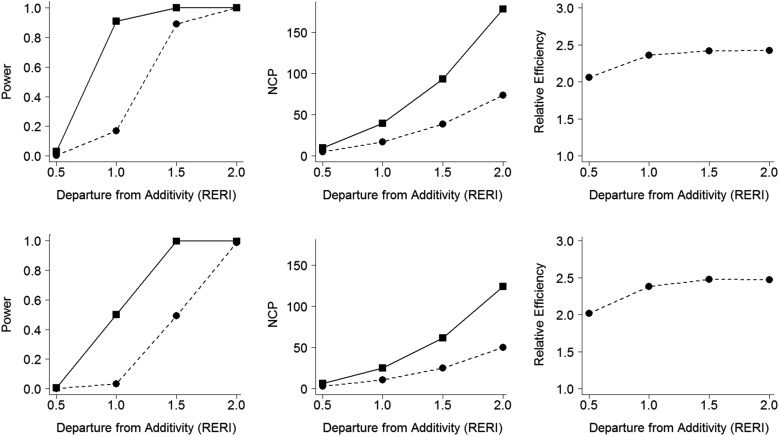
Figure 1.

Power simulation results of the tests for additive interaction (4,000 cases and 4,000 controls). The 3 columns, from left to right, show power, the noncentrality parameter (NCP), and the relative efficiency, respectively. For the top 3 panels, the marginal odds ratio (MOR) for the genetic factor G, MOR(G), is 1.2 and the MOR for the environmental factor E, MOR(E ), is 2.5. For the bottom 3 panels, MOR(G) is 1.2 and MOR(E ) is 3.5. The squares with solid lines in the first 2 columns represent results obtained using a likelihood ratio test (LRT) assuming gene-environment (G-E ) independence (retrospective likelihood). The dots with dashed lines in the first 2 columns represent results obtained using a likelihood ratio test without assuming G-E independence (prospective likelihood). The dots with dashed lines in the third column represent relative efficiency, calculated as the retrospective likelihood divided by the prospective likelihood (LRT_R /LRT_P). The relative excess risk due to interaction (RERI) is a measure of additive interaction defined as (δ₁₁/b₀) = exp(β_G1 + β_E1 + γ₁₁) − exp(β_G1) − exp(β_E1) + 1.

Table 1.

Parameter Values for the Logistic Regression Model (Equation 5) Used in the Simulation Studies

MOR	Parameter	RERIa
		0.5	1	1.5	2
MOR(G)b = 1.2	exp(βG1)	1.16	1.06	0.96	0.85
MOR(E)c = 2.5	exp(βE1)	2.45	2.21	1.98	1.74
	exp(γ11)	1.09	1.39	1.80	2.42
MOR(G) = 1.2	exp(βG1)	1.20	1.10	0.99	0.87
MOR(E) = 3.5	exp(βE1)	3.58	3.18	2.79	2.38
	exp(γ11)	0.99	1.22	1.55	2.05

Abbreviations: MOR, marginal odds ratio; RERI, relative excess risk due to interaction.

^a RERI is a measure of additive interaction defined as .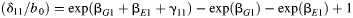

^b MOR for the genetic factor G.

^c MOR for the environmental factor E.

(see Appendix for definition of RR_jk). We choose appropriate parameter values for β_G1, β_E1, and γ₁₁ in the logistic model so that MOR(G), MOR(E), and RERI are fixed at given values (see Table 1). In each simulation, we generate G and E data for 4,000 cases and 4,000 controls. For the simulation of type I error rates, parameter values are chosen to correspond to the null hypothesis of RERI = 0; specifically, β_G1 = log(1.2), β_E1 = log(3.58), and γ₁₁ = log(0.87).

For each test in each model, power is calculated by counting the fraction of replicate data sets with significant P values using a significance level of α = 1.00 × 10⁻⁶. Since relative differences of power between tests depend on the significance level, we also calculate the noncentrality parameter (NCP) for each LRT in order to compare performances of tests regardless of significance levels. Using the fact that NCP is the expected value of an LRT under the alternative hypothesis, we take the average of LRT values over replicate data sets. We estimate the relative efficiency of LRT_R with regard to LRT_P by taking the ratio of the NCP of LRT_R to the NCP of LRT_P. All simulations are based on 5,000 replicates for evaluation of power and based on 10,000 replicates for evaluation of type I error.

RESULTS

Bladder cancer data example

For the model with 2 categories of G and E, both the prospective LRT and the retrospective LRT indicate evidence of supra-additive effects, with statistical significance appearing to be stronger under the retrospective method (P = 0.001) than under the prospective method (P = 0.007). Table 2 shows the joint effect of the SNP and smoking status using the prospective and retrospective likelihoods. For the model with 3 categories of G and E, the results show increased significance using the retrospective likelihood (P = 0.00038) but decreased significance for the prospective likelihood (P = 0.153). None of the tests for multiplicative interaction using 2 or 3 categories of exposure detected any supra-multiplicative effects, although the P value under the retrospective likelihood was consistently reduced in comparison with the prospective likelihood.

Table 2.

Odds Ratios for the Joint Association of Prostate Stem Cell Antigen Gene (PSCA) Polymorphism rs2294008 and Smoking Status With Bladder Cancer Risk^a

Method	PSCA Genotype	Smoking Status				RERIb	95% CI	Interaction P Value
		Never Smoker		Ever Smoker
		OR	95% CI	OR	95% CI
No G-E independence assumption	CC	1	Referent	2.53	2.03, 3.14b	0.53	0.17, 0.88	0.0076
(prospective likelihood)	CT + TT	1.05	0.86, 1.30	3.11	2.54, 3.81
G-E independence assumption	CC	1	Referent	2.55	2.10, 3.09	0.53	0.23, 0.83	0.0010
(retrospective likelihood)	CT + TT	1.07	0.89, 1.28	3.15	2.59, 3.83

Abbreviations: CI, confidence interval; G-E, gene-environment; OR, odds ratio; RERI, relative excess risk due to interaction.

^a Data were obtained from a National Cancer Institute-led genome-wide association study that included 3,577 cases and 5,280 controls from 5 different study centers (14).

^b RERI is a measure of additive interaction defined as .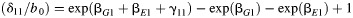

Power simulation results

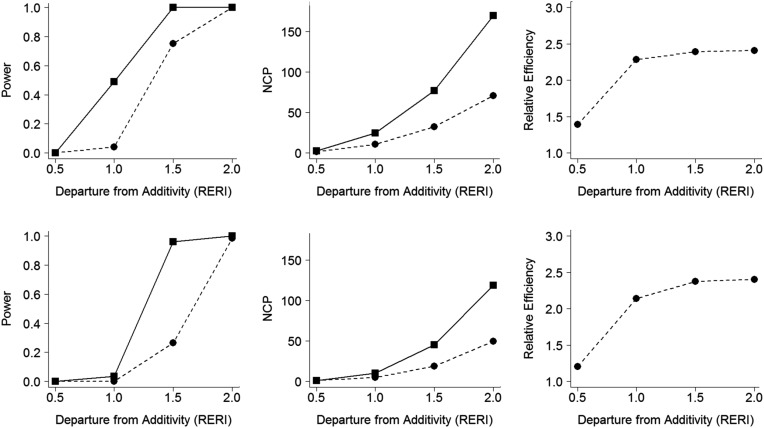
The estimated type I error rates are shown in Table 3, which demonstrates correct error rates across different significance levels. Power simulation results for additive interactions (displayed in Figure 1) show that LRT_R is more powerful than LRT_P across different values of RERI and different values of MOR(E) (left column in Figure 1). NCP values show correspondingly larger values for LRT_R than for LRT_P (middle column in Figure 1), which yield a relative efficiency of LRT_R to LRT_P ranging from 2.1 to 2.4 (right column in Figure 1). Figure 2 displays the analogous results for the multiplicative interaction, which show slightly lower power levels in comparison with the additive interaction tests, since the true models are under the additive interaction model. The relative efficiencies of the test using the retrospective likelihood over the test using the prospective likelihood for multiplicative interaction ranged from 1.3 to 2.5, which shows a bit wider range in comparison with the additive interaction tests.

Table 3.

Type I Error Rates Estimated Using Simulations With 4,000 Cases and 4,000 Controls

α	LRTRa	LRTPb
0.1	0.0989	0.1011
0.05	0.0513	0.0503
0.01	0.0135	0.0107
0.005	0.0059	0.0062
0.001	0.0016	0.0012

Abbreviation: LRT, likelihood ratio test.

^a LRT using the gene-environment independence assumption (retrospective likelihood).

^b LRT without the gene-environment independence assumption (prospective likelihood).

Figure 2.

Power simulation results of the tests for multiplicative interaction (4,000 cases and 4,000 controls). The 3 columns, from left to right, show power, the noncentrality parameter (NCP), and the relative efficiency, respectively. For the top 3 panels, the marginal odds ratio (MOR) for the genetic factor G, MOR(G), is 1.2, and the MOR for the environmental factor E, MOR(E), is 2.5. For the bottom 3 panels, MOR(G) is 1.2 and MOR(E ) is 3.5. The squares with solid lines in the first 2 columns represent results obtained using a likelihood ratio test (LRT) assuming gene-environment (G-E ) independence (retrospective likelihood). The dots with dashed lines in the first 2 columns represent results obtained using a likelihood ratio test without assuming G-E independence (prospective likelihood). The dots with dashed lines in the third column represent relative efficiency, calculated as the retrospective likelihood divided by the prospective likelihood (LRT_R/LRT_P). The relative excess risk due to interaction (RERI) is a measure of additive interaction defined as (δ₁₁/b₀) = exp(β_G1 + β_E1 + γ₁₁) − exp(β_G1) − exp(β_E1) + 1.

DISCUSSION

In this article, we have proposed an LRT for additive interaction that exploits G-E independence information by incorporating the retrospective likelihood proposed by Chatterjee and Carroll (7). To our knowledge, our method is the first approach to exploit G-E or G-G independence information for testing additive interaction. The general framework we utilize can also be easily extended to test for interactions in the “sufficient-component” framework (16), which has been shown to correspond to specific constraints on risk-difference parameters (17).

The simulation study showed that the proposed method gains major power over the alternative, which does not take into account the independence information; the relative efficiency of LRT_R to LRT_P ranges from 2.1 to 2.4, depending on the model parameters. The real-data example for testing gene × smoking status interaction for bladder cancer also illustrates the power advantage of the proposed method. We generalized our method so it can be flexibly applied to a setting where risk factors have any number of categories.

Our method employs a general logistic regression model for testing additive interactions instead of fitting an additive risk model directly. The approach enables us to utilize the logistic regression-based profile likelihood approach (7), which is computationally stable and is highly flexible in its ability to account for very general types of covariates. Within this framework, the assumption of rare disease, which is partly required to invoke the G-E independence assumption for the controls as opposed to the whole population, can be relaxed if the disease rate for the underlying population is known or is estimated from an underlying cohort. Further, even if a disease is not rare but an incidence sampling design is used in a case-control study, the odds ratio parameters can be interpreted as rate ratios instead of risk ratios (18).

A limitation of methods which exploit the G-E or G-G independence assumption to gain efficiency is that they can produce substantial bias when the underlying assumptions of independence are violated. Similar to results reported for multiplicative interactions, we observed that violation of the independence assumption can seriously bias the proposed test for additive interaction (Web Table 2). A major source of G-E association in large-scale studies could be the existence of hidden population stratification along which both the genotype distribution and the exposure distribution may vary. The proposed method can easily adjust for such population stratification bias by taking into account self-reported ethnicity, geographic regions, and/or principal components of large numbers of markers in the retrospective likelihood (12). Other approaches that may protect against bias irrespective of the source of G-E association would be empirical Bayes (19, 20) or model averaging (21) techniques that can data-adaptively relax the independence assumption. In the future, further development of these techniques for tests for additive interaction would be desirable.

APPENDIX

Null Hypothesis and a Likelihood Ratio Test

Let R_jk denote an absolute risk for a group of persons with G_i = j and E_i = k (see Appendix Table 1), and let RR_jk = R_jk/R₀₀ denote a relative risk (RR) for the group as compared with a reference group with j = 0 and k = 0.

Appendix Table 1.

Absolute Risk for Each Combination of Different Levels of a Genetic Factor G (Row) and an Environmental Exposure E (Column)^a

j	k = 0	k = 1	…	k = K
0	b0 (= R00)	b0 + bE1 (= R01)	…	b0 + bEK (= R0K)
1	b0 + bG1 (= R10)	b0 + bG1 + bE1 + δ11 (= R11)	…	b0 + bG1 + bEK + δ1K (= R1K)
2	b0 + bG2 (= R20)	b0 + bG2 + bE1 + δ21 (= R21)	…	b0 + bG2 + bEK + δ2K (= R2K)

^a Constructed from the additive risk model in equation 1.

The null hypothesis for testing additive interaction is H₀: δ_jk = 0 for j = 1, 2 and k = 1, 2, … , K. Simple algebra shows that this is equivalent to

(A1)

for j = 1, 2 and k = 1, 2, … , K—that is, increased risk due to exposure to G with level j and E with level k is the same as the sum of separate risk increments due solely to exposure to G or E of the same levels. Dividing equation A1 by R₀₀ gives the following relative risk relations:

(A2)

for j = 1, 2 and k = 1, 2, …, K, where RR_jk = R_jk/R₀₀. Approximating equation A2 through the use of odd ratios in Appendix Table 2 gives exp(β_Gj + β_Ek + γ_jk) = exp(β_Gj) + exp(β_Ek) − 1 for j = 1, 2 and k = 1, 2, … , K. Hence, we can rewrite the null hypothesis as

for j = 1, 2 and k = 1, 2, … , K. A likelihood ratio test (LRT) is constructed by comparing a fit without any parameter restrictions to a fit with the contrasts in equation 3 (see main text) imposed on the parameter space for testing an additive interaction:

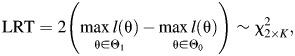where θ = (β₀, β_Gj, β_Ek, γ_jk) for j = 1, 2 and k = 1, 2, … , K; Θ₁ = {θ: θ ∈ R^p}, where p is the total number of parameters and Θ₀ = {θ: exp(γ_jk) = [exp(β_Gj) + exp(β_Ek) − 1]/exp(β_Gj + β_Ek) for j = 1, 2 and k = 1, 2, … , K}; and l(θ) is a log-likelihood—for example, a typical log-likelihood for logistic regression is a prospective likelihood given as

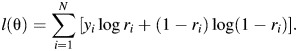Appendix Table 2.

Odds Ratio for Each Combination of Different Levels of a Genetic Factor G (Row) and an Environmental Exposure E (Column)^a

j	k = 0	k = 1	k = 2	…	k = K
0	1	exp(βE1)	exp(βE2)	…	exp(βEK)
1	exp(βG1)	exp(βG1 + βE1 + γ11)	exp(βG1 + βE2 + γ12)	…	exp(βG1 + βEK + γ1K)
2	exp(βG2)	exp(βG2 + βE1 + γ21)	exp(βG2 + βE2 + γ22)	…	exp(βG2 + βEK + γ2K)

^a Constructed from the multiplicative risk model in equation 2.