Abstract
Defective interfering particles (DIPs) are viral deletion mutants lacking essential transacting or packaging elements and must be complemented by wild-type virus to propagate. DIPs transmit through human populations, replicating at the expense of the wild-type virus and acting as molecular parasites of viruses. Consequently, engineered DIPs have been proposed as therapies for a number of diseases, including human immunodeficiency virus (HIV). However, it is not clear if DIP-based therapies would face evolutionary blocks given the high mutation rates and high within-host diversity of lentiviruses. Divergent evolution of HIV and DIPs appears likely since natural DIPs have not been detected for lentiviruses, despite extensive sequencing of HIVs and simian immunodeficiency viruses (SIVs). Here, we tested if the apparent lack of lentiviral DIPs is due to natural selection and analyzed which molecular characteristics a DIP or DIP-based therapy would need to maintain coadaptive stability with HIV-1. Using a well-established mathematical model of HIV-1 in a host extended to include its replication in a single cell and interference from DIP, we calculated evolutionary selection coefficients. The analysis predicts that interference by codimerization between DIPs and HIV-1 genomes is evolutionarily unstable, indicating that recombination between DIPs and HIV-1 would be selected against. In contrast, DIPs that interfere via competition for capsids have the potential to be evolutionarily stable if the capsid-to-genome production ratio of HIV-1 is >1. Thus, HIV-1 variants that attempt to “starve” DIPs to escape interference would be selected against. In summary, the analysis suggests specific experimental measurements that could address the apparent lack of naturally occurring lentiviral DIPs and specifies how therapeutic approaches based on engineered DIPs could be evolutionarily robust and avoid recombination.
INTRODUCTION
Defective interfering particles (DIPs) are mutant versions of viruses that contain significant genomic deletions such that they are unable to replicate except when complemented by wild-type virus replicating within the same cell (for reviews, see references 1 and 2). At the most fundamental level, DIPs arise because viral genomes encode both cis- and trans-acting elements. Trans-acting elements (trans elements) code for gene products, such as capsid proteins or transcription factors, and cis-acting elements (cis elements) are regions of the viral genome that interact with trans-element products to achieve productive viral replication, including viral genome amplification, encapsidation, and viral egress. In the case of RNA virus genomes, cis elements can include viral enhancers and promoters and also viral genome-packaging signals. Viral capsid and envelope proteins, on the other hand, are examples of trans elements. Mutations that result in the loss of at least one obligate trans element but retain all necessary cis elements required for productive replication can generate DIPs.
DIPs have been reported for several important human and animal pathogens, including murine leukemia virus (3), Rous sarcoma virus (4), vesicular stomatitis virus (5), influenza virus (6), and dengue fever virus (7, 8). Presumably, the characteristic error-prone replication of RNA viruses leads to frequent generation of defective mutants (1, 2). In some cases (e.g., murine leukemia virus), specific mutations within DIPs encode novel trans elements that enhance immune responses to infected cells or produce cytocidal or cytotoxic products that lead to enhanced virulence (3, 9–11). Many DIPs interfere with the in vivo replication of the wild-type pathogen and attenuate virulence and reduce disease in animal models (12–16). Based on these findings, therapies based on DIPs have been proposed for a number of diseases, including human immunodeficiency virus type 1 (HIV-1) (15, 17).
Here, we considered a broad class of DIP designs that represent HIV-1 with mutations or deletions in capsid proteins and Nef responsible for protection against superinfection. Possible designs range from minimal DIPs completely lacking any trans elements to DIPs expressing some trans elements, including transcriptional transactivating proteins (Tat) and genomic export proteins (Rev). All these HIV-1 mutants can be expressed, complemented, and packaged by either providing the missing viral proteins in trans (18) or coinfecting with a homologous replication-competent virus (19) (e.g., wild-type HIV or a “helper” virus) which provides the missing trans factors. This shunting of trans factors to the DIP interferes with the intracellular replication of the wild-type virus. Since DIPs coopt viral replication or packaging machinery and transmit their genetic material at the expense of the wild-type virus, they are essentially molecular parasites of wild-type viruses. However, whether coevolution might occur between HIV-1 and a DIP therapy and whether HIV-1 could escape from a DIP have not been explored.
Importantly, natural lentiviral DIPs have not been detected, despite extensive sequencing of HIV and simian immunodeficiency virus (SIV) strains. For example, although many cells infected with HIV-1 harbor permanently or transiently inactive variants of HIV-1 provirus, the vast majority of infected cells contain a single provirus (20). There is no evidence in humans or nonhuman primates of coinfection of cells with a replication-competent HIV-1 (or SIV) provirus and a replication-deficient HIV-1 (or SIV) mutant that is mobilized by a replication-competent virus and could be identified as a DIP. This absence of lentiviral DIPs could result from one of three possibilities: (i) a lack of assays sensitive enough to detect existing DIPs, (ii) molecular restrictions resulting from the unique biology of lentiviruses compared to other RNA viruses (i.e., a “molecular block” to DIP formation), or (iii) rapid evolutionary selection against DIPs that do spontaneously arise (i.e., lentiviral DIPs could be generated with appreciable frequency but are evolutionarily unstable and exist only transiently before being “selected out” of the viral population, either within an infected individual or at the level of the infected host population in a “boom-then-bust” scenario) (see Discussion).
A molecular block to DIP formation is unlikely in the case of HIV-1. While different viruses and target cells clearly vary in their ability to form and propagate DIPs (21–23), there do not appear to be any inherent blocks to the generation of large deletions within the HIV-1 genome (24) or in the packaging or mobilization of subgenomic HIV-1. Subgenomic HIV-1 strains are routinely produced from packaging cell lines during the generation of lentiviral vectors for gene delivery and gene therapy (18). Moreover, numerous studies have artificially engineered HIV-1 variants that lack trans elements but conditionally replicate in the presence of full-length HIV-1 and transmit through tissue cultures (25–30). A conditionally replicating HIV-1 construct termed VRX496, which is essentially a DIP encoding an antisense gene therapy element, has even been reported to mobilize within a humanized-mouse model of HIV-1 (31) and in patients infected with HIV-1 (15).
While a molecular block to lentiviral DIPs appears unlikely, it is unclear if DIPs are evolutionarily stable, since HIV-1 might escape by mutation. While studies have quantitatively explored the dynamics and dynamic stability (i.e., conditions for survival) of DIPs (17, 32–35), there have been no quantitative analyses of the long-term evolutionary stability of lentiviral DIPs. Experimentally, DIPs for vesicular stomatitis virus are known to exert strong selective pressures on their helper virus as a result of the divestment of cellular resources to the DIPs during intracellular replication (i.e., DIP-mediated resource stealing). In long-term cultures of cells infected with vesicular stomatitis virus and its DIP (T particle) over a period of 5 years and several hundred passages, Holland and coworkers observed significant coevolution of both wild-type virus and a DIP (23, 36), including the emergence of formerly susceptible wild-type virus that gained resistance to the DIP from previous passages (21, 37–39).
One would expect HIV-1 to be under pressure to change genetically to minimize its interaction with a DIP. Since HIV-1 demonstrates a considerable degree of evolutionary plasticity, it is likely to eventually escape the parasite. However, evolutionary plasticity of the DIPs would be similar to that of HIV-1 and under similar selective pressure to maintain the parasitization of HIV-1. This would establish a coevolutionary arms race between HIV-1 and the DIP, and the outcome of such a race would not be obvious, especially when the system is further complicated by dynamics at multiple scales of biological organization (e.g., the single-cell and individual levels), as is the case for HIV-1 and the DIP.
The appropriate tools for theoretically analyzing such complex coevolutionary processes are found in the field of population genetics. Simple models of HIV-1 population genetics, introduced in the 1990s, proved to be powerful tools for the analysis of HIV-1 sequence data and led to predictive experimentally tested theories on the rates of HIV-1 adaptation and selection and its effective recombination rate (40–50). Most relevantly, population genetics models estimated the fitness costs of HIV-1 mutations (including drug resistance and immune escape mutations) by calculating evolutionary selection coefficients from the data (40, 43, 46, 48, 51–54). Coupled with the well-established models of HIV-1 dynamics in individuals (55, 56), population genetics provides a rigorous approach to studying the coevolution of HIV-1 and DIPs and to addressing the question of whether lentiviral DIPs would be evolutionarily stable.
In this study, we calculated the likely direction of HIV-1 and DIP evolution within an infected individual to determine if DIP-based therapies would face an evolutionary disadvantage. Specifically, we asked whether two mechanisms of competition corresponding to two points in the viral replication cycle—cis stealing (e.g., competition between single-stranded HIV genomic RNA and single-stranded DIP RNA to bind a second strand of HIV genomic RNA) and trans stealing (e.g., competition for viral capsids)—are evolutionarily stable strategies of interference. The practical aim of this inquiry was to direct the design of future DIP vectors. Testing stability in cell culture is not a trivial matter, because the total number of cells, even in large flasks, is several logs lower than in an animal/human host, and the speed of evolution may be sensitive to rare double or triple mutations. Therefore, before attempting expensive long-term animal studies, it was important to test evolutionary stability in silico.
To do this, we considered a model of HIV-DIP interaction at two scales: (i) on the single-cell scale, a simplified intracellular model approximated the molecular mechanisms of HIV-1 particle formation and DIP formation (two models for two types of interference), and (ii) on the individual-patient scale, a standard model of HIV-1 dynamics in individuals (55, 56) was extended to include the presence of DIPs. We derived the fitness effect of mutation at the within-host scale (effective selection coefficient) directly from the underlying intracellular model and tested whether HIV-1 is likely to evolve to decrease DIP-mediated stealing of its products and hence escape suppression by the DIP.
THEORY
Preliminary analysis: DIP interference by the competition for HIV-1 genomic RNA leads to divergent evolution at the single-cell level.
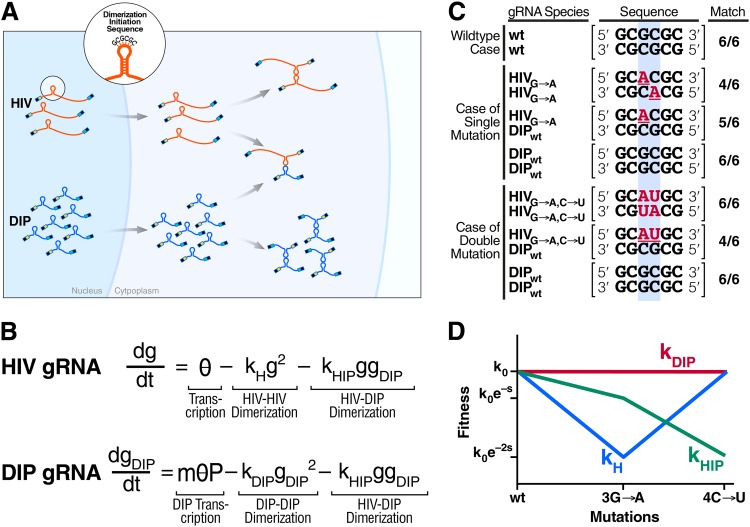
We begin by analyzing the stability of DIPs that interfere via binding to the genomic RNAs (gRNAs) of the wild-type lentivirus (i.e., genome stealing). Lentiviruses are diploid, and gRNAs are packaged into virions in pairs, where encapsidation of two copies of RNA is achieved by allowing the gRNAs to dimerize. This gRNA pairing is initiated at a six-nucleotide palindrome termed the dimerization initiation signal (DIS), which is located within stem-loop 1 (SL1) of the HIV-1 genome and has the consensus sequence GCGCGC (57).
A minimal mathematical model that considers only nondimerized and dimerized genomes (Fig. 1A and B) is used to describe gRNA pairing and to analyze how the gRNA pairing would coevolve for a DIP and HIV-1. The model describes the homozygous pairing of HIV-1 genomes (g) and DIP genomes (gDIP) as well as the heterozygous pairing between DIP genomes and HIV-1 in dually infected cells. The model also captures experimental evidence demonstrating that subgenomic RNAs that share the consensus DIS palindrome of HIV-1 can dimerize to gRNA HIV-1 genomes (57, 58) and that partitioning of diploid genomes between homozygous and heterozygous virions is binomial (58). Importantly, the heterozygous virions that contain one copy of the HIV-1 genome and one copy of the DIP genome (subgenomic) are largely nonviable (59).
Fig 1.
Divergent evolution of the HIV-1 and DIP dimerization initiation sequences (DIS) by double mutations in HIV-1 indicates that DIP interference by genome stealing is evolutionarily unstable. (A) Genomic RNA (gRNA) monomers of HIV-1 and a DIP form three types of dimer complexes (HIV-HIV, HIV-DIP, and DIP-DIP) based upon a “kissing-loop” formation between the dimerization initiation sequences of HIV-1 and DIP, which contain a palindromic sequence (e.g., the consensus sequence GCGCGC). Due to a higher rate of transcription and multiple provirus copies, DIP monomers are more abundant, so most HIV-1 RNA is wasted on nonviable HIV-DIP heterodimers. (B) A simplified model representing the abundance of gRNA monomers for HIV-1 and a DIP in the cytoplasm of the infected cell: g(t) and gDIP(t), respectively. θ is a lumped parameter representing the linear rate of gRNA production, and P is the expression asymmetry between HIV-1 and DIP. kH, kDIP, and kHIP are dimerization coefficients for HIV-HIV, DIP-DIP, and HIV-DIP, respectively. (C) Potential mutations in the kissing loop lead to divergent evolution of HIV-1 and DIP. Top row, in the wild-type (wt) HIV-1 and DIP case, there is an exact match for any gRNA pair (HIV-HIV, HIV-DIP, and DIP-DIP), which is enumerated in the rightmost column. Middle rows, if a single mutation arises within HIV-1 (highlighted by the blue rectangle), HIV-HIV homodimers have two mismatches, whereas HIV-DIP heterodimers have only a single mismatch and DIP-DIP homodimers have no mismatches. Bottom rows, in the (likely) scenario where the second compensatory mutation occurs in HIV, heterodimerization is disfavored compared to homodimerization. (D) Evolutionary fitness of homodimers and heterodimers qualitatively estimated based on dimerization coefficients in panel B and the number of sequence matches in panel C. In this idealized model, fitness takes the canonical functional form of an exponential where the selection coefficient, s, is based only upon the dimerization coefficients and the degree of sequence matching. Although a single mutation in the DIS of HIV-1 is more deleterious to HIV-1 homodimerization than to DIP-to-HIV-1 heterodimerization, a second mutation within the DIS will rescue HIV-1 dimerization and generate a further decrease in DIP-to-HIV-1 genome stealing.
Furthermore, the model includes recent evidence that the overwhelming majority of HIV-1-infected cells harbor a single integrated HIV-1 provirus (60), most likely, due to the short lifetime of infected cells (61, 62) and molecular restrictions to superinfection, such as nef downregulation of surface CD4 (61). However, the model does not restrict DIP proviral integrations to a single copy, since multiple infections of the cell require expression of trans elements, which the DIP would lack. Here, specifically, we consider a DIP that does not express Nef or any other trans elements responsible for protection against superinfection. Multiple copies of integrated DIP provirus, whose number we denote m (m = 1, 2, 3, …), lead to the DIP gRNA monomers being more abundant than the HIV-1 gRNA in the cytoplasm of the cell by a factor of m, which varies among cells and is determined in part by the abundance of circulating virus in the body (i.e., viral dynamics). In addition, we assume that DIP genome architecture (e.g., the lack of splicing sites [63, 64]), leads to an expression asymmetry between a DIP and HIV, such that DIP monomers are more abundant in the cytoplasm of the cell by an additional fixed factor, which we denote P (where P is >1). This “expression asymmetry” has been observed for lentiviral vectors (25, 59, 63–65), including HIV-1-derived lentiviral vectors (25, 59). The enrichment of the DIP gRNA over HIV gRNA in the cytoplasm is a product of both m and P. Due to enrichment of the DIP, most HIV-1 genomic RNA copies in the cell are stolen by the DIP to produce nonviable virions with HIV-DIP heterodimers, thereby generating a mechanism of interference.
To examine the evolutionary stability of interference by genome stealing (i.e., heterodimerization), we first consider single-residue mutations in the HIV-1 DIS (e.g., GCGCGC → GCGAGC). Such mutations lead to mismatches and decreases in the probability of heterodimerization but result in more severe decreases in the levels of HIV-1 homodimerization (Fig. 1C). However, compensatory double-residue mutations reestablish a new DIS palindrome (e.g., GCGCGC → GCUAGC) and generate a situation in which DIP-to-HIV-1 heterozygous dimerization is far less favorable than homozygous dimerization (Fig. 1C). By this logic, the idealized model that considers dimerization coefficients to be a function of only the number of mismatches leads to divergent evolution of the DIS sequences between HIV-1 and a DIP due to double mutations in HIV-1 DIS (Fig. 1D). Although a single mutation in HIV-1's DIS is more deleterious to HIV-1 homodimerization than to DIP-to-HIV-1 heterodimerization, a second mutation within the DIS will rescue HIV-1 dimerization and generate a further decrease in DIP-to-HIV-1 genome stealing.
This analysis does not explicitly account for the cost of the palindromic DIS being different than the consensus GCGCGC sequence, since different HIV-1 strains encode different DIS palindromes (57). Another limitation of this analysis is that it only considers a single round of mutation. However, these assumptions are not critical for the conclusion of evolutionary instability of genome stealing. More realistic models that capture multiple rounds of mutation still lead to progressive decreases in heterodimerization levels relative to those of homodimerization (see Fig. S1 in the supplemental material).
An alternative mechanism of interference: capsid stealing by DIPs.
Given that interference by genome stealing is unstable (see above), we next considered whether interference by DIP competition for trans elements, such as the capsid, was evolutionarily stable. Since DIPs carry the full complement of cis elements but lack one or more trans elements (e.g., capsid, envelope), DIPs must rely on the trans elements of the wild-type lentivirus to package and mobilize out of the infected cell. Thus, DIPs compete for and parasitize trans elements, leading to interference with the wild-type virus.
To calculate DIP interference on HIV-1 viral loads and the associated evolutionary stability, we used a recently developed multiscale modeling approach (17) to integrate a single-cell model of competition for capsid with an individual-patient model. Unlike previous multiscale modeling of virus infections (66–68), this multiscale model is designed specifically for HIV-1 in the presence of a DIP. The model applies to a range of DIP vectors, from a minimal DIP that does not code for any trans elements to a DIP that codes for tat and rev (allowing for the expression and export of genomes to the cytoplasm even in the absence of an HIV-1 provirus), but does not express capsid proteins or Nef (which mediates protection against superinfection). In the following subsections, we describe the single-cell and individual-host models, their integration, and their parameters. In the last subsection, we introduce the notion of an effective selection coefficient. Detailed analytical derivations are presented in Supplemental Methods in the supplemental material. Numerical solutions for all figures were performed in MATLAB (version R2011a).
The single-cell model with capsid stealing.
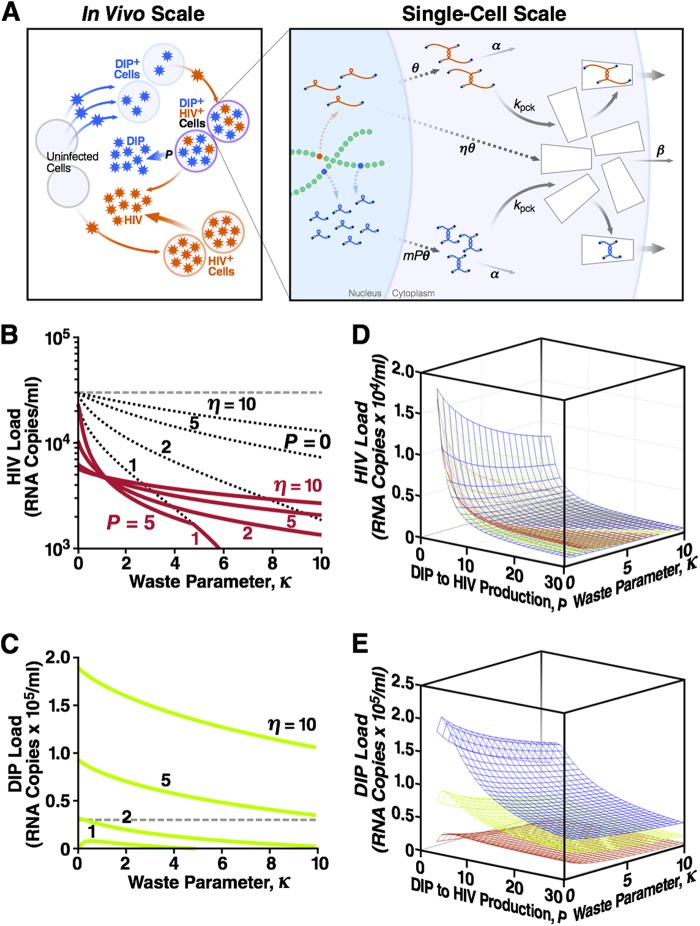
For tractability, the single-cell model considered here (Fig. 2A) is simplified and considers only intracellular replication events relating to dimerized wild-type HIV-1 RNA genomes (G), encapsidation-competent capsid (C), and dimerized DIP RNA genomes (GDIP). The equations have the following form:
| (1) |
| (2) |
| (3) |
The model parameters are defined in Table 1. Briefly, the model describes the production and decay of dimerized HIV-1 genomes, the packaging of these dimerized genomes into capsids that are produced at a rate proportional to that of genome dimers, and the competition for encapsidation between DIP genomes and HIV-1 genomes. The model neglects heterozygous genomes since, as demonstrated above, the dimerization initiation sequence for HIV-1 and the DIP will diverge so that heterozygous pairing is eliminated. As in the genome-stealing model (above), we allow each DIP provirus to express more RNA than an HIV-1 provirus by a fixed factor of P (25, 59, 63–65). This expression asymmetry (P > 1) is due to differences in genome architecture, such as mutated alternative splicing sites (63, 64). We classify dually infected cells by the number of DIP provirus copies m (m = 1, 2, 3, …). The net asymmetry between a DIP and HIV-1 expression in a dually infected cell is the product m × P. Based on previous results (17), we assume that the HIV-1 and DIP levels inside of the cells rapidly reach a steady state; the steady-state values of G, GDIP, and C are derived analytically in Supplemental Methods in the supplemental material (see equations S6 to S14).
Fig 2.
DIPs that steal capsid proteins stably suppress the HIV-1 load across a broad range of parameters. (A) The model comprises two scales of biological organization. The in vivo (individual host) scale is the standard model of HIV-1 replication, expanded to include DIPs (see Supplemental Methods, equations S28 to S33, in the supplemental material). Uninfected cells can be infected with either HIV-1 or DIP, and DIP+ cells can be superinfected with HIV-1 to become dually infected cells. The single-cell model is described by equations 1 to 3. A dually infected cell has one integrated HIV-1 provirus and multiple, m, copies of DIP provirus. A fraction of HIV-1 gRNA is translated into proteins that form “empty” capsids. The DIP does not express proteins. Dashed arrows represent multistage processes (including the loss of RNA monomers and capsid proteins). A fraction of stable dimer genomes and full capsids is also lost. Remaining genomes, HIV-1 or the DIP, are packaged within capsids and released as infectious particles. Shown also are the steady-state HIV-1 load (B) and the steady-state DIP load (C) at different values of two single-cell parameters: the capsid waste parameter, κ, and the capsid-to-genome production ratio, η (Table 1). The dashed line indicates the HIV-1 viral load in the absence of capsid waste and the DIP (κ = P = 0), which is assumed to be the average load in untreated humans (3 × 104 RNA copies/ml blood). Calculations use a DIP/HIV-1 production ratio (i.e., expression asymmetry) of P = 5 and a basic reproduction ratio of R0 = 10 (Table 1). The decrease in HIV-1 load in the presence of capsid waste (κ > 0, red lines), compared to the untreated HIV-1 “set-point” level (dashed line), is partly due to the loss of HIV-1 products (black dotted lines calculated at P = 0) and partly due to the DIP, which competes with HIV-1 for available target cells and steals HIV-1 capsid in dually infected cells. The first effect is more important at η = ∼1, and the DIP suppression factor is stronger at a large η value (see Fig. S2 in the supplemental material). Shown also are the steady-state HIV-1 load (D) and the steady-state DIP load (E) as functions of both expression asymmetry, P, and capsid waste parameter, κ, at three values of the capsid-to-genome ratio: η = 2 (red), η = 5 (green), and η = 10 (blue). These 3D plots act as a partial sensitivity analysis showing that HIV-1 and DIP loads depend strongly on the value of P.
Table 1.
State variables and model parameters for the intracellular capsid-stealing modela
| Notation | Definition | Unit | Value | Reference(s) |
|---|---|---|---|---|
| State variables | ||||
| G | Concentration of full-length dimerized HIV genomic mRNAs | 1/μl | ||
| GDIP | Concentration of full-length dimerized DIP genomic mRNAs | 1/μl | ||
| C | Concentration of encapsidation-competent capsids in cytoplasm | 1/μl | ||
| m | DIP (integrated) provirus copy number (i.e., MOI) | Dimensionless | ||
| Model parameters | ||||
| θ | Rate of accumulation of encapsidation-competent HIV genomes in cytoplasm | 1/μl/day | 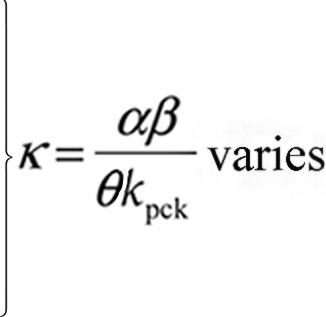 |
|
| kpck | Packaging constant | μl/day | ||
| α | Loss of genome rate | 1/day | ||
| β | Loss of capsid rate | 1/day | ||
| η | Capsid-to-genome accumulation ratio | Dimensionless | 1.2 to 5 | 10 and 72 |
| P | Expression asymmetry between DIP and HIV | Dimensionless | 8 to 10 | 13 |
See Fig. 2A and equations 1 to 3.
The individual-host model.
Similar to the method previously used (17), the output of the single-cell model is used to calculate HIV-1 and DIP viral loads within an individual patient using a standard model of HIV-1 in vivo dynamics (55, 61, 69) that is generalized to include the production of DIPs. The generalized model includes coinfection of cells with DIPs and HIV-1 so that the dually infected cells produce less HIV-1. Based on the results of recent in vivo studies (60), we assume a single HIV-1 provirus per (singly or dually) infected cell but allow for multiple DIP provirus copies per cell, as previously proposed (35). Briefly, the model describes uninfected CD4+ T cells permissive for viral replication (T), cells infected with HIV-1 only (I), CD4+ T cells harboring m copies of DIP provirus but not infected with HIV-1 (TDIP m) (by definition, TDIP 0 = T), dually infected cells harboring a copy of HIV-1 and m copies of DIP provirus (ID m), HIV-1 load (V) (free virus concentration in peripheral blood plasma), and DIP load (VDIP). The system of equations has the following form:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
The model parameters, which are well described in the literature and summarized in Table 2, are the linear production rate of uninfected cells (b), the natural death rate of uninfected cells (d), the infectivity factor (k), the death rate of singly and dually infected cells (δ), and the HIV-1 burst size from a singly infected cell (n). There are two additional parameters in the presence of a DIP: ψm, the ratio of HIV-1 burst size between a singly infected cell, I, and a dually infected cell with m copies of DIP provirus ID m, and ρm, the ratio of the DIP to HIV-1 burst size from a dually infected cell with m copies of DIP provirus.
Table 2.
See equations 4 to 9.
In the two bottom rows, G, GDIP, and C are steady-state values of state variables for the intracellular model (see equations 1 to 3 and Table 1) and are derived in Supplemental Methods, equations S6 to S20, in the supplemental material.
The steady states of the single-cell model (equations 1 to 3) define the following burst sizes for HIV-1 and a DIP (see equations S6 to S20 in Supplementary Methods in the supplemental material):
| (10) |
| (11) |
| (12) |
These expressions serve as input parameters for the individual-host model. The individual-host model (equations 4 to 9) is similar to the model described by Metzger et al. (17), except that here we relax the restriction of a single DIP copy per cell and allow cells to have multiple DIP infections. We assume that the state variables of the individual-host model (equations 4 to 9) are in a steady state, which corresponds to chronic infection. Equations 4 to 9 are used to calculate steady-state levels, as described in equations S34 to S43 and the following subsection in Supplementary Methods in the supplemental material.
Parameter values.
The full list of model parameters is given in Tables 1 and 2. Using a standard approach, we reduce the number of parameters to a smaller number of composite parameters by changing units to those in which the state variables are measured (see Supplemental Methods in the supplemental material). As a result of this nondimensionalization, all results can be conveniently expressed in terms of two nondimensional parameters that capture the evolutionary potential of HIV-1: (i) the composite “waste” parameter κ = (αβ)/(θkpck), which reflects the loss of HIV-1 genomes (rate α, equation 1) and capsids (rate β, equation 2), and (ii) the ratio of the encapsidation-competent capsids to the dimerized HIV-1 genomes produced per unit time (η) (referred to as the capsid-to-genome production ratio). The remaining parameters are determined from the basic reproductive ratio (R0), which is estimated from in vivo data as R0 ∼ 10 (the case of an exponentially distributed production delay with an average between 24 h and 12 h) (see reference 70) (Table 3), and by using fixed values of P. Lentiviral DIPs with P values of 8 to 10 have been engineered (65). We focus on the conservative value of P = 5 below, but the interval P = 2 to 30 is also studied (see Supplemental Methods).
Testing evolutionary stability: the effective selection coefficient.
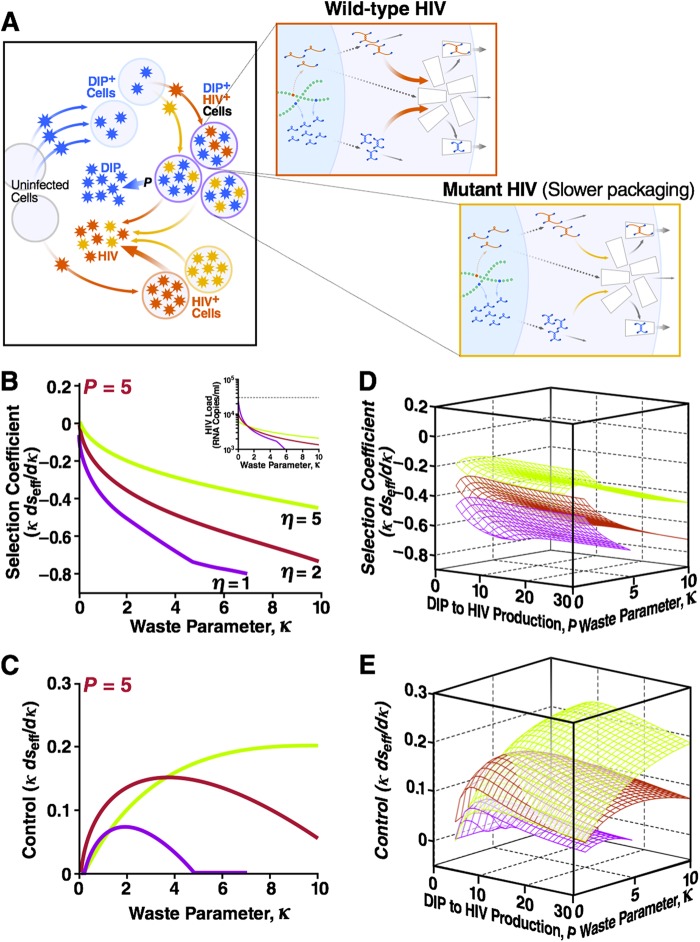
To determine if HIV-1 mutates to increase or decrease capsid waste (or the capsid-to-genome rate ratio), we capitalized on previous studies that applied concepts from Darwinian evolution, based on the notion of the selection coefficient (s), to analyze the evolution of single-locus mutations in the HIV-1 genome (41, 48). Negative values of s denote that a mutation decreases the progeny of an infected cell and is selected against, and positive values of s denote that a mutation is selected for. Calculating s is complicated by the compartmental structure of a population of infected cells that includes both dually (HIV+ DIP+) and singly (HIV+ DIP−) infected cells that may contribute differently to the fitness effect of mutation (number of progeny). The calculation of s is also affected by the dynamic interaction of HIV-1 and DIP within dually infected cells. To account for these complexities, we introduce the effective selection coefficient (∂seff), defined as the exponential rate of increase or decrease of a mutant virus normalized to the death rate of infected cells. To calculate ∂seff, we begin with a DIP–HIV-1 coinfection at steady state and perturb the system by adding a small amount of mutant HIV-1. In particular, we consider mutations that increase capsid waste (κ→κ + ∂κ, ∂κ > 0), achieved by slightly reducing the value of kpkg (Fig. 3A). We then calculate the expansion (contraction) rate of the mutant subpopulation from the model equations (equations 1 to 12) and arrive at normalized value ∂seff/(∂κ/κ). The normalized selection coefficient for mutations affecting the capsid-to-genome production ratio η is calculated in analogous fashion (detailed derivations are given in Supplemental Methods, equations S48 to S57, in the supplemental material).
Fig 3.
A DIP-HIV interaction is evolutionarily stable over a broad parameter range: HIV-1 cannot escape DIP by decreasing packaging resources. (A) The two-scale model for an individual infected by two strains of HIV, wild type (red) and mutant (orange), as well as a DIP (blue). Mutation causes a small decrease in the packaging constant of both HIV-1 and DIP kpck and, hence, an increase in capsid waste parameter, κ = αβ/(θkpck), when ∂κ is >0. (B) Normalized effective selection coefficient, ∂seff/(∂κ/κ), for that mutation as a function of κ for a range of capsid-to-genome production ratios η. Fixed parameters are as described for Fig. 2B and C: R0 = 10 and P = 5. The negative values of ∂seff/(∂κ/κ) imply that the mutation has net deleterious effects on HIV-1 replication. Overall, HIV-1 mutations that increase capsid waste are selected against. Inset, HIV-1 load as a function of the waste parameter from Fig. 2B. (C) A negative control showing ∂seff/(∂κ/κ) within HIV+ DIP+ dually infected cells when burst size changes due to increased capsid waste (the first term in equation S54 in the supplemental material) are neglected. Only in this specific context, when burst size changes are ignored, are HIV-1 mutations that increase capsid waste selected for. Shown also are the net ∂seff/(∂κ/κ) (D) and control ∂seff/(∂κ/κ) (i.e., when burst size changes are neglected) (E) as functions of both P and κ. These 3D plots act as a partial sensitivity analysis and show that the selection coefficient weakly depends on the value of P. Detailed calculations are given in Supplementary Methods in the supplemental material.
RESULTS
Evolutionary stability of capsid-stealing interference: general approach.
Our preliminary analysis (see “Preliminary analysis”) showed that the genome-stealing mechanism of DIP interference with HIV-1 replication is evolutionarily unstable due to divergence of the HIV-1 and DIP dimerization initiation sequences (Fig. 1). Here, we determine whether interference by DIP competition for trans elements, such as the capsid protein, leads to stable and sustained interference. We use our recently developed multiscale modeling approach to integrate a single-cell model with an individual-patient model (17). The single-cell model (equations 1 to 3) captures the reported ability of minimal lentiviral vectors to express more RNA in the cytoplasm than HIV-1 (25, 59, 63–65), and this expression asymmetry is represented by the parameter P (where P is >1). The output from this single-cell model (i.e., DIP and HIV-1 burst sizes) is used as the input for the individual-patient model (equations 4 to 9) (Table 2)—a generalized form of the standard model of HIV-1 in vivo dynamics (55, 61, 69) that includes the production of DIP particles—to ultimately calculate HIV-1 and DIP viral loads within a patient (Fig. 2A). Detailed analytical derivations and numeric calculations are presented in Supplemental Methods in the supplemental material.
DIP interference by competition for the capsid within single cells leads to sustained suppression of HIV-1 at the individual-patient level.
To test whether DIP lowers HIV-1 viral load, we examined the steady-state values of HIV-1 and the DIP at the individual-patient scale as a function of parameters in the single-cell model. As detailed above, the results are expressed in terms of a pair of intuitive and nondimensional parameters that capture the evolutionary potential of HIV-1 and the DIP: the composite waste parameter (κ) and the ratio of encapsidation-competent capsids to dimerized HIV-1 genomes produced per unit time (η).
Analytical solutions demonstrate that HIV-1 viral load is stably decreased across a broad range of κ values (Fig. 2B, red lines). In most cases, the viral load is decreased by more than 1 order of magnitude, which is associated with significantly reduced HIV-1 transmission and disease progression (71). Stable DIP-mediated suppression of HIV-1 depends upon the expression asymmetry (P > 1) (17, 35) and, importantly, is amplified by the large average multiplicity of DIP infection (see next section; see also Fig. S3a in the supplemental material). However, the decrease in HIV-1 viral load is not completely due to the DIP and is partly due to the loss of HIV-1 capsids and genomes by increased capsid waste (black dotted lines). Nevertheless, DIP-mediated suppression contributes to a significant fraction of this decrease through the stealing of HIV-1 capsids within dually infected cells and through competition for available target cells within the infected individual (see Fig. S2 in the supplemental material). At high κ values, there is a loss of dynamic stability because at such high capsid waste, HIV-1 crosses the threshold of its own extinction.
Even at modest values of expression asymmetry (P), the high multiplicity of DIP infection generates relatively high DIP viral loads (see next section; see also Fig. S3 in the supplemental material) and allows the DIP to be dynamically stable even when η is just greater than 1 (Fig. 2C).
Thus, DIPs that steal capsids can stably suppress HIV-1 viral load even if the expression asymmetry (P) of the DIP is modest. These results are robust and qualitatively similar across a broad range of P and η values (Fig. 2D and E).
Robust suppression of HIV-1 is due to a high multiplicity of DIP infection.
As previously noted (35), DIP-infected cells would not be restricted to harboring only a single DIP provirus, since DIP-infected cells are long lived and could be readily reinfected multiple times by the DIP before HIV-1 infects the cell. DIP superinfection will lead to multiple integrated DIP genomes per cell. The number of DIP copies (denoted m) varies among dually infected cells as predicted by the individual-patient model (see equations 4 to 9). We calculated the average DIP copy number, denoted E[m], as a function of capsid waste (κ) and expression asymmetry (P) for different values of the capsid-to-genome ratio (η) (see Supplemental Methods and Fig. S3a in the supplemental material). The results are dependent upon P in a positive manner: increases in the value of P lead to more DIP virions, which results in a greater multiplicity of DIP infection. It is useful to note that, according to the standard individual-patient model we use here, the probability that a DIP+ HIV− cell is infected with another DIP copy is proportional to the concentration of DIP virions. Dually infected “producer” cells contain higher levels of DIP gRNA than HIV-1 gRNA (i.e., P > 1), and these cells generate more DIP than HIV-1 virions, which results in an increase of the average DIP copy number with P. Thus, the ratio of DIP/HIV-1 gRNA within a cell is determined by P in two ways: directly (through the molecular architecture of the DIP) and indirectly through the increase in the multiplicity of DIP infection (m).
To further explore the contribution of m to HIV-1 interference and suppression, we artificially limited DIP multiplicity to a single copy per cell (i.e., m = 1 or m = 0) and recalculated the HIV-1 viral loads (see Fig. S3b in the supplemental material). This control demonstrates that when m is ≤1, DIP-mediated suppression contributes very little to the decrease in the HIV-1 viral load (i.e., when m is ≤1, HIV-1 suppression is modest and arises primarily due to increased capsid waste). The analysis further shows that when m is ≤1, the DIP loses stability at low η values as κ increases. Hence, when m is ≤1, a high η value is needed for even modest suppression of the HIV-1 viral load. In summary, the multiplicity of integrated DIP genomes (m) is critical for DIP-mediated suppression of HIV-1.
Capsid interference is evolutionarily stable.
We next examined the direction of the evolution of the DIP and HIV-1 to test whether the DIP would be selected against in an ongoing HIV-1 infection. Conceivably, HIV-1 could escape a DIP by mutating to effectively increase the capsid waste parameter (κ). One possible mechanism for increasing κ is for HIV-1 to mutate its packaging signal Ψ and thus decrease the packaging efficiency, allowing more genomes, or capsids, to be degraded instead of packaged. Under this increased-waste scenario, capsid stealing by the DIP would be more affected than HIV-1 packaging in dually infected cells due to the DIP expression asymmetry (P > 1) and integration multiplicity (m > 1). Thus, increased capsid waste would benefit HIV-1 due to a decrease in DIP interference. However, in the absence of a DIP, mutation toward increased capsid waste would be deleterious for HIV-1, since an increased loss of capsid products lowers the HIV-1 burst size. With these competing pressures, it is not clear which evolutionary direction dominates. These competing effects of mutation in the packaging loop are in fact evident from the steady-state HIV-1 load versus κ (Fig. 2B), where there are two components of HIV suppression: one due to a decrease in HIV-1 burst (black dotted curves versus the dashed line in Fig. 2B) and another due to DIP interference (red curves versus black dotted curves in Fig. 2B). As κ is increased, one component becomes larger and another smaller. It is not immediately clear which effect is stronger.
To determine if HIV-1 mutates to increase or decrease capsid waste, we calculate the effective selection coefficient (∂seff), defined as the exponential rate of increase, or decrease, of mutant HIV-1 normalized to the death rate of infected cells (see Theory; see also Supplemental Methods, equations S48 to S57, in the supplemental material). Negative values of seff indicate that a mutation decreases the progeny of an infected cell and is selected against, while positive values of seff indicate that a mutation is selected for. We consider mutations that slightly increase the value of κ by reducing the packaging efficiency (Fig. 3A). Because the effect of a mutation on κ, denoted ∂κ, is unknown and may vary among bases, the selection coefficient is expressed in a normalized form: ∂seff/(∂κ/κ).Unlike previous work, this study is unique in that it calculates an in vivo selection coefficient value directly from a molecular model. Previous studies were only able to estimate s by fitting (40, 43, 46, 48, 52–54).
Analyzing the effective selection coefficient as a function of capsid waste (κ) demonstrates that, overall, HIV-1 mutants with increased capsid waste are selected against, since ∂seff/(∂κ/κ) is <0 for a range of η and κ values (Fig. 3B). Importantly, HIV-1 mutants with high capsid waste are selected against despite DIP interference being decreased at high capsid waste (see Fig. 2B for low values of η).
As a negative control, we next examined the effective selection coefficient keeping the burst size of HIV-1 in singly infected cells constant as capsid waste increases. As expected, in this scenario HIV-1 does evolve toward high capsid waste, as shown by ∂seff/(∂κ/κ) being >0 for a range of η and κ values (Fig. 3C). The direction of evolutionary selection appears robust across a broad range of P values (Fig. 3D and E). Hence, it is the decrease in HIV-1 burst size that causes the negative selection coefficient shown in Fig. 3B.
Essentially, these results indicate that the base HIV-1 burst size (which affects both singly and dually infected cells)—and not the DIP interference within dually infected cells—would dominate HIV-1 evolution within the individual patient.
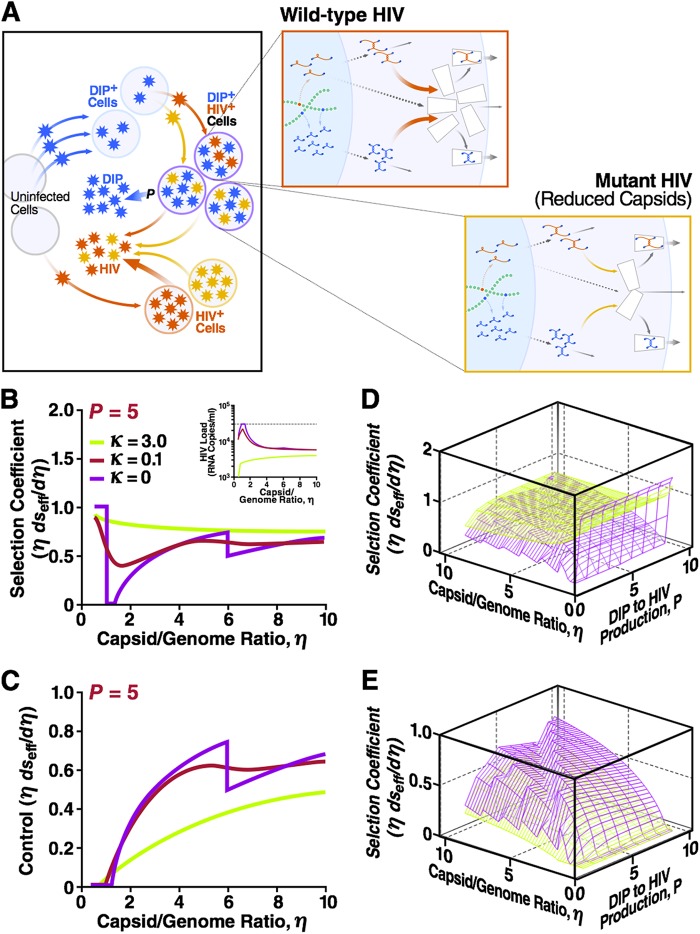
Next, we sought to determine if HIV-1 could escape DIPs by mutating to reduce the available capsid material (i.e., decreasing its capsid-to-genome ratio η) (Fig. 4A). The analysis shows that the DIP is unstable only at low values of η, and as expected, HIV-1 evolves toward high values of η, i.e., mutants that produce more capsid are selected for since ∂seff/(∂η/η) is >0 for a large range of κ and η values (Fig. 4B). In fact, there is only a narrow band (1 < η < (P + 1)R0/[P(R0 − 1)]) where the DIP is unstable and HIV-1 replication does not evolve toward increasing values of η (in this narrow band, the selection coefficient is zero). As a control, we examined keeping the HIV-1 burst size constant as the value of η increases (see the first term in equation S54 in the supplemental material). The control analysis shows that the effective selection coefficient is positive in the interval where the DIP is stable (Fig. 4C). Finally, a partial sensitivity analysis shows that the selection coefficient depends only weakly on the values of P, and the direction of evolutionary selection appears robust across a broad range of P values (Fig. 4D and E).
Fig 4.
DIV-HIV interaction is evolutionarily stable over a broad parameter range: HIV-1 cannot escape a DIP by decreasing the capsid-to-genome ratio. (A) The two-scale model for an individual infected by two strains of HIV-1, wild- type (red) and mutant (orange), as well as a DIP (blue). Mutation causes a small increase in the capsid-to-genome ratio η by ∂η > 0. (B) Normalized effective selection coefficient ∂seff/(∂η/η) for that mutation as a function of η for three values of the waste parameter κ. Fixed parameters used are as described for Fig. 2B and C: R0 = 10 and P = 5. Inset, corresponding HIV-1 viral load as a function of η at three values of the waste parameter κ. The positive values of ∂seff/(∂η/η) imply that mutation is selected for, and HIV-1 evolves toward an increasing η value. When κ is 0 and η is <1, the DIP is not dynamically stable in vivo, and the selection coefficient is due exclusively to an increase in the HIV-1 burst size. In a narrow adjacent interval, 1 < η < (P + 1)R0/[P(R0 − 1)], DIP is still unstable, and HIV-1 replication does not require more capsid, which is why the selection coefficient is zero. (C) A negative control neglecting HIV-1 burst size changes due to mutation (the first term in equation S54 in the supplemental material) and showing that the effective selection coefficient is positive in the interval where the DIP is stable. The discontinuity at κ = 0 and η = 1 + P is due to DIP gRNA competition with HIV gRNA for capsids at η < 1 + P but not at η > 1 + P, when there are enough capsids for both the DIP and HIV. Shown also are the net ∂seff/(∂η/η) (D) and control ∂seff/(∂η/η) (E) as functions of both P and η. Discontinuities at η = 1 + mP, m = 1, 2, …, are analogous to the discontinuity described for panel C. These 3D plots act as a partial sensitivity analysis and show that the selection coefficient depends weakly on the value of P.
DISCUSSION
This study examined the questions of whether lentiviral DIPs face evolutionary blocks and if DIPs would stably interfere with and suppress HIV-1. The analysis identified certain classes of DIPs that will not constitute an evolutionarily stable strategy of interference. Specifically, the analysis indicates that DIPs that suppress HIV replication via genome stealing will be unstable due to divergence between the HIV-1 DIS and the DIP DIS (i.e., interference and recombination via genome heterodimerization are minimized). This analytical finding raises doubts regarding the validity of a recent computational model that analyzes the evolutionary stability of conditionally replicating HIVs (i.e., DIPs) based exclusively on genome stealing (72). That DIS divergence is, in principle, possible is supported by the finding that different HIV-1 subtypes display diverse DIS sequences (73). Nevertheless, direct evidence demonstrating that the DIS is under selection from DIPs will require an intrapatient longitudinal data set showing evolution in the DIS.
As with all models, our analysis is a relatively simple representation of a complex system and necessarily makes certain assumptions. One potential caveat of our model is that it may not account for the finding that simple gammaretroviruses (not considered in the present work) exhibit spontaneous formation of DIPs (16), while lentiviruses do not. However, there are significant quantitative and qualitative differences in replication cycles between these two groups of viruses, and the model and parameters herein cannot be applied to the gammaretroviral life cycle. Most notably, HIV-1-infected cells are rapidly destroyed in a day or less, while in the gammaretrovirus setting, infected cells do not appear to display nearly as much cell death (except for mutants with poor protection against superinfection and an atypically broad host range) (74). Even more importantly, HIV-1 displays exclusively horizontal replication within a host (i.e., infection of new uninfected cells), which was taken into account in our model, while gammaretroviruses rely mostly on vertical replication (i.e., division of infected cells); their horizontal transmission is relatively infrequent and occurs between hosts or organs within a host. To determine whether these replication cycle differences account for the discrepancy in DIP formation between gammaretroviruses and lentiviruses or whether additional factors are at play will require additional experimental and theoretical analysis. Additional simplifications of our model are designed to capture basic features of the lentiviral cycle inside of cells in conjunction with the within-host level. Specifically, we assumed that all process times are Poisson distributed and that all dynamic variables are at steady state at both levels of modeling. A more complex model would include deterministic chaos that is present in all but the simplest dynamic systems, as well as various stochastic effects. For example, Kirkwood and Bangham (32) considered a generic virus and DIP coinfection in cell culture by introducing age-structured dynamics of infected cells and making the key assumption that wild-type virions are only produced from singly infected cells (i.e., perfect interference). In contrast, artificial lentiviral DIPs (25, 26, 29) do not exhibit perfect interference, and such DIPs would face strong negative selection pressures. Thus, it is unlikely that age-structured dynamics or time fluctuations would lead to chaotic dynamics for DIPs and HIV-1 or alter the main conclusions of our analysis, as long as the system remains far from instability.
Despite the caveats and assumptions inherent to any modeling exercise, the results herein provide a principled theoretical argument, based on the available data, that capsid stealing (competition for capsid proteins) is a dynamically and evolutionarily stable form of interference, provided that the ratio of capsid-to-dimerized genome production, η, is somewhat greater than 1. Capsid stealing is dynamically stable, primarily due to a multiplicity of DIP infection (i.e., multiple copies of integrated DIP provirus) that is higher than that of HIV-1, which appears to have a multiplicity of infection (MOI) of ≈1 (60). High MOIs are likely for DIPs that have deletions in transactivating elements, since these DIP-infected cells would not be subject to rapid virus-mediated or immune-mediated death; HIV-1-infected cells have an average life span of ∼1 day (61, 75) or less (76) and would therefore provide a long-lived target population for DIP superinfection. Also, cells infected with DIPs that lack trans-acting factors (such as HIV-1 Nef and Vpu) would not downregulate the cellular CD4 entry receptor that typically prevents HIV-1 superinfection of the cell (77).
The analysis also finds that capsid stealing is evolutionarily stable because the obvious mechanism that HIV-1 could use to escape DIP—increasing capsid waste (κ) by decreasing packaging efficiency (kpck)—ultimately harms HIV-1 replication significantly more than DIP production. HIV-1 could conceivably negate the deleterious effect of high capsid waste by generating compensatory mutations to ensure that DIP packaging is affected more than HIV-1 packaging (i.e., different kpck in equations 1 and 3). However, to escape in this manner, HIV-1 would need to mutate both cis and trans elements (e.g., generate correlated double mutations in both the capsid protein and the packaging signal), while the DIP could counteract with a single mutation in its cis sequence. Thus, this escape approach would not benefit HIV-1 in the long run.
In principle, there are a number of possible scenarios for the value of η and its rate of evolution within an individual patient. The model predicts that effective selection coefficients for mutation in η are positive (Fig. 4). If η is <1, then the analysis above argues that HIV-1 will evolve to η equaling 1 rapidly (Fig. 4B), probably on the time scale of years, given the high rate of HIV-1 evolution. The evolution to η equaling 1 is predictable, since each genome requires a capsid. When η is >1 in the absence of a DIP, HIV is still predicted to increase the value of η but at a much lower rate. The reason why HIV-1 evolves to a larger η, even when η is >1, is to compensate for capsid waste, but the rate of evolution in this regime is low because capsid waste is small (small κ). Determining the rapidity of this evolution will be critical for determining when DIPs may arise and transmit in the population. Once η reaches the DIP stability threshold (slightly above η = 1), HIV-1 evolution toward larger η values accelerates again due to the decrease of DIP interference (until η reaches a molecular limit) (Fig. 4B). The central findings of this analysis, the evolutionary instability of genome stealing and the evolutionary stability of capsid stealing when η is >1, conform to the conventional wisdom that a parasite (DIP) that harms its host (HIV-1) without need will be not be evolutionarily stable. Conversely, in the capsid-stealing scenario, a DIP that depletes a surplus of HIV-1 capsids is expected to survive.
While the value of η was not directly measured, analysis of the fraction of empty capsids versus capsids “filled” with RNA genomes can provide estimates of η (see Fig. S4 in the supplemental material). In vivo measurements (78, 79) suggest that the fraction of filled capsids is ∼20%, which implies η being ∼5 (80). While in vitro measurements in a tissue culture viral expression system (293T human embryonic kidney cells) estimated the fraction of filled capsids to be 90% (58), which sets a bound of η being ≤1.1, it is not unlikely that viral production in this 293T tissue culture setting is optimized compared to the in vivo setting. Thus, direct empirical measurements of η should be carried across a large sample of patients, and theoretical studies of HIV-1 evolution in a population of animal hosts could be used to predict the values of η that could evolve in the natural host.
The DIP stability condition (η slightly above 1) hints at a hypothetical schematic for the apparent absence of lentiviral DIPs. For example, historically, HIV-1 (or SIV) variants limited to η being <1 due to intrinsic molecular and cellular factors might have penetrated a population already harboring HIV-1 (or SIV) strains with η at >1 and already coinfected with a DIP. This new penetrating strain (with η < 1) would transmit more efficiently, since it would likely not be suppressed by DIPs, and could spread across the population, causing depletion of DIPs. However, as HIV-1 evolves toward large η values within patients and η exceeds the DIP stability threshold, DIPs could reemerge and spread in a population, causing another round of preferential spread of an HIV-1 strain with η being <1. This cycle could repeat and lead to repeated boom-then-bust cycles for the prevalence of DIPs and HIV-1 strains with η values of >1 and <1 over time. We emphasize that we know of no evidence to support this historical speculation, and systematic population level theoretical studies will be required to determine the likelihood of this scenario over others and to determine when DIPs may arise and transmit in the population, as has occurred for dengue virus (7).
Regarding the safety of DIPs as an antiviral strategy, there is a long-standing concern of the possibility of rescuing a virulent phenotype by recombination between DIPs and the full-length HIV-1. However, the analysis here argues that, for HIV-1, this recombination is unlikely, since recombination requires heterodimerization via the DIS, and the HIV-1 and DIP DIS sequences diverge. Moreover, production of such a recombinant, even if possible, would be equivalent to the production of an HIV strain with lower fitness than that of the wild type. Because this recombinant is selected against, in order to be significant, it would need to occur in each and every DIP-infected cell, which is highly unlikely.
To conclude, our analysis argues that DIPs would be evolutionarily stable within an individual, provided that the capsid-to-genome production ratio is sufficiently large. Our previous analysis argued that a DIP would be dynamically stable in a population level infection of HIV-1 (17). However, to address whether DIPs would be evolutionarily stable at the population level, further multiscale analysis is needed, since complex coevolutionary dynamics will exist between HIV-1 and a DIP, and these dynamics will be compounded by the existence of multiple circulating HIV-1 strains encoding different levels of capsid production.
Supplementary Material
ACKNOWLEDGMENTS
We thank Timothy Notton for technical and writing assistance and members of the Weinberger lab for critical reading of the manuscript.
This work was supported by the Pew Scholars Program in the Biomedical Sciences (to L.S.W.), an Alfred P. Sloan Foundation Research Fellowship (to L.S.W.), and the NIGMS National Center for Systems and Synthetic Biology at UCSF (grant P50 GM081879).
Footnotes
Published ahead of print 5 December 2012
Supplemental material for this article may be found at http://dx.doi.org/10.1128/JVI.02741-12.
REFERENCES
- 1. Holland J. 1990. Generation and replication of defective viral genomes, p 77–99 In Fields BN, Knipe DM. (ed), Virology. Raven Press, New York, NY [Google Scholar]
- 2. Huang AS, Baltimore D. 1970. Defective viral particles and viral disease processes. Nature 226:325–327 [DOI] [PubMed] [Google Scholar]
- 3. Chattopadhyay SK, Morse HC, 3rd, Makino M, Ruscetti SK, Hartley JW. 1989. Defective virus is associated with induction of murine retrovirus-induced immunodeficiency syndrome. Proc. Natl. Acad. Sci. U. S. A. 86:3862–3866 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Voynow SL, Coffin JM. 1985. Truncated gag-related proteins are produced by large deletion mutants of Rous sarcoma virus and form virus particles. J. Virol. 55:79–85 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Holland JJ, Villarreal LP. 1975. Purification of defective interfering T particles of vesicular stomatitis and rabies viruses generated in vivo in brains of newborn mice. Virology 67:438–449 [DOI] [PubMed] [Google Scholar]
- 6. McLain L, Armstrong SJ, Dimmock NJ. 1988. One defective interfering particle per cell prevents influenza virus-mediated cytopathology: an efficient assay system. J. Gen. Virol. 69:1415–1419 [DOI] [PubMed] [Google Scholar]
- 7. Aaskov J, Buzacott K, Thu HM, Lowry K, Holmes EC. 2006. Long-term transmission of defective RNA viruses in humans and Aedes mosquitoes. Science 311:236–238 [DOI] [PubMed] [Google Scholar]
- 8. Li D, Lott WB, Lowry K, Jones A, Thu HM, Aaskov J. 2011. Defective interfering viral particles in acute dengue infections. PLoS One 6:e19447 doi:10.1371/journal.pone.0019447 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Cook WJ, Green KA, Obar JJ, Green WR. 2003. Quantitative analysis of LP-BM5 murine leukemia retrovirus RNA using real-time RT-PCR. J. Virol. Methods 108:49–58 [DOI] [PubMed] [Google Scholar]
- 10. Kubo Y, Kakimi K, Higo K, Kobayashi H, Ono T, Iwama Y, Kuribayashi K, Hiai H, Adachi A, Ishimoto A. 1996. Possible origin of murine AIDS (MAIDS) virus: conversion of an endogenous retroviral p12gag sequence to a MAIDS-inducing sequence by frameshift mutations. J. Virol. 70:6405–6409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Paun A, Shaw K, Fisher S, Sammels LM, Watson MW, Beilharz MW. 2005. Quantitation of defective and ecotropic viruses during LP-BM5 infection by real time PCR and RT-PCR. J. Virol. Methods 124:57–63 [DOI] [PubMed] [Google Scholar]
- 12. Barrett AD, Dimmock NJ. 1986. Defective interfering viruses and infections of animals. Curr. Top. Microbiol. Immunol. 128:55–84 [DOI] [PubMed] [Google Scholar]
- 13. Cave DR, Hendrickson FM, Huang AS. 1985. Defective interfering virus particles modulate virulence. J. Virol. 55:366–373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Dimmock NJ. 1985. Defective interfering viruses: modulators of infection. Microbiol. Sci. 2:1–7 [PubMed] [Google Scholar]
- 15. Levine BL, Humeau LM, Boyer J, MacGregor RR, Rebello T, Lu X, Binder GK, Slepushkin V, Lemiale F, Mascola JR, Bushman FD, Dropulic B, June CH. 2006. Gene transfer in humans using a conditionally replicating lentiviral vector. Proc. Natl. Acad. Sci. U. S. A. 103:17372–17377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Marriott AC, Dimmock NJ. 2010. Defective interfering viruses and their potential as antiviral agents. Rev. Med. Virol. 20:51–62 [DOI] [PubMed] [Google Scholar]
- 17. Metzger VT, Lloyd-Smith JO, Weinberger LS. 2011. Autonomous targeting of infectious superspreaders using engineered transmissible therapies. PLoS Comput. Biol. 7:e1002015 doi:10.1371/journal.pcbi.1002015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Dull T, Zufferey R, Kelly M, Mandel RJ, Nguyen M, Trono D, Naldini L. 1998. A third-generation lentivirus vector with a conditional packaging system. J. Virol. 72:8463–8471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Turner AM, De La Cruz J, Morris KV. 2009. Mobilization-competent lentiviral vector-mediated sustained transcriptional modulation of HIV-1 expression. Mol. Ther. 17:360–368 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Kearney M, Maldarelli F, Shao W, Margolick JB, Daar ES, Mellors JW, Rao V, Coffin JM, Palmer S. 2009. Human immunodeficiency virus type 1 population genetics and adaptation in newly infected individuals. J. Virol. 83:2715–2727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. DePolo NJ, Holland JJ. 1986. Very rapid generation/amplification of defective interfering particles by vesicular stomatitis virus variants isolated from persistent infection. J. Gen. Virol. 67:1195–1198 [DOI] [PubMed] [Google Scholar]
- 22. Giachetti C, Holland JJ. 1988. Altered replicase specificity is responsible for resistance to defective interfering particle interference of an Sdi− mutant of vesicular stomatitis virus. J. Virol. 62:3614–3621 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. O'Hara PJ, Horodyski FM, Nichol ST, Holland JJ. 1984. Vesicular stomatitis virus mutants resistant to defective-interfering particles accumulate stable 5′-terminal and fewer 3′-terminal mutations in a stepwise manner. J. Virol. 49:793–798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Li Y, Kappes JC, Conway JA, Price RW, Shaw GM, Hahn BH. 1991. Molecular characterization of human immunodeficiency virus type 1 cloned directly from uncultured human brain tissue: identification of replication-competent and -defective viral genomes. J. Virol. 65:3973–3985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Bukovsky AA, Song JP, Naldini L. 1999. Interaction of human immunodeficiency virus-derived vectors with wild-type virus in transduced cells. J. Virol. 73:7087–7092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Chen CJ, Banerjea AC, Harmison GG, Haglund K, Schubert M. 1992. Multitarget-ribozyme directed to cleave at up to nine highly conserved HIV-1 env RNA regions inhibits HIV-1 replication—potential effectiveness against most presently sequenced HIV-1 isolates. Nucleic Acids Res. 20:4581–4589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Evans JT, Garcia JV. 2000. Lentivirus vector mobilization and spread by human immunodeficiency virus. Hum. Gene Ther. 11:2331–2339 [DOI] [PubMed] [Google Scholar]
- 28. Finzi D, Blankson J, Siliciano JD, Margolick JB, Chadwick K, Pierson T, Smith K, Lisziewicz J, Lori F, Flexner C, Quinn TC, Chaisson RE, Rosenberg E, Walker B, Gange S, Gallant J, Siliciano RF. 1999. Latent infection of CD4+ T cells provides a mechanism for lifelong persistence of HIV-1, even in patients on effective combination therapy. Nat. Med. 5:512–517 [DOI] [PubMed] [Google Scholar]
- 29. Klimatcheva E, Planelles V, Day SL, Fulreader F, Renda MJ, Rosenblatt J. 2001. Defective lentiviral vectors are efficiently trafficked by HIV-1 and inhibit its replication. Mol. Ther. 3:928–939 [DOI] [PubMed] [Google Scholar]
- 30. Paik SY, Banerjea A, Chen CJ, Ye Z, Harmison GG, Schubert M. 1997. Defective HIV-1 provirus encoding a multitarget-ribozyme inhibits accumulation of spliced and unspliced HIV-1 mRNAs, reduces infectivity of viral progeny, and protects the cells from pathogenesis. Hum. Gene Ther. 8:1115–1124 [DOI] [PubMed] [Google Scholar]
- 31. Mukherjee R, Plesa G, Sherrill-Mix S, Richardson MW, Riley JL, Bushman FD. 2010. HIV sequence variation associated with env antisense adoptive T-cell therapy in the hNSG mouse model. Mol. Ther. 18:803–811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Kirkwood TB, Bangham CR. 1994. Cycles, chaos, and evolution in virus cultures: a model of defective interfering particles. Proc. Natl. Acad. Sci. U. S. A. 91:8685–8689 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Nelson GW, Perelson AS. 1995. Modeling defective interfering virus therapy for AIDS: conditions for DIV survival. Math. Biosci. 125:127–153 [DOI] [PubMed] [Google Scholar]
- 34. Thompson KA, Yin J. 2010. Population dynamics of an RNA virus and its defective interfering particles in passage cultures. Virol. J. 7:257 doi:10.1186/1743-422X-7-257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Weinberger LS, Schaffer DV, Arkin AP. 2003. Theoretical design of a gene therapy to prevent AIDS but not human immunodeficiency virus type 1 infection. J. Virol. 77:10028–10036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Perrault J, Holland JJ. 1972. Absence of transcriptase activity or transcription-inhibiting ability in defective interfering particles of vesicular stomatitis virus. Virology 50:150–170 [PubMed] [Google Scholar]
- 37. DePolo NJ, Giachetti C, Holland JJ. 1987. Continuing coevolution of virus and defective interfering particles and of viral genome sequences during undiluted passages: virus mutants exhibiting nearly complete resistance to formerly dominant defective interfering particles. J. Virol. 61:454–464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Horodyski FM, Holland JJ. 1980. Viruses isolated from cells persistently infected with vesicular stomatitis virus show altered interactions with defective interfering particles. J. Virol. 36:627–631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Steinhauer DA, de la Torre JC, Meier E, Holland JJ. 1989. Extreme heterogeneity in populations of vesicular stomatitis virus. J. Virol. 63:2072–2080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Batorsky R, Kearney MF, Palmer SE, Maldarelli F, Rouzine IM, Coffin JM. 2011. Estimate of effective recombination rate and average selection coefficient for HIV in chronic infection. Proc. Natl. Acad. Sci. U. S. A. 108:5661–5666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Coffin JM. 1995. HIV population dynamics in vivo: implications for genetic variation, pathogenesis, and therapy. Science 267:483–488 [DOI] [PubMed] [Google Scholar]
- 42. Frost SD, Dumaurier MJ, Wain-Hobson S, Brown AJ. 2001. Genetic drift and within-host metapopulation dynamics of HIV-1 infection. Proc. Natl. Acad. Sci. U. S. A. 98:6975–6980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Frost SD, Nijhuis M, Schuurman R, Boucher CA, Brown AJ. 2000. Evolution of lamivudine resistance in human immunodeficiency virus type 1-infected individuals: the relative roles of drift and selection. J. Virol. 74:6262–6268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Frost SD, Wrin T, Smith DM, Kosakovsky Pond SL, Liu Y, Paxinos E, Chappey C, Galovich J, Beauchaine J, Petropoulos CJ, Little SJ, Richman DD. 2005. Neutralizing antibody responses drive the evolution of human immunodeficiency virus type 1 envelope during recent HIV infection. Proc. Natl. Acad. Sci. U. S. A. 102:18514–18519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Brown AJ. 1997. Analysis of HIV-1 env gene sequences reveals evidence for a low effective number in the viral population. Proc. Natl. Acad. Sci. U. S. A. 94:1862–1865 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Neher RA, Leitner T. 2010. Recombination rate and selection strength in HIV intra-patient evolution. PLoS Comput. Biol. 6:e1000660 doi:10.1371/journal.pcbi.1000660 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Rouzine IM, Coffin JM. 1999. Linkage disequilibrium test implies a large effective population number for HIV in vivo. Proc. Natl. Acad. Sci. U. S. A. 96:10758–10763 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Rouzine IM, Coffin JM. 1999. Search for the mechanism of genetic variation in the pro gene of human immunodeficiency virus. J. Virol. 73:8167–8178 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Rouzine IM, Rodrigo A, Coffin JM. 2001. Transition between stochastic evolution and deterministic evolution in the presence of selection: general theory and application to virology. Microbiol. Mol. Biol. Rev. 65:151–185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Rouzine IM, Weinberger L. The quantitative theory of within-host viral evolution. J. Stat. Mech. Theor. Exp, in press [Google Scholar]
- 51. Bonhoeffer S, Chappey C, Parkin NT, Whitcomb JM, Petropoulos CJ. 2004. Evidence for positive epistasis in HIV-1. Science 306:1547–1550 [DOI] [PubMed] [Google Scholar]
- 52. Ganusov VV, Goonetilleke N, Liu MK, Ferrari G, Shaw GM, McMichael AJ, Borrow P, Korber BT, Perelson AS. 2011. Fitness costs and diversity of the cytotoxic T lymphocyte (CTL) response determine the rate of CTL escape during acute and chronic phases of HIV infection. J. Virol. 85:10518–10528 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Hinkley T, Martins J, Chappey C, Haddad M, Stawiski E, Whitcomb JM, Petropoulos CJ, Bonhoeffer S. 2011. A systems analysis of mutational effects in HIV-1 protease and reverse transcriptase. Nat. Genet. 43:487–489 [DOI] [PubMed] [Google Scholar]
- 54. Wang D, Hicks CB, Goswami ND, Tafoya E, Ribeiro RM, Cai F, Perelson AS, Gao F. 2011. Evolution of drug-resistant viral populations during interruption of antiretroviral therapy. J. Virol. 85:6403–6415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Nowak M, May R. 2000. Virus dynamics: mathematical principles of immunology and virology. Oxford University Press, Oxford, UK [Google Scholar]
- 56. Perelson AS, Bonhoeffer S, Mohri H, Ho DD. 1999. T cell turnover in SIV infection. Science 284:555c doi:10.1126/science.284.5414.555a [Google Scholar]
- 57. Moore MD, Fu W, Nikolaitchik O, Chen J, Ptak RG, Hu WS. 2007. Dimer initiation signal of human immunodeficiency virus type 1: its role in partner selection during RNA copackaging and its effects on recombination. J. Virol. 81:4002–4011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Chen J, Nikolaitchik O, Singh J, Wright A, Bencsics CE, Coffin JM, Ni N, Lockett S, Pathak VK, Hu WS. 2009. High efficiency of HIV-1 genomic RNA packaging and heterozygote formation revealed by single virion analysis. Proc. Natl. Acad. Sci. U. S. A. 106:13535–13540 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. An DS, Morizono K, Li QX, Mao SH, Lu S, Chen IS. 1999. An inducible human immunodeficiency virus type 1 (HIV-1) vector which effectively suppresses HIV-1 replication. J. Virol. 73:7671–7677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Josefsson L, King MS, Makitalo B, Brannstrom J, Shao W, Maldarelli F, Kearney MF, Hu WS, Chen J, Gaines H, Mellors JW, Albert J, Coffin JM, Palmer SE. 2011. Majority of CD4+ T cells from peripheral blood of HIV-1-infected individuals contain only one HIV DNA molecule. Proc. Natl. Acad. Sci. U. S. A. 108:11199–11204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Furtado MR, Callaway DS, Phair JP, Kunstman KJ, Stanton JL, Macken CA, Perelson AS, Wolinsky SM. 1999. Persistence of HIV-1 transcription in peripheral-blood mononuclear cells in patients receiving potent antiretroviral therapy. N. Engl. J. Med. 340:1614–1622 [DOI] [PubMed] [Google Scholar]
- 62. Goudsmit J, De Ronde A, Ho DD, Perelson AS. 1996. Human immunodeficiency virus fitness in vivo: calculations based on a single zidovudine resistance mutation at codon 215 of reverse transcriptase. J. Virol. 70:5662–5664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. D'Costa J, Brown H, Kundra P, Davis-Warren A, Arya S. 2001. Human immunodeficiency virus type 2 lentiviral vectors: packaging signal and splice donor in expression and encapsidation. J. Gen. Virol. 82:425–434 [DOI] [PubMed] [Google Scholar]
- 64. Koldej RM, Anson DS. 2009. Refinement of lentiviral vector for improved RNA processing and reduced rates of self inactivation repair. BMC Biotechnol. 9:86 doi:10.1186/1472-6750-9-86 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. D'Costa J, Mansfield SG, Humeau LM. 2009. Lentiviral vectors in clinical trials: current status. Curr. Opin. Mol. Ther. 11:554–564 [PubMed] [Google Scholar]
- 66. Guedj J, Neumann AU. 2010. Understanding hepatitis C viral dynamics with direct-acting antiviral agents due to the interplay between intracellular replication and cellular infection dynamics. J. Theor. Biol. 267:330–340 [DOI] [PubMed] [Google Scholar]
- 67. Haseltine EL, Yin J, Rawlings JB. 2008. Implications of decoupling the intracellular and extracellular levels in multi-level models of virus growth. Biotechnol. Bioeng. 101:811–820 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Krakauer DC, Komarova NL. 2003. Levels of selection in positive-strand virus dynamics. J. Evol. Biol. 16:64–73 [DOI] [PubMed] [Google Scholar]
- 69. Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. 1996. HIV-1 dynamics in vivo: virion clearance rate, infected cell life span, and viral generation time. Science 271:1582–1586 [DOI] [PubMed] [Google Scholar]
- 70. Nowak MA, Lloyd AL, Vasquez GM, Wiltrout TA, Wahl LM, Bischofberger N, Williams J, Kinter A, Fauci AS, Hirsch VM, Lifson JD. 1997. Viral dynamics of primary viremia and antiretroviral therapy in simian immunodeficiency virus infection. J. Virol. 71:7518–7525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Fraser C, Hollingsworth TD, Chapman R, de Wolf F, Hanage WP. 2007. Variation in HIV-1 set-point viral load: epidemiological analysis and an evolutionary hypothesis. Proc. Natl. Acad. Sci. U. S. A. 104:17441–17446 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Ke R, Lloyd-Smith JO. 2012. Evolutionary analysis of human immunodeficiency virus type 1 therapies based on conditionally replicating vectors. PLoS Comput. Biol. 8:e1002744 doi:10.1371/journal.pcbi.1002744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Paillart JC, Shehu-Xhilaga M, Marquet R, Mak J. 2004. Dimerization of retroviral RNA genomes: an inseparable pair. Nat. Rev. 2:461–472 [DOI] [PubMed] [Google Scholar]
- 74. Rainey GJA, Coffin JM. 2006. Evolution of broad host range in retroviruses leads to cell death mediated by highly cytopathic variants. J. Virol. 80:562–570 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Markowitz M, Louie M, Hurley A, Sun E, Di Mascio M, Perelson AS, Ho DD. 2003. A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J. Virol. 77:5037–5038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Rouzine IM, Sergeev RA, Glushtsov AI. 2006. Two types of cytotoxic lymphocyte regulation explain kinetics of immune response to human immunodeficiency virus. Proc. Natl. Acad. Sci. U. S. A. 103:666–671 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Michel N, Allespach I, Venzke S, Fackler OT, Keppler OT. 2005. The Nef protein of human immunodeficiency virus establishes superinfection immunity by a dual strategy to downregulate cell-surface CCR5 and CD4. Curr. Biol. 15:714–723 [DOI] [PubMed] [Google Scholar]
- 78. Kuroda MJ, Schmitz JE, Charini WA, Nickerson CE, Lifton MA, Lord CI, Forman MA, Letvin NL. 1999. Emergence of CTL coincides with clearance of virus during primary simian immunodeficiency virus infection in rhesus monkeys. J. Immunol. 162:5127–5133 [PubMed] [Google Scholar]
- 79. Letvin NL, Mascola JR, Sun Y, Gorgone DA, Buzby AP, Xu L, Yang ZY, Chakrabarti B, Rao SS, Schmitz JE, Montefiori DC, Barker BR, Bookstein FL, Nabel GJ. 2006. Preserved CD4+ central memory T cells and survival in vaccinated SIV-challenged monkeys. Science 312:1530–1533 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Sergeev RA, Batorsky RE, Rouzine IM. 2010. Model with two types of CTL regulation and experiments on CTL dynamics. J. Theor. Biol. 263:369–384 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.