The behavioral economics of drug self-administration: A review and new analytical approach for within-session procedures

Abstract

Rationale

Behavioral-economic demand curve analysis offers several useful measures of drug self-administration. Although generation of demand curves previously required multiple days, recent within-session procedures allow curve construction from a single 110-min cocaine self-administration session, making behavioral-economic analyses available to a broad range of self-administration experiments. However, a mathematical approach of curve fitting has not been reported for the within-session threshold procedure.

Objectives

We review demand curve analysis in drug self-administration experiments and provide a quantitative method for fitting curves to single-session data that incorporates relative stability of brain drug concentration.

Methods

Sprague-Dawley rats were trained to self-administer cocaine, and then tested with the threshold procedure in which the cocaine dose was sequentially decreased on a fixed ratio-1 schedule. Price points (responses/mg cocaine) outside of relatively stable brain cocaine concentrations were removed before curves were fit. Curve-fit accuracy was determined by the degree of correlation between graphical and calculated parameters for cocaine consumption at low price (Q₀) and the price at which maximal responding occurred (Pmax).

Results

Removing price points that occurred at relatively unstable brain cocaine concentrations generated precise estimates of Q₀ and resulted in Pmax values with significantly closer agreement with graphical Pmax than conventional methods.

Conclusion

The exponential demand equation can be fit to single-session data using the threshold procedure for cocaine self-administration. Removing data points that occur during relatively unstable brain cocaine concentrations resulted in more accurate estimates of demand curve slope than graphical methods, permitting a more comprehensive analysis of drug self-administration via a behavioral-economic framework.

Introduction

Law of demand

Behavioral economics is “the study of the allocation of behavior within a system of constraint” (Bickel et al. 1995). This umbrella term may be used to describe several unique economic perspectives; e.g., it has been used to describe the reduction in value of a delayed vs. immediate reward (Bickel and Marsch 2001). Here, however, we specifically consider the area of behavioral economics known as consumer demand theory, i.e., how demand for a commodity varies as a function of price (Hursh et al. 1988). Demand in this context is the experimentally derived magnitude of consumption of a commodity at a given price (Hursh 1980). When demand is plotted across different prices, a demand curve is produced (Hursh 1980). This curve typically follows the law of demand, which states that demand decreases as the price increases (Samuelson and Nordhaus 2004).

Demand curve analysis of drug self-administration

Demand curve analysis is a particularly useful tool for characterizing drug self-administration (Bickel et al. 2011; Hursh and Winger 1995). The utility of demand curve analysis for studying drug self-administration is the multiple, unique measures that it produces (Bickel et al. 2000; España et al. 2010; Oleson et al. 2011) and its unique ability to directly compare different types of reinforcers (Hursh and Silberberg 2008; Hursh and Winger 1995). A single demand curve produces values for the following variables: Omax¹, Pmax¹, Q₀ and α (Hursh and Silberberg 2008). Although Pmax, Omax, and Q₀ may be estimated graphically from response curves, α must be calculated using the exponential demand equation (Equation 1) (Hursh and Silberberg 2008).

$$lnQ=ln{Q}_0+k(e^{-\alpha Q_{0}C}-1)$$ (1)

Q in Equation 1 is demand, the experimentally derived measure of drug consumption, and Q₀ is the level of demand that occurs when cost², C, approaches 0 (Hursh and Silberberg 2008). k specifies the range of Q, and α is a measure of demand curve elasticity, i.e. how quickly demand falls with increases in price (Hursh and Silberberg 2008).

Q₀ has been defined as a measure of consummatory behavior (Oleson et al. 2011). Taking into account that cost is a measure of effort (Hursh et al. 1988), then Q₀ is the level of consumption when no effort is required to acquire the commodity of interest. Similarly, Q₀ can also be described as a measure of “hedonic set point”, i.e., the consumption of drug under unrestricted conditions (Ahmed and Koob 1999; Ahmed and Koob 1998). This set point model predicts that animals will maintain a specific brain concentration of drug when price for drug is null (Zittel-Lazarini et al. 2007). Because effort is a restriction on consumption, assessments of this hedonic set point can only be obtained when no effort is required to obtain drug. Q₀ is a prediction of consumption at null effort extrapolated from the animal’s consumption at low price (Hursh and Silberberg 2008); hence, it is an especially appropriate measure of the consummatory behavior required to bring an animal’s brain drug concentration up to its hedonic set point. When measured in humans, Q₀ and other similar behavioral-economic variables that represent demand at low price have been shown to significantly correlate with several clinically relevant indices of both alcohol (MacKillop et al. 2010a; MacKillop and Murphy 2007; MacKillop et al. 2010b; Murphy et al. 2009) and nicotine (MacKillop et al. 2012; Murphy et al. 2011) addiction.

The other behavioral-economic parameters, Pmax, Omax, and essential value (α) are best understood in the context of elasticity. Elasticity is a measure of how sensitive demand is to changes in price, and it is represented by the slope of the demand curve (Hursh 1980). The more elastic demand for a commodity is the quicker demand falls in response to rising price. Pmax is the simplest method of measuring elasticity. It is the price at which the point slope of the demand curve is equal to −1, and it represents the price that elicits maximum responding (Hursh 1991). Stated otherwise, at prices lower than Pmax consumption is relatively stable and similar to Q_0, but after Pmax is crossed consumption falls more rapidly with rising price. Considering that price is a measure of effort (Hursh et al. 1988), Pmax is then the maximum effort that the animal is willing to expend to defend Q₀. Pmax as a measure of maximal effort is also supported by its correlation with progressive ratio breakpoint (Bickel and Madden 1999; Lenoir and Ahmed 2008; Oleson and Roberts 2008; Rodefer and Carroll 1997).

In comparison to Pmax, the utility of Omax is not as clear. Omax is the maximum number of responses that occurs at Pmax, and is directly proportional to the consumption at Pmax (Hursh and Winger 1995). Hursh and Winger proposed that the utility in Omax is its sensitivity to both elasticity and demand, in contrast to Pmax, which is just sensitive to elasticity, and in contrast to Q₀, which is sensitive only to demand (1995). In the human literature, like Q₀, Omax has been shown to be a particularly reliable measure (Murphy et al. 2009), and one that correlates well with several clinically relevant indices of both alcohol (MacKillop et al. 2010b; MacKillop et al. 2010a; MacKillop and Murphy 2007; Murphy et al. 2009) and nicotine (MacKillop et al. 2012; Murphy et al. 2011) addiction. Additionally, Omax is currently the only behavioral-economic variable that has been shown to predict treatment outcome (MacKillop and Murphy 2007). Thus, Omax may prove to be an appropriate measure for drug-addiction treatment efficacy in preclinical and clinical models.

One of the unique advantages of demand curve analysis is the ability to directly compare across reinforcers of various magnitudes, potencies, and types. This feat is made possible by normalizing demand and price with respect to Q₀, with demand set relative to Q₀ and price set as a multiple of Q₀ (Hursh et al. 2005; Hursh and Silberberg 2008; Hursh and Winger 1995). This normalization process results in normalized values of Omax (nOmax) and Pmax (nPmax) that allow for comparison across various reinforcers (Ko et al. 2002; Wade-Galuska et al. 2007; Winger et al. 2006; Winger et al. 2002; Winger et al. 1996). As an alternative to nPmax, when Equation 1 is employed, essential value (α) may take its place. α is an inherently normalized parameter (Hursh and Silberberg 2008) and equivalent to nPmax, as the these variables are inversely proportional.

α has several advantages over non-normalized Pmax as a measure of demand elasticity. Foremost, the inherent normalization in α allows for the comparison of elasticity across reinforcers (Hursh and Silberberg 2008). In the first prospective use of Equation 1, α was used to determine that food has a significantly greater essential value (lower α) compared to cocaine in rats (Christensen et al. 2008a). Christensen et al. then showed that extended exposure to cocaine self-administration resulted in an increase in essential value for cocaine, but that extended exposure to food self-administration did not result in an increase in essential value for food, highlighting a change in essential value with exposure to a reinforcer as a fundamental characteristic of drugs of abuse (2008b). More recently, α was used to show that food also has a greater essential value than methamphetamine in rats (Galuska et al. 2011). These comparisons between food and drugs of abuse cannot be realized with conventional measures of reinforcing efficacy or non-normalized behavioral-economic variables, because there is no absolute dose equivalency between different reinforcers (Hursh and Winger 1995). However, when reinforcer dose is scaled in relation to the hedonic set point of a subject (Q₀), the change in demand as a function of price can be directly compared across reinforcers (Hursh et al. 2005; Hursh and Silberberg 2008; Hursh and Winger 1995).

Normalized measures of demand elasticity also allow for the assessment of genetic factors, treatments, and other manipulations on a subject’s essential value for a reinforcer. Non-normalized parameters can sometimes, but not always, accomplish this, because manipulations may alter the subject’s hedonic set point (Q₀) and willingness to maintain this set point as price is increased (Pmax) independently of one another. In an example given by Hursh and Winger, lesions of the ventromedial nuclei of the monkey hypothalamus (VMA) resulted in an increase in Q₀ but a decrease in non-normalized Pmax (1995). Thus, the VMA lesion resulted in greater consumption of food at low price and decreased consumption of food at high price, blurring whether the monkeys’ essential value for food had increased or decreased. However, when Hursh and Winger normalized food consumption and price, the demand curve for monkeys with VMA lesions became identical to the demand curve produced by monkeys without VMA lesions, indicating that a VMA lesion increased the monkeys’ hedonic set point for food without altering its essential value (1995). In another example, normalized elasticity was employed for the investigation of a genetic component of essential value. Christensen et al. used α to show that the essential value of food and cocaine varies between rat strains, indicating that essential value for a reinforcer has a partly genetic basis (2009). Similarly, normalized elasticity has been correlated with impulsive choice for nicotine but not alcohol in rats (Diergaarde et al. 2012). In both of these previous examples, normalization was required to compare elasticity, because the hedonic set point (Q₀) for reinforcer was significantly different between groups.

Normalized values of elasticity have also been shown to correlate with a greater number of clinically relevant variables than non-normalized values. For example, Murphy et al. found that α was a more reliable measure than non-normalized Pmax and that α, but not Pmax, correlated with alcoholic drinks per weak, alcohol related problems, and the proportion of expenditure on alcohol in college students (2009). Similarly, MacKillop et al. demonstrated that compared to neutral cues, exposure to alcohol cues resulted in significantly higher nPmax but not Pmax in heavy drinkers (2010b). Finally, these differences in clinical correlation between normalized and non-normalized behavioral economic-parameters are not limited to alcohol as Murphy et al. have also found that α, but not Pmax, correlates with number of cigarettes smoked per day in adolescent smokers (2011).

Polydrug abuse remains a national public health problem (Montoya and McCann 2010). Hence, it is imperative to map the interactions between concurrently available drugs of abuse in order to inform appropriate policy (Petry 2001). When drugs and/or non-drug reinforcers are concurrently available, 3 possible interactions may occur. One reinforcer may act as either a substitute or a complement for the other, leading to a decrease or an increase in demand for the other reinforcer, respectively, or the reinforcers may act independently of one another (Petry 2001). Demand curve analysis is particularly helpful in understanding these interactions because such interactions are price dependent (Sumnall et al. 2004). For example, in monkeys remifentanil and cocaine act as economic substitutes for each other; increases in the price of cocaine lead to an increase in consumption of remifentanil when remifentanil’s price was held constant and vice versa (Wade-Galuska et al. 2007), and the combination of these 2 drugs has been found to be no more reinforcing than either drug alone (Winger et al. 2006), an effect that can only be realized when normalized demand curves are employed. Furthermore, the type of interaction between drugs of abuse may not coincide with predictions based on molecular action. Intuition would predict that drugs with similar molecular actions would act as substitutes for each other; however, despite pharmacological similarities between diazepam and alcohol, demand for each has been shown to be independent of the price of the other (Petry 2001). Similarly, drugs with very different molecular actions may act as substitutes; e.g., diazepam and cocaine have been found to act as substitutes for heroin (Petry and Bickel 1998).

Safer, alternative reinforcers that act as substitutes for an abused drug are often sought for the treatment of drug addiction. Demand curve analysis has been beneficial to this area of investigation by testing for possible substitutes and by describing the price dependency of these substitutive effects. For example, concurrent availability of denicotinized cigarettes, but not nicotine gum, has been shown to reduce demand for nicotine-containing cigarette puffs (Johnson et al. 2004; Shahan et al. 2000), and the amount of denicotinized cigarette puffs occupies a greater proportion of total cigarette puffs at higher nicotine-containing cigarette price (Johnson et al. 2004). Non-drug related reinforcers may also act as effective substitutes for drugs of abuse; e.g., food has been found to reduce the essential value of heroin in rats exposed to long-access heroin self-administration (Lenoir and Ahmed 2008).

In summary, demand curve analysis of drug self-administration produces several unique measures of drug consumption as a function of price. These measures may be used to directly compare reinforcing efficacy across reward type, magnitude, and potency; they have been used to track changes in the essential value of reinforcers; they have been shown to correlate with clinically-relevant aspects of drug addiction; and they have helped explain the interactions between reinforcers that underlie both polydrug abuse as well as reinforcer replacement therapies.

Multi-session paradigm for behavioral-economic analyses

Conventionally, in preclinical studies data sets to create demand curves that can be modeled with Equation 1 are produced via a series of daily sessions that each determine the demand at one specific price (Christensen et al. 2009; Christensen et al. 2008b; Christensen et al. 2008a; Galuska et al. 2011; Koffarnus and Woods 2011; Oleson and Roberts 2008; Wade-Galuska et al. 2007; Winger 1993; Woolverton et al. 1997). The advantage of this approach is that each assessment of demand per price is taken over a period of time (e.g., 1 hr or more) after the animal’s behavior has stabilized. Furthermore, when separate sessions are used for each price, the effects of satiety or fluctuating brain concentrations of a drug do not influence behavior at subsequent prices. The independent assessment of demand at each price allows Equation 1 to model multi-session data extremely well. However, schedules that analyze different prices across multiple sessions are time consuming and preclude many neural manipulations that are relatively transient or are repeatable only a limited number of times, e.g., microinjections of compounds into brain nuclei. Fortunately, this limitation on demand curve analysis has recently been lifted for intravenous cocaine (Oleson et al. 2011; Oleson and Roberts 2012) and heroin (Lenoir and Ahmed 2008) self-administration with the advent of within-session procedures.

Can behavioral-economic analyses be applied to a within-session self-administration paradigm?

The within-session threshold procedure for cocaine self-administration has previously been described in detail (España et al. 2010; Oleson et al. 2011; Oleson and Roberts 2012; Zimmer et al. 2012). This procedure exposes animals to a series of decreasing doses of intravenous cocaine under a fixed ratio-1 (FR-1) schedule of reinforcement in a single 110-min operant conditioning session. Every 10 min, the dose of cocaine reinforcing a response on the active lever decreases by decreasing the infusion duration. This effectively raises the unit price of cocaine every 10 min. Unit price is defined as the amount of effort required to earn a unit of commodity (Hursh et al. 1988). The unit price here is the number of responses required to obtain 1 mg of cocaine. In contrast, within-session procedures for heroin have held the injection volume constant while increasing FR requirement every 33-min (Lenoir and Ahmed 2008).

In accordance with the law of demand and multi-session threshold paradigms, the within-session procedures result in consumption that decreases throughout the session as price increases (España et al. 2010; Lenoir and Ahmed 2008; Oleson et al. 2011; Zimmer et al. 2012). It is then plausible that Equation 1 may be mathematically fit to within-session procedure data. Yet, to our knowledge, a mathematical fit of Equation 1 to within-session procedure data has not been reported.

Previous studies employing within-session procedures have relied on graphical methods to estimate Q₀ and Pmax (España et al. 2010; Lenoir and Ahmed 2008; Oleson et al. 2011; Zimmer et al. 2012). The graphical method has an advantage over calculating behavioral-economic parameters from a mathematically fit demand curve in that it is straightforward and can be used to quickly estimate behavioral-economic parameters directly from data without the need of further processing. However, the graphical method has several limiting shortcomings. Its resolution of estimating Pmax is limited to the sampling rate of price set by the procedure. Because price typically ascends on a logarithmic scale, the resolution of Pmax estimations decreases logarithmically as price increases. In contrast, Pmax calculated from a mathematically fit demand curve is a continuous variable that can fall anywhere, including between price points. Furthermore, although essential value (or normalized Pmax) can be estimated using graphical estimations of Q₀ and Pmax, the result would be subject to the multiplicative error of both graphical estimations. Hence, a high-resolution calculation of the important essential value parameter must be garnered from a best-fit demand curve regression that employs Equation 1. Finally, when a demand curve is fit to consumption data, all data are used to calculate elasticity. Whereas graphical estimations of elasticity are insensitive to changes in demand at other prices, elasticity calculated from a best-fit demand curve is sensitive to changes in demand at all prices.

One report fit Equation 1 to within-session threshold procedure data for cocaine self-administration; however, the technique used relied on matching calculated values of Q₀ and Pmax to graphical estimations (Oleson et al. 2011). Thus, this technique is bound by the same limitations as graphical estimation alone. Another report attempted to fit an older demand equation (Hursh et al. 1988) to within-session heroin self-administration data; however, aberrant calculated Pmax values resulted and were not reported (Lenoir and Ahmed 2008).

Although it would be advantageous to mathematically fit Equation 1 to within-session threshold procedure data, there are differences in the brain drug concentration-price relationship between the within-session and multi-session approaches that predict that Equation 1 may not be fit to within-session data with the conventional techniques used for multi-session approaches. In the multi-session approach, the brain drug concentration during each session depends only on the drug consumed at the price for that session, so there is a direct relationship between brain drug concentration and price. In contrast, brain drug concentration during the within-session approach depends on the consumption of drug at a given price as well as drug consumed at lower prices, so there is an indirect relationship between price and brain drug concentration.

Equation 1 describes a monotonic relationship between demand and price, but demand is also a function of brain drug concentration, a relationship highlighted by studies that found significant differences in rates of cocaine self-administration by pre-treating animals with cocaine analogs (Hiranita et al. 2009; Roberts et al. 2003). Although demand varies with price and brain drug concentration, a monotonic relationship between demand and price is preserved when a multi-session approach is used, because price and brain drug concentration are directly related for multi-session approaches. In contrast, the price and brain drug concentration are not directly related for a within-session approach; thus, a monotonic function such as Equation 1 may not accurately model data produced by a within-session approach. Importantly, the fundamental difference that predicts that Equation 1 may not necessarily model data from the within-session procedures is not that within-session designs produce different magnitudes of cocaine brain concentration, but that there is not a direct relationship between price and brain drug concentration in current within-session paradigms as concentration at any price is influenced by concentrations at lower prices.

However, a monotonic relationship between price and demand can be preserved for a within-session approach if the demand curve analysis is focused on behavior that occurs during relatively stable brain drug concentration. When demand is only assessed at a relatively stable brain drug concentration, the effects of brain drug concentration are approximately equal at every price and need not be accounted for. This is not necessary for multi-session paradigms, because brain concentration is directly related to price. Thus, multi-session procedures effectively conceal the effects of brain drug concentration within price.

In the case of the within-session threshold procedure for cocaine self-administration, after the animal brings its brain drug concentration up to its hedonic set point, Q₀, during the first 10 minutes of the session, its brain drug concentration remains relatively stable until Pmax is reached (Zimmer et al. 2012; Zittel-Lazarini et al. 2007). At Pmax the animal begins to fail to maintain its brain drug concentration, and as price increases consumption of drug quickly approaches zero (Zimmer et al. 2012; Zittel-Lazarini et al. 2007). As a consequence of decreased consumption, brain drug concentration will decay at a predictable rate. For example, previous studies show that brain cocaine concentration drops to ~17% of its maximum value by 20 min after cessation of cocaine intake (Pan et al. 1991). In the case of cocaine, if the animal’s Pmax occurs early during the session, then there is ample time for brain cocaine concentration to markedly fall compared to its concentration pre-Pmax. Thus, behavior that occurs exclusively at relatively stable brain drug concentration occurs up to and just after Pmax.

We predicted that the increase in the rate of decay of brain drug concentration that occurs at high prices after Pmax would increase the animal’s motivation for drug, because past reports have indicated that lower brain drug concentrations of cocaine analogs resulted in higher rates of cocaine self-administration (Hiranita et al. 2009; Roberts et al. 2003). This led to the hypothesis that focusing the behavioral-economic analysis on demand that occurs only at relatively stable brain drug concentration will enable Equation 1 to more accurately model within-session data.

We set out to compare conventional and novel mathematical methods of fitting the exponential demand equation (Equation 1) to demand curves generated by the within-session threshold procedure for cocaine self-administration. We hypothesized that our novel method that focuses the analysis on behavior that occurs only at relatively stable brain drug concentration would yield a more accurate description of the behavioral-economic parameters compared to conventional methods. Hence, we applied both analysis methods to a group of animals to compare accuracy, i.e. overall concordance between graphical and calculated parameters. Our results indicate that our novel method produces a demand curve for within-session data with a more accurate prediction of elasticity.

Methods

Animals

Male Sprague-Dawley rats (n = 9) with an initial weight of approximately 250–275g (Charles River, Raleigh, NC) were single-housed under a reversed 12-h light/dark cycle (lights on 6 p.m.) and had ad libitum access to food and water. Animals were housed in a temperature and humidity-controlled animal facility at MUSC (AAALAC-accredited). All experiments were approved by the IACUC at MUSC and conducted according to specifications of the NIH as outlined in the Guide for the Care and Use of Laboratory Animals (2011).

Intravenous catheter surgery

Animals were implanted with intravenous jugular catheters after acclimation to the housing facilities as previously described (Smith et al. 2009). Animals were anesthetized prior to surgery using a ketamine/xylazine mixture (56.6/8.7 mg/kg i.p.). Meloxicam was administered as an analgesic (1 mg/kg, s.c.). After obtaining a deep plane of anesthesia (lack of corneal reflex), the free end of the catheter was inserted into the right external jugular vein. The tubing was run subcutaneously and exited through the skin via a biopsy hole placed 2 cm caudal to the mid-scapular region. Beginning 3 days after surgery, catheters were flushed daily with 0.1 ml of heparin (100 mg/mL) and 0.1 ml of cefazolin (100 U/mL). Animals were allowed to recover for at least 1 week before cocaine self-administration training.

Drugs

Cocaine HCl powder was provided by the National Institute on Drug Abuse (Research Triangle Park, NC, USA) and was dissolved in 0.9% sterile saline.

Self-administration and threshold procedure

Self-administration sessions were carried out in operant conditioning chambers housed in sound-attenuating cubicles and controlled by a MED-PC IV program (Med-Associates, St Albans, VT, USA). Before beginning the threshold procedure, rats learned to lever-press for 0.16 mg infusions of intravenous cocaine on an FR-1 schedule in 2-hr daily sessions. Infusions were delivered over 3 sec in 52 μL of saline via a motorized pump with a 20-sec timeout after each infusion during which lever presses were recorded but did not result in further infusions. Cocaine infusions were paired with discrete tone and light cues (78 dB, 2900 Hz; white stimulus light above the active lever). The red house light on the wall opposite the levers was turned off during cocaine infusions and 20-sec timeouts. Presses on an inactive lever had no programmed consequences but were recorded. Rats remained on the FR-1 schedule until they achieved at least 20 infusions per session for 5 consecutive days. Rats were then switched to the threshold procedure for training and testing.

The day after completion of FR-1 training, rats were trained and then tested on the within-session threshold procedure (Oleson and Roberts 2012). In this paradigm rats received access to decreasing doses of cocaine in successive 10 min intervals on a quarter logarithmic scale (358.4, 201.5, 113.3, 63.7, 35.8, 20.2, 11.3, 6.4, 3.6, 2.0, 1.1 μg per infusion), by decreasing pump infusion duration. The pump rate infusion times (7640, 4296, 2416, 1359, 764, 430, 242, 136, 76, 43, 24 ms) were based on an averaged measurement of the flow rates of 16 individual PMH100 pumps (Med-Associates, St Albans, VT, USA) with a 10 ml syringe (BD, Franklin Lakes, NJ, USA). The volume of infusion was determined to be accurate to within 5% at the highest dose (358.4 μg) and to within 20% at the lowest dose (1.1 μg). Similarly to the FR-1 paradigm, during an infusion while the pump was on the house-light was turned off and the light and tone cues were presented. However, during the threshold-procedure sessions, there was no timeout, allowing rats to press for the next infusion as soon as the current infusion was finished. The only exception was that while the pump was on presses on the active lever were recorded but did not elicit a second infusion. The animals were run daily on the threshold procedure for a minimum of 6 sessions and until the last 3 sessions produced an approximate Pmax that was within a range of 3 price points. The data from the last 3 days of threshold procedure testing were then used for analysis.

Determining graphical values for Q₀ and Pmax

Graphical values for Q₀ and Pmax were determined using methods similar to those previously reported (España et al. 2010; Oleson et al. 2011; Oleson and Roberts 2008; Zimmer et al. 2012). The graphical Pmax was defined as the first price point that was followed consecutively by two price points with lower numbers of responses. In every case, descending response values flanked the graphical Pmax, making determination unambiguous. In cases where there were 2 adjacent maximum response values that were within 15% of their mean, the graphical Pmax was taken at the midpoint of the prices at which these response values occurred. Q₀ was taken as the average of the consumption at the second through fourth price points.

Calculating Brain Cocaine Concentration

Brain cocaine concentration was continuously calculated and plotted in minute-to-minute resolution to aid in demand curve fitting as described below. The technique employed to calculate brain cocaine concentration was developed by Pan et al. (1991) and has successfully been used to model rat brain cocaine concentration during the within-session threshold procedure (Zimmer et al. 2012). The brain cocaine concentration of each intravenous infusion of cocaine as a function of time was calculated with Equation 2 and then summed over the course of a session.

$$c=\frac{dk}{v(\alpha -\beta )}(e^{-\beta t}-e^{-\alpha t})$$ (2)

Equation 2 includes the brain cocaine concentration (c, mg/L), the dose of cocaine in an infusion (d, mg/kg), the rate constant for transfer of cocaine between the blood and the brain (k = 0.233 min⁻¹), the apparent volume of distribution of the brain (v = 0.15 L/kg), and the rate constants for removal of cocaine from the blood through redistribution (α = 0.642 min⁻¹) and elimination (β = 0.097 min⁻¹).

Fitting the Exponential Demand Equation

Demand curves were fit via conventional methods and via our novel approach. As is done conventionally, demand curves were fit to each subject’s full data set using standard linear and non-linear regression techniques (Bickel and Madden 1999; Hursh et al. 1988; Jacobs and Bickel 1999; Murphy et al. 2009). In this approach, the values α and Q₀ in Equation 1 were manipulated to minimize the residual sum of squares, i.e. the square of the difference between the experimentally measured demand and the demand predicted by Equation 1 was found for each price and then summed across all prices. The parameter k in Equation 1 represents the range of the consumption data in Log_e units and was held constant at a value of 8.85 (3.84 in Log₁₀ units) across all animals (Hursh and Silberberg 2008). This value of k was chosen based on the maximum observed range of consumption. All data points were used in these fits except for the first price point as it represents a loading dose (Oleson et al. 2011).

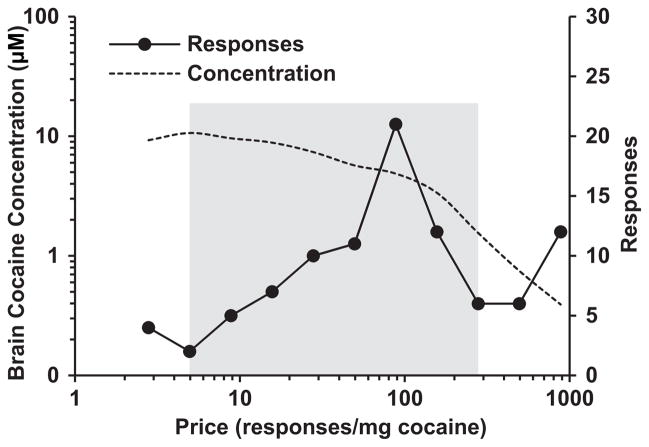
Demand curves were also fit using a novel approach that we developed specifically for data acquired via the within-session threshold procedure. This approach was set to exclusively model demand that occurs when brain drug concentration is relatively stable. This was accomplished by employing an Excel macro that removed data points associated with rapidly changing brain cocaine concentrations over time. This custom macro first used Equation 2 to determine the brain cocaine concentration during each minute of the session. It then calculated the point slope for that minute by performing a linear least-sum-of-squares regression using 3 flanking data points. The point slopes that occurred within each 10-min bin that defined each price point were then averaged. Unstable brain cocaine concentration was defined as having an average slope magnitude greater than one standard deviation from 0, the theoretical limit of stability. One standard deviation was set at the average standard deviation of the minute point slopes across all animals and sessions (0.02 Log₁₀(μM)/min). Using this method, the consumption at the first price point was removed in every case, because it had a slope greater than one standard deviation above 0. By the second price point all animals reached relative stability. All succeeding price points were included up to the first 2 unstable points. The 2 unstable price points were included, because it ensured that at least the minimum number of data points required to estimate Pmax, i.e. at least one data point past graphical Pmax, would be included in every data set. An example of truncated data can be seen in Fig. 1.

Fig. 1.

Example of within-session threshold data from a single animal with a response-price relationship that produces 2 valleys, a marked departure from data produced from a multi-session procedure. The data points indicated by arrows were removed before demand curve regressions were calculated by the focused fitting approach. The shaded area represents the data included in the focused analysis. The brain cocaine concentration was calculated and plotted concurrently with response data to highlight the relative stability of brain cocaine concentration included in the focused analysis.

After truncating the data in this manner, demand curves were fit by setting k to the same constant value of 8.85 as was used for the conventional method, and α and Q₀ were manipulated via a custom Excel macro to minimize the residual sum of squares. Hereafter, we will refer to this method as “focused fitting.”

Calculating Pmax

Elasticity of demand is the point slope of the demand equation (Hursh and Winger 1995). Solving for the first derivative of Equation 1 yields Equation 3, which describes the elasticity of the demand curve.

$$\mathit{Elasticity}=-\alpha Q_0{\mathit{Cke}}^{-\alpha Q_{0}C}$$ (3)

After determining the values of α and Q₀ that produce the best-fit demand curve (Equation 1), Pmax³ is the value of C that sets elasticity equal to −1 (Equation 3). Pmax was determined via an automated, iterative process performed by a custom Excel macro, because Equation 3 cannot be solved algebraically.

Statistics

All statistics were performed using SPSS Statistics (Version 19). Pmax and Q₀ data were found to be positively skewed and were logarithmically transformed to obtain a normal distribution. Pearson’s correlation coefficient was used to relate Pmax and Q₀ values. Pearson’s r-values were compared by subjecting the z-scores of transformed Pmax and Q₀ values to a repeated-measures ANOVA. The slopes of the linear regressions were compared via a technique described by Zar (1984). The differences in fit of linear regressions were determined by comparing the absolute values of the residuals for each regression. Bivariate comparisons were conducted with a paired-samples t-test for parametric data and a related-samples Wilcoxon signed rank test for non-parametric data.

Results

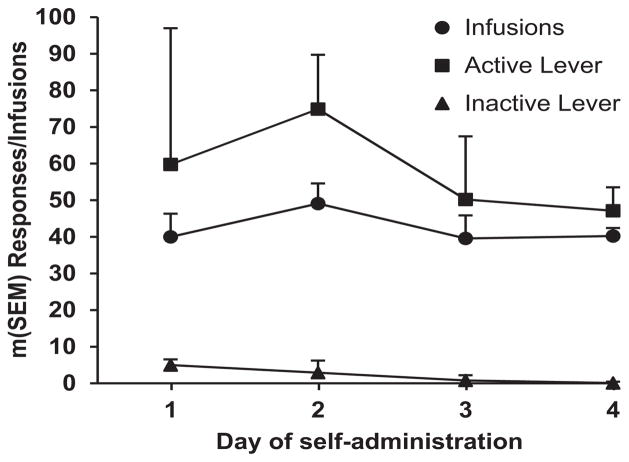
Rats (n = 9) met the FR-1 acquisition criterion after a mean of 8.4 (±0.6) days (±standard error of the mean). The means for the last 2 days of FR-1 cocaine self-administration were 39.6 (±2.2) and 40.2 (±2.3) infusions and 50.2 (±6.4) and 47.1 (±2.7) active lever presses (Fig. 2). Rats were then trained on the within-session threshold procedure for a mean of 4.8 (±0.6) days before the 3 days of threshold testing with data acquisition.

Fig. 2.

Cocaine self-administration under an FR-1 (20-sec timeout) schedule of reinforcement 4 days before training and testing on the within-session threshold procedure (n = 9).

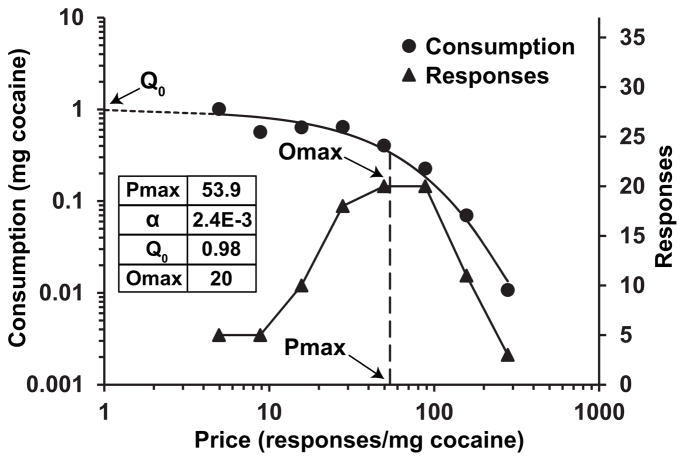
Twenty-seven separate demand curves were fit, employing both the conventional (non-truncated) method and focused fitting. The focused fitting technique truncated data in 19 demand curves, preserving a mean of 2.15 (±0.09) data points past graphical Pmax. Although there is no consensus on what qualifies as an appropriate measure of demand curve fit, we used the criterion of R² ≥ 0.30 in consensus with recent work (Murphy et al. 2009). All demand curves met this criterion with a mean R² of 0.90 (range from 0.62 to 0.98) when demand curves were fit with conventional methods, and an R² of 0.93 (range from 0.82 to 0.98) when demand curves were fit via focused fitting. A representative demand curve with values for calculated parameters can be seen in Fig. 3.

Fig. 3.

Example of within-session threshold data from a single animal. Data points outside of relatively stable brain cocaine concentrations have been removed using the focused-fit procedure, and an exponential demand curve (Equation 1) has been added. Q₀ is the theoretical demand (consumption) at a unit price of 0. Omax is the peak response output and Pmax is the unit price at which Omax occurs. Pmax is calculated from the exponential demand curve that is fit to the consumption data.

The correlation was then determined between graphically derived values of Pmax and Q₀ and values calculated from the best-fit demand curves. This was done to compare the ability of demand curves fit via conventional vs. focused fitting methods to predict values that can be approximated by graphical methods. As stated above, consumption is relatively stable at low prices; thus, consumption at the lowest price points should approximate consumption at null price, Q₀ On the other hand, Pmax can be estimated graphically only to within the resolution of price sampling, i.e. to a pre-determined price point. This is in contrast to the continuous distribution of Pmax values calculated from a demand curve that is fit to the data. Although a strong 1:1 correlation should exist between graphical and calculated parameters, the discordant resolutions of the two methods precludes the possibility of a perfect correlation.

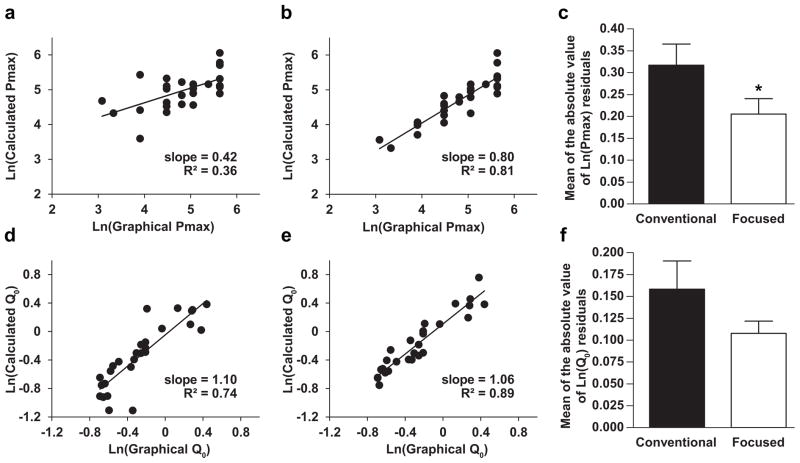
Both methods of demand curve fitting yielded statistically significant correlations between graphical Pmax and calculated Pmax (p < 0.001). Pearson’s r-value was 0.60 when demand curves were fit with conventional methods and 0.90 when demand curves were fit via focused fitting. The difference in Pearson’s r-values was significant (F(1, 25) = 7.26, p < 0.05). A linear regression yielded an R² value of 0.36 with a slope of 0.42 when demand curves were fit with conventional methods (Fig. 4a) and an R² of 0.81 with a slope of 0.80 when demand curves were fit via focused fitting (Fig. 4b). The difference in the slopes of the linear regressions was determined to be statistically significant (p < 0.01); thus, focused fitting produced a slope closer to 1, indicating a more accurate prediction of Pmax. A paired-samples t-test of the absolute values of the normally distributed residuals of each linear regression revealed a statistically significant difference between the conventional and focused methods of demand curve fitting (p < 0.05) (Fig. 4c).

Fig. 4.

Comparison of accuracy of conventional vs. focused demand curve fitting. a. Pmax values obtained from conventionally fit demand curves plotted against Pmax values obtained from graphical analysis. b. Pmax values obtained from focused-fit demand curves plotted against Pmax values obtained from graphical analysis. c. Mean of the absolute values of the residuals for the linear regressions of graphically determined Pmax vs. Pmax calculated from either a conventional or focused-fit demand curve (*p < 0.05). d. Q₀ values obtained from conventionally fit demand curves plotted against Q₀ values obtained from graphical analysis. e. Q₀ values obtained from focused-fit demand curves plotted against Q₀ values obtained from graphical analysis. f. Mean of the absolute values of the residuals for the linear regressions of graphically determined Q₀ vs. Q₀ calculated from either a conventional or focused-fit demand curve. Each circle represents a single operant conditioning session (n = 27) from a single animal (n = 9).

Both methods of demand curve fitting yielded statistically significant correlations between graphical Q₀ and calculated Q₀ (p < 0.001). Pearson’s r-value was 0.86 when demand curves were fit with conventional methods and 0.95 when demand curves were fit via focused fitting. The difference in Pearson’s r-values was not significant (F(1, 25) = 0.477, p = 0.50). A linear regression yielded an R² value of 0.74 with a slope of 1.10 when demand curves were fit with conventional methods (Fig. 4d) and an R² of 0.89 with a slope of 1.06 when demand curves were fit via focused fitting (Fig. 4e). The difference in the slopes of the linear regressions was not statistically significant (p = 0.76). A paired-samples t-test of the absolute values of the normally distributed residuals of each linear regression revealed that there was no statistically significant difference between the conventional and focused methods of demand curve fitting for Q₀ (p = 0.12) (Fig. 4f).

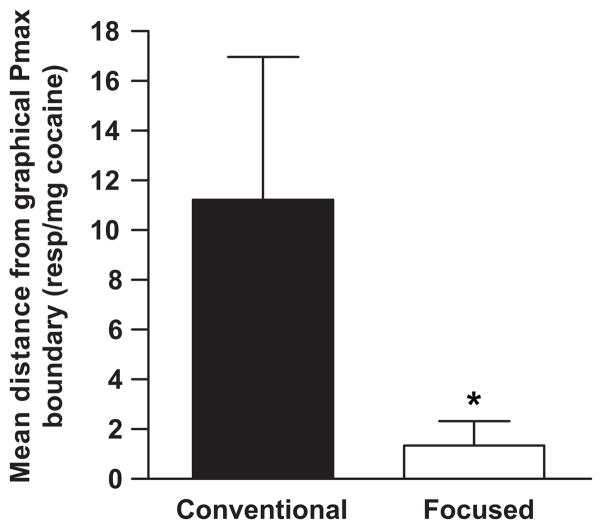
Estimating Pmax values graphically is limited to a resolution of ±1 price points. Hence, a final analysis was carried out that compared the magnitude of the distance of calculated Pmax from a ±1 price point interval centered at the graphical Pmax. The mean distances were 11.23 and 1.35 responses/mg cocaine for Pmax values calculated from conventionally fit and focused fit demand curves, respectively (Fig. 5). These non-parametric distances were compared via a related-samples Wilcoxon signed rank test and were found to be significantly different (p < 0.05).

Fig. 5.

Comparison of accuracy of conventional vs. focused demand curve fitting that takes into account a ±1 price point error in the estimation of graphical Pmax. Distance from Pmax boundary is the magnitude of the distance in units of price of the calculated Pmax to ±1 price point from graphical Pmax; *p < 0.05.

Discussion

The present study indicates that a demand curve analysis of the within-session threshold procedure that focuses on behavior at relatively stable brain drug concentrations yields accurate measures of the elasticity of cocaine demand. In particular, there was a closer correlation and tighter linear fit between graphical Pmax and Pmax calculated from the demand curve when the demand curve was fit with focused fitting than with the conventional method. Considering that Pmax is a measure of elasticity (Hursh and Winger 1995), this indicates that our novel method of focused fitting enables greater accuracy when predicting elasticity. Hence, we conclude that essential value (α) will also be more accurately obtained when focused fitting is used for the within-subjects threshold procedure of cocaine self-administration. However, as α cannot be directly measured from a graphical analysis, we are unable to test predicted values of α against a clear graphical value as we did here for Pmax and Q₀.

The conclusion that the focused fitting technique results in a more accurate prediction of demand curve elasticity rests on the premise that the graphical Pmax represents the true Pmax within the error of ±1 price point. Graphical estimation of Pmax, although imprecise, is highly accurate within the limits imposed on it by the sampling rate of price set by the procedure. This is because the response-price relationship produces a robust inverted U-shaped function across reinforcer types with an easily identifiable apex (Hursh 1991). Graphically estimated Pmax has been used exclusively to describe data from the within-session threshold procedure for cocaine self-administration (España et al. 2010; Oleson et al. 2011; Zimmer et al. 2012), and in cases when calculated and graphical estimations of Pmax have been discordant, the graphical values were taken in place of the calculated values (Lenoir and Ahmed 2008). However, simply defining the Pmax as the price that elicits maximal responding allows for possible aberrantly high response outputs to dictate the estimation of elasticity. That is why in the current analysis response-price relationships were graphed for every session. Visual inspection ensured that the assigned graphical Pmax was flanked by an increasing trend from low price and a decreasing trend to high price. Finally, in several cases the apex of the response-price graph contained adjacent similar values, and in these cases the graphical Pmax was taken at the midpoint price.

In contrast to Pmax, both focused and conventional techniques of demand curve fitting predicted Q₀ with near equal accuracy with a trend towards a better correlation for the focused fitting method. This is not surprising given that focused fitting only alters data that occurs after brain cocaine concentration becomes relatively unstable at high prices. In contrast, the data that predict Q₀ occur at low prices, before Pmax is reached. Thus, the advantage of focused fitting resides in its ability to more accurately describe elasticity.

Eliminating data that falls outside of relatively stable brain cocaine concentration has, in this case, resulted in a more accurate prediction of elasticity than when conventional multi-session approaches are applied to single session data. However, the focused fitting approach resulted in rejecting mostly data points at high prices. Although this fits with an hypothesis of relative brain drug stability, it also fits with an hypothesis that unit price is not equivalent between designs that either 1) employ a static dose of cocaine while increasing the FR schedule or 2) decrease dose on a static FR-1 schedule of reinforcement. Different doses of cocaine may simply carry non-equivalent essential values. For example, for the same unit price different levels of consumption have been reported for i.v. cocaine self-administration in rhesus monkeys depending on whether unit price was varied via FR requirement or via dose (Winger 1993; Woolverton et al. 1997). However, in these examples lower doses of cocaine resulted in lower consumption at equivalent unit prices; whereas, the data here show that inclusion of high price (low dose) data points results in an overestimation of consumption and demand. Furthermore, in animals that had a high Pmax, equivalent data points were used for both conventional and focused methods with neither method failing to produce an accurate measure of Pmax. Hence, it is unlikely that the difference between these methods is due to a decreasing essential value of cocaine with decreasing dose.

With the ability to easily describe elasticity by recording the graphical Pmax, the reader may question the utility in conducting an exponential regression on their data sets. Modeling the data from the within-session threshold procedure produces two distinct advantages over a simple graphical analysis: 1) A more precise measure of Pmax is obtained than allowed by the graphical method. The graphical approach is limited in its resolution of Pmax. This is because, unlike graphical measures of Q₀, graphical measures of Pmax are restricted to discrete price points that are pre-determined in the threshold procedure and vary logarithmically. Consequently, the precision of estimating Pmax graphically is coarse and decreases as the price increases. By calculating the Pmax based on a regression curve, the graphical constraints on possible Pmax values are removed and greater precision in estimating Pmax is obtained. 2) A high-resolution estimate of essential value (α) can also be resolved. Normalized graphical measures of elasticity such as essential value depend on graphical estimates of both Q₀ and Pmax; thus, any error incurred in graphically estimating these parameters will result in multiplicative error in the essential value estimate, making regression analysis the preferred method of estimating essential value.

A possible barrier to adopting focused fitting as a method of demand curve analysis of the within-session threshold procedure for cocaine self-administration may be in the technical challenge of writing custom software to perform the analysis. Several hundred infusions are typically administered during a session, requiring software to calculate brain cocaine concentration as well as the point slope of brain cocaine concentration vs. time. A separate program is then used to determine which price points should be included based on the average slope of the cocaine concentration vs. time curve at that price. Fortuitously, this method resulted in maintaining a mean of 2.15 (±0.09) data points after graphical Pmax; thus, for cocaine threshold procedures with similar parameters this method can be approximated by removing the first data point and truncating all data points that occur 2 price points following the graphical Pmax. Then, focused fitting may easily be applied to other data sets allowing for further experimental validation.

The technique described here for accurately fitting demand curves to data produced by the within-session threshold procedure allows the tools of behavioral-economic demand curve analysis to be applied to neuroeconomics. A particularly appropriate application within neuroeconomics may be in modeling the behavioral correlate of expected value, which could be used to better understand the underlying neural substrates of expected value. Similarly to how the exponential demand equation describes a monotonic relationship between price and demand, monotonic relationships that describe neural firing properties as a function of expected and received reward magnitude have been described in the orbital frontal cortex, striatum, amygdala, and midbrain dopaminergic neurons (Bermudez and Schultz 2010; Cromwell and Schultz 2003; Padoa-Schioppa and Assad 2006; Tobler et al. 2005). By having a mathematical description of self-administration behavior via demand curve analysis, behavioral results can be interfaced with the mathematical functions that underlie the brain substrates of expected value. Such analyses, and integration with other neural modeling efforts, will permit a more extensive and rigorous mathematical examination of neural-behavioral relationships than previously possible.

Conclusion

Normalized measures of demand curve elasticity have proven to be useful in the analysis of both preclinical and clinical drug self-administration. Here we have presented a focused quantitative technique for demand curve fitting that takes into consideration the pharmacological influence of the consumed substance and results in a demand curve fit for within-session cocaine self-administration data in rats with a more accurate prediction of elasticity. Demand curve fitting of the within-session threshold procedure allows for a high-resolution analysis of all the parameters that the field of behavioral economics has to offer within a single 110-minute operant conditioning session. Although the tools of demand curve analysis have largely been limited to the field of psychology, the exponential demand equation can now be applied to discovering the neural substrates that underlie the exponential demand curve model.