Abstract
Interpreting information on diagnostic accuracy is an area that health professionals struggle with. In this paper, we use the example of Mr Samways, a 45-year-old man with joint symptoms, to illustrate how to apply the results of a diagnostic accuracy study in clinical practice. We consider the various measures used to quantify diagnostic accuracy and discuss their clinical utility. We provide an overview of potential biases to consider when evaluating a diagnostic accuracy study and consider how to determine whether the results can be applied to a particular patient.
Introduction
New diagnostic tests may be introduced into clinical practice if they are more accurate, less invasive or painful, cheaper, quicker or easier to perform than existing tests. Before a clinician decides to introduce a new test into clinical practice s/he needs to be sure that it distinguishes patients with and without the target condition with sufficient accuracy, and hence that its use benefits patients.
Methods
In this paper, we use the example of Mr Samways (Box 1), a 45-year-old man with joint symptoms, to illustrate how to apply the results of a diagnostic accuracy study in clinical practice. The article has developed from a chapter on the same topic aimed at undergraduate medical students.2 We consider the various measures used to quantify diagnostic accuracy and discuss their clinical utility. We discuss potential biases to consider when evaluating a diagnostic accuracy study and consider how to determine whether the results can be applied to a particular patient.3–5 To help you to learn more about interpreting the accuracy of diagnostic tests, assess your knowledge and provide us with information about how doctors use diagnostic information, we have developed a web tutorial that accompanies this article, at www.diag-tutorial.co.uk.
Box 1. Example Scenario.
Mr Samways is a 45-year-old man who presents to his general prectitioner (GP) with knee pain and malaise. He recalls swelling of the same knee three years previously that resolved following a corticosteroid injection. On this occasion the knee has been increasingly uncomfortable for three months. There are no other joints involved. He has no significant past medical or family history. He drinks 21 units of alcohol weekly. On physical examination there was a marked right knee effusion, and some tenderness of the metatarsophalangeal joints (MTPJs), proximal interphalangeal joints (PIPJs) and metacarpophalangeal joints (MCPJs). Aspiration of the affected knee joint reveals no evidence of sepsis, nor of a crystal arthropathy. At review, two weeks later, Mr Samways reports stiffness in both shoulders and an effusion at both elbows. He is now significantly disabled by loss of arm function. Examination of his hands and wrists is unremarkable. There is no evidence of a spondylitis.
As his GP, you suspect a possible diagnosis of rheumatoid arthritis (RA) but are not sufficiently confident to make the diagnosis based on his clinical features. You decide to find out whether there are any studies reporting on new diagnostic tests for RA. You search PubMed (http://www.ncbi.nlm.nih.gov/pubmed) using the term ‘rheumatoid arthritis’ combined with PubMed's inbuilt clinical query for diagnosis studies. You identify a study that evaluated the accuracy of anti-cyclic citrullinated peptide (anti-CCP) antibodies for making an early diagnosis of RA1 and are considering ordering this test to help with the diagnosis. However, you need to decide whether you can trust the results of this study, whether they apply to Mr Samways and whether the test will help you reach a diagnosis.
Evaluating test accuracy
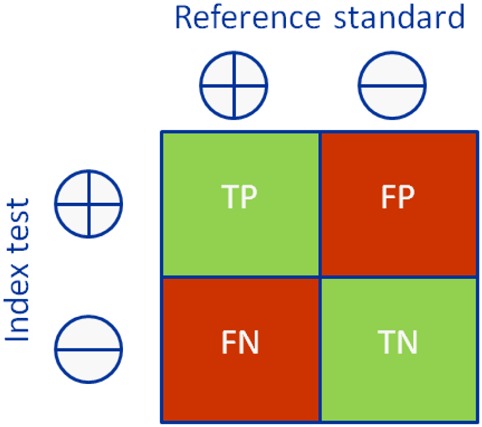
Diagnostic accuracy studies compare the results of a test of interest (‘index test’) to the best available method for determining disease status (‘reference standard’ or ‘gold standard’).6 Consider the example in Box 1 – anti-cyclic citrullinated peptide (CCP) antibodies for the early diagnosis of rheumatoid arthritis (RA). Clinical follow-up is the best available method for the early diagnosis of RA, and so the results of the anti-CCP test (index test) are compared with the American College of Rheumatology (ACR) criteria applied after a period of follow-up (reference standard); the results are cross-tabulated to produce a 2 × 2 table (Box 2). Based on this, estimates of the diagnostic accuracy of anti-CCP can be calculated (Box 2).
Box 2. 2 × 2 tables showing the cross-classification of index test and reference standard results and overview of measures of accuracy that can be calculated from these data.
| General table and formulae | Example: anti-CCP for diagnosing RA | ||
|---|---|---|---|
 |
 |
||
| True positives | People with the target condition who have a positive test result | TP | 82 |
| True negatives | People without the target condition who have a negative test result | TN | 301 |
| False-positives | People without the target condition who have a positive test result | FP | 13 |
| False-negatives | People with the target condition who have a negative test result | FN | 71 |
| Sensitivity | Proportion of patients with the target condition who have a positive test result | TP/(TP + FN) | 82/(82 + 71) = 54% |
| Specificity | Proportion of patients without the target condition who have a negative test result | TN/(FP + TN) | 301/(13 + 301) = 96% |
| Positive predictive value (PPV) | Probability that a patient with a positive test result has the target condition | TP/(TP + FP) | 82/(82 + 13) = 86% |
| Negative predictive value (NPV) | Probability that a patient with a negative test result does not have the target condition | TN/(FN + TN) | 301/(71 + 301) = 81% |
| Prevalence | The proportion of patients in the whole study population who have the target condition | (TP + FN)/(TP + FP + FN + TN) | (82 + 71)/(82 + 13 + 71 + 301) = 33% |
| Positive likelihood ratio (LR+) | The number of times more likely a person with the target condition is to have a positive test result compared with a person without the target condition | (TP/(TP + FN))/(FP/(FP + TN)) or sensitivity/(1 – specificity) | 0.54/(1–0.96) = 13.5 |
| Negative likelihood ratio (LR−) | The number of times more likely a person with the target condition is to have a negative test result compared with a person without the target condition | (FN/(TP + FN))/(TN/(FP + TN)) or (1 – sensitivity)/specificity | (1–0.54)/0.96 = 0.48 |
Sensitivity and specificity

Test sensitivity is the proportion of those with the target condition who have a positive test result, while specificity is the proportion of those without the target condition who have a negative test result. These measures are not directly clinically relevant because they quantify test performance given that the patient does or does not have the condition. The clinical question of most interest is ‘What is the probability that the patient has the target condition given their test result?’ High specificity (few false-positives) implies that if the test is positive we can be confident that the patient has the target condition (we can ‘rule in’ the diagnosis) while high sensitivity (few false-negatives) implies that if the test is negative we can be confident that the patient does not have the condition (‘rule out’ the diagnosis). ‘SpPin’ and ‘SnNout’ are useful acronyms summarizing these principles. However, they should be interpreted with caution as the ability of a test with high sensitivity to rule out a diagnosis is also affected by specificity, and similarly the ability of a test with high specificity to rule in a diagnosis is also affected by sensitivity.7
Example Scenario: From Box 2, specificity is high (96% – the proportion of patients with a false-positive test is only 4%) suggesting that if Mr Samways has a positive anti-CCP test we can be fairly confident in our diagnosis of RA. However, sensitivity is less good (54% – the proportion of false-negative results is 46%) so that if his test is negative we can be less confident about ruling out the diagnosis.
Pretest probability of the target condition
The pretest probability of the target condition can be defined either at the population or the patient level. At the population level it corresponds to the prevalence of the target condition. For a diagnostic cohort study (a study that enrols patients with suspected disease rather than patients whose disease status is known), it can be obtained from the 2 × 2 results table. The pretest probability of the target condition for an individual patient can be estimated based on their clinical history, results of physical examination, and clinical knowledge and experience. This corresponds to the expected prevalence of the condition in a series of similar patients.
Example Scenario: Based on Box 2, we can estimate the prevalence of RA (population-level pretest probability) in the population in which the study was carried out as 33%. However, based on Mr Samways' history and physical examination combined with our clinical knowledge and experience, we estimate that he has a 45% probability of having RA (individual-level pretest probability).
Positive and negative predictive values
The positive predictive value (PPV) is the (post-test) probability that a patient with a positive test result has the target condition, while the negative predictive value (NPV) is the probability that a patient with a negative test result does not have the target condition (Box 2). Predictive values are thus directly clinically relevant. However, they are strongly dependent on the pretest probability, as well as the test's sensitivity and specificity. For example, the prevalence of the target condition is likely to be higher in hospital than general practice settings, and the positive predictive value will be correspondingly higher in hospital settings, even if test sensitivity and specificity are the same. For this reason, the PPV and NPV estimated from a primary diagnostic test accuracy study should not be assumed to apply in other settings, for which the pretest probability of disease may be very different.
For a given pretest probability, it is possible to calculate the post-test probability of disease if data on the sensitivity and specificity of the test are available. A convenient way to do this is via likelihood ratios – this is discussed further below. When evaluating a diagnostic test it can be helpful to think about how the test modifies the probability of the target condition. By considering how the pretest probability is modified to give a post-test probability of the target condition, for either a positive or negative test, we can assess the clinical usefulness of the test.
Example Scenario: Based on the example study, in which the population pretest probability was 33%, the PPV is 86%, so that patients who test positive have an 86% probability of having RA. The negative predictive value is 81%, so that patients who test negative have a 19% probability of having RA (Box 2). This supports the conclusions above, based on test sensitivity and specificity, that anti-CCP is more useful for ruling in than ruling out a diagnosis of RA. In this population, its accuracy may not be sufficient to either confirm or exclude RA. However, because Mr Samways’ pretest probability of having RA is 45% we cannot apply these PPV and NPV estimates directly to him. Positive and negative predictive values based on a pretest probability of 45% are calculated below.
Likelihood ratios
Positive and negative likelihood ratios (Box 2) describe how much more likely a person with the target condition is to have a positive or negative test result than a person without the target condition. A positive likelihood ratio is usually a number greater than 1, while the negative likelihood ratio usually lies between 0 and 1. The further away is the value from 1, the more useful is the test.8 The Supplementary Table S1 summarizes the interpretation of different values of likelihood ratios and shows where the anti-CCP test lies in relation to other well-known diagnostic ‘tests’ (including symptoms elicited during clinical history taking).
Likelihood ratios are more clinically useful than other measures of accuracy because they directly quantify the ability of a test to rule in or rule out the target condition.8 Using Bayes’ theorem, they can be combined with any estimate of the pretest probability to estimate the post-test probability of the target condition. To do this, the pretest probability is transformed into the pretest odds (note that odds = probability/(1 − probability), and that probability = odds/(1 + odds)). This is multiplied by the likelihood ratio to give the post-test odds, which can be transformed into the post-test probability of the target condition. Methods other than hand calculation for obtaining the post-test probability include online calculators (e.g. http://www.dokterrutten.nl/collega/LRcalcul.html) and Fagan's nomogram (Figure 1).9 To use this nomogram, select a pretest probability and likelihood ratio, join these with a straight line and extrapolate the line to the right to read off the post-test probability.
Figure 1.
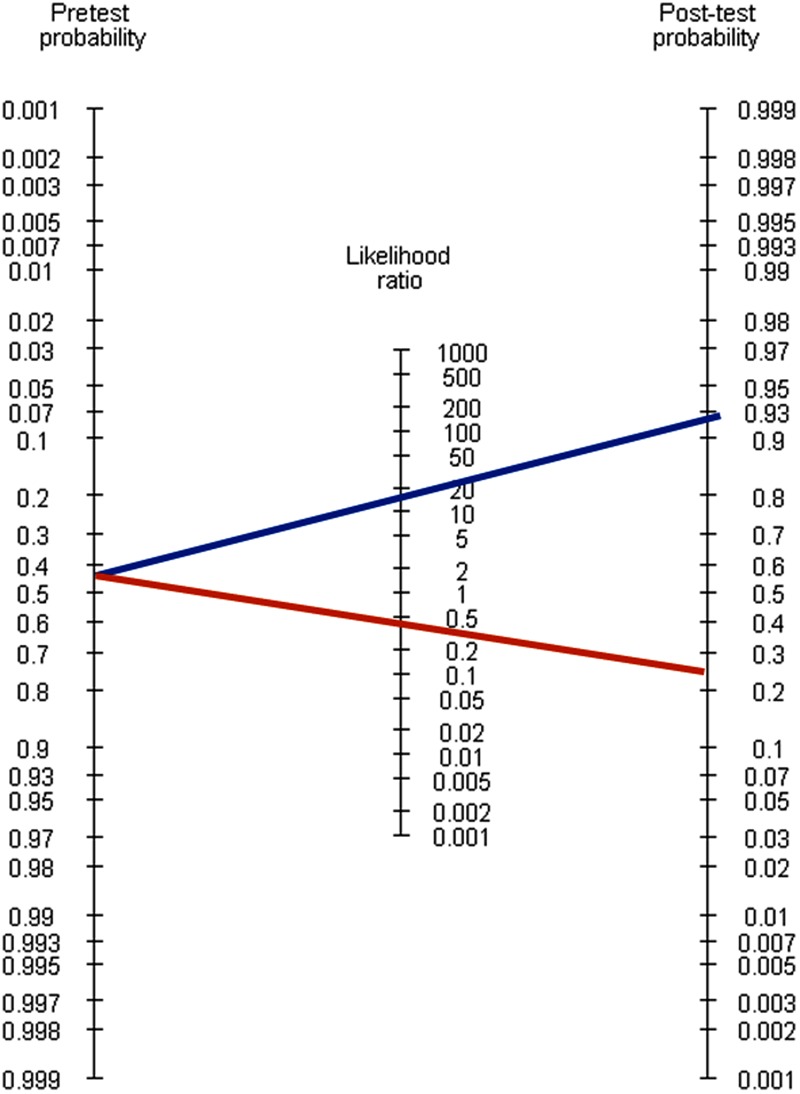
Fagan's nomogram9
Example Scenario: The positive likelihood ratio for anti-CCP is 13.5 and the negative likelihood ratio is 0.48. Thus, a patient with RA is 13.5 times more likely to have a positive test result than a person without RA, and 0.48 times as likely to have a negative test result. Based on Mr Samways’ pretest probability of 45%, his pretest odds are 0.45/0.55 = 0.818, post-test odds (following a positive result) are 11.05, and therefore his post-test probability of RA based on a positive anti-CCP result is 11.05/(1 + 11.05) = 92%. Corresponding calculations show his probability based on a negative test result to be 28%. For a patient such as Mr Samways, a positive anti-CCP result increases his probability of RA from 45% to 92%, so this test would be helpful in reaching a diagnosis. However, a negative test result only decreases his probability of RA from 45% to 28%, which is not sufficient to rule out the diagnosis. Mr Samways’ post-test probabilities differ from the predictive values obtained directly from the 2 × 2 table (PPV 86% and NPV 19%), which highlights that it is important not to rely on positive and negative predictive values estimated from primary studies.
Can I trust the results of a diagnostic study?
If a study is not well designed, estimates of diagnostic accuracy can be biased. Details of how to evaluate the potential for bias in diagnostic accuracy studies are given in Box 3. Such evaluations should be based on consideration of four key areas: patient selection, index test, reference standard and patient flow.4 The importance of different sources of bias is likely to vary according to the particular test, target condition and patient population being studied. This makes it difficult to provide general guidance on when a study should be described as ‘biased’, and the stage at which a study becomes so biased that the results are unlikely to be reliable. Determining whether a study is biased therefore requires some degree of subjective judgement. The areas outlined in Box 3 provide a framework to help in making this judgement.
Box 3. Evaluation of risk of bias in diagnostic accuracy studies.
| General description of source of bias | Potential effects in anti-CCP example |
|---|---|
| Patient selection | |
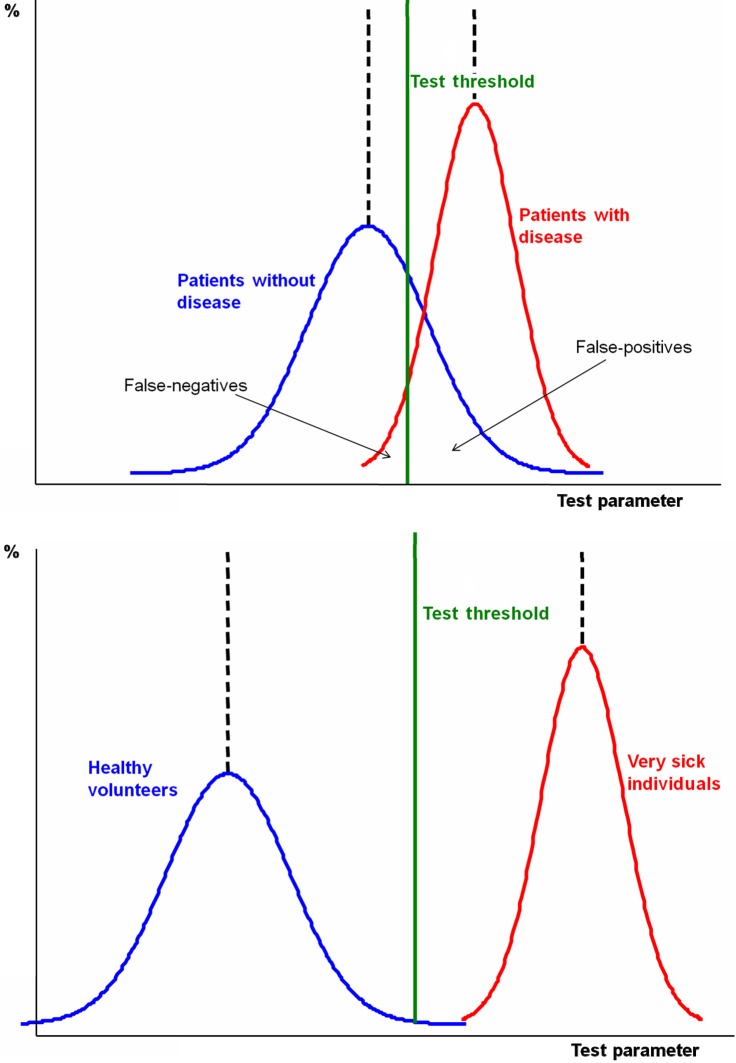
| Consecutive patients, or a random sample of patients, with suspected disease should be enrolled and criteria for enrolment should be clearly stated. Studies that avoid inclusion of ‘difficult to diagnose’ patients or ‘grey cases’ (in whom diagnostic tests are often most useful) may result in overoptimistic estimates of accuracy (‘spectrum bias’) (Supplementary Figure S1). | A study that enrols patients with definite RA and a control group of healthy people without symptoms may produce overoptimistic estimates of sensitivity and specificity that exaggerate the utility of the test in clinical practice. |
| Index test | |
| The results of the index test should be interpreted without knowledge of the results of the reference standard, because knowledge of the reference standard may lead to inflated measures of accuracy (test review bias). The testing sequence and degree of subjectiveness in test interpretation will impact on the potential for bias. | As anti-CCP is a biochemical test the potential for bias is less than had it involved more subjective interpretation (e.g. X-ray). The anti-CCP test result will probably be interpreted without knowledge of whether included patients have RA, because the reference standard (ACR criteria) is applied after a period of follow-up. |
| Reference standard | |
| Estimates of diagnostic accuracy assume that the reference standard is measured without error (100% sensitive and specific). Disagreements between the reference standard and index test are assumed to result from incorrect test results. In practice, a perfect reference standard may not exist. For example, interpretation of a reference standard such as this may be influenced by knowledge of the index test result (diagnostic review bias). A related source of bias is when the reference standard consists of compound criteria that include the index test (incorporation bias). | There is no definite way to make an early diagnosis of RA. The ACR criteria are applied some time after the anti-CCP test and could therefore be influenced by knowledge of test results; an explicit statement that the person interpreting the ACR criteria was blinded to the anti-CCP test results is therefore required. Incorporation bias was avoided as the ACR criteria did not include anti-CCP when the study was conducted. |
| Patient flow | |
| Ideally all patients should undergo both the index test and reference standard within a short time, and all should be included in the analysis or accounted for. There is a potential for bias if the number of patients enrolled differs from the number included in the 2 × 2 table. A potential consequence of withdrawals is verification bias, which occurs when the index test result influences patients’ probability of receiving the reference standard, or receiving a different reference standard. If there is a delay between application of the index test and reference standard, misclassification due to recovery or progression to a more advanced stage of disease may occur (disease progression bias). | As the reference standard is not costly or invasive it is unlikely that the decision to apply it will be influenced by a patient's anti-CCP result. All patients enrolled into the study should be included in the 2 × 2 table, any omissions, should be explained. The reference standard incorporates a period of follow-up, so that a minimum rather than maximum period between index test and reference standard is required. |
CCP, cyclic citrullinated peptide; RA, rheumatoid arthritis; ACR, American College of Rheumatology
Can I apply the results to my patient?
Differences in demographic and clinical features, the index test and the way the target condition is defined cause considerable variations in diagnostic accuracy.3,5,10 Reported estimates of accuracy, even if unbiased, may have limited generalizability if the patients in the study differ from the patient of interest; if the test methods vary (for example, in terms of test technology or how the test was conducted or interpreted), or if the target condition is defined differently. To decide if the results of a diagnostic accuracy study are applicable to Mr Samways in a primary care setting, you should consider whether the study was conducted in general practice, enrolled patients presenting with similar symptoms of a similar duration to Mr Samways, included patients of a similar age and involved patients who had undergone a similar pattern of testing. For the results to be applicable to Mr Samways, the anti-CCP test that you are considering ordering should also match that evaluated in the study. Different generations of anti-CCP test differ biochemically from one another and there are different commercial manufacturers. All have the potential to alter test accuracy. Applicability also depends on how the target condition was defined.10 For example, accuracy of anti-CCP differs according to the stage of disease – sensitivity is higher for the detection of more advanced disease. For the study to be applicable to Mr Samways it should aim to diagnose RA at an early stage: RCT evidence indicates that prognosis is improved with earlier diagnosis.11
DECLARATIONS
Competing interests
None
Funding
This paper was funded by the United Kingdom Medical Research Council (Grant Code G0801405)
Ethical Approval
None required
Guarantor
PW
Contributorship
PW and RMM developed the idea for this paper. PW drafted the manuscript and approved the final version. RMM, YB-S, DG and JACS commented on the manuscript and approved the final version
Acknowledgements
We would like to thank Dr Shane Clarke for developing the clinical scenario used in the example
Appendix
Supplementary Figure S1.
Distribution of test results in patients with and without the target condition. (a) Diagnostic cohort study (unbiased design). (b) Diagnosis case-control study (potentially biased design).
Supplementary Table S1.
Interpretation of likelihood ratios (LRs) with some examples.
| LR | Effect on likelihood of the target condition | Example | Value | |
|---|---|---|---|---|
| Positive likelihood ratio | >10 | Strong increase | CAGE questionnaire, 4 positive responses (alcohol dependency)1 |
25 |
| Positive anti-CCP (RA)2 | 13.5 | |||
| 5–10 | Moderate increase | High probability ventilation-perfusion scan (pulmonary embolus)3 |
7.3 | |
| 2–5 | Small increase | Ultrasound (pancreatic cancer)3 | 4.7 | |
| 1–2 | Minimal increase | Free/total (f/t) prostate-specific antigen (PSA) test >0.25 (prostate cancer)4 |
1.7 | |
| 1 | No change | |||
| Negative likelihood ratio | 0.5–1.0 | Minimal decrease | No loss of urine with coughing/exercise (ruling out stress incontinence)3 |
0.74 |
| 0.2–0.5 | Small decrease | Negative anti-CCP (ruling out RA)2 | 0.48 | |
| <0.2 | Strong decrease | Normal ventilation-perfusion scan (ruling out pulmonary embolus)5 |
0.05 |
References
- 1.Aertgeerts B, Buntinx F, Kester A The value of the CAGE in screening for alcohol abuse and alcohol dependence in general clinical populations: a diagnostic meta-analysis. J Clin Epidemiol 2004;57:30–39 [DOI] [PubMed] [Google Scholar]
- 2.Whiting PF, Smidt N, Sterne JA, et al. Systematic review: accuracy of anti-citrullinated Peptide antibodies for diagnosing rheumatoid arthritis. Ann Intern Med 2010;152:456–464 [DOI] [PubMed] [Google Scholar]
- 3.Black ER, Bordley DR, Tape TG, Panzer RJ Diagnostic strategies for common medical problems. 2nd edn. Philadelphi, Pennsylvania: American College of Physicians, 1999 [Google Scholar]
- 4.Guo X, Xu H, Zhang X, Wang H, Shi J The accuracy of f/t-PSA for diagnosing prostate cancer with a t-PSA level of 4–10 ng/mL: A systematic review and meta-analysis. Chin J Evid Based Med 2010;10:1164–1168 [Google Scholar]
- 5.Roy PM, Colombet I, Durieux P, Chatellier G, Sors H, Meyer G Systematic review and meta-analysis of strategies for the diagnosis of suspected pulmonary embolism. BMJ 2005;331:259. [DOI] [PMC free article] [PubMed] [Google Scholar]
References
- 1.Hyrich KL Patients with suspected rheumatoid arthritis should be referred early to rheumatology. BMJ 2008;336:215–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ben-Shlomo Y, Hickman M, Brookes S, eds. Lecture Notes: Epidemiology, Evidence-based Medicine and Public Health. Oxford: John Wiley & Sons, 2013 [Google Scholar]
- 3.Whiting P, Rutjes AW, Reitsma JB, Glas AS, Bossuyt PM, Kleijnen J Sources of variation and bias in studies of diagnostic accuracy: a systematic review. Ann Intern Med 2004;140:189–202 [DOI] [PubMed] [Google Scholar]
- 4.Whiting PF, Rutjes AW, Westwood ME, et al. QUADAS-2: a revised tool for the quality assessment of diagnostic accuracy studies. Ann Intern Med 2011;155:529–36 [DOI] [PubMed] [Google Scholar]
- 5.Irwig L, Bossuyt P, Glasziou P, Gatsonis C, Lijmer J Designing studies to ensure that estimates of test accuracy are transferable. BMJ 2002;324:669–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sackett DL, Haynes RB The architecture of diagnostic research. BMJ 2002;324:539–41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pewsner D, Battaglia M, Minder C, Marx A, Bucher HC, Egger M Ruling a diagnosis in or out with ‘SpPIn’ and ‘SnNOut’: a note of caution. BMJ 2004;329:209–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Deeks JJ, Altman DG Diagnostic tests 4: likelihood ratios. BMJ 2004;329:168–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fagan TJ Letter: Nomogram for Bayes theorem. N Engl J Med 1975;293:257. [DOI] [PubMed] [Google Scholar]
- 10.Lord SJ, Staub LP, Bossuyt PM, Irwig LM Target practice: choosing target conditions for test accuracy studies that are relevant to clinical practice. BMJ 2011;343:d4684. [DOI] [PubMed] [Google Scholar]
- 11.Whiting PF, Smidt N, Sterne JA, et al. Systematic review: accuracy of anti-citrullinated peptide antibodies for diagnosing rheumatoid arthritis. Ann Intern Med 2010;152:456–64 [DOI] [PubMed] [Google Scholar]