Adjusted Exponentially Tilted Likelihood with Applications to Brain Morphology

Summary

In this paper, we develop a nonparametric method, called adjusted exponentially tilted likelihood, and apply it to the analysis of morphometric measures. The adjusted exponential tilting estimator is shown to have the same first order asymptotic properties as that of the original exponentially tilted likelihood. The adjusted exponentially tilted likelihood ratio statistic is applied to test linear hypotheses of unknown parameters, such as the associations of brain measures (e.g., cortical and subcortical surfaces) with covariates of interest, such as age, gender, and gene. Simulation studies show that the adjusted exponential tilted likelihood ratio statistic performs as well as the t-test when the imaging data are symmetrically distributed, while it is superior when the imaging data have skewed distribution. We demonstrate the application of our new statistical methods to the detection of statistically significant differences in the morphology of the hippocampus between two schizophrenia groups and healthy subjects.

1. Introduction

Anatomical magnetic resonance imaging (MRI) have been widely collected to understand brain structure in various neuroimaging studies. For instance, various measures of the morphology of the cortical and subcortical structures (e.g., hippocampus) are extracted from anatomical MRI for understanding neuroanatomical differences in brain structure across subjects. Nowadays, studies of brain morphology have been conducted widely to characterize differences in brain structure across groups of healthy individuals and persons with various diseases, and across time (Thompson and Toga, 2002; Thompson et al., 2002; Chung et al., 2005; Styner et al., 2005; Zhu et al., 2007).

The statistical analysis of morphometric measures usually involves two procedures executed in sequence. The first procedure includes fitting a general linear model to the data from all subjects at each voxel, and then producing a map of some statistic (for instance, a p—value) calculated at each voxel (Worsley et al., 2004; Friston, 2007). However, the general linear models are often fitted under the assumption that the variance of the imaging data is homogeneous across subjects at each voxel, and that the data conform to a Gaussian distribution at each voxel. The second procedure identifies regions where the statistic significantly deviates from its nominal value under some null hypothesis, by methods range from random field theory, false discovery rate, and permutation method, to account for the effect of multiple hypothesis testing (Benjamini and Hochberg, 1995; Nichols and Holmes, 2002; Nichols and Hayasaka, 2003; Genoveses et al., 2002; Logan and Rowe, 2004; Worsley, 1994; Worsley et al., 2004).

This paper develops and applies new statistical methods for the analysis of morphometric measures that are free from Gaussian assumptions. Specifically, we develop a new nonparametric method, called adjusted exponentially tilted (ET) likelihood, along with a nonparametric likelihood ratio test for hypotheses of parameters in the functional form of β = β (F), where F is the unknown distribution function in general, or the distribution of morphometric measures in particular. Assuming only a set of estimating equations, the adjusted ET likelihood hence works on a nonparametric extension of general linear model. This extension is particularly desirable for the analysis of brain morphometry, because the distribution of the morphometric measures often deviates from the Gaussian distribution (Ashburner, 2001; Salmond et al., 2002; Luo and Nichols, 2003; Zhu et al., 2007; Viviani et al., 2007; Lepore et al., 2008). Moreover, the adjusted exponential tilting estimator, β̃_aET, and its associated estimator of the distribution function F are asymptotically efficient (Qin and Lawless, 1994). Furthermore, because the adjusted ET likelihood ratio statistic is well approximated by a χ² distribution, it is easy to calculate p-values across all voxels, and hence the overall p-values taking into account of the multiple comparisons using random field theory and the notion of false discovery rate (Worsley et al., 2004; Benjamini and Hochberg, 1995).

To motivate the proposed methodology, we consider a neuroimaging data set from 123 haloperidol-treated schizophrenia patients, 115 olanzapine-treated schizophrenia patients, and 56 healthy controls (Lieberman et al., 2005). We built medial shape description of the left and right hippocampi from all subjects (Fig. 1a). Here, it is of interest to investigate whether the shape of the left and right hippocampus structures differs in two schizophrenia groups and healthy controls. We fitted a general linear model, in which the logarithm of the m-rep thickness (or radius) measure for each medial atom of the left and right hippocampi is response and gender, diagnostic status, and race are included as covariates, and computed the Shapiro-Wilk and Cook-Weisberg test statistics based on the residuals. As shown in Figure 2, the Shapiro-Wilk test rejected the normality assumption at many atoms of the both left and right hippocampus structures, whereas the Cook-Weisberg (CW) test did not reject the constant variance assumption. Consequently, applying a non-parametric method for the analysis of this data set is a good choice. More details regarding this example are given in Section 3.2. To further illustrate the methodology, we also examine the proposed methods using simulated data.

Figure 1.

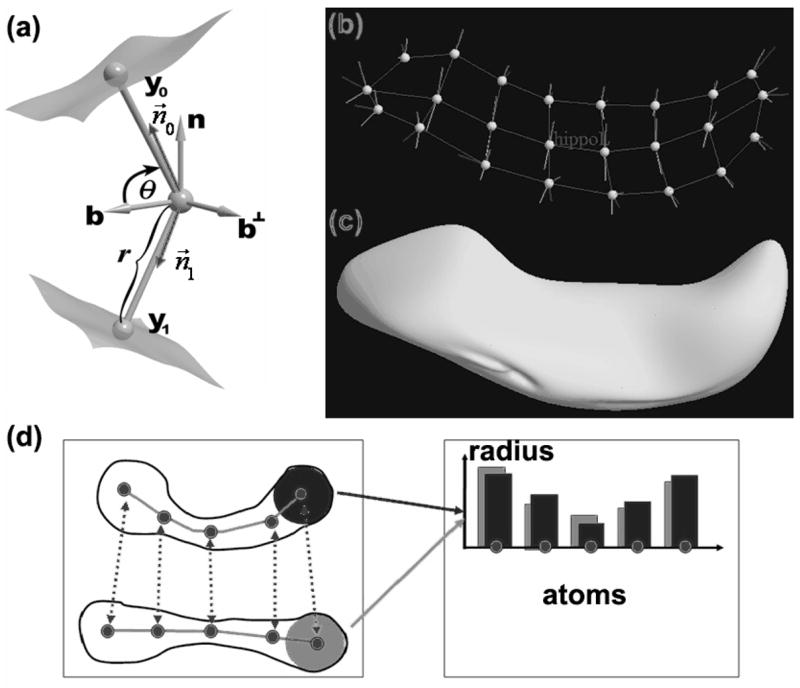
An rn-rep model of a hippocampus: (a) a medial atom with a cross-section of the boundary surface it implies; (b) an m-rep model of the hippocampus; (c) the boundary surface of the m-rep model of hippocampus; (d) m-rep radius (or thickness) measures at the five atoms from two m-rep objects.

Figure 2.

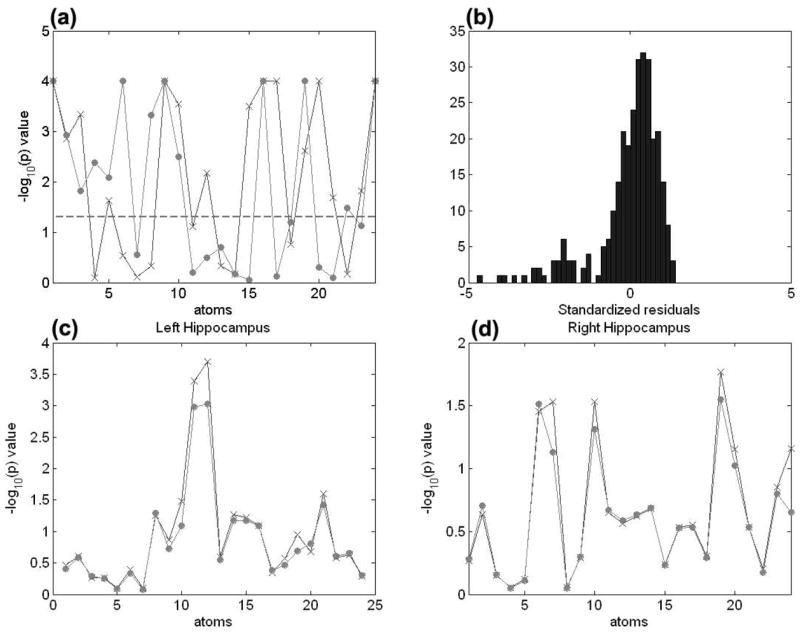
Results from the analyses of the m-rep models of the Hippocampus structures. Panel (a) shows the uncorrected −log₁₀(p)-value for the Shapiro-Wilk test of normality at each atom of the m-rep models for the left hippocampus (circle) and right hippocampus (‘x’). Panel (b) shows the histogram of the standardized residuals obtained from general linear model based on data at the first atom of the left hippocampus. Panels (c) & (d) show the uncorrected −log₁₀(p) values (LR_aET: ‘x’; the F test: circle) of group effect on the left and right hippocampi. Using LR_aET increases the − log₁₀ (p) values for these significant atoms of the hippocampus in each hemisphere.

The rest of this paper is organized as follows. In Section 2, we introduce moment model for the analysis of brain morphometry and develop the adjusted ET likelihood and associated ET likelihood ratio statistic for testing linear hypotheses of unknown parameters. In Sections 3, we examine the adjusted ET likelihood ratio statistic using simulated data and a hippocampus data set from the neuroimaging study of Schizophrenia. We conclude the paper with some discussion in Section 4.

2. Methods

We introduce the estimating functions or equations suitable for the analysis of brain morphometry. Then, we develop the adjusted ET likelihood and associated ET likelihood ratio statistic for testing linear hypotheses of unknown parameters.

2.1 The Moment Model

Consider a cross-sectional study with n subjects, in which an imaging data set consists of morphometric measures ${\mathbf{y}}_i=\{y_i(d):d\in \mathcal{D}\}$, over a specific brain region $\mathcal{D}$ with d being a voxel, and a c₀ × 1 vector of clinical outcomes, x_i. The morphometric measures of different subjects are assumed independent, whereas the morphometric measures at different voxels but of the same subject are correlated. The morphometric measure y_i(d) at each voxel d can be either univariate or multivariate. For instance, gray matter density and signed Euclidean distance of cortical/subcortical surfaces are univariate measures, whereas the spherical harmonic shape description (SPHARM) of subcortical surfaces is a three dimensional MRI measures (Thompson and Toga, 2002; Thompson et al., 2002; Chung et al., 2005; Chung et al., 2007; Styner et al., 2005; Styner and Gerig, 2003; Zhu et al., 2007). Clinical data may include demographic characteristics (e.g., age, gender, weight and height), diagnostic status, and depression measures, among many others. For notational simplicity, we assume that y_i(d) are univariate MRI measures.

We temporarily drop voxel d from our notation. At a specific voxel d, we postulate a model for z_i = (x_i,y_i) via the following moment conditions

$$E_F\{g({\mathbf{z}}_i;\beta )\}=E_F\{{\mathbf{x}}_i(y_i-{\mathbf{x}}_i^T\beta )\}=0,\text{ for }i=1,\cdots ,n,$$ (1)

where β is a C0 × 1 vector and E_F denotes the expectation with respect to the common distribution of (x_i,y_i), F. We call g(z; β) an estimating function, and we do not place any parametric assumptions on F. However, the standard linear regression model (LRM) assumes that

$$y_i={\mathbf{x}}_i^T\beta +{\epsilon }_i\text{ for }i=1,\cdots ,n,$$ (2)

and that ε_i has Gaussian distribution N(0,σ²). Model (2) is a special case of (1), because ${\mathbf{x}}_i(y_i-{\mathbf{x}}_i^T\beta )$ is associated with the score function of model (2). Parametric inference based on (2) often heavily depends on the Gaussian distribution assumption. Our nonparametric model (1) is also referred as an estimating equation model or a moment model (Qin and Lawless, 1994; Owen, 2001).

2.2 Adjusted ET Likelihood and the Likelihood Ratio Test

Exponentially tilted likelihood is a powerful tool to carry out non-parametric statistical inferences (Owen, 2001; Qin and Lawless, 1994; Kitamura and Stutzer, 1997; Imbens et al., 1998). For i = 1,…,n, let p_i = dF(z_i) = Pr(Z_i = _Zi). The ET likelihood can be characterized as the Kullback-Leibler distance between the empirical frequencies 1/n and p_i subjected to some constraints on p_i. More specifically, the ET estimator β̃_ET is the solution to the Kullback-Leibler information criterion:

$$\underset{p_1,\cdots ,p_n,\beta }{inf}\sum _{i=1}^n{p}_{i}log{p}_i$$ (3)

subject to ${\sum }_{i=1}^n{p}_i=1,p_i\ge 0$ and ${\sum }_{i=1}^n{p}_{i}g({\mathbf{z}}_i;\beta )=\mathbf{0}$. Clearly, a solution β̃_ET exists only if the convex hull of {g(z_i, β), i = 1, …, n} contains vector 0 as an interior point. According to a duality theorem in the convex analysis (Imbens et al., 1998; Kitamura and Stutzer, 1997; Newey and Smith, 2004), β̃_ET is also the solution to the saddle point problem

$${\stackrel{\sim }{\beta }}_{\text{ET}}={argmax}_{\beta }\underset{\lambda }{inf}{\ell }_{ET}(\lambda ,\beta ),$$ (4)

where λ is a C0 × 1 vector Lagrange multiplier and ${\ell }_{ET}(\lambda ,\beta )=log[{\sum }_{i=1}^{n}exp\{{\lambda }^{T}g({\mathbf{z}}_i;\beta )\}]$. Denote the saddle point as (β̃_ET, λ̃_ET). We further obtain, for i = 1, …, n,

$${\widehat{p}}_{et,i}=\frac{exp\{{\stackrel{\sim }{\lambda }}_{ET}^{T}g({\mathbf{z}}_i;{\stackrel{\sim }{\beta }}_{ET})\}}{{\sum }_{j=1}^{n}exp\{{\stackrel{\sim }{\lambda }}_{ET}^{T}g({\mathbf{z}}_j;{\stackrel{\sim }{\beta }}_{ET})\}}.$$ (5)

Moreover, F can be estimated by ${\stackrel{\sim }{F}}_{et}(\mathbf{z})={\sum }_{i=1}^n{\stackrel{\sim }{p}}_{et,i}\mathbf{1}({\mathbf{z}}_i<\mathbf{z})$, where 1(·) is an indicator function.

Next, we consider testing the linear hypotheses:

$$H_0:R\beta =b_0\text{ vs}\text{. }{H}_1:R\beta \ne b_0,$$ (6)

where R is a r × c₀ matrix with full row rank and b₀ is a, r × 1 specified vector. Most scientific questions in imaging studies can be formulated into linear hypotheses, such as a comparison of brain region across diagnostic groups and a detection of changes in brain region across time. An ET likelihood ratio test can be constructed as follows:

$$L{R}_{ET}=-2n\{\underset{\beta :R\beta =b_0}{sup}\underset{\lambda }{inf}{\ell }_{ET}(\lambda ,\beta )-\underset{\beta }{sup}\underset{\lambda }{inf}{\ell }_{ET}(\lambda ,\beta )\}.$$ (7)

Under the null hypothesis H₀, LR_ET has a limiting chi-squared distribution with r degrees of freedom (Kitamura and Stutzer, 1997; Imbens et al., 1998). However, if the alternative hypothesis is true, E{g(z;β)} = 0 may not have any solution in β such that Rβ = b₀-Consequently, the convex hull of {g(z_i, β) : i = 1, …,n} may not contain vector 0 as an interior point for any β satisfying Rβ = b₀, and it further implies that the saddle point β̃_ET,0 under the constraint Rβ = b₀ does not exist.

A convention method for solving the solution problem is to set LR_ET = +∞ or a 0 p-value whenever a saddle point does not exist. The 0 p—value apparently does not imply there is an overwhelm evidence to reject the null hypothesis at the voxel under investigation. When two voxels have the same 0 p—value, we lack quantitative judgement on at which voxel the MRI signals deviate from the null model more significantly. Moreover, locating the significant regions where the null hypothesis is doubtful is precisely the goal of the image data analysis. A new technique is clearly needed.

2.3 Adjusted Exponential Tilting Likelihood

We introduce an adjustment to ET likelihood as follows. Let

$$g_{n+1}(\beta )=g({\mathbf{z}}_{n+1};\beta )=-\frac{a_n}{n}\sum _{i=1}^{n}g({\mathbf{z}}_i;\beta ),$$ (8)

where a_n = max{1, log(n)/2}, and z_n+1 is introduced purely for notational simplicity. We calculate β̃_aET by minimizing ${\sum }_{i=1}^{n+1}{p}_{i}log{p}_i$ subject to

$$\sum _{i=1}^{n+1}{p}_i=1,p_i\ge 0,\text{ and }\sum _{i=1}^{n+1}{p}_i{g}_{n+1}({\mathbf{z}}_i;\beta )=0.$$ (9)

Using the duality theorem leads to that

$${\stackrel{\sim }{\beta }}_{\mathit{aET}}={argmax}_{\beta }\underset{\lambda }{inf}\{{\ell }_{\mathit{aET}}(\lambda ,\beta )\},$$ (10)

where ℓ_aET (λ, β) is given by

$$log[\sum _{i=1}^{n+1}exp\{{\lambda }^{T}g({\mathbf{z}}_i,\beta )\}]-log(n+1).$$ (11)

Similarly, we can calculate β̃_aET,0 under the null hypothesis Rβ = b₀. It is particularly important to emphasize here that the convex hull of {g(z_i, β),i = l, …,n+ 1} always contains 0 as an interior point, for any β value. Therefore, the ET likelihood is well defined for all β. The algorithm for computing β̃_aET,0 and β̃_aET can be found in the Web Appendix A. The adjusted ET likelihood ratio statistic for testing Rβ = b₀ becomes:

$$L{R}_{\mathit{aET}}=-2(n+1)\{\underset{\beta :R\beta =b_0}{sup}\underset{\lambda }{inf}{\ell }_{\mathit{aET}}(\lambda ,\beta )-\underset{\beta }{sup}\underset{\lambda }{inf}{\ell }_{\mathit{aET}}(\lambda ,\beta )\}.$$ (12)

The adjusted ET likelihood has many additional advantages that are particularly important to the imaging analysis. The adjusted ET likelihood completely eliminates the solution problem as discussed in Section 2.2. Compared to the empirical likelihood (EL) (Owen, 2001), the adjusted ET is robust against model mis-specification because no model can be exact at all voxels (Imbens et al., 1998; Kitamura and Stutzer, 1997; Schennach, 2007). The adjusted ET is also computationally more efficient at each voxel, which number in the thousands to hundreds of thousands in each imaging data set, because the adjusted ET avoids imposing inequality constraints λ^Tg(z_i, β) > 0 for all i and β.

2.4 Extension and Theoretical Justification

Our adjusted ET likelihood can be applied to various models. For instance, a nonlinear regression between y and x can be specified by g(z; β) = ∂_βμ(x; β){y−μ (x; β)}, where μ (x; β) is the conditional mean of y given x, and ∂_β denotes the first order differentiation with respect to β. Other examples of g(z;β) can be found in Qin and Lawless (1994), Owen (2001), and among many others. Then, we can define g_n+1(β). Similar to the developments from (9)–(12), we can define β̃_aET and LR_aET for the estimating functions g(z_i,β) and g_n+1(β).

Under some conditions on g(z_i, β), we have the following results, whose detailed proofs can be found in the Web Appendix B.

Theorem 1

We assume that following conditions: (a) The parameter space of β, $\mathcal{B}$ is compact; (b) β₀, an interior point of $\mathcal{B}$, is the unique solution to E{g(z,β)} = 0; (c) g(β) = g(z,β) is continuous at each $\beta \in \mathcal{B}$ with probability one; (d) $E\{{sup}_{\beta \in \mathcal{B}}\parallel g(\mathbf{z},\beta ){\parallel }^{\alpha }\}<\infty$ for some α > 2; (e) Ω = E{g_i(β₀)g_i(β₀)^T} is finite and nonsingular. Then, we have

1. $\sqrt{n}({\stackrel{\sim }{\beta }}_{\mathit{aET}}-{\beta }_0)$ converges to N(0,V) in distribution, where V = (D^TΩ^−lD}⁻¹, where D = E_F{∂_βg(z, β₀)};

2. under the null hypothesis, LR_aET converges to a χ²(r) distribution in distribution.

Theoretically, we have established the consistency and asymptotical normality of β̃_aET and the asymptotic χ² distribution of LR_aET. Thus, these asymptotic properties based on the adjusted ET likelihood are the same as those based on the ET likelihood (Kitamura and Stutzer, 1997; Imbens et al., 1998). It will be shown in Section 3 that the chisquare approximation of the adjusted ET or EL likelihood ratio statistics is found precise, resulting in more reliable p-values over the the entire regions of voxels. The improvement is the greatest when the sample size is small to moderate, where the traditional ET and EL are known to have poor approximating precisions (Tsao, 2004; Owen, 2001; Chen and Cui, 2006). Providing a reliable p-value at each voxel is crucial for controlling family-wise error rate and false discovery rate (FDR) across the entire brain region (Benjamini and Hochberg, 1995; Worsley et al., 2004).

3. Simulations and Real-World Example

3.1 Simulation Studies

We conducted two sets of Monte Carlo simulations to examine the finite performance of LR_aET at the single-voxel level. In particular, we compared LR_aET with the gold standard t-test and the adjusted empirical likelihood ratio statistic, denoted by LR_aEL (Chen et al., 2008). The first simulated data are from

$$y_i=\beta +{\epsilon }_i,$$ (13)

for i = 1, …, n, where ε_i was a random error with zero mean. We set n = 20, 40, and 60, and β = 0. We calculated the rejection rates of the null hypothesis H₀ : β = 0 to assess the Type I error of LR_aET, LR_aEL and the t-test. Furthermore, we simulated data from (13) with incremental β values from 0.1 to 1.0 to study the power of these three tests. In both cases, R = (1) and b₀ = (0). For each set of simulations, the significance levels were set at α = 5%, and 10,000 replications were used to estimate the rejection rates. Additional simulation results can be found in the Web Appendix C. For a fixed α, if the Type I rejection rate is smaller than a, then the test is conservative, whereas if the Type I rejection rate is greater than α, then the test is anticonservative, or liberal.

We considered four error distributions and examined their effects on the finite sample performance of LR_aET, LR_aEL and the t-test. First, ε_i, were generated from N (0,1). The Gaussian errors with homogeneous variance were commonly assumed for general linear model. Second, we assumed ε_i, = χ²(3) − 3, in which χ²(3) represented a chi-squared random variable with 3 degrees of freedom. The skewed distribution %²(3) — 3 differs substantially from any Gaussian distribution. Third, ε_i were generated from a t(3) distribution, which represented a distribution with heavy tail. Fourth, we assumed that ε_i, came from a mixture of normal distributions, 0.5N(2,1) + 0.5N(−2, 1).

For model (13), the Type I errors rates of LR_aET, LR_aEL, and the t-test were found accurate for all sample sizes (n = 20, 40, or 60) considered and for all different distributions of error terms at the 5% significant levels (Table 1). We observed that Type II error rates for the three test statistics were similar under symmetric errors and for all sample sizes (Table 1). However, the power of LR_aET and LR_aEL to reject the null hypothesis increased modestly when the distribution of error terms followed skewed distribution χ²(3) – 3 (Table 1). This decline in Type II error was caused by the fact that the distribution of the t-test was not in fact t-distributed.

Table 1.

Comparison of the rejection rates (×10⁻²) of the null hypothesis H₀: β = 0 for the t test, the adjusted ET likelihood ratio test and the adjusted EL likelihood ratio test at the 0.05 significance level. Four error distributions are N(0,1), χ²(3) − 3, 0.5N(2,1) + 0.5N(−2,1), and t(3). Four different β and 10,000 simulated data sets were used.

		N(0,1)			χ2(3) −3
Methods	β	n=20	n=40	n=60	n=20	n=40	n=60
t	0.0	5.01	5.01	5.32	7.34	6.07	5.77
LRaET	0.0	4.51	4.57	4.77	5.09	5.22	5.04
LRaEL	0.0	4.68	4.54	4.75	6.20	5.40	4.97
t	0.5	56.30	86.93	97.20	8.28	19.50	29.48
LRaET	0.5	53.60	85.77	96.61	9.60	22.18	34.78
LRaEL	0.5	54.41	85.56	96.48	12.58	26.60	38.62
t	0.8	92.09	99.88	100	21.47	53.30	74.20
LRaET	0.8	90.97	99.79	100	24.87	58.03	78.79
LRaEL	0.8	91.14	99.84	100	32.38	62.96	81.22
t	1.0	98.80	100	100	37.35	77.65	92.93
LRaET	1.0	98.50	100	100	42.69	81.58	94.67
LRaEL	1.0	98.54	100	100	50.60	84.14	95.86
		0.5N(2, 1) + 0.5N(− 2, 1)			t(3)
Methods	β	n=20	n=40	n=60	n=20	n=40	n=60
t	0.0	5.07	4.88	4.72	3.91	4.36	4.71
LRaET	0.0	4.37	4.18	4.20	4.71	5.08	5.31
LRaEL	0.0	3.89	4.12	4.10	6.03	5.92	5.85
t	0.5	15.10	27.55	38.76	32.26	52.74	67.59
LRaET	0.5	13.66	26.51	38.88	34.71	51.54	66.23
LRaEL	0.5	12.44	26.10	37.92	33.50	50.05	62.78
t	0.8	30.86	59.19	78.08	62.59	85.28	94.22
LRaET	0.8	30.25	59.49	77.16	61.33	83.48	92.26
LRaEL	0.8	30.58	59.45	78.20	61.14	80.46	90.46
t	1.0	45.52	79.05	93.16	78.10	93.85	97.94
LRaET	1.0	45.34	78.23	93.03	76.18	92.80	97.26
LRaEL	1.0	46.36	79.16	93.02	73.04	90.22	95.92

The second set of simulations generated data from

$$y_i={\mathbf{x}}_i^T\beta +{\epsilon }_i$$ (14)

for i = 1,…n, where ε_i was a random error with zero mean and β = (β₁, β₂, β₃)^T is a 3 × 1 unknown parameter vector. The x_i = (1, x_i2, x_i3)^T was a 3 × 1 vector of covariates. We generated x_i2 independently from a Bernoulli distribution with the probability of success parameter being 0.5, and generated x_i3 independently from the uniform distribution in [0, 1]. The x_i2 and x_i3 were chosen to represent group identity and standardized age, respectively. We set n = 20, 40, and 60.

We first assumed β = (0, 0, 0)^T and set the null hypothesis H₀ : β = 0 to assess the Type I error rates of LR_aET, LR_aEL and the t test. Second, the simulations were done with incremental β₂ values from 0.1 to 1.0, and then we examined the Type II errors of LR_aET, LRa_EL and the t test. In both cases, R = (0, 1, 0) and b₀ = (0).

We considered the effects of six different error distributions and examined their effects on the finite performance of LR_aET, LR_aEL and the t-test at the single-voxel level. The first four distributions of ε_i were the same as those for the first set of simulations. Fifth, we assumed that ε_i = σ(i)z, σ(i) = exp(u) for x_i2 = 0 and σ (i) = exp(u + 1) for x_i2 = 1, where z and u were independently generated from a N(0,1) distribution. Given u, the variances of ε_i were highly heterogeneous (Zhu et al., 2007). Sixth, we assumed that ε_i = 2z for x_i2 = 1 and z otherwise, in which z were independently generated from a N(0,1) distribution. We tried to mimic that the two groups may have different variances.

For model (14), except that LR_aET and LR_aEL had slightly inflated Type I error under Gaussian distribution with severe heterogeneous variances, the Type I errors rates for the three test statistics were accurate for all sample sizes (n = 20, 40, or 60) considered and for almost all different distributions of error terms at the 5% significant level (Table 2). The type II error rates of the three test statistics were similar under symmetric errors and for all sample sizes. However, for skewed distribution χ²(3) – 3 and Gaussian distribution with severe variance heterogeneity, the power of LR_aET and LR_aEL to reject the null hypothesis increased modestly. Consistent with our expectations, the statistical power for rejecting the null hypothesis increased with the sample size n.

Table 2.

Comparison of the rejection rates (×10⁻²) of the null hypothesis H₀: β₂ = 0 for the t test, the adjusted ET likelihood ratio test and the adjusted EL likelihood ratio test at the 0.05 significance level. Six error distributions are N(0,1), χ²(3) − 3, heter1, heter2, 0.5N(2,1) + 0.5N(−2,1), and t(3). Moreover, heter1 and heter2 denote Gaussian distributions with heterogeneous variance σ(i). For heter1, σ (i) = exp(u) when x_i2 = 0 and σ(i) = exp(u + 1) when x_i2 = 1, where u ~ N(0,1); however, for heter2, σ(i) = 1 for x_i2 = 0 and σ(i) = 4 for x_i2 = 1. Four different (β and 10,000 simulated data sets were used.

		N(0, 1)			χ2(3)−3			0.5N(2, 1) + 0.5AT(−2, 1)
Methods	β	n=20	n=40	n=60	n=20	n=40	n=60	n=20	n=40	n=60
t	0.0	5.12	5.22	4.67	4.72	5.32	5.12	4.86	5.18	5.20
LRaET	0.0	5.65	4.63	4.85	6.63	6.02	5.52	5.93	4.93	5.15
LRaEL	0.0	7.00	5.62	5.43	8.87	6.55	5.74	6.70	5.00	4.28
t	0.5	17.41	32.32	46.58	7.25	10.12	11.37	7.14	10.56	12.77
LRaET	0.5	19.74	34.78	48.27	8.40	11.41	13.15	7.81	9.74	13.19
LRaEL	0.5	20.55	33.44	46.99	11.96	12.48	14.16	8.50	11.22	12.66
t	0.8	35.70	66.69	84.95	10.33	17.06	24.65	10.01	17.53	25.70
LRaET	0.8	39.10	69.25	84.15	13.42	19.37	25.16	12.14	19.04	27.02
LRaEL	0.8	40.94	68.97	84.11	16.85	21.34	25.32	12.88	18.68	26.88
t	1.0	50.83	85.41	96.33	14.28	25.47	35.11	12.98	26.27	38.44
LRaET	1.0	53.38	84.87	97.03	16.60	26.75	36.92	15.31	25.03	40.34
LRaEL	1.0	57.74	86.45	95.92	20.19	26.62	35.53	16.23	26.12	39.23
		t(3)			heter1			heter2
Methods	β	n=20	n=40	n=60	n=20	n=40	n=60	n=20	n=40	n=60
t	0.0	4.16	4.40	4.58	3.60	3.93	4.67	5.43	4.88	5.40
LRaET	0.0	5.63	5.68	5.50	7.80	7.46	7.19	5.45	4.97	5.33
LRaEL	0.0	8.17	6.70	5.93	11.82	9.62	9.36	7.00	6.00	5.26
t	0.5	10.71	17.71	22.64	6.11	6.23	7.05	10.51	16.40	22.13
LRaET	0.5	14.44	19.48	25.40	9.24	10.38	9.96	12.03	16.78	24.29
LRaEL	0.5	16.32	20.54	25.36	13.22	12.76	11.50	14.46	16.82	22.08
t	0.8	20.09	36.00	48.65	8.15	9.26	11.78	17.91	33.08	46.74
LRaET	0.8	24.68	37.85	51.60	11.82	13.70	16.04	20.59	34.72	48.03
LRaEL	0.8	27.29	37.95	48.27	15.90	15.84	16.08	21.81	33.02	47.33
t	1.0	29.10	50.31	64.80	9.46	12.46	15.04	25.48	47.51	65.86
LRaET	1.0	31.72	52.02	66.59	14.54	17.20	19.24	25.53	48.42	66.10
LRaEL	1.0	36.69	52.05	64.57	18.36	18.24	19.88	31.32	48.17	64.79

3.2 Analysis of Hippocampus Morphometric Measures

We investigate the shape of the left and right hippocampus structures in two schizophrenia groups and healthy controls while controlling other factors including gender, race and age.

We analyzed a neuroimaging data set from schizophrenia (SC) patients and healthy controls, collected at 14 academic medical centers in North America and western Europe, with partial funding from Lilly Research Laboratories (Lieberman et al., 2005). In this study, we included 294 subjects (123 haloperidol SC, 115 olanzapine SC, 56 healthy controls; mean [SD] age, halopepridol SC, 24.13 [4.89] years; olanzapine SC, 23.56 [4.63] years; healthy control, 25.28 [3.97] years). The SC groups contained fewer females (halopepridol SC, 17.23%; olanzapine SC, 22.61%; healthy control, 33.93%; p=0.043). The data set had more Caucasian (CA) and African American (AA) subjects ((CA, AA, others) halopepridol SC, (48, 65, 10); olanzapine SC, (45, 57, 13); healthy control, (15, 34, 7)). All schizophrenia patients enrolled in the study, met the following criteria: age 16 to 40 years; onset of psychiatric symptoms before age 35; diagnosis of schizophrenia, schizophreniform, or schizoaffective disorder according to DSM-IV criteria; and various treatment and substance dependence conditions. Neurocognitive assessments and MRI were performed at the enrollment.

The hippocampi were segmented with a fully automatic, highly stable deformable registration based segmentation procedure that employs a probabilistic hippocampus definition in an average atlas image (Gouttard et al., 2007). Then, we built medial shape description, called m-rep, on the left and right hippocampi from all subjects, with the right hippocampi mirrored at the interhemispheric plane prior to the model generation. The detailed procedure for generating the m-rep model was reported in Styner and Gerig (2003). The resulting m-rep was a linked set of 24 medial primitives named medial atoms, which were formed from two equal length vectors and were composed of a position, a radius, a frame implying the tangent plane to the medial manifold and an object angle (Fig. 1a). The individual m-rep descriptions were computed by fitting this model into each object’s boundary. We computed the overall average structure as the template for medial shape analysis.

We considered the moment model based on the 7 × 1 estimating function x(y − x^Tβ), where the response of interest y was the logarithm of the m-rep thickness (or radius) measure for each medial atom of the left and right hippocampi (Figs, 1a and 1d). Moreover, β = (β₁, … , β₇)^T and x was a 7 × 1 vector given by x = (1, g, age, SC₁, SC₂,r₁,r₂), where g denoted gender (male=l, female=0), SC₁ and SC₂ were, respectively, dummy variables for haloperidol-treated SC patient and healthy controls, and r₁ and r₂ were, respectively, dummy variables for Caucasian and African American. Computer code for implementing this analysis is available at Biometrics website under the link “Paper Information”.

The basis of existing analysis methods of the image data includes the assumptions that the error distribution is Gaussian and the variance is constant. Because the SW test rejected the normality assumption at many atoms of the both left and right hippocampus structures, we chose the adjusted ET likelihood for the analysis of this data set (Fig. 2). Next, we use LR_aET to detect the localized differences in the morphology of the hippocampus across groups. We tested the null hypotheses H₀ : β₄ = β₅ = 0 at all 48 medial atoms of the left and right hippocampi, hence, the constraint under the null model is formed by

$$R=\left(\begin{array}{ccccccc}0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\end{array}\right)\text{ and }b={(0,0)}^T.$$

The − log₁₀(p)-values of the LR_aET of the null hypothesis Rβ = 0 across the atom of the reference hippocampus were color-coded in (Figs. 3a & b). For better illustration purpose, we presented these – log₁₀(p)-values of all atoms on the smoothed reference hippocampus. To correct for multiple comparisons, we applied false discovery rate approach to calculate the adjusted – log₁₀(p)-values across the reference hippocampus (Figs. 3c & d). We compared the uncorrected – log₁₀(p) values obtained using general linear model and the LR_aET test. We observed that the use of LR_aET test increased the significance level at those significant atoms of the hippocampus in each hemisphere (Figs. 2c & d).

Figure 3.

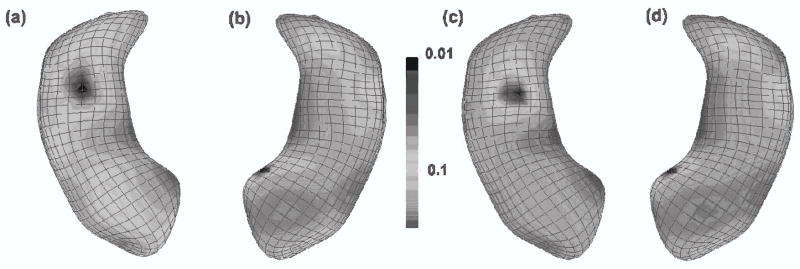
Significance testing at the atoms of the m-rep models of the Hippocampus structures: Color-coded maps of p—values and adjusted p—values for LR_aET. (a) and (c): left hippocampus; (b) and (d): right hippocampus, (a) and (b): raw p—values of LR_aET based on a χ² distribution, (c) and (d): adjusted p—values of LR_aET based on false discovery rate procedure for the correction of multiple comparisons. After correction for multiple comparisons, statistically significant group effects remain in the body of both the right (d) and left (c) hippocampus structures. We present the − log₁₀(p) values of all atoms on the smoothed left and right hippocampus surfaces.

As previously reported in studies of schizophrenia, especially in studies of first episode schizophrenics (Narr et al., 2004), there is a clear asymmetric aspect in that the left hippocampus shows larger regions of significance than the right hippocampus. In our experiment, the significant hippocampal locations of difference were found primarily in the lateral dentate gyrus and medial CA4 body regions for the left hippocampus, as well as a smaller area in the medial hippocampal head portion of the right hippocampus. In Narr et al., (2004), they also found differences in the lateral dentate gyrus, slightly more anterior-laterally located, when comparing first episodes schizophrenics with controls. Our studies thus seem to confirm these earlier results obtained with an alternative method that employed simple local t-tests without covarying for age, gender, and race.

4.Conclusions and Discussion

Our simulation studies suggest that the adjusted ET likelihood as a nonparametric method is an useful tool for the analysis of brain morphometry. The use of the adjusted ET likelihood avoids the assumption of Gaussian distribution of morphometric measures, that we have shown to be invalid in some imaging datasets (Ashburner, 2001; Salmond et al., 2002; Zhu et al., 2007). The LR_aET test provides accurate control of the Type I error rate for relatively small to moderate sample sizes and various error distributions. When the imaging data follow skewed distribution, the LR_aET test may offer better power compared with the t (or F)-test. Furthermore, when the homogeneous variance and Gaussian assumptions underlying the linear model are appropriate, the LR_aET test has almost the same power as the t-test (Tables 1 and 2). Our analysis of a real-world dataset demonstrates the applicability of our test procedure to morphometric measures. However, we also note several limitations of our procedures. For instance, for distributions with severe variance heterogeneity, the LR_aET test increases Type I error slightly.

Many aspects of this work merit further research. We may examine the performance of the adjusted ET likelihood in the analysis of data from other imaging modalities, including diffusion tensor images and functional MRI. We may consider robust estimating equations in the adjusted ET likelihood, because the estimating equations in (1) may be sensitive to outliers. These outliers may lead to reduced power and increased false positive rates in neuroimaging analyses (Wager et al., 2005). We may extend the LR_aET test to the imaging data from longitudinal and family studies. The estimating functions for data from longitudinal and family studies can be adapted from the existing literature and are used to set up the adjusted ET likelihood (Diggle et al., 2002; Duncan, 2004).

5.Supplementary Materials

Web Appendices and Computer code referenced in Sections 2 and 3 are available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.