Skip to main content
PMC home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2012 Jul 11;21(3):332–337. doi: 10.1038/ejhg.2012.143

Adaptive clustering and adaptive weighting methods to detect disease associated rare variants

Qiuying Sha 1, Shuaicheng Wang 1, Shuanglin Zhang 1,*
PMCID: PMC3573192  PMID: 22781093

Abstract

Current statistical methods to test association between rare variants and phenotypes are essentially the group-wise methods that collapse or aggregate all variants in a predefined group into a single variant. Comparing with the variant-by-variant methods, the group-wise methods have their advantages. However, two factors may affect the power of these methods. One is that some of the causal variants may be protective. When both risk and protective variants are presented, it will lose power by collapsing or aggregating all variants because the effects of risk and protective variants will counteract each other. The other is that not all variants in the group are causal; rather, a large proportion is believed to be neutral. When a large proportion of variants are neutral, collapsing or aggregating all variants may not be an optimal solution. We propose two alternative methods, adaptive clustering (AC) method and adaptive weighting (AW) method, aiming to test rare variant association in the presence of neutral and/or protective variants. Both of AC and AW are applicable to quantitative traits as well as qualitative traits. Results of extensive simulation studies show that AC and AW have similar power and both of them have clear advantages from power to computational efficiency comparing with existing group-wise methods and existing data-driven methods that allow neutral and protective variants. We recommend AW method because AW method is computationally more efficient than AC method.

Keywords: rare variants, association studies, adaptive weights, sequencing data

Introduction

Studies of the genetic architectures of several common diseases as well as simulation studies suggest that causal variants can be either common or rare.1, 2, 3, 4, 5, 6, 7 The main purpose of current genome-wide association studies (GWAS) is mapping common variants using indirect mapping methods based on tagging SNPs. GWAS have successfully detected many common variants responsible for complex diseases.8, 9, 10, 11 However, it has also been observed that the variants identified through GWAS account for only a small portion of the presumed phenotypic variation, and hence many variants remain to be discovered.12 Therefore, there is a great interest to investigate the function of rare variants in the etiology of common diseases and rare variant association studies become more and more popular.7, 13, 14, 15, 16, 17 In order to perform rare variant association studies, direct association mapping method in which all variants must be indentified should be used. New technologies allow sequencing of parts of the genome—or, in the future, the whole genome—of large groups of individuals.18 Sequencing can directly identify millions of rare mutations in the genome, and may therefore be able to identify rare mutations that are not tagged by tagging SNPs, which makes rare variant association studies feasible.19

Based on the idea of collapsing or aggregating rare variants in a gene or a pathway, several statistical methods to detect associations of rare variants have recently been developed, which includes the cohort allelic sums test (CAST) method,20 the combined multivariate and collapsing (CMC) method,21 the weighted sum (WS) method,22 the variable minor allele frequency (MAF) threshold method,23 and the cumulative minor-allele test (CMAT) method24 among others. These group-wise methods have been proved to be more powerful than the variant-by-variant methods. However, two factors may affect the power of these methods. One is that some of the causal variants may be protective. The other is that not all variants in the group are causal; rather, a large proportion is believed to be neutral. The group-wise methods assume that all causal variants are risk variants. This assumption may be reasonable for some diseases,7 but it is possible that some variants are protective.25 When both risk and protective variants are presented, it may lose power by collapsing or aggregating all variants because the effects of risk and protective variants will counteract each other. When a large number of neutral variants are included, the group-wise methods will also lose power because more neutral variants mean more noise and smaller signal–to-noise ratio. One way to reduce the number of neutral variants in the analysis is focusing on non-synonymous variants in gene coding regions.7, 26 In addition, bioinformatics tools such as SIFT,27 PMUT,28 and PolyPhen29 can be used to predict functionality of non-synonymous variants. We can further focus on non-synonymous variants that lead to putatively deleterious mutations. However, empirical studies have shown that predictive errors of these tools are high and agreement among them is low.17, 25, 30 Therefore, the usefulness of the bioinformatics tools is limited. As pointed by Liu and Leal,30 even when functionality can be correctly inferred, whether the identified variants affect the phenotype of interest is still unknown. Thus, we expect that a large proportion of variants under study are neutral and the group-wise methods by collapsing or aggregating all variants in the group may not be optimal. New methods that can combine the effects of risk and protective variants and can reduce the noise produced by neutral variants are needed.

Recently, several adaptive or data-driven methods have been proposed to detect rare variant association.25, 31, 32, 33 Han and Pan31 proposed to use a statistic to determine whether a variant should be protective or risk and change sign of genotypic scores of protective variants when aggregating. However, neutral variants are not carefully considered in this method. All of Bhatia et al,32 Hoffmann et al,25 and Zhang et al33 proposed to find the ‘best' subgroup in the group of variants considered and only collapse or aggregate the variants in the ‘best' subgroup. Some of other methods that are robust to the direction and magnitude of the effects of causal variants have been also proposed, which include C-alpha test,34 sequence kernel association test (SKAT),35 and weighted Goeman's test (WGT).36, 37 C-alpha, SKAT, and WGT, by testing the variance rather than the mean, are robust to the direction of the effects of causal variants.

In this article, we propose two alternative methods to test association between a group of rare variants and the phenotype in the presence of neutral and protective variants. One method, called adaptive clustering (AC), clusters variants into risk, neutral, and protective variants based on the optimal threshold of a statistic, and then tests association by combining the effects of risk and protective variants and deleting the effects of neutral variants. The other method, called adaptive weighting (AW), gives a continuous weight for each variant instead of clustering variants in a rigid manner. In this method, the variants that have strong associations with the phenotype will be given higher weights, which can potentially distinguish risk, neutral, and protective variants. Extensive simulation studies are used to evaluate and compare the performance of the proposed methods with existing group-wise methods and a data-driven method. Results show clear advantages of our proposed methods from power to computational efficiency.

Methods

Consider a sample of n individuals. Each individual has been genotyped at m variants in a genomic region (a gene or a pathway). As discussed in Introduction, there may be risk, neutral, and protective variants among the m variants. Collapsing all the m variants together, the protective variants will offset the effects of risk variants and the neutral variants will produce noise. If we know which variants are risk, neutral, or protective, then we can delete the neutral variants and combine the effects of risk and protective variants. However, for a specific phenotype, it is hard to separate the three kinds of variants by using bioinformatics tools. We propose to use an adaptive method that uses data at hand to separate the three kinds of variants. Specifically, we use the score test statistic to separate the variants. Denote yi (1 for cases and 0 for controls in a case–control study) and Xi as the trait value and genotypic score of the ith individual, where Xi can be multidimensional. Under the assumption of the generalized linear model,38 the score test statistic to test association between the trait and genotype is given by Chapman et al39

graphic file with name ejhg2012143e1.jpg

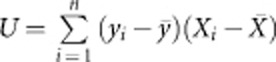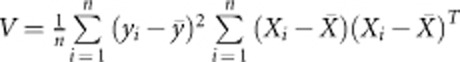where Inline graphic and Inline graphic.

When Xi is one dimension, we also say that 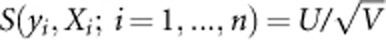Inline graphic is score test statistic. We use the score test to test association between the trait and each of the m variants. Let xi1,...,xim denote the genotypic scores of the ith individual at the m variants, where xik=0,1, or 2 (the number of the minor allele), and 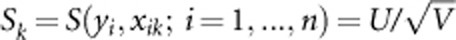Inline graphic denote the value of the score test statistic to test association between the trait and the kth variant. For a given threshold C, we consider the kth variant as a risk, neutral, or protective variant, if Sk>C, |Sk|≤C, or Sk<−C, respectively. When the information of risk, neutral, and protective variants is available, we use the following method to construct a test that can reduce the noise produced by neutral variants and can combine the effects of risk and protective variants.

Let RC and PC denote the sets of risk and protective variants, respectively. The genotypic scores of the ith individual across risk variants, across protective variants, and across all variants are given by

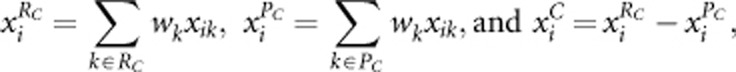graphic file with name ejhg2012143e6.jpg

respectively, where 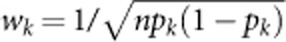Inline graphic is the weight suggested by Madsen and Browning22 and pk is the estimated MAF with pseudo-counts at the kth variant using controls only for case–control studies and using all sampled individuals for quantitative traits. The test statistic to test association between the trait and the genomic region is the score test statistic

graphic file with name ejhg2012143e8.jpg

Two adaptive tests combining effects of risk and protective variants

The test SC is intuitively appealing. However, the test statistic depends on the threshold C and choosing an appropriate value of threshold C is crucial to the performance of the test. It is difficult to choose the optimal value of the threshold C because the optimal value depends on many factors and different data sets may have different optimal values. To overcome the difficulty of choosing the optimal value, we propose the following two methods.

(1) Instead of using a fixed threshold in SC, we use a variable-threshold approach. We call the test with variable-threshold as Adaptive Clustering test combining effects of both risk and protective variants (AC2). The statistic of AC2 maximize the value of SC across values of threshold C, that is,

graphic file with name ejhg2012143e9.jpg

Statistical significance of AC2 can be evaluated by a permutation test. To calculate AC2, we only need to maximize SC across m values of C: S1, S2,..., Sm, the values of score test statistic at the m variants. Thus, the computational cost of AC2 for analyzing a genomic region with m variants is O(m).

(2) Instead of using a threshold in SC, we use continuous weights. We call the test with continuous weights as Adaptive Weighting test combining effects of both risk and protective variants (AW2). In AW2, the genotypic score of the ith individual is given by

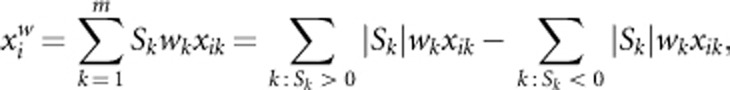graphic file with name ejhg2012143e10.jpg

where wk is the weight suggested by Madsen and Browning22 and Sk is the value of score test statistic applied to the kth variant. AW2 is the score test and test statistic is given by

graphic file with name ejhg2012143e11.jpg

In AW2, the variants that have strong association with the trait will be given higher weights which can potentially distinguish risk, neutral, and protective variants. The computational cost of AW2 for analyzing a genomic region with m variants is O(1).

Two adaptive tests using effects of risk variants only

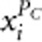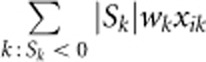To incorporate the effects of protective variants, AC2 and AW2 include the terms Inline graphic and Inline graphic in their genotypic scores. However, in the case of no protective variants, including Inline graphic and Inline graphic means including noise terms and may make AC2 and AW2 lose power. Here, we propose another two tests for the case of no or small proportion of protective variants: AC method using risk variants only (AC1) and AW method using risk variants only (AW1). AC1 is the same as AC2 but replacing genotypic score 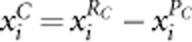Inline graphic in AC2 by 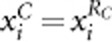Inline graphic. AW1 is the same as AW2 but replacing genotypic score 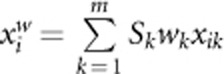Inline graphic in AW2 by 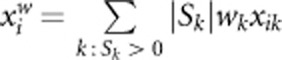Inline graphic. We expect that AC1 and AW1 are more powerful than AC2 and AW2 in the case of no or small proportion of protective variants.

Comparison of methods

We compare the performance of the four proposed tests with that of the WS test,22 the CMC method,20 STEP-UP method,25 aSum,31 and WGT.36, 37 If we use a permutation test to evaluate the P-value, then the Goeman's test is equivalent to T=UTU, where 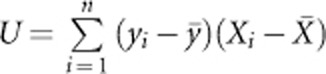Inline graphic and Xi=(xi1,…, xim)T. WGT is the weighted version of Goeman's test in which the weight suggested by Madsen and Browning22 is used to weight genotypes. For quantitative traits, the rank sum test used by WS is replaced by the score test, the T2 test used by CMC is also replaced by the score test, and the logistic model used by aSum is replaced by a linear model.

Simulation

We perform our simulation studies based on the empirical Mini-Exome genotype data provided by Genetic data Analysis Workshop 17 (GAW17). This data set contains genotypes of 697 unrelated individuals on 3205 genes. The genotypes are extracted from the sequence alignment files provided by the 1000 Genomes Project for their pilot3 study (http://www.1000genomes.org). In the first set of simulations, we generate genotypes based on the empirical Mini-Exome genotype data of two genes: MSH4 gene (gene1) and ADAMTS4 gene (gene2) (see Supplementary Tables S1 and S2 for haplotypes and their frequencies). In all, 16 SNPs out of 20 SNPs in gene1 are rare (MAF<1%) while 33 SNPs out of 40 SNPs in gene2 are rare. In the second set of simulations, we generate genotypes based on the empirical Mini-Exome genotype data of the Sgene. The Sgene with 100 variants is formed by merging four genes (gene1, gene2, ELAVL4, and PDE4B). We choose this Sgene because the distribution of MAFs in rare variants of Sgene can represent the distribution of MAFs in rare variants of the 3205 genes in the empirical Mini-Exome genotype data provided by GAW17 (Supplementary Figure S1). We use the program fastPHASE40 to infer haplotypic phase for the 697 individuals for gene1, gene2, and Sgene. According to the haplotype frequencies, we can generate genotypes. To evaluate type I error, we generate trait value by the standard normal distribution and independent of genotypes.

To evaluate power, we generate trait value under three disease models. In the first set of simulations, we randomly choose nc=10 rare variants as causal variants. In the second set of simulations, we randomly choose nc variants (can be common variants) as causal variants, where nc is determined by the percentage of causal variants. Denote nr and np as the number of risk variants and protective variants, respectively, where nr+np=nc. 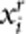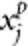For an individual, let Inline graphic and Inline graphic denote the genotypic scores of the ith risk variant and the jth protective variant, respectively. In disease model 1, we assume that all the nc causal variants have the same heritability. 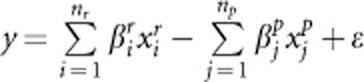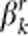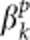Under this assumption, disease model 1 is given by Inline graphic, where ɛ is a standard normal random number; Inline graphic and Inline graphic are constants and their values depend on the total heritability. Disease model 2 is given by y=β(xr−xp)+ɛ, where 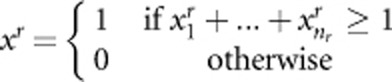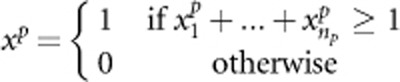Inline graphic, Inline graphic. Disease model 3 is given by 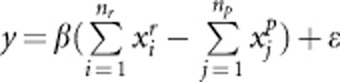Inline graphic. β is constant and its value depends on the total heritability.

Results

To evaluate the type I error, we consider different sample sizes and different haplotype structures. In each simulation scenario, P-values are estimated by 1000 permutations and type I error rates are evaluated using 1000 replicated samples. For 1000 replicated samples, the standard deviation for type I error rates is 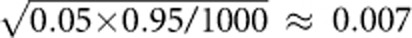Inline graphic and the 95% confidence interval is (0.036, 0.064) for the nominal level of 0.05. The estimated type I error rates of the seven tests are summarized in Table 1. From this table, we can see that all the estimated type I error rates are within the 95% confidence intervals, which indicate that the estimated type I error rates are not significantly different from the nominal level. Thus, the seven tests are all valid tests.

Table 1. The estimated type I error rates (in percentage) of the seven tests.

    Significance level 5%
Sample size Gene CMC WS AW1 AW2 AC1 AC2 STEP-UP
500                
  Gene1 4.7 5.0 4.9 4.9 4.8 4.9 3.7
  Gene2 4.7 4.9 5.0 4.1 5.0 4.5 5.5
1000
  Gene1 3.8 5.5 4.4 3.6 4.7 3.9 4.5
  Gene2 5.9 5.6 4.9 5.3 4.9 5.5 5.8
1500
  Gene1 3.6 4.3 4.3 4.7 4.6 4.7 5.5
  Gene2 4.5 5.5 4.3 4.7 4.4 4.4 4.0
Open in a new tab

For power comparisons, we consider two different cases: candidate gene association studies and regional association studies. In candidate gene studies, P-values are estimated by 1000 permutations and powers are calculated at a significance level of 0.05. In regional association studies, P-values are estimated by using 10 000 permutations and powers are calculated at a significance level of 0.001. In both cases, power is evaluated using 200 replicated samples.

In power comparisons, we first notice that AC1 has almost identical power with AW1 and AC2 has almost identical power with AW2 in all the simulation scenarios (Supplementary Figures S2–S5). Thus, in following discussions, we omit AC1 and AC2.

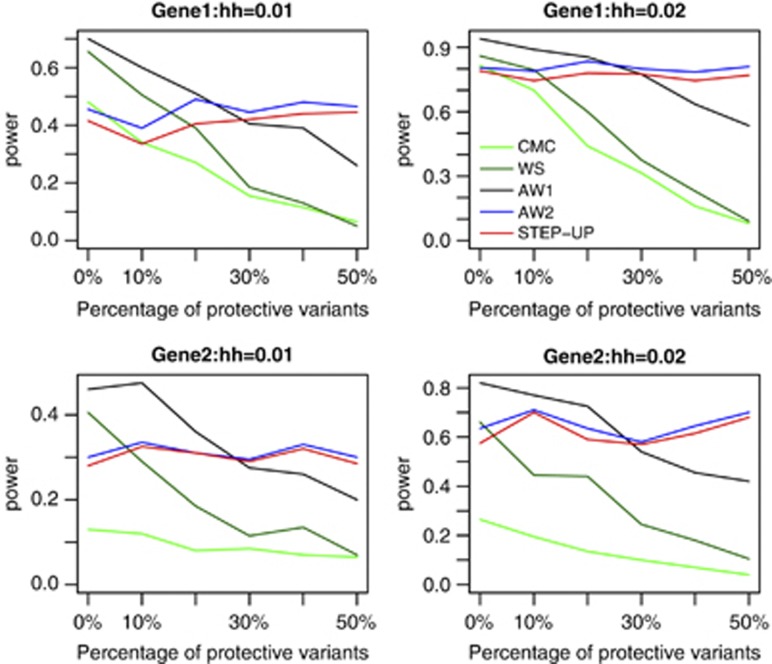
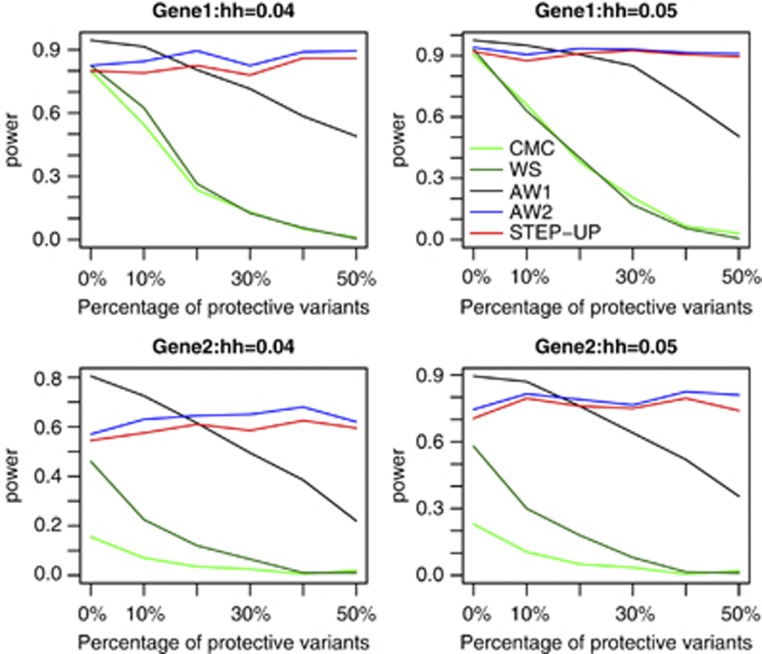
In the first set of simulations, we compare the power of five tests: CMC, WS, AW1, AW2, and STEP-UP. The power comparisons under disease model 1 in the case of candidate gene association studies and in the case of regional association studies are given in Figures 1 and 2, respectively. From these figures, we can draw following conclusions: (1) AW1 is consistently more powerful than CMC and WS regardless of different values of heritability, disease models, and the number of protective variants. In general, the power improvement of AW1 over CMC and WS becomes larger in the presence of the protective variants. (2) With the increase of the number of protective variants, the power of CMC, WS, and AW1 decreases, but the power of AW1 decreases not as much as that of CMC and WS. This is because protective variants would offset the effects of risk variants for CMC and WS. For AW1, although protective variants do not provide more information, protective variants do not offset the effects of risk variants. (3) The pattern of powers of AW2 and STEP-UP is different from that of CMC, WS, and AW1. The powers of AW2 and STEP-UP do not decrease with the increase of the number of protective variants because AW2 and STEP-UP can combine the effects of both risk and protective variants. AW2 and STEP-UP may be not as powerful as CMC, WS, and AW1 when there is no protective variant. However, AW2 and STEP-UP will be more powerful than CMC, WS, and AW1 when there are a large proportion of protective variants. (4) Although AW2 and STEP-UP have similar power, AW2 is more powerful than STEP-UP in >90% of simulation scenarios. The two sample t test based on all the simulation scenarios and 200 replications for each simulation scenario shows that AW2 is significantly more powerful than STEP-UP with P-value 1.7 × 10−10. Furthermore, AW2 is computationally much more efficient than STEP-UP (see Discussion for details). (5) Comparing power of AW1 and AW2, when protective variants are <10%, AW1 is more powerful than AW2; when protective variants are >40%, AW2 is more powerful than AW1; when protective variants are between 10 and 40%, which one is more powerful depends on disease models, haplotype structures, and values of heritability. (6) The power improvements of AW1 and AW2 over CMC and WS in regional association studies are larger than those in candidate gene association studies. This is not difficult to interpret. To reach certain power in regional association studies in which a more stringent significance level is used, the effects of causal variants or sample size should be larger than that in candidate gene studies, and in either case, it is easier to separate risk, protective, and neutral variants. Power simulation results based on models 2 and 3 yield the same conclusions (Supplementary Figures S6–S9).

Figure 1.

Figure 1

Open in a new tab

The power comparisons of the five tests based on disease model 1. hh represents the total heritability of the 10 causal variants. Since there are 10 causal variants in total, 0, 10, 20, 30, 40, and 50% protective variants represent 0, 1, 2, 3, 4, and 5 protective variants. Sample size is 1000. P-values are estimated using 1000 permutations and power is evaluated at a significance level of 0.05 using 200 replicates for each scenario. This simulation mimics candidate gene association studies.

Figure 2.

Figure 2

Open in a new tab

The power comparisons of the five tests based on disease model 1. hh represents the total heritability of the 10 causal variants. Since there are 10 causal variants in total, 0, 10, 20, 30, 40, and 50% protective variants represent 0, 1, 2, 3, 4, and 5 protective variants. Sample size is 1000. P-values are estimated using 10 000 permutations and power is evaluated at a significance level of 0.001 using 200 replicates for each scenario. This simulation mimics regional association studies.

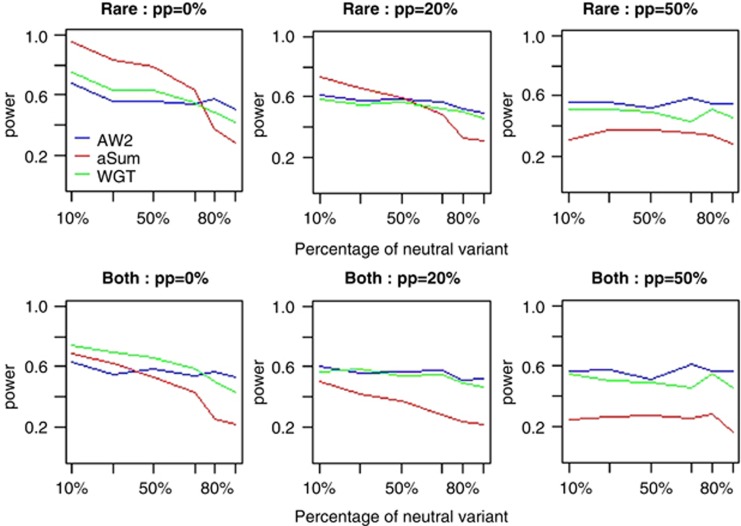
In the second set of simulations, we compare the power of three tests: AW2, aSum, and WGT. The power comparisons under disease model 1 are given in Figure 3. As shown in Figure 3, AW2 and WGT have similar power in general. WGT is more powerful than AW2 when there are no protective variants and the percentage of neutral variants is small; AW2 is more powerful than WGT otherwise. The power of AW2 and WGT is not affected by the percentage of neutral variants, while the power of aSum decreases as the increase of the percentage of neutral variants. When only rare variants are considered, aSum is more powerful than AW2 and WGT when the percentage of neutral variants is small and aSum is less powerful than AW2 and WGT when the percentage of neutral variants is large. When common variants are added, the power of AW2 and WGT is not affected much because AW2 and WGT put small weights on common variants. However, the power of aSum decreases significantly when common variants are added because common neutral variants will introduce large noises for aSum.

Figure 3.

Figure 3

Open in a new tab

The power comparisons of the three tests based on disease model 1 and using the haplotype structure of the Sgene. The total heritability of the all causal variants is 0.03. Sample size is 1000. P-values are estimated using 1000 permutations and power is evaluated at a significance level of 0.05 using 200 replicates for each scenario. pp represents for the percentage of protective variants. ‘Rare' means that only rare variants (MAF<0.01) are considered. ‘Both' means that both rare and common variants are considered. This simulation mimics candidate gene association studies.

Discussion

New sequencing technologies such as ABI SOLiD and Illumina HiSeq that allow sequencing of parts of the genome—or, in the future, the whole genome—of large groups of individuals have made rare variant association studies feasible. However, statistical methods to test association between rare variants and phenotypes are still under developed. In this article, we have developed two novel methods, AC and AW, aiming to test rare variant association in the presence of neutral and/or protective variants. Our results show that AC and AW have very similar performance. We recommend AW because AW is computationally more efficient than AC. Two tests, AW1 and AW2, are proposed under the AW method. AW2 is designed to test rare variant association in the presence of neutral and protective variants while AW1 is designed to test rare variant association in the presence of neutral with no or small proportion of protective variants. We use extensive simulation studies to compare the performance of our proposed methods with existing methods. Our results show that AW1 is consistently more powerful than CMC and WS (two typical group-wise methods) in all the simulation scenarios, while AW2 is more powerful than STEP-UP (one recently developed data-driven method that allows neutral and protective variants) in >90% of simulation scenarios.

In population-based association studies, it has been long recognized that population stratification can seriously confound association results. In common variant association studies, several methods that use a set of unlinked genetic markers genotyped in the same samples have been developed to control for population stratification.41, 42, 43, 44 All of the four tests proposed in this article can be easily modified such that they can be robust to population stratification. Principal component (PC) approach that summarizes the genetic background through the PC analysis of genotypes at genomic markers43, 44 can be used to modify our four tests. We take AW2 as an example. Let Ti=(ti1, ti2,..., tiK)T denote the first K PCs of genotypes at genomic markers of the ith individual. We adjust both the trait yi and genotypic score 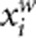Inline graphic for the PCs by applying linear regression. That is,

graphic file with name ejhg2012143e31.jpg

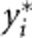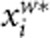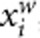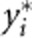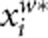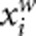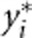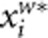Let Inline graphic and Inline graphic denote the residuals of yi and Inline graphic, respectively. We can consider Inline graphic and Inline graphic as the trait value and genotypic score of the ith individual after adjusted for population stratification. AW2 will be robust to population stratification if we replace yi and Inline graphic by Inline graphic and Inline graphic, respectively.

In rare variant association studies, the use of asymptotic distributions of test statistics is not appropriate because very small MAF can lead sparse data. Almost all of existing methods for testing rare variant association use a permutation test to evaluate P-values. The use of the permutation test makes us to consider the computational efficiency of each method. Data-driven methods are usually computationally more intensive than other methods. Analyzing a single gene with m variants, the computational complexity of variable MAF threshold method23 that considers all possible MAF thresholds is at order of O(m) and STEP-UP method is at order of O(m2), while our proposed AW method is at order of O(1). The running time of AW method to analyze one gene with 20 variants, 1000 individuals, and 1000 permutations is <0.5 s. To perform genome-wide studies, we can first select genes that show evidence of association based on a small number (eg, 1000) of permutations, and then, a large number of permutations are used to test the selected genes.

Each of AW1 and AW2, the two tests we proposed under AW method, has its advantages. In general, AW2 is more powerful when a large proportion of causal variants are protective; AW1 is more powerful otherwise. In practice, we suggest to apply both of the two tests because it is hard to know which test is more powerful for a specific data set. We can also construct a test that combine AW1 and AW2 by

graphic file with name ejhg2012143e40.jpg

where p1 and p2 are the P-values of AW1 and AW2, respectively. The power of AWcom is expected to be between that of AW1 and AW2. However, further investigation is needed to evaluate the performance of AWcom.

Acknowledgments

The Genetic Analysis workshops are supported by NIH grant R01 GM031575 from the National Institute of General Medical Sciences. Preparation of the Genetic Analysis Workshop 17 Simulated Exome Data Set was supported in part by NIH R01 MH059490 and used sequencing data from the 1000 Genomes Project (www.1000genomes.org).

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies the paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)

Supplementary Material

Supplementary information
Click here for additional data file. (280KB, doc)

References

  1. Pritchard JK. Are rare variants responsible for susceptibility to complex diseases. Am J Hum Genet. 2001;69:124–137. doi: 10.1086/321272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Pritchard JK, Cox NJ. The allelic architecture of human disease genes: common disease-common variant...or not. Hum Mol Genet. 2002;11:2417–2423. doi: 10.1093/hmg/11.20.2417. [DOI] [PubMed] [Google Scholar]
  3. Weiss KM, Terwilliger JD. How many diseases does it take to map a gene with SNPs. Nat Genet. 2000;26:151–157. doi: 10.1038/79866. [DOI] [PubMed] [Google Scholar]
  4. Stratton MR, Rahman N. The emerging landscape of breast cancer susceptibility. Nat Genet. 2008;40:17–22. doi: 10.1038/ng.2007.53. [DOI] [PubMed] [Google Scholar]
  5. Walsh T, King MC. Ten genes for inherited breast cancer. Cancer Cell. 2007;11:103–105. doi: 10.1016/j.ccr.2007.01.010. [DOI] [PubMed] [Google Scholar]
  6. Frikke-Schmidt R, Nordestgaard BG, Jensen GB, Tybjaerg-Hansen A. Genetic variation in ABC transporter A1 contributes to HDL cholesterol in the general population. J Clin Invest. 2004;114:1343–1353. doi: 10.1172/JCI20361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cohen JC, Kiss RS, Pertsemlidis A, Marcel YL, McPherson R, Hobbs HH. Multiple rare alleles contribute to low plasma levels of HDL cholesterol. Science. 2004;305:869–872. doi: 10.1126/science.1099870. [DOI] [PubMed] [Google Scholar]
  8. Plenge RM, Cotsapas C, Davies L, et al. Two independent alleles at 6q23 associated with risk of rheumatoid arthritis. Nat Genet. 2007;39:1477–1482. doi: 10.1038/ng.2007.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Thomson W, Barton A, Ke X, et al. Rheumatoid arthritis association at 6q23. Nat Genet. 2007;39:1431–1433. doi: 10.1038/ng.2007.32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Saxena R, Voight BF, Lyssenko V, et al. Genomewide association analysis identifies loci for type 2 diabetes and triglyceride levels. Science. 2007;316:1331–1336. doi: 10.1126/science.1142358. [DOI] [PubMed] [Google Scholar]
  11. Zeggini E, Weedon MN, Lindgren CM, et al. Replication of genome-wide association signals in UK samples reveals risk loci for type 2 diabetes. Science. 2007;316:1336–1341. doi: 10.1126/science.1142364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. McCarthy MI, Abecasis GR, Cardon LR, et al. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat Rev Genet. 2008;9:356–369. doi: 10.1038/nrg2344. [DOI] [PubMed] [Google Scholar]
  13. Ji W, Foo JN, O'Roak BJ, et al. Rare independent mutations in renal salt handling genes contribute to blood pressure variation. Nat Genet. 2008;40:592–599. doi: 10.1038/ng.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ahituv N, Kavaslar N, Schackwitz W, et al. Medical sequencing at the extremes of human body mass. Am J Hum Genet. 2007;80:779–791. doi: 10.1086/513471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Cohen JC, Pertsemlidis A, Fahmi S, et al. Multiple rare variants in NPC1L1 associated with reduced sterol absorption and plasma low-density lipoprotein levels. Proc Natl Acad Sci USA. 2006;103:1810–1815. doi: 10.1073/pnas.0508483103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Romeo S, Pennacchio LA, Fu Y, et al. Population-based resequencing of ANGPTL4 uncovers variations that reduce triglycerides and increase HDL. Nat Genet. 2007;39:513–516. doi: 10.1038/ng1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Romeo S, Yin W, Kozlitina J, et al. Rare loss-of-function mutations in ANGPTL family members contribute to plasma triglyceride levels in humans. J Clin Invest. 2009;119:70–79. doi: 10.1172/JCI37118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hodges E, Xuan Z, Balija V, et al. Genome-wide in situ exon capture for selective resequencing. Nat Genet. 2007;39:1522–1527. doi: 10.1038/ng.2007.42. [DOI] [PubMed] [Google Scholar]
  19. Andre′s A, Clark A, Shimmin L, et al. Understanding the accuracy of statistical haplotype inference with sequence data of known phase. Genetic Epidemiol. 2007;31:659–671. doi: 10.1002/gepi.20185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Morgenthaler S, Thilly WG. A strategy to discover genes that carry multiallelic or mono-allelic risk for common diseases: a cohort allelic sums test (CAST) Mutat Res. 2007;615:28–56. doi: 10.1016/j.mrfmmm.2006.09.003. [DOI] [PubMed] [Google Scholar]
  21. Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet. 2008;83:311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009;5:e1000384. doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Price AL, Kryukov GV, de Bakker PI, et al. Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet. 2010;86:832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Zawistowski M, Gopalakrishnan S, Ding J, et al. Extending rare-variant testing strategies: analysis of noncoding sequence and imputed genotypes. Am J Hum Genet. 2010;87:604–617. doi: 10.1016/j.ajhg.2010.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hoffmann TJ, Marini NJ, Witte JS. Comprehensive Approach to Analyzing Rare Genetic Variants. PLoS One. 2010;5:e13584. doi: 10.1371/journal.pone.0013584. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kryukov GV, Shpunt A, Stamatoyannopoulos JA, Sunyaev SR. Power of deep, all-exon resequencing for discovery of human trait genes. Proc Natl Acad Sci USA. 2009;106:3871–3876. doi: 10.1073/pnas.0812824106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ng PC, Henikoff S. Sift: predicting amino acid changes that affect protein function. Nucleic Acids Res. 2003;31:3812–3814. doi: 10.1093/nar/gkg509. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Ferrer-Costa C, Orozco M, de la Cruz X. Sequence-based prediction of pathological mutations. Proteins. 2004;57:811–819. doi: 10.1002/prot.20252. [DOI] [PubMed] [Google Scholar]
  29. Ramensky V, Bork P, Sunyaev S. Human non-synonymous snps: server and survey. Nucleic Acids Res. 2002;30:3894–3900. doi: 10.1093/nar/gkf493. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Liu DJ, Leal SM. A novel adaptive method for the analysis of next generation sequencing data to detect complex trait associations with rare variants due to gene main effects and interactions. PLoS Genet. 2010;6:e1001156. doi: 10.1371/journal.pgen.1001156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Han F, Pan W. A data-adaptive sum test for disease association with multiple common or rare variants. Hum Hered. 2010;70:42–54. doi: 10.1159/000288704. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Bhatia G, Bansal V, Harismendy O, et al. A covering method for detecting genetic associations between rare variants and common phenotypes. PLoS Comput Biol. 2010;6:e1000954. doi: 10.1371/journal.pcbi.1000954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Zhang L, Pei Y-F, Li J, Papasian CJ, Deng H-W. Efficient utilization of rare variants for detection of disease-related genomic regions. PLoS One. 2010;5:e14288. doi: 10.1371/journal.pone.0014288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Neale BM, Rivas MA, Voight BF, et al. Testing for an unusual distribution of rare variants. PLoS Genet. 2011;7:e1001322. doi: 10.1371/journal.pgen.1001322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wu M, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare variant association testing for sequencing data using the sequence kernel association test (SKAT) Am J Hum Genet. 2011;89:82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Goeman JJ, van de Geer S, van Houwelingen HC. Testing against a high dimensional alternative. J Royal Stat Soc B. 2006;68:477–493. [Google Scholar]
  37. Uh HW, Tsonaka R, Houwing-Duistermaat JJ. Does pathway analysis make it easier for common variants to tag rare ones. BMC Proc. 2011;5 (Suppl 9:S90. doi: 10.1186/1753-6561-5-S9-S90. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Nelder J, Wedderburn R. Generalized linear models. J R Stat Soc Ser A. 1972;135:370–384. [Google Scholar]
  39. Chapman JM, Cooper JD, Todd JA, Clayton DG. Detecting disease associations due to linkage disequilibrium using haplotype tags: a class of tests and the determinants of statistical power. Hum Hered. 2003;56:18–31. doi: 10.1159/000073729. [DOI] [PubMed] [Google Scholar]
  40. Scheet P, Stephens M. A fast and flexible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase. Am J Hum Genet. 2006;78:629–644. doi: 10.1086/502802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55:997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
  42. Pritchard JK, Stephens M, Rosenberg NA, Donnelly P. Association mapping in structured populations. Am J Hum Genet. 2000;67:70–181. doi: 10.1086/302959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Zhang S, Zhu X, Zhao H. On a semi-parametric test to detect associations between quantitative traits and candidate genes using unrelated individuals. Genet Epidemiol. 2003;24:44–56. doi: 10.1002/gepi.10196. [DOI] [PubMed] [Google Scholar]
  44. Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. PCs analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary information
Click here for additional data file. (280KB, doc)

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES