Abstract
One of the fundamental open questions in condensed matter science is the origin of the unique universal characteristics of glasses. Among them, the Boson peak (BP) and the first sharp diffraction peak (FSDP) are directly related with the disordered nature of these solids. The lack of widely accepted understanding of the origin of these features makes the characterization of glass forming systems on the microscopic level challenging. Moreover a strong and open debate exists on the possible correlation between BP and FSDP and its origin. Here we present the first detailed concomitant Raman and x-ray diffraction study of these two features under hydrostatic pressure. Surprisingly, we find that the previously proposed correlations between the positions of BP and FSDP do not hold under pressure. Based on the anticorrelation of the characteristic dimensions, we conclude that, BP and FSDP probe different spatial scales corresponding to dynamical and structural dimensions, respectively.
Glass forming systems, exhibit unique universal characteristics related with the absence of a long-range order. Among them, the low frequency broad peak in the Raman spectra, the Boson peak (BP) and the first sharp diffraction peak (FSDP) in x-ray and neutron diffraction patterns are considered to be related to the disordered nature of these materials1,2,3.
Despite numerous experimental and theoretical studies over the past decades, the scattering mechanism responsible for the BP is still a matter of debate and controversy4,5,6,7. However, it is generally concluded that the BP spectrum involves vibrations of the disordered solid beyond the atomic distance scale. In inorganic network glasses, this scale has been suggested to represent the medium-range order (MRO) of the glasses4,5,6,7. The FSDP in network glasses has also been associated with the MRO8. As in the case of the BP the precise origin of FSDP and its relation to the structure of glasses remains controversial9,10,11,12. Among the various interpretations for its origin, two have attracted most of the attention in the case of covalent network glasses (mainly chalcogenide and oxide glasses): a) the FSDP is a consequence of the partial periodicity (order) of the MRO (cages) existing in the glass13 and b) it is due to the chemical ordering of interstitial voids around cation centered clusters8. On the other hand, for elemental glasses such as Se, S and amorphous red P FSDP has been attributed to the existence of disordered rings (Se8 and S8) and/or chains14, while FSDP of metallic glasses is believed to arise from the presence of atomic clusters, quasicrystal-like, connected via a fractal network15.
In the case of polymer glasses, the term structural correlation length is used to describe the correlation between polymeric chains. The so-called polymerization (or van der Waals) peak represents real space distances consistent with the expected inter-backbone distances16 and so is the analogous feature of the FSDP peak. Hence, hereafter we will refer to this as FSDP for either network or polymer glasses. Additionally, main (backbone) and side chains are expected to contribute to the long wavelength vibrations and BP may be related to fluctuations (density or elasticity) between the space filed with backbones and side chains of the polymer.
Several approaches have been made to establish a correlation between the BP and the FSDP1,2,17,18,19. A possible universal correlation would be a general feature of amorphous solids, independent of specific structures and bonding. It might also clarify the issue about a possible correlation between the origin of the low frequency excitations (BP) and the structural characteristics of glasses. Diverse proposals have been reported in the recent literature: a) supporting a simple relation between them1,17,19 b) questioning the previous concept of a simple relation with the suggestion of a more complicated relation2,18 and c) completely rejecting any relation between BP and FSDP. Therefore, the relation, if any, between FSDP and BP is a matter of an open strong debate. The intensity and the position of both features are known to vary with temperature and pressure1. It is well known, from both Raman scattering20 and x-ray diffraction19 measurements, that MRO is more strongly affected by pressure than the short range order (SRO). This is directly related with the large free volume of glasses that results to a higher compressibility of glasses compared to the crystalline counterparts, since SRO is practically the same. Hence, the pressure behavior of both features will aid in our understanding the BP and FSDP and possible relationships between them.
In a theoretical study using the soft-potential model (SPM), Gurevich et al.21 have proposed the following expression for the frequency of the BP as a function of pressure:
where ωb(0) is the BP frequency at ambient pressure and P0 is a parameter proportional to the ambient-pressure bulk modulus K0 of the glass. Although equation (1) represents a simple phenomenological approach, its prediction is in good overall agreement with in situ Raman BP data for several network glasses19,22,23, in which there is no significant variation of K with pressure. In contrast, significant deviations from equation (1) have been found24 for polymer glasses because of the strong pressure dependence of their bulk modulus. Recent theoretical studies (e.g. Ref. 25), aimed to provide exact equations, are still in an early stage and therefore could not be used towards a direct comparison with experimental findings. As for the FSDP, the quantitative pressure behavior is still not well understood. In the past, very few studies have attempted to record in situ both the BP and FSDP features under pressure, mainly due to experimental difficulties associated with the recording of BP inside a diamond anvil cell (DAC). To the best of our knowledge, only for SiO2 a simple empirical relation between BP and FSDP was suggested17,19, which were in contrast with each other. In addition the true underlying nature of these relations, i.e. the correlation between the origins of the two features, was not examined.
In this work we present a detailed in situ high-pressure study of both FSDP and BP for a polymer glass, namely Kel F-800. The results are combined and analyzed along with pressure-dependent sound velocities data reported previously26. Our aim is twofold: a) to provide further input to the debate about a possible correlation between the two features through comparisons of their pressure dependence and b) to test if the existing models for the origin of BP are in agreement with experimental findings.
Results
Representative Raman spectra of the Kel F-800 polymeric glass as a function of pressure are shown in Fig. 1(a). As in previous studies19,22,23,24 the BP hardens with pressure and this is accompanied by a decrease of its intensity. The pressure dependence of the BP frequency ωb (Fig. 2) deviates from the theoretical predictions at high densities. Presumably this behavior is due to the large increase of bulk modulus with pressure for this glass, which amounts to nearly an order of magnitude by 14 GPa26.
Figure 1.
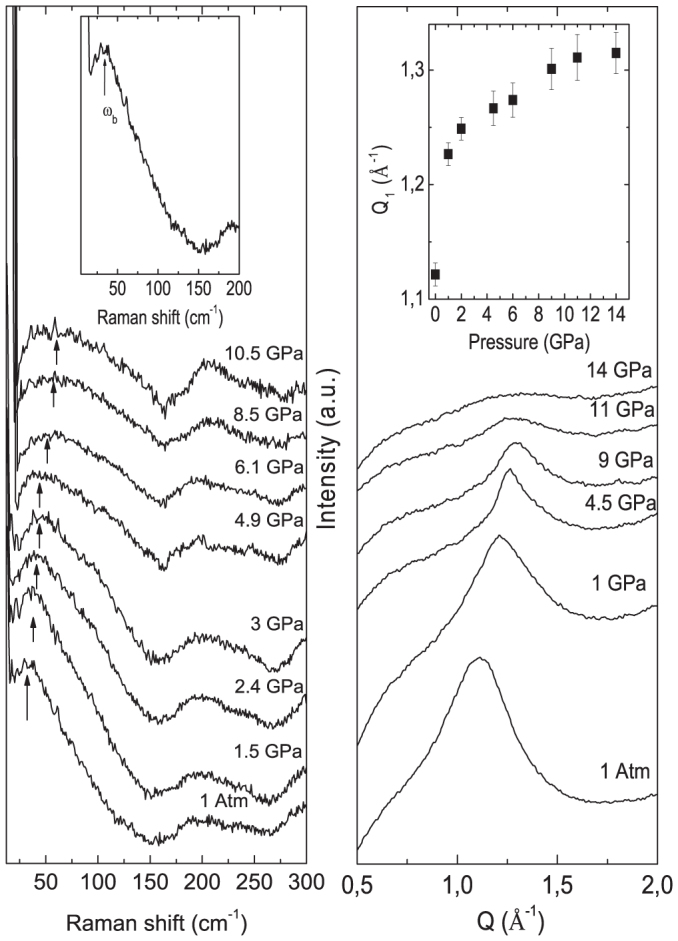
(a) Raman spectra of Kel F-800 polymer glass at various pressures for the compression run.The temperature was 278 K. The inset shows a detailed spectrum of the Boson peak at ambient conditions outside the high-pressure diamond anvil cell and (b) x-ray diffraction patterns of Kel F-800 glass with increasing pressure. The inset shows the plot of the position Q1 of the FSDP against pressure.
Figure 2. Pressure dependence of the normalized ωb(P )/ωb(0) BP frequency and the normalized sound velocity Vs(P )/Vs(0) for the Kel F-800 polymer glass.
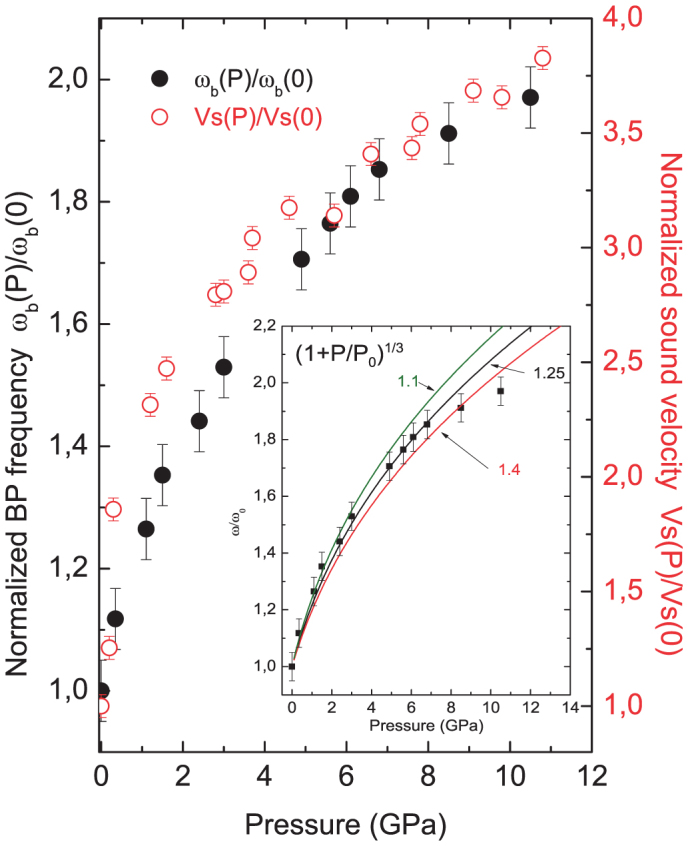
The fitting procedures applied for the determination of peak frequency of the asymmetric Boson band can be found elsewhere20,34. The inset shows fitting attempts of ωb, using equation (1), for three different values of the parameter P0.
Fig. 1(b) shows the x-ray diffraction patterns of Kel F-800 glass with increasing pressure. As in the case of the BP, the intensity of the FSDP decreases with pressure. With increasing pressure the position of the FSDP Q1 increases in qualitative agreement with all previous reports (e.g. Ref.19) for different types of glasses.
As already mentioned, several studies have related the BP frequency to a characteristic dynamical length R (correlation length). The physical meaning of R varies in different models. For instance R may be: (i) a cluster size inside the glass27, (ii) the scattering localization length due to density, elastic or elasto-optic property fluctuations7,28,29, and (iii) the length of propagation of high-frequency stress30. Independently from the proposed model ωb can be related to R through a simple equation1,28,31
where Vs is the sound velocity, and A is a constant depending on the particular model. Equation (2) represents the expected phenomenological relation between 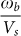 and the inverse of a dynamical characteristic length. Here we use equation (2) in the form
and the inverse of a dynamical characteristic length. Here we use equation (2) in the form 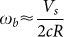 where c is the speed of light. Previous studies1 have shown that, although ωb(0) may vary from 10 to 200 cm−1 for different glasses, R usually takes values in a narrow range of 1 to 2 nm. This implies that ωb(0) is mainly defined by the elastic constants. Although equation (2) is not an exact equation and “microscopic” sound velocities with nm wavelengths should be used32, it provides a simple and straightforward prediction about the R trend under pressure. Moreover, it is difficult to obtain “microscopic” sound velocities under pressure, and this is why this equation was used by most of the previous studies.
where c is the speed of light. Previous studies1 have shown that, although ωb(0) may vary from 10 to 200 cm−1 for different glasses, R usually takes values in a narrow range of 1 to 2 nm. This implies that ωb(0) is mainly defined by the elastic constants. Although equation (2) is not an exact equation and “microscopic” sound velocities with nm wavelengths should be used32, it provides a simple and straightforward prediction about the R trend under pressure. Moreover, it is difficult to obtain “microscopic” sound velocities under pressure, and this is why this equation was used by most of the previous studies.
Normalized sound velocity Vs(P )/Vs(0) from26 as a function of pressure is plotted in Fig. 2. The pressure behavior of Vs(P ) is broadly similar to that displayed by ωb, but the overall increase is almost doubled (ωb(Pmax) ≈ 1.9 ωb(0) vs Vs(Pmax) ≈ 3.9 Vs(0)). Therefore, the rate at which the BP hardens with pressure lags considerably the stiffening of the elastic medium. It appears that the relation between the rate of increase of ωb and Vs(P ) with pressure is not the same for all glasses (see Ref.24,33). According to equation (2), this means that R should increase with pressure in contrast to the previously reported experimental results for other polymers24 and also contrary to the expectation of the structural models of BP27 as one expects a decrease of the MRO structural dimensions under pressure.
Discussion
From equation (2) we have calculated the inverse correlation length 1/R values using ωb values from this study and Vs values from Ref.26 (Fig. 3). Fig. 3 also shows the FSDP peak position Q1 plotted as a function of pressure. It is clearly seen that 1/R decreases with pressure (rapidly during the first step of compression), while the FSDP shifts to higher momentum transfers. The latter implies a decrease of the inter-backbone characteristic structural dimensions3. This is not compatible with the increase of R, if we consider the structural models of BP. R may be also attributed to a dynamical scattering length (localization length) which, according to the Ioffe-Regel condition, is the phonon's wavelength when equal to phonon's mean free path35. Another point of view is to attribute R to the crossover point between the phonon thermalization length and the propagation length due to elastic properties fluctuations36. In this case, the increase of R under pressure means that the phonon localization length increases.
Figure 3. Pressure dependence of the inverse correlation length (1/R) and FSDP position Q1 for the Kel F-800 polymer glass.
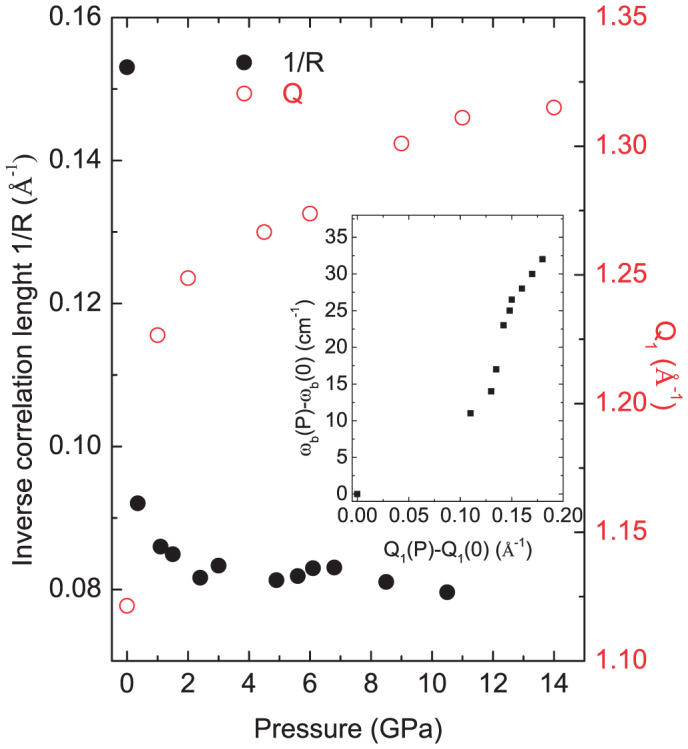
The inset shows the relative shifts between ωb and Q1 against each other19.
This is in favor of the various proposed fluctuation models of BP. Thus, BP and FSDP probe different spatial scales, i.e. structural dimensions in the case of FSDP and fluctuation dimensions for BP. The increase of R with pressure may be interpreted as the result of the free volume decrease and a consequent “homogenization” of the intermediate range structure of the glass, i.e. limited density or elastic fluctuations and a decrease of topological disorder. It is generally known37 that the BP relative intensity increases with increasing disorder for a given glass. Since the decrease of the BP intensity with increasing pressure is a universal observation1,3, it may also be related with the increase of R (decrease of disorder). In a previous study on GeO2 glass, a similar analysis between BP and Vs has been used by Deschamps et al.38. They concluded that the decrease of BP intensity is related with the anomalous softening of the elastic moduli, in a narrow pressure interval, and the consequent increase of R due to the elastic homogenization. Moreover, a similar interdependence between 1/R and BP intensity was also observed by Levelut et al.18 around the glass transition.
Here we concentrate on possible correlation between BP and FSDP using the pressure behavior of these two features. The first proposed1 and simplest relation between BP and FSDP is in the form 1/R ~ Q1. This relation is based on the assumption that R represents an effective size of the clusters. Although this relation holds relatively well for different glasses at ambient conditions1, it is obvious from Fig. 3 that it fails when applied to Kel F-800 glass under pressure. In another approach3 the relation R ~ 1/ΔQ1 has been proposed, where ΔQ1 is the width of the FSDP. This relation was based in the hypothesis that the Scherrer equation for microcrystalline samples, also holds for glasses. However, the available experimental data (including those of the present work) do not show any substantial decrease of ΔQ1 with pressure.
Apart of the above mentioned generally proposed relations between BP and FSDP there has also been further number of attempts to relate their pressure dependencies. Sugai and Onodera17 suggested an empirical relation in the form ωb ~ Vs ΔQ1which is compatible with the R~ 1/ΔQ1 one. They found that there is a linear relation between ωband ΔQ1. In this event, Vs should be constant under pressure, in contrast to all previously reported results. Elsewhere, Hemley et al.19 and Inamura et al.39 proposed a linear relation between ωb(P ) − ωb(0) and Q1(P ) − Q1(0) based on 1/R ~Q1 relation. This result has been attributed in Ref.40 to the fact that the increase of ωb means that R decreases and so that the relation 1/R ~ Q1 is fulfilled. However, this conclusion is not valid for the glass of this study since R effectively increases with pressure.
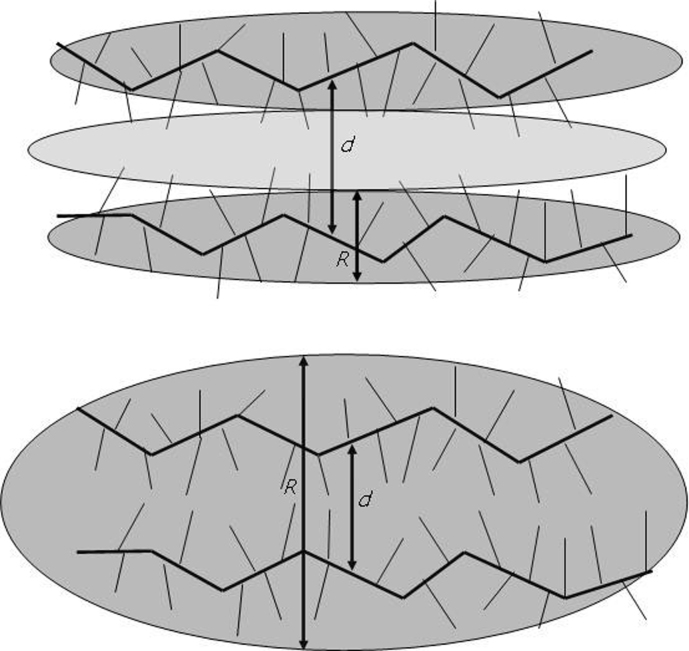
Although a near linear relation ωb ~ Q1 can be valid under pressure (see inset of Fig. 3) it may not reflect the true correlation between BP and FSDP. Our results suggest that the correlation length (see equation (2) ) is the main factor that affects frequency and intensity of the BP, since Vs is a bulk property. Consequently, we propose that under pressure the structural correlation length (distance between backbones for a polymer) decreases, however the dynamical correlation length increases due to “homogenization”. The latter is consistent with the BP intensity decrease. These proposals are schematically illustrated in Fig. 4. At low pressures the distance between backbones is large because of the voids created from the side chains. With increasing pressure the free volume decreases and backbones approach each other. This compression mechanism is in agreement with the high compressibility of the Kel F-800 polymer glass26. According to this, the density and/or elasticity fluctuations becomes less influential as the void space collapses. Consequently, the dynamical correlation length R increases upon pressure exertion. We conclude that, BP and FSDP are not directly correlated because they probe different spatial scales corresponding to fluctuation and structural dimensions, respectively. Thus, the previously proposed phenomenological relations, although may be valid, are coincidental and doesn't reflect the actual anticorrelation behavior under pressure between the microscopic characteristic lengths of these features.
Figure 4. Schematic representation of low (a) and high (b) pressure configuration of polymer back- bones and voids for a representative polymer.
The dimensions of the structural (d) and scattering (R) correlation lengths are indicated with arrows.
Further studies are necessary to confirm the universality of this observation and for better understanding of the simple model we propose here. First, the dynamical correlation length under pressure should be examined for other types of glasses (network and polymeric), in order to better understand the origin of the difference in its pressure behavior. Second, different techniques (for example inelastic and elastic neutron scattering) may be used to probe the different spatial scales and to fully identify the above experimental findings. This may also provide useful input for theoretical attempts aiming on a better understanding of the origin of the BP and FSDP features in glasses and on a possible correlation between them.
Methods
Kel F-800 fluorocarbon polymer is a 3 M copolymer derived from the monomers chlorotri- fluorethylene (CTFE) and vinylidine (VF2). A small piece of Kel F-800 polymer was loaded inside the DAC without any pressure transmitting medium. Small quantities of ruby and gold powder were also loaded, for determination of pressure through ruby luminescence and gold EOS, respectively. Raman spectra were measured with a backscattering geometry using the 532 nm line from a solid state laser for excitation. An experimental setup capable to record Raman spectra at very low wavenumbers (<10 cm−1) using solid state notch filters was used. Diffraction data were collected at the GSECARS (sector 13), using a MAR355 CCD detector. The monochromatic x-ray beam (wavelength λ = 0.3344 Å ) was focused to a nominal diameter of 4 μm. For this glass Tg ≈ 307 K at ambient pressure41, and is expected to increase with pressure. Raman experiments were performed at room (293 K) and at low temperature (278 K) well below Tg, yielding very similar results for the BP position, but BP is much better resolved at low temperatures.
Author Contributions
E.S. and A.G designed research. E.S. M.A. and A.G. conducted the experiments. All authors reviewed the manuscript.
Acknowledgments
E. S. would like to thank C. Raptis for fruitful discussions and critical reading of the manuscript. The authors would like to thank D. M. Dattelbaum for the Kel F-800 polymer samples, also V. Prakapenka and GSECARS staff for help in conducting synchrotron experiments. We thank V. V. Struzkin and B. Mysen for useful comments on the manuscript. This work was supported by the US Army Research Office, the Carnegie/DOE Alliance Center and DARPA. GSECARS is supported by the National Science Foundation Earth Sciences (EAR-0622171) and Department of Energy Geosciences (DE-FG02-94ER14466). Use of the Advanced Photon Source was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357.
References
- Novikov V. N. & Sokolov A. P. A correlation between Low-energy Vibrational-spectra and 1st Sharp Diffraction Peak in Chalcogenide Glasses. Sol. State Commun. 77, 243–247 (1991). [Google Scholar]
- Borjesson L., Hassan A. K., Swenson J., Torell L. M. & Fontana A. Is there a Correlation Between the 1st Sharp Diffraction Peak and the Low-frequency Vibrational Behavior of Glasses. Phys. Rev. Lett. 70, 1275–1278 (1993). [DOI] [PubMed] [Google Scholar]
- Sokolov A. P., Kisliuk A., Soltwisch M. & Quitmann D. Medium-range Order in Glasses - Comparison of Raman and Diffraction Measurements. Phys. Rev. Lett. 69, 1540–1543 (1992). [DOI] [PubMed] [Google Scholar]
- Mermet A. et al. Inelastic neutron and Raman scattering of poly (methyl methacrylate): Nanostructure of polymer glasses. J. Europhy. Lett. 36, 277–282 (1996). [Google Scholar]
- Parshin D. A., Schober H. R. & Gurevich V. L. Vibrational instability, two-level systems, and the boson peak in glasses. Phys. Rev. B 76, 064206 (2007). [Google Scholar]
- Schirmacher W., Ruocco G. & Scopigno T. Acoustic attenuation in glasses and its relation with the boson peak. Phys. Rev. Lett. 98, 025501 (2007) [DOI] [PubMed] [Google Scholar]
- Schmid B. & Schirmacher W. Raman scattering and the low- frequency vibrational spectrum of glasses. Phys. Rev. Lett. 100, 137402 (2008). [DOI] [PubMed] [Google Scholar]
- Elliott S. R. Medium-range Structural Order in Covalent Amorphous Solids. Nature 354, 445–452 (1991). [Google Scholar]
- Gaskell P. H. & Wallis D. J. Medium-range order in silica, the canonical network glass. Phys. Rev. Lett. 76, 66–69 (1996). [DOI] [PubMed] [Google Scholar]
- Massobrio C. & Pasquarello A. Origin of the first sharp diffraction peak in the structure factor of disordered network-forming systems: Layers or voids? J. Chem. Phys. 114, 7976–7979 (2001). [Google Scholar]
- Zaug J. M., Soper A. K. & Clark S. M. Pressure-dependent structures of amorphous red phosphorus and the origin of the first sharp diffraction peaks. Nature Mat. 7, 890–899 (2008). [DOI] [PubMed] [Google Scholar]
- Wilson M. & Madden P. A. Voids, layers, and the first sharp diffraction peak in ZnCl2. Phys. Rev. Lett. 80, 532–535 (1998). [Google Scholar]
- Wright A. C. Longer range order in single component network glasses?. Phys. Chem. Glasses B 49, 103–117 (2008). [Google Scholar]
- Jovari P., Delaplane R. G. & Pusztai L. Structural models of amorphous selenium. Phys. Rev. B 67, 172201 (2003). and references therein. [Google Scholar]
- Ma D., Stoica A. D. & Wang X. –L. Power-law scaling and fractal nature of medium-range order in metallic glasses. Nature Mater. 8, 30 (2008). [DOI] [PubMed] [Google Scholar]
- Chiba A. et al. Pressure-induced structural change of intermediate- range order in poly(4-methyl-1-pentene) melt. Phys. Rev. E 85, 021807 (2012). [DOI] [PubMed] [Google Scholar]
- Sugai S. & Onodera A. Medium-range order in permanently densified SiO2 and GeO2 glass. Phys. Rev. Lett. 77, 4210–4213 (1996). [DOI] [PubMed] [Google Scholar]
- Levelut C. et al. Glass-transition temperature - Relation between Low-frequency Dynamics and Medium-range Order. Phys. Rev. B 51, 8606–8609 (1995). [DOI] [PubMed] [Google Scholar]
- Hemley R. J., Meade C. & Mao H. K. Medium-range order in permanently densified SiO2 and GeO2 glass-comment. Phys. Rev. Lett. 79, 1420–1420 (1997). [Google Scholar]
- Stavrou E., Raptis C. & Syassen K. Effects of pressure on the boson peak of Tellurite TeO2(1-x) ZnOx glasses: Evidence of an elastic glass-to-glass transition. Phys. Rev. B 81, 174202 (2010). [Google Scholar]
- Gurevich V. L., Parshin D. A. & Schober H. R. Pressure dependence of the boson peak in glasses. Phys. Rev. B 71, 014209 (2005). [Google Scholar]
- Andrikopoulos K. S., Christofilos D., Kourouklis G. A. & Yannopoulos S. N. Pressure dependence of the boson peak in glassy As2S3 studied by Raman scattering. J. Non-Cryst. Solids 352, 4594–4600 (2006). [Google Scholar]
- Yamaguchi M., Nakayama T. & Yagi T. Effects of high pressure on the Bose peak in a-GeS2 studied by light scattering. Physica B 263, 258 (1999). [Google Scholar]
- Hong L. et al. Pressure and density dependence of the boson peak in polymers. Phys. Rev. B 78, 134201 (2008). [Google Scholar]
- Srivastava D. & Sarkar S. K. Pressure dependence of the boson peak for repulsive homogeneous potentials. Phys. Rev. B 85, 024206 (2012). [Google Scholar]
- Stevens L. L., Dattelbaum D. M., Ahart M. & Hemley R. J. High-pressure elastic properties of a fluorinated copolymer: Poly(chlorotrifluoroethylene-co-vinylidene fluoride) (Kel-F 800). J. Appl. Phys. 112, 023523 (2012). [Google Scholar]
- Duval E., Boukenter A. & Achibat T. Vibrational Dynamics and the Structure of Glasses. J. Phys.: Condens Matter 2, 10227–10234 (1990). [Google Scholar]
- Elliott S. R. A Unified Model for the Low-energy Vibrational Behavior of Amorphous Solids. Europhys. Lett. 19, 201–206 (1992). [Google Scholar]
- Duval E., Mermet A. & Saviot L. Boson peak and hybridization of acoustic modes with vibrations of nanometric heterogeneities in glasses. Phys. Rev. B 75, 024201 (2007). [Google Scholar]
- Trachenko K. & Brazhkin V. V. Understanding the problem of glass transition on the basis of elastic waves in a liquid. J. Phys.: Condens. Matter 21, 425104 (2009). [DOI] [PubMed] [Google Scholar]
- Shuker R. & Gammon R. W. Raman-scattering Selection-rule Breaking and Density of States in Amorphous Materials. Phys. Rev. Lett. 25, 222 (1970). [Google Scholar]
- Monaco G. & Giordano V. N. Breakdown of the Debye approximation for the acoustic modes with nanometric wavelengths in glasses. Proc. Natl. Acad. Sci. 106, 3659 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monaco A. et al. Effect of Densification on the Density of Vibrational States of Glasses. Phys. Rev. Lett. 97, 135501 (2006). [DOI] [PubMed] [Google Scholar]
- Boulmetis Y. C. et al. Composition and temperature dependence of the low- frequency Raman scattering in Ge-As-S glasses. J. Non-Cryst. Solids 347, 187 (2004). [Google Scholar]
- Schroeder J. et al. Raman scattering and Boson peaks in glasses: temperature and pressure effects. J. Non-Cryst. Solids 349, 88 (2004). [Google Scholar]
- Pronin A. A., Trachenko K., Kondrin M. V., Lyapin A. G. & Brazhkin V. V. Nonlocal dielectric relaxation in glycerol. Phys. Rev. B 84, 012201 (2011). [Google Scholar]
- Malinovsky V. K. & Sokolov A. P. The Nature of Boson Peak in Raman-scattering in Glasses. Sol. State Commun. 57, 757–761 (1986). [Google Scholar]
- Deschamps T., Martinet C., de Ligny D., Bruneel J. L. & Champagnon B. Correlation between boson peak and anomalous elastic behavior in GeO2 glass: An in situ Raman scattering study under high-pressure. J. of Chem. Phys. 134, 234503 (2011). [DOI] [PubMed] [Google Scholar]
- Inamura Y. et al. Intermediate range structure and low-energy dynamics of densified vitreous silica. J. Non-Cryst. Solids 293, 389 (2001). [Google Scholar]
- Chmel A. The role of the dynamic structural correlation in glasses in the initiation of brittle fracture. J. Non-Cryst. Solids 319, 65–73 (2003). [Google Scholar]
- Cady W. E. & Caley L. E. Technical report, UCRL-12439, Lawrence Livermore National Laboratory, Livermore, CA. (1977).