Abstract
The role of temporal stimulus parameters in the perception of across-frequency synchrony and asynchrony was investigated using pairs of 500-ms tones consisting of a 250-Hz tone and a tone with a higher frequency of 1, 2, 4, or 6 kHz. Subjective judgments suggested veridical perception of across-frequency synchrony but with greater sensitivity to changes in asynchrony for pairs in which the lower-frequency tone was leading than for pairs in which it was lagging. Consistent with the subjective judgments, thresholds for the detection of asynchrony measured in a three-alternative forced-choice task were lower when the signal interval contained a pair with the low-frequency tone leading than a pair with a high-frequency tone leading. A similar asymmetry was observed for asynchrony discrimination when the standard asynchrony was relatively small (≤20 ms) but not for larger standard asynchronies. Independent manipulation of onset and offset ramp durations indicated a dominant role of onsets in the perception of across-frequency asynchrony. A physiologically inspired model, involving broadly tuned monaural coincidence detectors that receive inputs from frequency-selective onset detectors, was able to accurately reproduce the asymmetric distributions of synchrony judgments. The model provides testable predictions for future physiological investigations of responses to broadband stimuli with across-frequency delays.
INTRODUCTION
Temporal disparity between different frequency components often indicates the presence of different sound sources, and so the processing of across-frequency timing information is a critical aspect of auditory perception and scene analysis. Noninvasive physiological measures of peripheral auditory responses in humans have shown that frequency-dependent basilar-membrane (BM) traveling-wave delays result in a progressive delay of low frequencies relative to higher frequencies in the representation of a stimulus transmitted to the auditory nerve (AN) and subsequent processing stages (e.g., Elberling, 1974; Eggermont, 1979; Neely et al., 1988; Schoonhoven et al., 2001; Shera et al., 2002; Sisto and Moleti, 2007; Harte et al., 2009). Auditory brainstem responses (ABRs) to a chirp designed to counteract the frequency-dependent delays and to synchronize the BM responses across locations with different characteristic frequencies (CFs) exhibit a greater amplitude of wave V (Dau et al., 2000; Fobel and Dau, 2004), greater amplitudes of high-frequency (HF) components of the ABR spectrum, and a smaller phase variance of the main ABR components (Petoe et al., 2010b) than the ABRs to a click with the same overall energy. These results suggest that differences in response latencies across CFs introduced by cochlear filtering are preserved at least up to the level of the brainstem. On the other hand, psychophysical measurements of the perceived compactness of brief upward chirps, downward chirps of the same duration, and a click, performed by Uppenkamp et al. (2001), showed that the click was perceived as the most compact, suggesting that across-frequency differences in cochlear-response delays might be compensated for at a higher neural level, although it was difficult to separate within-channel from across-channel effects in that study.
Recently, additional support for the hypothesis of a compensating mechanism was provided by Wojtczak et al. (2012), who measured the perceived synchrony of tone pairs at different frequencies with varying delays between the tones. To eliminate the confounding effect of within-channel cues, the frequencies of the tones were at least two octaves apart and were presented with a band of noise that masked regions of potential overlapping excitation on the BM. Based on a linear model of BM mechanics by de Boer (1980), the difference in cochlear response delays between the CFs of 100 Hz and 10 kHz is about 10.5 ms, with the greatest changes in delay occurring in the range of CFs below 2 to 3 kHz. If cochlear delays were preserved throughout the auditory system, the greatest perceived synchrony should correspond to tone pairs with the low-frequency (LF) tone leading by the difference between cochlear response times to the test tones. Instead, it was found that listeners judged the tones as synchronous on the greatest proportion of trials when the tones were physically synchronous, thereby suggesting the presence of a compensation mechanism that results in veridical perception. In addition, the results revealed a significant asymmetry in the perception of asynchrony between two tones with remote frequencies. For a given delay between the tones, pairs with a LF lead yielded a lower proportion of “synchronous” judgments compared to pairs with the corresponding HF lead. This pattern was observed for all the frequency separations and stimulus levels used in that study. Consistent with the subjective judgments, Wojtczak et al. (2012) also found lower (i.e., better) thresholds for the detection of asynchrony for pairs of tones with LF leading than with HF leading in a three-alternative forced-choice task. An asymmetry in the same direction was observed in the judgments of compactness in the study by Uppenkamp et al. (2001) and in thresholds for discriminating timbre differences introduced by monotonically shifting phases of components with increasing and decreasing frequencies in a harmonic complex (Patterson, 1987). Since Wojtczak et al. (2012) took special measures to eliminate within-channel cues (i.e., potentially detectable changes in excitation level in the regions of overlapping excitation occurring during the onset of the delayed component and the offset of the leading component), the asymmetry in all three studies may reflect the characteristics of a mechanism underlying the perception of across-channel timing information.
There is currently no physiological evidence for a mechanism devoted specifically to compensating for frequency-dependent cochlear delays. Since frequency-dependent delays are shown by measures that reflect neural synchrony at the level of the AN and brainstem (e.g., Dau et al., 2000; Petoe et al., 2010b), the hypothesized compensating mechanism could be involved in the transmission of information from the brainstem to the midbrain or/and the central nuclei or could be more central in origin. Given the millisecond scale of the phenomenon, however, a brainstem or midbrain locus seems more plausible than a cortical one. It is also unknown whether this mechanism is “hard-wired” or whether it is subject to learning and plasticity and, if so, whether there exists a “critical period.”
The aim of this study was to identify stimulus parameters relevant for the perception of across-frequency asynchrony. The study investigated whether the recent findings of Wojtczak et al. (2012) generalize to longer stimulus durations and whether onset and offset ramp durations have systematic effects on the ability to detect and discriminate across-frequency asynchronies. In most of the earlier studies of asynchrony detection, the asynchrony between two (or more) tones was introduced by desynchronizing the onsets while gating the tones off simultaneously (Parker, 1988; Zera and Green, 1993; Mossbridge et al., 2006) or by desynchronizing the offsets while preserving simultaneity of the onsets (Zera and Green, 1993; Mossbridge et al., 2006; Mossbridge et al., 2008). These strategies forced the listeners to use temporal disparity of the onsets or offsets, respectively. The results showed that listeners were better at detecting onset asynchronies than offset asynchronies. Other studies measured asynchrony detection by delaying one tone in a pair relative to the other so that both the onsets and offsets were desynchronized by the same amount (Micheyl et al., 2010; Wojtczak et al., 2012). For these stimuli, listeners could use the asynchrony of the onsets, offsets, or a change in the duration of the overall stimulus (tone pair) as cues to perform the asynchrony-detection task. In all the studies except for Wojtczak et al. (2012), within-channel cues could have been used because of the relatively close frequency spacing between the tones and/or rapid gating that resulted in energy splatter over a wide range of frequencies. Based on the existing data it is not clear which stimulus parameters are dominant for the perception of asynchrony in the absence of within-channel cues. This study investigated the role of onset, offset, and overall-duration cues with the broader aim of providing further data for the search of a physiological mechanism involved in compensating for frequency-dependent cochlear delays and a mechanism underlying the asymmetry in asynchrony perception found in the previous studies (Patterson, 1987; Uppenkamp et al., 2001; Wojtczak et al., 2012). A physiologically inspired model based on monaural coincidence detection is proposed to account for the data. The present results and model thus provide data, a conceptual framework, and testable hypotheses in the search for the neural correlates of cochlear-delay compensation.
EXPERIMENT 1: SUBJECTIVE JUDGMENTS OF ACROSS-FREQUENCY ASYNCHRONY
Wojtczak et al. (2012) found that pairs of 40-ms tones with remote frequencies were perceived as synchronous on the maximum proportion of trials when they were physically synchronous but the functions relating the proportion of synchronous responses to the delay between the tones were asymmetric about the 0-ms delay. In apparent contrast, Micheyl et al. (2010) found that for 100-ms tones, asynchrony detection thresholds estimated from separate tracks within a block for the pairs with LF- and HF-tones leading were not significantly different. The different outcomes may reflect the different tone durations, and possibly different resulting detection strategies. Alternatively, because of the relatively small frequency separations used by Micheyl et al. (2010), it is possible that their subjects used within-channel cues that do not exhibit the asymmetries characterizing across-channel processing of relative-timing cues. The present experiment tested these possibilities by measuring asynchrony perception for longer tone durations while ruling out the detection of within-channel cues.
Stimuli and procedure
The perceived synchrony of two tones with remote frequencies was measured as a function of the delay between the tones, using a method of constant stimuli. The experimental procedure was the same as that in the study of Wojtczak et al. (2012) but the stimulus durations and some of the delays were different. Four tone pairs were used in separate blocks. Each pair consisted of a 250-Hz tone and a tone with a higher frequency of 1, 2, 4, or 6 kHz. The tones had durations of 500 ms including 10-ms raised-cosine onset and offset ramps. Within each block of trials, the same pair of tones was presented with different delays between the tones that included 0 ms, and ±2, 4, 8, 12, 20, 40, 60, and 100 ms, where the negative delays represented pairs with the LF-tone leading, and the positive delays represented pairs with the HF-tone leading. Each trial consisted of one presentation of a tone pair with a selected delay. After each trial the listener was asked to decide whether the tones sounded synchronous or asynchronous. The listeners were advised to use any information that was most helpful in performing the task, i.e., they could focus on the temporal disparity of the onsets or offsets, or evaluate the overall duration of the tone pairs. The listeners were told that each block will contain both synchronous and asynchronous tone pairs but not in the same numbers, and they were asked to respond according to the perceived relative timing and to avoid trying to balance the two (“synchronous” and “asynchronous”) response types. No feedback was provided in the experiment. Ten random permutations of all the delays were used within each block and the listeners completed ten blocks for each pair of frequencies used. This resulted in 100 synchrony judgments per listener for each delay and frequency pair.
The experiment was performed for two levels of the tones, 20 dB sensation level (SL) and 85 dB sound pressure level (SPL). For both levels, the tones were presented with a half-octave-wide noise band centered on the geometric mean of the frequencies of the two tones. The noise was used to mask potential within-channel cues that could otherwise have been available in the regions of overlapping excitation. For the 85-dB SPL tones, the level of the noise was set 20 dB below the level of the tones. For the 20-dB SL tones, the level of the noise was 20 dB below the SPL of the less intense tone. These levels were deemed sufficient for eliminating within-channel cues based on the outputs of level-dependent gamma-chirp filters (Irino and Patterson, 1997). In each trial, the tone pair was temporally centered in the noise. The noise was longer than the tone pair by 800 ms with a 400-ms fringe preceding and following the pair. The masking noise was generated in the frequency domain by setting the components outside of the passband to zero, and so the roll-offs below and above the cutoff frequencies were determined only by the temporal gating of the noise waveform. The noise waveforms were gated on and off with 10-ms raised-cosine ramps.
The SPLs corresponding to the 20 dB SL for the tones used for synchrony judgments were determined by measuring thresholds in dB SPL for detecting the individual 500-ms tones using an adaptive three-interval, three-alternative forced-choice procedure (3I-3AFC) coupled with a 2-down 1-up tracking technique estimating the 70.7% correct point on the psychometric function (Levitt, 1971), as described in Wojtczak et al. (2012).
All the stimuli were generated on a PC with a sampling rate of 48 kHz via a 24-bit LynxStudio Lynx22 sound card and presented to the left ear via the earphone of a Sennheiser HD 580 headset. During the experiment the listeners were seated in a double-walled sound-attenuating booth. The equipment was calibrated using a Sound Level Meter (2260 Observer, Brüel & Kær, Denmark) by measuring the headphone outputs for tones and noise with specified root-mean-squared amplitudes. The headphones were mounted on a Brüel & Kær artificial ear (4153) with a half-inch pressure microphone (4192).
Listeners
Six listeners participated in the experiment. Five of the six listeners were also the participants in the study by Wojtczak et al. (2012). The audiometric thresholds tested using an ANSI certified audiometer (Madsen Conera) indicated that all the listeners had normal hearing [thresholds at or below 15 dB hearing level (HL)] at octave frequencies between 0.25 and 8 kHz. The listeners received about an hour of training during which they could try different cues and settle on one that made them most confident about their judgments. No additional training was given to the one new listener since the data were stable and within the range of the data from the other listeners. All subjects provided informed written consent. The protocol for this and all the other experiments within this study was approved by the Institutional Review Board of the University of Minnesota.
Results and discussion
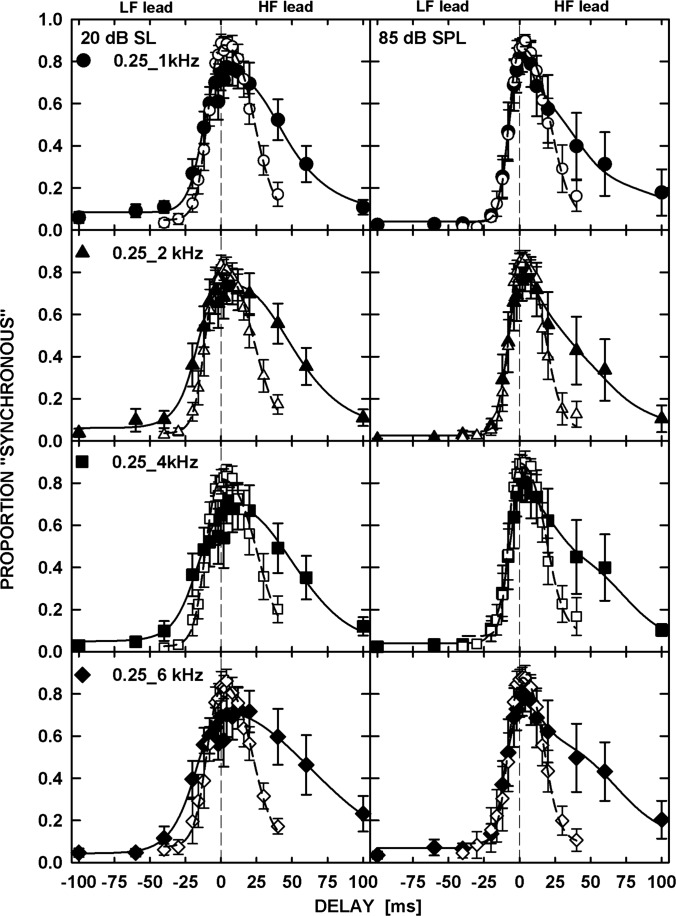
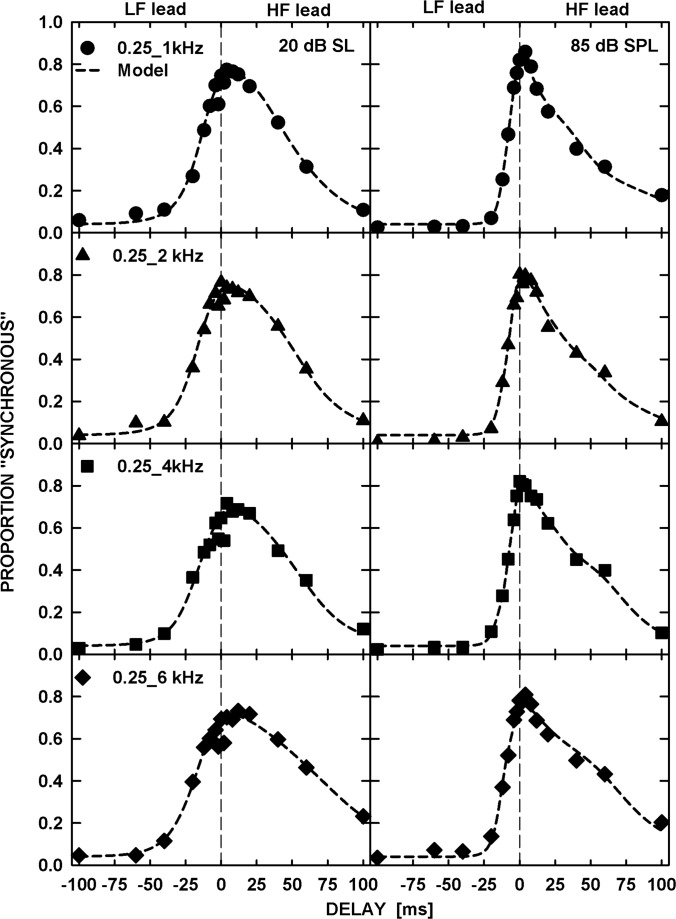
The patterns of results were similar for all six listeners and so only the averaged data (filled symbols) are shown in Fig. 1. Each panel shows the proportion of synchronous responses plotted as a function of the delay between the tones in a pair. The frequencies of the tones are specified in the left panels. As mentioned above, the data corresponding to the negative delays on the abscissa are for tone pairs with the LF leading while those corresponding to the positive delays are for pairs with the HF leading. The left and right panels show data for the tone levels of 20 dB SL and 85 dB SPL, respectively. The error bars represent one standard error of the mean. For visual comparison, data for the same tone pairs but with 40-ms duration are replotted from the study by Wojtczak et al. (2012) using open symbols.
Figure 1.
Mean proportion of synchronous responses (filled symbols) plotted as a function of delay between the two tones. The negative and positive delays represent tone pairs with LF leading and HF leading, respectively. The left column shows data for tones presented at 20 dB SL and the right column for tones at 85 dB SPL. Different rows show data for different frequency pairs. The open symbols show data for 40-ms tones replotted from the study by Wojtczak et al. (2012) for comparison. The solid and dashed curves show predictions by a model based on signal detection theory, for the 500- and 40-ms tones, respectively.
The patterns of results were very similar across the frequency pairs and the levels used. In all the panels of Fig. 1, the proportion of synchronous responses reached a maximum as the delay between the tones approached 0 ms (i.e., physical synchrony). In addition, the synchronous-response functions were highly asymmetric, with a steeper slope for the pairs with the LF leading than the HF leading. This asymmetry was also observed in the data for the 40-ms tones (open symbols) from our previous study, although it appears to be stronger for the 500-ms tones, mainly due to the shallower slope for the side representing delays with the HF leading.
To estimate the delay corresponding to the maximum proportion of synchronous responses and to quantify the degree of asymmetry, the data were fitted with a decision-theoretic model that was used to fit the synchronous-response functions for the 40-ms tones in our previous study (see the Appendix in Wojtczak et al., 2012). The fits, represented by the solid (for 500-ms tones) and dashed (for 40-ms tones) curves in Fig. 1, were performed using the maximum likelihood procedure with a binomial distribution (Wichmann and Hill, 2001; Dai and Micheyl, 2011). The delays corresponding to the peak of the functions fitted to the individual data (not shown) were subjected to a repeated-measures analysis of variance (ANOVA) with factors of frequency separation and level. The ANOVA showed that the frequency separation had no effect on the delay corresponding to the maximum proportion of synchronous responses [F(3,15) = 0.587, p = 0.633] but there was a significant effect of level [F(1,5) = 9.864, p = 0.026]. A one-sample t-test performed separately for each level showed that the peak position was significantly different from 0 ms for the tones at 20 dB SL [t(23) = 3.491, p = 0.002] but not at 85 dB SPL [t(23) = 2.010, p = 0.056]. For tones at 20 dB SL, the mean peak position corresponded to a 4.3-ms HF lead. However, an analysis of 95% confidence intervals around the peak positions, estimated using the individual data, showed that the confidence interval included 0 ms in 36 out of 48 cases (6 listeners × 4 frequency separations × 2 levels), and cases for which the lower bound did not include 0 ms were not systematically related to the frequency separation and were not consistently observed for any given listener.
The asymmetry between the slopes of the synchronous-response functions was estimated based on the values of parameter β (see the Appendix in Wojtczak et al., 2012) obtained from the fits to the individual data (not shown). Briefly, the unitless parameter β scales the standard deviation of the distribution representing the proportion of synchronous responses above the peak relative to that below the peak. Thus, parameter β has a value of 1 when the synchronous-response function is symmetric about the position of the peak, and a value greater than 1 when the slope is steeper below than above the peak of the function. A repeated-measures ANOVA with factors of frequency separation and level, with the Greenhouse-Geisser correction applied in cases where the sphericity assumption was violated, showed no significant effect of either factor on the log-transformed value of β, and no significant interaction [Frequency separation: F(3,15) = 0.325, p = 0.808; Level: F(1,5) = 4.716, p = 0.082; Interaction: F(1.352,6.761) = 2.336, p = 0.172]. For each listener, the values of β were averaged across the 8 conditions (4 frequency separations ×2 levels). A one-sample t-test showed that the log-transformed average value of β was significantly greater than zero [t(5) = 5.528, p = 0.003, compared with Bonferroni corrected significance criterion α = 0.006] indicating significantly shallower slopes of the synchronous-response functions above than below the peak. The mean value of parameter β for the 500-ms tones was 4.1, nearly twice the mean value of 2.3 obtained for the 40-ms tones in our previous study. An independent-sample t-test performed on log-transformed values of β from the individual fits to the synchronous-response functions for the four frequency pairs and two levels tested showed that the asymmetry of the synchronous-response functions was significantly greater for the 500- than for the 40-ms tones [t(76.076) = 3.138, p = 0.002, Bonferroni corrected α = 0.006]. A paired t-test performed on the log-transformed values of parameter β only using the five listeners who participated in the experiments for both 40- and 500-ms tones also showed a significant effect of tone duration on the asymmetry [t(39) = 4.728, p < 0.001]. Because of the significant differences between the asymmetry of the functions representing subjective judgments of synchrony for the two tone durations, the same values of the model parameters could not be used without compromising the accuracy of the fits.
In summary, the new results using 500-ms tones were generally consistent with the earlier results of Wojtczak et al. (2012) in showing maximum perceived synchrony when the tones were indeed synchronous. The results also show that the asymmetry between the responses to LF- and HF-leading pairs observed in Wojtczak et al. (2012) was not simply due to their use of short-duration tones; if anything, the asymmetry observed with 500-ms tones was even greater.
EXPERIMENT 2: ASYNCHRONY DISCRIMINATION
For the 40-ms tones used in the study by Wojtczak et al. (2012), the steeper slope of the synchronous-response functions for the pairs with the LF tone leading than the HF tone leading was consistent with lower (better) asynchrony-detection thresholds in the LF-leading condition. For longer (100 ms) tones, Micheyl et al. (2010) did not observe the dependence of asynchrony detection on tone-frequency order. The results from Experiment 1 suggest that the asymmetry between the LF- and HF-leading pairs is observed over a wide range of tone durations. However, a more direct comparison with the results of Micheyl et al. (2010) requires a discrimination task, rather than the subjective judgments measured in Experiment 1. In this experiment, thresholds for detecting increments in asynchrony were measured for the 500-ms tones used in Experiment 1, to test whether the subjective judgments of asynchrony could be used to predict asynchrony-detection thresholds in the same way as was done for the 40-ms tones.
Stimuli and procedure
Thresholds for detecting an increase in the asynchrony between two tones were measured as a function of the standard asynchrony using an adaptive 3I-3AFC procedure combined with a 2-down 1-up tracking rule estimating the 70.7% correct point on the psychometric function (Levitt, 1971). The experiment was performed for a 250-Hz tone paired with a 1-, 2-, 4-, or 6-kHz tone. Conditions in which the HF or LF tone was leading were tested in separate runs. For each condition (LF and HF leading), five standard delays between the tones were used: 0, 10, 20, 60, and 100 ms. The different conditions and the standard delays were tested in random order. One tone pair with a fixed standard delay between the tones was used within each run. Two of the three intervals in each trial contained the pair with the same (standard) delay and the third interval, chosen at random with uniform a priori probability, contained the same tone pair with an increased delay (signal). The observation intervals were separated by 500-ms silent intervals. The listeners were asked to choose the interval with the different delay and enter their responses via a computer keyboard or a mouse click. Feedback indicating the correct response was provided after each trial. At the beginning of a run, the delay in the signal interval was clearly distinguishable from the standard delay. The difference between the signal and standard delays, ΔAsynch, was varied adaptively using multiplicative steps. ΔAsynch was decreased by a factor of 2 after two consecutive correct responses and increased by a factor of 2 after one incorrect response until the second reversal was reached. After that, the multiplicative step was reduced to a factor of 1.41 for the subsequent two reversals, and a factor of 1.19 for the remainder of the run. The run terminated after a total of 12 reversals. A single-run threshold estimate was calculated as the geometric mean of the ΔAsynch values at the final eight reversal points. The final threshold estimate for each listener and condition was obtained by geometrically averaging three single-run thresholds.
The tones had a duration of 500 ms and were gated on and off with 10-ms raised-cosine ramps. The experiment was run with the tones presented at two levels, 20 dB SL and 85 dB SPL. As in Experiment 1, half-octave noise bands were used to mask areas of overlapping excitation from the tones on the BM. The noise started 300 ms before the first observation interval and ended with the end of the third observation interval. The methods for stimulus generation and presentation (monaural to the left ear) were the same as in Experiment 1.
Listeners
Five listeners were recruited for the experiment. Three of the listeners participated in Experiment 1 and four of the listeners had participated in the asynchrony-discrimination task in the study by Wojtczak et al. (2012). One new participant was given a hearing test that confirmed normal hearing and received an extensive (at least 4 h) practice before data collection began.
Results and discussion
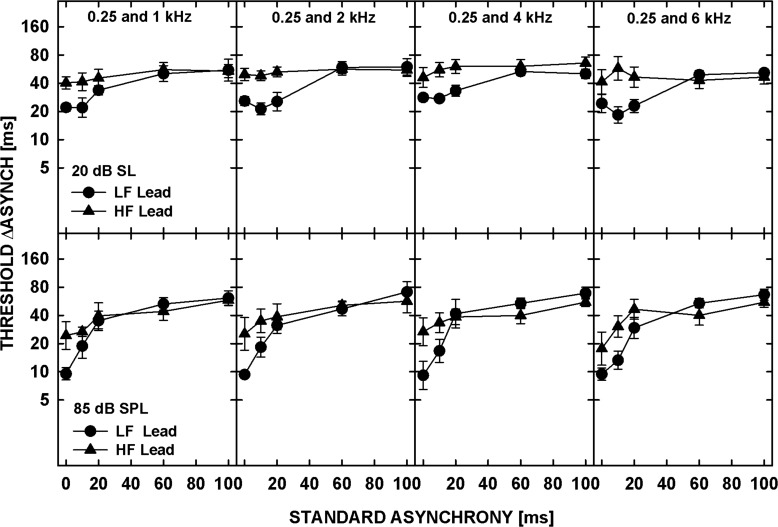
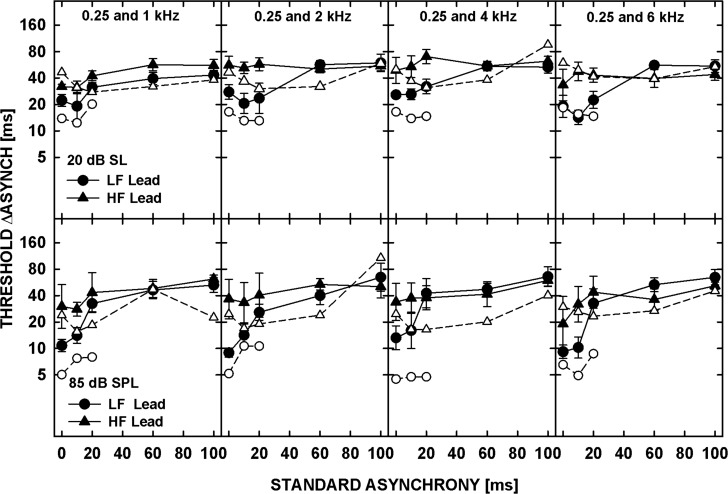
Geometric mean asynchrony discrimination thresholds across the five listeners are shown in Fig 2. In each panel, the just-detectable increase in asynchrony, ΔAsynch, is plotted as a function of the standard asynchrony. For the standard asynchrony of 0 ms, the task was asynchrony detection, whereas for all the other standard asynchronies the task required an ability to discriminate between different amounts of asynchrony (asynchrony discrimination). The top and bottom panels show data for the 20-dB SL and 85-dB SPL tones, respectively. Each column shows data for a different frequency separation, as indicated at the top of the upper panels. The circles and triangles represent thresholds for the LF- and HF-lead conditions, respectively. For the tones presented at 20 dB SL, thresholds in the LF-lead condition were lower than those for the HF-lead and varied little with the standard asynchrony for standard asynchronies up to 20 ms. For larger standard asynchronies, thresholds from the two conditions converged. For the 85-dB SPL tones, thresholds in the LF-lead condition were lower than those in the HF-lead condition, for standard asynchronies up to 10 ms, and converged for larger delays. At this higher level, the thresholds from both LF- and HF-lead conditions progressively increased with increasing standard asynchrony at short delays (≤20 ms), and increased less or remained relatively constant for the standard asynchronies between 20 and 100 ms.
Figure 2.
Geometrically averaged thresholds for detecting changes in the asynchrony between two tones plotted as a function of the standard asynchrony. The circles and triangles show thresholds for the LF and HF tone leading, respectively. The top panels show data for the tones presented at 20 dB SL, and the bottom panels for the tones at 85 dB SPL. Data for different frequency pairs are shown in different columns as indicated by the titles in the upper panels. The error bars represent the standard error of the mean.
All the statistical analyses described below were performed on log-transformed thresholds obtained in Experiment 2. A repeated-measures ANOVA performed on asynchrony-discrimination thresholds with factors of standard asynchrony, direction of delay (LF or HF lead), frequency separation, and level showed a significant effect of standard asynchrony [F(4,16) = 16.219, p < 0.0001] but no significant main effect of any of the other factors [Direction of delay: F(1,4) = 3.420, p = 0.138; Frequency separation: F(3,12) = 1.370, p = 0.299; Level: F(1,4) = 0.718, p = 0.444]. There were, however, significant interactions between the factors [Direction of delay and Standard asynchrony: F(4,16) = 8.036, p = 0.001; Level and Standard asynchrony: F(4,16) = 5.502, p = 0.006]. The first interaction reflects the lower thresholds in the LF-lead than the HF-lead condition for small but not for large standard asynchronies. A t-test performed on asynchrony-detection thresholds (for a 0-ms standard asynchrony) showed that the listeners were significantly more sensitive to the asynchrony between the tones when the LF was leading than when the HF was leading, both at 20 dB SL [t(19) = −4.835, p < 0.001] and at 85 dB SPL [t(19) = −3.383, p = 0.003]. This result is qualitatively consistent with the asymmetric shape of the synchronous-response functions measured in Experiment 1 but appears inconsistent with the data of Micheyl et al. (2010), suggesting that a smaller frequency separation between the tones in that study rather than a relatively long tone duration (100 ms) led to the lack of asymmetry in asynchrony detection. The smaller frequency separation (and lack of a noise band between the tones) may have enabled the listeners to use within-channel envelope cues in the region of overlapping excitation from the test tones. The availability of this cue would not depend on whether the LF or HF tone was gated on and off first. Another possible explanation for the lack of asymmetry in asynchrony-detection thresholds observed by Micheyl et al. (2010) is offered below in Sec. 6D .
Although the ANOVA did not show a significant main effect of level on the data pooled across all the conditions, the interaction between level and standard asynchrony reflects significantly lower asynchrony-detection thresholds for tones at 85 dB SPL than at 20 dB SL, for both the LF-lead condition [t(19) = 7.976, p < 0.001] and HF-lead condition [t(19) = 2.571, p = 0.019]. This result is qualitatively consistent with the broader shape (especially around the peak) of the synchronous-response functions measured in Experiment 1 for the tones presented at the lower level.
The patterns of results from Experiment 2 were very similar to those observed for the 40-ms tones in Wojtczak et al. (2012). However, the thresholds compared for the three standard asynchronies that were common in the two studies were generally higher for the 500-ms tones than for the 40-ms tones, particularly at the low level. To illustrate this point, data from Fig. 2 (filled symbols) were replotted along with the corresponding data from Wojtczak et al. (2012) shown by the open symbols in Fig. 3 (for tones presented at 20 dB SL) and Fig. 4 (for tones presented at 85 dB SPL). In both figures, the data for the LF- and HF-lead conditions are shown in the upper and lower panels, respectively.
Figure 3.
Comparison of (geometric) mean thresholds for detecting changes in the asynchrony between tones with a duration of 500 ms (filled symbols) and 40 ms (open symbols), for the same listeners. The 40-ms data are replotted from the study by Wojtczak et al. (2012). The upper panels show data for tone pairs with LF leading, and the lower panels for tones with HF leading. The data are for tones presented at 20 dB SL. The error bars show the standard error of the mean.
Figure 4.
As in Fig. 3 but for tones at 85 dB SPL.
A repeated-measures ANOVA with factors of duration, standard asynchrony, direction of delay, frequency separation, and level was performed on the log-transformed data from the four listeners who participated in the asynchrony-discrimination experiments with the 500- and 40-ms tones in the study by Wojtczak et al. (2012). Only the thresholds for the three standard asynchronies that were common in both studies were used in the analysis. The ANOVA showed that thresholds for the 500-ms tones were significantly higher than those for the 40-ms tones [F(1,3) = 12.457, p = 0.039]. In addition to the duration, the standard asynchrony was the only other significant factor [F(2,6) = 9.317, p = 0.014].
For asynchrony detection (i.e., a 0-ms delay), independent-sample t-tests were performed to compare the mean log-transformed thresholds for the 500- and 40-ms duration using data from all the listeners participating in the two experiments. The effect of tone duration on asynchrony detection was not significant for pairs with the LF leading with tones presented at 85 dB SPL [t(42) = −1.615, p = 0.114]. For the pairs of tones presented at 20 dB SL with the LF leading and the pairs with the HF leading at both levels used, thresholds were significantly higher for the 500- than for the 40-ms tones [t(23.73) = −6.339, p < 0.001, for LF lead at 20 dB SL; t(20.38) = −2.169, p = 0.042, for the HF lead at 85 dB SPL; and t(25.54) = −4.300, p < 0.001, for the HF lead at 20 dB SL].
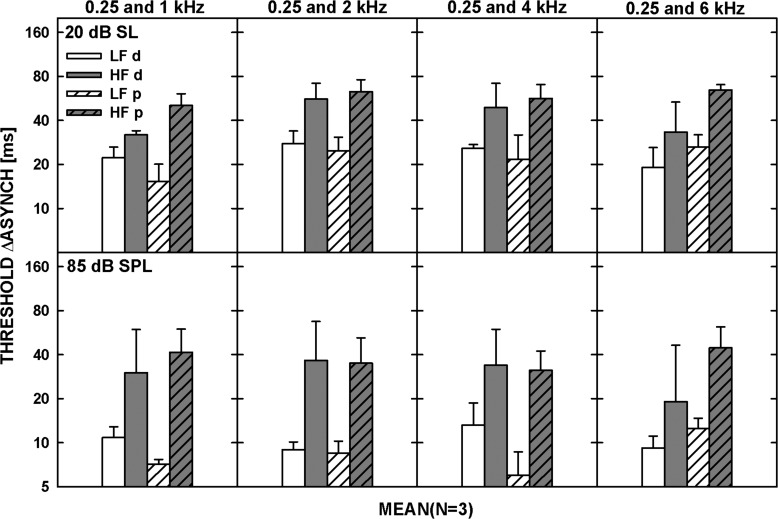
The model used to fit the synchronous-response functions for the individual listeners in Experiment 1 (and the average functions shown in Fig. 1) was used to predict asynchrony-detection thresholds in the 3I-3AFC task, as was done for the 40-ms tones in the study by Wojtczak et al. (2012). Since only three listeners participated in both experiments, only their data could be used for this analysis. The asynchrony-detection thresholds were predicted by deriving functions relating d′ to the delay between the tones from the curves fitted to the synchronous-response functions for each frequency pair and level. From these functions, the delays corresponding to a d′ of 1.26 (the value corresponding to the 70.7% in the 3I-3AFC task) were obtained separately for the LF-lead and HF-lead conditions. Figure 5 shows the geometrically-averaged measured (the plain bars denoted by “d” in the legend) and predicted (the hatched bars, denoted by “p”) thresholds. Consistent with the data, the model predicted lower thresholds in the LF-lead than the HF-lead condition and captured the effect of level (thresholds were lower for the tones at 85 dB SPL than 20 dB SL, as shown in the lower and upper panel, respectively).
Figure 5.
Data (plain bars indicated by d in the legend) and predictions (hatched bars indicated by p) from the model based on signal detection theory described in the Appendix in Wojtczak et al. (2012). Both sets of bars represent the geometric mean of data (and predictions) for three listeners. The predictions were obtained using the synchronous response functions measured in Experiment 1. The lower and upper panels are for tones at 20 dB SL and 85 dB SPL, respectively, and the different columns show the results for different frequency pairs, as indicated on top of the upper panels. The error bars represent the standard error of the mean.
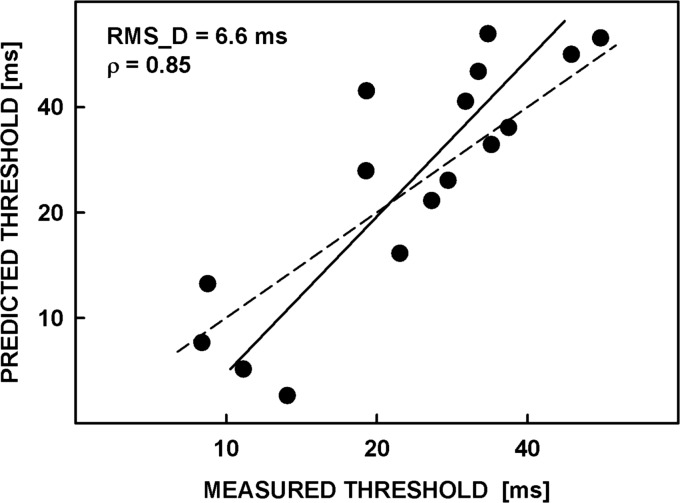
Figure 6 illustrates the relationship between the average measured and predicted asynchrony-detection thresholds. Because neither the predicted nor measured thresholds were free of error, the same errors were assumed for both and the data were analyzed using orthogonal regression (Deming, 1964), represented by the solid line in Fig. 6. A relatively uniform scatter of the points around this line indicates that the model did not systematically under- or over-predict the data. The root-mean-squared deviation (RMS_D) of the data points from the line was 6.6 ms. The correlation coefficient between the observed and predicted thresholds was ρ = 0.85. Overall, the predictions are in reasonably good agreement with the measured thresholds suggesting that the two tasks, i.e., the subjective judgments of the perceived asynchrony and the asynchrony detection measured in the 3I-3AFC procedure, were generally equivalent with respect to the cues used to perform them.
Figure 6.
Correlation between the (geometric) mean predicted and measured asynchrony-detection thresholds. The solid line represents orthogonal regression which takes into account variability in both thresholds. The dashed line has a slope of 1 and represents ideal agreement between the data and predictions.
In summary, the results from the asynchrony-discrimination experiment with the 500-ms tones followed the same general pattern as previously observed using a shorter tone duration (40 ms). However, thresholds for the 500-ms tones were generally higher than those for the 40-ms tones, although the difference was not significant for the pairs with the LF leading at 85 dB SPL. One possibility is that the effect of tone duration reflects the use of the overall duration of a tone pair as a cue for performing the task. Since duration-discrimination threshold increases with increasing baseline (reference) duration, higher thresholds would be expected for the 500- than the 40-ms tones (Abel, 1972). Another possibility is that the higher thresholds for the 500-ms tones are due to an interfering effect of longer exposure to irrelevant information, which may affect the memory trace when comparing the synchrony of onsets across observation intervals (Pastore et al., 1982). In the following experiment, the role of different cues is further investigated by manipulating the durations of the onset and offset ramps for a fixed duration of the tones.
EXPERIMENT 3: THE EFFECTS OF ONSET AND OFFSET RAMPS ON ASYNCHRONY DETECTION AND DISCRIMINATION
Comparisons of results from Experiment 2 in this study with those from the asynchrony-discrimination task performed with shorter tones by Wojtczak et al. (2012) showed that for the pairs with the HF leading at 85 dB SPL and for all tone pairs at 20 dB SL, asynchrony detection and discrimination thresholds were significantly higher for the 500-ms tones than the 40-ms tones. Pastore et al. (1982) showed that thresholds for detecting onset asynchrony increased with increasing common duration of the test tones after the onsets, even though that part of the stimuli provided no additional information about the asynchrony (the tones were gated off simultaneously). Thus, in our data, the effect of duration may have resulted from the listeners' inability to ignore an increased proportion of the overall stimulus that did not carry information about the relative timing of the onsets. Alternatively, the higher thresholds observed for the 500- than 40-ms tones may reflect the use of a change in overall duration of a tone pair as a cue in performing the asynchrony-detection task since the offsets were desynchronized along with the onsets. Duration discrimination has been shown to decline with increasing duration of the baseline stimulus (Abel, 1972).
All the previous studies of asynchrony detection used only one relatively high level of the tones. Physiological evidence suggests that neural responses to onsets are less precise for low-intensity stimuli than for high-intensity stimuli (e.g., Kitzes et al., 1978; Winter and Palmer, 1995). Thus, the relative contribution of onsets to the perceived asynchrony may decrease at low levels, making it more likely for tone duration to interfere with the accuracy of the decision regarding the relative timing of the tones. In this experiment, the relative role of onset and offset cues was examined by independently manipulating the duration of the onset and offset ramps, for two levels of the test tones. The assumption was that lengthening the duration of either ramp would render it less reliable as a cue.
Stimuli and procedure
Thresholds for detecting a change in asynchrony were measured for two standard asynchronies, 0 ms (asynchrony detection) and 60 ms (asynchrony discrimination). The stimuli were identical to those used in Experiment 2 except for ramp duration, which was manipulated across conditions. Four different gating configurations were used: 10-ms onset and offset ramps (10/10), 10-ms onset and 250-ms offset ramps (10/250), 250-ms onset and 10-ms offset ramps (250/10), and 250-ms onset and offset ramps (250/250). The ramps were included in the overall 500-ms tone duration. The experiment was performed at two levels, 20 dB SL and 85 dB SPL. All the remaining parameters of the stimuli, the masking noise, the procedure, and the equipment were the same as in Experiment 2.
Listeners
Five listeners participated in the experiment. Two of the listeners also participated in Experiment 2. All listeners had thresholds at or below 15 dB HL for the octave frequencies between 0.25 and 8 kHz. The new listeners were given practice, until asymptotic performance was observed, which typically took less than 2 h.
Results and discussion
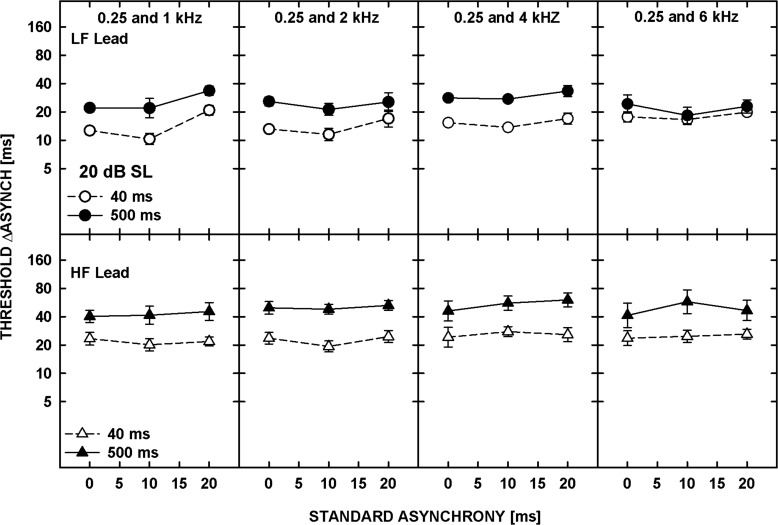
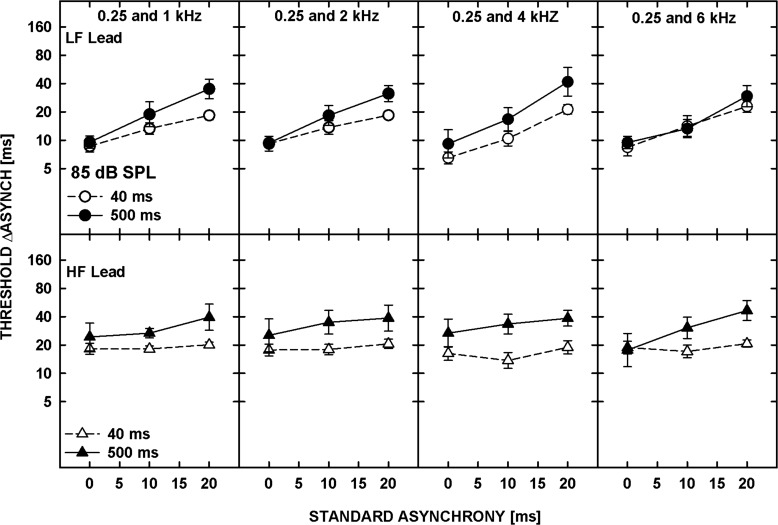
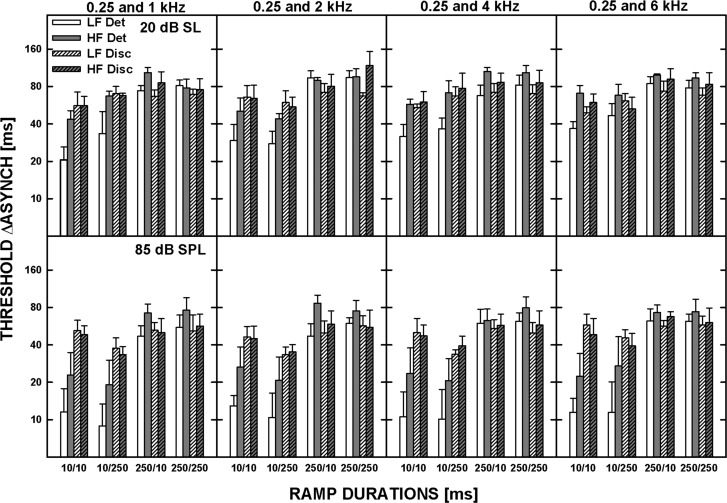
The patterns of the results were similar for the five listeners and thus only the geometric means of the individual thresholds are shown in Fig. 7. The top and bottom panels show the data for tones presented at 20 dB SL and 85 dB SPL, respectively. Data for different frequency separations are shown in different columns, as indicated at the top of the upper panels. Each panel shows data for the four ramp configurations. The bars with the plain and hatched fill represent thresholds for the standard asynchrony of 0 and 60 ms, respectively. The white and gray bars are for the LF-lead and HF-lead conditions, respectively.
Figure 7.
Thresholds for asynchrony detection (plain bars) and discrimination from the standard asynchrony of 60 ms (hatched bars), averaged geometrically for five listeners, for different ramp-duration configurations: (10/10)—10-ms onset and offset ramps, (10/250)—10-ms onset and 250-ms offset ramps, (250/10)—250-ms onset and 10-ms offset ramps, and (250/250)—250-ms onset and offset ramps. The upper and lower panels show data for 20 dB SL and 85 dB SPL, respectively. Data for different frequency pairs are shown in different columns. The error bars represent the standard error of the mean.
The data were analyzed using a repeated-measures ANOVA performed on log-transformed thresholds. Overall, thresholds shown in Fig. 7 were significantly higher for the 20-dB SL than for the 85-dB SPL tones [F(1,4) = 35.166, p = 0.004] and were significantly affected by the duration of the onset ramp [F(1,4) = 59.394, p = 0.002] but not by the duration of the offset ramp [F(1,4) = 0.892, p = 0.398]. Because of multiple significant interactions, additional ANOVAs were performed on some subsets of the data. Thresholds for asynchrony detection (i.e., the 0-ms standard asynchrony) were significantly lower for the LF-tone leading than the HF-tone leading [F(1,4) = 9.003, p = 0.04] while thresholds for asynchrony discrimination (for the 60-ms standard asynchrony) did not depend on the order of the tones [F(1,4) = 1.708, p = 0.261], consistent with the results from Experiment 2. Asynchrony detection was also significantly better for the 10- than the 250-ms onset ramp duration [F(1,4) = 52.283, p = 0.002] while the duration of the offset ramp had no significant effect [F(1,4) = 2.288, p = 0.205]. Similarly, for the standard asynchrony of 60 ms, asynchrony discrimination thresholds were significantly lower for the 10-ms than the 250-ms onset ramp [F(1,4) = 20.248, p = 0.011] while the offset ramp had no significant effect [F(1,4) = 0.181, p = 0.693].
In summary, asynchrony detection and discrimination thresholds were adversely affected by a longer duration of the onset ramp, presumably because gradual ramps provide less precise timing cues (e.g., Biermann and Heil, 2000). In contrast, gradual offset gating had no effect on the thresholds, suggesting that neither the temporal disparity of the offsets nor the overall duration were used to determine the relative timing between the tones. Overall, the results suggest that the temporal disparity of the onsets was a dominant cue in performing the task.
A PHYSIOLOGICALLY INSPIRED MODEL OF ASYNCHRONY PERCEPTION
In this section, a new model is proposed that, unlike the decision-theoretic model used to fit the data in Fig. 1, suggests a specific physiological process that could account for some important trends in the subjective judgments of synchrony and in the thresholds for asynchrony detection and discrimination. The model is inspired by physiology but remains speculative, due to the current lack of physiological data showing responses to synchronous and asynchronous stimuli with wide frequency separations. The model is based on the hypothesis that the perception of across-frequency synchrony is mediated by the activity of broadly tuned across-frequency onset-coincidence detectors in the midbrain or in the central auditory system. The onset-coincidence detectors are assumed to receive inputs from frequency-selective onset detectors. It is assumed that each of these onset detectors “fires” once when it registers the onset of a tone. The latency of the onset-detector response varies randomly across tone presentations, and its probability distribution can vary depending on the characteristics (frequency and level) of the evoking tone.
The mathematical details of the model are as follows. The probability density functions for onset-response latencies are modeled using asymmetric Gaussians,1
| (1) |
and
| (2) |
The superscripts, l and h, refer to the LF and HF channels, respectively. The index, i, denotes the level condition and can take on two values, i = 1 for 20 dB SL, and i = 2 for 85 dB SPL. The index, j, takes on values from 1 to 4, for frequencies 1, 2, 4, and 6 kHz, respectively. The variables , , , and , denote the standard deviations (in milliseconds) of the lower (−) and upper (+) sides of the distributions, subject to the constraints: , , , and ; these constraints were used to prevent the occurrence of negative standard deviations, or of negatively skewed distributions. The standard deviations and do not feature the index j because the same LF tone (250 Hz) was used for all tone pairs, and thus, for simplicity, the index j can also be thought of as representing pairs consisting of 250 Hz and each of the respective higher-frequency tones.
Assuming that the random across-trial fluctuations in the latencies of the onset responses to the two tones are statistically independent, the activation probability of an onset-coincidence detector can be computed as
| (3) |
Consequently, the expected value of the number of activated onset-coincidence detectors (out of a population containing ni,j detectors) for condition {i, j} equals
| (4) |
The fact that the number of coincidence detectors, ni,j, depends on the condition reflects an assumption that this number can vary depending on the level of the tones and on their frequency separation.
Finally, the probability that two tones having a level indexed by i, a frequency separation indexed by j, and an onset-time difference equal to δ (ms) are judged synchronous, ψi,j(δ), is related to the mean number of activated coincidence detectors, , via a logistic function
| (5) |
where
| (6) |
The constant, b, represents the listener's proclivity toward synchronous responses. The value of this constant determines the probability of a synchronous response when the number of activated detectors, , equals 0: The larger b is, the higher the probability of a “false alarm,” i.e., of a synchronous response to a pair of asynchronous tones. Here, as in the main text, the onset-time difference, δ, is defined as the onset time of the LF tone minus the onset time of the HF tone, so that negative values correspond to tone pairs with the LF tone leading, whereas positive values correspond to the pairs with the HF tone leading.
The values of the free parameters in the model, , , , , ni,j, and b, were found by fitting the model defined by Eqs. 1, 2, 3, 4 to the data from Experiment 1. Parameters corresponding to all possible combinations of the indices i and j (i.e., all level and frequency-separation conditions) were estimated simultaneously and conjointly, using all of the data from a given listener. The fits for different listeners were computed separately, using the constrained-minimization function, fmincon, of the Matlab Optimization Toolbox (The MathWorks, MA). The predicted synchronous-response functions for individual listeners were averaged and plotted in Fig. 8 by dashed lines along with the averaged data (replotted from Fig. 1). As in Fig. 1, the left and right panels show the predictions for the tones presented at 20 dB SL and 85 dB SPL, respectively, and different rows show the functions for different frequency pairs. The model predictions closely follow the shapes of the synchronous response functions.
Figure 8.
Data replotted from Fig. 1 (symbols) with predictions (dashed curves) by the model based on a broadly tuned monaural coincidence detector.
Table TABLE I. shows the average values of the model parameters that produced the best fits to the individual data. The parameter values suggest that the distributions of onset latencies for LF onset detectors are narrower than those for HF onset detectors; standard deviations, and , producing the best fits to the data were smaller than the standard deviations, and , at both stimulus levels. This outcome of the model implies higher temporal acuity of low-CF than high-CF neural pathways, which is at least qualitatively consistent with the results reported by Middlebrooks and Snyder (2010), who showed that electrically stimulated low-CF neurons in the central inferior colliculus (IC) can synchronize up to higher pulse rates than high-CF neurons. The best-fitting parameters of the model also suggest that the distributions of onset latencies are narrower for higher stimulus levels; standard deviations indexed with i = 2 were smaller than those for i = 1. This result is consistent with physiological data showing a decreased variability of neural onset responses with increasing level (Kitzes et al., 1978; Winter and Palmer, 1995; Heil et al., 2008).
TABLE I.
Average values of best-fitting model parameters.
| Level | Frequency [kHz] | Parameter name | Parameter average value |
|---|---|---|---|
| b | −3.81 | ||
| 20 dB SL | 0.25 | 10.71 | |
| 24.66 | |||
| 1 | 12.17 | ||
| 59.95 | |||
| 478 | |||
| 2 | 12.92 | ||
| 62.51 | |||
| 509 | |||
| 4 | 13.66 | ||
| 61.11 | |||
| 481 | |||
| 6 | 17.51 | ||
| 85.54 | |||
| 614 | |||
| 85 dB SPL | 0.25 | 3.04 | |
| 8.87 | |||
| 1 | 5.07 | ||
| 48.06 | |||
| 303 | |||
| 2 | 5.44 | ||
| 49.96 | |||
| 323 | |||
| 4 | 4.36 | ||
| 49.60 | |||
| 343 | |||
| 6 | 7.79 | ||
| 60.45 | |||
| 400 |
In a second step, the coincidence-detection model was used to generate “predicted” asynchrony-discrimination thresholds. To this aim, the model parameters were set to their best-fitting values (computed from Experiment 1 data in the previous step) and the decision variable, zi,j(δ), was evaluated separately for each stimulus condition and for each listener, for δ values ranging from δ0—the value corresponding to the standard asynchrony in the considered condition of Experiment 2 (e.g., +20 ms, for the “20-ms HF-leading condition”)—to δ0 + s512 ms, where s was equal to −1 for the conditions in which the LF tone was leading, and to +1 for the conditions with a HF-tone leading.
The zi,j(δ) values were used to form the decision variable
| (7) |
Intuitively, this decision variable represents the perceived difference in degree of synchrony between a pair of tones separated by δ ms (the comparison pair) and a pair of tones separated by δ0 ms (the standard pair).
Finally, the predicted thresholds, θi,j, were computed as the δ values corresponding to yi,j(δ) = 1.26σ, where 1.26 is the d′ corresponding to 70.7% correct in the 3I-3AFC task used to measure thresholds in the asynchrony-discrimination experiment, and σ denotes the standard deviation of the internal noise that limited the performance of the observers. The latter quantity was not directly observable; its value was estimated by minimizing the sum of squared deviations between the predicted and measured thresholds.
The mean predicted thresholds, averaged geometrically across the three listeners who participated in Experiments 1 and 2, are shown in Fig. 9 by open symbols, along with the (geometric-mean) thresholds that were measured in the same three listeners (filled symbols). For the LF-tone leading, asynchrony-discrimination thresholds could only be predicted for the standard asynchronies ≤20 ms. For larger standard asynchronies the distributions of onset-response latencies became separated for the LF and HF tones, and thus the coincidence detector could no longer contribute to the decision about the change in asynchrony. Interestingly, this limit coincides with the range of standard asynchronies, for which lower thresholds were observed for the pairs with the LF-tone leading than for the pairs with the HF-tone leading. For standard asynchronies greater than 20 ms, thresholds for the two stimulus configurations converged, perhaps indicating a change in the decision variable used by the listeners to perform the task.
Figure 9.
Geometrically averaged predicted (open symbols) and measured (filled symbols replotted from Fig. 2) asynchrony-discrimination thresholds for three listeners who participated in Experiments 1 and 2. The predictions were made based on the model fits to the individual data obtained in Experiment 1. The error bars show the standard error of the mean.
The predicted thresholds were highly correlated with the measured thresholds across conditions (Spearman's ρ = 0.78; p < 0.0001) indicating that the model captured the effect of level and the direction of delay (LF vs HF lead). However, in many cases the model produced lower thresholds than those observed in Experiment 2, although it generally was not the case for asynchrony detection measured with the LF-tone leading. One possible explanation for this discrepancy between the data and the predictions is in terms of the interfering effect of the relatively large proportion of the stimulus overall duration, over which no information about asynchrony was available (Pastore et al., 1982). As a consequence of such interference, the memory trace between the observation intervals in the 3I-3AFC task could be disrupted, leading to elevated thresholds. Since the model described in this section is based on the assumption that onset detectors constitute the input to the coincidence detector, the model cannot account for any effects that depend on stimulus duration. Note that since the interfering effect would be expected to raise thresholds, if incorporated in the model, it would bring the predictions closer in line with the data.
GENERAL DISCUSSION
Summary of experimental results
Experiment 1 involved subjective judgments of synchrony. In a majority of the individual results, for all four frequency pairs used in the experiment the maximum proportion of synchronous responses occurred at or very close to the 0-ms delay, i.e., the synchronous gating of the tones. In addition, the synchronous-response functions showed a significantly shallower slope for the pairs of tones with the HF leading than for the LF leading. The results from Experiment 2 measured thresholds for the detection and discrimination of asynchrony between the same tone pairs used in Experiment 1, using a forced-choice procedure with feedback indicating the correct response. Similar asymmetries were found in both experiments, and it was possible to use a model based on signal detection theory to predict the asynchrony detection results from the subjective judgments. Finally, Experiment 3 compared results with onset and offset ramps of different durations, and established that the onset ramps were critical and that changes in the offset ramp durations had no significant effect on detection or discrimination thresholds.
Overall, the patterns of results are consistent with those of Wojtczak et al. (2012), who used shorter tone durations (40 ms versus 500 ms used here). In addition, the results provide further support for the hypothesis for perceptual compensation for frequency-dependent cochlear delays, and show that the mechanisms involved in the processing of relative across-frequency timing information are asymmetric with respect to the ordering of the component frequencies.
Cochlear delays and neural synchrony throughout the auditory system
Evidence from animal physiology (Recio-Spinoso et al., 2005; Siegel et al., 2005; Temchin et al., 2005; Palmer and Shackleton, 2009; Temchin et al., 2011) and from measurements performed using non-invasive physiological techniques in humans (e.g., Elberling, 1974; Eggermont, 1979; Neely et al., 1988; Schoonhoven et al., 2001; Shera et al., 2002; Sisto and Moleti, 2007; Harte et al., 2009) shows that latencies of cochlear and auditory-nerve responses to low frequencies are longer than those for high-frequencies. Analysis of the relative across-frequency response timing at higher processing stages is complicated by non-homogeneity of the neural structures and responses in higher-level nuclei. Frequency-dependent latencies, similar to those observed in the peripheral responses, have been shown in neurons that appear to be specialized in coding of stimulus onsets in the cochlear nucleus (CN) of the cat (Kitzes et al., 1978) and the guinea pig (Winter and Palmer, 1995). In humans, the increased amplitude of the ABR wave-V in response to an up-chirp that presumably produces a synchronous response throughout the cochlea, compared to that for a click (Dau et al., 2000; Fobel and Dau, 2004; Petoe et al., 2010b,a), also supports the notion that frequency-dependent latencies are preserved at the level of the CN. These results suggest that any mechanism compensating for peripheral frequency-dependent delays is likely to originate central to the CN. However, little is known about the frequency dependence of onset latencies in the higher-level nuclei. Langner and Schreiner (1988) performed single- and multi-unit recordings in the IC of the cat. In a plot showing the response latency as a function of the CF of the unit, the shortest latency observed at the CF of 40 kHz was similar to that observed for the CF of 500 Hz. However, for each CF, the data in the plot were scattered over a large range of latencies with the upper boundary of that range increasing with decreasing CF. Onset latencies measured in the auditory cortex of the cat for neurons with different CFs (Heil, 1997; Heil and Irvine, 1997) also showed considerable scatter, precluding any conclusions about the presence or absence of the CF-dependent delays. Based on their data, it is impossible to infer if the differences in latency across CFs are absent at that site or if any systematic dependence of the latency on CF is simply obscured by the large variability. Similarly, response latencies in the human auditory cortex derived from evoked magnetic fields by Biermann and Heil (2000) show no systematic dependence on CF but the variability in the data precludes any strong conclusions. Thus, the physiological evidence for the compensating mechanism is currently lacking but the existing physiological and psychophysical data suggest that the mechanism probably originates from sites central to the CN. Another important question is whether the hypothesized neural compensation for frequency-dependent cochlear-response delays can adapt to changes in the shape of the latency-frequency function that may accompany cochlear damage, or whether the mechanism is hard wired. The capability of the auditory system to develop new neural maps in response to peripheral changes has been shown for sound source localization in humans (Hofman et al., 1998) and in barn owls (Knudsen and Knudsen, 1986; Knudsen et al., 1994). No comparable data are available from tasks that involve the use of across-frequency timing information.
Effect of overall duration and onset or offset ramps on asynchrony detection and discrimination
When two tones with remote frequencies are delayed relative to one another, the delay leads to temporal disparity of the onsets and offsets and an increase in the duration of the overall stimulus. All these cues could potentially be used, separately or in combination, for the detection of asynchrony between the tones. Previous studies have shown that thresholds for detecting onset asynchrony for stimuli with simultaneous offsets were substantially lower than thresholds for detecting offset asynchrony for stimuli with simultaneous onsets (Zera and Green, 1993; Mossbridge et al., 2006). Because of superior sensitivity to onset asynchrony, it has been suggested that asynchrony detection involves the operation of monaural coincidence detectors (Mossbridge et al., 2006; Micheyl et al., 2010). Physiological correlates for monaural coincidence detectors were implicated by Winter and Palmer (1995), who found facilitation of responses to CF tones in the onset neurons within the CN of the guinea pig by presenting these tones simultaneously with off-CF tones that, when presented alone, did not produce measurable excitation at the CF. In another study, Palmer and Winter (1996) showed that the facilitation was not limited to the cases where the CF and off-CF tones were gated synchronously but was also observed when the off-frequency tone preceded the CF tone by as much as 20 ms, or was delayed relative to the CF tone by up to ∼10 ms. These results suggested that the monaural onset coincidence detectors may have relatively long integration times and, consequently, may exhibit limited precision in coding across-frequency asynchrony. Because the location of the hypothesized compensation mechanism would have to be central to the CN, broadly tuned monaural coincidence detectors at higher processing stages may be involved in the processing of relative timing between tones that are several octaves apart in frequency. To our knowledge, no study has investigated responses from pairs of asynchronous tones at sites central to the CN.
The idea of onset disparity being the sole cue for detecting across-frequency asynchrony appears intuitive given that neurons with particularly strong onset (compared with ongoing) responses are found at every stage of the auditory system. However, if onsets alone were used, one would expect asynchrony detection thresholds to be independent of stimulus duration (at least as long as the duration exceeded the integration time of coincidence detectors). In an apparent contrast to this expectation, Pastore et al. (1982) found that thresholds for detecting onset asynchrony between two tones with simultaneous offsets increased as the duration of the tones increased. Since the overall duration did not change while the asynchrony between the tones was manipulated, it was not clear why detecting the disparity between the onsets was affected by the common duration of the tones that did not provide any additional information about the asynchrony. Comparisons of the data from 500-ms tones of Experiment 2 in this study with the data from 40-ms tones of Wojtczak et al. (2012) also revealed higher asynchrony detection thresholds for a longer tone duration, although the effect was not significant for the pairs of tones presented at 85 dB SPL with the LF leading.
Data from Experiment 3 suggested that the onset asynchrony (rather than overall duration or offset asynchrony) dominated performance. Thus, given these results and the duration effects on onset-asynchrony detection reported by Pastore et al. (1982), it can be argued that the increase in asynchrony detection and discrimination thresholds with increasing duration of the stimuli may simply reflect interference by an increased overlapping duration of the stimuli that on its own does not provide any information about the relative timing between the tones. It is not clear why the listeners seem unable to ignore parts of the stimuli that do not provide any cues for the task at hand and adversely affect performance but examples of such interference are plentiful in auditory perception (e.g., informational masking reported by Kidd et al., 2003).
Speculations on the physiological mechanisms for coding across-frequency timing
The model presented in Sec. 5 successfully predicted the asymmetry of synchrony judgments, and the parameters of the model that yielded the best fits to the data suggested that the distribution of onset latencies at the input to a monaural coincidence detector was narrower in neurons with low CFs than in neurons with high CFs. To our knowledge, no physiological study has systematically investigated changes in variability of onset latencies with CF, especially at sites central to the CN, and this outcome of the model should be considered as a hypothesis that needs experimental verification. It can be argued that variability in onset latency would be expected to increase with increasing mean latency since such a trend has been consistently observed in a number of studies that measured changes in onset latency with level (e.g., Kitzes et al., 1978; Winter and Palmer, 1995; Heil, 1997; Tan et al., 2008). However, if one assumes that a mechanism compensating for cochlear delays exists, then the argument may not hold at neural sites following the compensation. At least one study provides data that are consistent with this reasoning. Middlebrooks and Snyder (2010) found that neurons with low CFs in the IC of a cat exhibit superior temporal acuity over neurons with high CFs, when cochlear processing is bypassed by using electrical stimulation of the AN. Their data showed that the upper limit for coding high pulse rates was significantly higher in low-CF than high-CF neurons, suggesting that low-CF neurons may be more precise at coding onset-timing information. This, in turn, may result in a narrower distribution of the onset-response times. In another study, a narrower distribution of onset latencies for a population of low-CF compared with high-CF neurons was shown by multi-unit responses recorded from the primary auditory cortex (A1) of the macaque monkey (Fishman and Steinschneider, 2009). The distributions of multi-unit responses were also asymmetric, with a steeper slope before than after the maximum of the distribution, in agreement with the asymmetric Gaussian probability density functions in the model presented above in Sec. 5 (see Table TABLE I.).
In the model, narrower distributions of onset latencies had to be used to predict the data at 85 dB SPL than at 20 dB SL. This assumption has strong physiological support from studies that measured level effects on onset latencies at different sites of the auditory pathways, from the AN (Heil et al., 2008), through the CN (Kitzes et al., 1978, cat; Winter and Palmer, 1995, guinea pig), the IC (Tan et al., 2008, mice), to the auditory cortex (Heil, 1997, cat). Since the frequency separation was large for all the tone pairs used in this study, no specific trend for changes in the variance around the mean response latency with frequency was implicated by the best-fitting model parameters for the higher-frequency tones, i.e., 1, 2, 4, and 6 kHz. However, an implicit assumption in the model is that for pairs of tones with small frequency separations, the distributions of onset latencies would have similar bandwidths. This would lead to predicting symmetric shapes of synchronous response functions, and thus similar asynchrony-detection thresholds for pairs of tones with LF and HF leading, consistent with the data of Micheyl et al. (2010).
In summary, although the model is speculative, some of its assumptions have physiological support, some provide strong testable predictions for further physiological study, and none appear to be directly contradicted by the available physiological data. In addition to level effects on onset latencies and their variability, the widths (on the time scale) of the assumed distributions were within the physiological range given the scope of the integration window suggested for a monaural coincidence detector in the CN of guinea pig by Palmer and Winter (1996) and the temporal span of onset latencies from multiunit recordings in the A1 of macaque monkey (Fishman and Steinschneider, 2009).
SUMMARY
The purpose of this study was to investigate the effect of stimulus parameters on the perception of relative across-frequency timing. The following main results were obtained:
-
(1)
Functions relating the proportion of synchronous responses to the delay between two tones with remote frequencies (i.e., exciting separate auditory channels) showed a peak around a 0-ms delay, for most of the listeners and conditions tested in the study, although in some conditions the peak corresponded to pairs with a small HF lead. The generally veridical perception of across-frequency synchrony for the 500-ms tones is consistent with the earlier results of Wojtczak et al. (2012), who used 40-ms tones. Overall, the data support the hypothesis that frequency-dependent cochlear delays are compensated for at higher neural processing stages.
-
(2)
The subjective synchrony judgments showed a marked asymmetry, with a HF-leading tone pair perceived as synchronous on a larger proportion of trials than a LF-leading pair with the same absolute delay.
-
(3)
For the standard asynchrony of 0 ms and for small non-zero standard asynchronies, asynchrony detection and discrimination thresholds were lower (better) for LF-leading tone pairs than for HF-leading tone pairs. The lower thresholds for LF-leading tone pairs were predicted by a model based on signal detection theory, in which the data from subjective synchrony judgments were used to derive psychometric functions underlying the perception of across-frequency asynchrony.
-
(4)
Asynchrony detection and discrimination thresholds were generally higher (worse) for the 500-ms tones than for the 40-ms tones (Wojtczak et al., 2012), although the overall pattern of results was similar.
-
(5)
Increasing the onset ramp durations from 10 to 250 ms led to a significant worsening in detection and discrimination thresholds, whereas changing the offset ramp durations had no significant effect, suggesting that the dominant cues used in the perception of relative across-frequency timing information are temporal disparities of the onsets.
-
(6)
The asymmetry in the perception of across-frequency asynchrony was modeled assuming a narrower distribution of onset latencies for neurons with low CFs than for neurons with high CFs at the input to a monaural coincidence detector. Physiological data that would support or disprove this assumption are currently lacking, and the model should be treated as a motivation for investigating the physiological mechanisms involved in coding relative onset responses for tone pairs with remote frequencies at the sites central to the CN.
ACKNOWLEDGMENTS
The study was supported by Grant No. R01 DC 010374 from the National Institutes of Health. The authors thank the three anonymous reviewers for helpful suggestions and comments on the earlier version of the manuscript.
Portions of this manuscript were presented at the 34th Annual Midwinter Meeting of the Association for Research in Otolaryngology [M. Wojtczak and A. J. Oxenham, ARO (2011), A#185].
Footnotes
Gaussian distributions were chosen purely for mathematical convenience to provide a proof of concept. The choice of Gaussians does not imply that other distributions could not result in similar (or better) fits to the data.
References
- Abel, S. M. (1972). “ Duration discrimination of noise and tone bursts,” J. Acoust. Soc. Am. 51, 1219–1223. 10.1121/1.1912963 [DOI] [PubMed] [Google Scholar]
- Biermann, S., and Heil, P. (2000). “ Parallels between timing of onset responses of single neurons in cat and of evoked magnetic fields in human auditory cortex,” J. Neurophysiol. 84, 2426–2439. [DOI] [PubMed] [Google Scholar]
- Dai, H., and Micheyl, C. (2011). “ Psychometric functions for pure-tone frequency discrimination,” J. Acoust. Soc. Am. 130, 263–272. 10.1121/1.3598448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dau, T., Wegner, O., Mellert, V., and Kollmeier, B. (2000). “ Auditory brainstem responses with optimized chirp signals compensating basilar-membrane dispersion,” J. Acoust. Soc. Am. 107, 1530–1540. 10.1121/1.428438 [DOI] [PubMed] [Google Scholar]
- de Boer, E. (1980). “ Auditory physics. Physical principles in hearing theory I,” Phys. Rep. 62, 87–174. 10.1016/0370-1573(80)90100-3 [DOI] [Google Scholar]
- Deming, W. E. (1964). Statistical Adjustment of Data (Dover, New York: ), 261 p. [Google Scholar]
- Eggermont, J. J. (1979). “ Narrow-band AP latencies in normal and recruiting human ears,” J. Acoust. Soc. Am. 65, 463–470. 10.1121/1.382345 [DOI] [PubMed] [Google Scholar]
- Elberling, C. (1974). “ Action potentials along the cochlear partition recorded from the ear canal in man,” Scand. Audiol. 3, 13–19. 10.3109/01050397409044959 [DOI] [Google Scholar]
- Fishman, Y. I., and Steinschneider, M. (2009). “ Temporally dynamic frequency tuning of population responses in monkey primary auditory cortex,” Hear. Res. 254, 64–76. 10.1016/j.heares.2009.04.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fobel, O., and Dau, T. (2004). “ Searching for the optimal stimulus eliciting auditory brainstem responses in humans,” J. Acoust. Soc. Am. 116, 2213–2222. 10.1121/1.1787523 [DOI] [PubMed] [Google Scholar]
- Harte, J. M., Pigasse, G., and Dau, T. (2009). “ Comparison of cochlear delay estimates using otoacoustic emissions and auditory brainstem responses,” J. Acoust. Soc. Am. 126, 1291–1301. 10.1121/1.3168508 [DOI] [PubMed] [Google Scholar]
- Heil, P. (1997). “ Auditory cortical onset responses revisited. I. First-spike timing,” J. Neurophysiol. 77, 2616–2641. [DOI] [PubMed] [Google Scholar]
- Heil, P., and Irvine, D. R. (1997). “ First-spike timing of auditory-nerve fibers and comparison with auditory cortex,” J. Neurophysiol. 78, 2438–2454. [DOI] [PubMed] [Google Scholar]
- Heil, P., Neubauer, H., Brown, M., and Irvine, D. R. (2008). “ Towards a unifying basis of auditory thresholds: distributions of the first-spike latencies of auditory-nerve fibers,” Hear. Res. 238, 25–38. 10.1016/j.heares.2007.09.014 [DOI] [PubMed] [Google Scholar]
- Hofman, P. M., Van Riswick, J. G. A., and Van Opstal, A. J. (1998). “ Relearning sound localization with new ears,” Nat. Neurosci. 1, 417–421. 10.1038/1633 [DOI] [PubMed] [Google Scholar]
- Irino, T., and Patterson, R. D. (1997). “ A time-domain, level-dependent auditory filter: The gammachirp,” J. Acoust. Soc. Am. 101, 412–419. 10.1121/1.417975 [DOI] [Google Scholar]
- Kidd, G., Jr., Mason, C. R., Arbogast, T. L., Brungart, D. S., and Simpson, B. D. (2003). “ Informational masking caused by contralateral stimulation,” J. Acoust. Soc. Am. 113, 1594–1603. 10.1121/1.1547440 [DOI] [PubMed] [Google Scholar]
- Kitzes, L. M., Gibson, M. M., Rose, J. E., and Hind, J. E. (1978). “ Initial discharge latency and threshold considerations for some neurons in cochlear nuclear complex of the cat,” J. Neurophysiol. 41, 1165–1182. [DOI] [PubMed] [Google Scholar]
- Knudsen, E. I., Esterly, S. D., and Olsen, J. F. (1994). “ Adaptive plasticity of the auditory space map in the optic tectum of adult and baby barn owls in response to external ear modification,” J. Neurophysiol. 71, 79–94. [DOI] [PubMed] [Google Scholar]
- Knudsen, E. I., and Knudsen, P. F. (1986). “ The sensitive period for auditory localization in barn owls is limited by age, not by experience,” J. Neurosci. 6, 1918–1924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langner, G., and Schreiner, C. E. (1988). “ Periodicity coding in the inferior colliculus of the cat. I. Neuronal mechanisms,” J. Neurophysiol. 60, 1799–1822. [DOI] [PubMed] [Google Scholar]
- Levitt, H. (1971). “ Transformed up-down methods in psychoacoustics,” J. Acoust. Soc. Am. 49, 467–477. 10.1121/1.1912375 [DOI] [PubMed] [Google Scholar]
- Micheyl, C., Hunter, C., and Oxenham, A. J. (2010). “ Auditory stream segregation and the perception of across-frequency synchrony,” J. Exp. Psychol. Hum. Percept. Perform. 36, 1029–1039. 10.1037/a0017601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks, J. C., and Snyder, R. L. (2010). “ Selective electrical stimulation of the auditory nerve activates a pathway specialized for high temporal acuity,” J. Neurosci. 30, 1937–1946. 10.1523/JNEUROSCI.4949-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mossbridge, J. A., Fitzgerald, M. B., O'Connor, E. S., and Wright, B. A. (2006). “ Perceptual-learning evidence for separate processing of asynchrony and order tasks,” J. Neurosci. 26, 12708–12716. 10.1523/JNEUROSCI.2254-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mossbridge, J. A., Scissors, B. N., and Wright, B. A. (2008). “ Learning and generalization on asynchrony and order tasks at sound offset: implications for underlying neural circuitry,” Learn. Memory 15, 13–20. 10.1101/lm.573608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neely, S. T., Norton, S. J., Gorga, M. P., and Jesteadt, W. (1988). “ Latency of auditory brain-stem responses and otoacoustic emissions using tone-burst stimuli,” J. Acoust. Soc. Am. 83, 652–656. 10.1121/1.396542 [DOI] [PubMed] [Google Scholar]
- Palmer, A. R., and Shackleton, T. M. (2009). “ Variation in the phase of response to low-frequency pure tones in the guinea pig auditory nerve as functions of stimulus level and frequency,” J. Assoc. Res. Otolaryngol. 10, 233–250. 10.1007/s10162-008-0151-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer, A. R., and Winter, I. M. (1996). “ The temporal window of two-tone facilitation in onset units of the ventral cochlear nucleus,” Audiol. Neuro-Otol. 1, 12–30. 10.1159/000259199 [DOI] [PubMed] [Google Scholar]
- Parker, E. M. (1988). “ Auditory constraints on the perception of voice-onset time: the influence of lower tone frequency on judgments of tone-onset simultaneity,” J. Acoust. Soc. Am. 83, 1597–1607. 10.1121/1.395914 [DOI] [PubMed] [Google Scholar]
- Pastore, R. E., Harris, L. B., and Kaplan, J. K. (1982). “ Temporal order identification: some parameter dependencies,” J. Acoust. Soc. Am. 71, 430–436. 10.1121/1.387446 [DOI] [Google Scholar]
- Patterson, R. D. (1987). “ A pulse ribbon model of monaural phase perception,” J. Acoust. Soc. Am. 82, 1560–1586. 10.1121/1.395146 [DOI] [PubMed] [Google Scholar]
- Petoe, M. A., Bradley, A. P., and Wilson, W. J. (2010a). “ On chirp stimuli and neural synchrony in the suprathreshold auditory brainstem response,” J. Acoust. Soc. Am. 128, 235–246. 10.1121/1.3436527 [DOI] [PubMed] [Google Scholar]
- Petoe, M. A., Bradley, A. P., and Wilson, W. J. (2010b). “ Spectral and synchrony differences in auditory brainstem responses evoked by chirps of varying durations,” J. Acoust. Soc. Am. 128, 1896–1907. 10.1121/1.3483738 [DOI] [PubMed] [Google Scholar]
- Recio-Spinoso, A., Temchin, A. N., van Dijk, P., Fan, Y.-H., and Ruggero, M. A. (2005). “ Wiener-kernel analysis of responses to noise of chinchilla auditory-nerve fibers,” J. Neurophysiol. 93, 3615–3634. 10.1152/jn.00882.2004 [DOI] [PubMed] [Google Scholar]
- Schoonhoven, R., Prijs, V. F., and Schneider, S. (2001). “ DPOAE group delays versus electrophysiological measures of cochlear delay in normal human ears,” J. Acoust. Soc. Am. 109, 1503–1512. 10.1121/1.1354987 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., and Oxenham, A. J. (2002). “ Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements,” Proc. Natl. Acad. Sci. U.S.A. 99, 3318–3323. 10.1073/pnas.032675099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel, J. H., Cerka, A. J., Recio-Spinoso, A., Temchin, A. N., van Dijk, P., and Ruggero, M. A. (2005). “ Delays of stimulus-frequency otoacoustic emissions and cochlear vibrations contradict the theory of coherent reflection filtering,” J. Acoust. Soc. Am. 118, 2434–2443. 10.1121/1.2005867 [DOI] [PubMed] [Google Scholar]
- Sisto, R., and Moleti, A. (2007). “ Transient evoked otoacoustic emission latency and cochlear tuning at different stimulus levels,” J. Acoust. Soc. Am. 122, 2183–2190. 10.1121/1.2769981 [DOI] [PubMed] [Google Scholar]
- Tan, X., Wang, X., Yang, W., and Xiao, Z. (2008). “ First spike latency and spike count as functions of tone amplitude and frequency in the inferior colliculus of mice,” Hear. Res. 235, 90–104. 10.1016/j.heares.2007.10.002 [DOI] [PubMed] [Google Scholar]
- Temchin, A. N., Recio-Spinoso, A., and Ruggero, M. A. (2011). “ Timing of cochlear responses inferred from frequency-threshold tuning curves of auditory-nerve fibers,” Hear. Res. 272, 178–186. 10.1016/j.heares.2010.10.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temchin, A. N., Recio-Spinoso, A., van Dijk, P., and Ruggero, M. A. (2005). “ Wiener kernels of chinchilla auditory-nerve fibers: Verification using responses to tones, clicks, and noise and comparison with basilar-membrane variations,” J. Neurophysiol. 93, 3635–3648. 10.1152/jn.00885.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uppenkamp, S., Fobel, S., and Patterson, R. D. (2001). “ The effects of temporal asymmetry on the detection and perception of short chirps,” Hear. Res. 158, 71–83. 10.1016/S0378-5955(01)00299-4 [DOI] [PubMed] [Google Scholar]
- Wichmann, F. A., and Hill, N. J. (2001). “ The psychometric function: I. Fitting, sampling, and goodness of fit,” Percept. Psychophys. 63, 1293–1313. 10.3758/BF03194544 [DOI] [PubMed] [Google Scholar]
- Winter, I. M., and Palmer, A. R. (1995). “ Level dependence of cochlear nucleus onset unit responses and facilitation by second tones or broadband noise,” J. Neurophysiol. 73, 141–159. [DOI] [PubMed] [Google Scholar]
- Wojtczak, M., Beim, J. A., Micheyl, C., and Oxenham, A. J. (2012). “ Perception of across-frequency asynchrony and the role of cochlear delays,” J. Acoust. Soc. Am. 131, 363–377. 10.1121/1.3665995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zera, J., and Green, D. M. (1993). “ Detecting temporal onset and offset asynchrony in multicomponent complexes,” J. Acoust. Soc. Am. 93, 1038–1052. 10.1121/1.405552 [DOI] [PubMed] [Google Scholar]