Wave motion on the surface of the human tympanic membrane: Holographic measurement and modeling analysis

Abstract

Sound-induced motions of the surface of the tympanic membrane (TM) were measured using stroboscopic holography in cadaveric human temporal bones at frequencies between 0.2 and 18 kHz. The results are consistent with the combination of standing-wave-like modal motions and traveling-wave-like motions on the TM surface. The holographic techniques also quantified sound-induced displacements of the umbo of the malleus, as well as volume velocity of the TM. These measurements were combined with sound-pressure measurements near the TM to compute middle-ear input impedance and power reflectance at the TM. The results are generally consistent with other published data. A phenomenological model that behaved qualitatively like the data was used to quantify the relative magnitude and spatial frequencies of the modal and traveling-wave-like displacement components on the TM surface. This model suggests the modal magnitudes are generally larger than those of the putative traveling waves, and the computed wave speeds are much slower than wave speeds predicted by estimates of middle-ear delay. While the data are inconsistent with simple modal displacements of the TM, an alternate model based on the combination of modal motions in a lossy membrane can also explain these measurements without invoking traveling waves.

INTRODUCTION

Sound-induced motions of the tympanic membrane (TM) or eardrum are coupled to the inner ear via vibration of the ossicular chain. Therefore, the TM plays an important early role in the reception and transmission of sound energy to the inner ear.

The sound-induced vibration of the entire TM surface is highly frequency dependent and the spatial patterns of the vibrations qualitatively vary from simple in-phase displacement patterns to more complex patterns with many spatial maxima and minima moving with different phase angles as frequency increases (Tonndorf and Khanna, 1970; Khanna and Tonndorf, 1972; Decraemer et al., 1989, 1999; Rosowski et al., 2009; Cheng et al., 2010). Attempts have been made to describe the complex motion patterns observed on the TM surface in response to high frequency sound in terms of combinations of wave motions (de La Rochefoucauld and Olson, 2010; Cheng et al., 2010). Based on the stroboscopic holography measurement of TM motion on cadaveric human temporal bones (TBs) at four frequencies (Cheng et al., 2010), we hypothesized that the relatively uniform acoustic stimulation on the TM surface from the ear canal produced large standing-wave-like modal motions and smaller traveling waves on the TM surface. de La Rochefoucauld and Olson (2010) came to similar conclusions in their study of gerbil TM surface motions. Here, we expand our description of the motion of the surface of the cadaveric human TM to include more TB specimens and more frequency sampling points. We also use a simple two-wave phenomenological model to separate out different motion components on the surface of the TM and describe the relative magnitudes and spatial frequencies of the different surface waves. Furthermore, we used our holographic techniques to measure the motion of the umbo of the malleus, as well as the complex volume velocity of the entire TM to directly compute middle-ear (ME) input impedance and reflectance at the TM. These measurements are compared to others in the literature.

Theories of TM function

While we describe complicated surface motions of the TM that result from the combination of modal motions of the entire TM surface and possible traveling waves on the TM surface, it is not known how these different motion components contribute to the vibration of the manubrium and ossicular chain necessary for normal sound conduction to the inner ear. Several contrasting theories have been proposed to explain the coupling of sound-induced TM surface motions and the vibration of the manubrium and ossicular chain. These theories are either based on limited experimental observations of temporal and spatial motions of the TM or modeling approaches.

One of the oldest theories of TM motion is the catenary lever theory postulated by von Helmholtz (1868). Based on its curved shape, von Helmholtz considered the TM provided a catenary lever that aided the transformer function of the ME, where large displacements of the central ring of the membrane resulted in smaller displacements of the manubrium and the coupled ossicles (von Helmholtz, 1868). Later, von Békésy used a capacitive probe to describe the sound-induced motion at multiple points on the TM surface in response to low frequency sound stimuli. von Békésy's interpretation of his results was that the TM moved as a stiff plate that was hinged near the pars flaccida of the TM. In his theory, the ME transformer function was mainly accomplished by the ratio between TM and stapes footplate areas and was not greatly affected by any catenary process within the TM (von Békésy, 1941). In the 1970s, Tonndorf and Khanna used time-averaged holography (TAH) to study the magnitude of the vibration of the entire surface of the TM in humans and cats (e.g., Khanna and Tonndorf, 1972; Tonndorf and Khanna, 1972). Their results suggested the presence of frequency-dependent modes of TM surface motion, similar to the modes of the vibrating diaphragm of a microphone. Furthermore, they observed that the TM locations coupled to the umbo and manubrium of the malleus moved with much smaller displacements than did the areas of the TM between the manubrium and the TM rim. Such decreased motion of the manubrium relative to other regions on the TM surface is consistent with von Helmholtz's curved membrane theory (Tonndorf and Khanna, 1970). With stimulus frequencies between 2 and 8 kHz, Khanna and Tonndorf (1972) observed complex TM motion patterns with multiple spatial maxima and minima of motion. Tonndorf and Khanna (1970) interpreted these complicated patterns in terms of higher-order modal motions, where they suggested the different maxima were separated by nodal regions. The presence of higher-order modal motions in man-made sound-transducing surfaces, e.g., microphone or loudspeaker diaphragms, is a sign that the surface is “breaking-up” and no longer acting efficiently (Beranek, 1993; Fletcher, 1992). Keeping this in mind, Tonndorf and Khanna (1970, 1972) and Shaw and Stinson (1983) suggested that such break ups would decouple the motion of the more distant parts of the membrane surface from the center of the TM, and lead to a decrease in the sensitivity of the ME's response to high-frequency sound. With this decoupling in mind, Tonndorf and Khanna suggested that the primary function of much of the TM surface at high frequencies was to act as a baffle that maintained a significant sound pressure difference between the ear canal and ME cavity (Tonndorf and Khanna, 1970).

Other hypotheses for the role of the TM in hearing have been proposed. Puria and Allen (1998) fit measurements of ME input admittance and ME sound transfer in cats with a transmission line model that assumes there are forward-going and reflected surface waves traveling on the TM surface as well as longitudinal waves in the ossicular sound conducting path. This model formalized the concept of impedance matching at multiple places within the ossicular system: Between air in the ear canal and the TM, between the TM and the ossicular chain, and between the ossicular chain and the inner ear. These ideas are further developed in the TM transmission-line models of Parent and Allen (2007, 2010), and the string model of Goll and Dalhoff (2011).

A variation on the modal model of TM function was proposed by Fay et al. (2006). In their model, the function of the TM in ME sound conduction is tightly connected to both the material properties of the fibers that course through the middle lamina of the TM, and the shape of the TM. They concluded the “combination of its (TM) shape, angular placement and composition” contributes to the “eardrum's success as an instrument of hearing” (Fay et al., 2006). In particular, they suggested the high density of TM modal resonances at high frequencies, where “all the resonances are summed at the malleus attachment… produce a smooth transfer of pressure across all frequencies” (Fay et al., 2006). The idea of the modal resonances of the TM at high frequencies is in line with the descriptions of Tonndorf and Khanna (1970) but the interpretation of the complex modal patterns at high frequencies is quite different. Tonndorf and Khanna (1970, 1976) suggest the high frequency modes are uncoupled from the motion of the ossicles while Fay et al. (2006) suggest that the closely spaced high-frequency modes actually average together to produce a smoothed frequency dependence of ossicular motion.

Measurements of the magnitude and phase angle of TM motion

Holographic data (Khanna and Tonndorf, 1972; Tonndorf and Khanna, 1972; Rosowski et al., 2009) only provide information about the magnitude of motion of the TM surface, and generally do not identify regions that move at different phase angles, or traveling waves that are marked by regions where the phase angle of motion varies regularly with position. A technique that measures both the magnitude and phase angle of TM motion is laser Doppler vibrometry (LDV). LDV has been used repeatedly to measure the sound-induced motion at specific locations on the TM surface, such as the umbo, over a wide frequency range (0.1 to 20 kHz) (e.g., Decraemer et al. 1989; Goode et al., 1993, 1994, 1996; Gan et al., 2004; Rosowski et al., 2008). These results provide more quantitative views of a vibrating TM: The displacement magnitude of the TM at the umbo varies with frequency and peaks around 1 kHz while the phase angle of the displacement and stimulus sound pressure is near 0 up to about 1 kHz and then decreases with increasing frequency. The limited spatial sampling density of the LDV measurement is partially overcome by using scanning LDV to measure displacement of the TM at multiple locations (Decraemer et al., 1999; de La Rochefoucauld and Olson, 2010).

Our group has been studying the sound-induced motion of the TM using fiber-optic-based opto-electronic holographic (OEH) interferometery (Furlong and Pryputniewicz, 1998; Furlong et al., 2009; Hernández-Montes et al., 2009; Flores-Moreno et al., 2011). Our previous studies have shown that sound-induced motions of the mammalian TM follow different patterns (simple, complex, ordered) within different stimulus frequency ranges (Rosowski et al., 2009). We have also suggested that the complex and ordered patterns result from the interaction of modal motions and traveling waves on the TM surface (Cheng et al., 2010; Rosowski et al., 2011). However, the magnitudes and wave numbers of the different modes of motion have not yet been quantified and questions, such as how modal motions and putative surface waves traveling on the TM surface are related to ME sound transmission, remain unanswered and need further investigation.

In this study, we measured the sound-induced displacement of the TM in human TBs at 8 to 25 frequencies between 0.2 and 18 kHz. The opto-electronic holography system (Hernández-Montes et al., 2009) was operated in the stroboscopic mode, and provided measurements of both the magnitude and phase angle of the displacement of the TM at about 300 000 points on the TM surface. A phenomenological model analysis has been applied to identify different modal motions or waves generated on the TM surface by sound and quantify their amplitudes and spatial frequencies. These results allowed estimation of the apparent speed of traveling-wave-like phenomena along the TM and the relative magnitude of modal motions and “traveling waves.” Our results are also used to test predictions of various models of TM motion.

METHODS

Stroboscopic holography

The design and specifications of our OEH system in stroboscopic mode can be found in Hernández-Montes et al. (2009) and Cheng et al. (2010). Briefly, opto-electronic holography records spatially and temporally dependent interference patterns (optical fringe patterns) produced by the interaction of a fixed reference laser beam and a beam reflected from a moving object. In our studies, the optical path length between the TM and the recording camera is affected by the sound-driven vibrations of the TM, producing time-related variations in the intensity of the interference pattern at each camera pixel. In stroboscopic mode, the camera records holographic images while the object is illuminated by a train of brief laser pulses that are locked to one of eight phases of the acoustic stimulus. Two holograms illuminated at different stimulus phases are used to compute the deformation of the TM between the two phases by the change in the optical interference path [see Eqs. (2) and (3) in Cheng et al., 2010].

Data acquisition

Following previously described procedures (Cheng et al., 2010), seven fresh human TBs (TB09_I, TB09_II, TB10_4, TB10_5, TB10p1, TB10p2, and TB10p3) without history of otologic disease were prepared. Most of the bony external ear canal was removed to expose 80% to 90% of the TM surface area without damage to the TM or its support. The experimental setup is described in Fig. 1 of Cheng et al. (2010). Briefly, the TB was positioned with the bony rim of the TM perpendicular to the illumination beam such that the holograms measure displacements that are perpendicular to the TM rim. In this position the bony rim is also orthogonal to the sound field that stimulates the TM. A calibrated prepolarized microphone (PCB Piezotronics, Depew, NY, Model 377C10) with a probe-tube was used to monitor the stimulus sound pressure at the edge of the TM. In order to increase the amount of light reflected from the TM, the holographic measurements we report in Sec. 3 were obtained with the lateral surface of the TM painted with a suspension of zinc oxide (ZnO) powder (Z52-500 Fisher Scientific) in normal saline at a concentration of 90 mg/ml. The effects of painting the TM on the motion of the TM and the ossicular chain are discussed later.

Continuous voltage sinusoids from 0.2 to 18 kHz of varied magnitude were generated by the stimulus generator (AFG 3102 Tektronix), amplified (Crown D45), and coupled to the sound source (Tucker-Davis Technologies, Alachua, FL, CF1) to produce tonal sound pressures between 80 and 120 dB sound pressure level (SPL). The stimulus levels were selected to produce resolvable sound-induced holographic fringes over the entire TM surface: A too small sound pressure will produce little change in the brightness level of the image associated with small motion of the TM while a too large sound pressure will generate high density fringe patterns on the TM surface due to a relatively large motion of the TM that are not readily distinguishable. Because of these limitations and the fact that the entire TM surface moves non-uniformly, the effective stimulus dynamic range is about 20 dB at each frequency. The pressure-induced microphone voltage was captured over a few milliseconds using an A/D converter controlled by LabView software, and a fast-Fourier transform (FFT) was applied to the captured time waveform. The FFT revealed stimulus distortions generally less than 30 to 40 dB relative to the stimulus frequency component and always less than 20 dB. A previously determined calibration characteristic was used to convert the measured microphone voltages to sound pressures.

The stimulus generator also generated the “strobe” pulses, which activated an acousto-optic modulator used to temporarily alter the path of the laser source. The pulses were of a duration equal to 5% to 10% of the sinusoidal period of each tone, and were phase-locked to the stimulus at 9 evenly spaced stimulus phases (0, π/4, π/2, … , 7π/4, 2π) with one pulse per acoustic stimulus period. During the short on-periods of the phase-locked pulses the laser path was set to illuminate the object and provide a reference beam at repeated identical phase-locked instants during the 25 ms period (40 frames/s) when a camera frame was exposed. During the longer off-periods the laser beam was diverted away from the fiber-optic pathways that provided the object and reference beams. By using the hologram taken at stimulus phase 0 as the base position, the relative deformations of the TM at each of the eight stimulus phases were derived, and used to reconstruct the motion of the sinusoidally driven TM. Detailed descriptions of the measurement steps are found in Cheng et al. (2010). Ideally it took about a second to record the nine stroboscopic images needed to reconstruct the displacement of over 300 000 points on the TM surface at a single frequency and stimulus level; however, it took more than an hour to take data at 20 to 30 stimulus frequencies due to additional time needed in between each measurement to switch the stimulus frequency, choose an appropriate level, adjust camera exposure time, check measurement stability, etc.1

Data analysis

Displacement on the surface of the TM from holograms

While gathering the optical fringes took about a second for one complete measurement, the analysis and synthesis of one measurement with nine 300 000 point images required a much longer time. The conversion of the gathered holographic images of the TM into displacement magnitude and phase angle on the surface of the TM was done in five steps: (1) Computation of the holographic optical phase difference between each of eight stimulus phases and the base measurement; (2) spatial phase unwrapping of the displacement phase angle over the TM surface to quantify optical-path-length differences larger than a wavelength; (3) masking of the images to restrict the analysis to the area of the TM and remove the effect of random noise-driven variations in non-TM regions; (4) edge normalization to define zero displacement along the TM annulus; and (5) Fourier transformation of the recorded displacement waveforms to derive the magnitude |D| and phase angle ∠D of the fundamental and harmonic components of motion at each of over 300 000 points on the TM surface. The detailed descriptions of these analytic steps are in Cheng et al. (2010). Correlation coefficients were computed between the raw displacements of the TM recorded by the holograms and the Fourier-derived fundamental displacement component (Cheng et al., 2010) at each point. The average of these correlations over the surface of the TM was generally higher than 0.95, consistent with sinusoid responses with relatively low distortion (Cheng et al., 2010).

Averaged Umbo displacement normalized by sound pressure

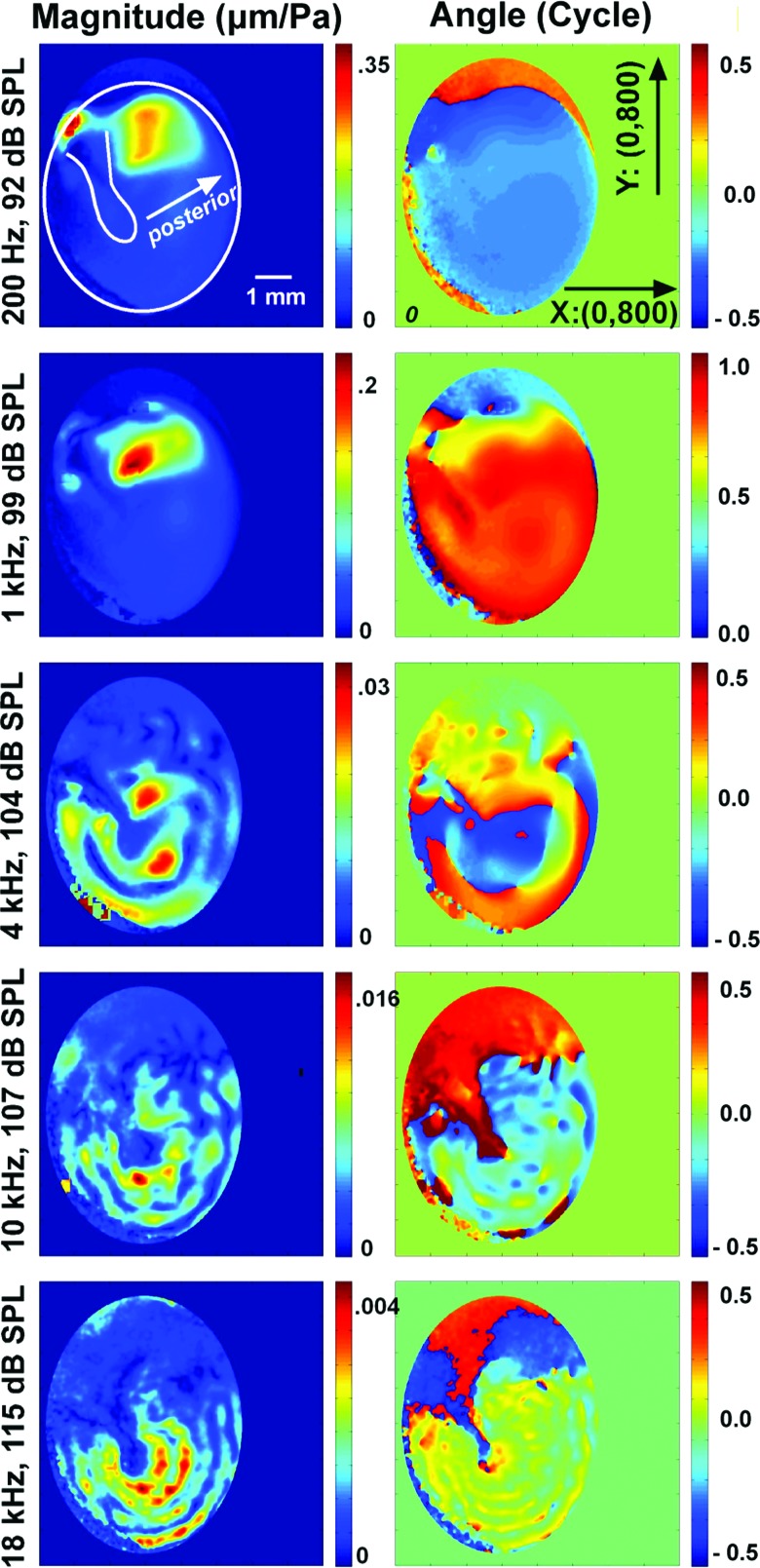
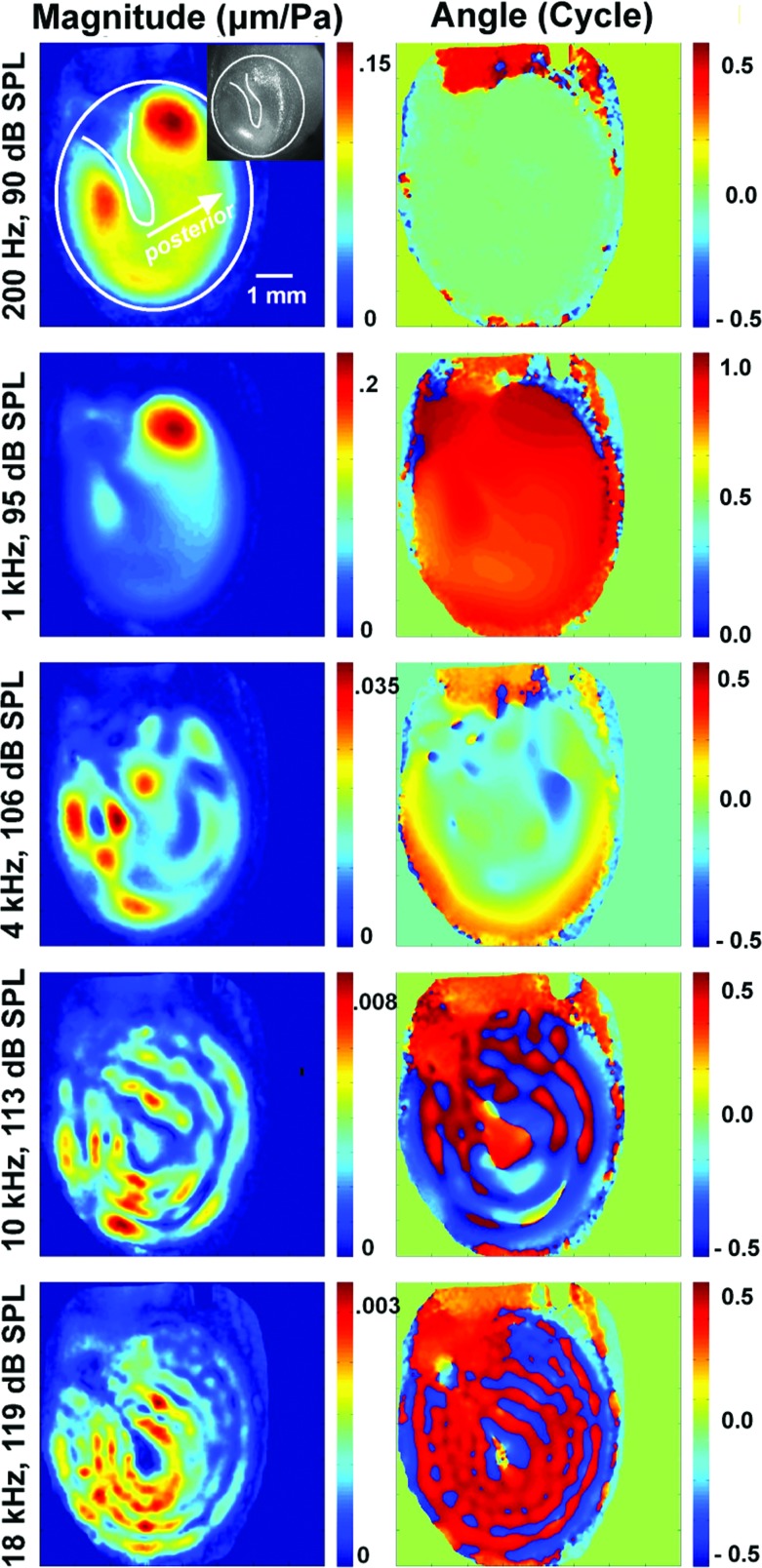
The Fourier-derived fundamental components of displacement were normalized by the sound pressure monitored at the edge of the TM and plotted as normalized displacement magnitude and phase angle maps on the TM surface (Fig. 1 from TB09_I and Fig. 2 from TB10_5). These maps are displayed in rectangles and each consist of 640 000 pixels (an 800 × 800 pixel array along the X-Y axes as shown in the phase angle plot of TB09_I at 200 Hz in Fig. 1), and about 50% of the plot area codes TM surface motion. The position of the umbo and the manubrium were identified on these maps based on the live image of the TM taken before painting (see a live image of TB10_5 in the inset within the magnitude map at 200 Hz in Fig. 2). The locations of the umbo and the manubrium identified through the live image are consistent with regions of low displacement magnitude observed with high-frequency stimuli: Compare the location of the manubrium in the inset of the top left-hand panel in Fig. 2 with the displacement magnitude maps produced with 10 and 18 kHz stimuli in the two bottom left panels in Fig. 2; there is a good match between the location of the manubrium and the umbo and the centrally located dark blue area in the 18 kHz data. There is also a good match at 10 kHz, although the magnitude map suggests the umbo (marked by the lighter-blue ellipse) is moving more than the rest of the manubrium. After the umbo was identified, the average stimulus normalized motion of a 10 × 10 square pixel area at the center of the umbo was computed.

Figure 1.

TM surface displacements measured by stroboscopic holography on TB 09_I normalized by pressure. The displacement magnitude |D| normalized by the stimulus sound pressure (units of μm/Pa; left column) and phase angle in cycles (right column) are coded with different colors as shown in the color bar on the right side of each plot. The stimulus frequencies from top to bottom are 0.2, 1, 4, 10, and 18 kHz, with an appropriate stimulus level given at each frequency to produce measurable TM displacement. The shapes of the TM and the manubrium are outlined in the magnitude plot at 200 Hz (top left), with arrows pointing to the posterior side of the TM. The size of each image is 800 × 800 pixels along the X-Y axes, as shown in the phase angle plot at 200 Hz (top right). An ellipse-shaped mask has been applied to exclude non-TM regions in data analysis.

Figure 2.

Similar plots of normalized TM surface displacement to pressure measured by stroboscopic holography on TB 10_5. The displacement magnitude |D| and phase angles normalized by the stimulus sound pressure are coded with color bars shown on the right side of each plot. The stimulus frequency and levels are given on the left side of each plot. The shapes of the TM and the manubrium are outlined in the magnitude plot at 200 Hz (top left), with arrows pointing to the posterior side of the TM. A live image of TB10_5 was inserted within the magnitude map at 200 Hz (top left), which identified locations of the umbo and the manubrium. The irregular mask was made by manually tracing around the area within the bony annulus in data analysis.

ME input impedance and power reflectance

The ME input impedance Z_T is the ratio of the sound pressure P_T on the lateral TM surface and the volume velocity of the TM U_T, i.e., Z_T = P_T/U_T. In this study, we assumed the sound pressure monitored by the probe-tube microphone near the edge of the TM described the average sound pressure acting on the surface of the TM. This assumption is based on measurements of the distribution of the sound pressure over the entire surface of an artificial membrane that demonstrated relatively uniform pressures (within ±3 dB) at frequencies below 20 kHz (Rosowski et al., 2009). The complex sinusoidal TM volume displacement was computed from the sum of the complex displacement (the real and imaginary parts of the fundamental Fourier component) of all points on the TM surface multiplied by the effective area of each image pixel (∼170 μm²). Since our measurements were made using continuous sinusoids, the complex volume velocity was equal to j2πf times the complex volume displacement, where j is the complex number $\sqrt{-1}$ and f is the stimulus frequency. To the best of our knowledge, this is the first time the complex ME input impedance at the TM has been computed from a direct measure of the volume velocity over the TM surface.

External ear power reflectance has been used to evaluate ME function (Stinson et al., 1982; Keefe et al., 1993; Voss and Allen, 1994). The power reflectance $R^2$ measures the ratio between the sound power reflected from the TM and the sound power incident at the TM, and can be computed from the ME input impedance $Z_T$ and the characteristic impedance of the ear canal at the TM $Z_0$, where

$$Z_0=\frac{{\rho }_{o}c}{S},$$ (1)

and

$$R^2={\left|\frac{Z_0-Z_T}{Z_0+Z_T}\right|}^2.$$ (2)

In the ear canal at 35 °C, ${\rho }_0$, the density of air, is 1.15 kg/m³ and c, the speed of sound, is 352.0 m/s. S is the nominal cross sectional area of the ear-canal near the TM, which we estimate as ∼51 mm² in this study.

RESULTS

Normalized TM displacement magnitude and phase angle map

Stroboscopic holography quantifies both the magnitude and relative phase of the displacement at each point (pixel) on the TM surface. Figures 12 show normalized displacement magnitude and phase angle maps of two TMs from this study (TM #1: TB09_I, from a 61-year-old male, and TM #2: TB10_5, from a 79-year-old male), at selected frequencies (0.2, 1, 4, 10, and 18 kHz) and SPLs. The sound levels were selected to produce measurable displacements. Results from the other TMs are similar.

In Figs. 12 the normalized displacement magnitudes (μm/Pa) and phase angles (in cycle) are coded with different colors (see the color bar on the right side of each plot). The approximate shapes of the TM and the manubrium are outlined in the magnitude plot at 200 Hz (top left), with arrows pointing to the posterior side of the TM. In the analysis of TM #1, we applied an ellipse-shaped mask during data analysis (see Sec. 2C1), and these maps show small nonzero-displacements outside of the TM area. For TM #2, an irregular mask was made by manually tracing around the area within the bony annulus. The tracing was imperfect and included parts of the tympanic ring and the ear canal wall but these included areas show motions of low magnitude and irregular phase angle.

The displacement phase angle maps at 0.2 and 1 kHz in Figs. 12 clearly demonstrate in-phase motion of the TM with a uniform phase angle distribution (uniform blue and orange for TM #1 and uniform green and red for TM #2) over much of the TM surface. Both TMs show a local region of maximal displacement magnitude in the superior-posterior quadrant of the TM (red to yellow areas), and TM #2 shows an additional peak in displacement magnitude in its superior-anterior quadrant as well. These in-phase motions of the TM at low frequencies are consistent with observations from others in cats (Decraemer et al., 1989, 1999) and humans (Cheng et al. 2010). At 0.2 kHz, TM #1 also shows a small area of large displacement superior to the manubrium; this region almost certainly represents low-frequency motion of the pars flaccida of the TM (Kohllöffel, 1984; Teoh et al., 1997).

At 4 kHz and above, the displacement patterns become more complicated: The magnitude maps show multiple local peaks with similar displacement magnitudes and phase angle (regions coded with the same color) that are circularly arranged around the manubrium. The circular arrangements of magnitude and phase values are consistent with the “ordered” motions of the TM that we described using TAH with high frequency sound stimuli (Rosowski et al., 2009).

The phase angle maps at frequencies of 4 kHz and higher in Figs. 12 show significant variations in the relative displacement phase angles over the TM surface. However, there are only a few clear cases where we observe a sudden half a cycle (π radian) shift in phase angle with space. One example of such a shift is in Fig. 1 at 4 kHz stimulation, where the phase map shows several rapid transitions from medium blue to orange that are consistent with a spatially rapid half-cycle change in displacement phase angle. Another obvious example of a half-cycle phase angle change is the presence of the dark-red phase angle values along the manubrium in Fig. 1 at 10 kHz, compared to the surrounding region where the phase angle is coded by a lighter blue. Other near half-cycle sudden phase angle changes are apparent at 18 kHz in Fig. 1 and at 4, 10, and 18 kHz in Fig. 2. Other than these observed above, the phase angle differences that occur between local regions of maximal displacement are much smaller than half a cycle, and also tend to vary cyclically in space. For example, the displacement phase angles over large areas of the TM at 10 and 18 kHz in Fig. 2 tend to vary by less than [1/4] period, between the medium to darker blues and the medium to darker reds.2

At 10 and 18 kHz in Figs. 12, one sees clear ring-like displacement patterns that are circularly organized around the umbo in both magnitude and phase angle; the magnitude rings show alternative peaks and valleys around the umbo, with the number of rings increasing as the frequency increases. The associated phase angle rings show cyclic variations in phase, from light blue to light green in TM #1, and deep red to dark blue in TM #2 (note the phase angle values in these plots have been wrapped between [+1/2 to −1/2 cycle], so that the phase angle in dark blue [−1/2 cycle] is nearly equal to the phase angle in deep red [+1/2 cycle]), suggesting the entire TM is moving nearly in-phase but with the addition of small oscillating phase angle “ripples.”

Quantitative descriptions of TM motion: Level dependence

Past comparisons of TM and ossicular motions with different level stimuli have demonstrated a strict proportionality between stimulus sound pressure and response: One of the hallmarks of linear system behavior (Guinan and Peake, 1967; Buunen and Vlaming, 1981; Goode et al., 1994). In this study, we used stroboscopic holography to measure the displacements of the TM induced by sound stimuli that varied over a wide frequency range (0.2 to 18 kHz), and with multiple stimulus levels to test the linearity of the TM response and limits of our measurement technique.

Displacement at the Umbo with varied stimulus levels

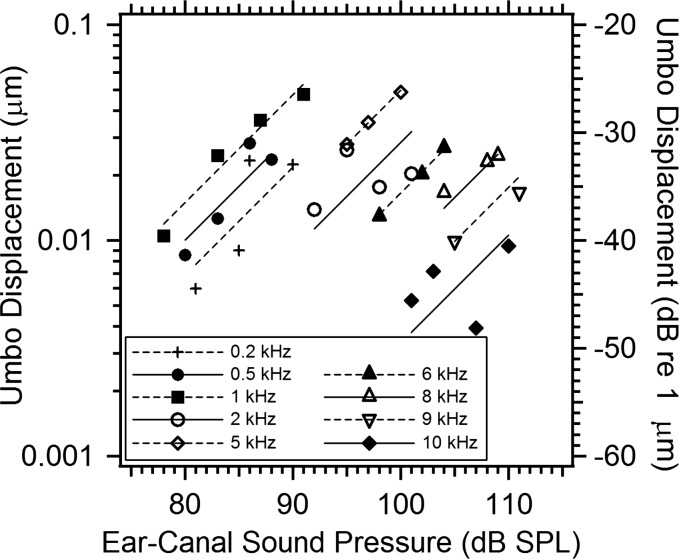
Figure 3 plots the magnitude of the umbo displacement of TB09_II measured at 9 frequencies from 0.2 to 10 kHz, and 2 to 4 stimulus levels at each frequency. The symbols illustrate the measured displacement magnitude in μm (y-axis to the left) or dB re 1 μm (y-axis to the right) plotted vs stimulus levels in dB SPL (x-axis). Figure 3 also includes line segments that pass through the mean displacement and stimulus level at each frequency with unit slope. Comparisons of the data points to the line segments indicate that the displacements at 0.5, 1, 5, 6, 8, and 9 kHz are consistent with a proportional relationship between stimulus drive and displacement while the displacements at 0.2, 2, and 10 kHz are less consistent with proportionality. One issue related to observations of umbo displacement is that the motion of the umbo tends to be small compared to the motion at other TM locations, and some of the non-proportional behavior observed in Fig. 3 may be related to attempts to quantify displacements that are near or below the 10 to 20 nm resolution of our measurement system.3

Figure 3.

Growth of the umbo displacement with stimulus level in TB09_II. The umbo displacement magnitudes in micrometers (left axis label) or dB per micrometer (right axis label) are estimated from the complex average displacement in a 10 × 10 pixel array centered on the umbo location, at 9 stimulus frequencies from 0.2 to 10 kHz and 2 to 4 stimulus levels at each frequency. The measured magnitudes at each frequency are plotted vs stimulus level in dB SPL as individual symbols. The figure also includes unit-slope line segments fit through the mean dB displacement and dB level of the stimulus at each frequency.

Average displacement of the TM surface with varied stimulus levels

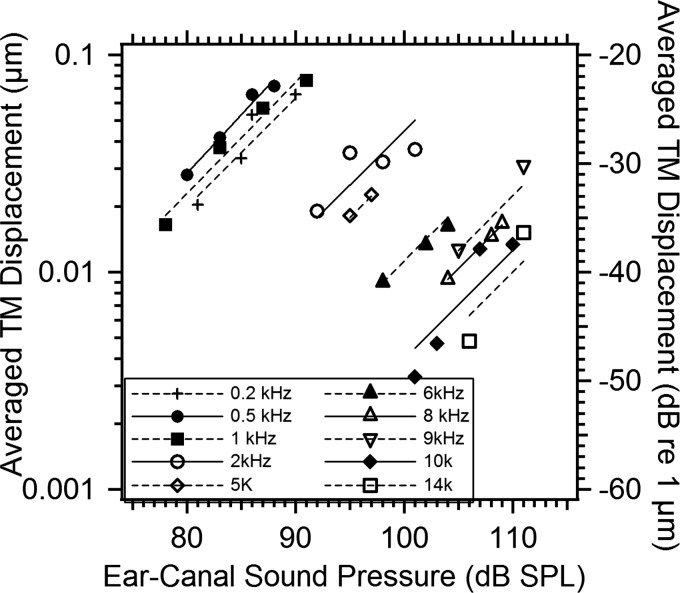
An alternative way to look at the growth of TM motion with stimulus level is through the average displacement of the entire TM surface. Figure 4 plots the average magnitude of the complex displacement on the entire surface of the TM against ear-canal SPL for frequencies from 0.2 to 14 kHz. Again we also plot unit-slope line segments that pass through the mean dB level and dB displacement of each frequency set as a standard for proportional growth. At 5 kHz and below, the average TM displacement magnitudes are about a factor of 2 larger than the umbo displacement magnitude (Fig. 3). This is consistent with other observations of these two quantities in a cat (Khanna and Tonndorf, 1972; Lynch et al., 1994) that suggest the umbo moves less than other parts of the TM. However, above 5 kHz, phase angle variations across the TM surface can lead to reductions in the average displacement, where the “positive” displacements of the TM cancel “negative” displacements, thus the magnitudes of the umbo displacement and the average TM displacement are similar. Note the average displacement data grow generally linearly with stimulus levels and are less affected by measurement noise, perhaps because of the reduction in noise associated with averaging the displacement at the nearly 300 000 points on the TM surface, as well as the inclusion of large regions with motion magnitudes larger than those at the umbo.

Figure 4.

Growth of the averaged magnitude of the TM displacements over the entire surface with ear-canal SPL (2 to 4 levels) for frequencies 0.2 to 14kHz. The left axis label shows linear averaged TM displacement in micrometers, and the right axis label shows dB per micrometer. Both individual symbols and unit-line segments between displacement and stimulus level are given for each frequency.

Frequency dependence: Normalized Umbo displacement

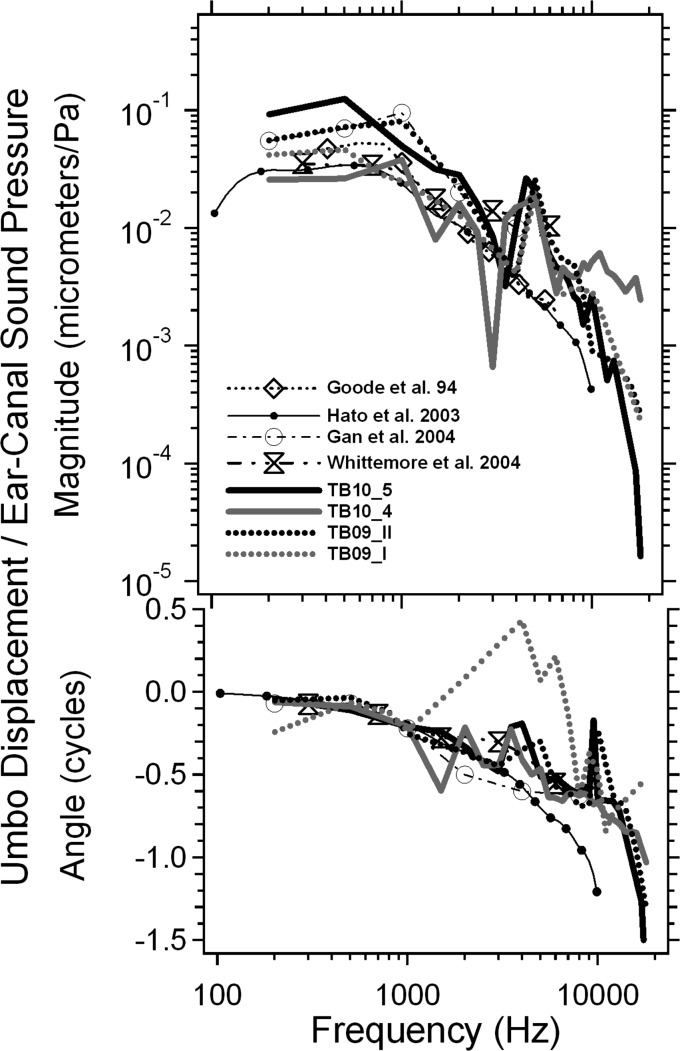
Our estimates of the umbo displacement normalized by the ear canal pressure are plotted versus frequency from 0.2 to 18 kHz for 4 TBs in Fig. 5: The magnitude in the top panel and phase angle in the bottom panel. These measurements are compared with published umbo displacements in live and cadaveric humans measured by LDV (Goode et al., 1994; Hato et al., 2003; Gan et al., 2004; Whittemore et al., 2004). In general, the umbo displacement magnitudes from four TBs measured by stroboscopic holography are similar, with small variations across different bones. The displacement magnitudes all peak between 0.5 and 1 kHz, and then decrease as frequency increases, which is consistent with previous published results. The phase angles start around 0 cycles at low frequency and gradually decrease as frequency increases, reaching about −1 or −1.5 cycles at a frequency of 18 kHz for 3 of the TBs in the plot. We also note the phase angle in 4 bones does not accumulate smoothly with frequency: There are backward (positive) steps between 2 and 10 kHz in all the bones. The presence of these steps may be due in part to the relatively sparse frequency sampling of the data points, where phase unwrapping of rapidly accumulating phase may introduce unnecessary shifts in the estimated phase angle of displacement. The sparse sampling is especially troublesome in TB09_I where there are only 8 sample points between 1 and 10 kHz. The frequency dependence of umbo motion in the other 3 bones were sampled with higher resolution: 15 to 25 frequency points between 0.2 and 18 kHz. Note that at frequencies greater than 10 kHz the inter-specimen variations become larger in this study as the data approach the displacement resolution limit (∼10 to 20 nm) of our holography measurement system.

Figure 5.

The umbo displacements normalized by the ear canal pressure versus frequency from 0.2 to 18 kHz measured from 4 TBs (TB10_5, TB10_4, TB09_II, and TB09_I), compared with published umbo displacements in live and cadaveric human ears measured by LDV (Goode et al., 1994; Hato et al., 2003; Gan et al., 2004; Whittemore et al., 2004). Both magnitude (top panel) and phase angle (bottom panel) are plotted.

While there is reasonable agreement between the frequency dependence of the umbo displacements in our measurements and published data, one of the more prominent differences between our measurements and the means of the other studies is the fairly sharp dip that appears in our magnitude data near 3 kHz. This dip was likely related to a narrow-band stimulus artifact that shook the entire table at that frequency. There are also less-prominent variations between our data and the others but such variations are common between measurements of function in individual ears, and especially so when one compares individual and mean measurements.

Another point of comparison between ours and other data is the group delay calculated from the change of phase angle with frequency. The group delays calculated from our individual measurement data vary between 40 and 60 μs. This is similar to the group delays estimated from the data of Gan et al. (2004) and Whittemore et al. (2004) but smaller than the ∼80 μs delay suggested by the data of Hato et al. (2003).

ME input impedance and power reflectance

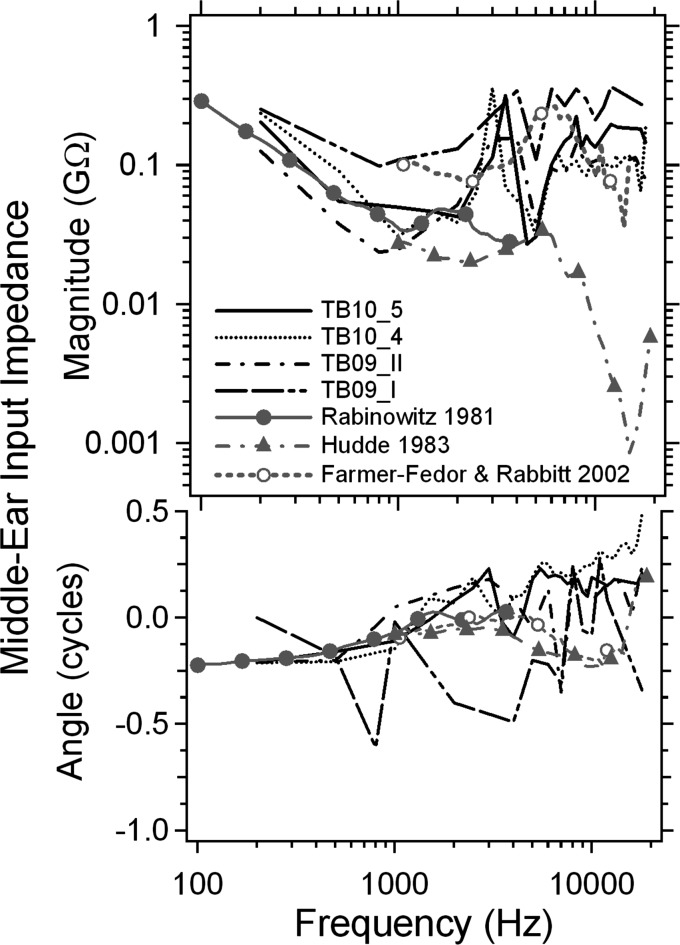
The ME input impedance computed from the directly measured volume velocity of the TM surface and the sound pressure monitored at the TM rim is shown in Fig. 6 for 4 TBs, in magnitude (GΩ) and phase angle (cycles) from 0.2 to 18 kHz. These are compared to the ME input impedance data of Rabinowitz (1981) and impedances calculated from the complex ear canal reflection coefficient measurements of Hudde (1983) and Farmer-Fedor and Rabbitt (2002). Rabinowitz (1981) measured the ME input impedance over the 0.2 to 4 kHz range in a group of young live adults. Hudde (1983) and Farmer-Fedor and Rabbitt (2002) used reflectance techniques to measure the impedance in a higher frequency range in a similar population. Note the wide differences between these estimates at frequencies above 10 kHz.

Figure 6.

The human ME input impedance computed from the holographic measured volume displacement of the TM surface and the sound pressure monitored at the edge of the TM from 4 TBs (TB10_5, TB10_4, TB09_II, and TB09_I), in magnitude (GΩ) and phase angle (cycles), from 0.2 to 18 kHz, compared to the ME input impedance data of Rabinowitz (1981) and impedances calculated from the complex ear canal reflection coefficient measurements of Hudde (1983) and Farmer-Fedor and Rabbitt (2002).

The impedance from TB09_I (the double dotted-double dashed line) shows different behavior from the other 3 TBs: Its impedance magnitude is higher over most of the frequency range, and the impedance phase angle jumps around with multiple half-cycle changes, e.g., at 1 and 4 kHz. The impedance phase angles from the other three bones are less variable and generally fall into the ±0.25 cycle range.

The impedance magnitudes from the other 3 TBs (TB09_II, TB10_4, and TB10_5) are similar to each other over the entire frequency range from 0.2 to 18 kHz. As frequency increases, the impedance magnitude starts around 0.2 GΩ at 0.2 kHz, decreases to about 0.03 GΩ around 1 kHz, peaks (0.2 GΩ) at around 3.5 kHz, decreases to a new minimum (0.03 GΩ) around 4.5 kHz, and finally increases to a near stable level of 0.1 to 0.2 GΩ at about 8 kHz. The Rabinowitz (1981) impedance magnitude data show similar frequency dependence from 0.2 to 2 kHz. Hudde's (1983) impedance magnitude data are generally lower than our measurements from 1 to 20 kHz. The impedance magnitudes from Farmer-Fedor and Rabbitt (2002) are more similar to our results at frequencies above 4 kHz. Unlike the other data, our impedances show a peak and near 0.25 cycle phase change around 3 kHz, which may be related to the narrow decrease in the displacement of the umbo in the same frequency range (Fig. 5) caused by a narrow-band motion artifact from motion of the table.

The impedance phase angles from our measurements are also consistent with the Rabinowitz data below 1 kHz as shown in the bottom panel of Fig. 6, where the phase angle starts around −0.25 cycles at the lowest frequency and gradually increases to 0 cycles around 1 kHz. The impedance phase angle in the comparison data remains around 0 from 2 to 4 kHz while our data suggest a continuous increase to about 0.25 cycles around 3 kHz, and then a drop to 0 around 4 kHz. Perhaps this difference is related again to the 3 kHz artifact that we mentioned before. Above 4 kHz the impedance phase angles we measured increase to a peak of 0.25 cycles around 6 kHz, and then remain fairly constant until 18 kHz. Above 4 kHz Hudde's and Farmer-Fedor and Rabbitt's data suggest a decrease of phase angle first, with a sudden increase between 15 and 20 kHz. (This sudden phase increase is associated with a minimum in the magnitude of the impedance.) It is also noted in Fig. 6 that the impedance phase angle at high frequency becomes less consistent across different bones. For instance, the impedance phase angle of TB10_4 (dotted line) increases to 0.5 cycle at 18 kHz while the impedance phase angles of TBs 10_5 and 09_II remain near 0.25 cycle.

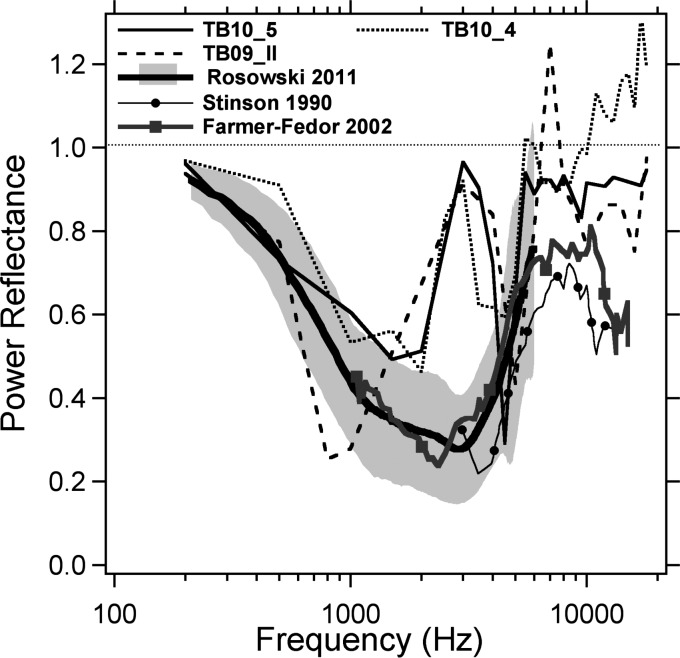
The power reflectance in the three TBs were computed from the impedance estimates described above (we excluded TB09_I with its variable impedance phase angle) via Eqs. 1, 2. The resultant power reflectances are shown in Fig. 7 and compared with published measurements from 52 adult humans ears with normal hearing that are being used as a clinical standard in our lab (Rosowski et al., 2012) and studies on a small number of young adults described by Stinson (1990) and Farmer-Fedor and Rabbitt (2002). Between 0.2 and 2 kHz, our holographic results agree well with the live human data, with the power reflectance value decreasing from 0.9 to 0.4. However, we see a difference between our data and live human data in the mid-frequency range. The power reflectance from live humans is relatively constant at a value near 0.3 between 1 and 3 kHz and then increases to a value between 0.6 and 0.8 as the frequency increases from 3 to 6 kHz. Our data show a rapid increase in reflectance near 3 kHz, the same frequency where we suspect an artifact leads to anomalous estimates of umbo velocity and ME impedance. This increase is followed by a rapid fall of power reflectance to about 0.2 or 0.3 at 5 kHz, and a rapid rise again to 0.9 at 6 kHz. While the magnitude of the power reflectance we report in our individuals near 6 kHz is larger than any of the clinical mean data, a significant increase in reflectance magnitude near 6 kHz is also seen in the data from all of the other studies. Finally the reflectance estimated from the holographic measurements stabilizes between 0.8 and 0.9 at frequencies above 8 kHz in ears TB 09_II and TB 10_5. The live human data of Stinson (1990) and Farmer-Fedor and Rabbitt (2002) show a smaller high power reflectance of between 0.5 and 0.8 at frequencies above 6 kHz.

Figure 7.

The human ME power reflectance computed from the ME impedance estimated from holographic measurements of 3 TBs (TB10_5, TB10_4, and TB09_II), compared with recent measurements in 52 adult humans ears with normal hearing by Rosowski et al. (2012) and studies on a small number of young adults described by Stinson (1990) and Farmer-Fedor and Rabbitt (2002).

Probable errors of a computed power reflectance greater than 1 are observed in 2 bones at a few frequencies (TB 09_II near 7 kHz and TB10_4 above 9 kHz) in Fig. 7, which will be discussed further in Sec. 4A. Despite differences and potential errors, there are regions of good agreement (below 2 kHz and above 4 kHz) between our power reflectance estimates and those in the literature.

DISCUSSION

Stroboscopic holographic measurements of TM motion

In this study we measured sound-induced displacement magnitude and phase angle of about 300 000 points on the surface of the TM of cadaveric human TBs. The surface maps of displacement magnitude and phase angle from these measurements (Figs. 12) demonstrate in-phase motion of the entire TM surface at frequencies of 1 kHz and less. They also demonstrate spatial variations in magnitude and phase angle of TM displacements at higher frequencies. Some of the spatial variations can be explained by the presence of nodal boundaries on the TM surface where a near zero minimum in magnitude is paired with a half a cycle phase change on either side of the minimum. However, we also see cyclic variations in displacement magnitude and phase angle across the TM surface at frequencies above 4 kHz, where the phase angle changes are too small to be explained by “nodes.”

We used the measured displacement magnitudes and phase angles on the TM surface to define the displacement of the umbo and the average volume displacement of the entire TM surface. In general, the umbo displacement and the average displacement of the entire TM grow linearly with stimulus levels, although the measured umbo displacements at high frequencies and low stimulus levels may fall below the 10 to 20 nm limit of resolution of our displacement estimates. Calculations of the average displacement of the entire TM surface are less affected by such limits because large areas of the TM move more than the umbo and the benefits of averaging the measurements over 300 000 points.

The frequency dependence of the extracted umbo displacements and the ME input impedance and reflectance computed from the average displacement show similarities to other published reports of these quantities, although there are differences in the 3 to 4 kHz range. One possible source of these differences is the artifactual motion of the bone in our measurements. We have noted in previous experiments (Aarnisalo et al., 2009) the presence of significant motions of the entire TB in the sound field due to resonances in the table and the support clamps that hold the bone and holographic head.4 While these resonances produce errors in the estimate of absolute motion of the TM, they should have a minimal effect on our measurements of the relative motion of the different points on the TM surface.

While our impedance and reflectance estimates in three ears at frequencies less than 2 kHz and greater than 4 kHz fall within the range of published data, there are clear indications of isolated errors in our individual measurements: Impedance phase angles that are greater than 0.25 cycles yield reflectances greater than 1. Possible sources for these errors include inaccuracies in the estimated volume displacement (the distribution of displacement magnitude and phase angle across the TM surface gets more complicated at high frequency, which complicates volume displacement calculation) or errors in the estimated sound pressure. The latter could be related to a breakdown at higher frequencies in our assumption that the sound pressure measured near the rim of the TM is a good estimator of the average sound pressure acting on the TM. We have demonstrated that the sound pressure varies within 3 dB in magnitude and 0.05 cycles in phase angle over an artificial flat membrane surface up to 20 kHz (Rosowski et al., 2009), and over the human TM surface with an artificial ear canal up to 15 kHz (Cheng et al., 2012). However, when the impedance is dominated by reactive terms, a small phase error can produce significant errors in the estimation of the real part of the input impedance and the estimated reflectance that may explain many of the instances of reflectance greater than 1 in Fig. 7.

Effect of painting the TM

All of the measurements we report in this manuscript come from TMs that have been painted with solutions to increase the opacity of the membrane and improve the reflected laser signal. The paint was applied to the lateral surface of the TM before positioning the bone in the holographic laser beam.

We investigated the effects of painting the TM by using two different paints, TiO₂ and ZnO, at several concentration levels mixed in normal saline with repeated measurements in three TBs. In 2 bones (TB10p1 and TB10p2) the surface motion of the TM was measured with stroboscopic holography after applying sequential 60, 90, and 125 mg/ml ZnO solutions, then followed by 35 mg/ml TiO₂ in saline. Repeated measurements were made for each paint condition. In between measurements, the bone was removed from the holography setup and a weak acetic acid solution was used to remove ZnO paint (ZnO is soluble in acetic acid) before applying the next layer of paint. TiO₂ was the last paint used because it was difficult to remove. In a third bone (TB10p3), we looked at the effect of painting the TM on stapes velocity. LDV measurements of stapes motion (the beam was focused on the posterior crus) were made before and after painting the TM with increasing concentrations of ZnO in saline (Trial 1). ZnO was removed from the TM by bathing the TM in weak acetic acid, and Trial 2 started with the no-paint condition followed with 125 mg/ml ZnO in saline. In all of these measurements the SPLs near the surface of the TM were monitored via the probe microphone placed at the TM rim.

We compared the change of umbo displacement and volume displacement with respect to the unpainted TM condition from measurements made in 1 bone at 4 frequencies (0.5, 1, 4, and 8 kHz) and a second bone at 3 frequencies (0.4, 2, and 8 kHz) in four painting conditions (60, 90, and 120 mg/ml ZnO and 35 mg/ml TiO₂) for a total of 28 conditions. Many but not all of the measurement conditions were repeated, yielding 52 measurements of paint induced change in both the umbo and volume displacement. The mean and standard deviation of the change in volume displacement from all 52 measurements was −0.41 ± 4.4 dB, with 3 instances of change larger than 10 dB. The mean change in umbo displacement after painting from the same measurement set was −0.03 ± 6.5 dB, with 2 instances of change larger than 10 dB. There was no apparent pattern relating the size of the changes to the paint concentration, and many of the changes were of magnitudes similar to those seen after simply soaking the bone in saline and repositioning the bone in the measurement apparatus.

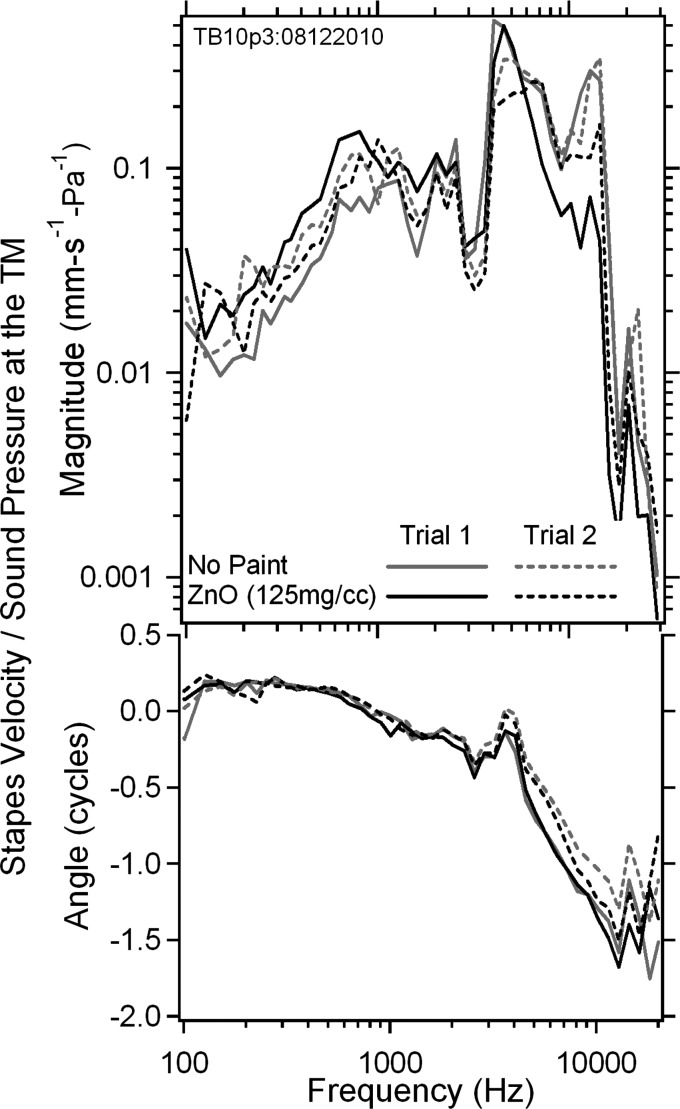
We also compared the stapes velocity normalized by the sound pressure measured in a third bone (TB10p3) by LDV, as shown in Fig. 8 (top panel magnitude, bottom panel phase), from 4 measurements with either no paint or painted with 125 mg/cc ZnO with 2 trials. Trial 1 results show some small changes in stapes velocity magnitude with/without painting across most of the frequency range from 0.1 to 20 kHz, except near 14 kHz where 10 dB variations are observed. Trial 2 results are more consistent, with smaller than 3 dB changes in magnitude between the unpainted and painted TM over a majority of the measurement frequency range. The phase data between unpainted and painted measurements are more consistent within each trial over the whole measurement frequency range, with a small variation observed between the 2 trials at frequencies above 6 kHz. Such changes can also be observed after soaking the TM in saline (Rosowski et al., 1990; Voss et al., 2000).

Figure 8.

(Color online) The stapes velocity in magnitude (upper panel) and phase angle (lower panel) measured in TB10p3 by LDV normalized by the sound pressure monitored at the TM rim from 0.1 to 20 kHz, with no paint and after painting the TM surface with 125 mg/ml ZnO in saline solution. Two trials were performed for each case.

Displacement vs distance from the Umbo on TM surface

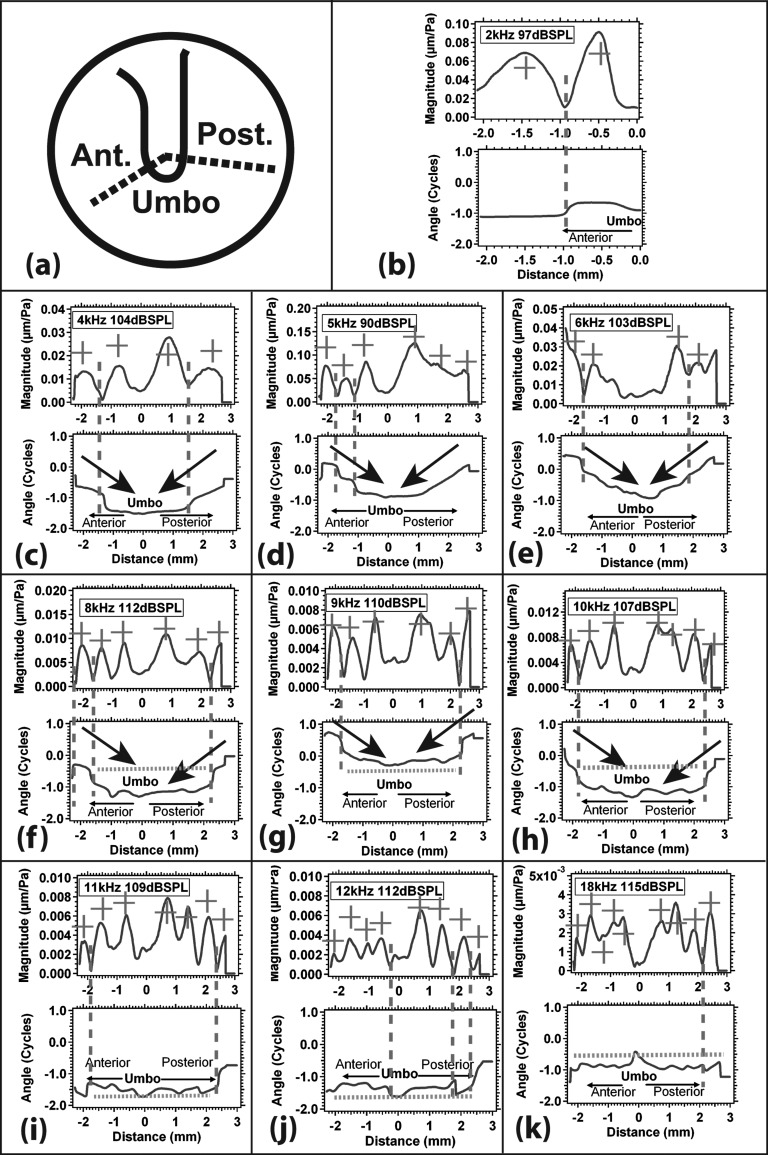
Stroboscopic holography measures displacement magnitude and phase angle in response to acoustic stimuli at a large number of points on the TM surface. While observations of the two-dimensional normalized magnitude and phase angle maps of Figs. 12 give an overall sense of the patterns of the response, it is difficult to extract quantitative information from such maps because of the lack of explicit scales. To help in such quantification we have extracted plots of the displacement magnitude and phase angle along two radial line segments that start at the rim of the TM and end at the umbo [as shown in Fig. 9a]. We have chosen line segments that (1) cover both the anterior and posterior halves of the TM; (2) pass through regions of large displacement; and (3) are nearly perpendicular to the apparent wave fronts defined by the rings of displacement magnitude and phase angle that surround the umbo at frequencies above 4 kHz. The resultant plots of displacement vs radial distance from two TMs (TB09_I and TB10_5) are shown in Figs. 910 at multiple stimulus frequencies between 2 and 18 kHz. The other bones show similar patterns of displacement vs radial distance.

Figure 9.

(Color online) The normalized displacement magnitude and phase angle of the TM from TB09_I as a function of the distance from the umbo along two radial lines (a), at 9 selected frequencies between 4 and 18 kHz (b)–(k). In each plot from (b) to (k), the x-axis represents the distance along two radial lines from the umbo (where x = 0), with x < 0 along the anterior radial line and x > 0 along the posterior radial line; the y-axis represents normalized displacement magnitude in micrometers/Pa (upper panel) and phase angle in cycles (lower panel). Multiple local displacement magnitude maxima are marked by red + signs. The pairing of deep minima in magnitude and half-cycle phase angle change (“modal node”) is marked by the red vertical dashed line. Black arrows are plotted at locations where traveling waves are suggested. Green dashed lines mark regions where “phase ripples” (slow back-and-forth phase angle changes of less than 0.3 cycles) are observed along the radial lines.

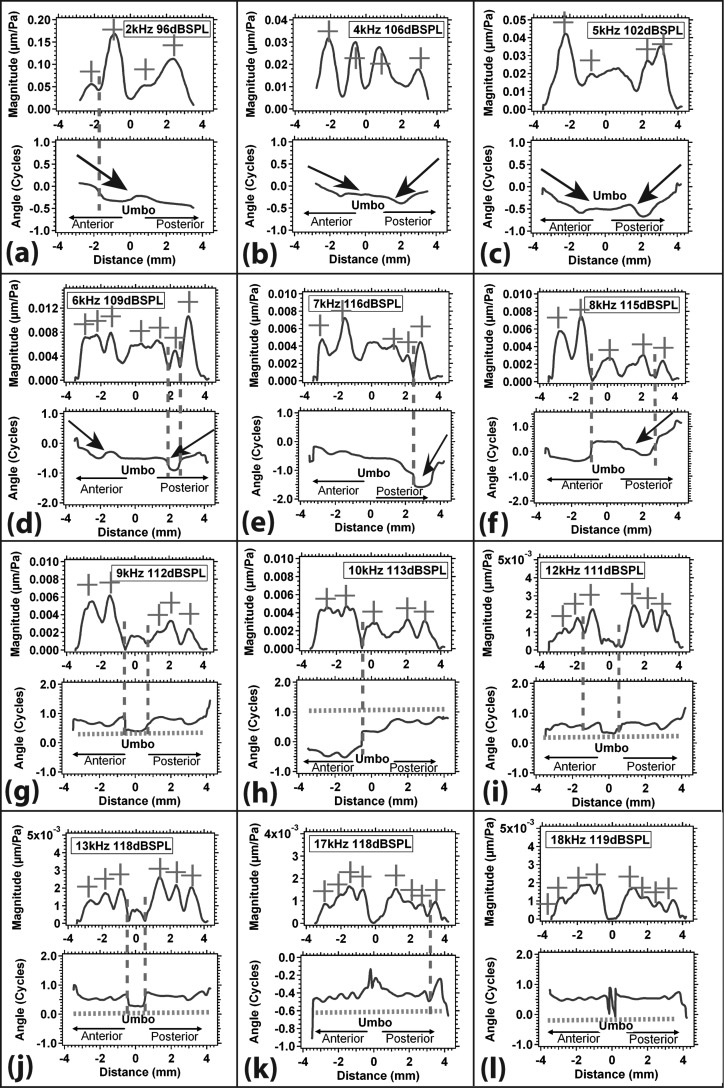
Figure 10.

(Color online) The normalized displacement magnitude and phase angle of the TM along two similar radial lines [as in Fig. 11a] for TB 10_5 between 2 and 18 kHz (a)–(l). Again, the x-axis represents the distance along two radial lines from the umbo (where x = 0), and the y-axis represents normalized displacement magnitude and phase angle. The red + sign marks local displacement magnitude maxima, the red vertical dashed line marks modal node, the black arrow suggests traveling wave, and the green dashed line marks phase ripples.

Figure 9 plots the normalized displacement magnitude and phase angle of the TM from TB09_I as a function of the distance from the umbo at 10 selected frequencies between 2 and 18 kHz. In each plot, the x-axis represents the radial distance from the umbo (where x = 0): Displacements along the anteriorly pointing radial line are plotted in the negative half of the plot (x < 0); displacements along the radial line that points posterior-inferiorly are plotted in the positive half (x > 0). The y axes represent the normalized displacement magnitude (in μm/Pa) and phase angle (in cycles).

At stimulus frequencies less than 8 kHz [Figs. 9b, 9c, 9d, 9e] these plots show several notable features:

• (1)Multiple local displacement magnitude maxima (marked by “+” signs) are seen along each radial line.
• (2)Several of these maxima are separated from each other by deep magnitude minima associated with rapid half-cycle phase changes (marked by red vertical dashed lines). The pairing of deep minima and half-cycle phase changes is consistent with a modal node.
• (3)The magnitude of the displacement at the umbo (x = 0) is less than that at many locations along the radial line segments.
• (4)Phase angle gradients (marked by black arrows) are consistent with traveling waves, where the direction of travel is the direction in which negative phase angle accumulates. The gradients presented here suggest traveling waves that propagate from the edge of the TM toward the umbo in the center. As we point out later in Sec. 4I, such phase angle gradients can also result from the presence of losses within a membrane or plate that is responding to uniform pressure stimulation with purely modal motions; such oscillations are stationary and do not travel along the membrane surface.

At stimulus frequencies of 8 to 10 kHz [Figs. 9f, 9g, 9h] the radially arranged motion patterns show multiple displacement maxima and minima on the TM surface; again, the umbo tends to move with a smaller displacement than much of the TM. Some of the displacement minima (especially those closer to the TM rim) are associated with rapid half-cycle phase changes (marked by a red dashed vertical line) but the majority are associated with slow back-and-forth phase angle changes of less than 0.3 cycles (the regions noted by the horizontal green dashed line). These oscillating phase angle ripples are most pronounced with stimulus frequencies greater than 10 kHz as shown in Figs. 9i, 9j, 9k. The oscillations in phase angle are generally matched by oscillations in magnitude but the magnitude minima associated with the phase angle oscillations tend to be less deep than the minima observed at the locations of rapid [1/2] cycle phase changes.

Figure 10 displays normalized displacement magnitude and phase angle of TM from TB10_5, along two radial lines similar to those in Fig. 9a (anteriorly and posterior-inferiorly) vs distance from the umbo (x = 0) at 12 selected frequencies (2 to 18 kHz). Many of the features seen in Fig. 9 are also observed in this data set. We again see multiple displacement maxima (marked by + signs) and minima along the radial lines across the TM surface. The umbo displacement magnitude is usually smaller than the displacement magnitude along the radii across the TM surface. The phase angle variations take similar forms as we see rapid half-cycle phase changes indicative of nodes, long phase angle glides suggesting waves that travel toward the umbo, and paired oscillations in phase angle and magnitude, especially at the higher frequencies. However, there is a significant difference between the two data sets: In Fig. 9, the nodal regions (marked by the [1/2] cycle phase change and magnitude minimum) were generally near the rim of the TM; in Fig. 10, a large fraction of the apparent nodes are on either side of the umbo, and there is evidence that the umbo moves out-of-phase with the rest of the TM at frequencies of 12 and 13 kHz and maybe higher.5

Combinations of waves in a phenomenological model

The data we gathered on TM surface motions at frequencies of less than or equal to 1 kHz suggest the entire TM moves in-phase with one or more spatially localized maxima in magnitude; such patterns are consistent with very low-order modal motion of the membrane (Fletcher, 1992). At frequencies above 1 kHz, we see evidence of spatial nodes and nodal lines (regions of near zero motion) that divide the motion of the membrane into sections that move in opposite phases; such patterns are consistent with modal motions of somewhat higher order (Fletcher, 1992). These modal-like motions occur in combination with traveling-wave-like phase angle glides, especially in the middle frequencies. At frequencies above 8 kHz the membrane motions describe a small number of nodal boundaries in combination with regions where the phase angle varies regularly around a near constant baseline while the magnitude goes through a series of maxima and minima. We suggest that all of these motion patterns are consistent with a combination of lower-order (low spatial frequency) modal motions and higher-order (larger spatial frequency) modes or waves.

This hypothesis is consistent with simulations of a phenomenological model in which two waves, one modal standing wave and one traveling wave, of different magnitude and spatial frequency, are summed in space. The basis of our model is that different displacement patterns (modal motions and traveling waves) with different spatial frequencies can simultaneously exist on the TM. This can occur because the spatial frequency of a traveling wave depends on the local properties of the medium (the TM) through which the wave travels. In contrast, the spatial frequency of a particular modal motion depends on constraints placed on the membrane by its boundary conditions, as well as the stiffness and mass of the membrane. Such constraints allow the existence of multiple modal patterns. Low-order modal motions contain a small number of spatially distributed motion maxima and nodal lines consistent with lower spatial frequencies. Higher-order modal motions contain a larger number of local maxima and nodal lines consistent with higher spatial frequencies (e.g., Fletcher, 1992).

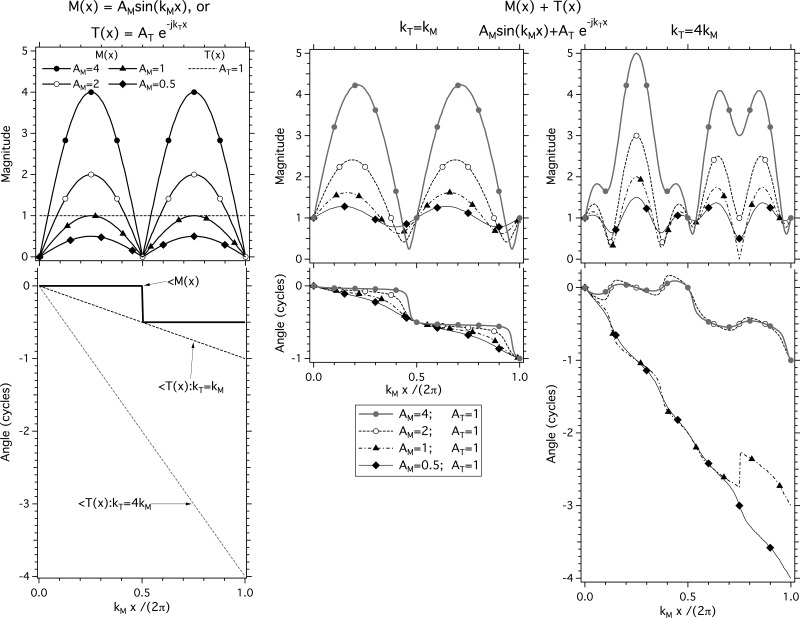
Simulations of the combination of a modal motion and a traveling wave are illustrated in Fig. 11. Wave M(x) = A_M sin(k_Mx) is a modal standing wave of magnitude A_M and spatial frequency k_M, where the magnitude of the modal wave varies sinusoidally in space, and the phase angle is either 0 (when the sine term returns a positive number) or [1/2] cycle (when the sine term returns a negative number). Wave T(x) = A_T e^−jk_Tx is a traveling wave of magnitude A_T and spatial frequency k_T, where the magnitude of the wave is invariant in space but the phase angle varies regularly with x. In Fig. 11, the left-most panel with its two vertically aligned plots describes the spatially varying magnitude and phase angle of six basic waves M(x) and T(x) with a closed set of parameters: A_T = 1; A_M = {0.5, 1, 2, 4}, and either k_T = k_M or k_T = 4k_M.

Figure 11.

Models of combinations of two waves [a modal wave M(x) = A_M sin(k_Mx) and a traveling wave T(x) = A_T e^−jk_Tx], with varied magnitudes and spatial frequencies. The left-most panel with its two vertically aligned plots describes the spatially varying magnitude and phase angle of six basic waves M(x) and T(x) with a closed set of parameters: A_T = 1 (horizontal dotted line in magnitude plot); A_M = {0.5, 1, 2, 4} (four solid lines with symbols in magnitude plot), and either k_T = k_M (solid dotted line in the phase angle plot) or k_T = 4k_M (gray dotted line in the phase angle plot). The two right-hand panels describe the spatial variations in displacement magnitude and phase angle predicted by various combinations of one of four modal wave patterns M(x) with one of two traveling waves T(x) (middle panel: k_T = k_M, right-most panel: k_T = 4k_M). The top plot of each panel illustrates the variation in the wave magnitudes as k_Mx and k_T x (plotted on the abscissa) vary. The bottom plot of each panel illustrates the spatial variations in the phase angle of the waves.

The two right-hand panels describe the spatial variations in displacement magnitude and phase angle predicted by various combinations of one of four modal motion waves M(x) with one of two traveling waves T(x). The top plot of each panel illustrates the variation in the wave magnitudes as k_Mx varies. The bottom plot of each panel illustrates the spatial variations in the phase.

The middle panel of Fig. 11 shows the spatial dependence produced by the sum of each of the four modal motion waves with varied modal magnitudes, with a traveling wave of magnitude 1, and k_T = k_M. When A_M/A_T = 4, the spatial pattern of the sum of the modal and traveling waves is similar to the pattern of the modal wave alone, with the most obvious differences occurring in the variation of phase angle with space: The phase angle transitions in the sum are slightly more gradual, and the total phase angle lag accumulated by the sum of the waves when k_Mx = 2π is a full cycle. As A_M is reduced so that A_M/A_T equals 2, 1, and 0.5, the spatial patterns of the summed waves looks more and more like the pattern of the traveling wave, with a nearly uniform phase angle gradient when A_M/A_T = 0.5, and the node within the modal motion becomes more difficult to see. At the same time, the spatial variations in the magnitude of the summed waves become smaller. With A_M/A_T = 0.5, the magnitude of the summed waves shows small cyclic variations around a near constant magnitude, and the phase angle varies fairly regularly from 0 to 1 as k_Mx and k_Tx vary between 0 and 2π; as is expected for a wave pattern dominated by wave travels.

The right-most panel of Fig. 11 shows the spatially varying magnitudes and phase angles produced by the sum of each of the four modal motions with varied modal magnitudes and a traveling wave of magnitude 1 and k_T = 4k_M. These summed waveforms show similarities and significant differences from the middle panel of the figure. When k_T = k_M in the middle panel, we always see two local magnitude maxima while in the right-most panel, with k_T = 4k_M, we see that each of the model predictions shows five local maxima. Also, when A_M/A_T ≤ 1, on the right we see phase angle accumulations of more than 2 cycles over the distance of k_Mx = 2π, and when A_M/A_T ≥ 2 we see ripples in phase angle around the modal wave values of 0 or 0.5 cycles where the ripples have a spatial extent that approximates one wavelength of the traveling wave (x = 2π/k_T). Finally, note the complete loss of any sign of a modal node on the right when A_M/A_T ≤ 1, and the introduction of a pseudo node with the coupling of a deep minima in magnitude with a quarter cycle phase angle step when k_Mx /2π = 0.75 and A_M/A_T = 1.

It is important to realize that the details of the model predictions we present in the center and right-hand panels of Fig. 11 depend on the precise spatial phase angle relationship between the modal and traveling wave components. The introduction of some constant phase angle term in the traveling wave component can change the specific patterns of the sums that we compute. However, several features of these predictions are relatively robust to such alterations including the ability to see nodal minima and coupled half-cycle phase changes when A_M/A_T ≥ 2 and k_M ∼ k_T, the presence of phase angle glides in the sum when A_M/A_T ≤ 1, and the ripples in phase angle about the relatively constant modal values when A_M/A_T ≥ 2 and k_M > 3k_T. These three features are prominent components of our holographic results.

Wave patterns in our measurements and modeling

The common features in the wave patterns from our measurements that are summarized in Figs. 910 and the simulations of the simple combination of modal and traveling waves in Fig. 11 include:

• (1)The presence of motion nodes marked by regions of localized low-magnitude that are accompanied by rapid half-cycle phase changes: Such patterns are observed in the model simulations only under the conditions where the magnitude of the modal wave is at least twice the magnitude of the traveling wave (A_M/A_T ≥ 2), and are best observed when the spatial frequency of the modal and traveling wave are similar (k_M ∼ k_T). These cues to prominent modal motions are most apparent in our holographic measurements with stimulus frequencies of 4 kHz and above, and are observed near the edge of the TM in Figs. 910 and on either side of the umbo at stimulus frequencies of 9 kHz and higher in Figs. 10g, 10h, 10i, 10j.
• (2)The phase angle ramps or glides of near constant phase angle gradient are obvious in the simulations when the magnitude of the traveling wave is equal to or larger than the magnitude of the modal wave (A_M/A_T ≤ 1) and the spatial frequency of the traveling wave is equal to or greater than the spatial frequency of the modal wave (k_T ≥ k_M). Under these conditions, the spatial phase angle gradient of the ramp (Δθ/Δx) in radians per unit x is a good estimator of the spatial frequency of the traveling wave, k_T. Prominent phase angle ramps are observed in our holographic data with stimulus frequencies between 3 and 8 kHz. These ramps are generally but not always, centripetal in nature with phase angle accumulating as the wave travels toward the center. Furthermore, the ramps are most prominent near the rim of the TM, and often die out before reaching the area of the umbo [Figs. 9c, 9d, 9e, 9f, 9g, 9h; 10a, 10b, 10c, 10d, 10e, 10f].
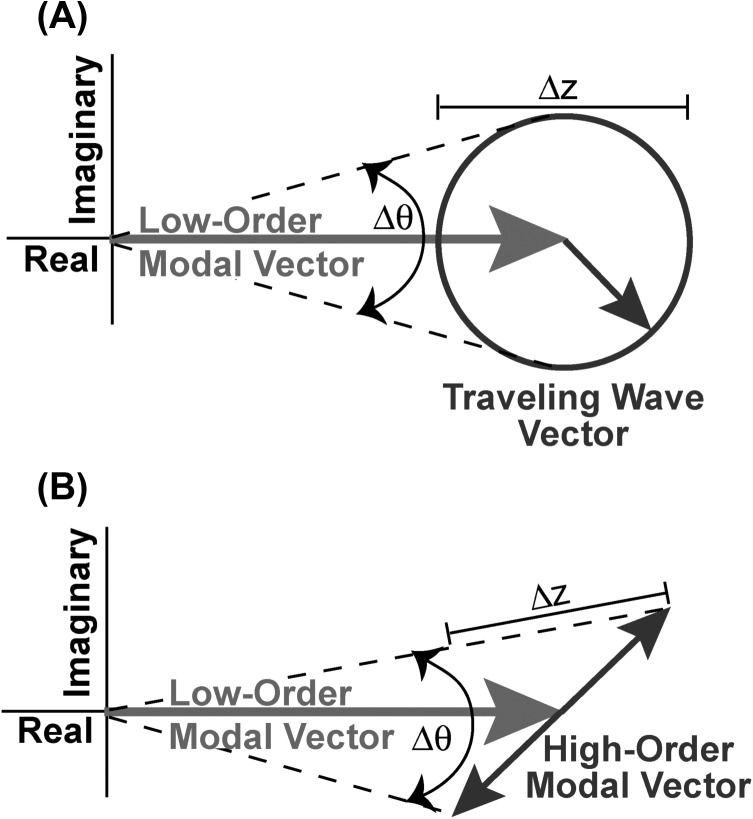
• (3)Our data also show multiple instances of the phase angle and magnitude ripples seen in the simulations that result from the combination of a larger modal wave magnitude (A_M/A_T ≥ 2) with a traveling wave of much higher spatial frequency k_T ≥ 4k_M. The number of phase angle ripples observed without a more significant phase angle deviation is an indicator of the difference in spatial frequency between the traveling wave and the modal motion. In the right-hand panel of Fig. 11, when A_M/A_T ≥ 2 we see two phase angle ripples per half modal wavelength, consistent with the model values of k_T ≥ 4k_M. A similar number of ripples around a near steady mean angle are observed in Figs. 9f, 9g, 9h, 9i and Figs. 10f, 10g, 10h when the stimulus frequency is between 8 and 12 kHz. A larger number of phase angle ripples (3 to 4) per region of near constant mean phase angle are observed in Figs. 9j, 9k and Figs. 10i, 10j, 10k, 10l (with stimulus frequencies of 12 kHz and larger), which suggests that k_T ≥ 6 k_M in these data sets. Also, as in the simulations, in the data regions where phase angle ripples are observed, the number of phase angle ripples is roughly matched by cyclic variations in the magnitude of the wave pattern. Such phase angle and magnitude ripples are perfectly consistent with Fig. 12A, which illustrates the summing of a modal pattern that varies slowly in space (low spatial frequency) and a traveling wave of smaller magnitude that varies rapidly in space (high spatial frequency). The ripples in magnitude and phase angle [Δz and Δθ in Fig. 12A] represent the rapid rotation of the smaller higher-spatial-frequency traveling wave vector around the larger, slowly changing low-spatial-frequency modal.

Figure 12.

Complex plane representations of a combination of displacement patterns with large magnitude and a low-spatial frequency and a pattern with smaller magnitude and a much higher spatial frequency. (A) Sum of a modal vector with large magnitude that varies slowly in space (low spatial frequency), and a traveling wave vector with smaller magnitude that varies rapidly in space (high spatial frequency). We have chosen to illustrate the combination around a spatial location where the magnitude of the modal vector is near maximum. As we look at locations adjacent to the starting point, the magnitude of the modal vector varies slowly along the real axis while the traveling wave is represented by a vector of constant magnitude that rotates as the location changes. The summation of the two patterns produces a displacement vector with cyclic variations (ripples) in the magnitude Δz and phase angle Δθ of the measured displacement. (B) Sum of a modal vector with large magnitude that varies slowly in space (low spatial frequency), and a higher-order modal vector with smaller magnitude that varies rapidly in space (high spatial frequency). As above, we illustrate the combination around a spatial location where the magnitude of the low-order modal vector is near maximum. As we move away from the start location, each of the two modal vectors moves back and forth along their assigned track, although at greatly different spatial frequencies. The magnitude of the modal vector varies slowly along the real axis while the influence of a significant damping term in the denominator of Eq. 3 when the stimulus frequency is near the natural frequency of the higher-order mode gives a mode a track that varies in both the real and imaginary planes by a vector of constant magnitude that rotates as the location changes. The summation of the two patterns produces a displacement vector with cyclic variations (ripples) in the magnitude Δz and phase angle Δθ of the measured displacement.

Estimates of traveling wave speed and ME group delay

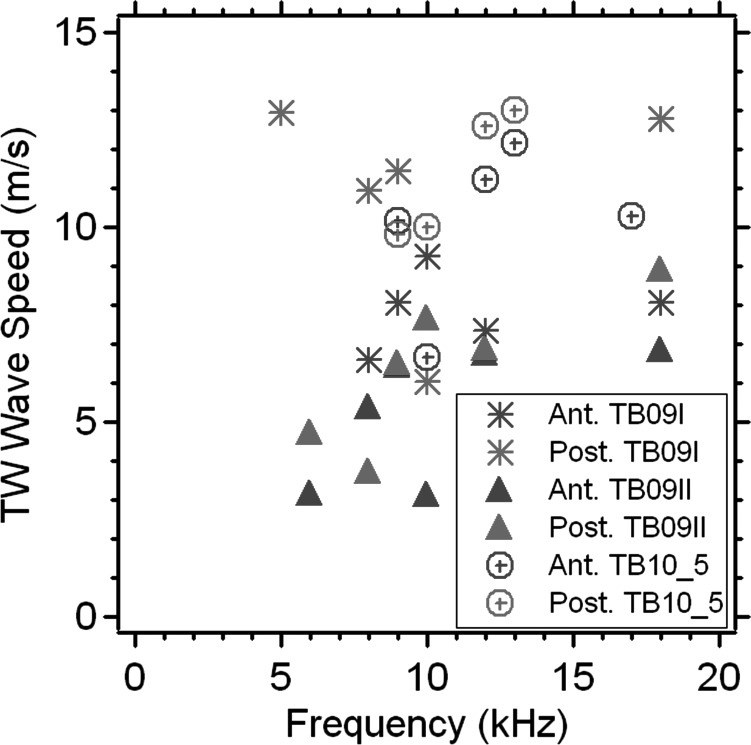
The similarity of the spatial variations of magnitude and phase angles that we see from our measured TM displacement results (Figs. 910) and our simulation (Fig. 11) suggests two methods for quantifying the speed of the traveling-wave-like components in TM displacement: (1) The presence of obvious phase angle glides in response to sound stimuli of 2 to 8 kHz allows direct estimation of the spatial frequency of the putative traveling wave, where k_T = Δθ/Δx, the gradient of the phase angle glide; (2) when the phase angle and magnitude ripples are prominent in the stimulus frequencies region of 8 to 18 kHz, the spatial frequency of the putative traveling wave is 2π divided by the distance required for one complete ripple cycle. The propagation velocity or wave speed, c, of a traveling wave is related to the spatial frequency of the wave, k_T, and the stimulus frequency f, where c = 2πf/k_T.

Estimates of the speed of putative traveling waves from three TBs in response to eight stimulus frequencies are illustrated in Fig. 13, where separate estimates of the wave speed are made from the anterior and posterior portions of the three TMs. The estimated wave speeds vary between 3 and 15 m/s with a tendency to see lower wave speeds at lower frequencies. These wave speeds, together with the 4 mm radius of the TM, suggest delays of 0.3 to 1.3 ms for wave travel from the TM rim to the umbo.

Figure 13.

(Color online) Estimates of the speed of the traveling wave based on the analysis of phase angle vs position plots (e.g., Figs. 910) from 3 TBs (TB09_I, TB09_II, and TB10_5) in response to 8 stimulus frequencies (between 5 and 18 kHz) at the anterior and posterior side of the TM.

The time needed for putative traveling waves on the TM surface to travel from the rim to the center (the umbo) has been used to explain observations of a signal transmission delay between the sound pressure in the ear canal just lateral to the TM, and sound entering the inner ear. This ME transmission delay has been characterized by computations of the group delay in ME sound transfer based on comparisons of stapes motion or inner-ear sound pressure to the sound pressure in the ear canal (O'Connor and Puria, 2008; Nakajima et al., 2009). The human ME group delays calculated from such measurements are between 40 and 90 μs, a factor of 3 to 10 shorter than the putative wave delays (0.3 to 1.3 ms) that we quantified above from our holographic data. Put another way, the ME delays measured by O'Connor and Nakajima are consistent with wave speeds (40 to 100 m/s) 3 to 10 times faster than the putative wave speeds (3 to 15 m/s) we estimate here. In discussing ours and others umbo displacement data (Sec. 3C), we also quantified group delays that varied between 40 and 60 μs that would also result in wave speeds considerably faster than those in Fig. 13. Therefore, it seems unlikely that the putative traveling waves we describe here are responsible for observations of group delay either in umbo motion or ME sound transmission.

The significance of uniform pressure stimulation

The interpretation of our results in terms of modal motions depends, in part, on the assumption that the sound pressure stimulus to the TM is uniform. Such an assumption is natural at frequencies less than 5 kHz, given that the wavelength of sound in air at 5 kHz is about 70 mm and the diameter of the TM is about 8 mm, and that the wavelength increases as frequency decreases. The simple wavelength argument, however, breaks down as frequency increases and the sound wavelength approximates the dimensions of the TM. An important factor in the higher frequency range is the direction of wave propagation relative to the surface of the TM.

Stinson (1985), among others, pointed out that the human TM is normally acutely angled relative to the long axis of the ear canal, with the posterior edge of the TM being about 4 mm closer to the entrance of the ear canal. He demonstrated that this angulation led to differences in sound pressure magnitude across the TM surface of about ±10 dB at 15 kHz in a human ear with an intact ear canal. Our measurements are made with the ear canal removed and with the plane of the TM ring in our specimens oriented nearly perpendicular to the direction of sound stimulus propagation. Such an arrangement is different from the TM attached to the natural ear canal.

While the significance of ear canal removal on our data should be minimal at frequencies of less than 5 kHz, it is possible that the effect of the canal on the motion patterns we observe is greater at higher frequencies. For example, Goll and Dalhoff (2011) suggest that the ME delay they see in their model depends on the location of the reference stimulus along their string. We are investigating the possibility that the ear canal delays can alter the wave motions we see by using a glass-backed artificial ear canal that mimics the angulation of the TM ring and the canal terminus but allows observation of most of the TM surface. Whether or not these investigations point to a significant ear canal effect on the surface motions of the TM, our existing data will provide a useful view of TM function isolated from the ear canal.

Relevance to other observations and models of TM motion and function

The data we present and our analytic descriptions can be used to test other observation-based and model descriptions of TM motion and function.

• (a)Our data fairly consistently demonstrate that the parts of the TM attached to the manubrium of the malleus move much less than other parts of the TM. As pointed out by Tonndorf and Khanna (1970), this observation is consistent with the ossicular lever hypothesis of von Helmholtz (1868). Our measurements extend this observation to frequencies as high as 18 kHz.
• (b)Our measurements of the variations of displacement magnitude across the TM surface are consistent with earlier time-average holography measurements (Tonndorf and Khanna, 1972; Rosowski et al., 2009), which described multiple local regions of maximum and minimum motion magnitude. These earlier papers suggested that the observed magnitudes were consistent with a succession of purely modal displacement patterns that greatly increased in order as stimulus frequency increases, with different regions of the TM surface either moving in-phase or perfectly out-of-phase (a phase angle difference of [1/2] cycle). Our measurements of the phase angle of TM surface displacements demonstrate that the motion patterns we observe cannot be explained by a succession of single modes. In particular, we observed high frequency displacement patterns with multiple local maxima separated by minima but the minima have displacement magnitudes greater than zero and the phase angle difference between adjacent maxima is generally less than [1/4] cycle.
• (c)Parent and Allen (2007, 2010) have suggested that the TM acts as a two-dimensional transmission line, where sound power in air is matched to the membrane at its rim and then conducted to the umbo via traveling waves on the membrane surface. In their idealized model, the impedance at the umbo is matched to the output impedance of the TM transmission line so that no reflections occur and there are no mode-like standing waves on the membrane surface.6

  While we have observed traveling-wave-like phase angle variations on the TM surface consistent with wave propagation toward the umbo, we have also described significant standing-wave like modal motion patterns of TM motion that do not occur in the idealized models of Parent and Allen (2007, 2010). While we do see evidence of putative traveling waves of larger magnitude than the modal patterns (e.g., the phase angle glides seen in response to stimulus frequencies of 1 to 4 kHz in spatial regions between the rim and the umbo), in general the membranes' motion response at other frequencies point to the dominance of modal motions.

• (d)Puria and Allen (1998) also used a transmission line model of the TM to describe a set of ME input impedance and sound transmission measurements made in cats. Since they saw indications of temporally occurring standing waves, especially when the cochlear load was removed, their model parameters allowed for the presence of mode-like standing waves on the TM surface. However, in their model, sound energy was still carried along the TM surface by traveling waves, and the delay associated with that wave travel was on the order of the 0.04 ms ossicular transmission delay estimated from group delay measurements (Puria and Allen, 1998; Olson, 1998). The wave delays, which we calculate from our estimates of propagation velocity on the TM surface in our cadaveric ears, are about a factor of 10 longer than the group delays estimated from measurements of ossicular sound transmission in a similar TB preparation (Nakajima et al., 2009). Therefore, the traveling waves we observe on the TM surface are fundamentally different from those predicted by Puria and Allen (1998).
• (e)In a variation of the transmission line model, Goll and Dalhoff (2011) assume the TM is a collection of strings that are bound at the TM ring, and the umbo at the center of the TM. They also assume that the force acting on the surface of the string varies linearly with distance along the string. These assumptions lead them to a simple three-wave model that sums a simple modal pattern of motion with a combination of a backward and forward traveling wave along the string. Variations in the magnitude of the traveling waves allow this combination to approximate a one directional traveling wave (when the magnitude of one of the traveling waves is significantly larger than the other), a standing wave (when the two wave magnitudes are of equal magnitude), or some combination of traveling and standing wave. While the combination of a modal displacement and traveling waves is similar to our model simulations (Fig. 11), the low-order modal patterns we see in our data are more complex than the modal pattern suggested by Goll and Dalhoff (2011) (e.g., we see evidence of nodes). Also, many of the patterns we see suggest that the low-order modal displacements are of larger magnitude than the displacements produced by putative traveling waves.
• (f)Fay et al. (2006) used modal motion theory to suggest the motion of the TM results from the sum of many possible modal motions (e.g., Fletcher, 1992), and specifically hypothesize that the high density of higher-order modal motions at frequencies above a few kilohertz were gathered in a weighted sum that smoothed the frequency response of the motion of the umbo and attached ossicles at high frequencies. While we see indications of summed motions, the small number of nodes we identify suggest the presence of relatively low-order modal motions on the TM surface even at frequencies as high as 18 kHz. The best evidence we see in support of the dominance of low-order modes at these high frequencies is the repeated phase angle ripples that cover much of the TM surface at frequencies above 6 to 8 kHz: We argue that these ripples are consistent with the combination of a larger magnitude low-spatial frequency modal motion and smaller magnitude higher-spatial frequency waves (either traveling waves or a higher-order modal motion). If our interpretation is correct, relatively low-order modal motions contribute significantly to TM motion even at high frequencies and are likely a major contributor to umbo and ossicular motion.
• (g)de La Rochefoucauld and Olson (2010) presented scanning laser data from the gerbil TM that support the data we present, as well as our interpretation of the combination of modal and traveling waves. Their measurements included high density scans along a radial line of the gerbil TM ending at the umbo, and along the surface of the TM lateral to the gerbil manubrium. They saw TM surface motions consistent with both traveling waves and what they described as “more piston-like” motions of the entire TM surface (what we might describe as a low-order modal motion). They also argued, based on comparisons of the TM surface and umbo motions, that the stimulus to the ossicles was the “piston-like” motion of the TM, and not the traveling wave.
• (h)The suggestion that displacement of the TM in our experiments is dominated by low-order (low spatial frequency) modal patterns of motion is incompatible with the notion that the delay between the sound pressure in the ear canal and the motion of the umbo is caused by a delay in wave travel along the surface of the TM. Furthermore, the putative wave speeds we estimated from the spatial variations in the displacement phase angle are much slower than the speeds required to explain the measurements of ME delay. The suggestion is that the phase angle variations we observe are not related to stimulus transmission between the sound and umbo velocity. A hypothesis that needs further investigation is that the group delay observed in umbo-velocity to sound pressure transfer functions may reflect a concatenation of impedances that govern the sound-induced motion of the TM and the ossicular chain (de La Rochefoucauld et al., 2010). It may also be that some other form of TM motion, e.g., longitudinal waves traveling along the TM fibers, may be responsible for TM sound transmission (Jackson et al., 2012).

The consequences of a lossy membrane

The spatial patterns of the magnitude and phase angle of displacement on the surface of the TM can also be described by purely modal motions of TM without invoking traveling waves when sufficient membrane losses are included. Equation 3 is a simplification of Eq. (5.19) of Fletcher (1992) that describes the motion of a circular membrane in response to a uniform sinusoidal load on the surface with $\omega =2\pi \times$ the stimulus frequency

$$z(x,y,t)=\frac{p}{{\rho }_{s}d}{\displaystyle \sum _{m,n}\frac{A_{m,n}(x,y){A^{\prime }}_{m,n}}{\left({{\omega }^2}_{m,n}-{\omega }^2\right)+2j\mathrm{\omega \alpha }(\omega )}{e}^{j\omega t}},$$ (3)

where z is the time varying displacement at location (x,y); p is the magnitude of the uniform pressure stimulus; ${\rho }_s$ is the density of the membrane; d is the membrane thickness; m and n are the orders of the possible circular and radial modal motion modes (Fletcher, 1992); $A_{m,n}(x,y)$ is the eigenfunction describing the spatial pattern of mode m, n; $A_{m,n}^{\prime }$ is a spatial integral of the modal function over the TM surface in space; ${\omega }_{m,n}$ is the natural radian frequency of each mode; j is the imaginary number, and $\alpha (\omega )$ is a frequency dependent damping term, which in practice increases with frequency.

The modal patterns that contribute to the TM motion depends on the proximity of the stimulus frequency to the natural frequency (${\omega }_{m,n}-\omega$) and the amount of damping. In Figs. 12910, the response of the TM to stimulus frequencies of less than 4 kHz can be produced by the sum of one or two low-order modes of motion. The phase glides observed with tonal stimuli in the 4 to 8 kHz range can be accounted for by the presence of the damping term, which slows the spatial transitions in phase angle between regions that move out-of-phase with each other. The phase angle and magnitude ripples observed at higher frequency can be produced by the summation of a low-order (low-spatial frequency) modal motion summed with a higher-order (high-spatial frequency) modal motion that is significantly damped and of lower magnitude [Figs. 12B]. The damping is required to produce a difference in the phase angle of the two summing modal vectors.

Other wave motions on the TM surface

While the majority of our TM surface motion data are adequately summarized by the figures and analyses we present here, we have seen signs of other modes of TM motion that need more investigation. We have mentioned that occasionally we see phase angle glides on the TM surface consistent with wave travel from the center of the TM toward the rim. We also see signs of circular traveling-wave-like phase angle glides consistent with wave travel along one of the rings of displacement maxima that we see with sound stimuli of frequencies greater than 6 to 8 kHz. The causes and significance of these putative traveling waves are unclear.

CONCLUSIONS

In this study, we used stroboscopic holographic interferometry to measure the vibration of the human TM stimulated by tones from 0.2 to 18 kHz. This technique quantifies both the magnitude and phase angle of the displacement at over 300 000 points on the TM surface, allowing us to define spatial patterns of sound-induced wave motion. The measurements of umbo displacement and total volume displacement of the TM extracted from these data appear linear and show a frequency dependence that is generally similar to data in the literature. The ME input impedance and reflectance were computed from direct measurements of the volume displacement of the TM and the pressure at the edge of the TM from cadaveric human TBs over a wide frequency, from 0.2 up to 18 kHz. Using a simple two-wave model we were able to separate out different wave motion patterns and identify frequencies and regions where the patterns of motion were consistent with (1) simple modal motion (at low frequencies, where phase angle is constant on the TM surface, and by the presence of nodes at higher frequencies), (2) dominant traveling-wave-like motions (regions where the phase angle changes regularly with location), and (3) a combination of a larger low-order (low spatial frequency) modal disturbance and a smaller high-order (high spatial frequency) traveling-wave-like motion. The traveling-wave-like motion could also be attributed to damped modal motion. These data were used to test various models and interpretations of TM motion in the literature, and were found to be consistent with the interpretation of de La Rochefoucauld and Olson (2010) and others (Cheng et al., 2010; Rosowski et al., 2011). The contribution of these different motion patterns to ME function is a point of continuing study. However, our results suggest that relatively low-order modal motions of the TM surface are capable of providing significant stimulation to the manubrium over a wide range of frequencies.