Reduced-order constrained optimization (ROCO): Clinical application to head-and-neck IMRT

Abstract

Purpose: The authors present the application of the reduced order constrained optimization (ROCO) method, previously successfully applied to the prostate and lung sites, to the head-and-neck (H&N) site, demonstrating that it can quickly and automatically generate clinically competitive IMRT plans. We provide guidelines for applying ROCO to larynx, oropharynx, and nasopharynx cases, and report the results of a live experiment that demonstrates how an expert planner can save several hours of trial-and-error interaction using the proposed approach.

Methods: The ROCO method used for H&N IMRT planning consists of three major steps. First, the intensity space of treatment plans is sampled by solving a series of unconstrained optimization problems with a parameter range based on previously treated patient data. Second, the dominant modes in the intensity space are estimated by dimensionality reduction using principal component analysis (PCA). Third, a constrained optimization problem over this basis is quickly solved to find an IMRT plan that meets organ-at-risk (OAR) and target coverage constraints. The quality of the plan is assessed using evaluation tools within Memorial Sloan-Kettering Cancer Center (MSKCC)’s treatment planning system (TPS).

Results: The authors generated ten H&N IMRT plans for previously treated patients using the ROCO method and processed them for deliverability by a dynamic multileaf collimator (DMLC). The authors quantitatively compared the ROCO plans to the previously achieved clinical plans using the TPS tools used at MSKCC, including DVH and isodose contour analysis, and concluded that the ROCO plans would be clinically acceptable. In our current implementation, ROCO H&N plans can be generated using about 1.6 h of offline computation followed by 5–15 min of semiautomatic planning time. Additionally, the authors conducted a live session for a plan designated by MSKCC performed together with an expert H&N planner. A technical assistant set up the first two steps, which were performed without further human interaction, and then collaborated in a virtual meeting with the expert planner to perform the third (constrained optimization) step. The expert planner performed in-depth analysis of the resulting ROCO plan and deemed it to be clinically acceptable and in some aspects superior to the clinical plan. This entire process took 135 min including two constrained optimization runs, in comparison to the estimated 4 h that would have been required using traditional clinical planning tools.

Conclusions: The H&N site is very challenging for IMRT planning, due to several levels of prescription and a large, variable number (6–20) of OARs that depend on the location of the tumor. ROCO for H&N shows promise in generating clinically acceptable plans both more quickly and with substantially less human interaction.

INTRODUCTION

In previous work, we proposed the reduced order constrained optimization (ROCO) method that applies machine learning techniques to IMRT treatment planning, demonstrating its success in generating acceptable plans for the prostate¹ and lung² sites. In this paper, we extend ROCO to the head-and-neck (H&N) site, which is substantially more complex given the numerous organs at risk (OARs) involved. In our current implementation, ROCO H&N plans can be generated using about 1.6 h of offline computation followed by 5–15 min of semiautomatic planning time on a modest desktop workstation (an Intel Core 2 Duo, clock speed 2.66 GHz, with 3.5 GB of RAM). We estimate this saves an average of 3 h of online planning time compared to current clinical practice at MSK on a similar platform.

H&N cancers account for 3%–5% of all cancers in the United States. An estimated 52 610 people will develop H&N cancer and an estimated 11 500 deaths will occur in 2012.³ Long term survival rates are high (55%–80%) when combining radiation therapy with chemotherapy, and the cure rate is also high for early-stage disease.⁴ IMRT is often preferred to standard radiation therapy for nasopharynx tumors, since it has been shown to offer significant improvement in quality of life factors including fatigue, taste/smell, dry mouth, and ill feeling during the recovery phase of acute toxicity.⁵ However, the concave shape of the target volume and the close proximity to a large number of radiation-sensitive normal tissues makes this site extremely difficult to plan. We estimate that it currently takes an expert planner at Memorial Sloan-Kettering Cancer Center (MSKCC) an average of 5 h to create a clinically acceptable IMRT plan for H&N cancer.

It is still common clinical practice to obtain H&N IMRT plans by minimizing an unconstrained objective function composed of a weighted sum involving several competing clinical goals specified by the physician.^{6, 7} Since the clinical goals cannot be directly enforced in such a formulation, planners require an iterative loop of trial-and-error interaction with optimization software until a suitable plan is achieved. This process can take up to 8 h for a H&N case; part of this time is spent in evaluating a plan, deciding on changes in optimization parameters to get closer to the treatment goals, and iterating the optimization/evaluation process. The key advantage to the ROCO method is that it involves a constrained optimization step in which hard clinical constraints are directly imposed on the optimization structures, made computationally feasible by reducing the dimensionality of the intensity space.

Previous methods have attempted to apply a constrained optimization over the beamlet weights,^{8, 9} which provides direct control and steerability of the treatment plans.¹⁰ However, due to the large number of beamlets (on the order of tens of thousands), these very large optimization problems are computationally time-consuming. Binary integer variables have been introduced¹¹ to flag the voxels violating the dose-volume constraints (DVCs), so that the problem becomes a mixed integer program. The mixed integer program instances explicitly include the constraints and require no tunable parameters; however, the number of binary variables is equal to the total number of evaluation points in all structures, which is on the order of tens of thousands. On such a scale, the time required to implement this approach is far from being clinically feasible.

The planning problem has also been posed as a multiobjective optimization that allows the planner to interactively choose from a family of Pareto-optimal plans.^{12, 13} This method requires a reasonably large number of pre-computed plans to be generated on the Pareto front, each of which takes several minutes to compute, though some studies indicate that the Pareto front is spanned by a relatively small number of plans.¹⁴ More recent studies¹⁵ explore the possibility of including multiple beam angle configurations in the multicriteria formulation that introduce nonconvexity to the problem, as well as a method for navigating multiple Pareto surfaces. Further work¹⁶ introduces a method to compare convex Pareto surfaces and suggests that even complex cases with many objectives often have a limited number of “strong” competing objectives between which the planner has to decide according to clinical importance. We believe this reflects our observation that viable treatment plans can generally be found in a low-dimensional space discovered using machine learning.

Other studies¹⁷ investigate how expanding the search space to a wider range of penalty functions using a multiobjective evolutionary algorithm (MOEA) can result in improved IMRT plans. However, each MOEA optimization can take up to 7 h for a complex head-and-neck case, limiting clinical feasibility.

Here, we present our results for the ROCO method applied to ten previously treated H&N cases, demonstrating that ROCO is able to achieve clinically acceptable treatment plans and does so quickly and semiautomatically. We also describe a live ROCO session performed together with an experienced planner for a given H&N patient, illustrating the potential of the method to be used in clinical practice.

SUBJECTS AND METHODS

Treatment plan criteria

IMRT planning for H&N at MSKCC is typically a dose-painting (or “concomitant boost”) technique where 2–3 different planning target volumes (PTVs) are delineated, each to be treated to a different dose level. For the patients in this study, the lowest prescription level ranged between 54 and 59.4 Gy. The second level varied between 59.4 and 66 Gy, and the third level of prescription was usually 70 Gy. In our study, we deemed coverage acceptable if for each PTV, D₉₅ (the highest dose encompassing 95% of the structure) was ⩾95% of the prescription dose for that target.

We used the MSKCC treatment planning system for our study, which uses a radiological pathlength corrected pencil beam algorithm for dose calculation;¹⁸ the optimization algorithm employed by default in the TPS has been described previously.^{4, 7} At MSKCC, H&N IMRT plans are delivered at 1.6–1.8 Gy/fraction to the lowest dose level, using the sliding window technique. Up to nine planner-chosen 6 MV beam directions are used. The ROCO algorithm used these beam directions to retrospectively replan ten H&N patients who had already been treated with IMRT, including larynx, oropharynx, and nasopharynx cases. The anonymized clinical data, including image sets, structure contours, and clinical treatment plans, were provided by MSKCC under IRB approval.

A number of the cases that we studied were treated with a low anterior neck (LAN) non-IMRT AP field with the same isocenter as the IMRT fields; the junction was established by nondivergent or minimally divergent settings of the jaws as placed by the physician. This is a common treatment technique. To prevent the IMRT intensity from falling off suddenly at the junction (which could result in small setup errors causing cold spots in a tumor-bearing region) our clinical practice is to use optimization PTVs and optimization fields that extend below the junction by ∼2 slices (∼5 mm). The jaws used for final plan evaluation and for delivery are defined by the physician-specified matchline, and the evaluation PTV terminates at ∼2 slices superior to the matchline. Thus, we refer to longer “extended” structures that are used during optimization and shorter “evaluation” structures that are used when assessing plan acceptability.

For H&N patients, there are typically three “critical” organs at risk (OARs)—the spinal cord, brainstem and chiasm—as well as several additional OARs that enter into the optimization depending on the position of the target. The parotids are particularly important, but it is difficult to impose a patient-independent constraint that can be consistently met by the optimization without compromising PTV coverage. Here, we impose the mean dose constraint on the parotid glands calculated using the heuristic proposed by Hunt et al.,¹⁹ which takes into account the overlap between the parotids and the PTVs to determine the minimum parotid mean dose that can be actually attained for each of the glands. Table 1 summarizes the departmental guidelines for OAR dose distributions at MSKCC.

Table 1.

Clinical goals for organs at risk to be satisfied by H&N plans. In difficult cases, the physician might allow the relaxation of a goal to the number observed in parenthesis. The achievable parotid gland mean dose constraint is estimated per patient using the heuristic proposed by Hunt et al.¹⁹ In addition to the structures in the table, hot spots more than ≈1 cm outside of the envelope of the lowest dose PTV are not allowed.

Structure	Constraint
Cord	Dmax ⩽ 45 Gy (50 Gy)
Brainstem	Dmax ⩽ 50 Gy (60 Gy)
Chiasm	Dmax ⩽ 54 Gy (60 Gy)
Mandible excluding all PTVs	Dmax ⩽ 104% of low PTV Rx
Cochlea	Dmax ⩽ 50 Gy
Brachial plexus	Dmax ⩽ 65 Gy
Lens	Dmax ⩽ 5 Gy (10 Gy)
Eyes/retina	Dmax ⩽ 45 Gy
Optic nerve	Dmax ⩽ 54 Gy
Larynx	Dmean ⩽ 40 − 45 Gy
Parotid	Dmean ⩽ 26 Gy
Oral cavity	Dmean ⩽ 35 − 40 Gy

However, declaring a plan “clinically acceptable” depends on the intuition of the planner as well as the physician's requests. Some goals may be relaxed if the physician is unhappy with the tradeoffs in the plan and needs to improve the coverage of the PTVs. For example, even though the cord, brainstem, and chiasm have the highest clinical priority, in difficult cases in which the coverage of the PTVs is highly compromised, the physician might allow the relaxation of a goal to the number observed in parenthesis (Table 1), for each one of these structures, but will not allow further relaxation. On the other hand, for other structures such as the optic nerve or oral cavity, doses might be allowed to exceed the values in Table 1 after the planner has tried hard and still not been able to achieve the desired coverage. Excessive modulation of the intensity profiles, which can lead to delivery problems and unnecessarily increased delivery time, is also not desirable in the clinic. Planners can visually inspect the profiles for each beam, and use cues provided by the planning system to direct them to problematic beams. In our experience, overmodulation is the result of pushing too hard on competing objectives.

PTV volumes treated to the 100% prescription level (lowest prescription dose) ranged from 77.25 to 1170 cm³ (median 301.40 cm³). Several of these patients presented challenging clinical scenarios, in which the treatment planner had required more than 15 optimization cycles to arrive at an acceptable plan. Table 2 summarizes the characteristics of the ten patients in the study.

Table 2.

Characteristics of the ten patients in the study including treatment site, number of parameters and fields used in the clinical optimization, and the number of optimization cycles (≈0.5 × run no.) that were required to achieve an acceptable IMRT plan.

Patient	Treatment site	No. of parameters	No. of fields	Run no.
1	Floor of mouth	34	7	45
2	Nasopharynx	65	9	48
3	Nasopharynx	59	7	37
4	Nasopharynx	52	9	15
5	Oropharynx	43	7	75
6	Base of tongue	37	7	19
7	Nasopharynx	52	7	19
8	Nasopharynx	54	7	16
9	Larynx	47	7	35
10	Larynx	45	7	65

The ROCO method

The ROCO method has been described in detail in previous work,¹ and is briefly summarized here. The method consists of three major phases as follows.

1. Unconstrained optimization.

   In this phase we randomly sample the parameter space of a quadratic dose-based objective function, computed as the weighted sum of several competing objectives for the structures listed in Sec. 2A. For the kth target, the corresponding objective function term is:

   $$\begin{array}{ccc}\hfill F_k^{\mathrm{target}}& =& \frac{1}{N_k}\left(\sum _{i=1}^{N_k}{\left(D_i-D_k^{\mathrm{Rx}}\right)}^2+w_k^{\min }\sum _{\left\{i\right|D_i<D_k^{\min }\}}{\left(D_i-D_k^{\min }\right)}^2\right.\hfill \\ \hfill & & \left.+w_k^{\max }\sum _{\left\{i\right|D_i>D_k^{\max }\}}{\left(D_i-D_k^{\max }\right)}^2\right),\hfill \end{array}$$ (1)

   where N_k is the number of points in the target, D_i is the dose to the ith point in the target, $D_k^{\mathrm{Rx}}$ is the prescription dose, $D_k^{\min }$ and $D_k^{\max }$ are the minimum and maximum dose allowed without penalty, and $w_k^{\min }$ and $w_k^{\max }$ are the penalties (weights) for under- and overdosing. The parameter set $P_k=\{D_k^{\mathrm{Rx}},D_k^{\min },D_k^{\max },w_k^{\min },w_k^{\max }\}$ completely specifies the objective function for target k.
   A similar objective function term is defined for each organ at risk, which also includes parameters $D_k^{\mathrm{mean}}$ and $w_k^{\mathrm{mean}}$ that define the mean dose constraints (as discussed previously,^{1, 2} ROCO can also handle dose-volume constraints, but they were not required in this study):

   $$\begin{array}{ccc}\hfill F_k^{\mathrm{OAR}}& =& \frac{1}{N_k}\left(w_k^{\max }\sum _{\left\{i\right|D_i>D_k^{\max }\}}^{N_k}{\left(D_i-D_k^{\max }\right)}^2\right.\hfill \\ & & \left.+w_k^{\mathrm{mean}}\sum _{i=1}^{N_k}{\left(D_i-D_k^{\mathrm{mean}}\right)}^2\right).\hfill \end{array}$$ (2)

   The minimum and maximum values for each parameter are determined by inspecting a population of previously generated clinical plans; this range is patient independent and only depends on the treatment site. We use Latin hypercube sampling²⁰ to randomly select N parameter sets within this range. Each set of parameters corresponds to an unconstrained objective function for the current patient that is minimized with the conjugate gradient method used in clinical practice at MSKCC.^{4, 7}

   The ith optimization results in an intensity vector I_i corresponding to a given set of parameters P_i, constructed by stacking the intensity values from all seven to nine treatment fields into a very high-dimensional vector. In this study, the dimension of this vector ranged from 14 935 to 45 362. The parameter sampling process is performed offline (i.e., prior to planner interaction).

2. PCA dimensionality reduction and mode dose calculation.

   Given N optimized intensity distributions {I₁, I₂, …, I_N} resulting from the unconstrained optimization with score function parameter sets {P₁, P₂, …, P_N}, the dimensionality of the intensity space can be reduced by linear or nonlinear feature extraction methods. We use Principal Component Analysis (PCA)²¹ for the reduced-order approximation. This procedure shifts the independent variables of the problem from the tens of thousands of beamlets that specify the intensity profile of a treatment plan to the N_modes PCA modes with the greatest variance. As described in our previous work,¹ the cumulative sum of the eigenvalues from the PCA process can be used to compute the amount of variance in the dataset accounted for by the top modes. We discuss the selection of the parameter N_modes for the head and neck site in more detail in Sec. 3A. These modes, denoted {U_j}, span a reduced solution space.

   As we noted in our previous work,² a simplified (short-range kernel) dose calculation is sufficient for the sampling step for the purposes of performing many dose calculations rapidly. However, we have found the simplified dose to result in inaccuracies if used in subsequent steps of ROCO. After the U_j are determined, it is critical to accurately calculate the dose for the PCA modes, so that during the next step of constrained optimization, the solver has precise information about OAR doses and target coverage. Therefore, at this stage we use a full dose calculation to evaluate the dose distributions for the PCA modes, using a radiological pathlength corrected pencil beam algorithm.¹⁸

   However, the full dose calculation algorithm only allows non-negative intensities (i.e., physically deliverable fields). Since the modes generally contain negative values, we compute the full dose for mode U_j, represented as a vector, as

   $$\begin{array}{ccc}& & (\max \left(U_j\right)-\min \left(U_j\right))·FD\left(U_j-U_j^{\min }\right)\hfill \\ & & +\min \left(U_j\right)·FD\left(-U_j^{\min }\right),\hfill \end{array}$$ (3)

   where FD corresponds to the full dose calculation that operates only on non-negative values. Here, max (U_j) and min (U_j) are scalars equal to the maximum and minimum values of the vector U_j, and $U_j^{\min }$ is a constant vector the same size as U_j in which each entry equals min (U_j). This approach of scaling and shifting to compute the mode doses is justified due to the linear relationship between doses and intensities. The principal component analysis and full dose calculation for the modes are performed offline (i.e., prior to planner interaction).

3. Constrained optimization.

   Given the reduced-dimension space that captures the effective degrees of freedom in the intensity variables, the final step is to find a clinically acceptable solution in terms of the reduced basis. At this stage, the optimizer has N_modes degrees of freedom: the coefficients of the PCA modes. The objective function for the optimization is

   $$\min \sum _{i\in T}{(D_i-D^{\mathrm{Rx}})}^2,$$ (4)

   for the voxels T in the target structures, each with a given prescription dose. This encourages the optimizer to reward uniform PTV coverage. The doses to voxel i are given by

   $$D_i=\sum _{j=1}^{N_{\mathrm{modes}}}{A}_{ij}{\xi }_j+{\mu }_i,$$ (5)

   where ξ_j are the coefficients of the principal components, which are the independent variables of the optimization. A_ij is the dose to voxel i from principal component j, and μ_i is the dose to this voxel from the plan corresponding to the mean of the N intensity distributions. The intensities of these modes were determined during the dimensionality reduction step, and the A_ij and μ_i are obtained by calculating the doses for each intensity mode U_j and for the mean.
   For each organ, the point dose hard constraints are specified by

   $$D_i\le D^{\max },$$ (6)

   where i runs over the set of voxels in each organ or target. Mean dose constraints are specified by

   $$\sum _{i=1}^{N_{\mathrm{vox}}}{D}_i\le N_{\mathrm{vox}}{D}^{\mathrm{mean}},$$ (7)

   where N_vox is the number of voxels in the structure.

   This reduced-dimensionality hard-constrained problem is feasible to solve quickly; we use the quadratic programming solver ILOG CPLEX^TM.

   The step of converting the ideal fluence profile to a deliverable leaf sequence, including realistic parameters (e.g., leaf transmission specific to the DMLC) is not unique to the MSKCC planning system. This step is also required in several modern commercial systems (e.g., Eclipse^TM, RaySearch^TM). Since the ideal fluences are somewhat modified by these MLC-specific effects, it is critical to perform a final dose calculation with the deliverable fluence and evaluate the resulting treatment plan. The module in the MSKCC planning system that creates the deliverable leaf sequence is called DMLCG. This module also provides the metrics that indicate the possible presence of an unacceptably high degree of modulation. After DMLCG and a final full dose calculation are performed, the planner checks the plan once more to make sure that all the desired constraints are still met. We were able to incorporate this vital step into ROCO by writing an algorithm that converts the intensity files to the required format in order to run DMLCG using the MSKCC TPS.

In our study, for both patients with and without a LAN field, we used the previously described extended structures in the sampling stage to ensure sufficient PTV coverage, and then optimized over the previously described evaluation structures in the constrained optimization stage. We also used the number of beams and beam angles defined by the planner. The original extended fields were used for optimization and then shortened at the evaluation stage.

Overall workflow

Many radiation therapy departments (including our own) have well-developed plan protocols for common disease sites. For such situations, much of the ROCO process can be carried out by a technical assistant (or eventually in automated fashion) without skilled planner input. Specifically, a physician and a skilled planner contour the target and important organs, the physician specifies the prescription, and the planner studies the case and chooses beam directions. The site-specific planning protocol defines the target coverage, OAR protection goals, and location and sizes of artificial dose-control structures such as “rinds”. For ROCO-based planning, the sampling space range, number of samples and number of modes (in clinical use, this would be established when the ROCO module of the planning system is commissioned) would be included in the protocol. A technical assistant would initiate the automatic process of sampling, solving unconstrained optimization problems, and computing PCA modes and mode doses. At this point, an experienced planner takes over to apply the protocol constraints, interactively run the constrained optimization phase of ROCO, and evaluate the resulting plan. The planner can modify the constraints if he or she thinks the plan can be improved. While there is still an element of experimentation, the process is much more directed than the trial-and-error process that characterizes unconstrained optimization, since the constraints the planner requests are actually achieved (or reported to be infeasible). The overall process is illustrated in Fig. 1.

Figure 1.

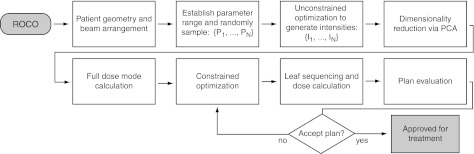
A flowchart illustrating the application of ROCO to clinical treatment planning.

RESULTS

Numbers of samples and modes

A critical aspect of the ROCO method is the choice of an appropriate number of samples and modes to achieve an acceptable plan. For the prostate and lung sites, we chose constant values for these quantities after investigating several training cases by varying the number of samples and modes to find the values at which desired PTV coverage was achieved. However, H&N cases exhibit higher variability, increasing in complexity from the oropharynx to the nasopharynx, so constant values across all cases would be inappropriate.

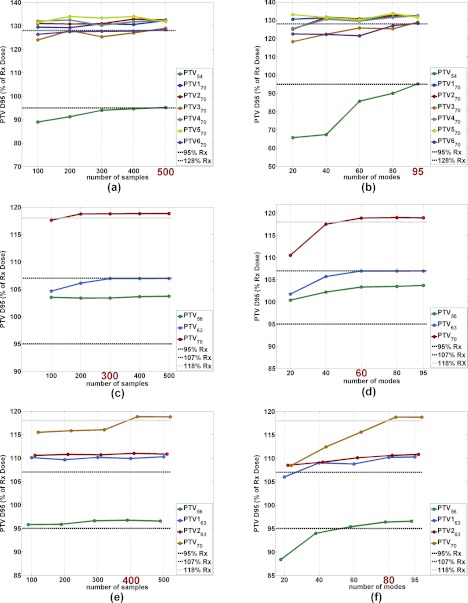
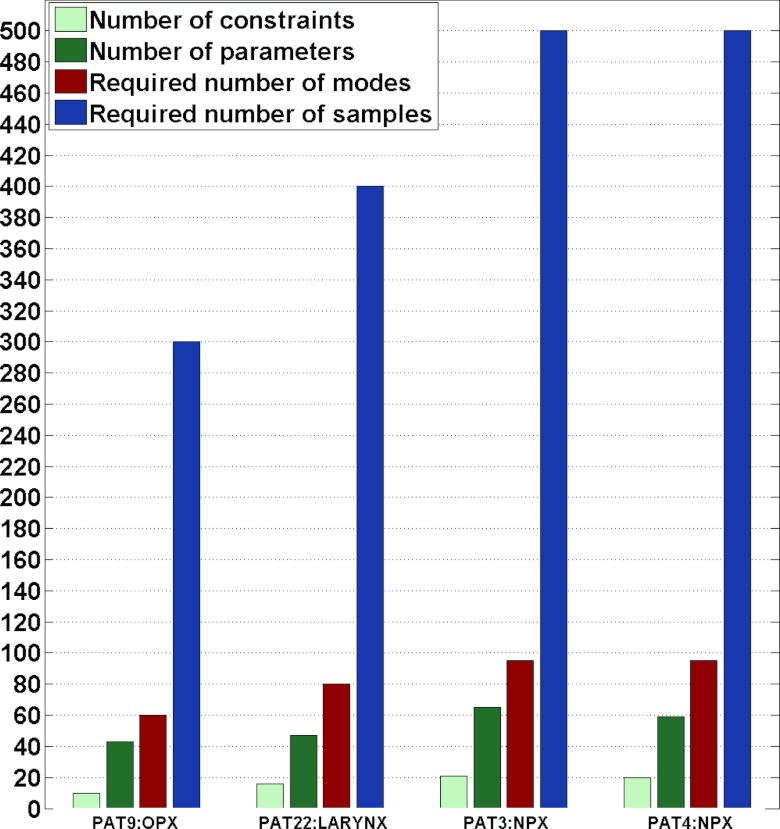
Figure 2 shows plots for three H&N patients illustrating PTV D₉₅ values for all the contoured PTVs per patient at different numbers of samples and modes. Figures 2a, 2b correspond to a nasopharynx case; (c) and (d) correspond to an oropharynx case; and (e) and (f) correspond to a larynx case. For each patient the sample/mode numbers at which PTV coverage was satisfactory are highlighted on the x-axis. We noticed that patients with fewer contoured structures (and hence, fewer unconstrained objective function parameters and clinical constraints) required both fewer samples in the sampling stage and fewer modes in the dimensionality reduction stage to achieve acceptable PTV coverage. Thus, we recommend deciding the starting values of the number of samples and modes based on the number of parameters. For example, Fig. 3 shows that oropharynx cases tend to have the least number of parameters in the unconstrained optimization, and in turn they require the fewest samples in the unconstrained phase. We would advise the planner to start an oropharynx case with 300 samples. On the other hand, nasopharynx cases generally have the largest number of parameters in the unconstrained optimization, so we would recommend the planner start these cases with 500 samples. Larynx patients generally have an intermediate number of parameters. The number of modes can be determined in a similar fashion as can be observed in Fig. 3; for oropharynx cases we would advise using 60 modes as the starting point in the constrained optimization stage and for nasopharynx cases we recommend starting with 95 modes.

Figure 2.

(a), (c), and (e) PTV D95 for all contoured PTVs at different prescription levels as the number of samples is increased for three H&N patients. (b), (d), and (f) PTV D95 for all contoured PTVs at different prescription levels as the number of modes is increased for three H&N patients. The highlighted number on the x-axis indicates the number of samples and modes that were sufficient to achieve satisfactory PTV coverage for all PTVs in the given patient. Plots (a) and (b) correspond to a nasopharynx case, plots (c) and (d) correspond to an oropharynx case, and plots (e) and (f) correspond to a larynx case.

Figure 3.

The number of samples and modes required for four H&N patients in order to achieve target coverage. For each patient, the left two bars indicate the number of constraints used in the constrained optimization and the number of parameters used in the unconstrained optimization, respectively; a lower number of parameters corresponds to fewer required modes (third bar) and samples (fourth bar) to achieve coverage.

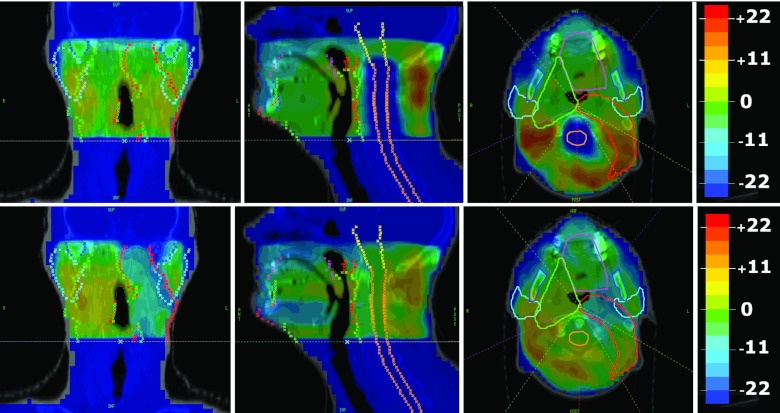
The modes, when interpreted as dose distributions, can correspond to planning tradeoffs for a particular patient. For example, Fig. 4 illustrates dose distributions corresponding to the first two modes for a two-PTV patient in our study. We can see that the first mode spares the cord while delivering similar doses to the PTVs, and the second mode concentrates dose to PTV59, while sacrificing dose to PTV66 and sparing the left parotid (generally shifting dose to the patient's right). Of course, the final ROCO plan is the superposition of tens of mode doses with different weights that are optimized to not violate the clinical constraints. The degree of sparing and dose concentration will vary depending on the sign and magnitude of the optimized coefficient for each mode.

Figure 4.

(Top) Dose distributions corresponding to the first mode for one patient. (Bottom) Dose distributions corresponding to the second mode for the same patient. In this case, the first mode spares the cord while delivering similar doses to the PTVs, and the second mode concentrates dose to PTV59, while sacrificing dose to PTV66 and sparing the left parotid. Warmer colors represent positive doses and cooler colors represent negative doses. The contoured structures include the brainstem (yellow), cord (orange), oral cavity (pink), parotid glands (cyan), mandible (blue), PTV59 (green), and PTV66 (red).

Clinical comparison

Each ROCO IMRT plan was compared to the corresponding historical clinical plan to assess its clinical acceptability. For the purpose of comparison, the ROCO plans were normalized to the D₉₅ value of one of the PTVs (generally the lowest dose PTV) in the plan used for treatment. This step is done to facilitate direct comparison between two plans for the same patient and would not be a step in the clinical implementation of ROCO. All of the ROCO plans were inspected to confirm that the intensity profiles were sufficiently smooth using several departmental criteria. First, the intensity profiles were visually inspected to confirm that there were no large peaks. Second, since overmodulation causes inefficient delivery which increases the monitor units (MU), we confirmed that the plan delivery did not require an excessive number of MU; Table 3 compares ROCO and clincal MUs, showing that in both cases the MUs are similar. Finally, the TPS reports the delivery efficiency of each beam; these were acceptable by the clinical planning standards.

Table 3.

Monitor units comparison between the ROCO and clinical plans. The number reported per patient corresponds to the sum of the MUs over all the beams.

Patient	1	2	3	4	5	6	7	8	9	10
ROCO plan MU	855	1476	1235	1367	1896	1478	1132	1100	1830	1650
Clinical plan MU	966	1580	1245	1162	1523	1241	1019	994	1263	1828

Our goal was to determine whether ROCO would be able to achieve plans that were competitive with respect to the clinical plans. Since the general treatment protocol constraints are not always optimal (or achievable) given the diversity of cases, in our study we applied the hard constraints corresponding to the recorded clinical plan. In all cases, the directly output intensities for the ROCO plans met the input hard constraints on the OARs while achieving satisfactory PTV coverage, measured using clinical full dose calculation, as illustrated in Fig. 5. The process of normalizing the ROCO plans to have the same D₉₅ as the one of the PTVs in the clinical plan for direct comparison resulted in a slight modification of the ROCO intensities and doses. We also found that after processing the intensity matrices to produce a deliverable set of leaf motions for the DMLC, the doses often increased (particularly the parotid mean doses), which can be attributed to dose leakage through the leaves. We noted that in the clinical plans we studied, the planner seemed to anticipate the DMLC effect by constraining the parotid mean doses to a lower value during optimization. If at this point, the parotid mean doses increased beyond the desired constraint, a second run through the constrained optimization in ROCO would attempt to tighten the parotid mean dose constraints while making sure that PTV coverage was still satisfactory.

Figure 5.

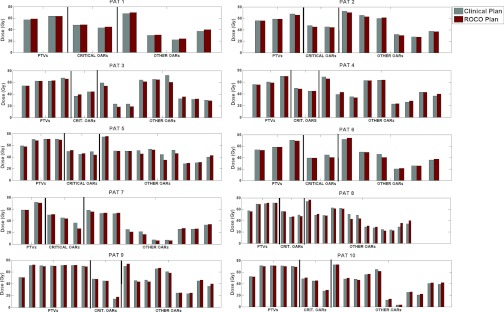
The clinical vs ROCO plan results for all ten patients, indicating doses for the PTVs, critical OARs (cord, brainstem, and chaism), and remaining patient-specific OARs. Due to both normalization for the purpose of comparison and the leaf-sequencing effect, some of the ROCO doses increased slightly, but remain close to the desired constraint.

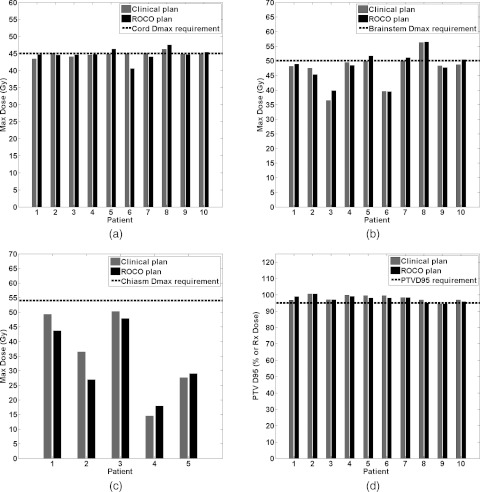
Figure 6 compares the ROCO plans that were achieved after leaf-sequencing (DMLCG) to the clinical plans for the cord, brainstem, chiasm, and PTV treated to the 100% level of prescription. The cord and brainstem were present in all of the H&N cases; as can be observed in Figs. 6a, 6b, the ROCO D_max values compare well to those achieved by the clinical plan. The chiasm was constrained in only half of the clinical plans; Fig. 6c shows that the ROCO plans were able to achieve D_max values in the chiasm generally lower than the clinical ones. Finally, Fig. 6d shows that the target coverage for the lower dose PTV is generally similar for both plans. All other levels of prescription, which are equally important, also achieved the desired coverage across the patients; the number of contoured higher-prescription PTVs varies from patient to patient and the results are illustrated in Fig. 5. As mentioned in Sec. 2A, for very difficult cases, the physician will allow the relaxation of some of the constraints. In Figs. 6a, 6b, we can see that in a few cases the planner decided to relax the cord and/or brainstem D_max constraint to the values listed in Table 1.

Figure 6.

Comparisons of ROCO vs Clinical IMRT plan results for the H&N critical constraints: (a) Cord D_max, (b) Brainstem D_max, and (c) Chiasm D_max. (d) Comparison of ROCO vs Clinical IMRT plan PTV D₉₅ for the 100% prescription dose level.

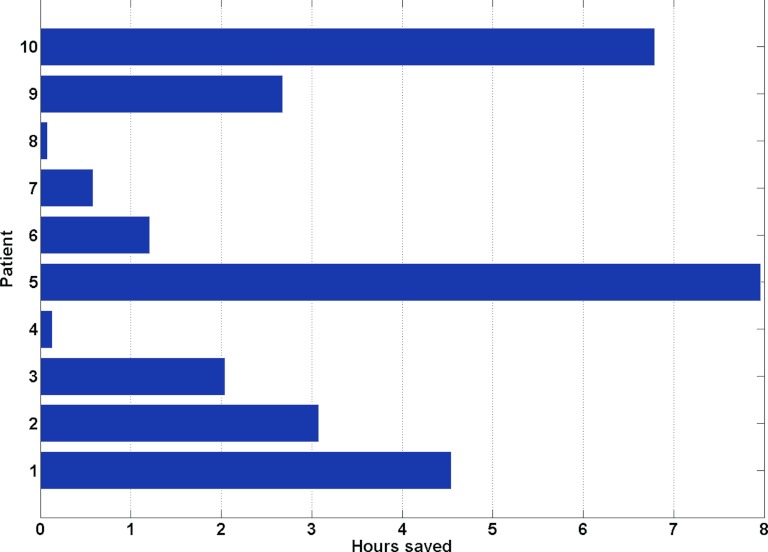
In addition to being able to satisfy hard clinical constraints directly, the main advantage of ROCO is its speed. Treatment planners using conventional IMRT optimization require up to 8 h to generate satisfactory H&N treatment plans. Using ROCO, the plans in our study were achieved on average within 109 min on a modest desktop workstation (an Intel Core 2 Duo, clock speed 2.66 GHz, with 3.5 GB of RAM). Of this time, approximately 99 min of computation are “offline” and require no user intervention. For example, the samples, modes, and mode doses can all be automatically computed before a planner begins to work. Each interactive constrained optimization takes approximately 10 min on our platform, of which only 2–3 min is taken by the CPLEX^TM solver. The rest of the time is spent looking at the results, evaluating them and deciding whether the plan is acceptable. This “online” time could be shortened even further since our current implementation still requires a human in the loop to transfer files and data between different programs. For eight out of the ten patients in the study, an acceptable plan was achieved after going through the constrained optimization one to two times. The second run was typically done to adjust the constraints on the parotid mean doses to account for the DMLC effect. The guideline used to choose the number of samples and modes described in Sec. 3A was effective for eight out of the ten patients; in only two cases did the number of modes at the constrained optimization stage need to be slightly increased. Assuming that each reoptimization cycle requires 15 min for a treatment planner to complete, Fig. 7 illustrates that ROCO offers a median time savings of 2.36 h, and that for difficult cases, more than 6 h would be saved.

Figure 7.

Hours of computation saved by ROCO per patient, assuming that each reoptimization cycle takes an experienced planner 15 min. The median time saved is 2.36 h.

Live ROCO session

As a proof of principle, we set up a live ROCO session between a nonplanner author (LR) and an expert H&N planner from MSKCC (AK). A nasopharynx patient with two discrete high-dose PTVs (named PTV70 and PTV7000) both with prescription doses of 70 Gy and a larger PTV intended for a prescription dose of 59.4 Gy (PTV5940) was chosen. The experienced planner reviewed the contours and chose the beam directions. The nonplanner ran all the pre-constrained optimization steps from a remote site; based on the sample and mode analysis described in Sec. 3A, 600 samples and 95 modes were chosen. The sampling took approximately 90 min and the PCA and mode dose calculation approximately another 30 min, all without human supervision. The experienced planner then provided the constraints he determined to be viable for this patient and the ROCO CPLEX^TM constrained optimization was performed, producing an intensity result in approximately 2 min. The ROCO intensities were then converted into deliverable DMLC compensator files, the full dose was computed, and the expert planner evaluated the results. Although the planner was satisfied with the coverage, he decided that the plan could be improved by further constraining the mandible and parotid mean doses. A second run with the modified constraints was performed (CPLEX^TM, DMLCG, full dose calculation) and the planner felt that overall the plan was acceptable, although, given a third run, he could further improve the plan by pushing the parotid mean doses lower and reducing the D_max constraint on one of the high-dose PTVs (PTV70).

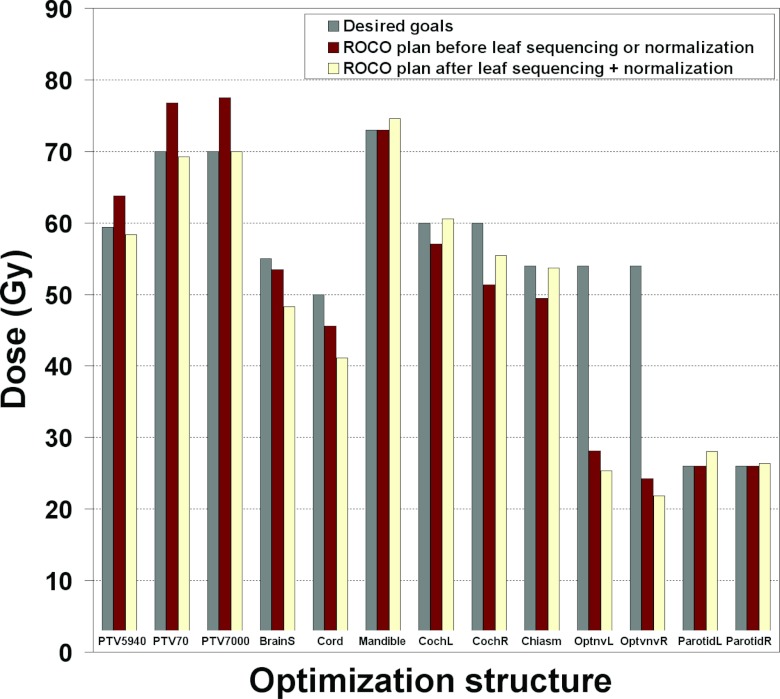
Figure 8 illustrates the resulting values for the constraints in the ROCO plan compared to what was requested by the planner. First, we compare the doses from the ROCO plan (middle bars) to the requested clinical constraints (left bars). As expected, all goals are met since ROCO directly, not approximately, imposes constraints. Next, we applied a common normalization used in the clinic; the D₉₅ value for the PTV7000 structure of the ROCO plan is scaled to equal the planner constraint. We then leaf-sequenced the plan for clinical delivery (right bars). After these two steps, the beamlet intensities and doses change slightly, but the ROCO plan still generally meets the constraints that were requested. Figure 9 presents sagittal and coronal slices of the final ROCO plan; they show that the ROCO plan is able to achieve good target coverage for both levels of prescription specified for this patient. As a final step, the ROCO plan was compared to the original plan used for treatment. Overall, the ROCO plan was competitive and even superior in some aspects, including the D_max of the cord and brainstem. This experience demonstrates the promise of using ROCO to improve expert planners' efficiency by deferring routine preliminary calculations to a junior planner or a technical assistant, and reserving planner expertise for adjusting plans and evaluating clinical tradeoffs after initial setup.

Figure 8.

Comparison of the requested planner constraints (left bars), the resulting ROCO plan prior to leaf sequencing or normalization (middle bars), and the ROCO plan after leaf sequencing and normalization (right bars) for the live session. The ROCO plan meets all the constraints prior to leaf sequencing or normalization, and meets most constraints after the D₉₅ value for the PTV7000 structure of the ROCO plan is scaled to equal the planner constraint. For several structures the ROCO plan does much better than requested (e.g., D_max for the cord and brainstem).

Figure 9.

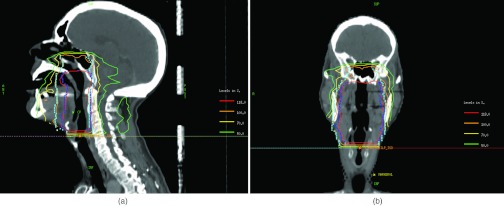
(a) Sagittal and (b) coronal slices of the ROCO plan from the live session. The 100% and 118% isodose levels show that the ROCO plan conforms well to the two levels of prescription specified in cyan (PTV5940) and blue (PTV70) respectively.

DISCUSSION AND CONCLUSIONS

We demonstrated the potential of the ROCO method to quickly and semiautomatically generate clinically acceptable IMRT plans for H&N cases. The dimensionality reduction of the problem allows ROCO to quickly solve a constrained optimization in which maximum and mean dose hard constraints are imposed on the desired structures. The ten ROCO plans in our study, as well as the additional plan from the live session, were compared to those achieved by an experienced planner and shown to be competitive. The ROCO plans were leaf-sequenced and evaluated using a full dose calculation as well as several treatment planning evaluation tools from MSKCC TPS. This study further confirms the applicability of ROCO as a general approach for IMRT treatment planning, after previous reports of its success in the prostate and lung sites. The head and neck site is the most complex and general scenario for IMRT planning since it contains many normal tissues and multiple PTVs at different dose levels (i.e., dose painting instead of uniform PTV dose).

While we have always applied ROCO to optimization objective functions of the form 1, 2 to conform with clinical practice at MSKCC, we could easily investigate alternative objective functions, e.g., based on generalized equivalent uniform dose (EUD) or biological responses. The key challenge would be that optimization packages that can handle nonlinear objectives and constraints would be necessary instead of our current tool, CPLEX^TM. We are currently evaluating alternative packages (e.g., SNOPT^TM) for these types of problems.

We also note that the ROCO approach is not restricted to MSKCC's in-house treatment planning system. As long as we have access to the relevant portions of the computer code, ROCO could be used with treatment planning systems that work like MSKCC's in the sense of generating intensities that minimize an objective function (e.g., Eclipse^TM or Pinnacle^TM).

The intended workflow of ROCO is illustrated by the flowchart in Sec. 2B and the live experiment discussed in Sec. 3C. First, a physician and/or planner contours the important organs, and an experienced planner studies the case and chooses beam directions; these steps must occur whether ROCO is used or not. Next, a sampling space range, number of samples, and number of modes are selected for the given case; these parameters depend on the site, number of targets, and their doses, and are established when ROCO is commissioned. A technical assistant or junior dosimetrist initiates the automatic process of sampling parameters, solving unconstrained optimization problems, and computing PCA modes and mode doses; this process may take 1–2 h but need not be supervised. Finally, the experienced planner applies his or her expert knowledge to the case to determine the initial set of constraints, and interactively runs the constrained optimization phase of ROCO to arrive at a plan. The planner evaluates the result and modifies the constraints through experimentation; however, this process is much more directed than the trial-and-error process that characterizes unconstrained optimization since the constraints the planner requests are actually achieved (or reported to be infeasible).

Improving planner efficiency is one of the primary goals of the development of ROCO. Our future work involves the parallelization of the sampling stage and the full dose calculation of the PCA modes. The ROCO process would thus be sped up significantly and become an even more efficient IMRT planning tool. At the same time, in order to avoid several constrained optimization loops to adjust the hard constraints, in an attempt to anticipate the planner's unwritten methodology, we plan to develop a prioritized optimization scheme which would initially try to meet the protocol constraints, first imposing the constraints on the most critical structures, then enforcing the protocol constraints for the remaining OARs. Once a plan that meets these requirements with acceptable PTV coverage is achieved, the constraints would be pushed until the PTV coverage becomes unacceptable. We also plan to further explore the way in which the leaf-sequencing step causes some of the doses to increase and attempt to automatically adjust for this effect.