Computational modeling of electrocardiograms: Repolarization and T-wave polarity in the human heart

Abstract

For more than a century, electrophysiologists, cardiologists, and engineers have studied the electrical activity of the human heart to better understand rhythm disorders and possible treatment options. While the depolarization sequence of the heart is relatively well characterized, the repolarization sequence remains a subject of great controversy. Here we study regional and temporal variations in both depolarization and repolarization using a finite element approach. We discretize the governing equations in time using an unconditionally stable implicit Euler backward scheme and in space using a consistently linearized Newton-Raphson-based finite element solver. Through systematic parameter-sensitivity studies, we establish a direct relation between a normal positive T-wave and the non-uniform distribution of the controlling parameter, which we have termed refractoriness. To establish a healthy baseline model, we calibrate the refractoriness using clinically measured action potential durations at different locations in the human heart. We demonstrate the potential of our model by comparing the computationally predicted and clinically measured depolarization and repolarization profiles across the left ventricle. The proposed framework allows us to explore how local action potential durations on the microscopic scale translate into global repolarization sequences on the macroscopic scale. We anticipate that our calibrated human heart model can be widely used to explore cardiac excitation in health and disease. For example, our model can serve to identify optimal pacing sites in patients with heart failure and to localize optimal ablation sites in patients with cardiac fibrillation.

1. Introduction

For more than a century, the electrocardiogram has served as a cheap, non-invasive, highly accurate, and easily reproducible diagnostic tool to monitor the electrical activity of the human heart. In the healthy heart, the electrocardiogram consists of three characteristic segments: a small hump, the P-wave, associated with atrial depolarization; a sharp dip-rise-dip sequence, the QRS-complex, associated with ventricular depolarization; and a small hump, the T-wave, associated with ventricular repolarization (Noble and Cohen 1978; Keener and Sneyd 1998), see Figure 1. While the depolarization sequence and the QRS-complex are relatively well characterized, the repolarization sequence and the T-wave remain poorly understood (Opthof et al. 2009; Patel et al. 2009). However, the clinical significance of the T-wave cannot be underestimated: Inverted T-waves can indicate coronary ischemia, Wellens’ syndrome, left ventricular hypertrophy, or central nervous system disorders; tall and narrow symmetrical T-waves can indicate hyperkalemia; flat T-waves can indicate coronary ischemia or hypokalemia (Klabunde 2005). In the healthy heart, the T-wave is positive in all three limb leads. Positive T-waves reflect the fact that the last cells to depolarize are the first to repolarize (Franz et al. 1991). The central hypothesis of this work is that we can incorporate this regional information through a novel non-uniform material parameter, the refractoriness, and that the heterogeneity of this parameter is critical to accurately capture the T-wave profile in the electrocardiogram.

Figure 1.

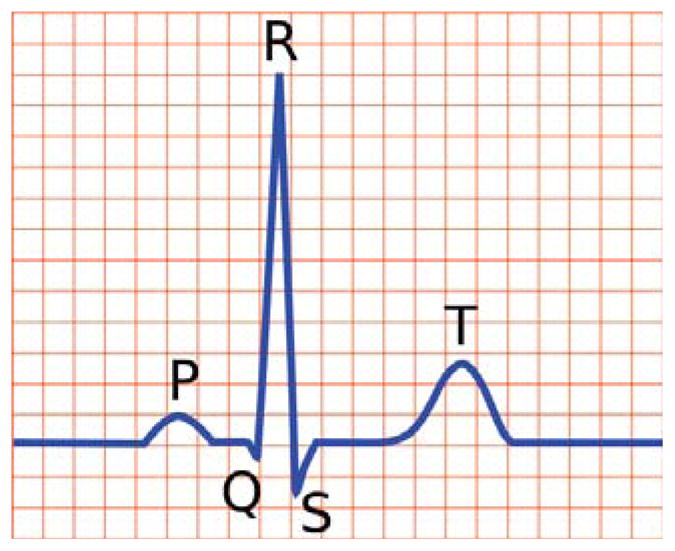
Schematic of electrocardiogram sequence for a healthy human heart, showing the P-wave, QRS-complex and T-wave.

Within the past three decades, computer models of the heart have gained increasing popularity (Clayton et al. 2011). Computer models have the potential to visualize regional depolarization and repolarization sequences of the heart (Kotikanyadanam et al. 2010), to localize disturbances (Bacharova et al. 2011), to identify optimal locations for intervention, and to virtually probe different treatment options. Conceptually speaking, we can distinguish two classes of electrophysiological models: Ionic models and phenomenological models.

Ionic models characterize the electrophysiological behavior by explicitly considering the transport of charged ions across the cell membrane (MacLachlan et al. 2007; Wong et al. 2011). Their major advantage is that they are mechanistic in origin, providing detailed information about ion concentrations and ion channel dynamics. However, their inherent disadvantages are their high computational cost and their large number of material parameters. Because of the inherent lack of human tissue samples, the calibration of these parameters is traditionally based on experiments with non-human cells, usually under conditions that barely represent the full physiological regime (Pullan et al. 2005).

Phenomenological models characterize the electrophysiological behavior by capturing empirical observations on the macroscopic scale. One inherent advantage is their low computational cost. As such, they have played a significant role in advancing the frontiers of computer simulation in cardiac electrophysiology. The majority of cardiac cell models derive from the Hodgkin-Huxley model of the giant squid axon (Hodgkin and Huxley 1952). Simplified two-variable versions of the Hodgkin-Huxley model, e.g., the FitzHugh-Nagumo model (Fitzhugh 1961; Nagumo et al. 1962), have enabled further progress in the mathematical analysis and numerical simulation of cardiac electrophysiology. A modification of the FitzHugh-Nagumo model, the Aliev-Panfilov model for cardiomyocytes (Aliev and Panfilov 1996), has shown excellent agreement with all the salient features of the depolarization and repolarization cycle of individual cardiomyocytes, including the dependance of action potential duration on cycle length.

The major disadvantage of phenomenological models is that they typically introduce several material parameters, which lack a direct physiological interpretation. In general, those parameters are calibrated by tuning the proposed model to fit available experimental data. To simplify the calibration process, a common assumption in cardiac electrophysiology is to consider a uniform distribution of the model parameters throughout the entire cardiac domain (Clayton et al. 2011). In reality, however, electrophysiological properties of cardiomyocytes may display large regional variations, sometimes also referred to as dispersion. The observed heterogeneity can be attributed to locally varying densities of gap junctions, ion channels, pumps, and exchangers to name but a few (Burton and Cobbe 2001). Spatial heterogeneities gives rise to non-uniform conduction velocities and non-uniform action potential durations. Experimental evidence supports the heterogeneity of the action potential duration, both regionally and transmurally (Antzelevitch et al. 1991; Viswanathan et al. 1999; Stoll et al. 2008). In particular, the last regions to depolarize are commonly known to be the first to repolarize, giving rise to positive T-waves in the electrocardiogram (Franz et al. 1987; Cowan et al. 1988; Conrath and Opthof 2006).

Mathematical models of electrophysiology have been solved numerically using finite-difference methods (Panfilov and Keener 1995; Winslow et al. 2000), finite-volume methods (Johnston 2010) and finite-element methods (Rogers and Mc Culloch 1994). In addition to their complete geometric flexibility, finite-element methods have the advantage of seamlessly coupling the primary potential field with other fields, e.g., with a second potential field in bidomain models (Dal et al. 2012), with a mechanical field in excitation-contraction coupling (Göktepe and Kuhl 2010), or with an optical field in optogenetics (Abilez et al. 2011; Wong et al. 2012). Furthermore, they allow us to use existing finite element infrastructures, e.g., adaptive time stepping schemes, which can reduce the computational time down to the order of minutes or seconds (Wong et al. 2011). Here, we make use of yet another benefit of finite element schemes that comes at almost no additional cost: Finite element algorithms allow us to extract computational electrocardiograms in a simple, standard post-processing step (Bacharova et al. 2011; Kotikanyadanam et al. 2010; Okada et al. 2011).

In this work, we use a novel robust, stable, and efficient finite element algorithm to systematically explore how the regional variation of cellular action potential profiles affects the repolarization sequence in a human heart. After briefly summarizing the continuous problem of cardiac excitation in Section 2, we illustrate the algorithmic realization in Section 3. In Section 4, we identify a functional relation between the local action potential duration and a phenomenological model parameter, which we introduce as the refractoriness. In Section 5, we utilize this relation to calibrate our model by means of clinically measured action potential durations at different locations in the human heart. We confirm our simulations by computational electrocardiograms which display a normal positive T-wave. Finally, we demonstrate the potential of our model by comparing computationally predicted and clinically measured depolarization and repolarization profiles across the left ventricle. We conclude with a brief discussion and outlook in Section 6.

2. CONTINUOUS PROBLEM OF CARDIAC EXCITATION

In what follows, we model the excitation of cardiac tissue through a coupled system of equations (Fitzhugh 1961; Nagumo et al. 1962), which characterize the electrical response through the action potential φ and the biochemical response through the recovery variable r (Aliev and Panfilov 1996; Göktepe and Kuhl 2009). To account for the propagating nature of excitation waves, we introduce a flux term in the electrical conservation law, while the recovery variable r remains strictly local and governed by local kinetics.

2.1 The global electrical problem

We model the electrical problem through the spatio-temporal evolution of the action potential φ, initiated by the flux div q and by the source f^φ,

$$\stackrel{.}{\phi }+\text{div}\mathit{q}(\phi )=f^{\phi }(\phi ,r).$$ (1)

The flux term characterizes the propagating nature of excitation waves,

$$\mathit{q}=-\mathit{D}·\nabla \phi ,$$ (2)

parameterized in terms of the second order diffusion tensor D = d^isoI + d^anin ⊗ n, which can account for both isotropic diffusion d^iso and anisotropic diffusion d^ani along a preferred direction n. The source term characterizes the local action potential profile,

$$f^{\phi }=c\phi [\phi -\alpha ][1-\phi ]-r\phi ,$$ (3)

parameterized in terms of a cubic polynomial, c φ [φ − α][1 − φ], and a coupling term, r φ, introducing the recovery variable r. Herein c is a scaling parameter and α is the oscillation threshold. While positive α values characterize stable non-pacemaker cells, negative α values characterize oscillatory pacemaker cells. Experimentally, we can calibrate the global flux term q using microelectrode array recordings (Chen et al. 2012) and the local source term f^φ using single cell patch clamp experiments (Abilez et al. 2011).

2.2 The local biochemical problem

While we assume that the electrical signal φ can propagate in space, we model the biochemical problem through the temporal evolution of the recovery variable r, initiated exclusively by the source f^r,

$$\stackrel{.}{r}=f^r(\phi ,r).$$ (4)

The source term characterizes the slow features of the action potential profile,

$$f^r=[\gamma +r\overline{\gamma }(\phi )][-r-c\phi [\phi -b-1]],$$ (5)

parameterized in terms of the weighting factor [γ + r γ̄] with γ̄ = μ₁/[ μ₂ + φ] and the additional phenomenological parameter b. The parameters μ₁ and μ₂ are essential to calibrate the shape of the restitution curve. In this manuscript, we adopt common parameter values from the literature for the standard FitzHugh-Nagumo parameters c, α, and b (Fitzhugh 1961; Keener and Sneyd 1998) and for the non-standard parameters μ₁ and μ₂ (Aliev and Panfilov 1996). In what follows, we focus in particular on the parameter γ, its physiological interpretation, and its role in cardiac excitation across the scales.

Remark

To simulate physiological values of the transmembrane potential and of the time, it is common to scale the non-dimensional field φ and the non-dimensional time t using the following the expressions,

$$\mathrm{\Phi }=100\phi -80\text{mV}\text{and}\tau =12.9t\text{ms}.$$

This implies that the transmembrane-potential Φ will range from −80 mV to +20 mV and a typical action potential will last a real time τ of 200 ms to 300 ms, which is in agreement with the physiological values for healthy human hearts.

3. DISCRETE PROBLEM OF CARDIAC EXCITATION

For an efficient and robust computational solution of the governing equations (1) and (4), we follow (Göktepe and Kuhl 2009) and use a finite difference scheme for time discretization and a finite element scheme for the spatial discretization. For the sake of completeness, we summarize the formulation and key aspects of the method in the following. We introduce the action potential φ as 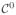-continuous global degree of freedom on each finite element node and the recovery variable r as 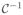-continuous internal variable on the integration point level. To solve the resulting system of equations, we apply an incremental iterative Newton-Raphson solution strategy, which allows us to adopt an adaptive time stepping scheme (Wong et al. 2011).

3.1 The global electrical problem

On the global level, we transform the electrical problem (1) into its residual format evaluated in the domain 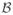, and complement it with the corresponding boundary conditions on the Dirichlet and Neumann boundary ∂ 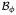and ∂ 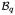, respectively,

$$\begin{array}{lll}\hfill {\text{R}}^{\phi }=\stackrel{.}{\phi }+\text{div}(\mathit{q})-f^{\phi }=0& \text{in}\hfill & \hfill \mathcal{B}\hfill \\ \hfill \phi =\overline{\phi }& \text{on}\hfill & \hfill \partial {\mathcal{B}}_{\phi }\hfill \\ \hfill \mathit{q}·\mathit{n}=\overline{q}& \text{on}\hfill & \hfill \partial {\mathcal{B}}_q.\hfill \end{array}$$ (6)

By multiplying the residual equation (6.1) by admissible test functions, integrating it over the domain 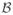, applying the standard integration by parts, and including the Neumann boundary conditions (6.3), we obtain the weak form of the electrical residual. For the spatial discretization, we discretize the domain of interest with n_el finite elements as $\mathcal{B}={\cup }_{e=1}^{n_{\text{el}}}{\mathcal{B}}^e$ and apply the standard isoparametric concept to interpolate the trial functions φ^h and the test functions δφ^h,

$$\delta {\phi }^h{\mid }_{{\mathcal{B}}^e}=\sum _{i=1}^{n_{\text{en}}}{N}^i\delta {\phi }_i\text{and}{\phi }^h{\mid }_{{\mathcal{B}}^e}=\sum _{j=1}^{n_{\text{en}}}{N}^j{\phi }_j.$$ (7)

Here, N are the standard shape functions on the element level and i, j = 1, …, n_en are the element nodes. For the temporal discretization, we partition the time interval of interest into n_stp subintervals [t_n, t_{n + 1}] as $\mathcal{T}={\cup }_{n=0}^{n_{\text{stp}}-1}[t_{\text{n}},t_{\text{n}+1}]$ and apply a standard backward Euler time integration scheme in combination with a finite difference approximation of the first order time derivative φ̇,

$$\stackrel{.}{\phi }=[{\phi }^h-{\phi }_{\text{n}}^h]/\mathrm{\Delta }t.$$ (8)

Here, we have introduced the common abbreviation Δt: = t − t_n > 0 for current time increment. For the sake of clarity, we omit the index (∘)_n+1 of the current time point of interest. With the discretizations in space (7) and time (8), the discrete algorithmic residual ${\text{R}}_I^{\phi }$ takes the following explicit representation,

$${\text{R}}_I^{\phi }=\underset{e=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}^e}{N}^i\frac{{\phi }^h-{\phi }_{\text{n}}^h}{\mathrm{\Delta }t}-\nabla N^i·\mathit{q}\text{d}V+{\int }_{\partial {\mathcal{B}}_q^e}{N}^i\overline{q}\text{d}A-{\int }_{{\mathcal{B}}^e}{N}^i{f}^{\phi }\text{d}V\doteq 0.$$ (9)

The operator A symbolizes the assembly of all element contributions at the element nodes i = 1, …, n_en to the overall residual at the global node points I = 1, …, n_nd. To solve the discrete system of nonlinear equations (9), we apply an incremental iterative Newton Raphson solution scheme based on the consistent linearization of the residual (9), which introduces the global iteration matrix,

$${\text{K}}_{IJ}^{\phi }={\text{d}}_{\phi J}{\text{R}}_I^{\phi }=\underset{e=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}^e}{N}^i\frac{1}{\mathrm{\Delta }t}{N}^j+\nabla N^i·\mathit{D}·\nabla N^j-N^i{\text{d}}_{\phi }{f}^{\phi }{N}^j\text{d}V.$$ (10)

For each incremental iteration step, we update the global vector of unknowns ${\phi }_I\leftarrow {\phi }_I-{\sum }_{J=1}^{n_{\text{nd}}}{\text{K}}_{IJ}^{\phi -1}{\text{R}}_J^{\phi }$ at all I = 1, …, n_nd global nodes. In the following subsection, we illustrate the iterative calculation of the source term f^φ(φ, r) required to evaluate the global residual (9) and the calculation of its sensitivity with respect to the action potential φ,

$${\text{d}}_{\phi }{f}^{\phi }=c[-3{\phi }^2+2[1+\alpha ]\phi -\alpha ]-r-\phi {\text{d}}_{\phi }r,$$ (11)

required to evaluate the global iteration matrix (10). We end this section by noting that all integrals in (9) and (10) are calculated using standard numerical quadrature techniques, where values of φ at quadrature points for time t = t_n+1 result from evaluating the corresponding finite-element interpolation (7).

3.2 The local biochemical problem

On the local level, we introduce the recovery variable r as an internal variable and store it locally at each integration point. For the temporal discretization, we apply a finite difference approximation

$$\stackrel{.}{r}=[r-r_{\text{n}}]/\mathrm{\Delta }t,$$ (12)

combined with a classical implicit Euler backward time integration scheme. With the discretization in time (12), the discrete residual R^r of the recovery equation (4) takes the following representation

$${\text{R}}^r=r-r_{\text{n}}-[[\gamma +r\overline{\gamma }][-r-c\phi [\phi -b-1]]]\mathrm{\Delta }t\doteq 0.$$ (13)

Its consistent linearization

$${\text{K}}^r={\text{d}}_r{\text{R}}^r=1+[\gamma +\overline{\gamma }[2r+c\phi [\phi -b-1]]]\mathrm{\Delta }t$$ (14)

defines the iteration scheme for the incremental update of the recovery variable r ← r − K^{r − 1} R^r on the integration point level. At local equilibrium, we finally compute the source term f^φ from equation (5) for the global electrical problem (9) and its consistent algorithmic linearization d_φf ^φ from equation (11) for the global Newton iteration (10). To evaluate this linearization, we calculate the sensitivity

$${\text{d}}_{\phi }r=-{[{\text{K}}^r]}^{-1}{\partial }_{\phi }{\text{R}}^r$$ (15)

where K^r is the tangent (14) at local equilibrium, and ∂_φR^r is the sensitivity of the residual,

$${\partial }_{\phi }{\text{R}}^r=[[\gamma +r\overline{\gamma }]c[2\phi -b-1]+r{\partial }_{\phi }\overline{\gamma }[r+c\phi [\phi -b-1]]]\mathrm{\Delta }t,$$ (16)

with ∂_φγ̄ = −μ₁/[μ₂ + φ]². Within a classical finite element setting, these source and tangent terms are passed to the higher scales, from the biochemical problem (13) and (14) at the integration point level to the electrical problem (9) and (10) at the node point level. Once the global Newton iteration has converged, we store the updated recovery variable r on the integration point level.

4. Local excitation of individual cells

In this section, we study the temporal evolution of the local action potential to gain insight into the excitation of individual cardiac muscle cells. This implies that we can neglect the diffusion term divq in (1). The local electrical and biochemical equations (1) and (4) reduce to the following set of ordinary differential equations,

$$\begin{array}{l}\stackrel{.}{\phi }=c\phi [\phi -\alpha ][1-\phi ]-r\phi \\ \stackrel{.}{r}=[\gamma +r\overline{\gamma }(\phi )][-r-c\phi [\phi -b-1]]\end{array}$$

with γ̄ = μ₁/[μ₂ + φ], which we solve numerically using standard integration schemes. The dynamics of this system and the role of the standard FitzHugh-Nagumo parameters c, α, and b have been studied intensely in the past (Fitzhugh 1961; Keener and Sneyd 1998). Here, we have added the non-standard parameters μ₁ and μ₂ to calibrate different restitution curves (Aliev and Panfilov 1996). The additional parameter γ controls the action potential duration. To date, this parameter has not been thoroughly explored, although it plays a critical role in cardiac repolarization, as we will demonstrate in the sequel. Since the action potential duration directly controls the effective refractoriness of the system (Conrath and Opthof 2006), from now on, we will refer to the parameter γ as the refractoriness.

To quantify the relation between the action potential duration and the refractoriness γ, we solve the local excitation problem and systematically vary the refractoriness γ. In all simulations, we choose c = 8, α = 0.05, b = 0.15, μ₁ = 0.2, μ₂ = 0.3, which are common parameter values for human cardiomyocytes (Aliev and Panfilov 1996; Kotikanyadanam et al. 2010). As initial conditions, we choose Φ|_t=0=−50mV and r|_t=0=0, such that the cardiomyocyte is excited with a transmembrane potential slightly above the critical excitation threshold. Figure 2, left, displays the sensitivity of the action potential profile with respect to the refractoriness γ. Despite the inherent nonlinearity of the underlying system of equations, the only property affected by changes in γ is the duration of the action potential itself, while all other features, i.e., the slope of the upstroke, the slope of the recovery, and the baseline voltage at the resting stage, remain virtually unchanged. Figure 2, right, displays the corresponding action potential duration APD₉₀, i.e., the time until the cardiomyocyte is repolarized by 90%. The curve suggests that the functional relation between APD₉₀ and γ can be approximated by the following logarithmic expression,

Figure 2.

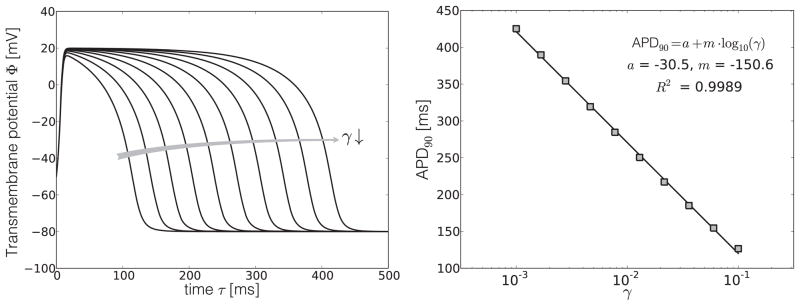
Sensitivity of the action potential profile Φ with respect to the refractoriness γ, left, and functional relation between the action potential duration APD₉₀ and the refractoriness γ, right. The refractoriness γ affects the duration of the action potential, but not the slopes of the upstroke, nor the slope of the repolarization, and neither the baseline voltage at the resting stage.

$${\text{APD}}_{90}=a_{\text{cell}}+m_{\text{cell}}·{log}_{10}(\gamma ).$$

Using a least-squares linear regression, we obtain the values a_cell = −30.5 and m_cell = −150.6 for the constants of this model, see Figure 2, right. In further sensitivity studies, we confirmed that these model constants are insensitive to the initial conditions of the boundary value problem.

5. Global excitation of a human heart

Next, we study the spatio-temporal evolution of the action potential to gain insight into the baseline excitation pattern of a human heart. In the healthy heart, the last cells to depolarize are the first to repolarize. As anticipated in section 1, this characteristic depolarization-repolarization pattern explains the positive T-wave in normal electrocardiograms. This observation has also been confirmed by electrophysiological studies in human hearts (Cohen et al. 1976; Franz et al. 1987). By mapping the transmembrane potential in different regions of the left and right ventricles, both in the endocardium and epicardium, clinical studies have revealed a linear relation between action potential duration and activation time (Cowan et al. 1988; Franz et al. 1987). This empirical relation can be summarized by the following linear expression,

$${\text{APD}}_{90}=a_{\text{heart}}+m_{\text{heart}}·t_{\text{act}},$$ (17)

where t_act is the activation time, i.e., the interval between the onset of the QRS-complex and the upstroke of the individual action potential. The constants a_heart and m_heart are determined from a least-squares fit of expression (17) to the experimental data. Typical values for the slope m_heart range from −0.83 to −2.11, with a mean of −1.32 and a standard deviation of 0.45, for healthy patients with positive T-waves (Cowan et al. 1988; Franz et al. 1987).

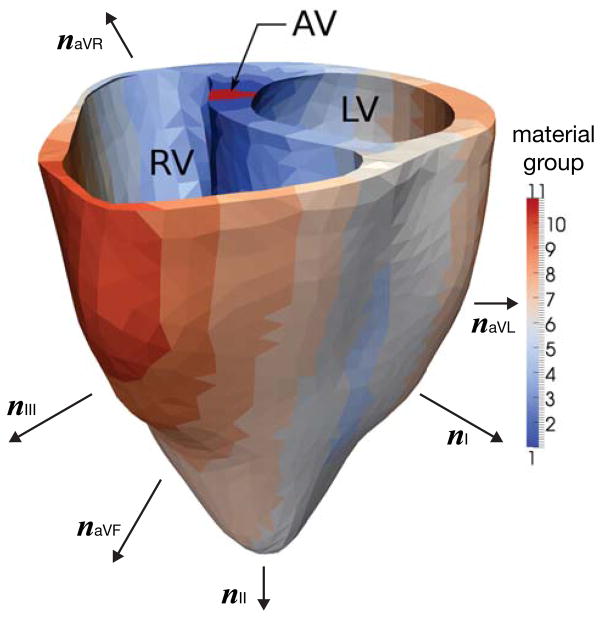
Motivated by these clinical observations, we partition the geometry of a patient-specific human heart (Kotikanyadanam et al. 2010) into subdomains according to their activation times. To this end, we solve the global electrical and biochemical equations (1) and (4) described in Section 3 using a finite-element implementation. The elements in the atrio-ventricular node region are electrically excited, generating wavefronts that travel throughout the entire heart domain. As the initial wavefront propagates, it activates cells in different locations at different times. The time elapsed between the excitation of the elements in the atrio-ventricular node and the activation of a particular element defines its activation time t_act. We then partition the domain into ten subdomains and assign each element its corresponding subdomain according to its local activation time t_act, see Figure 3. For each subdomain, we calculate the average APD₉₀ using the empirical relation APD₉₀ = a_heart + m_heart · t_act with a_heart = 360 and m_heart = −1.8 (Cowan et al. 1988; Franz et al. 1987). For each APD₉₀, we calculate the refractoriness γ using the local equation APD₉₀ = a_cell +m_cell · log₁₀(γ) with a_cell = −30.5 and m_cell = −150.6. Finally, for each refractoriness γ, we define an individual cell type and assign it to the corresponding subdomain. In a finite element setting, this assignment is performed simply via introducing individual material groups, see Figure 3. Table 1 summarizes the average activation times t_act, the action potential durations APD₉₀, and refractoriness parameters γ considered for all ten subdomains.

Figure 3.

Human heart model partitioned into ten subregions based on activation times obtained from simulation. The color code indicates that the dark blue regions depolarize first, while the dark red regions depolarize last. In the healthy heart, the regions to depolarize last are the ones to repolarize first. This is modeled through a heterogeneous refractoriness γ with largest values in the red regions and smallest values in the blue regions. Notation: RV = right ventricle, LV = left ventricle, AV = atrioventricular node, n_I, n_II, n_III = limb leads, n_aVR, n_aVL, n_aVF = augmented limb leads.

Table 1.

Regional variation of refractoriness γ in a healthy human heart model. The heart is partitioned into ten subdomains. For each subdomain we calculate the average activation time t_act using the global electrical and biochemical equations. For each activation time t_act, we calculate the average APD₉₀ using the global equation for the action potential duration. For each APD₉₀, we calculate the refractoriness γ using the local equation for the action potential duration.

material group region [−]	average activation time tact [ms]	action potential duration APD90 [ms]	refractoriness γ [−]
1,11	7.5	346.5	0.0031
2	17.5	328.5	0.0041
3	27.5	310.5	0.0055
4	37.5	292.5	0.0072
5	47.5	274.5	0.0095
6	57.5	256.5	0.0124
7	67.5	238.5	0.0164
8	77.5	220.5	0.0216
9	87.5	202.5	0.0284
10	97.5	184.5	0.0374

Once the refractoriness is assigned to the different regions in the heart domain, we proceed to solve the electrical propagation problem using the finite element formulation described in section 3. The parameters c, α, b, μ₁ and μ₂ are considered uniform in the domain of analysis, and take the same values reported in section 4. The isotropic and anisotropic conduction parameters have been set to d^iso = 2mm²/ms and d^ani = 8mm²/ms, respectively. The tetrahedral mesh consist in 11,347 elements and 3,129 nodes (Kotikanyadanam et al. 2010), where linear shape functions have been selected as the interpolation basis. We set Φ = −80mV in the entire domain as initial conditions. Boundary conditions reflect the flux-free condition q · n = 0 at the domain surface. The time step is set to Δt = 5ms.

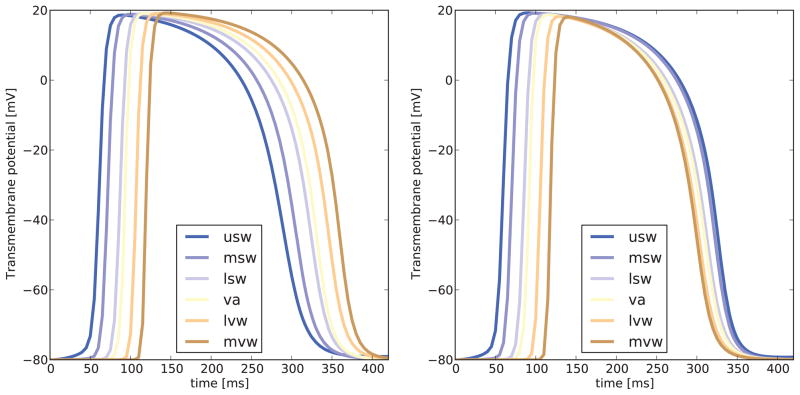
Figure 4 illustrates the action potential profile at different locations in the left ventricle for simulations considering a uniform and a non-uniform distribution of the refractoriness γ, respectively. In the uniform case shown in Figure 4, left, the action-potential duration is similar for all cardiomyocytes, irrespective of their location and their activation time. In the non-uniform case shown in Figure 4, right, the action-potential duration varies with location and time, in keeping with experimental observations where last regions to depolarize are the first to repolarize. Action potentials in cells immersed in an aggregate can differ from the behavior of single isolated cells. In particular, one is to expect some differences in the action potential durations for these cases. Since we have established a relation between the refractoriness and APD₉₀ based on single-cell simulations, we assessed the error between the target APD₉₀ described in Table 1 and the APD₉₀ obtained from biventricular simulations. To this end, we computed the APD₉₀ from curves in Figure 4, right, and compared them to their corresponding target values in Table 1, and found a maximum relative error of 8%. Thus, we can use activation time, the empirical relation between activation time and action potential duration, and the relation that defines the refractoriness to calibrate our model on the microscopic cell. We will now elaborate how this microscopic calibration translates into clinically relevant macroscopic readouts.

Figure 4.

Action potential profiles for seven representative subregions in the heart. Uniform distribution of refractoriness γ, left, generates similar action potential profiles at all locations. Non-uniform distribution of refractoriness γ, right, generates spatially varying action potential profiles, where the regions to depolarize last are the ones to repolarize first. Notation: usw = upper septal wall, msw = mid septal wall, lsw = lower septal wall, va = ventricular apex, lvw = lower ventricular lateral wall, mvw = mid ventricular lateral wall.

Using the non-uniform distribution of the refractoriness γ as summarized in Table 1, we simulate the excitation of a healthy human heart (Kotikanyadanam et al. 2010) based on our fully-implicit finite element algorithm (Göktepe and Kuhl 2009). In an additional post-processing step, we compute the electrical flux q from the diffusion-weighted transmembrane potential gradient ∇φ, and integrate it numerically over the entire domain to obtain the mean electrical vector q_♡, also known as the heart vector,

$$\mathit{q}♡={\int }_{\mathcal{B}}\mathit{q}\text{d}V\text{with}\mathit{q}=-\mathit{D}·\nabla \phi .$$

To calculate the chest electrocardiogram, we project the heart vector q_♡ onto the standard six chest leads (Kotikanyadanam et al. 2010) characterized through the six vectors n as illustrated in Figure 3,

$$\begin{array}{ccc}\text{I}=\mathit{q}♡·{\mathit{n}}_{\text{I}}& \text{II}=\mathit{q}♡·{\mathit{n}}_{\text{II}}& \text{III}=\mathit{q}♡·{\mathit{n}}_{\text{III}}\\ \text{aVR}=\mathit{q}♡·{\mathit{n}}_{\text{aVR}}& \text{aVL}=\mathit{q}♡·{\mathit{n}}_{\text{aVL}}& \text{aVF}=\mathit{q}♡·{\mathit{n}}_{\text{aVF}}.\end{array}$$

The first set of vectors, i.e., the vectors between the left and the right arm n_I, between the left leg and the right arm n_II, and between the left leg and the left arm n_III characterizes the limb leads I, II, and III. The second set of vectors, i.e., n_aVR, n_aVL, and n_aVF, characterizes the augmented limb leads, aVR, aVL, and aVF, which are linear combinations of the standard limb leads.

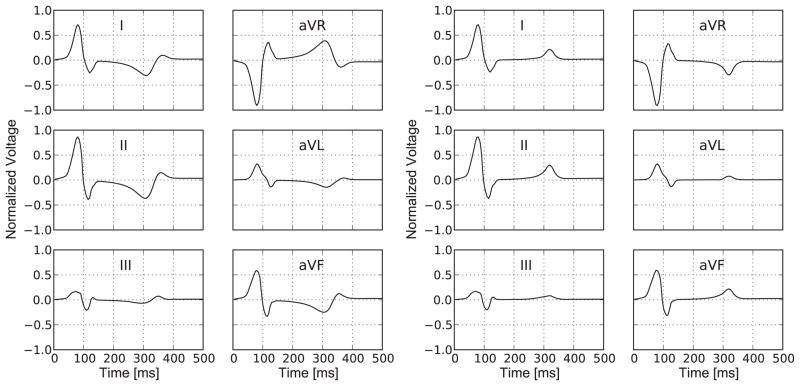
Figure 5, left, displays the electrocardiogram simulated with the uniform parameter distribution according to Figure 4, left. The uniform-parameter model nicely captures the QRS-complex, i.e., the downward-upward-downward sequence at the beginning of the cardiac cycle associated with a normal depolarization wave. However, the model generates a markedly inverted T-wave, i.e., a negative hump at time τ ~ 300 ms associated with a disturbed repolarization wave. We conclude that the uniform-parameter model is capable of correctly predicting the depolarization phase of a healthy human heart, but that it is incapable of correctly predicting the repolarization phase.

Figure 5.

Electrocardiogram for a representative cardiac cycle with limb leads I, II, and III and augmented limb leads aVR, aVL, and aVF. Uniform distribution of refractoriness γ, left, generates an inverted T-wave, i.e., a negative hump in leads I and II at time τ = 300 ms. Non-uniform distribution of refractoriness γ, right, generates a normal T-wave, i.e., positive hump in leads I and II at time τ=300 ms. The QRS-complex, i.e., the downward-upward-downward sequence at the beginning of the cardiac cycle, is captured nicely by both models, left and right.

Figure 5, right, displays the electrocardiogram simulated with the non-uniform parameter distribution according to Figure 4, right. The non-uniform-parameter model nicely captures the QRS-complex, i.e., the downward-upward-downward sequence at the beginning of the cardiac cycle associated with a normal depolarization wave. In contrast to the uniform-parameter model, the non-uniform-parameter model generates a normal T-wave, i.e., a positive hump at time τ ~ 300 ms associated with a normal repolarization wave. We conclude that the non-uniform-parameter model is capable of correctly predicting the electrophysiology of the healthy human heart, both in the depolarization and repolarization phases.

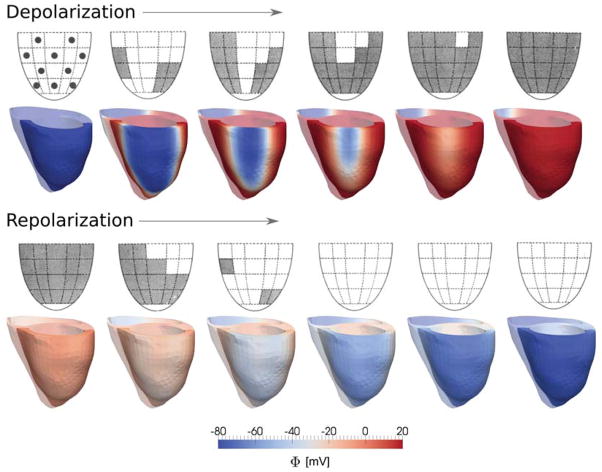
Finally, to validate our model, we compared the sequences of cardiac depolarization and repolarization in the lateral left ventricular wall with clinically measured sequences averaged over ten patients with healthy hearts and normal T-waves (Cowan et al. 1988). Figure 6 shows the clinically measured and the computationally predicted depolarization sequences, top row, and repolarization sequences, bottom row. During the depolarization phase, the action potential propagates bottom-up and inside-out across the left ventricular free wall. The computational simulations agree nicely with these findings and closely match the clinical excitation pattern. During the repolarization phase, the action potential returns to its resting state top-down and outside-in. The last regions to depolarize are the first to repolarize. Since the repolarization time is the sum of activation time and action potential duration, in contrast to the depolarization pattern, the repolarization pattern is rather uniform. Again, the computational simulations are in excellent agreement with the clinical observations. Unfortunately, the clinical measurements do not include data on the repolarization of the septum. Our simulations indicate that the cardiomyocytes in the septal region repolarize later than the cardiomyocytes in the ventricular free walls. Overall, this repolarization sequence results in the formation of a positive T-wave characteristic for the electrocardiogram of healthy human hearts.

Figure 6.

Depolarization and repolarization sequences in the healthy human heart. The experimental sequences, top rows, represent the depolarization and repolarization of the left ventricle, averaged over ten healthy individuals, where grey regions indicate activated epicardium; reprinted with permission from (Cowan et al. 1988). The computational sequences, bottom rows, represent the depolarization and repolarization of a healthy human heart, where the red regions indicate activated myocardium.

6. Concluding Remarks

In the healthy heart, the last cells to depolarize are the first to repolarize. This implies that the action potential durations display significant regional and transmural variations. Here we reinterpret a phenomenological scaling parameter as the refractoriness, and establish a functional relation between the local action potential duration and this material parameter. We then utilize this function to calibrate our model by means of clinically measured action potential durations at different locations in the human heart. Our calibrated model displays the major characteristic features of a healthy human heart; in particular, it correctly reproduces the normal positive T-wave. When mapped across the left ventricle, its depolarization and repolarization sequences are in excellent agreement with its clinically measured counterparts.

Transmural variations of action potential durations (Myles et al. 2010; Tsamis et al. 2011) have recently been incorporated into numerical simulations of cardiac electrophysiology to obtain more realistic electrocardiograms (Boulakia et al. 2010). In particular, the experimentally observed linear relation between action potential duration and activation time (Franz et al. 1987) has been successfully integrated into computational models to assure an upright T-wave (Winslow et al. 2000). However, to date, the importance of non-uniform action potential durations has only been recognized phenomenologically, and the regional assignment of the corresponding model parameters has been rather heuristic. Using the concept of a non-uniform refractoriness, our proposed approach offers an elegant framework to calibrate phenomenological models by means of clinically measured excitation sequences obtained under physiological conditions.

Although the relation between global T-wave polarity and local action potential durations has been recognized more than a century ago (Mines 1913), the heterogeneity of cardiac repolarization remains largely controversial (Opthof et al. 2009; Patel et al. 2009). In particular, the relative contributions of regional and transmural action potential variations to the genesis of a positive T-wave are still a matter of ongoing debate (Bakker and Opthof 2002; Conrath and Opthof 2006). There is strong experimental evidence, which supports that action potential duration and activation time are closely correlated under physiological conditions, irrespective of the location in the heart (Cowan et al. 1988; Franz et al. 1987; Myles et al. 2010). The proposed model could help to further elucidate this hypothesis by using a high-resolution patient-specific model with a non-uniform refractoriness distribution. Numerical simulations would then allow us to study the complex interplay between regional and transmural action potential durations, and assess their role in the formation of positive T-waves in electrocardiograms of healthy individuals (Okada et al. 2011; Winslow et al. 2000). We anticipate that our correctly calibrated baseline model of the human heart has the potential to be widely applicable to explore cardiac excitation profiles in health and disease.