Abstract
Animals are capable of enhanced decision making through cooperation, whereby accurate decisions can occur quickly through decentralized consensus. These interactions often depend upon reliable social cues, which can result in highly coordinated activities in uncertain environments. Yet information within a crowd may be lost in translation, generating confusion and enhancing individual risk. As quantitative data detailing animal social interactions accumulate, the mechanisms enabling individuals to rapidly and accurately process competing social cues remain unresolved. Here, we model how motion-guided attention influences the exchange of visual information during social navigation. We also compare the performance of this mechanism to the hypothesis that robust social coordination requires individuals to numerically limit their attention to a set of n-nearest neighbours. While we find that such numerically limited attention does not generate robust social navigation across ecological contexts, several notable qualities arise from selective attention to motion cues. First, individuals can instantly become a local information hub when startled into action, without requiring changes in neighbour attention level. Second, individuals can circumvent speed–accuracy trade-offs by tuning their motion thresholds. In turn, these properties enable groups to collectively dampen or amplify social information. Lastly, the minority required to sway a group's short-term directional decisions can change substantially with social context. Our findings suggest that motion-guided attention is a fundamental and efficient mechanism underlying collaborative decision making during social navigation.
Keywords: collective behaviour, vision, topological, selective attention, social information, speed–accuracy trade-offs
1. Introduction
To survive organisms must adapt quickly and accurately to changes in their environment. Social organisms can enhance this process by disseminating cues among themselves in a manner that either dampens or amplifies local information [1–5]. The fluid manoeuvres observed in flocks of birds and schools of fish have long epitomized the speed at which such collective processes can occur [1–4,6–10]. The constituents of these groups can dampen directional errors by adopting the average decisions of their neighbours [8], while any abrupt movements by only a single startled individual can trigger rapid directional shifts across the ensemble [9]. Discerning how group members distinguish salient from spurious social information in a manner that harmonizes these opposing qualities remains a fundamental paradox [3,11]. Our objective is to discern what individual-level mechanism(s) can promote adaptive social communications during navigation, thereby complementing a group's capacity to collectively dampen or amplify information.
Numerous models have explored how social individuals may integrate local information [6,8,10,12–15]. These theoretical efforts are complemented by an equally diverse set of empirical findings supporting various alternatives [6,7,9,10,15–19]. Most models of collective behaviour assume that behavioral interactions change with distance (i.e. metric models) and that individuals integrate all available information within their sensory range [10,12,20–22]. This causes an important sensory processing issue because by simply averaging across all available information group members invariably dampen out any novel signal or cue. It is therefore unlikely that this approach alone can catalyse collective adaptability across contexts without requiring higher-order cognitive computations, e.g. memory [21].
Recent work suggests that group members can resist disruptions more effectively by limiting their attention to a set of n-nearest neighbours (approx. 6 or 7 if n can only be a whole number), resulting in topological interactions that are particularly effective with regard to changes in separation distance [6]. We will refer to this mechanism as a numerical threshold, since the term topological has much broader cognitive implications related to visual object recognition and association [23]. It is hypothesized that such numerically limited attention is, in fact, essential to explain robust collective coordination [6]. While this mechanism suggests a mathematically elegant solution, it is unlikely to be cognitively tenable across taxa. Experimental evidence indicates that, in general, species ranging from fish to human children can only visually identify and track 3 or 4 discrete objects simultaneously [24–26]. Furthermore, a numerical limit does not address the sensory processing issue because all available information is still treated equitably.
We recently proposed an alternative mechanism based on Weber's Law to explore how selective visual attention can influence collective behaviour [14]. Visual motion cues are a primary feature in sensory processing [26–28], conveying information that directly impacts individual fitness, such as with navigation, foraging, courtship and predator avoidance [26,29–31]. The amount of information within a scene generally exceeds the capacity of the visual system, so neural selectivity compensates by sifting salient features from the scene to limit processing [26–29]. Both numerical and motion thresholds are features that can guide visual attention, although there is stronger evidence supporting selective attention to motion [28] and movement behaviour is an inherent component of social navigation. Here, we extend our previous efforts by modelling how these visual features can influence the flow of social information across a variety of conditions.
We proceed by drawing analogy to social foragers who are often dispersed and disorganized when searching for food within a patch, yet must remain vigilant to minimize competitive effects, conflict and predation risk [4,32,33]. These effects can lead to a range of social conditions, spanning from seemingly normal to disturbed group departures. However, regardless of context, group members must integrate competing movement cues from their neighbours in order to come to a directional consensus. Modelling this scenario allows us to address several pertinent questions. First, how does coupling individual attention to movement behaviour influence information transfer during social navigation? Second, can alternative visual features (numerical versus motion thresholds) provide a mechanism to catalyse adaptive social coordination across a wide range of ecological contexts? Specifically, can these attention mechanisms influence a social individual's ability to display prolonged resistance to environmental uncertainty, yet remain equally responsive to sudden disturbances? Last, if individual attention and behaviour can influence the flow of social information, how then will these factors influence collective coordination as group size increases?
2. Model
(a). Visual interactions
Individuals are initialized with random positions xi and orientations 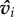 , as may be expected of social animals foraging within a patch. Social interactions in the model are first scaled by visual perception. This process begins by relating how the relative motion of a neighbour, vj,i = vj − vi, changes visually along an individual's line-of-sight, dj,i = xj − xi. Individual i ‘sees’ neighbour j as an arc of angular size:
, as may be expected of social animals foraging within a patch. Social interactions in the model are first scaled by visual perception. This process begins by relating how the relative motion of a neighbour, vj,i = vj − vi, changes visually along an individual's line-of-sight, dj,i = xj − xi. Individual i ‘sees’ neighbour j as an arc of angular size:
| 2.1 |
where rL is the particle's radius and dj,i is the intervening distance (e.g. 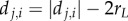 ). Length units are scaled to body length
). Length units are scaled to body length 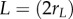 and time is in generic units, t. At each time step, neighbours are sorted by increasing distance to reflect the group from the individual's perspective. Neighbour detection is limited by a minimal image size, Ωmin, and occlusion (see the electronic supplementary material, appendices S.1 and S.2). Each subject therefore sees the group as a set of apparent neighbours, Ai.
and time is in generic units, t. At each time step, neighbours are sorted by increasing distance to reflect the group from the individual's perspective. Neighbour detection is limited by a minimal image size, Ωmin, and occlusion (see the electronic supplementary material, appendices S.1 and S.2). Each subject therefore sees the group as a set of apparent neighbours, Ai.
A neighbour's motion is perceived as
| 2.2 |
where directional information is provided by 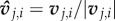 and weighted by
and weighted by 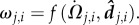 ωj,i essentially quantifies the speed at which an image Ωj,i moves along, or across, an individual's line of sight,
ωj,i essentially quantifies the speed at which an image Ωj,i moves along, or across, an individual's line of sight, 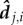 . The primary effect is that interactions are proportional to a neighbour's relative speed and decay exponentially with distance, dj,i. A secondary effect is that individuals do not explicitly align with the heading of their neighbours
. The primary effect is that interactions are proportional to a neighbour's relative speed and decay exponentially with distance, dj,i. A secondary effect is that individuals do not explicitly align with the heading of their neighbours 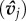 , but, rather, respond to how images move with respect to a neighbour's position (see the electronic supplementary material, appendix S.1).
, but, rather, respond to how images move with respect to a neighbour's position (see the electronic supplementary material, appendix S.1).
(b). Attention mechanisms
While the above equations characterize visual perception, we are primarily interested in how individuals identify influential neighbours from among competing visual stimuli. Here, individuals select influential neighbours based on one of two alternative mechanisms: the motion or number of apparent neighbours, as proposed by Lemasson et al. [14] and Ballerini et al. [6], respectively.
Individuals reacting to motion cues direct their attention towards any apparent image(s) whose relative speed exceeds some proportion of their optic flow [14]:
| 2.3 |
In this case, individual attention level at time t is defined by the number of influential neighbours, 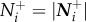 , optic flow is the average relative speed of all apparent neighbours,
, optic flow is the average relative speed of all apparent neighbours, 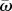 , and m is a motion-sensitive attention threshold. Equation (2.3) is based on a fundamental signal-to-noise property inspired by Weber's law, where the perception of a stimulus is a constant proportion m of the background physical intensity, given by
, and m is a motion-sensitive attention threshold. Equation (2.3) is based on a fundamental signal-to-noise property inspired by Weber's law, where the perception of a stimulus is a constant proportion m of the background physical intensity, given by 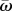 . Here, the number of motion signals that stand out from the background drop as m increases continuously, which serves to narrow the individual's attention.
. Here, the number of motion signals that stand out from the background drop as m increases continuously, which serves to narrow the individual's attention.
Alternatively, individuals reacting to a fixed number of neighbours limit their attention to their n-nearest apparent neighbours [6]:
| 2.4 |
Here, the number of influential neighbours increases discretely in direct proportion with increasing values of n (e.g. 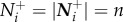 ).
).
Parameters m and n are thresholds that control attention level and represent changes in the individual's internal state, e.g. hunger or fear [6,12–15,20–22]. Note that individuals are exposed to the same visual stimuli when adopting either the motion or numeric mechanism (equation (2.3) or (2.4), respectively).
(c). Social navigation
The relative velocities of any influential neighbours that are selected by equation (2.3) or (2.4) are then averaged to adjust an individual's intended course:
| 2.5 |
Intended speed is bounded by 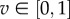 with a maximum turning arc of
with a maximum turning arc of 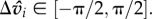 These constraints ensure continued, yet limited motion. Individuals then move in their intended direction with some degree of uncertainty:
These constraints ensure continued, yet limited motion. Individuals then move in their intended direction with some degree of uncertainty:
| 2.6 |
Function U independently adjusts individual speed and direction according to a noise scalar, η; a parameter generating disorientation, such as may arise from environmental turbulence or panic behaviour [12,14]. Speed is adjusted as 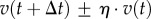 , where
, where 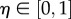 and heading
and heading 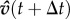 is rotated by
is rotated by 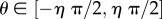 .
.
3. Measuring information transfer
We quantify information transfer by measuring how directional information is distributed and the accuracy with which it is transmitted at both the individual and group level. At the individual level, we select transmitter–receiver (T–R) pairs, each of which is chosen at random from within a group to measure pairwise coordination (one pair per group). Across replicate departures, receivers represent a typical member's attention level (how many neighbours one is responding to; equation (2.3) or (2.4); figure 1a), while transmitters represent social influence (the number of neighbours responding to one's motion, figure 1b). The median values of these metrics across replicates (attention, 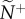 and influence,
and influence, 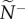 ) quantify how information is initially distributed in the communication networks that emerge.
) quantify how information is initially distributed in the communication networks that emerge.
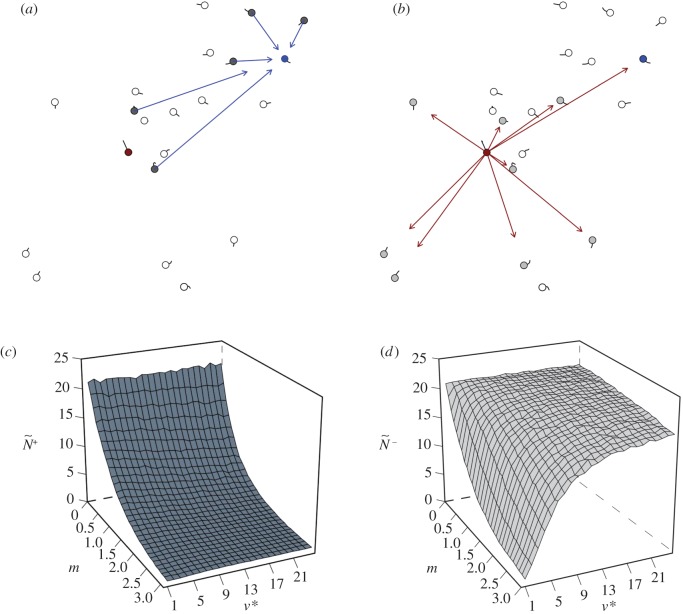
Figure 1.
Snap shots of the initial communication networks that emerge when a single member, acting as a transmitter, ignores its neighbours and departs with motion cue v*. Average attention level, 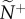 , reflects the median number of neighbours that influenced a receiver (ex. a, receiver in blue). Average transmitter influence,
, reflects the median number of neighbours that influenced a receiver (ex. a, receiver in blue). Average transmitter influence, 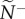 , reflects the median number of neighbours that were influenced by its movement behaviour (ex. b, transmitter in red). The resulting attention/influence communication networks are defined by
, reflects the median number of neighbours that were influenced by its movement behaviour (ex. b, transmitter in red). The resulting attention/influence communication networks are defined by 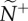 (c) and
(c) and 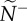 (d), respectively. The decay in attention level with m reflects the physical nature of dispersed neighbours, whose motion cues decay exponentially with distance (c;
(d), respectively. The decay in attention level with m reflects the physical nature of dispersed neighbours, whose motion cues decay exponentially with distance (c; 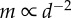 ; see the electronic supplementary material, appendix S.1). There are 1000 replicates per parameter combination, η = 0.1 and
; see the electronic supplementary material, appendix S.1). There are 1000 replicates per parameter combination, η = 0.1 and 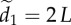 . Results are for motion-guided attention only (see the electronic supplementary material, appendix S.3 for corresponding figures related to communications under numerically limited attention).
. Results are for motion-guided attention only (see the electronic supplementary material, appendix S.3 for corresponding figures related to communications under numerically limited attention).
Coordination between any given T–R pair begins by measuring their directional deviation from one another, 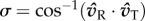 . The accuracy of all pairwise coordinations is then measured by the angular concentration in σ values across departure events:
. The accuracy of all pairwise coordinations is then measured by the angular concentration in σ values across departure events:
| 3.1 |
where E is the expected value of σ. This statistic provides an individual-level distillation of the group-level order parameter [12,14,21]:
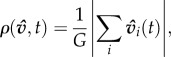 |
3.2 |
which measures collective coordination at time t across all individuals in a group of size G = |G|. The final value of this metric at the end of each simulation is then averaged across departures, 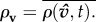 Coordination improves from 0 to 1 in both ρσ and ρv. We initially focus on measuring information transfer among individuals, ρσ, yet directional agreement between any two individuals does not guarantee collective consensus. We therefore compare ρσ and ρv to confirm or deny such associations.
Coordination improves from 0 to 1 in both ρσ and ρv. We initially focus on measuring information transfer among individuals, ρσ, yet directional agreement between any two individuals does not guarantee collective consensus. We therefore compare ρσ and ρv to confirm or deny such associations.
4. Simulations
(a). Motion-guided attention
The first objective is to quantify how coupling individual attention to neighbour motion cues can influence the transfer of social information through a group. Here, we focus on the motion threshold because it directly links attention and movement behaviour, whereas 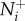 is not directly affected by motion under the numerical mechanism and its effects have been explored elsewhere [6]. We measure information transfer between T–R pairs in moderately sized groups of 25 individuals; a size that enables interactions to realistically range from local to global and meets both theoretical and empirical expectations related to individual attention level
is not directly affected by motion under the numerical mechanism and its effects have been explored elsewhere [6]. We measure information transfer between T–R pairs in moderately sized groups of 25 individuals; a size that enables interactions to realistically range from local to global and meets both theoretical and empirical expectations related to individual attention level 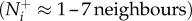 [6,18–20]. We then record how changes in the transmitter's motion cue relate to the receiver's direction. Transmitter speed in this case is presented in relation to the group average:
[6,18–20]. We then record how changes in the transmitter's motion cue relate to the receiver's direction. Transmitter speed in this case is presented in relation to the group average:  . The influence of attention and motion on information transfer are measured by how changes in m and v* influence the initial communication networks that emerge across all 25 group members (using
. The influence of attention and motion on information transfer are measured by how changes in m and v* influence the initial communication networks that emerge across all 25 group members (using 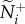 and
and 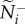 ), followed by the resulting T–R coordination patterns across time and replicate departures, ρσ. Corresponding simulations are conducted for the numerical mechanism (see the electronic supplementary material, appendix S.3).
), followed by the resulting T–R coordination patterns across time and replicate departures, ρσ. Corresponding simulations are conducted for the numerical mechanism (see the electronic supplementary material, appendix S.3).
(b). Ecological context
For the second objective, we determine if either attention mechanism can catalyse adaptive social coordination across ecological contexts. We measure the performance of these two mechanisms using ρσ and ρv as a function of individual cost, e.g. the attention level required to generate the observed degree of coordination. Recall that incremental changes in the m and n thresholds have an inverse effect on individual attention (equations (2.3) and (2.4)). Therefore, comparisons are facilitated by translating changes in m and n into the resulting attention level, 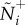 (see the electronic supplementary material, appendix S.4).
(see the electronic supplementary material, appendix S.4).
Ecological context is defined as the combination of one's physical and social environment. We alter the physical environment by varying environmental noise (η) and the initial nearest-neighbour distance (d1). These physical changes occur under two extreme social contexts: normal and disturbed patch departures. During normal departures all 25 individuals in a group behave similarly without any inherent movement biases, and both ρσ and ρv are recorded at t = 1000 to measure navigational coordination over an extensive period (i.e. resistance to persistent environmental uncertainty). Under disturbed conditions, each group's transmitter ignores its neighbours and moves off rapidly in a random direction at speed v*, following the ‘leading according to need’ hypothesis [22] (figure 1a,b). Here, the disturbance is dramatic (v* = 10) and mimics the initial moments of a reflexive startle response [34], as when an individual avoids an attack from a predator, neighbour aggression or responds to producer–scrounger dynamics [4,32,33]. In these scenarios ρσ and ρv are sampled at t = 100 to measure how responsive individuals are to such sudden disruptions (see the electronic supplementary material, appendix S.5). Additionally, it is important to quantify whether pairwise coordination, ρσ, is either amplified or dampened by the remaining group members. For this, we control for social feedbacks by repeating the above simulations, but remove all group members save the selected T–R pairs to compare how ρσ changes in groups of 25 versus two.
(c). Group size
Lastly, we extend our analyses by exploring how the two attention mechanisms affect navigational coordination as group size increases (10–200 individuals) [4,12,22]. Here, attention thresholds (m or n) and environmental conditions (η, d1) are fixed at operable levels determined from the preceding analyses (see the electronic supplementary material, appendix S.8). In groups capable of self-organization, we then measure how the strength of a cue (ν*) influences the proportion of transmitters, PT, necessary to sway a group's ability to come to a directional consensus, e.g. ρv ∼ f(PT,ν*). To measure this, we run simulations that are initiated with a single transmitter at t = 2. We then assume that some proportion PT of the group members that are influenced by a transmitter will copy its behaviour and become transmitters themselves, thereby mimicking a visually contagious response. Transmitter departure ranges from subtle to dramatic and we constrain ourselves to short time periods under both departure scenarios (ν* : {1,10}; t = 100 time steps).
5. Results
(a). Motion-guided attention
Under motion-guided attention movement cues (v*) and attention threshold (m) can interact to generate striking structural asymmetries in the communication networks that emerge (figure 1c,d). Average individual attention level is unaffected by changes in a particular neighbour's motion cue, ν* (figure 1c). However, a transmitter's ν* can range from having little influence across the group, to instantly becoming public (figure 1d, ν* → 20), even when members are largely ignoring one another (corresponding to figure 1c, m → 3.0, 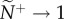 ). Over time, weak directional cues (low v*) are generally dampened or ignored, while strong cues (high v*) are nearly always accurately transmitted, regardless of the average individual's attention level (figure 2a). Individuals can therefore tune their response to weaker cues either through social indifference (high m threshold, resulting in low attention levels), or unintentionally through collective averaging (low m threshold, resulting in high attention levels). The trade-off between these behavioural endpoints is that higher attention levels slow down response time because of collective dampening, but generate slightly better pairwise coordination (figure 2b and [14]). However, intermediate levels of attention can enhance both the speed and accuracy with which social information is transmitted, albeit at the price of increased sensitivity to weaker motion cues (figure 2a,b). Information distribution and transmission patterns differ substantially when individuals adopt the numerical mechanism (see the electronic supplementary material, appendix S.3).
). Over time, weak directional cues (low v*) are generally dampened or ignored, while strong cues (high v*) are nearly always accurately transmitted, regardless of the average individual's attention level (figure 2a). Individuals can therefore tune their response to weaker cues either through social indifference (high m threshold, resulting in low attention levels), or unintentionally through collective averaging (low m threshold, resulting in high attention levels). The trade-off between these behavioural endpoints is that higher attention levels slow down response time because of collective dampening, but generate slightly better pairwise coordination (figure 2b and [14]). However, intermediate levels of attention can enhance both the speed and accuracy with which social information is transmitted, albeit at the price of increased sensitivity to weaker motion cues (figure 2a,b). Information distribution and transmission patterns differ substantially when individuals adopt the numerical mechanism (see the electronic supplementary material, appendix S.3).
Figure 2.
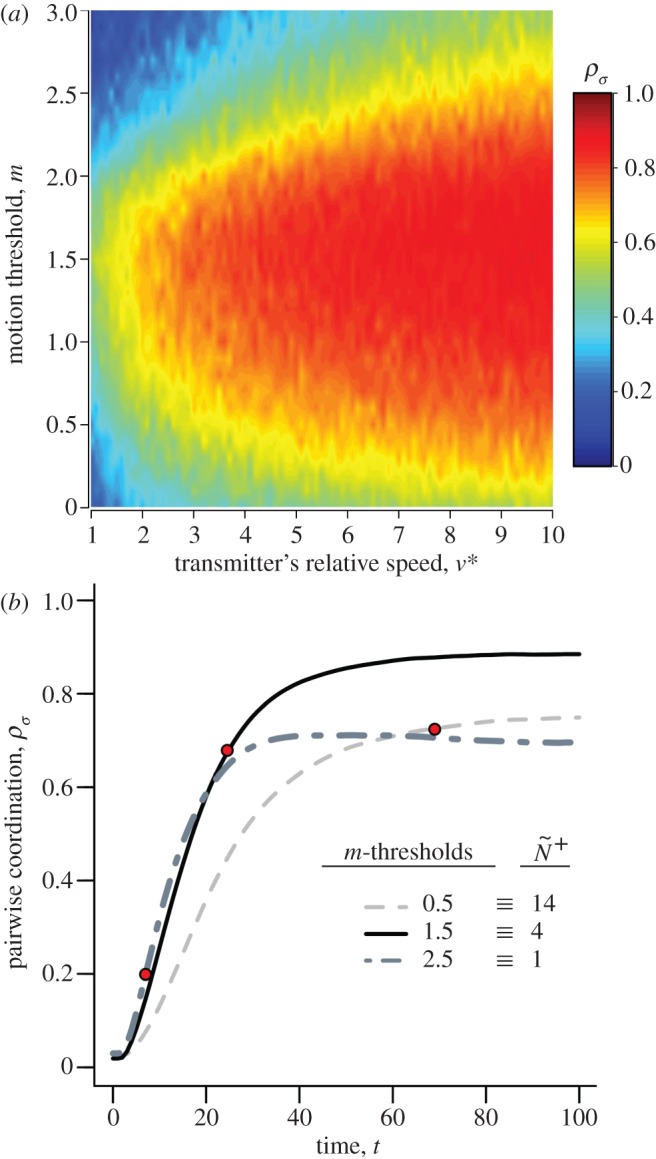
(a) Coordination accuracy between transmitter–receiver pairs (T–R, t = 100) as a function of the transmitter's motion cue, v*, and the receiver's motion threshold, m. (b) Time series of the average trends in T–R coordination during a social disturbance (v* = 10) for three attention levels. Red dots indicate the median time that receivers tracked their transmitter's motion through the crowd (i.e. 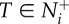 ; equation (2.3)). v* is limited to
; equation (2.3)). v* is limited to  to reflect the saturation point seen in (a) and corresponds to the relative speeds displayed by startled fish [34]. Trend lines in (b) reflect median values that are all smoothed by the same exponential moving average. Parameter values and conditions match those in figure 1.
to reflect the saturation point seen in (a) and corresponds to the relative speeds displayed by startled fish [34]. Trend lines in (b) reflect median values that are all smoothed by the same exponential moving average. Parameter values and conditions match those in figure 1.
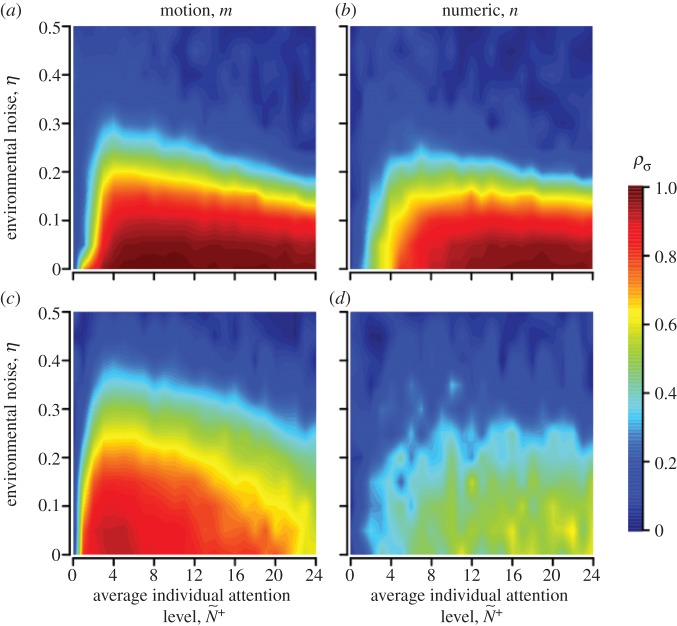
(b). Ecological context
As environmental noise or panic levels increase, motion-guided attention enables individuals within a group to maintain directional coordination across contexts more effectively than when they adopt the numerical mechanism (ρσ, figure 3). During normal patch departures, individuals can achieve high levels of navigational performance at half the attention level required by those adopting numerically limited attention (figure 3a,b). Resistance to noise is not limited by n under the numeric mechanism because pairwise coordination accuracy peaks well before 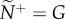 (figure 3b). Motion-guided attention also enables individuals to retain high levels of coordination accuracy during a sudden disturbance, suggesting a robust means to optimize social communications across large changes in context (figure 3a,c). Moreover, this rapid response occurs without requiring receivers to alter their internal state (i.e. m). In contrast, coordination accuracy breaks down during a disturbance when individuals adopt the numerical mechanism (figure 3b,d). While both attention mechanisms can result in a receiver not responding to a transmitter's motion cue, missed or dampened cues are much more prevalent with the numerical mechanism (see the electronic supplementary material, movies S1 and S2 for example).
(figure 3b). Motion-guided attention also enables individuals to retain high levels of coordination accuracy during a sudden disturbance, suggesting a robust means to optimize social communications across large changes in context (figure 3a,c). Moreover, this rapid response occurs without requiring receivers to alter their internal state (i.e. m). In contrast, coordination accuracy breaks down during a disturbance when individuals adopt the numerical mechanism (figure 3b,d). While both attention mechanisms can result in a receiver not responding to a transmitter's motion cue, missed or dampened cues are much more prevalent with the numerical mechanism (see the electronic supplementary material, movies S1 and S2 for example).
Figure 3.
Coordination accuracy between T–R pairs as a function of ecological context, environmental noise (η) and attention. Individuals adopt either a motion threshold (a,c) or a numerical threshold (b,d). Under normal patch departures all individuals interact socially and move at similar speeds (a,b). During disturbed departures a startled transmitter ignores its neighbours and departs with a motion cue of v* = 10 (c,d). Coordination is shown as a function of individual attention level to facilitate comparison between the attention mechanisms (see the electronic supplementary material, appendix S.4 and movies S1–S3 for example). Simulations lasted 1000 and 100 time steps for normal and disturbed scenarios, respectively; 500 replicates per parameter combination; initial dispersion level is 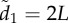 (see electronic supplementary material, table A1 and appendix S.2 for parameter values and rationale).
(see electronic supplementary material, table A1 and appendix S.2 for parameter values and rationale).
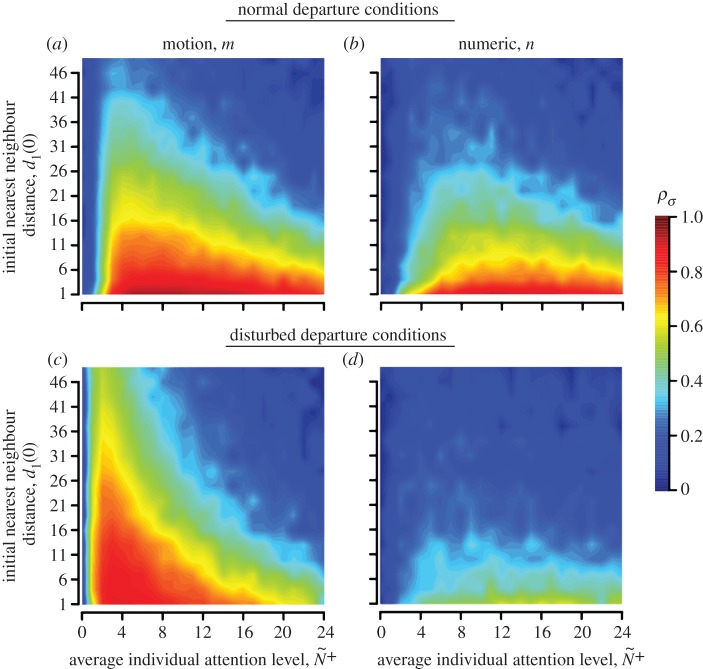
We find qualitatively similar patterns between the attention mechanisms within and across contexts when group dispersion levels vary from crowded to sparse (ρσ, figure 4). Additionally, coordination accuracy between T–R pairs within groups of 25 individuals is generally reflected at the group level across these ecological contexts, confirming collective coordination (ρv; see the electronic supplementary material, appendix S.6). Lastly, social feedbacks play a critical role in amplifying information transfer through groups, which only occurs under the motion mechanism. The result is that pairwise coordination within full groups (G = 25) can be substantially enhanced beyond what is observed in isolated pairwise interactions (see the electronic supplementary material, appendix S.7).
Figure 4.
Coordination accuracy between T–R pairs as a function of ecological context, initial nearest-neighbour distance (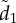 at t = 0) and attention. Individual attention level is dictated by either a motion threshold, m (a,c), or a numerical threshold, n, (b,d). Additional parameter values match those in figure 3, albeit with noise fixed at η = 0.1.
at t = 0) and attention. Individual attention level is dictated by either a motion threshold, m (a,c), or a numerical threshold, n, (b,d). Additional parameter values match those in figure 3, albeit with noise fixed at η = 0.1.
(c). Group size
Under normal conditions motion-guided attention enables individuals to self-organize across a broad range of group sizes, albeit more slowly as group size increases (figure 5a). When the numerical mechanism is employed at n=7, the biological upper limit for this mechanism [24–26], larger groups fail to self-organize (see figure 5a inset and electronic supplementary material, appendix S.8). One reason for these differences in group-level coordination is that the motion mechanism enables individual attention to scale with group size, thereby enhancing social connectivity. However, a receiver's Nj nearest neighbours become less influential with increasing separation distance, regardless of the attention mechanism (as ωj,i, decays in strength with increasing distance; see electronic supplementary material, appendix S.1). This results in distal neighbours having diminishing navigational influence as G and Nj increase, which is shown by the cumulative influence that each successive neighbour adds to a receiver's optic flow (figure 5b). So, although median attention levels rise with group size (figure 5b, inset), movement decisions remain locally biased and show little change in the proportion of influential neighbours across group sizes (figure 5b, inset; see the electronic supplementary material, movie S3).
Figure 5.
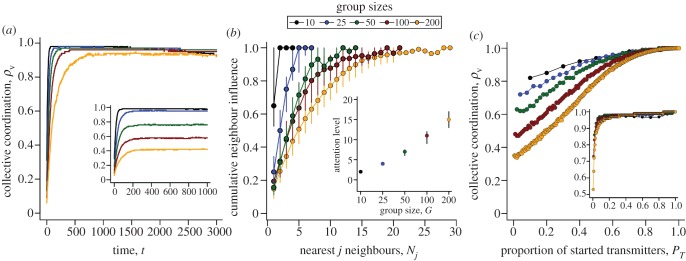
The effects of group size, movement behaviour and attention mechanisms on collective coordination. Average trends in collective coordination in groups of 10–200 individuals over time when members adopt either motion (a; main) or numerical (a; inset) thresholds. (b) The cumulative influence of G and the Nj nearest influential neighbours on the magnitude of the typical receiver's response. Each successive influential neighbour provides additional movement information whose proportional contribution is given by 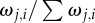 . The sum of all influential motion weights is then averaged to scale the receiver's response to its social stimuli (equations (2.2) and (2.5)). Inset (b) shows the median receiver attention levels as a function of group size under a fixed motion threshold. Points and error bars represent 25, 50 and 75% quantiles. (c) Collective coordination across groups of varying size as a function of the number of transmitters and their motion cue, where v* = 1 (main) and 10 (inset). Starting values of ρv equate to those at t = 100 in (a) for each group size. When v* = 1 transmitters have limited social influence, but their directional influence increases dramatically when v* = 10 (Note the lower limits in the y-axis.). Parameter values for all simulations: m = 1.5, n = 7 (a; inset only),
. The sum of all influential motion weights is then averaged to scale the receiver's response to its social stimuli (equations (2.2) and (2.5)). Inset (b) shows the median receiver attention levels as a function of group size under a fixed motion threshold. Points and error bars represent 25, 50 and 75% quantiles. (c) Collective coordination across groups of varying size as a function of the number of transmitters and their motion cue, where v* = 1 (main) and 10 (inset). Starting values of ρv equate to those at t = 100 in (a) for each group size. When v* = 1 transmitters have limited social influence, but their directional influence increases dramatically when v* = 10 (Note the lower limits in the y-axis.). Parameter values for all simulations: m = 1.5, n = 7 (a; inset only), 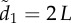 at t = 0, η = 0.1.
at t = 0, η = 0.1.
Motion-guided attention also affects the proportion of group members necessary to sway a group's directional consensus during short time periods (t = 100). When transmitters display a persistent directional bias, but move no faster than the average individual (v* = 1), it takes a greater proportion of them to successfully bias the group's direction as group size increases (figure 5c). This is because it simply takes larger groups longer to self-organize (ρv values at PT = 0 in figure 5c equate to those at t = 100 in figure 5a). However, we see a dramatic shift in the influence that a minority of individuals can exert over a group during a sudden social disturbance across all group sizes (v* = 10; figure 5c, inset; see electronic supplementary material, movie S4). These dynamics are largely driven by the underlying pairwise interactions, which increase more rapidly (see the electronic supplementary material, appendix S.8, figure A-11).
6. Discussion
The central finding of this study is that motion-guided attention can catalyse adaptive social communications across a broad range of ecological contexts. This mechanism enables individuals to become temporary information hubs simply through their actions, without requiring a shift in the average receiver's attention level, thereby increasing both the speed and accuracy with which information is locally disseminated. In turn, these properties can substantially influence the proportion of individuals necessary to sway a group's responsiveness to a social disturbance. Our results do not support the hypothesis that numerically limited interactions are essential to generate robust collective behaviour, particularly with regard to large changes in ecological context. As arguments for and against a numerical mechanism are nicely presented elsewhere [6,35], we will discuss how the motion mechanism may extend our understanding of coordinated social behaviour.
Motion-guided attention provides an intuitive means of generating adaptive communications in animal groups on the move. For instance, animals tend to optimize their travel speeds to balance ecological and energetic trade-offs [36]. The high energetic costs associated with bursts of motion would therefore minimize the risk of behavioral cascades from false alarms (type I errors), while enabling individuals to tune their attention to hedge their bets against type II errors (failing to respond to a neighbour's predator avoidance manoeuvre) [37]. Additionally, biasing social sensory processing according to the strength of any perceivable cues effectively removes distracting cues from the integration process, thereby reducing the dampening effects of weaker cues that can frequently arise simply through minor random motions. The result is that individuals sift energetically salient information from a scene while avoiding the associated costs, such as time lost for other activities (e.g. foraging–vigilance trade-offs [4,32,33,38]).
The simulation results also provide interesting parallels to recent laboratory studies. For instance, fish swimming in small groups of 2–30 individuals have been shown to primarily respond to their nearest 1–3 neighbours and these kinematic interactions appear largely driven by changes in individual speed [18,19]. Speed drives the interactions in the model when individuals adopt motion-guided attention. Likewise, motion-guided attention generates very similar kinematic associations among nearest neighbours in similarly sized groups (G = 10 and 25; figure 5b). Interestingly, as group size expands beyond the limits of the empirical data [18,19], the influence of one's nearest neighbours becomes progressively muted as group size increases. In the model, this occurs from local density effects over time, as groups compact and an individual's neighbours become more evenly distributed around it. While additional effects certainly play a role in local interactions (occlusion, collision avoidance), our results suggest a mechanism that may underlie both the limited interaction patterns observed in small groups [18,19] and the theoretical and empirical evidence supporting density-driven interactions in larger groups (i.e. attraction/avoidance of crowded horizons) [39,40]. The model also predicts that the role of minorities within a group can shift considerably when groups are exposed to different social contexts, which suggests that the quorum necessary to bias collective decision making may be equally affected (i.e. behavioural inter-dependencies and social context dictate the quorum; [1,2,41]). Our study focused on the short term, reflexive motions that may occur during rushed decisions [1], whereas time and the addition of social cohesion may serve to shift the long-term leader–follower dynamics in social groups [12].
Selective attention is likely to be an important mechanism promoting collaborative decision-making processes in social organisms [13,14]. The basic properties of selective attention appear across a broad taxonomic range [26,37,42–44], which suggests a fundamental mechanism underlying basic social interactions in taxa spanning from bacteria to humans. These findings have broad inter-disciplinary potential, from re-evaluating vigilance trade-offs in foraging theory, advancing information exchange in distributed systems and expanding our biological understanding of dynamic networks.
Acknowledgements
The authors would like to thank Colby Tanner, Eric Dimperio and Mary Hunsicker for discussions and constructive comments. We also thank two anonymous referees for their insightful feedback. Jim Johnson, US Fish and Wildlife Service-Migratory Bird Management, and Bob Christensen provided access to the Chiloé Island Shorebird Conservation Program, which inspired this work. This research was sponsored by the US Army's Network Science research initiative through the US Army Engineer Research & Development Center's Environmental Quality and Installations Basic Research Program. Permission was granted by the Chief of Engineers to publish this information.
References
- 1.Ward AJW, Herbert-Read JE, Sumpter DJT, Krause J. 2011. Fast and accurate decisions through collective vigilance in fish shoals. Proc. Natl Acad. Sci. USA 108, 2312–2315 10.1073/pnas.1007102108 (doi:10.1073/pnas.1007102108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Conradt L, List C. 2009. Group decisions in humans and animals: a survey. Phil. Trans. R. Soc. B 364, 719–742 10.1098/rstb.2008.0276 (doi:10.1098/rstb.2008.0276) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Couzin ID, James R, Mawdsley D, Croft D, Krause J. 2006. Social organization and information transfer in schooling fishes. In Fish cognition and behavior (eds Brown C, LaLand K, Krause J.), pp. 166–185 Oxford, UK: Blackwell [Google Scholar]
- 4.Krause J, Ruxton G. 2002. Living in groups. Oxford, UK: Oxford University Press [Google Scholar]
- 5.Danchin É, Giraldeau LA, Valone TJ, Wagner RH. 2004. Public information: from nosy neighbors to cultural evolution. Science 305, 487–491 10.1126/science.1098254 (doi:10.1126/science.1098254) [DOI] [PubMed] [Google Scholar]
- 6.Ballerini M, et al. 2008. Interaction ruling animal collective behavior depends on topological rather than metric distance: evidence from a field study. Proc. Natl Acad. Sci. USA 105, 1232–1237 10.1073/pnas.0711437105 (doi:10.1073/pnas.0711437105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nagy M, Ákos Z, Biro D, Vicsek T. 2010. Hierarchical group dynamics in pigeon flocks. Nature 464, 890–894 10.1038/nature08891 (doi:10.1038/nature08891) [DOI] [PubMed] [Google Scholar]
- 8.Grünbaum D. 1998. Schooling as a strategy for taxis in a noisy environment. Evol. Ecol. 12, 503–522 10.1023/A:1006574607845 (doi:10.1023/A:1006574607845) [DOI] [Google Scholar]
- 9.Potts W. 1984. The chorus-line hypothesis of manoeuvre coordination in avian flocks. Nature 309, 344–345 10.1038/309344a0 (doi:10.1038/309344a0) [DOI] [Google Scholar]
- 10.Viscido SV, Parrish JK, Grünbaum D. 2004. Individual behavior and emergent properties of fish schools: a comparison of observation and theory. Mar. Ecol. Progr. Ser. 273, 239–249 10.3354/meps273239 (doi:10.3354/meps273239) [DOI] [Google Scholar]
- 11.Couzin ID. 2009. Collective cognition in animal groups. Trends Cogn. Sci. 13, 36–43 10.1016/j.tics.2008.10.002 (doi:10.1016/j.tics.2008.10.002) [DOI] [PubMed] [Google Scholar]
- 12.Couzin I, Krause J, Franks N, Levin S. 2005. Effective leadership and decision-making in animal groups on the move. Nature 433, 513–516 10.1038/nature03236 (doi:10.1038/nature03236) [DOI] [PubMed] [Google Scholar]
- 13.Romanczuk P, Couzin ID, Schimansky-Geier L. 2009. Collective motion due to individual escape and pursuit response. Phys. Rev. Lett. 102, 010602. 10.1103/PhysRevLett.102.010602 (doi:10.1103/PhysRevLett.102.010602) [DOI] [PubMed] [Google Scholar]
- 14.Lemasson B, Anderson J, Goodwin RA. 2009. Collective motion in animal groups from a neurobiological perspective: the adaptive benefits of dynamic sensory loads and selective attention. J. Theor. Biol. 261, 501–510 10.1016/j.jtbi.2009.08.013 (doi:10.1016/j.jtbi.2009.08.013) [DOI] [PubMed] [Google Scholar]
- 15.Bode NWF, Faria JJ, Franks DW, Krause J, Wood AJ. 2010. How perceived threat increases synchronization in collectively moving animal groups. Proc. R. Soc. B 277, 3065–3070 10.1098/rspb.2010.0855 (doi:10.1098/rspb.2010.0855) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fernández-Juricic E, Kacelnik A. 2004. Information transfer and gain in flocks: the effects of quality and quantity of social information at different neighbour distances. Behav. Ecol. Sociobiol. 55, 502–511 10.1007/s00265-003-0698-9 (doi:10.1007/s00265-003-0698-9) [DOI] [Google Scholar]
- 17.Bazazi S, Buhl J, Hale J, Anstey M, Sword G, Simpson S, Couzin ID. 2008. Collective motion and cannibalism in locust migratory bands. Curr. Biol. 18, 735–739 10.1016/j.cub.2008.04.035 (doi:10.1016/j.cub.2008.04.035) [DOI] [PubMed] [Google Scholar]
- 18.Katz Y, Tunstrom K, Ioannou C, Huepe C, Couzin ID. 2011. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl Acad. Sci. USA 108, 18 720–18 725 10.1073/pnas.1107583108 (doi:10.1073/pnas.1107583108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Herbert-Read JE, Perna A, Mann RP, Schaerf TM, Sumpter DJT, Ward AJW. 2011. Inferring the rules of interaction of shoaling fish. Proc. Natl Acad. Sci. USA 108, 18 726–18 731 10.1073/pnas.1109355108 (doi:10.1073/pnas.1109355108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Inada Y, Kawachi K. 2002. Order and flexibility in the motion of fish schools. J. Theor. Biol. 214, 371–387 10.1006/jtbi.2001.2449 (doi:10.1006/jtbi.2001.2449) [DOI] [PubMed] [Google Scholar]
- 21.Torney C, Neufeld Z, Couzin ID. 2009. Context-dependent interaction leads to emergent search behavior in social aggregates. Proc. Natl Acad. Sci. USA 106, 22 055–22 060 10.1073/pnas.0907929106 (doi:10.1073/pnas.0907929106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Conradt L, Krause J, Couzin ID, Roper TJ. 2009. ‘Leading according to need’ in self-organizing groups. Am. Nat. 173, 304–312 10.1086/596532 (doi:10.1086/596532) [DOI] [PubMed] [Google Scholar]
- 23.Chen L. 2005. The topological approach to perceptual organization. Vis. Cogn. 12, 553–637 10.1080/13506280444000256 (doi:10.1080/13506280444000256) [DOI] [Google Scholar]
- 24.Nieder A. 2005. Counting on neurons: the neurobiology of numerical competence. Nat. Rev. Neurosci. 6, 177–190 10.1038/nrn1626 (doi:10.1038/nrn1626) [DOI] [PubMed] [Google Scholar]
- 25.Agrillo C, Dadda M, Bisazza A. 2007. Quantity discrimination in female mosquitofish. Anim. Cogn. 10, 63–70 10.1007/s10071-006-0036-5 (doi:10.1007/s10071-006-0036-5) [DOI] [PubMed] [Google Scholar]
- 26.Shettleworth S. 2010. Cognition, evolution and behavior. New York, NY: Oxford University Press [Google Scholar]
- 27.Desimone R, Duncan J. 1995. Neural mechanisms of selective visual attention. Annu. Rev. Neurosci. 18, 193–222 10.1146/annurev.ne.18.030195.001205 (doi:10.1146/annurev.ne.18.030195.001205) [DOI] [PubMed] [Google Scholar]
- 28.Wolfe J, Horowitz T. 2004. What attributes guide the deployment of visual attention and how do they do it? Nat. Rev. Neurosci. 5, 1–7 10.1038/nrn1411 (doi:10.1038/nrn1411) [DOI] [PubMed] [Google Scholar]
- 29.Lehrer M, Srinivasan MV, Zhang SW, Horridge GA. 1988. Motion cues provide the bee's visual world with a third dimension. Nature 332, 356–357 10.1038/332356a0 (doi:10.1038/332356a0) [DOI] [Google Scholar]
- 30.Fleishman L. 1992. The influence of the sensory system and the environment on motion patterns in the visual displays of anoline lizards and other vertebrates. Am. Nat. 139, S36–S61 10.1086/285304 (doi:10.1086/285304) [DOI] [Google Scholar]
- 31.Ioannou C, Krause J. 2009. Interactions between background matching and motion during visual detection can explain why cryptic animals keep still. Biol. Lett. 5, 191–193 10.1098/rsbl.2008.0758 (doi:10.1098/rsbl.2008.0758) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Giraldeau LA, Caraco T. 2000. Social foraging theory. Princeton, NJ: Princeton University Press [Google Scholar]
- 33.Fernández-Juricic E, Erichsen JT, Kacelnik A. 2004. Visual perception and social foraging in birds. Trends Ecol. Evol. 19, 25–31 10.1016/j.tree.2003.10.003 (doi:10.1016/j.tree.2003.10.003) [DOI] [PubMed] [Google Scholar]
- 34.Domenici P, Blake R. 1997. The kinematics and performance of fish fast-start swimming. J. Exp. Biol. 200, 1165–1178 [DOI] [PubMed] [Google Scholar]
- 35.Bode NWF, Franks DW, Wood AJ. 2011. Limited interactions in flocks: relating model simulations to empirical data. J. R. Soc. Interface 8, 301–304 10.1098/rsif.2010.0397 (doi:10.1098/rsif.2010.0397) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Alexander R. 1999. Bioenergetics: One price to run, swim or fly? Nature 397, 651–653 10.1038/17687 (doi:10.1038/17687) [DOI] [PubMed] [Google Scholar]
- 37.List C. 2004. Democracy in animal groups: a political science perspective. Trends Ecol. Evol. 19, 168–169 10.1016/j.tree.2004.02.004 (doi:10.1016/j.tree.2004.02.004) [DOI] [PubMed] [Google Scholar]
- 38.Dukas R. 2004. Causes and consequences of limited attention. Brain Behav. Evol. 63, 197–210 10.1159/000076781 (doi:10.1159/000076781) [DOI] [PubMed] [Google Scholar]
- 39.Viscido SV, Miller M, Wethey DS. 2002. The dilemma of the selfish herd: the search for a realistic movement rule. J. Theor. Biol. 217, 183–194 10.1006/yjtbi.3025 (doi:10.1006/yjtbi.3025) [DOI] [PubMed] [Google Scholar]
- 40.Moussaïd M, Helbing D, Theraulaz G. 2011. How simple rules determine pedestrian behavior and crowd disasters. Proc. Natl Acad. Sci. USA 108, 6884–6888 10.1073/pnas.1016507108 (doi:10.1073/pnas.1016507108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sumpter DJT, Pratt SC. 2009. Quorum responses and consensus decision making. Phil. Trans. R. Soc. B 364, 743–753 10.1098/rstb.2008.0204 (doi:10.1098/rstb.2008.0204) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Swinderen BV. 2005. The remote roots of consciousness in fruit-fly selective attention? Bioessays 27, 321–330 10.1002/bies.20195 (doi:10.1002/bies.20195) [DOI] [PubMed] [Google Scholar]
- 43.Zanker J. 1995. Does motion perception follow Weber's law? Perception 24, 363–372 10.1068/p240363 (doi:10.1068/p240363) [DOI] [PubMed] [Google Scholar]
- 44.Tu Y, Shimizu T, Berg H. 2008. Modeling the chemotactic response of Escherichia coli to time-varying stimuli. Proc. Natl Acad. Sci. USA 105, 14 855–14 860 10.1073/pnas.0807569105 (doi:10.1073/pnas.0807569105) [DOI] [PMC free article] [PubMed] [Google Scholar]