Geographical variation in the spatial synchrony of a forest-defoliating insect: isolation of environmental and spatial drivers

Abstract

Despite the pervasiveness of spatial synchrony of population fluctuations in virtually every taxon, it remains difficult to disentangle its underlying mechanisms, such as environmental perturbations and dispersal. We used multiple regression of distance matrices (MRMs) to statistically partition the importance of several factors potentially synchronizing the dynamics of the gypsy moth, an invasive species in North America, exhibiting outbreaks that are partially synchronized over long distances (approx. 900 km). The factors considered in the MRM were synchrony in weather conditions, spatial proximity and forest-type similarity. We found that the most likely driver of outbreak synchrony is synchronous precipitation. Proximity played no apparent role in influencing outbreak synchrony after accounting for precipitation, suggesting dispersal does not drive outbreak synchrony. Because a previous modelling study indicated weather might indirectly synchronize outbreaks through synchronization of oak masting and generalist predators that feed upon acorns, we also examined the influence of weather and proximity on synchrony of acorn production. As we found for outbreak synchrony, synchrony in oak masting increased with synchrony in precipitation, though it also increased with proximity. We conclude that precipitation could synchronize gypsy moth populations directly, as in a Moran effect, or indirectly, through effects on oak masting, generalist predators or diseases.

1. Introduction

The pursuit of explanations for the pervasiveness of spatial synchrony in the fluctuations of populations advances ecological understanding of the dominant forces influencing population dynamics [1]. Spatial synchrony of population fluctuations is generally thought to result from two classes of mechanism: spatially synchronous environmental perturbations, or dispersal (of a focal species or its natural enemies) between populations. Spatial synchrony of populations brought on by regional environmental perturbations may arise through a process known as the Moran effect, where synchrony among populations matches that of the environment, but this is a special case where populations are governed by identical density-dependent dynamics [2]. Moran effects are generally thought to be caused by the direct effects of weather on the survival and reproduction of individuals. There is also increasing recognition from empirical and theoretical work that spatial synchrony of a focal species owing to regional environmental perturbation can be transferred to other species that are directly or indirectly linked through food web interactions [3–6].

Determining the class of mechanisms (much less the specific drivers) responsible for the spatial synchrony of populations in nature is notoriously difficult [7]. In some species, spatial synchrony has been detected among populations separated by vast distances (e.g. 1000 km in the spruce budworm [8]), making experiments in such systems impractical. However, the observation that spatial synchrony in population fluctuations typically declines with the distance between populations has informed the search for underlying mechanisms. Because dispersal is limited in space, it is commonly assumed that dispersal can contribute only to population synchrony over relatively small distances and that synchrony over long distances is likely to be due to regional environmental perturbations [1,9,10]. Furthermore, observations of synchrony in weather over long distances, along with similar distance decay in synchrony of weather and population fluctuations, have provided support for the hypothesis that population synchrony is environmentally driven [8,11]. However, there are problems with both lines of evidence. First, Ranta et al. [12] showed that exchange of even low numbers of individuals between distant populations can bring them into synchrony when the populations are locally cyclic, through a process known as phase locking. Second, local variability in other environmental conditions may mask the synchronizing effects of an environmental driver. For example, the spatial synchrony of gypsy moth (Lymantria dispar) populations declines faster with distance than does synchrony in weather, possibly because of geographical variability in local conditions such as forest type [8]. These complications hamper efforts to disentangle the effects of regional environmental perturbations and dispersal on population synchrony based on distance–decay relationships alone.

A method that has recently been gaining some traction as a tool for discerning the underpinnings of population synchrony is to partition variance in geographical synchrony into environmental and spatial sources. For example, Hegel et al. [10] found that spatial synchrony in caribou (Rangifer tarandus) recruitment was correlated with the similarity of elevational variation (standard deviation) in calving locations between herds. In addition, Powney et al. [13] evaluated how synchrony of butterfly populations was correlated with climatic dissimilarity and geographical distance. However, mere similarity in environmental conditions such as climate (mean weather over time) or habitat condition would not actively synchronize populations. The key feature of an environmental synchronizing agent is that it fluctuates synchronously [2].

To date, very few studies have examined whether geographical variation in the strength of synchrony of environmental conditions leads to geographical variation in population synchrony. A notable exception is Drever's study [14] of the effects of spatial synchrony in wetland availability on the synchrony of duck populations. Drever [14] also examined how the strength of population synchrony was related to distance. Quantifying the relationships between population synchrony and synchrony in environmental conditions (e.g. weather), while controlling for distance, allows the researcher to investigate the importance of environmental forces as well as spatial drivers such as dispersal.

In this study, we examine the sources of geographical variation in the synchrony of gypsy moth outbreaks in North America. The gypsy moth is an ideal study organism for this topic because of the availability of extensive spatio-temporal data on gypsy moth outbreaks, and accompanying data on weather and forest characteristics throughout the gypsy moth's range. In addition, spatial synchrony in gypsy moth outbreaks is detectable over distances of up to approximately 900 km [6,8]. Peltonen et al. [8] reported that the distance–decay pattern of synchrony in June precipitation was similar to that of gypsy moth outbreaks. A modelling study [6] showed that weather-driven synchrony in oak (Quercus spp.) mast production is capable of indirectly synchronizing gypsy moth populations via a series of consumer–resource interactions. Spatial synchrony in acorn production was hypothesized to synchronize mammalian predator populations that depend on acorns for overwinter survival and, by extension, lead to synchrony in gypsy moth populations. However, we have no evidence directly linking the synchrony in outbreaks to any particular driver. Pathogens of the gypsy moth are known to be influenced by humidity and temperature [15,16], so these may provide additional top-down enhancement of synchrony.

Here, we statistically partition geographical variation in the strength of synchrony into variation explained by synchrony in weather or spatial proximity while controlling for similarity in forest type. We also examine the influence of synchrony in weather conditions and spatial proximity on synchrony in oak masting to explore the possibility that weather-driven synchrony in acorn production indirectly synchronizes gypsy moth outbreaks.

2. Methods

(a). Study system

Gypsy moth populations exhibit complex cyclical behaviour, with outbreaks in some forest types (e.g. oak/hickory) exhibiting an 8–10-year period as well as a subharmonic 4–5-year period [17]. By contrast, gypsy moth cycles in oak/pine forest exhibit only a 4–5-year period [17]. These cycles are thought to result from the gypsy moth's capacity for rapid population growth and delayed density-dependent feedback owing to host–pathogen interactions [18–20]. Although outbreaks are terminated primarily by pathogens such as the gypsy moth nucleopolyhedrosis virus (LdNPV) and the fungus Entomophaga maimaiga, the timing of outbreaks may be strongly influenced by predation of pupae by generalist mammalian predators [21,22]. In years of low gypsy moth density, predation by generalist predators is the largest source of mortality and the dominant factor determining population growth [18,21]. The chief predator of the gypsy moth is the white-footed mouse (Peromyscus leucopus), the abundance of which is influenced by mast seeding of oaks; mice depend on acorns as a food source for overwinter survival [21,23–26].

In North American gypsy moth populations, the main natural dispersal mechanism is larval ballooning because adult females are flightless [27,28]. Mason & McManus [27] showed that the vast majority of ballooning larvae travel less than 200 m.

(b). Analyses of drivers of spatial synchrony in defoliation

The purpose of our analysis was to isolate the effects of regional environmental forcing and other spatial processes (e.g. dispersal) on the spatial synchrony of gypsy moth outbreaks. Specifically, we evaluated the extent to which the strength of synchrony in gypsy moth defoliation between paired locations was related to spatial proximity or the strength of synchrony in weather conditions, while controlling for similarity of forest type. Synchrony of gypsy moth outbreaks was assessed using spatially referenced data (figure 1a) on gypsy moth defoliation in the northeastern United States over a period of 35 years (1975–2009). The spatio-temporal defoliation data were obtained from an archive of annual aerial survey maps, which were digitized as sequential raster maps in a geographical information system. We used the fraction of forest defoliated within 64 × 64 km quadrats as a proxy for gypsy moth density [8,17]. Defoliation data are available over the 35-year period at a maximum resolution of 2 × 2 km; however, these data are binary (1 = defoliated, 0 = not defoliated), and fine-scale defoliation data are subject to a high degree of spatial error [22,30]. By aggregating the fine-scale data into 64 × 64 km quadrats, we were able to reduce the influence of fine-scale error and derive a proxy of gypsy moth density that varied continuously. We restricted the analysis to areas included with the 1973 ‘generally infested area’ in US Department of Agriculture gypsy moth quarantine regulations (US Code of Federal Regulations, title 7, ch. III, §301.45), which includes much of the northeastern United States. More recently, infested areas were not included in our analysis, because the history of defoliation in these areas is not comparable. Finally, we excluded quadrats where defoliation was detected for less than 3 years to avoid singular correlation matrices when computing synchrony. These steps led us to use 70 quadrats in the analyses (figure 1a). These defoliation data are freely available on the Knowledge Network for Biocomplexity (KNB) Metacat server (http://knb.ecoinformatics.org/data.jsp). Synchrony of defoliation for each pair-wise combination of quadrats was determined by computing the Spearman rank correlation (for this as well as all other synchrony calculations below).

Figure 1.

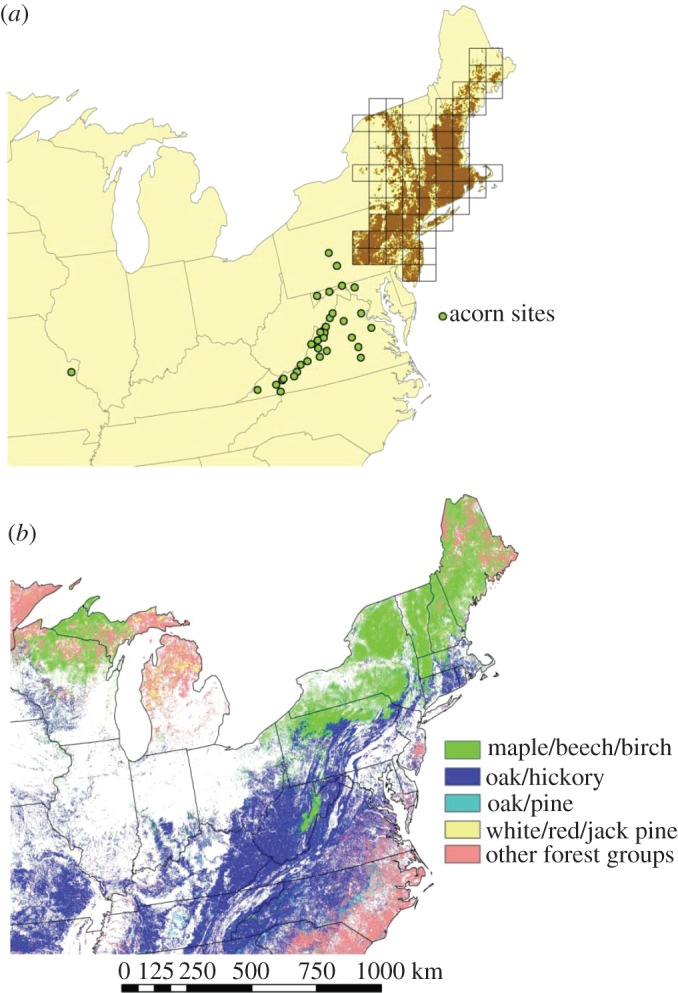
(a) Locations of red oak (Erythrobalanus) acorn abundance and gypsy moth defoliation datasets. The percentage of forest canopy defoliated in a given year was measured for 70 forest quadrats (open black squares). Brown shading represents areas defoliated by gypsy moths from 1975 to 2009. (b) Spatial arrangement of forest type groups (which we refer to as ‘forest types’) generated from Ruefenacht's [29] map layer.

Weather data for each of the 70 quadrats were obtained from the PRISM climate mapping project (http://www.prism.oregonstate.edu/index.phtml) [31]. These data consist of 1 km raster spatial interpolations from historical weather variables collected at a network of stations across the conterminous USA. Variables were monthly precipitation, mean monthly maximum temperature and mean monthly minimum temperature in each year (a total of 36 variables; three variables for each month), which were each averaged across the 64 × 64 km quadrats. We obtained these variables for each year from 1975 to 2009, generating a separate 35-year time series for each variable. We chose to use all 36 weather variables rather than selecting a smaller number of variables a priori because of inconsistent and sometimes contradictory findings among previous studies examining correlations between weather variables and gypsy moth density or extent of defoliation [18]. However, analysis of such a large number of weather variables when testing for relationships between weather and outbreak synchrony would lead to an unacceptable type I error rate. Additionally, many of the variables were collinear. Therefore, we characterized variation in weather based on a smaller number of dimensions using principal component analysis (PCA). The data used in the PCA were the values of each variable in each year from 1975 to 2009. After finding two dominant components (see electronic supplementary material, figure S1), we measured the strength of synchrony in the scores for these components over the 35-year time series.

Because gypsy moth outbreak dynamics is known to vary by forest type [17], we controlled for the influence of forest type on outbreak synchrony. Ruefenacht [29] published a 250 m resolution map based on ground surveys of forest plots (conducted by the USDA Forest Inventory and Analysis Programme) and remote sensing data that classified forests within our study area into 11 forest type groups (hereafter, forest types). Using a geographic information system (GIS), we determined the relative amount of each forest type (percentage of forested area) within each quadrat from the georeferenced map [29]. Covariates consisting of the percentages of each forest type were used to determine the overall dissimilarity for each pair-wise combination of quadrats by calculating Mahalanobis distance (D), a distance measure that accounts for differences in variance and correlations among the covariates [32]. To avoid bias from disproportionate influence of rare forest types, three forest types (pinyon/juniper, exotic softwoods and oak/gum/cypress) constituting less than 1 per cent of total forested area were excluded from the computations. The dominant forest types in the study area were maple/beech/birch (48.8%) and oak/hickory (29.8%; figure 1b).

To isolate the influences of weather, spatial proximity and forest type on the spatial synchrony of gypsy moth outbreaks, we performed multiple regression on resemblance (or distance) matrices (MRMs) [33–35]. This technique is an extension of the more widely used partial Mantel test, a procedure for determining the partial correlation between two distance or resemblance matrices while controlling for the influence of a third matrix [35,36]. MRM is used to examine relationships between a dependent distance or resemblance matrix and any number of explanatory distance or resemblance matrices. By using explanatory matrices for both spatial proximity and any measures of environmental similarity, variance in the dependent matrix can be partitioned into environmental sources or spatial sources such as dispersal. Because it may not be possible to account for all important sources of environmental variation, it is important to note that spatially structured environmental variation that is not accounted for will be attributed to purely spatial effects [35,37].

To carry out the MRM procedure, we created resemblance matrices where the elements were the similarities (synchrony, forest type similarity or spatial proximity) for all pair-wise combinations of locations. Forest type dissimilarities and geographical distances for each pair of quadrats i, j were converted to similarities (forest type similarity and spatial proximity) using the computation 1 − (distance from i to j)/(maximum distance), using Mahalanobis distances and Euclidean distances, respectively.

Following Lichstein [35], we investigated the roles of environmental versus spatial factors by fitting a ‘space model’, an ‘environment model’ and a ‘combined model’ (space + environment). The sole explanatory matrix in the space model was proximity. The environment model included the explanatory matrices for synchrony in weather (Spearman rank correlations of the scores for the two dominant components) and similarity in forest types. The combined model included all of the explanatory matrices. The use of linear models was found to be adequate based on inspection of the residuals resulting from fitting the combined model. The statistical significance of each explanatory matrix was determined by a permutation procedure appropriate for spatially structured data, whereby each observed regression coefficient was compared with a distribution of coefficients generated from 999 permutations of the dependent matrix [35]. The MRM procedure was carried out using the Ecodist package [38] running in the R language [39].

(c). Analyses of drivers of spatial synchrony in oak masting

We also examined the role of synchrony in weather and proximity on oak masting. We used time-series data on acorn production at 34 sites (figure 1a) in eastern deciduous forest derived from several field studies [40–43]. These data have been made available on the KNB Metacat server. We used only time series in which the acorns were predominantly or only from the Erythrobalanus (red oak) subgenus, because these are especially critical to the overwinter survival of granivorous rodents [44]. The source studies contain acorn abundance time series from five additional sites, but these were excluded because of insufficient temporal overlap with other sites (i.e. less than three overlapping observations). Temporal overlap in the acorn abundance data was limited to the years 1973–2000. From a 4 km² area centred on each site, we acquired monthly measures of precipitation and mean maximum and minimum temperatures from the PRISM data for 1973–2000. PCA was applied to these weather data, and we measured the synchrony in the scores for the two dominant components. We then evaluated the effects of synchrony in weather and spatial proximity on the synchrony of acorn production using MRM.

3. Results

(a). Principal component analysis on weather variables in defoliation quadrats

PCA allowed us to reduce the dimensionality of the weather data from 36 variables (three weather measures for each month: precipitation, mean maximum temperature, mean minimum temperature) to two variables composed of PC scores (see the electronic supplementary material, figure S1). These components explained 42.9 per cent and 5.8 per cent, respectively, of the variation in weather variables. Minimum and maximum monthly temperatures primarily had high loadings on the first component (figure 2a). By contrast, monthly precipitation variables tended to load onto the second component. Maximum temperature in May was an exception; it loaded heavily on both components (figure 2a).

Figure 2.

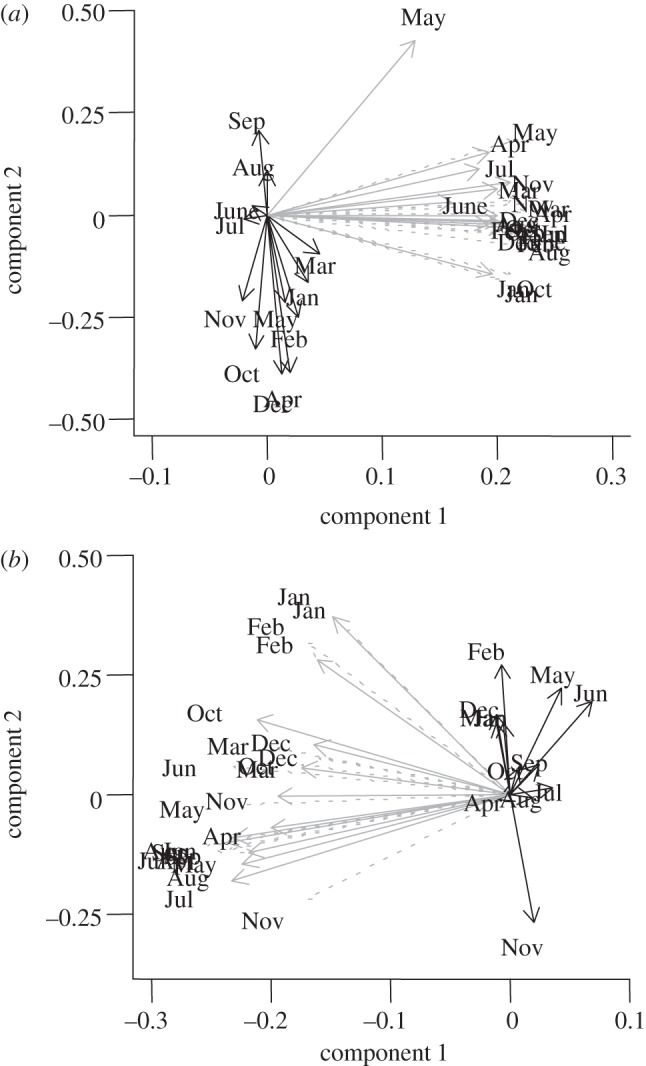
Ordination plot generated from principal component analysis of precipitation and mean maximum and minimum temperature in each month among the locations of the (a) defoliation and (b) acorn datasets. Precipitation variables are displayed with solid black lines, mean maximum temperatures with solid grey lines and mean minimum temperatures with dotted grey lines.

(b). Principal component analysis on weather variables at mast sites

PCA of the weather data at the sites of acorn abundance data resulted in retention of two PCs (see the electronic supplementary material, figure S1), which explained 32.3 per cent and 8.8 per cent of the variation in weather observations among masting sites, respectively. The interpretations of the first two components derived from the defoliation quadrats and the sites of acorn abundance data are similar; in both cases, the first component largely represented variation in monthly temperatures and the second was more associated with monthly precipitation amounts (figure 2a,b). However, minimum and maximum temperatures in autumn and winter months also loaded heavily onto the second component derived for the acorn abundance sites (figure 2b).

(c). Spatial synchrony in defoliation

Pair-wise synchrony in defoliation between quadrats was highly variable, but tended to be moderately strong (0.406 ± 0.237; mean Spearman rank correlation ± 1 s.d.). Weather was considerably more synchronous than defoliation (based on the synchrony of the first (0.847 ± 0.079) and second PCs (0.990 ± 0.845; electronic supplementary material, table S1).

In the space model, we detected significantly higher synchrony of defoliation in more proximal quadrats (table 1); however, this model explained only 10.7 per cent of the variance in the pair-wise synchrony of defoliation (figure 3a). The environment model explained more than twice as much variation in the synchrony of defoliation as the space model (figure 3a). The only significant predictor of synchrony in the environment model was synchrony in the scores for the second PC (table 1), which largely represented monthly precipitation. Forest type similarity and synchrony in the first PC scores were not significantly related to synchrony of defoliation. The combined (space + environment) model explained only slightly more variance than the environment model (figure 3a). Although proximity was a significant predictor of the synchrony of defoliation in the space model, proximity had no significant effect in the combined model (table 1). As in the environment model, the only significant predictor of the synchrony of defoliation in the combined model was synchrony in the scores for the second PC (table 1).

Table 1.

MRM results on spatial and environmental factors affecting synchrony of gypsy moth outbreaks. Significant results are shown in bold.

variable	coefficient	p
space-only model
proximity	0.456	0.001
environment-only model
synchrony in PC1 scores	0.183	0.296
synchrony in PC2 scores	1.140	0.001
forest type similarity	0.222	0.078
space + environment model
proximity	0.032	0.801
synchrony in PC1 scores	0.137	0.600
synchrony in PC2 scores	1.115	0.001
forest type similarity	0.222	0.075

Figure 3.

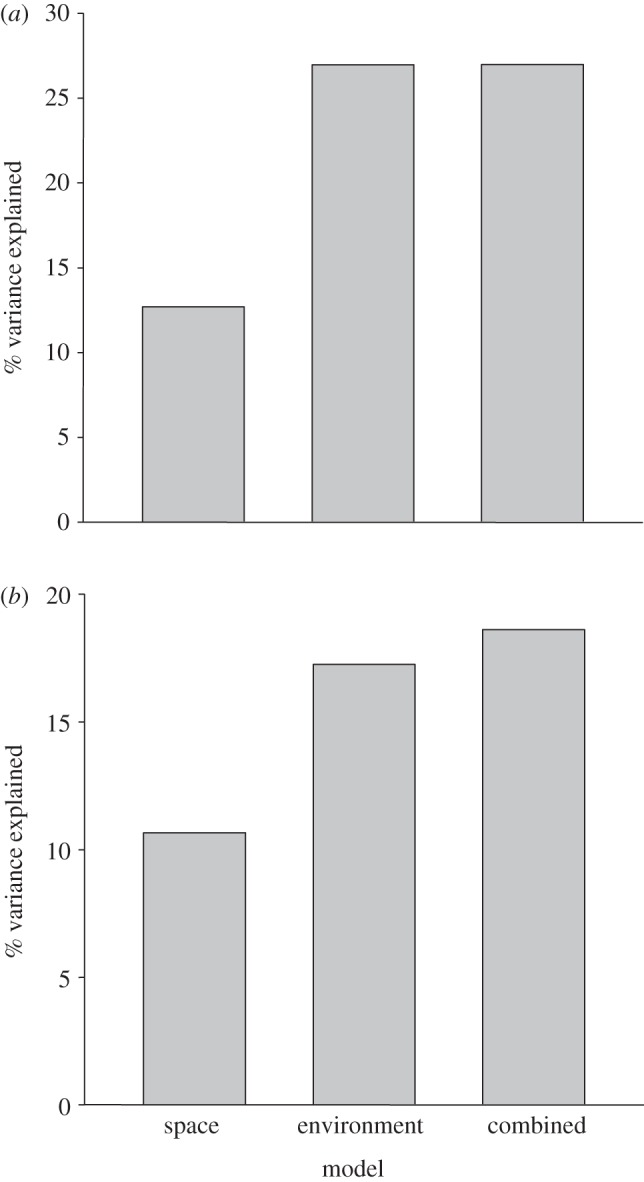
Percentages of the variation of spatial synchrony in (a) gypsy moth defoliation and (b) acorn abundance explained (based on r²) by the space, environment and combined (space + environment) MRM models.

Additional analyses to test the sensitivity of the MRM analyses to the number of PCs used to characterize weather conditions yielded qualitatively similar results when more PCs were used (see the electronic supplementary material, table S2). Analyses conducted to identify whether the seasonal timing of precipitation determines the importance of precipitation to the synchrony of gypsy moth outbreaks were somewhat uninformative, because the synchrony of precipitation in almost any month (10 of 12) was a significant predictor of defoliation synchrony (see the electronic supplementary material, table S3), probably due to collinearity of precipitation among months. Synchrony in mean maximum temperature in May was also correlated with the synchrony of gypsy moth outbreaks (see the electronic supplementary material, table S3).

(d). Spatial synchrony in oak masting

Synchrony in weather conditions between the source locations of the acorn abundance data was strong, and roughly equivalent to the synchrony in weather between defoliation quadrats (see the electronic supplementary material, table S1). The synchrony of acorn production, however, was generally weak (0.292 ± 0.307; mean Spearman rank correlation ± 1 s.d.).

Similar to our findings for defoliation, synchrony in the scores for the second PC (primarily representing rainfall) was positively correlated with synchrony in acorn production in both the environment and combined models (table 2). Proximity was also a significant predictor of synchrony in oak masting (table 2). The combined model explained substantially more variation in the synchrony of masting than both the environment and space models (figure 3b). The space model explained slightly more variation in the synchrony of acorn production than the environment model (figure 3b).

Table 2.

MRM results on spatial and environmental factors affecting synchrony in oak masting. Significant results are shown in bold.

variable	coefficient	p
space-only model
proximity	0.534	0.004
environment-only model
synchrony in PC1 scores	−0.139	0.642
synchrony in PC2 scores	2.203	0.001
space + environment model
proximity	−0.451	0.001
synchrony in PC1 scores	−0.143	0.629
synchrony in PC2 scores	3.472	0.001

4. Discussion

We present evidence that synchrony in weather is an important driver of the spatial synchrony of gypsy moth outbreaks in North America. In addition, spatial proximity appears to play no role in explaining the synchrony of gypsy moth outbreaks after synchrony of weather is taken into account. The lack of direct effects of proximity on the synchrony of gypsy moth outbreaks is a strong indication that dispersal (either by the gypsy moth or its natural enemies) is not important in the synchronization of gypsy moth populations. If dispersal were a synchronizing agent, spatial proximity should have been a significant factor even after controlling for synchrony in weather and similarity in forest type in the combined model (table 1).

Previous studies have found little evidence that gypsy moth dispersal plays a significant role in synchronizing gypsy moth populations [4,6,8]. This conclusion was based in part on the flightlessness of gypsy moth females in North America, the limited dispersal capability of larvae via ballooning (less than 200 m [27]) and limited impact of anthropogenic transport of egg masses [45]. However, theory indicates that exchanges of small numbers of individuals can lead to synchrony of distant cyclical populations [12]. Thus, low dispersal ability alone does not preclude dispersal as a driver of spatial synchrony. The results presented here appear to rule out the hypothesis that dispersal plays an important role in synchronizing gypsy moth populations.

The positive relationship between synchrony of the second PC scores and synchrony of defoliation suggests that precipitation and springtime temperature (specifically, maximum temperatures in May) may be the critical aspects of weather involved in synchronizing gypsy moth outbreaks. Although maximum May temperature loaded strongly on both the first and second PC, only synchrony in the second component showed a strong relationship with the synchrony of defoliation (table 1). Thus, precipitation may be the main aspect of weather responsible for synchronizing gypsy moth populations, despite indications that both temperature and precipitation can influence gypsy moth densities [18].

Precipitation could synchronize gypsy moth populations directly by influencing survival or reproduction, as in a Moran effect, or indirectly through effects on diseases, predators or oak masting. One potentially important indirect effect of precipitation on gypsy moth populations involves the role of rainfall in the transmission of LdNPV. An experiment using artificial rain showed that rainfall effectively transfers LdNPV from branch to branch [15]. As transmission of LdNPV occurs through larvae consuming foliage contaminated by viral particles, rainfall could potentially impact rates of virus-induced mortality. It is also possible that rainfall synchronizes gypsy moth outbreaks by affecting rates of infection by the fungal pathogen E. maimaiga. Rainfall coincident with larval development is associated with higher rates of E. maimaiga infection [16,46]. However, it is important to keep in mind that E. maimaiga was largely absent from North American gypsy moth populations prior to 1989 [47]. Alternatively, weather might indirectly synchronize gypsy moth populations through synchronization of oak masting and generalist mammalian predators that depend upon acorns for overwinter survival. This hypothesis was shown to be viable using a mechanistic model of interactions between gypsy moths, LdNPV, the white-footed mouse (the gypsy moth's main predator) and acorns (a critical food source for white-footed mice) [6]. The fact that the synchrony in precipitation seems to influence the synchrony of both gypsy moth populations and oak masting provides indirect support for this hypothesis. The acorn abundance data were obtained at sites outside the quadrats where defoliation was measured, but weather conditions were about equally synchronous where acorn production and defoliation were measured (see the electronic supplementary material, table S1), suggesting that precipitation is sufficiently synchronous within the gypsy moth's range to synchronize acorn production there. Unlike synchrony in gypsy moth populations, synchrony in oak masting also appeared to be influenced by spatial proximity. Limitation in pollen transfer among individuals is known to be capable of driving synchronous mast seeding [48,49], though its role in synchronizing oak mast seeding is not clear. The observed relationship between proximity and synchrony in acorn production suggests that spatially restricted pollen dispersal may be a significant factor in the synchronization of mast seeding in oaks.

Gypsy moth population outbreaks are known to occur at different frequencies in different forest types [17,50]. It is therefore somewhat surprising that the effect of forest type on the synchrony of gypsy moth outbreaks (coefficient = 0.222, p = 0.075; table 1) was not stronger. One possible explanation for why heterogeneity in forest type does not strongly diminish synchrony is that the period lengths with which gypsy moth populations oscillate in different forest types tend to be multiples of approximately 5 years. For example, the dominant period length of gypsy moth population cycles is approximately 5 years in oak/pine forest, and harmonic oscillations with period lengths of approximately 5 and approximately 10 years predominate in oak/hickory forest [17]. In addition, the georeferenced data on forest types across our study area are not entirely free of classification errors [29], possibly diminishing our ability to detect a significant relationship with the synchrony of defoliation.

Despite the large body of work on the importance of regional environmental perturbations to the synchrony of plant and animal populations, much of which was inspired by Moran [2], this is one of the first studies to statistically associate geographical variation in population synchrony directly with synchrony in weather. The approach adopted here provides a robust tool for isolating the drivers of population synchrony in that the effects of environmental forcing can be disentangled from non-environmental spatial processes such as dispersal. Application of this procedure more widely could significantly advance our understanding of the origins of population synchrony.