Basal metabolic rate is positively correlated with parental investment in laboratory mice

Abstract

The assimilation capacity (AC) hypothesis for the evolution of endothermy predicts that the maternal basal metabolic rate (BMR) should be positively correlated with the capacity for parental investment. In this study, we provide a unique test of the AC model based on mice from a long-term selection experiment designed to produce divergent levels of BMR. By constructing experimental families with cross-fostered litters, we were able to control for the effect of the mother as well as the type of pup based on the selected lines. We found that mothers with genetically determined high levels of BMR were characterized by higher parental investment capacity, measured as the offspring growth rate. We also found higher food consumption and heavier visceral organs in the females with high BMR. These findings suggested that the high-BMR females have higher energy acquisition abilities. When the effect of the line type of a foster mother was controlled, the pup line type significantly affected the growth rate only in the first week of life, with young from the high-BMR line type growing more rapidly. Our results support the predictions of the AC model.

1. Introduction

The ability to maintain an elevated body temperature by means of metabolic heat production (endothermy) is the most unique physiological trait of birds and mammals. The mechanism of the evolution of endothermy is still the subject of an ongoing debate. One of the recent hypotheses for the evolution of endothermy proposes parental care as the most plausible explanation for the development of this costly strategy of energy use [1–3]. According to life-history theory, the highest fitness advantage can be achieved by decreased mortality early in life rather than by a comparable decrease at an older age [4]. The most obvious way to achieve this effect is to provide parental care by feeding (e.g. foraging) and guarding the young. All these activities, however, require substantially increased locomotor performance and, thus, higher rates of daily energy expenditures over long periods (weeks or months). It has been proposed that such an intense effort can be maintained only through a higher, sustained capacity for aerobic respiration, inevitably leading to higher costs of metabolic maintenance and thus higher levels of basal metabolic rate (BMR) [1,2]. However, as assumed by the assimilation capacity (AC) hypothesis [1,2], these costs are repaid by higher growth rates and a decreased mortality of offspring. Thus, the evolutionary strategy promoting parental care should be strongly favoured by natural selection.

The amount of energy that an organism can acquire, process and/or dissipate is limited and must be divided among basic physiological processes such as maintenance, growth and reproduction. Therefore, as assumed by the principle of resource allocation, an increase in the allocation of energy to one process (e.g. maintenance) restricts the energy available for other uses [5]. It may therefore appear that individuals with high metabolic rates have less energy available for reproduction owing to their high costs of maintenance. However, high metabolic rates may reflect higher rates of biosynthesis and/or the higher costs of maintenance of enlarged internal organs essential for sustaining faster growth and perhaps higher rates of milk production [1,6–16]. If this is the case, the larger guts of individuals with a higher BMR should fuel all of the basic and additional processes and should even result in higher reproductive success. However, only a few studies succeeded in finding a positive correlation between the level of the BMR and reproductive output measured as the growth rate of the young, litter size or litter mass [7,8,10,15–21].

The AC model [1,2] assumes a genetic correlation between the amount of energy expended on parental care and maternal BMR. To test the AC model, one would therefore need to demonstrate that both traits evolved in a concerted fashion. Although the lack of applicable palaeontological data makes a direct test of the AC model impossible, the model can still be tested on extant species with the methods of experimental evolution. This approach is represented by experiments on animals subjected to artificial selection resulting in changed frequencies of alleles directly related to energy expenditure (for review [22,23]). In this study, we provide a test of the AC hypothesis with mice from a long-term divergent-selection experiment involving high basal metabolic rate (H-BMR) and low basal metabolic rate (L-BMR). Our experimental animals from the selected high-BMR line are characterized not only by higher basal metabolism but also by larger visceral organs, higher food intake and higher levels of spontaneous activity [11,24,25]. These significant between-line differences in BMR level and intestine mass are maintained even after a reproductive bout (J. Sadowska & A. K. Gębczyński 2011, unpublished data), demonstrating that these animals furnish a useful model for such studies.

If the AC model is correct, then we should be able to show that the females from the high-BMR line type have a greater capacity for parental effort/investment, i.e. these females would allocate more energy to the growth of their offspring. We also hypothesize that this increased parental investment should be matched by a higher growth rate of the pups from the H-BMR line type. Furthermore, we predict that a higher capacity for parental effort and growth of the mice from the H-BMR line type should be particularly evident under metabolically challenging environmental conditions. To test this prediction, we exposed families from both line types to a low ambient temperature (17°C) during the most energetically demanding phase of lactation.

However, a meaningful test of the AC model requires that possible differences be discriminated at the level of parental effort and in the potential for individual pup growth. Because adult animals from the H-BMR line type have a considerably higher food intake and larger guts than their L-BMR counterparts [11,24,26], it is possible that young individuals from both line types may also differ inherently with respect to developmental rate (e.g. owing to faster growth of the alimentary tract) or energy acquisition. Therefore, we created cross-fostered litters consisting of the offspring from both of the selected line types and nursed by the H-BMR or L-BMR mothers to discriminate between the effects of the mother's parental care quality and the pups' line type.

2. Material and methods

(a). Selected animals

We used outbred Swiss Webster mice from the 32nd generation of a selection experiment performed in the Institute of Biology, University of Bialystok, Poland. The experiment is based on two non-replicated lines of animals selected for high (H-BMR line) and low (L-BMR line) BMR. In subsequent generations, we maintain 30–35 families per line type. At the age of 12 weeks, three randomly chosen males and females from each family are subjected to BMR measurements. No more than two individuals per family with the highest (H-BMR line type) and lowest (L-BMR line type) body mass-corrected BMR are chosen as progenitors and mated outside their families [11,25,26].

In this study, we used 30 females, 15 from each line type originating from 25 families (in five cases, i.e. two L-BMR and three H-BMR, families were represented by two females) that were not used as progenitors of the next selective generation. The body mass-corrected BMR differed considerably between the L-BMR and H-BMR females entering the experiment (50.8 ± 0.6 and 63.6 ± 0.5 ml O₂ h⁻¹, respectively; ANCOVA, F_1,23 = 214.4, p < 0.001; body mass was significant as a covariate, F_1,4 = 202.2, p < 0.001), a difference equivalent to 3.7 phenotypic standard deviations.

(b). Experimental design

Two days after parturition, pups were individually marked (with xylene-free markers) and cross-fostered between cages. Independent of the original litter size, each female received a litter consisting of eight pups (four from the H-BMR and four from the L-BMR line type), none of which was her own offspring. The use of cross-fostered litters consisting of the offspring from both of the selected line types and nursed by the H-BMR or L-BMR mothers enabled us to discriminate between the effects of the mother's parental care quality and the pups’ line type. Litters nursed by H-BMR and L-BMR type mothers did not differ with respect to sex ratio (mean male/female ratio averaged 0.70 ± 0.06 and 0.58 ± 0.06 in litters of H-BMR and L-BMR type mothers, respectively; F_1,22 = 2.1; p = 0.159).

The families were placed in cages equipped with plastic grids. The grids allowed faeces and food remains to fall freely to the bottom of the cage. No bedding was provided during the entire experimental trial. For the first 8 days of the experiment, all families were maintained at an ambient temperature of 23°C and 12 L : 12 D photoperiod, the standard housing conditions in our mouse colony. On day 8 of the experiment, we reduced the ambient temperature to 17°C. Such conditions effectively increase the energy burden on the mothers without incurring increased risks of pup mortality owing to hypothermia [27,28]. We recorded the individual body mass of the mothers and pups every 2 days (±0.1 g) with an Ohaus Port-O-Gram electronic balance (Parsippany, NJ, USA).

(c). Food consumption, digestibility and morphometrics

The food consumption of the mother mice was estimated at the peak of lactation (days 10–14). Because the location of the food dispenser prevented the pups from nibbling, we were confident that the estimates of the mothers’ food consumption were not confounded by food ingestion by the pups. Every 2 days, we provided each mother mouse with an excessive, known amount of food (murine laboratory chow, Labofeed H, Kcynia, Poland). Every 2 days, we also collected the food remains and faeces from the bottom of the cage, then dried them and weighed them to the nearest 0.01 g. We calculated the food consumption for each adult mouse during two consecutive days as the mass of food disappearing from the food dispenser minus orts. The apparent dry matter digestibility (D) was calculated as the difference between the food intake and the faecal output, divided by food intake and multiplied by 100 per cent.

We terminated the experiment on day 14 of the pups life, as later they start to nibble solid food and no longer exclusively rely on maternal milk [29]. All females and their offspring were killed by cervical dislocation and pups were sexed. The metabolically active internal organs (the heart, liver, kidneys and intestine) were removed, cleaned of blood and food remains, weighed to the nearest 0.001 g, dried (60°C) and weighed again.

(d). Statistics

The body mass of the pups at the beginning of the experiment (second day after parturition) was analysed with an ANOVA with the pup line type as a fixed factor and the family affiliation nested within-line type as a random factor. We defined the individual growth rate of a pup as the slope of a linear regression of the individual's changes in body mass against the age of the pup. We calculated the individual slopes separately for each of the two weeks of the experiment (from the second to the eighth day and from the eighth to the 14th day after parturition). We then analysed the growth rate of the pups in each week using a mixed ANCOVA with the foster female line type and cross-fostered pup line type as fixed factors, the pup family affiliation nested within pup line type as a random factor and the individual pup body mass (on the first day of a particular experimental week) as a covariate.

In all analyses, pup sex was initially included as a main factor, however it was dropped from the final models as it was never significant (p = 0.5). In 15 cases (nine L-BMR and six H-BMR experimental families), individual pups were killed by the mothers or had to be removed from the experiment owing to abnormally slow growth. To account for these cases, we used the number of pups in the experimental litter (at the end of each experimental week) as a covariate.

We also analysed the mass gain of total litters. First, for each of the litter, we computed regression coefficients of total litter mass gains, separately in the first and second week of the experiment. We then analysed thus obtained coefficients by means of ANCOVA with female line type as a fixed factor, female family affiliation nested within the line type as a random factor and litter mass measured on the beginning of a particular experimental week as a covariate.

Female food consumption and food digestibility in consecutive days of the experiment were analysed with a repeated-measures ANCOVA, with the female line type as a fixed factor, the family affiliation nested within the female line type as a random factor, and the final litter size and female body mass as covariates. Six females (three H-BMR, three L-BMR) that killed and ate at least one of their young were excluded from the analysis.

The dry masses of the female visceral organs were analysed with an ANCOVA with the female line type as a fixed factor, the family affiliation nested within the line type as a random factor and the carcass mass as a covariate.

Assumptions of the parametric tests were verified before the tests were performed and by analysing the resulting residuals [30]. Female body mass before reproduction and initial pup body mass are reported as absolute means, whereas BMR, food consumption, digestibility, pup and total litter growth rate, as well as organ masses are presented as least square means (±s.e.m.) from the respective ANCOVA models. Statistical analyses were performed with SAS software (SAS Institute 1990, Cary, NC, USA).

Because our selection line types are not replicated, one cannot eliminate the possibility that the between-line type differences in the traits studied may be owing to genetic drift rather than a genuine effect of artificial selection. Therefore, we also analysed the differences in growth rate at both the foster mother's and pup's level separately according to Henderson's guidelines (only if the ANCOVA between-line type results were significant) [31,32]. First, we analysed the differences at the mother level by calculating the within-line type means of the analysed trait (computed from the female family averaged growth rates of all pups nursed by a given female). Then, we calculated the within-line type phenotypic standard deviations (SD's) and used them to calculate the weighted SD_X as follows:

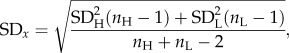2.1

where SD_H and SD_L are the phenotypic standard deviations of the studied trait X for the H-BMR and L-BMR line types, respectively, and n_H and n_L represent the number of families in particular line types. In the next step, we expressed the magnitude of separation of the two line types within the studied trait as the difference between the within-line mean values divided by the weighted phenotypic SD:

2.2

To estimate the 95% confidence intervals (CI) for d_X, we used eqn (16) from Henderson [31]:

2.3

where h² is heritability, F the inbreeding coefficient and n the number of families used in the experiment. We calculated the CIs using h² = 0.18 for growth rate in mice [33] and the inbreeding coefficient F = 0.22. We estimated F for the effective population size in our selected mouse lines according to eqn 3.6 given by Falconer & Mackay [34]. Please note that the value of F = 0.22 used therein is lower than values erroneously reported earlier for our selection experiment [11,25,26,35].

For analysis of differences at the pup level, we calculated the within-line type means of growth rate, which we computed from the pups’ original family means. We then calculated the within-line SDs, weighted SD and the magnitude of separation, as described earlier. Finally, we calculated the confidence intervals (using eqn (16) from Henderson [31]).

3. Results

(a). Female body mass and internal organs

Before reproduction, the body mass of the H-BMR and L-BMR females did not differ (H-BMR = 30.2 ± 0.7, L-BMR = 28.6 ± 0.7 g; F_1,28 = 2,8; p = 0.105). After parturition, however, the body mass was significantly higher in the H-BMR mother mice (H-BMR = 41.7 ± 0.9, L-BMR = 37.3 ± 0.8 g; F_1,28 = 13.4; p = 0.001) and remained higher until the last day of the experiment (H-BMR = 42.1 ± 1.0, L-BMR = 39.1 ± 1.0 g; F_1,28 = 4.6; p = 0.041). The primary litter size (i.e. the number of pups born) was not affected by the female line type (F_1,34 = 0.2; p = 0.683).

The masses of the visceral organs of the lactating mothers (intestine, liver, kidneys and heart, corrected for carcass mass with the ANCOVA model) were significantly affected by the female line type and heavier in the H-BMR animals (table 1).

Table 1.

ANCOVA results of dry masses of visceral organs of lactating females from the line types selected for high (H-BMR) and low (L-BMR). (Values are adjusted means (g) ± s.e.m. from the respective ANCOVAs with degrees of freedom as shown in brackets.)

	line type (1,23)	carcass mass (1,4)	H-BMR (g)	L-BMR (g)
intestine	F = 40.0, p < 0.001	F = 9.0, p = 0.040	0.711 ± 0.021	0.530 ± 0.020
liver	F = 47.4, p < 0.001	F = 55.2, p = 0.002	1.052 ± 0.016	0.897 ± 0.016
kidneys	F = 7.6, p < 0.011	F = 11.2, p = 0.029	0.172 ± 0.007	0.145 ± 0.007
heart	F = 21.1, p < 0.001	F = 3.1, p = 0.152	0.054 ± 0.001	0.045 ± 0.001

(b). Food consumption and digestibility

A repeated-measures ANCOVA showed that the females’ food consumption between the 10th and the 14th day of the experiment significantly increased in both line types in the course of the experiment (i.e. F_1,23 = 23.6; p < 0.001). The female line type (F_1,19 = 5.4; p = 0.031) and female body mass (F_1,23 = 7.9; p = 0.010) also affected the food consumption and were higher in the H-BMR line type individuals (days 10–12: H-BMR = 36.6 ± 1.0, L-BMR = 32.9 ± 1.0 g; days 12–14: H-BMR = 38.5 ± 1.0, L-BMR = 36.0 ± 1.0 g).

The food digestibility between the 10th and the 14th day did not differ between the line types (days 10–12: H-BMR = 73.2 ± 0.5%, L-BMR = 72.8 ± 0.5%; days 12–14: H-BMR = 72.9 ± 0.5%, L-BMR = 72.6 ± 0.5%; F_1,19 = 0.2; p = 0.630; see the electronic supplementary material). Moreover, it was not affected by the time course (F_1,423 = 0.9; p = 0.357) or the body mass (F_1,23 = 0.01; p = 0.921) and was only weakly affected by the litter size (F_1,23 = 4.3; p < 0.050). There was no interaction between the line type affiliation and the day of the experiment (F_1,23 = 0.04; p = 0.843).

(c). Pup growth rate

The initial pup body mass (measured on the second day of life) did not differ between the line types (H-BMR: 2.3 ± 0.1, L-BMR: 2.2 ± 0.1 g; F_1,35 = 2.4; p = 0.130). The effects of the line type of the foster mother and the initial pup body mass were significant throughout the first week (days 2–8; table 2). Irrespective of the pups’ original line type, all pups nursed by the H-BMR foster mothers had a higher body mass gain per day (table 2). However, the standardized between-mother line type difference in the offspring growth rate during the first week was smaller than that expected owing to the possible effect of genetic drift alone (d = 0.42 versus d_drift = 0.56).

Table 2.

Summary results of nested ANCOVA for pup growth rate and mean pup body mass gain per day in the first and second experimental weeks in animals selected for high (H-BMR) and low (L-BMR) BMR (adjusted means (g per day) ± s.e.m.). BM, body mass.

	female line type	pup line type	initial pup BM	litter size	H-BMR foster mother		L-BMR foster mother
					H-BMR pups (g per day)	L-BMR pups (g per day)	H-BMR pups (g per day)	L-BMR pups (g per day)
growth rate (days 2nd–8th)	F1,28 = 5.4, p = 0.028	F1,35 = 5.1, p = 0.030	F1,157 = 9.2, p = 0.003	F1,157 = 0.4, p = 0.528	0.96 ± 0.04	0.84 ± 0.04	0.89 ± 0.03	0.81 ± 0.04
growth rate (days 8th–14th)	F1,28 = 27.4, p < 0.001	F1,35 = 1.3, p = 0.262	F1,144 = 0.1, p = 0.752	F1,144 = 14.0, p < 0.001	0.35 ± 0.04	0.31 ± 0.04	0.20 ± 0.04	0.14 ± 0.04

The effect of the pups’ original line type was significant during the first week, with H-BMR pups showing a higher mass gain (table 2). The magnitude of the standardized between-line type difference suggests the presence of a genetic correlation between the pups’ growth rate and the BMR, the primary selected trait (d = 0.85 versus d_drift = 0.52). There was no interaction between the foster mother and pup line types (F_1,158 = 1.3; p = 0.256).

In the second week of the experiment (days 8–14), the body mass of the pups was significantly affected by the line type of the foster mother but not by the line type affiliation of the pups themselves (table 2 and figure 1; see the electronic supplementary material). The H-BMR mothers raised heavier offspring (table 2). There was no interaction between the female and juvenile line types F_1,144 = 0.3; p = 0.585). The standardized between-mother line type difference in offspring growth rate calculated for the second week was higher than d_drift (d = 0.64 versus d_drift = 0.56), suggesting a positive correlation between the mother's BMR and the juvenile growth rate.

Figure 1.

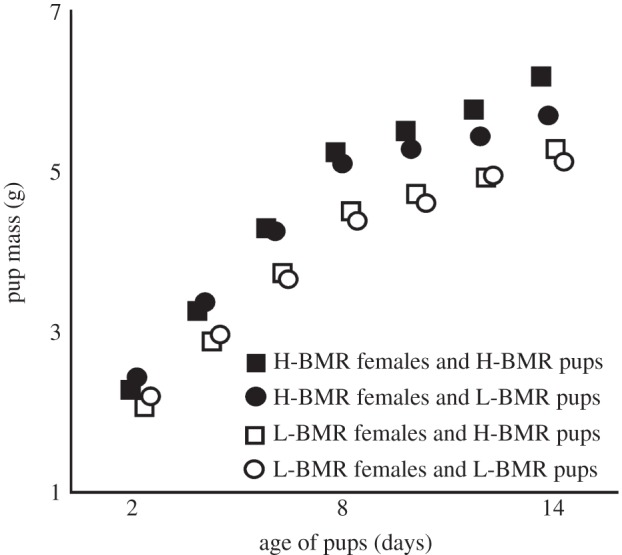
Unadjusted body mass of pups nursed by females from line types selected for high (H-BMR) and low (L-BMR) BMR. Symbols represent mean values ± s.e.m. Note that s.e.m. are smaller than symbol size in all cases.

The line type affiliation of the nursing mother did not affect the rate of the total litter mass gain during the first week of the experiment (F_1,21 = 1.5; p = 0.240). Litter mass (at the beginning of this part of the experiment) did not affect total litter mass gain (F_1,3 = 0.1; p = 0.748). In the second week, female line type significantly affected litter mass gain (F_1,21 = 9.3; p = 0.006), and the results are indicative of a genetic correlation between mother's BMR level and litter mass (d = 1.1 versus d_drift = 0.56). Litter mass (measured at the beginning of this part of the experiment) had no effect on total litter mass gain in the second week (F_1,3 = 0.3; p = 0.608).

4. Discussion

Our study demonstrated a positive correlation between the BMR of the mother mice and the parental investment capacity, measured as the growth rate of the nursed pups, after controlling for the effect of the pups’ original line type. The effect of the mother's line type on the pups’ growth rate was significant throughout the entire 14 day trial. However, it was considerably stronger during the second week of the experiment, when the energy demands of the offspring were at their maximum.

The between-line type differences in the pups’ growth rate, expressed in phenotypic SD, for the first experimental week did not indicate the presence of a genetic correlation despite the significance of the ANCOVA results at α = 0.05. It is probable that this outcome was most likely owing to a relatively low energetic load (i.e. smaller pups, warm environment), at which the H-BMR animals were not forced to use their full capacity for energy acquisition and/or milk production. Throughout the second week of our experiment, both the H- and L-BMR females suffered additional energetic costs resulting from cold exposure. As we predicted, the between-line type differences in parental investment, measured as the pup's daily body mass gain as well as total litter mass gain, were particularly prominent under those metabolically challenging conditions. This finding supports the assumptions of the AC model.

Although the body mass of the pups did not differ significantly between the line types at the beginning of our trial, we found that the H-BMR young showed a higher body mass gain than the L-BMR offspring during the first week of the experiment. Because the litters in our experiment were cross-fostered, we were able to control for the effect of the mothers’ line type and discriminate between the mothers’ parental investment capacity and the pups’ own growth abilities. Moreover, the optimal number of eight pups per experimental family [29] assured us that there was no competition between H-BMR and L-BMR offspring to access milk and that all young had sufficient time for suckling. The between-line type differences in the first week were therefore not owing to higher competitive abilities of H-BMR pups or their higher initial body mass but rather to their greater ability to acquire food and/or their higher potential for biosynthesis. It is possible that young H-BMR mice are characterized by a higher developmental rate of the alimentary tract, which enables them to fuel their more rapid growth. In a study on juvenile cotton rats, Derting [8] manipulated their rates of ‘basal’ metabolism by implanting the animals with thyroxine and demonstrated that elevated metabolic rates were correlated with higher food intake, energy assimilation and, ultimately, faster growth (body mass gain per day), compared with unmanipulated controls. Moreover, Sadowska et al. [36] found a positive correlation between post-weaning growth rate and BMR in bank voles fed a low-quality diet. These results suggest that the metabolic rate of the pups may be positively associated with the rates of energy assimilation and tissue biosynthesis.

If, however, as suggested by the resource limitation principle [5], individuals with a higher BMR are expected to have less energy available for growth or reproduction owing to their high maintenance costs, how are H-BMR mice capable of sustaining this higher parental effort? The answer may lie in different energy acquisition abilities associated with the individual BMR level. Females from the H-BMR line type have substantially larger visceral organs (table 1) and higher rates of energy turnover than L-BMR individuals. A positive association between alimentary tract morphology, maximal food intake and BMR has been well documented [37–40]. However, all the intra- and interspecific research on the relationship between BMR and parental investment capacity has analysed phenotypic correlations [7,10,14–16,18–21,41,42]. Such correlations may differ in strength (or even sign) from genetic ones [43,44] and therefore do not always provide credible information on the joint evolvability of both traits. Our study builds upon the results of a long-term artificial selection programme that caused a change in the frequencies of alleles directly related to energy expenditures and whose results are therefore useful for testing the AC model in a quantitative genetics context. Males from the H-BMR line type of our selection experiment are characterized by larger organs (intestines, liver, kidneys, heart) and a higher food consumption than L-BMR individuals of the same body mass [11,25,35]. In this study, we found that lactating adult females from the H-BMR line type have larger internal organs (e.g. liver, intestines and kidneys). This characteristic should allow the females to meet the higher requirements of growing pups. By contrast, L-BMR mothers have smaller guts and are therefore unable to provide their young with amounts of nutrients equal to those provided by H-BMR mothers.

As the energy burden increased throughout the second experimental week, food consumption increased in both line types. This finding is consistent with other studies performed on cold-stressed lactating rodents [15,20,27,45–49]. As we predicted, however, the increase was higher in the H-BMR type females. Nevertheless, the dry matter digestibility remained unaffected by the female line type, in agreement with earlier findings from studies conducted on animals from our selection experiment [11,25,26].

Several studies reported a significant increase of intestinal (as well as liver) mass in lactating female mice [18,27,42,45,47,50]. Such gut hypertrophy has also been demonstrated in other lactating rodents and is interpreted as a mechanism of allowing the mothers to cope with the high energy demands of rapidly growing offspring [18,27,45,47,50,51]. This hypertrophic effect on energy-acquiring organs (i.e. intestines, liver) is not completely reversible after lactation [52]. As those organs significantly contribute to the BMR [37], their elevated metabolic costs of maintenance during and after reproduction may explain the weak correlation between the BMR measured before and after a reproductive bout [42]. The flexibility of the gut size (and its metabolic costs of maintenance) may also explain the weak correlation between the BMR measured prior to reproduction and reproductive performance reported by many studies [7,8,10,15,17–21,41,42]. Note that in our selected line types, the between-line type differences in BMR level and organ masses do not disappear even after reproduction and remain higher in the H-BMR type females (J. Sadowska & A.K. Gębczyński 2011, unpublished data).

The experimental testing of the AC hypothesis on an extant species must recognize the effect of possible physiological constraints on parental performance and therefore on the strength of its correlation with the BMR. Hammond et al. [29] showed that limits on lactation (and thus parental investment) may not reside centrally (at the level of the energy-acquiring intestines) but may lie peripherally, within the mammary glands themselves. Simply stated, if the capacity of the mammary glands for milk production is at its maximum, then higher energy intake will not necessarily translate into higher milk production. This hypothesis has been questioned in a series of studies which demonstrated that milk production in lactating mice was inversely related to the ambient temperature [19,28,47] (for review, see [53,54]). Speakman and Krol's ‘heat dissipation limit’ (HDL) hypothesis suggests that animals are constrained by the maximal capacity to dissipate body heat. This principle implies that lactational performance may be limited neither centrally at the gut nor peripherally at the mammary gland level. However, a recent study by Valencak et al. [55] demonstrated that the HDL hypothesis may not adequately identify the limitations on mammalian parental investment. Contrary to the HDL predictions, Valencak et al. [55] showed that female European hares reached maximum energy turnover even under thermoneutral conditions. They concluded that energy expenditures in lactating European hares are not set by physiological constraints but are restricted to maximize lifetime reproductive success. Additionally, a study on striped hamsters lactating in the cold demonstrated that despite an increased food intake, they were not capable of producing milk, contradicting the assumptions of the HDL hypothesis [15]. Likewise, shaved lactating laboratory mice increased their energy intake but were not able to nurse heavier pups in comparison with non-shaved females [56]. On the other hand, McDonald & Nielsen [16] found that mice selected for high heat loss capacity achieved a higher reproductive performance (measured as litter mass and milk production) than individuals from the low heat loss line.

Regardless of the validity of the HDL hypothesis, we conducted our study under conditions that did not restrict the heat loss capacity of lactating animals, as shown by the lactation of the mice in our experiment at an ambient temperature of 17°C. Therefore, we are confident that our results provide a strong test of the AC model. We conclude that the female mice characterized by high levels of BMR achieved a higher reproductive output, measured as pup growth rate and mean pup body mass. We also demonstrated that the quality of parental care (i.e. mother type) is not the only factor determining the growth rate of the offspring. The growth ability of the pup alone also plays an important role.