Abstract
We employ quantum mechanical/molecular mechanical umbrella sampling simulations to probe the free energy surfaces of a series of increasingly complex reaction models of RNA 2’-O-transesterification in aqueous solution under alkaline conditions. Such models are valuable for understanding the uncatalyzed processes underlying catalytic cleavage of the phosphodiester backbone of RNA, a reaction of fundamental importance in biology. The chemically reactive atoms are modeled by the AM1/d-PhoT quantum model for phosphoryl transfer, whereas the aqueous solvation environment is modeled with a molecular mechanics force field. Several simulation protocols were compared that used different ionic conditions and force field models. The results provide insight into how variation of the structural environment of the nucleophile and leaving group affects the free energy profile for the transesterification reaction. Results for a simple RNA backbone model are compared with recent experiments by Harris et al. on the specific base catalyzed cleavage of a UpG dinucleotide. The calculated and measured free energies of activation match extremely well (ΔF‡ = 19.9–20.8 versus 19.9 kcal/mol). Solvation is seen to play a crucial role and is characterized by a network of hydrogen bonds that envelopes the pentacoordinate dianionic phosphorane transition state and provides preferential stabilization relative to the reactant state.
Keywords: quantum mechanics/molecular mechanics, catalysis, phosphoryl transfer, mechanism, free energy
Introduction
Cleavage of the phosphodiester backbone of RNA is an essential reaction in biology that is fundamental to many important biological processes ranging from gene splicing and regulation to viral replication and cell signaling.1 It is thus significant that several small RNA molecules, such as the hammerhead,2 hairpin,3 hepatitis delta virus,4 Varkud satellite,5 and glmS6 ribozymes, catalyze the phosphoryl cleavage of their own backbones. While the secondary and tertiary structure of these ribozymes are all distinct and their optimal ion identity and concentration requirements differ significantly, they all catalyze the same intramolecular 2’-O-transesterification reaction and form a 2’,3’-cyclic phosphate and 5’-hydroxyl as products.7–9
As with all catalytic reactions, the mechanistic features of ribozymes and protein enzymes are inherently related to their rate enhancement relative to the background rate of the non-catalytic reaction, in this case the cleavage of an RNA backbone in aqueous solution. Hence, a logical starting point for determining the key mechanistic characteristics of self-cleaving ribozymes would be to first determine the characteristics of the uncatalyzed mechanism. Indeed, there is an established literature concerning model compounds for phosphate 2’-O-transesterification,10–14 but these studies frequently focus on non-native, enhanced leaving groups,15–17 reactions perturbed by chemical markers needed for spectroscopic analysis,18 or temperature ranges far from normal biological conditions.15,19 Nonetheless, these studies provide a firm experimental baseline for comparisons between native uncatalyzed and catalyzed reactions.
Theoretical and computational approaches, particularlymolecular dynamics (MD), have emerged as a valuable tool in the study of chemical reactions because they allow access to full atomistic detail. However, the degree to which meaningful insights into mechanism can be gained from simulations relies on the accuracy of the models that are employed for the particular system under study. This leads to a natural synergistic relationship between experiment and theory, with experiment providing key benchmarks and theory providing detailed molecular level interpretations and testable predictions. This approach is well illustrated by the development of fast and accurate quantum mechanical/molecular mechanical (QM/MM) methods calibrated to specific experimental and ab initio data,20 which has opened the door for accurate tests of explicit reaction pathways, even for large biomolecules.21,22 The free energy surfaces of such pathways can be rigorously compared to experimental kinetics measurements and also have strong connections to highly sensitive mechanistic probes such as thio and isotope23 as well as mutational24 effects.
In order to rationally decompose the complexity of RNA backbone cleavage, the present work focuses on mapping the free energy profiles of a series of molecules undergoing transphosphorylation to form cyclic phosphates under basic conditions (Figure 1). The systems are akin to the simple UpG dinucleotide recently studied experimentally by Harris, et al.25 The dinucleotide UpG matches the sequence at the cleavage site of the self-cleaving hepatitis delta virus ribozyme26 and is an active substrate for ribonuclease A.27 Its cleavage mechanism in solution is therefore a valuable benchmark. In solution, the observed first order rate constant for UpG cleavage increases linearly from pH 10–13, becoming pH independent beyond that point; extrapolating to “infinite” pH gives an intrinsic rate constant of 0.06 s−−1.25 Using novel techniques,25,28 Harris, et al. also measured primary and secondary kinetic isotope effects (KIEs) for base catalyzed UpG cleavage, as well as the solvent D2O effect. The lack of any significant solvent D2O effect combined with an estimated correction for equilibrium isotope effects on the nucleophile confirms the conventionally accepted specific base mechanism. Taken together, the KIEs suggest that UpG undergoes a concerted mechanism with a “late,” product-like, transition state.
Figure 1.
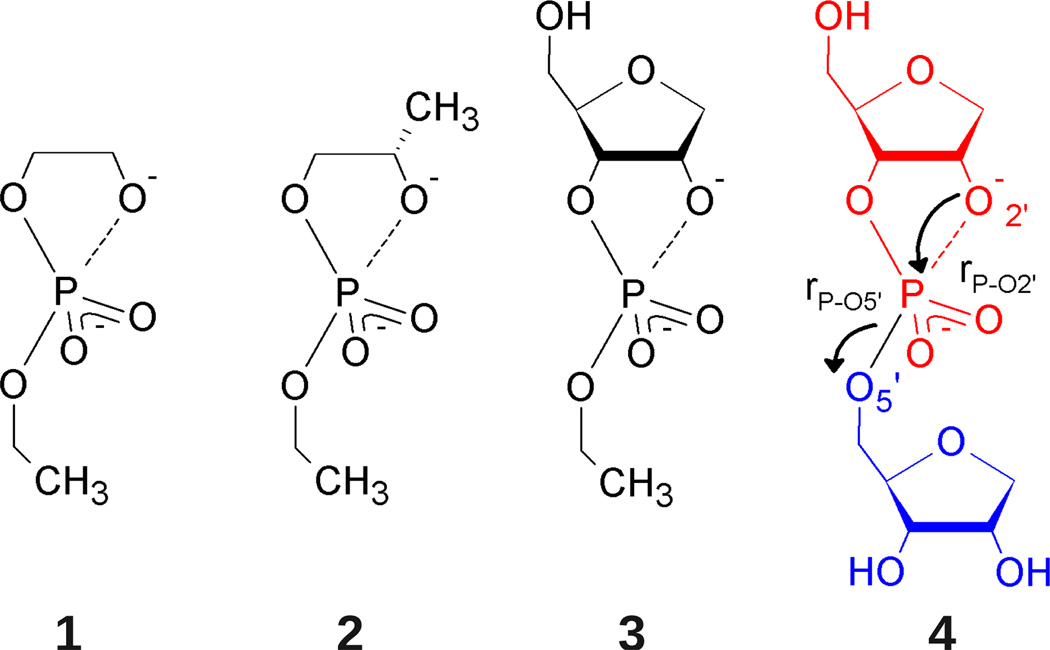
Reaction models for base-catalyzed phosphoryl transfer. Structural complexity increases from model 1 (2-hydroxy-ethyl ethyl phosphate) to model 4 (an abasic RNA dinucleotide) to bridge the gap between simple alkyl phosphates and the more complex RNA backbone. Ribose ring naming conventions are adopted for consistency such that all systems are said to undergo cleavage of the P-O5’ bond, yielding a primary alkoxide (blue), and formation of a P-O2’ bond, yielding a cyclic phosphate (red).
On the basis of QM/MM MD simulations, a theoretical free energy of activation is calculated here that allows direct comparison to the experiments of Harris, et al. The quality of the comparison begets significant confidence in also using the simulations to characterize the reactant and transition states structurally, as well as analyze the role of water and ions in the reaction. Additionally, because of the wide range of models available for (and commonly used in) QM/MM studies, the sensitivity of the results to different water models and Lennard-Jones parameters is compared and discussed.
Computational Methods
Molecular Dynamics
MD simulations were performed using the AMBER 1229 suite of programs. An integration step of either 1 or 2 fs was used depending on whether or not the SHAKE30 algorithm (tolerance = 1.0×10−8) was used to constrain bonds with hydrogen in the solute; the SETTLE31 algorithm was always used to constrain rigid water molecules. Temperature and pressure were regulated with the methods of Andersen32 (310 K, “massive” collisions every 2000 steps) and Berendsen33 (1 bar, time constant of 5 ps, compressibility = 44.6×10−6 bar−1), respectively. Long range electrostatics were treated using periodic boundary conditions in a rhombic dodecahedron cell and the particle mesh Ewald (PME) method for both molecular mechanical (MM)34,35 and QM/MM36,37 calculations. PME calculations employed 6th order B-spline interpolation with 50 grid points (≈1 point/Å) along each axis; the Ewald coefficient was chosen such that the estimated error in the direct space energy was on the order of 10−5 kcal/mol. QM/MM Ewald calculations used a reciprocal space defined by kmax = 7 and ; the QM/MM Ewald coefficient was separately chosen as 10V−1/3, where V is the cell volume in Å3 (see Supporting Information for details). Lennard-Jones and direct space Coulombic interactions were truncated at 10 Å. For the QM/MM direct space, an atom based switching function was applied between 8 and 10 Å.
All QM/MM simulations used the AM1/d-PhoT semi-empirical Hamiltonian,20 with the QM region defined as the entire solute. Lennard-Jones parameters were taken from either the AMBER FF1038–41 or CHARMM2742,43 nucleic acid force fields, with the exception of select interactions with sodiumions (see Discussion and Supporting Information). The solvent environment was modeled using either the TIP3P44 or TIP4P-Ew45 rigid water model and the associated alkali metal and halide ion parameters of Joung and Cheatham.46 Simulations contained 2,640 solvent molecules (e.g., water molecules or water molecules in approximately 140 mM NaCl, see Supporting Information).
The selected model is appropriate for several reasons and similar QM/MM models have been successfully used elsewhere in studies of both enzymatic21,22,47 and non-enzymatic48,49 phosphoryl transfer. First, AM1/d-PhoT is specifically parameterized to reproduce gas phase ab initio calculations of an extensive set of phosphate containing compounds and reactions (see Ref. 20 and 50 and the Supporting Information) and has also been shown to be the best choice for reproducing geometries and energies of penta-coordinated phosphorous systems amongst several common semi-empirical methods.51 Second, a QM/MM approach to solvation (i.e. neglecting a QM description of the solvent) is well suited for the current application since chemical participation of water (e.g. via hydrolysis or proton transfer) is not expected to occur.13,25 An intermediate description including some water in the QM region in an adaptive fashion (a necessary consequence of diffusion in a fully solvent exposed reaction) could potentially be advantageous, but such an approach is difficult to implement with smooth gradients suitable for dynamics and not yet widely available.52 Therefore, at present, a QM/MM model is expected to be preferable to a full QM description due to the vastly decreased cost needed to obtain adequate sampling and since the bulk properties of MM water models are generally superior to both semi-empirical53 and even certain ab initio quantum models.54
Umbrella Sampling
QM/MMMD umbrella sampling55 trajectories were performed along a mass weighted atom transfer coordinate, , where rA-B is the distance between atoms A and B and the factor of one half arises from the leaving group and nucleophile masses being the same (it should be noted that, in the present case, this has no effect on the thermodynamics). Although such a coordinate has been widely used in the literature, especially with regards to phosphoryl transfer reactions,21–23,47–49,56 a recent study by Rosta, et al. has suggested that the calculated free energy barrier is potentially sensitive to this choice properly capturing orthogonal chemical events such as proton transfer.57 This is not anticipated to be an issue here because the reactions take place in the high pH regime where the assumption of rapid, uncoupled deprotonation of the nucleophile is well-justified.25 The orthogonal events are thus entirely structural and not chemical (i.e. they involve solvent rearrangement).
After an extensive initial equilibration protocol (see Supporting Information) production consisted of 1 ns (2 ns for the dinucleotide system) for each window, with sampling omitting the first 250 ps for relaxation/equilibration within the window. The value of the progress coordinate was stored at 0.5 ps intervals for analysis using the multistate Bennett acceptance ratio (MBAR).58 Approximately uncorrelated data sets were obtained by subsampling configurations at intervals equal to the statistical inefficiencies, which were estimated in each simulation by direct integration of the autocorrelation function of the progress coordinate using the fast, adaptive integration scheme of Chodera, et al.59
MBAR Analysis and Free Energy Profiles
MBAR provides a general formalism for re-weighting mechanical observables for estimation in arbitrary thermodynamic states provided that the relative statistical weight in those states is known. The MBAR estimator for the expectation of an observable, 〈A〉, that depends only on the configuration, x, is given by:58
| (1) |
where M is the number of states, Nm is the number of samples from state m, f̂l is the MBAR estimate of the free energy of state l relative to an arbitrary state (here f1 ≡ 0), and ul(x) ≡ βUl(x) is the “reduced potential” characterizing state l.58,60 β and U(x) are the inverse temperature (for simplicity assumed to be the same in all states) and potential energy. This expression is quite general, but in the present context of umbrella sampling the unindexed values refer to the unbiased state and the sample configurations, xmn, are drawn from M biased states.
One method of estimating the free energy profile, F(ξ), is to estimate the marginal distribution, ρ(ξ) = 〈δ(ξ(x)−ξ)〉; the free energy profile, up to an additive constant, is then simply F(ξ) = (−1/β) ln ρ(ξ). Since the delta function is only a function in the distributional sense, an approximate estimator is needed for finite sampling. A broad class of such estimators are known in the statistics literature as kernel density estimators,61–64 and may take the following form:
| (2) |
The function K is often referred to as a kernel and the parameter h as the bandwidth. A case more common to the chemical literature is when K is an indicator function;59,65,66 this returns the familiar histogram estimator and h is recognized as the bin width, with an additional parameter defining the bin center. The results obtained with a histogram estimator are often qualitatively, and even quantitatively, similar to those obtained using a kernel density estimator. This general trend is confirmed in the present work (see Supporting Information). The marginal distribution could also be calculated using other estimators, such as those with a parametric form,67,68 although this may require slight variation of the MBAR formalism.
In order to obtain a kernel based estimator for F(ξ), Eq. (2) is substituted into Eq. (1) and the logarithm is taken:
| (3) |
As noted above, the additive constant f̂ can be arbitrarily set to zero (or any other convenient value). This work employs a standard normal kernel density estimator with the bandwidth chosen in each window as twice that given by the data based algorithm of Sheather and Jones69 (see Supporting Information), hence the bandwidth is shown to vary amongst states.
A more unusual class of observables can be defined as expectations along a coordinate ξ:
| (4) |
Note that Eq. (4) is expressed as a ratio of expectations in an unconstrained ensemble, rather than as an expectation in a constrained ensemble (i.e. the momentum conjugate to ξ is non-zero). Following a similar process as above and recognizing the denominator as being related to Eq. (3), the following estimator is obtained:
| (5) |
Note that in this context f̂ is not arbitrary, although it could be made zero in certain contexts.
All of the estimators shown here were implemented in a locally modified version of the Python MBAR implementation by Shirts and Chodera (pymbar v2.0).58 Visualization and other analyses were performed using Visual Molecular Dynamics (v1.8.7),70 particularly the VolMap plugin (default, unscaled radii, 0.5 Å resolution).
Results
Validation of QM/MM Model and Reaction Coordinate
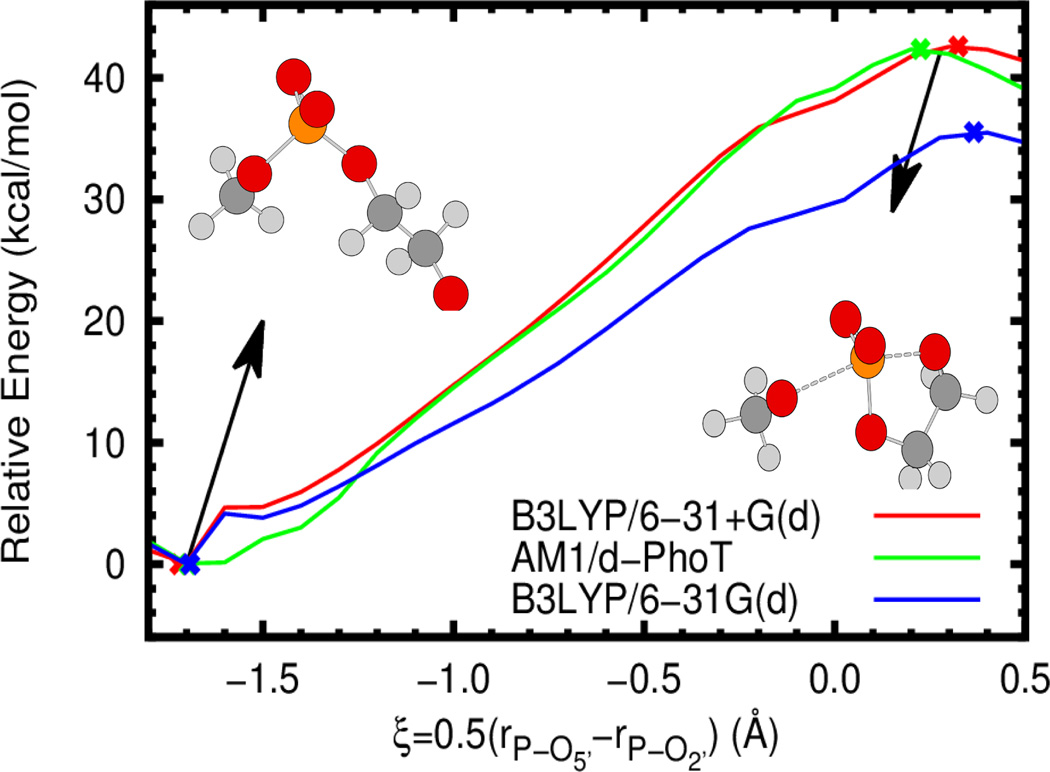
Both semi-empirical quantum methods and approximate reaction coordinates require some degree of caution when used in simulations; both can lead to significant deviation from physical behavior. In addition to the extensive validation and use in the literature of AM1/d-PhoT in conjunction with the simple atom transfer coordinate used here,21–23,47–49,56 we briefly present potential energy profiles comparing AM1/d-PhoT to standard B3LYP results as well as the reaction coordinate paths with the optimized stationary points. For simplicity, the gas phase 2’-O-transesterification reaction of 2-hydroxy ethyl phosphate (similar to model 1 in Figure 1) is considered. As is clear from Figure 2 and Table 1, AM1/d-PhoT provides excellent agreement with B3LYP/6-31+G(d), both in the energy barrier and geometry and location of minima and saddle points. In all cases, the approximate reaction coordinate correctly follows the reaction progress from reactant to product and predicts stationary points that are similar in geometry. Interestingly, B3LYP with a slightly smaller basis set (as one might consider using in QM/MM simulations due to lower cost) yields a substantial underestimate of the reaction barrier compared to both the higher basis set and AM1/d-PhoT, although the geometries are still comparable. Lastly, it is worthwhile to note that AM1/d-PhoT was actually trained and tested on even higher level results (B3LYP/6-311++G(3df,2p)//B3LYP/6-31++G(d,p)),20,50 which, at the very least, explains the existence of the minor deviations in energy and geometry visible in Figure 2.
Figure 2.
Gas phase potential energy profiles for the 2’-O-transesterification of 2-hydroxy ethyl methyl phosphate (see inset) at the B3LYP/6-31+G(d) (red), B3LYP/6-31G(d) (blue), and AM1/d-PhoT (green) levels (as implemented in Gaussian 0986 and AMBER12/AmberTools1229,37,87 respectively). The approximate reaction coordinate paths are obtained via constrained optimization at different coordinate values (using the DL-FIND library88). Crosses denote the location of optimized minima and transition states. All energies are relative to the optimized minimum at the relevant level of theory.
Table 1.
Potential energy barriers and select geometric quantities at the transition state at different levels of theory using multiple reaction coordinates. The intrinsic reaction coordinate (IRC) is defined so as exactly to connect the minimum and first order saddle point. However, the approximate reaction coordinate (ARC) used in simulations is not guaranteed to connect either point on the potential energy surface. In this case the minimum and saddle point are defined by the reduced set of coordinates. It should be noted that the ARC values are obtained under the additional approximation that , with Δξ=0.1 Å and m is some integer. Energies are in kcal/mol and lengths are in Å.
| ΔE‡ | rP-O5’,TS | rP-O2’,TS | ||
|---|---|---|---|---|
| B3LYP/6-31+G(d) | IRC | 42.6 | 2.49 | 1.84 |
| ARC | 42.5 | 2.44 | 1.84 | |
| AM1/d-PhoT | IRC | 42.4 | 2.33 | 1.88 |
| ARC | 42.3 | 2.27 | 1.87 | |
| B3LYP/6-31G(d) | IRC | 35.5 | 2.56 | 1.83 |
| ARC | 35.5 | 2.63 | 1.83 |
Free Energy Profiles and Mechanical Observables
The principle results of the present work are the free energy profiles, F(ξ), for each of the specific base catalyzed reactions calculated from umbrella sampling simulations. The values of the progress coordinate, ξ, corresponding to the reactant and transition state (ξR and ξ‡, respectively) are determined as:
| (6) |
The free energy barrier is then calculated as ΔF‡ = F(ξ‡)−F(ξR). Additionally, the averages of select mechanical observables, 〈A〉ξ, and their standard deviations, , were estimated at fixed values of the reaction coordinate [Eq. (5)].
Throughout this work the term “reaction model” is used to refer to a molecule that undergoes a reaction analogous to RNA transesterification (i.e., contains a phosphodiester that reacts to form a cyclic phosphate). The reaction models used here are illustrated and numbered in Figure 1. In QM/MM simulations of these reaction models a “force field model” must also be chosen to describe the (non-bonded) MM and QM/MM interactions between the (QM) solute and solvent. Here the force field models for the solutes take parameters from either the AMBER (A) or CHARMM (C) force fields in conjunction with solvent (water or water + NaCl) defined by the TIP3P (3) or TIP4P-Ew (4) water models. A full simulation model is then given by both a reaction model and force field model. For example, an abasic RNA dinucleotide (reaction model 4 in Figure 1) with AMBER force field parameters in a simulation cell containing TIP4P-Ew water and sodium chloride is designated as 4-A4/NaCl. All models will hereafter be referred to with this nomenclature.
Abasic Dinucleotide Models
Solvent Environments
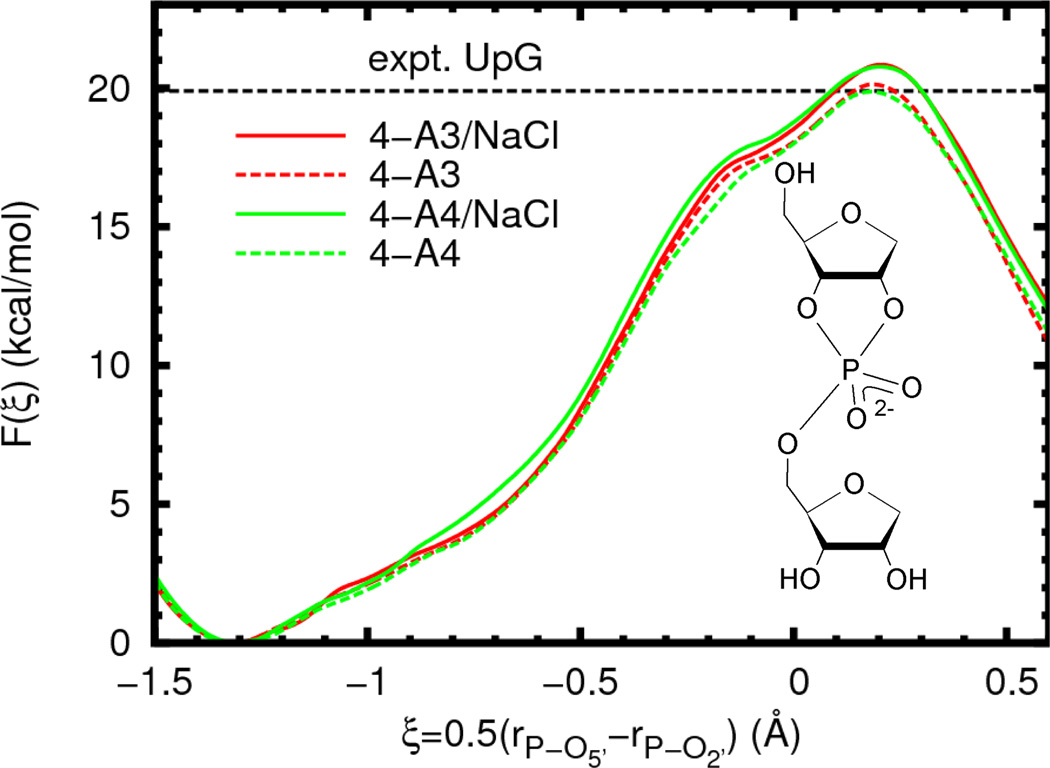
We begin by examining several possible solvation models of an abasic RNA dinucleotide, for which a wealth of experimental data is available.10,11,13,25 In particular, we examine differences in the free energy profile due to variations in the water model and ion atmosphere. The results (Figure 3, Table 2) show no statistically significant variation in the reaction barrier or geometry when the water model is changed from TIP3P to TIP4P-Ew. The removal of ions (infinite dilution limit) appears to slightly lower the barrier for both water models by the same amount, although this difference is very similar in magnitude to the estimated error (0.8 ± 0.6 kcal/mol).
Figure 3.
Free energy profiles for reaction model 4 (inset) in different solvent environments. The experimental value is given for a UpG dinucleotide (Ref. 25, 310 K and ionic strength of 1 M in NaOH/NaCl, dashed line). In order to aid visual comparison of barrier heights, the plots are shifted such that F(ξR) = 0.0. The average error bars (estimated 95% confidence interval, not shown for clarity) for all of the curves are less than 0.4 kcal/mol relative to the appropriate reactant state.
Table 2.
Free energy profile extrema and select average geometric quantities at fixed values of the reaction coordinate for reaction model 4 in different solvent environments. For barrier heights, error bars represent approximate 95% confidence intervals, for all other quantities they represent twice the population standard deviation. Energies are in kcal/mol, lengths are in Å, and angles are in degrees.
| reactant state | |||||
|---|---|---|---|---|---|
| model | ξR | ΔF‡ | 〈rP-O2’〉ξR | 〈rP-5’〉ξR | 〈θO2’-P-O5’〉ξR |
| 4-A3/NaCl | −1.31 | - | 4.27 ± 0.11 | 1.65 ± 0.06 | 95 ± 28 |
| 4-A3 | −1.31 | - | 4.27 ± 0.12 | 1.66 ± 0.06 | 97 ± 29 |
| 4-A4/NaCl | −1.30 | - | 4.26 ± 0.12 | 1.66 ± 0.06 | 94 ± 26 |
| 4-A4 | −1.31 | - | 4.28 ± 0.10 | 1.66 ± 0.06 | 90 ± 21 |
| transition state | |||||
| model | ξ‡ | ΔF‡ | 〈rP-O2’〉ξ‡ | 〈rP-O5’〉ξ‡ | 〈θO2’-P-O5’〉ξ‡ |
| 4-A3/NaCl | 0.20 | 20.8 ± 0.5 | 1.78 ± 0.08 | 2.20 ± 0.22 | 161 ± 8 |
| 4-A3 | 0.18 | 20.1 ± 0.4 | 1.78 ± 0.08 | 2.18 ± 0.22 | 162 ± 9 |
| 4-A4/NaCl | 0.20 | 20.8 ± 0.4 | 1.78 ± 0.09 | 2.19 ± 0.22 | 161 ± 9 |
| 4-A4 | 0.18 | 19.9 ± 0.4 | 1.78 ± 0.09 | 2.15 ± 0.18 | 162 ± 8 |
Solute-Solvent Interaction Models
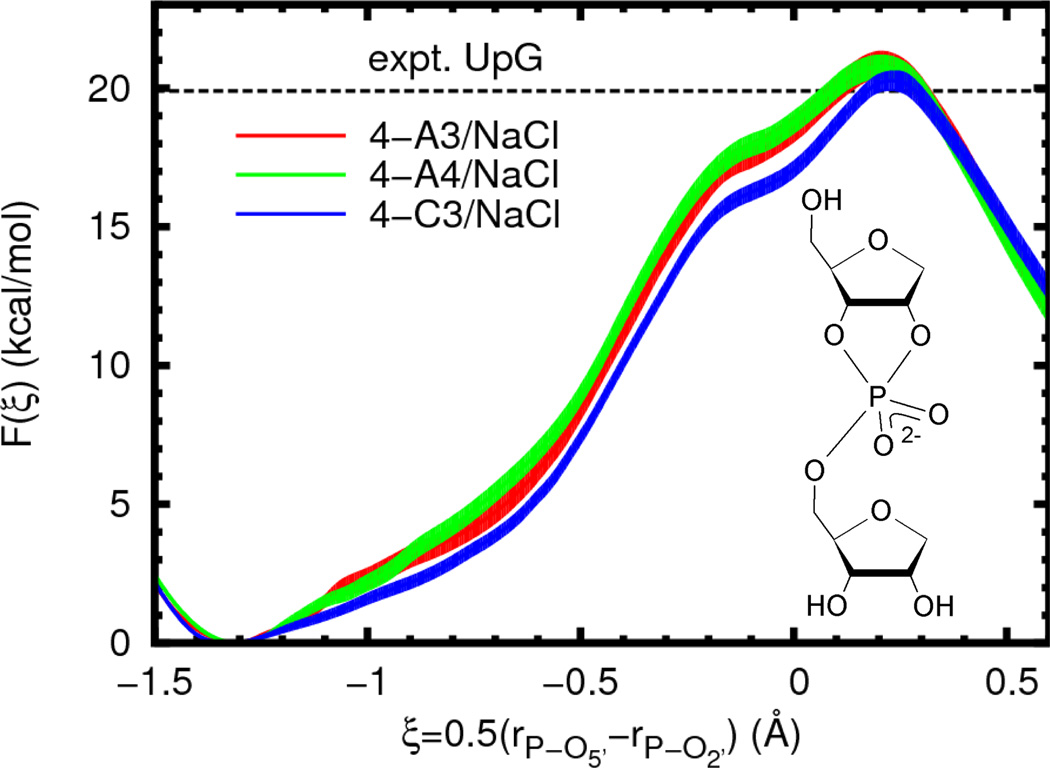
A necessary aspect of QM/MM simulations is to select a non-bonded, non-electrostatic interaction model for QM/MM interactions. Here, as is generally done, the choice is made from existing standard force field models. However, these models usually only aim to describe a fixed valence chemical structure and are thus not necessarily appropriate for describing chemical reactions.71 As an investigation of the accuracy of the models used here, we compare the free energy profiles calculated with different force field models. Three solute/solvent combinations were examined using common parameters from the AMBER and CHARMM nucleic acid force fields and the TIP3P and TIP4P-Ew rigid water models.72 A summary of these parameters is given in the Supporting Information. The free energy profiles largely display the same shape and only slight quantitative differences (Figure 4, Table 3). The change from AMBER to CHARMM Lennard-Jones parameters leads to a slight lowering of the profile between the reactant and transition states by roughly 1 kcal/mol, but without changing the reaction barrier to a statistically significant degree.
Figure 4.
Free energy profiles for reaction model 4 (inset) with different force field models in the presence of sodium chloride. The experimental value is given for a UpG dinucleotide (Ref. 25, 310 K and ionic strength of 1 M in NaOH/NaCl, dashed line). In order to aid visual comparison of barrier heights, the plots are shifted such that F(ξR) = 0.0. Filled curves represent estimated 95% confidence intervals relative to the appropriate reactant state.
Table 3.
Free energy profile extrema and select average geometric quantities at fixed values of the reaction coordinate for reaction model 4 with different force field models in the presence of sodium chloride. For barrier heights, error bars represent approximate 95% confidence intervals, for all other quantities they represent twice the population standard deviation. Energies are in kcal/mol, lengths are in Å, and angles are in degrees.
| reactant state | |||||
|---|---|---|---|---|---|
| model | ξR | ΔF‡ | 〈rP-O2’〉ξR | 〈rP-O5’〉ξR | 〈θO2’-P-05’〉ξR |
| 4-A3/NaCl | −1.31 | - | 4.27 ± 0.11 | 1.65 ± 0.06 | 95 ± 28 |
| 4-A4/NaCl | −1.30 | - | 4.26 ± 0.12 | 1.66 ± 0.06 | 94 ± 26 |
| 4-C3/NaCl | −1.32 | - | 4.29 ± 0.12 | 1.65 ± 0.06 | 95 ± 23 |
| transition state | |||||
| model | ξ‡ | ΔF‡ | 〈rP-O2’〉ξ‡ | 〈rP-05’〉ξ‡ | 〈θO2’-P-05’〉ξ‡ |
| 4-A3/NaCl | 0.20 | 20.8 ± 0.5 | 1.78 ± 0.08 | 2.20 ± 0.22 | 161 ± 8 |
| 4-A4/NaCl | 0.20 | 20.8 ± 0.4 | 1.78 ± 0.09 | 2.19 ± 0.22 | 161 ± 9 |
| 4-C3/NaCl | 0.23 | 20.3 ± 0.4 | 1.77 ± 0.08 | 2.24 ± 0.14 | 164 ± 10 |
Varying the Structural Environment of the Nucleophile and Leaving Group
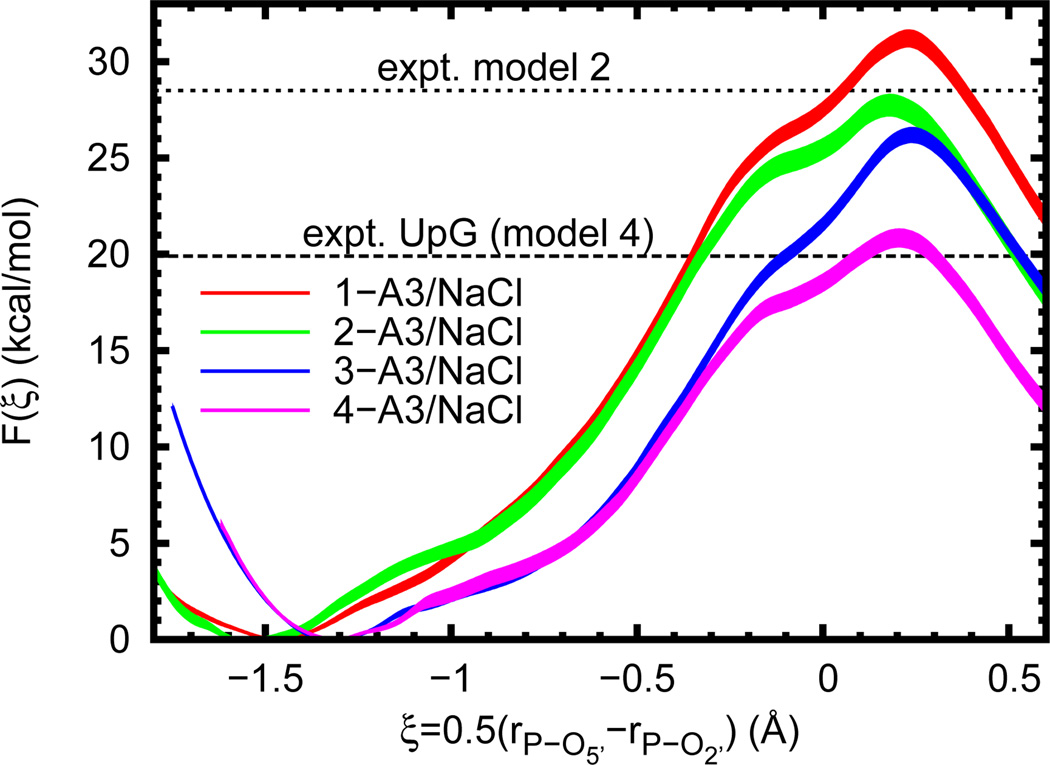
In our final analysis, a series of reaction models that undergo phosphoryl transfer were established in order to systematically dissect levels of model complexity (Figure 1). In each case the general reaction scheme is identical to that of RNA cleavage. The nucleophile is either part of a simple alkyl chain or ribose ring and the leaving group is either ethoxide or 5’-deprotonated ribose. The calculated free energy profiles (Figure 5) show the barrier magnitudes clustering into three groups depending on whether or not the nucleophile is part of a ribose ring and the size of the leaving group (, Table 4). A slightly different classification is obtained when comparing the location of the profile minimum (i.e. the reactant state); in this case the presence of a ribose ring is the most obvious factor.
Figure 5.
Free energy profiles for several reaction models (n-A3/NaCl, where n = 1–4 as in Figure 1). Experimental values are given for a UpG dinucleotide (Ref. 25, 310 K and ionic strength of 1 M in NaOH/NaCl, dashed line, for comparison to model 4) and model 2 (Ref. 15, 353 K and 0.05 N in NaOH, dotted line). In order to aid visual comparison of barrier heights, the plots are shifted such that F(ξR) = 0.0. Filled curves represent estimated 95% confidence intervals relative to the appropriate reactant state.
Table 4.
Free energy profile extrema and select average geometric quantities at fixed values of the reaction coordinate for several reaction models (n-A3/NaCl, where n = 1–4 as in Figure 1). For barrier heights, error bars represent approximate 95% confidence intervals, for all other quantities they represent twice the population standard deviation. Energies are in kcal/mol, lengths are in Å, and angles are in degrees.
| reactant state | |||||
|---|---|---|---|---|---|
| model | ξR | ΔF‡ | 〈rP-O2’〉ξR | 〈rP-O5’〉ξR | 〈θO2’-P-O5’〉ξR |
| l-A3/NaCl | −1.47 | - | 4.58 ± 0.14 | 1.65 ± 0.06 | 130 ± 42 |
| 2-A3/NaCl | −1.55 | - | 4.74 ± 0.14 | 1.65 ± 0.06 | 112 ± 60 |
| 3-A3/NaCl | −1.32 | - | 4.29 ± 0.12 | 1.65 ± 0.06 | 100 ± 33 |
| 4-A3/NaCl | −1.31 | - | 4.27 ± 0.11 | 1.65 ± 0.06 | 95 ± 28 |
| transition state | |||||
| model | ξ‡ | ΔF‡ | 〈rP-O2’〉ξ‡ | 〈rP-O5’〉ξ‡ | 〈θO2’-P-O5’〉ξ‡ |
| l-A3/NaCl | 0.23 | 31.2 ± 0.5 | 1.78 ± 0.09 | 2.22 ± 0.24 | 166 ± 9 |
| 2-A3/NaCl | 0.18 | 27.7a± 0.6 | 1.77 ± 0.08 | 2.20 ± 0.24 | 162 ± 9 |
| 3-A3/NaCl | 0.24 | 26.2 ± 0.4 | 1.77 ± 0.08 | 2.26 ± 0.33 | 164 ± 10 |
| 4-A3/NaCl | 0.20 | 20.8b± 0.5 | 1.78 ± 0.08 | 2.20 ± 0.22 | 161 ± 8 |
Discussion
Comparison with Experiment: UpG Dinucleotide
A primary motivation of this work was the recent publication by Harris, et al. of pH-rate and kinetic isotope effect data for the specific-base catalyzed cleavage of a UpG dinucleotide.25 In that work a rate constant of 0.06 ± 0.002 s−1 was extrapolated at “infinite” pH near biological conditions (310 K, ionic strength of 1 M in NaOH/NaCl).73 Applying transition state theory (and standard error propagation) then gives a free energy of activation of 19.9 ± 0.02 kcal/mol. This is important because it provides optimal comparison to the constant protonation state simulations performed here. Other experimental work has demonstrated small (< 5.0×10−4 s−1), but detectable, variations of the rate constant with respect to nucleobase sequence,14 but we do not consider these effects in the present work.
As seen in Figure 3 (and Figure 4), in all cases the agreement is very good (between 19.9 and 20.8 versus 19.9 kcal/mol), and within statistical errors. However, one must be wary that this agreement may, at least to some degree, be serendipitous. The model parameters related to solvation (water and solute Lennard-Jones parameters), which are known to influence barriers in reactions where local changes in charge state occur along the reaction coordinate as in the present example, have not been tuned for the specific reaction considered here.
The most prominent difference between the parameters of our simulations and those of experiment is the ionic strength. By necessity, experiments at high pH require high concentrations of NaOH or some other base, usually buffered with a salt.12,14,25 Such conditions have been known to be problematic in periodic boundary simulations74,75 and it was only recently that models (employed here) were developed that robustly reproduce experimental bulk behavior.46 However, “local,” solvation properties, such as binding coefficients,76 are often not well reproduced by many ion models, at least not on the time scales accessible in typical simulations. The modified sodium interactions used here (see Supporting Information) were designed to prevent direct binding of sodium to the phosphate in a minimally perturbative fashion so at least to enforce consistency across all umbrella sampling simulation, which might otherwise sample different bound conformations. This is justifiable based on the low binding coefficient between sodium and phosphates,76 but could be problematic at higher concentrations where the fraction of bound sodium ions is expected to be non-negligible. Li and Breaker have noted that the observed rate constant of base catalyzed RNA cleavage increased with increasing potassium concentration.14 However, they were only able to hypothesize that this effect was primarily due to influence on the pKa of the 2’-hydroxyl group and not on the intrinsic rate constant, as they were unable to establish simultaneously high pH and low potassium conditions. Although the system studied in that work was a DNA 22-mer with a single embedded RNA dinucleotide, the observed free energy barriers (21.5–22.5 kcal/mol, 296 K, 3.15 M K+) are reasonably close to those measured and calculated for a simple dinculeotide. The results reported here are thus, at the very least, consistent with that hypothesis. Although it is tempting to suggest that the hypothesis is supported by the lack of a catalytic effect when sodium is removed, additional data would be required, for example (as suggested by a referee) examining the concentration dependence of the nucleophile pKa or more rigorously considering sodium binding.
Free Energy Barriers and Solvent Structure
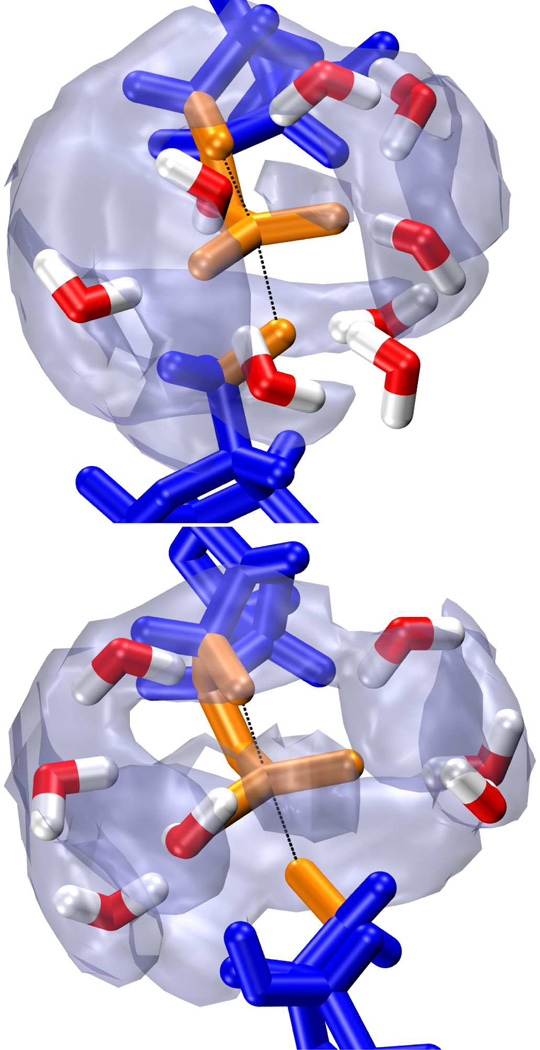
While the effects of solvation models on free energy profiles are obvious and easily compared, this does not necessarily make them an optimal metric for assessing solvation model quality. That is, there is not necessarily a direct, or even one-to-one, correspondence between empirical parameters that give the “correct” free energy barrier and those that are physically sensible. An ideal model would satisfy both criteria. As a qualitative check of the TIP3P and TIP4P-Ew water models, we examine the radial and three dimensional distribution of water molecules (or rather the water oxygens) around the phosphorane transition state (Figure 6). The results for both models are very similar, with distinct gaps of density around each of the non-bridge oxygen bond axes as well as parallel to the breaking and forming bonds (although a clear patch of density appears along the non-bridge oxygen angle bisector). Viewing a representative transition state-like configuration shows tetrahedral coordination of water around each of the non-bridge oxygens. As would be expected, the water molecules neatly reside on a density isosurface roughly corresponding to the first peak of the radial distribution function.
Figure 6.
Snapshots from umbrella sampling simulations near the transition state of model 4-A3 (top) and 4-A4 (bottom). Both transition state structures consist of a pentacoordinated phosphorane (orange) with advanced bond formation between the phosphorous and 2’ oxygen (upper black line) and bond cleavage between the phosphorous and 5’ oxygen (lower black line). This is indicative of a “late” transition state. Density maps of the water oxygens [transparent gray, isosurfaces correspond to 4πρbulkg(rmax)] indicate three distinct areas of low solvation around the phosphorane.
There have been some discussions in the literature concerning the choice of Lennard-Jones parameters for atoms in the QM region.71,77,78 Mulholland and co-workers showed that modified parameters for nucleobases in the quantum region can improve hydrogen bond geometries with MM water molecules,79 and further demonstrated that changing between a point charge and ab initio electronic density for several common rigid water models can lead to unexpected (and potentially unsatisfying) results.80 By examining extreme choices of radii and well depths, Riccardi, et al. demonstrated that both a reduction potential and proton transfer barrier, as well as hydrogen bonding interaction energies, display a systematic dependence on Lennard-Jones parameters.81 However, their conclusion was that physical accuracy (in the sense of properly balancing enthalpic and entropic effects, rather than agreement with experimental data or ab initio calculations) would be more profitably improved through other aspects of the QM/MM model.
The present work appears to support the view that simple tuning of Lennard-Jones parameters is not a fruitful avenue to producing more physically accurate free energy profiles in QM/MM simulations. However, that is not to say that the parameters cannot non-trivially affect the profile or that the expected change cannot be predicted. In the present case, although not contrived to be so, the CHARMM potential for the highly charged non-bridge oxygens have somewhat weaker repulsive components (both Lennard-Jones ε and coefficients) than the related AMBER parameters (see Supporting Information). This would seem to correlate with the near systematic lowering of the CHARMM free energy profiles in comparison to the AMBER profiles (Figure 4). That is, with identical electrostatic interactions, the CHARMM parameters allow more preferential stabilization of the dianionic transition state relative to the monoanionic phosphate and nucleophile reactants since the weaker repulsion is overwhelmed by electrostatic attraction. It is not clear as to whether this systematic behavior is desireable. For example, a more physically correct profile might possess a steeper approach to a transition state that is lower in energy, a scenario not obviously attainable by simple modification of the Lennard-Jones potentials. This suggests the merit of a different approach. Developments in our group have sought to replace the empirical Lennard-Jones potential with a more physical model that inserts directly into the QM/MM self-consistent field calculation.82,83 This would allow for charge dependent exchange and dispersion interactions and would not rely on static atom type based parameters. The potential advantage would arise from non-systematic changes in the free energy profile, thereby inserting more of the physical behavior that Riccardi, et al. found lacking.
Dependence of the Barrier on Ground State
Amongst the free energy profiles of the four different reaction models studied here, the most obvious differences are the locations of the reactant state and height of the free energy barrier (Figure 5). A comparison of the average geometries at all four reactant states (Table 4) shows nearly identical bond lengths between phosphorous and the O5’ leaving group, but quite different distances to the O2’ nucleophile. This is sensible, as the ring structure effectively prevents the secondary alkoxide from getting too far from the negatively charged phosphate, even though it would be electrostatically favorable to do so. However, when no ring is present (as in models 1 and 2) much larger separation is possible. In this case the barrier to phosphoryl transfer is effectively increased by the added conformational change. The sizable difference in the reaction barriers of models 1 and 2 (3.5 ± 0.8 kcal/mol) is likely explained by differing solvation of the nucleophiles. That is, in principle, the additional methyl substituent on model 2 should stabilize the alkoxide more than in model 1, thereby lowering the energy of the (deprotonated) reactant state and raising the barrier. However, this is clearly not the case. The dominating effect is the increased solvent exposure of the primary alkoxide due to the presence of fewer substituents. It therefore experiences a higher energetic cost when moving towards the transition state and thus a higher reaction barrier.
Near the transition state, all four models are strikingly similar both in the shape of the free energy profile and in the average geometry (Table 4). The exception to this is model 3, which has a slightly longer bond breaking distance (rP-O5’), as well as a “looser” bonding environment, as indicated by increased fluctuations. This variation is not enough, however, to change the classification of the transition state; the progressed bond breakage in all of the models clearly indicates a “late” transition state characterized by a nearly fully formed bond with the nucleophile, and a nearly fully broken bond to the leaving group. However, unlike the difference between the reaction barriers of models 1 and 2, the difference between models 3 and 4 (5.4 ± 0.6 kcal/mol) seems more anomalous. The obvious departure point for examining this is the nature of the leaving groups. In the current AM1/d-PhoT QM model, the gas-phase proton affinities of these compounds are quite dissimilar (ΔΔHPA = ΔHPA,EtOH − ΔHPA,5’-ribose ≈ 18 kcal/mol) and indicative of a higher cost to remove the ethoxide leaving group (if one is willing to assume the solvation properties are not too different). This rather dramatic difference also seems to be semi-quantitatively in line with high level density functional theory (DFT) calculations84 (ΔΔHPA ≈ 10 – 16 kcal/mol). However, a DFT model using continuum solvation similar to 3 was also recently shown to give a free energy barrier in very close agreement with that for an RNA dinucleotide,85 implying that the present result is in fact anomalous, but for reasons other than the proton affinity difference. Because of the reasonable agreement of models 2 and 4 with experimental results, we suspect that there is an imbalance of solvent effects when the nucleophile is large and the leaving group is small. This is in line with the clear importance of solute/solvent and QM/MM interactions and allows for the results for model 3 to be seen as anomalous.
Conclusion
A significant aspect of understanding enyzmatic mechanism is understanding the nature of rate enhancement over the native (solution) mechanism. In this work we have studied several variants of non-enzymatic phosphoryl transfer, a reaction catalyzed by a wide range of proteins and the most ubiquitous amongst known ribozymes. Using QM/MM MD umbrella sampling simulations, the free energy profiles were calculated along a simple atom transfer coordinate.
The calculated barrier for an abasic dinucleotide agrees almost exactly with the experimental result for the UpG dinucleotide under similar conditions. Analysis of the transition state structure indicates a “late” transition state, also in agreement with inferences from the experimental kinetic isotope effects. Although ionic conditions are a necessity of most high pH experiments, removing all monovalent ions did not lead to any significant change in the barrier. However, it should be noted that the model used here effectively precluded the possibility of direct coordination of cations to the phosphate. The obvious corollary to this result is that changes in the rate constant observed in conjunction with changes in ionic environment are likely due to the types of coordination neglected here. Such coordination is likely to be electrostatically favorable, but will come at the cost of disrupting extensive hydrogen bond networks surrounding the dianionic transition state if it occurs at the non-bridge oxygens.
The conclusions made here are strengthened by extensive testing of the available QM/MM models, including the commonly used TIP3P and TIP4P-Ew water models, as well as Lennard-Jones parameters from the AMBER FF10 and CHARMM27 force fields. Changing any one of these aspects of the model also does not lead to substantial change in the calculated reaction barrier. This does not suggest that these parameters are not important, as it has been demonstrated previously by our group and others that free energy profiles involving local changes in charge are highly sensitive to solvation and Lennard-Jones parameters. Rather, the combinations of parameters examined here appear to be similarly balanced in terms of overall solvation.
The structural complexity of the leaving group and nucleophile has a subtle effect on the structure of the transition state, and a significant effect on the magnitude of the free energy barrier. This is most evident according to the presence or absence of a ribose ring, which acts to constrain the degree of separation between the deprotonated nucleophile and monoanionic phosphate in the reactant state. Lastly, improper balancing of model pKas for the nucleophile and leaving group can lead to abnormally disparate reaction barriers and should be considered when embedding QM regions into larger systems such as ribozymes. Next-generation models that are able to consider adjustments of non-electrostatic non-bonded interactions as a function of local charge are likely to considerably improve the robustness of QM/MM simulations for chemical reactions or processes that involve charge migration or change of local charge state.
Supplementary Material
Acknowledgement
The authors are grateful for financial support provided by the National Institutes of Health (GM62248 to DY, GM096000 to MH), as well as for the use of computational resources from the Minnesota Supercomputing Institute for Advanced Computational Research. This research was also partially supported by the National Science Foundation through TeraGrid resources provided by Ranger at TACC and Kraken at NICS under grant number TG-CHE100072.
Footnotes
Supporting Information Available
A more detailed description of the umbrella sampling simulation protocol and data analysis is provided. The Lennard-Jones parameter sets used here are also described and discussed. Finally, a brief assessment of the kernel density estimation approach is given along with comparisons to the more conventional histogram approach. This material is available free of charge via the Internet at http://pubs.acs.org/.
Notes and References
- 1.Nelson DL, Cox MM. In: Lehninger Principles of Biochemistry. 4th Edition. Freeman WH, editor. New York, NY: 2005. [Google Scholar]
- 2.Prody GA, Bakos JT, Buzayan JM, Schneider IR, Bruening G. Science. 1986;231:1577–1580. doi: 10.1126/science.231.4745.1577. [DOI] [PubMed] [Google Scholar]
- 3.Buzayan JM, Gerlach WL, Bruening G. Proc. Natl. Acad. Sci. USA. 1986;83:8859–8862. doi: 10.1073/pnas.83.23.8859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sharmeen L, Kuo MY, Dinter-Gottlieb G, Taylor J. J. Virol. 1988;62:2674–2679. doi: 10.1128/jvi.62.8.2674-2679.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Saville BJ, Collins RA. Cell. 1990;61:685–696. doi: 10.1016/0092-8674(90)90480-3. [DOI] [PubMed] [Google Scholar]
- 6.Winkler WC, Nahvi A, Roth A, Collins JA, Breaker RR. Nature. 2004;428:281–286. doi: 10.1038/nature02362. [DOI] [PubMed] [Google Scholar]
- 7.Scott WG. Curr. Opin. Struct. Biol. 2007;17:280–286. doi: 10.1016/j.sbi.2007.05.003. [DOI] [PubMed] [Google Scholar]
- 8.Harris ME, Cassano AG. Curr. Opin. Chem. Biol. 2008;12:626–639. doi: 10.1016/j.cbpa.2008.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ferré-D’Amaré AR, Scott WG. Cold Spring Harb Perspect Biol. 2010;2:a003574. doi: 10.1101/cshperspect.a003574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Koike T, Inoue Y. Chem. Lett. 1972;1:569–572. [Google Scholar]
- 11.Anslyn E, Breslow R. J. Am. Chem. Soc. 1989;111:4473–4482. [Google Scholar]
- 12.Järvinen P, Oivanen M, Lönnberg H. J. Org. Chem. 1991;56:5396–5401. [Google Scholar]
- 13.Oivanen M, Kuusela S, Lönnberg H. Chem. Rev. 1998;98:961–990. doi: 10.1021/cr960425x. [DOI] [PubMed] [Google Scholar]
- 14.Li Y, Breaker RR. J. Am. Chem. Soc. 1999;121:5364–5372. [Google Scholar]
- 15.Brown DM, Usher DA. J. Chem. Soc. 1965;87:6558–6564. [Google Scholar]
- 16.Usher DA, Richardson DI, Jr, Oakenfull DG. J. Am. Chem. Soc. 1970;92:4699–4712. doi: 10.1021/ja00718a037. [DOI] [PubMed] [Google Scholar]
- 17.Davis AM, Hall AD, Williams A. J. Am. Chem. Soc. 1988;110:5105–5108. [Google Scholar]
- 18.Hengge AC, Bruzik KS, Tobin AE, Cleland WW, Tsai MD. Bioorg. Chem. 2000;28:119–133. doi: 10.1006/bioo.2000.1170. [DOI] [PubMed] [Google Scholar]
- 19.Oivanen M, Mikhailov SN, Padyukova NS, Lönnberg H. J. Org. Chem. 1993;58:1617–1619. [Google Scholar]
- 20.Nam K, Cui Q, Gao J, York DM. J. Chem. Theory Comput. 2007;3:486–504. doi: 10.1021/ct6002466. [DOI] [PubMed] [Google Scholar]
- 21.Nam K, Gao J, York DM. J. Am. Chem. Soc. 2008;130:4680–4691. doi: 10.1021/ja0759141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wong KY, Lee TS, York DM. J. Chem. Theory Comput. 2011;7:1–3. doi: 10.1021/ct100467t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wong K-Y, Gu H, Zhang S, Piccirilli JA, Harris ME, York DM. Angew. Chem. Int. Ed. 2012;51:647–651. doi: 10.1002/anie.201104147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lee T-S, York DM. J. Am. Chem. Soc. 2010;132:13505–13518. doi: 10.1021/ja105956u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Harris ME, Dai Q, Gu H, Kellerman DL, Piccirilli JA, Anderson VE. J. Am. Chem. Soc. 2010;132:11613–11621. doi: 10.1021/ja103550e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tanner NK, Schaff S, Thill G, Petit-Koskas E, Crain-Denoyelle AM, Westhof E. Curr. Biol. 1994;4:488–498. doi: 10.1016/s0960-9822(00)00109-3. [DOI] [PubMed] [Google Scholar]
- 27.Vitagliano L, Merlino A, Zagari A, Mazzarella L. Protein Sci. 2000;9:1217–1225. doi: 10.1110/ps.9.6.1217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dai Q, Frederiksen JK, Anderson VE, Harris ME, Piccirilli JA. J. Org. Chem. 2008;73:309–311. doi: 10.1021/jo701727h. [DOI] [PubMed] [Google Scholar]
- 29.Case DA, et al. AMBER 12. San Francisco, CA: University of California, San Francisco; 2012. [Google Scholar]
- 30.Ryckaert JP, Ciccotti G, Berendsen HJC. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 31.Miyamoto S, Kollman PA. J. Comput. Chem. 1992;13:952–962. [Google Scholar]
- 32.Andersen HC. J. Chem. Phys. 1980;72:2384–2393. [Google Scholar]
- 33.Berendsen HJC, Postma JPM, van Gunsteren WF, Dinola A, Haak JR. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 34.Darden T, York D, Pedersen L. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 35.Essmann U, Perera L, Berkowitz ML, Darden T, Hsing L, Pedersen LG. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 36.Nam K, Gao J, York DM. J. Chem. Theory Comput. 2005;1:2–13. doi: 10.1021/ct049941i. [DOI] [PubMed] [Google Scholar]
- 37.Walker RC, Crowley MF, Case DA. J. Comput. Chem. 2008;29:1019–1031. doi: 10.1002/jcc.20857. [DOI] [PubMed] [Google Scholar]
- 38.Cornell WD, Cieplak P, Bayly CI, Gould IR, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 39.Wang J, Cieplak P, Kollman PA. J. Comput. Chem. 2000;21:1049–1074. [Google Scholar]
- 40.Pérez A, Marchán I, Svozil D, Šponer J, Cheatham TE, III, Laughton CA, Orozco M. Biophys. J. 2007;92:3817–3829. doi: 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zgarbová M, Otyepka M, Šponer J, Mládek A, Banáš P, Cheatham TE, III, Jurečka P. J. Chem. Theory Comput. 2011;7:2886–2902. doi: 10.1021/ct200162x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Foloppe N, MacKerell AD., Jr J. Comput. Chem. 2000;21:86–104. [Google Scholar]
- 43.MacKerell AD, Jr, Banavali NK. J. Comput. Chem. 2000;21:105–120. [Google Scholar]
- 44.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 45.Horn HW, Swope WC, Pitera JW, Madura JD, Dick TJ, Hura GL, Head-Gordon T. J. Chem. Phys. 2004;120:9665–9678. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 46.Joung IS, Cheatham TE., III J. Phys. Chem. B. 2008;112:9020–9041. doi: 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.López-Canut V, Martí S, Bertrán J, Moliner V, Tuñón I. J. Phys. Chem. B. 2009;113:7816–7824. doi: 10.1021/jp901444g. [DOI] [PubMed] [Google Scholar]
- 48.Nam K, Gao J, York DM. In: Multiscale Simulation Methods for Nanomaterials. Ross RB, Mohanty SS, editors. John Wiley & Sons Inc.; 2008. pp. 201–218. [Google Scholar]
- 49.López-Canut V, Ruiz-Pernía J, Tuñón I, Ferrer S, Moliner V. J. Chem. Theory Comput. 2009;5:439–442. doi: 10.1021/ct800470f. [DOI] [PubMed] [Google Scholar]
- 50.Giese TJ, Gregersen BA, Liu Y, Nam K, Mayaan E, Moser A, Range K, Nieto Faza O, Silva Lopez C, Rodriguez de Lera A, Schaftenaar G, Lopez X, Lee T, Karypis G, York DM. J. Mol. Graph. Model. 2006;25:423–433. doi: 10.1016/j.jmgm.2006.02.011. [DOI] [PubMed] [Google Scholar]
- 51.Marcos E, Anglada JM, Crehuet R. Phys. Chem. Chem. Phys. 2008;10:2442–2450. doi: 10.1039/b719792f. [DOI] [PubMed] [Google Scholar]
- 52.Park K, Götz AW, Walker RC, Paesani F. J. Chem. Theory Comput. 2012;8:2868–2877. doi: 10.1021/ct300331f. [DOI] [PubMed] [Google Scholar]
- 53.Monard G, Bernal-Uruchurtu MI, van der Vaart A, Merz KM, Jr, Ruiz-López MF. J. Phys. Chem. A. 2005;109:3425–3432. doi: 10.1021/jp0459099. [DOI] [PubMed] [Google Scholar]
- 54.Yoo S, Zeng XC, Xantheas SS. J. Chem. Phys. 2009;130:221102. doi: 10.1063/1.3153871. [DOI] [PubMed] [Google Scholar]
- 55.Torrie GM, Valleau JP. J. Comput. Phys. 1977;23:187–199. [Google Scholar]
- 56.Rosta E, Nowotny M, Yang W, Hummer G. J. Am. Chem. Soc. 2011;133:8934–8941. doi: 10.1021/ja200173a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rosta E, Woodcock HL, Brooks BR, Hummer G. J. Comput. Chem. 2009;30:1634–1641. doi: 10.1002/jcc.21312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Shirts MR, Chodera JD. J. Chem. Phys. 2008;129:124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Chodera JD, Swope WC, Pitera JW, Seok C, Dill KA. J. Chem. Theory Comput. 2007;3:26–41. doi: 10.1021/ct0502864. [DOI] [PubMed] [Google Scholar]
- 60.Bennett CH. J. Comput. Phys. 1976;22:245–268. [Google Scholar]
- 61.Rosenblatt M. Annal. Math. Statist. 1956;27:832–837. [Google Scholar]
- 62.Parzen E. Annal. Math. Statist. 1962;33:1065–1076. [Google Scholar]
- 63.Silverman B. Density Estimation for Statistics and Data Analysis. New York: Chapman and Hall; 1986. [Google Scholar]
- 64.Wand M, Jones M. Kernel Smoothing. Chapman and Hall; Boca Raton, FL: 1995. [Google Scholar]
- 65.Kumar S, Bouzida D, Swendsen R, Kollman P, Rosenberg J. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 66.Souaille M, Roux B. Comput. Phys. Commun. 2001;135:40–57. [Google Scholar]
- 67.Kästner J, Thiel W. J. Chem. Phys. 2005;123:144104. doi: 10.1063/1.2052648. [DOI] [PubMed] [Google Scholar]
- 68.Maragakis P, van der Vaart A, Karplus M. J. Phys. Chem. B. 2009;113:4664–4673. doi: 10.1021/jp808381s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Sheather SJ, Jones MC. J. R. Statist. Soc. B. 1991;53:683–690. [Google Scholar]
- 70.Humphrey W, Dalke A, Schulten K. J. Mol. Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 71.Ridder L, Mulholland AJ. Curr. Top. Med. Chem. 2003;3:1241–1256. doi: 10.2174/1568026033452005. [DOI] [PubMed] [Google Scholar]
- 72.For consistency with the ion parameters the modified TIP3P model commonly used with the CHARMM force field is not employed here. Since the present purpose is simply to test whether and to what extent the models lead to different results (not to evaluate their relative quality) this potentially improper use should not be of consequence.
- 73.The fitting error on this quantity was not reported in the original publication.
- 74.Auffinger P, Cheatham TE, III, Vaiana AC. J. Chem. Theory Comput. 2007;3:1851–1859. doi: 10.1021/ct700143s. [DOI] [PubMed] [Google Scholar]
- 75.Chen AA, Pappu RV. J. Phys. Chem. B. 2007;111:11884–11887. doi: 10.1021/jp0765392. [DOI] [PubMed] [Google Scholar]
- 76.Haake P, Prigodich RV. Inorg. Chem. 1984;23:457–462. [Google Scholar]
- 77.Bash PA, Ho LL, MacKerell AD, Jr, Levine D, Hallstrom P. Proc. Natl. Acad. Sci. USA. 1996;93:3698–3703. doi: 10.1073/pnas.93.8.3698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Tu Y, Laaksonen A. J. Chem. Phys. 1999;111:7519–7525. [Google Scholar]
- 79.Pentikäinen U, Shaw KE, Senthilkumar K, Woods CJ, Mulholland AJ. J. Chem. Theory Comput. 2009;5:396–410. doi: 10.1021/ct800135k. [DOI] [PubMed] [Google Scholar]
- 80.Shaw KE, Woods CJ, Mulholland AJ. J. Phys. Chem. Lett. 2010;1:219–223. [Google Scholar]
- 81.Riccardi D, Li G, Cui Q. J. Phys. Chem. B. 2004;108:6467–6478. doi: 10.1021/jp037992q. [DOI] [PubMed] [Google Scholar]
- 82.Giese TJ, York DM. J. Chem. Phys. 2007;127:194101. doi: 10.1063/1.2778428. [DOI] [PubMed] [Google Scholar]
- 83.Giese TJ, York DM. Theor. Chem. Acc. 2012;131:1145. doi: 10.1007/s00214-012-1145-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Moser A, Range K, York DM. J. Phys. Chem. B. 2010;114:13911–13921. doi: 10.1021/jp107450n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Gu H, Zhang S, Wong K, Radak BK, Dissanayake T, Kellerman DL, Dai Q, Miyagi M, Anderson VE, York DM, Piccirilli JA, Harris ME. doi: 10.1073/pnas.1215086110. Submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Frisch MJ, et al. Gaussian 09, Revision A.02. Wallingford, CT: Gaussian, Inc.; 2009. [Google Scholar]
- 87.Lee T, Götz AW, Giese TJ, Radak ER, anda Kuechler Brian K, Brozell SR, Crowley MF, Case DA, Walker RC, York DM. In Preparation. [Google Scholar]
- 88.Kästner J, Carr JM, Keal TW, Thiel W, Wander A, Sherwood P. J. Phys. Chem. A. 2009;113:11856–11865. doi: 10.1021/jp9028968. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.