Incorporating scientific knowledge into phenotype development: Penalized latent class regression

Abstract

The field of psychiatric genetics is hampered by the lack of a clear taxonomy for disorders. Building on the work of Houseman and colleagues (Feature-specific penalized latent class analysis for genomic data. Harvard University Biostatistics Working Paper Series, Working Paper 22, 2005), we describe a penalized latent class regression aimed at allowing additional scientific information to influence the estimation of the measurement model, while retaining the standard assumption of non-differential measurement.

In simulation studies, ridge and LASSO penalty functions improved the precision of estimates and, in some cases of differential measurement, also reduced bias. Class-specific penalization enhanced separation of latent classes with respect to covariates, but only in scenarios where there was a true separation. Penalization proved to be less computationally intensive than an analogous Bayesian analysis by a factor of 37.

This methodology was then applied to data from normal elderly subjects from the Cache County Study on Memory and Aging. Addition of APO-E genotype and a number of baseline clinical covariates improved the dementia prediction utility of the latent classes; application of class-specific penalization improved precision while retaining that prediction utility. This methodology may be useful in scenarios with large numbers of collinear covariates or in certain cases where latent class model assumptions are violated. Investigation of novel penalty functions may prove fruitful in further refining psychiatric phenotypes.

1. Introduction

In order to show an association between a genotype and a disorder, one must first define that disorder. Traditionally, psychiatric diagnoses have been based predominantly on presentation [2], but it is possible that etiologically or genetically relevant subgroups exist within groups of patients with the same diagnosis. The goal is then to ‘carve nature at its joints’ [3] and to produce phenotypic definitions that are as distinct as possible from one another, for the purposes of identifying risk factors or etiologies specific to each phenotype.

Toward that end, it may be appropriate to model psychiatric phenotypes (diagnoses) as latent variables. Latent variable models typically consist of a measurement model, which relates the latent variable to its observed indicators, and a structural model, which relates the latent variable to other variables (e.g. genotypes) [4]. Methods exist to simultaneously estimate the measurement and structural models [5], but assumptions imposed by the model may result in distorted phenotypic definitions that, if used to classify individuals, would produce subgroups that were not etiologically or genetically relevant. We believe it is possible to improve on such phenotypic definitions by including additional substantive information in the model. This paper will describe an adaptation to the latent class regression model that seeks to ‘reconcile’ standard internally validating assumptions with scientifically motivated criteria through the use of penalization.

A penalized latent class model has been developed, but is distinct from the model described here in both its aim and its form. Houseman and colleagues [6] describe a model for use with genomic data, where the number of variables (indicators) is large relative to the sample size. Their work penalizes parameters of the measurement model, whereas we aim to penalize parameters of the structural model. This form of penalization requires different estimating algorithms. Most importantly, the approach of Houseman and colleagues has the primary goal of regularization, that is, achieving estimation that would have been intractable otherwise given the large-p-small-n structure of their data. Our goal is the development of a new approach to defining latent states that can be focused on validation, not only on feasibility.

2. Methods

2.1. Latent class regression model

The problem described in the introduction involves relating a gene (or other biomarkers) to a psychiatric (latent) phenotype. The categorical nature of psychiatric diagnoses and their observed indicators (typically whether or not a particular symptom is present) suggests the use of latent class analysis. Let Y_i =(Y_i1,…,Y_{i M})’ denote a vector of M dichotomous observed indicators for the ith of n individuals in a sample. It is assumed that the indicators are not independent within individuals, but that any dependence is ‘explained’ after conditioning upon individuals’ membership (C_i = j) in exactly one of J latent classes. This assumption is referred to as conditional independence [7]. Letting = η_j =Pr[C_i = j] and π_mj =Pr[Y_im = y|C_i = j], we have the following distribution of Y (1) as the standard latent class analysis model [5].

$$\mathrm{Pr}[Y_{i1}=y_1,\dots ,Y_{iM}=y_M]=\sum _{j=1}^J{\eta }_j\prod _{m=1}^M{\pi }_{m_j}^{y_m}{(1-{\pi }_{\mathit{mj}})}^{1-y_m}$$ (1)

The next step is to incorporate predictors of the latent phenotype. Letting η_j(x_i’β) denote the mean model of a regression of latent class membership (a polytomous variable representing psychiatric phenotype) on a P×1 vector of covariates for the ith individual (x_i’), where β=(β₁’,…,β_J’)’, we have the following log-likelihood function (2) for the standard latent class regression model [5], with η(ν) typically

$$L_i(\pi ,\beta \mid {\tilde{y}}_i)=\log \left(\sum _{j=1}^J{\eta }_j\left({\tilde{x}}_i\beta \right)\prod _{m=1}^M{\pi }_{\mathit{mj}}^{y_m}(1-{\pi }_{\mathit{mj}})1-y_m\right)$$ (2)

specified as the generalized logistic function of ν. The interpretation of exp(β₁₁), then, is the odds ratio for the association between membership in class one (compared to the reference class) and the covariate x_i1. A key assumption is that of non-differential measurement (NDM), such that $\mathrm{Pr}[{\tilde{Y}}_i={\tilde{y}}_i\mid C_i,{\tilde{x}}_i]=\mathrm{Pr}[{\tilde{Y}}_i-{\tilde{y}}_i\mid C_i]$. Essentially, the observed indicators of the latent phenotype are independent of the covariates given class membership (C_i) [5]. Explicit modeling of relationships between covariates and latent class indicators is possible but may exacerbate difficulties with identifiability. Conditions for local identifiability have been described [8], but they entail an assumption that covariate effects on latent class indicators are constant across classes, and may require the fixing of other parameters.

2.2. Proposed methodology

In the model of Houseman and colleagues, each conditional probability (π_mj) is modeled as a function of the covariates h(x_im’ α_j), and the estimation of the parameters {α_j; j = 1,…,J – 1} is penalized through the inclusion of a penalty function in the likelihood equation [6]. We propose an adaptation, similar to that of Houseman and colleagues, in which conditional probabilities are not modeled as explicit functions of the covariates but rather treated as (unknown) constants per item and class, thus allowing an assumption of non-differential measurement. Here, estimation of β is penalized per (3), with penalty function C and tuning parameter λ, with $L(\pi ,\beta \mid \tilde{y})$ as in 1.2. While the proposed penalty is on parameters characterizing the latent class probabilities η_j, not π_mj, it is expected that penalization

$$L_C(\pi ,\beta \mid \tilde{y})=L(\pi ,\beta \mid \tilde{y})-C(\beta ,\lambda )$$ (3)

of covariate coefficients will alter the composition of latent classes, and therefore indirectly affects the estimation of the conditional probabilities (π_mj).

2.3. Incorporation of scientific information for phenotype development

We see at least four ways in which this can be achieved in the framework we have proposed. The first is by the inclusion of covariates that are hypothesized to distinguish phenotypic classes. Then, penalization primarily aims to minimize error of prediction of individuals’ class memberships. We have found this approach to be most tractable in a paper focused on introductory exposition and evaluation of the methodology we have developed, and it is our primary focus here. To this end, we will employ two commonly used penalty functions and will select the tuning parameter by cross-validation.

To illustrate the remaining three ways we might incorporate scientific information, consider a scenario like that which motivated our study: researchers aim to develop psychiatric phenotypes, and they believe there are two distinct subtypes—exactly one of which is genetically linked. A first method of incorporating this belief is to constrain the genetic marker coefficient to be 0 for one of the two subtype classes (say, 1 and 2, with the non-disordered subpopulation as class 3). Our methodology aims to avoid this rigid an imposition. A second method is through choice of the penalty function, or equivalently, prior distribution on the parameters at issue. For example, one might encode the genetic coefficients in the two subtype classes as β₁₁ = pβ; β₁₂ =(1 – p)β and impose a beta prior on p, so as to allow the possibility of concentrating mass at the extremes of the support. The final method is through the choice of the tuning parameter. This might occur in conjunction with a specific penalty—for instance, through the choice of beta parameters in the example just given. It might also occur through selective penalization of parameters in some classes but not others; we illustrate this approach in our simulation study and our culminating data analysis.

2.4. Penalization

In this paper, we develop penalization methodology for the ridge penalty, $C(\beta ,\lambda )={\Sigma }_{j=1}^J{\Sigma }_{i=1}^N{\lambda }_{\mathit{ij}}{\left({\beta }_{\mathit{ij}}\right)}^2$ [9], and the LASSO penalty $C(\beta ,\lambda )={\Sigma }_{j=1}^J{\Sigma }_{i=1}^N{\lambda }_{\mathit{ij}}\mid {\beta }_{\mathit{ji}}\mid$ [10]. From a Bayesian perspective, penalization can be viewed as the assumption of a prior distribution on β. The bridge penalty λ∑|β_j|^γ then becomes the logarithm of the prior distribution subject to a constraint [11]. In the case of the ridge penalty, this prior distribution is Gaussian, with a mean of 0 and variance 1/λ [11]. With the LASSO, the prior distribution is double exponential, with a scale parameter of 1/λ [11]. From a frequentist perspective, this penalization is equivalent to fitting a mixed effects model, where the regression coefficients are modeled as crossed random effects [12].

Parameter estimation with the ridge penalty is straightforward, and identical to the gradient EM algorithm described by Bandeen-Roche and colleagues [5] for the standard latent class regression model, except that here the ‘score’ equation, u^(t) and Hessian matrix, H^(t) for β become (4) and (5), respectively. Here, θ_{i j} represent individual posterior probabilities of membership in class j, and ϕ_jk = 1 if j = k and 0 otherwise. The ‘score’ equation and Hessian matrix for π (not shown) are unchanged.

$$\frac{\partial \log L_C}{\partial {\beta }_{\mathit{pj}}}=\sum _{i=1}^N{x}_{\mathit{ip}}\left\{{\theta }_{\mathit{ij}-{\eta }_j}\right(x_j^{\prime }\mathrm{B}\}-\sum _{i=1}^{N}2\Lambda {\beta }_{\mathit{pj}}$$ (4)

$$\frac{{\partial }^2\log L_C}{\partial {\beta }_{\mathit{pj}}\partial {\beta }_{\mathit{qk}}}=\sum _{i=1}^N{x}_{\mathit{ip}}{x}_{\mathit{iq}}\left({\theta }_{\mathit{ij}}\right({\varphi }_{\mathit{jk}}-{\theta }_{\mathit{ik}})-{\eta }_j(x_j^{\prime }\mathrm{B}\left)\right({\varphi }_{\mathit{jk}}-{\eta }_k\left(x_i^{\prime }\mathrm{B}\right)\left)\right)-\sum _{i=1}^{N}2\Lambda$$ (5)

Standard errors were calculated as H⁻¹nV H⁻¹, where V is an estimate of the asymptotic variance of the score [6]. In order to reduce computing time, the SQUAREM algorithm, an iterative scheme that is a hybrid of reduced rank extrapolation and minimal polynomial extrapolation [13], was implemented for all ridge penalty simulations.

Implementation of the LASSO penalty is not straightforward, as the resultant penalized log-likelihood is not differentiable with respect to β. Iterative re-weighting was used to reformulate the optimization as a quadratic programming problem within the generalized linear model framework. The algorithm is based on that of Houseman and colleagues [6] (pp. 33–34), but adapted to the current application. In the first step, μ_{i j} = η_{i j}(x_i’ β_j), to reflect that the class prevalences, rather than the conditional probabilities, are functions of x and β. Likewise, residuals are calculated as e_{i j} = θ_{i j} – μ_{i j}, where θ_{i j} is the posterior probability of class membership. Further, the weighting matrix, W, now corresponds to casting of the polytomous latent regression in the standard iteratively re-weighted least-squares generalized linear modeling form. The full algorithm is included in Appendix A.

2.5. Choice of the tuning parameter

In addition to choosing the form of the penalty, one must also choose a value for λ, the tuning parameter. Here we pursue the typical aim of trading off accuracy and precision of prediction in subsequent data sets, and λ is chosen to minimize prediction error. A measure of prediction error can be obtained through cross-validation [14]. Since the latent class regression model involves non-Gaussian (binomial) distributions, deviance is used as the measure of discrepancy, and R, the log-likelihood loss $R=2{\Sigma }_{i=1}^n{L}_i({\widehat{\beta }}_{-i},{\widehat{\pi }}_{-i})$, where ${\widehat{\beta }}_{-i},{\widehat{\pi }}_{-i}$ are parameter estimates obtained with the ith subject left out is approximated by (6), where H_C is the Hessian matrix of the penalized log-likelihood, and nV is the estimated variance of the score equation.

$$\widehat{R}=2\mathrm{tr}\left(H_C^{-1}nV\right)-2L(\beta ,\pi )$$ (6)

Since the LASSO-penalized likelihood is not differentiable, H_C in that case is approximated by H + W, where W is a diagonal matrix with W[(j–1)*p]+p,[(j–1)*p]+p=|β_jp|⁻¹ [15].

Minimization of prediction error was not our only goal; we were also interested in the effects of penalization on external validity. In light of the penalties examined here, we focused our investigation on quality of prediction, made operational as the area (AUC) under a receiver operating characteristic (ROC) curve. ROC curves plot sensitivity (probability of a positive test result given the presence of disease) versus 1-specificity (probability of a negative test result given the absence of a disease) for a binary outcome based on varying cutoff values on a continuous ‘test’ variable [16]. The greater the AUC, the more predictive the test, with an AUC of 1.0 representing a perfect test with 100 per cent sensitivity and specificity. In our setting, we will use posterior probability of being in the highest risk latent class as the test value, and dichotomous disease status as the outcome.

3. Simulation studies

A number of simulation studies were conducted. In each case, 100 data sets with three ‘latent’ classes (η={0.05,0.15,0.80}) were generated with sample sizes of 500 and 5000. Here, the initial ηs refer to means over the population of the covariates. Both the latent class prevalences and conditional probabilities (π₁={0.75,0.75,0.75,0.25,0.25,0.25}, π₂={0.25,0.25,0.25,0.75,0.75,0.75}; π₃={0.05,0.05,0.05,0.05,0.05,0.05}) were chosen to reflect what might be expected in a scenario where a disorder has two distinctively different potential profiles, with the majority of the sample having no disease. Runs were first conducted with a range of λ values from 0 (no penalty) to 10 with an increment of 1 (‘gross mapping’). Subsequent ‘further mapping’, with an increment of 0.1, was then done in the most promising region (based on cross-validation of log-likelihood loss, R) identified by gross mapping, or in increments of 1, 10, or 100 beyond the initial region.

In order to assess the effects of penalization on external validity, external distal outcome variables were simulated from a Uniform (0,1) distribution, and were then dichotomized using latent class-specific outcome prevalences (0.70, 0.05, 0.05), such that individuals in class 1 would be expected to have the distal outcome 70 per cent of the time, and individuals in class 2 or 3 would be expected to have the distal outcome 5 per cent of the time. Following each simulation, parameter estimates corresponding to λ=0 and each λ value evaluated in the ‘further mapping’ phase were used to calculate posterior probabilities of class membership for each simulated individual. These posterior probabilities, along with the simulated outcome statuses were then used to calculate AUC for each λ value.

The first set of simulations was intended to examine the effects of penalization in the context of varying strengths of association between the class of interest (class 1) and a single covariate (β₁₁=0.69 or 1.79) in the case of a correctly specified latent class regression model—i.e. where all model assumptions are met. In this case, penalization of non-intercept βs(β_pj, p≠0) to minimize prediction error may add precision in identifying classes but is not expected to meaningfully improve over analyses without the penalty. The log odds ratio (β₁₂) for association between the single covariate and class 2 was always 0. The covariate itself was generated from a Uniform (−0.5,0.5) distribution. A number of summary measures were calculated for ${\widehat{\beta }}_{11}$: bias, empirical and estimated precision, accuracy of the precision, and mean-squared error (MSE). Table I shows fine-mapping results with sample size equal to 5000 and a ridge penalty. As expected, non-zero values of λ resulted in small increases in precision, at the expense of small increases in bias. These effects were larger in identical simulations (not shown) with the smaller sample size of 500. Standard errors accurately estimated the coefficient sampling distributions in both cases. In no case did AUC (not shown) vary with λ.

Table I.

Ridge penalty: variations of β₁₁ and δ (N =5000).

β * 11	δ †	λ ‡	Bias§	Empirical precision¶	Accuracy of precision∥	MSE**
0.69	0	0.0	0.001	0.033	−0.004	0.033
		1	−0.036	0.030	−0.010	0.031
1.79	0	0.0	0.011	0.035	0.007	0.036
		0.2	−0.016	0.033	0.006	0.033
1.79	0.69	0.0	0.297	0.051	0.039	0.139
		0.1	0.279	0.048	0.038	0.126
1.79	1.79	0.0	1.146	0.056	0.041	1.369
		0.1	1.113	0.051	0.036	1.290
1.79	−1.79	0.0	−0.296	0.046	0.036	0.134
		0.2	−0.317	0.044	0.035	0.144

^*Simulated log odds ratio for association between x₁ and membership in class 1, relative to class 3.

^†Simulated log odds ratio for the independent association between covariate and the first of six latent class indicators.

^‡Candidate value for tuning parameter. Results are shown for λ=0 and the candidate λ value which minimized R, the cross-validated log-likelihood loss for the largest number of simulated data sets.

^§${\beta }_{11}-\left[\right(1∕\mathit{nsi}){\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}{\widehat{\beta }}_{11,\mathit{si},\lambda },],$, where si are simulation iterations.

^¶${\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}{({\widehat{\beta }}_{11,\mathit{si},\lambda }-{\beta }_{11,\lambda })}^2∕(n-1)$.

^∥$(1∕\mathit{nsi}){\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}v\widehat{a}r\left({\widehat{\beta }}_{11,\mathit{si},\lambda }\right)$—empirical precision_λ.

^**Mean square error = empirical ${\text{precision}}_{\lambda }+{\text{bias}}_{\lambda }^2$.

The next set of simulations was conducted to determine the effects of penalization in the context of differential measurement that was not accounted for in the model. Differential measurement is present when there is dependence between one or more covariates and one or more latent class indicators after conditioning on latent class membership. In the presence of such differential measurement, the standard latent class regression model (1) would be misspecified, as its form implies independence of covariates and latent class indicators after conditioning on class membership. Typically, differential measurement is ascertained by creating a set of ‘pseudoclass assignments’ based on individuals’ vectors of posterior probabilities of class membership, and then testing for dependence within each pseudoclass [5]. This set of simulations regarding differential measurement is of primary concern for our methodological development, which aims to tradeoff between construct validating assumptions that may not all be correct. Data sets were simulated with a range of log odds ratios (δ={−1.79,0.0,0.69,1.79}) for the conditional dependence between the covariate and the first of the six latent class indicators; this δ was constant across classes. Conditional probabilities and latent class prevalences were as in the previous set of simulations, and β₁₁=1.79. We will refer to instances where both the conditional dependence between the covariate and the latent class indicator as well as the relationship between the covariate and class membership are in the same direction as ‘positive differential measurement’ (δ={0.69,1.79}), and when they are in the opposite direction (δ={−1.79}) as ‘negative differential measurement’. The second half of Table I shows results from these simulations using the ridge penalty and a sample size of 5000. In comparing bias across values of δ, but where λ=0 (no penalty), it is clear that the presence of positive differential measurement leads to overestimation of β₁₁. This is because the relationship between the latent class of interest and the indicator (here, π₁₁=0.75) and between the covariate and the indicator (δ) are both in the same direction. As in the previous set of simulations, imposition of the penalty decreased empirical variances, but bias was decreased. In this case, the typical downward biasing effect of the penalty (partially) neutralized the upward biasing effect of the differential measurement. In the case of negative differential measurement, unpenalized estimation was biased downward, and imposition of the ridge penalty exacerbated that bias. It is therefore important that users considering use of a penalty first conduct diagnostics on the unpenalized model to determine the degree and direction of differential measurement. Here, the standard errors overestimated the coefficient sampling distributions, both with and without penalization. In cases where differential measurement is suspected, users may want to employ an alternate method of standard error estimation, such as bootstrap or Huber–White.

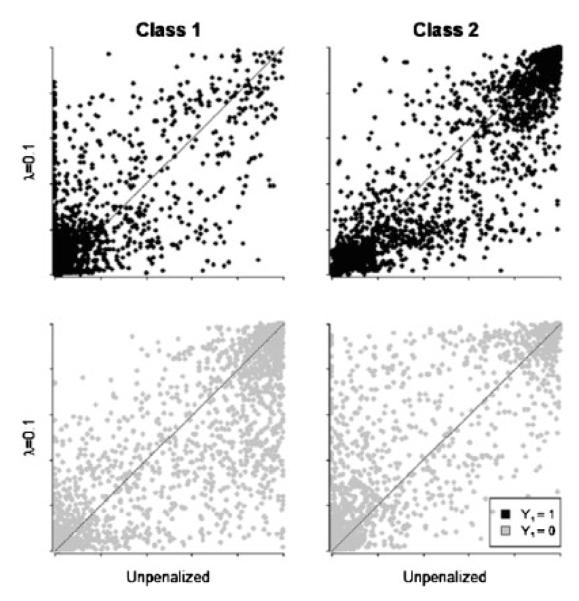
In none of the simulations we performed did the conditional probability estimates change dramatically as a result of penalization, though there were subtle alterations. Figure 1 shows scatter plots for the posterior probabilities of class membership based on parameter estimates for λ=0 and λ=0.1 from a simulation analogous to that in Table I where β₁₁=1.79 and δ=1.79, but with a sample size of 500. Black points represent simulated cases where the first latent class indicator (the indicator with the independent relationship with the covariate) is 0, while for gray it is 1. Points above the diagonal line represent cases where the posterior probability of membership in that class had increased as a result of the penalty, and those below represent cases where that probability had decreased. The pattern of posterior probabilities suggests that use of the ridge penalty ‘moved’ some individuals with a positive value for the first indicator out of the first class and into the second, and likewise some individuals with negative value for the first indicator out of the second class and into the first.

Figure 1.

Posterior probability of class membership as a function of λ and Y₁. Each graph plots posterior probability of class membership for λ=0 and λ=0.01 from the differential measurement scenario in Table I, where β₁₁=δ=1.79. Points above the diagonal line represent cases where the posterior probability of membership in that class had increased as a result of the penalty, and those below represent cases where that probability had decreased.

Given that traditionally both the ridge and LASSO penalty are useful in situations with large numbers of covariates, we next explored scenarios with nine dichotomous covariates. These nine covariates were generated from a multivariate normal distribution with means of 0, variances of 1, and covariances of either 0 (first set) or 0.9 (second set). These were then dichotomized to produce covariates with specified frequencies, φ=(0.5,0.2,0.3,0.1,0.2,0.3,0.4,0.5,0.6). Simulated β values for the nine covariates were β_•1 =(1.79,0,0,–1.39,1.39,–0.40,0.40,–0.69,0.69), and β_•2 =(0,0.69,–0.69,0.40,–0.40,1.39,–1.39,0.40,–0.40). Table II shows results using a ridge penalty and sample size of 5000. As in the previous simulations, imposition of the penalty increased bias but improved precision, resulting in a modest improvement in MSE.

Table II.

Ridge penalty: nine covariates, variations of ρ (N =5000).

Penalized estimates*	ρ †	λ ‡	Bias§	Empirical precision¶	Accuracy of precision∥	MSE**
	0	0.0	−0.023	0.058	0.006	0.058
	0.9	0.0	−0.022	0.138	0.024	0.139
${\widehat{\beta }}_{1j}$	0	0.1	−0.046	0.054	0.008	0.056
	0.9	0.2	−0.128	0.109	0.031	0.125
${\widehat{\beta }}_{\mathit{pj}}$, p=(1,…,9)	0	0.4	−0.071	0.048	−0.002	0.054
	0.9	0.4	−0.101	0.127	0.004	0.137

^*Values for bias, precision, etc. refer to ${\widehat{\beta }}_{11}$, where the simulated value of β₁₁ is 1.79.

^†Bivariate correlations among covariates.

^‡Candidate value for tuning parameter. Results are shown for λ=0 and the candidate λ value which minimized R, the cross-validated log-likelihood loss for the largest number of simulated data sets.

^§${\beta }_{11}-\left[\right(1∕\mathit{nsi}\left){\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}{\widehat{\beta }}_{11,\mathit{si},\lambda }\right]$, where si are simulation iterations.

^¶${\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}{({\widehat{\beta }}_{11,\mathit{si},\lambda }-{\beta }_{11,\lambda })}^2∕(n-1)$.

^∥$(1∕\mathit{nsi}){\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}v\widehat{a}r\left({\widehat{\beta }}_{11,\mathit{si},\lambda }\right)$—empirical precision_λ.

^**Mean square error = empirical ${\text{precision}}_{\lambda }+{\text{bias}}_{\lambda }^2$.

We have previously described penalization from a Bayesian perspective, and next wished to compare our penalization approach to a Bayesian analysis, both in terms of parameter estimation and computational burden. To achieve this, Bayesian estimations of the latent class regression models were performed using WinBugs. Priors were defined for parameters on the logit scale for the conditional probabilities within classes to be logit(π_mj)~N(0,5). On the probability scale, this provides a rather flat prior over the range of 0.05–0.95, suggesting a relatively uninformative prior, but it bounds estimates away from the boundaries of the parameter space. The same prior distribution was used for the intercept in the regression portion of the model, and each of the remaining regression coefficients was specified with a prior that was ~N(0,1/λ), to be consistent with the ridge penalty. A fully Bayesian analysis might also have included a hyperprior on λ itself, but this was not undertaken here, as such a hyperprior would have altered the interpretation of the penalty itself [17], and would have produced parameter estimates which were not directly comparable to those obtained via penalization. For each simulated data set, a burn-in of 10 000 iterations was performed. Based on exploration of chains, we found that convergence occurred within 5000 iterations so that doubling the burn-in should have ensured convergence for all simulated data sets. The chain was then run for an additional 50 000 iterations with every 10th iteration saved for inferences. It is possible for ‘label switching’ to occur among the classes during each Bayesian estimation. To correct this, chains were post-processed so that class definitions were consistent throughout the chains using an approach similar to that described by Stephens [18]. Additionally, we inspected histograms of final estimates and scatterplots of standard errors versus parameter estimates across all simulated data sets and found no evidence of lack of convergence. The same simulated data files were used for both the Bayesian and penalized estimation to facilitate comparisons between the two methods.

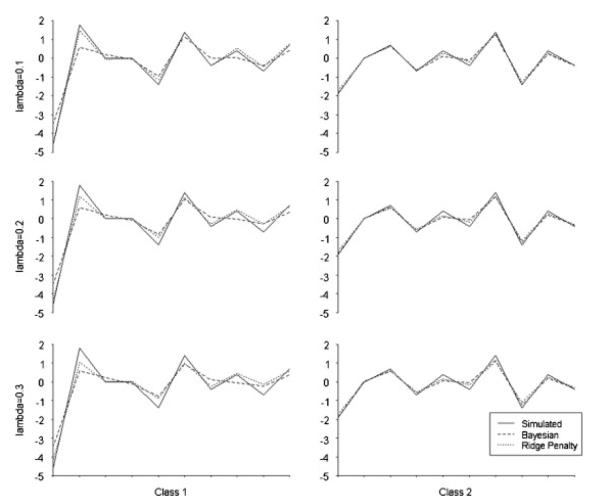
Figure 2 shows simulated β values, Bayesian posterior means, and penalized parameter estimates from the scenario presented in Table II with nine highly correlated covariates, but with a sample size of 500. Comparing the penalized estimates to the Bayesian posterior means, it appears that the penalized estimates were more accurate. Empirical standard errors were similar between the two methods, but for penalization were larger for class one but smaller for class two. We believe it worth noting that, notwithstanding the different patterns as observed, the two methods produced remarkably similar estimates in all scenarios, with absolute differences not exceeding 0.04 and generally considerably lower. In addition to potential gains in accuracy, the penalized estimation was far less time-consuming. Using the same computer, (2.13 GHz, 2 M RAM), the Bayesian analyses took an average of 35.55 h for each λ value shown in Figure 2. By contrast, penalized estimation took an average of 0.95 h per λ value.

Figure 2.

Comparison of estimates from Bayesian and penalization simulations. Estimates are analogous to the scenario in Table II, with ρ=0.9, and all non-intercept coefficients penalized, but with N=500. The optimal λ value was 0.2. Each graph plots ${\widehat{\beta }}_{\mathit{pj}}$ (Y-axis) for the intercept and nine covariates by class and λ value.

In the simulations described so far, imposition of either the ridge or LASSO penalties resulted in a downward bias in the regression coefficients. Ideally, though, one would like to maximize separation between the classes, such that the coefficient for just one of the classes (the one that, in truth, was not associated with the covariate) was biased downwards. In the context of a strong a priori hypothesis, it might be appropriate to employ class-specific penalization. Table III includes results from simulations with a sample size of 5000, β₁₁ of 0.69 or 1.79, and the log odds ratio between the covariate and the other non-reference class, β₁₂ equal to 0 in both cases. Here, the ridge penalty was imposed only on ${\widehat{\beta }}_{12}$. On comparing these results to those from Table I, where both ${\widehat{\beta }}_{11}$ and ${\widehat{\beta }}_{12}$ were penalized, one sees that much higher values of λ are now optimal, that neither ${\widehat{\beta }}_{11}$ nor ${\widehat{\beta }}_{12}$ are substantially biased, and that imposition of the penalty still results in modest improvements in MSE. Table IV shows the results from analogous simulations that used the LASSO penalty.

Table III.

Class-specific ridge penalization (only β₁₂ penalized) (N =5000).

			β 11		β 12
β * 11	β † 12	λ ‡	Bias§	MSE¶	Bias	MSE
0.69	0	0	0.001	0.033	0.015	0.010
		1000	0.001	0.034	0.001	0.000
1.79	0	0	0.011	0.036	−0.009	0.013
		1000	0.011	0.036	0.000	0.000
1.79	0.69	0	−0.010	0.038	0.011	0.008
		1	−0.013	0.035	−0.001	0.007
1.79	1.79	0∥	0.049	0.038	0.005	0.009
		1	0.031	0.033	−0.028	0.010

^*Simulated log odds ratio for association between x₁ and membership in class 1, relative to class 3.

^†Simulated log odds ratio for association between x₁ and membership in class 2, relative to class 3.

^‡Candidate value for tuning parameter. Results are shown for λ=0 and the candidate λ value which minimized R, the cross-validated log-likelihood loss for the largest number of simulated data sets.

^§${\beta }_{1j}-\left[\right(1∕\mathit{nsi}\left){\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}{\widehat{\beta }}_{1j,\mathit{si},\lambda }\right]$, where si are simulation iterations.

^¶Mean square error =${\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}{\left(\right({\widehat{\beta }}_{1j,\mathit{si},\lambda }-{\stackrel{‒}{\beta }}_{1j,\lambda })}^2∕(n-1))+{\text{bias}}_{\lambda }^2$.

^∥In the case of β₁₁=β₁₂=1.79, R was minimized with λ=0 in all 100 simulated data sets.

Table IV.

Class-specific LASSO penalization (only β₁₂ penalized) (N =5000).

			β 11		β 12
β * 11	β † 12	λ ‡	Bias§	MSE¶	Bias	MSE
0.69	0	0	0.001	0.033	0.015	0.010
		1.1	−0.039	0.031	0.015	0.009
1.79	0	0	0.011	0.036	−0.009	0.012
		0.1	−0.003	0.034	−0.009	0.012
1.79	0.69	0.0	−0.011	0.037	0.010	0.008
		0.1	−0.024	0.036	0.009	0.008
1.79	1.79	0.0	0.049	0.038	0.005	0.009
		0.1	0.037	0.036	0.002	0.009

^*Simulated log odds ratio for association between x₁ and membership in class 1, relative to class 3.

^†Simulated log odds ratio for association between x₁ and membership in class 2, relative to class 3.

^‡Candidate value for tuning parameter. Results are shown for λ=0 and the candidate λ value which minimized R, the cross-validated log-likelihood loss for the largest number of simulated data sets.

^§${\beta }_{1j}-\left[\right(1∕\mathit{nsi}\left){\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}{\widehat{\beta }}_{1j,\mathit{si},\lambda }\right]$, where si are simulation iterations.

^¶Mean square error = ${\Sigma }_{\mathit{si}=1}^{\mathit{nsi}}{\left(\right({\widehat{\beta }}_{1j,\mathit{si},\lambda }-{\stackrel{‒}{\beta }}_{1j,\lambda })}^2∕(n-1))+{\text{bias}}_{\lambda }^2$.

A concern with our approach is that spurious relationships between covariates and class membership may be created, or legitimate ones obscured. With class-specific penalization, this could manifest as an artificial separation between classes. Included in Tables III and IV are additional simulations in which β₁₁ was 1.79, but β₁₂ was now also non-zero. For both the ridge and LASSO penalties, optimal values of λ were much smaller than when β₁₂ was 0, and bias in ${\widehat{\beta }}_{12}$ for these optimal λ values is not large. With the ridge penalty, in the case where both β₁₁ and β₁₂ were 1.79, the optimal value of λ was always 0, providing reassurance that class-specific ridge penalization does not create an artificial separation between classes with respect to the regression coefficient estimates.

4. Application

The Cache County Study on Memory and Aging is a prospective, population-based study of cognition and aging. Accurate prediction of who is likely to develop dementia would be useful both in terms of targeting prevention and treatments as well as opening a window on the pathological process. Even among non-demented elderly, there is substantial variability in cognitive performance. This is attributable to a combination of innate abilities, normal senescence, and prodromal dementia. We hypothesize that latent classes of cognitive performance exist, and that APO-E4 genotype, a well-replicated dementia risk factor [19], will usefully refine the estimation of these latent classes, along with other known risk factors.

In April 1995, all current identified residents of Cache County, Utah (N=5677) were invited to participate, and 5092 were enrolled. Individuals were screened for dementia and those who were dementia-free were re-screened 3 (wave 2) and seven (wave 3) years later. Screening included administration of the 3MS-R [20], an adaptation of the 3MS [21], an expanded 100-point version of the MMSE [22], which included measures of verbal fluency and abstract reasoning as well as additional delayed recall items. These analyses include only those individuals who were dementia free at wave 1, though individuals with CIND (cognitive impairment no dementia) were included. Seven 3MS-R items (knowledge, word registration, orientation to time, verbal fluency, sentence writing, pentagon drawing, and combined word recall) were chosen as latent class indicators. In all cases, ‘1’ was better, and ‘0’ was worse. In this sample, the 2-class model had the lowest BIC (31 204.21) and the 3-class model had the second-lowest BIC (31 245.88). However, based on the bootstrap likelihood ratio test, the 3-class model fit the data significantly better than the 2-class model (-2LL difference: 24.87, p=0.03). Since simulations have shown the BLRT to be superior to the BIC for choosing the appropriate number of classes [23], and since it was consistent with a priori theory, a 3-class model was chosen. This model consisted of an ‘impaired’ group (class 1), characterized by uniformly lower probabilities of correctly answering items, particularly knowledge and combined recall, an ‘intermediate’ group (class 2) with higher conditional probability estimates, and an ‘unaffected’ group (class 3) with the highest item probabilities. Parameter estimates for the measurement model are shown in Table V; conditional probability estimates from models with and without covariates, penalized or unpenalized, were all very similar.

Table V.

Latent class regression measurement model.

Class	1—‘Impaired’	2—‘Intermediate’	3—‘Unaffected’
$\widehat{\eta }$	0.10	0.51	0.39
Knowledge	0.148(0.032)*	0.434(0.020)	0.705(0.019)
Registration	0.716(0.033)	0.902(0.010)	0.982(0.006)
Time	0.391(0.043)	0.766(0.015)	0.871(0.012)
Fluency	0.262(0.037)	0.512(0.020)	0.804(0.018)
Sentence	0.600(0.035)	0.757(0.014)	0.908(0.012)
Pentagons	0.585(0.037)	0.807(0.013)	0.896(0.011)
Combined Recall	0.158(0.030)	0.506(0.022)	0.743(0.017)

^*Conditional probability ${\widehat{\pi }}_{\mathit{mj}}$ (SE).

Next, we fit a series of latent class regressions, with the final models including covariates for the presence of one and two APO-E4 alleles, age, education, history of cerebrovascular accident (CVA, or stroke), head injury, hypertension, high cholesterol, coronary artery bypass graft surgery (CABG), myocardial infarction, or diabetes, lifetime history of two weeks or more of sadness or apathy, and parental history of memory loss. A priori theory guided the imposition of a class-specific penalty. We believed that while both classes 1 and 2 were characterized by cognitive deficits, only the more severe class 1 represented individuals at imminent risk for dementia, with class 2 representing individuals experiencing normal/non-pathological cognitive decline. As such, we expected membership in class 1 to be more strongly associated with risk factors for dementia, and we chose to penalize only associations between covariates and membership in class 2. A priori theory also drove the choice of which covariates to penalize. Since age and education have been shown to be associated with both dementia and normal cognitive decline, these covariates were left unpenalized. By contrast, APO-E4 has been strongly and specifically associated with dementia, and the choice to impose a class-specific penalty on that covariate was straightforward. The scientific support for specific associations between the remaining covariates and dementia risk as opposed to more general associations with any degree of cognitive decline was less strong, so we fit two penalized models, (a) and (b), representing different assumptions regarding those covariates. In model (a), only the covariates for the association between membership in class 2 and APO-E4 genotype were penalized. In model (b), covariates for the association between membership in class 2 and all risk factors except age and education were penalized. We chose the ridge penalty over the LASSO based on the class-specific simulations in Tables III and IV, which showed better performance in cases where covariates were associated with both classes 1 and 2.

Table VI shows estimates from the penalized latent class regression models (a) and (b), along with estimates from an unpenalized model. In the unpenalized model: age, education, and CVA were strongly associated with increased odds of membership in both classes 1 and 2, relative to class 3. APO-E4 hetero- and homozygosity, head injury, and myocardial infarction were associated with increased odds of membership in class 1 only. Unexpectedly, hypertension was associated with decreased odds of membership in either class 1 or 2, and lifetime history of two or more weeks of sadness was associated with decreased odds of membership in class 1. Model (a), which only penalized APO-E4 genotypes, yielded a modest improvement in R (28 929.00–28 927.30) at the optimal (based on R) λ of 9.7. Compared to the unpenalized model, model (a) showed improvement in precision for APO-E4 genotype coefficients for both classes, and a substantial decrease in the absolute magnitudes of the estimates for class 2, thus representing an increase in the separation between classes 1 and 2. Model (b), which penalized all of the dementia risk factors except age and education, resulted in a further modest improvement in R (to 28 926.75) at the optimal λ value of 1.1. As expected, penalization resulted in decreases in absolute magnitude and improvements in precision of the estimates of the associations between membership in class 2 and each of the penalized risk factors.

Table VI.

Latent class regression parameter estimates.

	Class 1			Class 2
	Unpenalized*	Penalized (a)†	Penalized (b)‡	Unpenalized	Penalized (a)	Penalized (b)
Age (y)	0.381 (0.032)Ÿ	0.377 (0.032)	0.373 (0.031)	0.204 (0.029)	0.200 (0.026)	0.197 (0.026)
Education (y)	−0.741 (0.081)	−0.733 (0.080)	−0.719 (0.079)	−0.431 (0.059)	−0.431(0.053)	−0.408 (0.054)
APO-E4	1.327 (0.347)	1.177 (0.299)	1.311 (0.335)	0.359 (0.234)	0.178 (0.161)	0.329 (0.210)
APO-E44	2.800 (0.761)	2.468 (0.652)	2.659 (0.734)	0.543 (0.716)	0.050 (0.215)	0.272 (0.468)
CVA	2.549 (0.979)	2.597 (0.955)	1.628 (0.565)	2.067 (0.905)	2.139 (0.895)	1.077 (0.423)
Head injury	0.833 (0.342)	0.824 (0.333)	0.780 (0.333)	0.428 (0.291)	0.398 (0.267)	0.382 (0.270)
Cholesterol	0.117 (0.299)	0.106 (0.278)	0.090 (0.286)	0.310 (0.255)	0.306 (0.225)	0.273 (0.238)
Hypertension	−1.487 (0.427)	−1.462 (0.383)	−1.438 (0.432)	−0.454 (0.226)	−0.443 (0.215)	−0.370 (0.206)
CABG	0.118 (1.141)	0.179 (0.941)	−0.189 (1.035)	0.934 (0.535)	0.961 (0.526)	0.608 (0.365)
Myocardial infarction	0.970 (0.452)	0.956 (0.431)	0.972 (0.413)	0.316 (0.431)	0.299 (0.384)	0.318 (0.358)
Diabetes	0.687 (0.415)	0.672 (0.393)	0.707 (0.402)	0.126 (0.302)	0.119 (0.297)	0.153 (0.265)
Parental memory loss	−0.351 (0.353)	−0.312 (0.336)	−0.346 (0.359)	0.026 (0.212)	0.044 (0.211)	0.031 (0.193)
Sadness	−0.833 (0.398)	−0.811 (0.388)	−0.781 (0.394)	−0.485 (0.314)	−0.485 (0.298)	−0.393 (0.277)
Apathy	0.213 (0.510)	0.197 (0.499)	0.149 (0.500)	0.225 (0.340)	0.210 (0.334)	0.135 (0.288)

^*No penalization, R=28929.00.

^†Only genotype covariates for class 2 penalized, optimal λ=9.7, R=28927.30.

^‡All non-intercept covariates for class 2 penalized except age and education, optimal λ=1.1, R=28926.75.

^§Estimates (SE) for log odds of association between covariate and class membership ${\widehat{\beta }}_{\mathit{pj}}$, relative to class 3.

Though addition of covariates had little or no effect on conditional probability estimates (${\widehat{\pi }}_{\mathit{mj}}$), addition of covariates to the latent class model did affect the measurement model through changes in latent class probabilities. Prevalence estimates for classes 1–3, respectively, went from (0.05,0.44, 0.52) to (0.10, 0.51, 0.39), suggesting that some individuals in class 3 ‘moved’ into classes 1 and 2. Latent class probabilities and conditional probabilities for both penalized models were virtually unchanged from the unpenalized latent class regression model. Model diagnostics using pseudoclass assignments [5, 24] showed no evidence of conditional dependence or differential measurement in any of the latent class regression models.

Since study participants were re-evaluated at two subsequent waves, it was possible to examine the external validity of the latent classes by observing who progressed to either CIND [25] (Cognitive Impairment, No Dementia) or dementia. ROC curves [16] were constructed using posterior probability of membership in class 1 (‘Impaired’) as the test value. At wave 3, addition of the covariates improved prediction (from AUC of 0.709–0.788), but AUCs for penalized estimation models (a) and (b) were the same as that for the unpenalized model with covariates to three decimal places. Posterior probability of membership in class 2 ‘intermediate’ showed no predictive value for progression to CIND or dementia.

5. Discussion

The ultimate goal of this work was to adapt the standard latent class regression model to allow covariates to influence class definition in such a way as to produce a distinct phenotype that was preferentially associated with the known risk factors or predictors. Toward that goal, and building on work by Houseman and colleagues [6], a model in which estimation of the regression covariates was penalized was developed. Simulation studies using two stock penalties, the ridge and LASSO, were conducted under of variety of conditions. The LASSO penalty, even with very small values of λ, resulted in unacceptably large biases, typically reducing all penalized coefficient estimates to 0. Its weak utility for the modeling scenarios we studied is not surprising, as the LASSO typically shows utility in scenarios with larger numbers of covariates. The ridge penalty, as expected, biased coefficient estimates downwards, but improved precision and convergence. In cases of positive differential measurement, penalization also resulted in improved accuracy, but in cases of negative differential measurement, penalization decreased accuracy. As such, penalties that shrink coefficients toward the null should only be imposed in cases of differential measurement after diagnostics of the unpenalized model have demonstrated that the differential measurement is positive. In cases with multiple correlated covariates, ridge penalization again increased bias somewhat, but improved precision.

Simulations with class-specific penalization were the most promising. When one class had a true regression coefficient value greater than the other class, penalization increased separation between the classes, but in simulations of scenarios in which both classes were similarly associated with the covariate, optimal λ values were close to or equal to 0, and penalization did not increase the separation between the classes. This suggests that class-specific penalization is a useful tool in enhancing the separation between classes, but does not create an artificial separation. In practice, choice of which classes to penalize would be guided by the existing scientific knowledge; this, along with choice regarding which covariate coefficients to penalize are the avenues through which penalization allows for the incorporation of such knowledge.

We applied the ridge penalty to experimental data from the Cache County Study on Memory and Aging. As in the simulation studies, absolute magnitudes of regression coefficient estimates were lowered, and precision was improved. Class-specific penalization resulted in a wider separation between the classes with respect to the covariates. ROC curves, based on prediction of dementia as a function of posterior probabilities of membership in the impaired class, demonstrated that penalization did not adversely affect the external validity of the latent classes, but did not appreciably improve prediction.

We predict that our method would have utility in a number of situations. First, our simulations have shown that the typical action of these penalties, regularization in the context of a small sample size or large numbers of collinear covariates, also occurs when applied to latent class regression. Our method should also be useful when observed variables (latent class indicators) show considerable imprecision in measuring latent classes. Additionally, our method may be useful in some cases where measurement model assumptions are incorrect, as shown in our simulation studies of positive differential measurement.

Methodologically, several areas for fruitful investigation remain. The ridge and LASSO penalties were chosen because they are used commonly, and their behavior in a variety of settings has been previously described. Given the stated goal of producing distinct classes, a ‘penalty’ that both rewards increased strength of covariate association with one class and penalizes associations with other classes might be more appropriate. Simulation studies of a wider variety of scenarios (e.g. more classes, more covariates, different parameter values) are also needed. Bayesian analyses are a clear alternative to those we have proposed, replacing cross-validated distributions through which penalties may be made operational with prior distributions. Clarity of translation of prior beliefs about, say, gene–class relationships into posterior ones is an advantage of such an approach. Our simulations comparing penalization to an analogous Bayesian approach suggest that penalization is at least as accurate and far less computationally intensive. It is possible that a fully Bayesian approach (with a hyperprior on λ) would produce a gain in accuracy to offset this computational burden.

The primary drawbacks to this work lie in the substantive assumptions of our approach. First, it assumes that psychiatric phenotypes are discrete; this is quite possibly not the case. In the dementia example, the conditional probabilities for the indicators showed a clear gradient from the ‘impaired’ to the ‘unaffected’ class. Use of a continuous latent variable method, such as latent trait analysis, might have been more appropriate, and penalization of these models has also been explored [26]. Further, the model we have described suggests a one-to-one relationship between genotype and phenotype; for most psychiatric conditions, this is clearly not the case. It is likely that a given phenotype is the result of a number of genes acting singly or in concert. However, this model can be easily expanded to include multiple genes, environmental factors, and interactions, thus addressing genetic variability. Pleiotrophy presents a more fundamental difficulty; it is not clear how this model would be adapted for scenarios in which a gene or set of genes and other factors is expressible as any of a number of phenotypes.

It should be noted that, as described in Bollen [27], there are (at least) two schools of thought regarding the nature of latent variables. The first is that they are only hypothetical constructs, and the second is that they do represent something ‘real’ but can only be measured imperfectly. Our paper has in mind applications for which the second school of thought is tenable. We would argue that the modeling of phenotypes (effects of genotypes) as latent variables is predicated on the assumption that the latent variable is measuring something real—in this case, the underlying pathophysiology. As Sobel [28] noted, only this type of conceptualization is compatible with treatment of latent variables as causes or effects.

Potential applications for this method extend beyond genetics. Possibilities include studying which types of depression are most likely to respond to specific treatments, or which characteristics among children might signal increased risk of future violence or drug use. In all cases, because the outcome itself is aiding in the formation of the phenotypic definition, findings cannot be viewed as confirmatory in their own right. External validation will always be necessary. Instead, such findings can be used to focus researchers’ efforts in a process of ‘iterative validation’ [29].

In conclusion, methodology for the implementation of penalization for latent class models has been developed, and performance of these methods with two commonly used penalty functions has been examined. Further exploration, particularly with novel penalty functions is needed. Penalized latent class regression models may become a useful tool in understanding the nature and antecedents of psychiatric disorders, working as a compromise between the goals of identifying homogenous subgroups and distinguishing classes by subgroup.

Appendix A. Iteratively re-weighted quadratic programming

IRQP-0 set $\tilde{\sigma }=\text{sign}\left({\tilde{\beta }}_{\mathit{pj}}\right)$

IRQP-1 set ${\mu }_{\mathit{ij}}={\eta }_{\mathit{ij}}\left(x_i^{\prime }{\tilde{\beta }}_j\right)$ where each μ_i is a 1×(J–1) vector.

IRQP-2e_{i j}=θ_{i j}–μ_{i j} where e is a n×(J–1) matrix

IRQP-3 ${\sigma }_{\mathit{pj}}=\text{sign}\left({\beta }_{\mathit{pj}}\right)\cdot I({\beta }_{\mathit{pj}}\ne 0)-{\tilde{\sigma }}_{\mathit{pj}}\cdot I({\beta }_{\mathit{pj}}=0)$

IRQP-4 $\tilde{\sigma }=\sigma$

IRQP-5 ${\stackrel{.}{\mu }}_i$ is a (J–1)×(J–1) matrix:

$$\left[\begin{array}{cc}\hfill {\mu }_{i1}(1-{\mu }_{i1})\hfill & \hfill -{\mu }_{i1}{\mu }_{i2}\hfill \\ \hfill -{\mu }_{i1}{\mu }_{i2}\hfill & \hfill {\mu }_{i2}(1-{\mu }_{i2})\hfill \end{array}\right]$$

$U_i=X_i{\stackrel{.}{\mu }}_i{X}_i^{\prime }$ where

$$X_i=\left[\begin{array}{cc}\hfill x_{i0}\hfill & \hfill 0\hfill \\ \hfill x_{i1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill x_{i0}\hfill \\ \hfill 0\hfill & \hfill x_{i1}\hfill \end{array}\right]$$

IRQP-6Z_i=X_ie_i’–Λσ where

$$W=\sum _{i=1}^N{U}_i$$

IRQP-7 $Z_0=-{\sigma }^{\prime }{\tilde{\beta }}_{\mathit{pj}}$ (where multiplication is element-wise)

IRQP-8 set δ equal to solve. QP minimum of (δ*Wδ*–Z’δ*) Such that σδ*≥Z₀

IRQP-9 set β_t+1=β_t+δ