Abstract
Background
Three binary representations of the genetic code according to the ancient I Ching of Fu-Xi will be presented, depending on their defragging capabilities by pairing based on three biochemical properties of the nucleic acids: H-bonds, Purine/Pyrimidine rings, and the Keto-enol/Amino-imino tautomerism, yielding the last pair a 32/32 single-strand self-annealed genetic code and I Ching tables.
Methods
Our working tool is the ancient binary I Ching's resulting genetic code chromosomes defragged by vertical and by horizontal pairing, reverse engineered into non-binaries of 2D rotating 4×4×4 circles and 8×8 squares and into one 3D 100% symmetrical 16×4 tetrahedron coupled to a functional tetrahedron with apical signaling and central hydrophobicity (codon formula: 4[1(1)+1(3)+1(4)+4(2)]; 5:5, 6:6 in man) forming a stella octangula, and compared to Nirenberg's 16×4 codon table (1965) pairing the first two nucleotides of the 64 codons in axis y.
Results
One horizontal and one vertical defragging had the start Met at the center. Two, both horizontal and vertical pairings produced two pairs of 2×8×4 genetic code chromosomes naturally arranged (M and I), rearranged by semi-introversion of central purines or pyrimidines (M' and I') and by clustering hydrophobic amino acids; their quasi-identity was disrupted by amino acids with odd codons (Met and Tyr pairing to Ile and TGA Stop); in all instances, the 64-grid 90° rotational ability was restored.
Conclusions
We defragged three I Ching representations of the genetic code while emphasizing Nirenberg's historical finding. The synthetic genetic code chromosomes obtained reflect the protective strategy of enzymes with a similar function, having both humans and mammals a biased G-C dominance of three H-bonds in the third nucleotide of their most used codons per amino acid, as seen in one chromosome of the i, M and M' genetic codes, while a two H-bond A-T dominance was found in their complementary chromosome, as seen in invertebrates and plants. The reverse engineering of chromosome I' into 2D rotating circles and squares was undertaken, yielding a 100% symmetrical 3D geometry which was coupled to a previously obtained genetic code tetrahedron in order to differentiate the start methionine from the methionine that is acting as a codifying non-start codon.
Background
The single-strand self-annealing ability of the long coding strand known as the genetic code is presented here for the first time, demonstrating the ordered sequential pairing of codons, i.e., TTT with AAA, CCC with GGG, etc., with 32 of its codons matching the remaining 32.
The four nucleotides of the genetic code: T, A, C, G have specific physicochemical properties deserving a careful analysis, as also do the codons and amino acids produced by them; however, it is important to first recognize the value of binary systems in bioinformatics as applied to the DNA genetic code. The most ancient 64-grid representation seems to predate the Chinese civilization but somehow was preserved by them, representing faithfully the binary order of the genetic code through the most ancient or primeval pairs of trigrams that integrate each of the 64 hexagrams of the I Ching table, also called the Book of Changes or Book of Mutations. This article shows that some basic principles of software engineering can be applied to this ancient binary genetic code system.
At the same time that I was looking for the most modern 3D representation of the genetic code [1], I was also exploring the oldest possible representation of the genetic code in existence today, finding that the I Ching of Fu-Xi, a binary and open-ended system, was already representing with precision the genetic code [2]; this 2D square representation seemed capable to make easier a storage of codon units into bits, and to be adaptable to concepts of bioinformatics.
Due to the fact that the I Ching is the oldest antecedent of a binary system, we are going to use it in its full extent, even when we may have obtained the binaries presented here independently of it. If we look for a definition of the word "defrag" or "defragmentation" from at least three specialized sources, we obtain the next highly related definitions:
"The reorganization of data on a hard disk to optimize performance" [3],
The verb "defragging" appears in [4], with the explanation that this process "rearranges the information stored on the drive into larger contiguous blocks, typically freeing up previously unusable space and making the drive work more efficiently",
While in [5] we read the description of a program that "not only unites fragmented files", but also places them "in the most optimal positions", "files that you open most frequently are placed near the center of a platter, where seek times are lowest".
We are going to apply here this defragging information over the I Ching binary genetic code.
I decided to try all the possible combinations between the three known characteristics of the DNA nucleotides that integrate the double helix, comparing their resulting graphics first with the use of a 3D Euclidean vector environment (a finding submitted elsewhere since Dec. 2011 while still awaiting response); on doing such exercise, I was deeply surprised to find that the four components of the Yin/Yang were manifested, mimicking both the directions of the transcription and replication exhibited by the nucleic acids.
Then, when defragging the binary I Ching tables of the genetic code, both by horizontal and by vertical pairing of codons, for the first time I was able to observe synthetic and quasi-identical genetic code chromosomes (m, i, M and I), a novel representation of the genetic code clearly visible through its resulting amino acids, which I also rearranged into two additional genetic code chromosomes (M' and I') while seeking, not only to align all the hydrophobic amino acids horizontally at the center of the genetic code (in its 8×8 rows four and five) while keeping all their pairings, but also for a semi-introversion per correspondence of codons, a step needed to obtain a 100% symmetrical geometry; so, a slightly modified version of the originally resulting chromosomes M and I will be analyzed in more detail in this article: the two pairs of genetic code chromosomes M' and I'.
On seeking to optimize the speed of DNA analysis and/or of the transcription/translation of its sequences, we are seeking for those binary representations that will allocate, through defragging, the starting codon Met (M) at the center of the 8×8 = 64 grids; we will also analyze the resulting quasi-identities derived from such arrangements, their reverse engineering into rotating 2D non-binaries, and its 3D 100% symmetrical counterpart, coupling its base to the base of the other functional genetic code tetrahedron recently discovered [1] while further compressing them into a novel digenetic code stella octangula.
The pair of genetic code chromosomes I' are the reworked product of comparing the Keto/Amino tautomerism in axis x with the nucleotide rings Pur/Pyr in axis y, and it is this one (and its reciprocal not analyzed here) the one producing a perfectly paired representation of the I Ching table, where every unbroken horizontal line (with a value of 1), was paired to its broken horizontal line (with a value of 0), with 32 of its hexagrams perfectly pairing its remaining 32; meaning that if we stretch linearly the T. 2 shown in Figure 1, starting with 000/000 and ending with 111/111, as if it were a cord, then 000/000 (cell 1, GGG) will be paired to 111/111 (cell 64, CCC), then cell 2 (GGA) will pair cell 63 (CCT), cell 3 (GAG) will pair cell 62 (CTC), etc., until reaching cell 32 (ACC), which theoretically could be capable of pairing with cell 33 (TGG), as seen horizontally in App. B and vertically in App. E, where we have side-by-side the perfect complement of all the opposites within the 64 codons (32/32), with every 0 (broken horizontal line) pairing with every 1 (unbroken horizontal line), according to the Chinese binary system; i.e.:
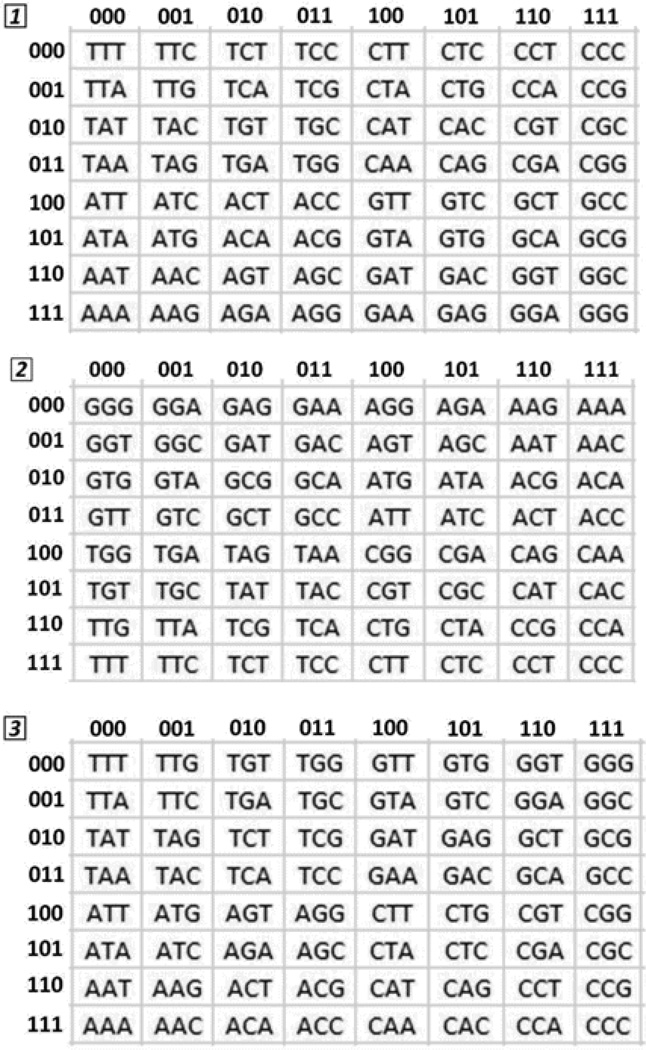
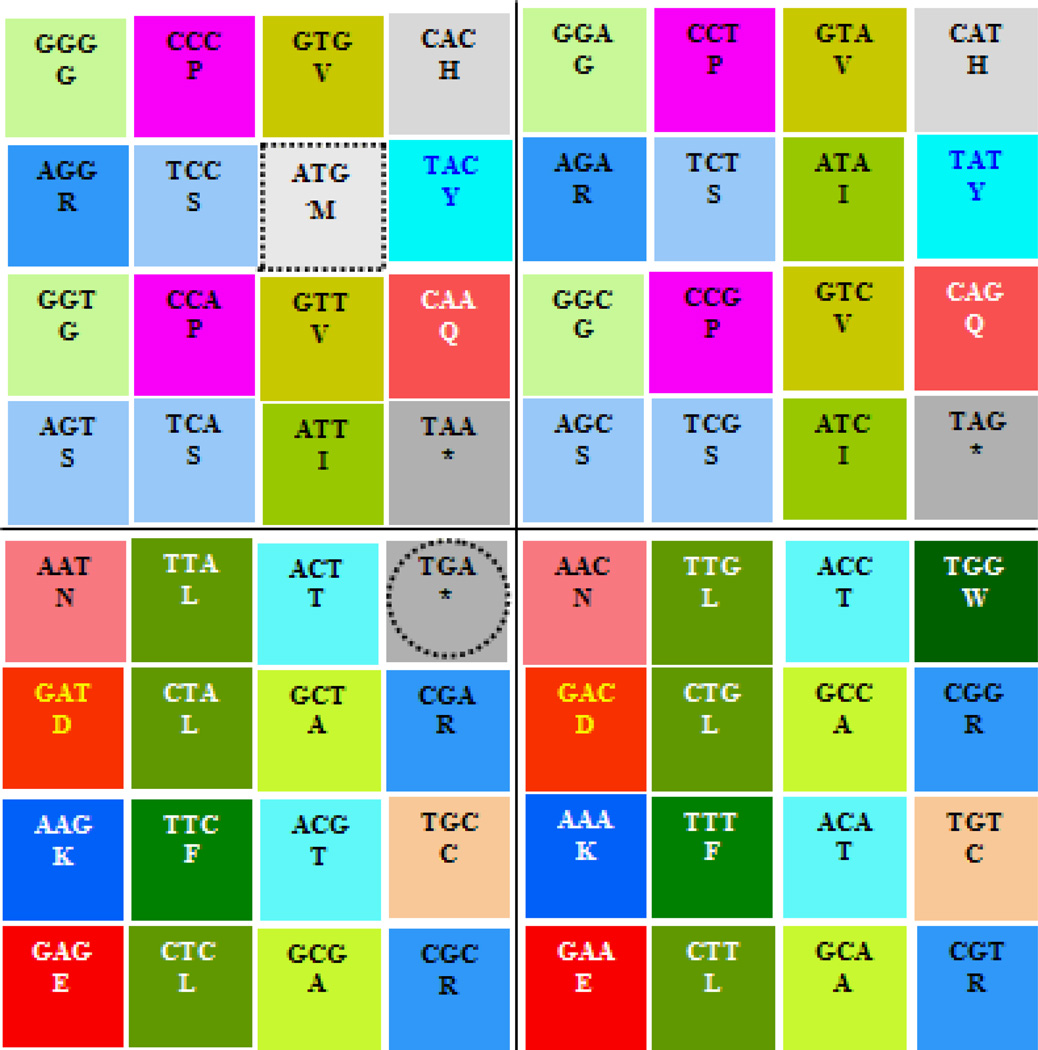
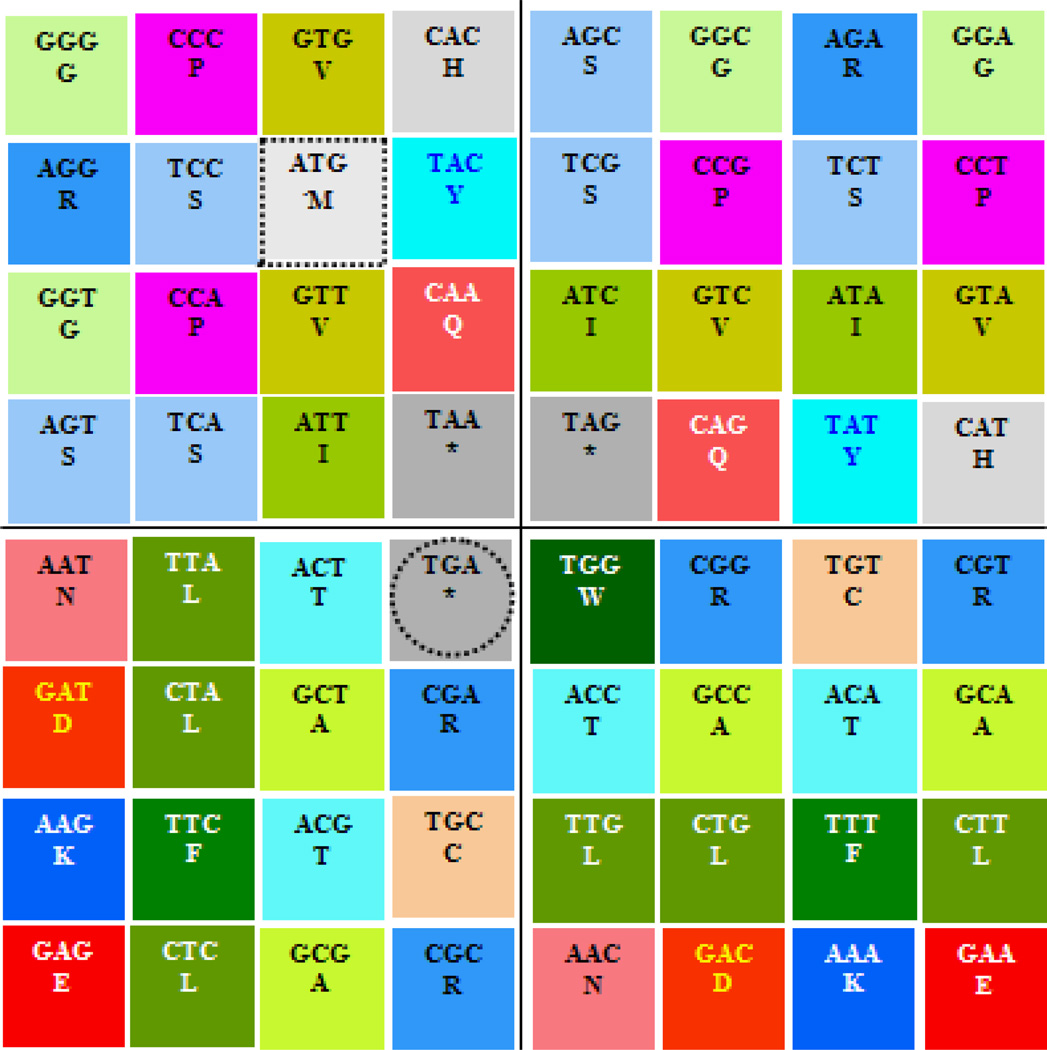
Figure 1.
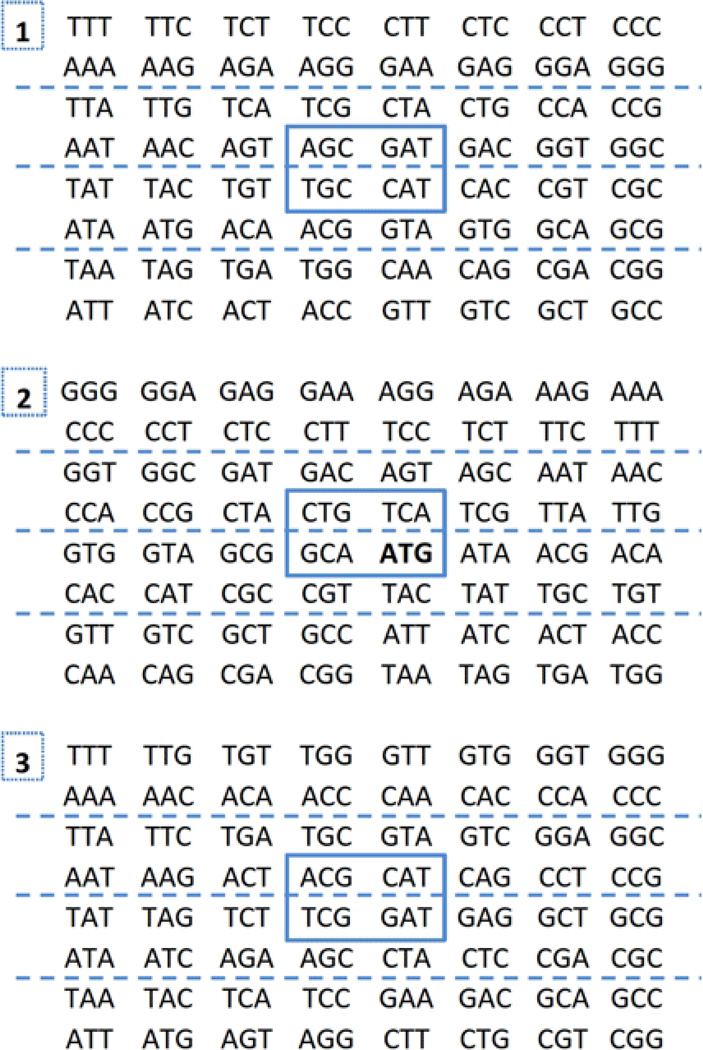
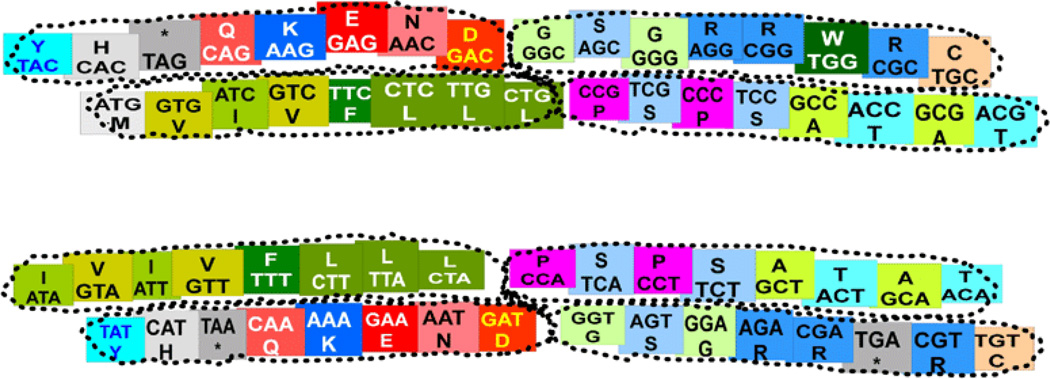
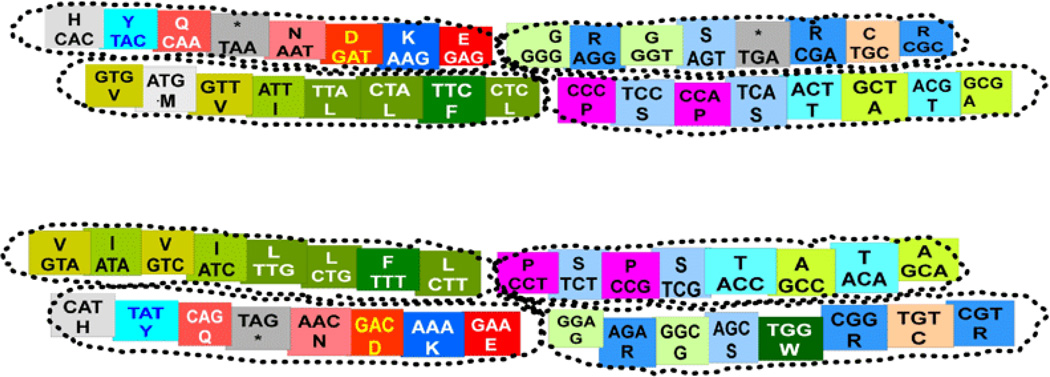
Three binary representations of the genetic code according to the numerical order of the I Ching (the prime matter for this article): T. 1 axis x: 2-H bond = 0 = A, T; 3-H bond = 1 = C, G; axis y: Purine = 0 = A, G; Pyrimidine = 1 = T, C, T. 2 axis x: Keto/Amino (G = T = 0, A = C = 1); axis y: Pur/ Pyr (A = G = 0, C = T = 1). T. 3 axis x: H-bonds (A = T = 0, C = G = 1); axis y: Keto/Amino (G = T = 0, A = C = 1). [Note: T in this DNA corresponds to U in the RNA].
![]()
etc.; I expect to explore elsewhere additional details on the peculiarities of these remarkable I Ching genetic codes and, like Leibnitz, who reported it in 1703 [6], I am only interested in the scientific aspects of this ancient table and derived structures. The paired tables source of the genetic code chromosomes shown here, are composed by four 8 bp self-annealed single-strands.
In sum, we will start by exploring here the genetic code taken as software, applying what we did learn before [2] to further decode its properties and peculiarities, i.e., the unique way in which it can be defragged by single-strand self-annealing which is the pairing of sequences, both horizontally and vertically, and their 2D and 3D geometries and heterogeneous (synthetic) genetic code chromosomes obtained form them.
The rearranged representations of the I Ching will be shown in this article and its Appendixes.
Additionally, a recent discovery of the 1965 unpublished handwritten first codon table by Nirenberg [7] will be displayed comparing its resulting genetic code chromosomes with those obtained from the binary defragged I Ching.
Methods
The original, open-ended and binary representation of the genetic code in the I Ching received presumably from Fu-Xi, the first Emperor of China, can be seen at: http://www.webcitation.org/649aaKNQN. Figure 1 shows the raw binary products of the three I Ching tables that are possible (their reciprocals not shown), while App. A to F show the ancient hexagrams products of their pairs of trigrams (3×2=6), having each table 64 hexagrams, being each of them the result of locating first, at the base of each hexagram, the trigram or three lines representing the codons of each row of the vertical axis or y, while locating secondly on top of them the trigram of the codons that are present in each column of the horizontal axis or x. The specific comparisons are indicated in each table.
The red, green and blue (RGB) color model (Microsoft OfficeTM) with 0% of transparency for all the amino acids is as follows: P: 255,0,255; R: 51,153,255; A: 204,255,51; M: 234,234,234; G: 204,255,153; S: 153,204,255; V: 204,204,0; W: 0,102,0; I: 153,204,0; Q: 255,80,80; E: 255,0,0; C: 255,204,153; F: 0,128,0; L: 102,153,0; T: 102,255,255; N: 255,124,128; D: 255,51,0; K: 0,102,255; Y: 0,255,255; H: 221,221,221; *: 178,178,178. Letter Y: 0,0,255; letter D: 255,255,0; being the extremes the white letters (F, L, W, E, Q, K) with a saturated key (255,255,255), and for the rest the black letters with an absolute lack of color (0,0,0). The colors for the upper part of Figures 21 and 23 when folded, and the complete Figure 22 are the same ones but with a 50% of transparency, having those amino acid letters a dark purple key of 102,0,102 to differentiate them, while to distinguish its unique function as starting codon, their color key of M is 153,0,204.
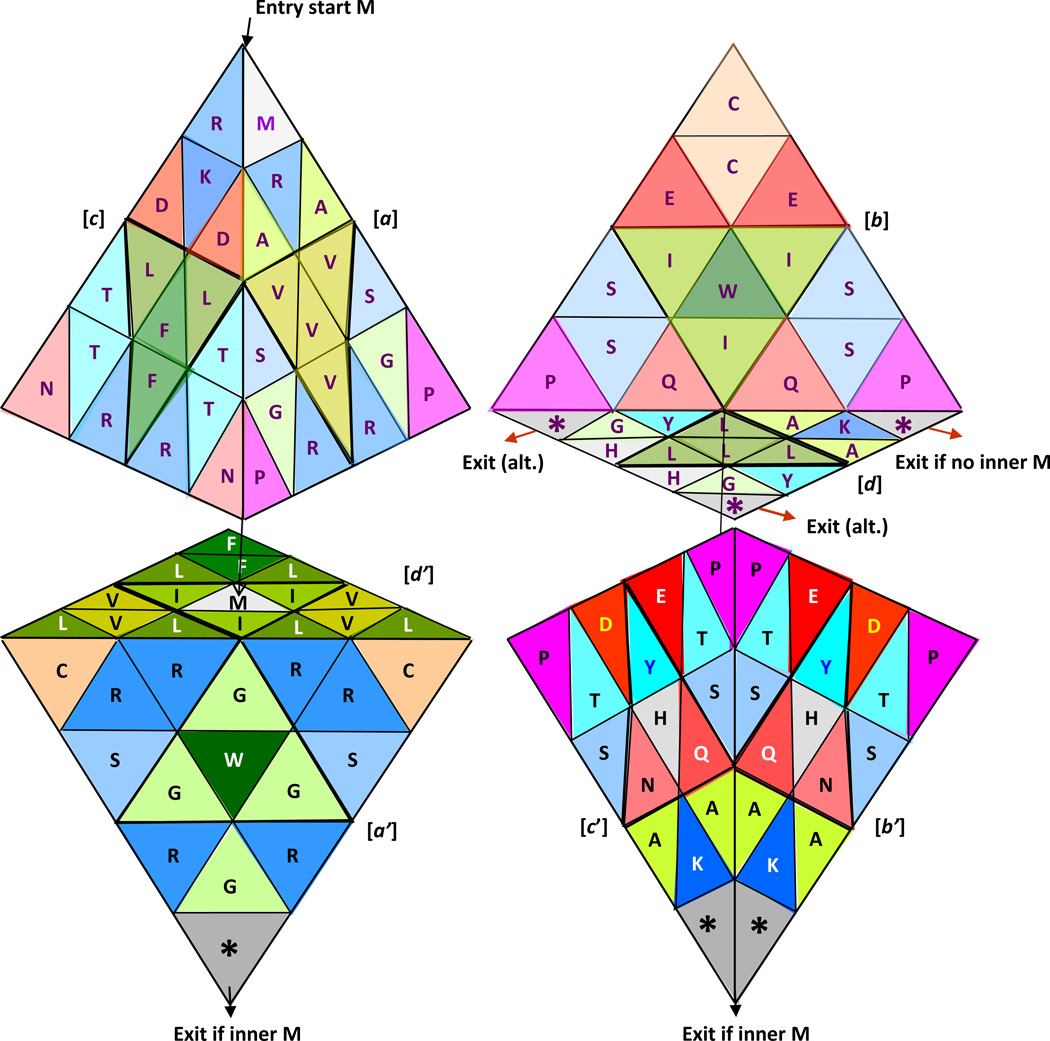
Figure 21.
A 3D diagram of flow for the translation of genes into proteins; two views of the double tetrahedron representing twice the genetic code, as a visual and/or computational strategy to differentiate the start M (ATG) from the non-start M if present, in both a genetic sequence (ATG) or in a peptide/protein; the entry start M (in purple) for the formation of the protein (translation) is indicated by the upper left arrow; if a non-start M is absent, the peptide or protein leaves at one of the three basal apical stop codons from the upper tetrahedron, with the words Exit if no inner M, plus the other two alternative exits: Exit (alt.), shown by the red exit arrows (upper); while on the other hand, if a non-start M is present in a genetic sequence, and in its resulting peptide or protein, as soon as one is detected, the translation moves to the second tetrahedron, being in this case the exit point located at the final apex, at the end, as indicated by Exit if inner M and by the exit black arrows (lower).
Figure 23.
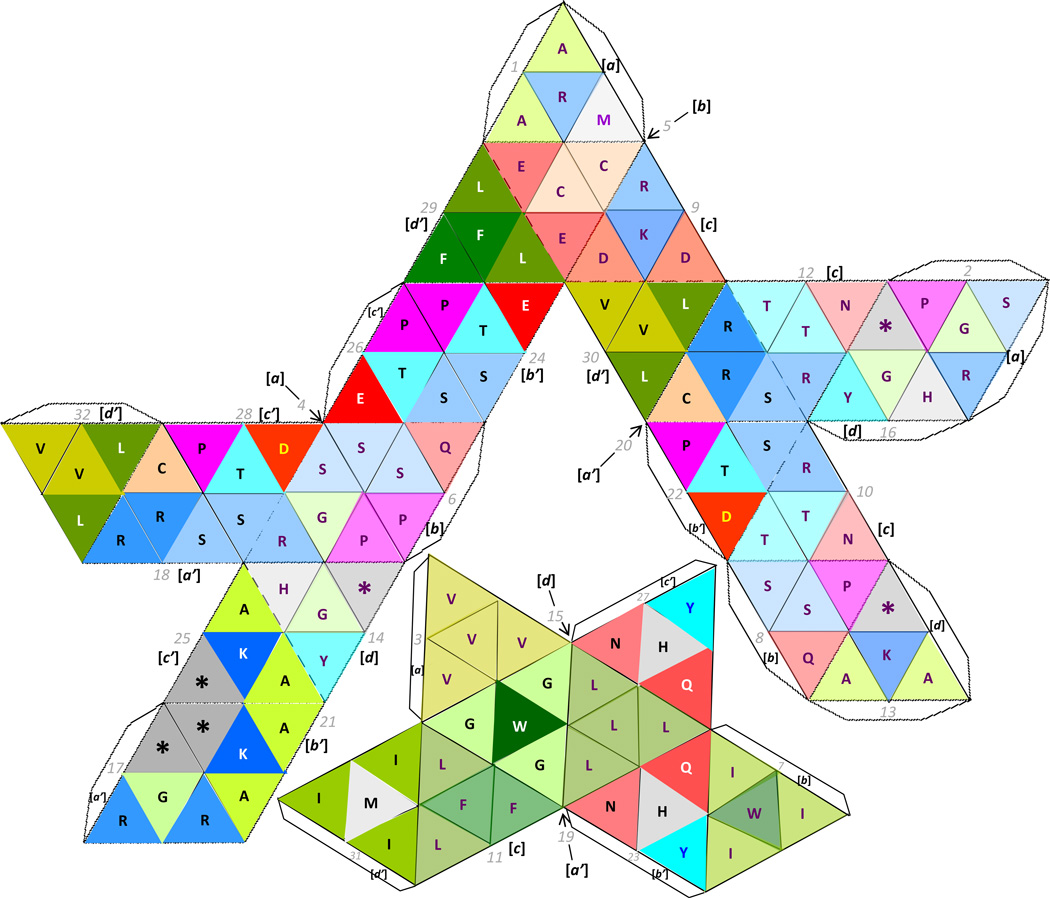
Stella octangula formed when compressing into a single geometrical figure the two genetic code tetrahedra shown in Figure 21, with each group of four amino acids being classified according to their corresponding letter [a to d'], and according to is sequential position from top to bottom and from left to right [i.e., starting with numbers 1 to 4 that correspond to a, and ending with numbers 29 to 32 corresponding to d']; notice that this geometry needs to be translucent in order to make visible its interior integrated by the smaller octahedron shown through its net below; or both structures can computationally rotate side by side in synchrony.
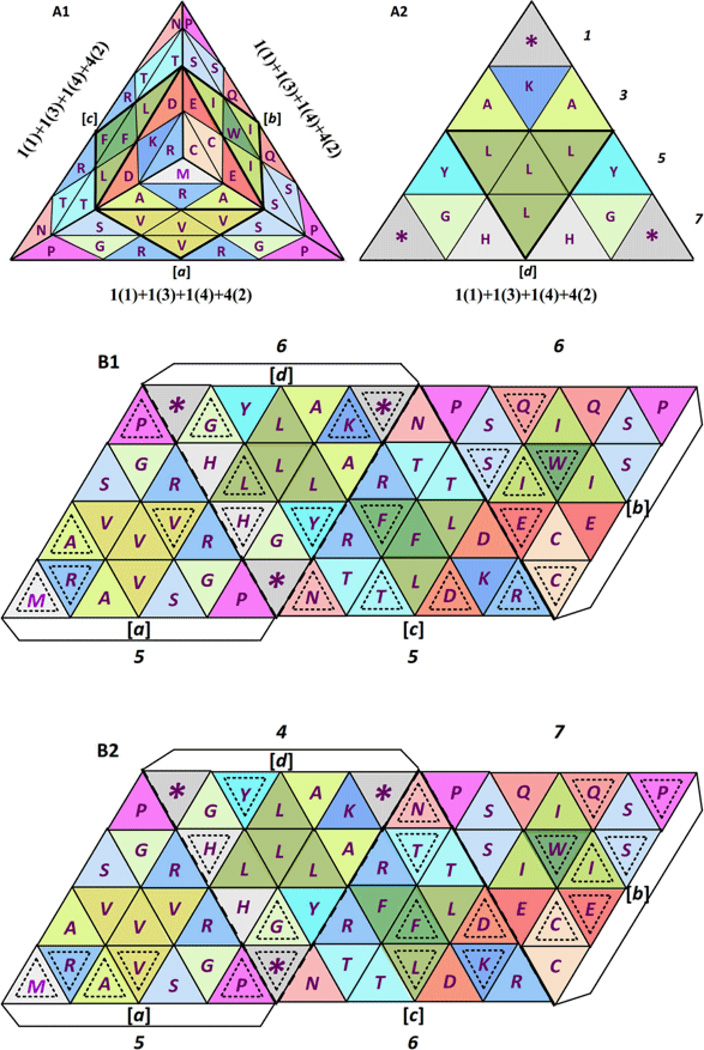
Figure 22.
Codon balance in the standard functional genetic code tetrahedron, seen here from the top (A1) and from the bottom (A2) [1], showing the expanded formula for the balance of codons in the standard functional genetic code tetrahedron: 4[1(1)+1(3)+1(4)+4(2)], where a = b = c = d [1]. Numbers at the right side of A2 show the odd pattern of equilateral triangles per row (1+3+5+7 = 16); comparing in B its alternative 2D parallelogram pattern from which an identical 3D tetrahedron results, like the one shown in A1 and A2, and in the upper half of Figure 21, showing here the position of most used codons per amino acid in man (Homo sapiens): a = c with 5:5 and b = d with 6:6 (B1), compared to the position of most used codons per amino acid in octopus (Octopus vulgaris): d ≠ a ≠ c ≠ b, or 4 ≠ 5 ≠ 6 ≠ 7 (B2).
In this work T (DNA) instead of U (RNA) will be used in order to emphasize the need for a paired DNA analysis, defining here the specific binary I Ching genetic code defragging as the pairing of complementary sequences originated from the homogeneous single-strand self-annealing as seen in the square representations, or single-codon self-annealing as seen in the circular representations, either horizontally or vertically.
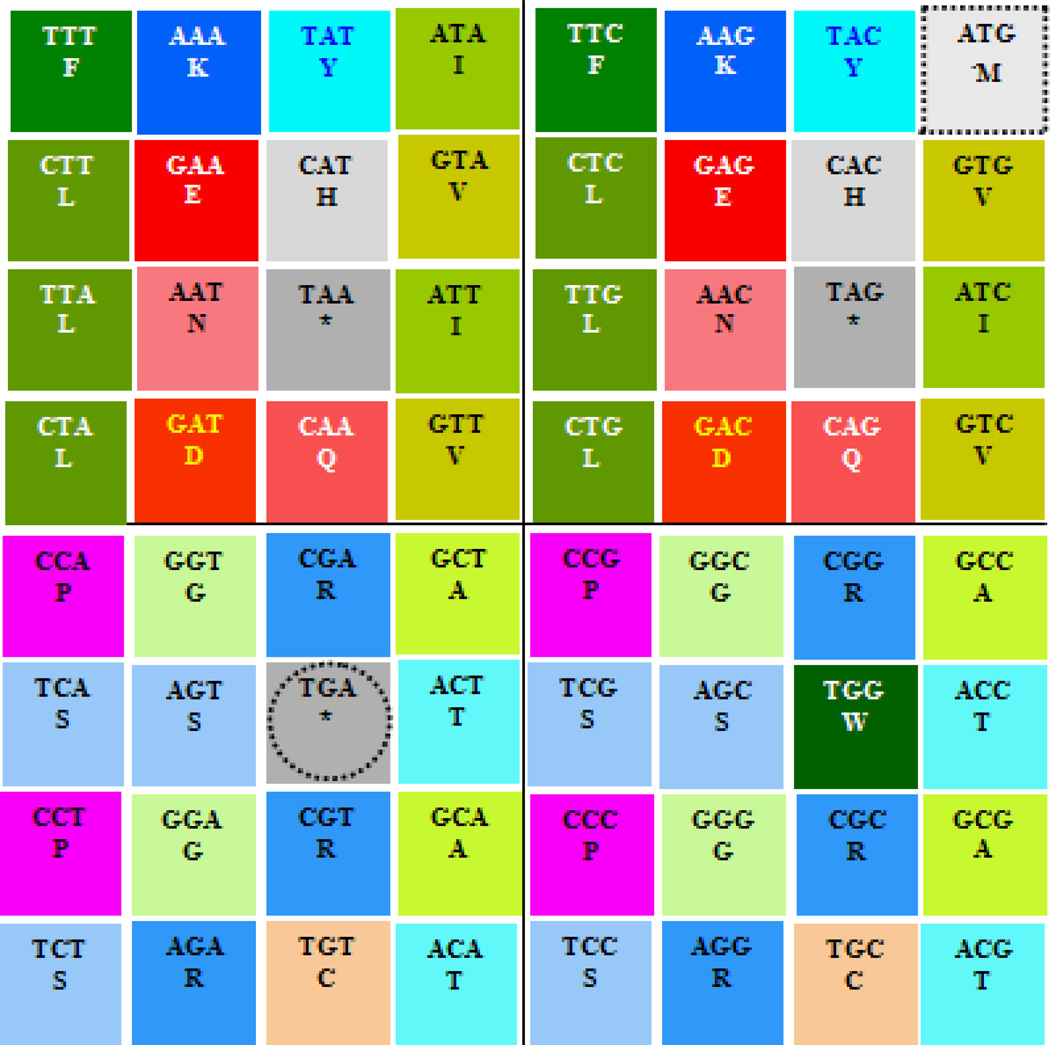
The genetic code chromosomes derived from the I Ching were here compared to the unpublished handwritten representation of the 64 codons drawn by Nirenberg in his laboratory notebook [7] according to Crick's table nucleotide sequence T (or U), C, A, G [8], also followed by Bresch and Hausmann in their classic circular genetic code [9]. The original handwritten laboratory note of the 16×4 codons by Nirenberg is at: http://profiles.nlm.nih.gov/ps/access/JJBBJX.pdf A 5' – 3' or plus orientation is assumed in every strand or sequence of codons presented here.
Additionally, an Internet search was done (05/28/2012) to determine the frequency of mention of individual amino acids using the Google Scholar search engine (http://scholar.google.com) looking for the frequency of appearances of each amino acid name (with no abbreviations), using the next conditions: 1) Find Articles with all the words (in our case this means putting in this row one amino acid at a time; amino acids with double words were searched with quote marks such as "Glutamic Acid"), 2) Date: Return articles published between: 2010 - 2012, 3) where my words occur: in the title of the article (allintitle:), of 4) Collections: Articles and patents: Search articles in all subject areas 'include' patents.
The specific pattern for the nets to obtain the stella octangula and its inner octahedron were taken from the geometrical websites of Altes [Altes GK. Stella Octangula. Paper Models of Polyhedra (1998–2012), http://www.webcitation.org/68B4BdM1a] and of the Mathematica™ software [Weisstein, EW. Octahedron (1999 – 2012), From MathWorld--A Wolfram Web Resource. http://liveweb.archive.org/http://mathworld.wolfram.com/Octahedron.html], respectively.
Results
Based on the I Ching table as originally preserved and attributed to Fu-Xi, we have simplified the resulting codons from their binary comparisons, obtaining thus the three tables shown in Figure 1.
If we defrag them, first by horizontal pairing of their codons, we obtain the results shown in Figure 2, where we are seeking for the optimal defragging that has the start codon (M) at its center (within one of the four central nucleotides). In App. A to C these horizontal defragmentations are seen in their ancient pairs of trigrams.
Figure 2.
Three binary representations of the genetic code defragged by horizontal pairing according to the numerical order of the I Ching: T. 1 Pairing the resulting binaries of H bonding with the nucleotide rings Pur/Pyr. T. 2 Pairing the resulting binaries of Keto/Amino with Pur/Pyr. T. 3 Pairing the resulting binaries of H-bonds with Keto/Amino.
The 4×8 bp tables shown in Figures 2 and 3 are divided in four horizontal pairings, while Figures 4 and 5 are divided in four vertical pairings.
Figure 3.
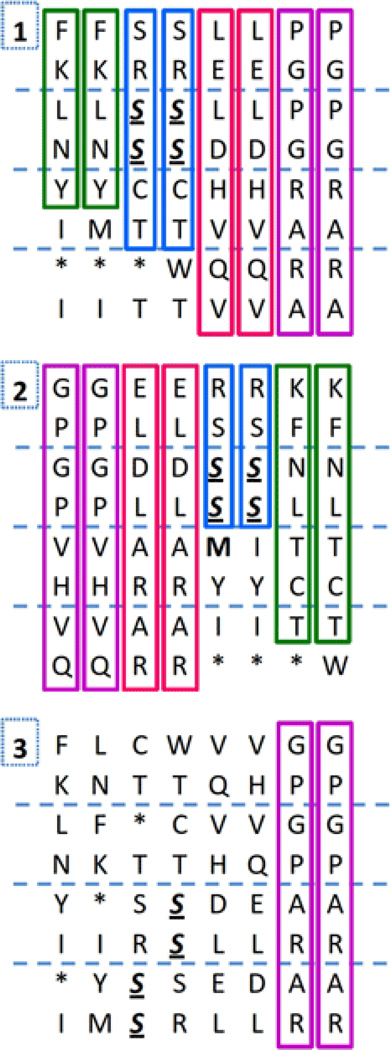
Three binary amino acid representations of the genetic code defragged by horizontal pairing according to the numerical order of the I Ching: T. 1 Pairing the resulting binaries of H bonding with the nucleotide rings Pur/Pyr. T. 2 Pairing the resulting binaries of Keto/ Amino with Pur/Pyr. T. 3 Pairing the resulting binaries of H-bonds with Keto/Amino. Vertical rectangles, the continuous amino acid strand similarities. The exclusively reciprocal codons for serine are in bold italics underlined. The M present at the center of T. 2 is in bold.
Figure 4.
Three binary triplet representations of the genetic code defragged by vertical pairing according to the numerical order seen in the I Ching: T. 1 Pairing the resulting binaries of H bonding with the nucleotide rings Pur/Pyr. T. 2 Pairing the resulting binaries of Keto/Amino with Pur/ Pyr. T. 3 Pairing the resulting binaries of H-bonds with Keto/Amino.
Figure 5.
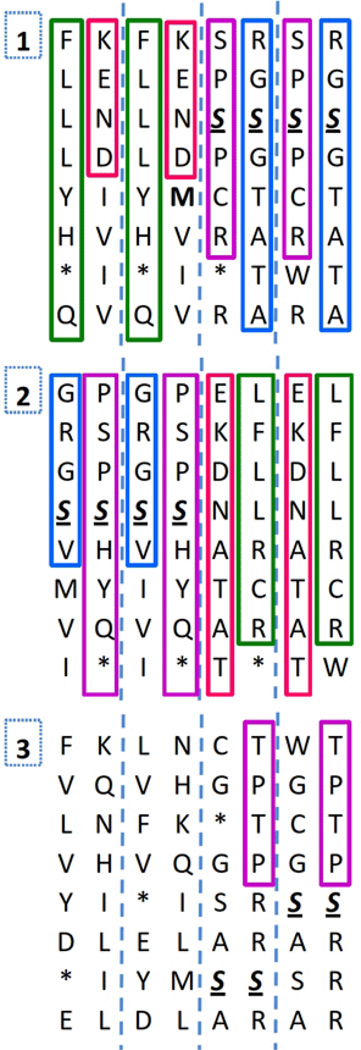
Three binary amino acid representations of the genetic code defragged by vertical pairing according to the numerical order of the I Ching: T. 1 Pairing the resulting binaries of H bonding with the nucleotide rings Pur/Pyr. T. 2 Pairing the resulting binaries of Keto/ Amino with Pur/Pyr. T. 3 Pairing the resulting binaries of H-bonds with Keto/Amino. Vertical rectangles, the continuous amino acid strand similarities. The codons for serine are in bold italics underlined. M at the center of T. 1 is in bold.
If we now move one step forward by simplifying these images as we did before [2] by only placing the corresponding amino acids instead of their codons, we will improve the ease to identify patterns, as it will be seen in Figures 3 and 5.
In Fig. 3 we can see that the only horizontal desfragmentation (defragging) by pairing locating the starting codon or Met at the center is its T. 2, in which we also see one S touching the center and side-by-side, the two pairs of codons producing Ser; two of the three horizontal desfragmentations by pairing were able to reproduce an amino acid quasi-identity for the pairs of genetic code chromosomes shown below, but only when seen vertically (see the colored rectangles Figure 3).
Ser is peculiar because it is the only amino acid (and its codons) matching always, or occupying, the same paired relative positions in every single-strand self-annealed comparison.
Figures 2 and 3 show the horizontal defragging by comparing the three properties of nucleotides within this single-strand self– annealed genetic code, pairing them both by codons and by amino acids, respectively.
Next, we will see the vertical defragmentation through pairing, both by codons (Figure 4), and by their corresponding amino acids (Figure 5).
In Figures 4 and 5 the central codons and corresponding amino acids will again be emphasized, while their defragmentation using the ancient pairs of trigrams will be seen in App. D to F.
In this article, the codon sequences derived from defragging by vertical pairing are the ones that will be analyzed in detail; the horizontal ones and the directionality obtained by the four elements of such molecular Yin/Yang, as mentioned, I expect to be able to present elsewhere.
We need to notice the central position of the functional start, Met (M) in T. 1 of Figure 5, resulting from defragging the codons by vertical pairing.
The successful combinations providing the ordered result of an almost identical duplicate of two sets of chromosomes by looking at their amino acids, were the ones comparing two and three H-bonds (0 and 1, respectively) or the nucleotide tautomerism Keto/Amino (0 and 1, respectively), with the nucleotide rings Pur/Pyr (0 and 1, respectively).
The pairing that did not show any of these quasi-identities vertically or horizontally is the one that compared H-bonds with the Keto/Amino tautomerism or its reciprocal (not shown). The amino acids within the pairs of genetic code chromosomes shown both in T. 1 and T. 2 of both Figures 3 and 5 where, respectively, almost a perfect replicate, a quasi-identity, except for the two one-codon amino acids: 1) the start, which can only be contributed by one codon: Met, which did break the identity of the genetic code chromosomes by matching to Ile in the opposite chromatid, while 2) Trp was also breaking the identity by matching with the peculiar stop TGA, the one that not only is the most frequent releaser of the completed proteins from human ribosomes, but also a solitary or unique stop codon when compared to its other two counterparts, the stop pair that starts with TA_.
This break of identity due to the presence of odd codons in the genetic code happened in all the quasi-identities shown in this article, being only sorted out by the triangle that was 100% symmetrical having 64 triangular grids and source of the 100% symmetrical tetrahedron shown respectively in Figure 20 and in the lower part of Figure 21, and of Figure 23, when folded.
Figure 20.
The 3D 16×4 100% symmetrical genetic code tetrahedron, where the logic within the 2D binary I Ching according to Fu-Xi from the pair of genetic code chromosomes I', the 'horizontalized' defragged vertical pairing for its second binary genetic code combination [Keto/Amino, axis x (G = U = 0, A = C = 1); Pur/Pyr, axis y (A = G = 0, C = U = 1)], was transferred into a 3D tetrahedron. The pairing shown in Figure 17 of codons has been lost in this representation while the functional, positional resonance has been kept between b and c, while d and a have individual symmetry within themselves. The allocating logic consists on transferring from Figure 17: row 4 and 5 to d, rows 2 and 7 to a, rows 3 and 8 to b, and rows 1 and 6 to c.
It needs to be noticed that I', a modified version of the pair of genetic code chromosomes I represented within T. 2 of Figure 5, will be our pair of chromosomes of choice to illustrate the reverse engineering of the binary I Ching genetic code into its unique symmetrical 3D geometry.
Next, and in order to obtain a global perspective of how deep each amino acid is currently studied worldwide (since 2010 to present), we did a browsing using the search engine of Google Scholar (as mentioned in Methods) with the results shown in Table 1.
Table 1.
Academic use of amino acids in the literature as observed on the Internet
| Amino Acid | Use | Amino Acid | Use | Amino Acid | Use |
|---|---|---|---|---|---|
| Tyrosine, Y | 4,690 | Proline, P | 1,410 | Histidine, H | 912 |
| Glutamate, E* | 4,288 | Methionine, M | 1,330 | Phenylalanine, F | 772 |
| Glycine, G | 2,900 | Tryptophan, W | 1,330 | Threonine, T | 574 |
| Cysteine, C** | 2,633 | Aspartate, D*** | 1,206 | Valine, V | 266 |
| Arginine, R | 2,210 | Alanine, A | 1,090 | Asparagine, N | 184 |
| Serine, S | 2,040 | Glutamine, Q | 1,020 | Isoleucine, I | 148 |
| Lysine, K | 1,950 | Leucine, L | 948 | Stop, # | 76 |
Limits: Google Scholar search engine, articles and patents, title, full amino acid name, since 2010 to 05/28/12.
Notes:
Sum of Glutamate: 3,670 + “Glutamic Acid”: 618 = 4,288;
Sum of Cysteine: 2,390 + Cystine: 243 = 2,633;
Sum of Aspartate: 918 + “Aspartic Acid”: 288 = 1,206;
Sum of “Stop Codons”: 18 + “Stop Codon”: 52 + “Nonsense Codons”: 4 + “Nonsense Codon”: 2 = 76; for comparison with the normal Stops, “Nonsense Mutation”: 135 + “Nonsense Mutations”: 54 + “Stop Mutation”: 10 = 199, locating these mutations with 15 hits above N [05/28/2012].
Table 1 indicates that the amino acid most currently investigated is Tyr, the star of the signal transduction, followed by Glu, the polar acidic amino acid, and by Gly, the smallest of them all, in that order and from more to less; on the other hand, the less investigated functions and/or amino acids of the genetic code were: the stop codons (*), then Ile, which is an essential hydrophobic amino acid, followed by Asn, an amide, in that order and from less to more.
And, even when a book could be written for each of these amino acids, and more than one for the ones that are the most used, here the emphasis will be made on the importance of the start codon, Met, by seeking for it at the center of the defragged binary genetic code, being this the best theoretical way to start the comparison of genes when using the genetic code as its engine.
Table 1 also shows that, both the stop codons and the Ile codons, each of them belonging to the only two odd groups that only have three codons, appear together and are currently the two less investigated, while Met and Trp, the only two odd amino acids having only one codon, were also side-by-side, occupying positions 9th and 10th, respectively, both with 1,330 hits, in the last search done on 05/28/12, being in reality in the same theoretical position of the table, while serine occupied the 6th position.
In Table 1 we see that each set of functional amino acids falls in a different column according to the research invested on them, and/ or in their scholarly interest, with Ser in the first column, where we also see at the top, as mentioned, the hydroxy phosphorylatable Tyr, which molecularly is also the head of the cellular signal transduction. Cys is also present in the first column, the binder of peptides and of proteins. In the second column, as mentioned before, we see side-by-side the amino acids that only have one codon: Trp, and Met the starter; as head of the second column we have Pro, the bender. In the third and last column, which is also the end of the whole table, we have the groups with only three codons: Ile and the Stops, headed by the aromatic His, which is the catalyzer of enzymes, and by the aromatic Phe, while Thr, the third phosphorylatable amino acid, was also present in this third column.
Table 1 also shows that the functional importance of amino acids is independent of their number of codons: Tyr is at the head of the list having only two codons, while Ile and Stop are at the end of the list having three codons each, while the ones with only one codon are tied in the positions 9th and 10th. The possessors of six codons are distributed near the end of column one and ending column two, while the ones with two and four codons are spread throughout the three columns.
In order to perceive their trend, I did the same analysis shown in Table 1 more than two months ago (03/09/12), compared to my last analysis done on 05/28/12, showing in order from the most to the least, the next increase in the study of amino acid and/or of function between the two analysis: E (Glutamate: 430, "Glutamic Acid": 90, with an E total increase of 520), Y: 480, G: 460, C (Cysteine: 260, Cystine: 30, with a C total increase of 290), R: 260, K: 240, S: 230, M: 200, P: 190, A: 174, W: 170, D (Aspartate: 105, "Aspartic Acid": 36, with a D total increase of 141), L: 138, Q: 131, H: 112, F: 112, T: 59, V: 47, N: 21, I: 21, and * (Stop Codons: 5, Stop Codon: 8, Nonsense Codons: 4, Nonsense Codon: 2, with a total increase of 19).
If we go back now to the Chinese binary code, we notice that since the days of Leibnitz [6] its potential was clearly perceived for the study of mathematics, and at least since Stent also for the study of genetics [10], something corroborated by Schonberger [11], while Swanson analyzed the importance of binary systems to understand the genetic code, being her study independent of the I Ching [12]; so, the potential of binary systems and/or of the I Ching for genetics has clearly been acknowledged by these pioneers and by others mentioned in [2] after them, a study that I attempt to advance with this and other related publications.
For every possible combination of nucleotide properties in the context of single-strand self-annealing, we are finding that, as it happens in informatics in general, also the genetic code and its conformational grids can be defragged to optimize the informational flow, with the peculiarity here that we can enhance its molecular pattern through geometries, both in 2D and in 3D.
We found that the best defragmentation according to our background references is the strategy where the most used bits of information are located at the center, and we are seeking here for the starting codon to be in this optimal position, the central location deemed to be the most important for starting translation, because without it, there will be no peptides or proteins at all. So, we are aiming to find Met at a central position, noticing that this was the case for only one instance of the horizontal and also for only one instance of the vertical defragging by pairing.
And apart of the well known importance of serine as the phosphorylatable determinant for the activation and/or function of enzymes and proteins, and of its vital function in signal transduction, recent studies seem to indicate that the Ser built from glucose is also very important in brain development, in neuronal survival, and in neuronal signaling, being this remarkably achieved by either of its two amino acid isoforms: l-serine [13] and, after being additionally processed by the enzyme serine racemase, also by d-serine [14], having both of them a balanced presence, and a reciprocal shuttling [15].
Now, if we were to design a model for the ideal compatible pair of chromosomes based on the results of single-codon self-annealing by pairing of the genetic code, while also looking at the similarity of its resulting amino acids that in the end will produce similar peptides and proteins, then, a system of choice to use a pair of genetic code chromosomes in bioinformatics could be the first table (T. 1) of Figure 5; however, in the same way that this table has its specific advantages and properties, we will see below that also a product of T. 2 has some unique attributes (i.e., the 100% pairing of its I Ching hexagrams, etc.)
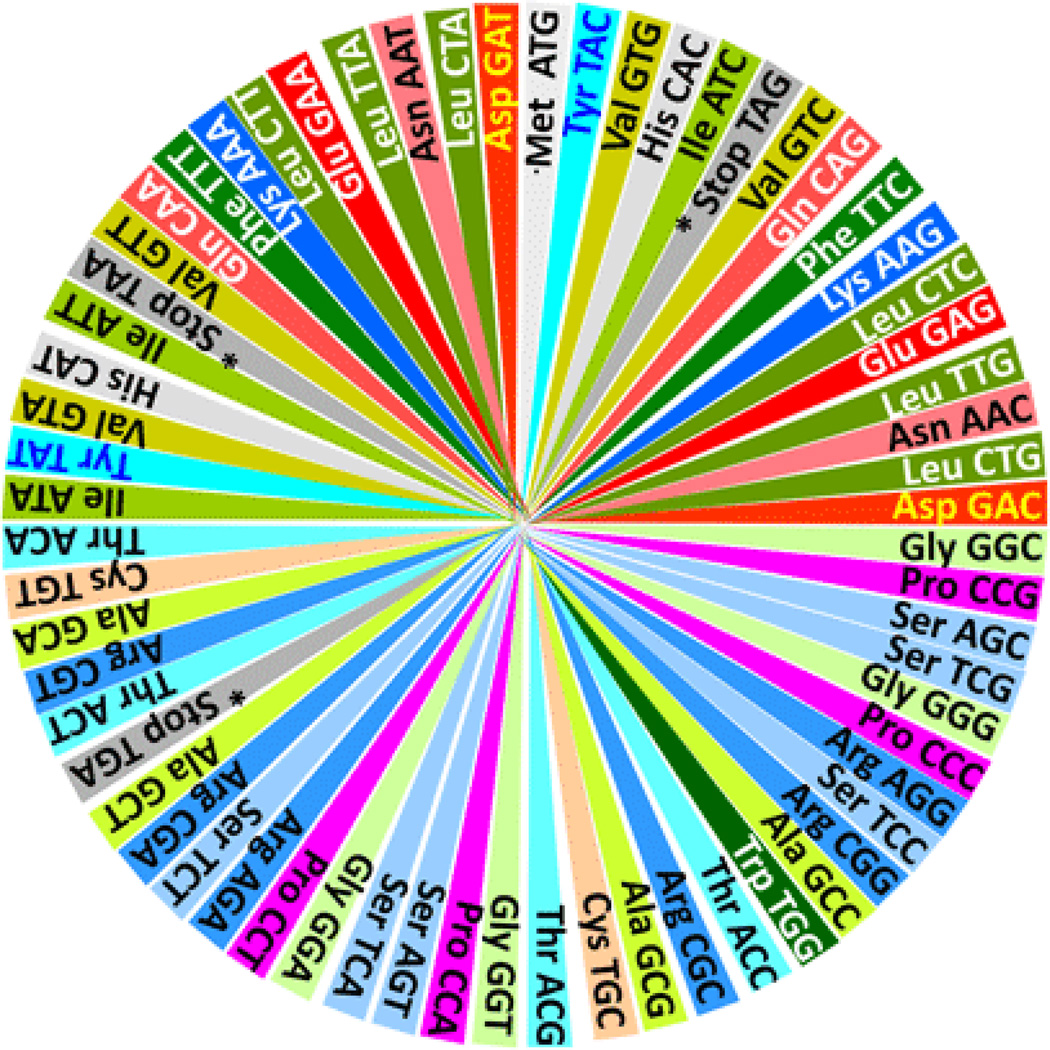
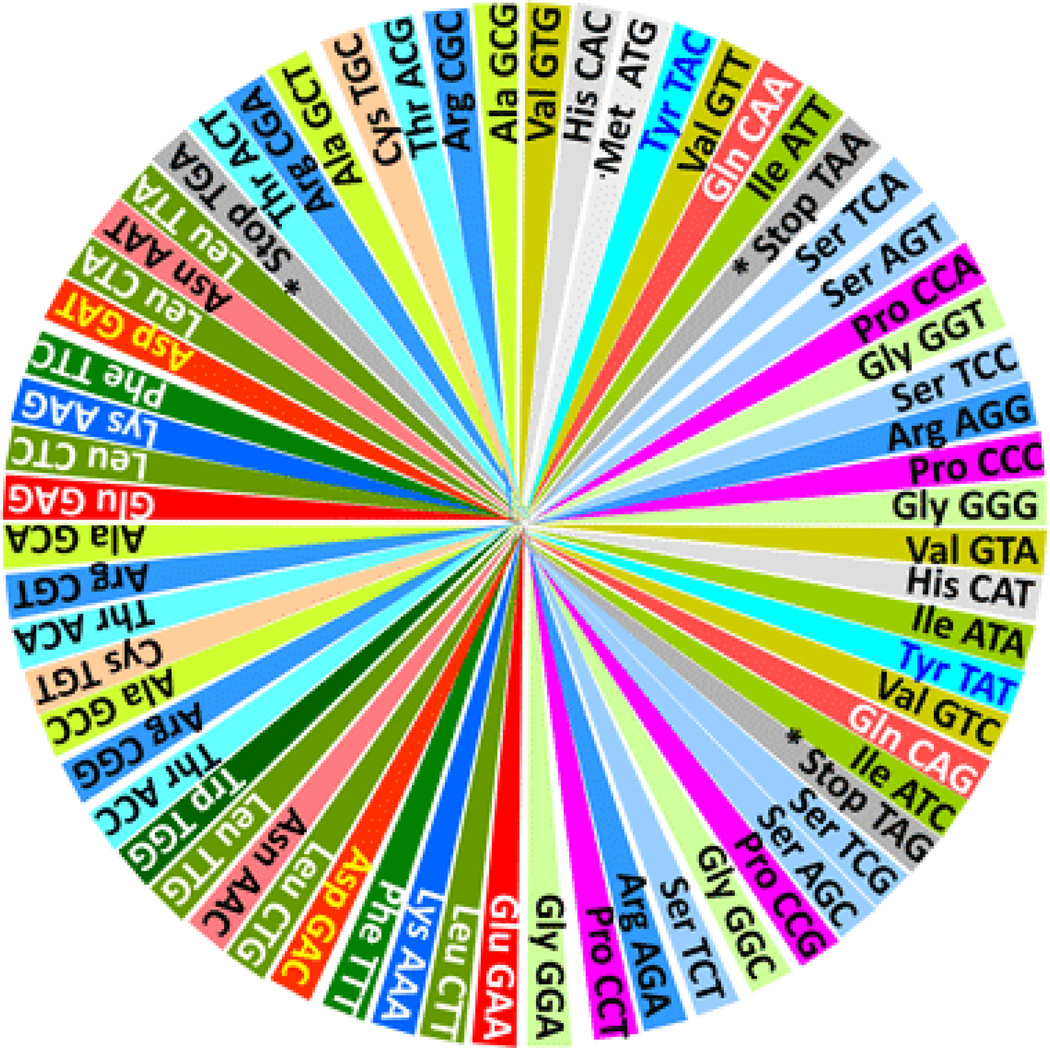
And, as we have seen before, the first two tables (T.1 and T.2) presented in Figure 5 will also be arranged in the two quasi-identical synthetic pairs of chromosomes (M and I) shown at the right side of Figure 6, representing the whole genetic code through each pair of genetic code chromosomes.
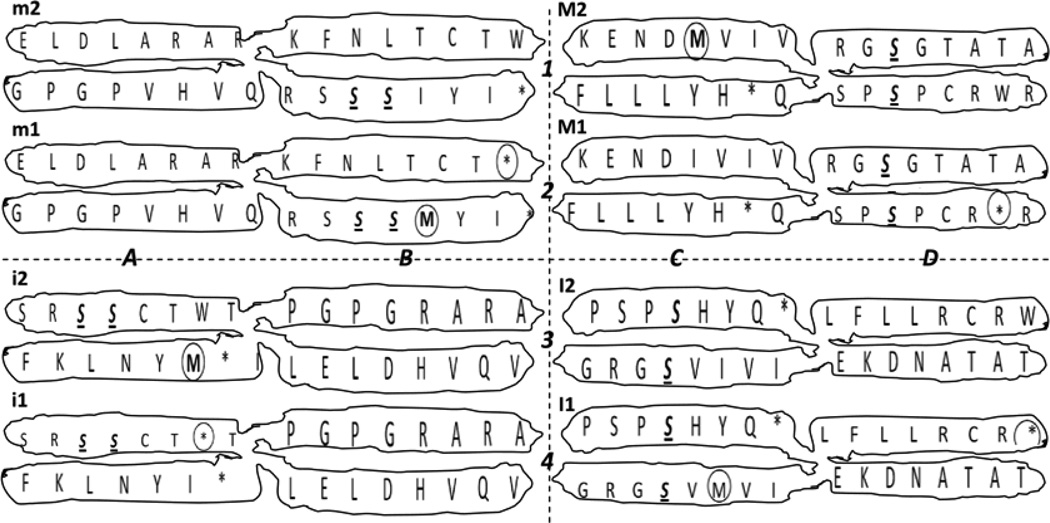
Figure 6.
Quasi-identical synthetic genetic code chromosomes obtained by defragging. Upper rows 1 and 2, left side: Chromosomes m (m1 and m2, obtained by the vertical view of the horizontal defragging shown in T. 2 of Figure 3) and, right side: M (M1 and M2, obtained by the vertical view of the vertical defragging shown in T. 1 of Figure 5). Lower rows 3 and 4, left side: Chromosomes i (i1 and i2, obtained by the vertical view of the horizontal defragging shown in T. 1 of Figure 3) and, right side: I (I1 and I2, obtained by the vertical view of the vertical defragging shown in T. 2 of Figure 5). Note: the single-codon self-annealed Ser, S, always fell in the same relative position of both of the chromatids per chromosome, being indicated in italics, bold and underlined, while the odd or uneven functional codons for the start (ATG, M) and for the end (TGA, *) are noticed by a small dotted circle. Each pair of chromosomes is the complete representation of the genetic code, so we have here half or four of its alternate genetic code chromosomal representations.
It needs to be noticed that none of these binary codon codes, or their amino acids, exhibits a numerical balance of codons such as the one seen in some alternate functional resonating genetic code models [1, 2, 16, etc.].
The vertical view of the horizontal defragging also produced two pairs of genetic code chromosomes, the two pairs of genetic code chromosomes m and i seen at the left side of Figure 6.
The quasi-identical patterns seen in these four pairs of synthetic genetic code chromosomes remind us of the protective strategy of enzymes with a same function through nature, with the pair of synthetic genetic code chromosomes M (upper right pair of (Figure 6) mimicking the bias reported elsewhere in humans and mammals having a three H-bond preference for the third nucleotide of most used codons per amino acid (chromosome M2, where Met is located in its upper left arm), while on the other hand, invertebrates and plants have a two H-bond preference for their third nucleotide of most used codons per amino acid (chromosome M1, where the TGA stop codon, the most used in man [17], is located, in the lower right arm), a phenomenon also seen in the pair of genetic code chromosomes i1 and i2 shown in the lower left side of Figure 6.
An explanation of the logic for the amino acid transfer from the binary systems shown in Figures 3 and 5, to the four pairs of genetic code chromosomes shown in Figure 6, can be seen in App. G.
If we now transition to a quantum logic, we proceed to rearrange codons for two pairs of the obtained genetic code chromosomes, starting by slightly modifying the genetic code chromosomes shown in the right side of Figure 6, in order to keep all hydrophobic amino acids with T at the center in only one arm, then for a positional quasi-identity and to improve semi-introversion, we obtain two related chromosomes:
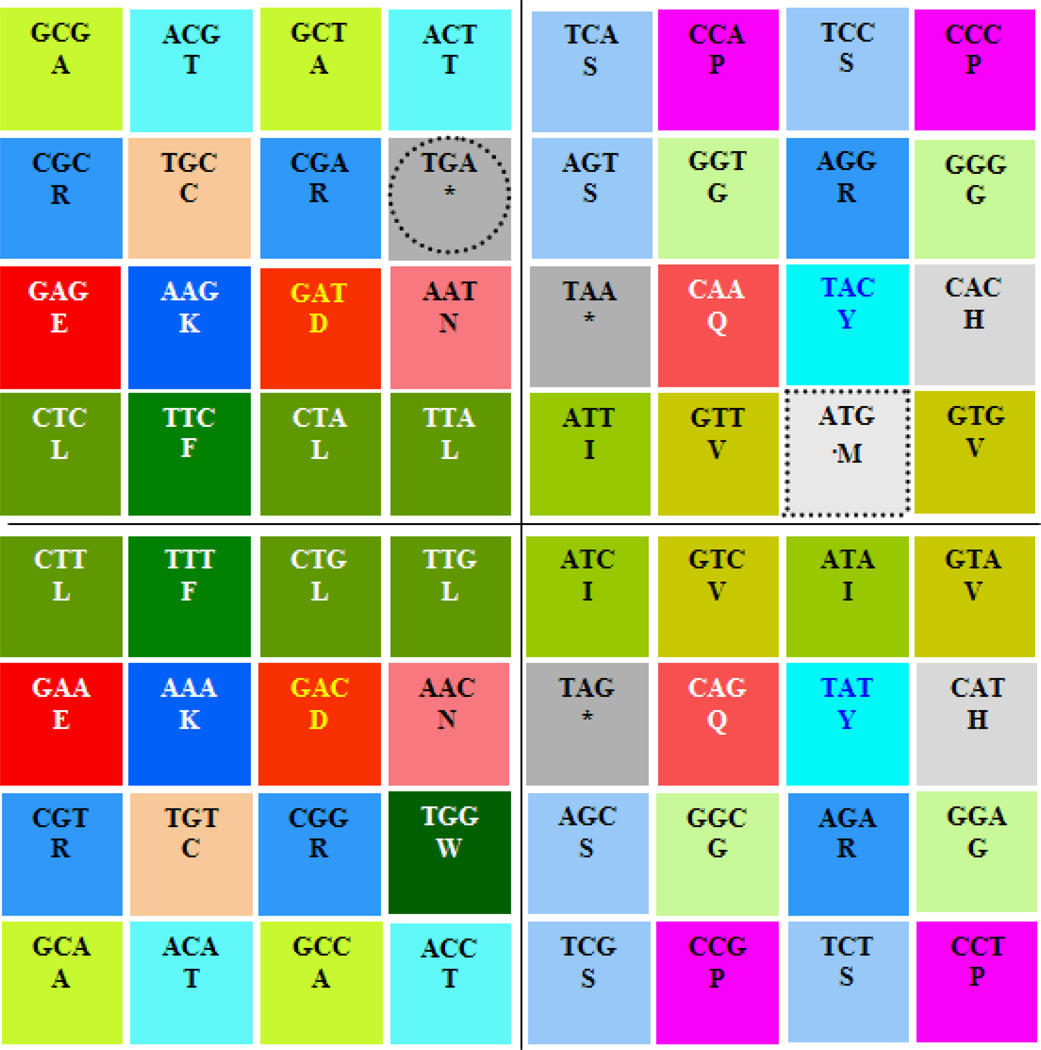
a) The chromosome M' shown in Figure 7, with one example of semi-introversion for its upper chromatid being: TAC-CAC-TAG-CAG-AAG-GAG-AAC-GAC / GGC-AGC-GGG-AGG-CGG-TGG-CGC-TGC, etc., showing here in bold italics the A/G exchange within central nucleotides; the accompanying M' hexagrams within the I Ching are shown in Figure 8 ; and b) The chromosome I' is shown in Figure 9, while its respective I' hexagrams within the I Ching are shown in Figure 10.
Figure 7.
Pair of genetic code chromosomes M', their quasi-identical correspondence can be seen horizontally, between the upper and the lower chromosomes and their chromatids (except M and W); the semi-introversion can be seen vertically, between the left side arms and the right side arms (where only the central nucleotides are reciprocally replaced, G for A (r by r) or C for T (y by y). Notice the uniform location of essential hydrophobic codons with T at the center in one left arm per chromosome.
Figure 8.
I Ching hexagrams paired reshuffled from the product of a Cartesian comparison of trigrams: H-bonds for the axis x (A = U = 0, C = G = 1) and Pur/Pyr nucleotide rings in axis y (A = G = 0, C = U = 1). The four sets of single-strand self-annealed double-helixes run vertically in this representation lacking the 0 to 1 match seen in Figure 10.
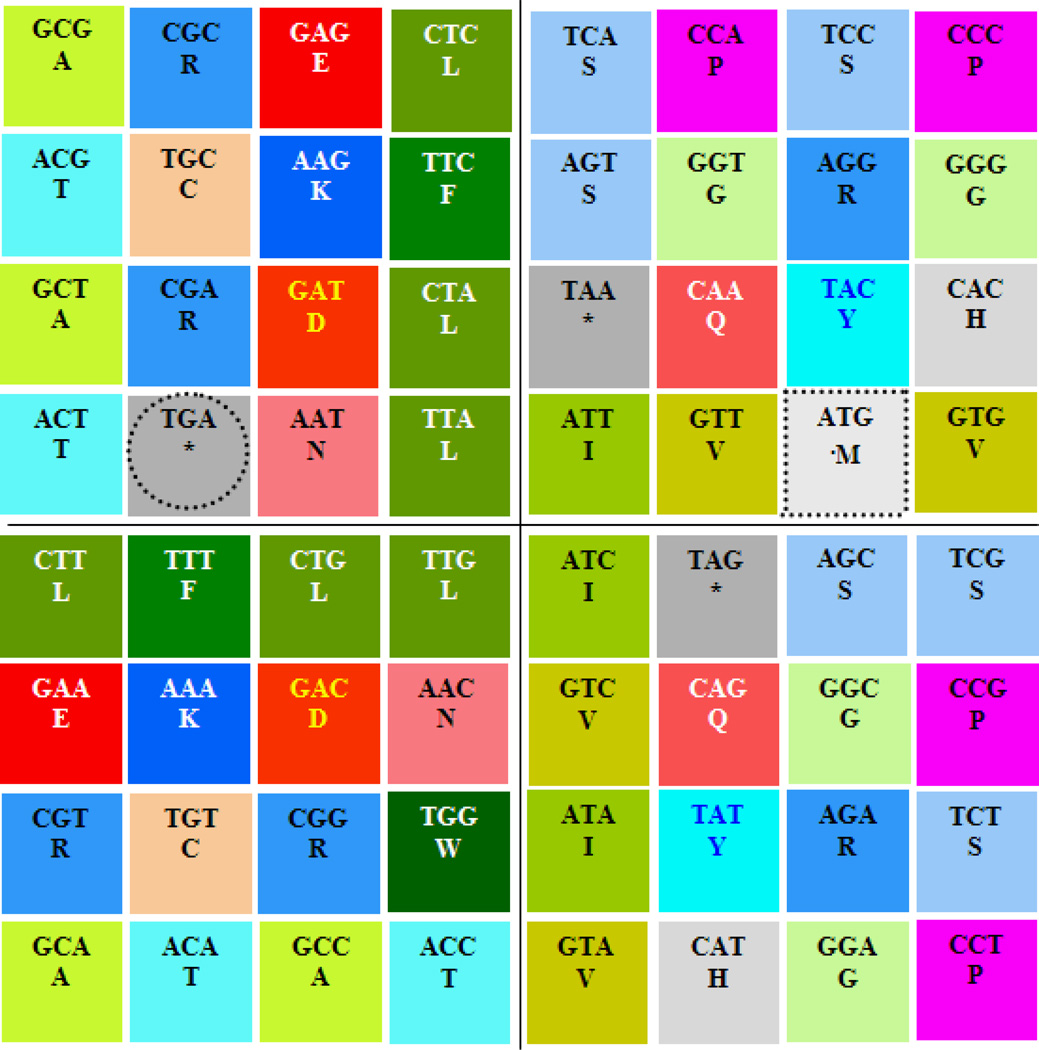
Figure 9.
Pair of genetic code chromosomes I', their quasi-identical correspondence can be seen horizontally, between the upper and the lower chromosomes and their chromatids (except M and W); the semi-introversion can be seen vertically, between the left side arms and the right side arms (where only the central nucleotides are reciprocally replaced, G for A (r by r) or C for T (y by y). Notice the uniform location of essential hydrophobic codons with T at the center in one left arm per chromosome.
Figure 10.
I Ching hexagrams reshuffled from the product of a Cartesian comparison of trigrams: Keto/Amino tautomerism, axis x (G = U = 0, A = C = 1); Pur/Pyr, axis y (A = G = 0, C = U = 1); this 2D binary comparison (and its reciprocal not shown here), where the only ones that exhibited a unique pairing of its vertical pairs of hexagrams, showing the pairing of every 0 with every 1 along all the 32 pairings that constitute this table. The four sets of single-strand self-annealed double-helixes run vertically in this representation (four pairs of 8 bp).
The double pairs of genetic code chromosomes M' and I' have both a horizontal quasi-identity by amino acids (except M and W), and a vertical semi-introversion in the second nucleotide of all their codons when we compare the left half of each chromosome with its right half as exemplified, with a reciprocal exchange of purines within themselves (A for G and vice versa), and of pyrimidines within themselves (T for C and vice versa), as seen in Figures 7 and 9.
In Figure 7 we can see the rearrangement and coloring of the upper right part of Figure 6, obtaining the pair of genetic code chromosomes M’. It needs to be noticed that the upper genetic code chromosome M' shown in Figure 7, as its parental genetic code chromosome M2 had, has only C and G at its third nucleotide, which again is what dominantly happens in humans and mammals, while the lower genetic code chromosome M' only has A and T at its third nucleotide, as it happens dominantly in plants and invertebrates, keeping this property in common also with its original or parental genetic code chromosome M1.
The pattern for the third nucleotide seen in the pair of genetic code chromosomes M' shown in Figure 7 is, for the upper or 'mammal' M' chromosome: 2(2C-4G-2C) and 2(2G-4C-2G) for its upper and lower chromatids, respectively; while for the lower or 'invertebrate' M' chromosome we have: 2(2A-4T-2A) and 2(2T-4A-2T) for its upper and lower chromatids, respectively.
Special care has been taken to show in both pairs of genetic code chromosomes (M' and I'), not only a quasi-identity between the upper and the lower chromatid and the grouping of essential hydrophobic amino acids with T at the center in only one of their left arms, but also as indicated, a semi-introversion within the two arms of each chromatid consisting of the exchange at the central nucleotides of purines for purines and of pyrimidines for pyrimidines.
Figure 8 does not produce the perfect correspondence of 0s and 1s seen in Figures 10, 18, 26 and 29. The logic behind the reshuffling to obtain the pair of genetic code chromosomes M' (Figure 7) and the pair of genetic code chromosomes I’ (Figure 9) can be seen in App. H.
Figure 18.
Modified alignment of the binary genetic code with double trigrams (hexagrams) of the I Ching as seen in the pair of genetic code chromosomes I'; the defragging by vertical pairing has been modified once more to an horizontal pairing to keep the logic of a 64-grid composed by four quadrants keeping the starting codon Met, ATG, in quadrant one. The four sets of single-strand self-annealed double-helixes run horizontally in this representation (four pairs of 8 bp).
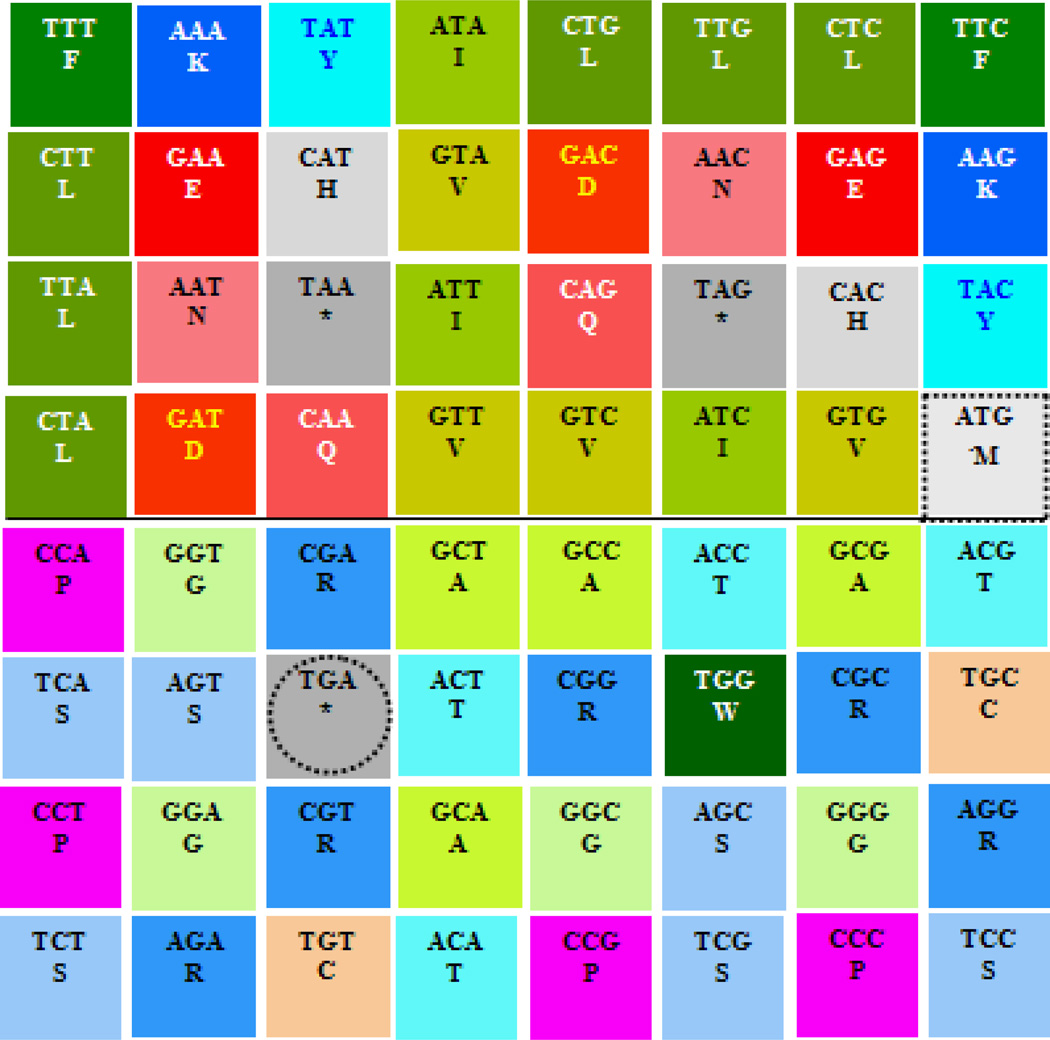
Figure 9 shows the synthetic pair of genetic code chromosomes I’, a modified version of the parental pair of genetic code chromosomes I that were directly obtained as shown at the lower right side of Figure 6.
The pattern for the third nucleotide seen in the pair of genetic code chromosomes I' (Figure 9) is, for the upper chromosome and for the left and right arm of its upper chromatid: 2C-2A-2T-2G and 2G-2T-2A-2C, respectively, while it appears transposed to 2G-2T-2A- 2C and 2C-2A-2T-2G for the left and right arm of its lower chromatid, respectively; for the lower chromosome, the pattern is 2A-2C-2G-2T and 2T-2G-2C-2A for the left and right arm of its upper chromatid, respectively, being also transposed to 2T-2G-2C-2A and 2A-2C-2G- 2T for the left and right arm of its lower chromatid, respectively. So, Figure 9 shows the even distribution (50/50) of third nucleotides (Pur/Pyr) in the codons that are present along the whole pair of genetic code chromosomes I’.
Figure 10 shows that the pair of genetic code chromosomes I' produced a vertically aligned side-by-side pairing of hexagrams where the 0s were paired to the 1s in all of its 32+32 I Ching components.
The two pairs of genetic code chromosomes represented in both Figure 7 and Figure 9 will be transferred next into their related 2D, 64-grid and circular representations, with the end to obtain in both cases a 90° rotational resonance of amino acids.
Figure 11 and Figure 14 show that the result of respectively transferring the two pairs of genetic code chromosomes M' and I' into a 64-grid vertical paired distribution does not directly produce an immediate rotational resonance, which is what happened when the circular representation of the genetic code was transferred to a related 8×8 distribution using quantum logic [2]; however, if we focus in the resulting amino acids, we can see that in these particular results, the right half of the figure can almost perfectly be superimposed to the left side, except again for the two unavoidable breaks of identity: an "I" occupying in the one half the place where "M" is located in the other half, while an "*" (TAG) occupies in the one half the place where "W" is located in the other half of this quasi-perfect overlapping.
Figure 11.
Resulting 64-grid 2D representation of the reverse engineered pair of genetic code chromosomes M'. The start and the most used stop codon in man are indicated with dotted geometries, while M and W are the amino acids with only one codon that are breaking the identity. Semi-introversion has been intended between the upper and the lower half, where every A and T in the second nucleotide of the upper codons has been replaced by their alternative purine or pyrimidine G and C nucleotides in the lower half, respectively. Notice the four sets of single-strand self-annealed double-helixes running vertically (four pairs of 8 bp).
Figure 14.
Resulting 64-grid 2D representation of the reverse engineered pair of genetic code chromosomes I'. The start and the most used stop codon in man are indicated with dotted geometries, the odd codon functions that are breaking with the identity. Notice the four sets of single-strand self-annealed double-helixes running vertically (four pairs of 8 bp).
And also, the semi-introversion of codons can be clearly seen in Figure 11, where the only replacements between the upper and the lower half of this genetic code representation occurred at the second or central nucleotide; for example, the As and Ts in the upper half (and only As and Ts are present at the center of all the codons of the upper part of this 64-grid table), have been all replaced by Gs and Cs in the lower half (and only Gs and Cs are present at the center of all the codons that integrate the lower part of this table).
Figure 12 shows that when the pair of genetic code chromosomes M' are transferred by paired bases (i.e., ATG pairing TAC, GTG pairing CAC, etc.) to a circular representation, differently to what happened in the 64-grid conformation, the 90° positional resonances were kept for almost all the amino acids within the two quadrants of the upper half (quadrants 4 and 1), and also within the two quadrants of the lower half (quadrants 3 and 2), except again for Met and Trp.
Figure 12.
Resulting circular 2D representation of the reverse engineered pair of genetic code chromosomes M'. Notice the horizontal semi-introversion (the upper part semi-introverted with the lower part, where the central purines/pyrimidines are replaced by their alternative purines/ pyrimidines, in a replacement of C for T and A for G), and of the vertical resonance, the right half is resonating at 90° with the left half (quadrant 1 with 4, and quadrant 2 with 3). This is different of what we see in Figure 15. The four sets of single-strand self-annealed double-helixes running vertically in Figure 11 have been lost, being reduced here to 32 base pairs (32 bp). Again, M and W are the unique codons with no match.
In Figure 12 we can also see that the semi-introversion works identically in the circular representation, dividing the circle horizontally in two parts, as it worked in its 64-grid representation, where the central nucleotides As and Ts in its upper half (only As and Ts were present in the second nucleotide of all the codons of the upper half of the circle), have been replaced by the nucleotides Gs and Cs in all the codons present in its lower half (only Gs and Cs were present in the second nucleotide of all the codons of the lower half of this geometry), while a single paired self-annealing of codons was kept in all cases.
The semi-introversion was preserved between these two 2D representations, the 8×8 square and the 4×4×4 circular, as well as the parallel pairing side-by-side of all their codons, which is easily perceptible in the square representation through four sets of 8 bp, but that by a geometrical necessity, it was only alternated by pairs (32 pairs of 1 bp each) in the circular representation; however, the perfect 90° positional rotation is only seen at this point in the circular representation (upper quadrants among themselves, and lower quadrants among themselves), while as mentioned, it was lost in the 8×8 square shown in Figure 11; in that figure and in its corresponding circle (Figure 12), the clustering of essential hydrophobic amino acids for codons with T at the center is not present yet.
In order to recover for the 64-grid square of Figure 11 the positional 90° rotational resonance that is seen in the genetic code circle of Figure 12, the upper right quadrant (quadrant 1) needed to be rotated 90° clockwise in order to be able to rotationally match is related amino acids present in its left counterpart (quadrant 4), excepting M; while for the lower half of Figure 11, quadrant 2 also needed to be rotated 90°, but this time counterclockwise in order to obtain an almost perfect rotational resonance with its left counterpart (quadrant 3), excepting W.
A notable peculiarity of these 64-grid rotational transformations is that, even when these double rotations change their pairings from being initially vertical to now being horizontal for the right side of the tables, the exact and complete semi-introversion between the upper half and the lower half of this right side, was still preserved as seen in Figure 13, where the restored rotational ability for this 64-grid genetic code representation of the pair of genetic code chromosomes M' is shown. Only the pairing within the codons of quadrants 3 and 4 was untouched and continued running vertically (two sets of 8 bp), while the right side changed to now run horizontally in four sets of 4 bp.
Figure 13.
Restoring the 90° rotational ability of the 64-grid 2D representation of the reverse engineered pair of genetic code chromosomes M'; the unique start and the most used stop codon in man are indicated with dotted geometries. The semi-introversion was kept between the upper and the lower half, where every A and T that is only present in the second nucleotide of the upper codons has been replaced by their alternative purine or pyrimidine G and C nucleotides that are only present in the lower half, respectively. The two left-side sets of single-strand self-annealed double-helixes are running vertically (two pairs of 8 bp) while the four right-side sets of single-strand self-annealed double-helixes are now running horizontally (four pairs of 4 bp).
Figure 13 also shows that the hidden symbol within these rotational results is something as old as the I Ching, something open-ended that can both be represented clockwise or counterclockwise, which is a rotational resonance of groups of amino acids that have the implicit shape of a swastika (i.e., in Figure 13, for the bigger one rotating counterclockwise and starting with the outer amino acids, please track the 2(FLLLDQV) of the upper half plus the 2(SRCTATA) of the lower half, then for a medium size counterclockwise swastika, track the 2(KENDQV) and 2(PGRATA). For the bigger one rotating clockwise: 2(FKY(I/M)VIV) and 2(SPSPGRA), and for a medium size clockwise: 2(LEHVIV) and 2(RGSGRA), etc.) The heterogeneous break of identical correspondence caused by Ile vs Met, represented here as (I/M), was present in the upper half of the figure.
The primeval swastika with a meaning of fertility or sexual reproduction is a symbol that appeared in the currently known archaeological record since around 2,800 B.C., or even earlier, in the Civilization of the Indus Valley [18, etc.], being this a symbol initially evoking the shakti, 'the agent of change' [19] like the codons and their amino acids, and/or of 'fertility' [20], where we find these codons; so, this symbol seems to have been related to genetics in the remote past, but shouldn't have had anything to do with the late destructive eugenic attempts of the Third Reich [21].
Figure 14 shows the transference of the pair of genetic code chromosomes I' into one 8×8 grid representation, with a semi-introversion of codons where the G, C, T, and A, that are present at the center of codons in the upper half of the table, have been replaced in its lower half with their alternative A, T, C and G, respectively (being these replacements of purines for purines and of pyrimidines for pyrimidines).
Figure 15 shows that when the pair of genetic code chromosomes I' is transferred to a circular representation, the 90° rotating positional resonances are again preserved for almost all of the amino acids between the two quadrants (except again for Met and Trp), in this case between the quadrants of the right half (quadrants 1 and 2 amongst themselves), and also between the quadrants of the left half (quadrants 3 and 4 amongst themselves).
Figure 15.
Resulting circular 2D representation of the reverse engineered pair of genetic code chromosomes I'. Notice the vertical semi-introversion (the left part is semi-introverting the right part, where the center purines/pyrimidines are replaced by their alternative purines/pyrimidines, C for T and A for G), and the horizontal resonance, the upper half resonating at 90° with the lower half (quadrant 1 with 2 and quadrant 3 with 4). This resonance is different of what we see in Figure 12. The four sets of single-strand self-annealed double-helixes that are running vertically in Figure 14 have been lost, being reduced to 32 single base pairs (32 bp). M and W are the unique codons with no match.
Figure 15 also shows the semi-introversion between the left half and the right half of the circle, where once again only the central nucleotides of the codons alternate within their respective purines or pyrimidines (pur exchanged by pur, while pyr by pyr), being here all the nucleotides evenly represented at the center (which means that here, eight of each: G,C,T,A at the right side are replaced by eight of each: A,T,C,G, at the left side, respectively), a phenomenon also seen horizontally in Figures 14 and 16 (upper half vs lower half).
Figure 16.
Restoring the 90° rotational ability of the 64-grid 2D representation of the reverse engineered pair of genetic code chromosomes I'; the start and the most used stop codon in man are indicated with dotted geometries, being these the odd codons that are breaking with the identical correspondence. The semi-introversion was kept between the upper and the lower half, where every A, T, G, C in the second nucleotide of the upper codons has been replaced by their alternative purine or pyrimidine G, C, A, T in the lower half, respectively. The two left-side sets of single-strand self-annealed double-helixes are running vertically (two pairs of 8 bp) while the four right-side sets of double-helixes are now running horizontally (four pairs of 4 bp).
And again, in Figure 16 we have restored the rotational ability for the 64-grid representation of Figure 14 (the pair of genetic code chromosomes I’).
To obtain Figure 16 we again rotated quadrant one 90° clockwise while also rotating quadrant two 90° counter-clockwise while keeping the semi-introversion of the upper part of the table with the lower part of the table in a similar way as in its original Figure 14. Here, the hidden representations of anticlockwise swastikas were obtained by tracking the 2(GRGSSI*) of the upper half plus the 2(ELARCR(W/*)) of the lower half; then, for a smaller one the 2(PSPSI*) plus 2(KFTCR(W/*)), etc. Here, the heterogeneous identity caused by * vs W was present in the lower half of the figure.
And again, in Figure 16 the pairing within the codons of quadrants 3 and 4 continued running side-by-side, vertically (2×8 bp), while the pairing within the codons of quadrants 1 and 2, the ones that where rotated, changed, to now be run horizontally (4×4 bp), exactly as it happened in the previous case analyzed and shown in Figure 13, while keeping again horizontally the semi-introversion of central nucleotides within the rotated quadrants 1 and 2, amongst themselves (exchange of compatible rings, pur by pur and pyr by pyr). Now, in order to group at the two central rows of the table (rows four and five) all the essential hydrophobic codons having T at the center, an additional procedure was undertaken as shown in Figure 17, where we can see modified horizontally all the strands that were originally paired vertically in Figure 14, a figure that also corresponds to the pair of genetic code chromosomes I’.
Figure 17.
Modified alignment of the binary genetic code derived from the I Ching through 'horizontalization' of the defragged vertical pairings shown in Figure 14; the semi-introversion has changed to the third nucleotide between the upper and the lower half, where every A, T, G, C in the third nucleotide of the upper codons has been replaced to their alternative purine or pyrimidine G, C, A, T nucleotides in the lower half, respectively. Notice the four sets of single-strand self-annealed double-helixes running horizontally (four pairs of 8 bp).
It is interesting to notice that when the vertical results of Figure 14 were made horizontal in Figure 17 to have all the essential hydrophobic amino acids parallel and aligned at the center while keeping their pairings intact at the same time, a different semi-introversion between the upper part and the lower part unexpectedly appeared, changing the semi-introversion from the second to the third nucleotide as the one being exchanged, resembling somewhat what happens in nature with the compatible wobbling of third nucleotides. This exchange, as in all the previous examples, was once more restricted to purines for purines and to pyrimidines for pyrimidines. This 64-grid genetic code table was the only one exhibiting a semi-mirroring for all its amino acids (Figure 17).
The logic for the conversion of the columns of Figure 14 into the rows of Figure 17 is given in App. I, always dividing the columns in two equal halves while rotating them clockwise, with the first half of the columns filling the first half of the rows, and the same for their second halves.
When the semi-introversion was focused on the nucleotides of codons directly derived from the I Ching, they always prevailed after the 90° rotation of two of their quadrants (as shown between Figures 11 and 13 and between Figures 14 and 16), however, this did not happen with the third nucleotides between rearranged Figures 17 and 19 (see below).
Figure 19.
Restoring the 90° rotational ability of the 64-grid 2D representation of the reverse engineered and horizontalized pair of genetic code chromosomes I'. The start and the most used stop codon in man are indicated with dotted geometries, while M and W always are the amino acids with only one codon that are breaking the identities. The upper left-side and the lower right-side single-strand self-annealed double-helixes are running vertically (four pairs of 4 bp), while the upper right-side and the lower left-side of single-strand self-annealed double-helixes are still running horizontally (another four pairs of 4 bp). The semi-introversion has been lost in this representation that had in total eight pairs of 4 bp each.
Figure 18 shows the horizontal transformation of the pair of genetic code chromosomes I' using the hexagrams of the I Ching, showing an horizontal correspondence of 0s with 1s.
Figure 19 shows how Figure 17 was transformed into a 90° positional rotating 64-grid genetic code.
Here, to obtain Figure 19 was more complicated than the previous conversions from non-rotational (Figures 11 and 14) to rotational (Figures 13 and 16, respectively) representations, because here quadrants two and four of Figure 17 needed to be turned to the back and then rotated 90° counterclockwise.
In Figure 19, the hidden representations of the bigger swastika symbols were seen by tracking this time the 2(PSPSS*I) of the right half of the table plus the 2(ATAT(W/*)NL) of its left half; then, for a smaller one, 2(GRGS*I) plus 2(RCR(W/*)NL), etc. Here, the heterogeneous identity caused by W vs *, represented as (W/*), was present in the left half of the figure.
It needs to be emphasized that all of these tables and chromosomes were defragged by a continuous pairing or single-strand self-annealing (Figures 2–11, 13–14,16–19,25–30); however, as mentioned before, this continuous pairing was lost by necessity in the circular representations of the genetic code, where only individual base pairs were preserved, as well as the semi-introversion of the two halves of the circles, while the 90° rotational resonances flowed naturally in all the circular representations, as exemplified in Figures 12 and 15, with the positional replacement of the semi-introverted Gly GGT and its companion Pro CCA in Figure 12, for Ala GCT and its companion Arg CGA in Figure 15.
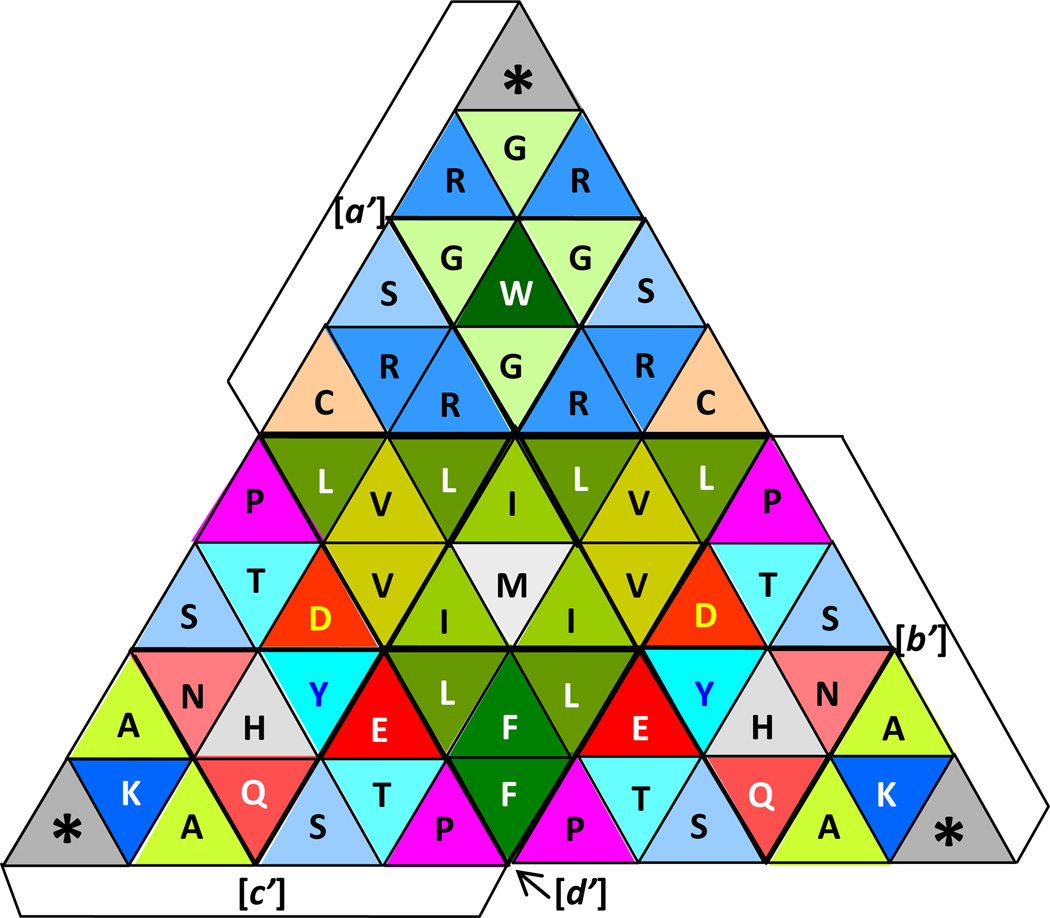
Remarkably, through the use of quantum logic, it was possible to transfer the genetic code from the horizontal binary genetic code chromosomes I' shown in Figure 17, into a 100% symmetrical 3D 16×4 genetic code tetrahedron shown in Figure 20. This could be considered one of the highest achievements of this work.
Notice once more that the essential hydrophobic amino acids that appear distributed at the center rows of Figure 17 are the ones that were located at the bottom of this 100% symmetrical tetrahedron, and as its 2D triangular pattern shows (Figure 20), we can see that the two equilateral triangles surrounding the central triangles are able of a compatible exchange among themselves (faces b and c), while preserving a positional resonance between identical (A, S, H, P, T, Y, K, *), or equivalent (N and Q, and D and E) amino acids. The two central triangles (faces a and d) can experience a compatible exchange separately or individually only within themselves.
The 2D triangular net or pattern with 64 smaller triangular grids to obtain a 3D tetrahedron as shown in Figure 20, was the product of a quantum transfer of the genetic code chromosomes I' seen in the Figure 17; however, it seems that it is not possible to transfer the actual paired products side-by-side of any binary defragging into the current four faces of a 16×4 tetrahedron.
Figure 20 shows the first 3D genetic code tetrahedron obtained thus far to my knowledge that is both perfectly symmetrical and still meaningful, with its logic including the relocation of all the essential hydrophobic amino acids that were at the central rows of Figure 17 (rows 4 and 5), into its bottom face or d, while the three remaining faces of Figure 20 were integrated by the alternated combination of rows 2 and 7 of Figure 17 in its face a, then of rows 3 and 8 in face b, and finally of rows 1 and 6 in face c of this tetrahedron; with this arrangement, the three functional stop codons ended up notably at its top three sides of the apex.
Notice here that the start codon, Met, is now located at an inner position, being at the center of the bottom of this tetrahedron, while, as mentioned before, the three stop codons are now located at the three sides of the top apex, being this a bottom-up representation, starting at the bottom and ending at the top, being this symmetrical genetic code tetrahedron the opposite of the functional genetic code tetrahedron that was initially inspired by the classic circular genetic code representation [1].
This symmetrical genetic code tetrahedron balances perfectly by position, both the amino acids and the functions; however, it is not numerically symmetrical or numerically balanced as the functional one is [1]. So, the quantum transfer of the pair of genetic code chromosomes I', product of a binary I Ching comparison into a 3D genetic code tetrahedron (Figure 20), lacks of the codon balance seen in other geometrical representations of the genetic code [1,16].
In Figure 21 we can see the culminating results of this work, a double design, an assembly of two tetrahedra coupled at their bases, being the one derived from this article shown at the lower half, while an earlier functional genetic code tetrahedron [1] is shown at the upper half, with the end to visually, and possibly computationally, help to distinguish with precision between the starting M, which is easy to be removed from its proteins [22], here represented in purple (upper half), from the more permanent, non-starting or inner M (lower half).
Figure 21 also shows that while a functional set of logical reasons was used to obtain the first tetrahedron (upper half or row, [1]), the systematic and sequential quantum logic derived from the binary system, as present in the vertically defragged I Ching comparing Keto/Amino to Pur/Pyr, was the basis for the second tetrahedron (lower half or row, this study).
These two different tetrahedral genetic code representations obtained by very different strategies complement each other, and for that reason, these two genetic code tetrahedra could be called, the upper one the Yin, being this the functional one in numerical balance of codons, having this also an equilibrium of most used codons per amino acid in man (Figure 22), while the lower one could be called the Yang, being this the one that is out of numerical balance of codons or of equilibrium between the usage of codons in man while having a 100% geometrical symmetry, something that the other one is lacking.
Additional aspects of the directionality of the Yin/Yang arrows derived from the binary I Ching genetic code will be shown elsewhere in a manuscript currently stuck in Australia for 7 months: (see in a related matter the 'accountability of peers' at the beginning of the Discussion below).
A detailed explanation of the five logical principles for the design of the standard functional genetic code tetrahedron shown here in the upper half of Figure 21 has been published elsewhere [1]; here, I just want to add that Figure 22 is showing the mathematical counterpart of those principles, the perfect numerical balance of codons (upper), and the equilibrium of most used codons per amino acid in the code of man (having the third nucleotides of human codons a distinctive signature or password of: 12-8-2, C-G-A), compared to the octopus (12-3-7, U-G-A) according to the parallelogram (lower), an alternate geometry that when folded produces an identical result to the one shown in the upper part of both Figures 21 and 22; these arithmetic features are not present in the lower tetrahedron of Figure 21, the 100% symmetrical one derived from the binary I Ching.
In an effort to compress the two different genetic code tetrahedra shown in Figure 21, a stella octangula has been obtained with its inner smaller octahedron shown separately through their two nets presented here (Figure 23).
If we now compare the pair of genetic code chromosomes I to the genetic code chromosome obtained form Nirenberg's first codon table of 1965 never published before (Table 2) [7], here modified to follow the classic order of codons [8,9] and their corresponding amino acids, we obtain the arrangement of codons and of amino acids shown in Figure 24.
Table 2.
Rearrangement of Nirenberg's handwritten, previously unpublished, first representation of the codons that integrate the genetic code.
| 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|
| → | T | C | A | G | |
| 1 | TT | TTT = F | TTC = F | TTA = L | TTG = L |
| 2 | TC | TCT = S | TCC = S | TCA = S | TCG = S |
| 3 | TA | TAT = Y | TAC = Y | TAA = * | TAG = * |
| 4 | TG | TGT = C | TGC = C | TGA = * | TGG = W |
| 5 | CT | CTT - L | CTC - L | CTA - L | CTG = L |
| 6 | CC | CCT = P | CCC = P | CCA = P | CCG = P |
| 7 | CA | CAT = H | CAC = H | CAA = Q | CAG = Q |
| 8 | CG | CGT = R | CGC = R | CGA = R | CGG = R |
| 9 | AT | ATT = I | ATC = I | ATA = I | ATG = M |
| 10 | AC | ACT = T | ACC = T | ACA = T | ACG = T |
| 11 | AA | AAT = N | AAC = N | AAA = K | AAG = K |
| 12 | AG | AGT = S | AGC = S | AGA = R | AGG = R |
| 13 | GT | GTT = V | GTC = V | GTA = V | GTG = V |
| 14 | GC | GCT = A | GCC = A | GCA = A | GCG = A |
| 15 | GA | GAT = D | GAC = D | GAA = E | GAG = E |
| 16 | GG | GGT = G | GGC = G | GGA = G | GGG = G |
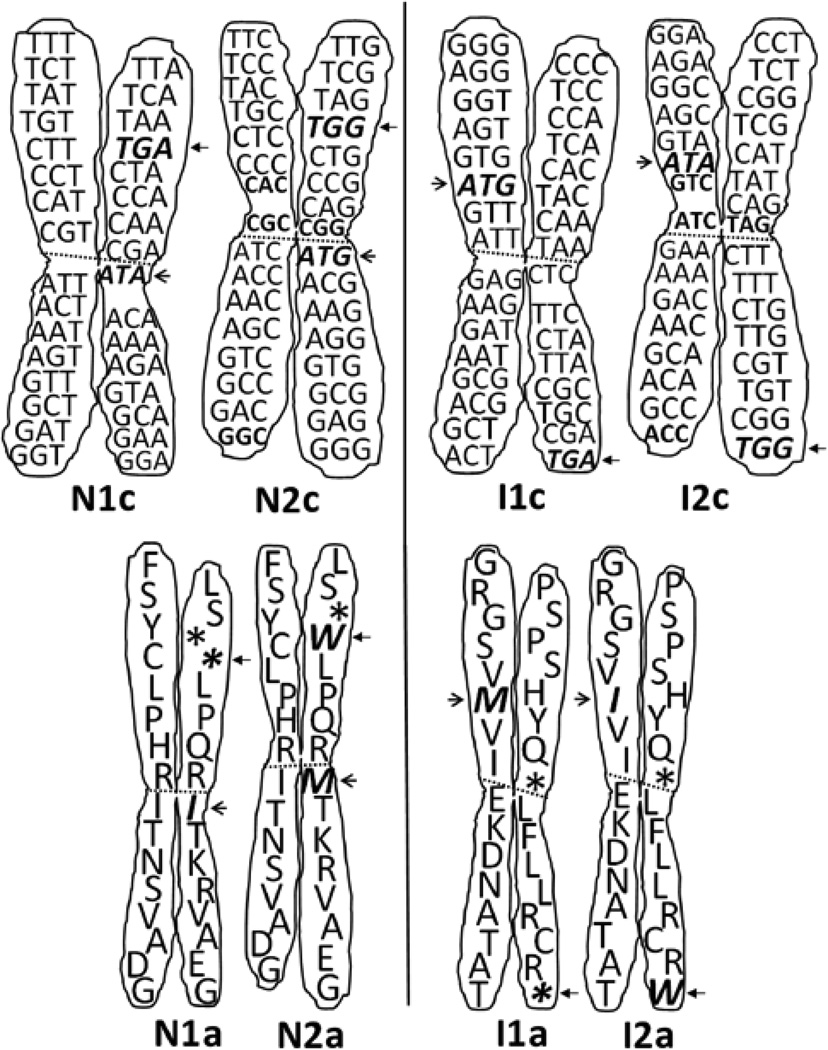
Figure 24.
Pair of Nirenberg's genetic code chromosomes compared to the I Ching ones. The complete genetic code is represented at each side, either through the quasi-identical codon chromosomes (having these the suffix c, for codon), showing partial wobbling or exchange of pyr by pyr (C for T and vice versa), and of pur by pur (G for A and vice versa), or through their respective amino acids (suffix a, for amino acid), either resulting from the rearranged codon table of Nirenberg (N1 and N2), or derived from the I Ching as stated in the text (I1 and I2). The arrows indicate the two points of discrepancy per chromosome due to the odd codons (M and W, always matching ATA and TGA, respectively). Note: Only the sense strand is shown, assuming that for the genetic code chromosomes I the antisense strand hides below them, having such strand an identical conformation to the one shown here via their companion chromatids.
As shown in Figure 24, a unique feature of the pair of genetic code chromosomes I (I1 and I2) derived from defragging by horizontal pairing of the I Ching binary comparison of Pur/Pyr in axis x versus Keto/Amino in axis y, is that, as stated in its legend, the antisense strand is assumed to be present below or hidden behind the illustrated codons, having that strand an identical conformation to the one shown by the companion chromatids, where GGG pairs with CCC, AGG matches TCC, etc., a feature not seen in the pair of genetic code chromosomes N (N1 and N2), obtained from the codon Table 2; just a reminder that the antisense reading goes in the opposite direction, from right to left or – 5'; the order of Nirenberg's pair of genetic code chromosomes N lacks of such pairing and correspondence and of its identical hidden annealing, being rather a sequential arrangement of codons, in a similar way that Crick’s table is [8].
The logic to obtain the pair of Nirenberg's genetic code chromosomes N consisted in locating the components of the columns that represent the 3rd nucleotide: of columns one (T) and three (A) in the corresponding chromatids one and three (seeing them also from left to right), while locating the columns two (C) and four (G) in the chromatids two and four; once again, the products are shown in the novel 2×8×4 representation of the genetic code introduced with this article.
The arrangement in all the chromatids of the chromosomes obtained from Nirenberg's codon table (Figure 24) is a uniform sequence of four codons for each nucleotide: T, C, A, G, following the classic order of nucleotides with which we rearranged Nirenberg's table (Table 2). On the other hand, the pattern seen in the pair of genetic code chromosomes I produced a heterogeneous set of chromatids in which the left ones of both chromosomes had similar first alternating nucleotides (G-A) while also the right chromatids of both chromosomes had first alternating nucleotides (C-T), etc.
Nirenberg’s unpublished codon table [7] reordered as T,C,A,G [8, 9], changing U for T and numbering coordinates of axis x, with their codified amino acids.
An interesting feature seen both in the I Ching derived genetic code chromosomes and in Nirenberg's (Figure 24), is that the mammal/invertebrate exchange of most used third-nucleotides per amino acid in real life follows in general a similar pattern such as the one shown in these figures, having a G/A or a C/U exchange [17].
Discussion
Being this my most important article to date, and prompted by both a critical reviewer who, similarly to the journal of [23], "do not recommend publishing this manuscript in JPSCB or in any other journal", while we seek for the accountability of peers, I wish to develop a detailed discussion of the available works that are also representing the genetic code with tetrahedra, starting with Trainor [24], who labeled her four tetrahedral apices with identical three letter codons: AAA for the top, while CCC, GGG, and UUU were the basal apices; however, smaller 3D tetrahedra were included within the bigger ones, making her model not only "fractal" but also highly intricate.
Trainor used a tetrahedral genetic code derived from a parallelogram divided into four groups of nine equilateral triangles per side [24]. It was Trainor who noticed that "the molecular basis of life is so conceptually simple, so wonderfully understandable, that anyone with an interest can grasp its basics within an afternoon" [25], being this a generalization of modeling in biology where things are simplified to understand one by one their principles; however, the closer we look at them, i.e., by looking at an electronic microscope, or by tracking real-time metabolism, plus the introduction of additional variables, then things get more and more intricate and complex, as they really are; Trainor also declared that her tetrahedral representation of the genetic code was probably inspired by an analogous representation used for elementary particle quantum numbers [26].
Trainor [24] provided 10 intersecting points per side plus one unique point at the center of each face, while the remaining 9 points were shared by the other triangular faces, with each face of the tetrahedron being later filled with 27 components per face, with 27×4=108 codons in total.
In Trainor [24], the biological meaning of her 44 extra codons was left unexplained, as well as the lack of correspondence between amino acids and codons between her different figures, while including erroneously the stop codons within "the twenty families of codons", a confounding factor that she repeated again when declaring that "sixty-four codons are related to twenty amino acids", when we know that only 61 codons are related to 20 amino acids while the remaining three are the non-sense functional stop codons (*).
Then, a "complex representation" of codons, or rather a mixed pool of discrepant representations was also published [27], with one of its many confounding factors being that the 'tetrahedral' representation was entangled to a "vectorial (3D) representation", further intertwining them with extra "complex (2D)" figures plus a "genetic code vectorial representation" within a cube, also having 21 superimposed and extremely hard to recognize codons or amino acids in its x,y,z coordinates, changing out of a sudden to an uneven representation.
Added to those hard to understand images lacking sequential logic, a pyramid with no base was also presented [27], showing 'the complex plane' with 16 amino acids per side, while there, if we include each touching flank, we find 20 dots per pyramidal side, plus some unexplained 9 central squares and 7 lateral triangles, omitting in its last representation the important stop codons as several others have also done before [24,29] and after [30,31].
And, as if these highly complicated images were not enough, in [27] we also see two incomplete interlocking tetrahedra with the letters A, C, T, G at each angle, where, as it was done before in [24] and later in [28], "each of the codons is attached to one of the vertices in a resulting three-level fractal-like tetrahedron structure", which adds additional 3D "representations of an amino acid… mapped in neighboring points."
This complex set of disconnected representations presented by [27] seems to be unclear for either educational purposes or bioinformatics; recently, even [27] gave up those to rather "use the simpler two-dimensional nucleotide representation" [23]. We also read in [27] that "the separation within the amino-keto classes is less significant as compared to the strong-weak and purine/pyrimidine dichotomies", and in [23] that "it is possible, and desirable, to give up the less important amino-keto separation"; however, as we have seen through my current article, the biochemical aspect of nucleotides based on the content of radicals and their tautomerism is as important, as also seen below, as their H-bonds and their rings if we attempt to obtain a better understanding of the complete genetic code, both for its binaries shown here and for their vectors that I expect to hopefully show elsewhere.
A similar reasoning showed the geometry of a 'single stranded' DNA as a tetrahedron inside a cube, and of a 'double stranded' DNA as two tetrahedra superimposed in opposite directions also inside a cube, "the star tetrahedron" [28], which according to the Mathematica™ website is an inappropriate term [Weisstein EW. Stella Octangula. MathWorld - A Wolfram Web Resource (1998–2012). http://mathworld.wolfram.com/StellaOctangula.html] touching the inner eight angles of the cube. I obtained here a similar structure (Figure 23) by following a completely different logic and a systematic methodology, representing not a 'double stranded' DNA as these authors attempted to do, but two complete and different genetic codes to differentiate between the start and the non-start Met.
On the other hand and as done before [24, 27], these authors [28] also showed a "higher order level tetrahedral" subdivision per triangular side of the tetrahedron, with one tetrahedron in the first order, four in the second, and 'ten' in the third; however, only nine tetrahedra integrate this order [24].
Also in [28], each angle of an inner tetrahedron was represented by the letters G, A, A, and U, respectively, having at the side the written words: "Start codon = Methionine = AUG", and "Stop codons = UAG, UGA, UAA"; these apical letters can produce the next possibilities rotating the individual nucleotides clockwise for its four sides (underlining start and stops): left (GAA, AAG, AGA), right (GUA, UAG, AGU), bottom (AUA, UAA, AAU), back (GAU, AUG, UGA), while leaving unexplained as seen, the non underlined codons and the complete left side; for that figure, its authors wrote that: "If we consider that each face rests upon that of an octahedral 'codon' face then this tetrahedron is likely to be the one in the very centre of the third order level tetrahedron which is completely surrounded by octahedra"; thus, they are hiding the functional codons at the innermost center of their three-level tetrahedron, being this the complete opposite of what I am doing here with my pair of genetic code tetrahedra, where the start Met and the three non-sense stop codons are external, having both a functional and an apical role for the computational entrance and exit of information (Figure 21 and 23).
In [29] we have a tetrahedron divided in 20 parts, representing only the 20 amino acids while ignoring again the stop codons; here, the mapping showed that the hydrophobic and hydrophilic amino acids were distributed at distinct regions of the 3D space, noticing that hydrophobic codons were constituted dominantly by bases of the keto group (G and T/U) while hydrophilic codons were constituted dominantly by bases of the amino group (A and C). These observations also seem to emphasize the importance of the “amino-keto separation” minimized by [23, 27].
In [30] we see added the tRNA factor to a rectangular table based on the division of amino acids into two classes of aminoacyl-tRNA synthetases, ordered by their molecular masses and by their coding bases; the resulting tetrahedron, not shown but clearly described there, is a 3D representation similar, but not identical, to the ones described before, where at the center of each tetrahedral face is located one amino acid: Ala (A), Leu (L), Phe (F), and Asn (N), while its apices contain Gly (G), Lys (K), Pro (P) and Tyr (Y), plus six contiguous pairs of amino acids at each of its six tetrahedral edges, i.e.: V and D; H and Q; S and E; T and R; I and M; and C and W, being each of these pairs shared by two tetrahedral faces. According to [31], these 20 amino acids are D-amino acids having a L tetrahedron mirror image; however, both of them [30 and 31], only represented the amino acids while once more failing to include the three functional non-sense stop codons.
Furthermore, a patented representation of the genetic code in a 3D tetrahedron was done by Fujimoto [32], seemingly the closest to the ones that I present here in Figures 20–23, also showing a 16×4 tetrahedron while exhibiting a different logic and arrangement of codons based on Crick's table [8], grouping in each face all the codons that start with the same letter (T, C, A, or G, respectively); in [32] we find figures superimposing simultaneously codons and amino acids within the small 64 equilateral tetrahedra, or superimposing amino acid one-letter symbols with ideograms, or even including a drawing of four-diamond figures with an heterogeneous space for the allocation of codons in an attempt to represent the different size of their products.
In Fujimoto [32], we read that the "tetrahedral 4 faces may be transcribed over the surface of a sphere", and also that "the 64 small-triangular phases could be transcribed preferably over the full surface of a sphere without any limitations of a tetrahedron model", with nobody to date, to my knowledge, having been able to do so; however, in Fujimoto's last statement we can see that he himself thought that his model had limitations, because he mentioned "limitations of a tetrahedron model" without stating which where those limitations that he saw in it.
And something similar can be said of Fujimoto's statement that his patented representation was "highly useful in the field of genetic engineering" [32]; here, even when that may be one of the potential uses of the genetic code as an engine, this has not yet been demonstrated, being this, one incentive for our own research, together to the statements that "a good representation of a system is an important part in solving various problems related to that system" [27], and that "a genome resembles less to a plain text, which simply expresses semantics in accordance to certain grammar rules, and more to a poem, which also obeys additional rules, such as those that generate rhythm and rhyme" [23].
It needs to be noticed that there may be additional properties and more patterns hidden, apart of the ones presented in this article in these 2D and 3D genetic code models, plus precise mathematical periodicities still undiscovered. For example, the semi-introversion was preserved, like in the two central nucleotide examples here shown (Figures 13 and 16), by rotating quadrant one 90° clockwise and quadrant two 90° counterclockwise, for first nucleotides of the upper and the lower half by rearrangement of Figure 11, and of third nucleotides by rearrangement of Figure 14, which were also re-enabled to rotate with a 90° resonance while retaining all their semi-introversion; (data not shown) being the 90° rotational recovery of Figure 17 shown in Figure 19, the only one unable to restore the property of semi-introversion as it was done by the mentioned transformations.
On the other hand, the quantum logic presented in this article could be called subjective or artistic; however, it may also be framed within the backbone of mathematics within the interface where art and science collide, in the place where the subjectivity of the artist may be measured by the theories of probability and with the statistics of the scientist.
It is due to this phenomenon within the human thinking that we are able to differentiate the artistic styles; for example, compare the clear difference between the elongated characters of El Greco [33] and the fat characters of Botero [34], just to show an example so evident that even intuitively it is possible to detect the differences; and even more surprising are the collective differences between complete groups of people and their cultures, such as the rude and elongated works of the African tribal art, i.e., the Guro of the Ivory Coast [35], contrasted to the more exquisite and rounded works of the ancient south American Moche [36].
Once the innate mathematics within the thinking patterns of an artist are extracted from his works, I think that a universe following his general set of rules could be generated.
Here, the conflict between the artistic and the rational mind can easily be solved, as stated, if the later one wishes to measure with precision the products generated by the previous one, being such discrepancy equated to the conflict held between the precise order that Einstein wanted to find in the universe (I may call this one 'Yin') versus the more fuzzy and quantic way of thinking of Bohr, who was more open to a wide array of equally valid spatial and numerical possibilities ('Yang') [37].
Maybe Einstein just ignored or forgot that it was the attempted prediction of gambling, subject to numbers, the origin of our current mathematical theory of probability, started by Pascal and by Fermat in 1654 [38]; also remembering that probability is what apparently mainly intervenes in the apportioning of genes within our gametes; and if such was the statistical origin of probability based on gambling, with more logic and reason we could be able to do the same for the arts, some of them already found within a numerical interface (architecture, graphic design, music, etc.).
Leonardo Da Vinci, in his anatomical drawings fused art and science with such precision and realism as to make them timeless [39,40]; we are attempting to do here something similar with the genetic code, and with the molecular realm in general.
In relation to that, Fujimoto wrote that his genetic code tetrahedral patent, "which is made of paper", according to the end of his claim number 12, can be made "available for an interior ornament or a table-top object because the whole features of the tetrahedron can be esthetically enjoyed as a kind of decorative arts" [32].
And also in this regard, to my 3D representations presented here I must add the word "freely", because anybody is welcome to build a 3D paper representation of a genetic code tetrahedron based on the patterns shown here and in [1], for the benefit of the students by providing them with educational tools, but also for professionals due to its potential in bioinformatics, medicine, biology, ecology, bioengineering, etc.
If we allow a more wider use of metaphors in science, I think that it will inspire a new generation of researchers, i.e., by showing that once the double tetrahedron is assembled into its two 3D representations (Figures 21 and 23), the start codon (Met, M) will be seen located at the top apex of the first tetrahedron (upper) while the three stop codons (*) will be located at the bottom apex of the second tetrahedron (lower); evocating, not only the difference between the starting Met (upper) and the non-starting Met (lower), but also the whole process of translation of mRNA into proteins within the ribosome.
Being the functional and numerical codons of my model a metaphor of the mRNA translation, we can say then that at the top of my first 3D genetic code tetrahedron the start codon ATG is located, representing that entrance, like a receptor antenna or lighting rod, the receiver of the first tRNA that carries the first amino acid Met within the ribosome, while the three stop codons TGA, TAA and TAG, located at the pointy apex looking down of the second tetrahedron, are representing the actual non-coding exit point of the protein or enzyme recently completed and coming out of the ribosome.
So, if the functional genetic code tetrahedron [1] can be called the entry or the receiver, the 100% symmetrical geometry or more artistic genetic code tetrahedron here obtained is its opposite, being deemed as the exit or volcano, as shown in Figures 21 and 23.
Here, we need to stop and once more be reminded of the non-random nature of the stop codons and of the entire genetic code; if it were random, we should have some 30 stop codons per mRNA when only one stop codon is actually needed per mRNA [41].
Fujimoto also declared that "an intuitive grasp of the meaning of these 21 alphabet characters is extremely important for investigation and discussion of codons and/or amino acids or physico/biochemical properties of resultant peptide chain" [32]; but again, we need to clearly distinguish between the two different properties of Met as a starting function and also as a non-starting amino acid, as it has been geometrically demonstrated in Figures 21 and 23; such difference will increase our understanding of the genetic code, and its alphabet [1]. In a related statement, shCherbak wrote about his surprise of, not only being able to study the genetic code in a binary way as we do here, but in a decimal way: "Metaphorically, in our denary dialect of the arithmetical language we have written down the names of certain cardinal numerals of the genetic code. This is the answer the genetic code gave: These inscriptions are their inborn names. The names have been given them in the time of genesis. Now, in their native numerical language these names are reproduced in written form again because the current dialect turns out to be identical to that primordial numerical language" [42] the link: http://tinyurl.com/shcherbak
So we have seen that the genetic code is a logic and intelligible system, being this the reason of why we are capable to decode it, not only as it has been done here in its 2D representations, but also now in 3D, coupling it to geometry, to arithmetic [42], to bioinformatics, to mathematics in general, and now to art, as it has already been done with other aspects of science [43–45], etc.
Such aspects and more are also present in the genetic code when compared to any other meaningful code currently known to man, both the ones already deciphered and those that are still encrypted just waiting to be decoded.
It is the intelligent design inherently present within the genetic code the reason why we can adventure ourselves to explore it with our own intelligence, both with our simplest, but also with the most advanced tools of logic.
The 16×4 tetrahedral 3D representations of the genetic code shown in Figures 21 – 23 demonstrate that, being the genetic code a biological reality, composed of material codons with mass, it has, and by inference it had, a beginning or a start from the top or above, depicted here by the strategic location of the first or starting upper Met (in pale purple); but also an end, either located at the three non-coding stop codons that are present at the three exiting lower apexes of the upper tetrahedron (if the gene lacks of an internal Met), but also located at the lowest or exiting apex of the lower tetrahedron (if the gene has one or more internal Met); except for possible quasi-spherical representations of the genetic code, this observation seems to be incompatible with alternative scenarios attempting to portray the genetic code as a continuum lacking of beginning and end.
Here, we may also equate the rotational ability of the genetic code, in a limited way, with the theoretical representation of an atom, having here the essential hydrophobic amino acids at the nucleus, as shown in Figure 22, and related portions of Figures 21 and 23, while the rest of amino acids and functions (start, stop) are orbiting around them as electrons, and due to the multiple locations in which the identical exchangeable codons per amino acid can be allocated, or even the equivalent codons, the functional tetrahedral representation could be considered as a quantic representation of the genetic code, remembering that each compatible set of codons is restrained within its own orbit or boundary, similar to their compatible genomes and Themes in nature [16].
However, the results obtained here seem to indicate that both the numerical symmetry and the numerical balance are in need to be sacrificed in order to obtain a perfectly 100% geometrical symmetry in a 3D genetic code tetrahedron and vice versa, being this a unique symmetry that it is not possible to be displayed by the 2D 8×8 square, or by the 4×4×4 circular representations, or by the 2×8×4 genetic code chromosomes presented here for the first time. This impossibility is due to the necessary presence of odd codons within the genetic code, the ones that are breaking the possibility of symmetry for non-triangular or non-tetrahedral configurations. The search for a biomedical programming independent of operating systems has been contemplated at least for a decade [46]; however, its advances today seem to be limited to diverse and complex 2D diagrams of flow, and of a rather cumbersome administrative archival task where the most notable problem seems to be the semantic heterogeneity of the collected data, mostly focused currently in cancer research [47].
Being the genetic code a more permanent correlation capable of a 64-binary-grid representation, it appears that it can be used independently of any operating system, by pairing or aligning its codons both horizontally and vertically.
The efforts of this article attempt to expand the perspectives of, not only a grid, or of 2D flow diagrams coupled to "logic and sets", but also to include the use of other geometries such as the 3D diagram of flow displayed in Figure 21 and 23, capable potentially to help in the study of, not only cancers, but also of any hereditary disease, and to compare those compatible sequences that are present within the biodiversity of today.
These results may help us to see that, when we keep the product of the transfer from one set of representations of the genetic code to another in a sequential manner, such as it was done for the double pairs of genetic code chromosomes M and I, but also in a more unpredictable quantum logic as it was also demonstrated here (M', I'), there is always an array of alternatives like a nebulae of electrons, starting with the free and deliberate (subjective) correlation of nucleotides to the I Ching symbols of 0s and 1s [2,6,10,11, etc.], a multitude of possible representations, being the ones presented here just single examples taken from that multitude of possibilities.
So, we now have a start at the center of the table, in the first uneven spot, ATG, but also a specific end, or stop codon of choice, in the second uneven spot, being this, the stop TGA, the most used stop codon in man [17]; so here, if we start in Met (ATG), we will end in TGA.
In this work, synthetic, heterogeneous and quasi-identical genetic code chromosomes (m, M, M' and i, I, I') have been presented (with M' and I' exhibiting an additional semi-introversion plus an integration of the codons for essential hydrophobic amino acids with T at their center), being this a positive theoretical use for the single-strand self-annealing; however, in a previous work, I have experimentally demonstrated its negative side because there, synthetic single-strand self-annealed palindromes that are real products of molecular methodologies, are also resistant to digestion by restriction enzymes, and are currently contaminating millions of nucleic acids that are present in databases such as the Genbank [48]; such negative single-strand self-annealing is the opposite of the theoretical positive basis for the defragging by pairing presented here for the genetic code; and as said at the beginning, all the analyses done here used only the coding strand, while it is assumed that the non-coding strand is hidden below or behind the coding strand that is shown.
Our initial studies of the genetic code were done independently of binary systems or of vectors, being rather aligned by periodicity, by functionality, and/or according to their compatible variation [1,2,16,17,49]; here however, I am exploring the novelty of the quantum logic as applied to the genetic code in order to pursue the reverse engineering of these two, apparently independent sets of representations: 1) the binaries derived from the I Ching, successfully transferred in this article into 2D and 3D genetic codes, and 2) the genetic codes based in the functional associations of amino acids and their codons, being these last ones independent of binary arrangements and/or pairings. It seems to me at this point that the informational flow from binaries to geometries is easier than the opposite.
It may be that from all the possible representations of the genetic code, including the two different approaches mentioned in the previous paragraph, some of them may run in parallel, never touching themselves, even if all of them, or almost all of them, could be equally efficient for the comparison of sequences, and/or for the generation of data in bioinformatics [2,17]; for example, through the efforts displayed recently by Petoukhov and He [50,51].
Somebody else found a 0.82 correlation of the 20 amino acids encoded by 61 codons between hydrophobicity and three physicochemical properties (mu, Hb, MW), separating them in acidic and basic and in aromatic and heterocyclic through the different quadrants of an octagon, concluding that "this is in agreement with the ancient Chinese Ying-Yang theory embedded in the classical I-Ching" [52]; however, as we have seen before [24,27,29–31], their omission of the three non-coding stop codons is taking out of balance the last consideration, leaving incomplete the I Ching, with three empty spaces or cells. In my case, I found that in a similar way to the number of cells in each row or column of the I Ching, there are also eight quasi-identical pairs of defragging products (pairs of genetic code chromosomes), without modification and directly derived from the I Ching; being half of them presented in this article, having compared one of them with the additional historical discovery presented here for the first time, the differences between Nirenberg's Table 2 and the open-ended binary I Ching, being one more difference between them that the last one can be re-ordered or defragged both by horizontal or by vertical pairing as seen in Figure 6, a feature that is absent in the pair of Nirenberg's genetic code chromosomes N shown in Figure 24.
Conclusions
The peculiar property of single-strand self-annealing displayed by the genetic code has been demonstrated here for the first time to my knowledge, together with the dynamic plasticity of the genetic code as to be represented and adapted from and to, multiple geometries and numerical systems, evocative of the adaptability and variability displayed by the real genomes and genes within living systems.
This work also indicates that, as with any other computational software, it was possible to defrag the genetic code obtained by its binary representations according to the Chinese hexagrams that were preserved in the I Ching; these original open-ended binary numbers are not committed to any specific codon, being possible to reorder them sequentially according to the three sets of Cartesian combinations shown in Figure 1, and by their reciprocals not shown in this article, being these combinations based on the equally important comparisons between the three properties displayed by nucleotides: Pur/Pyr being compared to either H-bonds or to the Keto/Amino tautomerism, and of the two last ones amongst themselves.
From the defragmentation strategies presented here (Figures 2–5), one that we have subjectively favored is T. 1 from Figure 5, due to the strategic location at its center of the start codon, Met, coupled to the almost perfect identity between its two sets of chromosomes, except for M and W; the discovery of quasi-identities within the binary representations of the genetic code far exceeded our initial expectations.
In the results, the comparison of the two figures representing the allocation of amino acids, either when defragged by horizontal (Figure 3), or by vertical pairing (Figure 5), did indicate that the quasi-identity of amino acids, when arranged on the basis of their codons, was easily present in the vertical pairing, but it was also present in the horizontal pairing when viewed vertically.
The theoretical importance to represent the complete genetic code as amino acids was revealed through the shape of the double pair of genetic code chromosomes obtained in this article. Apart of these findings, an unexpected result was obtained when the vertical pair of genetic code chromosomes I' from the binary defragged I Ching was first rendered horizontal, to be then reverse engineered using quantum logic, obtaining in the end a perfectly symmetrical 3D tetrahedron genetic code (Figure 20), a symmetry that, as said before, is impossible to be obtained by any of the other representations here explored (circular, square, and chromosomal) due to the presence of the necessary four sets of odd codons: one Met or start, one Trp, then three Ile, and three Stops.
The pair of genetic code chromosomes I and their derivatives I' were binary comparisons that presented their I Ching hexagrams side by side in a 100% pairing (i.e., Figures 18 and 26 for the horizontal pairing, and Figures 8, 10 and 29 for the vertical pairing), something also attainable by their reciprocals not shown here.
This 100% 3D genetic code tetrahedral symmetry may help us in our pursuit to further develop the field of bio-architecture, where molecular aesthetics in biology goes hand in hand with logic, geometry, and mathematics, an aspect that is highly important when looking for novel tools and approaches in bioinformatics.
The results presented here also show the high plasticity of the genetic code, which is capable of representation in apparently limitless ways that are both meaningful and rich in information, having obtained several in 2D and several in 3D, and of the last ones, the quasi-spherical representations seems to be the logical next step. Also, it may be possible to introduce these different representations as diverse engines for software and for programming in bioinformatics, to compare sequences, and/or to verify which one of these genetic code geometries, or even several them, could be the best in providing, not only an educational benefit, but also a computational, biomedical, and/or biological one. A grant in bioinformatics, still locked to me until now, will greatly help me to pursue these goals.
Now, and given the constant presence of the unique and solitary stop codon TGA as one disruptor of the identical correspondence, being this one apparently the most used in man [17], being the other stopper of identical correspondence the start Met. A deeper consideration needs to be done on the stop codons, especially when we found that them, with TGA included, are the less studied or talked about in research and/or in academic circles today, as Table 1 shows, they are even easily forgotten in related literature [24,27,29–31,52]. Hopefully, with these observations, we could be able to do a deeper and more detailed study of the non-coding stop codons, and particularly of that one that differs, or TGA.
The ordered defragging by vertical pairing of genetic code products derived from the I Ching resulted in the double pair of genetic code chromosomes M (for Met) and I (for Ile), showing a new way to represent the genetic code through quasi-identical and semi-introverted chromosome representations that can also be useful in bioinformatics; and here, as stated before, one chromosome is most expected to be used when studying humans and mammals in general (the one with codons ending only in C and G), while the other one is most expected to be used when studying invertebrates and plants (the one with codons ending in T and A).
So, an additional rule of variation [2,17] seemed to be here confirmed, a rule dealing with the most used third nucleotide within codons per amino acid, showing that there is a bias in dominance of three H-bonds in the third nucleotides of the most used codons per amino acid of humans and of mammals, as we saw in the upper i, M and M', with an opposite set of bias in the dominance of two H-bonds in the third nucleotide of the most used codons per amino acid of invertebrates and of plants, a dominance seen in the other member chromosome of these synthetic pairs of genetic code chromosomes, being these the lower i, M or M'.
The theoretical exchange of G for A and of C for T seen in our semi-introversions seems to be similar to the differential choices seen in the most used codons per amino acid in mammals versus invertebrates and plants, an intriguing aspect of patterns, logic, and mathematics to be further developed.
The quasi-identity seen in the double pairs of genetic code chromosomes M and I is also an analogy of the protective duplicity of valuable codifying information that is available in chromosomes through strategies and mechanisms still waiting to be discovered. For example, each gene has two pairs of two almost identical replicas, with each one of them located in one of its four almost-identical chromatids: two of them coming from the chromosome inherited by the father plus the remaining two coming from the chromosome inherited by the mother. This reiterated information is protecting us as much as it can, according to the limits established by the quality control mechanisms within cells and organisms, preventing anarchy while keeping the order within the genomics of populations, being these their compatible Themes [16,17]; safeguarding thus functional efficacy of protein products, while indirectly, also of the metabolic sub-products manufactured by them through this protected integrity of genes.
The pairs of genetic code chromosomes M, M', and I, I' studied here were within their groups quasi-identical in their amino acids, as shown in Figures 6, 7 and 9, being heterogeneous in their codons. The 64-grid genetic code shown in Figure 11 was restored to its 90° rotational resonance as shown in Figure 13, while Figure 14 was also restored to its 90° rotational resonance as shown in Figure 16, and finally Figure 17 was 90° rotationally restored with the differential results shown in Figure 19.
Both pairs of figures: the pair of Figures 11 and 13 and the pair of Figures 14 and 16 surprisingly preserved their respective semi-introversions in their second nucleotides; however, in Figure 17 we had the third nucleotide exhibiting a semi-introversion (also by replacement of pur by pur and of pyr by pyr), a semi-introversion that was lost when the figure was 90° rotationally restored (Figure 19). As seen in the discussion, the genetic code is able to manifest mathematics such as precise geometries and arithmetic because it is actually representing a group of real third dimensional molecules, the enzymes and proteins with their proper symmetries and stoichiometries.
This article also demonstrates that the basic principles of an intelligent design present in the genetic code can easily be expanded, not only to bioengineering, but also to a novel bio-architecture.
Some of the perspectives derived from this work, as stated earlier, are: 1) the search for quasi-spherical representations of the genetic code, 2) the reverse engineering of the functional genetic code tetrahedron shown in the upper part of Figures 21 and 23 (when folded), and in Figure 22, 3) the search of compressed versions of the genetic code in order to increase the practical speed of computational programs that may be able to compare genetic and genomic sequences on the basis of the genetic code, etc.
Maybe an alternative representation of the genetic code is still hidden and undiscovered in some corner of the remote Chinese, Hindu, Moche, Inca, Maya, etc., just waiting to be discovered.
For example, in relation to the ancient finding described here as hidden within binary paired and rotationally restored representations of the genetic code, a similar double swastika was found on a replicating stamp seal from about 2,800 B.C. [53], http://www.webcitation.org/67OW4dh79 matching the approximate date given for the origin of the I Ching [54]; after that time, the swastika of fertility did spread all over the world, from Troy, where two different female characters were found by H. Schliemann, having both a right-handed or clockwise motion swastika stamped on their reproductive organs and/or belly, respectively [55–57], to Peru, where it was the opposite, a left-handed or counterclockwise swastika found stamped at approximately the height of the breast [58,59; to see a collage with these three last images, go to: http://www.webcitation.org/67Q3DxXYD].
And while the archaeological evidence for the previous paragraph is very scant, not so for the one related to the I Ching and its presumed discoverers: Fu-Xi and Nu-Wa, frequently shown intertwined in their 'double-helix'-like lower bodies, being them like two strands, something found by the hundreds or more in China and related nations [60–64; my collage with some of those images can be seen http://www.webcitation.org/680MQgzjL].
It is notable that, in a similar way that the first representation of the 64 codons in modern times went unnoticed while accumulating dust in a handwritten notebook [7], also the first open-ended representation of the genetic code currently known to man, the millenary and binary I Ching of Fu-Xi, also went unnoticed for centuries, until Stent represented it in a book [10]; however, I think that a research article may be able to have a wider distribution than a book.
This is the first time, to my knowledge, that part of the handwritten and unpublished codon table of the modern age from the pen of Nirenberg (1965) [7], has been shown (Table 2). It is also to be noticed that each of the other most recent representations of the genetic code through tetrahedrons (Figures 21–23) follows an identical mathematical multiplication corresponding to Nirenberg's 16×4. On the other hand, any pair of the genetic code chromosomes introduced here follows a new multiplicative logic for the genetic code: 2×8×4.
It is interesting to notice the correspondence of Crick's table [8] to Nirenberg's unpublished one [7] when turning the last to the back, rotating it 90° counterclockwise and dividing it by four.
The full, theoretically translucent stella octangula or stellated octahedron obtained in this article (Figure 23), is a structure made by 128 codons (64+64 or two complete genetic codes coupled in order to separate the two different methionines), including the 32 codons or 1/4 of the total, hidden on the inner octahedron. This stella and its core resulted by further compressing the slightly separated 'pair of tetrahedra' shown in Figure 21 into a cube to save space, suggesting the ease for the transformation of 2D cell 'bits' into 3D cubes.
The basic nets or patterns to build a 3D tetrahedron from a 2D triangle (shown in Figure 20) and from a 2D parallelogram (shown in Figure 22) are known at least since 1636 [65], http://www.gutenberg.org/files/26752/26752-page-images/p0255.png]."
Finally, it needs to be stressed once more that the core aspect explored in this article was the inherent ability of the genetic code to experience a complete and sense or positive single-strand self-annealing. While the earlier (1619) tetrahedral subdivision in 16 triangular grids per face corresponds to Kepler [66, http://books.google.com/books?id=rEkLAAAAIAAJ (D on p. 104)].
Acknowledgments
Tracy L. Duncan helped preparing this manuscript and Angelina G. Castelli and J. Christós suggested important elements of the 3D tetrahedral representations; my parents María Cristina Chávez de Castro and Manuel Castro Dávila encouraged me to pursue this investigation, funded in part by the NIH grant T32 HL-07812; this article is also available at PubMed. I wish to thank Tilda McLean and the Emergency Unemployment Compensation (EUC) of the Texas Workforce Commission for helping me to survive while preparing this work; if anyone likes my work and wants to sponsor me to pursue it, please email me, this is the time to help; i.e., through a faculty/tenure position derived from my works, a good grant in bioinformatics, an invite and/or income from publishing/speaking, etc.
Abbreviations
Amino acids
- A
alanine (Ala)
- V
valine (Val)
- I
isoleucine (Ile)
- L
leucine (Leu)
- M
methionine (Met)
- F
phenylalanine (Phe)
- W
tryptophan (Trp)
- D
aspartic acid (Asp)
- N
asparagine (Asn)
- E
glutamic acid (Glu)
- Q
glutamine (Gln)
- R
arginine (Arg)
- K
lysine (Lys)
- S
serine (Ser)
- T
threonine (Thr)
- G
glycine (Gly)
- P
proline (Pro)
- H
histidine (His)
- C
cysteine (Cys)
- Y
tyrosine (Tyr)
Glossary
Nucleotides
- C
cytosine
- A
adenine
- G
guanine
- T
thymine
- U
uracil
- r
purine
- y
pyrimidine
- bp
base pairs
Appendixes
Appendix A
Figure 25: Horizontal defragging shown in T. 1 of Figure 2 according to the original pairs of trigrams called the hexagrams of the I Ching.
Appendix B
Figure 26: Horizontal defragging shown in T. 2 of Figure 2 according to the original pairs of trigrams called the hexagrams of the I Ching.
Appendix C
Figure 27: Horizontal defragging shown in T. 3 of Figure 2 according to the original pairs of trigrams called the hexagrams of the I Ching. This comparison does not generate a pair of genetic code chromosomes.
Appendix D
Figure 28: Vertical defragging shown in T. 1 of Figure 4 according to the original pairs of trigrams called the hexagrams of the I Ching.
Appendix E
Figure 29: Vertical defragging shown in T. 2 of Figure 4 according to the original pairs of trigrams called the hexagrams of the I Ching.
Appendix F
Figure 30: Vertical defragging shown in T. 3 of Figure 4 according to the original pairs of trigrams called the hexagrams of the I Ching. This comparison does not generate a pair of genetic code chromosomes.
Appendix G
The logic for the amino acid transfer from binary tables to genetic code chromosomes
An intuitive strategy has been used to fill the genetic code chromosomes shown in the right side of Figure 6, first by giving a naturally vertical sight to the originally vertical pairings of single-strand self-annealed sets of eight codons, here transformed into their resulting sets of 8 amino acids. T. 1 of Figure 5 was converted into a pair of genetic code chromosomes called M by rotating this table 90 degrees counterclockwise and stacking its first original four columns (1–4), counting them from left to right, in the left side arms of the chromosomes shown in the upper right part of Figure 6, or genetic code chromosomes M (M1 and M2), starting here from their bottom arm with column 1, and going to the top arm, while the rest of the original columns (5–8) have been used in the same way to fill their right-side arms, again starting from the bottom arm and ending at the top arm with column 8; the same has been done to T. 2 of Figure 5, rotating it 90 degrees counterclockwise and locating its original first four columns in the left-side arms of the genetic code chromosomes I (I1 and I2) from bottom to top as shown in the lower right half of Figure 6, while the remaining original columns (5–8) have been used to fill the right-side arms, going again from bottom to top. This completes the two pairs of genetic code chromosomes shown at the right side of Figure 6.
A more counter-intuitive strategy has been used to fill the genetic code chromosomes shown in the left side of Figure 6, first by giving a vertical sight to the originally horizontal pairings of single-strand self-annealed sets of eight codons, here transformed into their resulting sets of 8 amino acids, selecting T. 1 of Figure 3 to design the pair of genetic code chromosomes shown in the lower left side of Figure 6, again rotating 90 degrees counterclockwise the tables while keeping the original column numbering from 1–4 for the left-side arms of the chromosomes while selecting them this time in an alternated way, i.e., column 1 fills the lower left-side arm of chromosome i1 while column 3 fills its upper-left side arm; likewise, the lower left-side arm of chromosome i2 is filled with the contents of column 2 while its upper left-side arm was filled with the amino acid contents of column 4; for the right side a similar strategy was followed to obtain their right-side arms: using the originally numbered columns 5 and 7 to respectively fill the lower and upper right-side arms of the genetic code chromosome i1, and columns 6 and 8 to respectively fill the lower and upper right-side arms of the genetic code chromosome i2. The same logic was followed to obtain the genetic code chromosomes m that are shown in the upper left side of Figure 6, using T. 2 of Figure 3, selecting its originally numbered columns 1 and 3 to respectively fill the lower and upper left-side arms of the genetic code chromosome m1 while using the columns 5 and 7 to respectively fill its lower and upper right side arms; the same was done to its companion, the genetic code chromosome m2, using columns 2 and 4 to respectively fill its lower and upper left-side arms, to finally use columns 6 and 8 to fill its lower and upper right-side arms. This completes the two pairs of genetic code chromosomes shown at the left side of Figure 6. Each of these genetic code chromosomes pairs (m, i, M, I) is a different and independent representation of the complete genetic code.
Appendix H
The logic behind the transformation of M into M'
The logic behind the transformation of the original pair of genetic code chromosomes M into the first semi-introverted codon system, here called the M' pair of chromosomes, consists in taking groups of four amino acids as seen in the original quadrants of the table from which the original pairs of chromosomes were derived (T. 1 of Figure 5); for the genetic code chromosomes M' seen in Figure 7, we took the next arm's halves following the number and letter coordinates seen in Figure 6, for the essential hydrophobic arm of the upper chromosome M': 1C up right half + 1C down left half, while for the lower chromosome M' we took 2C up right half + 2C down left half; for the acidic arm (E, D) of the upper chromosome M' we took 1C down right half + 1C up left half, while for the lower chromosome M' we took 2C down right half + 2C up left half. This completes the arms of the left side.
The arms of the right side of the chromosomes M' shown in Figure 7 have been integrated by always taking backwards from Figure 6 the next segments for both chromosomes, for the Arg (R) arm of the upper chromosome M' we took: 1D up left half + 1D down right half, while for the lower chromosome M', we took the 2D up left half + 2D down right half; and finally, for the Pro (P) arm of the upper chromosome M' we took 1D down left half + 1D up right half, while for the lower chromosome M' we took 2D down left half + 2D up right half.
The logic behind the transformation of I into I'
Now, the logic behind the conversion of the original pair of genetic code chromosomes I into a second semi-introverted codon system, here called the I' pair of chromosomes, also consists in taking groups of four amino acids as seen in the original quadrants of the table from which the original pairs of chromosomes were derived (T. 2 of Figure 5); for the genetic code chromosomes I' seen in Figure 9 we took the next arm's halves following the number and letter coordinates seen in Figure 6, for the essential hydrophobic arm of the upper chromosome I': 4C down right half + backwards 4D up left half, while for the lower chromosome I' we took 3C down right half + backwards 3D up left half; for the acidic arm (E, D) of the upper chromosome I' we took 4C up right half + backwards 4D down left half, while for the lower chromosome I' we took 3C up right half + backwards 3D down left half. This completes the arms of the left side.
The arms of the right side from the chromosomes I' shown in Figure 9 have been integrated by taking from Figure 6 the next segments for both chromosomes, for the Arg (R) arm of the upper chromosome I' we took: 4C down left half + backwards 4D up right half, while for the lower chromosome I' we took the 3C down left half + backwards 3D up right half; and finally, for the Pro (P) arm of the upper chromosome I' we took 4C up left half + backwards 4D downright half, while for the lower chromosome I', we took 3C up left half + backwards 3D downright half. A careful observation of the mentioned figures and of the previous ones will help the reader to visually identify the given allocations.
Appendix I
The logic for the conversion of the comparison of Keto/Amino vs Pur/Pyr columns into rows
The quantum logic behind the conversion of the columns of Figure 14 into the rows of Figure 17 is as follows: dividing them in two and rotating them 90° clockwise, first numbering the columns of Figure 14 from 1 to 8 from left to right, calling the first half (1–4) A and the second half (5–8) B, to then also number the rows of Figure 17 from 1 to 8 and from top to bottom while calling here the first half (1–4) a and the second half (5–8) b, following as our order reference the rows of Figure 17: B3 to a1, A2 to b1; B4 to a2, A1 to b2; B1 to a3, A4 to b3; B2 to a4, A3 to b4; B6 to a5, A7 to b5; B5 to a6, A8 to b6; B8 to a7, A5 to b7; ending with B7 to a8, and A6 to b8. Here underlined, the two rows with the codons for the essential hydrophobic amino acids with T at the center (corresponding to rows 4 and 5).
References
- 1.Castro-Chavez F. A tetrahedral representation of the genetic code emphasizing aspects of symmetry. Bio-Complexity. 2012a;2:1–6. doi: 10.5048/BIO-C.2012.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Castro-Chavez F. The Quantum Workings of the Rotating 64-Grid Genetic Code. Neuroquantology. 2011;9(4):728–746. doi: 10.14704/nq.2011.9.4.499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alpern NJ, Alpern J, Muller R. IT career JumpStart: An introduction to PC hardware, Software, and Networking. Indiana: Wiley; 2012. p. 92. [Google Scholar]
- 4.Rutenbeck J. Tech terms: what every telecommunications and digital media person should know. Boston: Elsevier; 2006. p. 66. [Google Scholar]
- 5.Smith W. Ultimate PC toolkit. Maximum PC. 2003:28. [Google Scholar]
- 6.Leibnitz M. Explication de l’arithmetique binaire, qui se sert des seuls caracteres 0 et 1; avec des remarques sur son utilite, et sur ce qu’elle donne le sens des anciennes figures Chinoises de Fohy. [Explanation of binary arithmetic, using only the characters 0 and 1; emphasizing its usefulness, and how it gives sense to the ancient Chinese Figures of Fuxi]. Memoires de l’Academie Royale des Sciences. 1703;3:85–89. [in French] [Google Scholar]
- 7.Nirenberg MW. 64 triplets and complementary triplets. Unpublished laboratory note. 1965 [Google Scholar]
- 8.Crick FH. The Croonian lecture, 1966. The genetic code. Proc R Soc Lond B Biol Sci. 1967;167(9):331–347. doi: 10.1098/rspb.1967.0031. http://profiles.nlm.nih.gov/ps/access/SCBCBX.pdf. [DOI] [PubMed] [Google Scholar]
- 9.Bresch C, Hausmann R. Der genetische code. Klassische und Molekulare Genetik [The genetic code. In: Classical and Molecular Genetics] Berlin: Springer; 1972. pp. 243–278. [in German] [Google Scholar]
- 10.Stent GS. The coming of the golden age. A view of the end of progress. New York: Natural History Press; 1969. [Google Scholar]
- 11.Schonberger M. I Ching and the genetic code: The hidden key to life. New Mexico: Aurora Press; 1992. [Google Scholar]
- 12.Swanson R. A unifying concept for the amino acid code. Bull Math Biol. 1984;46(2):187–203. doi: 10.1007/BF02460068. [DOI] [PubMed] [Google Scholar]
- 13.Hirabayashi Y, Furuya S. Roles of l-serine and sphingolipid synthesis in brain development and neuronal survival. Prog Lipid Res. 2008;47(3):188–203. doi: 10.1016/j.plipres.2008.01.003. [DOI] [PubMed] [Google Scholar]
- 14.Fuchs SA, Berger R, de Koning TJ. D-serine: the right or wrong isoform? Brain Res. 2011;1401:104–117. doi: 10.1016/j.brainres.2011.05.039. [DOI] [PubMed] [Google Scholar]
- 15.Wolosker H. Serine racemase and the serine shuttle between neurons and astrocytes. Biochim Biophys Acta. 2011;1814(11):1558–1566. doi: 10.1016/j.bbapap.2011.01.001. [DOI] [PubMed] [Google Scholar]
- 16.Castro-Chavez F. The rules of variation expanded, implications for the research on compatible genomics. Biosemiotics. 2012b;5(1):121–145. doi: 10.1007/s12304-011-9118-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Castro-Chavez F. Most used codons per amino acid and per genome in the code of man compared to other organisms according to the rotating circular genetic code. NeuroQuantology. 2011b;9(4):747–766. doi: 10.14704/nq.2011.9.4.500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lee JHX, Nadeau KM. Encyclopedia of Asian American folklore and folklife. Santa Barbara: ABC-CLIO; 2010. p. 87. [Google Scholar]
- 19.Feuerstein G. The Shambhala encyclopedia of yoga. Boston: Shambhala Publications; 2000. p. 27. [Google Scholar]
- 20.Tiwari BM. The path of practice: A woman's book of Ayurvedic healing. New Delhi: Motilal Banarsidass Press; 2002. p. 55. [Google Scholar]
- 21.Weiss SF. The Nazi symbiosis: Human genetics and politics in the Third Reich. Chicago: University of Chicago Press; 2010. [Google Scholar]
- 22.Zimmermann R. Protein transport into the endoplasmic reticulum. Texas: Landes Bioscience; 2009. [Google Scholar]
- 23.Cristea PD. Symmetry in genomics. Symm Cult Sci. 2010;21(1–3):71–86. [Google Scholar]
- 24.Trainor LEH. The triplet genetic code: key to living organisms. California: World Scientific; 2001. 8.3 The tetrahedral representation of codon space; pp. 62–70. [Google Scholar]
- 25.Freeland SJ. Book review: The triplet genetic code: key to living organisms. LEH Trainor. Heredity. 2002;89:236–237. [Google Scholar]
- 26.Close F. The quark structure of matter. In: Davies P, editor. The new physics. Cambridge: Cambridge University Press; 1992. pp. 396–424. [Google Scholar]
- 27.Cristea PD. Representation and analysis of DNA sequences. In: Dougherty ER, Shmulevich I, Chen J, Wang J, editors. Genomic signal processing and statistics. New York: Hindawi Publishing Corporation; 2005. pp. 15–65. [Google Scholar]
- 28.Hill V, Rowlands P. Nature's code. In: Rowlands P, editor. Zero to infinity: the foundations of physics. California: World Scientific; 2007. pp. 502–555. [Google Scholar]
- 29.Zhang R. Distribution of mapping points of 20 amino acids in the tetrahedral space. Amino Acids. 1997;12(2):167–177. [Google Scholar]
- 30.Filatov F. A molecular mass gradient is the key parameter of the genetic code organization. 2009 arXiv:0907.3537v1 [q-bio.OT] [Google Scholar]
- 31.Negadi T. The irregular (integer) tetrahedron as a warehouse of biological information. [Manuscript] [Google Scholar]
- 32.Fujiomoto M. 4,702,704. Tetrahedral codon stereo-table. U.S. Patent. 1987
- 33.Baccheschi E. El Greco: the complete paintings. London: Granada; 1980. [Google Scholar]
- 34.Spies W. Botero: Paintings and drawings. New York: Prestel; 2007. [Google Scholar]
- 35.Fischer E. Guro: Masks, performances, and master carvers in Ivory Coast. Zurich: Museum Rietberg; 2008. [Google Scholar]
- 36.Quilter J. The Moche of ancient Peru: Media and messages. Massachusetts: Peabody Museum of Archaeology and Ethnology, Harvard University Press; 2011. [Google Scholar]
- 37.Kumar M. Quantum: Einstein, Bohr, and the great debate about the nature of reality. New York: Norton; 2011. [Google Scholar]
- 38.Tattao LA. Basic concepts in statistics. Manila: Rex; 2007. p. 7. [Google Scholar]
- 39.Da Vinci L. Leonardo on the human body. New York: Henry Schuman; 1952. [Google Scholar]
- 40.Clayton M, Philo R. Leonardo Da Vinci: The mechanics of man. Los Angeles: Getty Publications; 2010. [Google Scholar]
- 41.Strachan T, Read AP. Human molecular genetics. 2nd ed. New York: Wiley; 1999. [Google Scholar]
- 42.shCherbak V. The arithmetical origin of the genetic code. In: Barbieri M, editor. The Codes of Life. Berlin: Springer; 2008. pp. 153–188. [Google Scholar]
- 43.Sommerer C, Mignonneau L. Art@science. Berlin: Springer; 1998. [Google Scholar]
- 44.Glass CS. The convergence of art & science. California: Green Museum; 2005. [Google Scholar]
- 45.Shlain L. Art & physics: Parallel visions in space, time, and light. New York: Harper Perennial; 2007. [Google Scholar]
- 46.Chien A, Foster I, Goddette D. Grid technologies empowering drug discovery. Drug Discov. Today. 2002;7(20 Suppl):S176–S180. doi: 10.1016/s1359-6446(02)02369-3. [DOI] [PubMed] [Google Scholar]
- 47.Gonzalez-Beltran A, Tagger B, Finkelstein A. Federated ontology-based queries over cancer data. BMC Bioinformatics. 2012;13(Suppl 1):S9. doi: 10.1186/1471-2105-13-S1-S9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Castro-Chavez F. Escaping the cut by restriction enzymes through single-strand self-annealing of host-edited 12-bp and longer synthetic palindromes. DNA Cell Biol. 2012c;31(2):151–163. doi: 10.1089/dna.2011.1339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Castro-Chavez F. The rules of variation: amino acid exchange according to the rotating circular genetic code. J Theor Biol. 2010;64(3):711–721. doi: 10.1016/j.jtbi.2010.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Petoukhov S, He M. Symmetrical Analysis Techniques for Genetic Systems and Bioinformatics. Pennsylvania: IGI Global; 2010. [Google Scholar]
- 51.He M, Petoukhov S. Mathematics of Bioinformatics: Theory, Methods and Applications. New Jersey: Wiley; 2011. [Google Scholar]
- 52.Lien EJ, Das A, Nandy P, Ren S. Physicochemical basis of the universal genetic codes--quantitative analysis. Prog Drug Res. 1997;48:9–25. doi: 10.1007/978-3-0348-8861-5_1. [DOI] [PubMed] [Google Scholar]
- 53.Oude culturen in Pakistan. Brussel: Kon Musea voor Kunst & Geschiedenis; 1989. p. 246. [Google Scholar]
- 54.Huang A. The complete I Ching. Rochester: Inner Traditions; 2010. p. XVII. [Google Scholar]
- 55.Wilson T. The swastika, the earliest known symbol, and its migrations: with observations on the migration of certain industries in prehistoric times. Washington: Govt Print Off; 1896. p. 829.p. 831. [Google Scholar]
- 56.Schliemann H. Troja. Results of the latest researches and discoveries on the site of Homer’s Troy. New York: Harper & Brothers; 1884. p. 191. [Google Scholar]
- 57.Schliemann H. Ilios. The city and country of the Trojans. New York: Harper & Brothers; 1880. p. 337. [Google Scholar]
- 58.Chero-Zurita L. Sipán, temporada de excavaciones 2007. Chiclayo – Trujillo, edición especial, Compendio de Arqueología, Lundero, Publicación Cultural del Diario La Industria, Mayo [Sipan, 2007 excavation season. Chiclayo - Trujillo, special edition, Compendium of Archaeology, Lundero, Cultural Publishing of Journal The Industry, May] 2008 [in Spanish] [Google Scholar]
- 59.Alva W, Chero-Zurita L. Perú puede sorprender al mundo con nuevos hallazgos arqueológicos. Lima, Agencia Peruana de Noticias, Agencias/RES [Peru can surprise the world with new archaeological finds. Lima, Peru News Agency, Agencies / RES], 07/02/2009. http://www.andina.com.pe/Espanol/Noticia.aspx?id=2OZIV9X48Mw= [in Spanish] [Google Scholar]
- 60.Ruey YF. [Miao stories of a Great Flood and the legends of a Fu-hsi and Nu-wa] Com on Anthropol. 1938;1:155–204. [in Chinese] [Google Scholar]
- 61.Rudolph RC. Han tomb reliefs from Szechwan. Archives of the Chinese Art Society of America [currently: Arch Asian Art] 1950;4:29–38. [Google Scholar]
- 62.En-lin Y. Die sagenhaften kaiser in der chinesischen urgeschichte. Versuch eines vergleichs zwischen alten klassischen überlieferungen und neuen archäologischen funden in China. Forschungen und Berichte, Kunsthistorische und volkskundliche Beiträge [The legendary emperor of China's ancient history. Attempt of a comparison between the old classical traditions and new archaeological discoveries in China. Research and Reports, Historical art and ethnographic contributions] 1979;19 37-48+T1-T7 [in German] [Google Scholar]
- 63.Powers MJ. An archaic bas-relief and the Chinese moral cosmos in the first century A.D. Ars Orientalis. 1981;12:25–40. [Google Scholar]
- 64.Whitfield S, Sims-williams U. The Silk Road: Trade, Travel, War and Faith. Chicago: Serindia Publications; 2004. p. 328. [Google Scholar]
- 65.Ramus P. The way to geometry. London: Thomas Cotes; 1636. p. 255. [Google Scholar]
- 66.Keppleri I. Harmonices mundi. Austriae, Johannes Plancus MDCXIX [Kepler J. The harmony of the world. Austria, John Plancus 1619], Fig. D of insert after p. 58 [In Latin] [Google Scholar]