Humans, geometric similarity and the Froude number: is ‘‘reasonably close’’ really close enough?

Summary

Understanding locomotor energetics is imperative, because energy expended during locomotion, a requisite feature of primate subsistence, is lost to reproduction. Although metabolic energy expenditure can only be measured in extant species, using the equations of motion to calculate mechanical energy expenditure offers unlimited opportunities to explore energy expenditure, particularly in extinct species on which empirical experimentation is impossible. Variability, either within or between groups, can manifest as changes in size and/or shape. Isometric scaling (or geometric similarity) requires that all dimensions change equally among all individuals, a condition that will not be met in naturally developing populations. The Froude number (Fr), with lower limb (or hindlimb) length as the characteristic length, has been used to compensate for differences in size, but does not account for differences in shape.

To determine whether or not shape matters at the intraspecific level, we used a mechanical model that had properties that mimic human variation in shape. We varied crural index and limb segment circumferences (and consequently, mass and inertial parameters) among nine populations that included 19 individuals that were of different size. Our goal in the current work is to understand whether shape variation changes mechanical energy sufficiently enough to make shape a critical factor in mechanical and metabolic energy assessments.

Our results reaffirm that size does not affect mass-specific mechanical cost of transport (Alexander and Jayes, 1983) among geometrically similar individuals walking at equal Fr. The known shape differences among modern humans, however, produce sufficiently large differences in internal and external work to account for much of the observed variation in metabolic energy expenditure, if mechanical energy is correlated with metabolic energy. Any species or other group that exhibits shape differences should be affected similarly to that which we establish for humans. Unfortunately, we currently do not have a simple method to control or adjust for size–shape differences in individuals that are not geometrically similar, although musculoskeletal modeling is a viable, and promising, alternative. In mouse-to-elephant comparisons, size differences could represent the largest source of morphological variation, and isometric scaling factors such as Fr can compensate for much of the variability. Within species, however, shape differences may dominate morphological variation and Fr is not designed to compensate for shape differences. In other words, those shape differences that are “reasonably close” at the mouse-to-elephant level may become grossly different for within-species energetic comparisons.

Introduction

Assessing the energy that animals expend on locomotion is critically important, because locomotion is a mandatory feature of subsistence and energy is a finite, non-recyclable resource (Borgerhoff-Mulder, 1992), intimately tied to reproduction (Ellison, 2008). Approximately 6–30% of the daily activity budget of non-human primates is spent on locomotion (A.D. Sylvester, The decoupling hypothesis: a new theory for the origin of hominid bipedalism, PhD thesis, University of Tennessee, 2006, and references therein) and modern hunter–gatherers routinely engage in subsistence rounds of >10 km (e.g. Hilton and Greaves, 2003). Individuals require substantial amounts of (metabolic) energy to reproduce, especially mothers who gestate, lactate and frequently transport dependent young (Altmann and Samuels, 1992; Kramer, 1998; Wall-Scheffler et al., 2007; Watson et al., 2008). Consequently, much effort has been devoted to understanding the energy expenditure of locomotion and the features that affect locomotor efficiency.

For extant species that can be directly studied in laboratory settings, statistical equations can be used to predict metabolic energy expenditure from a variety of potential locomotor (e.g. velocity) and morphological (e.g. body mass) parameters. Usually, the rate of volumetric consumption of oxygen ( 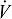O₂) is used as a proxy of metabolic energy expenditure. Frequently however, the goal is to understand the energy expenditure of extinct creatures or extant ones that are not amenable to laboratory experiments. Some extant species are difficult to obtain for experimentation (e.g. Pan sp.), less than cooperative (e.g. male Papio sp.) or hard to accommodate in laboratory settings (e.g. Rhinoceros sp.), thus making mechanical modeling an attractive option to explore issues associated with their metabolic energy expenditure. Often in paleoanthropology, the research goal is to understand differences in energy expenditure between groups, populations, or species whose absolute size are relatively similar, but whose shape varies in interesting ways (e.g. modern humans and Neandertals). Given this, it is critical that the effect of size differences on metabolic energy expenditure be distinguishable from those caused by shape differences.

Empirically-determined equations can be extrapolated to estimate the energy expenditure of extinct groups (e.g. Sorensen and Leonard, 2001; Steudel-Numbers and Tilkens, 2004) or those engaged in locomotor tasks in their natural environments (e.g. Altmann and Samuels, 1992), but caution is warranted: the causal link between locomotor parameters and metabolic energy consumption is not entirely understood. Because the variables that affect metabolic energy consumption may affect specific locomotor systems (or particular species) differently (Kramer and Sylvester, 2009), the assumptions that underlie the extrapolations are questionable and the conclusions reached are tenuous at best.

As an alternative to extrapolating from metabolic equations, a different approach seeks to use the equations of motion to understand metabolic energy expenditure. The mechanical energy required to produce motion can be calculated for any machine, if that machine can be mathematically described (Meriam, 1978). In forward dynamics, the forces applied to the machine are known, while in inverse dynamics, motions are known. Either approach can be used to calculate the mechanical energy expenditure of a machine. Importantly, for a given machine in a perfect world, these techniques yield the same results as is dictated by the equations of mechanical motion and has been shown empirically to be true for walking humans (Kramer and Sylvester, 2011). Nonetheless, error is always present in the data collected as inputs to mechanical analyses and the magnitude of the error varies among kinds of data or methods of collection, e.g. positional data obtained using external markers and infrared cameras are more error prone than that acquired from fluoroscopy, but less than that from digitization of videotape.

Using mechanical energy to estimate metabolic energy is mathematically rigorous and offers unlimited opportunity to explore how small changes in individual components affect the total machine. One difficulty in using the mechanics of motion is that all important components need to be adequately defined. The mechanical energy of movement (i.e. kinetic and potential energy) does not predict the metabolic energy expenditure of a sample of individuals with fidelity or precision when elastic storage is important, as in running, or when muscles work at different points on their force–velocity curves, as can happen when small and large animals are aggregated (Heglund et al., 1982). We recently tested the ability of seven approaches, based on mechanical energy calculations, to predict metabolic energy and found that they are as good as empirical methods among walking humans (Kramer and Sylvester, 2011). The inverse kinematics approach with individualized segment parameters predicted metabolic energy expenditure within individuals (i.e. that due to velocity) well (r² = 0.87), but variability among individuals was not well predicted (r² = 0.17) (Kramer and Sylvester, 2011).

This difficulty in predicting variability between individuals is interesting, because mechanical tenets clearly specify how size differences should affect the motion of animals: individuals moving in dynamically similar ways should expend equal amounts of mass-specific metabolic energy when moving at the same speed for their body size (Alexander and Jayes, 1983). Determining a size-equivalent speed is critical, and the nearly universal choice is the Froude number (Fr). Fr is a dimensionless speed calculated as Fr = V/(g*l)^0.5 where V is velocity (in m/s), g is the gravitational constant at sea level (9.81 m/s²) and l is a characteristic length (in m) (Alexander and Jayes, 1983). The characteristic length for terrestrial locomotion is usually taken to be lower limb (or hindlimb) length. Humans do not, however, use the same O₂ to move at equal Fr (Kramer and Sarton-Miller, 2008; Steudel-Numbers and Weaver, 2006), even when body mass and lower limb length are controlled.

This finding prompts a closer examination of dynamic similarity, the theoretical foundation for the use of Fr. The most basic requirement of dynamic similarity is geometric similarity, which states that all linear measurements of one individual can be transformed into those of another through multiplication by a single factor (Alexander and Jayes, 1983). In other words, individuals are strictly isometric for all linear measurements, including lengths and circumferences, and thus linear proportions are constant between individuals. We refer herein to this characteristic as shape – geometrically similar individuals are the same shape, regardless of their size (absolute dimensions) (Kramer and Sylvester, 2009).

The assumption of geometric similarity is violated in modern humans (Sylvester et al., 2008), but the importance of those deviations to the metabolic energy expenditure of humans remains obscure. Alexander and Jayes tested the geometric similarity proposition, including such disparately sized mammals as shrews and elephants, covering a range in body mass from 0.003 to 2500 kg (Alexander and Jayes, 1983). They found that while mammals are not perfectly geometrically similar, they “…tend to be reasonably close to geometric similarity, in some of their principal linear dimensions” and that “…these deviations from geometric similarity need not destroy the usefulness of the dynamic similarity hypothesis” (Alexander and Jayes, 1983; p.141). The deviation from geometric similarity is probably negligible for analyses of metabolic energy expenditure where the difference in absolute size is large (i.e. mouse-to-elephant analyses), but for analyses where absolute size is similar (e.g. within a hominin genus or species) shape differences may become important (Kramer and Sylvester, 2009). Another way of saying this is that size may be the predominant source of variation in mouse-to-elephant analyses, but shape could become an increasingly large source of variation when smaller taxonomic groups are analyzed.

Differences in shape, no matter how small they may appear, violate the foundational assumption of using Fr. Thus, one explanation for why Fr does not predict walking energy expenditure in humans as well as expected may simply be that humans are not a geometrically similar group, i.e. humans vary in their shape. This variation is, of course, a well-known phenomenon. A critical issue raised by Sylvester and colleagues is that the energetic effect of even small shape differences is unknown (Sylvester et al., 2008).

From the perspective of allometry, geometric similarity (and true isometry) requires that: 1) the slope of the regression line between all pairs of length measurements in log–log space equals 1.0; and 2) the correlation coefficient equals 1.0 for all bivariate comparisons. For samples that include mice-to-elephants, size is likely to dominate with little scatter about the regression line due to shape differences, i.e. correlation coefficients are high (e.g. r² = 0.95 body mass- effective lower limb/hindlimb length in terrestrial species (Pontzer, 2007)). In samples with less size difference, shape can assume a larger role in accounting for the total variance and lower correlation coefficients are found (e.g. r² = 0.41 body mass-lower limb length in modern humans (Steudel-Numbers and Tilkens, 2004)). The interesting question, then, is not “Are the individuals in a sample geometrically similar?”—they are certainly not, because the correlation coefficients among their morphological variable pairs are not all equal to 1.0—but rather “To what degree is geometric similarity violated?”. And, how does this level of shape variability affect energy expenditure and the use of Fr?

To answer that question, we have simulated the shape variability present in a modern human population, using the inverse kinematics model that was validated against the metabolic data of 8 modern humans (Kramer and Sylvester, 2011). This model predicted metabolic energy expenditure as well as, or better than, other techniques and is sensitive to the effect of shape (via morphological variables). In the current use of this model, we used the morphological inputs (described below) as variables in mechanical simulations to predict mechanical energy expenditure. Our goal is to understand if the shape variation in a typical population is discernible in mechanical energy calculations. We considered cases where the linear measurements (lengths and circumferences) of the limb segments varied in accordance with human population-level variation. Our goal was to understand whether or not this shape variation could produce variation in mechanical energy expenditure that was of similar magnitude to the variation among individuals in metabolic cost of transport that has been previously documented empirically. Thus, we explicitly test the proposition that population-level variability is “reasonably close” enough to geometric similarity for intraspecific comparisons of metabolic energy expenditure.

Materials and Methods

Variability in metabolic cost of transport

Numerous studies over 100 years of investigation have documented the metabolic energy consumption of modern humans using the metabolic currency of 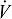O₂. A review of this literature indicates that although data are often aggregated to form average curves, substantial variability exists within studies at a velocity and for a body mass. To demonstrate this variability, representative studies, chosen through a review of the literature supplemented with unpublished data available to the authors, are summarized in Table 1. Inclusion criteria for the studies included the ability to discern multiple, individual values of 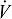O₂ at normal walking velocity (1.1–1.5 m/s). In order to determine the variability, data for multiple individuals are necessary and normal walking velocity allows us to compare the metabolic energy variability with that of the mechanical energy described below.

Table 1. Studies chosen through a review of the literature supplemented with unpublished data available to the authors.

Inclusion criteria include the ability to discern multiple individual values of 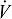O₂ at normal walking velocity (1.1–1.5 m/s). We acquired the 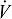O₂ data through 3 mechanisms: tables with individual values were presented in the published information, figures in the published sources indicated individual values which could be digitized by us, or the original data were either ours or made available to us. Many authors report only average data or had their walk-subjects walk at velocities other than normal, while some studies provide exemplary data of one individual and averages for all others or included small numbers of subjects. In order to determine the max./min. value, multiple individual data points are necessary.

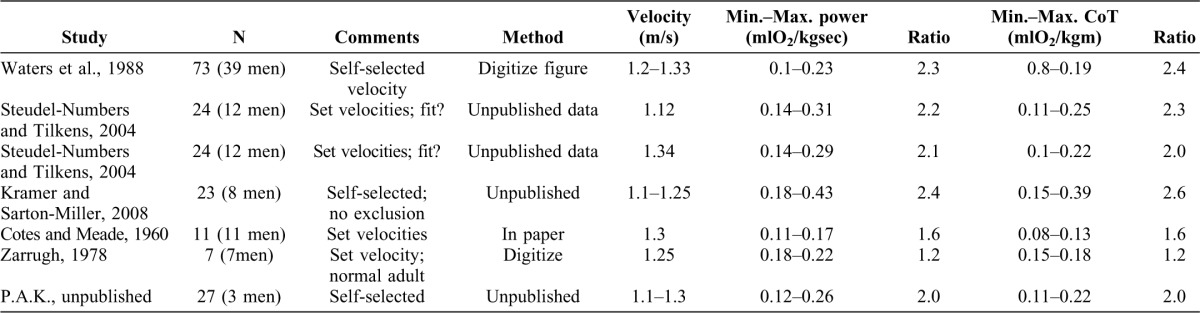
We obtained the 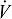O₂ data from three sources: tables with individual values presented in the published information (e.g. Cotes and Meade, 1960); figures in the published sources that indicated individual values and could be digitized by the authors (e.g. Waters et al., 1988); or original data, either the authors' own data (e.g. Kramer and Sarton-Miller, 2008) or data made available to the authors (e.g. Steudel-Numbers and Tilkens, 2004). Many authors report only average data (e.g. Minetti et al., 1994) or had their walk subjects walk at velocities other than normal (e.g. Mercier et al., 1994), while some studies provide exemplary data of one individual and averages for all others (e.g. Workman and Armstrong, 1963) or included small numbers of subjects (e.g. Benedict and Murschhauser, 1915). The maximum and minimum values of mass-specific 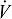O₂ and cost of transport in a velocity range are given and the ratio of maximum to minimum calculated.

Mechanical model

We previously developed a mechanical model, which was based on the inverse kinematics approach, using SimMechanics, the mechanical simulation module of Matlab (MathWorks, Natick, MA), to predict the kinetic and potential energy of segments. This model was previously validated against, and found to be comparable to, other methods of predicting metabolic energy expenditure, such as those focusing on (muscular) force production or joint moments, as described by Kramer and Sylvester (Kramer and Sylvester, 2011). In that work, internal and external work were denoted as INT-MAT and EXT-MAT, respectively, and their sum as COMB-MAT. The model was able to predict 87% of the variation in metabolic energy consumption (net 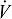O₂) within any particular walking subject. The model included rigid bodies representing the left and right thigh, calf, and foot segments and a pelvis that linked the two lower limbs. Motion of the knee and ankle joints was restricted to the parasagittal plane while that of the hip joints was allowed in all three planes. We chose this mechanical method over the others, because it allows us to vary limb proportions and segmental variables (Kramer and Sylvester, 2011).

Model inputs

Two groups of inputs were required by the SimMechanics model: angular displacements and segment parameters. Angular displacements of the ankle, knee, and hip joints were obtained for average adult humans walking at normal velocities (Inman et al., 1981; Winter, 1987) and were similar to those used elsewhere (Kramer, 1999; Kramer and Sylvester, 2011). All iterations of segmental variables used the same angular displacements. Thigh and calf segmental variables include segment length and proximal and distal circumferences and a constant density was used for all individuals. Mass moments of inertia and segment masses were calculated assuming that the thigh and calf were idealized truncated cones. Foot segmental variables include segment length, width and thickness. Mass and mass moment of inertia were calculated assuming that the foot was a rectangular brick. Mass for the pelvic segment was the difference between total body mass and the sum of left and right lower limbs and inertial properties were calculated assuming the pelvis was cylindrical.

Nine “populations” were created in an attempt to cover the two most basic (external) geometrical features of lower limb shape that can differ among individuals or groups: crural indices and segmental robusticity (Table 2; Fig. 1). In each population, nineteen individuals represented variation from 50–150% of the lower limb length of the mean individual (individual 10) in ∼5% increments. We chose to create individuals who had lower limbs half the size of the mean individual in order to include lower limb lengths approximately equal to the smallest known hominins. We chose to mirror the distribution around the mean modern human (i.e. have an individual with twice the limb length of the mean individual), even though this choice produces individuals with longer lower limbs and higher body masses than are typically seen. All individuals within each population were geometrically similar (i.e. the same shape), but of different size. We created populations of individuals to determine if the effect of shape variation on mechanical energy expenditure varied with size, knowing that it should not.

Table 2. Population parameters.

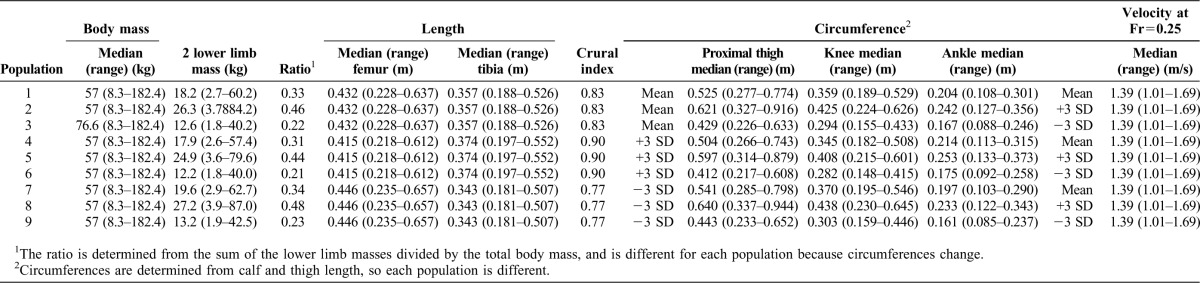
Fig. 1. Relative proportions of the mean individual (individual 10) in each population.

Other individuals in a population are isometrically scaled versions of individual 10.

Population 1 has the mean shape of modern Americans. Segment lengths for individual 10 of population 1 were derived from tibial and femoral lengths of the individuals in the Forensic Anthropology Data Bank of the University of Tennessee (Jantz and Moore-Jansen, 2000), while body mass, circumferences and pelvic width were determined from the 1988 anthropometric survey of US Army male and female soldiers (Gordon et al., 1989). The parameters of the other individuals were scaled isometrically from these values of individual 10.

Populations 2 and 3 were created with circumferences that were +3 and −3 standard deviations from the mean, respectively, but the same lengths as population 1. Populations 4–6 were +3 standard deviations in crural index from populations 1–3, while populations 7–9 were −3 standard deviations in crural index (Table 2; Fig. 1).

For this work, we used the same model as previously, but simulated 3 full strides and filtered the resultant velocity data of the segments. When the average angular profiles of each joint are combined into the full model, the trajectories of each limb segment are not perfectly smooth, producing local maxima/minima in the velocities. Irregular position or velocity curves produce jagged energy curves, which can artificially increase the total energy required to take a stride. To remove these artifacts, we applied a zero phase shift lowpass Butterworth filter (Giakas and Baltzopoulos, 1997). Smoothing to remove local maxima/minima in energy is typically done; for instance, Willems and colleagues considered only those maxima that were separated by 20 ms in their calculation of kinetic energy (Willems et al., 1995). In all subsequent analyses, we used the results from the first step of the second of the three strides (100–150%) to avoid end effects. The second step of the second stride (150–200%) produced identical values to the first.

Mechanical calculations

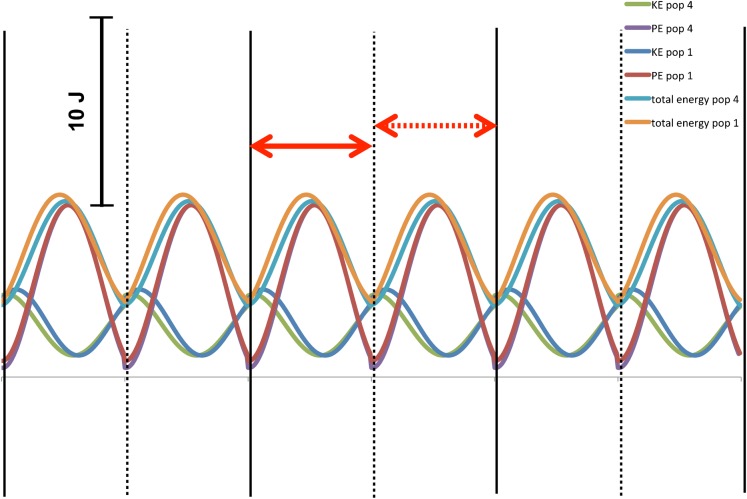
The mechanical calculations are described elsewhere (Kramer and Sylvester, 2011), but the most important details are repeated here. Linear velocities of the limb segmental centers of gravity and angular velocity of the limb segments were output from the Simulink model (using an inverse dynamic solution) and were reported for each limb segment for temporal increments from 0–300% of stride cycle. The filtered values from the first step of the second stride (100–150%) were used to calculate internal work at each temporal increment from the standard equations, similar to the procedure of Cavagna and Kaneko (Cavagna and Kaneko, 1977). As has been done previously, full (100%) energy transfer was allowed between the segments of the same limb, but not between a limb and the body (Kramer, 1999; Willems et al., 1995). Intra-limb energy transfers are feasible because the accelerations and masses and, consequently, forces, are similar, but this is not the case between the body and the limbs (Willems et al., 1995). Fig. 2 depicts the change in internal energy for each segment and the entire limb across the stride cycle.

Fig. 2. Internal work (from potential and kinetic energy) in the segments (A) and summed for a limb (B) for the mean individual (individual 10) in the mean population (population 1) and in the population with mean crural index, but +3 standard deviation circumferences (population 2).

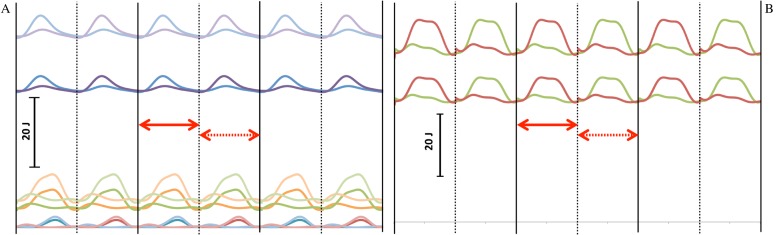
Three strides are shown; heelstrike for the right leg is shown with the solid black vertical line and for the left with a dashed black vertical line. The interval over which the analysis was done (first step of second stride) is indicated with a solid red double-headed arrow. The interval that was used to check the analysis (the second step of the second stride) is indicated with a dashed double-headed arrow. In A, the upper curves are for the thigh, the middle curves for the calf, and the lower curves are for the foot. Darker shades are population 1 while lighter shades are population 2. In B, the sum of the energies of the left (rust) and right (green) lower limbs are shown. The lower set of curves is for population 1, while upper set is population 2.

The energy of a limb at one temporal increment was compared to that of the next temporal increment. If the energy of a later increment was greater than that of the previous increment, extra energy was required to create motion. If a subsequent increment had a lower energy than the previous, this energy was not stored for later use and was set to zero. This approach is similar to previous work (Browning et al., 2009; Doets et al., 2009; Kramer, 1999; Willems et al., 1995). The extra energy required for each interval was summed across the step for left and right lower limbs. Internal work for that iteration was the sum of the extra energy required by the left and right lower limbs.

External work was calculated from the effective change in position of the body's center of gravity as calculated from the motion of the limbs. In other words, the motion of the center of gravity occurs as the result of the motion of the hip, knee and ankle joints. This approach differs from the typical approach (e.g. Willems et al., 1995), who use ground reaction forces to determine the motion of the body center of gravity. We agree with Willems and colleagues that using ground reaction force data would result in less error in the calculation of body's mechanical energy (external work) (Willems et al., 1995), but we are not aware of existing data that detail how ground reaction forces vary with lower limb segment lengths. If we had used a generic curve for ground reaction forces, it would have not been sensitive to differences in segment lengths, i.e. external work would not have varied among populations. Fig. 3 depicts the change in external energy across the stride cycle. Similarly to internal work, external work needed for a step is the sum of the energy that needs to be added between temporal increments.

Fig. 3. External work and kinetic and potential energy of the whole body for the mean individual (individual 10) in the mean population (population 1) and in the population with mean circumferences, but +3 standard deviation crural index (population 4).

Three strides are shown; heelstrike for the right leg is shown with the solid black vertical line and for the left with a dashed black vertical line. The interval over which the analysis was done (first step of second stride) is indicated with a solid red double-headed arrow. The interval that was used to check the analysis (the second step of the second stride) is indicated with a dashed double-headed arrow.

Internal work and external work were both scaled to their mass-specific forms, which is appropriate because all terms in the energy equation contain mass. Mass-specific power was created by dividing work per step by step time and mechanical mass-specific cost of transport was calculated by dividing power by the horizontal velocity of the body averaged over a step. Calculations were undertaken with Fr = 0.25 and the characteristic length set to the lower limb length of each individual. When moving at the same Fr, larger individuals move absolutely faster and the range of velocities can be found in Table 1.

Results

Within a study, the mass-specific 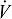O₂ or cost of transport can vary by a factor of 2.5. Unsurprisingly, studies with more participants (e.g. Waters et al., 1988) or less exclusive inclusion criteria (e.g. Kramer and Sarton-Miller, 2008), which had no age, activity level or body composition requirements) had higher ratios. Even with more stringent inclusion criteria (e.g. P.A.K., unpublished data from normally-active 18–40 year olds), the ratio is 2.0.

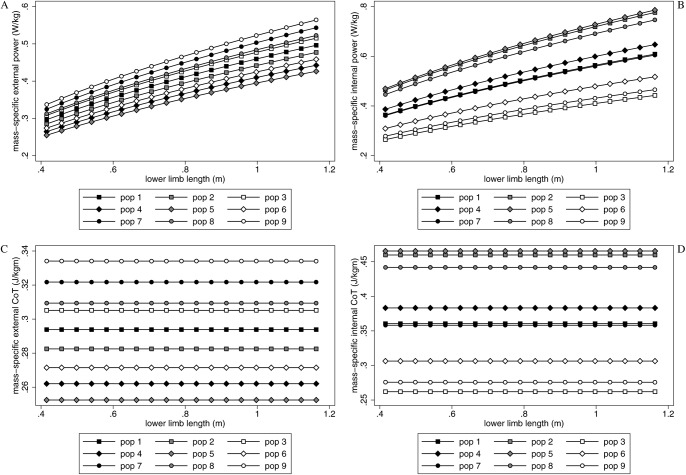
The internal and external mass-specific powers and mechanical costs of transport for the nine populations walking at Fr = 0.25 are shown in Fig. 4. External power (the power required to move the body's center of gravity at a velocity) was less than internal power (the power required to move the lower limbs relative to the body at a velocity). For internal power values, populations with smaller circumferences (i.e. less robust) used less mass-specific mechanical energy than those with larger circumferences (i.e. more robust) and the populations with the lowest crural index (relatively long thighs) (populations 7–9) used less mass-specific mechanical energy than either the populations with average (populations 1–3) or highest crural index (relatively long calves) (populations 4–6). For external values, limb circumferences are irrelevant, but the lowest crural index populations (populations 7–9) used more mass-specific mechanical energy than either of the other configurations.

Fig. 4. Mass-specific power or cost of transport versus lower limb length for Fr = 0.25.

(A) External power, (B) internal power, (C) external cost of transport, and (D) internal cost of transport. Populations 1–3, which have the average crural index, are indicated with squares; populations 4–6, which have a relatively high crural index, are indicated with diamonds; populations 7–9, which have a relatively low crural index, are indicated with circles. Populations 2, 5 and 8 have circumferences that are +3 standard deviations above the mean; populations 3, 6, and 9 have circumferences that are −3 standard deviations above the mean.

Geometrically similar individuals had the same mechanical cost of transport when moving at equal Fr in all populations (Fig. 4C,D), but larger individuals used more mass-specific power than smaller ones (Fig. 4A,B).

For the average individual (lower limb length = 0.78 m), the difference among crural indices in mass-specific internal and external work or cost of transport was ∼10% (internal = +1%/−6%; external = +11%/−12%). The difference in mass-specific internal work or cost of transport within a crural index, but between circumferences was +40%/−30%. The ratio of the smallest to the largest internal work or cost of transport across all crural indices and circumferences was 2.1.

Discussion

For geometrically similar individuals traveling at equal Fr, our model shows that size does not affect mass-specific mechanical cost of transport in accordance with the predictions of Alexander and Jayes (Alexander and Jayes, 1983). Power was, however, affected by size. Larger individuals, when moving at equal Fr, had a higher mass-specific rate of mechanical energy expenditure (power) than smaller ones. Larger individuals move absolutely faster when traveling at equal Fr, and power, the rate of doing work, is directly related to velocity.

When (mass-specific) cost of transport is used as the metric by which geometrically similar individuals are compared, the cost of transport of larger individuals is not different from that of smaller individuals when walking at an equivalent Fr, because the velocity difference has been factored into the calculation of cost of transport ( = power/velocity). In other words, the penalty of a fast velocity for large individuals that is apparent in the rate of mechanical energy expenditure (power) is removed in cost of transport. Indeed, this compensatory effect is the reason that cost of transport is the preferred variable that is used as a proxy of energetic efficiency (Kramer and Sylvester, 2009; Pontzer et al., 2010; Steudel, 1994).

The literature on the metabolic energy expenditure required to walk is vast, and the variation among people in their total metabolic energy expenditure of walking is substantial. Within studies of more than 20 people, the ratio of the maximum to minimum 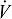O₂ or cost of transport is ≥2.0. This would on the surface seem to indicate that shape variation with its contribution of <20% is unimportant. This superficial assessment may be wrong, however, because the variability between any two individuals can be due to many factors, including the effect of external (such as size and shape) and internal (such as respiratory capacity, muscle architecture and mass distribution) characteristics, and it is difficult or impossible to tease these apart.

In order to understand how metabolic energy expenditure varies with shape, either people of the same size but different shape need to be compared or the shape of individuals needs to be changed so that the individuals can serve as their own control on size and physiology. To our knowledge, no study has explicitly attempted to compare the metabolic energy expenditure of (unmodified) individuals with the same lower limb length but different segment mass. The closest studies have artificially modified the length of the calf (Leurs et al., 2011) or the mass and inertial properties of the limb segments (e.g. Browning et al., 2007; Myers and Steudel, 1985; Royer and Martin, 2005). Using the data in figure 5 from Leurs and colleagues (Leurs et al., 2011), people use ∼15% greater metabolic energy to walk with artificially lengthened calves than they did when they walked without the stilts but at the same velocity. The 0.4 m stilts increased the average lower limb length by ∼40%, but the data are not available to determine the magnitude of change in crural index. It is possible that balancing on stilts is more energetically demanding than balancing on feet and the increase in metabolic energy expenditure is due to stilt walking rather than limb lengthening.

When mass is added to the limb, metabolic energy expenditure increases (Browning et al., 2007; Myers and Steudel, 1985; Royer and Martin, 2005). Royer and colleagues increased limb mass and moment of inertia by adding 2 kg to the mass of the calf of 14 adults (Royer and Martin, 2005). They found that as mass or mass moment of inertia increased, mechanical and metabolic power increased similarly. In their study, increasing mass or mass moment of inertia of the limb by 5% increased metabolic power by 4% and 3.4%, respectively. In our study, we approximately double limb mass within a crural index (i.e. between the +3 and −3 SD circumferences) and also double internal work for individual 10.

Browning and colleagues added 4, 8 and 16 kg loads to the thigh, shank and foot in various combinations and found that an increase in mass and limb mass moment of inertia increased metabolic energy expenditure (Browning et al., 2007). They do not, however, calculate internal work, so it is difficult to compare directly results between their study and ours.

From this, it seems clear that limb properties affect metabolic energy expenditure in a manner predicted by internal work. But the question remains, how much of the difference among individuals in metabolic energy that is demonstrated by the literature is explainable by shape? Comparing metabolic energy expenditure from different studies can be misleading due to differences in protocol, but the difference between the highest individual value of mass-specific metabolic energy expenditure at a velocity is over 2 times that of the person with the lowest value within a study (Table 1). From our simulation, doubling of internal work is possible from circumferential changes alone, so if the relationship found by Royer and colleagues holds (Royer and Martin, 2005), then shape differences could account for the majority of the observed variation in metabolic energy expenditure.

From this previous work and our current analysis, it seems reasonable to expect that it is important to consider shape variation when seeking to understand energy expenditure within species. We chose to simulate the energetics of modern humans, because humans exhibit shape variability, are readily available, and our research interest lies in hominin evolution. There is no reason to believe, however, that our result would not also hold for other species or groups that are of similar size, but variable shape. Thus, researchers who use Fr as a way to compensate for size in comparisons at lower taxonomic levels (e.g. species and genera) must also be conscious of, and compensate for, variation in shape, a source of variation that is always present in such populations. Individuals in intraspecific comparisons may simply not be “reasonably close” (Alexander and Jayes, 1983) enough in shape to be evaluated using the assumption of isometry (geometric similarity).

We think it important at this point to reiterate the logic of using geometric similarity in energetic comparisons. If two individuals (or groups) are geometrically similar—if the slope of the regression line for all their measurements is equal to 1.0 in log–log space and the correlation coefficient is also 1.0—then their mass-specific mechanical cost of transport will be the same (as shown herein). Their metabolic cost of transport may be different, but this difference is not caused by shape (because they have no shape differences). Instead, any difference in metabolic cost of transport must be caused by other characteristics.

If two individuals or groups are not geometrically similar, then their mechanical cost of transport will, in part, reflect the effect of the difference in the shape of the body segments included in the model. Their metabolic cost of transport is also likely to be different, but the difference could arise from the known difference in size, shape and/or internal characteristics and there is currently no way to tease apart these reasons. This problem exists even if two individuals are “reasonably close” to geometric similarity or if techniques are used to “account” for one aspect of size (like total body mass or limb length). This study shows that small absolute differences in segment lengths (<10%) and/or circumferences (<20%) can make discernible differences in the mechanical cost of transport of individuals of the same species. It is logical to believe that this difference in mechanical cost of transport would be reflected in metabolic cost of transport.

Bullimore and Burn make the critical point that almost all simulations of reality require compromises (Bullimore and Burn, 2004), if for no other reason than the need to decrease the number of variables (Langhaar, 1951). In engineering, where simulations are used extensively, they are developed to test the effect of a narrow set of parameters on an important feature of the system (Duncan, 1953; Langhaar, 1951), because in order to get one aspect of the model correct, simplifications or compromises have to be made in other aspects. William Froude developed the Froude number in the context of his simulation of ships with the goal of creating similar wave patterns (Vaughan and O'Malley, 2005) with drag as the feature of importance (Langhaar, 1951), but his concept has been extended to other mechanical phenomena that are driven by gravity and inertia (Duncan, 1953). As has been pointed out (Steudel-Numbers and Weaver, 2006), the explicit intent of Alexander and Jayes was to use Fr to assess the locomotion of animals of widely varying size (Alexander and Jayes, 1983). The broader the variation in size, the greater the correlation of a size may be to metabolic energy expenditure, because shape contributes less to the total morphological variation.

Because Fr is usually calculated using limb length, Fr directly compensates for differences in velocity that accrue from limb length. Differences in velocity that are due to other factors, like shape, are not controlled. Steudel-Numbers and Weaver suggested that another characteristic length—the cube root of body mass—might provide a better control, but they found that it was no better than lower limb length (Steudel-Numbers and Weaver, 2006). This is completely compatible with the causality discussed above: using the cube root of body mass in the Fr calculation controls for the effect of mass, but not lower limb length (and consequently velocity), because the individuals were not geometrically similar (e.g. mass-lower limb length r² = 0.41 (Steudel-Numbers and Tilkens, 2004)), as the authors note. All other characteristic lengths that could be considered have the same failing when applied to naturally—developing populations—individuals have different shapes, and shape matters.

Fr cannot compensate for a factor that violates the foundational assumption of its development. While Fr is a necessary control so that individuals are compared at the same intensity of activity (relative velocity); it is simply not sufficient to control for shape. This is not because Fr is flawed, but rather because no simple parameter is adequate to account for the myriad effects of difference in shape. We believe that if the goal is to understand the energetics of groups that vary in shape, more complicated simulations are required that directly simulate the critical elements. To our knowledge, the only way of doing this for any animal group or species is musculoskeletal modeling (e.g. Delp et al., 2007; Hamner et al., 2010; Liu et al., 2008; Nagano et al., 2005; Ogihara et al., 2010; Sellers et al., 2003; Sellers and Manning, 2007; Umberger, 2010; Wang et al., 2004). Musculoskeletal modeling allows for perceived differences in shape between known groups to be simulated by modifying inputs, such as segmental properties or motion trajectories. Then, virtual experiments on hypothetical situations can be conducted, allowing insight into what aspects of that difference contribute to important features.

We should add that empirical evidence suggests that animals “distort” their morphology to accommodate the observed conservation in basic musculoskeletal properties (i.e. these properties do not scale isometrically with length (size)) (Bullimore and Burn, 2004). Increasing size should increase bone stress, for instance, necessitating an increasing bone allowable stress with size, but mammalian bone ultimate stress (or strain) has been shown to be relatively constant (Biewener, 1982). Animals appear to compensate by changing other aspects of their morphology, such as that demonstrated by the allometry of limb moment arms described by Biewener (Biewener, 1989; Biewener, 1990). Changing joint angles is a method of changing shape, when shape is understood as a functional rather than simply a static parameter. Another way to describe Biewener's finding is that animals adjust their shape to maintain safe levels of musculoskeletal stress/strain.

Finally, we want to make explicit that we believe that size differences remain important even in the face of shape differences. Despite our finding that the shape differences that are seen intraspecifically produce discernible differences in mechanical energy expenditure, size remains a critical factor. Both size and shape need to be accounted. Consequently, we do not recommend ignoring the Fr correction for size, especially for velocity. Rather, we point out that Fr correction, while necessary, is not sufficient to adequately compensate for differences among individuals, groups, or species.

One limitation of this study is that all populations were evaluated using the same angular excursions. While this approach allows an uncomplicated appraisal of the effect of shape variation, it remains to be determined to what degree the internal and external power and mechanical cost of transport will vary with angular changes associated with variations in (walking) velocity. As with segmental lengths and circumferences, people vary in their angular excursion profiles even when traveling at equivalent velocities (same Fr) and these kinematic changes may be related to size or shape variation. In other words, the allometry of joint moment arms reported among species (Biewener, 1989; Biewener, 1990; Polk et al., 2009), which is mediated by joint angular excursion, might be expressed within a species. We tentatively found that the effect of crural index differs between internal and external calculations, but the significance of this finding is limited because individuals may vary their angular motion to accommodate their morphology. Future work will address this question.

Although this research could be extended in many ways, we have re-established that cost of transport does not vary among geometrically similar individuals that are compared at the same Fr (Alexander and Jayes, 1983), although power (the rate of using energy) does. While the internal characteristics that vary among individuals remain difficult to assess at this time, the externally apparent characteristics of size and shape are knowable and appear to be important for understanding metabolic energy expenditure. The use of a model organism that can be experimentally manipulated and invasively examined, such as the Guinea fowl used by Marsh and colleagues (Carr et al., 2011a; Carr et al., 2011b; Ellerby et al., 2003; Ellerby et al., 2005; Ellerby and Marsh, 2006; Ellerby and Marsh, 2010; Henry et al., 2005; Marsh and Ellerby, 2006; Marsh et al., 2004; Marsh et al., 2006; Rubenson et al., 2006; Rubenson and Marsh, 2009), could provide unique insights into the interplay among the many parameters that influence the relationship between metabolism and mechanical energy.

Size and shape differences among individuals and groups are both important and need to be included in any comparison of metabolic or mechanical energy expenditure, but the appropriate scaling parameters are dependent on the specifics of the comparison to be made. As Duncan wrote in 1953: “The extreme easiness of the process of…[scaling] should not blind us to the fact that the successful use of the process demands intelligence and a close study of the physical problem” (Duncan, 1953). For the comparison of groups that vary in shape, the physical problem demands consideration of both size and shape.

Conclusions

Our results indicate that size does not affect mass-specific mechanical cost of transport (Alexander and Jayes, 1983). The known shape differences among modern humans are, however, sufficiently large to account for much of the observed variation in metabolic energy expenditure and we expect this to be the case for any group that is of similar size but different shape. Unfortunately, we currently do not have a simple method to control or adjust for size–shape differences in individuals that are not geometrically similar. Musculoskeletal modeling is the only method that accounts for both size and shape. Those shape differences that are “reasonably close” at the mouse-to-elephant level may become “grossly different” for within-species energetic comparisons.