Specific Binding of Chloride Ions to Lipid Vesicles and Implications at Molecular Scale

Abstract

Biological membranes composed of lipids and proteins are in contact with electrolytes like aqueous NaCl solutions. Based on molecular dynamics studies it is widely believed that Na⁺ ions specifically bind to 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) membranes, whereas Cl⁻ ions stay in solution. Here, we present a careful comparison of recent data from electrophoresis and isothermal titration calorimetry experiments as well as molecular dynamics simulations suggesting that in fact both ions show very similar affinities. The corresponding binding constants are $0.44\left(\pm 0.05\right)$ M⁻¹ for Na⁺ and $0.40\left(\pm 0.04\right)$ M⁻¹ for Cl⁻ ions. This is highlighted by our observation that a widely used simulation setup showing asymmetric affinities of Na⁺ and Cl⁻ for POPC bilayers overestimates the effect of NaCl on the electrophoretic mobility of a POPC membrane by an order of magnitude. Implications for previous simulation results on the effect of NaCl on polarization of interfacial water, transmembrane potentials, and mechanisms for ion transport through bilayers are discussed. Our findings suggest that a range of published simulations results on the interaction of NaCl with phosphocholine bilayers have to be reconsidered and revised and that force field refinements are necessary for reliable simulation studies of membranes at physiological conditions on a molecular level.

Introduction

Biological membranes consist of a complex mixture of a variety of lipids and proteins surrounded by aqueous solutions containing various types of ions that may specifically bind to these membranes. Interactions of ions with lipid bilayers as model membranes have been studied extensively. It has long been established that ions may interact significantly with charged lipid bilayers. Studies of the interaction of monovalent ions with zwitterionic membranes, however, have yielded conflicting results. Here, we refer to the behavior of phosphocholine (PC) bilayers in aqueous NaCl solutions. Traditional studies have used electrophoresis to investigate this interaction. Typically, no effect of NaCl on electrophoretic mobilities of PC liposomes was observed leading to the conclusion that Na⁺ and Cl⁻ ions do not bind to PC bilayers (1–4). From electrophoretic mobilities of eggPC liposomes though, small but significant binding affinities were deduced in the presence of divalent cations (5). Intrinsic binding constants inferred were 0.15 M⁻¹ for Na⁺ and 0.20 M⁻¹ for Cl⁻ ions, respectively. Thus, besides the fact these binding affinities were small, they were similar in magnitude, such that the effect of Na⁺ and Cl⁻ ions on electrophoretic mobilities would largely cancel out, as a possible reason why no net effect could be resolved earlier.

PC vesicles in aqueous buffer at neutral pH usually show negative electrophoretic mobilities (6–8). The negative electrophoretic mobilities could arise from impurities (9) or excess adsorption of hydroxide (6) or buffer ions (7) at the vesicle membranes. We have recently observed that addition of up to 500 mM NaCl to aqueous solutions containing 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) vesicles rendered the electrophoretic mobilities of the vesicles progressively less negative (7). The effects seen for monocomponent PC vesicles were more than an order of magnitude smaller than those observed for PC/phosphatidylserine mixtures and required a higher resolution of the experimental setup; this is probably why they were discovered much later when the technical equipment was more advanced (10).

Interactions of NaCl with PC bilayers have been studied in atomic detail in a range of studies using molecular dynamics (MD) simulations, see (11) for a review. The results depended on the molecular force fields chosen. Simulations describing the lipids using parameters by Berger et al. (in conjunction with GROMOS parameters for the ions (12)) or with the generalized Amber force field (GAFF) indicate that PC headgroups bind Na⁺ ions, whereas Cl⁻ ions form a diffuse counterion layer in the water phase (10,13–19). First studies using CHARMM at short timescales and at constant volume showed weak binding of Na⁺ and Cl⁻ ions at similar positions normal to the bilayer. Later simulations at constant pressure with a more recent version of the CHARMM force field indicated that Na⁺ ions bind more deeply in the bilayer than Cl⁻ ions, as observed for the Berger/GROMOS, though with lower affinity (20).

Recently, we have used isothermal titration calorimetry (ITC) to measure the heat exchange with a thermal reservoir occurring when NaCl was added to solutions containing POPC vesicles (7). In agreement with MD simulations of PC bilayers in aqueous NaCl solutions we assumed that only Na⁺ is adsorbed at the vesicle membranes and hence determined binding constants for the interaction of Na⁺ with POPC. These binding constants were found to be consistent with the adsorption strength occurring in MD simulations using the Berger/GROMOS setup (10).

The simulation results that only Na⁺ adsorbs at the PC headgroups, whereas Cl⁻ ions stay in solution, however, appear to disagree with the experiments, which could not resolve any effect of NaCl on the electrophoretic mobilities of PC vesicles, suggesting negligible or similar membrane affinities of Na⁺ and Cl⁻ ions (1–5). On the other hand, electrophoretic mobilities depend on the position of the shear plane such that a more detailed consideration of the distribution of Na⁺ and Cl⁻ ions at PC-water interfaces is necessary. In simulations, Na⁺ ions bind at the interface between the headgroup and the tail region of PC bilayers, whereas Cl⁻ ions form a layer at the interface between the headgroups and the water. If the shear plane resided between the Cl⁻ layer and the bulk, the net charge of the moving entity would be small. In this case, the simulations, though showing that Na⁺ ions bind more deeply in PC bilayers than Cl⁻ ions, would be in agreement with measured electrophoretic mobilities.

In a recent study we have probed the position of the shear plane using MD simulations (V. Knecht, B. Klasczyk, R. Dimova, unpublished). To this aim, we applied an electric field parallel to a POPC bilayer in an aqueous NaCl solution and determined the drift velocity ν of slabs parallel to the membrane ($xy$ plane) as a function of the z position of the plane. Here, the origin of the z axis was set to the position at which the water density equaled half the bulk density (Gibbs dividing surface), and $z<0$ or $z>0$ denoted the membrane or the water side, respectively, of the interface. According to the derivation of the Helmholtz-Smoluchowski equation, the shear plane location $z_{\text{s}}$ must have the properties $v\left(z_{\text{s}}\right)=v_{\text{m}}\text{and}v\left(z\right)<v_{\text{m}}\text{for}z>z_{\text{s}}$, where $v_{\text{m}}$ denotes the average drift velocity of the membrane. This property applied to $z_{\text{s}}=0.166\left(\pm 0.056\right)$ nm, which was between the Na⁺ and the Cl⁻ layer (V. Knecht, B. Klasczyk, R. Dimova, unpublished), such that a strong effect of NaCl on the electrophoretic mobility of POPC can be expected.

In this work we i), compare the electrophoretic mobilities from these simulations with experimental values, ii), check the consistency of the previous interpretation of the ITC experiments with measured electrophoretic mobilities, and iii), combine the calorimetric and electrophoretic data to determine individual binding constants for the association of Na⁺ and Cl⁻ ions with POPC bilayers. Our analysis indicates that Na⁺ and Cl⁻ ions bind almost equally strongly to PC bilayers. MD simulations overestimate the effect of NaCl on the electrophoretic mobilities by an order of magnitude. This is mainly because the simulations do not show significant penetration of Cl⁻ ions below the shear plane. Implications of our findings at a molecular scale are discussed.

Results and Discussion

MD simulations

Simulations overestimate effect of NaCl on electrophoretic mobility of PC bilayer by an order of magnitude

Experimental electrophoretic mobilities of POPC vesicles in 15 mM HEPES buffer are ${\mu }_{\text{E},0,\text{exp}}=-4.95\left(\pm 0.15\right)\times {10}^{-5}$ cm²/Vs. Makino et al. (6) proposed that negative electrophoretic mobilities of PC vesicles could arise from the anisotropic orientation of lipid headgroups normal to the bilayer. If the headgroup orientation alone were sufficient to induce electrophoretic motion, electrophoretic mobilities of PC membranes should also be observed in the absence of any ions. In our recent MD study, however, a PC bilayer in aqueous solution did not show significant electrophoretic motion when ions were absent (V. Knecht, B. Klasczyk, R. Dimova, unpublished), indicating that ions are required for electrophoretic motion, which can also be shown from thermodynamic arguments (21). Ionic species inducing negative electrophoretic mobilities of PC vesicles could be excess levels of hydroxide at the membrane surface (22), buffer molecules (7), or acidic impurities (9).

Experimental electrophoretic mobilities of POPC vesicles at 500 mM NaCl concentration are $1.1\pm 1.5\times {10}^{-5}$ cm²/Vs, thus being shifted by $\Delta {\mu }_{\text{E},\text{exp}}=3.98\pm 1.51\times {10}^{-5}$ cm²/Vs compared to NaCl free conditions. In our MD simulations, electrophoretic mobilities ${\mu }_{\text{MD}}$ were evaluated as ${\mu }_{\text{MD}}=v/E$, with ν denoting the drift velocity of the bilayer with respect to the bulk water, and E the electric field in the bulk, as valuated from the water polarization (V. Knecht, B. Klasczyk, R. Dimova, unpublished). Hence, we found that addition of 470 mM NaCl induced an electrophoretic mobility of ${\mu }_{\text{E},\text{MD}}=40.28\times {10}^{-5}$ cm²/Vs = $\Delta {\mu }_{\text{E},\text{MD}}$ (V. Knecht, B. Klasczyk, R. Dimova, unpublished). The simulations thus reproduced the sign of $\Delta {\mu }_{\text{E},\text{exp}}$ but overestimated its size by an order of magnitude, indicating force field issues.

Binding affinities from ITC and electrophoretic data

In this section, we check the consistency of the interpretation of the calorimetric and electrophoretic data in our recent experimental work (7) using the double layer theory to analyze the electrophoretic data. Central to our analysis is to infer corresponding binding constants from ITC and electrophoretic data. Thus, in the following, we will first review and introduce measures for binding affinities obtained from the two kinds of experiments, give links between the measures, and check for consistency of the previous interpretation of the experiments.

An apparent binding constant for ion-lipid association for a 1:1 stochiometry is defined as

$$K_{\text{app}}=\frac{\alpha }{c\left(1-\alpha \right)},$$ (1)

where c denotes the ion concentration in the bulk and α the fraction of ions binding an ion (10,14). Experimentally, the ion concentration in the bulk is about equal to the average ion concentration (7,10). This definition in fact depends on the definition of bound, which, inversely, depends on the experimental method used to determine binding constants. The corresponding definitions for electrophoresis and ITC will be explained in the following.

Binding constant from electrophoresis

From electrophoretic mobilities, the electrostatic potential at the shear plane, denoted as ζ potential, is usually determined using either the Smoluchowski or the Henry equation (23). From ζ and for 1:1 electrolytes, the surface charge σ is deduced using the Gouy or Grahame equation

$$\sigma ={\left(8c_{\text{el}}\mathit{\epsilon }{\mathit{\epsilon }}_0{k}_{\text{B}}T\right)}^{1/2}\text{sinh}\left(\frac{e{\Psi }_0}{2k_{\text{B}}T}\right)\equiv {\sigma }_{\text{TH}},$$ (2)

where e is the proton charge and ${\Psi }_0$ denotes the surface potential and it is assumed that ${\Psi }_0=\zeta$. Here, $c_{\text{el}}$ denotes the electrolyte concentration, $k_{\text{B}}$ the Boltzmann constant, and T the temperature. Equation 2 implies that at a molecular scale

$$\sigma =\underset{z_{\mathrm{c}}}{\overset{z_{\mathrm{s}}}{\int }}\rho \left(z^{\prime }\right)\text{d}{z}^{\prime }\equiv {\sigma }_{\text{MD}}$$ (3)

holds. Here, $z^{\prime }$ is the position normal to the membrane, with $z_{\text{c}}$ residing in the center of the membrane, and $z_{\text{s}}$ at the shear plane. The symbol ρ denotes the charge density from Na⁺ and Cl⁻ ions. To check whether the surface charges from Eqs. 3 and 2 are consistent we have used both equations to estimate the surface charge for the POPC bilayer studied in our recent MD simulations (V. Knecht, B. Klasczyk, R. Dimova, unpublished). To this aim, the electrophoretic mobility observed in the simulations, ${\mu }_{\text{E},\text{MD}}$, was converted into a zeta potential using the Helmholtz-Smoluchowski equation, leading to $\zeta =28.2\left(\pm 2.1\right)$ mV. Equation 2 yields ${\sigma }_{\text{TH}}=0.255\left(\pm 0.020\right)$ e/nm². The corresponding surface charge from Eq. 3 skipping the initial 20 ns for equilibration was ${\sigma }_{\text{MD}}=0.263\left(\pm 0.017\right)$ e/nm². Hence, within the statistical uncertainty ${\sigma }_{\text{TH}}={\sigma }_{\text{MD}}$, that is, the surface charges from Eqs. 3 and 2 are consistent. Thus, plugging ζ into Eq. 2 yields a correct estimate for σ.

On the other hand, from σ obtained via Eq. 2 and if the membrane is neutral in the absence of ions, the fraction of hydrodynamically bound ions, ${\alpha }_{\text{hyd}}$, may be deduced according to

$${\alpha }_{\text{hyd}}=\frac{\sigma }{{\sigma }_1},$$ (4)

with ${\sigma }_1=q/a_{\text{lip}}$ where $a_{\text{lip}}$ denotes the area per lipid and q the charge of the surface-active ions. Experiments yield is $a_{\text{lip}}$ = 0.683 nm² for POPC (24). We note that whereas NaCl leads to a decrease in $a_{\text{lip}}$ in MD simulations it does not affect $a_{\text{lip}}$ significantly for NaCl concentrations below 1 M experimentally. According to Eq. 3, Eq. 4 implies that ${\alpha }_{\text{hyd}}$ obeys

$${\alpha }_{\text{hyd}}=a_{\text{lip}}\underset{z_{\mathrm{c}}}{\overset{z_{\mathrm{s}}}{\int }}n\left(z^{\prime }\right)\text{d}{z}^{\prime },$$ (5)

with $n\left(z^{\prime }\right)=n_{+}\left(z^{\prime }\right)+n_{-}\left(z^{\prime }\right)$, where $n_{+}\left(z^{\prime }\right)$ and $n_{-}\left(z^{\prime }\right)$ denote the local concentrations of cations and anions, respectively. If only cations are hydrodynamically adsorbed, $n_{-}\left(z^{\prime }\right)=0$ and $n\left(z^{\prime }\right)=n_{+}\left(z^{\prime }\right)$ for $z<z_{\text{s}}$. Hence, and following Eq. 1, the apparent hydrodynamic binding constant shall be defined as

$$K_{\text{app},\text{hyd}}\equiv \frac{{\alpha }_{\text{hyd}}}{c\left(1-{\alpha }_{\text{hyd}}\right)}.$$ (6)

Binding constant from ITC

Following Eq. 1, the apparent calorimetric binding constant shall be defined as

$$K_{\text{app},\text{cal}}=\frac{{\alpha }_{\text{cal}}}{c\left(1-{\alpha }_{\text{cal}}\right)}.$$ (7)

A criterion for the fraction of lipids calorimetrically binding ions, ${\alpha }_{\text{cal}}$, will be given in the following and related to a geometric criterion, enabling to derive a connection between calorimetric and hydrodynamic binding constants. Experimentally, $K_{\text{app},\text{cal}}$ is obtained by fitting the heats per injection (after subtracting the heats of ion and lipid dilution, as well as the heat associated with the mechanical work of the actual injection) as a function of ion concentration to a 1:1 binding model with $K_{\text{app},\text{cal}}$ and the energy change $\Delta E$ upon formation of a single ion-lipid complex as fit parameters. On the other hand, the binding constant from DSC experiments, ${\tilde{K}}_{\text{app},\text{cal}}$, is defined as ${\tilde{K}}_{\text{app},\text{cal}}\equiv 1/C_{\text{max}}$, where $C_{\text{max}}$ is the ion concentration at which the heat capacity is maximal (25). The heat capacity is related to the energy fluctuations of the system, and we show in the Supporting Material that ${\tilde{K}}_{\text{app},\text{cal}}\equiv K_{\text{app},\text{cal}}$. Simulations by Kim and Hummer indicate that bound according to the DSC criterion is equivalent to a minimum distance smaller than $0.8\text{nm}\equiv r_{\text{min}}$ (25). Analysis of our previous MD simulations of NaCl interacting with POPC bilayers shows that a minimum distance smaller than $r_{\text{min}}$ is equivalent to $z<0.93$ nm $\equiv z_{\text{max}}$. Together, this indicates that calorimetrically bound means $z<z_{\text{max}}$. Hence,

$${\alpha }_{\text{cal}}=a_{\text{lip}}\underset{z_{\mathrm{c}}}{\overset{z_{\max }}{\int }}n\left(z^{\prime }\right)\text{d}{z}^{\prime }.$$ (8)

Equation 6 means that ${\alpha }_{\text{hyd}}\ll 1$ implies $K_{\text{app},\text{hyd}}\approx {\alpha }_{\text{hyd}}/c$ and ${\alpha }_{\text{cal}}\ll 1$ implies $K_{\text{app},\text{cal}}\approx {\alpha }_{\text{cal}}/c$. In this approximation,

$$\Delta K_{\text{app}}\equiv K_{\text{app},\text{cal}}-K_{\text{app},\text{hyd}}\approx \Delta \alpha /c,$$ (9)

which becomes exact for small c, with $\Delta \alpha =a_{\text{lip}}{\int }_{z_{\text{s}}}^{z_{\text{max}}}n\left(z^{\prime }\right)\text{d}{z}^{\prime }$, such that

$$\Delta K_{\text{app}}=a_{\text{lip}}\underset{z_{\mathrm{s}}}{\overset{z_{\max }}{\int }}\frac{n\left(z^{\prime }\right)}{c\text{d}{z}^{\prime }}.$$ (10)

From the Gouy-Chapman theory (23) and for small electrostatic potentials relative to the bulk water, $\xi \equiv \left|e\Psi /k_{\text{B}}T\right|\ll 1$, $\Delta K_{\text{app}}$ is

$$\Delta K_{\text{app}}=2a_{\text{lip}}\Delta z,$$ (11)

up to first order in ζ, with $\Delta z=z_{\text{max}}-z_{\text{s}}$. The approximation for small electrostatic potentials appears reasonable, as for the experimental zeta potentials at NaCl concentrations between 35 and 100 mM, $e\zeta /k_{\text{B}}T$ was in the range 0.08 to 0.04 and thus small compared to 1.

Analysis of recent calorimetric and electrophoretic data

In this section, our calorimetric and electrophoretic data from (7) are tested for consistency and reanalyzed to determine individual binding constants for the association of Na⁺ and Cl⁻ ions with PC membranes.

Calorimetric and electrophoretic data appear inconsistent if specific binding of Cl⁻ ions to PC bilayers is excluded

Whereas NaCl concentrations of up to 500 mM were employed for the electrophoresis experiments, the ITC experiments were restricted to NaCl concentrations of up to 100 mM, which thus determines the upper limit of concentrations for which calorimetric and electrophoretic experiments can be compared.

Apparent binding constant from ITC

The apparent calorimetric binding constant inferred from our ITC experiments assuming that only Na⁺ but not Cl⁻ ions bind to POPC lipids was $K_{\text{app},\text{cal}}^{\text{ITC}}=1.25\left(\pm 0.05\right)$ M⁻¹ (7). Here and in the following, superscripts indicate whether estimates of observables are obtained from ITC (ITC) or electrophoretic experiments (EP). Hence, Eq. 11 yields the hydrodynamic binding constant $K_{\text{app},\text{hyd}}^{\text{ITC}}=0.87$ M⁻¹. Thus, according to Eqs. 9 and 11, the fraction of lipids hydrodynamically binding ions at given NaCl concentration c is given by

$${\alpha }_{\text{hyd}}^{\text{ITC}}=\frac{K_{\text{app},\text{hyd}}^{\text{ITC}}c}{K_{\text{app},\text{hyd}}^{\text{ITC}}c+1}.$$ (12)

Hence, for NaCl concentrations up to 100 mM, lipid fractions of up to ${\alpha }_{\text{hyd}}^{\text{ITC}}=0.08$ are obtained, as shown in Fig. S1.

Apparent binding constant from zeta potentials

When inferring the fraction of lipids binding ions from the surface charge according to Eq. 4 one has to consider that even in the absence of NaCl nonzero zeta potentials indicating negative surface charge are measured. The surface charge ${\sigma }_{\text{NaCl},\text{hyd}}$ from NaCl at given NaCl concentration is obtained from

$${\sigma }_{\text{NaCl},\text{hyd}}={\sigma }_{\text{hyd}}\left(c\right)-{\sigma }_{\text{hyd}}\left(0\right),$$ (13)

whereby ${\sigma }_{\text{hyd}}\left(0\right)$ and ${\sigma }_{\text{hyd}}\left(c\right)$ denote the surface charge in the absence of NaCl and at a NaCl concentration c, respectively, from Eq. 2. Here, $c_{\text{el}}=c+c_{\text{buf}}$ where $c_{\text{buf}}$ denotes the concentration of charged buffer molecules. The buffer used was HEPES in a concentration of 15 mM. A buffer acts such as to retain the pH at the pKa of the buffer molecules (7.55 here), which (for HEPES) means that half of the buffer molecules are zwitterionic, whereas the other half is ionized such that $c_{\text{buf}}=7.5$ mM. From the zeta potentials reported in (7) and using Eqs. 2 as well as 4, again assuming that only Na⁺ but not Cl⁻ ions bind to the lipids, ${\alpha }_{\text{hyd}}$ was inferred as a function of the NaCl concentration, as shown in Fig. S1. The error bars were estimated from the standard error of the zeta potentials $\text{se}\left(\zeta \right)$ via error propagation. The values for $\text{se}\left(\zeta \right)$ were obtained from the standard deviations of the zeta potentials, $\Delta \zeta$, obtained from 10 measurements as reported in (7), by dividing $\Delta \zeta$ by $\sqrt{10}$.

It is found that the estimates for ${\alpha }_{\text{hyd}}$ from the zeta potentials are an order of magnitude smaller than the estimates from the ITC data. The respective estimate for $K_{\text{app},\text{hyd}}$ is obtained by fitting Eq. 6 to the data, yielding $K_{\text{app},\text{hyd}}^{\text{EP}}=0.033$ mM which, accordingly, is an order of magnitude smaller than the estimate from the ITC data.

We hypothesize that the assumption that Cl⁻ ions do not specifically bind to PC lipids is wrong. To account for possible binding of Cl⁻ ions, we perform a joint analysis of the electrophoretic and calorimetric data to estimate the individual binding constants for Na⁺ and Cl⁻ ions in the following.

Joint analysis of ITC and electrophoresis data shows that the affinity of Na⁺ and Cl⁻ ions for PC bilayer is very similar

To consider the possibility that both Na⁺ and Cl⁻ might be adsorbed at the membrane, we treat the two ion species as indistinguishable and denote them as cosolvent, as done in the application of the Kirkwood-Buff theory to electrolyte solutions (26,27). The cosolvent concentration $c_{\text{ion}}^{\prime }$ is then twice the ion concentration, i.e., $c_{\text{ion}}^{\prime }=2c_{\text{ion}}$. In analogy to Eq. 7 we define the corresponding apparent calorimetric binding constant $K_{\text{app},\text{cal}}^{\prime }$ of the cosolvent according to

$$K_{\text{app},\text{cal}}^{\prime }\equiv \frac{{\alpha }_{\text{cal}}}{2c\left(1-{\alpha }_{\text{cal}}\right)}.$$ (14)

Here, ${\alpha }_{\text{cal}}$ is the fraction of lipids calorimetrically binding Na⁺ or Cl⁻ ions. Comparing Eqs. 7 and 14 yields $K_{\text{app},\text{cal}}^{\prime }=2K_{\text{app},\text{cal}}$ or $K_{\text{app},\text{cal}}=K_{\text{app},\text{cal}}^{\prime }/2$, where $K_{\text{app},\text{cal}}$ is the average calorimetric binding constant of Na⁺ and Cl⁻ ions. The corresponding average hydrodynamic binding constant of the ions according to Eqs. 9 and 11 is $K_{\text{app},\text{hyd}}=K_{\text{app},\text{cal}}-\Delta K_{\text{app}}$. Hence, the fraction of lipids hydrodynamically binding ions is

$${\alpha }_{\text{hyd}}=\frac{K_{\text{app},\text{hyd}}2c}{1+K_{\text{app},\text{hyd}}2c}.$$ (15)

The fraction of lipids hydrodynamically binding Na⁺ or Cl⁻ ions shall be denoted as x or y, correspondingly. Hence, $x+y={\alpha }_{\text{hyd}}$ and $x-y={\beta }_{\text{hyd}}$ with ${\beta }_{\text{hyd}}={\sigma }_{\text{NaCl}}/{\sigma }_1$ and ${\sigma }_1=e/a_{\text{lip}}$ with e denoting the proton charge. Here, ${\sigma }_{\text{NaCl}}=\sigma \left(c\right)-\sigma \left(0\right)$ denotes the surface charge from NaCl. The symbols $\sigma \left(c\right)$ and $\sigma \left(0\right)$ denote the surface charge as inferred from the zeta potential at a NaCl concentration c or in the absence of NaCl, respectively, via Eq. 2. Hence, x and y are determined from

$$x=\frac{{\alpha }_{\text{hyd}}+{\beta }_{\text{hyd}}}{2};y=\frac{{\alpha }_{\text{hyd}}-{\beta }_{\text{hyd}}}{2}.$$ (16)

Fig. 1 shows x and y as a function of the NaCl concentration. For NaCl concentrations in the range 35 to 100 mM, x and y are in the range 0.02 to 0.057 and scale linearly with c. At a given NaCl concentration, x tends to be higher than y but both values are close to each other, their error bars even overlapping. Fitting $x\left(c\right)$ and $y\left(c\right)$ to the equations

$$x=\frac{K_{\text{app},\text{hyd},\text{Na}}c}{K_{\text{app},\text{hyd},\text{Na}}c+1};y=\frac{K_{\text{app},\text{hyd},\text{Cl}}c}{K_{\text{app},\text{hyd},\text{Cl}}c+1}$$ (17)

yields apparent hydrodynamic binding constants for the association of POPC with Na⁺ and Cl⁻ ions of $K_{\text{app},\text{hyd},\text{Na}}=0.437\left(\pm 0.046\right)$ M⁻¹ and $K_{\text{app},\text{hyd},\text{Cl}}=0.401\left(\pm 0.038\right)$ M⁻¹, respectively. The affinity for NaCl for POPC is about twofold larger than for eggPC, see the Supporting Material.

Figure 1.

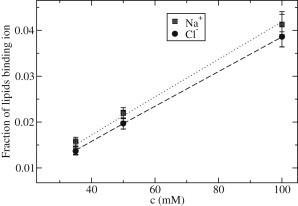
Fraction of lipids binding Na⁺ or Cl⁻ ions as a function of the NaCl concentration from joint analysis of ITC and electrophoretic data via Eq. 16. The lines are fits of Eq. 17 to the data, yielding binding constants of $0.44\left(\pm 0.05\right)$ M⁻¹ for Na⁺ ions and $0.40\left(\pm 0.04\right)$ M⁻¹ for Cl⁻ ions.

Comparison to simulation results

Simulations using the Berger/GROMOS setup yield an apparent hydrodynamic binding constant for Na⁺ ions of $K_{\text{app},\text{Na},\text{GRO}}=1.36\left(\pm 0.22\right)$ M⁻¹ (10). This value was determined by considering all ions as bound, which formed van der Waals contacts with lipids. Analyses of the simulations presented in ( V. Knecht, B. Klasczyk, R. Dimova, unpublished) suggested that this criterion is equivalent to the definition of the hydrodynamic binding constant, Eq. 6 such that the corresponding hydrodynamic binding constant for this setup $K_{\text{app},\text{hyd},\text{Na},\text{GRO}}$, is equal to $K_{\text{app},\text{Na},\text{GRO}}$. The estimate of $K_{\text{app},\text{hyd},\text{Na}}$ from the Berger/GROMOS setup is thus larger than the experimental binding constant inferred in this study by a factor of three. For comparison, we have also estimated $K_{\text{app},\text{hyd},\text{Na}}$ for the CHARMM force field, $K_{\text{app},\text{hyd},\text{Na},\text{CH}}$, by comparing the concentration profile of Na⁺ for the Berger setup in (10) with that of a corresponding profile obtained using the CHARMM force field (20). The value for $K_{\text{app},\text{hyd},\text{CH}}$ was obtained from

$$K_{\text{app},\text{Na},\text{CH}}=\frac{r_{\text{CH}}}{r_{\text{GRO}}}{K}_{\text{app},\text{Na},\text{GRO}},$$ (18)

with $r_{\text{CH}}=c_{\text{max},\text{CH}}/c_{\text{eff},\text{CH}}$ and $r_{\text{GRO}}=c_{\text{max},\text{GRO}}/c_{\text{eff},\text{GRO}}$. Here, $c_{\text{max},\text{CH}}$ or $c_{\text{max},\text{GRO}}$ denote the maximum of the corresponding peak in the ion distribution at the membrane, and $c_{\text{eff},\text{CH}}$ or $c_{\text{eff},\text{GRO}}$ are the effective bulk concentrations of the ions for the CHARMM and the Berger force field, respectively. For the simulations with the CHARMM force field, the box size was large enough such that the bulk concentration was reached within the simulation box and could be directly read from in the profile to be $c_{\text{eff},\text{CH}}=300$ mM. For the simulations with Berger, the bulk concentration was not reached in the box but could be determined from fitting a Poisson-Boltzmann distribution to the cation and anion concentrations in the region where the water density was equal to the bulk density. Here, we considered data for $c_{\text{eff},\text{CH}}=67\left(\pm 18\right)$ mM from which also $K_{\text{app},\text{hyd},\text{Na},\text{GRO}}$ had been determined in (10). Equation 18 yields $K_{\text{app},\text{hyd},\text{Na},\text{CH}}=0.269\left(\pm 0.030\right)$ M⁻¹. This is somewhat smaller than the experimental value obtained from our analysis.

From the binding constants, the relative surface charge at given ion concentration c may be determined using $\sigma \propto \left(K_{\text{app},\text{hyd},\text{Na}}-K_{\text{app},\text{hyd},\text{Cl}}\right)c\equiv \Delta {\tilde{K}}_{\text{app},\text{hyd}}$, if variations in the area per lipid are neglected. As for the Berger and the CHARMM force fields the Cl⁻ ions barely penetrate below the shear plane (which approximately coincides with the Gibbs dividing surface), $K_{\text{app},\text{hyd},\text{Cl}}\approx 0$ here. If ${\sigma }_{\text{exp}}$, ${\sigma }_{\text{GRO}}$, or ${\sigma }_{\text{CH}}$ denote the surface charge in experiment or simulations using the Berger or the CHARMM force field, respectively, we obtain ${\sigma }_{\text{GRO}}/{\sigma }_{\text{exp}}=\Delta {\tilde{K}}_{\text{app},\text{hyd},\text{GRO}}/\Delta {\tilde{K}}_{\text{app},\text{hyd},\text{exp}}=37.8\left(\pm 7.6\right)$ and ${\sigma }_{\text{CH}}/{\sigma }_{\text{exp}}=\Delta K_{\text{app},\text{hyd},\text{CH}}/\Delta K_{\text{app},\text{hyd},\text{exp}}=7.4\pm 1.2$. Thus, both the Berger/GROMOS and the CHARMM setup significantly overestimate the surface charge, though the latter is closer to the experimental value than Berger.

Implications

The joint analysis of data from electrophoretic and ITC experiments in this work suggests that both Na⁺ and Cl⁻ ions show significant affinity for POPC bilayers. The effect of the adsorption of chloride and sodium ions add up in the heat transfer measured by ITC but largely compensate each other in the electrophoretic mobilities. Our findings challenge the results from MD simulations suggesting that only Na⁺ ions are surface active, whereas Cl⁻ ions merely form a diffuse layer of counterions in solution close to the membrane.

Supporting our conclusions from the ITC and electrophoresis data, this setup overestimates the effect of NaCl on the electrophoretic mobility of POPC by a factor of 10. This indicates that the surface charge of POPC from the interaction with NaCl is highly overestimated, questioning results from previous simulation studies of POPC bilayers in the presence of NaCl (10,13–19,28,29). In the following. we review some findings from previous simulations of PC bilayers in aqueous NaCl solutions in the light of our present results. If not stated otherwise, the mentioned studies used the Berger/GROMOS setup.

Effect of NaCl on lipid diffusion

The effect of NaCl to decrease the diffusion constants of lipids, D, predicted from simulations using the Berger setup were in good agreement with experimental values from fluorescence correlation spectroscopy (13). This is plausible, as the decrease in D appeared to arise from the formation of complexes of multiple lipids mediated by ions that may not depend on the surface charge but, rather, the ratio of bound (Na⁺ and Cl⁻) ions to lipids, which appears to be only slightly overestimated by the Berger/GROMOS setup.

Effect of NaCl on membrane structure

MD simulations as well as x-ray experiments indicate that addition of NaCl leads to a decrease in the area per lipid, $a_{\text{lip}}$, as well as increases in membrane thickness, d, and the size of the order parameter of the lipid tails, $\left|S_{\text{CD}}\right|$ (10,13,20,30). However, the simulations with the Berger force field overestimate the size of the effect at given NaCl concentration. At 200 mM NaCl, the Berger force field yields a reduction in $a_{\text{lip}}$ by 15%, as well as increases in d by 7.7% and in $\left|S_{\text{CD}}\right|$ by 16%, compared to an ion-free system. The CHARMM force field predicts smaller changes at an even higher NaCl concentration of 300 mM. Here, $a_{\text{lip}}$ is reduced by only 2.2%, whereas d is increased by 1.3% and $\left|S_{\text{CD}}\right|$ by 1.5%, compared to an ion-free system; thus, the changes observed for CHARMM are an order of magnitude smaller than those seen with Berger (20). The absolute changes with CHARMM for this ion concentration were $\Delta a_{\text{L}}=-0.015$ nm², $\Delta d=0.05$ nm², and $\Delta \left|S_{\text{CD}}\right|=0.003$, in good agreement with the x-ray experiments that yielded $\left|\Delta a_{\text{lip}}\right|<0.01$ nm², $\Delta d<0.1$ nm², and $\Delta \left|S_{\text{CD}}\right|\approx 0$ at 200 mM NaCl (20,30).

The effect of NaCl on d in the simulations with the Berger parameters is likely related to the combination of the artificially high surface charge occurring there and the boundary conditions chosen as rationalized in the following. The simulations were conducted under periodic boundary conditions using a rectangular simulation box, with the same pressure of 1 bar both in the direction parallel ($xy$ plane) and normal to the bilayer (z axis), and a fixed number of water molecules per lipid (13). A high surface charge of the POPC due to the adsorption of Na⁺ ions would lead to an increased repulsion between the bilayer and its periodic images in the z direction, leading to a tendency of the system to increase the separation between the periodic images of the bilayer, as compared to a corresponding ion-free system. This would result in an increase in the thickness of the water layer by an increase of the box size in the z direction, $\Delta z$. As both the water and the lipid bilayer are incompressible with respect to their volume, the increase in $\Delta z$ is accompanied by a reduction in the lateral area of the box, A, which will be limited by the finite area compressibility of the bilayer. Because the lipid bilayer is incompressible with respect to its volume, the reduction in A will lead to an increase in membrane thickness. This will be accompanied by an increase in the size of the order parameter of the lipid tails. With the CHARMM force field, the effect on membrane structure is smaller than for the Berger parameters because of the smaller surface charge.

Our results may also have implications that question predictions on the effect of NaCl on water polarization and swelling of multibilayer stacks (13,20), the appearance of transmembrane potentials due to asymmetric binding of Na⁺ and Cl⁻ ions (29), and the mechanism of ion transport across lipid bilayers from previous MD studies (28), as explained in the Supporting Material. Our findings indicate that force field refinements are needed to achieve a realistic description of lipid membranes and conformational equilibria of membrane proteins under physiological ion conditions, as also explained in the Supporting Material.

Conclusions

A comparison of data from electrophoresis and ITC experiments as well as MD simulations suggest that chloride ions bind almost as strongly to PC bilayers as sodium ions. The strong asymmetry in membrane affinities, together with a range of associated effects seen in most simulations thus appears to be artificial. Our results show the importance of a detailed comparison between experimental and simulated data for understanding the interactions of ions with lipid membranes. Our findings suggest that a range of published simulation results on the interaction of NaCl with PC bilayers have to be reconsidered and revised.