Abstract
Signaling and regulatory networks are essential for cells to control processes such as growth, differentiation, and response to stimuli. Although many “omic” data sources are available to probe signaling pathways, these data are typically sparse and noisy. Thus, it has been difficult to use these data to discover the cause of the diseases and to propose new therapeutic strategies. We overcome these problems and use “omic” data to reconstruct simultaneously multiple pathways that are altered in a particular condition by solving the prize-collecting Steiner forest problem. To evaluate this approach, we use the well-characterized yeast pheromone response. We then apply the method to human glioblastoma data, searching for a forest of trees, each of which is rooted in a different cell-surface receptor. This approach discovers both overlapping and independent signaling pathways that are enriched in functionally and clinically relevant proteins, which could provide the basis for new therapeutic strategies. Although the algorithm was not provided with any information about the phosphorylation status of receptors, it identifies a small set of clinically relevant receptors among hundreds present in the interactome.
Key words: multiple network reconstruction, prize-collecting Steiner forest, signaling pathways
1. Introduction
High-throughput technologies including mass spectrometry, chromatin immunoprecipitation followed by sequencing (CHIP-Seq), RNA sequencing (RNA-seq), and microarray and screening methods have the potential to provide dramatically new insights into biological processes. By providing a relatively comprehensive view of the changes that occur for a specific type of molecule or perturbation, these approaches can uncover previously unrecognized processes in a system of interest. However, interpreting these data types together to provide a coherent view of the biological processes is still a challenging task. In order to discover how changes in different classes of molecules relate to each other, it is possible to map the data onto a network of known or predicted interactions. Ideally, the observed interactions would all lay near each other in a functionally coherent part of the interaction network (the interactome). However, due to false positives and false negatives in both the “omic” data and the interactome, the true situation is much more complex; advanced algorithms are needed to find meaningful connections among the data. Among the approaches that have been proposed to find these subnetworks from the interactome are network flow optimization (Lan et al., 2011; Yeger-Lotem et al., 2009), network propagation (Vanunu et al., 2010), the Steiner tree approach (Bailly-Bechet et al., 2010a; Dittrich et al., 2008; Huang and Fraenkel, 2009), network inference from gene expression (Bailly-Bechet et al., 2010b; Friedman, 2004), linear programming (Ourfali et al., 2007), maximum-likelihood (Yeang et al., 2004), electric circuits (Kim et al., 2011; Missiuro et al., 2009; Suthram et al., 2008), network alignment (Sharan and Ideker, 2006), and Bayesian networks (Akavia et al., 2010).
In our previous work, we used the prize-collecting Steiner tree formalism to find an optimum tree composed of nodes detected in experiments (terminals) and nodes that were not detected (Steiner nodes). We assigned costs to each interaction reflecting our confidence that the reported interaction was real and assigned prizes for excluding any of the terminals from the tree based on confidence in the proteomic or transcriptional data. By minimizing the sum of the total cost of all edges in the tree and the total prize of all nodes not contained in the tree, we were able to obtain compact and biologically relevant networks (Bailly-Bechet et al., 2010a; Huang and Fraenkel, 2009). Despite the power of the Steiner tree approach for identifying functionally coherent networks, it is restricted to discovering a connected subgraph, which may be an inadequate representation for many systems. In particular, we often expect there to be many simultaneously acting biological processes in the cell that may not be connected together by interactions in the currently known interactome. These processes may be unconnected either because they may involve essentially independent cell functions, or simply due to our imperfect knowledge of the interactome.
In this work, we formulate a forest (defined as a disjoint union of trees) approach to identify simultaneously acting pathways in biological networks using both proteomic and transcriptional data. We use a generalization of the message-passing algorithm for the Prize-collecting Steiner Tree (PCST) problem (Bailly-Bechet et al., 2010a; Bayati et al., 2008). We first demonstrate the forest approach by using it to integrate proteomic and transcriptional data in the yeast pheromone response, showing that the forest consists of trees enriched in specific and distinct biological processes. As an additional feature, directed edges, which are particularly useful for representing the effects of enzymes and transcriptional regulators on their targets, are also incorporated.
We reasoned that the Steiner forest approach could be utilized in modeling mammalian signaling where there are many more cell-surface receptors and downstream pathways than in yeast. In principle, the forest approach could uncover multiple, independent components of the biological response. Although the interactome data are much less complete for mammals than for yeast, we show that the same methods are applicable. We built prize-collecting Steiner forests derived from proteomic data from a model of glioblastoma multiforme (GBM) in which each tree was rooted in a different cell surface receptor representing independent signaling pathways and potential points of therapeutic intervention. The solution reveals several known pathways and some unexpected new ones that are altered in the disease and suggests potential therapeutic strategies. The modified algorithm can now be applied to a wide range of complex systems.
2. Methods
2.1. Datasets
Throughout this work, two different biological networks are used: the yeast interactome and the human interactome. We refer to nodes with prize values greater than zero as terminal nodes.
2.1.1. Yeast dataset
The yeast interactome contains 34,712 protein–protein and transcription factors to target interactions between 5,957 nodes. The terminal node set contains 106 differentially phosphorylated proteins detected by mass spectrometry (Gruhler et al., 2005) and 118 differentially expressed genes (Issel-Tarver et al., 2002) detected by microarray in response to the mating pheromone alpha factor. The node prizes are computed from the fold changes between treated and nontreated conditions. The edge costs are calculated by taking a negative log of the interaction probability. The details are available in Huang and Fraenkel (2009). In this study, we modified the transcription factor–DNA interactions to be directed edges. We also added to the interactome a set of directed edges that represent phosphorylation and dephosphorylation reactions between kinases, phosphatases, and their substrates (Breitkreutz et al., 2010). If these interactions are available in the original interactome, probabilities are retained. If they are not, the probabilities of these interactions are set uniformly to 0.8, based on the distribution of the probabilities in the original interactome. The final interactome contains 35,998 edges between 5,957 nodes. In both cases, the resulting interactomes are comprised of both undirected and directed edges.
2.1.2. Human dataset
Protein–protein interactions in the STRING database (version 8.3) are used as the data source for the human interactome (Jensen et al., 2009). Here, the probabilities from experiments and database evidence channels are combined to obtain the final probability of the interactions. Interactions with a combined probability greater than 0.8 are included in the interactome. The receptor molecules are collected from the Human Plasma Membrane Database (Ben-Shlomo et al., 2003), where 331 receptors are available in the interactome derived from STRING. The phosphoproteomic data in Huang et al. (2007) is combined with the human interactome for the GBM test case. From this dataset, 72 proteins containing phophorylated tyrosine peptides are present in our human interactome.
2.2. Prize-collecting Steiner tree problem
For a given, directed or undirected network G(V, E, c(e), p(v)) of node set V and edge set E, where a p(v) ≥ 0 assigns a prize to each node v ∈ V, and c(e) ≥ 0 assigns a cost to each edge e ∈ E. The aim is to find a tree T(VT,ET), by minimizing the objective function:
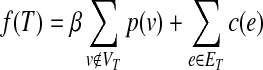 |
(1) |
where the first term is β times the sum of the node prizes not included in the tree T, and the second part is the sum of the edge costs of T. Note that
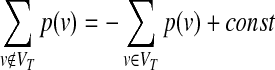 |
(2) |
so that minimizing f(T) amounts to collecting the largest set of high prize vertices while minimizing the set of large cost edges in a trade-off tuned by β. As a starting point, we consider the message-passing algorithm for the PCST problem introduced in Bailly-Bechet et al. (2010a). The message-passing algorithm converts the global problem of finding the optimal tree into a set of local problems that can be solved efficiently. These equations are solved iteratively in a computationally efficient way. Here we present a generalization of the message-passing algorithm designed to solve the PCST problem on directed networks [i.e., where, in general, c(e{i,j}) might be different from c(e{j,i})]. In this variant, the optimization will be done on directed rooted trees, where choice of the root (which will be part of the candidate tree) is an external parameter of the algorithm.
2.3. Prize-collecting Steiner forest problem
A type of prize-collecting Steiner forest (PCSF) has already been considered in Chekuri et al. (2010) and Gupta et al. (2007). In these works, penalties are assigned to each pair of nodes either directly connected in the tree (i.e., edges belonging to the forest) or completely disconnected (i.e., in different forest components). Here we consider a different PCSF construction for a given, directed, or undirected network G(V, E, c(e), p(v)) of node set V and edge set E, where a p(v) ≥ 0 assigns a prize to each node v ∈ V and c(e) ≥ 0 that assigns a cost to each edge e ∈ F. The aim is to find a forest F(VF,EF) that minimizes the objective function:
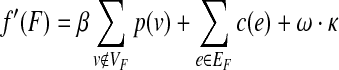 |
(3) |
where κ is the number of trees in the forest and ω is the new tuning parameter explained below. A practical way of minimizing f′ consists of casting the PCSF into a PCST on a slightly modified graph. The flowchart of this algorithm is illustrated in Figure S1 (Supplementary Data available online at www.liebertonline.com/cmb). The idea is to introduce an extra root node v0 into the network connected to each node v ∈ V by an edge (v, v0) with cost ω (Bailly-Bechet et al., 2009). The PCST algorithm is employed on the resulting graph H(V ∪ {v0,}, E ∪ V×{v0,}), and the solution will be called T. We define the forest F as T with all edges that point to the root removed. It is straightforward to see that the tree T is minimal for f if and only if the forest F is minimal for f′. Typically, the algorithm is run for different values of β and ω.
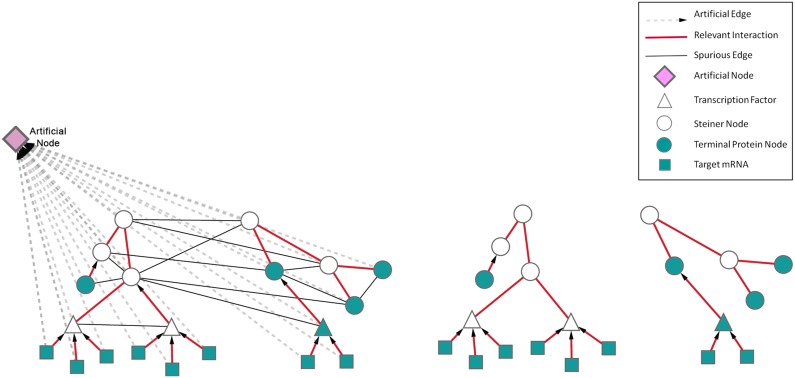
We used the previously published message-passing approach as the underlying implementation for this forest search (Bailly-Bechet et al., 2010a), as many of our networks exceeded the capacity of the linear programming approaches. The message-passing approach is computationally fast and robust to the noise in the network as well. Although this algorithm is not guarranteed to find the optimal solution, in practice the networks it discovers are very similar to the exact solution. Introducing the artificial edges allows the algorithm to identify one or more trees that are only connected to the artificial node and not to each other. Although this modification seems algorithmically straightforward, its biological implications are very important. The concept is illustrated in Figure 1. In that example, two distinct pathways are connected only through spurious edges. The main difference between the tree formalism and the forest formalism is that the former one connects as many of the experimental data as it can in a single network. As a result, it will either have to exclude some of the data that relate to distinct biological processes or add spurious edges to force these data to connect to the tree, while the latter one allows the corresponding nodes to be included in distinct trees. However, the forest formalism is able to locate distinct biological processes into different subtrees through the artificial node. The artifical node and edges give the flexibility of generating several subtrees without paying any penalty.
FIG. 1.
Conceptual illustration of the Prize-collecting Steiner Forest (PCSF) algorithm. The left panel shows an interactome and the right panel shows the Steiner forest constructed from that interactome. The direction of transcription factor to target and kinase/phosphatase to substrate interactions are pointing toward the root node (opposite to the biological direction). In this scenario, there are spurious edges between these two pathways in the interactome. The PCSF algorithm provides the advantage to connect these distinct pathways artificially.
2.4. Tuning the parameters
The parameters to be tuned in this problem are ω and β. The number of components of the solution (κ) depends strongly on the parameter ω, but it also depends on the β value: e.g., for β = 0 the optimal solution is the empty forest for all values of other parameters. For other values of β, while some subtrees are composed of a single node, some others are composed of a large number of nodes in the resulting forest. A forest with many very small trees (a single node each) would be obtained with very small artificial edge cost. The limiting case in the other direction is a single tree resulting from very large artificial edge cost. Therefore, there is a nontrivial interaction between the two parameters (β and ω). In principle, this two-dimensional (β, ω) space of parameters should be explored. In this way, we get many possible types of forest: many small trees, many large trees, few small trees, few large trees (see Supplementary Material and Fig. S2). The effect of ω and β intervals highly depends on the distribution of edge costs and node prizes in the targeted interactome, so these parameters will be different for different datasets. For the yeast dataset, ω values are tuned between [0.005, 0.1] and β values are tuned between [1, 20].
2.5. Functional annotation
For functional enrichment analysis, the BINGO plug-in (Maere et al., 2005) of Cytoscape (Shannon et al., 2003) was used. The p-value significance threshold of 0.05 was used, which is corrected for multiple hypothesis testing, and all yeast proteins were used as the background set for the yeast dataset. For the human dataset, the functional enrichment is performed by using all human proteins as background set. All network visualizations were performed in Cytoscape (Shannon et al., 2003).
3. Results
3.1. Practical advantages of the message-passing solution for biological networks
Previous work has shown that the message-passing approximation is faster than the branch-and-cut algorithm and typically finds a comparable value for the objective function. This comparison was performed on a benchmark set that is not related to biological data (Bailly-Bechet et al., 2010a). Since the message-passing approach only approximates the exact solution found by the branch-and-cut algorithm, we compared the performance of these two algorithms on phosphoproteomic and transcriptional data from the yeast pheromone response.
We performed an initial analysis to determine the appropriate paramater settings. In the branch-and-cut algorithm, the size of the network is controlled only by the beta parameter. In the message-passing algorithm, there is a second parameter, called depth, that can also be used to control the size of the resulting tree. Depth (D) represents the maximum allowed distance between the farthest node in the tree and the root node. Based on these observations, we tested several depth values on the yeast interactome and found that depth value equal to 20 produces the best objective function value in the PCST runs on yeast dataset (see Fig. S3a). To check the robustness of the message-passing algorithm we added noise to edge-weights and re-ran it (see Fig. S3b). We refer to the solutions of these noisy inputs as suboptimal solutions. The overlap between suboptimal solutions and the original solution is still very high up to a noise value; therefore, the solution is robust to noise on the yeast pheromone data.
Having identified a suitable range for the parameters, we compared the message-passing algorithm to the branch-and-cut algorithm on the original undirected yeast interactome. As mentioned previously, the message-passing algorithm finds a solution to the PCST problem in a computationally very effective way. For example, the branch-and-cut algorithm (Ljubic et al., 2006) takes 931 seconds to reach the exact solution with an objective value of 2.2123, while the message-passing algorithm reports a solution in 237 seconds with an objective value 2.2178. Critically, we find that the overlap of the nodes between these two solutions is 98.5%. This result shows that almost the same solution is obtained by both algorithms, but the message-passing approach is almost four times faster than the branch-and-cut approach (Table S1). The difference in speed becomes critical when exploring the space of parameters or testing the robustness of solutions.
To analyze the effects of the directionality in the solution, we added directed edges from enzymes to their substrates using the kinase and phophatase interaction network in Breitkreutz et al. (2010). The algorithm is able to find a smaller network that still includes the same number of terminals as when only the transcription factor–DNA edges were directed. In these two examples, having more directed edges in the starting interactome results in more compact PCST solutions that connect the same number of protein terminals using fewer intermediate nodes (Table S1). These more compact trees are likely to be more useful for generating testable biological hypothesis, since the Steiner nodes that they include are the ones that are most constrained by the experimentally derived terminals. Further, by adding directions between transcription factors to targets and enzyme to substrate interactions, we are able to obtain condition-specific transcription factors and compact networks.
3.2. The PCSF approach reveals parallel working pathways in addition to hidden individual proteins or genes in yeast pheromone response
High-throughput experimental methods like mass-spectrometry are capable of simultaneously detecting changes in many distinct biological processes that will not be connected by physical interactions. However, the PCST approach searches for a tree structure in the interactome that connects as many of the experimental data as it can. As a result, it will either have to exclude some of the data that relate to distinct biological process or add spurious edges to force these data to connect to the tree. The main advantage of the PCSF approach over PCST is that PCSF does not force the system to be connected in a single network, and it can automatically separate multiple pathways.
We tested the PCSF algorithm using data from the yeast pheromone response, which we had previously analyzed using the prize-collecting Steiner tree approach. The data consist of phosphoproteomic and transcriptional changes induced by mating pheromone, and the network is enriched with directed transcription factor–target and kinase/phosphatase–substrate reactions. The edge costs of the interactome were computed as the negative log of the interaction probabilities, and node prizes were obtained from the scheme detailed in Huang and Fraenkel (2009). To explore the space of solutions, we tuned the ω and β parameters between [0.005, 0.1] and [1, 20], respectively. The minimum, maximum, and average size and number of trees in the constructed PCSFs are extracted for each (ω, β) pair, and the distribution of these values along ω parameter is plotted. We looked for a solution in a region where the number of trees and average size of the trees in the forest are closest to each other. By these criteria, the best solution is found when ω = 0.025 and β = 13 (Fig. S4). We note that in order to explore these parameters, we constructed 400 solutions to the PCST problem. This number of calculations is only practical using the message-passing algorithm, but not with the integer linear-programming–based approaches.
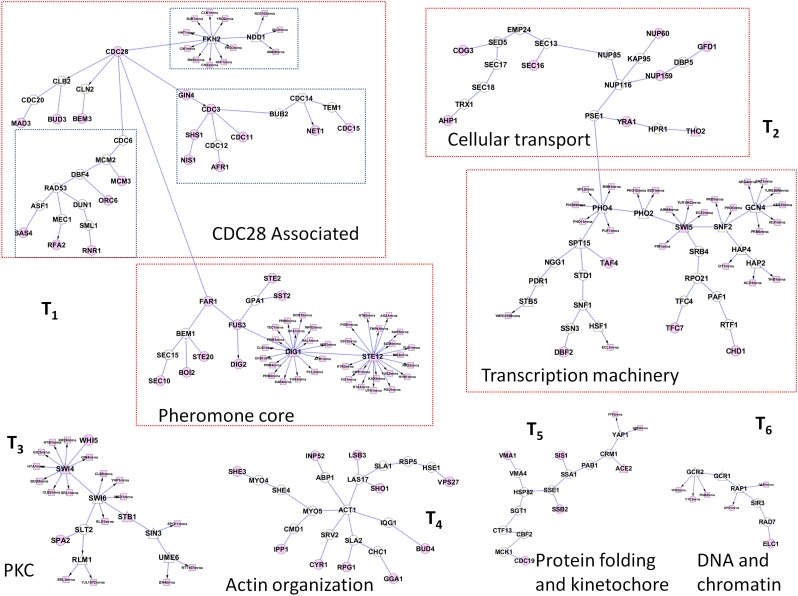
The solution to PCSF problem places distinct functional classes in seperate subtrees. In this solution, there are six trees, each containing more than 10 nodes. In Figure 2, each tree is labeled with its corresponding pathway. Small subtrees such as T3–6 are enriched in specific biological processes, including the protein kinase C (PKC) pathway, actin organization, protein folding and kinetochore, and DNA and chromatin pathways, while larger trees contain multiple processes. For example, the largest subtree, T1, contains the pheromone core mitogen-activated protein kinase (MAPK) pathway with CDC28-related proteins, and the second largest one, T3, contains transcription and transport processes (Fig. 2). There are two different yeast MAPK pathways; the pheromone-induced MAPK and the PKC pathways (Buehrer and Errede, 1997; Zarzov et al., 1996). The PCSF algorithm correctly separates these two pathways into different trees. The largest tree in size, T1, contains pheromone-induced MAPK pathway, but the PKC pathway is located in T3. While the former one induces cells to differentiate and be prepared for mating, the latter one is involved in cell integrity and new cell-wall synthesis.
FIG. 2.
Prize-collecting Steiner Forest (PCSF) of the Yeast Pheromone Response Network. Functional groups annotated by gene ontology (GO) are tagged with red boxes. In this PCSF, the rectangular nodes are genes, triangular nodes are transcription factors, and the circular nodes are proteins. Terminal nodes are colored red.
The core pheromone response pathway component in T1 includes the STE2 receptor. In this subtree, the STE2-GPA1-FUS3 interaction is in the core of pheromone response. In addition, the MAP kinase FUS3 activates several transcription factors, such as STE12, DIG1, and DIG2, for the expression of mating related genes. T1 contains DNA-replication proteins and cell-cycle proteins associated with CDC28 as well. Here, the connection between the MAP kinase pathway in the pheromone core and the CDC28-associated subnetwork is constructed through the interaction between FAR1 and CDC28. FAR1 is a direct inhibitor of CDC28/CLN2 complex and functions in orienting cell polarization. This association blocks the cell-cycle progression. FUS3 phosphorylates FAR1, and only phosphorylated FAR1 can associate with CDC28/CLN2 complex. All these interactions and these connected pathways are correctly located into the same subtree.
The algorithm correctly identifies SLT2, which was not detected in the phosphoproteomic data, as a key node in regulating new cell-wall synthesis. SLT2 is a serine/threonine MAP kinase activated in a cascade starting with PKC. The phosphoproteomic data are not sufficient for the algorithm to pick up the upstream pathway. However, in T3, the algorithm links SLT2 to several transcription factors that mostly function in cell-wall integrity and biosynthesis. SLT2 activates RLM1 (Garcia et al., 2004), SWI4 (Baetz et al., 2001), and SWI6 transcription factors. RLM1 functions in the maintenance of cell integrity. SWI4/SWI6 regulates the expression of genes functioning in cell-wall synthesis and G1/S transition of the cell cycle.
Transcriptional machinery and transport proteins are located in T2, seperate from other trees. The connection between transcriptional machinery and cellular transport part is achieved by the interaction between PHO4 and PSE1. Although these two proteins are experimentally undetected, the PCSF algorithm locates them in the same subtree. Direct association of PSE1 to PHO4 is required for the import of PHO4 into the nucleus (Kaffman et al., 1998). Nuclear pore components (NUP60, NUP85, NUP116, NUP159) are located in T2 because nuclear transport is achieved through the nuclear pore (Kaffman et al., 1998). In this subtree, the transcription factor PHO2 functions in a combinatorial manner with PHO4 and SWI5 (Bhoite et al., 2002).
In addition to the pathway analysis, we utilized the gene ontology (GO) biological process annotations to find the specific biological processes enriched in these trees. In Table 1, the top three annotations for each tree are tabulated along with their corrected p-values. These results show that this method effectively locates different biological processes into different trees. Instead of forcing all nodes to be connected in a single network, this “forest” representation composed of multiple subtrees is more useful for distinguishing distinct pathways. The forest solution retains more enrichment for the expected biological process, such as response to stress, cell cycle, signaling, and transport (Fig. S5). Further, by adding directions between transcription factors to targets and enzyme to substrate interactions, we are able to obtain more condition-specific transcription factors and a smaller network that still includes the same number of terminals (see Supplementary Material and Table S1).
Table 1.
Gene Ontology Enrichments of the Subtrees in the Prize-Collecting Steiner Forest Illustrated in Figure 2
| Subtree name | GO enrichment—biological process | Corr p-value |
|---|---|---|
| T1 | Regulation of cell cycle | 1.97 × 10−17 |
| Cell division | 2.60 × 10−17 | |
| Cell cycle | 3.02 × 10−17 | |
| T2 | Transcription | 7.07 × 10−13 |
| Regulation of nucleobase, nucleoside, nucleotide, and nucleic acid metabolic process | 2.36 × 10−12 | |
| Nuclear transport | 7.30 × 10−8 | |
| T3 | Positive regulation of gene-specific transcription | 2.20 × 10−5 |
| Regulation of gene-specific transcription | 7.75 × 10−5 | |
| Positive regulation of transcription, dna-dependent | 9.11 × 10−5 | |
| T4 | Actin filament-based process | 1.51 × 10−9 |
| Endocytosis | 4.42 × 10−9 | |
| Actin cytoskeleton organization | 9.32 × 10−9 | |
| T5 | Protein folding | 1.60 × 10−3 |
| Protein refolding | 1.60 × 10−3 | |
| Kinetochore assembly | 4.25 × 10−3 | |
| T6 | Positive regulation of glycolysis | 2.54 × 10−4 |
| Regulation of glycolysis | 2.54 × 10−4 | |
| Positive regulation of transcription | 2.54 × 10−4 |
To evaluate this approach further, we selected terminals from distinct biological processes assigned by GO annotations and constructed PCSFs. As we show in the Supplemental Material, these tests revealed that the approach was able to reconstruct functionally coherent trees based solely on the connectivity of the interactome. The detailed results and the list of biological processes used in this analysis are available in the supplementary text, Table S2, and Figure S6.
3.3. The PCSF algorithm reveals coordinately acting receptor molecules functioning in human GBM by integrating receptome, interactome, and proteomics data
Having demonstrated that the PCSF algorithm can successfully distinguish parallel-working pathways in yeast, we used it to identify cell-surface receptors associated with signaling pathways altered in disease. Cell-surface receptors are an interesting class of molecules to study, as they may be particularly easy to target with therapeutic agents. There is increasing evidence that some proteins are “undruggable,” in other words, hard or impossible to target with small molecule-based therapies because their three-dimensional shape does not have any appropriate concave sites to which these proteins can bind. In contrast, cell-surface receptors can be targeted with their natural ligand, modified forms of the natural ligand, or small molecules that insert into the naturally occurring binding pocket or antibodies.
We modified our approach to identify cell-surface receptors associated with phosphoproteomic changes that occur in a model of glioblastoma (Fig. S7). We use the artificial node to represent external stimuli (including autocrine loops) that potentially activates multiple receptor molecules, by connecting this node only to cell surface receptors, of which 331 are present in our human interactome. After running the prize-collecting Steiner tree algorithm and removing the artificial node, each subtree will contain one receptor as the starting node. The receptors selected in the solution of PCSF represent those most closely connected to the measured phosphoproteomic data and are therefore likely to be main contributors of the disease.
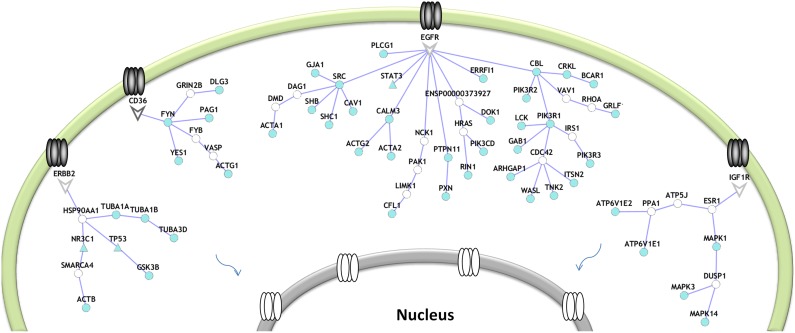
We applied this approach to phosphotyrosine data for a model of human GBM (Huang et al., 2007), representing phosphorylation differences between cells expressing an oncogenic mutation in the EGFR protein and cells with an inactive form of this receptor tyrosine kinase. The result is a set of 11 compact trees each rooted in one of the 331 potential receptors. The selected receptors in the order of their tree sizes are EGFR, ERBB2, CD36, IGF1R, PTCH1, A2MR, SDC2, MET, ITGB3, NPR1, and EPHA2 (Fig. 3). Although the algorithm had no direct knowledge that the data represented the results of mutation in EGFR, it selected this as the root of the largest tree. In fact, each of the four top receptors has a known link to cancer. EGFR and ERBB2 are EGF-family receptors, and it is known that EGFR is mutated in more than 50% GBM cases (Cancer Genome Atlas Research Network, 2008). IGF1R is overexpressed in many tumors and mediates proliferation and resistance to apoptosis, and it is currently an anti-cancer treatment target (Macaulay, 2004). Because IGF1R is also abnormally active in GBM, its inhibition is presented as a potential therapy to arrest the tumor growth (Kiaris et al., 2000).
FIG. 3.
Network representation of the PCSF for human glioblastoma dataset. Each tree is rooted from a cell-surface receptor. The receptor molecules are represented by the arrowheads, transcription factors in triangles, and other proteins as circles. Terminal nodes are colored in cyan.
It has been previously shown that the EGF and IGF pathways cross-talk (Adams et al., 2004), and IGF1R mediates resistance to anti-EGFR therapy in glioma cells (Chakravarti et al., 2002). Although CD36 functions in brain-specific angiogenic regulation (Kaur et al., 2009), and the interactions between CD36-Fyn-Yes lead to calcium and neurotransmitter release (Silverstein and Febbraio, 2009), its relation to GBM has not been studied in detail. Further, the downstream interactions in Fyn points out the glutamate-related proteins GRIN2B and DLG3. In addition to those receptors pictured in Figure 3, we identified PTCH1 as an important receptor in glioblastoma, which is the root of a small subtree. PTCH1 is a known tumor suppressor (Agren et al., 2004). These less-studied receptors, CD36 and PTCH1, suggest novel therapeutic targets for glioblastoma treatment.
Although the algorithm is constrained to identify independent trees, we can observe the potential for cross-talk between different receptors by adding back all the edges among the selected nodes (Fig. S8). We noticed two receptors selected by the algorithm, namely MET and ITGB3 (integrin-β3), are also very important, despite the fact that their corresponding subtrees each contain only two nodes. When all edges are put back in the Steiner forest, we observe extensive links between these two receptors and the EGFR subtree. MET has links to seven proteins out of nine first neighbors of EGFR and to 16 proteins in total of the EGFR-rooted subtree, and ITGB3 has links to 17 members of the EGFR subtree. By contrast, IGF1R has links only to three proteins, and ERBB2 has links only to two proteins in the first neighbors of EGFR. Although this information was not applied to the algorithm, MET is detected as differentially phosphorylated in the original data, and a MET inhibitor synergizes with an EGFR inhibitor (Huang et al., 2007).
Mammalian signaling systems frequently demonstrate a high degree of cross-talk. If two receptors share many common downstream components, the algorithm need only choose one of these as a root node to explain all the terminal nodes. We, therefore, introduce a perturbation-based approach to improve the sensitivity of the algorithm in identifying receptors that share many downstream components with the selected root nodes. In this analysis, selected receptor molecules (the root of the largest tree in the forest and other receptors in its corresponding subfamily available in the forest) and all their interactions are removed from the interactome, and PCSF algorithm is applied to the remaining network. Through this in silico knock-out experiment, we can find the other receptor molecules whose role may be masked in the presence of the receptors in the initial forest.
We first knocked out two EGF/ERBB subfamily receptors, EGFR and ERBB2, from the network and regenerated the PCSF. In the resulting network, 37 out of 42 nodes in the downstream of EGFR in the original tree are connected to other receptors. Platelet-derived growth factor receptor (PDGFR) is the root of the largest tree, covering 23 nodes linked to EGFR in the original network (shown in Fig. S9a). This observation suggests that PDGFR may have many overlapping functions with EGFR. In fact, several studies have shown that PDGFR is critical in brain tumorogenesis (Dai et al., 2001; Uhrbom et al., 1998); mutation of PDGFR causes alteration in the intracellular signaling (Clarke and Dirks, 2003), and it is a therapeutic target in GBM (Ziegler et al., 2008). Another 14 nodes downstream of EGFR are shared by MET (seven nodes), IGF1R (five nodes), and ITGB3 (two nodes). Although these four receptors (PDGFR, MET, IGF1R, and ITGB3) capture many of the nodes that were downstream of EGFR, five nodes are not captured by any other receptors. These may represent signaling that is uniquely downstream of EGFR.
To further explore the network, we removed PDGFR in addition to EGFR and ERBB2. In the new network, the MET receptor partially replaces PDGFR. It has been shown that the MET receptor is activated in GBM, and it might be a therapeutic target (Li et al., 2011). Similar to the MET receptor tree, the subtree containing ITGB3 receptor also collects several of the nodes previously associated with EGFR in its corresponding subtree (shown in Fig. S9b). It is interesting to note that integrins function as both upstream and downstream effectors of growth factor receptors, such as EGFR, IGF1R, PDGFR, MET (Alam et al., 2007). Integrins and their relation to GBM have not been studied in detail, which may have clinical importance in GBM.
During all these leave-one-receptor-out tests, IGF1R is present in the resulting PCSF, and it retains all proteins in the original network. The downstream network of IGF1R starts with the estrogen-receptor (ESR1) interaction, and it contains several MAPKs. It has been shown that ESR1 and IGF1R are cross-regulated in the brain and activate the MAPK/ERK pathway. This system of interactions results in some neural functional regulations in the brain, such as synaptic plasticity, neurotic growth, and neuronal survival (Cardona-Gomez et al., 2002). The size of the trees corresponding to the downstream of MET and ITGB3 receptors increases at each knock-out. Also, the FYN-related downstream pathway of CD36 is swapped to be downstream of MET receptor, although CD36 is not knocked out. This result implies that FYN-related pathway may be activated by several receptors.
To further validate the relevancy of these receptor molecules (EGFR, ERBB2, IGF1R, CD36, PDGFR, MET, and ITGB3), we used the TCGA GBM Gene Ranker (http://cbio.mskcc.org/tcga-generanker/). This server combines available literature information and TCGA data to score individual genes. All selected receptors are among highly ranked genes (genes having a score greater than 2.0) in GBM (calculated scores are as follows: EGFR: 15.75, MET: 11.75, ERBB2: 9.25, PDGFRB: 7.25, IGF1R: 4.0, ITGB3: 3.75, CD36: 2.0), with EGFR, MET, and ERBB2 having the highest ranks in the database.
We performed randomization tests to check the reliability of the output of the algorithm. Here, terminal nodes, their prizes, and the parameter set are kept same with the original PCSF analysis of GBM. In addition, number of nodes, edges, and edge costs are the same as in the original interactome. Only the edges are reshuffled randomly within the network. The randomization test is repeated ten times on different interactomes. The statistics for the average of the resulting forests are tabulated in Table S3. These characteristics show that random PCSFs contain many more subtrees when compared to the original PCSF, and these subtrees are not structured like the original trees; most of the trees in the random forests are “stringy,” composed of nine proteins at most. Further, random trees are not enriched for a specific biological process and none of the receptors found in the original PCSF are selected in the random PCSFs. The algorithm uses substantially more Steiner nodes to connect terminal nodes in random cases.
We performed another randomization test by reshuffling the nodes in the original interactome. In this way, the degree distribution is retained. In these randomizations, we retain the same terminal nodes; prizes and the parameter set are kept same with the original PCSF analysis, but these proteins have now been randomly mapped to other nodes. The results show that the characteristics of the subtrees in the random PCSFs are similar with the previous random case; they are “stringy,” not structured and not enriched for functions. However, this time the total number of nodes included in the PCSF is not as large as in the previous random case. These results show that the real PCSF solution is significantly different than the random solutions. It is particularly important that the receptors found by the algorithm run on the GBM data are not selected in the randomizations, supporting the hypothesis that these receptors are biologically relevant.
4. Discussion
We present a method for simultaneous discovery of multiple pathways by searching for “forests” consisting of multiple trees. We are able to solve this problem efficiently, even for large human networks, by a simple modification of the previously published message-passing solution for the Steiner tree problem. When applied to the pheromone response data on the directed yeast interactome, the PCSF approach reveals several parallel pathways affected by yeast pheromone. Some of these parallel pathways contain multiple, coherently acting processes such as pheromone response and the CDC28 associated pathway, or transport and transcriptional activity of PHO4. Others contain only one process, such as actin organization or protein folding. Independently from the pheromone response network, we also show that this approach can identify regions of the yeast interactome enriched in various biological processes using only the connectivity information (see Supplementary Material).
The advantages of the forest approach are most apparent when used to study mammalian cells, which respond to a large number of hormones, growth factors, and cytokines. Applying this approach to proteomic data from a model of GBM results in a forest composed of several subtrees, each of which is rooted from a receptor molecule. The PCSF algorithm is able to select receptors relevant to GBM from hundreds of molecules in the human receptome. The solution reveals several known pathways and some unexpected new ones. EGFR, ERBB2, IGF1R, and CD36 are starting nodes of the largest subtrees in the PCSF. This set of receptor molecules was selected by the algorithm among hundreds of receptors, and the literature search shows that each of the selected receptors is clinically relevant to GBM.
To find additional receptors whose downstream signaling pathways overlap with the selected receptors, we used an iterative approach that can be thought of as an in silico knock-out experiment. In this analysis, a selected receptor molecule and all its interactions are removed from the interactome, and PCSF algorithm is applied to the remaining network. These calculations revealed the roles of PDGFR, MET, and ITGB3, all of which have been previously linked to GBM.
Our method can be efficienly utilized to reconstruct networks that are enriched in functionally and clinically relevant proteins. Further, the algorithm is flexible, and can be modified for other types of data such as protein–small molecule inhibitor interactions and protein–metabolite interactions.
Supplementary Material
Acknowledgments
We thank Dr. Sara Gosline from MIT and Dr. Oznur Tastan from Microsoft Research for their critical reading and fruitful comments. This work is supported by NIH grants U54CA112967, R01GM089903, and Institute for Collaborative Biotechnologies through grant W911NF-09-0001 from the US Army Research Office (the content of the information does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred) and used computing resources funded by the National Science Foundation under Award No. DB1-0821391. E.F. receives support from the Eugene Bell Career Development Chair. R.Z. acknowledges the ERC grant OPTINF 267915. The support from the EC grant STAMINA 265496 is also acknowledged by A.B. and R.Z.
Disclosure Statement
The authors declare that no competing financial interests exist.
References
- Adams T.E. McKern N.M. Ward C.W. Signalling by the type 1 insulin-like growth factor receptor: interplay with the epidermal growth factor receptor. Growth Factors. 2004;22:89–95. doi: 10.1080/08977190410001700998. [DOI] [PubMed] [Google Scholar]
- Agren M. Kogerman P. Kleman M.I., et al. Expression of the PTCH1 tumor suppressor gene is regulated by alternative promoters and a single functional Gli-binding site. Gene. 2004;330:101–14. doi: 10.1016/j.gene.2004.01.010. [DOI] [PubMed] [Google Scholar]
- Akavia U.D. Litvin O. Kim J., et al. An integrated approach to uncover drivers of cancer. Cell. 2010;143:1005–17. doi: 10.1016/j.cell.2010.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alam N. Goel H.L. Zarif M.J., et al. The integrin-growth factor receptor duet. J. Cell. Physiol. 2007;213:649–53. doi: 10.1002/jcp.21278. [DOI] [PubMed] [Google Scholar]
- Baetz K. Moffat J. Haynes J., et al. Transcriptional coregulation by the cell integrity mitogen-activated protein kinase Slt2 and the cell cycle regulator Swi4. Mol. Cell. Biol. 2001;21:6515–28. doi: 10.1128/MCB.21.19.6515-6528.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailly-Bechet M. Borgs C. Braunstein A., et al. Finding undetected protein associations in cell signaling by belief propagation. Proc. Natl. Acad. Sci. U.S.A. 2010a;108:882–7. doi: 10.1073/pnas.1004751108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailly-Bechet M. Bradde S. Braunstein A., et al. Clustering with shallow trees. J. Stat. Mech. 2009:P12010. [Google Scholar]
- Bailly-Bechet M. Braunstein A. Pagnani A., et al. Inference of sparse combinatorial-control networks from gene-expression data: a message passing approach. BMC Bioinformatics. 2010b;11:355. doi: 10.1186/1471-2105-11-355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayati M. Borgs C. Braunstein A., et al. Statistical mechanics of steiner trees. Phys. Rev. Lett. 2008;101:037208. doi: 10.1103/PhysRevLett.101.037208. [DOI] [PubMed] [Google Scholar]
- Ben-Shlomo I. Yu Hsu S. Rauch R., et al. Signaling receptome: a genomic and evolutionary perspective of plasma membrane receptors involved in signal transduction. Sci. STKE. 2003;2003 doi: 10.1126/stke.2003.187.re9. RE9. [DOI] [PubMed] [Google Scholar]
- Bhoite L.T. Allen J.M. Garcia E., et al. Mutations in the pho2 (bas2) transcription factor that differentially affect activation with its partner proteins bas1, pho4, and swi5. J. Biol. Chem. 2002;277:37612–8. doi: 10.1074/jbc.M206125200. [DOI] [PubMed] [Google Scholar]
- Breitkreutz A. Choi H. Sharom J.R., et al. A global protein kinase and phosphatase interaction network in yeast. Science. 2010;328:1043–6. doi: 10.1126/science.1176495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buehrer B.M. Errede B. Coordination of the mating and cell integrity mitogen-activated protein kinase pathways in Saccharomyces cerevisiae. Mol. Cell. Biol. 1997;17:6517–25. doi: 10.1128/mcb.17.11.6517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cancer Genome Atlas Research Network. Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature. 2008;455:1061–8. doi: 10.1038/nature07385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardona-Gomez G.P. Mendez P. DonCarlos L.L., et al. Interactions of estrogen and insulin-like growth factor-I in the brain: molecular mechanisms and functional implications. J. Steroid Biochem. Mol. Biol. 2002;83:211–7. doi: 10.1016/s0960-0760(02)00261-3. [DOI] [PubMed] [Google Scholar]
- Chakravarti A. Loeffler J.S. Dyson N.J. Insulin-like growth factor receptor I mediates resistance to anti-epidermal growth factor receptor therapy in primary human glioblastoma cells through continued activation of phosphoinositide 3-kinase signaling. Cancer Res. 2002;62:200–7. [PubMed] [Google Scholar]
- Chekuri C. Ene A. Korula N. Prize-Collecting Steiner Tree and Forest in Planar Graphs. Data Structures and Algorithms 2010 [Google Scholar]
- Clarke I.D. Dirks P.B. A human brain tumor-derived PDGFR-alpha deletion mutant is transforming. Oncogene. 2003;22:722–33. doi: 10.1038/sj.onc.1206160. [DOI] [PubMed] [Google Scholar]
- Dai C. Celestino J.C. Okada Y., et al. PDGF autocrine stimulation dedifferentiates cultured astrocytes and induces oligodendrogliomas and oligoastrocytomas from neural progenitors and astrocytes in vivo. Genes Dev. 2001;15:1913–25. doi: 10.1101/gad.903001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dittrich M.T. Klau G.W. Rosenwald A., et al. Identifying functional modules in protein-protein interaction networks: an integrated exact approach. Bioinformatics. 2008;24:i223–31. doi: 10.1093/bioinformatics/btn161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman N. Inferring cellular networks using probabilistic graphical models. Science. 2004;303:799–805. doi: 10.1126/science.1094068. [DOI] [PubMed] [Google Scholar]
- Garcia R. Bermejo C. Grau C., et al. The global transcriptional response to transient cell wall damage in Saccharomyces cerevisiae and its regulation by the cell integrity signaling pathway. J. Biol. Chem. 2004;279:15183–95. doi: 10.1074/jbc.M312954200. [DOI] [PubMed] [Google Scholar]
- Gruhler A. Olsen J.V. Mohammed S., et al. Quantitative phosphoproteomics applied to the yeast pheromone signaling pathway. Mol. Cell. Proteomics. 2005;4:310–27. doi: 10.1074/mcp.M400219-MCP200. [DOI] [PubMed] [Google Scholar]
- Gupta A. Konemann J. Leonardi S., et al. An efficient cost-sharing mechanism for the prize-collecting Steiner forest problem. SODA '07 Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms.2007. [Google Scholar]
- Huang P.H. Mukasa A. Bonavia R., et al. Quantitative analysis of EGFRvIII cellular signaling networks reveals a combinatorial therapeutic strategy for glioblastoma. Proc. Natl. Acad. Sci. U.S.A. 2007;104:12867–72. doi: 10.1073/pnas.0705158104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S.S. Fraenkel E. Integrating proteomic, transcriptional, and interactome data reveals hidden components of signaling and regulatory networks. Sci. Signal. 2009;2:ra40. doi: 10.1126/scisignal.2000350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Issel-Tarver L. Christie K.R. Dolinski K., et al. Saccharomyces Genome Database. Methods Enzymol. 2002;350:329–46. doi: 10.1016/s0076-6879(02)50972-1. [DOI] [PubMed] [Google Scholar]
- Jensen L.J. Kuhn M. Stark M., et al. STRING 8–a global view on proteins and their functional interactions in 630 organisms. Nucleic Acids Res. 2009;37:D412–6. doi: 10.1093/nar/gkn760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaffman A. Rank N.M. O'Shea E.K. Phosphorylation regulates association of the transcription factor Pho4 with its import receptor Pse1/Kap121. Genes Dev. 1998;12:2673–83. doi: 10.1101/gad.12.17.2673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaur B. Cork S.M. Sandberg E.M., et al. Vasculostatin inhibits intracranial glioma growth and negatively regulates in vivo angiogenesis through a CD36-dependent mechanism. Cancer Res. 2009;69:1212–20. doi: 10.1158/0008-5472.CAN-08-1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiaris H. Schally A.V. Varga J.L. Antagonists of growth hormone-releasing hormone inhibit the growth of U-87MG human glioblastoma in nude mice. Neoplasia. 2000;2:242–50. doi: 10.1038/sj.neo.7900074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.A. Wuchty S. Przytycka T.M. Identifying causal genes and dysregulated pathways in complex diseases. PLoS Comput. Biol. 2011;7:e1001095. doi: 10.1371/journal.pcbi.1001095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan A. Smoly I.Y. Rapaport G., et al. ResponseNet: revealing signaling and regulatory networks linking genetic and transcriptomic screening data. Nucleic Acids Res. 2011;39:W424–W429. doi: 10.1093/nar/gkr359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y. Li A. Glas M., et al. c-Met signaling induces a reprogramming network and supports the glioblastoma stem-like phenotype. Proc. Natl. Acad. Sci. U.S.A. 2011;108:9951–6. doi: 10.1073/pnas.1016912108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ljubic I. Weiskircher R. Pferschy U., et al. An algorithmic framework for the exact solution of the Prize-Collecting Steiner Tree Problem. Mathematical Programming. 2006;105:427–449. [Google Scholar]
- Macaulay V.M. The IGF receptor as anticancer treatment target. Novartis Found Symp. 2004;262:235–43. discussion 243–6, 265–8. [PubMed] [Google Scholar]
- Maere S. Heymans K. Kuiper M. BiNGO: a Cytoscape plugin to assess overrepresentation of gene ontology categories in biological networks. Bioinformatics. 2005;21:3448–9. doi: 10.1093/bioinformatics/bti551. [DOI] [PubMed] [Google Scholar]
- Missiuro P.V. Liu K. Zou L., et al. Information flow analysis of interactome networks. PLoS Comput Biol. 2009;5:e1000350. doi: 10.1371/journal.pcbi.1000350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ourfali O. Shlomi T. Ideker T., et al. SPINE: a framework for signaling-regulatory pathway inference from cause-effect experiments. Bioinformatics. 2007;23:i359–66. doi: 10.1093/bioinformatics/btm170. [DOI] [PubMed] [Google Scholar]
- Shannon P. Markiel A. Ozier O., et al. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13:2498–504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharan R. Ideker T. Modeling cellular machinery through biological network comparison. Nat. Biotechnol. 2006;24:427–33. doi: 10.1038/nbt1196. [DOI] [PubMed] [Google Scholar]
- Silverstein R.L. Febbraio M. CD36, a scavenger receptor involved in immunity, metabolism, angiogenesis, and behavior. Sci. Signal. 2009;2:re3. doi: 10.1126/scisignal.272re3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suthram S. Beyer A. Karp R.M., et al. eQED: an efficient method for interpreting eQTL associations using protein networks. Mol. Syst. Biol. 2008;4:162. doi: 10.1038/msb.2008.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhrbom L. Hesselager G. Nister M., et al. Induction of brain tumors in mice using a recombinant platelet-derived growth factor B-chain retrovirus. Cancer Res. 1998;58:5275–9. [PubMed] [Google Scholar]
- Vanunu O. Magger O. Ruppin E., et al. Associating genes and protein complexes with disease via network propagation. PLoS Comput. Biol. 2010;6:e1000641. doi: 10.1371/journal.pcbi.1000641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeang C.H. Ideker T. Jaakkola T. Physical network models. J. Comput. Biol. 2004;11:243–62. doi: 10.1089/1066527041410382. [DOI] [PubMed] [Google Scholar]
- Yeger-Lotem E. Riva L. Su L.J., et al. Bridging high-throughput genetic and transcriptional data reveals cellular responses to alpha-synuclein toxicity. Nat. Genet. 2009;41:316–23. doi: 10.1038/ng.337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarzov P. Mazzoni C. Mann C. The SLT2(MPK1) MAP kinase is activated during periods of polarized cell growth in yeast. Embo. J. 1996;15:83–91. [PMC free article] [PubMed] [Google Scholar]
- Ziegler D.S. Wright R.D. Kesari S, et al. Resistance of human glioblastoma multiforme cells to growth factor inhibitors is overcome by blockade of inhibitor of apoptosis proteins. J. Clin. Invest. 2008;118:3109–22. doi: 10.1172/JCI34120. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.