Hap-seq: An Optimal Algorithm for Haplotype Phasing with Imputation Using Sequencing Data

Abstract

Inference of haplotypes, or the sequence of alleles along each chromosome, is a fundamental problem in genetics and is important for many analyses, including admixture mapping, identifying regions of identity by descent, and imputation. Traditionally, haplotypes are inferred from genotype data obtained from microarrays using information on population haplotype frequencies inferred from either a large sample of genotyped individuals or a reference dataset such as the HapMap. Since the availability of large reference datasets, modern approaches for haplotype phasing along these lines are closely related to imputation methods. When applied to data obtained from sequencing studies, a straightforward way to obtain haplotypes is to first infer genotypes from the sequence data and then apply an imputation method. However, this approach does not take into account that alleles on the same sequence read originate from the same chromosome. Haplotype assembly approaches take advantage of this insight and predict haplotypes by assigning the reads to chromosomes in such a way that minimizes the number of conflicts between the reads and the predicted haplotypes. Unfortunately, assembly approaches require very high sequencing coverage and are usually not able to fully reconstruct the haplotypes. In this work, we present a novel approach, Hap-seq, which is simultaneously an imputation and assembly method that combines information from a reference dataset with the information from the reads using a likelihood framework. Our method applies a dynamic programming algorithm to identify the predicted haplotype, which maximizes the joint likelihood of the haplotype with respect to the reference dataset and the haplotype with respect to the observed reads. We show that our method requires only low sequencing coverage and can reconstruct haplotypes containing both common and rare alleles with higher accuracy compared to the state-of-the-art imputation methods.

1. Introduction

Haplotype, or the sequence of alleles along each chromosome, is the fundamental unit of genetic variation, and inference of haplotypes is an important step in many analyses, including admixture mapping (Patterson et al., 2004), identifying regions of identity by descent (Gusev et al., 2009; Browning and Browning, 2010, 2011), imputation of uncollected genetic variation (Marchini et al., 2007; Li et al., 2010; Kang et al., 2010), and association studies (Beckmann, 2010). It is possible to use molecular methods for obtaining haplotypes (Patil et al., 2001), but they are expensive and not amenable to high throughput technologies. For this reason, most studies collect genotype information and infer haplotypes from genotypes, referred to as haplotype inference or haplotype phasing. One strategy for haplotype phasing is to collect mother-father-child trios and use the Mendelian inheritance patterns. However, this strategy is limited to related individuals.

Over the past two decades, there has been great interest in inference of haplotypes from genotypes of unrelated individuals (Clark, 1990). Traditionally, these methods were applied to genotypes of a cohort of individuals and utilized the insight that in each region a few haplotypes accounted for the majority of genetic variation. Using this insight, these methods identified the common haplotypes and used them to infer the haplotypes for each individual in the cohort (Stephens et al., 2001; Eskin et al., 2003; Gusfield, 2003; Halperin and Eskin, 2004; Browning and Browning, 2007). More recently, large reference datasets of genetic variation such as the HapMap (International HapMap Consortium, 2007) and 1000 Genomes (1000 Genomes Project, 2010) have become available, enabling a new class of methods, referred to as imputation methods (Marchini et al., 2007; Kang et al., 2010, Li et al., 2010). These use the information in the haplotypes in the reference datasets to both predict haplotypes from genotypes as well as predict the genotypes at uncollected variants. Since these methods use the reference datasets, they are able to infer haplotypes from a single individual's genotypes.

Recent advances in high-throughput sequencing have dramatically reduced the cost of obtaining sequencing information from individuals (Wheeler et al., 2008). One advantage of this data compared to microarray genotypes is that this information contains data on both common and rare variants. The initial approaches to inferring haplotypes from sequence data first infers genotype data from the sequencing data and then applies an imputation algorithm (Li et al., 2010). Unfortunately, since variants that are very rare or unique to an individual are not present in the reference datasets, phase information for these variants can not be recovered using this approach.

This commonly applied approach does not take into account an important source of information for haplotype inference. Each sequence read originates from a single chromosome, and alleles spanned by that read are on the same haplotype. A set of methods referred to as haplotype assembly methods (Levy et al., 2007; Bansal et al., 2008; Bansal and Bafna, 2008) have been developed around this idea. Since many reads overlap each other, these methods infer haplotypes by partitioning the reads into two sets corresponding to chromosomal origin in such a way that the number of conflicts between the reads and the predicted haplotypes is minimized. Recently, a dynamic programming method has been proposed, which obtains the optimal haplotype prediction from a set of reads (He et al., 2010). These methods worked well for sequencing studies in which the sequencing coverage is high and the reads are long (Levy et al., 2007) but perform very poorly for studies in which the sequencing coverage is low or the reads are short.

In this article, we propose a new method for haplotype inference from sequencing reads, Hap-seq, which combines information from a reference dataset with the information from the reads. We formulate the problem of haplotype inference using a likelihood framework. We use a hidden Markov model (HMM) to represent the likelihood model of the predicted haplotypes given the reference datasets, which is similar to imputation methods (Marchini et al., 2007; Kang et al., 2010; Li et al., 2010), and we compute the posterior probability of the predicted haplotypes given the reads averaging over all possible assignments of the reads to chromosomal origin. Since consistency with the reference dataset and the read errors are independent, our joint likelihood is the product of these likelihoods. We present a dynamic programming algorithm for predicting the optimal haplotypes under this joint likelihood. This dynamic programming algorithm nests the dynamic programming algorithm over the reads with a dynamic programming algorithm over the reference haplotypes.

Through simulations generated from the HapMap data (International HapMap Consortium, 2007), we show that our method significantly outperforms traditional imputation methods. We show that using our method, haplotypes can be accurately inferred using 1X coverage assuming a 0.01 error rate. Hap-seq achieved a 2.79% switch error rate, which is a 15% improvement over the number of switch errors over the state-of-the-art haplotype imputation algorithm. In addition, our method is the first practical method for predicting haplotypes for rare variants.

2. Likelihood Model

2.1. Overview

Previous methods for haplotype assembly (He et al., 2010) focused on finding the haplotype and the assignment of reads to each haplotype such that the number of conflicts between the reads and the predicted haplotypes is minimized. In our framework, we formulate the same intuition by computing the likelihood of a pair of haplotypes as the probability of the reads, given the haplotypes using a simple error model averaged over all possible partitions of the reads into chromosomal origin. Thus, we compute the likelihood with respect to the reads

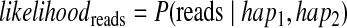where hap₁ and hap₂ are the (unknown) haplotypes of an individual.

We also take into account information from the reference dataset. We compute the probability of a pair of haplotypes in which each haplotype is represented as a mosaic of reference haplotypes, which is the standard HMM model for imputation. Thus, we compute the likelihood with respect to the reference dataset, or the imputation likelihood,

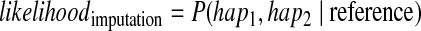Figure 1 shows the two types of data, sequencing reads and reference dataset. Since these two types of data are independent, we represent the likelihood of a haplotype given the reads and the reference dataset by the joint likelihood, which is the product of the two likelihoods

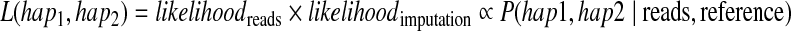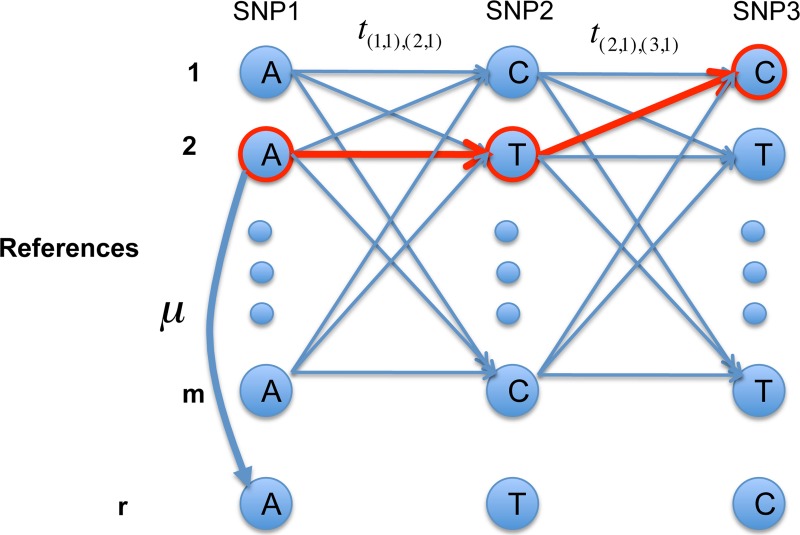
FIG. 1.

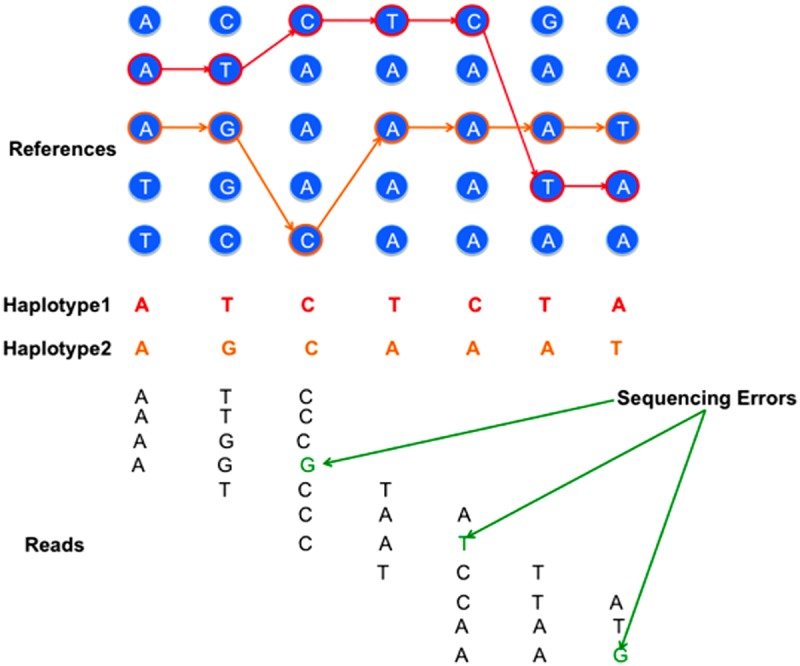
An illustration of reconstructing the pair of haplotypes as well as the imputation paths for each haplotype given a set of reference sequences and a set of sequencing reads that contains errors.

Our goal is to reconstruct a pair of haplotypes hap₁, hap₂ such that this likelihood is maximized. We call this objective function MIR (Most likely Imputation based on Reads).

2.2. Likelihood with respect to sequence reads

We will follow the notation by He et al. (2010) for the haplotype assembly problem. Given a reference genome sequence and the set of reads containing sequence from both chromosomes, we align all the reads to the reference genome. However, unlike the haplotype assembly problem, where the homozygous sites (columns in the alignment with identical values) are discarded, we need to maintain the homozygous sites that are polymorphic in the reference as well as the heterozygous sites (columns in the alignment with different values). The sites are labeled as 0 or 1 arbitrarily.

A matrix X of size m × n can be built from the alignment, where m is the number of reads and n is the number of SNPs (defined as the total number of positions that are either polymorphic sites in the reference and/or heterozygous in the sample). The i-th read is described as a ternary string 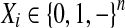, where “−” indicates a gap, namely that the allele is not covered by the fragment (again following the notation of He et al. [2010] for clarity). The start position and end position of a read are the first and last positions in the corresponding row that are not “−”, respectively. Therefore the “−”s in the head and tail of each row will not be considered as part of the corresponding read. However, there can be “−”s inside each read that correspond to either missing data for single reads or gaps connecting a pair of single reads (called paired-end reads). Reads without “−” are called gapless reads; otherwise they are called gapped reads. An example of the read matrix is shown in Table 1. As we can see, read5 is of length 4 and read6 is of length 9.

Table 1.

An Example of Read Matrix that Consists of 10 Reads Spanning 13 SNP Positions

Reads	0	1	2	3	4	5	6	7	8	9	10	11	12
Read1	0	1	-	-	-	-	-	-	-	-	-	-	-
Read2	-	-	1	1	-	-	-	-	-	-	-	-	-
Read3	1	0	0	0	-	-	-	-	-	-	-	-	-
Read4	-	-	1	0	1	-	-	-	-	-	-	-	-
Read5	-	-	0	-	-	0	-	-	-	-	-	-	-
Read6	-	-	-	0	-	-	-	-	-	-	1	1	-
Read7	-	-	-	-	1	0	0	-	-	-	-	-	-
Read8	-	-	-	-	0	1	1	0	-	-	-	-	-
Read9	-	-	-	-	-	-	-	-	1	1	-	-	-
Read10	-	-	-	-	-	-	-	1	0	0	-	-	0

The goal here is to describe our likelihood model of haplotypes with respect to reads. For this purpose, we should first describe the notion of a partial haplotype, which will be the unit of computation in our dynamic programming algorithm. Partial haplotypes are the prefix of full-length haplotypes that end with a suffix r of length k and the suffix starting position is i. For example, consider a full-length haplotype “00010100010.” When i = 4 and k = 4, the partial haplotype “0001010” has suffix r = “1010.” Similarly, r = “0100” is the suffix of the partial haplotype “00010100” when i = 5 and k = 4. Since there are two chromosomes, we must consider two partial haplotypes, and we refer to their two suffixes as r₁ and r₂. We note a difference from the haplotype assembly problem described in He et al. (2010), where r₁ and r₂ are always complementary because only heterozygous sites are considered. However, in our problem, we consider both homozygous sites and heterozygous sites and therefore r₁ and r₂ are not necessarily complementary.

Let H(i, r₁) and H(i, r₂) be the set of partial haplotypes that end with suffix r₁ and r₂ starting at position i, respectively. These sets contain 2ⁱ⁻¹ haplotypes. We define R(i, r₁, r₂) as the likelihood of the reads with starting position no greater than i that are generated from the pair of partial haplotypes 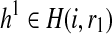and 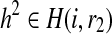, which maximizes the likelihood of the reads. The key idea behind our approach is that we will use dynamic programming to compute this quantity for larger and larger values of i, eventually allowing us to identify complete haplotypes with the highest likelihood.

Since reads are independent, we can decompose our computation of R(i, r₁, r₂) into the likelihood with respect to the reads starting at each position. Let R′(i, r₁, r₂) be the likelihood only for the reads starting at position i. For every position, we assume the reads span at most k sites; thus, all partial haplotypes with the same suffixes r₁, r₂ starting at position i ( 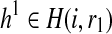and 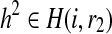) will have the same value for R′(i, r₁, r₂). Each read can originate from only one of the chromosomes corresponding to either r₁ or r₂. Since we do not know the origin of the reads, we consider all possible partitions of the reads. In each partition, a read is assigned to either r₁ or r₂ but not both. We can compute the number of mismatches between the reads and r₁ and r₂ and compute a likelihood given a partition using the following:

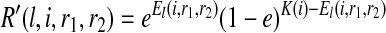(1)

where R′(l, i, r₁, r₂) is the likelihood corresponding to the l-th partition and E_l(i, r₁, r₂) is the number of mismatches for the l-th partition, K(i) is the total count of the alleles of all reads starting at position i, and e is the sequencing error rate. R′(i, r₁, r₂) is sum of the likelihoods of all the partitions weighted by the probability of each partition, namely

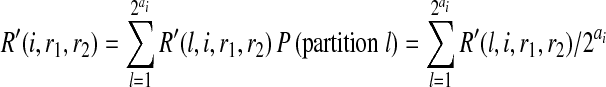(2)

assuming there are totally a_i reads starting at position i, 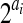is the total number of possible partitions and the probability of each partition is equal to .

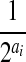Consider the two complete haplotypes 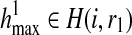and 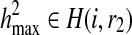that maximize the likelihood of the reads and by definition, their likelihood is R(i, r₁, r₂). For these haplotypes, R and R′ have the following relationship:

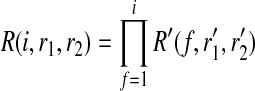(3)

where 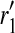and 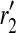are length k suffixes of the partial haplotypes of 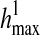and 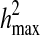with suffix starting position f.

R′ is computed for every possible suffix at each position of the dynamic programming. The dynamic programing uses the value of R′(i, r₁, r₂) and the four values of R(i − 1, x, y), where the suffix of x is a prefix of r₁ and the suffix of y is a prefix of r₂, to compute R(i, r₁, r₂) (see He et al., 2010, for details). For high sequencing coverage, we can compute just the likelihood of the most likely partition that approximates Equation (2).

2.3. Likelihood with respect to reference dataset

We use an HMM model, which is the basis of the widely used imputation methods (Marchini et al., 2007; Kang et al., 2010; Li et al., 2010). Given a binary string r, in the HMM, for each SNP at position i, we consider the HMM state with value S_i,j corresponding to the j-th reference haplotype h_j, where 1 ≤ j ≤ m. We define the transition probability from the state S_i,j to the state S_i+1,y as t_{(i,j),(i+1,y)} where 1 ≤ y ≤ m. We assume that t_{(i, j), (i+1, y)} is the same for all y ≠ j. (Once the transition occurs, the transition probabilities to all possible states are equal.) We also define the emission probability from the state S_i, j to the observed i-th SNP r[i] as μ_i, j. The emission probability models the mutations, and we assume that the mutation rate for all the SNPs are the same. The emission probability μ_i, j is defined as the following:

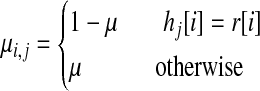where μ is the mutation rate. In this work, we assume we know the mutation rate and the transition probabilities. An example of the HMM is shown in Figure 2.

FIG. 2.

Example to illustrate the hidden Markov model (HMM). There are in total m reference sequences and 3 SNP locus. The given string r is “ATC,” and the optimal imputation path is highlighted in red.

Since we assume that we know μ as well as all t_{(i,j),(i+1,y)}'s, the most likely state sequence can be obtained by the Viterbi algorithm. We can also use the HMM to compute the likelihood of a partial haplotype. We define r as a length k binary string and l(i, r, j) as the imputation likelihood of the partial haplotypes starting at position 0 and ending at position i + k − 1, with suffix r, and whose imputation at position i + k − 1 (the last position) is from the j-th reference sequence. Also, l(i, r, j) is the maximum value among many possible partial haplotypes having the same suffix r and the same ending HMM state S_i, j. Let h_{l(i, r, j)} be the partial haplotype that maximized l(I, r, j), which can be traced back in the dynamic programming algorithm.

3. Hap-Seq

A naive algorithm to optimize MIR is to enumerate all possible pair of haplotypes and compute the likelihood, which requires time complexity O(4ⁿ), where n is the length of the haplotypes. Then for each pair, identify the number of mismatches between the reads and the haplotypes to compute the likelihood of the reads. After that, run the HMM to compute the likelihood of the imputation for both haplotypes. The complexity of this naive algorithm is obviously prohibitively large even for small n.

As the haplotype assembly problem can be optimally solved with a dynamic programming algorithm (He et al., 2010), and the imputation problem can be optimally solved using an HMM, we next propose a hybrid method combining a dynamic programming algorithm and an HMM, and we refer to the method as Hap-seq. The basic idea is to use a dynamic programming algorithm operating on partial haplotypes with suffixes r₁, r₂, which are the prefixes of full-length haplotypes similar to our algorithm for reconstructing haplotypes that maximize the likelihood of the reads. However, for each suffix, we also introduce a state encoding the current reference haplotype. Similar to the approach above, at each position we compute the likelihood of reads starting at the position. We also use an HMM to compute the likelihood of imputation for the partial haplotypes using the information on the reference state. For each position i, we store the MIRs corresponding to different partial haplotype suffixes and imputation states in the dynamic programming matrix. Then we compute the MIR values for position i + 1 using the previous values and repeat this process until we obtain the full-length haplotypes. To compute the MIRs for position i + 1 when extending the partial haplotypes, the MIR for the partial haplotypes from the previous position (i) is used in addition to the likelihood of reads for the new partial haplotypes (reads starting at position i + 1), and an HMM is used to compute the imputation likelihood for the extended partial haplotypes. The new MIR for the partial haplotypes is then the product of the three values (likelihood from previous step, imputation likelihood, and likelihood with respect to reads). We next discuss our Hap-seq algorithm in more details.

We define MIR(i, r₁, r₂, j₁, j₂) as the value of the MIR for the set of reads with starting positions no greater than i and the pair of partial haplotypes with suffix r₁, r₂, respectively, where the current references in the imputation model at position i + k − 1 are the j₁-th and j₂-th reference sequences, respectively. We also define MIR_max(i, r₁, r₂) as the maximum MIR for 1 ≤ j₁,j₂ ≤ m given m haplotypes in the reference dataset.

We build a dynamic programming matrix and at each position i we store MIR(i, r₁, r₂, j₁, j₂) for all r₁, r₂ and 1 ≤ j₁, j₂ ≤ m, respectively. For each pair of r₁, r₂, we call the HMM to compute the likelihood of the imputation l(i, r₁, j₁) and l(i, r₂, j₂). MIR at position i can be computed as

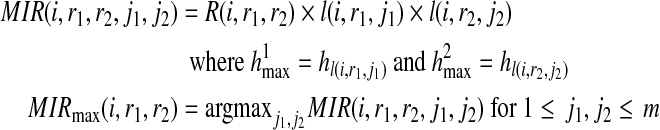The best MIR is the maximum MIR_max(n − k, r₁, r₂) over all r₁, r₂, where n is the full length of the haplotypes.

The objective function contains terms R(i, r₁, r₂), l(i, r₁, j₁), and l(i, r₂, j₂), each of which is a maximum likelihood value maximized by finding the corresponding haplotypes (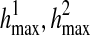), h_{l(i, r1, j1)}, and h_{l(i, r2, j2)} respectively. It should be noted that in our definition, we constrain the problem using the condition 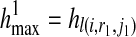and 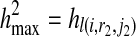, which forces the same haplotypes in each of the terms R(i, r₁, r₂), l(i, r₁, j₁), and l(i, r₂, j₂). Thus, we are searching for a single pair of haplotypes (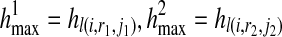) that maximize the product of these three terms.

We initialize MIR(0, r₁, r₂, j₁, j₂) by considering the reads starting at position 0. Given r₁, r₂, the HMM is called to compute the optimal likelihood l(0, r₁, j₁), l(0, r₂, j₂) for the imputation of r₁, r₂, respectively. Then MIR(0, r₁, r₂, j₁, j₂) = R(0, r₁, r₂) × l(0, r₁, j₁) × l(0, r₂, j₂) for 1 ≤ j₁, j₂ ≤ m.

3.1. Transition probability

The partial haplotypes at position i can be obtained by extending the partial haplotypes at position i − 1 with either a 0 or 1, as we consider homozygous sites and heterozygous sites. At position i, we again enumerate all length k binary strings for r₁ and r₂. Given a binary string r, l(i, r, j) is obtained by calling an HMM on the j-th reference haplotype to find the likelihood for the imputation of the suffix r ending at position i + k − 1. In the HMM, since we need to consider both haplotypes at the same time, we build a state for each SNP that contains m² different values as S _{(r1,r2), (i+k,j1,j2)} at position i + k of the j₁-th and j₂-th reference haplotype h_j1, h_j2, where 1 ≤ j₁, j₂ ≤ m for all pairs of partial haplotypes with suffix r₁ and r₂, respectively. We define the transition probability from the state with value 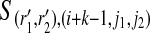to the state with value S_{(r1, r2),(i+k, f1, f2)}, where 1 ≤ f₁, f₂, j₁, j₂ ≤ m as t_(i+k−1,j1,_{j2),(i+k,f1,f2)}. As the assignment of the two partial haplotypes to the reference haplotypes are independent, we obtain the following formula:

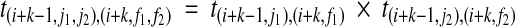where t_(i+k−1,j1),_(i+k,f1) and t_{(i+k−1,j2),(i+k,f2)} are the standard transition probabilities used in imputation methods. We assume t_{(i+k−1,j),(i+k,f)} is the same for all 1 ≤ f, j ≤ m, f ≠ j for all possible r₁'s and r₂'s. 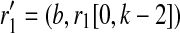where b is 0 or 1. The brackets [x, y] denote a substring starting from x and ending at y, both ends inclusive, where the index count starts from 0. A tuple of two strings denotes concatenation. Similarly, 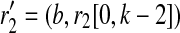where b is 0 or 1. For example, for k = 4, r₁ = “0000,” r₁′ = “1000,” we then have .

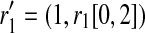3.2. Emission probability

We also define the emission probability from the state with value S_{(r1,r2),(i+k−1,j1,j2)} to the k-th observed SNPs in r₁,r₂, r₁[k − 1],r₂[k − 1], as μ_{(r1,r2),(i+k−1,j1,j2)}. Since the emissions from the two partial haplotypes are independent, we have the following formula:

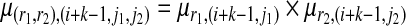The emission probability is defined using the mutation rate, and we assume the mutation rate for all SNPs is the same. The emission probability μ_{r,(i+k−1,j)} is defined as follows:

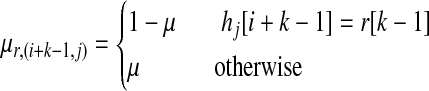where μ is the mutation rate, which is the same for all SNPs. Therefore if the two SNPs are identical, the emission probability is 1 − μ, otherwise it is μ. We assume the mutation rate and transition probabilities are known.

3.3. Recursions

Given the transition and emission probabilities, the MIR at position i for partial haplotypes with suffix r₁, r₂ is computed as the following:

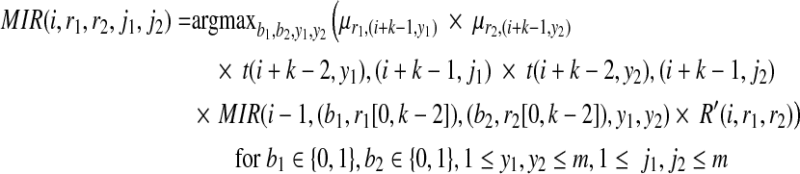which allows us to compute MIR_max(i, r₁, r₂) for each i for every r₁, r₂.

3.4. Complexity

The complexity of the Hap-seq algorithm is O(n × m⁴ × 4^k) where 4^k is from the enumeration of all pairs of length-k binary strings and m⁴ is from the HMM model on the m reference sequences, which is known to be reduced to m² by pre-computing and saving the transition probabilities (Li et al., 2010). Therefore, the complexity of Hap-seq is O(n × m² × 4^k), and typically m for imputation algorithms is around 100, for which Hap-seq is computationally feasible.

3.5. Read length

At each position, we enumerate all possible binary strings of length k, where k is the maximum number of SNPs the reads contain. Since the SNPs are usually far from each other, k is small. In our experiments, 99% of the reads contains no greater than three SNPs. Therefore, we set a threshold as k = 3. For reads containing more than three SNPs, we simply split them. For example, for a read “0001000” starting at position 0, we split it as “000” starting at position 0, “100” starting at position 3, and “0” starting at position 6. We show later in our experiments with k = 3 that Hap-seq can finish quickly.

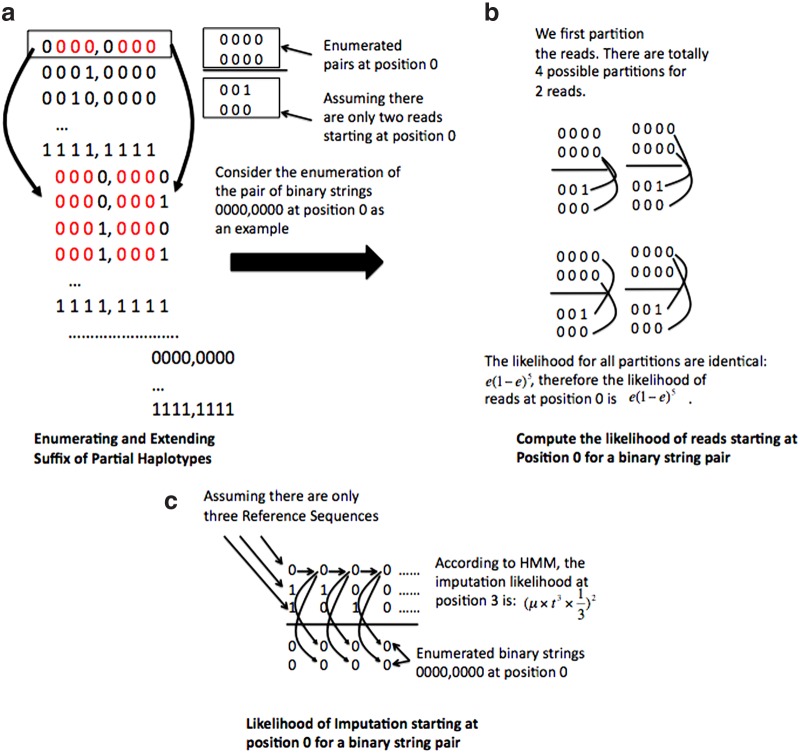
3.6. Illustrative example

For illustrative purpose, we show a running example of our Hap-seq algorithm in Figure 3. In Figure 3a, we show when k = 4, how we enumerate all length-4 binary strings at each position as suffixes of partial haplotypes and extend the suffix by one bit each time till the end of the haplotypes. As shown in the red color, the suffix of a binary string is identical to the prefix of the binary strings extended from it. In Figure 3b and c, we consider a pair of enumerated length-4 strings (0000, 0000) at position 0 as an example. We assume there are only two reads (001, 000) starting at position 0. In 3b, we compute the likelihood of these two reads by considering all four possible partitions. The likelihood is computed according to Equation (2). In 3c, we assume there are only three reference sequences. We apply HMM to compute the imputation likelihood for the pair of length-4 binary strings (0000,0000) at position 0. It is obvious that the best imputation path for both binary strings is through the first reference sequence without transition to other reference sequences. Then MIR(0, 0000, 0000) = MIR(0, 0000, 0000, 1, 1), which is simply the product of the two likelihoods: .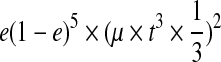

FIG. 3.

Example to illustrate the Hap-seq algorithm.

Next at position 1 (we do not show this step in the above figure), assuming we enumerate two binary strings as (0001, 0001), we can compute the likelihood R′(1, 0001, 0001) of reads starting at position 1 by considering all possible partitions similar to the one shown in Figure 3. Since 0000 = (0, 0001[0,2]), 1000 = (1, 0001[0,2]), we can then compute the new MIR at position 1 as follows:

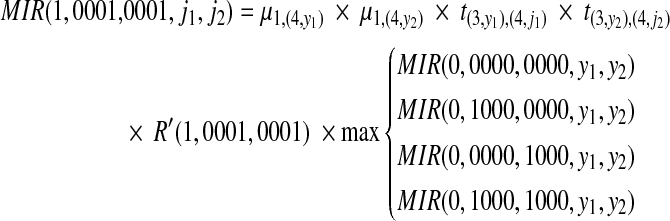where 1 ≤ j₁, j₂ ≤ 3 and 1 ≤ y₁, y₂ ≤ 3. Then MIR_max(1, 0001, 0001) = argmax_{1≤j1, j2≤3}MIR(1, 0001, 0001, j₁, j₂). We repeat the recursive procedure till we reach position n – 4, where n is the length of the full haplotypes.

3.7. Relationship to previous methods

Our method Hap-seq has a relationship to the standard imputation methods dealing with sequence reads in that the standard methods are a special case of our method. The standard methods such as MACH (Li et al., 2010) ignore the fact that alleles on the same sequence read originate from the same chromosome. Instead, the reads are split into SNP-wise information, where at each SNP we count how many times we observe 0 and 1. Then, the likelihood of the reads given a pair of haploytpes is modeled using a binomial distribution (Li et al., 2010).

Suppose a special case of our method such that we limit the read length k to 1. Then, r₁ and r₂ in Equation (1) corresponds to single allele 0 or 1. We can rewrite Equation (1)

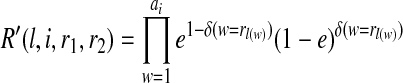where w iterates all a_i single-allele reads at SNP i, l(w) is the haplotype number that w is assigned in partition l (either 1 or 2), and δ() is the indicator function. Then the 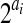terms in R′(i, r₁, r₂) in Equation (2) can be factorized into the product of a_i terms,

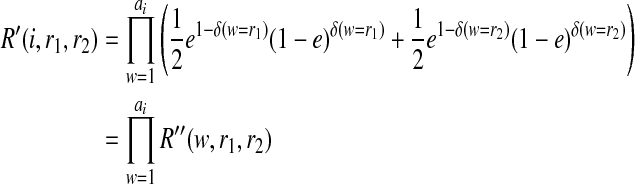Consider the case that r₁ = r₂ = 1. Then, R″(w, r₁, r₂) = e if w = 0 and (1−e) if w = 1. Thus,

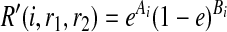where A are B are the counts how many times we observe 0 and 1 in the reads at SNP i respectively. Similarly, if r₁ = r₂ = 0, 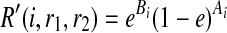. Now consider the case that r₁ ≠ r₂. Then, R″(w, r₁, r₂) = 1/2 regardless of w, and therefore .

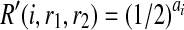Hence, the likelihoods of the reads at SNP i are equivalent to

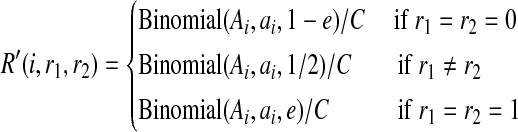which is exactly the same formulation of the probabilities of the observations presented in Li et al (2010), with only difference being the constant term 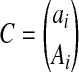. This constant term is due to whether we consider the reads ordered or unordered and does not affect the computation results. Consequently, the standard imputation method can be considered a special case of our method where the read length is limited to 1.

4. Experimental Results

We perform simulation experiments to compare the performance of our Hap-seq algorithm and the standard HMM. The implementations of the two methods are as follows. The standard HMM is our own implementation of the IMPUTE v1.0 model, which uses the pre-defined genetic map information for the transition probability. We use the genetic map data downloaded from the IMPUTE website. Since IMPUTE does not accept sequence read data, we allow our own implementation to accept sequence read by splitting the reads into SNP-wise information similarly to MACH (Li et al., 2010). Our implementation runs the Viterbi algorithm and gives the most likely haplotype phasing based on the IMPUTE model. To make a fair comparison, for the part of Hap-seq that computes the imputation likelihood, we use the same IMPUTE v1.0 model using the same genetic map data.

We use 60 parental individuals of CEU population of HapMap Phase II data downloaded from the HapMap website. We perform a leave-one-out experiment to measure the accuracy of our method. We choose one target individual, generate simulated sequence reads, and infer the genotypes and phasing of the target individual using the 59 individuals as the reference data set. We repeat this for all 60 individuals and the results are averaged. When we generate the data, we use the per-allele sequencing error rate of 1%. We assume that both IMPUTE and Hap-seq know the true error rate. In all datasets we generate, we assume a low coverage of 1x. That is, all heterozygous sites will be covered by two reads on average, since there are two chromosomes.

The first dataset we generate is the short region of 1,000 SNP sites at the beginning of chromosome 22. This region is approximately 1.8 Mb in length. We make an unrealistic assumption that each read covers a fixed number (F) of SNPs. Although this assumption is unrealistic, in this setting the performance gain of our Hap-seq over IMPUTE will be the most prominent because every read will contain phasing information when F > 1. We generate data for F = 2, F = 3, and F = 4. The results of switch error rate, which is the proportion of consecutive heterozygote genotypes that are incorrectly phased, for both algorithms are shown in the left of Table 2. As we can see, Hap-seq makes significant improvements over IMPUTE with respect to the number of switch errors. As F increases, the improvement becomes more significant. This is because as F increases, splitting reads loses more information that the SNPs in the same reads are from the same haplotype. Therefore, Hap-seq has more advantages as the reads gets longer. One thing to note is that the accuracy of both methods drops at F = 3 compared to F = 2. This is because when F increases, the total number of reads decreases, which can result in some regions not effectively covered by the reads. This raises an interesting question of what are the optimal read length and coverage that maximize the imputation and phasing accuracy given a cost, which requires further investigation.

Table 2.

Averaged Switch error Rate and the Improvement of Hap-seq over IMPUTE

F	IMPUTE	Hap-seq	Improvement
2	6.7%	6.2%	7.4%
3	5.4%	4.9%	8.2%
4	7%	5.7%	12.4%

W	IMPUTE	Hap-seq	Improvement
100	5.36%	5.2%	2.8%
200	6.4%	6.25%	2.5%
500	7.2%	6.9%	3.5%
1000	7.8%	7.3%	6.5%

Vary the number of SNPs F in the reads. Vary the length of the reads W.

The second dataset we generate is the same 1,000-SNP region where we generate a more realistic simulated read that has a constant size (W) in bp. We vary W between 100, 200, 500, and 1,000 bp. Thus, the number of SNPs contained in the reads is not fixed and can vary. However, as the SNPs are far from each other, over 99% of the reads contain no greater than three SNPs. The results of switch error rate for both algorithms are shown in the right of Table 2. We again observe over 2.5% improvement of Hap-seq over IMPUTE. The improvement is less significant compared with the last dataset. This is because we do not fix the number of SNPs in the reads and thus there are many reads containing just one SNP. Hap-seq does not have any advantages over IMPUTE for these reads. We again observe a general increase in the improvement ratio when the read length increases.

Finally, we generate the paired-end read data of the whole chromosome 22, which contains 35,412 SNPs. We randomly select one individual and generate the paired-end sequence reads of size 1,000 bp in each end. The gap size is assumed to follow a normal distribution of mean 1,000 bp, and a standard deviation of 100 bp. Therefore, the number of SNPs contained in the reads can vary. We use 1X coverage, and around 99% of the reads contain no greater than three SNPs, out of which 74% of the reads contain a single SNP. In order to parallelize our algorithm, we conduct a simple strategy. We split the chromosome 22 into chunks containing 1,000 SNPs each and run Hap-seq on each chunk in parallel only using reads in the chunk. In order to concatenate the reconstructed haplotypes from adjacent chunks seamlessly, we overlap adjacent chunks with a buffer region containing 200 SNPs. Therefore, the first chunk covers locus [0, 1000], the second chunk covers locus [800, 2000], the third chunk covers locus [1800, 3000], and so on. Our intuition is that the haplotypes from adjacent chunks in the overlapped buffer region should be highly consistent with each other. Therefore, when we concatenate them, we select the best option that is able to minimize the differences between the haplotypes from adjacent chunks in the buffer region.

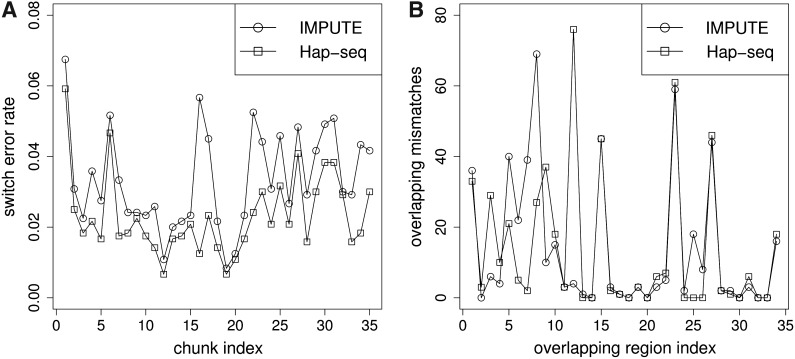
The program finished in nine hours on a cluster processing chromosome 22. We first compare the switch errors of Hap-seq and IMPUTE for each chunk containing 1,200 SNPs (the first and the last chunks contain different numbers of SNPs). As we can see in the left of Figure 4, it is obvious that for every chunk Hap-seq has lower switch error rate. For some chunks the improvement with respect to the number of switch errors is reduced by almost 80%. We also show the number of mismatches in the overlapping buffer regions for the haplotypes reconstructed by Hap-seq and IMPUTE in the right of Figure 4. We can see that although there are certain regions with relatively high inconsistencies, most of the buffer regions are highly consistent with mismatches close to 0. We then concatenate the haplotypes from all the chunks. After the concatenation, we obtain a 2.79% overall error rate for Hap-seq on the whole chromosome 22. Compared to the 3.28% overall error rate for IMPUTE, this is a 15% improvement with respect to the number of switch errors. This again indicates that our Hap-seq algorithm is more effective in reconstructing the haplotypes using sequencing reads compared to IMPUTE.

FIG. 4.

(A) The switch error rate when using IMPUTE and Hap-seq for each chunk of length 1,200 SNPs for whole chromosome 22. (B) The number of mismatches in the overlapping buffer regions for the haplotypes reconstructed by Hap-seq and IMPUTE.

5. Discussion

We have presented Hap-seq, a method for inferring haplotypes from sequencing data that takes into account both a population reference dataset as well as the information of alleles spanned by sequencing reads. Our method uses a dynamic programming approach to obtain the optimal haplotype prediction under a likelihood formulation of the haplotype inference problem.

Our approach is the first practical approach that can perform haplotype inference for both common and rare variants. The current imputation-based approaches that obtain genotype information from the sequencing and then apply imputation are ineffective for phasing rare variants. The reason is that reference datasets only contain common variants and since these are the only variants on the reference haplotypes, the variants that are unique to an individual can not be phased. Since our approach also uses read information, if a read is present in the data that spans a rare variant and a common variant, our method can recover the phase for the rare variant. To our knowledge, this is the first practical approach to phase rare variants.

Acknowledgments

D.H., B.H., and E.E. are supported by National Science Foundation grants 0513612, 0731455, 0729049, 0916676, and 1065276, and National Institutes of Health grants K25-HL080079, U01-DA024417, P01-HL30568, and PO1-HL28481. B.H. is supported by the Samsung Scholarship.

Disclosure Statement

The authors declare that no competing financial interests exist.