Median-Based Incremental Cost-Effectiveness Ratio (ICER)

Abstract

Cost-effectiveness analysis (CEA) is a type of economic evaluation that examines the costs and health outcomes of alternative strategies and has been extensively applied in health sciences. The incremental cost-effectiveness ratio (ICER), which represents the additional cost of one unit of outcome gained by one strategy compared with another, has become a popular methodology in CEA. Despite its popularity, limited attention has been paid to summary measures other than the mean for summarizing cost as well as effectiveness in the context of CEA. Although some apparent advantages of other central tendency measures such as median for cost data that are often highly skewed are well understood, thus far, the median has rarely been considered in the ICER. In this paper, we propose the median-based ICER, along with inferential procedures, and suggest that mean and median-based ICERs be considered together as complementary tools in CEA for informed decision making, acknowledging the pros and cons of each. If the mean and median-based CEAs are concordant, we may feel reasonably confident about the cost-effectiveness of an intervention, but if they provide different results, our confidence may need to be adjusted accordingly, pending further evidence.

1. Introduction

The economic burden of health care is a significant concern for all sectors of society. In response to the high cost of some interventions relative to their perceived benefits, individuals, businesses, and government are continually faced with difficult decisions regarding the allocation of health care resources. Not only is cost consciousness important, however; there is also a strong need to control health care costs and to consider which interventions produce the greatest value, based in part on an economic evaluation (Drummond et al., 2005; Gold et al., 1996).

Cost-effectiveness analysis (CEA) is a form of economic analysis that compares the expenditure and outcomes of two or more strategies for performing the same task. It has been popularly used in the health sciences over the past several decades, and, recently, the importance of cost analysis has been emphasized in the context of comparative effectiveness research and health care reform. Statistical methods for CEA have been developed, and a measure called the incremental cost-effectiveness ratio (ICER) has been widely adopted by researchers and policy makers (Weinstein and Stason, 1977). The ICER is expressed as the ratio of the difference in costs between two strategies to the difference in effectiveness. This one-dimensional summary measure can be interpreted as the cost of obtaining an extra unit of effectiveness, and it quantifies the trade-offs between patient outcomes gained and resources spent. The ICER threshold, often denoted by λ, may be understood as the upper limit of what society is willing to pay for an additional unit of health benefit (Blumenschein et al., 2001).

It does not take much time to realize, however, that there are not many analytic methods as controversial as the ICER, despite its popularity of usage. This is partly because ICER estimates can be highly variable or because the proper interpretation is not always straightforward (Briggs, 2000; Fan and Zhou, 2007; Fenwick, Claxton and Sculpher, 2001; Heitjan, Moskowitz and Whang, 1999b; Heshmat, 2003). The ICER has been calculated by using the mean for both cost and effectiveness measures, and other measures of central tendency have rarely been considered. The use of the mean is almost unanimously advocated primarily because the total cost can be directly computed from the mean, but not from alternative measures such as the median (Zhou, Melfi and Hui, 1997). Thus, the mean may better reflect the societal perspective because society must pay all costs incurred including a small proportion of very large ones (Siegel et al., 1996), and the mean-based ICER enjoys a solid theoretical foundation based on welfare economics (Garber and Phelps, 1997; Gardiner, Bradley and Huebner, 2000).

In general, however, costs are highly complicated data, and because the CEA can potentially have a great impact on our lives, it may well deserve more than one methodology and perspective. For severely skewed data, which are common in monetary data, the median is a simple and informative summary measure that is less sensitive to outliers or erroneous data. For instance, the median is more commonly reported than the mean in housing price, mortgage, and income/salary statistics. In the presence of a few high cost data, the median cost would be closer than the mean to what an ordinary individual would expect to spend. Moreover, the median is conventionally used in effectiveness analyses (e.g., median survival time) (Brookmeyer, 2005). For these reasons, the advantages of the median should not be ignored.

In this paper, we propose the median-based ICER and explain how to make statistical inference. We intend to provide systematic guidance on how to construct a confidence interval (CI) that can be used for the mean-based ICER as well as the median-based ICER, covering all possible scenarios in a unified fashion. Despite a substantial body of literature on the standard (i.e., mean-based) ICER, we believe that no systematic guidance has been provided, since different scenarios were investigated in different papers and a simplistic scenario has received the most attention (i.e., the NE scenario, see the next section). Based on our review of the literature, a considerable number of papers do not report CIs, and almost all of the reported CIs have closed intervals. So it is quite plausible that some or many researchers naively use standard (e.g., percentile-based) bootstrap methods regardless of the qualitatively different scenarios.

This paper is organized as follows: we explain statistical methods for estimation and inference of the mean and median-based ICERs in Section 2. These methods are applied to real data and the results are summarized in Section 3. Section 4 provides some discussions and concluding remarks.

2. Statistical Methods

Mean-based ICER

The ICER is defined as the ratio of the difference in costs between two competing strategies (e.g., a new intervention vs. a standard or no intervention) to the difference in effectiveness. Effectiveness is defined as a clinically meaningful event experienced by a patient such as survival time, quality-adjusted life years (QALYs), or symptom-reduced days, where a larger value generally implies a better outcome. As previously mentioned, cost and effectiveness are typically measured by the mean so the ICER is formulated as:

$${\mathit{ICER}}_{\mathit{mean}}=\frac{\mathit{mean}(C_1)-\mathit{mean}(C_2)}{\mathit{mean}(E_1)-\mathit{mean}(E_2)},$$

where C_i and E_i denote cost and effectiveness measures, respectively, for the i^th group (i=1,2), and mean(X) denotes the mean of variable X (Weinstein and Stason, 1977). The ICER_mean can be estimated by substituting the corresponding sample averages for the population means. [Remark: for simpler presentation, we will let the ICER represent both the population parameter and its estimator interchangeably.] Currently, several proposed inferential procedures for the ICER_mean are available, including those based on large sample normality assumptions and their nonparametric counterparts (Dinh and Zhou, 2006; Fan and Zhou, 2007; Gardiner et al., 2001; Wang and Zhao, 2008).

To improve asymptotic properties by symmetrizing a distribution, some researchers consider a log transformation and analyze the cost data on the log scale. However, certain limitations should be noted. Transformation produces less intuitive interpretations of the parameters involved or may entail back-transformation (Duan, 1983). Also, if the natural logarithm of a variable (X) is normally distributed with mean=μ and standard deviation (SD)=σ, then the mean of X is exp(μ+σ ²/2), whereas the median of X is exp(μ). It has been reported, in practice, that a wrong null hypothesis without accounting for skewness is frequently used in the t-test on log-transformed costs (Zhou et al., 1997). On the other hand, some compute the ICER_mean after excluding outliers or truncating the data. This can be subjective or result in a truncated or trimmed mean, whereas the median is robust in the presence or absence of extreme observations, preserving the original data/scale.

Median-based ICER

By applying the formula for the ICER_mean, we can calculate the median ICER:

$${\mathit{ICER}}_{\mathit{median}}=\frac{\mathit{median}(C_1)-\mathit{median}(C_2)}{\mathit{median}(E_1)-\mathit{median}(E_2)}.$$ (1)

Since the asymptotic distribution for the joint distribution of the difference between two median costs and the difference between two median effectiveness measures is inherently complicated, we propose the use of nonparametric methods to obtain a CI for the ICER_median via bootstrap sampling. The following method can be applied to the ICER_mean as well.

Confidence intervals for the median-based ICER

As a ratio, the ICER is neither a sufficient nor an unbiased statistic. Consequently, statistical inference can be complicated, and various methodological and practical issues have been documented for the standard, mean-based ICER (Chaudhary and Stearns, 1996; Dinh and Zhou, 2006; Gardiner, Sirbu and Rahbar, 2004; Heitjan, Moskowitz and Whang, 1999a; O’Brien and Briggs, 2002; Stinnett, 1996).

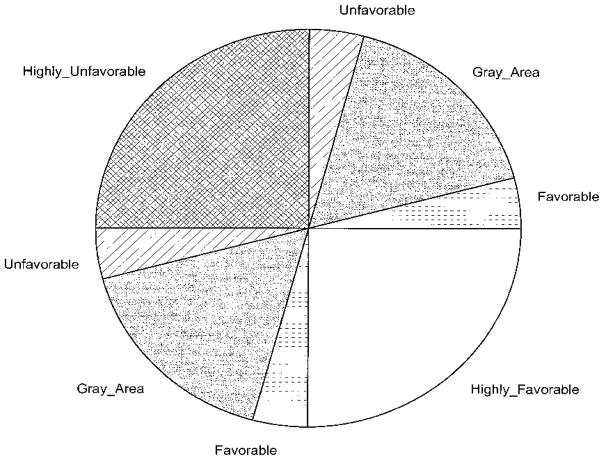
Perhaps, the best way of constructing a CI and interpreting it correctly is to plot the CE plane using bootstrap replicates. This offers a visual representation of the joint distribution and uncertainty (Black, 1990; Hwang, 1995; Jiang, Wu and Williams, 2000; O’Brien and Briggs, 2002; Wang and Zhao, 2008). To prevent misleading CIs, we strongly recommend that the CE plane be a prerequisite for statistical inference based on any ICER. The CE plane is formulated with the effectiveness difference as the x-axis and the cost difference as the y-axis, with the ICER represented by the slope. The plane can be divided into quadrants or regions representing different preference levels for comparing one intervention vs. another (O’Brien and Briggs, 2002; Obenchain, 1999) -see Appendix for five qualitatively different regions illustrating the full range of possible outcomes for a new vs. a standard treatment.

The CE plane can be constructed for both the mean-based and median-based ICERs. When the median-based ICER is concerned, each pair on the CE plane represents the difference of the median costs and the difference of the median effectiveness. The SE quadrant represents the situation when the new treatment is less costly and more effective, hence it is highly favorable. On the opposite side, in the NW quadrant, the new treatment is more costly and less effective, so it is highly unfavorable. In the NE quadrant, the new treatment is more costly and effective, hence, when the ICER (represents the tangent of the angle formed by the location of the pair of the difference in costs and the difference in effectiveness and the horizontal line) is small, the new treatment is still favorable, but when it is very large (i.e., closer to the vertical line), it is unfavorable. Between these two, there is a gray area where decision making can be less certain. Since the points in the SW quadrant represent the case when the new treatment is less costly and less effective, the ICER values in that quadrant have opposite meanings to the values in the NE quadrant despite the same sign, e.g., a larger ICER value in the SW quadrant means that the new treatment is more favorable. Note that a natural ordering of the negative ICERs in the SE and NW quadrants is not generally clear (O’Brien and Briggs, 2002; Obenchain and Sacristan, 1997; Stinnett and Mullahy, 1997) - instead, they represent the situation when the new treatment dominates (in SE) or when the standard treatment dominates (in NW).

The bootstrap samples for the median-based ICER can be generated and plotted in the CE plane by the following procedure, recapped below:

• Step 1: Sample the n₁ effectiveness-cost pairs (as correlated observations within subject) with replacement from the n₁ pairs in the treatment 1 arm. Compute the median effectiveness and the median cost.

• Step 2: Sample the n₂ effectiveness-cost pairs with replacement from the n₂ pairs in the treatment 2 arm. Compute the median effectiveness and the median cost.

• Step 3: Compute the ICER_median by plugging the sample medians into Eq.(1).

• Step 4: Repeat Step1 B-times to generate B sets of the bootstrap samples.

• Step 5: Plot each pair of values for the numerator and denominator of the ICER_median in the bootstrap samples on the CE plane.

Since the bootstrap samples can occupy from one to four quadrants (NE, NW, SE, SW) of the CE plane, great care should be taken when the CIs of the ICER_median are calculated.

1) One quadrant only

If the bootstrap replicates lie in the SE or NW quadrant only, the CI might not be necessary. Instead, we may conclude that the new treatment is preferable for the SE quadrant or not preferable for the NW quadrant. If all bootstrap replicates lie in the NE quadrant, we can form a CI by the standard bootstrap-percentile (BP) method, e.g., for the 95% CI, select the 2.5^th and 97.5^th percentiles of the bootstrap ICER_median replicates. The same procedure can be used for the SW quadrant, except that the interpretation is different; in the SW quadrant, the higher the ICER, the more desirable the new treatment (see Appendix).

2) Two quadrants

If the bootstrap replicates lie in the NE and SE quadrants, or the NW and SW quadrants, the BP method mentioned in 1) still works. However, if the ICER replicates lie in the NE and NW quadrants, or the SE and SW quadrants, then the ordinary percentile method should be avoided. Instead, the reordered BP method should be used (Wang and Zhao, 2008), in which the ICER replicates are ordered from the negative largest (smallest in absolute value) to the negative smallest (largest in absolute value) in descending order, followed by the positive largest to the positive smallest in descending order (for example, −1, −2, −5,…, −97, −500, −1000, 999, 864,….4, 2, 1). Then the 2.5^th and 97.5^th percentiles can be selected from these reordered ICER replicates. In this way, discontinuous open intervals that include positive infinity or negative infinity are allowed.

3) Three or four quadrants

When the bootstrap replicates occupy three or four quadrants of the ICER plane, which may happen when either the cost difference or the effect difference, or both, are not significantly far from zero, the CIs need to be based not only on the value of the ICER, but also on the signs of its numerator and denominator. In this case, the wedge-shaped method can be used (Obenchain, 1999). First, we calculate the polar angle of the observed ICER. The 100(1–2α)% confidence region is formed by going 50(1-α)% of the ICER angle clockwise from the observed ICER, and 50(1-α)% of the ICER angle counter-clockwise from the observed ICER. Again, open intervals can arise from angle-based wedge methods. Although these open intervals may seem to be less intuitive numerically, they are better understood when presented in the CE plane, as demonstrated in the examples below.

3. Examples

Using data collected from two clinical trials and one simulated dataset, we illustrate the mean and median-based ICER approaches.

Schizophrenia trial

In an international collaborative trial of olanzapine vs. haloperidol (Tollefson et al., 1997), a total of 1,996 subjects who met Diagnostic and Statistical Manual III revised criteria for schizophrenia-related disorders were enrolled at 174 sites in 17 countries between 1993 and 1995. A total of 817 subjects were enrolled at 66 sites within the US, and only they were considered for the CEA in order to avoid issues of cost conversion and between-country differences in medical practice patterns. A standard CEA based on the ICER_mean was performed (Obenchain and Johnstone, 1999), in which 812 subjects (548 in the olanzapine arm and 264 in the haloperidol arm) who had both cost and effectiveness data from the first post-baseline visit were included. All costs were calculated from standard pricing algorithms that used 1996 price lists for drugs and units of medical services. Effectiveness was defined as responder days.

Based on the standard analysis using mean values (see Table 1), olanzapine was both less costly ($27,765 vs. $38,066) and more effective (188 vs. 169 days) than haloperidol. Interestingly, however, the median cost was $7,790 for olanzapine and $6,486 for haloperidol, i.e., the order is reversed, while olanzapine was still more effective in terms of the median effectiveness (See Table 1). The ICER_mean and the ICER_median were −563 and 74.5 ($/day), respectively.

Table 1.

Summary statistics and cost-effectiveness analysis: Schizophrenia study

Mean-based analysis
Treatment	Cost	Cost difference (95% CI)	ICERmean (95% CI)
Olanzapine	$27,765	$-10,301 (−18,159, −2,256)	−563 ($/day) (−∞,−174) in SE (2110, ∞) in SW
Haloperidol	$38,066
	Effectiveness	Effectiveness difference (95% CI)
Olanzapine	188 (day)	19 (−2.1, 37) (day)
Haloperidol	169 (day)
Median-based analysis
Treatment	Cost	Cost difference (95% CI)	ICERmedian (95% CI)
Olanzapine	$7,790	$1,304 (−3,903, 5,574)	74.5 ($/day) (−152, ∞) in SE/NE (−∞, ∞) in NW/SW
Haloperidol	$6,486
	Effectiveness	Effectiveness difference (95% CI)
Olanzapine	200 (day)	18 (−21, 72) (day)
Haloperidol	182 (day)

CI denotes confidence interval. ICER denotes incremental cost-effectiveness ratio.

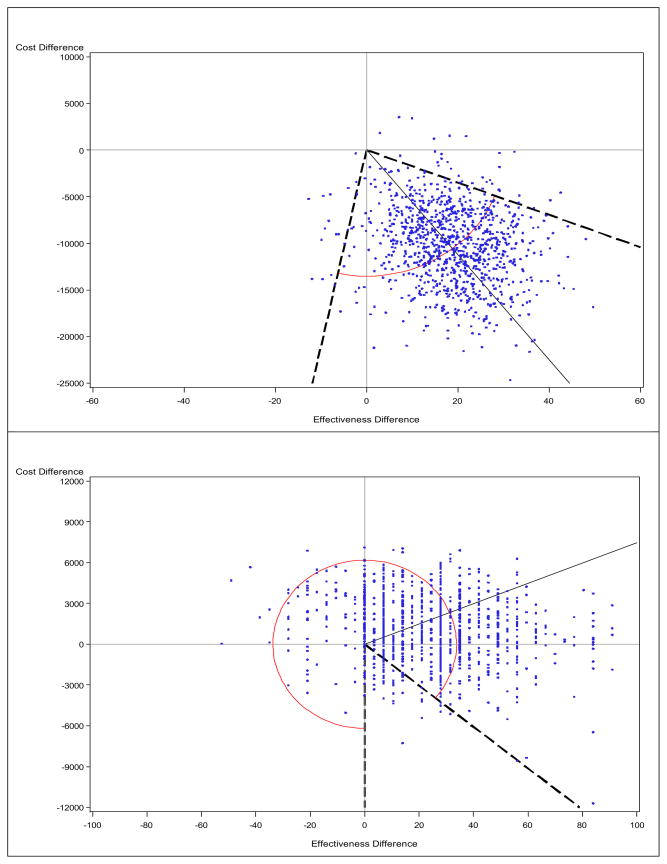
See Figure 1 for the cost-effectiveness plane and CIs.

548 patients in Olanzapine and 264 patients in Haloperidol were included.

We performed a bootstrap analysis with 1,000 replications. Since the ICER replicates lie in three or four quadrants, standard bootstrap methods that provide closed intervals will yield incorrect coverage probability. Therefore, we employed the wedge method for interval estimates. The inner angle formed by the two slopes of −174 and 2,110 in the SE and SW quadrants contained 95% of the bootstrap replicates of the ICER_mean, as shown in Figure 1. Numerically, we can write the 95% CI as (−∞,−174) in the SE quadrant and (2110, ∞) in the SW quadrant, which may look unusual. However, when they are overlaid in the CE plane, conjoined open intervals may no longer be surprising. The CE plane, coupled with the estimated CIs, strongly supports the dominance of olanzapine treatment, as almost all replicates lie in favorable or highly favorable regions in this study.

Figure 1. Cost-effectiveness plane using the mean (upper) vs. the median (lower): Schizophrenia study.

The solid line indicates the point estimate, and the broken line indicates a 95% confidence interval for the ICER (connected by arc), obtained from the bootstrap-wedge method. Note that the scale is different on the y-axis.

When we applied the same wedge method to the ICER_median, the outer angle formed by the two slopes of −152 and −∞ in the SE quadrant encompassed 95% of the bootstrap replicates. This ‘around the circle’ situation seems to mirror a 0/0 situation, as supported by a non-significant difference in cost as well as in effectiveness. Indeed, the CE plane shows that the cost difference is consistently around 0, while the effectiveness difference is more likely to be positive. Under these circumstances, we might choose either treatment or make a decision based on a pre-specified λ, the ICER threshold, using the cost-effectiveness acceptability curve (CEAC) (Van Hout et al., 1994), or Alice curve (Obenchain, 2008) methods to estimate the probability that one treatment dominates another.

In this example, disparities between mean and median results, as highlighted by reversed signs for both cost differences and ICERs, can make interpretation of the cost analysis and CEA challenging. We argue that all mean and median results (i.e., summary statistics and ICERs, with 95% CIs, and CE planes) should be presented together.

We repeated our analysis after 1) excluding very large cost data (>$125,000 corresponding to the top five percentiles) and 2) replacing costs >$125,000 by $125,000. The results show that the ICER_mean=62 and the ICER_median=157 in the former analysis, whereas the ICER_mean=−358 and the ICER_median=74.5 in the latter. The change in the ICER_mean was greater than in the median counterpart.

Prostate cancer trial

In a trial for the treatment of hormone-resistant prostate cancer, a total of 161 subjects were randomized to mitoxantrone plus prednisone (M+P) or P alone (Tannock et al., 1996). For the economic evaluation, investigators used retrospective chart reviews to collect cost data on 114 patients (61 patients for M+P and 53 patients for P) at the three largest centers, including the costs of hospital admissions, outpatient visits, investigations, therapies, and palliative care. All costs were calculated in Canadian dollars. For the effectiveness measure, quality-adjusted survival based on the European Organization for Research and Treatment of Cancer QLQ-C30 questionnaire was utilized (Bloomfield et al., 1998).

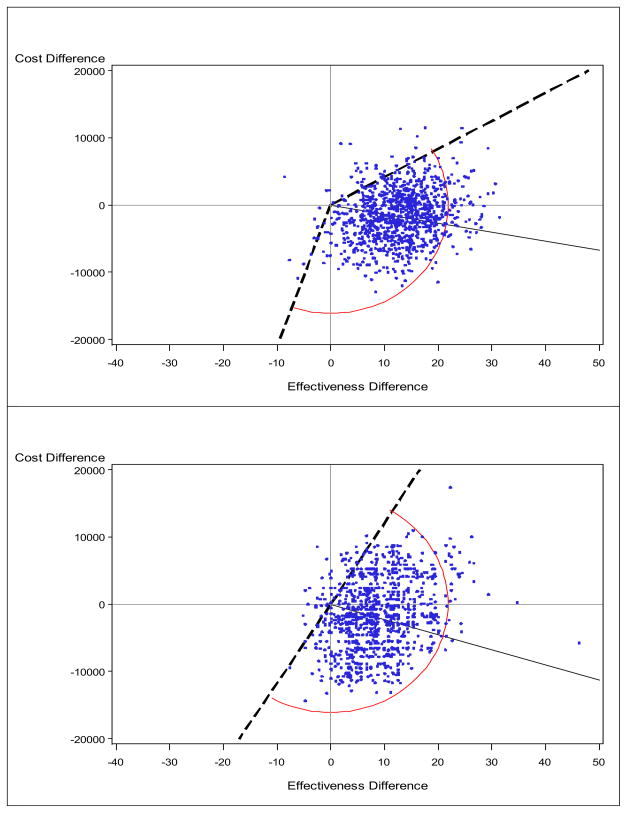
M+P tended to cost less, although the difference was not statistically significant, and to increase quality-adjusted survival, compared with P alone. The mean and median-based analyses provided results that were qualitatively similar (i.e., the same direction in cost and effectiveness differences and the same signs for the ICERs). Since the ICER replicates lie in all four regions, we used the wedge method again for computing CIs. Two slopes and the associated angle that form the 95% CI are visualized in Figure 2, and the numerical results are summarized in Table 2. Although the bootstrap samples for the medians are more variable than their mean counterparts, both planes seem to support the conclusion that M+P is superior.

Figure 2. Cost-effectiveness plane using the mean (upper) vs. the median (lower): Prostate cancer study.

The solid line indicates the point estimate and the broken line indicate a 95% confidence interval for the ICER (connected by arc), obtained from the bootstrap-wedge method.

Table 2.

Summary statistics and cost-effectiveness analysis: Prostate cancer study

Mean-based analysis
Treatment	Cost	Cost difference (95% CI)	ICERmean (95% CI)
M+P	$27,322	$-1,717 (−8,877, 5,882)	−134 ($/week) (−∞, 417) in SE/NE (2099, ∞) in SW
P	$29,039
	Effectiveness	Effectiveness difference (95% CI)
M+P	41 (week)	13 (0.29, 25) (week)
P	28 (week)
Median-based analysis
Treatment	Cost	Cost difference (95% CI)	ICERmedian (95% CI)
M+P	$24,655	$-1,871 (−10,777, 7,923)	−225 ($/week) (−∞, 1208) in SE/NE (1175, ∞) in SW
P	$26,526
	Effectiveness	Effectiveness difference (95% CI)
M+P	29 (week)	8 (−1.9, 22) (week)
P	21 (week)

CI denotes confidence interval. ICER denotes incremental cost-effectiveness ratio.

M denotes Mitxantron and P denotes Prednisone.

See Figure 2 for the cost-effectiveness plane and CIs.

61 patients in M+P and 53 patients in P were included.

Simulated example

In addition, we simulated a set of data to investigate another common scenario in practice; a new treatment is more effective, but costs more, as indicated either by the mean or median. We generated the effectiveness data (say, QALY) using N(mean=6, SD=1.2) for treatment A and N(7, 1.5) for treatment B, where N denotes a normal distribution, for 500 subjects in each arm. We generated cost data from log-normal distribution with mean = subject’s QALYs-1 and SD = 1 for treatment A and a log-normal distribution with mean = subject’s QALYs-1.8 and SD = 1.1 for treatment B. This scenario generated symmetric effectiveness data (thus, yielding similar mean and median values) and highly asymmetric cost data, where these two data were positively correlated with the correlation coefficient of about 0.47.

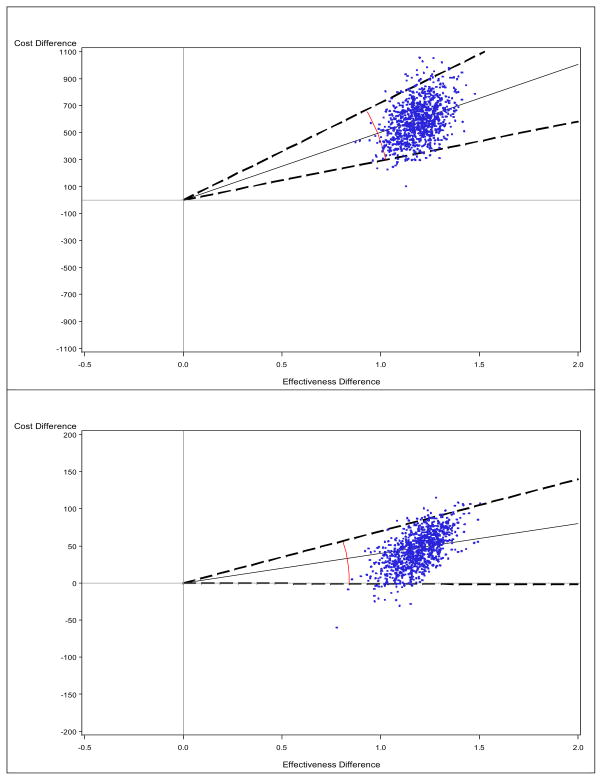
The cost difference is significantly far from 0 by the mean but not by the median. Moreover, the ICER_mean was almost 10 times larger than the ICER_median (502 vs. 40), as shown in Table 3. The ICER_mean formed an ellipse with larger angles in the CE plane, as displayed in Figure 3. Since the replicates are located only in the NE quadrant (for the mean) or the NE/SE quadrants (for the median), we employed the standard BP method for constructing CIs. For the ICER_mean, the 95% CI was estimated as (291, 721) in the NE quadrant, while for the ICER_median, it was estimated as (−0.99, 70) in the NE/SE quadrants. With these data, depending on the ICER threshold, different treatment decisions may be reached.

Table 3.

Summary statistics and cost-effectiveness analysis: Simulated data

Mean-based analysis
Treatment	Cost	Cost difference (95% CI)	ICERmean (95% CI)
A	$426	$597 (320, 897)	502 (291, 721) in NE
B	$1,023
	Effectiveness	Effectiveness difference (95% CI)
A	5.95	1.19 (1.02, 1.36)
B	7.14
Median-based analysis
Treatment	Cost	Cost difference (95% CI)	ICERmedian (95% CI)
A	$141	$49 (−1.06, 88)	40 (−0.99, 70) in SE/NE
B	$190
	Effectiveness	Effectiveness difference (95% CI)
A	5.92	1.21 (0.98, 1.38)
B	7.13

CI denotes confidence interval. ICER denotes incremental cost-effectiveness ratio.

See Figure 3 for the cost-effectiveness plane and CIs.

500 patients in treatment A and 500 patients in treatment B were included.

Figure 3. Cost-effectiveness plane using the mean (upper) vs. the median (lower): Simulated data.

The solid line indicates the point estimate and the broken line indicate a 95% confidence interval for the ICER (connected by arc), obtained from the bootstrap-percentile method. Note that the scale is different on the y-axis.

4. Discussion

Researchers and policy makers are increasingly interested in examining the comparative costs and effectiveness of health care interventions, and some large administrative and clinical databases are available nowadays for this purpose. But the analysis and interpretation of data are complex and can be affected by many factors. For example, because a few patients incur high costs relative to most patients, the distribution of cost data is often highly skewed. In addition, extreme values (outliers) in a distribution may at times be erroneous – say, being administrative errors.

In this article, we have presented two ICER approaches (ICER_mean and ICER_median) and have demonstrated that they could yield markedly different results with respect to point and/or interval estimates and conclusions. This is not surprising, because the mean and the median are different population quantities. The mean has been a dominating summary measure of data in cost-effectiveness literature, whereas other summary measures of distribution received limited attention. Actually, other measures beyond the mean are commonly considered in other scientific disciplines including clinical trials -effectiveness research - and other fields within economics.

We have also stressed that a naive application of standard methods that guarantee closed CIs (e.g., the BP method) can be problematic; up to now, there seemed to be no single inferential method that can be uniformly applied to all CE scenarios. Therefore, we also aimed to provide simple and systematic recommendations for inferential procedures that can be used for the mean and median-based ICERs together and can handle all possible CE scenarios in a unified framework. In particular, angle-based methods may be valid when the replicates lie in multiple quadrants/regions of the CE plane, which may indicate that the numerator and/or the denominator of the ICER is close to 0. Any inference that is not guided by the CE plane could be misleading.

The following methodological issues should be noted when we attempt to understand, implement, or extend the proposed method. First, the median may not be ideal for data with too many 0 observations or for binary effectiveness data. The mean would be better suited to these situations. Second, we used bootstrap-based methods for statistical inferences of the ICER_median. Although bootstrap methods have been widely accepted in CEA, more research is warranted to develop additional methods for statistical inference. However, inferential methods for median-based methods would be generally harder than mean-based methods. Third, the proposed method is for uncensored data for cost, as well as effectiveness. In the presence of right censoring, we need methods that properly account for censoring, possibly adapted from existing methods (Bang and Tsiatis, 2002; Zhao et al., 2007; Zhao and Tian, 2001; Zhao et al., In Press). Fourth, the median can be used in other CEA methodologies, including incremental net-benefit analysis and CEAC (Fenwick et al., 2001; Laska et al., 1999; Stinnett and Mullahy, 1998). In these methods, the willingness to pay can be based on the comparison of the median cost difference and the median effectiveness difference. The incremental net-health benefit is measured as the median health effectiveness gain. The decision rule of CEAC, similarly, can be based on comparing the median cost difference with the median effectiveness difference. Finally, our paper does not offer a theoretical justification for the median-based ICER. The foundation for economic evaluation and statistical theories (e.g., distributions of ratio of differences of medians) may be established in the future, just as it has been done in the past for the mean-based ICER (Weinstein and Stasson 1977; Garber and Phelps 1997).

The Task Force on Randomized Clinical Trials-Cost-Effectiveness Analysis of the International Society for Pharmacoeconomics and Outcomes Research recommended CEA be included in all clinical trials, and it should still be performed even if the study fails to show a statistically significant difference in clinical endpoints (Ramsey et al., 2005). We agree with this recommendation, but CEA under these conditions would require more particular caution in the analysis. Mathematically, it may involve a ‘division by 0’ situation, so that standard methods, as illustrated in our examples, may not work. Determining if the denominator is close to 0 is not straightforward, although the determination can be guided by statistical and/or clinical significance.

Investigators and evaluators may consider both the mean and median-based methods, coupled with robust inferential procedures. Accepting more than one method/perspective would be an important step in evidence-based practice that may advance the use of CEA in real world settings (Neumann, 2004; Rossner, Van Epps and Hill, 2007). Since the mean and median are conceptually and mathematically different and capture different aspects of the distribution, we do not view the two ICER methods as competing, just as the mean and median themselves do not compete. Instead, these two analytic methods can complement each other by performing different tasks; jointly, they would provide a more comprehensive economic analysis. In practice, if the results of mean and median-based analyses are qualitatively the same, our confidence about a given conclusion would be strengthened. However, if mean and median-based analyses provide different results, our confidence should be adjusted accordingly, pending further evidence.

Appendix. The five regions in the cost effectiveness plane for decision making

Reproduced with permission. Obenchain RL. J Biopharmaceut Stat. © 1999.