Abstract
We construct a stress p53-Mdm2-p300-HDAC1 regulatory network that is activated and stabilised by two regulatory proteins, p300 and HDAC1. Different activation levels of 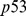 observed due to these regulators during stress condition have been investigated using a deterministic as well as a stochastic approach to understand how the cell responds during stress conditions. We found that these regulators help in adjusting p53 to different conditions as identified by various oscillatory states, namely fixed point oscillations, damped oscillations and sustain oscillations. On assessing the impact of p300 on p53-Mdm2 network we identified three states: first stabilised or normal condition where the impact of p300 is negligible, second an interim region where p53 is activated due to interaction between p53 and p300, and finally the third regime where excess of p300 leads to cell stress condition. Similarly evaluation of HDAC1 on our model led to identification of the above three distinct states. Also we observe that noise in stochastic cellular system helps to reach each oscillatory state quicker than those in deterministic case. The constructed model validated different experimental findings qualitatively.
observed due to these regulators during stress condition have been investigated using a deterministic as well as a stochastic approach to understand how the cell responds during stress conditions. We found that these regulators help in adjusting p53 to different conditions as identified by various oscillatory states, namely fixed point oscillations, damped oscillations and sustain oscillations. On assessing the impact of p300 on p53-Mdm2 network we identified three states: first stabilised or normal condition where the impact of p300 is negligible, second an interim region where p53 is activated due to interaction between p53 and p300, and finally the third regime where excess of p300 leads to cell stress condition. Similarly evaluation of HDAC1 on our model led to identification of the above three distinct states. Also we observe that noise in stochastic cellular system helps to reach each oscillatory state quicker than those in deterministic case. The constructed model validated different experimental findings qualitatively.
Introduction
The p53 is a 20-Kb tumor suppressor gene located on the small arm of human chromosome 17 that acts as a hub for a network of signalling pathways essential for cell growth regulation and apoptosis. It comprises of 393 amino acids and is divided into several structural and functional domains: the transactivation domain (TAD; residues 1–40), the proline-rich domain (PRD; residues 61–94), the DNA-binding domain (DBD; residues 100–300), the tetramerization domain (4D; residues 324–355) and the C-terminal regulatory domain (CTD; residues 360–393) [1]. Over the recent years many names have been accredited to p53 viz. Guardian of the Genome [2]; Death Star [3] and Cellular Gatekeper [4] and is regulated by a number of cellular proteins [5]. It is well established that p53 is accountable for preventing improper cell proliferation and maintaining genome integration following genotoxic stress. In normal proliferating cells, p53 is kept in low concentrations and exists mainly in an inactive latent form with a short half-life of 15–30 minutes [6]. This is due to interaction between p53 and Mdm2 the predominant negative regulator of p53. However, cellular insults activates p53 and its level increases rapidly. The activation of p53 is a result of several posttranslational modifications including phosphorylation, acetylation, sumoylation and neddylation [7]. Phosphorylation of Ser-15 and 37 at the amino terminus of p53 prevents Mdm2 binding, thus stabilizing p53. Also phosphorylation at Ser-15 increases p53 affinity for p300, thus promoting acetylation of p53 carboxy terminal by p300 [8]. Further the p53 in-turn activates the p53-targeted genes including those involved in cell cycle arrest and DNA repair, as well as apoptosis and senescence related genes. The activation of the p53-targeted genes leads to cell cycle arrest that forces cell to choose either to repair the DNA damage to restore its normal function or cell death (apoptosis). Further, it has been observed that p53 acetylation is a reversible process and for it Mdm2 recruits HDAC1 (a histone deacetylase) to form a Mdm2-HDAC1 complex which deacetylates p53. Interestingly, it was also shown that p300 can form a complex with Mdm2 in vitro and in vivo [9], [10] and this complex (Mdm2-p300) facilitate Mdm2 mediated p53 degradation. Moreover, it has also been reported that Mdm2-p53-p300 complex exists that is also thought to promote ubiquitylation and degradation of p53 [11]. Thus p300 plays dual role and exerts two opposite effects on p53 in cells i.e., it can either interact with Mdm2 promoting Mdm2-mediated ubiquitylation and degradation of p53 [9] or acetylate and stabilize p53. This remains puzzling.
There have been different mathematical techniques to study cellular and sub-cellular processes such as deterministic and stochastic models [12], [13]. Stochastic model provide detail picture of molecular interaction in the microscopic systems (small systems with small number of molecules accomodated in each system) that leads the system dynamics as noise-driven process [13], [14]. The model further highlights the important role of noise in the system dynamics, for example detection and amplification of weak noise, the phenomenon known as stochastic resonance [15], [16], lifting of cellular expression at different distinct expression state [17] and noise in gene expression can drive stochastic switching among such states [18], [19], noise induced stochastic phenotypic switching to different new level in living cells [20] etc. However, deterministic model provides qualitative picture of the cellular or sub-cellular processes.
The aim of the present study is (i) to understand some of the basic issues of p53 autoregulation induced by regulators p300 and HDAC1, (ii) to elucidate the functional relationship of p300 and HDAC1 in regulating p53 function, (iii) how do these regulators lifts the normal p53-Mdm2 network to different stress states and (iv) what could be the role of noise in such situations.
Materials and Methods
Stress 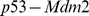 model regulated by
model regulated by 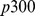 and
and 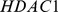
In normal proliferating cells, p53 is usually maintained at low levels due to p53 and Mdm2 protein feedback mechanism [21]. In unstressed condition the p53 binds to the regulatory region of Mdm2 gene and stimulates its transcription into messenger RNA (mRNA) with a transcription rate constant 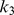 , followed by translation into Mdm2 protein with a rate constant
, followed by translation into Mdm2 protein with a rate constant 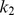 [22]. The degradation of Mdm2-mRNA, Mdm2 and genesis of p53 occurs with basal rate of
[22]. The degradation of Mdm2-mRNA, Mdm2 and genesis of p53 occurs with basal rate of 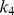 ,
, 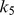 and
and 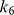 respectively. The Mdm2 protein then interacts physically with p53 to form Mdm2-p53 complex with the rate of
respectively. The Mdm2 protein then interacts physically with p53 to form Mdm2-p53 complex with the rate of 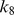 . Mdm2 functions as an E3 ubiquitin ligase and brings about ubiquitylation of multiple lysine residues (K370, K372, K373, K381, K382 and K386) [23] present in the C-terminal domain of p53 [11]. The ubiquitylation marks p53 for degradation via the 26S proteasome, with rate
. Mdm2 functions as an E3 ubiquitin ligase and brings about ubiquitylation of multiple lysine residues (K370, K372, K373, K381, K382 and K386) [23] present in the C-terminal domain of p53 [11]. The ubiquitylation marks p53 for degradation via the 26S proteasome, with rate 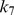 . The Mdm2-p53 complex can also dissociate to Mdm2 and p53 with rate constant
. The Mdm2-p53 complex can also dissociate to Mdm2 and p53 with rate constant 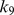 . Mdm2 and p300 have been shown to interact with rate constant
. Mdm2 and p300 have been shown to interact with rate constant 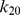 to form Mdm2-p300 complex, which facilitates p53 polyubiquitination and degradation at rate constant of
to form Mdm2-p300 complex, which facilitates p53 polyubiquitination and degradation at rate constant of 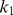 [9], [24]. Although there is no direct evidence reported to the best of author's knowledge in the literature for the degradation of Mdm2-p300 complex, however it has been shown that the p19ARF-binding domain of Mdm2 overlaps with its p300-binding domain suggesting that p19ARF could interfere with the Mdm2/p300 interaction [9]. Therefore, we can assume it is possible that Mdm2-p300 complex can be broken so as to interact with other proteins. Thus in normal unstressed cell, p53 is maintained at low level in an active state with short half-life of 15–30 minutes by Mdm2 and the cells are able to proliferate.
[9], [24]. Although there is no direct evidence reported to the best of author's knowledge in the literature for the degradation of Mdm2-p300 complex, however it has been shown that the p19ARF-binding domain of Mdm2 overlaps with its p300-binding domain suggesting that p19ARF could interfere with the Mdm2/p300 interaction [9]. Therefore, we can assume it is possible that Mdm2-p300 complex can be broken so as to interact with other proteins. Thus in normal unstressed cell, p53 is maintained at low level in an active state with short half-life of 15–30 minutes by Mdm2 and the cells are able to proliferate.
However, under stressed conditions the p53 is stabilized through various post translational modifications which lead to increase its level. Of the various mechanisms, phosphorylation of 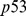 is the most well studied and it is reported that multiple kinases phosphorylate various residues which increase the level of
is the most well studied and it is reported that multiple kinases phosphorylate various residues which increase the level of 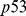 protein. One of these protein kinases is
protein. One of these protein kinases is 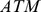 which upon activation by DNA damage phosphorylates
which upon activation by DNA damage phosphorylates 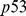 with a rate
with a rate 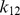 at serine 15 [25] which is critical for
at serine 15 [25] which is critical for 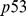 activation and stabilization. Strikingly, the phosphorylation of serine 15 mediated by
activation and stabilization. Strikingly, the phosphorylation of serine 15 mediated by 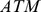 acts as a nucleation event that promotes subsequent sequential modification of many residues. To achieve this, interconversion of inactivated and activated
acts as a nucleation event that promotes subsequent sequential modification of many residues. To achieve this, interconversion of inactivated and activated 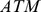 takes place, with rate constants
takes place, with rate constants 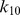 and
and 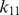 respectively. The
respectively. The 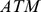 -initiated phosphorylation reduces the affinity of
-initiated phosphorylation reduces the affinity of 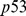 for
for 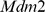 while increases interactions with HATs like
while increases interactions with HATs like 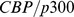 [8], [26]. Consequently, dephosphorylation of
[8], [26]. Consequently, dephosphorylation of 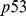 with a rate
with a rate 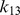 also takes place to counter this phosphorylation. It has been demonstrated that
also takes place to counter this phosphorylation. It has been demonstrated that 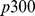 protein is a co-activator of
protein is a co-activator of 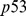 which potentiates its transcriptional activity as well as biological function in vivo [27]. However, it has also been shown that formation of
which potentiates its transcriptional activity as well as biological function in vivo [27]. However, it has also been shown that formation of 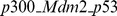 ternary complex leads to suppressing
ternary complex leads to suppressing 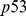 acetylation and activation [28]. The transcription activation domain (TAD) of
acetylation and activation [28]. The transcription activation domain (TAD) of 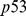 binds tightly to
binds tightly to 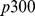 with formation rate constant
with formation rate constant 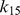 . The
. The 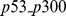 complex hence formed, causes
complex hence formed, causes 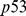 acetylation with rate constant
acetylation with rate constant 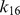 at multiple lysine residues (K370, K372, K373, K381, K382) of its C-terminal regulatory domain [27], [29]. The lysine residues (K370, K372, K373, K381, and K382) are the common sites for both acetylation and ubiquitination [30], [31]. Thus their acetylation causes the inhibition of ubiquitination resulting
at multiple lysine residues (K370, K372, K373, K381, K382) of its C-terminal regulatory domain [27], [29]. The lysine residues (K370, K372, K373, K381, and K382) are the common sites for both acetylation and ubiquitination [30], [31]. Thus their acetylation causes the inhibition of ubiquitination resulting 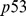 protein stability which is evident from the observation that acetylated
protein stability which is evident from the observation that acetylated 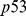 has half-life of greater than two hours [32]. Simultaneously, formation and degradation of
has half-life of greater than two hours [32]. Simultaneously, formation and degradation of 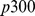 occurs with rate constants
occurs with rate constants 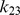 and
and 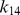 respectively.
respectively. 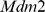 ,
, 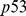 and
and 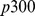 have also been demonstrated to exist in a ternary complex (
have also been demonstrated to exist in a ternary complex (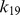 ) which is incapable of acetylating
) which is incapable of acetylating 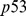 [28]. In the complex, TAD1 domain of
[28]. In the complex, TAD1 domain of 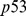 interacts with
interacts with 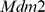 while TAD2 interacts with
while TAD2 interacts with 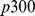 [11]. As mentioned earlier, phosphorylation increases the affinity of
[11]. As mentioned earlier, phosphorylation increases the affinity of 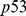 towards
towards 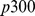 while decreasing its affinity towards
while decreasing its affinity towards 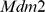 . After phosphorylation, the ternary complex dissociates, with rate constant
. After phosphorylation, the ternary complex dissociates, with rate constant  into
into 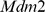 and
and 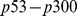 complex, in which both TAD1 and TAD2 of
complex, in which both TAD1 and TAD2 of 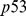 interact with
interact with 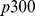 [11]. p300 can then acetylate and stabilize
[11]. p300 can then acetylate and stabilize 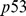 . Stabilized
. Stabilized 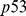 functions as a tumor suppressor and induces high levels of
functions as a tumor suppressor and induces high levels of 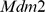 , which in turn promotes
, which in turn promotes 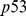 degradation by recruiting a
degradation by recruiting a 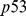 deacetylase,
deacetylase, 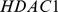 with rate constant
with rate constant 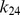 .
. 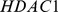 binds
binds 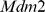 in a
in a 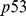 dependent manner with binding rate constant
dependent manner with binding rate constant 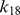 and deacetylates
and deacetylates 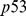 with rate constant
with rate constant 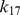 at all known acetylated lysines in vivo [33]. Moreover, analysis has indicated the presence of MDM2, SMAR1 and HDAC1 complex under conditions of inhibited translation only 12 h post damage rescue while there is lack of complex formation 24 h post damage rescue, thereby suggesting degradation of the Mdm2-HDAC1complex [34]. HDAC1 is generated and degraded in cells with rate constants
at all known acetylated lysines in vivo [33]. Moreover, analysis has indicated the presence of MDM2, SMAR1 and HDAC1 complex under conditions of inhibited translation only 12 h post damage rescue while there is lack of complex formation 24 h post damage rescue, thereby suggesting degradation of the Mdm2-HDAC1complex [34]. HDAC1 is generated and degraded in cells with rate constants 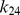 and
and 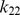 respectively. The unmodified lysine residues can then serve as the substrates for
respectively. The unmodified lysine residues can then serve as the substrates for 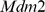 -mediated ubiquitylation resulting in
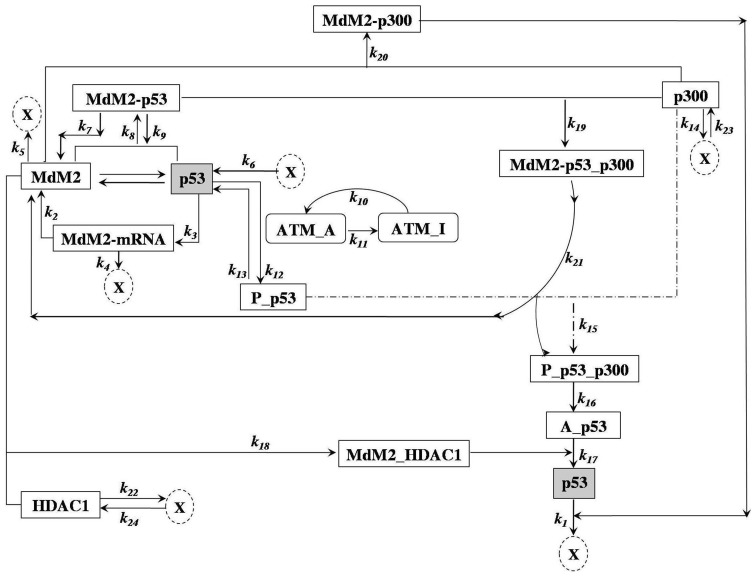
-mediated ubiquitylation resulting in 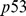 degradation and thus completing the feedback loop. The molecular species involved in the biochemical network are listed in Table 1 and the chemical reaction channels in the network are shown in Table 2. The schematic picture of the stress
degradation and thus completing the feedback loop. The molecular species involved in the biochemical network are listed in Table 1 and the chemical reaction channels in the network are shown in Table 2. The schematic picture of the stress 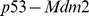 autoregulatory biochemical reaction network model via
autoregulatory biochemical reaction network model via 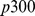 and
and 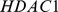 based on the experimental evidences and reports mentioned above is shown in Fig. 1.
based on the experimental evidences and reports mentioned above is shown in Fig. 1.
Table 1. List of molecular species.
| S.No. | Species Name | Description | Notation |
| 1. |
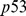
|
Unbounded 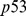 protein protein |
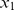
|
| 2. |
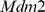
|
Unbounded 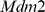 protein protein |
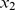
|
| 3. |
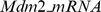
|
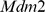 messenger messenger 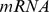
|
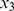
|
| 4. |
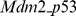
|
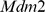 with with 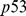 complex complex |
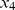
|
| 5. |
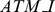
|
Inactivated 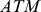 protein protein |
|
| 6. |
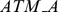
|
Activated 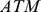 protein protein |
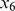
|
| 7. |
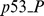
|
Phosphorylated  protein protein |
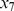
|
| 8. |
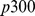
|
Unbounded 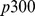 protein protein |
|
| 9. |
|
Phosphorylated 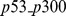 complex complex |
|
| 10. |
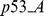
|
Acetylated 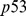 protein (capped p53) protein (capped p53) |
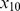
|
| 11. |
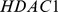
|
Unbounded 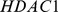 protein protein |
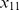
|
| 12. |
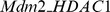
|
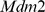 and and 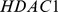 complex complex |
|
| 13. |
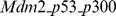
|
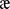 , ,  and and 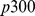 complex complex |
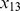
|
| 14. |
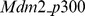
|
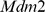 and and 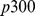 complex complex |
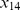
|
Table 2. List of chemical reaction, propensity function and their rate constant.
| S.No | Reaction | Name of the process | Kinetic law | Rate constant | References |
| 1 |
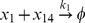
|
p53 degradation |
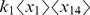
|
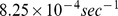
|
[9], [24]. |
| 2 |
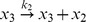
|
Mdm2 creation |
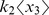
|
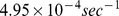
|
[22]. |
| 3 |
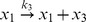
|
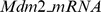 creation creation |
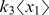
|
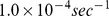
|
[22]. |
| 4 |
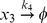
|
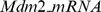 degradation degradation |
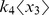
|
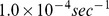
|
[22]. |
| 5 |
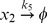
|
Mdm2 degradation |
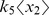
|
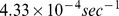
|
[22]. |
| 6 |
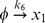
|
p53 synthesis |
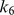
|
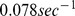
|
[22]. |
| 7 |
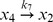
|
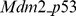 degradation degradation |
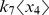
|
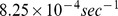
|
[11], [23]. |
| 8 |
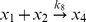
|
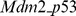 synthesis synthesis |
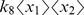
|
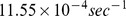
|
[22]. |
| 9 |
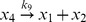
|
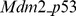 dissociation dissociation |
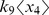
|
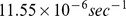
|
[22]. |
| 10 |
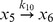
|
ATM activation |
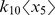
|
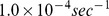
|
[12], [23]. |
| 11 |
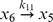
|
ATM deactivation |
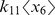
|
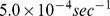
|
[12], [23]. |
| 12 |
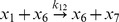
|
Phosphorylation of p53 |
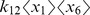
|
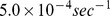
|
[23]. |
| 13 |
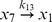
|
Dephosphorylation of p53 |
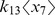
|
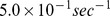
|
[12], [23]. |
| 14 |
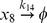
|
p300 degradation |
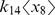
|
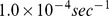
|
[30], [31]. |
| 15 |
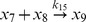
|
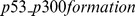
|
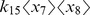
|
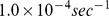
|
[28]. |
| 16 |
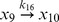
|
Acetylation of p53 |
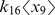
|
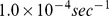
|
[27], [29]. |
| 17 |
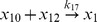
|
Deacetylation of p53 |
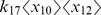
|
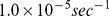
|
[29]. |
| 18 |
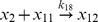
|
Creation of 
|
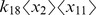
|
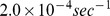
|
[29]. |
| 19 |
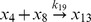
|
Creation of 
|
|
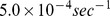
|
[28]. |
| 20 |
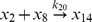
|
Formation of 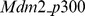
|
|
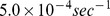
|
[9], [22]. |
| 21 |
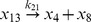
|
Dissociation of 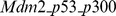
|
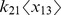
|
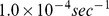
|
[11], [28]. |
| 22 |
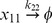
|
Degradation of HDAC1 |
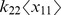
|
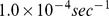
|
[29]. |
| 23 |
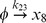
|
p300 synthesis |
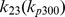
|
|
[30], [31]. |
| 24 |
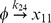
|
HDAC1 synthesis |
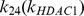
|
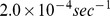
|
[29]. |
Figure 1. Biochemical network model of stress p53-Mdm2-p300-HDAC1.
The schematic diagram of stress p53-Mdm2-p300-HDAC1 model.
Stochastic description of biochemical reaction network
We now consider a configurational state  of the system of size
of the system of size 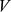 at any instant of time
at any instant of time  defined by
defined by 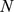 molecular species undergoing
molecular species undergoing 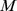 elementary reactions. The change in configurational state during any interval of time
elementary reactions. The change in configurational state during any interval of time 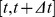 is due to random interaction of the participating molecules that leads to decay and creation of specific molecular species in state vector
is due to random interaction of the participating molecules that leads to decay and creation of specific molecular species in state vector 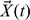 during the time interval [13], [14], [35]. Therefore the trajectory of this state vector
during the time interval [13], [14], [35]. Therefore the trajectory of this state vector 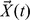 as a function of time in the configurational space follows Markov process [13], [14] and the dynamics of this vector becomes noise-induced stochastic process [13]. If we define
as a function of time in the configurational space follows Markov process [13], [14] and the dynamics of this vector becomes noise-induced stochastic process [13]. If we define 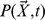 as the configurational probability of obtaining the state
as the configurational probability of obtaining the state 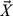 at time
at time  , then the time evolution of
, then the time evolution of 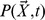 will obey Master equation [13], [14], [36]. Even though the Master equation for complex system could be very difficult to solve analytically, different algorithms have been devised to solve the system dynamics numerically depending on the nature of the system. For example, stochastic simulation algorithm (Gillespie algorithm) for reaction system without considering time delay [13], stochastic simulation algorithm for time delay reaction system [37], [38],
will obey Master equation [13], [14], [36]. Even though the Master equation for complex system could be very difficult to solve analytically, different algorithms have been devised to solve the system dynamics numerically depending on the nature of the system. For example, stochastic simulation algorithm (Gillespie algorithm) for reaction system without considering time delay [13], stochastic simulation algorithm for time delay reaction system [37], [38],  -leap algorithm which is approximated algorithm of stochastic simulation algorithm for very complex reaction network [39], hybrid algorithm for reaction networks consisting of both slow and fast reactions [40] etc.
-leap algorithm which is approximated algorithm of stochastic simulation algorithm for very complex reaction network [39], hybrid algorithm for reaction networks consisting of both slow and fast reactions [40] etc.
The Master equation for the stochastic system can be approximated to simpler Chemical Langevin equations (CLE) based on two important realistic approximations applied on the the system [41]. This can be done by defining a function 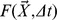 which is the number of a particular reaction fired during the time interval
which is the number of a particular reaction fired during the time interval 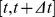 with
with 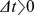 and applying the two approximations: first applying
and applying the two approximations: first applying 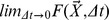 which leads to the prophensity functions (
which leads to the prophensity functions (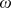 ) of the reactions fired remain constant during the time interval, and secondly applying
) of the reactions fired remain constant during the time interval, and secondly applying 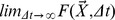 condition which gives rise
condition which gives rise 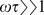 [41]. These two conditions are true for large population size of each variables in state vector
[41]. These two conditions are true for large population size of each variables in state vector 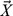 which is valid for natural systems. These two conditions allow the function
which is valid for natural systems. These two conditions allow the function 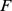 to approximate to Poisson distribution function and then to Normal distribution function with same mean and standard deviation. If molecular concentration is defined by
to approximate to Poisson distribution function and then to Normal distribution function with same mean and standard deviation. If molecular concentration is defined by 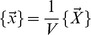 and linearize Normal distribution function, the Master equation leads to the following CLE of the vector
and linearize Normal distribution function, the Master equation leads to the following CLE of the vector 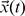 ,
,
| (1) |
where, 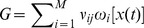 is the macroscopic contribution term and
is the macroscopic contribution term and 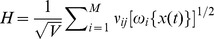 is the stochastic contribution term to the dynamics.
is the stochastic contribution term to the dynamics. 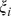 =
= 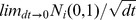 is uncorrelated, statistically independent random noise parameters which satisfy
is uncorrelated, statistically independent random noise parameters which satisfy 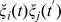 =
= 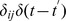 . {
. { } is the stoichiometric matrix of the reactions in the network.
} is the stoichiometric matrix of the reactions in the network.
The classical deterministic equations can be obtained from the CLE equation (1) at thermodynamics limit [41] i.e. at 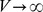 ,
, 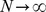 but
but 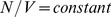 . This leads to
. This leads to 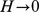 and the equation (1) becomes noise free deterministic equation,
and the equation (1) becomes noise free deterministic equation,
| (2) |
The same equation (2) can also be be retrieved from the biochemical reaction network by translating them into a set of differential equations based on standard principles of Mass-action law of biochemical reaction kinetics.
The stress 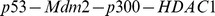 model network we study is defined by
model network we study is defined by 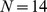 (14 molecular species) and
(14 molecular species) and 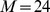 (24 reaction channels). The molecular species, possible reactions, kinetic laws and the rate constants in this model are listed in Table 1 and Table 2 respectively. The state vector at any instant of time
(24 reaction channels). The molecular species, possible reactions, kinetic laws and the rate constants in this model are listed in Table 1 and Table 2 respectively. The state vector at any instant of time  is given by,
is given by, 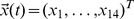 , where the variables in the vector are various proteins and their complexes which are listed in Table 1. The classical deterministic equations constructed from these reaction network are given by,
, where the variables in the vector are various proteins and their complexes which are listed in Table 1. The classical deterministic equations constructed from these reaction network are given by,
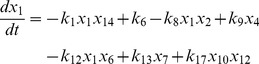 |
(3) |
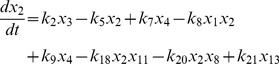 |
(4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
where, 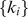 and
and 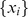 ,
, 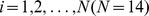 represent the sets of rate constants of the reactions listed in Table 2 and concentrations of the molecular populations listed in Table 1.
represent the sets of rate constants of the reactions listed in Table 2 and concentrations of the molecular populations listed in Table 1.
Following the same procedure as we have discussed above, we reach the following CLE for the network shown in Fig. 1, Table 1 and Table 2.
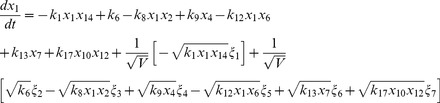 |
(17) |
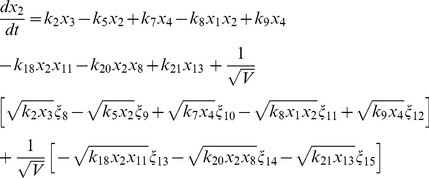 |
(18) |
| (19) |
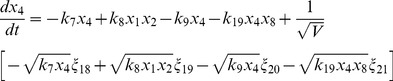 |
(20) |
| (21) |
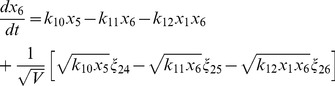 |
(22) |
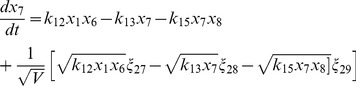 |
(23) |
| (24) |
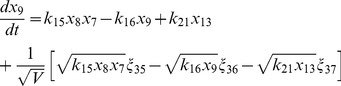 |
(25) |
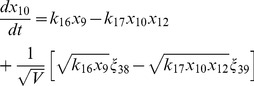 |
(26) |
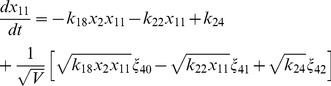 |
(27) |
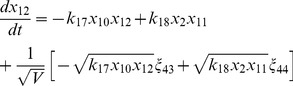 |
(28) |
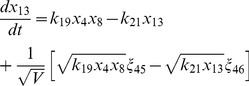 |
(29) |
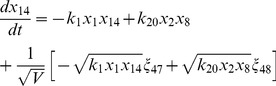 |
(30) |
where, 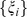 are random number which satisfy
are random number which satisfy 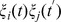 =
= 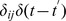 , and
, and 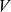 is the system's size.
is the system's size.
The CLE (3)-(17) and differential equations (18)-(32) can be solved numerically using standard algorithm of 4th order Runge-Kutta method of numerical integration [42].
Results and Discussion
Several researchers have studied the oscillations of 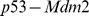 network in detail [22], [43]–[46], however to the best of our knowledge this study is the first one that uses systems biology approach for understanding the complex role of p300 and HDAC1 on p53. We numerically solved the set of deterministic differential equations (1)–(14), and stochastic CLE (15)–(29) by using standard algorithm of 4th order Runge-Kutta method of numerical integration [42]. We thus study the impact of p300 and HDAC1 on p53 activation and stabilization to understand the fate of the cell.
network in detail [22], [43]–[46], however to the best of our knowledge this study is the first one that uses systems biology approach for understanding the complex role of p300 and HDAC1 on p53. We numerically solved the set of deterministic differential equations (1)–(14), and stochastic CLE (15)–(29) by using standard algorithm of 4th order Runge-Kutta method of numerical integration [42]. We thus study the impact of p300 and HDAC1 on p53 activation and stabilization to understand the fate of the cell.
Impact of 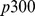 on
on 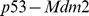 activation
activation
We first present the deterministic results on p53-Mdm2 regulatory network on exposure to different concentrations of 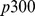 i.e. at different rate constants,
i.e. at different rate constants, 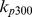 (Fig. 2). For small values of
(Fig. 2). For small values of 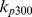 ( = 0.04) (lower
( = 0.04) (lower 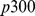 concentration),
concentration), 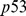 is first activated for some time (
is first activated for some time (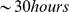 ) and then resumes its normal condition indicated by its constant level (
) and then resumes its normal condition indicated by its constant level (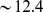 ) which is the level of stabilization. The range of activation is increased as
) which is the level of stabilization. The range of activation is increased as 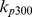 increases (increase of
increases (increase of 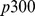 concentration) as well as there is rise in the level of stabilization. However, when
concentration) as well as there is rise in the level of stabilization. However, when 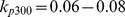 ,
, 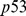 maintains sustain oscillations which leads to increasing level of activation as a consequence. With further increment of
maintains sustain oscillations which leads to increasing level of activation as a consequence. With further increment of 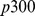 concentration level,
concentration level, 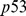 dynamics that was at sustain oscillations switched to damped oscillations and subsequently p53 concentration is stabilized at a constant level. This activity suggests that the capping of the c-terminal of
dynamics that was at sustain oscillations switched to damped oscillations and subsequently p53 concentration is stabilized at a constant level. This activity suggests that the capping of the c-terminal of 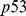 is higher and there is no decrement in the
is higher and there is no decrement in the 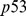 levels as a result of which
levels as a result of which 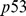 is stabilized. The results obtained are consistent with the experimental observations which indicates that acetylation of p53 is responsible for its activation [27], [31] and stabilization [29], [32]. If we further increase the value of
is stabilized. The results obtained are consistent with the experimental observations which indicates that acetylation of p53 is responsible for its activation [27], [31] and stabilization [29], [32]. If we further increase the value of 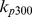 ,
, 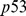 activation decreases maintaining
activation decreases maintaining 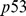 stability but at higher values (
stability but at higher values (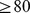 ). Hence we identify two conditions where p53 is stabilized, one at lower values (nearly normal cell condition) and the other at larger values (cell death condition) of
). Hence we identify two conditions where p53 is stabilized, one at lower values (nearly normal cell condition) and the other at larger values (cell death condition) of 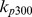 and in between
and in between 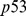 is activated.
is activated.
Figure 2.
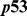 dynamics for various
dynamics for various 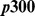 levels.
levels.
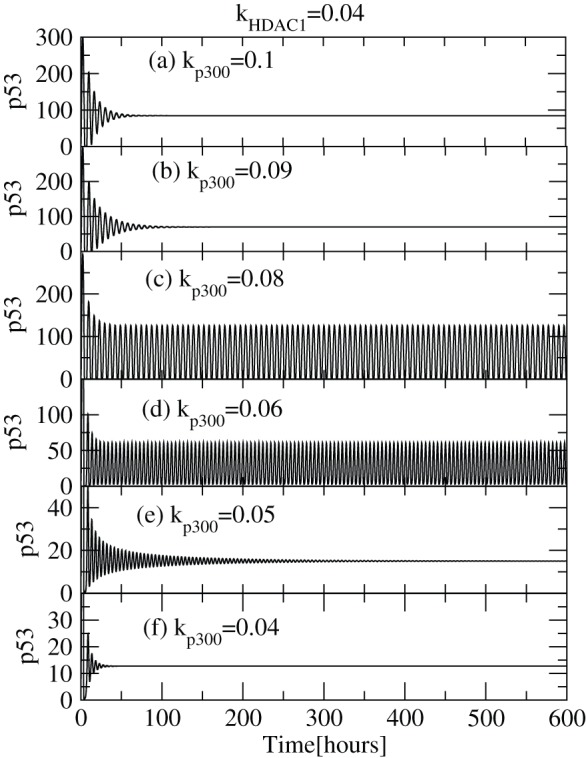
The plots of 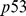 concentration levels as a function of time in hours for various
concentration levels as a function of time in hours for various 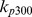 values: (a)
values: (a) 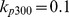 , (b)
, (b) 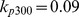 , (c)
, (c) 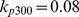 , (d)
, (d) 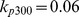 , (e)
, (e) 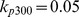 and (f)
and (f) 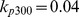 respectively at constant value of
respectively at constant value of 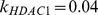 .
.
Similarly, 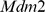 dynamics as a function of time for different values of
dynamics as a function of time for different values of 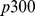 concentration levels is shown (Fig. 3) that demonstrates counter behaviour as expected. The two dimensional recurrence plots of (
concentration levels is shown (Fig. 3) that demonstrates counter behaviour as expected. The two dimensional recurrence plots of (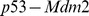 ), (
), (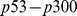 ) and (
) and (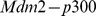 ) are presented in Fig. 4 which provides clear and qualitative picture of the above facts. The emergence of sustain/limit-cycle oscillation (activated
) are presented in Fig. 4 which provides clear and qualitative picture of the above facts. The emergence of sustain/limit-cycle oscillation (activated 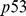 level) from fix point oscillation (stabilized
level) from fix point oscillation (stabilized 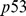 level), and then from sustain oscillation to again fix point oscillation is observed as one increase the concentration of
level), and then from sustain oscillation to again fix point oscillation is observed as one increase the concentration of 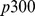 .
.
Figure 3.
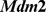 dynamics for various
dynamics for various 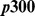 levels.
levels.

The plots of 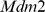 concentration levels as a function of time in hours for various
concentration levels as a function of time in hours for various 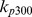 values: (a)
values: (a) 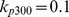 , (b)
, (b) 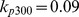 , (c)
, (c) 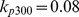 , (d)
, (d) 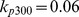 , (e)
, (e) 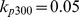 and (f)
and (f) 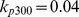 respectively at constant value of
respectively at constant value of 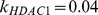 .
.
Figure 4. Two-dimensional recurrence plots of 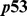 and
and 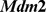 .
.
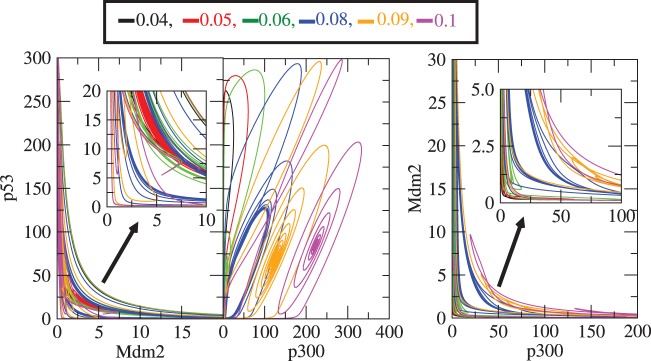
Recurrence plots between (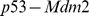 ), (
), (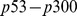 ) and (
) and (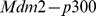 ) for different values of rate constants
) for different values of rate constants 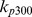 , i.e. 0.04, 0.05, 0.06, 0.08, 0.09 and 0.1 respectively.
, i.e. 0.04, 0.05, 0.06, 0.08, 0.09 and 0.1 respectively.
Impact of 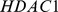 on
on 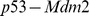 network
network
Several studies suggest that 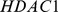 is involved in the deacetylation of p53 which has a potent impact on
is involved in the deacetylation of p53 which has a potent impact on 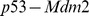 regulatory dynamics [29], [31], [47], [48]. It has been found that
regulatory dynamics [29], [31], [47], [48]. It has been found that 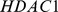 makes complex protein,
makes complex protein, 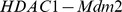 which deacetylates and then ubiquitinates the acetylated
which deacetylates and then ubiquitinates the acetylated 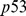 . Because of this process of interaction of
. Because of this process of interaction of 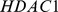 with
with 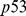 , both
, both 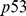 and
and 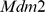 levels get stabilized. In our numerical simulation, we kept
levels get stabilized. In our numerical simulation, we kept 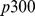 concentration level fixed by keeping
concentration level fixed by keeping 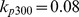 throughout the simulation and allow
throughout the simulation and allow 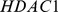 concentration to vary by changing
concentration to vary by changing 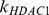 value. The results are shown in Fig. 5 (a)–(f). In these plots we observe that at lower concentration of
value. The results are shown in Fig. 5 (a)–(f). In these plots we observe that at lower concentration of 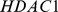 (
(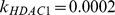 ), the
), the  activation is large due to pre-existing
activation is large due to pre-existing  , as indicated by the sustained oscillation (Fig. 5 (f)). This activity suggests that there is regular decay and creation of
, as indicated by the sustained oscillation (Fig. 5 (f)). This activity suggests that there is regular decay and creation of  , due to the presence of high levels of
, due to the presence of high levels of  and hence the impact of
and hence the impact of 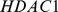 concentration level is not very significant. As the
concentration level is not very significant. As the 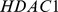 concentration increases (increasing
concentration increases (increasing 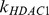 value), there is regular and competitive effect between
value), there is regular and competitive effect between 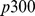 and
and 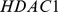 for
for 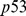 that decreases
that decreases 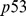 activation as indicated by decrease in
activation as indicated by decrease in 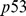 concentration level (Fig. 5 (c)–(e)). Further, if we increase the concentration of
concentration level (Fig. 5 (c)–(e)). Further, if we increase the concentration of 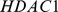 , the
, the 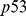 first activates for short period of time and then remains constant at same value (
first activates for short period of time and then remains constant at same value (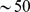 ) indicating
) indicating 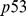 stabilization. This transition from
stabilization. This transition from 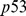 activation to stabilization is indicated by the transition from sustained oscillation to fixed point oscillations indicated in Fig. 5 (a) and (b). We observe this behaviour at
activation to stabilization is indicated by the transition from sustained oscillation to fixed point oscillations indicated in Fig. 5 (a) and (b). We observe this behaviour at 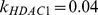 , where the activity of
, where the activity of 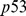 is low, stable and very much controlled.
is low, stable and very much controlled.
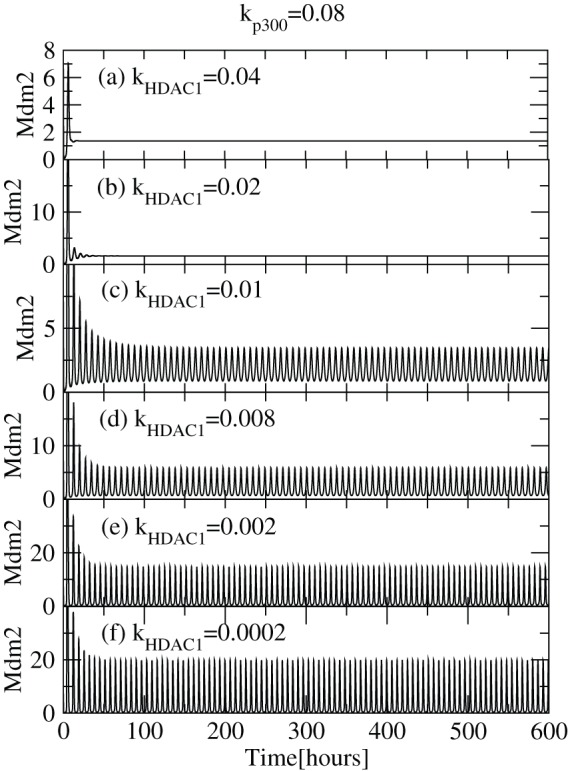
Figure 5. Activation of 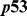 via variation of
via variation of  level.
level.
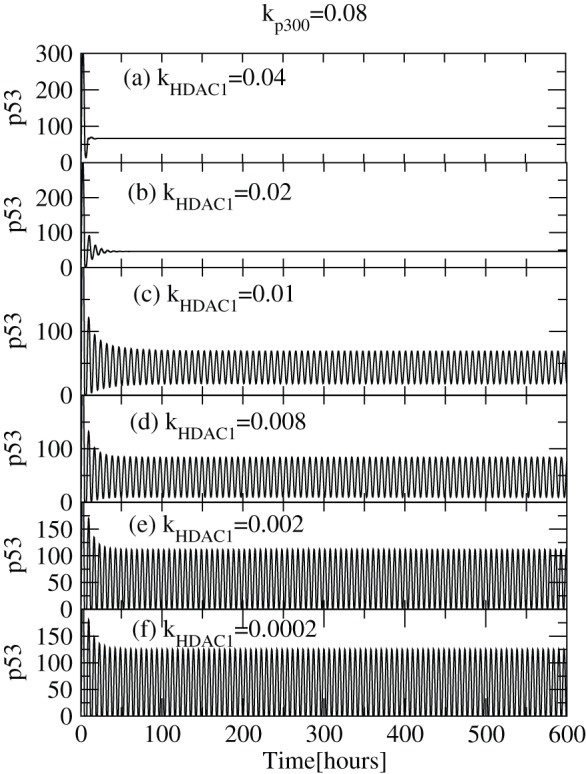
Plots of  concentration levels as a function of time in hours for various
concentration levels as a function of time in hours for various  values 0.0002, 0.002, 0.008, 0.01, 0.02 and 0.04 respectively (at constant value of
values 0.0002, 0.002, 0.008, 0.01, 0.02 and 0.04 respectively (at constant value of 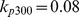 ), showing activation and stabilization of
), showing activation and stabilization of 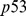 .
.
Similarly, we present the simulation results of 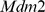 as a function of time for different
as a function of time for different 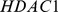 levels (Fig. 6 (a)–(f)). We observe similar behaviour of
levels (Fig. 6 (a)–(f)). We observe similar behaviour of 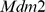 as
as 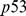 which shows a transition from sustain oscillation to fix point oscillation as one increase the
which shows a transition from sustain oscillation to fix point oscillation as one increase the 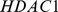 concentration level. These results indicate that
concentration level. These results indicate that 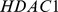 stabilizes
stabilizes 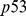 as well as
as well as 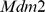 concentration levels.
concentration levels.
Figure 6. Activation of 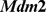 via variation of
via variation of 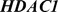 level.
level.
Plots of 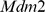 concentration levels as a function of time in hours for various
concentration levels as a function of time in hours for various 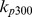 values 0.0002, 0.002, 0.008, 0.01, 0.02 and 0.04 respectively (at constant value of
values 0.0002, 0.002, 0.008, 0.01, 0.02 and 0.04 respectively (at constant value of 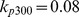 ), showing activation and stabilization of
), showing activation and stabilization of 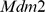 .
.
We also present the two dimensional recurrence plots of the (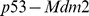 ), (
), (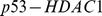 ) and (
) and (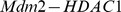 ) for demonstrating these facts (Fig. 7). The clear indication of transition from sustain/limit cycle oscillation to fix point oscillation as
) for demonstrating these facts (Fig. 7). The clear indication of transition from sustain/limit cycle oscillation to fix point oscillation as 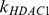 is increased, is shown in the plots indicating transition from activation of
is increased, is shown in the plots indicating transition from activation of 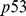 and
and 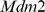 to stabilized state.
to stabilized state.
Figure 7. Recurrence plots of  and
and 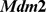 activated by
activated by 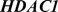 .
.
The two dimensional plots of the pairs ( ), (
), ( ) and (
) and (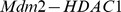 ) for different values of rate constants
) for different values of rate constants 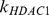 , i.e. 0.0002, 0.002, 0.08, 0.01, 0.02 and 0.04 respectively.
, i.e. 0.0002, 0.002, 0.08, 0.01, 0.02 and 0.04 respectively.
Stability analysis of 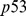 and
and 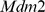
We then checked how concentration level of 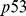 varies as a function of
varies as a function of 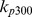 (
(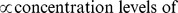
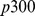 ). This is done by defining a parameter called expose time (
). This is done by defining a parameter called expose time (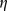 ) which can be stated as the amount of time the system is exposed to a particular concentration level of
) which can be stated as the amount of time the system is exposed to a particular concentration level of 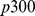 or
or 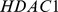 . The calculation of
. The calculation of 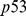 or
or 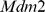 concentration level induced by the exposition of the system to
concentration level induced by the exposition of the system to 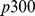 or
or 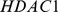 is done by obtaining its level just after the expose time (time slice calculation). Fig. 8 shows variation of
is done by obtaining its level just after the expose time (time slice calculation). Fig. 8 shows variation of 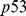 concentration levels as a function of
concentration levels as a function of 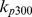 for different expose times of 10–100 hours for a fixed value of
for different expose times of 10–100 hours for a fixed value of 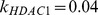 . The plots clearly show the activated and stabilized regimes. The activated regime is where the
. The plots clearly show the activated and stabilized regimes. The activated regime is where the 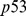 levels fluctuate as a function of
levels fluctuate as a function of 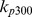 (induced by
(induced by 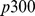 levels). In the plots,
levels). In the plots, 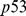 level starts activation from
level starts activation from 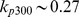 because of the interaction among
because of the interaction among 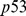 ,
, 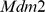 and
and 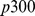 with small level of
with small level of  giving rise to fluctuation in
giving rise to fluctuation in 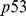 level. This could be due to acetylation and deacetylation which leads to capping (which prohibits
level. This could be due to acetylation and deacetylation which leads to capping (which prohibits 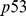 to decay) and uncapping (which leads to
to decay) and uncapping (which leads to 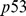 decay) of
decay) of 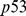 due to
due to 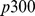 . This
. This 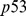 level fluctuation persists till
level fluctuation persists till 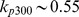 and then increases its level without fluctuation till
and then increases its level without fluctuation till 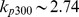 indicating only the capping of
indicating only the capping of 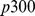 , then its level remain constant. Interestingly the range of activation of
, then its level remain constant. Interestingly the range of activation of 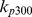 in
in  for all expose times remain the same in [0.27–2.74].
for all expose times remain the same in [0.27–2.74].
Figure 8. Stability curve induced by  .
.
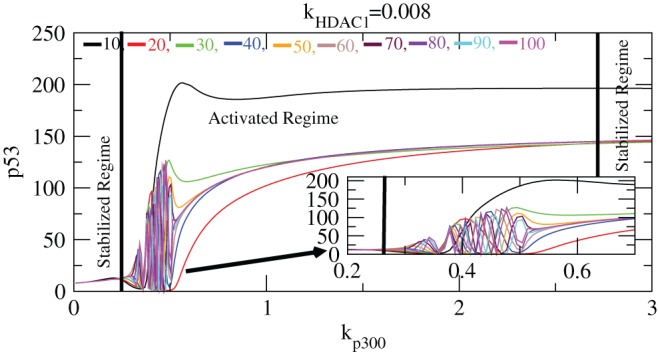
Plots of  concentration level as a function of
concentration level as a function of 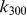 for different values of exposure times i.e.
for different values of exposure times i.e. 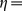 10-100 (at constant value of
10-100 (at constant value of 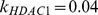 ). The inset is the enlarged portion of the activated regime. In the curve stabilized and activated regimes are demarcated.
). The inset is the enlarged portion of the activated regime. In the curve stabilized and activated regimes are demarcated.
The stabilized regimes are where 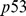 level is not affected by the variation in
level is not affected by the variation in 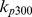 (
(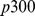 level variation). Initially, within the range of
level variation). Initially, within the range of 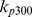 [0–0.27], the
[0–0.27], the 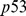 level is not much affected indicating that the cell resumes its normal condition maintaining its minimum level (
level is not much affected indicating that the cell resumes its normal condition maintaining its minimum level (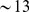 ) which we call first stabilization regime. However, in the second stabilization regime [2.74–
) which we call first stabilization regime. However, in the second stabilization regime [2.74– ],
], 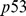 level remains constant at much higher value (
level remains constant at much higher value (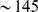 ) indicating the capping of
) indicating the capping of 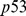 is maximum utilizing
is maximum utilizing 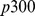 which prohibits decay. This case may be the condition where death of the cell could happen due to uncontrolled
which prohibits decay. This case may be the condition where death of the cell could happen due to uncontrolled 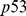 growth due to excess
growth due to excess 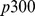 .
.
The activation and stabilization of 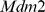 induced by
induced by 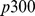 is shown in Fig. 9. Since
is shown in Fig. 9. Since 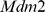 is counter part of
is counter part of 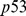 which is activated by
which is activated by 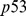 , similar results are obtained as in the case of
, similar results are obtained as in the case of 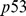 . The first stabilization regime is within [0–0.23] values of
. The first stabilization regime is within [0–0.23] values of 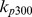 , followed by activation regime [
, followed by activation regime [ 0.23–0.7] and finally second stabilization regime [
0.23–0.7] and finally second stabilization regime [ 0.7–
0.7– ]. The increased level of
]. The increased level of 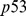 in the second stabilization regime are capped
in the second stabilization regime are capped 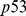 level which are prohibited from decay and taking part in any other reactions and therefore is not able to activate
level which are prohibited from decay and taking part in any other reactions and therefore is not able to activate 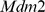 level. Hence its level reduces to minimum as soon as the second stabilization regime is reached.
level. Hence its level reduces to minimum as soon as the second stabilization regime is reached.
Figure 9. Stability curve induced by 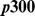 .
.
Plots of 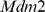 concentration level as a function of
concentration level as a function of 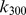 for different values of exposure times i.e.
for different values of exposure times i.e. 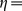 10–100 (at constant value of
10–100 (at constant value of 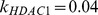 ). In the curve stabilized and activated regimes are demarcated.
). In the curve stabilized and activated regimes are demarcated.
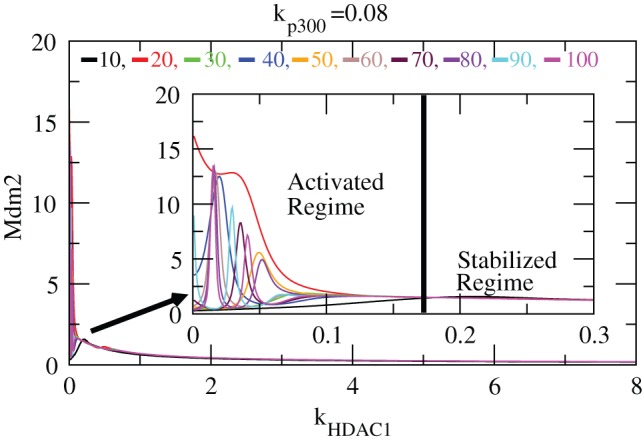
Next we study the impact of 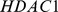 on
on 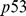 stabilization in our system. This is done by keeping the value of
stabilization in our system. This is done by keeping the value of 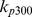 fixed at 0.08 and simulating the level of
fixed at 0.08 and simulating the level of 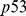 as a function of
as a function of 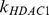 for different exposure times 10–100 hours (Fig. 10). From the plots one can see the activation of
for different exposure times 10–100 hours (Fig. 10). From the plots one can see the activation of 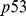 at low
at low 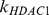 values due to
values due to 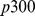 impact but not due to
impact but not due to 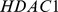 contribution. As
contribution. As 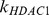 value increases, the
value increases, the 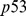 level starts decreasing due the deacetylation of
level starts decreasing due the deacetylation of 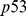 which allow it to degrade and take part in reactions. The activation of
which allow it to degrade and take part in reactions. The activation of 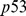 with fluctuation persists till
with fluctuation persists till 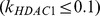 . After
. After 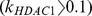 ,
, 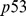 level remains constant for a short period of time and then its level starts increasing without fluctuation. This behaviour indicates that
level remains constant for a short period of time and then its level starts increasing without fluctuation. This behaviour indicates that 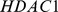 has suppressing impact on
has suppressing impact on 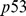 activation. This pattern is same for all exposure times as is shown in the plots (Fig. 10). The same pattern is found for
activation. This pattern is same for all exposure times as is shown in the plots (Fig. 10). The same pattern is found for 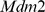 also which in fact is the counterpart of
also which in fact is the counterpart of 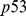 . The activated and stabilized regimes are shown in the Fig. 11.
. The activated and stabilized regimes are shown in the Fig. 11.
Figure 10. Stability curve induced by 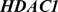 .
.
The variation of  concentration level versus
concentration level versus 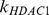 for different exposure times
for different exposure times  = 10–100, keeping
= 10–100, keeping 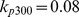 fixed. The inset is the enlarged portion of the actively activated regime.
fixed. The inset is the enlarged portion of the actively activated regime.
Figure 11. Stability curve induced by  .
.
The variation of  concentration level versus
concentration level versus 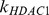 for different exposure times
for different exposure times 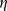 = 10–100, keeping
= 10–100, keeping 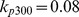 fixed. The inset is the enlarged portion of the activated and stabilized regimes.
fixed. The inset is the enlarged portion of the activated and stabilized regimes.
We then present the results of amplitudes of 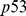 , (
, (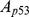 ) and time period, (
) and time period, (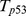 ) as a function of
) as a function of 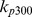 and
and 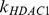 to understand the how
to understand the how 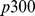 and
and 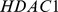 influence the amplitude and time period of
influence the amplitude and time period of 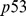 oscillations (Fig. 12). The calculation of
oscillations (Fig. 12). The calculation of 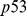 amplitude is done as in the following. For sustain oscillation we took time range of [100–200] hours in our calculation and then calculated the average of it. Then we take 50 such time series for different initial conditions and determine the average of p53 amplitude again (Fig. 12 and 13). The points in the plots are average points with error bars. For damped oscillations, we take the available number of oscillations and calculated the average of those oscillations which is found to be equivalent to the distance between x-axis and line which shows no oscillation (stable line) approximately. Similarly, for stabilized regime we determine distance between x-axis and stable line for each values of
amplitude is done as in the following. For sustain oscillation we took time range of [100–200] hours in our calculation and then calculated the average of it. Then we take 50 such time series for different initial conditions and determine the average of p53 amplitude again (Fig. 12 and 13). The points in the plots are average points with error bars. For damped oscillations, we take the available number of oscillations and calculated the average of those oscillations which is found to be equivalent to the distance between x-axis and line which shows no oscillation (stable line) approximately. Similarly, for stabilized regime we determine distance between x-axis and stable line for each values of 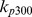 or
or 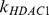 and average over 50 time series. Initially,
and average over 50 time series. Initially, 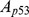 remains constant at lowest value for small values [0–0.05] of
remains constant at lowest value for small values [0–0.05] of 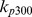 , then it monotonically increases and decrease in the interval [0.05–0.3] and finally its value remains constant. This in fact is the consequence of first stability (normal condition) where the impact of
, then it monotonically increases and decrease in the interval [0.05–0.3] and finally its value remains constant. This in fact is the consequence of first stability (normal condition) where the impact of 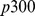 is negligible, then activation of
is negligible, then activation of 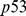 due to interaction of
due to interaction of 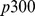 with
with 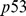 and other proteins and then stabilization of
and other proteins and then stabilization of 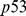 . These three regimes can also be seen in the case of
. These three regimes can also be seen in the case of 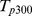 versus
versus 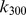 plot.
plot.
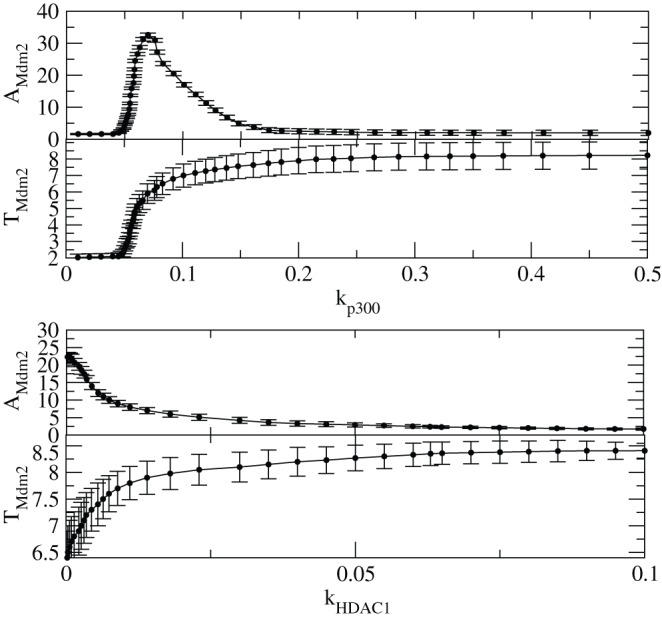
Figure 12. The variation of 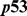 amplitude and time period induced by
amplitude and time period induced by  .
.
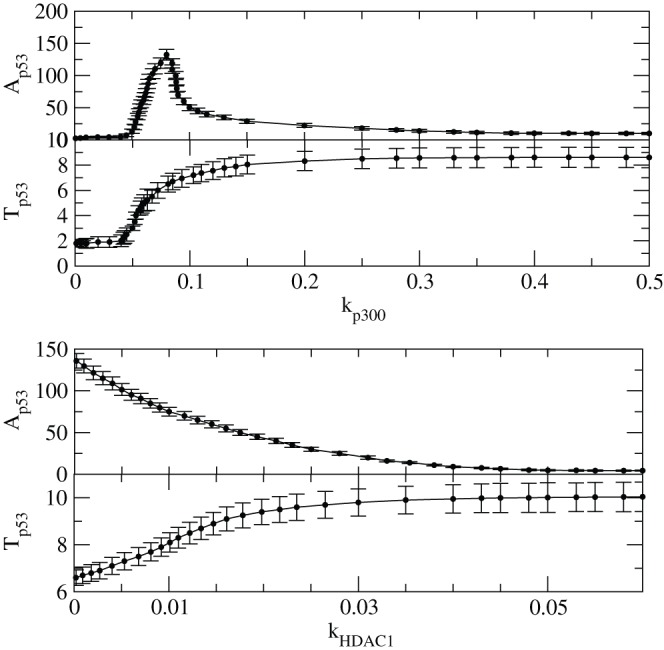
(a) Plots of  and
and  as a function of
as a function of 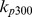 (upper two panels) which capture the stabilized and activated regimes. (b) Plots of
(upper two panels) which capture the stabilized and activated regimes. (b) Plots of 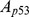 and
and 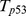 as a function of
as a function of 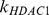 (lower two panels) which capture the stabilized and activated regimes.
(lower two panels) which capture the stabilized and activated regimes.
Figure 13. The variation of 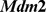 amplitude and time period induced by
amplitude and time period induced by 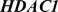 .
.
(a) Plots of 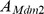 and
and 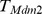 as a function of
as a function of 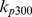 (upper two panels) which capture the stabilized and activated regimes. (b) Plots of
(upper two panels) which capture the stabilized and activated regimes. (b) Plots of 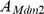 and
and 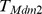 as a function of
as a function of 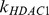 (lower two panels) which capture the stabilized and activated regimes.
(lower two panels) which capture the stabilized and activated regimes.
However, in the case of 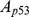 and
and 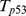 induced by
induced by 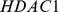 , the first stability condition is not observed because the cell is already activated with a constant
, the first stability condition is not observed because the cell is already activated with a constant 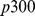 level i.e. at constant
level i.e. at constant 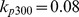 . In this case
. In this case 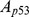 level decreases as
level decreases as 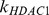 increases till
increases till 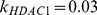 and the remains constant. However,
and the remains constant. However, 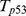 increases till
increases till 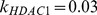 and then stabilized.
and then stabilized.
Similarly we calculated 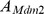 and
and 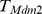 as a function of
as a function of 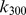 and
and 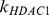 respectively and the results are shown in Fig. 12. For both the parameters similar behaviour was obtained as in the case of
respectively and the results are shown in Fig. 12. For both the parameters similar behaviour was obtained as in the case of 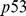 .
.
Deterministic steady state solutions: impact of 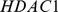 and
and 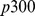 on
on 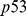
The steady state solutions in deterministic case can be obtained by putting the conditions 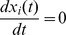 ,
, 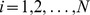 , where
, where 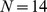 , to the set of differential equations (3)–(16) and solving for various variables
, to the set of differential equations (3)–(16) and solving for various variables 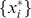 . Following this procedure we first solve for
. Following this procedure we first solve for 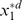 (steady state solution of p53) as a function of
(steady state solution of p53) as a function of 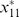 (steady state solution of HDAC1). The result is given by,
(steady state solution of HDAC1). The result is given by,
| (31) |
where, 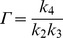 ,
, 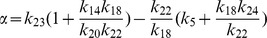 ,
, 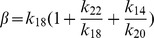 and
and 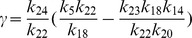 are constants. The equation (31) shows that the increase in
are constants. The equation (31) shows that the increase in 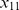 leads to increase in
leads to increase in  and second term in the equation is the main contributer. The reason being as
and second term in the equation is the main contributer. The reason being as  increases the third term
increases the third term 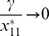 and the first term is a constant. Further, increase in
and the first term is a constant. Further, increase in 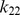 (degradation rate of HDAC1) and
(degradation rate of HDAC1) and 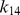 (degradation rate of p300) contribute increase in
(degradation rate of p300) contribute increase in 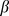 , and therefore increases the steady state level of
, and therefore increases the steady state level of 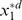 . From the expression of
. From the expression of  , one can see that if
, one can see that if 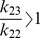 (p300 synthesis rate is larger than HDAC1 degradation rate),
(p300 synthesis rate is larger than HDAC1 degradation rate),  will contribute positive to
will contribute positive to 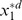 , otherwise it will give negative contribution.
, otherwise it will give negative contribution.
Proceeding in the same way, the steady state solution of 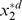 (Mdm2) can be obtained as a function of
(Mdm2) can be obtained as a function of 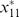 . The result is given by,
. The result is given by,
| (32) |
where, 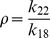 and
and 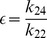 are constants. It can also be seen from the equation (32) that
are constants. It can also be seen from the equation (32) that 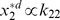 (
(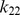 is degradation rate of HDAC1). Further for positive
is degradation rate of HDAC1). Further for positive 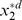 , we have the condition
, we have the condition 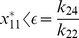 which means that the creation rate of HDAC1 (
which means that the creation rate of HDAC1 (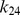 ) should be larger than degradation rate of HDAC1 (
) should be larger than degradation rate of HDAC1 (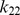 ) provided the condition. This behaviours can be seen in Fig. 8.
) provided the condition. This behaviours can be seen in Fig. 8.
Next we solve for steady state solution 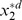 of
of 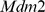 as a function of
as a function of 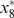 (steady state solution of p300) to study the impact of p300 on Mdm2. The result is given by,
(steady state solution of p300) to study the impact of p300 on Mdm2. The result is given by,
| (33) |
where, 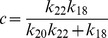 ,
, 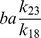 and
and 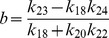 are constants. From equation (33) for positive
are constants. From equation (33) for positive 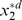 one can either
one can either 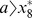 and
and 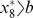 or
or 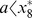 and
and 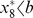 . Moreover
. Moreover 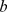 to be positive the condition
to be positive the condition 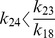 should be satisfied.
should be satisfied.
Now we solve steady state solution of 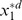 as a function of
as a function of 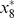 to understand the impact of p300 on p53. The result is given by,
to understand the impact of p300 on p53. The result is given by,
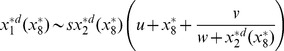 |
(34) |
where, 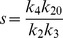 ,
, 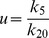 ,
, 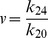 and
and 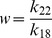 are constants.
are constants. 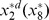 is given by the equation (33). The equation (34) indicates that
is given by the equation (33). The equation (34) indicates that 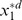 is increased by increase in
is increased by increase in 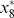 but decrease in
but decrease in 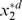 . Further if
. Further if 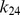 , the sysnthesis rate of HDAC1 is increased then
, the sysnthesis rate of HDAC1 is increased then 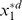 will also be increased. It can also be seen from
will also be increased. It can also be seen from  and (34) that
and (34) that 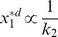 (synthesis rate of Mdm2).
(synthesis rate of Mdm2).
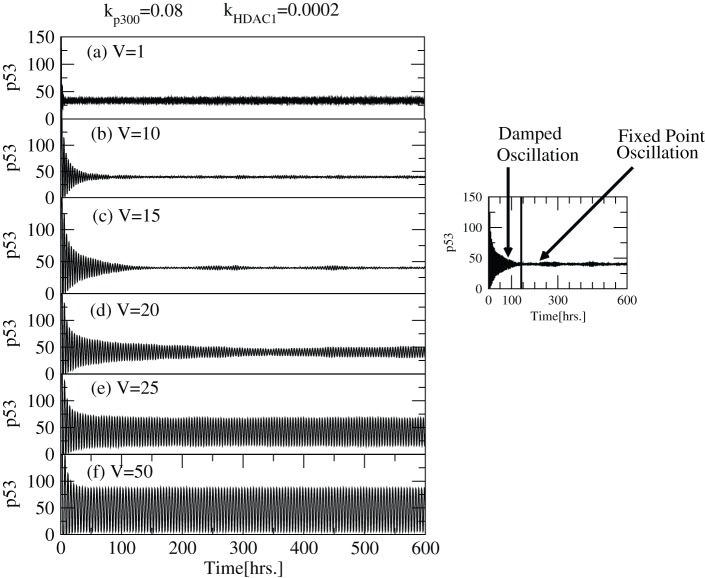
The role of noise and stabilization on 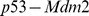 regulation
regulation
Now we present the role of noise on 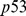 and
and 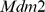 dynamics. This is done by solving the CLE equations (16)-(29) numerically. The results for different system size parameter,
dynamics. This is done by solving the CLE equations (16)-(29) numerically. The results for different system size parameter, 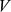 (1-50) at constant values of
(1-50) at constant values of 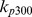 and
and 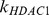 , are shown in Fig. 14 (a)–(f). It has been observed that for
, are shown in Fig. 14 (a)–(f). It has been observed that for 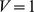 , no oscillation in
, no oscillation in 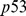 is seen. However, as
is seen. However, as 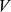 increases the oscillation starts emerging and when
increases the oscillation starts emerging and when 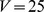 and 50 sustained oscillations are observed with increasing
and 50 sustained oscillations are observed with increasing 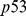 level. After
level. After  i.e. for
i.e. for 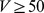 , the
, the 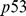 level remains constant i.e. it exhibits sustained oscillatory behaviour. The
level remains constant i.e. it exhibits sustained oscillatory behaviour. The 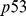 dynamics is noise induced stochastic process and the strength of noise decreases as
dynamics is noise induced stochastic process and the strength of noise decreases as 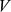 increases. The same behaviour is also seen in
increases. The same behaviour is also seen in 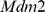 dynamics keeping all conditions the same (Fig. 14 (a)–(f)).
dynamics keeping all conditions the same (Fig. 14 (a)–(f)).
Figure 14. Noise contribution on 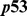 dynamics in stochastic system.
dynamics in stochastic system.
The variation of 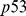 as a function of time in hours in stochastic system for different values of system size,
as a function of time in hours in stochastic system for different values of system size, 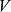 = 1, 10, 15, 20, 25, 50 (at constant values of
= 1, 10, 15, 20, 25, 50 (at constant values of 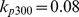 and
and 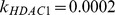 ).
).
Now we present the impact of 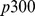 on
on 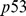 and
and 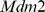 in stochastic system by simulating
in stochastic system by simulating 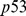 and
and 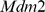 levels as a function of
levels as a function of 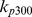 for different
for different 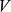 (Fig. 15). The result for
(Fig. 15). The result for 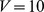 shows similar pattern as we found in the deterministic case, but the two conditions of stabilization and activation is achieved earlier with respect to
shows similar pattern as we found in the deterministic case, but the two conditions of stabilization and activation is achieved earlier with respect to 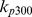 in stochastic case than that of the deterministic case as shown in the insets of the Fig. 15. Further, as one increases
in stochastic case than that of the deterministic case as shown in the insets of the Fig. 15. Further, as one increases 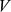 , the values
, the values 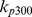 for getting the two conditions of stabilization and activation are increased.
for getting the two conditions of stabilization and activation are increased.
Figure 15. Noise contribution on 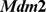 dynamics in stochastic system.
dynamics in stochastic system.

The variation of 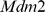 as a function of time in hours in stochastic system for different values of system size,
as a function of time in hours in stochastic system for different values of system size, 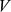 = 1, 10, 15, 20, 25, 50 (at constant values of
= 1, 10, 15, 20, 25, 50 (at constant values of 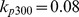 and
and 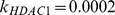 ).
).
The dynamics of  concentration remains constant with small fluctuations around the constant values of
concentration remains constant with small fluctuations around the constant values of  even though there is a small damping behavior at initial few hours. We then define
even though there is a small damping behavior at initial few hours. We then define  as the critical time below which the dynamics either shows damped or fixed point (stabilized) oscillations. The plot
as the critical time below which the dynamics either shows damped or fixed point (stabilized) oscillations. The plot  in Fig. 16 shows the damped, stabilized and oscillatory regimes. To generate this plot we took 50 simulations for a certain fixed set of parameters and points in the curves show average values with error bars which are correct up to of the order of 5-10 percent in our calculation as shown in Fig. 16. The plots show how system size, which can be taken as noise parameter (as V increases noise strength decreases and vice versa), drives the system at different states, namely, damped, stabilized (no oscillation) and sustain oscillation regimes.
in Fig. 16 shows the damped, stabilized and oscillatory regimes. To generate this plot we took 50 simulations for a certain fixed set of parameters and points in the curves show average values with error bars which are correct up to of the order of 5-10 percent in our calculation as shown in Fig. 16. The plots show how system size, which can be taken as noise parameter (as V increases noise strength decreases and vice versa), drives the system at different states, namely, damped, stabilized (no oscillation) and sustain oscillation regimes.
Figure 16. Phase diagram on  and
and  dynamics in stochastic system.
dynamics in stochastic system.
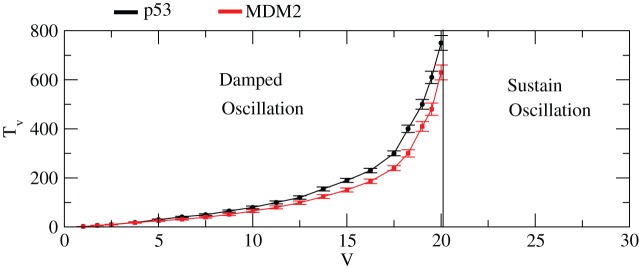
Phase diagram indicating damped and sustained oscillation regimes induced by system size,  .
.
We also study the impact of exposure time (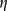 ) on
) on 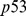 activation and stabilization for different values of
activation and stabilization for different values of 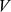 keeping the value of
keeping the value of 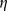 constant. We can see from the two left panels with insets in Fig. 15 that as
constant. We can see from the two left panels with insets in Fig. 15 that as 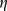 increases the conditions of stabilization and activation are obtained faster.
increases the conditions of stabilization and activation are obtained faster.
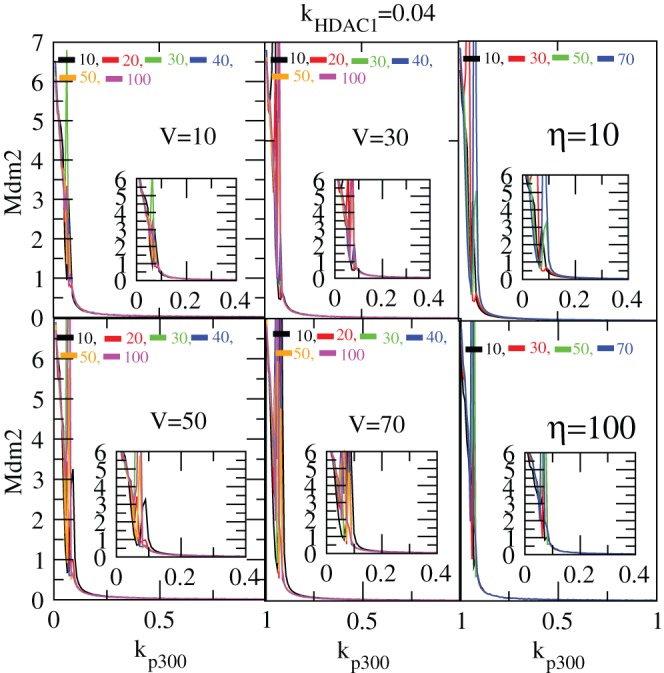
The results showing the impact of 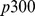 on
on 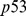 in stochastic system for different
in stochastic system for different 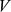 s and
s and 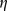 s are presented in Fig. 17. We also get the similar behaviour in the case as obtained in the case of
s are presented in Fig. 17. We also get the similar behaviour in the case as obtained in the case of 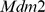 as shown in Fig. 18.
as shown in Fig. 18.
Figure 17. Stabilization of 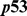 in stochastic system.
in stochastic system.
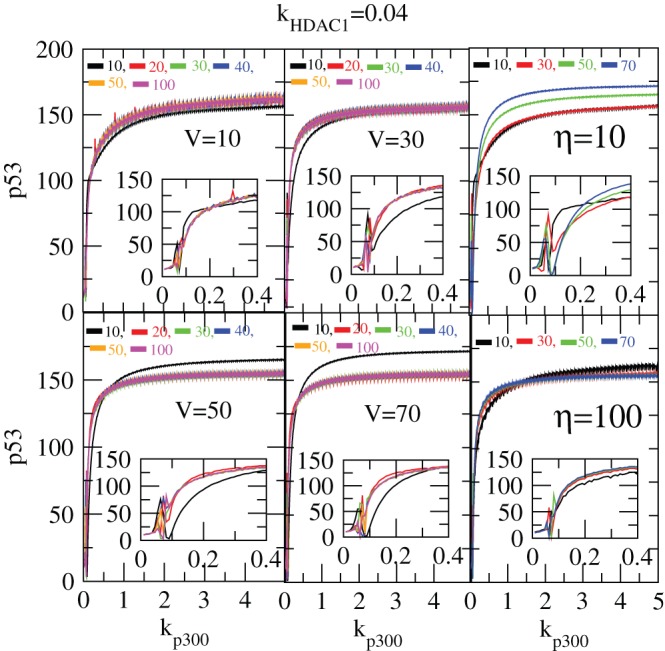
(a) Plots of  concentration levels as a function of
concentration levels as a function of  for different values of system size, V = 10, 30, 50 and 70 and for different values of
for different values of system size, V = 10, 30, 50 and 70 and for different values of  = [10–100] as shown in the four left panels. The insets show the enlarged portions of the activated regimes in each case. (b) Plots of
= [10–100] as shown in the four left panels. The insets show the enlarged portions of the activated regimes in each case. (b) Plots of 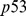 level versus
level versus 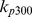 for different V = 10, 30, 50, 70 and for two different values of
for different V = 10, 30, 50, 70 and for two different values of 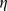 = 10 and 100 respectively as shown in two right hand panels.
= 10 and 100 respectively as shown in two right hand panels.
Figure 18. Stabilization of 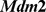 in stochastic system.
in stochastic system.
(a) Plots of 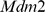 concentration levels as a function of
concentration levels as a function of 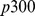 for different values of system size, V = 10, 30, 50 and 70 and for different values of
for different values of system size, V = 10, 30, 50 and 70 and for different values of  = [10–100] as shown in the four left panels. The insets show the enlarged portions of the activated regimes in each case. (b) Plots of
= [10–100] as shown in the four left panels. The insets show the enlarged portions of the activated regimes in each case. (b) Plots of 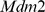 level versus
level versus 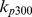 for different V = 10, 30, 50, 70 and for two different values of
for different V = 10, 30, 50, 70 and for two different values of 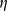 = 10 and 100 respectively as shown in two right hand panels.
= 10 and 100 respectively as shown in two right hand panels.
Stochastic steady state solutions: the noise effect
The steady state solutions of CLE can also be obtained as we did in deterministic case from the equations (17)–(30). We first impose steady state condition to the set of CLEs i.e. 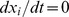 and got a set of steady state equations which are very difficult to solve. However, the steady state solutions can be obtained if we neglect negligible terms which have
and got a set of steady state equations which are very difficult to solve. However, the steady state solutions can be obtained if we neglect negligible terms which have  and
and 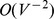 and rearrange the terms to solve the equations. Then one can easily solve simplified steady state equations. Proceeding in this way, the stochastic steady state solution of
and rearrange the terms to solve the equations. Then one can easily solve simplified steady state equations. Proceeding in this way, the stochastic steady state solution of 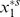 as a function of
as a function of 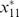 is obtained and given by,
is obtained and given by,
| (35) |
where, 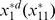 is given by equation (31) and we have taken the noise parameters
is given by equation (31) and we have taken the noise parameters 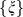 associated with each noise term are taken to be the same as
associated with each noise term are taken to be the same as 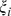 . The noise term
. The noise term 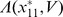 is given by,
is given by,
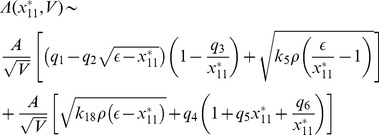 |
(36) |
where, 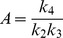 ,
, 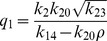 ,
, 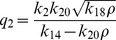 ,
, 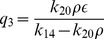 ,
, 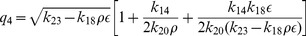 ,
, 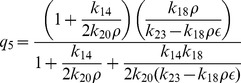 , and
, and 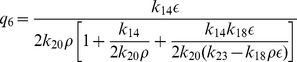 are constants. It can be seen from equation (36) that the terms apart from first term and last terms in the last paranthesis will contribute to
are constants. It can be seen from equation (36) that the terms apart from first term and last terms in the last paranthesis will contribute to  only when
only when 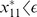 . Hence for
. Hence for 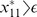 , the equation (36) will have the following expression,
, the equation (36) will have the following expression,
| (37) |
where, 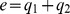 ,
, 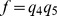 and
and 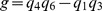 . It can also be seen from
. It can also be seen from 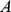 and equation (36)-(37)that
and equation (36)-(37)that 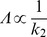 .
.
Next we calculated the steady state solution of 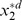 as a function of
as a function of  . The result can be expressed along with the deterministic result as shown in equation (32) with noise term. It is given by,
. The result can be expressed along with the deterministic result as shown in equation (32) with noise term. It is given by,
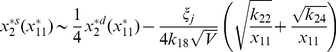 |
(38) |
where, 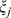 is the random noise parameter which we have taken same for all terms involved in the derivation. The noise contribution in this case is negative to the deterministic result which reduces steady state level of
is the random noise parameter which we have taken same for all terms involved in the derivation. The noise contribution in this case is negative to the deterministic result which reduces steady state level of 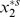 as the strength of noise increases. Further the increase in degradation and synthesis rate of HDAC1 (
as the strength of noise increases. Further the increase in degradation and synthesis rate of HDAC1 (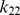 ) lead to increase in noise contribution which in turn decreases
) lead to increase in noise contribution which in turn decreases 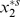 .
.
Similarly, the stochastic steady state solutions of 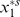 and
and 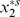 as a function of
as a function of  along with their respective deterministic solutions given by equations (33) and (34) can also be calculated. The results are given by,
along with their respective deterministic solutions given by equations (33) and (34) can also be calculated. The results are given by,
| (39) |
and
| (40) |
where, 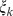 and
and 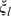 are random noise parameters for equations (39) and (40) respectively. The function
are random noise parameters for equations (39) and (40) respectively. The function  is given by
is given by
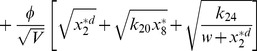 |
(41) |
where, 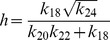 ,
, 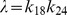 ,
, 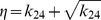 and
and 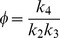 are constants. The noise function
are constants. The noise function 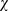 is mainly contributed from first, 5th and 6th terms in equation (41) and
is mainly contributed from first, 5th and 6th terms in equation (41) and 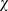 is positive contributor to the deterministic part. From these main contributing terms, the synthesis rate of HDAC1,
is positive contributor to the deterministic part. From these main contributing terms, the synthesis rate of HDAC1, 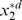 and
and 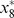 and their variation give significant contributions to the noise terms in equations (39) and (40). However noise contribution in equation (40) is negative contributor to the deterministic part.
and their variation give significant contributions to the noise terms in equations (39) and (40). However noise contribution in equation (40) is negative contributor to the deterministic part.
Conclusion
The interaction of 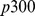 with
with 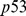 allows
allows 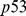 to be acetylated which prohibits it from decaying and allows it to participate in other reactions. This excess in
to be acetylated which prohibits it from decaying and allows it to participate in other reactions. This excess in 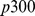 level eventually leads to increase in capped
level eventually leads to increase in capped 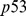 whose population cannot be controlled and subjects the cell to stress condition. If the excess in
whose population cannot be controlled and subjects the cell to stress condition. If the excess in 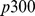 level is strong enough it may lead to cell death due to uncontrolled
level is strong enough it may lead to cell death due to uncontrolled  , similar to cancer. We observe this phenomena in our simulation results in qualitative sense via three different stages/conditions, namely, first stabilization or normal condition where impact of
, similar to cancer. We observe this phenomena in our simulation results in qualitative sense via three different stages/conditions, namely, first stabilization or normal condition where impact of  is negligible, second activation of
is negligible, second activation of  due to significant interaction between
due to significant interaction between  and
and 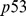 , and third uncontrolled growth of capped
, and third uncontrolled growth of capped 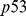 due to interaction with excess
due to interaction with excess 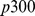 leading to second stabilization level which may represent cell death condition. The same behaviour is seen in
leading to second stabilization level which may represent cell death condition. The same behaviour is seen in 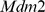 simulation results. The three conditions of stabilization and activation are obtained but the second stabilization level is obtained at lower level as compared to first stabilization level. This may be due to the fact that the increase of capped
simulation results. The three conditions of stabilization and activation are obtained but the second stabilization level is obtained at lower level as compared to first stabilization level. This may be due to the fact that the increase of capped 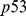 cannot activate
cannot activate 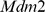 as is done normally, and goes to lower minimum level.
as is done normally, and goes to lower minimum level.
The interaction of 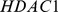 with
with 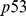 will cause deacetylation of capped
will cause deacetylation of capped 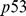 which leads
which leads 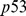 to participate in other reactions and able to decay. This may help the already stressed cell to bring back to its normal condition. However excess of
to participate in other reactions and able to decay. This may help the already stressed cell to bring back to its normal condition. However excess of 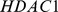 will cause excess deacetylation of
will cause excess deacetylation of 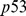 and will allow the cell to come back far beyond to its normal condition leading to stress. Our results supports these findings.
and will allow the cell to come back far beyond to its normal condition leading to stress. Our results supports these findings.
Noise has interesting but contrasting roles in stochastic system depending upon its strength. If its strength is strong then it has destructive impact on the signal processing in and outside the system etc. However if its strength is weak then it exhibit constructive role, for example weak signal detection, amplification and processing the signal etc. In our study, we found that if the system size is very small where the noise strength is very strong with respect to system size, the associated noise destroy the signal in the system which is in agreement with the theoretical claim. But if the system size is increased in our study where noise strength is comparatively weaker, the signal is resumed in normal with noise induced dynamics in each variable. Moreover, in stochastic system, the 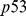 /
/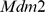 is activated by small concentration level of
is activated by small concentration level of 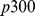 /
/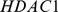 as compared to those in deterministic case and reach stabilization much much faster as compared to deterministic system. Further increase in system size reduces the noise fluctuation in the dynamics of each variable and when
as compared to those in deterministic case and reach stabilization much much faster as compared to deterministic system. Further increase in system size reduces the noise fluctuation in the dynamics of each variable and when 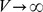 , the noise strength is negligible and the system goes to classical deterministic system.
, the noise strength is negligible and the system goes to classical deterministic system.
In the present study we determine only the impact of 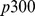 and
and 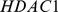 on
on 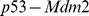 regulatory network. For developing any realistic model one needs to incorporate other proteins which influence
regulatory network. For developing any realistic model one needs to incorporate other proteins which influence 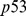 protein simultaneously and then study the impact collectively. Our study is just one step forward towards understanding p53 regulatory network.
protein simultaneously and then study the impact collectively. Our study is just one step forward towards understanding p53 regulatory network.
Acknowledgments
RKBS and Md. J. Alam gratefully acknowledge University Grants Commission (UGC) for the financial support to carry out some part of this work.
Funding Statement
Dr. Brojen Singh has received partial financial support for this work from University Grants Commission. However Dr. Subhash Agarwal has worked without any financial support from any funding agency. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Toledo F, Wahl GM (2006) Regulating the p53 pathway: in vitro hypotheses, in vivo veritas. Nat Rev Cancer 6: 909–23. [DOI] [PubMed] [Google Scholar]
- 2. Lane DP (1992) p53, guardian of the genome. Nature 358: 15–16 doi:10.1038/358015a0. [DOI] [PubMed] [Google Scholar]
- 3. Vousden KH (2000) p53: death star. Cell 103: 691–4. [DOI] [PubMed] [Google Scholar]
- 4. Levine AJ (1997) p53, the cellular gatekeeper for growth and division. Cell 88: 323–31. [DOI] [PubMed] [Google Scholar]
- 5. Bai L, Zhu W-G (2006) p53: Structure, Function and Therapeutic Applications. J. Cancer Mol. 2: 141–153. [Google Scholar]
- 6. Finlay CA (1993) The mdm-2 oncogene can overcome wild-type p53 suppression of transformed cell growth. Mol Cell Biol 13: 301–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Carter S, Vousden KH (2008) p53-Ubl fusions as models of ubiquitination, sumoylation and neddylation of p53. Cell Cycle 7: 2519–2528. [DOI] [PubMed] [Google Scholar]
- 8. Lambert PF, Kashanchi F, Radonovich MF, Shiekhattar R, Brady JN (1998) Phosphorylation of p53 serine 15 increases interaction with CBP. J Biol Chem. 273: 33048–53. [DOI] [PubMed] [Google Scholar]
- 9. Grossman SR, Perez M, Kung AL, Joseph M, Mansur C, et al. (1998) p300/MDM2 complexes participate in MDM2-mediated p53 degradation. Mol Cell. 2: 405–415. [DOI] [PubMed] [Google Scholar]
- 10. Zeng X, Chen L, Jost CA, Maya R, Keller D, et al. (1999) MDM2 suppresses p73 function without promoting p73 degradation. Mol Cell Biol (19) 3257–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Meek DW, Anderson CW (2009) Posttranslational Modification of p53: Cooperative Integrators of Function. Cold Spring Harb. Perspect. Biol. 00: a000950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Leslie PH (1958) A Stochastic Model for Studying the Properties of Certain Biological Systems by Numerical Methods. Biometrika 45: 16–31. [Google Scholar]
- 13. Gillespie DT (1977) Exact stochastic simulation of coupled chemical reactions. J. Phy. Chem. 31: 2340–2361. [Google Scholar]
- 14. Mc Quarrie DA (1967) Stochastic approach to chemical kinetics. J. Appl. Probab. 4: 413. [Google Scholar]
- 15. Anishchenko VS, Neiman AB, Moss F, Schimansky-Geier L (1999) Stochastic resonance: noise-enhanced order. Physcs-Uspekhi 42: 7–36. [Google Scholar]
- 16. Hanggi P (2002) Stochastic resonance in biology how noise can enhance detection of weak signals and help improve biological information processing. ChemPhysChem 3: 285–290. [DOI] [PubMed] [Google Scholar]
- 17. Blake WJ, Kaern M, Cantor CR, Collins JJ (2003) Noise in eukaryotic gene expression. Nature 422: 633637. [DOI] [PubMed] [Google Scholar]
- 18. Becskei A, Seraphin B, Serrano L (2001) Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion. EMBO J 20: 25282535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Weinberger LS, Burnett JC, Toettcher JE, Arkin AP, Schaffer DV (2005) Stochastic gene expression in a lentiviral positive-feedback loop: HIV-1 Tat fluctuations drive phenotypic diversity. Cell 122: 169182. [DOI] [PubMed] [Google Scholar]
- 20. Kussell E, Leibler S (2005) Phenotypic diversity, population growth, and information in fluctuating environments. Science 309: 20752078. [DOI] [PubMed] [Google Scholar]
- 21. Kubbutat MHG, Jones SN, Vousden KH (1997) Regulation of p53 stability by Mdm2. Natute 387: 299. [DOI] [PubMed] [Google Scholar]
- 22. Proctor CJ, Gray DA (2008) Explaining oscillations and variability in the p53-Mdm2 system. BMC Systems Biol. 2: 75 doi:10.1186/1752-0509-2-75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Rodriguez MS, Desterro JMP, Lain S, Lane DP, Hay RT (2000) Multiple C-Terminal Lysine Residues Target p53 for Ubiquitin-Proteasome-Mediated Degradation. Mol. Cell Biol. 20: 8458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Grossman SR, Deato ME, Brignone C, Chan HM, Kung AL, et al. (2003) Polyubiquitination of p53 by p300. Science 300: 342–344. [DOI] [PubMed] [Google Scholar]
- 25. Wagner J, Ma L, Rice JJ, Hu W, Levine AJ, et al. (2005) p53-Mdm2 loop controlled by a balance of its feedback strength and effective dampening using ATM and delayed feedback. IEE Proc-Syst. Biol. 152: 109. [DOI] [PubMed] [Google Scholar]
- 26. Dumaz N, Meek DW (1999) Serine 15 phosphorylation stimulates p53 transactivation but does not directly influence interaction with HDM2. EMBO J. 18: 7002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Gu W, Roeder RG (1997) Activation of p53 Sequence-Specific DNA Binding by Acetylation of the p53 C-Terminal Domain. Cell 90: 595–606. [DOI] [PubMed] [Google Scholar]
- 28. Kobet E, Zeng X, Zhu Y, Keller D, Lu H (2000) MDM2 inhibits p300-mediated p53 acetylation and activation by forming a ternary complex with the two proteins. Proc. Nat. Acad. Sc. 97: 1254712552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Ito A, Lai CH, Zhao X, Saito S, Hamilton MH, et al. (2001) p300/CBP-mediated p53 acetylation is commonly induced by p53-activating agents and inhibited by MDM2: EMBO J. 20: 1331–40 (2001).. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Knights CD, Catania J, Di Giovanni S, Muratoglu S, Perez R (2006) Distinct p53 acetylation cassettes differentially influence gene-expression patterns and cell fate: J Cell Biol. 173: 533–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Luo J, Li M, Tang Y, Laszkowska M, Roeder RG, et al. (2004) Acetylation of p53 augments its site-specific DNA binding both in vitro and in vivo: Proc. Natl. Acad. Sc. 101: 2259–2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Li, Luo J, Brooks CL, Gu W (2002) Acetylation of p53 Inhibits Its Ubiquitination by Mdm2. J Biol Chem. 277: 50607–50611. [DOI] [PubMed] [Google Scholar]
- 33. Ito A, Kawaguchi Y, Lai CH, Kovacs JJ, Higashimoto Y, et al. (2002) MDM2HDAC1-mediated deacetylation of p53 is required for its degradation. The EMBO J. 21: 6236–6245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Pavithra L, Mukherjee S, Sreenath K, Kar S, Sakaguchi K, et al. (2009) SMAR1 Forms a Ternary Complex with p53-MDM2 and Negatively Regulates p53-mediated Transcription. J. Mol. Biol. 388: 691. [DOI] [PubMed] [Google Scholar]
- 35. Gillespie DT (2007) Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 58: 35. [DOI] [PubMed] [Google Scholar]
- 36.van-Kampen NG (2007) Stochastic processes in Physics and Chemistry. Elsevier, New York.
- 37. Bratsun D, Volfson D, Tsimring LS, Hasty J (2005) Delay-induced stochastic oscillations in gene regulation. Proc. Nat. Acad. Sc. 102: 14593–14598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Cai X (2007) Exact stochastic simulation of coupled chemical reactions with delays. J. Chem. Phys. 126: 124108. [DOI] [PubMed] [Google Scholar]
- 39. Gillespie DT (2001) Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 115: 1716. [DOI] [PubMed] [Google Scholar]
- 40. Salis H, Kaznessis Y (2000) Accurate hybrid stochastic simulation of a system of coupled chemical or biochemical reactions. J. Chem. Phys. 122: 054103. [DOI] [PubMed] [Google Scholar]
- 41. Gillespie DT (2000) The chemical Langevin equation. J. Chem. Phys. 113: 297. [Google Scholar]
- 42.Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical Recipe in Fortran. Cambridge University Press.
- 43. Ciliberto A, Novak B, Tyson JJ (2005) Steady states and oscillations in the p53/Mdm2 network. Cell Cycle. 4: 488–493. [DOI] [PubMed] [Google Scholar]
- 44. Lev Bar-Or R, Maya R, Segel LA, Alon U, Levine AJ, et al. (2000) Generation of oscillations by the p53-Mdm2 feedback loop: a theoretical and experimental study. Proc Natl Acad Sci 97: 11250–11255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Zhang T, Brazhnik P, Tyson JJ (2007) Exploring mechanisms of the DNA-damage response: p53 pulses and their possible relevance to apoptosis. Cell Cycle. 6: 85–94. [DOI] [PubMed] [Google Scholar]
- 46. Lahav G, Rosenfeld N, Sigal A, Geva-Zatorsky N, Levine AJ, et al. (2004) Dynamics of the p53-Mdm2 feedback loop in individual cells. Nat Genet. 36: 147–150. [DOI] [PubMed] [Google Scholar]
- 47. Juan LJ, Shia WJ, Chen MH, Yang WM, Seto E, et al. (2000) Histone deacetylases specifically down-regulate p53-dependent gene activation. J Biol Chem. 275: 20436–20443. [DOI] [PubMed] [Google Scholar]
- 48. Luo J, Su F, Chen D, Shiloh A, Gu W, et al. (2000) Deacetylation of p53 modulates its effect on cell growth and apoptosis. Nature 408: 377–381. [DOI] [PubMed] [Google Scholar]