Center of Mass Acceleration Feedback Control of Standing Balance by Functional Neuromuscular Stimulation against External Postural Perturbations

Abstract

This study investigated the use of center of mass (COM) acceleration feedback for improving performance of a functional neuromuscular stimulation (FNS) control system to restore standing function to a subject with complete, thoracic-level spinal cord injury (SCI). The approach for linearly relating changes in muscle stimulation to changes in COM acceleration was verified experimentally and subsequently produced data to create an input-output map driven by sensor feedback. The feedback gains were systematically tuned to reduce upper extremity (UE) loads applied to an instrumented support device while resisting external postural disturbances. Total body COM acceleration was accurately estimated (> 89% variance explained) using three-dimensional (3-D) outputs of two accelerometers mounted on the pelvis and torso. Compared to constant muscle stimulation employed clinically, feedback control of stimulation reduced UE loading by 33%. COM acceleration feedback is advantageous in constructing a standing neuroprosthesis since it provides the basis for a comprehensive control synergy about a global, dynamic variable and requires minimal instrumentation. Future work should include tuning and testing the feedback control system during functional reaching activity that is more indicative of activities of daily living.

I. Introduction

The goal of this study was to develop and deploy a control system utilizing center of mass (COM) acceleration feedback to continuously adjust stimulation to paralyzed muscles so as to reduce the upper extremity (UE) loading required to maintain stable standing against postural perturbations. Functional neuromuscular stimulation (FNS) has been proven clinically effective for restoring basic standing function following spinal cord injury (SCI) [1]. Clinical usage relies on pre-programmed patterns of stimulation to produce sit-to-stand maneuvers and subsequently continuous, supramaximal stimulation to maintain upright posture. Under constant open-loop stimulation, the user is required to maintain balance against postural perturbations through voluntary UE interaction with a support structure (e.g., walker, countertop). Sustained UE loading compromises the utility of standing with FNS by limiting the functional use of the hands and arms and reducing standing time due to upper body fatigue. Feedback control of stimulation is necessary to provide automatic postural adjustments and reduce the burden on the UEs for balance and stability. A systematic perturbation paradigm was employed to evaluate basic controller operation prior to performance assessment in general clinical application.

Servo-type joint feedback has been extensively investigated for closed-loop control of standing with FNS. It has been implemented in isolation for individual joints including the knees [2, 3], hips [4, 5], and ankles [6]. These studies demonstrated moderate performance improvements in disturbance response but effectively constrained the standing system to single planes of movement using mechanical bracing or constant stimulation for joints not under direct feedback control. These limitations were justifiable given the initial challenges of implementing such control systems clinically with SCI subjects. Consequently, current standing systems still do not employ feedback control of FNS. Standing involves joint kinematics and multi-articulate muscle actions occurring in three-dimensional (3-D) space for functional movement [7]. The next step in advancing closed-loop FNS standing systems towards clinical utility is comprehensive operation by considering individual muscle effects in enacting control across the trunk, hip, knee, and ankle joints simultaneously and with minimal constraints to regulate balance posture in 3-D. We had previously investigated comprehensive FNS control in simulation and observed reduction (51%) in UE loading when utilizing active feedback of joint kinematics compared to the clinical analog of constant, maximal stimulation [8]. However, this system required tuning a total of 18 distinct gain parameters composed of proportional and derivative feedback from nine separate joints, which may be cumbersome and impractical for routine clinical deployment.

As an alternative to joint kinematics, linear acceleration of total body center of mass (COM) may be a more feasible option for feedback control of a standing neuroprosthesis. Acceleration has been previously shown as an effective means to assess standing balance [9 - 11], and it offers several potential advantages over joint-based control for standing with FNS. Firstly, it is sensitive to the inertial effects of rapidly acting perturbations and can facilitate control responses before significant changes in standing posture occur. Secondly, COM acceleration would provide a representation of global system dynamics, which have been focally implicated for standing balance control [12]. Finally, adequate measurement of COM acceleration may be plausible with only a few well-placed accelerometers since perturbed standing is well represented with a minimal number of synergies [13, 14] and nearly 75% of body mass is concentrated centrally across the pelvis, abdomen, and trunk [15]. We have previously conducted a simulation study [16] to conceptually develop and evaluate the potential of a control system for FNS standing using COM acceleration feedback inputs to produce optimal muscle excitation patterns that counter the effects of postural disturbances. This control system performed similarly to that relying on joint kinematics but utilized significantly fewer feedback parameters (2 versus 18) [17].

The current study serves as the next step in investigating this approach with a live-subject laboratory demonstration. We present the development and performance evaluation of a control system utilizing COM acceleration feedback to modulate stimulation delivered by a sixteen channel implanted pulse generator plus six additional channels of surface stimulation to an individual with complete paraplegia. The control system was tuned and evaluated according to the reduction in UE loading applied to an instrumented support device while resisting external disturbances from a laboratory perturbation system.

II. Methods

Development of the customized control system utilizing COM acceleration feedback for the subject participant involved a four-stage process: (1) Pilot perturbation sessions were performed to provide data for training a simple linear regression model that would accurately and reliably estimate total-body COM acceleration from a minimal set of acceleration measurements as inputs for feedback control. (2) Sessions were then performed to observe resultant changes in COM acceleration from normal, erect stance following changes in muscle stimulation from baseline levels. These data were then used to create an optimal acceleration-stimulation mapping represented by an artificial neural network (ANN). (3) The ANN was driven by proportional gain-modulated feedback of the anterior-posterior (AP) and medial-lateral (ML) components of COM acceleration to serve as the control system (Figure 1). Sessions to tune these controller gains to minimize UE loading against external perturbation were performed. (4) Finally, to evaluate controller performance, sessions were conducted to randomly apply perturbations with either the optimally-tuned feedback controller active or with application of clinically-determined constant stimulation levels.

Figure 1.

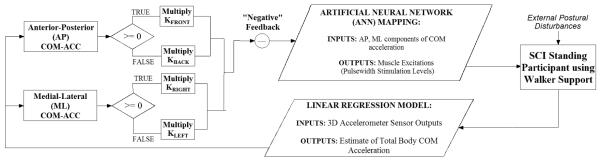
Flow Diagram for Overall Feedback Control System. Proportional feedback of total body center of mass (COM) acceleration (ACC) drove acceleration-stimulation mapping represented by artificial neural network (ANN) to modulate muscle stimulation levels and assist individual with spinal cord injury (SCI) to balance against postural disturbances while standing.

A. Subject and FNS Control System Hardware

The participant was a 54 year-old, female with T4 level complete paraplegia. She was approximately 170 cm tall and weighed 710 N. The subject signed informed consent forms approved by the Institutional Review Board of the Louis Stokes Cleveland Department of Veterans Affairs Medical Center. She was actively using a FNS system for restoration of basic standing function at the time of all experimental data collections. The system included a surgically implanted 16 channel stimulator-telemeter device (IST) [18] and universal external control unit (UECU) [19]. The UECU included toggle buttons and liquid crystal display (LCD) screen for operational control, lithium ion re-chargeable battery, inductive radiofrequency coil for implant communication, and serial communication control of 16 implant channels (delivered via intramuscular electrodes) and 8 surface channels of stimulation. Stimulation was applied via intramuscular electrodes implanted near innervation points to the following bilateral muscle groups: gastrocnemius/soleus (GS, ankle plantarflexion), tibialis anterior (TA, ankle dorsiflexion), quadriceps (QU, knee extension), semimembranosus/hamstrings (HS, hip extension), posterior adductor magnus (PA, hip extension), gluteus maximus (GM, hip extension), gluteus medius (ME, hip abduction) and erector spinae (ES, trunk extension). For QU, the electrode was surgically implanted near the femoral nerve to selectively activate all vasti groups and avoid recruitment of rectus femoris, which induces hip flexion that compromises erect neutral standing. The six additional surface stimulation channels were employed to introduce hip flexion and augment hip adduction and trunk extension via bilateral application to the erector spinae (ESs, trunk extension), rectus femoris (RF, hip flexion), and hip adductor (AD, hip adduction) muscle groups. The ground electrode for surface stimulation was placed on the abdomen or bony landmarks at either the kneecap or anterior superior iliac spine. Exact locations of surface electrode placement varied session to session based on clinical observation of which locations elicited the strongest stimulated responses along the desired anatomical planes of movement (i.e., hip flexion and trunk extension in sagittal plane, hip adduction in coronal plane).

Real-time control of stimulation was implemented with custom software developed to run in MATLAB®/SIMULINK® R14.3 and the xPC Target™ toolbox (Mathworks, Inc., Natick, MA). A Windows® (Microsoft, Inc., Redmond, WA) host computer was utilized to build customized applications, while a target computer with a Pentium Dual-Core 3 GHz microprocessor (Intel, Inc., Santa Clara, CA) with 2 GB of RAM was responsible for running the applications in real-time. The host and target communicated via TCP/IP protocol. Data were acquired using an NI PCI-6071E board (National Instruments, Inc., Austin, TX). Stimulation current was applied using charge balanced, biphasic pulses. Stimulation parameters under control included current pulse amplitude, duration (i.e., pulsewidth), and frequency. All real-time controller parameter updates and stimulation frequencies were fixed at 20 Hz. The pulse amplitude for all implanted stimulation channels was 20 mA except for those to the quadriceps and erector spinae, which were at 2 mA in accordance to clinical observation whereby the participant exhibited ample knee and trunk extension to stand erect without discomfort in respiratory function. Pulse amplitude for all surface stimulation channels was set at the maximum 100 mA. Stimulation pulsewidth (0 to 250 μs) was adjusted to modulate muscle excitation levels and produce controller-mediated corrections.

To ensure participant ability to comfortably and safely maintain near erect standing, non-zero minimum levels of stimulation pulsewidth were determined based on clinical observation for the channels activating the following core muscle groups bilaterally: QU, HS, PA, GM, and ES. Controller modulation of stimulation was never allowed to fall below these minimal levels to ensure the subject always maintained basic standing with FNS, including when no acceleration feedback was present (i.e., quiet erect standing). It was ultimately observed that even maximal increases in muscle stimulation from minimal levels for the core muscle groups did not elicit strong dynamic postural changes. Their contributions were subsequently omitted for feedback control of dynamic balance and were only activated for static postural support. This subject was able to maintain erect standing for between 1-2 hours each experimental session. Stimulated muscles, especially knee extensors, had developed high fatigue resistance from diligent daily use of the implanted FNS system and a commercially available rehabilitation bicycle.

B. Laboratory Perturbation Testing

Postural perturbations were applied while the subject performed neutral, bipedal standing (Figure 2) with each foot on a force platform (OR6-6-1000, Advanced Mechanical Technology, Inc., Watertown, MA). The participant balanced herself against postural disturbances by applying corrective loads with her upper extremities upon a customized support device composed of aluminum framing (80/20®, Inc., Columbia City, IN) and adjustable block mounts to interface left and right instrumented walker handles with 6-axis load cells (MCW-500, Advanced Mechanical Technology, Inc., Watertown, MA). All collected analog data were sampled at 100 Hz. For fall prevention, the participant wore a standard harness (distributed by McMaster-Carr, Inc., Elmhurst, IL) connected to a structurally reinforced overhead hook via safety lanyard (Guardian Fall Protection, Inc., Kent, WA).

Figure 2.

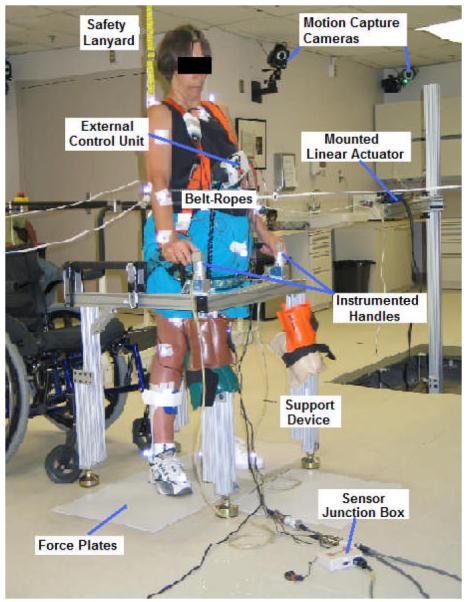
Photograph of study participant with SCI standing during external perturbation testing.

External perturbations were systematically applied as waist-level, force-pulse pulls by four electromagnetic linear actuators (STA2506, Copley Controls, Inc., Canton, MA). Each actuator was orthogonally directed (front, back, right, or left) to the standing participant along AP and ML planes. Simultaneous operation of the actuators was conducted through software developed in LabVIEW® (National Instruments, Austin, TX). The actuators were mounted on custom aluminum support structures (80/20®, Inc., Columbia City, IN) rigidly fixed to either the wall or laboratory subflooring. Nylon ropes were tied-off at one end to the weight belt worn at the subject’s waist, approximately at the level of her total body COM. At the other ends, ropes were quickly attached, length-adjusted, and released to the actuators using aluminum rope cleats (distributed by McMaster-Carr, Inc., Elmhurst, IL) fixed to the actuator piston rods. Actuator operation could be immediately halted according to experimenter discretion using a remote control power switch (SVAT WRC100 Indoor Remote Control Power Outlet).

All disturbances were 300 msec in duration. Five distinct disturbance magnitudes (M1 to M5) were determined for the subject in each direction. The maximum (M5) magnitude in each direction was determined as being barely tolerable according to the subject but still allowed efficient recovery to quiet, erect standing. In the forward direction, the five perturbation magnitude levels were 1, 3, 5, 7 and 9% BW. In both the right and the left directions, the five perturbation magnitude levels were 2, 4, 7, 10 and 12% BW. In the backward direction, the five perturbation magnitude levels were 1, 2, 3, 4 and 5% BW. Each external perturbation trial consisted of either 6 or 7 consecutive singular perturbations applied randomly as the subject did not know the direction or magnitude of the disturbance and the time between consecutive disturbances varied from 3 to 5 seconds. Three seconds was ample time for the subject to recover and return to quiet erect standing before onset of the next perturbation. The subject was instructed to keep eyes open and rely as little as possible on the support handles to maintain erect posture during steady-state standing and perturbation recovery.

C. STAGE 1: Estimating COM Acceleration for Feedback

Data Collection and Processing

Linear regression models to estimate COM accelerations were created during 10 pilot sessions with external perturbations applied to the subject while standing with constant stimulation. In each session, the subject was presented with each unique perturbation direction-magnitude pair three times for a total of 60 perturbations. The 3-D positions of body segments were measured with respect to a globally-fixed reference frame, with axes approximately aligned to anatomical AP and ML of the subject, using a VICON® MX digital motion capture system (Vicon Motion Systems and Peak Performance, Inc., Oxford, UK). All collected motion capture data were sampled at 100 Hz. Retro-reflective markers were placed on anatomical landmarks according to the defined PlugInGait marker set (C7 vertebra, clavicle, sacrum and bilateral shoulder, upper-arm, elbow, forearm, wrist, anterior superior iliac spine, thigh, knee, tibia, ankle, heel, and toe). These marker positions were used to estimate segment COM positions according to segment mass and COM location definitions from [15]. The segment COM positions were then used to calculate total body COM position. Retro-reflective marker data from these sessions were double-differentiated off-line and smoothed with a low-pass digital filter [20] to obtain 3-D acceleration of the aforementioned marker, segment COM, and total body COM positions.

Determination of Linear Regression Models

Using the data collected during external perturbation sessions and the Statistics Toolbox by MATLAB® (Mathworks, Inc., Natick, MA), a stepwise regression fit was applied to the set of segmental COM accelerations to determine a minimal set of segments most influential in estimating the total body COM acceleration with >90% variance accounted for (VAF). Ultimately, 80% of the collected trial data was selected randomly and utilized for determining the regression coefficients. The remaining 20% of the trial data were used as test data to verify goodness of fit. The 3-D acceleration data all segment COM locations defined were initially included in a stepwise regression as predictor variables to estimate the AP and ML components (AP, ML) of COM acceleration serving as the response variables. The segment sets that approximated the specified estimation accuracy of 90% VAF were identified, but the set with the fewest segments was identified as the target for instrumentation with 3-D accelerometers for subsequent feedback controller experiments.

A search algorithm was then applied to determine the location on each of the identified segments for placing a single 3-D accelerometer that would produce the best estimate of COM acceleration with simple linear regression. The algorithm applied a regression model at multiple test point locations between marker positions on the selected segments. The test locations that produced the best estimate were identified as the optimal accelerometer placements.

D. STAGE 2: Constructing Acceleration-Stimulation Map

Step 1

The first step was to determine the maximum COM acceleration (a_COM) induced from quiet erect standing due to the maximum change in activation for each muscle group targeted for stimulation (16 implant, 6 surface). The subject initially stood using the minimum stimulation levels previously described serving as baseline (M_base). From quiet erect standing, an instantaneous maximum change in muscle stimulation level (i.e., from baseline to maximum level) was applied for a single stimulation channel using a pulse train of 750 msec, which was the longest duration the subject could repeatedly tolerate. The maximum muscle stimulation level (M_max) for each corresponding muscle group equaled the maximum deliverable pulsewidth of 250 μs except right GS and left TA, which were limited to 50 μs and 125 μs, respectively, due to clinically observed subject tolerance.

For each trial, one pulse train was applied separately and consecutively to each muscle group with four seconds between applications. The maximum change (positive or negative) in COM acceleration in both the AP and ML dimensions occurring within a 500 msec window following onset of the stimulation pulse train was recorded as the trial value of a_COM for that stimulated muscle group. Selection of the 500 msec window was a methodological decision based on observations that it consistently captured the initial maximum acceleration occurring due to change in stimulation prior to subsequent maximal accelerations resulting from the subject’s reactions to stabilize with the arms. Four trials were conducted for each of 20 sessions yielding 80 test points for each muscle group. The average value across all 80 trials was assigned as the final a_COM for the given muscle group.

Step 2

The maximal changes in muscle stimulation, (ΔM_max = M_max - M_base) of individual muscle groups and the corresponding maximal changes in total body COM acceleration, a_COM, were used to determine the optimal mapping for feedback control. An optimization algorithm was formulated to determine the optimal muscle stimulation levels to produce a given COM acceleration target from the setpoint stance observed for quiet erect standing. The resultant acceleration-stimulation data served as the input-output data to train the ANN (see Step 3). For the optimization, the maximum stimulation level (M_max) and baseline muscle stimulation level (M_base) were normalized to equal 1 and 0, respectively, which bounded the corresponding normalized change in muscle stimulation (ΔM) over [0,1] for each muscle group.

Assuming initial muscle and joint kinematic states corresponding to quiet standing, instantaneous changes in muscle forces would be proportional to the respective induced accelerations. The instantaneous accelerations induced by individual muscles could be consequently summed to yield the net changes in total body COM acceleration. Given these assumptions, the linear constraint equations to be satisfied by the optimizer to yield targeted net COM acceleration targets (ACC_COM) were as follows:

$${\mathit{ACC}}_{\mathit{COM}-\mathit{AP}}=\sum _{i=1}^N{a}_{\mathit{COM}-\mathit{AP},j}{W}_j$$ (1)

$${\mathit{ACC}}_{\mathit{COM}-\mathit{ML}}=\sum _{i=1}^N{a}_{\mathit{COM}-\mathit{ML},j}{W}_j$$ (2)

The target COM acceleration was defined here by only two components, the AP and ML dimensions, with respect to a globally-fixed anatomical reference frame. The third dimension (i.e., inferior-superior) was assumed to be negligible provided certain physical constraints observed for basic standing [21], including feet remaining grounded and no knee buckling. Each component target represented an optimization constraint that was equal to the weighted sum of the a_COM values in that dimension induced by individual muscle groups (i) from baseline activation levels. The solution components (W_i) corresponded to the changes in muscle stimulation levels (ΔM_i) and serve as the weighting factors across all (N = 22) muscle groups to simultaneously satisfy both dimensional constraints. This construction also assumed that individual changes in muscle activation (W_i) were sufficiently proportional to the respective changes in muscle stimulation (ΔM_i), which presumes changes in posture were sufficiently small during muscle excitation-activation coupling [22]. Step 4 outlines methods to validate this assumption.

The Optimization Toolbox in MATLAB® (Mathworks, Natick, MA), was used to compute the solution vectors (W) for multiple COM acceleration targets specified from erect stance. The maximum targets of this space in each dimension direction were simply the sum of all the individual a_COM values recorded in that direction. These maximum target values were approximately 570, 190, 870, and 490 mm/sec² in the backward, forward, right, and left directions, respectively. A rectangular COM acceleration grid encompassed by these limits, in increments of 20 mm/sec², yielded 2584 targets. The optimization criterion minimized the sum of squares of increases in stimulation pulsewidths delivered (i.e., Σ(W_i)²). Optimization parameters included a maximum of 10000 iterations, constraint equation tolerance of 10 mm/sec² and function tolerance of 1 μs². If the optimizer produced a solution that met the tolerance criteria, for a given ACC_COM, then that target solution was classified as “feasible”. Only feasible solutions were retained in constituting the mapping for feedback control.

Step 3

Each feasible target solution served as a single data point to train the ANN. The two components (AP, ML) of ACC_COM served as the INPUTS, and the normalized changes in stimulations represented by solution vector W served as the OUTPUTS. Data points were randomly assigned for ANN training (70%), testing (20%), and validation (10%). The ANN was constructed with the Neural Network Toolbox in MATLAB (Mathworks®, Natick, MA). A three layer (input, hidden, output layers), feedforward ANN structure was employed for its universal mapping capability of nonlinear functions [23]. The number of hidden layer neurons was determined to be 18 by heuristically finding the number of neurons providing the lowest mean squared error after 1000 training epochs. All input and output data were normalized over [−1, +1] prior to training. The training function was the Levenberg-Marquardt algorithm [24]. A maximum of 10000 epochs were specified for training in lieu of an early stopping criterion of 250 consecutive epochs of increasing fitting error to the validation set. For feedback control, the ANN outputs were de-normalized to real stimulation pulsewidth (μs) values according to respective M_base and M_max for each muscle group.

Step 4

The construction of the acceleration-stimulation controller mapping depended on the assumption of linearity described in equations 1, 2. Validity of this assumption was explored in two ways. First, the magnitude response was investigated by observing if ramping optimal combinations of muscle stimulation along directional lines of the controller map produce linearly ramped responses in acceleration magnitude. The maximum induced COM acceleration in the forward, backward, rightward, and leftward directions on the controller map were designated as the 100% (i.e., maximum) response levels. Linearly interpolating from the 100% response point to the zero setpoint (i.e., no acceleration at quiet stance) identified the 25%, 50% and 75% response level points for each direction as shown in Figure 3.

Figure 3.

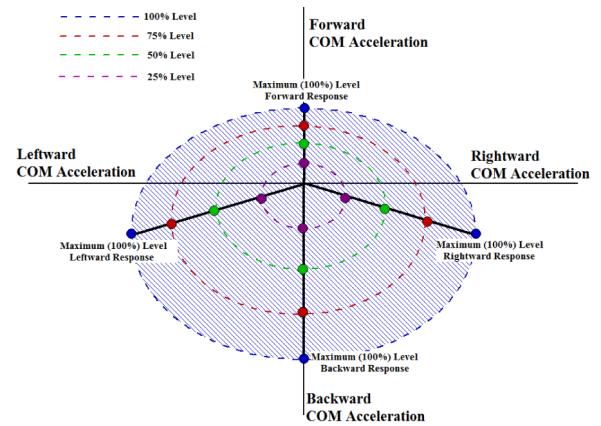
Diagram of theoretical 2-dimensional (2-D: anterior-posterior, medial-lateral) center of mass (COM) acceleration space for SCI subject composed of feasible 2-D COM acceleration targets that a particular subject can produce with optimal changes in muscle stimulation levels from erect stance (i.e., zero point).

In a theoretical or real COM acceleration space, the maximum right and left accelerations occur while coupled to naturally emergent backward accelerations. This results in peak right/left accelerations being below the horizontal. For a single trial, the muscle stimulation outputs at each response level were simultaneously applied as a 750 msec pulse train while the subject initially stood quietly with minimum baseline stimulations applied. The maximum COM acceleration was observed within the first 500 msec following onset of the stimulation pulse train was recorded with each trial. A total of 20 trials were performed for each response level in each direction over the course of 10 sessions.

The second basis for testing linearity was the summation response, which assessed if the acceleration effects induced by stimulating individual muscle groups separately can be summed to equal the observed acceleration effects when those muscle groups are stimulated together in combination. The same acceleration data collected for the magnitude response served as the combination values at each response level. The data collected from Step 1 were used to produce the individual summation values by applying equations 1 and 2 and multiplying the AP and ML a_COM values for each individual muscle group with the corresponding normalized (0 to 1) ANN output at each response level, then summing across all of the muscle groups.

E. STAGE 3: Tuning Feedback Controller

A negative feedback gain for each direction (front, back, right, and left) of the controller was tuned for outputting optimal muscle stimulation patterns that produced effects on COM acceleration opposing those generated by postural perturbations while minimizing UE loading. The controller map existed across two dimensions (AP and ML COM acceleration) resulting in the four distinct directions. For real-time controller feedback during external perturbations, COM acceleration was estimated from measurements of body-mounted 3-D analog accelerometers (CXL02LP3, Crossbow Technology, Milipitas, CA) according to the linear regression model and optimal locations determined in STAGE 1. Although only marker-based acceleration data were used to determine and validate regression model parameters, sensor measurements were used for real-time feedback estimation as with expected clinical application. It was previously shown that 3-D accelerometer readings during external disturbances applied from quiet standing compared favorably to double-differentiation of the 3-D position of a single retro-reflective marker affixed to the same accelerometer [25]. Accelerometer readings relative to a globally-fixed reference frame are susceptible to changes in orientation and the presence of gravity. Thus, sensors were carefully placed and oriented on the subject using medical tape with their readings re-zeroed prior to each trial.

Tuning a directional gain comprised of assigning a gain value, applying repeated M3-magnitude external perturbations to the subject in that direction, and observing the resultant standing performance as defined by the minimization in the total UE loading applied by the subject to stabilize. Total UE loading was calculated as the sum of the absolute net 3-D forces (vector sum across all dimensions) applied by the subject at both the left and right handles. For each perturbation, the absolute changes in total UE loading were tracked for 1 second from perturbation onset. It was noted that the maximum UE loading reactions consistently occurred within this 1-second time interval.

In each direction, the specific gain values examined were 0.0, 0.25, 0.50, 1.0, 1.5, and 2.0 while holding the other three gains to 0. Gains above 2.0 generally produced controller responses that the subject found to be intolerable. Each tuning trial involved applying six single perturbations in one direction, one at each gain value and presented in random order. Across 10 separate sessions, a total of 20 perturbation trials were applied at each unique direction and gain pair. A 3^rd order polynomial was then fit to the mean total UE loading calculated at each test point as a function of gain for each of the four directions. The gain corresponding to the minimum of each polynomial fit was designated as the “optimal” gain in that direction for resisting external perturbations.

F. STAGE 4: Testing Feedback Controller

Following protocol similar as in STAGE 1, five sessions of random external perturbation were conducted with stimulation conditions of either the optimally-tuned controller active or clinically-determined levels of constant stimulation used by the subject for standing at home with the neuroprosthesis. In each session, the subject was presented with each unique perturbation direction (front, right, back, left) and magnitude (M1 to M5) one time for each stimulation condition for a total of 40 perturbations. Each trial of perturbations involved either controller-active or constant stimulation conditions. Controller performance was ultimately compared against the constant stimulation case. Again, the changes in total UE loading were tracked for one second following each disturbance onset and then used for comparative evaluation. Comparisons were performed using one-way ANOVA at p < 0.01, a presumably high standard for clinical significance. If the null hypothesis of equal means was not rejected, significance at p < 0.05 was inspected.

III. Results

A. Estimation of COM Acceleration for Feedback Control

The stepwise linear regression results indicated that 3-D accelerations of only the pelvis and trunk segments are necessarily measured to accurately estimate total body COM acceleration during external perturbations by linear regression. The search algorithm determined that the optimal locations for accelerometer sensors during feedback control would be the anterior pelvis equidistant between the right and left superior iliac spine and posterior torso between the sacrum and right shoulder, ~40% closer to the right shoulder. The placement offset from midline for the torso sensor was an assumed byproduct of an asymmetric disturbance response for this subject. Table 1 lists the resultant regression coefficients to estimate total body COM acceleration in the AP and ML dimensions.

Table 1.

Linear Regression Model Coefficients for Estimation of Center of Mass Acceleration during External Perturbations

Segmental Acceleration Actively Measured	AP COM ACC	ML COM ACC
TORSO: Anterior Posterior	0.3160	0.0462
TORSO: Medial-Lateral	0.0934	0.3688
TORSO: Inferior-Superior	−0.0822	0.0299
PELVIS: Anterior-Posterior	0.3894	−0.0738
PELVIS: Medial-Lateral	−0.0808	0.4065
PELVIS: Inferior-Superior	−0.0983	0.0598
Correlation Coefficient (R2) across Testing Data	0.893	0.947

In both dimensions, high correlation (R² > 0.89) was observed for testing data between model output and the marker-measured COM accelerations. As expected, the largest positive regression coefficients were those multiplying measurement inputs in the same dimension as the component of COM acceleration being estimated.

B. Validating Controller Map Linearity

Results for the magnitude response test of linearity are shown in Figure 4. The data for average total COM acceleration induced by ramped stimulation in each direction were fitted with a simple linear regression (green trace). All correlation coefficients between the actual data and the linear fit were greater than 0.975. This indicates very high linearity in ramp responses in all four directions.

Figure 4.

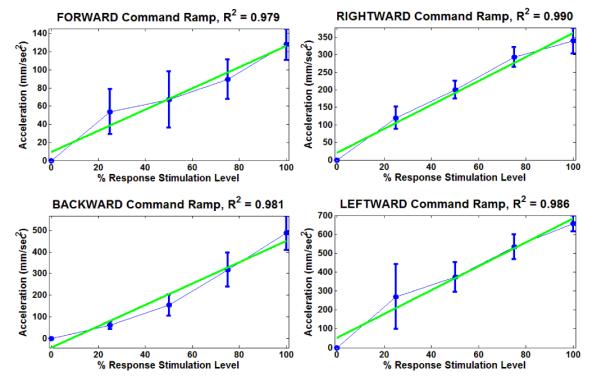
Results for magnitude response test of linearity.

Results for the summation response test showing the weighted sum of stimulated responses from individual muscle groups compared to the combined responses are shown in Figure 5. Only the results for the 100% response level are shown since high linearity from the magnitude response test indicated comparisons at the other response levels would be redundant.

Figure 5.

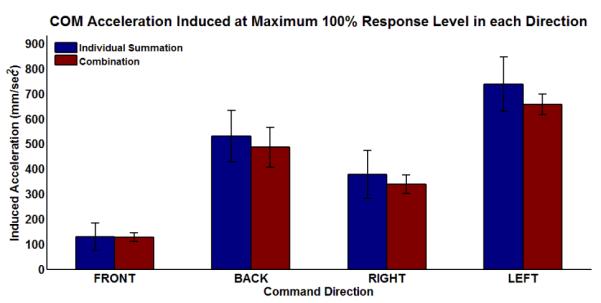
Results for summation response test of linearity.

For all four directions, the combination case produced a lower COM acceleration response. This indicates that actions of individual muscles did not sum ideally, thereby producing partially counter-effective interactions. Nevertheless, the differences between the two groups were not statistically significant at p < 0.05 in any direction.

C. Tuning Feedback Controller Gains

The tuning curves of mean total UE loading versus feedback gain value during external perturbations in each of the 4 directions are shown in Figure 6. Respective direction results were normalized by the mean total UE loading observed at “baseline” (gain = 0). For each direction, a 3^rd order polynomial was a good fit (R² > 0.90) and a distinct polynomial minimum was observed that was less than both the baseline and maximum (gain = 2.0) test values, indicating appropriate fit and sufficiently large range of test gains. The reduction in UE loading at p < 0.01 was significant between some test gain and baseline in every perturbation direction except backwards. The approximate minima values serving as optimal gains in the front, right, back, and left directions were 0.6, 0.7, 0.7, and 1.1, respectively. The corresponding reductions in UE loading at these minima were 46, 63, 30, and 53%, showing reductions in UE loading were greater along the ML (right, left) than the AP (front, back) dimension.

Figure 6.

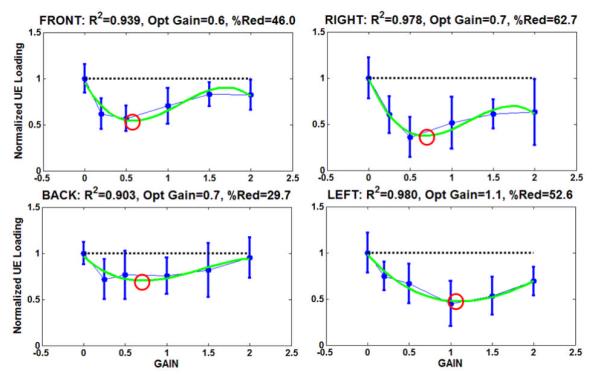
Normalized gain tuning curves along each perturbation direction. The 3^rd-order polynomial fits (i.e., green trace), correlation coefficients (R²), optimal feedback gains (polynomial minima circled in red), and percentage reduction (%Red) in UE loading at optimal gains from baseline are also indicated.

D. Testing Feedback Controller Performance

All UE loading test results were normalized such that 1.0 equals the mean UE loading (front = 190±30 N, right = 45±21 N, back = 86±16 N, left = 55±17 N) against the maximum disturbance magnitude (i.e., M5) in each direction. The mean normalized UE loading with the controller active (0.324 ± 0.097) was 32% less than with baseline constant stimulation (0.474 ± 0.146). This difference was statistically significant by one-way ANOVA at p < 0.05. As shown in Table 2, both the mean and standard deviation (S.D.) on UE loading was significantly reduced in the front, right, and left directions at either p < 0.05 or p < 0.01, between the feedback control and baseline groups. No significant differences were observed in the backwards direction.

Table 2.

Feedback Controller Performance Results

Perturbation Direction	Normalized Mean UE Loading		ANOVA ** p < 0.01 * p < 0.05 + no reject null
	Feedback Control	Baseline Stimulation	Mean	S.D.
FRONT	0.366±0.073	0.495±0.105	*	*
BACK	0.347±0.120	0.378±0.180	+	+
RIGHT	0.318±0.107	0.478±0.184	*	**
LEFT	0.310±0.095	0.513±0.191	*	**

The average increases in normalized stimulation levels (i.e., ANN outputs) delivered under feedback control taken over the 1 second interval immediately following perturbation onset in all cases was universally less than 0.4 for every muscle group. Multiplying these normalized stimulation levels by the corresponding maximum total COM acceleration value that can be induced yields the individual contribution to the overall controller response by a given muscle group. The relative contribution was the individual contribution for each muscle group divided by the summed contributions for all muscles groups. These results are shown in Figure 7.

Figure 7.

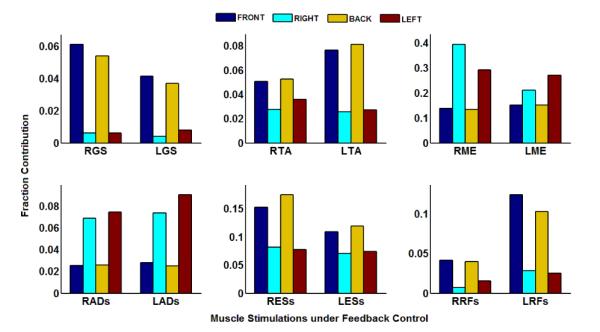
Fraction contributions to COM acceleration being induced by controller response during external perturbations. Notes: Preceding ‘L’ or ‘R’ denotes ‘Left’ or ‘Right’ side, respectively. Following ‘s’ denotes ‘surface’ stimulation.

The triceps surae, tibialis anterior, erector spinae, and rectus femoris groups had higher contributions to controller responses for disturbances in the AP dimension. The gluteus medius and thigh adductor muscles had higher contributions to controller response for disturbances in the ML dimension. These results are consistent with anatomical function. The triceps surae and tibialis anterior mediate ankle plantar/dorsiflexion and the rectus femoris and erector spinae produce notable flexion and extension changes at the pelvis and lower torso. These actions typically produce movements primarily along the sagittal plane. Gluteus medius and thigh adductor muscles mainly generate hip ab/adduction moments to produce shifts from erect standing primarily along the coronal plane. The right and left gluteus medius muscles alone contributed greater than 40% of the average controller response. Right and left surface-stimulated erector spinae contributed greater than 20% of the controller response. These relatively high contributions directly demonstrate that these muscle groups were capable of inducing strong absolute changes in COM acceleration following stimulation for this particular subject.

IV. Discussion

This study advances the scope of investigation for standing neuroprostheses that exhibit features important for clinical implementation. The proposed control system utilized total body COM acceleration as novel feedback for comprehensive 3-D control of standing by FNS for a single subject with SCI. The results of this study demonstrated the potential advantages and feasibility of COM acceleration feedback for FNS standing control.

Firstly, a simple linear regression model produced highly accurate estimates of total body COM acceleration for feedback during perturbed standing using only acceleration measurements from only two segments (pelvis, torso). For feedback controller experiments, the resultant linear regression model was applied with accelerometer sensor inputs instead of marker-based data. The controller was successfully tuned and tested to reduce UE loading. This was accomplished despite the possibility of aliasing errors whereby changes in orientation of the sensor would represent measured accelerations, including gravity, erroneously upon the presumed globally-fixed anatomical reference frame. This suggested that the changes in segment orientation were sufficiently small to attain robust estimation of feedback. While estimation of COM acceleration has not previously been a focus of investigation, it was critical to establish feasibility of this step in this study to demonstrate this controller paradigm in the laboratory environment. This feasibility was established based on the high correlation coefficient between the model-prediction of COM acceleration to the gold standard of the double-differentiated VICON data. Ultimately, feedback estimation was validated as reliable by the reduction in UE loading with active feedback control. This result is consistent with previous findings in simulation [16, 17] that showed expected levels of error in feedback would not degrade controller performance below that of baseline.

Secondly, changes in muscle stimulation were shown to be linearly related to changes in the controller feedback variable of total body COM acceleration from erect stance. The magnitude response test demonstrated that changes in COM acceleration magnitude were linearly proportional to the respective changes in stimulation level. The summation response test indicated that stimulated muscle responses can act synergistically in accordance to observed changes in COM acceleration. It was critical to demonstrate that stimulation patterns could be fundamentally organized according to these assumptions to validate the optimization constraints and reliably produce the expected control actions for postural balance function in the live, laboratory environment. While the concept of muscle-induced accelerations was originally constructed to assess contributions of individual muscles for motion analysis [7, 21], we have applied this concept for comprehensive feedback control of FNS standing in simulation [16] and in the laboratory for the current study.

Finally, this feedback control system exhibited significant potential for clinical implementation by enacting global, synergistic dynamic control with only a few feedback parameters for improved performance. Reduction in mean UE loading was used as the performance metric and was significantly minimized overall and for perturbations in the front, right, and leftward directions (p < 0.05) when utilizing the optimal feedback gains. The controller-active deviation on UE loading was also significantly reduced in the front, right, and left directions (p < 0.01), indicating that feedback control produced a less variable UE loading response. Typically, submaximal stimulation levels demonstrated that controller actions were finite to stabilize the system. Since the feedback control system only operated across two dimensions (AP, ML), only four directional gains needed to be tuned. No significant reduction was observed for perturbations in the backward direction. This may be due to insufficient musculature targeted for stimulation to initially accelerate the body forward against backward directions. This musculature may need to include abdominal muscles, which are typically not targeted by FNS systems since they do not as readily provide basic standing support and can induce discomfort in breathing function. We attribute the observed reductions in UE loading due to any learning effects by the user in responding to the applied external perturbations as common to both the controller-active and constant stimulation conditions.

In simulation [16], significant reductions in UE loading with controller feedback were observed across all perturbation conditions tested at p < 0.01. In this laboratory demonstration, reductions were only observed at p < 0.05 overall and in particular directions. This discrepancy may be attributable to the more idealized and robust simulation environment. In simulation, there was no inter- or intrasession response variability in muscle control or the presumed model for applying UE loading. Furthermore, the force-generating properties utilized in simulation representing SCI may be more generous than those for this particular subject. The simulated muscle properties were based on seated dynamometer measurements using a combination of surface and percutaneous electrodes that more fully recruited similar functioning muscle groups. This particular subject generally relied on a single channel of stimulation for each muscle group during functional standing conditions. Advanced stimulation paradigms (e.g., nerve cuff electrodes) may mitigate these problems with more targeted, consistent activation of paralyzed musculature. Furthermore, general controller robustness would have been better demonstrated by test perturbations in non-orthogonal directions as well. We prioritized orthogonal perturbations in this initial validation study to maximize limited resources including subject time and effort. Furthermore, orthogonal perturbations are common standard protocol standing balance studies [12-15].

Practical optimization of an FNS standing performance should focus on minimizing the user effort. Given the complexity of 3-D standing control and the limited number of paralyzed muscles typically available for stimulation, a moderate level of volitional UE support loading should be expected. However, this must be balanced against the potential for producing upper body fatigue and compromising user ability to reach and manipulate objects. Thus, UE loading provided an appropriate minimization function for optimizing performance since it readily reflects both user effort and compromised functional ability. Furthermore, UE loading reflects the combined contributions of feedback control of stimulation with volitional user inputs. Therefore, the integrated effects of postural mechanics, excitation-activation coupling delays, in addition to residual vestibular, somatosensory, and visual feedback of the user are simultaneously addressed by gain tuning according to UE loading performance. Further developments in FNS standing control require focal consideration of the coupled interactions between automatic and volitional control [26].

The linear actuators and instrumented support device conveniently provided the capability to apply force-pulse disturbances and instantly induce accelerations upon the subject COM along specified anatomical directions. This greatly simplified the tuning process to minimize UE loading accordingly. By exercising the feedback control system along all four principal directions, a set of gains was easily produced that could comprehensively control standing in both the AP and ML dimensions. Feedback control in the inferior-superior dimension was de-emphasized given its natural coupling in the AP and ML dimensions. Control in the inferior-superior direction has value in preventing accelerated collapse but is unexceptional for normative standing [21]. While previous investigations have focused on joint feedback, this study suggests that COM acceleration may also be a viable feedback signal for closed-loop FNS standing used clinically. Joint feedback potentially provides explicit, comprehensive description of the mechanical system under control, but only if several joints are instrumented. In simulation [8], significant reductions in UE loading were demonstrated with comprehensive proportional-derivative (PD) joint feedback for an FNS control system. However, this PD joint feedback system utilized 18 feedback signals from joints across the trunk and lower extremities. This is considerably more than the two bi-directional inputs for the analogously proposed COM acceleration feedback system with similar simulated performance [17]. Thus, the current live-subject, laboratory investigation into COM acceleration feedback control is the next natural step from the previous joint-based studies in providing a solution with clinical viability in mind.

Joint control, or similar position-based control, is ultimately necessary in theory to develop a “hands free” standing neuroprosthesis. But producing fine joint-based postural changes in addition to basic standing support may be beyond the capacity of current systems relying on stimulation of a limited number of paralyzed muscles. As such, at least moderate UE loading to fully stabilize against postural disturbances is required for clinical usage. These practical considerations facilitate approaches such as those employed in this study. Baseline stimulation was relied upon for basic standing support and optimized FNS control structures provided dynamic stabilization while minimizing volitional user effort. Future laboratory investigations could incorporate feedback from only select joints in conjunction with COM acceleration feedback to further improve performance [17] while still minimizing the sensor instrumentation deployed.

Certainly, muscle fatigue is a major issue for FNS systems [26], and fatigue at the quadriceps could produce knee-buckling and potential for collapse. In fact, acceleration has been previously evaluated for detecting knee unlock during FNS standing [27]. Muscle fatigue was not as significant for our particular subject and the issue was beyond the design scope of this study. While this control system rather focuses on disturbance rejection, muscle fatigue for FNS could be addressed by techniques proposed for online adaptation [28].

Since external perturbations are unknown disturbances to the user, they may not be as relevant for clinical usage. However, they provided a systematic mode to conceptually validate, develop, optimize and evaluate the basic operating characteristics of the feedback controller across a broad range of disturbances. Internal perturbations generated volitionally by the user while performing functional standing tasks are more pertinent to activities of daily living. The next modes by which to tune, test, and evaluate controller performance would include functional reaching activities while standing. These activities may include manipulating objects of varying weight and shape and completing 3-D reaching tasks according to time [29]. However, the external perturbation tests presented in this study represent important initial steps in controller performance evaluation.

A larger cohort of subjects would need to be tested in the future to generalize results or determine universal parameters of operation. This single-case study did serve our primary objective to initially evaluate this approach under live experimental conditions from its conception and validation in simulation. It outlined steps to practically devise, develop, tune, and test the control system accordingly.

V. Conclusions

This study investigated COM acceleration feedback as a feasible alternative for closed-loop control of FNS standing postural balance employed clinically. This feedback variable represented global system dynamics around which an optimal mapping relating changes in muscle stimulation was constructed. Only two body-mounted accelerometer sensors were required to estimate total body COM acceleration for controller feedback. Feedback gains were optimized to reduce upper extremity loading when resisting external perturbations. Compared to clinically-determined constant stimulation levels, the feedback control system significantly reduced the upper extremity loading required to resist postural disturbances. Future developments in FNS feedback control systems may expand testing to functional reaching tasks and consider incorporation of select joint feedback.