SUMMARY
The responses to sound of mammalian cochlear neurons exhibit many nonlinearities, some of which (such as two-tone rate suppression and intermodulation distortion) are highly frequency specific, being strongly tuned to the characteristic frequency (cf) of the neuron. With the goal of establishing the cochlear origin of these auditory-nerve nonlinearities, mechanical responses to clicks and to pairs of tones were studied in relatively healthy chinchilla cochleae at a basal site of the basilar membrane with cf of 8–10 kHz. Responses were also obtained in cochleae in which hair cell receptor potentials were reduced by systemic furosemide injection. Vibrations were recorded using either the Mössbauer technique or laser Doppler-shift velocimetry. Responses to tone pairs contained intermodulation distortion products whose magnitudes as a function of stimulus frequency and intensity were comparable to those of distortion products in cochlear afferent responses. Responses to cf tones could be selectively suppressed by tones with frequency either higher or lower than cf; in most respects, mechanical two-tone suppression resembled rate suppression in cochlear afferents. Responses to clicks displayed a cf-specific compressive nonlinearity, similar to that present in responses to single tones, which could be profoundly and selectively reduced by furosemide. The present findings firmly support the hypothesis that all cf-specific nonlinearities present in the auditory nerve originate in analogous phenomena of basilar membrane vibration. However, because of their lability, it is almost certain that the mechanical nonlinearities themselves originate in outer hair cells.
1. INTRODUCTION
The responses to sound of the mammalian auditory nerve contain many nonlinearities (see review by Ruggero (1992)) whose origins have not been fully specified, largely as a result of the scarcity of data on the representation of sounds in the vibration of the basilar membrane and in the receptor potentials of inner and outer hair cells. One useful distinction among auditory-nerve nonlinearities is whether they are frequency specific: i.e. whether the existence or extent of the nonlinearity is strongly dependent on the spectral content of the stimulus relative to the neuron’s characteristic frequency (cf, the frequency to which it is most sensitive). Examples of cf-specific nonlinearities are two-tone rate suppression, two-tone distortion and intensity-dependent phase shifts at near-cf frequencies. Examples of cf-independent nonlinearities are adaptation, reduction of the synchronized responses to one tone by a second tone (‘synchrony suppression’) and abrupt phase shifts (including ‘peak splitting’) in responses to tones with frequencies well below cf.
To clarify the cochlear origin of auditory-nerve nonlinearities, we have conducted studies on basilar membrane responses to two-tone and click stimuli. Our findings, reviewed in this paper, demonstrate striking cf-specific mechanical nonlinearities (including two-tone suppression and distortion) and thus strongly support the hypothesis that all frequency-specific auditory-nerve nonlinearities derive from counterparts present in the vibration of the basilar membrane. We also review evidence, based on the effects of furosemide on basilar membrane sensitivity and frequency tuning, that indicates that the frequency specificity of mechanical nonlinearities is not intrinsic to the basilar membrane but rather depends on the integrity of outer hair cell function.
2. METHODS
Mechanical responses to sound were measured from the basilar membrane of the chinchilla at a site located 3.5 mm from the round window. Animals were deeply anesthetized with sodium pentobarbital (initial dose: 65 mg kg−1), tracheotomized and intubated. Normal body temperature was maintained by means of a servo-controlled heating pad. The left pinna was resected, the bulla was widely opened and the tensor tympani muscle was sectioned. A small hole made in the basal turn of the otic capsule allowed direct visualization of the basilar membrane. Basilar membrane vibrations were recorded using either the Mössbauer technique (Robles et al. 1986) or laser velocimetry (Ruggero & Rich 1991a). Both methods, which detect velocity rather than displacement, are based on measurement of the Doppler shift of electromagnetic radiation due to relative motion between a radiation emitter or reflector attached to the basilar membrane and an immobile detector. In the Mössbauer technique, a source of gamma photons (57Fe annealed to a rhodium foil, 6 μm × 80 μm × 80 μm) was placed on the basilar membrane. In the case of laser velocimetry, coherent light from a He–Ne laser was reflected from glass microbeads (10–30 μm).
Acoustic signals (single tones, tone pairs or clicks) were produced under computer control by a custom two-channel waveform generator. The generator’s voltage outputs were fed into two Beyer DT-48 earphones mounted on the back of a plastic speculum sealed to the bony ear canal by means of ear-impression compound. A miniature microphone equipped with a probe tube was used to measure the sound pressure within 2 mm of the tympanic membrane.
3. RESULTS
(a) Two-tone suppression
Figure 1 illustrates suppression effects in the responses of a basilar membrane site with cf close to 8 kHz. The velocity-intensity function for an 8-kHz tone presented alone (dashed line) is typical of those obtained in relatively healthy cochleae for tones with frequency close to cf: at very low (and perhaps also at intense) stimulus levels the responses grow linearly but at moderate stimulus intensities responses grow at lower rates (i.e. less than 1 dB dB−1). Upon presentation of a second tone, with frequency lower than cf, the responses to the 8 kHz tone are reduced. In contrast with ‘classical’ findings in the auditory nerve (e.g. Javel et al. 1978), the mechanical suppression effect varies with probe intensity, being larger at low probe-tone levels. Thus, the input-output functions are not simply shifted to higher probe levels, but are also linearized. Recent findings in the auditory nerve indicate that, in fact, similar suppression-induced changes in rate-intensity functions can be demonstrated in the responses of high-threshold, low-spontaneous-rate cochlear afferents (Sokolowski et al. 1989).
Figure 1.
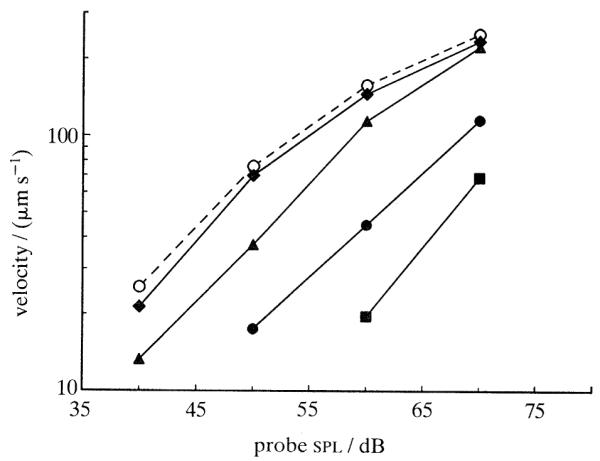
Effect of suppressor tones on basilar membrane intensity functions for a near-cf tone. Intensity functions are shown for an 8 kHz probe tone alone (open circles, dashed line) and in the presence of a 300 Hz suppressor at several intensities (filled symbols, solid lines): diamonds, 70 dB; triangles, 80 dB; circles, 90 dB; squares, 100 dB. Cochlea: L29.
As the intensity of the suppressor tone is raised, the magnitude of the mechanical suppression effect increases monotonically (figure 1). The slope of the function relating suppression to suppressor intensity depends on frequency of the suppressor tone relative to cf, both in the basilar membrane (Ruggero et al. 1992) and in the cochlear nerve (Costalupes et al. 1987; Delgutte 1990). For suppressors with frequency higher than cf, the rate is low, in the order of 0.4 dB dB−1; for suppressors with frequency well below cf (as illustrated in figure 1) the rate is substantially higher (between 0.65 and 1.42 dB dB−1).
Figure 2 shows that two-tone suppression in the basilar membrane, much as two-tone rate suppression in the auditory nerve (e.g. Abbas 1978; Schmiedt 1982), depends on probe frequency, being largest when probe frequency equals cf (10 kHz) and nonexistent for probe frequencies far removed from cf. The cf specificity of mechanical suppression also holds for suppressor tones with frequencies below cf (not shown). In this and several other respects, including its sensitivity to cochlear damage, two-tone rate suppression has mechanical counterparts in the basilar membrane and thus probably derives from these counterparts (Ruggero et al. 1992).
Figure 2.
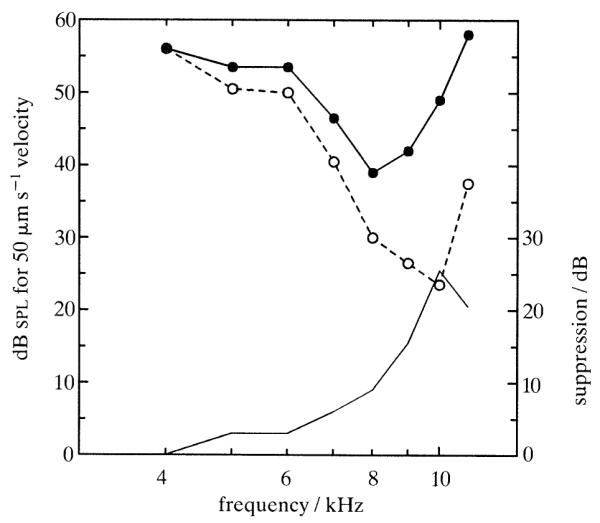
Changes in basilar-membrane frequency tuning produced by a 12 kHz suppressor tone presented at 63 dB spl. The isovelocity tuning curves (scale in left ordinate) were derived from intensity functions for probe tones presented alone (open circles, dashed line) and in the presence of the suppressor tone (filled circles, solid line). The thin solid line indicates suppression magnitude (scale in right ordinate) as a function of probe frequency. The 12 kHz suppressor tone evoked a response 7.4 dB smaller than the 50 μm s−1 isovelocity criterion. Cochlea: L14.
(b) Two-tone distortion
When listening to pairs of tones, humans hear additional tones – distortion products or combination tones – that are not present in the stimulus. Substantial psychophysical (e.g. Goldstein 1967; Smoorenburg 1972), neurophysiological (e.g. Siegel et al 1982) and acoustic (e.g. Mountain 1980) evidence suggests that combination tones arise on the basilar membrane. However, with the possible exception of an f2–f1 vibration component reported by Rhode (1977), searches for mechanical combination tones in the basilar membrane were until recently unsuccessful (Wilson & Johnstone, 1973; Rhode, 1977), perhaps due to a combination of inadequate vibration-measurement technologies and the poor physiological state of the experimental cochleae. During the last year mechanical combination tones have been finally measured, using laser velocimetry, in the cochleae of guinea pig and chinchilla (Nuttall et al. 1990; Robles et al. 1990, 1991).
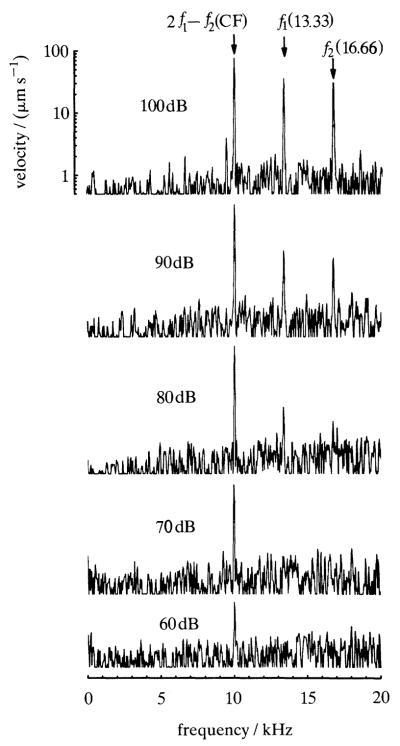
Figure 3 depicts the frequency spectrum of the mechanical response to a pair of tones, recorded from a basal site of the chinchilla basilar membrane. The tones were chosen with widely spaced frequencies (13.33 and 16.66 kHz) such that the cubic difference tone (2f1–f2) coincided with the cf (10 kHz) of the basilar membrane site. At high stimulus intensities the spectrum has components with frequencies corresponding to those of both primary tones and to the cubic difference tone 2f1–f2. However, at the lowest stimulus intensities (60 and 70 dB spl) the spectrum contains only one detectable component, the 10 kHz combination tone. The absence of detectable responses at the frequencies of the primary tones is due to the sharp filtering imposed by the cochlear partition on frequencies higher than cf. The fact that the responses to the primary tones are substantially lower than to the 2f1–f2 combination tone implies that the latter arose at a remote basal site, presumably one with cf intermediate between the frequencies of the primary tones, and subsequently propagated apically to the recording site with cf of 10 kHz.
Figure 3.
Frequency spectra of basilar membrane responses to a two-tone stimulus. The frequencies of equal-intensity tones (f1, 13.33 kHz;f2, 16.66 kHz) were chosen so that 2f1–f2 coincided with the cf of the basilar membrane site (10 kHz). Stimulus intensity (in dB relative to 20 μPa) is indicated in each panel. Cochlea: L47.
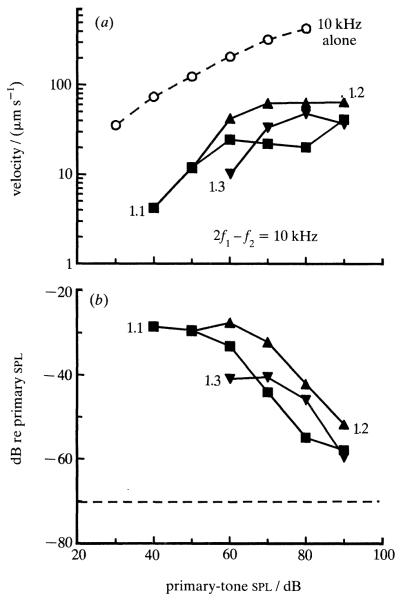
Figure 4 (top) shows distortion data obtained in the same cochlea from which the spectrum of figure 3 was recorded. The dashed line depicts a velocity-intensity function for responses to a cf tone. The other lines indicate velocities at 2f1–f2 for responses to primary tones with frequencies f1 and f2 chosen such that 2f1–f2 coincided with cf, and f2:f1 ratios were 1.1, 1.2 and 1.3. In general, the curves grow monotonically with stimulus intensity but saturate at levels of 60-80 dB spl. To permit comparison with neurophysiological and psychophysical findings, the data are replotted in the bottom panel of figure 4 with the magnitude of the distortion product being expressed as effective level: intensity of a single tone at the distortion-product frequency (in this case cf) required to produce a response of the same magnitude as the distortion product due to the two-tone stimulus. As previously shown for distortion products in the auditory nerve (Buunen & Rhode 1978) effective levels of the mechanical distortion products are largest at the lowest stimulus intensities and decline monotonically as intensity is raised. Even at stimulus levels as high as 90 dB spl the measured distortion products are larger than artifactual distortion products in the acoustic-stimulus system (dashed line), indicating that the distortion products originate in the cochlea. The largest magnitudes of basilar membrane distortion products are comparable with those measured neuro-physiologically. Unexpectedly, in figure 4 there is no clear monotonic reduction of distortion product magnitude as the f2:f1 ratio is increased from 1.1 to 1.3; such a monotonic reduction, which has been seen in recordings from guinea pig basilar membrane (Nuttall et al. 1990) and is a common (but not universal) feature of two-tone distortion measured from cochlear afferents (Buunen & Rhode, 1978), may have been absent in cochlea L47 due to organ of Corti damage at regions located basal to the recording site or may reflect a complex interaction between two-tone distortion and suppression.
Figure 4.
Magnitudes of 2f1–f2 distortion products as a function of primary-tone intensity and frequency ratio (solid lines). The frequencies of the two primary tones were chosen so that 2f1-f2 coincided with cf (10 kHz), (a) Open circles and dash line represent the velocity input–output function for a single tone at the distortion-product frequency. Closed symbols and solid lines indicate input–output functions for pairs of tones with f2:f1 ratios of 1.1, 1.2 and 1.3. (b) Distortion-product magnitudes are plotted as effective level, i.e. as intensity of a single tone at the distortion-product frequency required to produce a response of the same magnitude as the distortion product produced by the two-tone stimulus. Effective levels are expressed as decibels relative to primary-tone intensities. The dash line indicates that artifactual 2f1-f2 distortion products in the acoustic-stimulus system were about 70 dB less than the intensity of the primary tones. Cochlea: L47.
(c) Responses to clicks
Clicks have been previously used as stimuli in a single experimental series including relatively healthy cochleae with sharply tuned and nonlinear responses (Robles et al. 1976). Although those recordings were limited by the severely nonlinear input–output characteristic of the Mössbauer technique, which rectified and clipped the click responses, the findings were straightforward: they confirmed the existence of a frequency specific nonlinearity in the squirrel monkey basilar membrane and demonstrated time-domain counterparts of certain features of responses to tones (e.g. Rhode 1971). Taking advantage of a newly-developed method, laser vibrometry, which is essentially linear and much more sensitive than the Mössbauer technique (Ruggero & Rich 1991a), we now are able to extend the findings of the Mössbauer study.
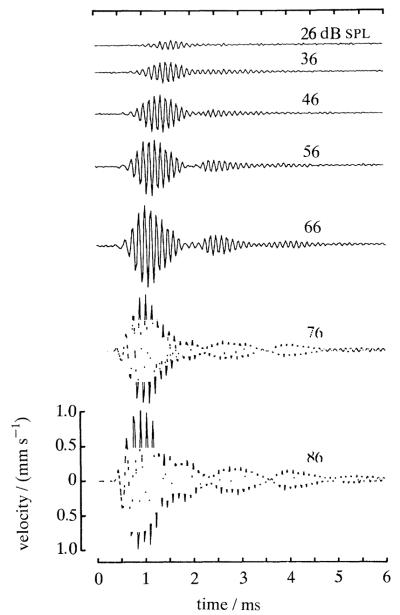
Figure 5 shows velocity responses to clicks of a basal site of a basilar membrane recorded in an exceptionally undamaged chinchilla cochlea. Responses to low-level clicks consist of high-frequency vibrations modulated by a spindle-shape envelope and are reminiscent of ‘revcors’ (reverse correlations) for low-cf auditory-nerve responses to noise (see, for example, de Boer & de Jongh 1978). With increases in click intensity, the responses grow monotonically but at rates lower than linear; further, different segments of the response grow at different rates, so that the responses at different click intensities are not scaled versions of each other. In general, the centre of gravity shifts to earlier times as intensity is raised. Although not obvious in figure 5, at the highest intensities the earliest vibration cycle (but no others) grow linearly, thus establishing an absolute, irreducible latency. This latency, which when measured from the onset of stapes displacement amounts to only 90 μs, presumably corresponds to the time that it takes the traveling wave to move from the oval window to the recording site 3.5 mm away (Ruggero et al. 1991a).
Figure 5.
Velocity responses to rarefaction clicks of a basilar membrane site with cf of 9 kHz. Click intensity, expressed as peak pressure (in decibels relative to 20 μPa), is indicated for each tracing. Modified from Ruggero & Rich (1991a). Cochlea: L13.
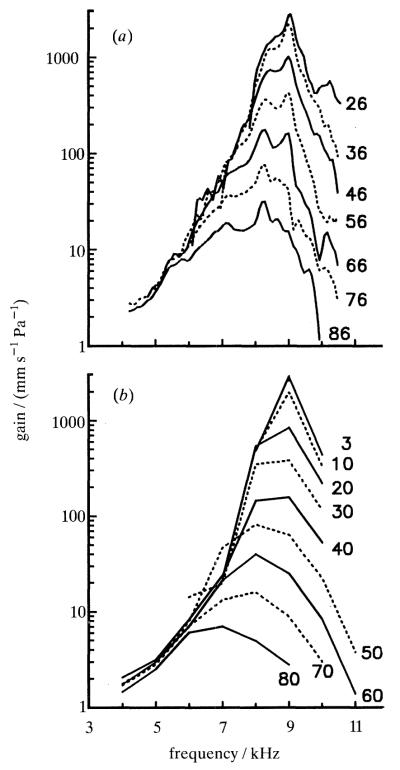
Figure 6 (top) shows gain-versus-frequency functions computed from the click responses of figure 5. In accordance with the compressive nonlinearity evident in the time-domain representations, the gain functions change systematically as a function of click level. Peak gains are largest (about 3 m s−1 Pa−1) at cf (9 kHz) at the lowest stimulus intensities; as click intensities are raised, the peak spectral velocities shift to lower frequencies and are reduced in magnitude. For a thousand-fold (60 dB) increase in click pressure, there is a hundred-fold (40 dB) reduction in peak gain. At frequencies well below cf the gain functions superimpose, indicating that at these frequencies responses grow linearly. For comparison with the click data, gain functions for responses to tones are plotted in the bottom panel of figure 6 using scales identical to those in the top panel. It is apparent that the two sets of gain functions are very similar. Thus, for example, responses to 26 dB clicks and 3 dB tones are nearly linear and yield nearly identical peak gains (about 3 m s−1 Pa−1); similarly, responses to stimuli about 1000-fold more intense (86 dB clicks and 60 dB tones) yield peak gains of 30–40 mm s−1 Pa−1. Thus, the cf specific compressive nonlinearities evident in responses to tones or clicks appear to be the same and do not preclude predicting the responses to one type of stimulus from these evoked by the other.
Figure 6.
Gain-versus-frequency functions for responses to (a) clicks and (b) tones of a single basilar membrane site. Gains were computed by dividing, frequency by frequency, spectral response magnitude by stimulus pressure. The spectral magnitudes for click responses were obtained by Fourier transformation of the data of figure 5. Click peak pressures are indicated next to each gain spectrum. Cochlea: L13.
(d) Lability of cf-specific nonlinear mechanical responses
Twenty years ago Rhode demonstrated that a cf-specific compressive nonlinearity existed in the response of the squirrel monkey basilar membrane (Rhode 1971) and that the nonlinearity disappeared upon death (Rhode 1973). With the advantage of hindsight, it now seems certain that failures to confirm the existence of cf-specific nonlinearities in basilar membrane responses during the next decade were due to the poor state of the experimental cochleae. More recent experiments (Sellick et al. 1982; Robles et al. 1986) suggest that basilar membrane nonlinearities are inextricably related to frequency tuning and that the same processes that abolish nonlinearities also destroy sharp frequency tuning. Thus, to the extent that nonlinearities in responses to two-tone or broadband stimuli are cf specific, one should expect them also to be labile. This indeed appears to be the case.
Cochleae that are relatively healthy, and thus yield sharply frequency-tuned and sensitive responses to tones, sustain strong two-tone mechanical suppression effects; conversely, poorly tuned and insensitive cochleae produce weak suppression effects (Ruggero et al. 1992). The lability of mechanical suppression is consistent with electrophysiological recordings from the auditory nerve: afferent fibers innervating cochlear regions devoid of outer hair cells do not exhibit rate suppression (see Schmiedt & Zwislocki 1980). Although we have not yet explored the lability of mechanical distortion-product generation in a systematic way, the absence of distortion products in insensitive cochleae and their presence in healthy cochleae suggests that the lability of two-tone distortion already demonstrated in auditory-nerve recordings (e.g. Siegel et al. 1982) must have correlates in the basilar membrane. Finally, the cf-specific nonlinearity and sensitivity of responses to clicks disappear after death, paralleling similar changes in responses to tones (Ruggero & Rich 1991a; Ruggero et al. 1991a).
The lability of basilar membrane sensitivity and cf-specific nonlinearities suggests that their origin does not reside in the largely acellular, and thus probably metabolically-insensitive, basilar membrane. Rather, there is a consensus belief that such basilar membrane properties reflect the activity of the living cells of the organ of Corti, probably the outer hair cells. Although substantial, evidence for this hypothesis has been mostly indirect. The strongest indirect evidence is the alteration of combination-tone otoacoustic emissions by electrical stimulation of the medial efferent system (Mountain 1980; Siegel & Kim 1982). We have recently taken advantage of a relatively specific and reversible cochlear manipulation, namely furosemide-induced reductions of receptor potentials, to test the hypothesis that the receptor potentials of outer hair cells control the mechanical frequency selectivity and sensitivity of basilar membrane vibrations (Ruggero & Rich 1991b).
Figure 7 shows alterations of responses to clicks caused by intravenous injections of furosemide, a loop-inhibiting diuretic that rapidly and reversibly reduces the hair cell receptor potentials. The spectra for responses to 48 dB and 68 dB clicks are drastically altered by furosemide: sensitivity drops by at least 20 dB at cf but it is not changed at frequencies well below cf. In a manner qualitatively similar to the effects of two-tone suppression (see figure 2) the sharpness of frequency tuning is reduced and the frequency of maximal sensitivity shifts to lower frequencies. Also similar to the effects of suppression, the effects of furosemide depend on stimulus intensity: they are largest for low-level clicks and small for intense clicks.
Figure 7.
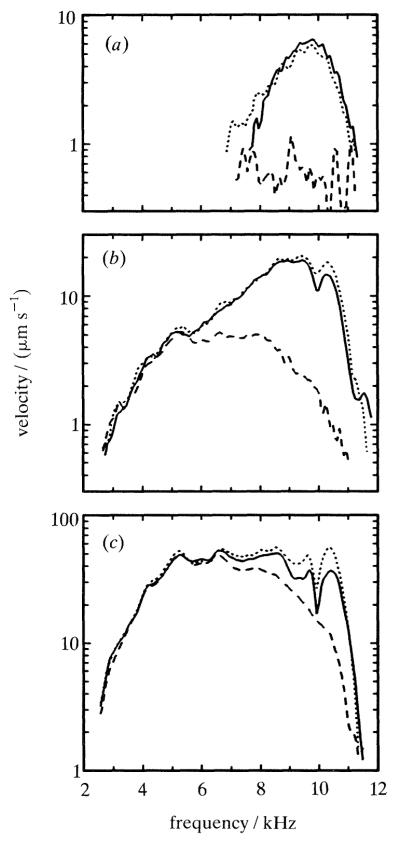
Frequency-specific effects of furosemide upon the magnitude of basilar membrane responses to clicks. The velocity-magnitude frequency spectra were computed by Fourier transformation of responses to clicks with peak pressures of (a) 48, (b) 68 and (c) 88 dB (relative to 20 μPa). For each stimulus level, three curves are displayed, representing responses immediately preceding (solid line, − 13 min) and following (long-dash line, +9 min) a furosemide injection and when full recovery had occurred (short-dash line, +100 min). Redrawn from Ruggero & Rich (1991b). Cochleae: L14.
We interpret the mechanical effects of furosemide as showing that the organ of Corti determines basilar membrane vibrations. More specifically, we argue, these effects almost inescapably imply that the receptor potentials of the outer hair cells participate in a feedback control system that normally boosts the vibration magnitude of the basilar membrane. Our argument is based on the following facts (reviewed by Ruggero & Rich (1991b)): (i) receptor potentials are produced by inner and outer hair cells, but not by supporting cells; (ii) furosemide alters the receptor potentials of hair cells either directly (unlikely), or indirectly (most likely) via reduction of the endocochlear potential; (iii) inner hair cells are unlikely to link furosemide-induced changes in receptor potentials to a mechanical effect: the effects of injecting negative extracellular dc current into scala media, a procedure (similar to reducing the endocochlear potential) which causes reduction of auditory-nerve and inner hair cell responses, cannot be mimicked by passing currents into inner hair cells via intracellular electrodes (Nuttall 1985). Furthermore, only outer hair cells display electrically induced motility (see Brownell et al. 1985) and they (but not inner hair cells) are positioned at sites favourable for influencing basilar membrane mechanics (see Lim 1980).
4. DISCUSSION
Our studies on the mechanical responses of the chinchilla basilar membrane to two-tone and broadband stimuli lead us to conclude that the main features of the cf-specific nonlinearities evoked by these stimuli in the auditory nerve derive from similar features of basilar membrane vibration. This conclusion is consistent with work of other laboratories on basilar-membrane responses to tones and clicks in the cochleae of squirrel monkeys (Rhode 1971; Robles et al. 1976) and guinea pigs (Sellick et al. 1982), on the low-frequency biasing of guinea pig basilar membrane responses to cf stimuli (Patuzzi et al. 1984) and on two-tone distortion at the guinea pig basilar membrane (Nuttall et al. 1990). There is a high likelihood that all cf-specific auditory-nerve nonlinearities have correlates in basilar membrane motion. The effects of furosemide on basilar membrane sensitivity and tuning imply that, in turn, the mechanical nonlinearities reflect an influence of the outer hair cells. The big unanswered question, of course, is whether the mild intrinsic frequency tuning of the basilar membrane (e.g. as measured during furosemide intoxication) is augmented by its interaction with the outer hair cells (and, indirectly, the tectorial membrane) or whether, alternatively, outer hair cells are intrinsically sharply tuned (e.g. Brundin et al. 1989) and thus responsible for sharp basilar membrane tuning in normal cochleae.
Having specified the basilar membrane – outer hair cell complex as the origin of cf-specific nonlinearities, it would seem that most other types of nonlinearities must arise in inner hair cells or at their synapses with cochlear afferent terminals. Compressive and rectifying nonlinearities exist in inner hair cells, at the process that transduces stereociliar displacement into electrical potentials (Russell et al. 1986), and at the synapses between inner hair cells and afferent terminals of the auditory nerve (see Greenwood, 1986). Because certain features of two-tone suppression can be generated by any process which exhibits compressive or rectifying properties (see Geisler, 1985) these two sites probably participate in generating ‘synchrony suppression’. An inner hair cell or synaptic origin of ‘synchrony suppression’ would also be consistent with its apparent insensitivity to outer hair cell loss (Javel et al. 1983). The inner hair cell compressive nonlinearity should also account for the nonlinear growth of auditory nerve responses to tones with frequency well below cf. On the other hand, the absence of adaptation in either basilar membrane or inner hair cell responses suggests that adaptation must arise at the chemical synapses between inner hair cells and type I cochlear afferents.
One type of auditory-nerve nonlinearity whose origin remains mysterious is the nearly universal intensity-dependent phase shift of responses to low-frequency tones: ‘peak splitting’, the appearance of two preferred times of phase locking and its slightly less-striking version, abrupt shifts in response phases (e.g. Kiang & Moxon 1972; Gifford & Guinan 1983; Ruggero & Rich 1989). We have obtained mechanical data ruling out a basilar membrane origin for these phenomena (Ruggero et al. 1991b). This is as expected on the basis of previously demonstrated linearity of responses to stimuli with frequency well below cf. What is puzzling is that clear counterparts of abrupt intensity-dependent phase shifts have been demonstrated in inner hair cells only rarely (Cody & Mountain 1989; Dallos & Gheatham 1989).
Acknowledgments
This investigation was financially supported principally by NIH (NIDCD) grants DC-00110 and DC-00419.
REFERENCES
- Brownell WE, Bader CR, Bertrand D, de Ribaupierre Y. Evoked mechanical responses of isolated outer hair cells. Science, Wash. 1985;227:194–196. doi: 10.1126/science.3966153. [DOI] [PubMed] [Google Scholar]
- Brundin L, Flock A, Canlon B. Sound-induced motility of isolated cochlear outer hair cells is frequency-specific. Nature, Lond. 1989;342:814–816. doi: 10.1038/342814a0. [DOI] [PubMed] [Google Scholar]
- Buunen TJF, Rhode WS. Responses of fibers in the cat’s auditory nerve to the cubic difference tone. J. acoust. Soc. Am. 1978;64:772–781. doi: 10.1121/1.382042. [DOI] [PubMed] [Google Scholar]
- Cody AR, Mountain DC. Low-frequency responses of inner hair cells: evidence for a mechanical origin of peak splitting. Hear. Res. 1989;41:89–100. doi: 10.1016/0378-5955(89)90002-6. [DOI] [PubMed] [Google Scholar]
- Costalupes JA, Rich NC, Ruggero MA. Effects of excitatory and non-excitatory suppressor tones on two-tone rate suppression in auditory nerve fibers. Hear. Res. 1987;26:155–164. doi: 10.1016/0378-5955(87)90107-9. [DOI] [PubMed] [Google Scholar]
- Dallos P, Cheatham MA. Nonlinearities in cochlear receptor potentials and their origins. J. acoust. Soc. Am. 1989;86:1790–1796. doi: 10.1121/1.398611. [DOI] [PubMed] [Google Scholar]
- de Boer E, de Jongh HR. On cochlear encoding: potentialities and limitations of the reverse-correlation technique. J. acoust. Soc. Am. 1978;63:115–135. doi: 10.1121/1.381704. [DOI] [PubMed] [Google Scholar]
- Delgutte B. Two-tone rate suppression in auditory-nerve fibers: dependence on suppressor frequency and level. Hear. Res. 1990;49:225–246. doi: 10.1016/0378-5955(90)90106-y. [DOI] [PubMed] [Google Scholar]
- Geisler CD. Effects of a compressive nonlinearity in a cochlear model. J. acoust. Soc. Am. 1985;78:257–260. doi: 10.1121/1.392568. [DOI] [PubMed] [Google Scholar]
- Gifford ML, Guinan JJ., Jr Effects of crossed-olivocochlear-bundle stimulation on cat auditory nerve fiber responses to tones. J. acoust. Soc. Am. 1983;74:115–123. doi: 10.1121/1.389728. [DOI] [PubMed] [Google Scholar]
- Goldstein JL. Auditory nonlinearity. J. acoust. Soc. Am. 1967;41:676–689. doi: 10.1121/1.1910396. [DOI] [PubMed] [Google Scholar]
- Greenwood DD. What is ‘synchrony suppression’? J. acoust. Soc. Am. 1986;79:1857–1872. doi: 10.1121/1.393194. [DOI] [PubMed] [Google Scholar]
- Javel E, Geisler CD, Ravindran A. Two-tone suppression in auditory nerve of the cat: rate-intensity and temporal analysis. J. acoust. Soc. Am. 1978;63:1093–1104. doi: 10.1121/1.381817. [DOI] [PubMed] [Google Scholar]
- Javel E, McGee JA, Walsh EJ, Farley GR. Studies of‘synchrony suppression’ in normal and hearing-impaired cats. In: Webster WR, Aitkin LM, editors. Mechanics of hearing. Monash University Press; Clayton, Victoria, Australia: 1983. pp. 46–51. [Google Scholar]
- Kiang NYS, Moxon EC. Physiological considerations in artificial stimulation of the inner ear. Ann. Otol. Rhinol. Laryngol. 1972;81:714–730. doi: 10.1177/000348947208100513. [DOI] [PubMed] [Google Scholar]
- Lim DJ. Cochlear anatomy related to cochlear micromechanics. A review. J. acoust. Soc. Am. 1980;67:1686–1695. doi: 10.1121/1.384295. [DOI] [PubMed] [Google Scholar]
- Mountain DC. Changes in endolymphatic potential and crossed olivocochlear bundle alter cochlear mechanics. Science, Wash. 1980;210:71–72. doi: 10.1126/science.7414321. [DOI] [PubMed] [Google Scholar]
- Nuttall AL. Influence of direct current on DC receptor potentials from cochlear inner hair cells in the guinea pig. J. acoust. Soc. Am. 1985;77:165–175. doi: 10.1121/1.392282. [DOI] [PubMed] [Google Scholar]
- Nuttall AL, Dolan DF, Avinash G. Measurements of basilar membrane tuning and distortion with laser Doppler velocimetry. In: Dallos P, Geisler CD, Matthews JW, Ruggero MA, Steele CR, editors. The mechanics and biophysics of hearing. Springer-Verlag; Berlin: 1990. pp. 288–295. [Google Scholar]
- Patuzzi R, Sellick PM, Johnstone BM. The modulation of the sensitivity of the mammalian cochlea by low frequency tones. III. Basilar membrane motion. Hear. Res. 1984;13:19–27. doi: 10.1016/0378-5955(84)90091-1. [DOI] [PubMed] [Google Scholar]
- Rhode WS. Observations of the vibration of the basilar membrane in squirrel monkeys using the Mössbauer technique. J. acoust. Soc. Am. 1971;49:1218–1231. doi: 10.1121/1.1912485. [DOI] [PubMed] [Google Scholar]
- Rhode WS. An investigation of post-mortem cochlear mechanics using the Mössbauer effect. In: Moller AR, editor. Basic mechanisms in hearing. Academic Press; New York: 1973. pp. 49–63. [Google Scholar]
- Rhode WS. Some observations on two-tone interaction measured with the Mössbauer effect. In: Evans EF, Wilson JP, editors. Psychophysics and physiology of hearing. Academic Press; London: 1977. pp. 27–41. [Google Scholar]
- Robles L, Rhode WS, Geisler CD. Transient response of the basilar membrane measured in the squirrel monkey using the Mössbauer effect. J. acoust. Soc. Am. 1976;59:926–939. doi: 10.1121/1.380953. [DOI] [PubMed] [Google Scholar]
- Robles L, Ruggero MA, Rich NC. Basilar membrane mechanics at the base of the chinchilla cochlea. I. Input-output functions, tuning curves, and response phases. J. acoust. Soc. Am. 1986;80:1364–1374. doi: 10.1121/1.394389. [DOI] [PubMed] [Google Scholar]
- Robles L, Ruggero MA, Rich NC. Two-tone distortion products in the basilar membrane of the chinchilla cochlea. In: Dallos P, Geisler CD, Matthews JW, Ruggero MA, Steele CR, editors. The mechanics and biophysics of hearing. Springer-Verlag; Berlin: 1990. pp. 304–311. [Google Scholar]
- Robles L, Ruggero MA, Rich NC. Two-tone distortion in the basilar membrane of the cochlea. Nature, Lond. 1991;349:413–414. doi: 10.1038/349413a0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero MA. Physiology and coding of sound in the auditory nerve. In: Fay R, Popper AN, editors. The mammalian auditory pathway: neurophysiology. Springer-Verlag; New York: 1992. (In the press.) [Google Scholar]
- Ruggero MA, Rich NC. ‘Peak splitting’: intensity effects in cochlear afferent responses to low-frequency tones. In: Wilson JP, Kemp DT, editors. Cochlear mechanisms-structure, function and models. Plenum; London: 1989. pp. 259–266. [Google Scholar]
- Ruggero MA, Rich NC. Application of a commercially-manufactured Doppler-shift laser veloci-meter to the measurement of basilar-membrane vibration. Hear. Res. 1991a;51:215–230. doi: 10.1016/0378-5955(91)90038-b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC. Furosemide alters organ of Corti mechanics: evidence for feedback of outer hair cells upon the basilar membrane. J. Neurosci. 1991b;11:1057–1067. doi: 10.1523/JNEUROSCI.11-04-01057.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC, Recio A. Basilar membrane responses to clicks. In: Cazals Y, Demany L, Horner K, editors. Auditory physiology and perception. Pergamon Press; Oxford: 1991a. pp. 85–91. [Google Scholar]
- Ruggero MA, Rich NC, Robles L. Comparison of cochlear-nerve and basilar-membrane responses to low-frequency tones: absence of macromechanical basis for ‘peak splitting’. Assoc. Res. Otolaryngol. Midwinter Meet. Abst. 1991b;14:78. [Google Scholar]
- Ruggero MA, Robles L, Rich NC. Two-tone suppression in the basilar membrane of the chinchilla cochlea: mechanical basis of auditory-nerve two-tone rate suppression. J. Neurophysiol. 1992 doi: 10.1152/jn.1992.68.4.1087. (Submitted.) [DOI] [PubMed] [Google Scholar]
- Russell IJ, Richardson GP, Cody AR. Mecha-nosensitivity of mammalian auditory hair cells in vitro. Nature, Lond. 1986;321:517–519. doi: 10.1038/321517a0. [DOI] [PubMed] [Google Scholar]
- Schmiedt RA, Zwislocki JJ. Effects of hair cell lesions on responses of cochlear nerve fibers. II. Single- and two-tone intensity functions in relation to tuning curves. J. Neurophysiol. 1980;43:1390–1405. doi: 10.1152/jn.1980.43.5.1390. [DOI] [PubMed] [Google Scholar]
- Sellick PM, Patuzzi R, Johnstone BM. Measurement of basilar membrane motion in the guinea pig using the Mössbauer technique. J. acoust. Soc. Am. 1982;72:131–141. doi: 10.1121/1.387996. [DOI] [PubMed] [Google Scholar]
- Siegel JH, Kim DO. Efferent neural control of cochlear mechanics? Olivocochlear bundle stimulation affects cochlear biomechanical nonlinearity. Hear. Res. 1982;6:171–182. doi: 10.1016/0378-5955(82)90052-1. [DOI] [PubMed] [Google Scholar]
- Siegel JH, Kim DO, Molnar CE. Effects of altering organ of Corti on cochlear distortion products f2–f1 and 2fi–f2. J. Neurophysiol. 1982;47:303–328. doi: 10.1152/jn.1982.47.2.303. [DOI] [PubMed] [Google Scholar]
- Smoorenburg GF. Combination tones and their origin. J. acoust. Soc. Am. 1972;52:615–632. [Google Scholar]
- Sokolowski BHA, Sachs MB, Goldstein JL. Auditory nerve rate-level functions for two-tone stimuli: possible relation to basilar membrane nonlinearity. Hear. Res. 1989;41:115–124. doi: 10.1016/0378-5955(89)90005-1. [DOI] [PubMed] [Google Scholar]
- Wilson JP, Johnston JR. Basilar membrane correlates of the combination tone 2f1–f2. Nature, Lond. 1973;241:206–207. doi: 10.1038/241206a0. [DOI] [PubMed] [Google Scholar]