Impact of Geometry Optimization on Base-Base Stacking Interaction Energies in the Canonical A- and B-forms of DNA

Abstract

Base stacking is known to make an important contribution to the stability of DNA and RNA and, accordingly, significant efforts are ongoing to calculate stacking energies using ab initio quantum mechanical methods. To date, impressive improvements have been made in the model chemistries used to perform stacking energy calculations, including extensions that include robust treatments of electron correlation with extended basis sets, as required to treat interactions where dispersion makes a significant contribution. However, those efforts typically use rigid monomer geometries when calculating the interaction energies. To overcome this, in the present work we describe a novel internal coordinate definition that allows the relative, intermolecular orientation of stacked base monomers to be constrained during geometry optimizations while allowing full optimization of the intramolecular degrees of freedom. Use of the novel reference frame to calculate the impact of full geometry optimization versus constraining the bases to be planar on base monomer stacking energies, combined with density-fitted, spin-component scaling MP2 treatment of electron correlation, shows that full optimization makes the average stacking energy more favorable by −3.4 and −1.5 kcal/mol for the canonical A and B conformations of the 16 5’ to 3’ base stacked monomers. Thus, treatment of geometry optimization impacts the stacking energies to an extent similar to or greater than the impact of current state of the art increases in the rigor of the model chemistry itself used to treat base stacking. Results also indicate that stacking favors the B form of DNA, though the average difference versus the A form decreases from −2.6 to −0.6 kcal/mol when the intramolecular geometry is allowed to fully relax. However, stacking involving cytosine is shown to favor the A form of DNA, with that contribution generally larger in the fully optimized bases. The present results show the importance of allowing geometry optimization, as well as properly treating the appropriate model chemistry, in studies of nucleic acid base stacking.

Introduction

The most common conformation of a deoxyribonucleic acid (DNA) duplex is a right-handed double helix. The helix exists in a number of canonical conformations, with the most common being the A- and B-forms. The B-form conformation is primarily observed in aqueous solution.¹ The A-form of DNA is observed in environments with low water activity associated with low relative humidity, or in solutions with high salt or high ethanol content.² The difference between the A- and B-form conformations is dominated by three major contributions: (i) intrinsic energies associated with the sugar/phosphodiester backbone and the glycosidic linkage, (ii) environmental interactions, including the hydration of minor and major grooves, and (iii) the intrinsic energy contributions associated with the base stacking.^3–10

The intrinsic π-stacking of the nucleic acid bases arises primarily from dispersion interactions, rather than electrostatic interactions, and thus accurately computing the stacking interaction is a significant computational challenge. Many studies have documented the need to use coupled-cluster methods along with large, diffuse basis sets to obtain accurate interaction energies between aromatic molecules.^11–15 However, such methods are extremely computationally intensive and time consuming and are not practical for larger systems.

Second-order perturbation theory (MP2) is a more computationally tractable method for larger systems, but MP2 is known to overestimate the interaction energy for base-stacking interactions.^11,16 One method to improve upon MP2 results is to use the so-called spin-component scaled (SCS) approach¹⁷, which uses different scale factors for the same-spin and opposite-spin contributions to the total energy. To assess the accuracy of this technique, Sherrill and co-workers have compared complete basis set coupled-cluster potential energy curves for several prototypical nonbonded interactions to those obtained using SCS-MP2 and several density functional methods.¹⁸ Overall, SCS-MP2 gave reasonable results, typically resulting in errors on the order of a few tenths of 1 kcal mol⁻¹. Further comparison of SCS-MP2 to CCSD(T) results for a revised S22 data set, including a parallel displaced benzene dimer, a uracil dimer, and a stacked adenine-thymine complex, yielded a mean absolute deviation between the SCS-MP2 and the CCSD(T) energy results of 0.80 kcal/mol and the root mean squared deviation was 0.96 kcal/mol.¹⁹

The computational cost of MP2 can be reduced through the use of the density-fitting (DF) approximation²⁰ which speeds up the evaluation of the two electron integrals by introducing an auxiliary basis set. Importantly, the DF approximation, which is also referred to as the resolution of identity (RI) method, does not significantly impact the obtained energies relative to canonical MP2. For a representative thymine-thymine dimer, while an MP2/aug-cc-pVTZ single-point energy computation takes approximately 22 hours, the corresponding DF-MP2/aug-cc-pVTZ calculation takes less than 1 hour. Using density-fitting in conjunction with SCS should provide satisfactory estimates of the base stacking interaction energy at a reasonable computational cost.

In addition to identification and application of the appropriate model chemistry for base stacking, as well as for other molecular interactions, another factor to consider is the treatment of the inter- and intramolecular degrees of freedom of the bases themselves. In the majority of studies to date the monomer (ie. individual nucleic acid base) geometries were fixed at experimental, empirical or QM monomer optimized geometries with the intermolecular degrees of freedom adjusted or optimized to varying degrees.^16,21–25 These studies include full optimization of a stacked uracil dimer to identify stationary points²⁶ to a number of studies where the intermolecular geometries correspond to experimentally observed stacking orientations of typically the A or B forms of DNA.^21,24,25,27 Such work has been extended to include systematic sampling of twist or roll.^28,29 However, the relative orientation of stacked bases may vary widely in DNA. This includes sequence dependent effects as well as the relative orientation of adjacent bases in non-canonical regions of DNA or RNA, which often deviate significantly from what would be consider stacked orientations.^30–32 In addition, the relative orientation of stacked bases can vary significantly during the course of the normal dynamics under which oligonucleotides undergo in aqueous and physiological environments at ambient temperatures.^33,34 Thus, in order to investigate the contribution of stacking interactions to the conformational properties of DNA and RNA, it is necessary to adopt a reference frame in which the relative orientation of stacked bases may be rigorously defined, in order to systematically control the intermolecular orientation between stacked base monomers or base pairs while also allowing for relaxation of the intramolecular degrees of freedom of the individual bases in the complex.

In this work, DF-SCS-MP2 is used to determine the base stacking energy of DNA base stacked monomers (e.g. Figures 5 and 6) in canonical A and B-form conformations for all 16 possible stacked base monomers. To perform such calculations while maintaining the relative orientation of the stacked bases and allowing the intramolecular geometries of the individual monomers to relax, we have recast the internal coordinate definition of base stacked monomers, separating the intramolecular and intermolecular coordinates. The intermolecular coordinates will be referred to in terms of the commonly understood parameters of rise, slide, shift, tilt, roll, and twist.^35–37 Our definitions of these parameters do not correspond directly to previously published definitions of relative base orientations,^35,37–40 and they are not intended to provide a general definition for relative base orientations. The focus of the work, rather, is to utilize a specific, controllable set of internal coordinates to examine the effect of various types of geometry optimization on the magnitude of base stacking interactions. Thus, we will refer to our definitions as rise_sm, and so on, where sm represents a stacked monomer configuration, to distinguish them from the standard definitions. And while the present definitions do approximate the standard convention, to obtain definitions that do correspond to previously published values the user must directly apply those published methods to the geometries obtained from optimization using the present definitions.

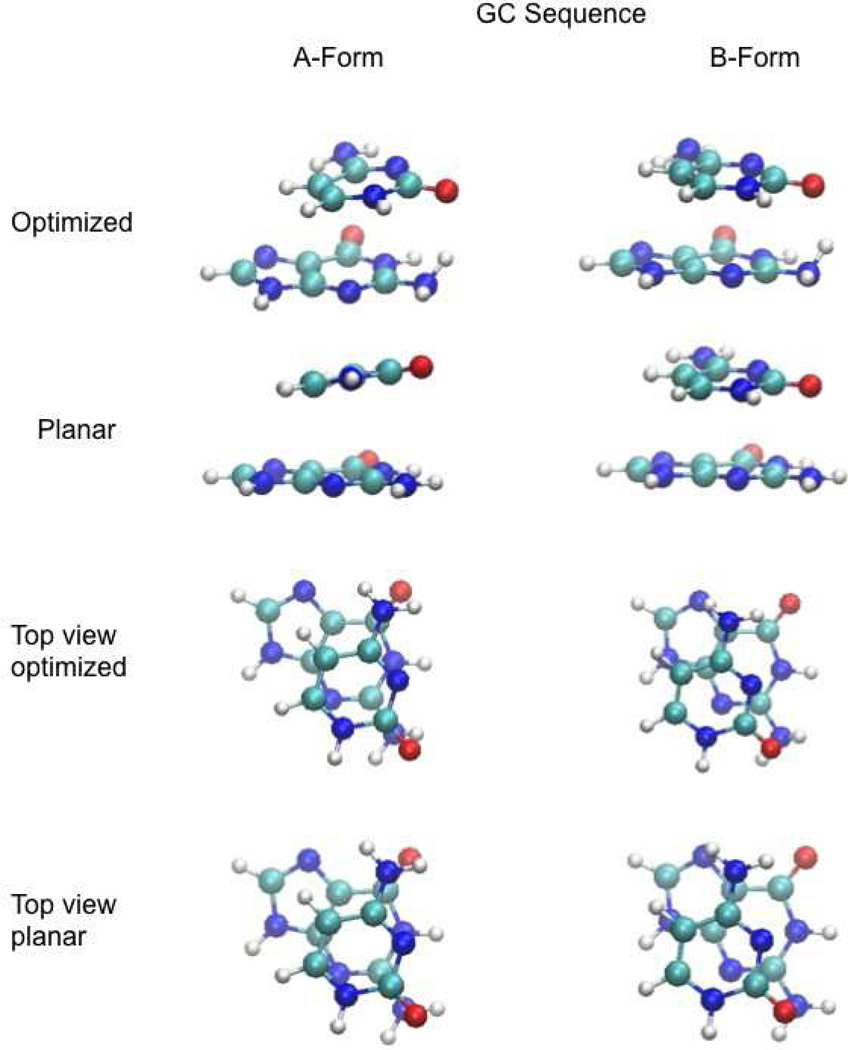
Figure 5.

Images of the GC stacked base monomers following full optimization (Optimized) and optimization with the planarity (Planar) of the bases constrained while all other intramolecular degrees of freedom of the individual bases were allowed to relax.

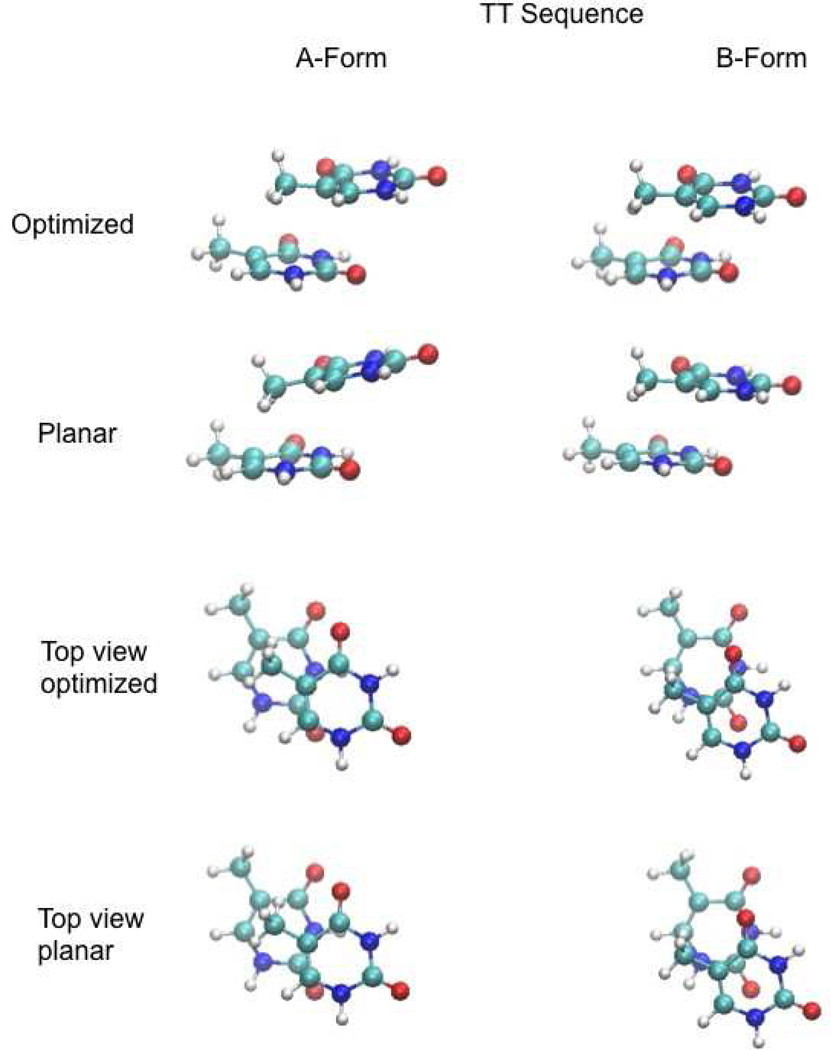
Figure 6.

Images of the TT stacked base monomers following full optimization (Optimized) and optimization with the planarity (Planar) of the bases constrained while all other intramolecular degrees of freedom of the individual bases were allowed to relax.

Methods

Representations of each possible base stack conformation in the canonical A- and B-forms based on fibre X-ray diffraction data⁴¹ were generated using MOE (Chemical Computing Group). A set of internal coordinates was defined for base stacked monomers that separated the intramolecular and the intermolecular coordinates. This provides a mechanism to input Cartesian coordinates from, for example, an X-ray crystallographic structure, constrain the relative (intermolecular) orientation of the two bases and fully optimize the intramolecular coordinates of the base monomers. Conversion from Cartesian to internal coordinates was performed using the program CHARMM⁴² in combination with in-house programs developed as part of the present work. Details of the implementation are presented below in the “Stacked Monomer Coordinate System Definition” section. For each base stacked configuration, two constrained geometry optimizations were performed. In the first optimization, all intramolecular coordinates were included in the optimization. In a separate optimization, the bases were restricted to planar geometries, but all other intramolecular coordinates were optimized. In both cases, the intermolecular coordinates were frozen. Monomer geometries were either fully optimized or restricted to be planar as required to calculate the respective fully optimized and planar interaction energies. All of the constrained geometry optimizations were performed at the MP2/cc-pVDZ level of theory using Gaussian03.⁴³

Using each of the optimized geometries, the total interaction energy was determined with MP2 and the aug-cc-pVTZ basis set. The density-fitting approximation,²⁰ or resolution of the identity (RI) method, was employed (DF-MP2/aug-cc-pVTZ). To provide an improved estimation of the interaction energy, the spin-component scaling method (SCS) was also employed using the scaling factors proposed by Grimme in his original formulation (same spin scaling factor 6/5 and opposite spin scaling factor 1/3).¹⁷ For all methods, the interaction energy was counterpoise-corrected using the method of Boys and Bernardi.⁴⁴ All interaction energy computations were performed in Molpro.⁴⁵

Stacked Monomer Coordinate System Definition

To assess the stacking interaction for stacked base monomers in a 5’ to 3’ DNA sequence, the relative orientation of the stacked bases for each conformation was defined based on a specific set of internal coordinates related to the base stacking orientation. In this approach the relative orientations of the bases are defined based on virtual or dummy atoms with the base atoms subsequently constructed relative to the virtual atoms. This type of system definition enables the optimization of the intramolecular coordinates, while retaining the intermolecular orientation of the bases.

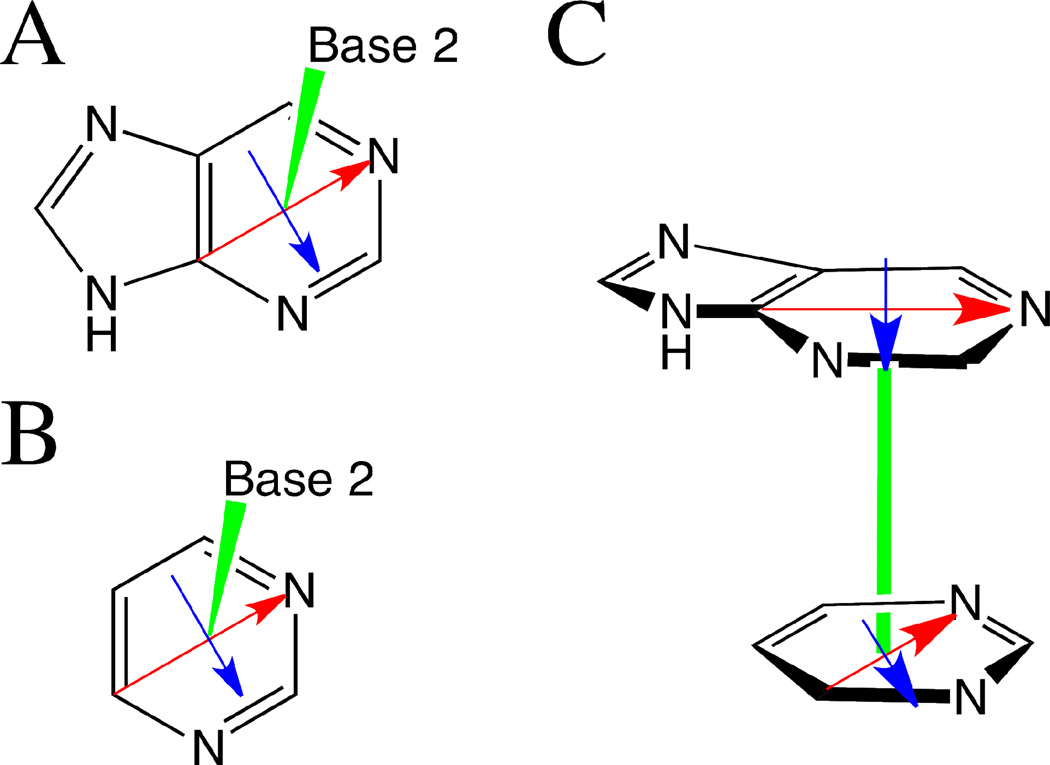
To define the relative orientation between two objects, six coordinates are required. The six coordinates could be defined in many equivalent formalisms, so we have selected a coordinate system that allows intuitive understanding of the orientation comprising three translational coordinates (rise_sm, slide_sm and shift_sm) and three rotational coordinates (twist_sm, tilt_sm and roll_sm; Figure S1 of the supporting information). The x-axis is defined as connecting C4 and N1 (for purines) or C6 and N3 (for pyrimidines) as shown in Figure 1A and 1B, respectively. The y-axis is defined as the perpendicular axis to the x-axis in the plane of the base, and the z-axis as the perpendicular vector to the plane of the base. In the initial construction of the stacked monomer configuration both bases are planar, although in subsequent geometry optimizations this constraint may be relaxed. For each base, we define a centroid at the midpoint connecting C4 and N1 or C6 and N3, which is very nearly the center of the six-membered ring for all bases. (If the six-membered ring is taken to be a perfect hexagon, this would be the exact center of the hexagon.) The C4 or C6 carbon in each purine or pyrimidine base, respectively, are considered the “seed” atom of that base, around which the rest of the base is constructed.

To specify the relative orientation between the two bases in the stacked conformation, we first assign the reference base (lower base in Figure 1C). The distance between the two defined centroids in the z-direction is defined as rise_sm, separation in the x-direction relative to the reference base as slide_sm, and separation in the y-direction relative to the reference base as shift_sm. The angle by which the upper base is rotated in the xy-plane is defined as twist_sm. If the two seed atoms from each base are aligned, this is defined as a twist_sm angle of 0 degrees. The rotation angle in the xz-plane is defined as tilt_sm. Since the x-axis is defined by the C4/N1 or C6/N3 vector, the tilt_sm is measured as the out-of-plane angle between the seed atom (C4 or C6) – centroid vector of the upper base and the plane parallel to the lower base. The rotation angle in the yz-plane is defined as roll_sm. Similarly, it is defined as the out of plane angle between a vector, with an origin at the centroid, perpendicular to the x-axis vector in the plane of the base and the plane parallel to the lower base (For additional details, see Figure S2 in the supporting information). Based on these definitions and the orientation of the bases in Figure 1C, rise_sm corresponds to the length of the green vector, both slide_sm and shift_sm are zero, the twist_sm angle is approximately −30° and both the tilt_sm and the roll_sm are 0°. Images depicting the displacements associated with tilt_sm, roll_sm, and twist_sm are shown in Figure S1 and a more detailed description of the coordinate system definitions is presented in Figure S2 in the supporting information.

Figure 1.

Definitions of the vectors and centroid of the A) purine and B) pyrimidine bases used to describe the relative orientation of the stacked bases, including an illustration of stacked monomers. X-axis (red): C4 and N1 for purines or C6 and N3 for pyrimidines; Y-axis (blue): perpendicular axis to the x-axis in the plane of the base; and Z-axis (green): perpendicular vector to the plane of the base originating from the centroid of the reference base. The base centroid is the midpoint connecting C4 and N1 for purines or C6 and N3 for pyrimdines. Based on these definitions, rise_sm corresponds to the length of the green vector, both slide_sm and shift_sm are zero, the twist_sm angle is approximately −30° and both the tilt_sm and the roll_sm are 0°.

To simplify the computational implementation, the tilt_sm and roll_sm angles are actually measured from the perpendicular rather than from the plane of the base. However, for ease of intuitive understanding of the geometry, we prefer to present the out-of-plane rotational angles. These differ by 90 degrees from our measured values. In addition, in contrast to definitions of the orientations of stacked base pairs that are direction independent,³⁸ the present reference frame is direction dependent such that the bases should be specified in the 5’ to 3’ direction for two bases that are stacked along the same strand.

To implement this internal coordinate system, a connectivity table (often called a Z-matrix) template is constructed for each base individually. In the Z-matrix template, initial values for the intramolecular coordinates must be defined. As these values will typically be optimized in our computations, the exact values of these initial parameters are not critical. We use the gas phase optimized MP2/cc-pVDZ bond lengths and bond angles for the initial values in our base templates, with the bases treated as planar. Any two base templates in any orientation are then joined in the specified order, yielding a new Z-matrix for the base stack conformation that defines the connecting intermolecular coordinates as the rise_sm, slide_sm, shift_sm, tilt_sm, roll_sm, and twist_sm coordinates defined above. Note that only intramolecular coordinates are included in the base templates and the intermolecular coordinates are not defined in terms of any of the intramolecular coordinates. This means that only the intermolecular coordinates must be specified and then any base stack conformation can be constructed in any orientation from the same base templates.

To enable the construction of a separated-coordinate z-matrix for a known base monomer stack conformation (eg. a conformation taken from a crystal structure), a CHARMM stream file was written which can measure the defined rise_sm, slide_sm, shift_sm, tilt_sm, roll_sm and twist_sm coordinates for any set of Cartesian coordinates that can be read by CHARMM. These coordinates can then be transformed into the general Z-matrix and used for any type of further calculation or analysis in any electronic structure program package. Programs to perform the above transformations and the CHARMM scripts to convert Cartesian coordinates are available on the MacKerell laboratory web page at http://mackerell.umaryland.edu/MacKerell_Lab.html.

While other software packages, such as Curves^46–48 or 3DNA^49,50, enable the specification of stacked base configurations with rigid intermolecular parameters, our system does not output coordinates, but rather constructs a Z-matrix that separates the inter- and intramolecular internal coordinates. This enables the manipulation of these intermolecular coordinates within electronic structure computations, allowing, for example, a scan over a particular intermolecular coordinate in a series of electronic structure computations. In addition, the impact of intramolecular coordinates on stacking energies may be systematically studied for a given intermolecular orientation. Indeed, in the present study the impact of enforcing planarity of nucleic acid bases on the stacking energy is investigated. Importantly, the Z-matrix output is quite general and can be used with a variety of electronic structure software packages. A representative Z-matrix is included in the supporting information (Figure S3), along with an image of the structure generated by the z-matrix, including the virtual atoms (Figure S4), and a PDB file of the structure (Figure S5).

Results and Discussion

To understand the relationship of the definitions in the present stacked monomer coordinate reader system with commonly used standard definitions, we constructed canonical conformations for all 16 possible base pair sequences for both canonical A- and B-form DNA. The defined rise_sm, slide_sm, shift_sm, tilt_sm, roll_sm, and twist_sm coordinates were then determined based on the input Cartesian coordinates generated for the canonical forms of DNA based on X-ray fibre data and are presented in Table 1. Table 1 also contains the standard values of rise, slide, shift, tilt, roll, and twist calculated with W3DNA⁵⁰ using the same Cartesian coordinates. Comparison of the stacked monomer versus standard definitions show them to be similar for rise, roll and tilt, although order of the values are reversed for roll with A versus B DNA. Larger, systematic differences are present for slide, shift and tilt and in all cases the RMS fluctuations of the stacked monomer parameters are significantly larger than those calculated with W3DNA. Thus, while the stacked monomer definitions may be used to construct base stacked monomers in orientations that approximate the standard definitions and perform the desired QM calculations, it is essential that published methods be applied on the final geometries to obtain the relative base orientations that correspond to the accepted definitions.^51,52

Table 1.

Base monomer stacking parameters for canonical base stacked configurations for 5’-3’ sequences in A-Form and B-Form DNA from the presented stacked monomer (SM) coordinate definition and calculated using the program W3DNA. Rise, slide, and shift are in angstroms. Tilt, roll, and twist are in degrees. A positive value for tilt_sm or twist_sm indicates the upper base is tilted away from the reference base. A positive value for twist_sm indicates rotation in the counterclockwise direction. Averages and RMS fluctuations over the base pairs are presented.

A-Form
	Rise		Slide		Shift		Tilt		Roll		Twist
	SM	3DNA	SM	3DNA	SM	3DNA	SM	3DNA	SM	3DNA	SM	3DNA
AA	3.49	3.27	2.16	−1.72	0.78	−0.23	1.73	−3.64	11.12	10.61	30.63	30.79
AC	3.32	3.26	0.17	−1.72	0.64	−0.14	−2.04	−3.56	11.23	10.66	11.99	31.99
AG	3.50	3.27	2.17	−1.82	0.81	−0.23	1.55	−3.74	11.10	10.58	29.52	30.02
AT	3.31	3.27	0.12	−1.74	0.62	−0.23	−1.83	−3.64	11.10	10.63	12.62	30.67
CA	3.49	3.26	4.22	−1.66	0.61	−0.33	1.67	−3.51	10.95	10.62	49.65	29.60
CC	3.31	3.25	2.29	−1.66	1.12	−0.25	−2.05	−3.43	11.05	10.67	30.99	30.80
CG	3.50	3.27	4.24	−1.77	0.63	−0.34	1.49	−3.61	10.93	10.59	48.54	28.83
CT	3.05	3.26	2.59	−1.69	1.12	−0.34	3.39	−3.51	7.71	10.65	31.70	29.48
GA	3.49	3.27	2.17	−1.64	0.70	−0.15	1.73	−3.69	11.18	10.58	31.74	31.58
GC	3.31	3.26	0.18	−1.64	0.60	−0.06	−2.07	−3.61	11.29	10.63	13.10	32.78
GG	3.50	3.28	2.19	−1.74	0.73	−0.15	1.54	−3.79	11.16	10.55	30.63	30.80
GT	3.31	3.27	0.14	−1.67	0.59	−0.15	−1.85	−3.69	11.17	10.60	13.76	31.46
TA	3.49	3.27	4.25	−1.70	0.68	−0.20	1.72	−3.67	11.10	10.58	48.94	30.92
TC	3.31	3.26	2.31	−1.70	1.16	−0.12	−2.05	−3.59	11.22	10.64	30.31	32.11
TG	3.50	3.28	4.27	−1.80	0.70	−0.21	1.54	−3.77	11.08	10.55	47.85	30.14
TT	3.31	3.27	2.27	−1.72	1.16	−0.21	−1.84	−3.68	11.10	10.61	30.98	30.80
Ave.	3.39	3.27	2.23	−1.71	0.79	−0.21	0.16	−3.63	10.91	10.61	30.81	30.80
RMS	0.12	0.01	1.45	0.05	0.21	0.08	1.92	0.10	0.83	0.04	12.70	1.01
B−Form
	Rise		Slide		Shift		Tilt		Roll		Twist
	SM	3DNA	SM	3DNA	SM	3DNA	SM	3DNA	SM	3DNA	SM	3DNA
AA	3.23	3.36	1.02	−0.34	1.24	−0.09	−2.91	−1.10	−2.59	−3.68	35.75	35.80
AC	3.22	3.38	1.03	−0.30	1.16	0.12	−2.43	−1.39	−3.67	−3.66	20.79	38.34
AG	3.23	3.36	1.03	−0.44	1.27	−0.10	−2.84	−1.07	−2.40	−3.68	34.57	35.06
AT	3.21	3.36	1.03	−0.37	1.24	−0.10	−1.93	−1.12	−3.40	−3.72	17.35	35.66
CA	3.22	3.35	3.21	−0.26	1.70	−0.29	−2.40	−1.01	−2.55	−3.78	50.68	33.25
CC	3.22	3.37	1.21	−0.22	2.16	−0.09	−1.95	−1.30	−3.50	−3.75	35.73	35.79
CG	3.22	3.35	3.23	−0.36	1.74	−0.31	−2.33	−0.98	−2.36	−3.78	49.51	32.50
CT	3.07	3.36	1.55	−0.29	2.24	−0.31	3.36	−1.03	−6.26	−3.82	32.34	33.11
GA	3.23	3.36	1.05	−0.27	1.19	−0.01	−3.07	−1.09	−2.78	−3.69	36.91	36.54
GC	3.21	3.38	1.00	−0.23	1.16	0.19	−2.53	−1.38	−3.89	−3.67	21.95	39.08
GG	3.23	3.36	1.07	−0.37	1.23	−0.03	−2.99	−1.06	−2.60	−3.69	35.74	35.80
GT	3.20	3.36	0.99	−0.30	1.24	−0.02	−2.03	−1.11	−3.63	−3.73	18.51	36.40
TA	3.23	3.36	3.31	−0.33	1.45	−0.06	−2.89	−1.05	−2.57	−3.67	54.14	35.95
TC	3.21	3.38	1.34	−0.28	2.03	0.14	−2.42	−1.34	−3.64	−3.64	39.18	38.48
TG	3.23	3.36	3.34	−0.43	1.49	−0.07	−2.82	−1.02	−2.38	−3.66	52.97	35.20
TT	3.20	3.36	1.37	−0.36	2.11	−0.07	−1.92	−1.07	−3.38	−3.71	35.74	35.80
Ave	3.21	3.36	1.67	−0.32	1.54	−0.07	−2.13	−1.13	−3.23	−3.71	35.74	35.80
RMS	0.04	0.01	0.94	0.06	0.38	0.14	1.47	0.13	0.95	0.05	11.52	1.78

Canonical A and B stacked monomer Cartesian coordinates were used to generate Z-matricies for all 16 base stacked monomers and constrained optimizations were performed which optimized the intramolecular coordinates while retaining the relative intermolecular orientation. For every conformation, the geometry was examined before and after the optimization to ensure that the relative orientation was the same and that it matched the relative orientation of the original canonical conformation. For each optimized structure, the stacking interaction energy was computed at the DF-MP2/aug-cc-pVTZ and DF-SCS-MP2/aug-cc-pVTZ levels of theory.

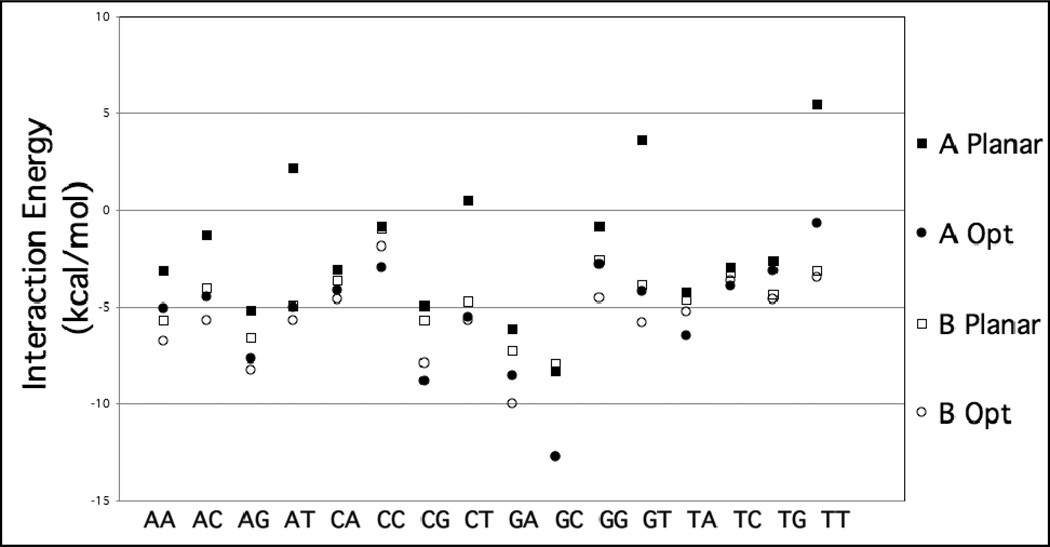
The total stacking interaction energies are presented graphically in Figure 2 for the A and B forms, and the associated data are presented in Tables S1 and S2 of the supporting information. In all cases, the DF-MP2 method consistently predicted more bound complexes than the DF-SCS-MP2. While density-fitting can offer significant speed-up of MP2 computations, it does not affect the accuracy of the underlying method, and MP2 is known to overestimate the stacking energy of aromatic complexes. The less favorable interaction energies from the SCS contribution correct for the systematic overestimation of dispersion contribution from canonical MP2, as reported in previous studies.¹⁷

Figure 2.

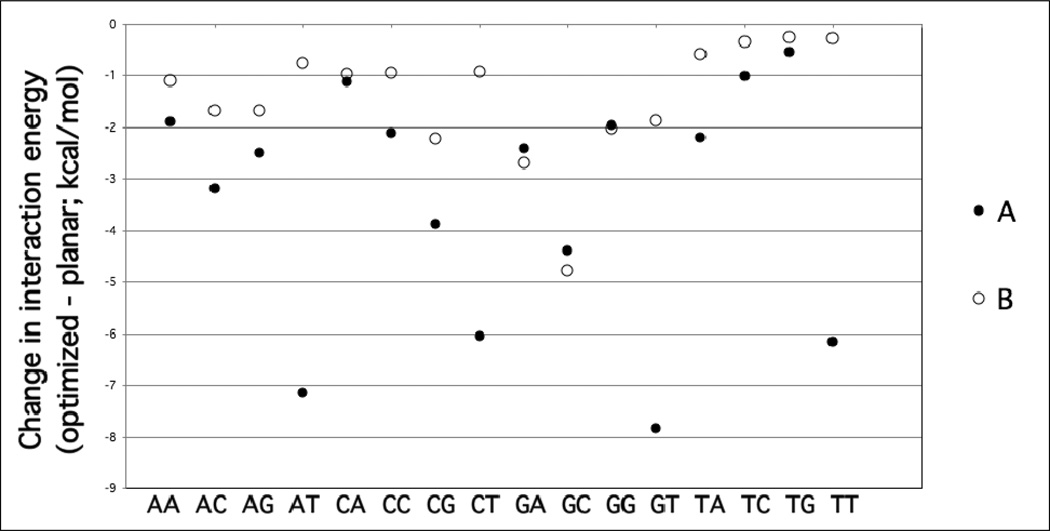
DF-SCS-MP2/aug-cc-pVTZ interaction energies (kcal/mol) for canonical A-form and B-form base-stacking conformations. The optimized geometry is the MP2/cc-pVDZ optimization of the intramolecular coordinates. The planar geometry restricts the base monomers to planar geometries, but allows other intramolecular coordinates to optimize.

To investigate the impact of relaxation of the internal (intramolecular) degrees of freedom on the bases, the stacking interaction energies were also determined with the bases restrained to be planar with all other internal degrees of freedom allowed to relax. Results are included with the fully optimized results in Figure 2. As expected full optimization led to more favorable binding energies, with the differences shown on Figure 3. In the case of A-form dimers, optimization lead to the interaction energy becoming more favorable by an average of −3.4±0.6 kcal/mol while the average difference was −1.5±0.3 kcal/mol in the case of B-form DNA (Data and statistical metrics shown in Table S3 in the supporting information). The additional optimization led to significant out-of-plane distortion of the individual bases leading to the more favorable interaction energies. For example, for the fully optimized geometries of the AT and GC stacked monomers, shown in Figures 4 and 5, respectively, out of plane distortions of the non-hydrogen atoms are evident, as are distortions of the amino groups. These distortions lead to “hydrogen bond-like” interactions between the stacked monomers, in particular the amino groups with the carbonyl oxygens, contributing to the more favorable interaction energies. While it is not surprising that additional degrees of freedom result in a lower energy structures, the role of these out-of-plane distortions in duplex DNA in solution is not clear.⁵³ Such out-of-plane distortions may be limited in stacked base dimers that occur in duplex DNA. In addition, interaction of amino groups with the environment, including base pairing and hydrogen bonding with solvent would compete for the intermolecular interactions occurring in the individual stacked dimers shown in Figures 4 and 5.

Figure 3.

Difference between the stacking energies of the fully optimized and planar (ΔE = IE_opt − IE_planar, kcal/mol) geometries.

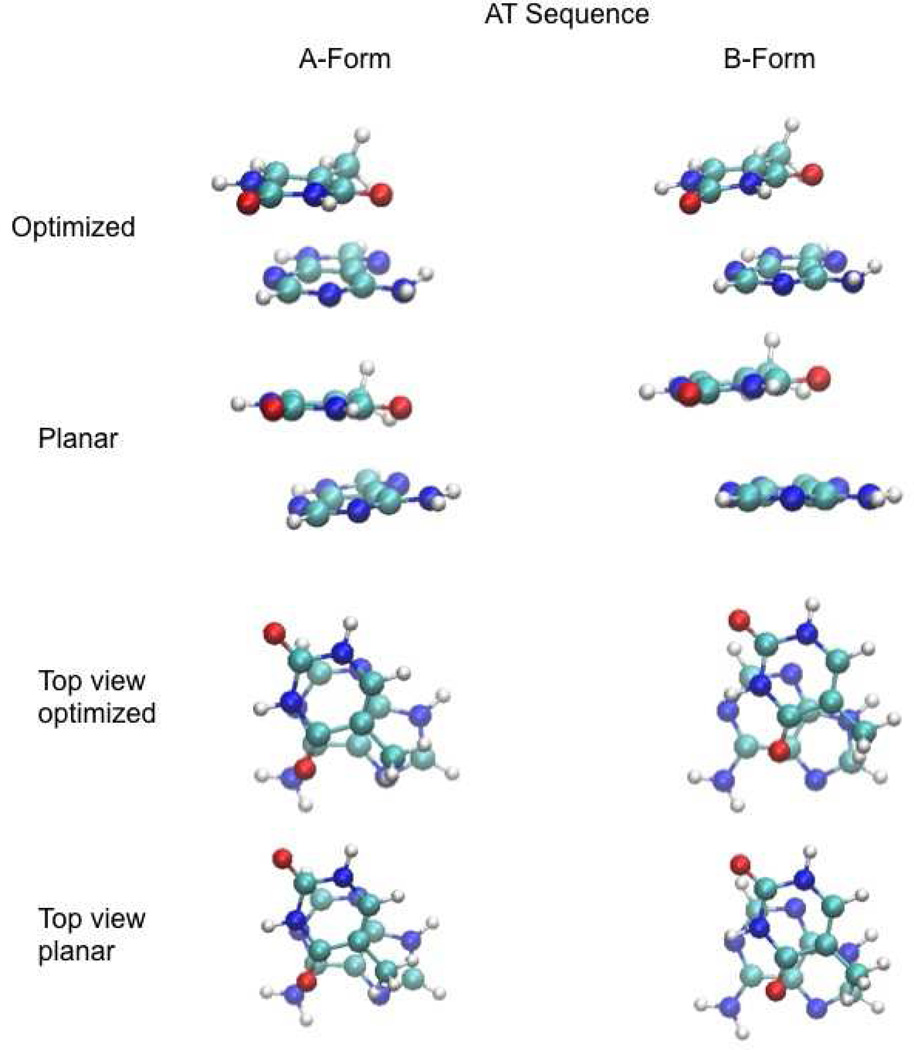
Figure 4.

Images of the AT stacked base monomers following full optimization (Optimized) and optimization with the planarity (Planar) of the bases constrained while all other intramolecular degrees of freedom of the individual bases were allowed to relax.

The largest impact of maintaining planarity was observed with the AT dimer. Using the DF-SCS-MP2/aug-cc-pVTZ stacking energies, for the A-form, restricting the monomers to planar geometries destabilized the complex by 7 kcal/mol. However, for the B form, the destabilization was only 0.8 kcal/mol. To understand this the planar conformations of AT are also shown in Figure 4 from a top view. This view best enables the comparison of the π-stacking in the A- and B-form conformations. In the B form the orientation is more parallel-displaced π-stacking as compared to the directly stacked (sandwich-like) A form (see Sinnokrot and Sherrill for the definition of parallel-displaced and sandwich-like configurations for benzene, Reference 14). This leads to the more favorable interaction energy for the B-form conformation in good agreement with previous studies of the benzene dimer that have consistently shown parallel-displaced configurations to be more favorable than sandwich configurations.^12,14 However, the directly stacked orientation for the A form also situates the amino and carbonyl group allowing for the formation of more hydrogen bond-like favorable interactions, leading to a greater gain upon full intramolecular optimization of the A form dimer.

Interestingly, in all the A-form base stacks involving thymine, DF-SCS-MP2/aug-cc-pVTZ interaction energies are actually unfavorable when the base intramolecular geometry was restricted to a planar geometry. For example, in the TT sequence, the DF-SCS-MP2/aug-cc-pVTZ interaction energy is 5.5 kcal/mol. In the B form, the TT sequence interaction energy is −3.2 kcal/mol. Both structures are shown in Figure 6; analysis of the top view enables the best comparison of the π-stacking overlap. In this case, the π-stacking for both conformations is similar; however, in the A form the carbonyl groups are in much closer proximity and the C5 methyl is pointed towards the C5 and C6 atoms of the lower base. This suggests that a combination of unfavorable electrostatic and van der Waals interactions between these moieties leads to the unfavorable interaction in the A form. However, upon full optimization of the TT dimer, the relative orientation of the carbonyls relaxes and the methyl group of the upper base moves out of plane, minimizing the unfavorable interactions and leading to a favorable stacking energy of −0.7 kcal/mol. These results further indicate the importance of including intramolecular geometry optimization in base stacking QM calculations.

Additional analysis involved the differences between the stacking interaction energies between the A and B forms, with the results presented in Figure 7 as IE_B – IE_A, and in Table S4 of the supporting information. On average, stacking in the B form is more stable with the average differences being −0.6 and −2.6 kcal/mol for the fully optimized and planar geometries, respectively. Again the impact of geometry optimization is evident, where the penalty associated with assumption of the A form is significantly decreased when the bases are allowed to relax. Previous studies reported that B stacking was more favorable than that in the A form, with the differences reported to be 6 kcal/mol for the stacked base pairs.²¹ While the present study only involved stacked monomers, the results indicate the difference between A and B form stacking to be less then in the previous work. This difference is consistent with the lack of optimization of the geometries of the bases in the previous study, though the smaller basis set could also contribute to the differences.

Figure 7.

Difference in MP2 interaction energies of the B form versus the A form (B-A) for each possible base stacking conformation. Energies in kcal/mol.

While B form stacking is more favorable on average than in the A form, this is not always the case. A number of stacked monomers are more stable in the A form with all of those including a C base, with the exception of the TA optimized stacked monomers (Figure 7). The contribution of C stacking towards favoring the A form of DNA has been observed in previous QM results,²¹ and is consistent with the known tendency of GC base pairs to favor assumption of the A form of DNA.^5,54–58 Thus, C intrinsically favors the A form of DNA due to stacking interactions as well as due to intrinsically favoring an A-like conformation of the glycosidic torsion χ and of the deoxyribose sugar pucker.⁵⁹

As stated above, the extent to which the stacking interaction energy became more favorable upon full relaxation was larger in the A form as compared to the B form (Figure 3). In the A form the average difference is approximately −3.4 kcal/mol versus the B form where the average is approximately −1.5 kcal/mol (Table S3 of the supporting information). A-form DNA is favored by low water activity, for example due to low humidity or high ion or ethanol concentrations. If the decreased water activity is associated with lower base-solvent interactions, it may be anticipated that the bases may sample conformations that are closer to the fully optimized geometries as compared to B-form DNA. This additional intrinsic relaxation of the bases would lead to a lower stacking penalty for assuming the A form, which is evident from the average B minus A differences (Table S4 of the supporting information) of −0.6 and −2.6 kcal/mol for the optimized and planar base geometries, respectively.

Summary

Results are reported for stacking energies of the 16 DNA base stacked monomers in canonical A and B-form conformations. Calculations use a novel Z-matrix representation of the intermolecular orientation of the stacked base monomers as well as of the intramolecular coordinates of the individual base monomers. This representation allows for the optimization of the internal degrees of freedom of the monomers while constraining the intermolecular orientation of the bases within an electronic structure computation. However, while the representation was designed to yield definitions of the intermolecular orientations of the bases similar to the standard definitions of rise, shift, slide, roll, twist and tilt, there are significant differences such that it is recommended that once optimized geometries are obtained using the presented Z-matrix representation standard definitions of base stacking be calculated using available programs such as W3DNA⁵⁰, Curves+⁴⁸ or FreeHelix⁶⁰.

Geometry optimizations at the MP2/cc-pVDZ level followed by single point energy calculations using DF-SCS-MP2/aug-cc-pVTZ represent a computationally feasible approach to obtaining stacking energy that approach CCSD(T) quality values. For example, calculation of the DF-SCS-MP2/aug-cc-pVTZ interaction energies, including all monomer and dimer calculations, required from 1.4 to 3.7 CPU hours for each base dimer on a single core (See Table S5 of the supporting information). Calculated interaction energies show the stacking to generally be more favorable in the B form, contributing to that being the dominant form of duplex DNA occurring in solution. However, in a number of stacked monomers involving C, the A form is favored, consistent with the presence of C in duplex DNA favoring the assumption of A form conformations. Notably, the inclusion of optimization of the intramolecular degrees of freedom of the bases in the calculations had a significant impact on the calculated stacking energies, with differences approaching 8 kcal/mol obtained going from base conformations constrained to be planar, with all other internal degrees of freedom relaxed, to those in which the bases were allowed to fully optimize. These differences also impact the relative stacking energies of the A versus B forms of DNA. In fact, the extent of these differences are similar to or greater than the energy differences observed between different model chemistries, including going from double to triple to quadruple zeta basis sets and different treatments of electron correlation.^21,24–27 Thus, the application of quantum mechanical methods to estimate base stacking energies must adequately treat relaxation of the internal base geometries in their respective environments as well as apply the appropriate QM model chemistries.