Abstract
Behavioral Disinhibition is a trait hypothesized to represent a general vulnerability to the development of substance use disorders. We used a large community-representative sample (N = 7188) to investigate the genetic and environmental relationships among measures of Behavioral Disinhibition, Nicotine Use/Dependence, Alcohol Consumption, Alcohol Dependence, and Drug Use. First, using a subsample of twins (N = 2877), we used standard twin models to estimate the additive genetic, shared environmental, and non-shared environmental contributions to these five traits. Heritabilities ranged from .42–.58 and shared environmental effects ranged from .12–.24. Phenotypic correlations among the five traits were largely attributable to shared genetic effects. Second, we used Genome-wide Complex Trait Analysis (GCTA) to estimate as a random effect the aggregate genetic effect attributable to 515,384 common SNPs. The aggregated SNPs explained 10–30% of the variance in the traits. Third, a genome-wide scoring approach summed the actual SNPs, creating a SNP-based genetic risk score for each individual. After 10-fold internal cross-validation, the SNP sumscore correlated with the traits at .03 to .07 (p<.05), indicating small but detectable effects. SNP sumscores generated on one trait correlated at approximately the same magnitude with other traits, indicating detectable pleiotropic effects among these traits. Behavioral disinhibition thus shares genetic etiology with measures of substance use, and this relationship is detectable at the level of measured genomic variation.
Keywords: Behavioral Disinhibition, Alcohol, Drug, Tobacco, GWAS, Twins, Polygenetic
Disinhibition is a behavioral trait hypothesized to represent a general vulnerability in the development of substance use disorders (Iacono, Malone, & McGue, 2008; Zucker, Heitzeg, & Nigg, 2011). Those with greater levels of disinhibition are thought to act more impulsively, be more thrill-seeking, and not consider as deeply the long-term consequences of their actions. Disinhibited individuals are also more likely to use substances and have a more difficult time quitting. Evidence for this hypothesis comes from a variety of research designs summarized inIacono et al. (2008). There is additional evidence that measures of substance use and disinhibition are heritable (e.g., 50% heritable as in the present study) and that the relationships among them are significantly genetically driven (Hicks, Schalet, Malone, Iacono, & McGue, 2011; Kendler, Jacobson, Prescott, & Neale, 2003; Kendler, Prescott, Myers, & Neale, 2003; Vrieze, Hicks, McGue, & Iacono, in press; Young, Stallings, Corley, Krauter, & Hewitt, 2000). However, research on measured genetic variants, such as single nucleotide polymorphisms (SNPs), has not been successful in locating individual genes or genetic variants responsible for the genetic variance in common substance use disorders, although there are notable exceptions (Bierut et al., 2012; Furberg et al., 2010; Luczak, Glatt, & Wall, 2006; Schumann et al., 2011).
It appears that for many complex traits the effects of individual genetic variants are small (Manolio et al., 2009). Genome-wide association studies (GWAS), which test for the relationship between a phenotype and individual common SNPs, have confirmed that individual SNPs have vanishingly small effects on complex traits (e.g., account for < 0.5% of the phenotypic variance). Compounding the problem, GWAS designs require around 1 million independent tests, and this creates a very substantial multiple testing burden requiring p-values of 5×10−8 (Hirschhorn & Daly, 2005). The result is that massive sample sizes have been required to reliably separate the genetic signal from noise. One successful approach to dealing with these challenges has been to assemble mega-samples of hundreds of thousands of individuals to obtain sufficient statistical power to detect these small effects. Such endeavors have identified hundreds of variants (Visscher, Brown, McCarthy, & Yang, 2012) for complex traits like height (Allen et al., 2010), body mass index (BMI) (Speliotes et al., 2010), and lipid levels (Teslovich et al., 2010), as well as for complex diseases such as Crohn’s disease (Franke et al., 2010) and Type-2 Diabetes (Voight et al., 2010).
The present study uses genome-wide scoring in a moderately-sized twin and adoptive family study sample (N = 7188) to investigate the genetic architecture of several measures of substance use pathology that have been described in detail previously (Hicks et al., 2011), including measures of nicotine use/dependence, alcohol consumption, alcohol dependence, illicit drug use, and behavioral disinhibition. A genome-wide association study of these same data was unsuccessful in identifying any genome-wide significant SNPs, reinforcing the need to aggregate SNPs in small- to moderately-sized samples (McGue et al., 2012).
In addition to genome-wide markers, the present sample contains a large number of twins, which allows estimation of heritability using standard twin methodology, as well as from Genome-wide Complex Trait Analysis (GCTA) (Yang, Lee, Goddard, & Visscher, 2011; Yang, Manolio, et al., 2011). Twin-based estimates, for example, provide estimates of the total additive genetic effect, which may be due to other forms of genetic variation than common SNPs (Vrieze, Iacono, & McGue, 2012). GCTA, on the other hand, provides the additive genetic effect due to common SNPs only. Comparison of the two methods provides insight into the non-SNP, rare SNP, or structural genetic variation that contribute to heritabilities estimated by twins.
Both twin-derived heritabilities and the GCTA method provide heritability estimates, but do not give individualized risk estimates for subjects. In contrast, Genome-wide scoring does provide individual risk estimates, and the scores can be applied in new samples to make risk predictions, although they typically return only a small fraction of the twin-estimated or GCTA-estimated heritability (Allen et al., 2010; Speliotes et al., 2010). In Genome-wide scoring individual SNPs are weighted based on their univariate association with the phenotype. All SNPs are then combined into a weighted sum to produce, for each person, a single aggregate SNP score. The score can then be used for a new individual to predict their phenotype value. Furthermore, twinand GCTA-estimated heritabilities are useful to inform the potential size and significance of the genome-wide scoring effect.
We computed twin- and GCTA-estimated heritabilities as well as genome-wide scores for our measures of nicotine use, alcohol consumption, alcohol dependence, illicit drug use, and behavioral disinhibition. The twin heritabilities and genome-wide scoring also allowed us to calculate the genetic correlations among the traits, providing estimates of pleiotropy among substance use disorders and behavioral disinhibition. The theory that behavioral disinhibition causes increased substance use would predict that genetic variants causing disinhibition should also be related to substance use—i.e., that there are pleiotropic genetic effects. In sum, the present results inform the extent and form of polygenetic heritability for substance use phenotypes, and provide guidance for future study of behavioral disinhibition and substance use traits and disease.
Method
The sample used in this research has been described in detail elsewhere (Iacono & McGue, 2002; Miller et al., in press). In short, it is composed of two studies of Minnesota families: a community-representative sample of twins and their parents, as well as a study of adoptive families. Sample sizes for the twin and adoptive families are provided in Table 1. Twin families are further divided into three prospective cohorts: (A) 17-year-old twins (N = 1139) first assessed between 1989–1996, followed regularly at ages 20, 24, and 29; (B) 11-year-old twins (N = 1167) assessed at ages 11, 14, 17, 20, 24, and 29, with their age-17 assessment occurring between 1996–2003; and (C) another sample (N = 571) of 11-year-old twins assessed at ages 11, 14, and 17, with their age-17 assessment occurring between 2005 and 2010. In the adoption study all families were composed of two families and two offspring. Some families had two biological offspring, some had two adopted offspring, and some had one biological offspring and one adopted offspring. Parents were typically assessed at intake, regardless of cohort. In total, the present study included 7188 Caucasian participants from 2300 families.
Table 1.
Means and Variances of Five Substance Use Phenotypes.
| Means | Variances | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample | Sex | N | Age | NIC | CON | DEP | DRG | BD | NIC | CON | DEP | DRUG | BD |
| M (SD) | |||||||||||||
| Twin Families | |||||||||||||
| Parents | Male | 1396 | 43.87 (5.65) | .53 | .80 | .86 | .41 | .63 | 1.16 | .42 | 1.64 | 1.36 | 1.10 |
| Female | 1587 | 41.67 (5.15) | .18 | .09 | −.06 | −.01 | −.33 | 1.11 | .35 | .63 | .83 | .55 | |
| MZ Twins | Male | 873 | 17.80 (0.61) | −.21 | −.23 | −.25 | −.17 | .24 | .70 | 1.38 | .63 | .90 | 1.17 |
| Female | 990 | 17.88 (0.77) | −.44 | −.64 | −.51 | −.39 | −.44 | .53 | 1.0 | .25 | .47 | .66 | |
| DZ Twins | Male | 457 | 17.75 (0.49) | −.22 | −.35 | −.26 | −.18 | .25 | .70 | 1.45 | .61 | .92 | 1.21 |
| Female | 557 | 18.03 (0.81) | −.32 | −.49 | −.40 | −.28 | −.26 | .65 | 1.05 | .46 | .65 | .82 | |
| Adoptive Families | |||||||||||||
| Parents | Male | 384 | 48.43 (4.46) | .22 | .49 | .44 | .45 | .22 | 1.13 | .49 | 1.21 | 1.35 | .73 |
| Females | 485 | 46.53 (4.11) | −.18 | −.11 | −.21 | .04 | −.50 | .91 | .32 | .47 | .78 | .28 | |
| Bio Sibs | Male | 168 | 18.16 (1.01) | −.26 | −.14 | −.09 | .15 | .35 | .65 | 1.52 | .78 | 1.37 | 1.31 |
| Female | 194 | 18.33 (1.14) | −.46 | −.49 | −.37 | −.15 | −.27 | .46 | 1.05 | .41 | .72 | .76 | |
| Adopted Sibs | Male | 50 | 18.54 (0.87) | .09 | .13 | .05 | .45 | .68 | .79 | 1.33 | .98 | 1.47 | 1.20 |
| Female | 47 | 18.37 (1.05) | −.24 | −.25 | −.29 | .04 | −.02 | .51 | .80 | .61 | .73 | .59 | |
Each variable in the full sample was scaled to have mean zero and variance one. NIC = Nicotine Use/Dependence; CON = Alcohol Consumption; DEP= Alcohol Dependence; DRG = Drug Dependence; BD = Behavioral Disinhibition; BD = Behavioral Disinhibition. MZ stands for monozygotic twins and DZ stands for dizygotic twins.
Phenotypic Measures
Development and construct validity of the composite measures for the phenotypes used in this study have been described extensively in a development report (Hicks et al., 2011). Phenotype values are factor scores computed from hierarchical factor analysis of items measuring substance use and behavioral disinhibition. Nicotine Use/Dependence (NIC) included lifetime symptoms of DSM-III-R nicotine dependence, as well as frequency and quantity of nicotine use during the period of an individual’s heaviest use. Alcohol Consumption (CON) included number of lifetime intoxications, maximum number of drinks consumed in a 24-hour period, and frequency of alcohol use during the period of heaviest use. Alcohol Abuse/Dependence (DEP) included the symptoms from several diagnostic systems including DSM-III-R, DSM-III, Research Diagnostic Criteria, and Feighner Criteria that assess pathological use of alcohol organized around the content domains of physiological tolerance and withdrawal, social and occupational problems due to drinking, and compulsive drinking (e.g., little time for anything but drinking). Drug Use (DRG) included the number of lifetime marijuana uses, a count of the number of classes of illicit drugs a person had ever tried (e.g., stimulants, hallucinogens, PCP, etc.), and DSM-III-R symptoms of abuse and dependence for the drug to which a person reported the most symptoms. Finally, Behavioral Disinhibition (BD) included DSM-III-R symptoms of conduct disorder, adult antisocial behavior (the adult criteria for antisocial personality disorder), and other measures of antisocial and non-normative behavior (e.g., precocious sexual intercourse) and disinhibited personality traits (e.g., impulsivity, aggression).
Genotyping
Details of the genotyping procedures are provided in (Miller et al., in press). In short, genome-wide genotyping was done on the Illumina Human660W-Quad Array, which contains a total of 561,490 SNPs. Markers were excluded if: 1) they had been identified as a poorly genotyped marker by Illumina; 2) had more than one mismatch in duplicated QC samples; 3) had a call rate <99%; 4) had a MAF <1%; 5) had more than 2 Mendelian inconsistencies across families; 6) significantly deviated from Hardy-Weinberg equilibrium at p<1e-7; 7) was an autosomal marker but associated with sex at p<1e-7; 8) had a significant batch effect at p<1e-7; or 8) there were more than 2 heterozygous X chromosome calls for males or mitochondrial calls for anyone. A total of 32,153, or 5.7% of the markers attempted, failed one or more of these quality control filters, leaving 527,829 markers that passed all QC filters. Of these, 515,384 were autosomal and used in the present study. Genotyping was attempted on samples from 7,438 participants. Samples were eliminated if: 1) they had >5000 no-calls; 2) had a low GenCall score; 3) had extreme heterozygosity or homozygosity; or 4) represented a sample mix-up or we could not confirm known genetic relationships. A total of 160 (2.2%) of samples failed quality control filters and were dropped from the present analysis. Only one MZ twin from each MZ twin pair was genotyped. Prior to genomewide genotyping, zygosity had been assigned through questionnaire-based methods (~99% accuracy). With genome-wide genotyping we determined that 1.5% of DZ twins (per the questionnaire) were in fact MZ. Zygosity for these 8 pairs of twins was therefore reassigned as MZ. For all other MZ twins genotypes were wholly imputed from the genotyped cotwin to the non-genotyped cotwin (n = 1127) for a final GWAS sample of 8405 individuals.
The majority of the full sample self-identified as White (90.4%), but we selected individuals for the current analysis on the basis of the first 10 genetic principal components computed with EIGENSTRAT (Price et al., 2006). Since EIGENSTRAT solutions are sensitive to close relatives, one member of each close relative pair was excluded. Full details are provided in Miller et al. (in press). To identify individuals as White for the present analysis we first found the centroid in the 10-dimensional principal component space for subjects thought to be white, and then computed the distance of every individual from this centroid. A small number closest to the centroid were used to compute the centroid and variance-covariance matrix to compute Mahalanobis distance to the centroid. A hyperellipsoid of constant Mahalanobis distance to the centroid was constructed such that points inside were those closest to the centroid of the white group. The hyperellipsoid was continuously expanded, updating the centroid and variance-covariance matrix every time another subject was added to the white group inside the hyperellipsoid. Expansion continued until further expansion started to bring in primarily subjects who were previously thought to be non-white on the basis of self-report. Thus, the white group was defined partly by self-report and partly by clustering in a principal-component space. The process resulted in a sample of 7702 putatively white individuals, including 101 for whom we did not have self-reported ethnicity and 46 who had originally self-reported as something other than white. Ten principal components were then computed on the newly defined white group and they were also used as covariates in all analyses to correct for any spurious effects arising from population stratification.
Heritability Estimates with Biometry and GCTA
The present sample allows several methods to estimate heritability of the phenotypes. First, a large portion of the sample is composed of twins. We used knowledge of twin zygosity and standard biometric statistical models to compute the additive genetic (A), shared environmental (C), and non-shared environmental (E) components of the 5x5 variance-covariance matrix of our five measures. This is the standard multivariate ACE model (Neale & Cardon, 1992). Variance-covariance component matrices were Cholesky-factorized and estimated by full information maximum likelihood after correcting for fixed effects of sex, age, year of birth, generational status, and the first 10 genetic principle components computed from EIGENSTRAT. Model fit was evaluated with accepted indexes of fit, including a likelihood ratio test and the Akaike Information Criterion (AIC). The likelihood ratio test is sensitive to sample size and correlational magnitude, and so is often augmented with measures of fit like the AIC, which have attractive theoretical properties not shared by the likelihood ratio, such as minimization of mean squared error of estimation (Vrieze, 2012).
A second way to estimate heritability is to consider the additive effect of all SNPs considered simultaneously using GCTA. GCTA has become increasingly used to provide an estimate of the heritability in a trait due to measured SNPs (Yang, Lee, et al., 2011; Yang, Manolio, et al., 2011). The method evaluates the joint effect of all SNPs considered simultaneously as a random effect, and estimates the variance in the phenotype attributable to this random effect. In practice, the method computes the genetic relatedness based on SNPs between all pairs of individuals in the sample. This genetic relatedness matrix (GRM) is then used as input in the random effects model, and the similarity among individuals in genetic relatedness predicts the similarity in phenotypic relatedness. In a sample of unrelated subjects the method produces the variance in the trait accounted for by the SNPs, because the relationships between genetically unrelated subjects are not influenced by shared environment or non-SNP genetic variance. In a sample of related subjects, such as the families used in the present study, phenotypic relatedness and genetic relatedness are confounded in important ways that must be addressed. If estimates are based on everyone, then SNP-based genetic relatedness and phenotypic relatedness are confounded with rare and non-additive genetic relationships (e.g., MZ twins share almost all variants, including rare and common SNPs) and shared environmental effects due to shared family experiences.
To account for familial confounding, we used GCTA on four samples. (1) The best way to estimate the random effect of SNPs (the aggregate effect of common SNPs on the phenotype) is with a large sample of unrelated individuals (Yang et al., 2010). The largest such sample in the present study consists of all genetically unrelated parents (n = 3542), under a simplifying assumption of no assortative mating. To determine genetic relatedness in this parent sample we excluded one individual of every pair of individuals who had a genetic relatedness of ≥ .025 as calculated by the GRM produced by GCTA on the full sample. (2) To help inform the biometric twin heritability estimates, we also estimated the random effect of SNPs on an unrelated sample of the youth offspring (n = 1784), including one member from each twin and sibling pair, as well as all adopted youth. Ideally, this would provide an estimate of the aggregate effect of common SNPs in the offspring youth sample and would be comparable to that produced by the unrelated parent sample. (3) We conducted the same analysis on the full sample of youth offspring (n = 3336), without concern for genetic relatedness. Because this analysis confounds phenotypes, genotypes, and shared environment, it should return a genetic random effect approximate to the sum of genetic and shared environment from the biometric analysis (i.e., approximately A + C). (4) Finally, we estimate the random genetic effect in the full sample (N = 7188), which should provide an estimate of the random effect somewhere between the unrelated sample and the youth offspring sample, as the full sample has less of a shared environment confound than the twin sample. That is, parents are phenotypically related due to shared environment, but the extent of shared environmental influence is less than that between twins, again under the simplifying assumption of no assortative mating.
Genome-wide Scoring Procedure
The biometric and GCTA methods provide variance component estimates of the aggregate effect of genetic variants. They are limited in that they do not provide weightings for individual SNPs, nor can they be applied to new samples in attempts to predict genetic loading for some trait. Genome-wide scoring, on the other hand, does return this information.
Scoring proceeded in a series of steps. First, the phenotype was residualized using a linear regression on covariates of sex, generational status (parent or child), age, year of birth, and the first 10 principal components produced by EIGENSTRAT. A GWAS was then conducted on the residualized phenotype, producing a univariate regression weight for the minor allele count for each SNP. Minor allele counts for each SNP were then multiplied by their corresponding regression weight and summed to form a single score for each participant in the sample. This sumscore was then validated by correlating it with the residualized phenotype. Squaring the correlation gives the variance in the phenotype accounted for by the SNP score.
Gross overfitting is expected when the same sample is used to generate and validate the SNP score, especially when the number of predictors is much greater than the number of subjects. To control for overfitting we employed a k-fold cross-validation technique (Breiman & Spector, 1992; Hastie, Tibshirani, & Friedman, 2009). For this study we set the number of k folds to be 10. To accomplish this, subjects were split into 10 roughly equal subsamples (707, 734, 719, 718, 724, 690, 737, 734, 725, 700). The scoring algorithm described above is conducted by combining 9 subsamples, providing a set of SNP weights based on the 9 subsamples combined. These weights were then applied to the minor allele counts in the 10th sample and correlated with the phenotype in that sample, producing an unbiased estimate of the cross-validated validity of the SNP score. This same procedure is used for every combination of the 10 samples, such that every single subject is in a development sample nine times and in the test sample once.
Because the full sample is composed of families, and individuals within families are correlated with respect to genotypes and phenotypes, we always kept individuals from the same family within the same subsample. This prevented the algorithm, for example, from deriving the SNP score on one twin and cross-validating it on the other – clearly in that case we expect prediction bias given correlation between twins on the phenotype and the genotype.
SNPs were also filtered on the basis of linkage disequilibrium (LD). If two tag SNPs are in LD with a causal variant and in LD with each other, then both SNPs will show a relationship with the phenotype, despite the fact that the two SNPs are redundant. To avoid over-counting such redundant SNPs prior studies have imposed strict LD cutoffs, such that no two SNPs included in the set of prediction SNPs can have LD r2 > .05 (e.g., (Allen et al., 2010)). We chose to evaluate three different LD cutoffs: r2 = .05, .50, and 1.0 (i.e., no cutoff). The cutoff was imposed in the following way. First, all SNPs were regressed on the phenotype and their univariate weights and p-values recorded. SNPs were then sorted according to p-value. The most significant SNP was selected, and all SNPs with LD greater than the cutoff were culled from the list of SNPs. Then the remaining second-most significant SNP was considered and all SNPs in LD with it were removed. This process was completed until the least significant SNP was considered. The proportion of SNPs included in the score was varied from .0001 (allowing only very highly significant SNPs in the score) to 1.0 (allowing all SNPs regardless of significance).
Finally, to increase our confidence in the scoring results, we simulated three types of phenotypes. First, we simulated a normally-distributed phenotype with no genetic association, which we refer to as “Random.” Second, we simulated phenotypes from 10,000, 50,000, and 100,000 causal SNPs under an additive model with normally distributed regression coefficients. Third, we simulated phenotypes from 10,000, 50,000, and 100,000 SNPs under an additive model with uniformly distributed regression coefficients. The phenotype in both the normal and uniform scenarios was simulated to be 17% heritable, in line with expectations based on the GCTA analyses reported in the current study.
Genome-wide scoring with 10-fold cross-validation is computationally demanding. This prevented us from conducting permutation or other tests of statistical significance. Fortunately, the cross-validation statistic in use here is the Pearson correlation and is amenable to short-hand tests of significance. The standard error of the Pearson correlation coefficient after z-transformation is 1/√ (N-3), and z = arctan(r). A significant t-score = 1.96. The p-value for z and any N is thus approximately 1 - Φ(z × √N), where Φ is the distribution function of the standard normal distribution. The average within-family correlation, averaging over all five phenotypes, was .24. Multiplying the total sample size by one minus the squared average within family correlation yields 7188×(1–.242)≈6774, an estimate of the effective sample size. When N = 6774, a correlation coefficient r must be greater than .02 to be significant at p < .05. If we are conservative, and set our effective sample size at 5,000 individuals, then a correlation coefficient must be r > .024 to be significant at p < .05. For all analyses we covaried out the linear effects of age, sex, year of birth, generational status (parent/offspring), and the first 10 genetic principal components.
The k-fold cross-validation algorithm was programmed in the R Environment 2.15.1 (R Development Core Team, 2011), and GWAS conducted using the GenABEL package 1.7–2 (Aulchenko, Ripke, Isaacs, & van Duijn, 2007). Biometric twin models were estimated with the OpenMx package 1.2 (Boker et al., 2011). GCTA analysis used the GCTA program 0.93.9 (Yang, Lee, et al., 2011). Scripts are available upon request.
Results
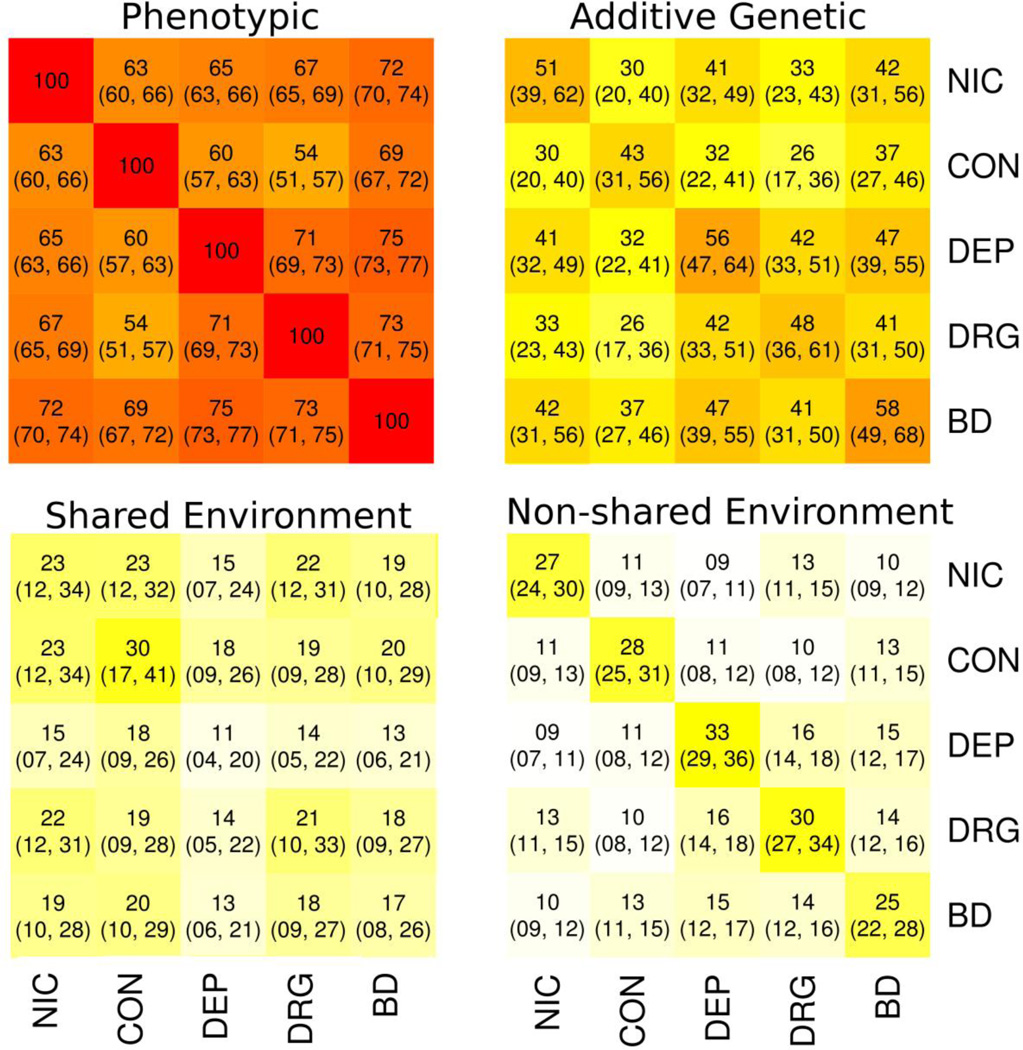
Descriptive statistics for the substance use phenotypes and behavioral disinhibition are provided in Table 1. Figure 1 provides the biometric estimates, based on the twin sample alone (average age = 17 years), of the heritable, shared environmental, and nonshared environmental components of the correlation matrix among the five phenotypes. The variance in each phenotype, as well as the covariance among phenotypes, is largely due to heritable variation. However, there are also significant shared environmental effects, both on the variances and covariances. Finally, there are significant non-shared environmental effects, especially on the variances. Fit statistics for the ACE, ADE, and AE models are listed in Table 2. The ACE model fit best, followed by the AE and ADE models, according both to likelihood ratio tests and the AIC.
Figure 1.
Phenotypic correlations and biometric decomposition (leading decimals were removed). Shown here are the phenotypic correlation matrix, as well as the additive genetic, shared environmental, and non-shared environmental component matrices. In parentheses are the 95% maximum likelihood confidence intervals. The component matrices are scaled such that they sum elementwise to produce the full phenotypic matrix. All entries are significant at p < .05. Estimates are based solely on the twins, who have an average age of 17 years. NIC = Nicotine Use/Dependence; CON = Alcohol Consumption; DEP = Alcohol Dependence; DRG = Drug Use; BD = Behavioral Disinhibition.
Table 2.
Fit of the Biometric Models.
| Model | -2LL | Free | χ2(df), p-value | AIC |
|---|---|---|---|---|
| Parameters | ||||
| ACE | 114287.4 | 50 | N/A | 85617.37 |
| ADE | 114365.3 | 50 | N/A | 85695.34 |
| AE | 114314.9 | 35 | 27.5(15), .02 | 85614.88 |
For the ACE, ADE, and AE models, the A refers to the additive genetic component, D to the dominant/recessive genetic component, C to the shared environmental component, and E to the non-shared environmental component. -2LL is minus to the log of the likelihood. AIC is the Akaike Information Criterion. The χ2 is for comparison between the AE and the ACE model. The significant p-value of .02 indicates that the AE leads to decrement in fit.
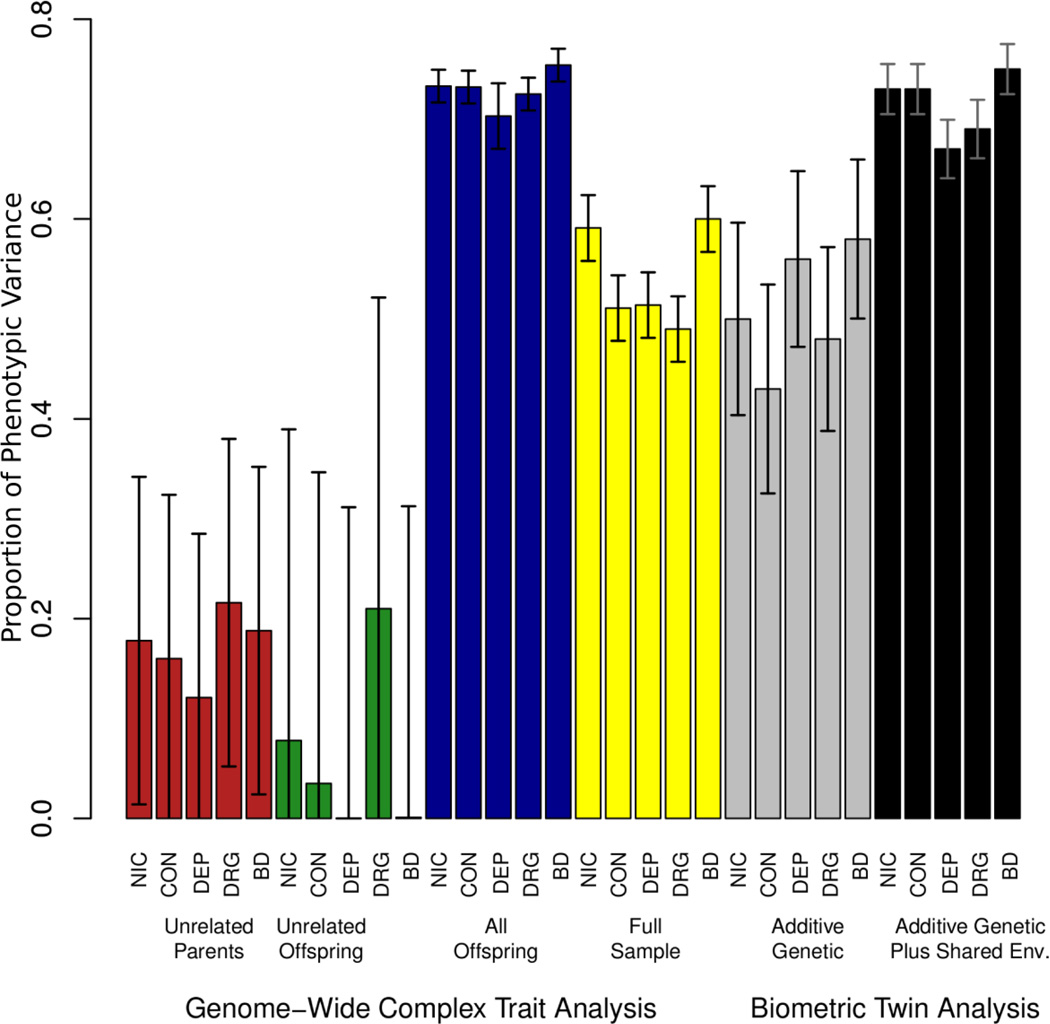
GCTA results are given in Figure 2 and differ depending on the sample and the GRM cutoff. For comparison, the twin-estimated heritabilities are provided (gray), as well as the sum of the heritabilities and shared environmental estimates (black). First, the best estimate of the aggregate effects of common SNPs was produced from the largest sample of genetically unrelated individuals (the parents), as determined by using a cutoff of < .025 on the genetic relatedness matrix. The parents share environments but not genes, and resulting GCTA estimates will not be confounded with non-common-SNP genetic effects and/or strong shared environmental effects. As can be seen in Figure 2, the estimates of phenotypic variance accounted for by the aggregated SNPs range from .16–.22 in the sample of unrelated parents (displayed in red). All estimates were statistically significant at one-tailed p<.05 except DEP (Alcohol Dependence). The full sample estimates (no GRM cutoff; displayed in yellow) yielded much higher estimates, consistent with the notion that rare-SNP, non-additive, non-SNP, and/or shared environmental effects are contributing to phenotypic similarity, sometimes substantially. It appears, however, that the GCTA estimates from the full sample are highly similar to the additive genetic estimates obtained in the biometric twin results, indicating only small inflation in the GCTA results due to shared environmental confound in the full sample.
Figure 2.
GCTA results with Biometric Comparison. The GCTA results are provided for each phenotype in a variety of samples. In grey are the additive genetic heritability estimates from the biometric twin analysis (also in Figure 1). In black is the sum of the additive genetic and shared environment estimates from the biometric analysis (also in Figure 1). Unrelated individuals were defined as those having a genetic relatedness estimated by GCTA to be < .025 (more distantly related than third cousins). The samples are: A) All unrelated parents (N = 3542), B) unrelated youths (N = 1784), C) All youths (N = 3336), and D) the full sample (N = 7188). Error bars are 95% confidence intervals. NIC = Nicotine Use/Dependence; CON = Alcohol Consumption; DEP = Alcohol Dependence; DRG = Drug Use; BD = Behavioral Disinhibition.
In the sample of unrelated youths (GRM cutoff of .025) estimates of the aggregate SNP effects are small and highly unstable (Figure 2 in green), perhaps due to less phenotypic variability and a relatively small sample. When evaluating the full sample of youths (blue), which does not control for non-SNP genetic relatedness and shared environmental confounding, estimates range from .70 to .75, perhaps indicating a stronger role of shared environment in the youth-only sample versus the full sample. In fact, if we sum the heritabilities and shared environmental components reported in Figure 1, we find that they are strikingly similar to the GCTA estimates on the full set of offspring.
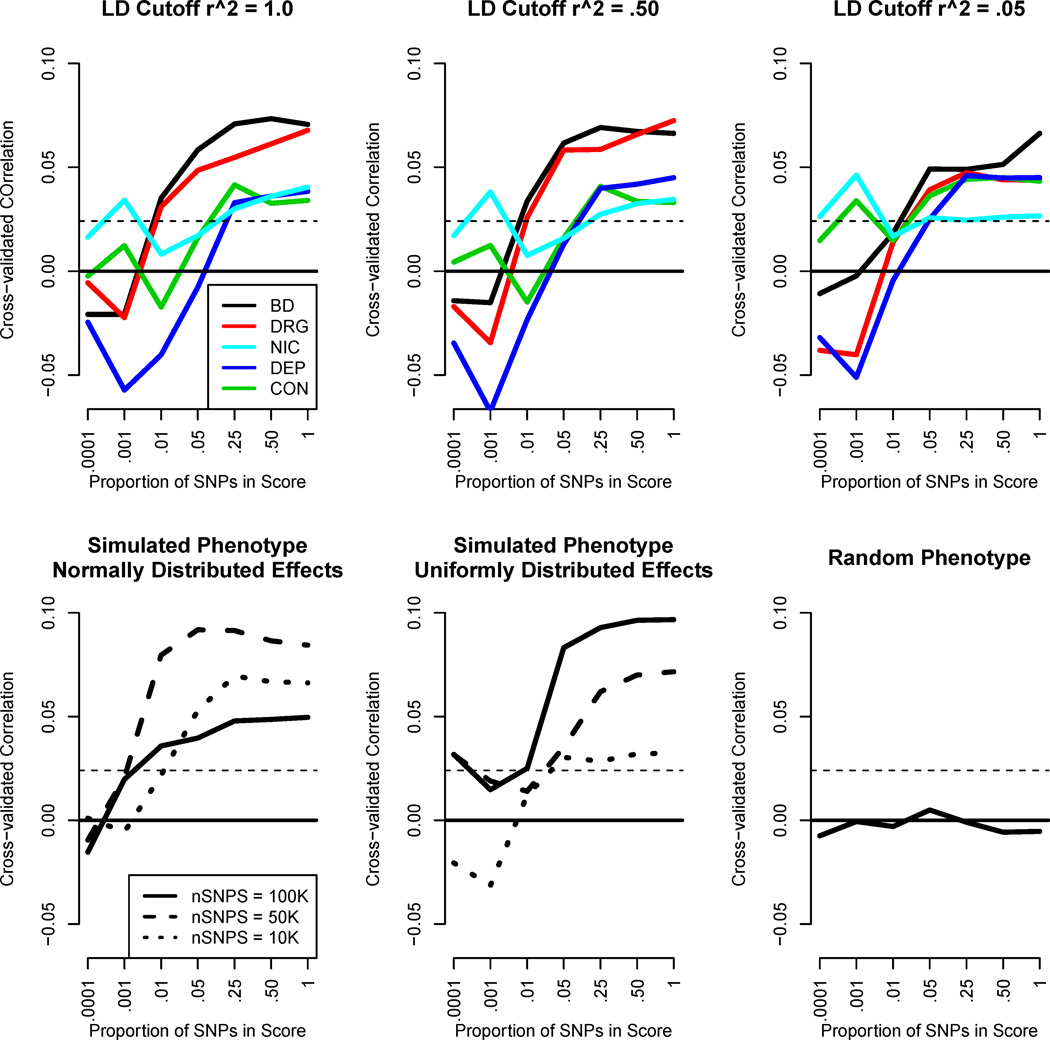
While moderately strong aggregate SNP effects were observed in the full sample by both GCTA and twin biometry, the genome-wide scoring procedure was unable to tap more than a small fraction of that variance. The results from the scoring procedure are given in Figure 3. The top row of sub-figures in Figure 3 provide the genome-wide scoring results for the five phenotypes, under seven SNP proportion thresholds and three LD thresholds. To explain, consider the top right figure. Here we imposed an LD threshold of .05. That is, SNPs were excluded whenever they were in LD > .05 with a nearby, more significant SNP. Each phenotype was then analyzed under seven thresholds for the proportion of SNPs to retain in the score. Stringent thresholds, such as including only .0001 of all SNPs produced essentially null results for every phenotype but nicotine. As the threshold was relaxed and more SNPs were included, improvement is seen for every phenotype (sans nicotine), until the effect plateaus at around .05. This pattern of results is generally true for each of the LD cutoffs (each of the three graphs in the top row of Figure 3). Most obviously, there appears to be a polygenetic effect—the variance accounted for in the phenotype increases substantially as the proportion of SNPs is increased. Results appear to be generally dampened by the choice of LD cutoff, although not substantially so. The polygenetic effect, and the pattern of results, is true for the phenotypic data as well as the simulated phenotypes, regardless of the number of SNPs contributing to the phenotype in the simulations. The random, non-genetically-related phenotype (bottom right figure in Figure 3) shows no association, as expected.
Figure 3.
Cross-validated Genome-wide Scoring Results. The top panel of three graphs provides the empirical results for the four substance use phenotypes and behavioral disinhibition. Each graph provides the seven p-value thresholds under consideration. The three top graphs only differ in the LD cutoff imposed (1.0, .50, and .05). The bottom row provides results from three kinds of simulated phenotypes. First, a simulated phenotype with a normal distribution of SNP regression coefficients, for each of the 7 p-value thresholds and three different polygenetic scenarios (100,000, 50,000, and 10,000 associated SNPs). Second, the same scenario except with uniformly distributed effects. Both of these simulated phenotypes were simulated such that the SNPs in aggregate accounted for 17% of the variance in the phenotype. Third, a completely random phenotype with no SNP associations. The bold horizontal line in each graph is zero. The dotted line represents a correlation that would be significant at p < .05, conservatively assuming an effective sample size of 5000. NIC = Nicotine Use/Dependence; CON = Alcohol Consumption; DEP = Alcohol Dependence; DRG = Drug Use; BD = Behavioral Disinhibition.
Table 3 reports cross-validated correlations between genome-wide scores generated on one phenotype and correlated with a different phenotype. Note that for some phenotypes (e.g., nicotine use with drug use) the off-diagonal value is greater than the diagonal. We expect this is due to sampling error. Correlations among the drugs are of smaller, but similar, magnitude, ranging from 0.03 to 0.07, suggesting small but detectable pleiotropic SNP effects in this sample.
Table 3.
Genome-wide Scores Created on One Phenotype and Applied to Another.
| NIC | CON | DEP | DRG | BD | RANDOM | |
|---|---|---|---|---|---|---|
| NIC | .040 | |||||
| CON | .030 | .034 | ||||
| DEP | .041 | .044 | .038 | |||
| DRG | .056 | .042 | .043 | .068 | ||
| BD | .046 | .054 | .050 | .069 | .071 | |
| RANDOM | −.008 | −.022 | −.013 | −.016 | −.015 | −.004 |
NIC = Nicotine Use/Dependence; CON = Alcohol Consumption; DEP = Alcohol Dependence; DRG = Drug Use; BD = Behavioral Disinhibition; RANDOM = randomly generated phenotype. The diagonal represents the cross-validated correlation between the genome-wide SNP score and the actual phenotypic measurements. Off-diagonals represent the mean correlation between trait 1’s genome-wide score and trait 2’s phenotypic measurements, plus the correlation between trait 2’s genome-wide score and trait 1’s phenotypic measurements. Scores here are taken from the models with no LD cutoff and no p-value cutoff. All correlations are significant at p < .05, assuming an effective sample size of 5000, as discussed in the Method.
Discussion
Like with other complex traits, our results demonstrate that substance use phenotypes are polygenetic and moderately to highly heritable. Using standard biometric twin models, heritabilities ranged from 43% for Alcohol Consumption to 58% for Behavioral Disinhibition (Figure 1). Additive SNP effects estimated by GCTA on the parent sample account for 16% of the variance in Alcohol Dependence to 22% of the variance in Drug Use. While the aggregate additive SNP effect, estimated by GCTA is relatively large (e.g., 10–30% of total phenotypic variance; Figure 2), identifying and summing actual individual SNPs with genome-wide scoring yields much weaker effects, accounting for around 0.25% of the variance in the substance use and behavioral disinhibition measures. Dividing the GCTA results estimated in the parent sample by the twin-estimated heritabilities allows us to estimate the total heritable variance accounted for by the aggregate SNP effect from GCTA. We estimate that the additive SNP effect accounts for 21% (Alcohol Dependence), 32% (Behavioral Disinhibition), 36% (Nicotine Use/Dependence), 38% (Alcohol Consumption), and 45% (Drug Dependence) of the heritable variance in these traits.
There were apparent pleiotropic effects observed in the biometric twin heritability estimates. The genetic correlations between disorders (Figure 1) were relatively high (.25 – .47), such that one can expect genetic variants for one disorder to predict from 7% to 22% of the phenotypic variance in another disorder. A genome-wide score developed on one phenotype accounted for .1% to 0.5% of the variance in other phenotypes (squaring the minimum and maximum correlation provided in Table 3), again indicating some extent of pleiotropy in the associated SNPs.
The disinhibitory hypothesis, that disinhibition represents a substantial source of general and genetically-based risk for substance use, was strongly supported by these results. First, that behavioral disinhibition shares genetic etiology with substance use disorders is supported by the biometric twin results given in Figure 1, in that the measure of behavioral disinhibition was highly genetically correlated with the other traits. What is more, the genome-wide scores generated on behavioral disinhibition were predictive of all the substance use traits (Table 3), indicating the existence of a polygenetic SNP-based relationship between disinhibition and substance use. Despite statistical significance, the predictive validity of the genome-wide scores was modest, indicating that the ratio of signal to noise is very small for a brute-force genome-wide approach. Clearly more samples are required to have sufficient precision in estimating weights at a genome-wide level. While the GCTA SNP-based estimates account for considerably more—21–45% of the twin-estimated heritable variance—there remains a majority of that heritable variance to be explained. There is much conjecture about the source of remaining additive genetic variance, including non-additive or rare SNP effects, additive and non-additive structural variation (e.g., CNVs, insertions/deletions), gene-environment interaction, or gene-gene interaction (Manolio et al., 2009; Zuk, Hechter, Sunyaev, & Lander, 2012). Further research involving much larger samples and more comprehensive genotyping, such as whole genome sequencing or rare variant chips, will be necessary to tackle these issues.
Future work would also do well to continue to evaluate both individual SNP effects as well as aggregate effects, as both can be informative about the genetic architecture of, and genetic relationships among, various psychological traits and other phenotypes. Applying diverse methods, such as twin biometry, GCTA, and genome-wide scoring provides an array of useful information. To be maximally informative, consortia might share more than GWAS p-values, and to report more than just the genome-wide significant values (e.g., the top 100 or 1000 in supplementary materials with all values available upon request). Supplemental materials could routinely include the top 100 or 1000 hits, including effect sizes, allele and strand information, standard errors, and p-values, which all would be extremely useful for the purposes of aggregating effects (as in the present study) as well as evaluating environmental and developmental moderation of genetic effects (Vrieze et al., 2012).
Indeed, environmental and developmental moderation of genetic effects are two possible reasons (of many) why genetic association studies have failed thusfar in identifying more variants associated with behavioral traits. Substance use development, for example, shows significant change in structure and heritability during adolescence Vrieze, Hicks, et al. (2012), which suggests a possible limitation of the present study, as we examined middle-aged parents along with their 17-year-old children. If genetic effects are substantially different between these age groups it may minimize the effects observed in the present study. Unfortunately, determining whether a SNP or other genetic variant is moderated by development (or environment) is greatly facilitated by a priori knowledge of SNPs known to be associated with the phenotype (Vrieze, Iacono & McGue, 2012), and there are very few such SNPs known at present. There has been preliminary work in evaluating developmental moderation for height and smoking (Vrieze, McGue, et al. [2011]; Vrieze, McGue, & Iacono [2012]), two phenotypes where there are strong SNP associations found through consortia with large meta-analytic GWAS results. Increased data sharing and the resulting larger samples will provide more hits for future work, which will allow powerful investigation of interaction effects for behavioral traits.
ACKNOWLEDGEMENTS
Support was provided by grants DA05147, AA09367, AA11886, DA13240, DA024417, MH66140, and MH017069 (SIV). We also thank Scott Sponheim for valuable laboratory support.
Footnotes
DISCLOSURES: No Authors have any conflict of interest in the present work.
References
- Allen HL, Estrada K, Lettre G, Berndt SI, Weedon MN, Rivadeneira F, Consortium P. Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature. 2010;467(7317):832–838. doi: 10.1038/nature09410. doi:Doi 10.1038/Nature09410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aulchenko YS, Ripke S, Isaacs A, van Duijn CM. GenABEL: an R library for genome-wide association analysis. Bioinformatics. 2007;23(10):1294–1296. doi: 10.1093/bioinformatics/btm108. doi:btm108 [pii] 10.1093/bioinformatics/btm108. [DOI] [PubMed] [Google Scholar]
- Bierut LJ, Goate AM, Breslau N, Johnson EO, Bertelsen S, Fox L, Edenberg HJ. ADH1B is associated with alcohol dependence and alcohol consumption in populations of European and African ancestry. [Meta-Analysis Research Support, N.I.H., Extramural] Mol Psychiatry. 2012;17(4):445–450. doi: 10.1038/mp.2011.124. doi: 10.1038/mp.2011.124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boker S, Neale M, Maes H, Wilde M, Spiegel M, Brick T, Fox J. OpenMx: An Open Source Extended Structural Equation Modeling Framework. Psychometrika. 2011;76(2):306–317. doi: 10.1007/s11336-010-9200-6. doi:DOI 10.1007/s11336-010-9200-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L, Spector P. Submodel Selection and Evaluation in Regression - the X-Random Case. International Statistical Review. 1992;60(3):291–319. [Google Scholar]
- Franke A, McGovern DPB, Barrett JC, Wang K, Radford-Smith GL, Ahmad T, Parkes M. Genome-wide meta-analysis increases to 71 the number of confirmed Crohn's disease susceptibility loci. Nature Genetics. 2010;42(12):1118-+. doi: 10.1038/ng.717. doi:Doi 10.1038/Ng.717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furberg H, Kim Y, Dackor J, Boerwinkle E, Franceschini N, Ardissino D, Sullivan PF. Genome-wide meta-analyses identify multiple loci associated with smoking behavior. Nature Genetics. 2010;42(5):441–U134. doi: 10.1038/ng.571. doi: 10.1038/ng.571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman JH. The elements of statistical learning : data mining, inference, and prediction. 2nd ed. New York, NY: Springer; 2009. [Google Scholar]
- Hicks BM, Schalet BD, Malone SM, Iacono WG, McGue M. Psychometric and genetic architecture of substance use disorder and behavioral disinhibition measures for gene association studies. Behavior Genetics. 2011;41(4):459–475. doi: 10.1007/s10519-010-9417-2. doi: 10.1007/s10519-010-9417-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirschhorn JN, Daly MJ. Genome-wide association studies for common diseases and complex traits. Nature Reviews Genetics. 2005;6(2):95–108. doi: 10.1038/nrg1521. doi:Doi 10.1038/Nrg1521. [DOI] [PubMed] [Google Scholar]
- Iacono WG, Malone SM, McGue M. Behavioral disinhibition and the development of early-onset addiction: Common and specific influences. Annual Review of Clinical Psychology. 2008;4:325–348. doi: 10.1146/annurev.clinpsy.4.022007.141157. doi:DOI 10.1146/annurev.clinpsy.4.022007.141157. [DOI] [PubMed] [Google Scholar]
- Iacono WG, McGue M. Minnesota Twin Family Study. Twin Res. 2002;5(5):482–487. doi: 10.1375/136905202320906327. [DOI] [PubMed] [Google Scholar]
- Kendler KS, Jacobson KC, Prescott CA, Neale MC. Specificity of genetic and environmental risk factors for use and abuse/dependence of cannabis, cocaine, hallucinogens, sedatives, stimulants, and opiates in male twins. American Journal of Psychiatry. 2003;160(4):687–695. doi: 10.1176/appi.ajp.160.4.687. [DOI] [PubMed] [Google Scholar]
- Kendler KS, Prescott CA, Myers J, Neale MC. The structure of genetic and environmental risk factors for common psychiatric and substance use disorders in men and women. Archives of General Psychiatry. 2003;60(9):929–937. doi: 10.1001/archpsyc.60.9.929. [DOI] [PubMed] [Google Scholar]
- Luczak SE, Glatt SJ, Wall TL. Meta-analyses of ALDH2 and ADH1B with alcohol dependence in Asians. Psychological Bulletin. 2006;132(4):607–621. doi: 10.1037/0033-2909.132.4.607. [DOI] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, Visscher PM. Finding the missing heritability of complex diseases. Nature. 2009;461(7265):747–753. doi: 10.1038/nature08494. doi:Doi 10.1038/Nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGue M, Miller MB, Basu S, Eskin E, Hicks BM, Irons DE, Iacono WG. A Genome-Wide Association Study of Behavioral Disinhibition. Submitted for publication. 2012 doi: 10.1007/s10519-013-9606-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MB, Basu S, Cunningham J, Oetting W, Schork NJ, Iacono WG, McGue M. The Minnesota Center for Twin and Family Research Genome-Wide Association Study. Twin Research and Human Genetics. doi: 10.1017/thg.2012.62. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale MC, Cardon LR. Methodology for genetic studies of twins and families. Dortrecht, The Netherlands: Kluwer Academic; 1992. [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics. 2006;38(8):904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. R: A language and environment for statistical computing. 2011 [Google Scholar]
- Schumann G, Coin LJ, Lourdusamy A, Charoen P, Berger KH, Stacey D, Elliott P. Genome-wide association and genetic functional studies identify autism susceptibility candidate 2 gene (AUTS2) in the regulation of alcohol consumption (vol 108, pg 7119, 2011) Proceedings of the National Academy of Sciences of the United States of America. 2011;108(22):9316–9316. doi: 10.1073/pnas.1017288108. doi: 10.1073/pnas.1106917108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speliotes EK, Willer CJ, Berndt SI, Monda KL, Thorleifsson G, Jackson AU, Magic Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nature Genetics. 2010;42(11):937–U953. doi: 10.1038/ng.686. doi: 10.1038/ng.686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teslovich TM, Musunuru K, Smith AV, Edmondson AC, Stylianou IM, Koseki M, Kathiresan S. Biological, clinical and population relevance of 95 loci for blood lipids. Nature. 2010;466(7307):707–713. doi: 10.1038/nature09270. doi:Doi 10.1038/Nature09270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Brown MA, McCarthy MI, Yang J. Five years of GWAS discovery. American Journal of Human Genetics. 2012;90(1):7–24. doi: 10.1016/j.ajhg.2011.11.029. doi:S0002-9297(11)00533-7 [pii] 10.1016/j.ajhg.2011.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voight BF, Scott LJ, Steinthorsdottir V, Morris AP, Dina C, Welch RP, Consortium G. Twelve type 2 diabetes susceptibility loci identified through large-scale association analysis. Nature Genetics. 2010;42(7):579–U155. doi: 10.1038/ng.609. doi:Doi 10.1038/Ng.609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vrieze SI. Model selection and psychological theory: A discussion of the differences between the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC) Psychological Methods. 2012;17(2):228–243. doi: 10.1037/a0027127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vrieze SI, Hicks BM, McGue M, Iacono WG. Genetic Influence on the Co-Occurrence of Alcohol, Marijuana, and Nicotine Dependence Symptoms Declines from Age 14 to 29. American Journal of Psychiatry. 169:1073–1081. doi: 10.1176/appi.ajp.2012.11081268. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vrieze SI, Iacono WG, McGue M. Confluence of genes, environment, development, and behavior in a post-GWAS world. Development & Psychopathology. 2012;24(4):1195–1214. doi: 10.1017/S0954579412000648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vrieze SI, McGue M, Iacono WG. The interplay of genes and adolescent development in substance use disorders: Leveraging findings from GWAS meta-analyses to test developmental hypotheses about nicotine consumption. Human Genetics. 2012;131(6):791–801. doi: 10.1007/s00439-012-1167-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vrieze SI, McGue M, Miller MB, Legrand LN, Schork NJ, Iacono WG. An assessment of the individual and collective effects of variants on height using twins and a developmentally informative study design. PLoS Genetics. 2011;7(12):e1002413. doi: 10.1371/journal.pgen.1002413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang JA, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Visscher PM. Common SNPs explain a large proportion of the heritability for human height. Nature Genetics. 2010;42(7):565–U131. doi: 10.1038/ng.608. doi:Doi 10.1038/Ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang JA, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome-wide complex trait analysis. American Journal of Human Genetics. 2011;88(1):76–82. doi: 10.1016/j.ajhg.2010.11.011. doi:S0002-9297(10)00598-7 [pii] 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang JA, Manolio TA, Pasquale LR, Boerwinkle E, Caporaso N, Cunningham JM, Visscher PM. Genome partitioning of genetic variation for complex traits using common SNPs. Nature Genetics. 2011;43(6):519–U544. doi: 10.1038/ng.823. doi:Doi 10.1038/Ng.823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young SE, Stallings MC, Corley RP, Krauter KS, Hewitt JK. Genetic and environmental influences on behavioral disinhibition. Amercan Journal of Medical Genetics. 2000;96(5):684–695. doi: 10.1002/1096-8628(20001009)96:5<684::AID-AJMG16>3.0.CO;2-G [pii] [PubMed] [Google Scholar]
- Zucker RA, Heitzeg MM, Nigg JT. Parsing the Undercontrol/Disinhibition Pathway to Substance Use Disorders: A Multilevel Developmental Problem. Child Development Perspectives. 2011;5(4):248–255. doi: 10.1111/j.1750-8606.2011.00172.x. doi: 10.1111/j.1750-8606.2011.00172.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuk O, Hechter E, Sunyaev SR, Lander ES. The mystery of missing heritability: Genetic interactions create phantom heritability. Proceedings of the National Academy of Sciences of the United States of America. 2012 doi: 10.1073/pnas.1119675109. doi:1119675109 [pii] 10.1073/pnas.1119675109. [DOI] [PMC free article] [PubMed] [Google Scholar]