IMPROVEMENT OF THE MODELLING OF THE LOW-TEMPERATURE OXIDATON OF N-BUTANE - STUDY OF THE PRIMARY REACTIONS

Abstract

This paper revisits the primary reactions involved in the oxidation of n-butane from low to intermediate temperatures (550-800 K) including the negative temperature coefficient (NTC) zone. A model which was automatically generated is used as a starting point and a large number of thermochemical and kinetic data are then re-estimated. The kinetic data of the isomerization of alkylperoxy radicals giving ·QOOH radicals and the subsequent decomposition to give cyclic ethers has been calculated at the CBS-QB3 level of theory. The newly obtained model allows a satisfactory prediction of experimental data recently obtained in a jet-stirred reactor and in rapid compression machines. A considerable improvement of the prediction of the selectivity of cyclic ethers is especially obtained compared to previous models. Linear and global sensitivity analyses have been performed in order to better understand which reactions are of influence in the NTC zone.

INTRODUCTION

While detailed kinetic models for the low-temperature oxidation of alkanes have been developed for more than 20 years (a first model of the oxidation of n-butane at low and intermediate temperatures was published in 1988 (1)), there are still important discrepancies between the kinetic parameters used in the different models from the literature as shown by the review of Battin-Leclerc (2). This explains why several experimental and theoretical studies have been recently undertaken to better categorize the kinetic data involved in the reactions of importance during the low temperature oxidation of alkanes as reviewed by Zádor et al. (3).

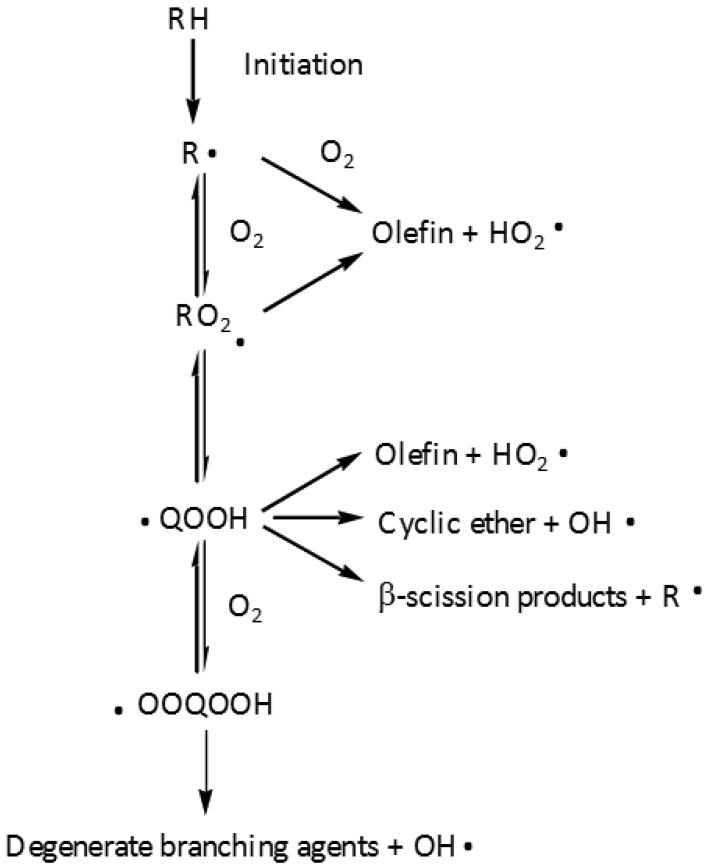
As this paper is concerned with the chemistry involved during the low-temperature oxidation of alkanes, let us first summarize briefly its main features (4)(5)(6). Figure 1 shows a simplified scheme of the main primary reactions which are now usually included in models of the oxidation of an alkane (RH). At low temperatures, i.e. below 900 K, alkyl radicals (R·) are produced by H-abstractions mostly by ·OH radicals. They add thereafter to O₂ and yield peroxy radicals ROO·. Some consecutive steps then lead to the formation of hydroperoxides, which are degenerate branching agents explaining the high reactivity of alkanes at low temperatures. ROO· radicals first isomerize to give hydroperoxyalkyl radicals (·QOOH). This first isomerization, which occurs via an internal H-abstraction going through a cyclic transition state, has a very large influence on the low-temperature oxidation chemistry. According to the size of the cyclic ring involved in the transition state, the formation of olefin + ·HO₂ can compete with isomerization, mainly, at low temperature, by direct elimination from ROO· as mentioned by Zádor et al. (3).

Figure 1.

General scheme of the low-temperature oxidation of an alkane (RH).

·QOOH radicals can thereafter add on O₂ and yield ·OOQOOH radicals that react by a second internal isomerization producing ·U(OOH)₂ radicals. The rapid unimolecular decomposition of ·U(OOH)₂ radicals leads to three radicals and is the source of the chain branching occurring at low temperatures:

$$\begin{array}{cc}\hfill \cdot \mathrm{U}& {\left(\mathrm{OOH}\right)}_2=\mathrm{R}(=\mathrm{O})\left(\mathrm{OOH}\right)+\cdot \mathrm{OH}\hfill \\ \hfill \mathrm{R}(=\mathrm{O})\left(\mathrm{OOH}\right)& =\mathrm{R}(=\mathrm{O})\mathrm{O}\cdot +\cdot \mathrm{OH}\left(\text{secondary reaction}\right)\hfill \end{array}$$

In this scheme, ·OH radicals reacting by H-abstraction with the initial alkane leads to the formation of three free radicals, two ·OH and a R(=O)O· radical. This auto-accelerating process strongly promotes the oxidation of alkanes below 700 K.

When the temperature increases, the equilibrium R· + O₂ = ROO· begins to be displaced back to the reactants and the formation of ROO· radicals is less favoured compared to the strongly inhibiting oxidation reaction R· + O₂ = ·HO₂ + conjugated olefin. This reaction is equivalent to a termination step since ·HO₂ radicals react mostly by a disproportionation reaction (2 ·HO₂ = H₂O₂ + O₂). Unimolecular decompositions of ·QOOH radicals compete with O₂ addition: ·QOOH radicals can decompose into cyclic ethers or ketones and ·OH radicals, or by β-scission into ·HO₂ radicals and conjugated olefins or smaller species. Because of the decrease in the production of hydroperoxides, the reactivity decreases in the 700 to 800 K temperature range. This temperature region is consequently called the Negative Temperature Coefficient (NTC) zone. At higher temperatures, the decomposition of H₂O₂ (H₂O₂ (+M) = 2 ·OH (+M)) is a new source of the chain branching leading to an increase of the reactivity. This reaction becomes very fast above 900 K.

Several detailed kinetic models of the low-temperature (below 800 K) oxidation of n-butane have already been published. Those proposed by Pitz et al. (1) and by Ranzi et al. (7) were used to model induction times measured in a static reactor (1). The model of Kojima (8) and the recent one of Healy et al. (9) were validated using their own shock tube and rapid compression machine data. Several models were also obtained using the automatic generation software EXGAS: that of Warth et al. (10) was used to model induction times measured in a static reactor (1) and jet-stirred reactor data (900-1200 K) (11), that of Buda et al. (12) to reproduce rapid compression machine ignition delay times (13) and finally that of Herbinet et al. (14) was tested for modelling their own jet-stirred reactor data (550-800 K).

The recent jet-stirred reactor data of Herbinet et al. (14) includes the quantification of 36 reaction products providing a valuable tool for model validation. Note that due to the small size of the reactant molecule, large amounts of three sizes of cyclic ethers have been found: tetrahydrofurans or oxolanes (five-member cycles), oxetanes (four-member cycles) and oxiranes (three-member cycles). These data are a good target for testing the validity of the rate constants used for ROO· radical isomerizations and cyclic ether formation. The purpose of the present paper is therefore to revisit the thermochemical and kinetic parameters used in the primary mechanism of a model automatically generated by the EXGAS software, in order to improve the modelling of the jet-stirred reactor data of Herbinet et al. (14). Additional tests of this new model for other literature data are also presented in the case of ignition delay times.

AUTOMATIC GENERATION OF THE MODEL

The initial model has been generated using the EXGAS software which has already been extensively described in the case of alkanes (10)(12)(15).

General features of EXGAS

The system provides reaction mechanisms made of three parts:

• ➢A C₀-C₂ reaction base including all the reactions involving radicals or molecules containing less than three carbon atoms,

  The kinetic data used in the C₀-C₂ reactions base were taken from the literature, mainly the values recommended by Baulch et al. (16)(17) and Tsang and Hampson (18). The pressure dependent rate constants follow the formalism proposed by Troe (19) and efficiency coefficients have been included.

• ➢A comprehensive primary mechanism, where the only molecular reactants considered are the initial organic compounds and oxygen,
  The primary mechanism includes only elementary steps; the reactions, which are considered to model the oxidation of alkanes are the following:

  • ◆
    Unimolecular and bimolecular initiation steps,
  • ◆
    Decomposition and oxidation of alkyl radicals (to form the conjugated alkene and ·HO₂ radicals),
  • ◆
    Addition to oxygen of alkyl and hydroperoxyalkyl radicals,
    Contrary to what has been considered in most recent models automatically generated using EXGAS (20), the reactions of ·OOQOOH radicals have been considered in detail.
  • ◆
    Isomerizations of alkyl and alkylperoxy radicals,
  • ◆
    Decompositions of hydroperoxyalkyl and di-hydroperoxyalkyl radicals to form cyclic ethers, alkenes, aldehydes, ketones and oxohydroperoxyalkanes,
  • ◆
    Metatheses involving the H-abstraction reactions from the initial reactants by a radical,
  • ◆
    Termination steps.
• ➢A lumped secondary mechanism, containing reactions consuming the molecular products of the primary mechanism, which do not react in the reaction bases (15). Note that the lumped secondary mechanism involves lumped reactants: the molecules formed in the primary mechanism, with the same molecular formula and the same functional groups, are lumped into one unique species without distinction between the different isomers. This is the case for butenes and oxiranes.

Thermochemical data for molecules or radicals are automatically calculated and stored as 14 polynomial coefficients, according to the CHEMKIN formalism (21). These data are calculated using the software THERGAS (22), based on the group and bond additivity methods proposed by Benson (23). The kinetic data of the reactions included in the primary or secondary mechanisms are either calculated using thermochemical kinetic methods or estimated using correlations (12)(15).

Performance of the initial model

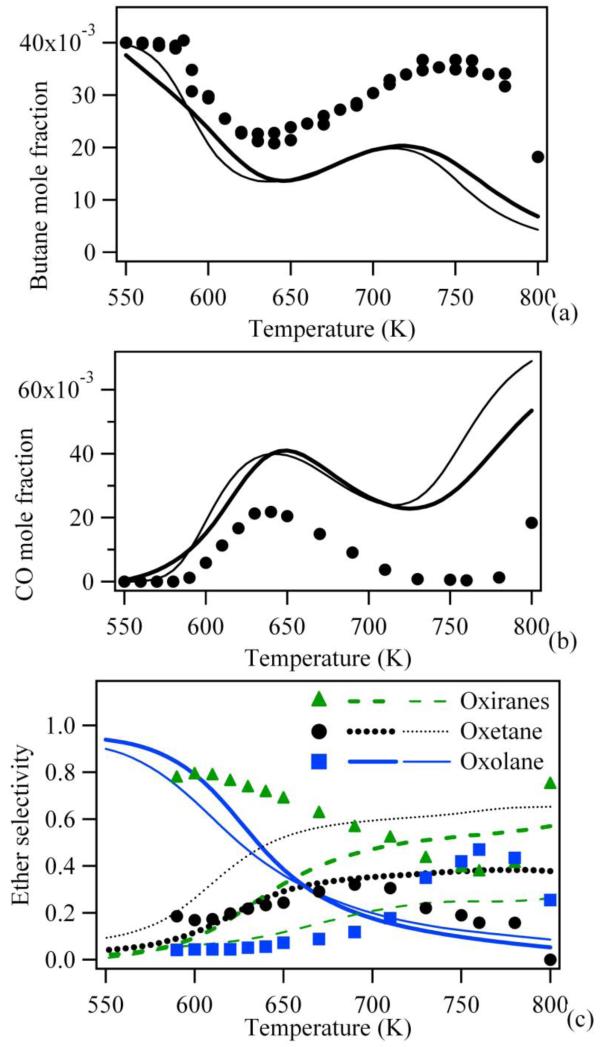
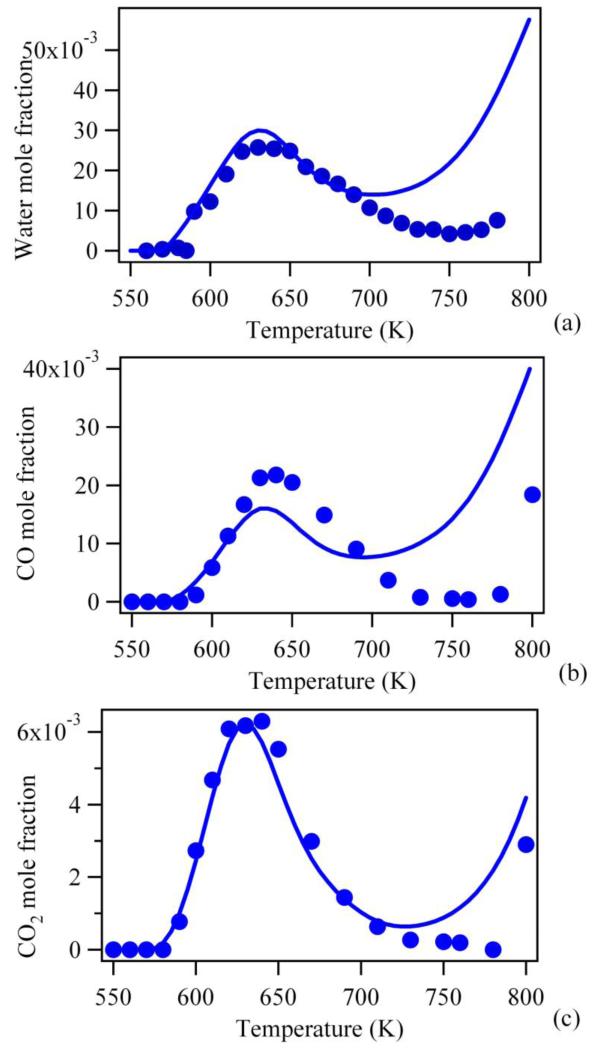
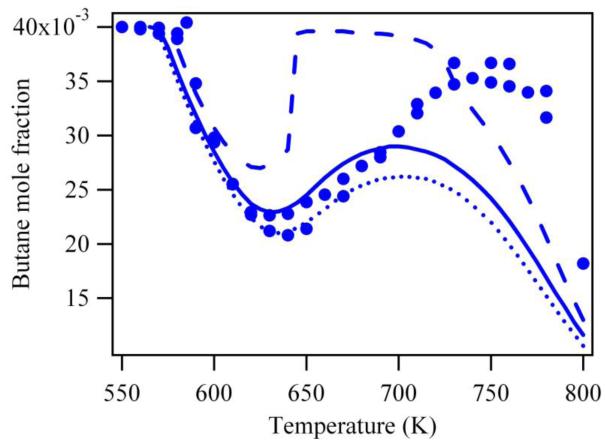
Figure 2 presents a comparison between the experimental results obtained by Herbinet et al. (14) in the case of the oxidation of n-butane in a jet-stirred reactor (analyses were performed using two methods: gas chromatography after sampling in the outlet gas and reflectron time-of-flight mass spectrometry with gas chromatography analysis) and simulations performed using a mechanism directly generated using EXGAS (15). A comparison with simulations performed using the recent mechanism of Healy et al. (9) is also displayed. Simulations have been performed using the PSR and SENKIN codes of the CHEMKIN software package (21). In all the figures hereafter presenting a comparison between simulated and experimental data, the points refer to experimental observations and the curves to simulations. Figure 2 shows that both mechanisms reproduce fairly well the global reactivity below 650 K: the fuel consumption (Figure 2a) and the formation of carbon monoxide (Figure 2b), a good indicator of the global reactivity, are only slightly overestimated. This agreement clearly deteriorates at higher temperatures. Another area for which the predictions of both models deviate significantly from experimental results is in the distribution of cyclic ethers. Figure 2c displays the selectivities (the ratio of the mole fraction of a given type of ether to the sum of ether mole fractions) of the three types of cyclic ethers observed: oxiranes (three-member ring ethers), oxetanes (four-member ring ethers) and oxolanes (five-member ring ethers) and shows that the prediction of the model considerably overestimates the formation of oxolanes at low temperature and underestimates that of oxiranes. The evolutions with temperature of the formation of these ethers are also badly predicted: the experimental selectivity of oxolanes increases with temperature while the simulated one decreases and the experimental selectivity of oxiranes decreases with temperature while the simulated one increases.

Figure 2.

Predictions of literature models (thick line (EXGAS (15)) and thin line (9)) for the oxidation of n-butane in a jet-stirred reactor (residence time of 6 s, atmospheric pressure, stoichiometric mixtures containing 4% (mol) n-butane diluted in helium, points are experiments from (14)).

IMPROVEMENTS OF THERMOCHEMICAL AND KINETIC PARAMETERS

In order to make the simulations more consistent with experiments, we have tried to improve the thermochemical and kinetic parameters used for several classes of reaction. Kinetic parameters have been investigated in the case of the reactions of alkyl radicals with oxygen, isomerizations, formation of cyclic ethers, and two β-scissions of hydroperoxyalkyl radicals. Moreover, the kinetic parameters of four reactions of the C₀-C₂ reactions base have also been up-dated: the rate constant proposed by Troe has been used for the reaction: H₂O₂ (+M) ↔ 2·OH (+M) (24), that proposed by You et al. (25) for the reaction: CO + ·HO₂ ↔ CO₂ + OH·, that proposed by Vasudevan et al. (26) for the reaction: ·OH + HCHO ↔ H₂O + ·HCO, and that proposed by DeSain et al. (27) for the reaction: ·HCO + O₂ ↔ CO + ·HO₂. Compared to the values used in EXGAS, the A-factors of the decompositions of hydroperoxydes and ketohydroperoxydes have been divided by 4 in order to be consistent with the value initially proposed by Sahetchian et al. (28).

Thermochemical data

At low-temperatures, a small energy difference in thermochemical data can have a significant impact on the global reactivity. Indeed, some reactions such as oxygen addition on alkyl or hydroperoxyalkyl radicals are strongly dependent on equilibrium constants. It is then important to use accurate thermochemical data. Enthalpies of formation, entropies and heat capacities of the major C₃ and C₄ alkyl, alkylperoxy, hydroperoxyalkyl, hydroperoxyalkylperoxy radicals radicals involved in the oxidation of n-butane have been calculated by quantum chemical methods. These calculations were performed at the CBS-QB3 level of theory (29) implemented in Gaussian 03 Rev. E.01 (30). For each species considered, the conformer with the lowest energy at 298 K has been identified, by performing relaxed scans, in particular for peroxy and hydroperoxyalkyl radicals, which can involve hydrogen bonding. Enthalpies of formation at 298 K have been obtained from isodesmic reactions. For vibrational partition function, Q_vib, the harmonic oscillator approximation has been assumed, except for low frequency vibrations which correspond to internal rotations. In these latter cases, a hindered rotor treatment was used. The rotational barriers have been estimated by relaxed scans at the B3LYP/cbsb7 level of theory and have been used to correct Q_vib from Pitzer and Gwinn tabulations (31). For transition states, we have used the same procedure, but by freezing the atoms involved in the reaction coordinate (i.e. the cyclic part of the transition states for isomerizations), and by taking into account the remaining torsions. Reduced moments of inertia for internal rotations as well as thermochemical properties as a function of temperature have been calculated using the CHEMRATE software (32) according to statistical mechanical principles.

Table 1 and 2 presents these calculated data at different temperatures, as well as a comparison with those obtained by group additivity methods using the THERGAS software (22) for C₃ and C₄ alkyl, alkylperoxy and hydroperoxyalkyl radicals and those calculated by Goos et al. (33) from quantum calculations at the G3B3 level of theory for C₃ and C₄ alkyl radicals.

TABLE 1. Enthalpies of formation (kcal.mol⁻¹), entropies and heat capacities (cal.mol⁻¹.K⁻¹) for alkyl, alkylperoxy and hydroperoxyalkyl radicals, calculated at the CBS-QB3 level of theory.

In brackets: EXGAS data. In square brackets: data from Goos et al. (33).

name	species	H298	S298	CP,300	CP,400	CP,500	CP,600	CP,800	CP,1000
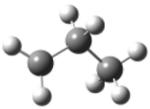
1-propyl radical		24.1 (23.9) [24.2]	69.5 (67.9) [69.4]	17.4 (17.6) [17.1]	21.5 (22.1) [21.1]	25.3 (25.9) [25.0]	28.5 (29.0) [28.3]	33.7 (34.2) [33.5]	37.8 (38.2) [37.6]
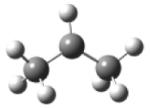
2-propyl radical		21.3 (21.5) [21.6]	69.2 (66.7) [69.3]	16.2 (17.3) [15.7]	20.1 (21.5) [19.5]	24.0 (25.2) [23.4]	27.4 (28.4) [26.9]	33.0 (33.7) [32.5]	37.3 (37.8) [36.9]
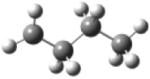
1-butyl radical		18.9 (18.6) [19.5]	79.0 (77.5) [73.5]	22.6 (23.3) [22.7]	28.3 (29.2) [28.4]	33.6 (34.2) [33.7]	38.1 (38.4) [38.4]	45.2 (45.3) [45.6]	50.5 (50.6) [51.1]
2-butyl radical		16.1 (16.4) [16.8]	80.1 (77.7) [76.9]	22.4 (23.1) [20.7]	27.6 (28.8) [26.2]	32.6 (33.7) [31.4]	37.0 (37.9) [36.2]	44.1 (44.8) [43.5]	49.6 (50.1) [49.1]
1-propylperoxy radical		−11.1 (−10.2)	83.5 (82.1)	23.5 (23.6)	28.9 (29.1)	33.7 (33.8)	37.7 (37.7)	43.7 (43.7)	48.2 (48.0)
2-propylperoxy radical		−15.6 (−14.7)	81.3 (79.6)	24.3 (24.2)	29.3 (29.9)	33.7 (34.6)	37.5 (38.5)	43.4 (44.3)	47.8 (48.5)
1-butylperoxy radical		−16.3 (−15.2)	93.0 (91.5)	28.6 (29.1)	35.8 (36.1)	42.1 (42.0)	47.3 (47.0)	55.2 (54.8)	60.9 (60.3)
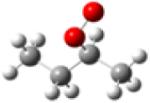
2-butylperoxy radical		−20.9 (−19.7)	90.2 (90.4)	29.6 (29.7)	36.5 (36.9)	42.4 (42.9)	47.4 (47.9)	55.0 (55.4)	60.6 (60.8)
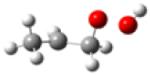
1-hydroperoxy- 2-propylradical		3.2 (1.3)	87.7 (88.8)	25.0 (25.2)	30.1 (30.1)	34.8 (34.2)	38.6 (37.7)	44.4 (43.0)	48.5 (47.0)
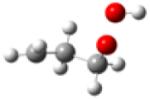
1-hydroperoxy- 3-propylradical		5.3 (3.5)	86.7 (88.7)	25.4 (25.3)	30.9 (30.5)	35.8 (34.8)	39.8 (38.2)	45.7 (43.6)	49.7 (47.5)
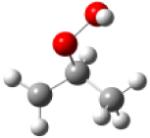
2-hydroperoxy- 1-propylradical		2.5 (−1.7)	84.4 (87.6)	26.3 (25.9)	31.7 (31.3)	36.3 (35.6)	40.0 (39.0)	45.4 (44.2)	49.3 (48.0)
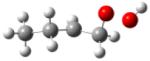
1-hydroperoxy- 2-butylradical		−1.7 (−3.7)	97.7 (98.2)	30.9 (30.7)	37.3 (37.3)	43.1 (42.7)	48.0 (47.1)	55.4 (54.1)	60.8 (59.3)
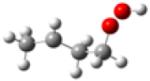
1-hydroperoxy- 3-butylradical		−2.7 (−3.7)	97.9 (98.2)	30.3 (30.6)	37.0 (37.1)	43.2 (42.5)	48.4 (47.0)	56.1 (54.1)	61.6 (59.4)
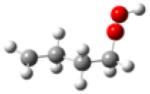
1-hydroperoxy- 4-butylradical		0.1 (−1.5)	96.7 (98.0)	30.4 (30.8)	37.7 (37.5)	44.1 (43.0)	49.3 (47.6)	56.9 (54.7)	62.1 (59.8)
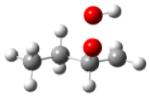
2-hydroperoxy- 1-butylradical		−2.7 (−6.7)	93.8 (96.9)	31.6 (31.4)	38.5 (38.3)	44.5 (43.8)	49.4 (48.4)	56.7 (55.3)	61.8 (60.3)
2-hydroperoxy- 3-butylradical		−6.3 (−8.2)	94.7 (97.1)	31.2 (31.2)	37.9 (37.9)	43.7 (43.3)	48.6 (47.8)	55.9 (54.7)	61.2 (59.9)
2-hydroperoxy- 4-butylradical		−3.6 (−6.0)	93.5 (96.9)	31.5 (31.4)	38.5 (38.3)	44.5 (43.8)	49.5 (48.4)	57.0 (55.3)	62.2 (60.3)

TABLE 2. Enthalpies of formation (kcal.mol⁻¹), entropies and heat capacities (cal.mol⁻¹.K⁻¹) for hydroperoxyalkylperoxy radicals, calculated at the CBS-QB3 level of theory.

In brackets: EXGAS data.

name	species	H298	S298	CP,300	CP,400	CP,500	CP,600	CP,800	CP,1000
1-hydroperoxy- 2-propylperoxy radical		−34.1 (−34.9)	97.2 (100.4)	31.7 (31.9)	38.3 (38.3)	44.1 (43.5)	48.9 (47.7)	55.8 (53.7)	60.5 (57.8)
1-hydroperoxy- 3-propylperoxy radical		−29.7 (−30.4)	100.4 (102.9)	30.8 (31.3)	37.6 (37.5)	43.7 (42.6)	48.6 (46.9)	55.9 (53.1)	60.7 (57.3)
2-hydroperoxy- 1-propylperoxy radical		−33.6 (−34.9)	96.1 (101.8)	31.5 (31.9)	38.2 (38.3)	44.1 (43.5)	49.0 (47.7)	56.1 (53.7)	61.0 (57.8)
1-hydroperoxy- 2-butylperoxy radical		−39.5 (−39.8)	105.6 (111.1)	36.9 (37.3)	45.3 (45.2)	52.7 (51.7)	58.7 (57.0)	67.5 (64.8)	73.4 (70.1)
1-hydroperoxy- 3-butylperoxy radical		−39.9 (−39.8)	107.0 (111.1)	36.9 (37.3)	45.2 (45.2)	52.5 (51.7)	58.4 (57.0)	67.2 (64.8)	73.2 (70.1)
1-hydroperoxy- 4-butylperoxy radical		−37.3 (−35.3)	108.0 (110.9)	35.5 (36.7)	44.1 (44.5)	51.8 (50.9)	58.2 (56.2)	68.0 (64.2)	74.8 (69.6)
2-hydroperoxy- 1-butylperoxy radical		−39.2 (−39.8)	105.1 (111.1)	36.7 (37.3)	45.1 (45.2)	52.6 (51.7)	58.7 (57.0)	67.6 (64.8)	73.7 (70.1)
2-hydroperoxy- 3-butylperoxy radical		−43.4 (−44.3)	102.9 (108.7)	37.6 (37.9)	45.5 (46.0)	52.5 (52.6)	58.4 (57.8)	67.2 (65.4)	73.4 (70.6)
2-hydroperoxy- 4-butylperoxy radical		−39.3 (−39.8)	105.6 (111.1)	36.7 (37.3)	45.1 (45.2)	52.5 (51.7)	58.6 (57.0)	67.7 (64.8)	73.8 (70.1)

In the case of alkyl radicals, the calculated enthalpies of formation (at 298 K) are very close to the THERGAS values and to those proposed by Goos et al. (33). A larger deviation is observed for entropies at 298 K. For alkyl radicals, the comparison with the THERGAS values leads to differences ranging from 1.6 to 2.5 cal.mol⁻¹.K⁻¹. If we compare our results with those obtained by Goos et al. (33) at the G3B3 level of theory, the entropies of C₃ alkyl radicals are very similar in both cases, while a larger deviation is observed for C₄ species, in particular for the 1-butyl radical for which a difference of 5.5 cal.mol⁻¹.K⁻¹ is observed. However, the value of 73.5 cal.mol⁻¹.K⁻¹ derived from the NASA polynomial of Goos et al. for 1- butyl radicals is doubtful since the entropy of n-butane, obtained at the same level of calculation, is equal to 74 cal.mol⁻¹.K⁻¹. A simple analysis shows that electronic and symmetry contributions (which represent important contributions) increase the entropy of the 1-butyl radical by a 2Rln2 (2.75 cal.mol⁻¹.K⁻¹) compared to that of n-butane.

For alkylperoxy and hydroperoxyalkyl radicals, the comparison with the THERGAS values shows that the calculated enthalpies of formation are about 1 kcal.mol⁻¹ lower for alkylperoxy radicals and about 2 kcal.mol⁻¹ higher for hydroperoxyalkyl radicals. Compared to the THERGAS values, calculated entropies are about 1 cal.mol⁻¹.K⁻¹ higher for alkylperoxy radicals, and about 2 cal.mol⁻¹.K⁻¹ lower for hydroperoxyalkyl radicals. Thus, according to our calculations, alkylperoxy radicals appear to be thermodynamically more stable and hydroperoxyalkyl radicals less stable, compared to what can be derived from the thermochemical values obtained by group additivity methods. The calculated enthalpies of formation of hydroperoxyalkylperoxy radicals are close to the THERGAS values, and the calculated entropies are 5 cal.mol⁻¹.K⁻¹ lower, so that these species appear to be thermodynamically less stable.

Reactions of alkyl radicals with oxygen

The reaction of alkyl radicals with oxygen is of particular importance at low temperature. The current understanding of these reactions for small alkyl radicals, such as ethyl or propyl radicals, is in agreement with the fact that the R· + O₂ reaction proceeds through a barrierless addition pathway to form the chemically activated ROO· adduct, which can either be stabilized or react via a concerted elimination of ·HO₂ to give the conjugated alkene (34). Combining theoretical calculations with an experimental investigation of the time-resolved formation of ·OH, DeSain et al. (34) reported kinetic parameters for the different possible channels at different pressures in the case of ethyl and propyl radicals. The data obtained by DeSain et al. (34) have been recently revisited by Huang et al. (35). In the EXGAS software, the kinetic parameters for the addition of oxygen to alkyl radicals and the formation of ·HO₂ and the conjugated alkene (oxidation) were estimated using correlations (12) based on values proposed by Benson in the first case (23) and on a study of Walker (36) in the second one.

In the present work, we used kinetic parameters for the reactions of butyl radicals with oxygen derived from values proposed by DeSain et al. (34) for propyl radicals. We have used the values at 1 atm for simulating the jet-stirred reactor experiments, and the values at 10 atm for ignition delay times. In the case of the addition, we have just considered whether the radical was primary or secondary. In the case of the formation of butenes and ·HO₂ radicals, we have calculated the contributions of the different types of abstracted H-atoms.

Isomerizations of peroxy radicals into hydroperoxyalkyl radicals

The first values for the rate parameters of a whole series of isomerizations of peroxy radicals to give hydroperoxyalkyl radicals were suggested by Baldwin et al. (37) from studies of the addition of various alkanes to slowly reacting mixtures of H₂ + O₂. Pilling and co-workers (38)(39) have later experimentally studied the isomerization of neopentylperoxy radicals between 660 and 750 K using the laser flash photolysis/laser induced fluorescence technique and revisited the values of Baldwin et al. (37). While the models generated by EXGAS use rate constants (12) close to those proposed by Pilling and co-workers (38)(39), the models of Curran et al. (40) used much faster values. In 1998, Chan et al. (41) were the first to use quantum mechanical calculations to derive rate constants for a large series of isomerisations and obtained activation energies between 5 and 7 kcal/mol higher than those proposed by the team of Pilling and co-workers (38)(39). Since then many theoretical studies have been focused on the rate constants of this class of reactions for specific alkyl radicals (e.g. DeSain et al. (42) and Zhu et al. (43) for butyl radicals, Asatryan et al. for pentyl radicals (44)). The calculations of DeSain et al. (42) were made using the QCISD(T) method, those of Bozzelli and co-workers (44) were mainly performed at the CBS-QB3 level of theory. Very recently, Sharma et al. (45) calculated the rate constants of isomerizations at the CBS-QB3 level of theory, with an emphasis on the treatment of the rotors, for a whole series of alkyl and hydroperoxyalkyl radicals. A similar study was also performed by Miyoshi (46) and Villano et al. (47). While the data of DeSain et al. (42) have been used for interpreting experimental results obtained for the time-resolved production of ·OH in the Cl-initiated oxidation of iso- and n-butane, none of the previously mentioned theoretical data have yet been used in a validated detailed kinetic model for the low-temperature oxidation of an alkane.

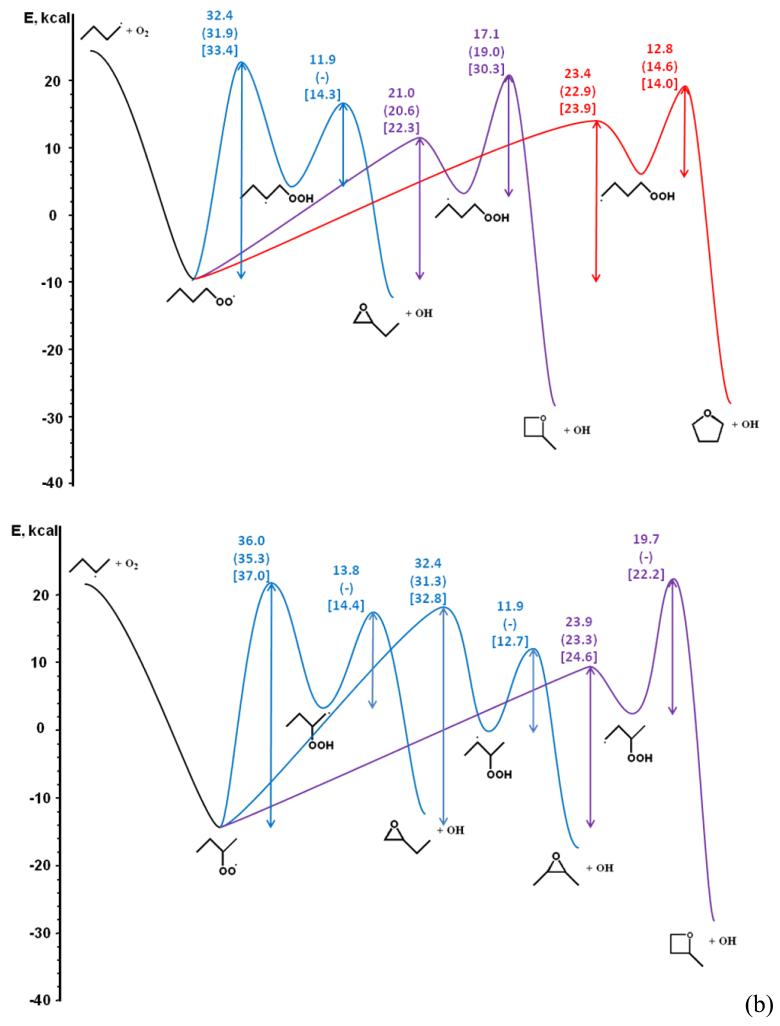
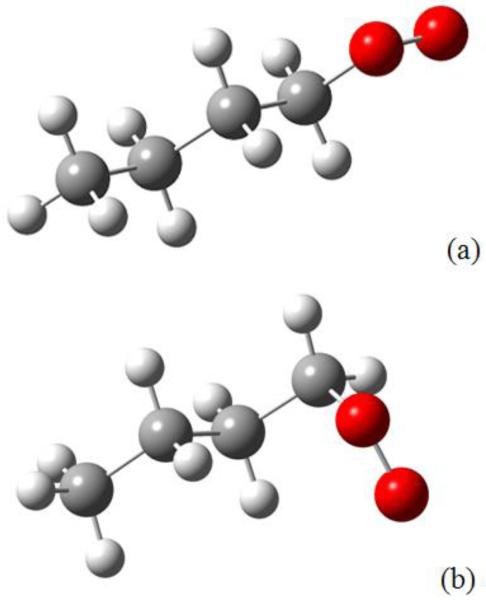
In the present work, the calculations of the kinetic parameters of isomerizations were performed with Gaussian 03 Rev. E.01 (30). The composite method CBS-QB3 (29) was applied for all stationary geometries and transition states involved in the reaction studied. Intrinsic Reaction Coordinates (IRC) calculations have been done at the B3LYP/cbsb7 level of theory to ensure that the transition states correctly connect the reactants to the products. Tunnelling effects have been taken into account for isomerizations based on the Eckart-1D method (48). Figure 3 presents a simplified potential energy surface (PES) for the isomerizations of the two possible butylperoxy radicals and for the reactions of the derived hydroperoxyalkyl radicals, with a comparison with energy barriers from the literature. Our values are based on the calculations reported on Tables 1-4: all the reactants and products of the PES were calculated, and we used analogies (same number of atoms in the cyclic part of the transition state, and same type of hydrogen abstracted and same type of radical for the isomerizations and the formation of cyclic ethers, respectively) to obtain the barrier heights of the reactions that have not been directly calculated. It can be observed that our ZPE-corrected barriers are close to those obtained recently by Sharma et al. (45) at the same level of theory, even if our values are slightly higher by 0.4 to 1 kcal.mol⁻¹. These variations can be mainly explained by the choice of different conformers for peroxy radicals, and by the analogies we used. The peroxy radicals considered by Sharma et al. (45) correspond to all-trans conformers with the five heavy atoms in the same plane, while those considered in this study have the oxygen atoms out of the plane defined by the three carbon atoms. Figure 4 shows the conformer taken into account by Sharma et al. (45) and that considered in this work for the peroxy radical deriving from 1-butyl radicals. The latter is more stable by 0.4 kcal.mol⁻¹. A similar difference can be observed with the values of DeSain et al. (42) obtained at the QCISD(T) level of theory although the trend is reversed (our ZPE-corrected barriers are lower by 0.4 to 1.3 kcal.mol⁻¹ compared to the values of DeSain et al. (42)).

Figure 3.

Simplified potential energy surface for the isomerizations of (a) 1-butylperoxy and (b) 2-butylperoxy radicals and for the reactions of the derived hydroperoxyalkyl radicals (the energies (in kcal mol⁻¹) are calculated at the CBS-QB3 level of theory at 0 K) and comparison with the energy barriers calculated by DeSain et al. (42) (in square brackets), Sharma et al. (45) (in brackets) and Wijaya et al. (52) (in brackets).

TABLE 4. Kinetic parameters calculated for the formation of cyclic ethers and comparison with the data used by EXGAS (12).

Reaction for which the calculation has been performed	Type of reaction*	log (A (s−1))	n	E (kcal.mol−1)	k / kEXGAS at 700 K
CH2(.)CH2OOH → oxirane + OH	3 - I	11.0	0.554	13.9	71
CH3CH(.)CH2OOH → 2-methyl-oxirane + OH	3 - II	10.8	0.468	12.1	100
(CH3)2C(.)CH2OOH → 2,2-dimethyl-oxirane + OH	3 - III	11.1	0.481	10.5	650
CH2(.)CH2CH2OOH → oxetane + OH	4 - I	10.6	0.303	19.8	0.43
CH3CH(.)CH2CH2OOH → 2-methyl-oxetane + OH	4 - II	10.2	0.275	17.3	0.78
(CH3)2C(.)CH2CH2OOH → 2,2-dimethyl-oxetane + OH	4 - III	9.77	0.523	15.0	8.7
CH2(.)CH2CH2CH2OOH → oxolane + OH	5 - I	9.61	0.277	12.5	0.16
CH3CH(.)CH2CH2CH2OOH → 2-methyl-oxolane + OH	5 - II	9.25	0.220	10.9	0.15
(CH3)2C(.)CH2CH2CH2OOH →2,2-dimethyl-oxolane + OH	5 - III	9.02	0.329	8.64	0.93

^*The first number is the number of atoms in the cyclic part of the transition state (from 3 to 5 atoms), and the second roman number refers to the type of radicals involved in the reaction (I: primary, II: secondary, III: tertiary).

Figure 4.

Conformers of butyl peroxy radical considered by (a) Sharma et al. (45) and (b) in the present work.

The high pressure rate constants involved in the mechanism were calculated with the software CHEMRATE (32), using canonical transition state theory (TST):

$$k_{\infty }=rpd\kappa \left(T\right)\frac{k_{b}T}{h}\exp \left(-\frac{\Delta G^{\ne }\left(T\right)}{RT}\right)$$ (eq. 1)

where ΔG^≠ is the Gibbs energy of activation, rpd the reaction path degeneracy, and κ the transmission coefficient. The kinetic parameters were obtained by fitting the rate constant values obtained from TST at several temperatures between 500 and 1200 K, using the modified-Arrhenius expression:

$$k_{\infty }=A{T}^n\exp \left(-\frac{\mathrm{E}}{\mathrm{RT}}\right)$$ (eq. 2)

Calculations were performed for the 11 reactions presented in Table 3, which are representative of the main isomerizations which can occur during the oxidation of linear and branched alkanes. These are the isomerizations for which the cyclic part of the transition state includes from 5 to 7 atoms. The isomerization involving 4-member transition states are in most cases of negligible importance. The rate constants of all the isomerizations of alkylperoxy radicals involving the transfer of primary or secondary H-atoms used in our new model have been recalculated based on the values presented in Table 3. Rates constants have also been calculated for the isomerizations of the most abundant ·OOQOOH radicals involving a 6-member ring in the transition state (see Table 3) and used in the new model. The rate constant for the other isomerizations are based on the previous EXGAS correlations (12).

TABLE 3. Kinetic parameters calculated for the isomerizations of alkylperoxy radicals and comparison with the data used by EXGAS (12).

Reaction for which the calculation has been performed	Type of isomerization*	log (A (s−1))	n	E (kcal.mol−1)	k / kEXGAS at 700 K
CH3CH2OO. → CH2(.)CH2OOH	5 - I	−2.88	4.53	27.0	1.4
CH3CH2CH2OO. → CH3CH(.)CH2OOH	5 - II	−0.52	3.66	24.8	0.9
(CH3)2CHCH2OO. → (CH3)2C(.)CH2OOH	5 - III	1.09	3.10	22.5	1.0
CH3CH2CH2OO. → CH2(.)CH2CH2OOH	6 - I	4.15	2.20	19.8	23
CH3CH2CH2CH2OO. → CH3CH(.)CH2CH2OOH	6 - II	4.80	1.83	17.2	10
(CH3)2CHCH2CH2OO. → (CH3)2C(.)CH2CH2OOH	6 - III	5.11	1.67	14.6	10
CH3CH2CH2CH2OO. → CH2(.)CH2CH2CH2OOH	7 - I	3.42	2.17	19.1	2.6
CH3CH2CH2CH2CH2OO. → CH3CH(.)CH2CH2CH2OOH	7 - II	4.30	1.71	16.1	1.5
(CH3)2CHCH2CH2CH2OO. → (CH3)2C(.)CH2CH2CH2OOH	7 - III	5.19	1.38	13.6	1.8
HOOCH2CH2CH(CH3)OO. → HOOCH(.)CH2CH(CH3)OOH	6 - II (O)**	4.48	2.03	15.7	12
HOOCH(CH3)CH2CH2OO. → HOOC(.)(CH3)CH2CH2OOH	6 - III (O)	5.24	1.78	14.5	7

^*The first number is the number of atoms in the cyclic part of the transition state (from 5 to 7 atoms), and the second roman number refers to the type of hydrogen atom abstracted for the isomerization (I: primary, II: secondary, III: tertiary).

^**(O) indicates that the hydrogen transferred is borne by a carbon linked to an atom of oxygen.

Table 3 also presents comparison with rate constants used by EXGAS (12). Similar rate constants are obtained at 700 K for the isomerizations for which the cyclic part of the transition state includes either 5 or 7 atoms. This is not the case for the isomerizations for which the cyclic part of the transition state includes 6 atoms, for which the newly calculated rate constants are considerably lower than those calculated by EXGAS (factors from 10 to 23).

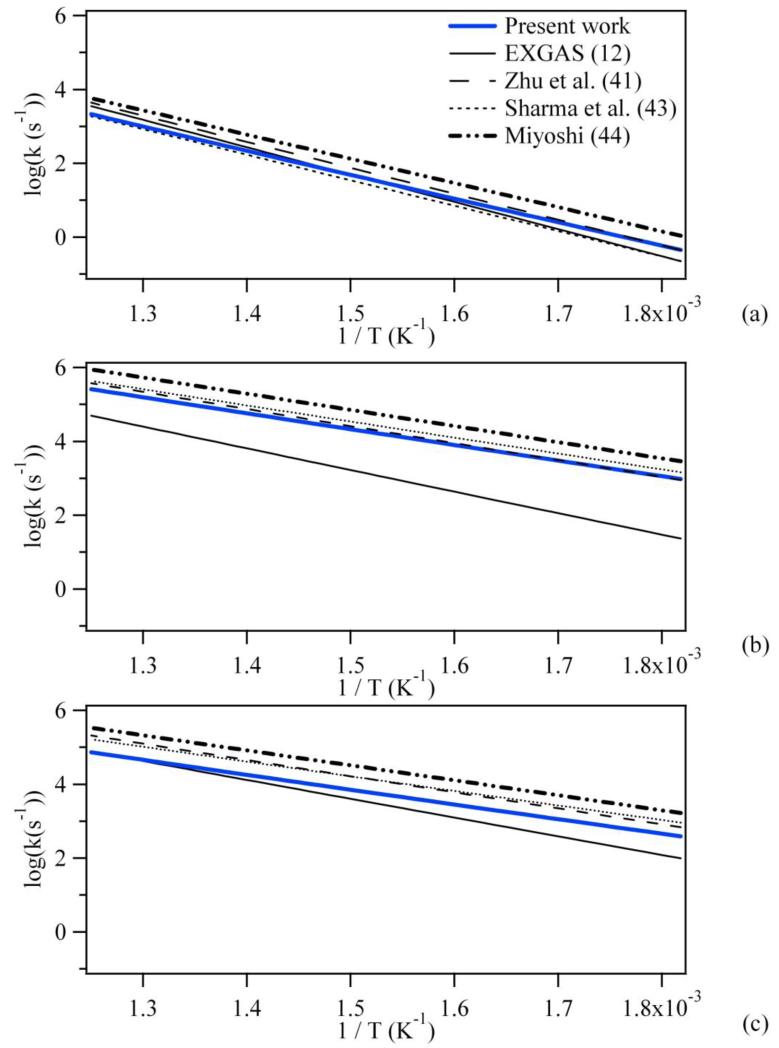
Figure 5 shows a comparison, at the same level of theory (CBS-QB3), between the rate constants using the newly calculated kinetic parameters, and those using the parameters proposed by Zhu et al. (43), Sharma et al. (45), Miyoshi (46) for the isomerizations involving the transfer of a secondary H-atom with a cyclic transition state including 5, 6 or 7 atoms. The rate constants currently used in EXGAS (12) are also presented for comparison. It can be noted that a rather good agreement between our values and those obtained by Sharma et al. (45) and Zhu et al. (43) is obtained with a maximum deviation of less than a factor of 3 for the isomerization passing through a seven member cyclic transition state. The gap slightly increases if we compare our values with those obtained by Miyoshi (46), with a maximum deviation of a factor 4.6 at 730 K. However this deviation is larger than what might be expected based on the agreement for the energy barriers. Several reasons can be put forward to explain these differences, such as the treatment of torsions or the use of tunnelling factors for the rate constants involving an H-transfer. For example, Sharma et al. (45) solved the one-dimensional Schrödinger (method 1D-HR (49)) to treat hindered rotors for peroxy and hydroperoxyalkyl radicals. This methodology is more accurate than the use of Pitzer and Gwinn tables (31) for taking into account non methyl or ·CH₂ torsions, even if it is a more time-consuming procedure. However, they used a Wigner approximation (50) to treat tunnelling effects. This method is less accurate than the one dimensional Eckart method used in this study. Miyoshi (46) considered all the conformers (for C₂-C₄ species) from the rotational-conformer distribution partition functions and treated internal rotors, consisting of heavy atoms as harmonic oscillators. Finally, the rate constants proposed by Mioyshi (46) were derived from structure-reactivity relationships based on his ab-initio calculations. Zhu et al. (43) calculated the contributions of hindered rotor to entropy and heat capacities using direct integration over energy levels of the internal potential. Moreover, they “corrected” the imaginary frequencies by a factor of 0.7 and used the Wigner approximation to take into account the tunnelling of the H atom. The treatment of hindered rotors for transition states could also explain the deviation between the results obtained by the different authors. As previously discussed, we chose to “freeze” all the atoms which constitute the reaction coordinate and performed relaxed scans for the remaining internal rotations of the transition state, but unfortunately no explicit information was given on this particular point by the other authors (43)(45)(46).

Figure 5.

Comparison between the rate constants the kinetic parameters calculated in this work and those using the parameters proposed by Zhu et al. (43), Sharma et al. (45), Miyoshi (46) and Buda et al. (EXGAS) (12) for the isomerizations involving the transfer of a secondary H-atom with a cyclic transition state including (a) 5, (b) 6 or (c) 7 atoms.

Note that the concerted elimination reaction from peroxy radicals to give the conjugated alkene and ·HO₂ radicals is a type of reaction which is not directly considered in the EXGAS generation. These reactions are taken into account in the new mechanism with rate constants derived from the values proposed by DeSain et al. (34) for propylperoxy radicals. As in the case of the formation of alkenes by reaction of alkyl radicals with oxygen, we have calculated the contributions of the different types of abstracted H-atoms.

Isomerization of one hydroperoxyalkyl radical into another hydroperoxyalkyl radical

Calculations of the kinetic parameter for the isomerization of the 1-hydroperoxy-4-butyl radical into the 1-hydroperoxy-1-butyl radical were performed using the same method as that previously described. This reaction is important because it is the fastest isomerization of one C₄-hydroperoxyalkyl radical into another C₄-hydroperoxyalkyl radical, since it involves a six-member ring transition state whereas the others involve cycles including 5 atoms or less. Moreover, this reaction is the major production channel of butanal. Indeed, the 1-hydroperoxy-1-butylradical is unstable and decomposes rapidly into butanal and a hydroxyl radical. The calculated rate constant is $k=212\times T^{2.679}\times e^{-\frac{7887}{T}}{s}^{-1}$. It is 59 times slower at 700 K than the EXGAS rate constant.

Formation of cyclic ethers

The kinetic parameters used in detailed kinetic models (e.g. (12)(40)) for the formation of cyclic ethers are also derived from values published by Baldwin et al. (37). In these models, the size of the cycle is the only variable taken into account for estimating the kinetic parameters, with activation energies consistently decreasing when increasing the size of the cycle. Much fewer theoretical studies of the formation of cyclic ethers have been performed than in the case of isomerizations. The first of these theoretical studies has been performed by Chan et al. (51) (BH&HLYP method) who obtained activation energies not consistently decreasing when increasing the size of the cycle. In addition, the calculations of Chan et al. (51) were the first showing the need to differentiate the type of carbon atom involved in the ring closure. Calculations have also been performed by DeSain et al. (42) using a QCISD(T) method and by Wijaya et al. (52) at the CBS-QB3 level of theory confirming the results of Chan et al. (51), but with action energies lower by about 2 kcal/mol. Using the same methodology as for isomerizations, Miyoshi (46) has also recently performed calculations for the formation of cyclic ethers from a series of hydroperoxyalkyl radicals and has reported an important spin contamination problem. Here also, none of the previously mentioned theoretical data have yet been used in a validated detailed kinetic model for the low-temperature oxidation of an alkane.

In the present work, the kinetic parameters of the formations of cyclic ethers were performed using the same method as that previously presented for isomerizations. Note that the transmission coefficient used for the estimation of the tunneling effect has not been calculated, since the imaginary frequency was low and then the tunneling effect was negligible. Figure 3 presents a comparison between the energy barriers obtained in this study for the formation of cyclic ethers and some from the literature. If a reasonable agreement was obtained between the ZPE-corrected barriers for isomerizations, a more important deviation can be observed for the reactions of cyclic ether formation. Even if the conformers of the hydroperoxyalkyl radical differ between authors, the most important issue deals with the spin contamination. For all the transition states involved in the formation of cyclic ethers, the spin contamination (<S²>) is important and reaches a value close to 1.3. In the CBS-QB3 method, an empirical correction for spin contamination (ΔE(Emp)) is provided for energy and is close to −3 kcal.mol⁻¹. Wijaya et al. (52) have performed their calculations with the old version of CBS-QB3 implemented in the Gaussian 98 software, which did not correctly estimate the empirical correction ΔE(Emp) and gives erroneous values which differ, for transition states, by +2.5 kcal.mol⁻¹ compared with the updated ones. This deviation is close to that observed on Figure 3. In the same manner, the QCISD(T) calculations performed by DeSain et al. (42) did not consider a correction for spin contamination. If we decrease their ZPE-corrected barriers by −3 kcal.mol⁻¹, which corresponds to the correction for spin contamination, we obtain a good agreement between the three sets of values. Only for the formation of methyloxetane from 1-butylperoxy, DeSain et al. (42) obtain values which are inexplicably considerably larger.

The empirical correction provided in the CBS-QB3 method has been taken into account in the present work even if it was shown not to be fully appropriate in the case of highly contaminated species (53). However the total removal of this correction can be also questionable: the effect of spin contamination on the barrier height is critical for the prediction of the branching ratios of the formation of cyclic ethers.

Calculations were performed for the 9 reactions presented in Table 4, which are representative of the main formation of cyclic ethers which can be observed during the oxidation of linear and branched alkanes. These are the formation of ether for which the cyclic part of the molecules includes from 3 to 5 atoms. As first observed by Chan et al. (51), the calculated activation energies do not consistently decrease when increasing the size of the ring: the formation of oxetane has systematically the largest activation energy. The rate constants of all the formation of cyclic ethers involving primary or secondary radicals used in our new model have been recalculated based on the values presented in Table 4.

Table 4 also presents comparison with the values used by EXGAS (12), for which an important point has to be noted: the correlations used by EXGAS depend only on the size of the cycle which is formed, while our calculations, as previous ones (51)(52), show the need to differentiate the type of carbon atom involved in the ring closure. In addition, the newly calculated rate constants for the formation of oxiranes at 700 K are faster than the EXGAS ones by factors from 71 to 650. Lower discrepancies are observed for the formation of the two other types of ethers.

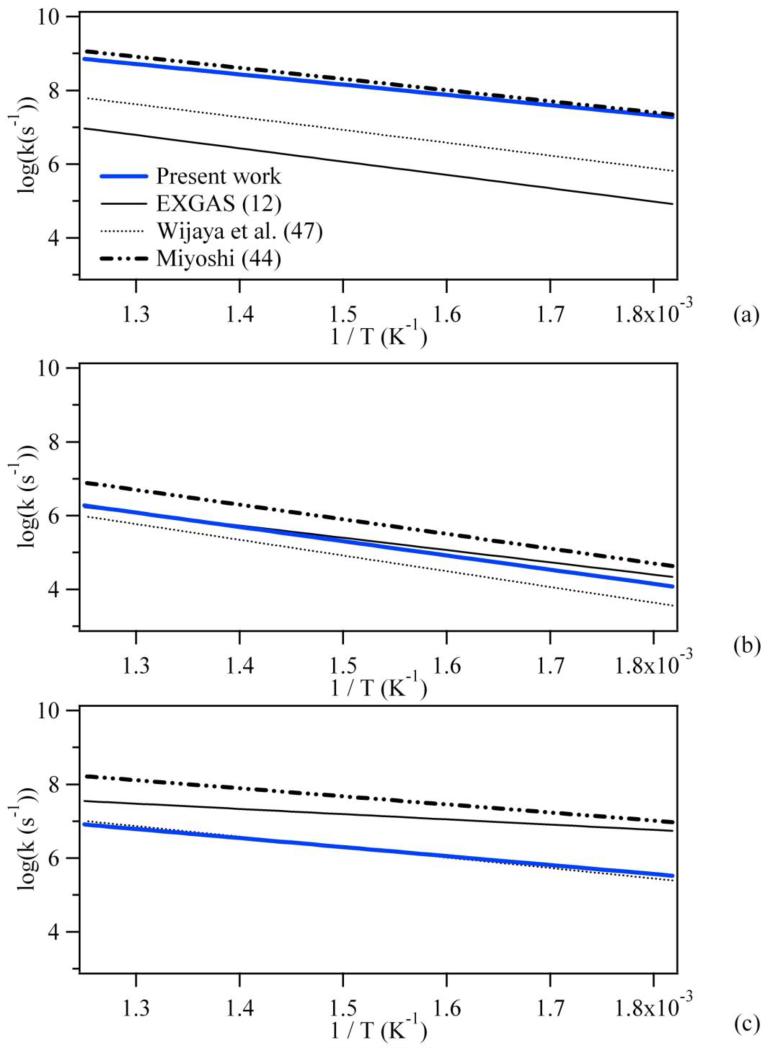
Figure 6 shows a comparison between the rate constants using the newly calculated kinetic parameters and those using the parameters proposed by Wijaya et al. (52), Miyoshi (46) and Buda et al. (EXGAS) (12) for the formation of cyclic ethers involving a secondary radical and a primary hydroperoxy function. Due to the problems encountered by Wijaya et al. (52), concerning the calculation of empirical corrections, their rate constants are always lower than ours, except for the formation of oxolane for which similar values are obtained. On the other hand, we obtained good agreement with the values of Miyoshi (46) for the formation of oxirane and an acceptable one in the case of oxetane with a maximum deviation lower than a factor of 4.2 at 800 K, but a large discrepancy appears for oxolane (a factor 30 at 550 K). If we compare our ZPE-corrected barriers to those of Miyoshi (46) calculated at the CBS-QB3 level of theory, we obtain the same values for oxirane and oxetane and a deviation of +0.8 kcal.mol⁻¹ for oxolane, that is to say a factor of 2.1 at 550 K, which cannot explain the deviation observed. Moreover, even if the treatment of hindered rotors or conformers is taken into account to explain the differences observed for oxiranes and oxetanes, it seems difficult to explain the factor of 30 difference observed between our rate constant and that proposed by Miyoshi (46) for the formation of oxolane.

Figure 6.

: Comparison between the rate constants obtained from the newly calculated kinetic parameters and those derived from the parameters proposed by Wijaya et al. (52), Miyoshi (46) and Buda et al. (EXGAS) (12) for the formations of (a) oxiranes, (b) oxetanes and (c) oxolanes involving the a secondary radical.

Beta-scission reactions

The rate constants of two beta-scissions have been calculated for the 1-hydroperoxy-3-butyl radical (R33C₄H₉O₂P) and the 2-hydroperoxy-4-butyl radical (R37C₄H₉O₂P). These radicals are the two QOOH radicals produced by the isomerizations of a C₄-alkylperoxy radical involving a six-member ring transition state. These reactions lead to an alkene and an α-QOOH. The latter is unstable and breaks into an aldehyde and a hydroxyl radical. The 1-hydroperoxy-3-butylradical leads to the formation of propene, formaldehyde and a hydroxyl radical:

$$\mathrm{R}33{\mathrm{C}}_4{\mathrm{H}}_9{\mathrm{O}}_2\mathrm{P}={\mathrm{C}}_3{\mathrm{H}}_6+\mathrm{HCHO}+\cdot \mathrm{OH},$$

whereas the 2-hydroperoxy-4-butylradical leads to the formation of ethylene, acetaldehyde and a hydroxyl radical:

$$\mathrm{R}37{\mathrm{C}}_4{\mathrm{H}}_9{\mathrm{O}}_2\mathrm{P}={\mathrm{C}}_2{\mathrm{H}}_4+{\mathrm{CH}}_3\mathrm{CHO}+\cdot \mathrm{OH}.$$

Calculations were performed using the same method as that previously presented for cyclic ether formation. The calculated rates constants are $k=2.62\cdot {10}^{11}\times T^{0.558}\times e^{-\frac{13844}{T}}{s}^{-1}$ for the beta-scission of the 1-hydroperoxy-3-butyl radical and $k=2.02\cdot {10}^{12}\times T^{0.413}\times e^{-\frac{12907}{T}}{s}^{-1}$ for the beta-scission of the 2-hydroperoxy-4-butyl radical. At 700 K, these values are 1.2 and 6.6 faster than the EXGAS rate constants, respectively.

COMPARISON BETWEEN EXPERIMENTAL RESULTS AND MODELLING

As discussed by Battin-Leclerc et al. (54), three types of apparatuses are mainly used to produce experimental data to validate detailed kinetic models for global gas phase oxidation at low-temperature: shock tubes, rapid compression machines, and heated flow reactors, such as flow tubes or jet-stirred reactors. The aim of models is to be able to reproduce data obtained in several of these apparatuses, e.g. (12)(40). According to the data existing for n-butane, we present here comparisons between modelling and experimental results obtained in rapid compression machines and jet-stirred reactors, this last type of device being particularly well suited for a detailed product speciation (54).

The complete new mechanism (at 1 and at 10 atm) described in this paper is available in CHEMKIN format as Supplementary Material on the web site of this journal. Simulations have been performed using the CHEMKIN software package (21). Simulations for a jet-stirred reactor were performed using the PSR code assuming a homogeneous isothermal reactor. Simulations for a rapid compression machine have been performed using the SENKIN code assuming a constant volume adiabatic reactor. No other changes other than those described above have been made to the mechanism generated by EXGAS. Pressure dependence was considered for reactions of the the C₀-C₂ reactions base and those the rate constant of which was derived was derived from the study of DeSain et al. (42). For the other reactions, the high-pressure rate rules have always been used. This assumption has been verified by Villano et al. (47) in the case of the reactions of ROO· radicals.

Validation using jet-stirred reactor data

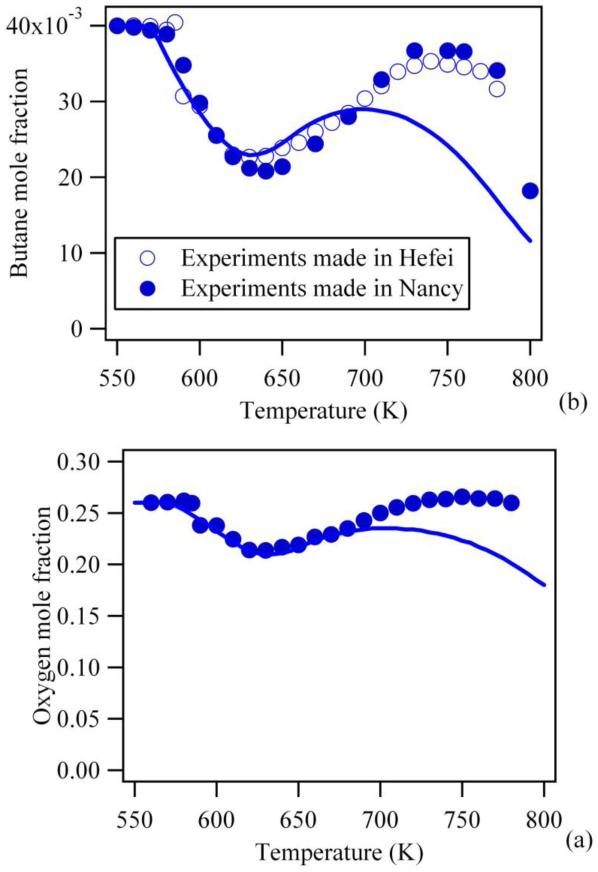
Jet-stirred reactors are well adapted for kinetic studies because the gas phase inside the reactor is well stirred and the concentration is homogenous with a limited effect of possible wall reactions (54). They have been used for more than 20 years and for many types of species, both in oxidation (15)(55)(56) and pyrolysis (57). A jet-stirred reactor consists of a heated sphere in which the stirring is achieved by four turbulent jets located at its centre. The sphere is attached to a quartz annular preheating zone in which the temperature of the gases is brought to the desired reactor temperature. The gas mixture residence time inside the annular preheater is very short compared to the residence time (strictly speaking “space time”) inside the reactor (about a few percent). The dilution by inert gas is kept high enough to avoid large temperature gradients inside the reactor due to the reaction exothermicity. The range of residence times accessible with this type of reactor is from 0.1 up to 10 s. With gas flow regulated by mass flow controllers, the uncertainty on the residence time is about 1%. With on-line gas chromatography analysis, the uncertainty on the quantification of species is about ± 5% (14). An example of the good reproducibility of the obtained data can be shown in Figure 7 which display the evolution with temperature of the mole fraction of n-butane measured by Herbinet et al. (14) in two separate similar reactors, one located in Nancy (France) with analysis by gas chromatography after sampling in the outlet gas the second in Hefei (China) with analysis by reflectron time-of-flight mass spectrometry after molecular beam sampling.

Figure 7.

Predictions of the new model for reactants mole fractions for the oxidation of n-butane in a jet-stirred reactor (residence time of 6 s, atmospheric pressure, stoichiometric mixtures containing 4% (mol) n-butane diluted in helium, points are experiments from (14)).

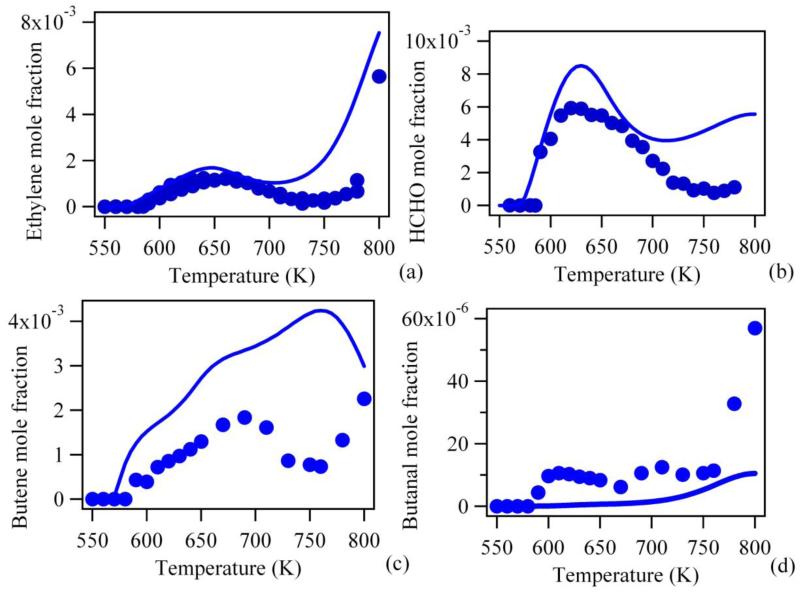
As the purpose of this study is to evaluate primary reactions, Figures 7 to 10 display comparisons between simulations performed using the new model and the experimental data of Herbinet et al. (14) for the reactants, the products which are good indicators of the global reactivity and the products mainly obtained through primary reactions.

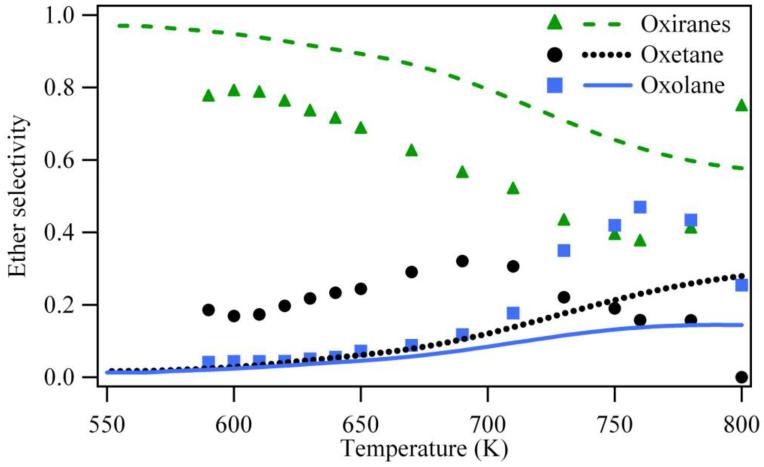
Figure 10.

Predictions of the new model for the selectivity of cyclic ethers for the oxidation of n-butane in a jet-stirred reactor (residence time of 6 s, atmospheric pressure, stoichiometric mixtures containing 4% (mol) n-butane diluted in helium, points are experiments from (14)).

Figure 7 presents the comparison for the evolution of the mole fractions of n-butane and oxygen with changes in temperature, and shows that the updates to the model lead to a significant improvement in the agreement with experimental results compared to the original mechanism (see Figure 2). The agreement is very good from 500 up to 720 K. At higher temperatures, some deviation is still observed. The acceptable modelling of the overall reactivity below 720 K is confirmed by the comparisons of the evolution of water (Figure 8a), carbon oxides (Figures 8b and 8c), ethylene (Figure 9a) and formaldehyde (Figure 9b). For these compounds, the new model performs even better than that of Herbinet et al. (14) which contained some arbitrary adjustments. In the case of butenes (Figure 9c) and butanal (Figure 9d), the predictions still require improvement. In the case of butenes which are mainly obtained from ROO· radicals by concerted elimination, this will require consideration of a more accurate mechanism for the reactions which consume this species. The formation of butanal with the new model is much lower than that predicted by Herbinet et al. (14). This is due to the large reduction of the rate constant for the isomerization of 1-hydroperoxy-4-butylradical into 1-hydroperoxy-1-butyl radical compared to the EXGAS value and to the fact that disproportionation reactions of two butylperoxy radicals to give oxygen, butanol, butanal or butanone have been not been considered here, while they were taken into account by Herbinet et al. (14). These reactions were not considered, because while Herbinet et al. (14) have analyzed ethanol, they were unable to detect butanol, whatever the efforts made for this purpose. More studies on barrierless disproportionation reactions are still required.

Figure 8.

Predictions of the new model for water and carbon oxides mole fractions for the oxidation of n-butane in a jet-stirred reactor (residence time of 6 s, atmospheric pressure, stoichiometric mixtures containing 4% (mol) n-butane diluted in helium, points are experiments from (14)).

Figure 9.

Predictions of the new model for ethylene, formaldehyde, butane and butanal mole fractions for the oxidation of n-butane in a jet-stirred reactor (residence time of 6 s, atmospheric pressure, stoichiometric mixtures containing 4% (mol) n-butane diluted in helium, points are experiments from (14)).

As shown in Figure 10, the most dramatic improvement has been obtained in the case of the formation of oxolanes and of oxiranes. The evolution of the mole fractions of these ethers with temperature is well predicted. On the other hand, the formation of oxetane is underestimated below 700 K. This could still be improved by an arbitrary fitting of the rate constant calculated for the formation of these cyclic ethers, but this was not the purpose of this study.

Validation using rapid compression machine tube data

A rapid compression machine is an instrument designed to simulate a single engine cycle of an internal combustion engine. The temperature after compression is derived from the initial pressure and temperature, the initial composition of the reactive mixture and the measured pressure after compression, assuming the adiabatic compression of a core gas. The temperature after compression can be varied by changing the composition of the inert gas (54). Heat losses and temperature gradients inside the combustion chamber of rapid compression machines are a source of uncertainties on estimated temperatures after compression and measured ignition delay times (58). For the largest ignition delay times for which the largest uncertainty in the experimental results is observed, heat losses have certainly some influence and the hypothesis of adiabaticity leads to some under-estimation of the delay times.

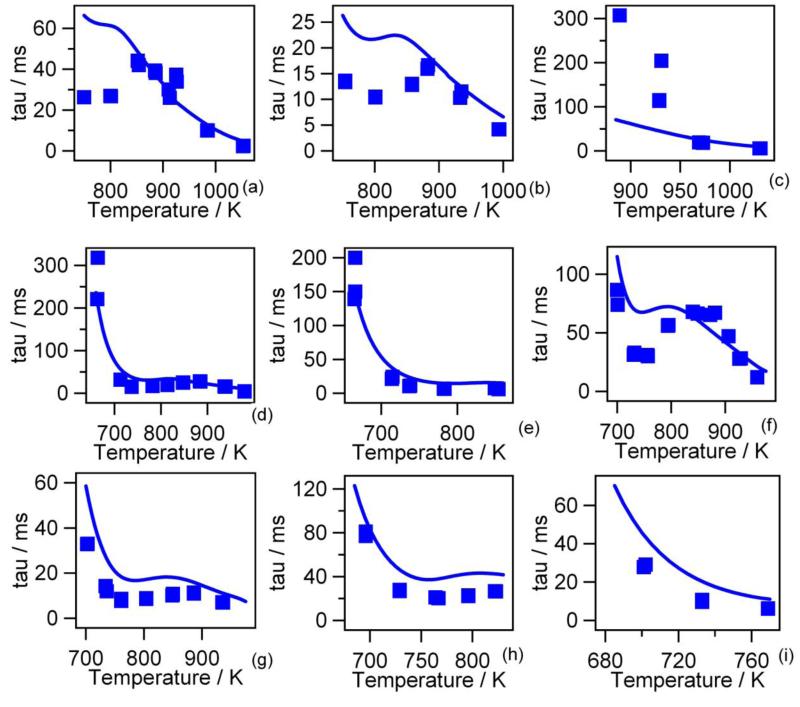
Figure 11 presents the comparison in the case of autoignition delay times recently obtained by Healy et al. (9) in a rapid compression machine for four stoichiometric ratios (0.3, 0.5, 1 and 2) and three pressures after compression (10, 20 and 30 atm). For stoichiometric and rich mixtures, the agreement is satisfactory for every studied pressure. At ɸ = 0.5, the agreement is also acceptable at 20 and 30 atm, but deteriorates at 10 atm, below 950 K where the ignition delays become very long. At ɸ = 0.3, the delays are significantly overestimated for temperatures below 850 K.

Figure 11.

Predictions of the new model ignition delay times in a rapid compression machine vs. temperature after compression (points are experiments from experiments from of Healy et al. (9) (φ=0.3: (a) P=20 atm, (b) P=30 atm); φ=0.5: (c) P=10 atm, (d) P=20 atm, (e) P=30 atm; φ=1.0: (f) P=10 atm, (g) P =20 atm; φ=2.0: (h) P=10 atm, (i) P=20 atm).

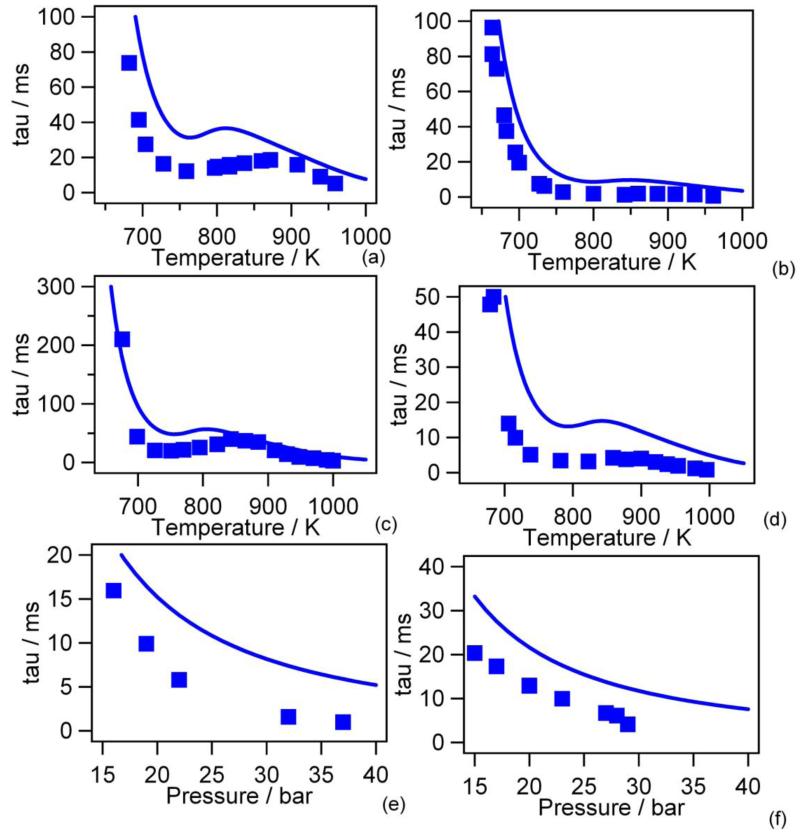
Figure 12 presents the comparison in the case of autoignition delay times recently obtained by Gersen et al. (59) in a rapid compression machine for stoichiometric mixtures for pressures after compression varying from 14 to 36 bar and at equivalence ratios ɸ = 1.0 and ɸ = 0.5. Here also the agreement is quite satisfactory.

Figure 12.

Predictions of the new model for ignition delay times vs. temperature after compression in a rapid compression machine (points are experiments from experiments from of Gersen et al. (58) (φ=1.0: (a) P=15 bar, (b) P=30 bar; φ=0.5: (c) P=15 bar, (d) P=30 bar; T=900K: (e) φ=1.0, (f) φ=0.5).

DISCUSSION

As shown in Table 1 and 2, there are significant uncertainties in thermochemical data, even in the case of alkyl radicals. These uncertainties can have a serious impact on the modelling since they influence the reaction equilibrium constants, through the free energy. For instance, the thermochemical data of alkyl and alkylperoxy radicals trigger the equilibrium of the reaction of addition to oxygen and a small variation in these data can have important consequence on the reactivity. To illustrate this, Figure 13 presents the result of a simulation under jet-stirred reactor conditions with changes of ± 2 cal.mol⁻¹.K⁻¹ on the entropies of C₃-C₄ alkyl radicals. It shows a dramatic influence of this small increase of entropy on the reactivity: the reaction is almost fully stopped from 650 to 725 K when the entropy is increased by 2 cal.mol⁻¹.K⁻¹.

Figure 13.

Predicted conversion of n-butane with changes on the entropies of the C₃- and C₄-alkyl radical under the conditions of figure 7 (points are experiments; lines simulations: full line unchanged mechanism, dotted line −2 cal.mol⁻¹.K⁻¹, broken line +2 cal.mol⁻¹.K⁻¹).

Clearly, discrepancies between the updated model predictions and experimental data still exist for certain temperatures and it is therefore worthwhile exploring the impact of remaining uncertainties in the input rate data on the model predictions of major species. Here sensitivity analysis was applied at several temperatures in order to indentify the key reactions which determine the predicted butane mole fraction within the jet-stirred reactor. Butane mole fraction was chosen as being representative of the overall reactivity of the scheme. The analysis may therefore suggest areas for further modelling and improved parameter estimation (60)(61) in order to try to improve the agreement between the model and the experiment in the NTC region.

Linear Screening Method

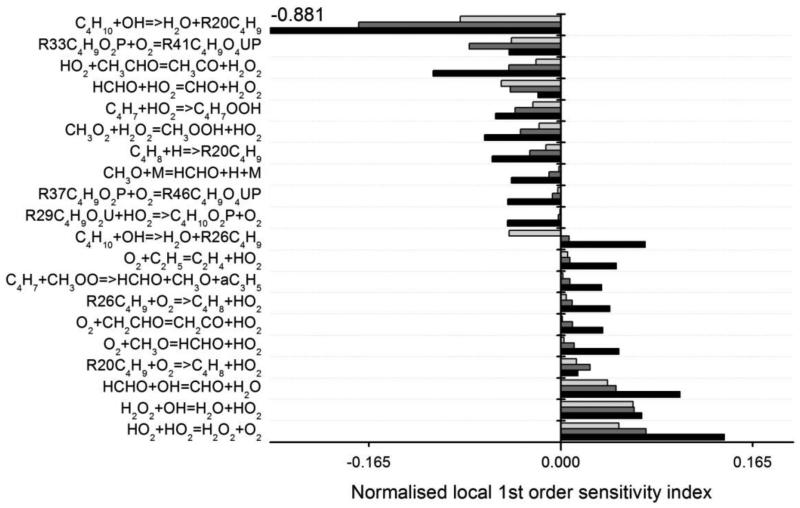
A screening method based on linear sensitivity analysis was first applied to all reactions in order to identify the key reactions to study in greater detail using a subsequent global sensitivity method. In the linear analysis the A-factor for each reaction was reduced by 25% and the change in predicted butane mole fraction was calculated at temperatures of 675, 750 and 775 K and atmospheric pressure. The most important reactions and their normalised sensitivity coefficients are shown in Figure 14. A negative sensitivity indicates that a reduction in reaction rate would reduce predicted butane mole fractions and vice versa. In this case the level of uncertainty of the input A-factors has not been accounted for and hence the most sensitive reaction at all temperatures is C₄H₁₀ + ·OH → H₂O + R20C₄H₉ (R20C₄H₉ being the 1-butyl radical). In the current analysis, this reaction is particulary dominant at lower temperatures. The reaction of butane + ·OH and its different product channels has been subject to detailed experimental and theoretical studies by Sivaramakrishnan et al. (62) across a broad temperature regime. Sivaramakrishnan et al. (62) suggest an uncertainty of 25% from their study which suggests that whilst this reaction has a high sensitivity coefficient, the level of uncertainty in its input value may be smaller than for many of the other reactions. Note also that the reaction C₄H₁₀ + ·OH → H₂O + R26C₄H₉ (R26C₄H₉ being the 2-butyl radical) has a significant impact especially at 675 K. Both channels of the reaction of butane + ·OH compete together with that leading to the 1-butyl radical having a large promoting effect on the reactivity because it is the only one for which the fast isomerization involving the transfer of a secondary H-atom with a cyclic transition state including 6 atoms is possible. In the case of 2-butyl radicals, only slower isomerizations involving either the transfer of a primary H-atom with a cyclic transition state including 6 atoms or the transfer of a secondary H-atom with a cyclic transition state including 5 atoms can occur.

Figure 14.

Normalised linear sensitivity coefficients for the most important reactions at 675 K (black), 750 K (dark grey) and 775 K (light grey) under the conditions of Figure 7. (The C₄ radicals are named in the same way as in the mechanism (see supplementary material): R20C₄H₉ is .ch2/ch2/ch2/ch3; R26C₄H₉ is .ch(/ch3)/ch2/ch3; R29C₄H₉O₂U is .o/o/ch(/ch3)/ch2/ch3; R33C₄H₉O₂P is .ch(/ch3)/ch2/ch2/o/oh; R37C₄H₉O₂P is .ch2/ch2/ch(/o/oh)/ch3; R41C₄H₉O₄UP is .o/o/ch(/ch3)/ch2/ch2/o/oh; R46C₄H₉O₄UP is .o/o/ch2/ch2/ch(/o/oh)/ch3).

At intermediate temperatures of 750 and 775 K there are several other reactions with high local sensitivities. The second oxygen addition to butylperoxy radicals shows a significant sensitivity, particularly at 750 K where the model shows poorer agreement with the experimental data. It is also interesting to note the significance of several reactions from the C₀-C₂ reactions base: ·HO₂ + ·HO₂ = H₂O₂ + O₂ and H₂O₂ + ·OH = H₂O + ·HO₂ in particular, as well as the reaction of HO₂ with formaldehyde and acetaldehyde and that of formaldehyde with ·OH.

Global Sensitivity Study

Whilst a simple linear method such as that described above can be used to screen out unimportant reactions, several potential issues arise with its use for the estimation of accurate sensitivity indices. Firstly, the response of the predicted outputs to changes in inputs may not be linear across the range of input uncertainty, and therefore focusing calculations around the nominal parameter values may give misleading results (Ziehn et al. (63)). There may also be interactions between parameters which cannot be addressed by a simple local linear approach. In addition, in order to assess the influence of each parameter on output predictability we must also take into account the input uncertainty assigned to each A-factor. It is acknowledged that for a complete uncertainty analysis, input uncertainties in the temperature dependence of the rates should be accounted for (64). However, the aim here is to identify key reactions for further kinetic study rather than to complete a rigorous uncertainty study and the temperature range under investigation is fairly narrow. Therefore the response to changes in the A-factor for each reaction is used as a way of indicating those reactions requiring better categorisation.

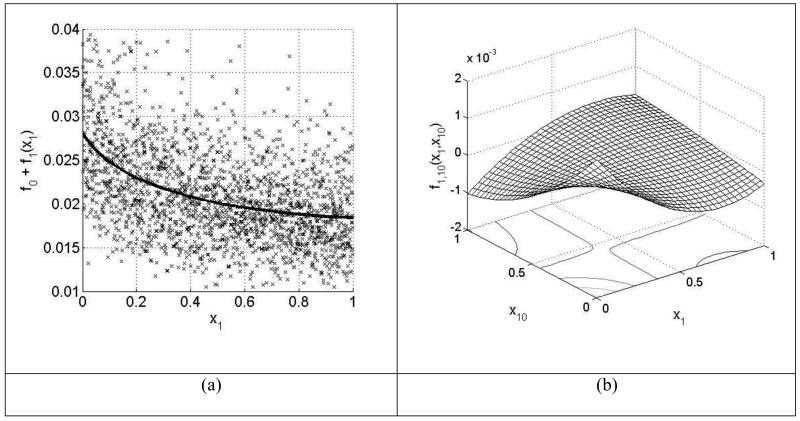
The global sensitivity method used here is based on High Dimensional Model Representations (HDMR) and has been described in detail elsewhere ((65)(66)). Essentially input uncertainty factors are first assigned to each A-factor. Then a quasi random sample is drawn from the input distribution and the butane mole fraction is predicted for each member of the quasi-random sample using the PSR code. In this case a uniform distribution is assumed between the minimum and maximum assigned values for each A-factor. The mapping between the input variables x₁,…,x_n and the output variable f(x) = f(x₁,…,x_n) in the domain Rⁿ is then fitted as a multi-variate hierarchical functional expansion of the following form:

$$f\left(\mathbf{x}\right)=f_0+\sum _{i=1}^n{f}_i\left(x_i\right)+\sum _{1\le i<j\le n}{f}_{ij}(x_i,x_j)+\dots +f_{12\dots n}(x_1,x_2,\dots ,x_n)$$

using orthonormal polynomial functions of up to 10^th order. Here f₀ denotes the mean effect (zeroth-order), which is a constant. The component function f_i(x_i) is a first-order term giving the effect of variable x_i acting independently (although generally nonlinearly) upon the output f(x). The function f_ij(x_i,x_j) is a second-order term describing the cooperative effects of the variables x_i and x_j upon the output f(x). The higher order terms reflect the cooperative effects of increasing numbers of input variables acting together to influence the output f(x). This study has been restricted to up to second order interactions. Sensitivity coefficients are then calculated from the polynomial coefficients using the method described in Li et al. (65) using the GUI-HDMR software (66). The component functions can be used to investigate the response of the predicted output to changes in input across the whole of the input range.

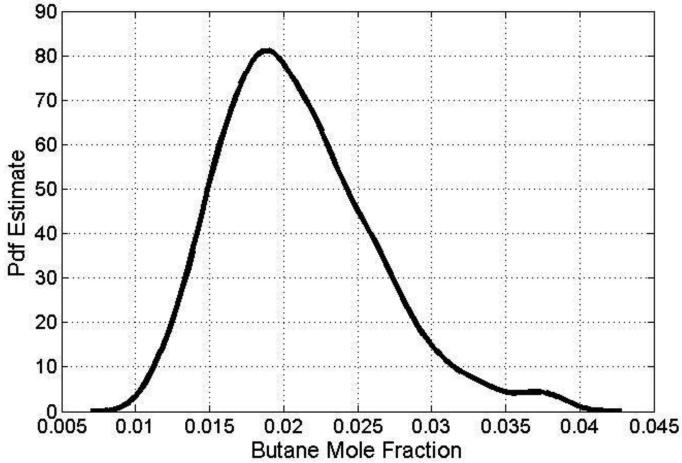
The analysis has been restricted to the most important reactions based on the linear screening method at 750 K and 31 reactions were included. Input uncertainty factors were assigned from appropriate evaluation studies where available (Baulch et al., (16)) and this was mostly the case for the C₀-C₂ reactions base. For the calculated parameters within the primary and secondary mechanisms, a factor of 3 was used except for butane + ·OH where a much smaller factor of 0.3 was used based on the detailed experimental and modelling studies of Sivaramakrishnan et al. (62). Figure 15 presents the output probability density function for the predicted butane mole fraction based on a quasi-random sample size of 4096. The calculation has been performed at 750 K, the temperature for which the largest deviation between experiments and simulations exists with the new model as shown in Figure 7. It shows that within the chosen uncertainty ranges for the A-factors, a wide range of possible predicted butane concentrations are possible ranging all the way from almost no consumption (0.4) to 75% consumption (0.1). The most frequently predicted value is significantly lower than the experimental measurements at 750 K. It can also be noted that there is a tail to the distribution at the higher mole fractions which is usually an indication of higher order effects i.e. parameter interactions (67).

Figure 15.

Probability density function (pdf) of predicted butane mole fractions from the global sensitivity analysis at 750 K.

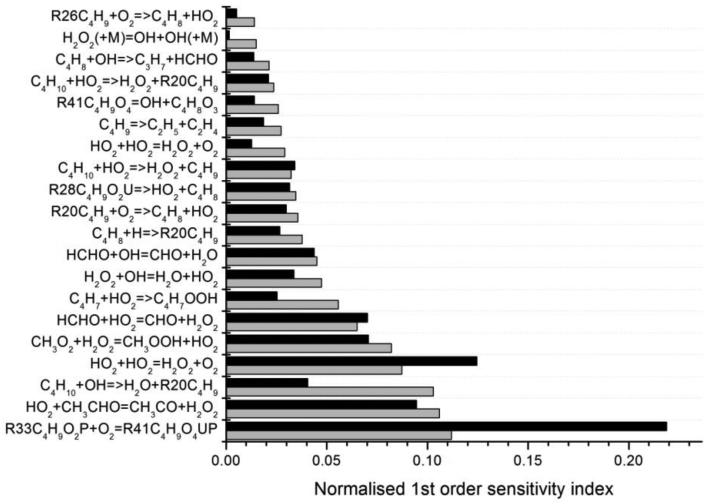
Figure 16 shows the comparison between the normalised global first order sensitivity indices and those based on a local linear analysis. In this case the local sensitivities have been scaled according to the relevant input uncertainties and normalised and therefore the ranking based on the linear method may be substantially different to the coefficients shown in Figure 14 since some reactions are much better categorised than others. Although Figure 16 shows that there is a broad agreement between the two methods in terms of the parameter importance ranking there are also some notable differences. The addition of hydroperoxyalkyl radicals to oxygen R33C₄H₉O₂P + O₂ = R41C₄H₉O₄UP has a higher global sensitivity index than local, which indicates that the response of the predicted butane mole fraction to changes in the A-factor for this reaction is non-linear. This is confirmed by Figure 17a which shows a scatter plot of the response to changes in this parameter within the full quasi-random sample, as well as its first order component function which indicates its independent first order effect. Its sensitivity clearly increases as the A-factor becomes lower i.e. the adopted rate is slower. It also shows a second order interaction with the A-factor for the reaction C₄H₁₀ + ·HO₂ = > H₂O₂ + R20C₄H₉ which is illustrated in Figure 17b. The figure shows that when the A-factors for both reactions are at the lower end of their adopted ranges, the predicted butane mole fraction increases further. In the global analysis the reaction R33C₄H₉O₂P + O₂ = R41C₄H₉O₄UP now dominates the sensitivity ranking, although it is clear that the performance of the butane mechanism depends also on the accuracy of several reactions in the C₀-C₂ reactions base and that further studies of these reactions within the NTC region could help to improve the predictability of the mechanism.

Figure 16.

Normalised estimates of first order contributions to the overall variance of predicted butane mole fraction at 750 K calculated using first order local sensitivities (grey) and the global HDMR method (black) under the conditions of Figure 7 (The C₄ radicals are named in the same way as in the mechanism (see supplementary material): R20C₄H₉ is .ch2/ch2/ch2/ch3; R26C₄H₉ is .ch(/ch3)/ch2/ch3; R28C₄H₉O₂U is .o/o/ch2/ch2/ch2/ch3; R33C₄H₉O₂P is .ch(/ch3)/ch2/ch2/o/oh; R41C₄H₉O₄UP is .o/o/ch(/ch3)/ch2/ch2/o/oh).

Figure 17.

a) Scatter plot of changes in output function (predicted butane mole fraction) in response to changes in the A-factor across the adopted input range for reaction R33C₄H₉O₂P+O₂=R41C₄H₉O₄UP. The solid line is the first order component function from the HDMR analysis which has been scaled by the constant value f₀ in order to compare with the scatter plot, and indicates the first order response to changes in the parameter, b) Second order component function showing the interaction between the A-factors for reactions R33C₄H₉O₂P+O₂=R41C₄H₉O₄UP and C₄H₁₀+HO₂=>H₂O₂+R20C₄H₉.

Many of the other influential reactions involve H₂O₂ molecules: CH₃CHO + ·HO₂ = ·CH₃CO + H₂O₂, ·HO₂ + ·HO₂ = H₂O₂ + O₂, CH₃OO· + H₂O₂ = CH₃OOH + ·HO₂, HCHO + ·HO₂ = ·CHO + H₂O₂, H₂O₂ + ·OH = H₂O + ·HO₂. Griffiths et al. (68) also noted the importance of H₂O₂ formation via the reaction of formaldehyde with HO₂ and HO₂ + HO₂ in multiple stage ignition modelling of propane oxidation within the NTC regime (although at a lower pressure). The reaction of formaldehyde with HO₂ does not seem to have been the subject of a great number of recent studies, although Li et al. (69) performed calculations at the B3LYP/cc-pVPZ level of theory for this reaction showing reasonable agreement with the Baulch evaluation (16). The recommendation of Baulch et al. (16) for the rate of formation of H₂O₂ from the reaction of acetaldehyde with HO₂ is for temperatures of 900 K and above. Further studies of this reaction in the NTC region could therefore be useful. There is some discrepancy between the Baulch evaluation (16) and more recent studies of the temperature dependency of the rate of the reaction H₂O₂ + ·OH = H₂O + ·HO₂. Subsequent work from Hippler et al. (70) suggested that the rate could be faster than that suggested by the Baulch evaluation by up to a factor of 2 at high temperatures. Their rate however is significantly higher than that suggested by the recent mechanism of Hong et al. (71), although this mechanism has been predominantly evaluated at temperatures above the NTC region.

The reaction of formaldehyde with ·OH radicals, HCHO + ·OH = ·CHO + H₂O, has also a significant impact. We use in this work the Arrhenius expression suggested by Vasudevan et al. (26) across a broad temperature range. These authors studied this reaction behind reflected shock waves in the high temperature region (934-1670 K) but also incorporated earlier low temperature measurements (202-399 K) of Sivakumaran et al. (72) and calculations at the CCSD(T) level of theory. Whilst they estimate the uncertainty in the suggested rate to be 25% at higher temperatures, there seem to be fewer studies in the NTC region, suggesting the uncertainty there may be higher. Further studies in this temperature region could also be very useful.

CONCLUSION

Theoretical calculations at the CBS-QB3 level of theory have been used to revisit the primary reactions involved in the oxidation of n-butane from low to intermediate temperature including the NTC zone and to propose a new model leading to improved simulations of the global reactivity and of the formation of intermediates products, such as cyclic ethers. If many studies have been devoted to theoretical calculations related to reactions included in mechanisms of alkanes oxidation, the present study is amongst the very rare ones presenting a validation of these calculated rate constants through a full simulation of observable experimental data (mole fraction profiles and ignition delay times).

In the case of isomerizations of peroxy radicals and the formation of cyclic ethers, a comparison between the rate constants obtained by theoretical calculations at the same level of theory (CBS-QB3) but from various authors has indicated surprisingly large differences (up to factor 30 in the worst case) which could be partly due to differences in the treatment of tunnelling effect, internal rotors, and of spin contamination, or in the description of reactant conformers.

While the predictions given by the models are overall satisfactory, there is still a significant overestimation of the reactivity observed in an atmospheric jet-stirred reactor around 750 K. A linear and global sensitivity analysis has indicated that at this temperature there is a large impact of the addition of oxygen molecules to hydroperoxyalkyl radicals, as well as of reactions of the C₀-C₂ reaction base, especially those involving H₂O₂. More studies on these reactions over the NTC temperature range would then be needed to improve the model predictions.