Physical Basis of Metal-Binding Specificity in Escherichia coli NikR

Abstract

In Escherichia coli and other bacteria, nickel uptake is regulated by the transcription factor NikR. Nickel binding at high-affinity sites in E. coli NikR (EcNikR) facilitates EcNikR binding to the nik operon, where it then suppresses transcription of genes encoding the nickel uptake transporter, NikABCDE. A structure of the EcNikR-DNA complex suggests that a second metal-binding site is also present when NikR binds to the nik operon. Moreover, this co-crystal structure raises the question of what metal occupies the second site under physiological conditions: K⁺, which is present in the crystal structure, or Ni²⁺, which has been proposed to bind to low- as well as high-affinity sites on EcNikR. To determine which ion is preferred at the second metal-binding site and the physical basis for any preference of one ion over another in both the second metal-binding site and the high-affinity sites, we conducted a series of detailed molecular simulations on the EcNikR structure. Simulations that place Ni²⁺ at high-affinity sites lead to stable trajectories with realistic ion–ligand distances and geometries, while simulations that place K⁺ at these sites lead to conformational changes in the protein that are likely unfavorable for ion binding. By contrast, simulations on the second metal site in the EcNikR-DNA complex lead to stable trajectories with realistic geometries regardless of whether K⁺ or Ni²⁺ occupies this site. Electrostatic binding free energy calculations, however, suggest that EcNikR binding to DNA is more favorable when the second metal-binding site contains K⁺. An analysis of the energetic contributions to the electrostatic binding free energy suggests that, while the interaction between EcNikR and DNA is more favorable when the second site contains Ni²⁺, the large desolvation penalty associated with moving Ni²⁺ from solution to the relatively buried second site offsets this favorable interaction term. Additional free energy simulations that account for both electrostatic and non-electrostatic effects argue that EcNikR binding to DNA is most favorable when the second site contains a monovalent ion the size of K⁺. Taken together, these data suggest that the EcNikR structure is most stable when Ni²⁺ occupies high-affinity sites and that EcNikR binding to DNA is more favorable when the second site contains K⁺.

Introduction

Monitoring the concentration of metal ions within the cell is of crucial importance, as a relatively small concentration of some metal ions is necessary for a number of cellular processes to occur, but often too much of that same ion may cause cell damage and death.^1–4 Nickel is an essential cofactor for a number of bacterial enzymes that are involved in cell survival, including hydrogenase and urease, two enzymes vital to the survival of the pathogenic bacteria Helicobacter pylori.¹ The concentration of nickel in many bacteria is regulated by the nickel-binding transcription factor, NikR, which transcriptionally represses genes encoding nickel-specific importers.⁵

The best-characterized NikR homologues are from Escherichia coli (EcNikR), H. pylori (HpNikR), and Pyrococcus horikoshi (PhNikR).^6–9 Each is a homotetramer composed of two domains: the central tetrameric metal-binding domain (MBD) and two flanking dimeric ribbon–helix–helix (RHH) domains (Figure 1a). The MBD is composed of C-terminal residues 48–133 (E. coli numbering), and each monomer contains a single high-affinity square-planar nickel-binding site composed of H87, H89, and C95 from one monomer and H76 from a neighboring monomer (Figure 1a). The RHH DNA-binding portion of the protein is composed of residues 1–47 and is arranged in a common DNA-binding motif such that the N-terminal ribbons from two monomers create a two-stranded β sheet that inserts into the major groove of DNA. The RHH domains are separated from the MBD by flexible linkers, and crystal structures have captured the RHH in a number of different arrangements with respect to the MBD, suggesting that the RHH domains are free to move with respect to the MBD.^8,9 However, the relevant DNA-binding conformation for the RHH domains appears to be a “down-cis” arrangement, as seen in the EcNikR-DNA crystal structure (Figure 1b).⁹ In addition, two identical second metal-binding sites are formed when NikR assumes a “down-cis” arrangement and are located at the interface of the RHH and MBD domains (Figure 1b). These second metal-binding sites are composed of two conserved amino acid residues from the RHH domain, E30 and D34, and a number of backbone carbonyls from residues in the MBD (Figure 1b).⁹

Figure 1.

Crystal structures of EcNikR and the metal-binding sites. Each of the four monomers is colored individually, and nickel ions are represented with green spheres and potassium ions with purple spheres. (a) Ni²⁺-bound EcNikR (PDB 2HZA) and the square-planar high-affinity nickel-binding site. (b) EcNikR-DNA complex (PDB 2HZV) and the second metal-binding site with potassium bound in an octahedral geometry.

Biochemical data and crystal structures of various NikR proteins have informed as well as raised interesting questions regarding these metal-binding sites. The high-affinity metal-binding sites have been well characterized as nickel-binding sites, which upon nickel binding induce a conformational change allowing NikR to bind DNA.^10,11 Interestingly, nickel binding does not appear to affect the conformation of the RHH DNA-binding domains that make specific contacts to DNA, instead altering the structure of the MBD that makes nonspecific DNA contacts (Figure 1).⁹ In particular, Ni²⁺ binding orders the α-helix 3 through its coordination of helical residue H76; conversely, H76 and α-helix 3 are disordered in the apo EcNikR structure.⁸

Crystallographic and mutagenesis data suggest that, like NikR’s high-affinity site, the second metal-binding sites are also important in modulating the affinity of NikR for DNA.⁹ The location of these sites at the interface of the MBD and RHH domains suggests that a metal in this site would stabilize the “down-cis” or the DNA-binding mode of EcNikR. Although there has been general agreement that these sites are functionally important, opinions have varied about which metal is likely to occupy them in vivo, with the contenders being Ni²⁺ and K⁺.^6,9 The suggestion that Ni²⁺ occupies these second sites comes from biochemical as well as crystallographic data. In particular, metal-binding studies have shown that the affinity of EcNikR for DNA increases from nanomolar, when stoichiometric Ni²⁺ ions are bound to the high-affinity nickel-binding sites, to picomolar, when excess nickel is present.^11,12 This increased DNA-binding affinity with excess nickel suggests the presence of one or multiple low-affinity Ni²⁺-binding sites on EcNikR. The idea that one of these low-affinity sites could be the second metal site is supported by crystallographic data on PhNikR.^6,13 Here, however, the high concentration of Ni²⁺ used (20 mM) and the need for phosphate in the crystallization conditions raises questions about the physiological relevance of these structural data. In addition, crystallographic data on EcNikR do not support the idea that Ni²⁺ binds in the second metal sites, instead showing multiple low-affinity sites on the surface of the EcNikR protein.⁹

The suggestion that K⁺ might be the relevant metal in the second metal-binding sites also comes from both biochemical and structural data. Sheila Wang and Deborah Zamble have recently shown that K⁺ is required for EcNikR-DNA binding under both stoichiometric and excess nickel conditions (personal communication). The localization of this K⁺ effect to the second metal-binding sites is derived from the structure of the EcNikR-DNA complex, in which a K⁺ ion from the crystallization buffer is modeled in this site.⁹ Although the binding of ions from the crystallization buffer is often an artifact, in this case the concentration of K⁺ in the crystallization buffer (200 mM) is slightly lower than that in E. coli (250 mM), indicating that the presence of K⁺ in the second metal-binding sites of this structure could be physiologically relevant.^9,14 If these second metal-binding sites are K⁺ sites, then they would not be regulatory sites but rather structural sites in which the binding of abundant cellular monovalent ions affords additional stability to the DNA-bound conformation of EcNikR.

To decipher the physical basis underlying any difference in metal-binding specificity at both the high-affinity and second metal-binding sites, we conducted a series of detailed molecular simulations on the EcNikR structure. We begin with an analysis of the EcNikR structure when either K⁺ or Ni²⁺ occupies the high-affinity or the second metal-binding sites. We then explore the effect of the identity of the ion in the second metal-binding site on EcNikR-DNA binding using a combined molecular mechanics Poisson–Boltzmann (MMPB) approach.¹⁵ Finally, we use detailed free energy simulations to explore the effect ion size in the second metal-binding site has on EcNikR-DNA association. In total, these data clarify the physical basis for metal ion specificity in both the high-affinity and second metal-binding sites in EcNikR.

Results

Conformation of High–Affinity Sites in the Presence of Ni²⁺ or K⁺

The high-affinity metal-binding sites on EcNikR have been well-characterized as square-planar Ni²⁺-binding sites (Figure 1a).^8,16,17 While this site is preferentially a Ni²⁺-binding site, in vitro metal-binding studies have shown that the coordinating species are flexible and can rearrange under different conditions.^8,17,18 In light of this, we explored whether high-affinity sites in EcNikR could rearrange to accommodate K⁺, which is present at much higher concentrations in the intracellular space than Ni²⁺. Starting our studies with the high-affinity sites allows us to explore the preference for Ni²⁺ versus K⁺ under conditions where the identity of the physiologically relevant metal is unquestioned.

Extensive energy minimizations of the Ni²⁺-containing high-affinity sites do not alter the geometry or the ion–ligand distances relative to those in the crystal structure (Figure 2a). To determine potential binding modes for K⁺ in the high-affinity sites, we replaced Ni²⁺ with K⁺ and energy-minimized the system. The objective of these calculations was to determine if there are flexible moieties in the vicinity of the high-affinity site that could participate in metal coordination, thereby yielding a geometry that was favorable for K⁺. However, the energy-minimized structure does not significantly deviate from a square-planar geometry (Figure 2b). While this geometry is expected for Ni²⁺, it is unprecedented for K⁺. A recent review of metal–ligand geometries of 4277 small-molecule crystal structures and 113 proteins structures suggests that the minimum coordination number for K⁺ is 5, with 6 being the most common number of coordinating ligands.¹⁹ In addition, the resulting coordinating species in this site consist of nitrogen and sulfur atoms, known Ni²⁺ ligands, but less common K⁺ ligands.^19,20 A search of the Cambridge Crystallographic Structural Database indicates that the average K⁺–N distances is 2.9 Å (from 3517 structures) and the average K⁺–S distance is 3.3 Å (from 297 structures), longer than those we see in our energy-minimized structure with K⁺ at the high-affinity sites (Figure 2b).

Figure 2.

Representative structures of the high-affinity metal-binding sites after energy minimization and MD simulation studies. High-affinity site with either (a) Ni²⁺ or (b) K⁺ after energy minimization. Metal–ligand distances are shown in Å. (c) Average structure from MD simulation of high-affinity site containing K⁺. Coloring is the same as in Figure 1. Water molecules are represented as red spheres.

Since typical energy minimization routines find local energy minima in the vicinity of the starting structure, we performed molecular dynamics (MD) simulations of EcNikR with K⁺ in the high-affinity sites to sample low-energy states over a larger region of conformational space. The goal was to determine whether the protein can adopt conformations that are consistent with our current understanding of favorable K⁺-binding geometries. Simulations of EcNikR with K⁺ in the high-affinity sites were performed for 3.1 ns in explicit solvent. The average structure arising from these simulations has K⁺ coordinated by six ligands arranged in an octahedral geometry (Figure 2c), consistent with prior analyses of K⁺-binding sites.¹⁹ In the average structure, three of the original high-affinity site ligands maintain their interactions with the ion with reasonable K⁺–ligand distances, while the H76 side chain is displaced by 3.7 Å and the backbone carbonyl of V88, along with two water molecules, aids in coordinating the K⁺ ion (Figure 2c). In short, in order for K⁺ to adopt its expected octahedral geometry, the protein “opens” to allow water molecules to enter the high-affinity site during the simulation. For comparison, we also conducted simulations in explicit solvent of EcNikR with Ni²⁺ in the high-affinity sites. After more than 3 ns, however, no water penetrates the high-affinity site when it is occupied by Ni²⁺, and the Ni²⁺ maintains its interactions with all four coordinating species as shown in Figure 2a.

These data suggest that the high-affinity sites in the protein cannot rearrange to form ion coordination numbers that are consistent with favorable K⁺-binding geometries. An octahedral geometry is obtained only when additional solvent molecules enter the site to participate in ligand coordination. Moreover, in all NikR structures where the high-affinity Ni²⁺ ion is appropriately coordinated by four ligands, this site is buried and not solvent exposed.^6,8,9 In total, these observations suggest that K⁺-containing high-affinity sites are associated with large conformational changes that cause the protein to significantly deviate from the prototypical NikR structure.

Conformation of the Second Metal–Binding Site in the Presence of Ni²⁺ or K⁺

In the crystal structure of EcNikR bound to DNA, ligands that coordinate the ion in the second metal-binding site are arranged in an octahedral geometry (Figure 1b), and energy minimization of this site does not significantly alter this geometry (Figure 3a). To explore whether the second metal-binding site can rearrange to adopt conformations that are favorable for Ni²⁺, we replaced K⁺ with Ni²⁺ in the crystal structure of EcNikR bound to DNA. Subsequent energy minimization resulted in a distorted square-pyramidal geometry, with a coordination number of 5, and shorter metal–ligand distances (Figure 3b). The shorter metal–ligand distances in the complex with Ni²⁺ bound at the second metal-binding site are consistent with Ni²⁺ having a smaller van der Waals radius than K⁺; studies of protein structures in the Protein Data Bank suggest that the typical Ni²⁺–O distance is 2.2 Å, while the average K⁺–O distance is 2.8 Å.^19,20 In our energy-minimized structures, we also find that the average Ni²⁺–O and K⁺–O distances are 2.2 and 2.8 Å, respectively (Figure 3). An analysis of Ni²⁺ coordination geometries obtained from eight structures in the Protein Data Bank and over 1000 structures in the Cambridge Structural Database reveals that similar geometries have been observed in other crystal structures that contain bound Ni²⁺ ions.^20–22

Figure 3.

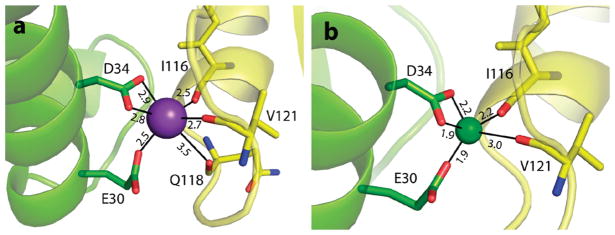
Representative structures of the second metal-binding site from minimization studies of the EcNikR-DNA complex with either (a) K⁺ or (b) Ni²⁺ bound in the second metal-binding site. Distances are in Å, and coloring is the same as in Figure 1.

Molecular dynamics simulations of EcNikR complexed to DNA with either K⁺ or Ni²⁺ in the second metal-binding site confirm that the octahedral geometry and the distorted square-pyramidal geometry for K⁺ and Ni²⁺, respectively, represent stable geometries for both ions. Over the course of a 2.1 ns simulation, both metals maintained the previously described binding geometries with reasonable metal–ligand distances. Hence, unlike the previous simulations that uncovered significant structural changes in high-affinity sites when the Ni²⁺ was replaced with K⁺, these data suggest that the second metal-binding site can accommodate either ion and substitution with Ni²⁺ does not lead to significant deviations in the EcNikR-DNA structure.

EcNikR–DNA Association with Either Ni2+ or K+ in the Second Metal–Binding Site

In light of these data, we explored the effect that K⁺ or Ni²⁺ binding at the second metal-binding site has on EcNikR-DNA association. We are interested in calculating the difference between the energy associated with EcNikR binding to DNA with K⁺ in the second site (ΔG_K) and DNA binding with Ni²⁺ in the second site (ΔG_Ni) (Figure 4). The difference between the two binding energies is equal to the free energy difference between two states; one state has K⁺ in the second site, and the other state has Ni²⁺ in the second site, and ΔΔG = ΔG_Ni − ΔG_K. The thermodynamic cycle used for the MMPB calculations is outlined in Figure 4. If ΔΔG is positive, EcNikR-DNA binding is preferred when K⁺ is in the second metal-binding site, and if ΔΔG is negative, EcNikR-DNA binding is preferred when Ni²⁺ is bound.

Figure 4.

Thermodynamic path comparing EcNikR-DNA binding with either K⁺ (ΔG_K) or Ni2+ (ΔG_Ni) at the second metal-binding site. Red rectangles represent the MBD, black triangles the RHH domains, and parallel green lines the DNA, and ions are explicitly shown in blue or orange. The ions not bound to the structure are infinitely distant from the protein.

We note that the individual binding free energies (ΔG_K and ΔG_Ni) can be decomposed into a sum of electrostatic and non-electrostatic contributions:^23,24

$$\mathrm{\Delta }{G}_{\text{K}}=\mathrm{\Delta }{G}_{\text{K}}^{\text{elec}}+\mathrm{\Delta }{G}_{\text{K}}^{\text{non}-\text{elec}}$$ (1)

$$\mathrm{\Delta }{G}_{\text{Ni}}=\mathrm{\Delta }{G}_{\text{Ni}}^{\text{elec}}+\mathrm{\Delta }{G}_{\text{Ni}}^{\text{non}-\text{elec}}$$ (2)

In each case, the non-electrostatic contributions can be expressed as a sum of a hydrophobic term plus additional terms that account for other contributions such as configuration entropy.^23–25 These non-electrostatic terms are typically estimated from an analysis of the unbound state and the bound complex; e.g., the hydrophobic term is calculated using the buried surface area of the complex.^23–25 We assume that the EcNikR-binding mode is the same regardless of whether Ni²⁺ or K⁺ is present in the second metal-binding site, i.e., that the structural changes at the second metal-binding site are small (Figure 3). Consequently, $\mathrm{\Delta }{G}_{\text{Ni}}^{\text{non}-\text{elec}}\approx \mathrm{\Delta }{G}_{\text{K}}^{\text{non}-\text{elec}}$, and hence $\mathrm{\Delta }\mathrm{\Delta }G\approx \mathrm{\Delta }{G}_{\text{Ni}}^{\text{elec}}-\mathrm{\Delta }{G}_{\text{K}}^{\text{elec}}$. We therefore use a combined MMPB approach to estimate the overall difference in binding free energy.¹⁵

We further express ΔΔG as a sum of physically meaningful terms, as outlined in Figure 5, in a manner similar to what has been done in previous studies.^23,24,26,27 First, the K⁺-bound EcNikR-DNA complex and two free Ni²⁺ ions are desolvated (1 → 2 in Figure 5). Next, in a vacuum, K⁺ ions are exchanged for Ni²⁺ ions at the second metal-binding sites in the EcNikR-DNA complex with the associated free energy difference of ΔG_e (2 → 3). However, the resulting structure has residues in the second metal-binding sites arranged in an orientation that is optimal for K⁺, not Ni²⁺. Therefore, we computed the electrostatic energy associated with residues at the second metal-binding sites rearranging to adopt a conformation that is favorable for Ni²⁺ binding (3 → 4). In the last step of the thermodynamic path, we calculated the energy associated with solvating the relaxed Ni²⁺-bound EcNikR-DNA complex and two free K⁺ ions (4 → 5). Each contribution is calculated from a set of 10 structures taken from a 1 ns MD simulation in explicit solvent. Values for the various contributions to ΔΔG are shown in Table 1 and represent the average value obtained from the 10 structures arising from the MD simulations.

Figure 5.

Thermodynamic cycle for calculating the electrostatic free energy difference associated with replacing potassium with nickel in the second metal-binding site. Numbers in circles delineate each structure in the pathway. Red rectangles represent the MBD, black triangles the RHH domains, and parallel green lines the DNA, and K⁺ ions are explicitly shown in purple. The Ni²⁺ ions are shown in either blue or orange, depending on the geometry of the groups that surround the ion. In structure 3, Ni²⁺ is placed in the secondary site; however, the coordinating species in the site are arranged in a manner that is consistent with a bound K⁺ ion (Ni²⁺ colored blue). In structure 4, the coordinating residues have been energy minimized, yielding a rearranged site that has Ni²⁺-preferred geometry and bond distances (Ni²⁺ colored orange).

Table 1.

Contributions to the Electrostatic Free Energy Difference for the Path Shown in Figure 5

contribution	value, kcal mol−1 site−1
$\mathrm{\Delta }{G}_{\text{d}}^{\text{C}-\text{K}}+\mathrm{\Delta }{G}_{\text{s}}^{\text{C}-\text{Ni}}$	932
$\mathrm{\Delta }{G}_{\text{d}}^{\text{Ni}}$	456
ΔGe	−501
ΔGr	−61
$\mathrm{\Delta }{G}_{\text{s}}^{\text{K}}$	−93
ΔΔG	733

The calculated value for ΔΔG is large, an average of 733 kcal mol⁻¹ site⁻¹, suggesting that EcNikR-DNA binding is preferred when K⁺ occupies the secondary site. To put this number into context, we note that the experimentally determined value for Ni²⁺ desolvation is also quite large, at 477 kcal/mol (and similar to the calculated value of 456 kcal/mol).²⁸ Interestingly, the value of the exchange term, ΔG_e, suggests that replacing K⁺ with Ni²⁺ is favorable; i.e., Ni²⁺ makes more favorable interactions with the protein and DNA relative to K⁺ (Table 1). However, this favorable contribution is largely offset by the unfavorable Ni²⁺ desolvation energy. The other major unfavorable contribution arises from the sum of the desolvation and solvation contributions for the protein DNA complex, $\mathrm{\Delta }{G}_{\text{d}}^{\text{C}-\text{K}}+\mathrm{\Delta }{G}_{\text{s}}^{\text{C}-\text{Ni}}=\mathrm{\Delta }{G}_{\text{s}}^{\text{C}-\text{Ni}}-\mathrm{\Delta }{G}_{\text{s}}^{\text{C}-\text{K}}=932\text{kcal}{\text{mol}}^{-1}{\text{site}}^{-1}$ (where $\mathrm{\Delta }{G}_{\text{s}}^{\text{C}-\text{K}}$ is the electrostatic energy associated with solvating the DNA-bound complex that has K⁺ in the second metal-binding site). The large positive value of this term suggests that solvating the DNA-bound complex is more favorable when K⁺ is in the second metal-binding site. Of note, the complex of EcNikR, DNA, and four high-affinity Ni²⁺ ions has a very large overall charge of −84. Addition of two K⁺ ions in the second metal-binding sites brings the total charge to −82, while the addition of two Ni²⁺ ions brings the total charge to −80. As the total charge of the system containing K⁺ is more negative, it is not surprising that it has a larger negative (i.e., more favorable) solvation energy relative to the complex with Ni²⁺ bound.

The Poisson–Boltzmann formalism allows us to calculate residue-specific contributions to the overall difference in free energy (ΔΔG). Figure 6 highlights the residues with the greatest contribution, positive (blue) or negative (red), to the overall difference in free energy. It is noteworthy that residues that are distant from the secondary site make significant contributions to the overall free energy change. That is, the relative preference for K⁺ in the secondary site cannot be explained using an analysis of the structure of the protein in the vicinity of the second metal-binding site alone.

Figure 6.

EcNikR-DNA structure, with residues with the most extreme contributions to ΔΔG colored in red and blue. Red residues contribute ≤−10 kcal/mol to ΔΔG and prefer Ni²⁺ ions in the second metal-binding sites (black spheres). Residues in blue contribute ≥10 kcal/mol to ΔΔG and prefer K⁺ ions in the second metal-binding sites. All backbone atoms are shown in ribbon form and are colored gray. Residues that contribute between −10 and 10 kcal/mol to the ΔΔG are not shown in stick form.

Effect of Ion Size on DNA Binding

The electrostatic calculations suggest that EcNikR-DNA association is more favorable when K⁺, and not the divalent ion Ni²⁺, occupies the second metal-binding site. This large difference is due, in part, to the fact that Ni²⁺ has a relatively large desolvation penalty. This raises the possibility that EcNikR DNA binding may be afforded by another monovalent cation in the second metal-binding site. In particular, we are interested in how the affinity of EcNikR for DNA changes when ions of different sizes occupy the second metal-binding site. For these studies we focus on Na⁺, which is considerably smaller than K⁺, and Cs⁺, which is larger than K⁺.

The thermodynamic cycle for these calculations is shown in Figure 7. We are interested in the difference between the binding free energies of two binding reactions. In the first reaction, EcNikR binds DNA with K⁺ in the second metal-binding site, and the associated free energy difference is ΔG_K. In the second reaction, EcNikR binds DNA with a monovalent ion denoted by X⁺, and again the associated free energy difference is given by ΔG_X. The relative binding free energy is $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{K}\to \text{X}}\equiv \mathrm{\Delta }{G}_{\text{X}}-\mathrm{\Delta }{G}_{\text{K}}=\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{P}}-\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{S}}$. The overall ΔΔG can therefore be calculated using the contributions along the alchemical paths, $\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{P}},\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{S}}$.

Figure 7.

Thermodynamic cycle for calculating the free energy difference associated with replacing a monovalent cation with the radius of potassium with a cation of larger or smaller radius. NikR representations are the same as in Figure 4, and “X⁺” represents an ion having different Lennard-Jones parameters than K⁺.

Ions can be characterized by a distinct van der Waals radius, σ, which determines the equilibrium interatomic distance, and the well-depth, ε. In Figure 7, X⁺ represents a monovalent ion having a van der Waals radius and well-depth different from those of K⁺. Therefore, we calculate $\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{P}}$ and $\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{S}}$ in a stepwise fashion, where first we calculate the effect of changing σ and then we compute the effect of changing the well-depth, ε. For example, we express the free energy differences along the alchemical paths associated with transforming K⁺ to Na⁺ as

$$\mathrm{\Delta }{G}_{\text{K}\to \text{Na}}^{\text{S}}=\mathrm{\Delta }{G}_{\text{K}({\sigma }_{\text{K}}+,{\epsilon }_{\text{K}}+)\to Y({\sigma }_{\text{Na}}+,{\epsilon }_{\text{K}}+)}^{\text{S}}+\mathrm{\Delta }{G}_{\text{Y}({\sigma }_{\text{Na}}+,{\epsilon }_{\text{K}}+)\to \text{Na}({\sigma }_{\text{Na}}+,{\epsilon }_{\text{Na}}+)}^{\text{S}}$$ (3)

$$\mathrm{\Delta }{G}_{\text{K}\to \text{Na}}^{\text{P}}=\mathrm{\Delta }{G}_{\text{K}({\sigma }_{\text{K}}+,{\epsilon }_{\text{K}}+)\to Y({\sigma }_{\text{Na}}+,{\epsilon }_{\text{K}}+)}^{\text{P}}+\mathrm{\Delta }{G}_{\text{Y}({\sigma }_{\text{Na}}+,{\epsilon }_{\text{K}}+)\to \text{Na}({\sigma }_{\text{Na}}+,{\epsilon }_{\text{Na}}+)}^{\text{P}}$$ (4)

While the individual contributions to the total free energy change are not state functions, the total free energy change is.²⁹ Therefore, the precise path chosen to calculate the overall free energy will not, in principle, affect the final result. Each term on the right-hand side of eqs 3 and 4 is computed using thermodynamic integration with a linear alchemical path. The overall free energy differences are listed in Table 2. For both Na⁺ and Cs⁺, the relative binding affinities are positive, suggesting that DNA binding is more favorable when the second site contains K⁺.

Table 2.

Free Energy Differences between EcNikR-DNA Complex with K⁺ and Other Monovalent Ions Bound in the Second Metal-Binding Site (Energies in kcal/mol)

	Na+	Cs+
ΔΔGvdW	4.02	0.41
ΔΔGε	1.05	0.45
ΔΔGtot	5.07	0.86

Discussion

The metal-binding sites of the transcriptional repressor EcNikR have been the subject of much attention.^{8–11,16–18,30} While the role of the high-affinity Ni²⁺-binding site as the main regulator of EcNikR’s affinity for DNA has not been in question, the function of the second metal site has been less clear. Possibilities include that this second site is an additional regulatory site to which excess Ni²⁺ ions can bind, yielding a tighter EcNikR-DNA complex. Alternatively, this second site could be non-regulatory, binding the abundant cellular K⁺ ion to further stabilize the EcNikR-DNA interaction. Here we consider whether both K⁺ and Ni²⁺ can stably bind this second site. Using unconstrained MD simulations of the EcNikR-DNA complex with either K⁺ or Ni²⁺ in the second metal site, we show that either of these metals is a reasonably good fit for the site. The overall backbone average root-mean-square deviations of the EcNikR-DNA complex with either metal bound at the second metal site are very similar, and in both cases, the second metal-binding site adopts realistic ion–ligand geometries. In light of these observations, we explored the effect of having either Ni²⁺ or K⁺ in the second metal-binding site on EcNikR-DNA association. Electrostatic free energy calculations suggest that, while the Coulombic interactions between Ni²⁺ and the EcNikR-DNA complex are more favorable relative to those with K⁺, this favorable contribution is counterbalanced by the unfavorable terms associated with the desolvation penalty of Ni²⁺ and the EcNikR-DNA complex. An analysis of the individual residue contributions to the overall binding free energies suggest that the preference for K⁺ at the second metal-binding site cannot be explained from an analysis of the local conformation of the protein in the vicinity of the second metal-binding site. Residues that are distant from the second metal-binding site have a significant effect on the identity of the ion in this site (Figure 6). These data raise the interesting possibility that mutations at sites that are distant from the second metal-binding site can affect the ion that is present in the bound complex.

As the high desolvation penalty of Ni²⁺ is partially responsible for the K⁺ being preferred in the second metal-binding site, EcNikR-DNA binding may be possible with any monovalent ion in the second metal-binding site, since these ions have much smaller desolvation penalties.^28,31 Additional free energy simulations that examine the effect of having other monovalent ions at the secondary site on EcNikR-DNA association suggest that the affinity of EcNikR for DNA is significantly reduced when the second metal-binding site contains Na⁺, a common monovalent cation in the cellular milieu (Table 2).

With the finding that desolvation is the main source of preference for K⁺ over Ni²⁺ in the second metal site, it is important to understand why the high-affinity site binds Ni²⁺ and not K⁺, especially given the high concentration of K⁺ compared to Ni²⁺ in E. coli. We found that the second metal site can rearrange to stably bind both metals, raising the question of whether the same is true for the high-affinity sites. Replacing Ni²⁺ with K⁺ at high-affinity sites, followed by energy minimization, however, does not lead to ion–ligand geometries that are consistent with what one would expect for K⁺. Energy-minimized high-affinity sites that contain K⁺ do not form an octahedral geometry, the preferred binding geometry for K⁺.¹⁹ Moreover, the coordination number for K⁺ at these sites is 4, whereas the minimum coordination number for K⁺ in both small-molecular and protein crystal structures is 5.¹⁹ Additional MD simulations of EcNikR with K⁺ at high-affinity sites suggest that realistic coordination geometries for K⁺ cannot be achieved with moieties that arise solely from the protein. That is, an octahedral geometry is achieved only when the protein undergoes significant conformational changes that cause the high-affinity sites to become solvent exposed. These data suggest that the EcNikR structure cannot accommodate K⁺ at the high-affinity sites.

Additional insights into the effect of K⁺ on the EcNikR structure are obtained from an analysis of its coordinating species in the MD simulations. After 3 ns of molecular dynamics, K⁺ achieves an octahedral geometry where two of the ligands are water molecules. The side chain of H76, which normally participates in ion coordination, shifts to a position where it can no longer coordinate the ion in the site (Figures 2c and S2 in the Supporting Information). This observation is of interest because structural studies have linked ion ligation at high-affinity sites by residue H76 with ordering of the α3 helix in the MBD, which contains residue H76.^9,18 The ordering of the α3 helix upon Ni²⁺ binding has been implicated in the mechanism of EcNikR-DNA binding, and solution studies suggest that metals that are capable of ordering the α3 helix are those that induce EcNikR-DNA binding.^{9,11,12,18,30} Metals that do use H76 as a ligand, such as Ni²⁺ and Cu²⁺, have well-ordered α3 helices.^8,18 However, when no metal or a metal like Zn²⁺ that does not induce strong DNA binding is bound at the high-affinity site, H76 is not utilized as a ligand, and the α3 helix is relatively disordered.¹⁸ Although the time scale of our simulations is not sufficiently long to reliably examine helix stability in the presence of K⁺, these data suggest that K⁺ does not induce the proper ligand ordering at the high-affinity site and may not support α3 helix stability or, in turn, proper DNA binding.

While classical dynamical simulations and continuum electrostatic calculations have a long history of providing useful insights into a number of biological problems, it is important to note that typically a number of approximations are made to yield results in a reasonable amount of CPU time.^33,34 In particular, our calculations account for only a relatively small region of DNA that is known to bind EcNikR and that was present in the EcNikR co-crystal structure.⁹ As DNA is highly charged and electrostatic interactions are long range in character, distant regions of DNA may influence the relative affinity of different ions for the second metal-binding site in vivo. Indeed, our results suggest that relatively distant residues on the EcNikR protein itself may influence the identity of the ion in the second metal-binding site.

Nevertheless, our data explain why Ni²⁺ is preferred over K⁺ at high-affinity sites and suggest that EcNikR binding to DNA is more favorable when K⁺ is present at the second metal-binding site. Recent studies have explored the effect of K⁺ on EcNikR-DNA binding using DNase footprinting and gel mobility shift assays. These results are consistent with our findings in that they demonstrate that K⁺ is required for EcNikR-DNA association in vitro (Sheila Wang and Deborah Zamble, personal communication).

In conclusion, EcNikR is exquisitely designed with a number of metal-binding sites of varying metal preferences. Other NikR homologues, such as HpNikR, have been shown to also require multiple metal-binding sites, and interestingly some of these sites are believed to be distinct from the sites in EcNikR.^35,36 Consequently, NikR proteins from different bacteria may have different metal-binding properties, and hence the NikR family represents a diverse and complex set of metal regulatory proteins. The central high-affinity Ni²⁺-binding sites, which are conserved among all NikR homologues, are sensory sites that specifically bind the scarce cellular Ni²⁺ ion, enabling binding to the nik promoter. The second metal-binding sites in EcNikR are located at the interface of the MBD and RHH domains and are composed solely of oxygen ligands from each domain. This conserved second metal-binding site is a structural site that prefers the cellularly abundant K⁺ ion to help stabilize the EcNikR-DNA interaction. By utilizing two different metals in each of these sites, EcNikR optimizes its specificity and strength of DNA binding.

Methods

Structure Preparation and Solvation

Structures of Ni²⁺-bound EcNikR and EcNikR-DNA were obtained from the Protein Data Bank (PDB IDs 2HZA and 2HZV, respectively).^9,32 Missing protein residues were added with only backbone and C_β atoms in approximate positions in COOT.³⁷ Missing heavy atoms and all hydrogen atoms were built with ICBuild and HBuild functions in CHARMM version 33b2 using the all-atom (CHARMM27) parameters for proteins, nucleic acids, and potassium ions.³⁸ Nickel parameters (van der Waals radius of 1.4125 Å and ε of −0.010) were obtained from Dr. Johan Bredenberg (personal communication) and thiolate parameters from published studies.³⁹ Histidines were modeled as δ- or ε-protonated, depending on the likely hydrogen-bonding pattern; i.e., heavy atoms of hydrogen-bonding residues that were within 3.5 Å of one another suggest that the corresponding nitrogen on His should be protonated. The high-affinity nickel ligand C95 was modeled as a deprotonated thiolate. Following these modifications to the protein–DNA complex, 100 steps of steepest decent minimization were run in a vacuum to remove bad contacts. For all simulations, the SHAKE command was used to restrain bonds involving hydrogen atoms near their equilibrium values, and the nonbonded cutoff was set to 13.0 Å.⁴⁰

Minimization and Molecular Dynamics of the High–Affinity Site in EcNikR

The EcNikR protein was prepared as described above with either four Ni²⁺ or four K⁺ ions filling the high-affinity metal-binding sites. Simulations with either Ni²⁺ or K⁺ ions in the high-affinity sites were performed in explicit solvent using a stochastic boundary approach.⁴¹ The system was solvated using TIP3P water molecules with a sphere of radius 39 Å centered around the metal-binding domain, and a stochastic boundary potential was used to maintain the water sphere around the system.^42,43 This water sphere allowed for a buffer of ~15 Å between the protein exterior and the boundary of the water sphere. There were a total of 5900 water molecules in the simulation, which were minimized using 500 steps of steepest decent, holding the protein portion fixed. Each of the high-affinity metal sites in both Ni²⁺-EcNikR and K⁺-EcNikR structures were minimized within 5 Å of each site using 500 steps of conjugate gradient and holding the rest of the protein and water fixed. Minimizations that employed a larger cutoff did not significantly change our results.

Following the minimization studies, the system was partitioned for the MD simulations in the following way. All solvent molecules and all protein atoms and ions within 39 Å of the center of the protein were in the reaction region and underwent full MD simulation. The protein molecules outside the sphere were constrained by force constants derived from the B-factors of the atoms in the X-ray crystal structure. The B-factors for atoms that were built into the structure and thus did not have crystallographic B-factors were set to the average B-factor, depending on that type of atom and its location in the main chain or side chain. B-factors were converted to force constants as previously described.⁴¹

Molecular dynamics simulations were run using CHARMM.³⁸ First, the protein was gently heated from 0 to 300 K at a rate of 5 K/ps using a Nosé-Hoover heat bath.⁴⁴ Dynamical simulations then ran at 300 K until the system had been allowed to fully equilibrate (Figure S1, Supporting Information). The total run time was 3.1 ns. Structures were saved every 10 ps. From the final 600 ps of the simulation, an average structure was calculated and briefly minimized to remove bad contacts using 100 steps of steepest descent.

Minimization and Molecular Dynamics of the Second Metal–Binding Site in the EcNikR–DNA Complex

For the studies of the second metal-binding site, the Ni²⁺-EcNikR-DNA structure was prepared as described above with either K⁺ or Ni²⁺ in the second metal-binding site and always with Ni²⁺ at all four high-affinity sites. The protein was solvated using a 57 Å sphere of water (with a total of 21 331 water molecules) in order to fully solvate each second metal-binding site with a water buffer of ~15 Å. In general, simulations with DNA require explicit solvent and counterions to achieve realistic geometries.⁴² However, the inclusion of specific counterions can lead to relatively long convergence times for systems of modest size.⁴⁵ Therefore, we again employed a stochastic boundary approach where the DNA is restrained using the crystallographically determined B-factors and no explicit counterions are used in the dynamic simulations.⁴⁶ This represents a compromise between computational efficiency and accuracy and helps to ensure that the DNA does not sample unrealistic conformations.

Minimization studies of the second metal-binding sites were performed as described for the high-affinity binding sites. For dynamics simulations, the system was partitioned such that all solvent, protein, and ions underwent full dynamics, but the DNA was constrained using harmonic restraints derived from B-factors. The same heating, equilibration, and production procedure described above was used (Figure S3, Supporting Information). The total MD run time was 2.1 ns, with the last 600 ps being used to construct the average structure.

MMPB Studies

For the Poisson–Boltzmann studies we first conducted additional dynamical simulations to obtain representative structures that could be used for electrostatic calculations. In these calculations, the four atoms directly coordinating each nickel ion at the high-affinity metal-binding sites were constrained using an improper dihedral angle of 0° with force constant of 100 kcal/Ų to ensure that optimal square-planar Ni²⁺ coordination geometry was maintained. The second metal sites were minimized as described above with either K⁺ or Ni²⁺ in the sites. After this minimization, the second metal sites were examined and then the final minimized geometry and distances noted (Figure 3). The second metal-binding sites were constrained to the distances defined in Figure 3 using the ’resdistance’ command with a force constant of 1.0 kcal/Ų. Similar approaches have been employed in other studies of protein complexes that contain metal-binding sites.^47–49

The protein–DNA complex was solvated in a water sphere of 35 Å centered around the MBD portion of the structure and fully solvating both second metal-binding sites. A total of 3062 water molecules were added, and the system was partitioned and heated as previously described. Given the restraints at the high-affinity and second metal-binding sites, only 80 ps of equilibration was needed, followed by 1 ns of production dynamics. Ten structures were taken from the 1 ns production trajectory, one every 100 ps. At that point the water molecules were deleted, and the 10 representative structures were ready for Poisson–Boltzmann calculations.

The program Delphi was used to solve the nonlinear Poisson–Boltzmann equation for each of the complexes. The initial grid size was 250 Å square with a grid spacing of 1 Å, which was then focused to a grid size of 125 Å with a grid spacing of 0.5 Å. The interior dielectric of the protein was set to 4 for all calculations. For the vacuum calculations, the exterior dielectric was set to 1, and for calculations in water the exterior dielectric was set to 80 with a salt concentration of 140 mM. The energies for all 10 structures in each of the five states along the pathway in Figure 5 were then averaged, and the electrostatic free energy differences were computed.

Thermodynamic Integration

We calculated the free energy difference between the EcNikR-DNA complex structure with K⁺ bound and the structure with an ion X⁺, where X⁺ is either Na⁺ or Cs⁺. The thermodynamic paths of interest are depicted as the horizontal legs of the thermodynamic cycle in Figure 7: EcNikR binding to DNA with potassium (ΔG_K) or to a monovalent ion with a radius larger or smaller than that of potassium (ΔG_X). We are interested in the difference of these energies, or ΔΔG, where $\mathrm{\Delta }\mathrm{\Delta }{\text{G}}_{\text{K}\to \text{X}}\equiv \mathrm{\Delta }{G}_{\text{X}}-\mathrm{\Delta }{G}_{\text{K}}=\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{P}}-\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{S}}$. We note that, for an exact calculation of $\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{S}}$ and $\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{P}}$, we must account for both the radius of the atom, σ, and the well-depth, ε. From eqs 3 and 4, $\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{S}}$ and $\mathrm{\Delta }{G}_{\text{K}\to \text{X}}^{\text{P}}$ can be decomposed into two steps, a ΔG_K→Y step where only the ionic radius is changed ( $\mathrm{\Delta }{G}_{\text{K}({\sigma }_{\text{K}}+,{\epsilon }_{\text{K}}+)\to \text{Y}({\sigma }_{\text{X}}+,{\epsilon }_{\text{K}}+)}^{\text{S}},\mathrm{\Delta }{G}_{\text{K}({\sigma }_{\text{K}}+,{\epsilon }_{\text{K}}+)\to \text{Y}({\sigma }_{\text{X}}+,{\epsilon }_{\text{K}}+)}^{\text{P}}$), and a ΔG_Y→X step where the well-depth is changed ( $\mathrm{\Delta }{G}_{\text{Y}({\sigma }_{\text{X}}+,{\epsilon }_{\text{K}}+)\to \text{X}({\sigma }_{\text{X}}+,{\epsilon }_{\text{X}}+)}^{\text{S}},\mathrm{\Delta }{G}_{\text{Y}({\sigma }_{\text{X}}+,{\epsilon }_{\text{K}}+)\to \text{X}({\sigma }_{\text{X}}+,{\epsilon }_{\text{X}}+)}^{\text{P}}$).

$\mathrm{\Delta }{G}_{\text{K}({\sigma }_{\text{K}}+,{\epsilon }_{\text{K}}+)\to \text{Y}({\sigma }_{\text{X}}+,{\epsilon }_{\text{K}}+)}^{\text{S}}$ from eq 3 and $\mathrm{\Delta }{G}_{\text{K}({\sigma }_{\text{K}}+,{\epsilon }_{\text{K}}+)\to \text{Y}({\sigma }_{\text{X}}+,{{\epsilon }_{\text{K}}}^{+})}^{\text{P}}$ from eq 4 correspond to the free energies associated with mutating the K⁺ atom to an atom Y⁺ with the van der Waals radius of X⁺ but the ε of K⁺ (−0.087) in solvent or in the EcNikR-DNA complex, respectively. To calculate $\mathrm{\Delta }{G}_{\text{K}({\sigma }_{\text{K}}+,{\epsilon }_{\text{K}}+)\to \text{Y}({\sigma }_{\text{X}}+,{\epsilon }_{\text{K}}+)}^{\text{S}}$, a single ion in a 20 Å radius sphere of TIP3P water was equilibrated for 100 ps. For $\mathrm{\Delta }{G}_{\text{K}({\sigma }_{\text{K}}+,{\epsilon }_{\text{K}}+)\to \text{Y}({\sigma }_{\text{X}}+,{\epsilon }_{\text{K}}+)}^{\text{P}}$, the EcNikR-DNA complex with K⁺ bound was solvated as described above with a 35 Å radius sphere centered around one of the two second metal-binding sites and equilibrated for 100, 200, or 500 ps. These structures were used as starting points for two separate alchemical transformation experiments described below.

The potential energy used for the alchemical transformation is given by V(λ) = V_K + λ(V_Y − V_K), where V_K and V_Y denote the potential energy of the EcNikR-DNA complex with either K⁺ or an ion Y⁺ bound or the ion free in solution. The free energy difference between the states of EcNikR-DNA with K⁺ or Y⁺ bound is given by $\mathrm{\Delta }{G}_{\text{K}({\sigma }_{\text{K}}+,{\epsilon }_{\text{K}}+)\to \text{Y}({\sigma }_{\text{X}}+,{\epsilon }_{\text{K}}+)}^{\text{P}}={\int }_0^1{\langle \mathrm{\Delta }V\rangle }_{\lambda }\text{d}\lambda$, where ΔV = V_Y − V_K. Simulations were performed for both the solvated EcNikR-DNA complex and the solvated free ions at λ = 0.02, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 0.98. At each λ value, 50 ps of equilibration was followed by 50 ps of production dynamics. The final free energy differences were computed using a standard quadrature. Electrostatic and non-electrostatic contributions to the free energy change were calculated separately as previously described.⁵⁰

To determine the contribution of the well-depth to the difference in free energy, we ran an experiment similar to that described above, but in this case we calculated the difference in free energy between having an atom Y⁺ with the size of X⁺ and the well-depth of K⁺, to an atom with both the size and well-depth of X⁺.