On the geometric modeling approach to empirical null distribution estimation for empirical Bayes modeling of multiple hypothesis testing

Abstract

We study the geometric modeling approach to estimating the null distribution for the empirical Bayes modeling of multiple hypothesis testing. The commonly used method is a nonparametric approach based on the Poisson regression, which however could be unduly affected by the dependence among test statistics and perform very poorly under strong dependence. In this paper, we explore a finite mixture model based geometric modeling approach to empirical null distribution estimation and multiple hypothesis testing. Through simulations and applications to two public microarray data, we will illustrate its competitive performance.

1 Introduction

The empirical Bayes modeling method has proven very useful for the large-scale multiple hypothesis testing problems, for example, the differential gene expression detection (Efron, 2003). In the empirical Bayes modeling approach, the selection of null distribution is critical for the appropriate control of false positives (Efron, 2004, 2007a,b). Efron (2010) discussed and illustrated in great detail the importance of adopting the empirical null distribution for the large-scale significance analysis of current biomedical data. Very novel analytic and geometric modeling approaches have been proposed for estimating the empirical null distribution in the significance analysis of two-class microarrays (Efron, 2008). In the analytical approach, a truncated normal distribution model was used to model the null statistics. In the geometric approach, a normal distribution was used to approximate the center of the marginal density, which is estimated non-parametrically using a splines based Poisson regression model.

In this paper we focus on the geometric modeling approach and show that the existing method could be unduly affected by the dependence among test statistics and perform very poorly under strong dependence. The commonly used Poisson regression based density estimation could not model the tail of the marginal distribution very well, and lead to irregular ranking of important genes based on the posterior differential expression probability. We propose a finite mixture model based geometric approach to simultaneously estimating the empirical null and marginal distributions. The finite mixture model is based on the normal distribution and could estimate the distribution tail very well yielding consistent ranking of important genes. We will illustrate its favorable performance through simulation and application studies.

The rest of the paper is organized as follows. In Section 2, we discuss a finite normal mixture model based geometric modeling approach to empirical null distribution estimation and multiple hypothesis testing. We conduct a simulation study in Section 3 and analyze a prostate and leukemia cancer microarray data in Section 4 to illustrate the proposed method. We end with a discussion in Section 5.

2 Geometric modeling of empirical null distribution estimation

Assume the appropriate normal transformation has been applied and we have some normally distributed test statistic z_i for the hypothesis i = 1, ···, m. Assume z_i has unit variance and we are interested in detecting those z_i with nonzero means. The theoretical null distribution is the standard normal distribution N(0, 1). The dependence among test statistics could make the theoretical null distribution a poor fit and calls for the empirical null distribution for the appropriate control of false positives.

Following Efron (2004), we use a normal distribution $N({\mu }_0,{\sigma }_0^2)$ with mean μ₀ and variance ${\sigma }_0^2$ to empirically model the null statistics. A Poisson regression based nonparametric approach has been proposed to estimate the empirical null distribution and true null proportion θ₀, and implemented in the R package ‘locfdr’ (Efron et al., 2011). Specifically the log densities at some pre-specified points are estimated with a splines based Poisson regression model. A quadratic regression model is then fitted to the log densities in a small region around zero to estimate the empirical null distribution parameters. Due to the nonparametric nature of the splines based Poisson regression, the tail of the marginal distribution is often poorly estimated, which will affect the calculation of posterior probability of differential expressions and often lead to irregular ranking of important genes when combined with the parametric empirical null distribution.

We propose to approximate the marginal distribution of {z_i} with a G-component finite normal mixture model

$$f(z)=\sum _{g=1}^G{\pi }_g\phi (z;{\nu }_g,{\sigma }^2),{\nu }_1=0,\sum _{g=1}^G{\pi }_g=1,$$ (1)

where φ(z; μ, σ²) is the probability density function of the normal distribution N(μ, σ²). Firstly we develop an EM algorithm (Dempster et al., 1977) for the maximum likelihood estimation of model (1), and select G based on the BIC (Schwarz, 1978). We then explore several approaches to geometric modeling of the empirical null distribution.

2.1 EM algorithm for model estimation

Define the class indicators, w_i ∈ {1, ···, G}, following the multinomial distribution, Pr(w_i = g) = π_g. Conditional on w_i = g, z_i follows the normal distribution N (ν_g, σ²). The complete data log likelihood is

$$\sum _{i=1}^m\sum _{g=1}^{G}I(w_i=g)log\left[{\pi }_g\phi (z_i;{\nu }_g,{\sigma }^2)\right],\text{where}\phi (z_i;{\nu }_g,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }exp\left\{-\frac{{(z_i-{\nu }_g)}^2}{2{\sigma }^2}\right\}.$$

At the b-th iteration, we firstly compute the conditional probabilities based on the current parameter estimates

$${\tau }_{ig}^{(b)}=\frac{{\pi }_g^{(b)}\phi (z_i;{\nu }_g^{(b)},{\sigma }^{2(b)})}{{\sum }_{k=1}^G{\pi }_k^{(b)}\phi (z_i;{\nu }_k^{(b)},{\sigma }^{2(b)})},g=1,\cdots ,G.$$

In the maximization step, for g = 1, ···, G, we compute (fixing ${\nu }_1^{(b)}=0$)

$${\pi }_g^{(b+1)}=\frac{{\sum }_{i=1}^m{\tau }_{ig}^{(b)}}{m},{\nu }_g^{(b+1)}=\frac{{\sum }_{i=1}^m{\tau }_{ig}^{(b)}{z}_i}{{\sum }_{i=1}^m{\tau }_{ig}^{(b)}},{\sigma }^{2(b+1)}=\frac{{\sum }_{i=1}^m{\sum }_{g=1}^G{\tau }_{ig}^{(b)}{\left[z_i-{\nu }_g^{(b+1)}\right]}^2}{m}.$$

We typically run the EM iteration multiple times with random initials to select the parameter estimate with the maximum likelihood. Given the estimated marginal distribution f(z), we discuss several geometric modeling approaches to estimating the empirical null distribution in the following section.

2.2 Geometric modeling of empirical null distribution

The intuitive idea of geometric modeling is to match the marginal distribution and the empirical null distribution based on some criterion, e.g., assuming similar distribution shape or minimizing their distance etc.

We approximate f(z) around zero with the empirical null distribution ${\theta }_0\phi (z;{\mu }_0,{\sigma }_0^2)$ by matching their moments. Specifically we expand log f(z) at zero into a quadratic function

$$logf(z)\approx logf(0)+{\alpha }_{1}z+\frac{1}{2}{\alpha }_2{z}^2,$$

where

$${\alpha }_1=\frac{f^{\prime }(0)}{f(0)},{\alpha }_2=\frac{f^{″}(0)}{f(0)}-\frac{f^{\prime }{(0)}^2}{f{(0)}^2}.$$

We then estimate

$${\sigma }_0^2=-\frac{1}{{\alpha }_2},{\mu }_0=-\frac{{\alpha }_1}{{\alpha }_2},{\theta }_0=min\left\{1,\frac{f(0)}{\phi (0;{\mu }_0,{\sigma }_0^2)}\right\}.$$

Alternatively we can use a linear regression model based on those observations in A₀ (a small interval around zero: we selected A₀ to contain the 10% smallest absolute test statistics in the simulation and application studies) to estimate α_j

$$logf(z_i)~{\alpha }_0+{\alpha }_1{z}_i+{\alpha }_2{z}_i^2,z_i\in A_0.$$

We can also minimize the Kullback-Leibler (KL) distance (Kullback and Leibler, 1951) between f(z) and the normal distribution $N({\mu }_0,{\sigma }_0^2)$ constrained in the region A₀

$$\underset{{\mu }_0,{\sigma }_0^2}{max}{\int }_{A_0}f(z)log\frac{\phi (z;{\mu }_0,{\sigma }_0^2)}{p_0}dz,p_0=Pr[A_0\mid N({\mu }_0,{\sigma }_0^2)].$$

Next we conduct simulation studies to compare the Poisson regression based geometric approach (denoted as ‘locfdr’) to the mixture model based central matching (denoted as ‘mcm’), linear regression (denoted as ‘mlr’), and KL distance minimization approach (denoted as ‘mkl’).

3 Simulation Study

We simulate 20 blocks, each with 500 test statistics following the multivariate normal distribution with a compound covariance matrix, where the marginal variance is 1 and covariance is ρ. Different blocks are simulated independently. For each block, 100(1−θ₀)% have the mean values simulated from a scaled Beta distribution, 2 × Beta(2, 2) + 1, and the rest have zero mean values. We then randomly change the sign of z_i with probability of 0.5 to create both positive and negative correlations.

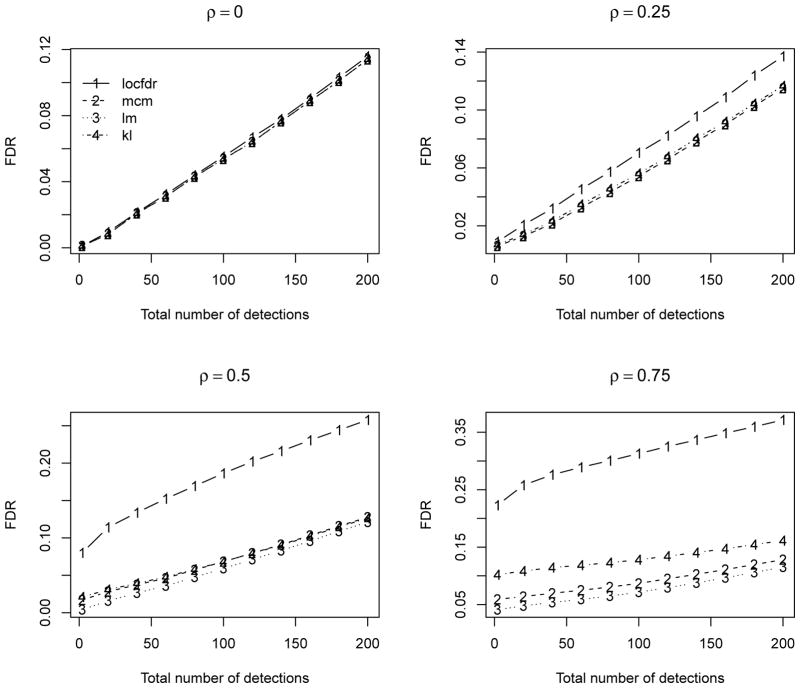
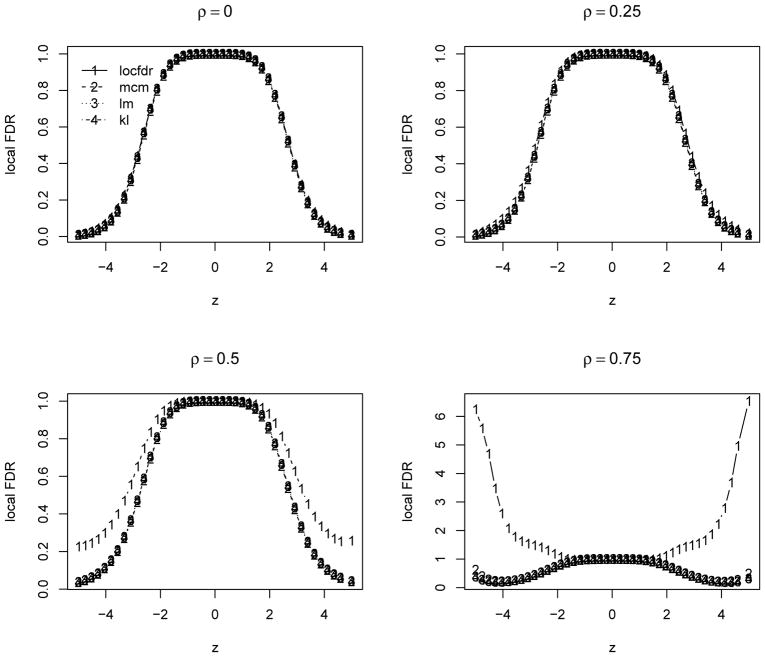
Here we report the results over 500 simulations for θ₀ = 0.9 and ρ = (0, 0.25, 0.5, 0.75) to investigate the performance under relatively weak to strong dependence. In each simulation, we compute the ‘oracle’ estimates with the mean and standard error computed based on the sample mean and variance of the set of 100θ₀% true null statistics. For the locfdr and mixture model based estimates, we compute the mean squared errors of their difference from the oracle estimates. We also compare the false discovery rate (FDR, Benjamini and Hochberg, 1995) for the top ranked 50/100 statistics, denoted as FDR₅₀ and FDR₁₀₀. Table 1 summarizes the results. Figure 1 compares the FDR for both methods. We can see that the locfdr approach is unduly affected by the strong dependence among statistics, especially the null proportion and variance estimates. The locfdr approach tends to detect more false positives under relatively strong dependence. While the mixture model based approaches are less affected by the test statistics dependence, and have relatively stable performance under all dependence structures. Overall the mixture model based approaches perform very favorably compared to the locfdr approach. Figure 2 compares the estimated local FDR, which is essentially the posterior probability of non-differential expression. The proposed approach has relatively more consistent estimation of the local FDR compared to the locfdr. When there are strong dependence among the test statistics, the locfdr has some irregular local FDR estimates in the tails, which is partially due to the nonparametric marginal density estimation unable to fit well the extreme tail probabilities.

Table 1.

Estimated mean squared errors of (θ₀, μ₀, σ₀) and FDRs for the top ranked 50 and 100 statistics over 500 simulations.

		θ0	μ0	σ0	FDR50	FDR100
0	locfdr	3.6e-3	7.5e-4	3.6e-3	0.026	0.053
	mcm	2.2e-3	7.4e-5	1.3e-3	0.025	0.052
	mlr	2.5e-3	7.0e-5	1.6e-3	0.025	0.052
	mkl	2.5e-3	7.0e-5	1.6e-3	0.025	0.052
0.25	locfdr	4.7e-3	8.2e-4	5.5e-3	0.026	0.056
	mcm	2.4e-3	7.2e-5	1.6e-3	0.025	0.055
	mlr	2.7e-3	6.8e-5	1.9e-3	0.025	0.055
	mkl	2.7e-3	6.8e-5	1.9e-3	0.025	0.055
0.50	locfdr	1.2e-2	9.8e-4	2.5e-2	0.072	0.105
	mcm	2.9e-3	7.2e-5	3.8e-3	0.022	0.047
	mlr	3.2e-3	6.9e-5	4.0e-3	0.021	0.046
	mkl	3.2e-3	6.9e-5	4.0e-3	0.024	0.049
0.75	locfdr	1.1e-1	8.4e-3	7.3e-1	0.232	0.268
	mcm	5.5e-3	1.1e-4	1.7e-2	0.032	0.055
	mlr	4.7e-3	8.8e-5	1.5e-2	0.023	0.047
	mkl	4.7e-3	8.8e-5	1.5e-2	0.041	0.061

Figure 1.

Estimated FDR over 500 simulations

Figure 2.

Estimated local FDR over 500 simulations

In the next section, we analyze the pairwise gene correlations in a prostate cancer microarray data (showing very strong interactions), and detect differential expressions in a leukemia microarray data (with relatively weak interactions). We compare the proposed mixture model based method to the locfdr.

4 Application to prostate and leukemia cancer microarray data

The prostate cancer microarray data (Singh et al., 2002) consists of 50 normal and 52 tumor prostate tissue samples with genes measured using the Affymetrix hgu95av2 genechip. We analyze the data using those genes with annotated molecular functions in the Gene Ontology (Ashburner et al., 2000), which leads to 5570 genes and K = 15509665 pairwise correlations.

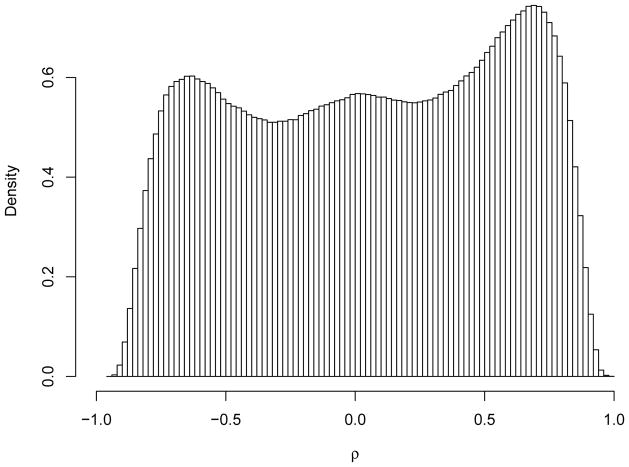
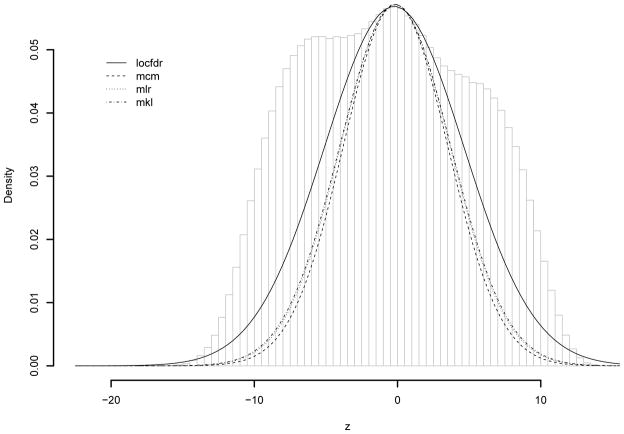
Denote ${\left\{{\rho }_k\right\}}_{k=1}^K$ as the sample correlations. Figure 3 shows its histogram for the prostate cancer microarray data. In general we can see many significantly non-zero correlations clustering around 1 and −1. When assuming normal distribution for the gene expressions, the statistic $t_k=\sqrt{99}{\rho }_k/\sqrt{1-{\rho }_k^2}$ follows the t-distribution with 99 degrees of freedom. We analyze the normally transformed statistic, z_k = Φ⁻¹{T₉₉(t_k)}, where Φ(·)/T₉₉(·) are the standard normal and t-distribution function with 99 degrees of freedom. The theoretical null distribution of z_k is the standard normal distribution. The pairwise sample correlations are strongly correlated with each other. The fitted mixture model selected 10 components based on the BIC. For both approaches, A₀ is chosen to contain the smallest 10% absolute correlations. Table 2 compares the estimated empirical null distributions and ${\widehat{\text{FDR}}}_{1.6e6}$, the estimated FDR when declaring the 1.6 × 10⁶ top ranked correlations as significant (approximately 10% of all correlations). Figure 4 shows the histogram of the transformed Z-statistics for the prostate cancer microarray data. The superimposed lines are estimated locfdr and mixture model based null distributions. Overall they provide similar fit around the center of the histogram. The histogram is a nonparametric estimate of the marginal distribution, and the fitted empirical null distribution should be smaller than the marginal distribution. The mixture model based approaches fit the tail of the histogram better than the locfdr, which tends to over estimate the tail of the null density.

Figure 3.

Pairwise gene correlations for the prostate cancer data

Table 2.

Empirical null distribution and FDR estimates for prostate cancer data.

	θ̂0	μ̂0	σ̂0	${\widehat{\text{FDR}}}_{1.6e6}$
locfdr	0.696	−0.233	4.887	0.354
mcm	0.524	−0.141	3.658	0.054
mlr	0.550	−0.159	3.834	0.079
mkl	0.557	−0.161	3.887	0.087

Figure 4.

Pairwise gene correlations for the prostate cancer data

The leukemia microarray data compared the gene expressions of 20 Mll-AF9 knockin and 23 wild type mice in four cell types (Chen et al., 2008). We analyzed 36,734 genes with unigene annotations among the 45,101 genes measured using the Affymetrix murine 430 2.0 genechip. We compare the Mll-AF9 and wild type expression differences with the following additive effects model

$$x_{ij}={\alpha }_j+{\beta }_j{y}_i+\sum _{k=1}^3{\gamma }_{kj}{z}_{ki}+{\epsilon }_{ij},{\epsilon }_{ij}~N(0,{\sigma }_j^2)i=1,\cdots ,n,$$

where {x_1j, ···, x_nj} are the expression values of gene j, y_i is the indicator for the Mll-AF9 /wild type, and (z_1i, z_2i, z_3i) are three indicators for the cell types. We use the empirical Bayes approach to further improve the estimation of ${\sigma }_j^2$ (Smyth, 2004). The normal transformed t-statistic for β_j is analyzed for detecting differential expressions. The three approaches based on the normal mixture model yield similar results, and we list the mcm results (denoted as ‘nmix’) in the following.

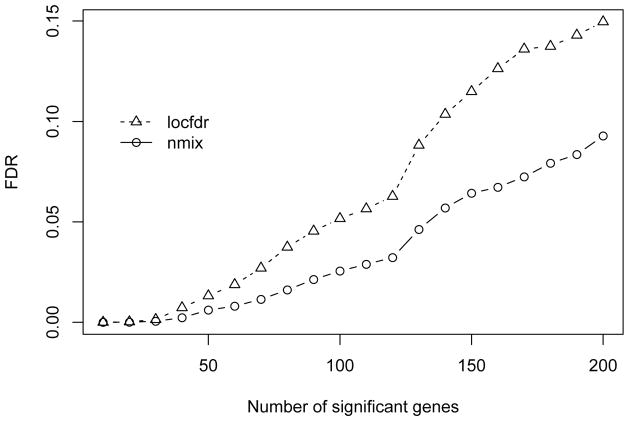
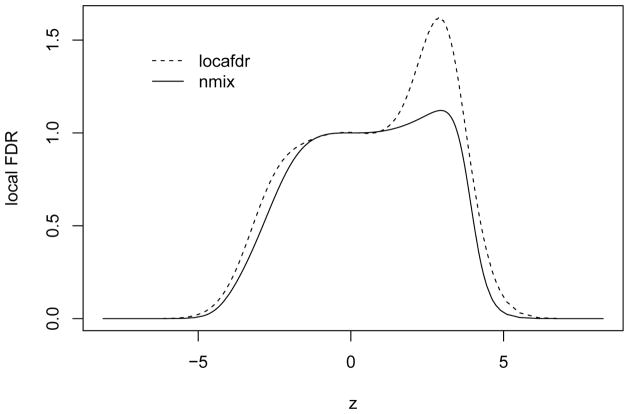
Figure 5 shows the estimated FDR for detecting differential expressions. In general, we can see that the proposed nmix can detect more significant genes than the locfdr. Controlling FDR at 0.1, the nmix identified 223 significant genes, while 165 genes are detected by the locfdr. Figure 6 compares the local FDR estimation for both methods. The local FDR is the posterior probability of non-differential expression and should be strictly between 0 and 1. The nmix approach has a more consistent estimate of the local FDR, while the locfdr approach has some irregular estimate in a positive interval.

Figure 5.

Estimated FDR of differential expression detection for the leukemia data

Figure 6.

Estimated local FDR of differential expression detection for the leukemia data

For the top ranked significant genes identified by each method, we analyze their enrichment of the KEGG pathways (Ogata et al., 1999). Controlling FDR at 0.1 for the enrichment significance, there were 13 significantly enriched KEGG pathways for the top 223 genes selected by the nmix, and 3 significantly enriched KEGG pathways for the top 165 significant genes selected by the locfdr. Table 3 and 4 summarize the detailed enrichment results. The number of genes column listed two numbers: the first is the total number of pathway genes (measured in the leukemia cancer data) and the second is the number of pathway genes ranked in the top 223/165 by each method. All the identified significantly enriched KEGG pathways have been studied and linked to leukemia (see, e.g., Cerny et al., 1971; Her and Zor, 1991; Walther et al., 1998; Perry et al., 1998; Mohle et al., 1998; Thomas and Anglaret, 1999; Puig-Kroger et al., 2000; Valentin et al., 2001; Zhao et al., 2004; Kandilci and Grosveld, 2005; Rizo, 2006; Gallay et al., 2007; Ramsay and Gribben, 2009; Dang et al., 2010; Heddleston et al., 2012).

Table 3.

Significantly enriched KEGG pathways for the top 223 genes identified by the nmix.

KEGG pathway	# genes	p-value	locfdr p-value
leukocyte transendothelial migration	244/8	2.0e-5	5.0e-3
biosynthesis of unsaturated fatty acids	37/3	7.5e-5	6.2e-4
glycine serine and threonine metabolism	51/3	2.6e-4	2.2e-2
regulation of actin cytoskeleton	477/9	7.3e-4	2.1e-2
inositol phosphate metabolism	128/4	1.1e-3	2.0e-2
tight junction	268/6	1.3e-3	1.4e-3
phosphatidylinositol signaling system	178/4	4.7e-3	4.7e-2
glioma	178/4	4.7e-3	8.7e-3
hematopoietic cell lineage	111/3	4.8e-3	1.6e-3
cell adhesion molecules cams	255/5	4.8e-3	1.1e-1
vibrio cholerae infection	112/3	4.9e-3	1.4e-2
long term potentiation	180/4	5.0e-3	4.8e-2
calcium signaling pathway	367/6	7.4e-3	6.5e-3

Table 4.

Significantly enriched KEGG pathways for the top 165 genes identified by the locfdr.

KEGG pathway	# genes	p-value	nmix p-value
biosynthesis of unsaturated fatty acids	37/2	6.2e-4	7.5e-5
tight junction	268/5	1.4e-3	1.3e-3
hematopoietic cell lineage	111/3	1.6e-3	4.8e-3

5 Discussion

As clearly demonstrated at Efron (2010), the empirical null distribution is critical for the appropriate control of false positives in the significance analysis of current large-scale biomedical data. The proposed three geometric modeling methods based on the mixture model are easy to implement and have shown very competitive performance in the simulation and application studies. Overall the central moment matching approach has the best performance. It can be very easily computed and does not need any tuning parameter selection. When we do not have very strong dependence among the test statistics, the linear regression and KL distance approaches have comparable performance as the central moment matching.

Highlights.

1. A flexible modeling approach to estimate empirical null distribution for appropriate control of false positives

2. Detailed simulation studies demonstrating the very competitive performance of the proposed method

3. Applications to two microarray data illustrating the favorable performance of the proposed method