Maternal effects on offspring mortality in rhesus macaques (Macaca mulatta)

Abstract

The genetics of primate life histories are poorly understood, but quantitative genetic patterns in other mammals suggest phenotypic differences among individuals early in life can be strongly affected by interactions with mothers or other caretakers. I used generalized linear mixed model extensions of complex pedigree quantitative genetic techniques to explore regression coefficients and variance components for infant and juvenile mortality rates across pre-reproductive age classes in the semi-free ranging Cayo Santiago rhesus macaques. Using a large set of records (max. n=977 mothers, 6240 offspring), strong maternal effects can be identified early in development but they rapidly “burn off” as offspring age and mothers become less consistent buffers from increasingly prominent environmental variation. The different ways behavioral ecologists and animal breeders have defined and studied maternal effects can be subsumed, and even blended, within the quantitative genetic framework. Regression coefficients identify loss of the mother, maternal age, and offspring age within their birth cohort as having significant maternal effects on offspring mortality, while variance components for maternal identity record significant maternal influence in the first month of life.

INTRODUCTION

Unless mating results in production of offspring who themselves survive infancy and the juvenile years and position themselves so as to reproduce, sex is only so much sound and undulation signifying nothing. [Hrdy, 1999, p. 81]

In response to Hrdy’s statement, one might ask: How much do primate mothers matter for the phenotypes of their offspring including mortality? While a long history of studying mother-infant interactions in primates implies mothers matter a great deal [e.g. Altmann, 1980; Goodall, 1986; Maestripieri, 2009], the answer to this question depends on a variety of conditions, such as which phenotypes one studies and at what ages—knowing that mothers interact more with their young offspring and mothers may affect some traits more than others. Furthermore, the answer must also be species- or even population-specific because evolved differences among species and their immediate local ecology can create larger or smaller opportunities for caretakers to affect offspring development [Charmantier & Garant, 2005; Dufour & Sauther, 2002]. In this paper, I offer a brief review of the theoretical background for describing how important mothers are for offspring mortality and then offer a case study with the free-ranging population of rhesus macaques (Macaca mulatta) on Cayo Santiago.

Imagine having the opportunity and resources to observe a primate population continuously for several decades. Over time, you amass a wealth of data on individual mothers and offspring. The influence of mothers on offspring mortality could be studied in two complementary ways. First, you could relate offspring loss to other measurable characteristics of mothers (e.g. maternal age, dominance rank, maternal style, milk composition) or the environment (e.g. food availability, population density, social group membership, group composition, predator abundance). This would identify trends (i.e. regression coefficients) for offspring mortality within the population, averaging over the individual mothers, to describe the dependence of mortality on these covariates. This influence of maternal phenotype on offspring phenotype is called a maternal effect [Wolf & Wade, 2009; Räsänen & Kruuk, 2007], and primatologists have been quite successful at finding them [reviewed in Maestripieri, 2009]. A familiar example seen in many primates would be primiparous mothers losing infants at higher rates than multiparae [e.g. Koyama et al., 1992; Bercovitch et al., 1998; Robbins et al., 2006].

A second approach would become available if you were able to observe individual mothers attempt to rear a series of offspring during their reproductive career. In this case, you might notice that some mothers tend to lose offspring while others are more successful at preventing their death. This implies there are stable differences among mothers in their influence on early life mortality. Those stable differences can be quantified with a variance component for mothers that accounts for some fraction of the total observable variance in offspring mortality. This fraction of total variance can be thought of as the repeatability of offspring mortality for mothers [Nakagawa & Schielzeth, 2010; Jones et al., 2010]. While useful in itself, the repeatability does little to identify what causes stable differences among mothers in risk to their offspring. It could be due to 1) genes mothers carry that influence her ability to provide care, 2) non-genetic factors, such as early life experiences of mothers, that influence the care they provide, 3) the genes mothers transmit to offspring in gametes that form half of an offspring genome and exert direct effects on offspring phenotypes like early life mortality, or 4) covariance between 1) and 3). In a large population, with several offspring measured per mother, mothers produced those offspring by mating with different identified fathers, and known pedigree relationships among mothers one can accurately estimate variance components for all four of these sources [Wilson et al., 2010; Lynch & Walsh, 1998; Cheverud & Moore, 1994]. In the absence of such a mating structure and rich pedigree information this is not possible, and it will not be attempted here. These steep requirements have prevented primatologists, and behavioral ecologists in general, from using this approach, though it is common in the animal breeding literature [Wilson & Réale, 2006]. Because it will likely become feasible to apply these techniques to wild and free-ranging primates in the near future [Kruuk et al., 2008; Morris et al., 2011], it is worth reviewing some of the theory behind the animal breeder’s model of maternal effects.

The breeder’s tradition of calculating variance components is an application of quantitative genetics. Quantitative genetics is a set of statistical techniques and related biological interpretations for the inheritance and evolution of phenotypes influenced by allelic variation at many loci scattered throughout the genome [Roff, 2007; Lynch & Walsh, 1998]. Phenotypes can be continuously distributed (e.g. birth weight) or even binary (e.g. survive/die) provided one assumes a continuous underlying genetic liability [Roff, 1997]. Crudely, these techniques take observable phenotypic measurements on sets of individuals of known genealogical relationship and decompose the total phenotypic variation (${\sigma }_p^2$) into several underlying components. For the model described in the previous paragraph, these are 1) maternal genetic variance (${\sigma }_m^2$), 2) maternal permanent environment variance (${\sigma }_c^2$), 3) additive genetic variance (${\sigma }_a^2$), and 4) covariance between additive and maternal genetic variance (${\sigma }_{am}$), respectively. Any remaining variance is residual error (${\sigma }_r^2$). Total phenotypic variance is just the sum of these components (${\sigma }_p^2={\sigma }_a^2+{\sigma }_m^2+{\sigma }_c^2+{\sigma }_{am}+{\sigma }_r^2$). These can be transformed into simpler ratios on a 0–1 scale like the narrow-sense heritability ($h^2={\sigma }_a^2∕{\sigma }_p^2$) or maternal gentic effect ($m={\sigma }_m^2∕{\sigma }_p^2$). For example, Southey et al. [2003] analyzed lamb mortality from birth to weaning in domestic sheep (Ovis aries) and found the heritability was about 0.05 with maternal genetic effect about twice that, and they had a negative covariance. In addition to estimating variance components, current “animal model” techniques also allow for very flexible modeling of covariates such as maternal age, parity, or social dominance rank that might also affect offspring phenotypes and incorporate the kinds of maternal influences that behavioral ecologists are more familiar with [Kruuk, 2004]. For example, lamb mortality was affected by lamb sex, litter size, maternal age, and type of rearing environment [Southey et al., 2003]. The variance components essentially partition the remaining variation after these factors have been accounted for [Wilson, 2008].

Variance components are useful for exploring maternal effects for at least two reasons. First, any maternal variance component indicates how much variation in offspring phenotypes is due to maternal variation. In other words, how much consistent differences among mothers matter even if it is unknown what it is about them affects their offspring (e.g. placenta quality, gestation length, maternal style, body mass). Second, variance components appear in simple equations for describing microevolutionary change [Cheverud & Moore, 1994]. Intergenerational response (change in the mean,) is predicted by additive genetic variation and strength of selection (β_P). Without maternal effects, this is simply the breeder’s equation ($R={\sigma }_a^2{\beta }_P$) and response will always be in the same direction as the trait is under selection. A more complicated equation describes response when maternal effects are present, where additive genetics becomes the whole portion in brackets of $R=[{\sigma }_a^2+\frac{3}{2}{\sigma }_{am}+\frac{1}{2}{\sigma }_m^2]{\beta }_P$. This is because a portion of offspring phenotypic variation is due to their own genes (${\sigma }_a^2$), some to genetic variation in the environment provided by mothers (${\sigma }_m^2$), and part to the covariance between the two (σ_am). It also means that offspring phenotypes can evolve strictly through changes in the environment provided by mothers (${\sigma }_a^2=0$, ${\sigma }_m^2$ > 0). In the sheep example quoted above, small variances mean response will be slow. Furthermore, the negative covariance will also curtail response. This implies coadaptation between maternal and additive genetics such that improvement in the direct effect of offspring genes that reduces risk of mortality is offset by increases in risk via maternal effect genes, or vice versa [Cheverud & Wolf, 2009; Cheverud & Moore, 1994].

There are far-reaching implications of maternal effects that few evolutionary biologists appreciated until the 1990s [Mousseau & Fox, 1998; Rossiter, 1996]. Whether or how maternal effects are adaptive and for whom (mothers v. offspring) is a topic of current debate and research [Marshall & Uller, 2007; Jones, 2005]. Adaptive interpretations primarily emphasize the strategies of mothers to adjust offspring phenotypes, functioning as a form of phenotypic plasticity [Räsänen & Kruuk, 2007]. This means that these are shared phenotypes between the two parties being negotiated with mothers in a position to signal adaptive patterns of development. Mothers adjusting how offspring develop can have large-scale demographic results influencing population growth rates, dispersal patterns, and phenotypic divergence among populations or sexes [Badyaev et al., 2002; Badyaev, 2005; Mousseau & Fox, 1998]. Many anthropologists and human biologists have become interested in maternal effects under the guise of the developmental origin of health and disease [Kuzawa & Quinn, 2009; Wells, 2007], to understand variation in adult phenotypes from fetal and early post-natal experiences [Lummaa & Clutton-Brock, 2002].

In this paper, I pursue describing maternal influences on offspring mortality through both the behavioral ecologist (regression coefficients) and animal breeder (variance component) traditions. As noted above, only the later of these is novel. Attention to variance components in the literature is currently very uneven for different sorts of primate phenotypes. For morphological traits, there have been a good number of studies, particularly of the skull, that describe its genetic architecture and are now adding molecular details [e.g. Koh et al., 2010; Roseman et al., 2010; Visscher et al., 2008; Cheverud & Dittus, 1992; Cheverud, 1982]. Unfortunately, this is almost entirely about static adult morphology and has little to say about early life ontogeny when mothers are likely most influential. Life history and reproductive traits have had very little treatment, especially if humans are excluded, and all of it comes from captive colonies [Gagliardi et al., 2010; Martin et al., 2002; Ha et al., 2002; Jaquish et al., 1996; Williams-Blangero & Blangero, 1995]. Other captive studies of the genetics of early life mortality have focused on the effects of inbreeding [Van Coillie et al., 2008; Ralls & Ballou, 1982].

The major obstacle to quantitative genetic research in primates is the large samples of pedigreed individuals needed. This is especially true for life history traits that are expected to have low heritabilities and large residual effects [Price & Schluter, 1991]. Because of this, the Cayo Santiago rhesus macaques are a valuable study population [Rawlins & Kessler, 1986; Sade et al., 1985]. Cayo Santiago is a small, 15 ha island about 1 km off the coast of mainland Puerto Rico inhabited by a population of about 1000 rhesus macaques. These monkeys are descendants of 409 individuals trapped in India that were released on the island in 1938. Demographic data have been collected in a regular census taken on weekday mornings with frequent, but brief interruptions since 1959 [Sade et al., 1985]. Animals are also annually trapped for tattooing and tissue sampling. They are provisioned with commercial monkey chow, and the population has been managed by removal of individuals, but matings are unmanaged and animals live in naturally formed social groups.

Several authors have used Cayo Santiago for quantitative genetic research [e.g. Blomquist, 2009; Havill, 2003; Cheverud et al., 1990]. Previous work on the heritability of female lifetime fitness (n = 590) in the population produced some unexpected results suggesting weak maternal influences on early life mortality [cf. Blomquist, 2010]. The heritability of having ever reproduced was roughly quantified by coding 1=if a female ever reproduced and 0=she never reproduced and analyzing the variable as normal/Gaussian, as is typical of quantitative traits. This had a low heritability of 0.27 and no maternal effect. The low heritability is not surprising, but the lack of maternal effect is unexpected when maternal characteristics are predicted to make a large contribution to early life phenotypes including mortality. Moreover, the pedigree information for this population of monkeys is not rich enough to satisfactorily separate maternal effects from direct genetic effects (see below).

Here, I use a much larger dataset of male and female demographic records from Cayo Santiago and generalized linear mixed model techniques [Wilson et al., 2010; Bolker et al., 2009] to estimate variance components for the binary phenotype of offspring death. I adopt a simple approach of focusing on the repeatability of offspring death for mothers. A heritability of offspring mortality for some age classes as a trait of mothers [Pettay et al., 2005] is also presented but it must be cautiously interpreted as it does not follow the strict decomposition in the animal breeder model of maternal effects (described above) and instead represents a familial patterning among mothers in offspring mortality of ambiguous genetic origin. With this new method and larger dataset I explore the age-course of maternal effects across infant and juvenile periods, rather than treating it as a single pre-reproductive stage of life. Maternal effects of both the ecologist’s (regression coefficients) animal breeder’s (variance components) tradition are statistically significant and, for some offspring ages, show strong maternal influences on early life death.

METHODS

Data were extracted from the Cayo Santiago demographic database in 2005 [Blomquist, 2007]. I scored individual mortality data from birth to 900 days of life on 6240 offspring of 977 mothers. I used this maximum age because I was strictly interested in pre-reproductive mortality. This is the approximate age (2.46 years) females begin to mate successfully such that they give birth when they are three years old. In addition to the 0–900 day interval, I also scored a series of five 180-day (≈ 6 month) age classes (Figure 1). Equal length age classes were chosen to avoid any circularity in defining classes based on prior knowledge of death rates, but they were required to be long enough that there was appreciable mortality (≥2%) in all the age classes (precluding a longer series of shorter classes). Because mother-infant interactions are more intense in the first few weeks after birth and mortality in this period is common, I also explored dividing the first interval into an initial 0–30 day and subsequent 30–180 day age classes [Maestripieri & Hoffman, 2012]. Offspring were only included if they came from cohorts prior to or including 2002 to ensure they could have survived to 900 days by the time the data were extracted in early 2005. Furthermore, infant ages are only recorded precisely after 1962. Maternal ages need not be known as precisely and were accepted from cohorts back to 1956. Births at Cayo Santiago are strongly seasonal making such assignments to cohorts simple [Rawlins & Kessler, 1985]. Any twins were also excluded because of their high death rates and extreme rarity [Bercovitch et al., 2002; Geissmann, 1990]. A small number of unsexed individuals were also excluded.

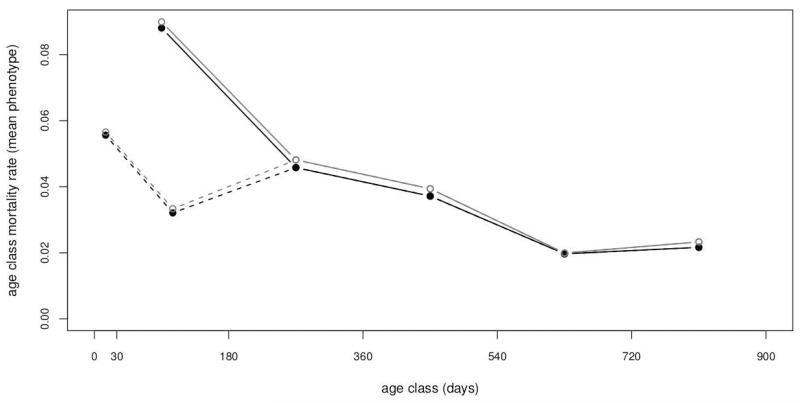
Figure 1.

Death rates in the analyzed dataset (dots) and for all sexed infants born in the same cohorts (circles).

Death was scored as a separate binary variable for each of the age classes with 1=death and 0=survived. All 6240 offspring were scored for each age class. Any individuals removed through colony management during an age class or prior to it were set to a missing value (NA) that is omitted from the analysis. Age class death rates can then be computed from the complement of a Kaplan & Meier [1958] survival rate that accounts for the censoring due to removals ($\text{death}\text{rate}=1-\frac{survived}{enter-removed}$). These death rates are also the mean phenotype of each age class. For example, if a monkey lived past 900 days it had a 0 for each age class. If a monkey died in the 180–360 age class it had a 1 for 180–360, 0 for any younger age class (e.g. 0–180), and missing value for all the later age classes (e.g. 360–540). Finally, to ensure repeatabilities were interpretable (see below) only mothers having two or more infants scored with non-missing values in an age class were retained in the analysis of that age class. These restrictions for constructing the dataset cause only a small downward bias in the death rates versus those seen in the full set of infants born in the 1962–2002 cohorts (Figure 1). Final numbers of offspring retained for the analysis were between 5859 and 3094 depending on the age class

I analyzed offspring death with univariate generalized linear mixed models (GLMM), running a single model for each age class to explore the age-course of effects predicting mortality (Equation 1). Offspring death was treated as a trait of the mothers with all mothers having multiple offspring scored if they were included for the model for an age class.

$$y=X\beta +\sum _i^n{Z}_i{u}_i+r$$ (1)

In equation 1, is the vector of phenotypic measurements of offspring death, X is an incidence matrix for fixed effects with β as their vector of regression coefficient estimates, Z_i is an incidence matrix for random effect i with u_i as the vector of solutions for the random effect, and r is residual error [Kruuk, 2004; Lynch & Walsh, 1998]. All fixed effects in the model were covariates with regression coefficients estimated in. Offspring sex was dummy coded with 1=male. Offspring age in cohort is the number of days deviating from the median birth date within the offspring’s cohort. Positive values are birth dates after the cohort median. Mother’s age at birth was recorded in years and the average age at birth (8 years) subtracted to ease interpretation of regression coefficients and baseline mortality rates. A set of dummy variables also indicated whether mothers were primiparous, whether they had given birth in the previous cohort, whether they exited due to death or removal during the current offspring age class, or whether they had done so prior to it. These final two variables are collectively referred to as maternal presence. Maternal age, primiparity, previous reproductive state, and presence are clearly maternal effects of the kind often studied by behavioral ecologists. Offspring age in cohort might also be considered one as a consequence of maternal conception or gestation time.

For all age classes models were initially run with a pair or random effects: maternal identity and offspring birth cohort. These have variance components estimated (${\sigma }_i^2$, and ${\sigma }_b^2$, respectively) and solution predicted (i, and b, respectively). Maternal identity solutions correspond to the variance in offspring mortality explained by stable differences among individual mothers, regardless of their cause. These are referred to as repeatability models as they partition variation in mortality a simple manner such that maternal repeatability can be calculated.

For age classes with high repeatabilities (${\sigma }_i^2$ > 0) I also explored an augmented model included three random effects and attempts to break the stable differences among which mothers into additive genetic and non-genetic (permanent environment) sources. Thus there are three variance components estimated (${\sigma }_a^2$, ${\sigma }_{pe}^2$, and ${\sigma }_b^2$, respectively) and solution predicted (a, pe, and b, respectively). In these models, ${\sigma }_a^2+{\sigma }_{pe}^2$ is approximately the individual variance and a+pe individual solutions.

The means of all random effects in repeatability or augmented models are zero. The maternal identity, permanent environment, and cohort effects have covariances given by ${\sigma }_i^2$, $I{\sigma }_{pe}^2$ and $I{\sigma }_b^2$ where I is an identity matrix having the number of mothers or cohorts as its dimensions. The additive genetic covariance is ${\sigma }_a^2$, where the elements of A are twice the kinship coefficients of a pair of individuals x and y [A_xy=2Θ_xy, Lynch & Walsh, 1998]. Pedigree relationships are known from behavioral interactions of mothers and infants and a smaller number of paternities in the 1988–1998 birth cohorts determined from 10 microsatellites (Table 1). Further details of the paternity analysis can be found in Bercovitch et al. [2003]. The paternity of nearly all monkeys dying during their first year of life is unknown because they were never trapped to have tissue collected. This prevents analyzing early life mortality as a phenotype of the offspring because a maternal identity effect and direct genetic effect would be confounded for most all offspring. This explains why Blomquist [2010] found significant heritability and no maternal effect when running this type of model, and implies great caution is required interpreting his results.

Table 1.

Pedigree statistics for the mothers analyzed in each offspring age class.

	0–900	0–180	0–30	30–180	180–360	360–540	540–720	720–900
phenotyped IDs	783	949	977	916	859	816	779	666
pedigree members	909	1100	1130	1070	1013	966	924	786
maximum generations	8	8	8	8	8	8	8	7
founders	73	78	79	77	72	68	65	63
maternities	836	1022	1051	993	941	898	859	723
paternities	175	221	224	218	217	213	204	142
maternal grandmothers	734	891	914	866	819	784	756	628
maternal grandfathers	64	88	90	87	87	84	80	49
paternal grandmothers	175	221	224	218	217	213	204	142
paternal grandfathers	64	88	90	87	87	84	80	49
maternal sibs	687	859	884	836	798	758	720	589
paternal sibs	129	169	172	166	166	162	153	97
maternal half-sibs	687	857	882	834	796	756	720	589
paternal half-sibs	129	167	170	164	164	160	153	97
full sibs	0	2	2	2	2	2	0	0
F > 0	17	26	26	25	25	25	22	13
F ≥ 1/16	4	4	4	4	4	4	4	4
F ≥ 1/8	4	4	4	4	4	4	4	4
F ≥ 1/4	2	2	2	2	2	2	2	2
% largest family	84.598	82.545	82.389	82.991	84.205	85.300	86.364	85.623
% disconnected	3.080	1.909	1.681	2.243	1.876	1.863	2.165	2.799
x̄ offspring per mother	2.297	2.371	2.372	2.364	2.388	2.382	2.347	2.231
x̄ offpsring per father	1.989	2.105	2.113	2.076	2.087	2.068	2.040	1.797
x̄ maternal sibship (n > 1 )	3.195	3.205	3.203	3.179	3.179	3.198	3.172	3.100
x̄ paternal sibship (n > 1 )	3.071	3.189	3.185	3.132	3.132	3.115	3.122	2.853
Ā ij	0.005	0.005	0.005	0.005	0.005	0.006	0.006	0.006
% Aij > 0	10.621	10.828	10.824	11.042	11.641	11.876	11.980	10.138
% Aij ≥ 1/16	2.878	2.584	2.521	2.641	2.829	2.962	3.026	3.045
% Aij ≥ 1/8	1.641	1.440	1.402	1.474	1.577	1.652	1.689	1.758
% Aij ≥ 1/4	0.770	0.662	0.644	0.679	0.728	0.766	0.794	0.845

Treating offspring mortality as a trait of mothers requires no paternity information on offspring. In fact, offspring are only part of the pedigree if they survive to become mothers themselves or are genealogical links between mothers. This means dead offspring do not appear in the pedigree—they are simply repeat measurements of a phenotype assigned to their mother. As such, only paternities of the mothers remain in the pedigree. Errors in these should only lower heritability estimates [Pemberton, 2008]. However, infant stealing potentially complicates the assignment of offspring to mothers and introduces a potential bias to heritability and repeatability measures because stolen infants typically die within a few days unless their mothers retrieve them. However, the physical signs of pregnancy, typical possessiveness of rhesus mothers, and pursuit of stolen infants which should all be recorded through regular observation of the population suggest this is unlikely to be very common [Quiatt, 1979]. Furthermore, this would only induce a downward bias to repeatability by shuffling offspring among mothers unless there were mothers which frequently managed to steal infants, undetected by observers, which then died. Heritability would be affected in similar ways only if related mothers frequently managed to steal infants undetected.

A binomial distribution with logit link function was used to account for the binary nature of the offspring mortality data [Southey et al., 2003; Nakagawa & Schielzeth, 2010]. Modeling mortality with the logit link produces regression coefficients for the logarithm of the odds of death. These are more interpretable when transformed. The baseline probability of death is calculated from the intercept coefficient (β₀) as $\frac{e_0^{\beta }}{1+e_0^{\beta }}$. Other coefficients are easily interpreted as proportionate change in the probability of death for a unit change in the covariate as $\frac{e^{{\beta }_0+{\beta }_1}}{1+e^{{\beta }_0+{\beta }^1}}∕\frac{e_0^{\beta }}{1+e_o^{\beta }}$ (e.g. probability of death increases 26.4 × baseline with maternal loss). I report these transformed regression coefficients giving the baseline mortality rate and proportionate changes in the mortality rate due to a unit increase in the covariate. Baseline mortality is for a female offspring, born on her cohort’s median date, to a 8-year old, multiparous female who did not give birth the previous year and was present throughout the offspring age class.

All data preparation and analysis was performed in R 2.15 [R Development Core Team, 2012] with the repeatability and augmented models analyzed via functions in the MCMCglmm package [Hadfield, 2010]. MCMCglmm relies on Bayesian Markov Chain Monte Carlo techniques [O’Hara et al., 2008] to provide estimates of variance components and regression coefficients by repeated sampling of a long-running simulation of the posterior distributions of model terms. Following Postma et al. [2011] and the MCMCglmm documentation [Ch. 8 of “CourseNotes” vignette; Hadfield, 2010], I used parameter expanded priors with ${\sigma }_i^2$, ${\sigma }_a^2$, ${\sigma }_{pe}^2$, and ${\sigma }_b^2$ set to 1 with a degree of belief parameter of 1. In these models, where each offspring’s death/survival is only observed once, ${\sigma }_r^2$ cannot be estimated and was fixed at 10. The logit link-specific variance also contributes π²/3 to the total variance in these models. Estimated values of ${\sigma }_i^2$, ${\sigma }_a^2$, ${\sigma }_{pe}^2$, and ${\sigma }_b^2$ are dependent on the residual and link variance. Ratios of these variance components to the total are easier to interpret because they are independent of the fixed residual, though dependence on the link variance remains. These are the repeatability ($\frac{{\sigma }_i^2}{{\sigma }_a^2+{\sigma }_{pe}^2+{\sigma }_b^2+10+{\pi }^2∕3}$ or $\frac{{\sigma }_a^2+{\sigma }_{pe}^2}{{\sigma }_a^2+{\sigma }_{pe}^2+{\sigma }_b^2+10+{\pi }^2∕3}$), heritability ($\frac{{\sigma }_a^2}{{\sigma }_a^2+{\sigma }_{pe}^2+{\sigma }_b^2+10+{\pi }^2∕3}$), and cohort effect ($\frac{{\sigma }_b^2}{{\sigma }_a^2+{\sigma }_{pe}^2+{\sigma }_b^2+10+{\pi }^2∕3}$).

The repeatability and cohort effect are the most important of these. The repeatability represents the fraction of variance on the logit scale accounted for by differences among mothers. If greater than 0, it indicates there are stable differences among mothers across the repeated measurements of offspring death in an age class. A similar interpretation applies to the cohort effect, that a fraction of total variance is explained by differences in risk of death among years. The heritability is difficult to interpret because, although offspring death is treated as a phenotype of mothers here, it is likely a complex mixture of direct genetic effects in offspring that influence risk of death (half of which come from mothers), direct genetic effects in the mother affecting her care of offspring (maternal genetic effects from the offspring’s perspective), and their covariance. I consider it to reflect familial similarity in early life mortality rates of unknown origin, and focus interpretation on the repeatability as a crude measure of maternal effects.

For each univariate model, I ran a single chain for 2005000 iterations and saved every 1000th sample after a 5000 iteration burn-in. This provides 2000 samples of the posterior distributions of the variance components, random effect solutions, and regression coefficients. Effective sample sizes for the non-fixed variance components were always greater than 1615. Autocorrelation of the retained samples was less than 0.065 in all cases and there were no trends in diagnostic plots of the chain over simulation time. Minimum effective size for the regression coefficients was 1296 and maximum autocorrelation was 0.074. Shape and location of these distributions of regression coefficients or variance components can be used to infer whether parameters are greater or less than 0. Credible intervals covering 95% of the posterior distribution are often used for these tests. These are appropriate for regression coefficients in this study but variance components and ratios have a lower boundary at 0 and thus cannot include it within their 95% interval. Instead, I simply visualize a ratio’s posterior distribution and modal value and interpret the resulting patterns. The mode is declared different from 0 if the lower tail of the visualized distribution does not approach 0 and the lower boundary of the 95% interval is greater than 0 at three digits past the decimal. Formal comparison of alternative models with different random effects using information criteria (e.g. DIC) is unreliable for GLMM [Wilson et al., 2010]. Ratios were not converted to the proportion scale [by equation 23 in Nakagawa & Schielzeth, 2010] because the resulting values are dependent on the mean which would complicate comparisons across age classes. Nevertheless, posterior distributions for repeatabilities on the proportion scale had an identical shape to those presented here. Regression coefficient dependence on fixing ${\sigma }_r^2=10$ was removed through their multiplication by $\frac{1}{\sqrt{1+10c^2}}(\text{where}=\frac{16\sqrt{3}}{15\pi })$, which rescales ${\sigma }_r^2=0$. Random effect solutions for cohort or individual mother effects were rescaled by $\frac{1}{1+10c^2}$ [Hadfield et al., 2010].

Research reported here relies on data collected over several decades by many observers under different funding auspices and IACUC approvals which should be consulted for further details. All research reported here, and occurring at Cayo Santiago today, adheres to the ASP’s Principles for the Ethical Treatment of Non-human Primates.

RESULTS & DISCUSSION

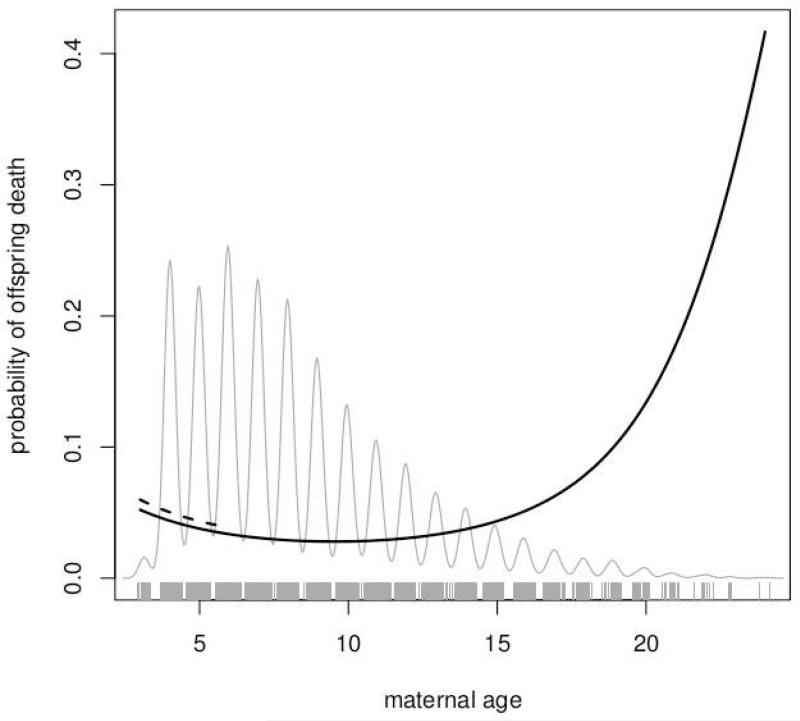
The regression coefficients and variance components record a number of statistically significant maternal effects on offspring mortality in rhesus macaques. In general, these are strongest on the youngest age classes. Among the regression coefficients, maternal age effects are significant in age classes prior to 180 days whether pooled or separate (Table 2). The linear effect of age is negative meaning offspring of older mothers are less likely to die, while the quadratic effect is positive meaning that offspring of very young and very old mothers are more likely to die (Figure 2). This recovers a pattern already known in offspring mortality at Cayo Santiago [Hoffman et al., 2010]. The maternal presence variables have by far the largest coefficients and index the dramatic risks posed to offspring by loss of the mother. The effect of losing a mother during an age class diminishes with offspring age, but it is statistically significant even in the final age class (720–900 days). By this final age class, offspring have been fully weaned for at least one year and spend very little time in contact or close proximity with their mothers except in stressful situations [Suomi, 2005]. Loss of the mother during an age class causes a 2.1–26.4× increase in the probability of offspring death, depending on the age class examined. For example, in the 720–900 day age class the mortality increases from a baseline of 0.007 to 0.020 (=0.007 × 2.808) when the mother is lost. In the 0–180 day class, this is a much greater change from 0.048 to 0.581. The absence of any maternal presence effect and change in sign of estimated coefficient in the 360–540 age class is atypical. This is likely due to the crudity of coding with 1=exit, which includes both maternal death or removal through population management. The ratio of the number of mother deaths to mother removals is lowest in this period. If removal of the mother is less damaging than death of the mother, then this decreased ratio of deaths to removals will diminish the maternal exit effect on offspring death. Separating death and removal into separate dummy variables is not possible because there are very few of each in most age classes.

Table 2.

Regression equations for death in each age class. β are posterior means and their 95% credible interval given on the logit scale. These are transformed into baseline death rate (intercept) and a proportionate change in probability of death due to a unit change in the variable (β′).

	β ′	β	95% CI		β ′	β	95% CI
	0–900 days				0–180 days
intercept	0.149	−1.744	−2.010	−1.479*	0.048	−2.997	−3.285	−2.722*
male	1.129	0.144	0.013	0.273*	1.021	0.021	−0.127	0.172
age in cohort	0.998	−0.002	−0.004	0.000	0.996	−0.004	−0.007	−0.002*
primiparous	1.236	0.254	−0.036	0.541	1.288	0.267	−0.061	0.587
rep. previous	1.151	0.167	−0.037	0.373	1.178	0.172	−0.065	0.421
age	0.981	−0.023	−0.057	0.011	0.941	−0.063	−0.102	−0.026*
age2	1.006	0.007	0.002	0.011*	1.015	0.015	0.011	0.020*
exit during	2.691	1.340	1.160	1.531*	12.110	3.303	2.949	3.673*
exit prior
	0–30 days				30–180 days
intercept	0.029	−3.514	−3.869	−3.169*	0.020	−3.881	−4.287	−3.505*
male	0.934	−0.071	−0.245	0.113	1.245	0.224	0.012	0.443*
age in cohort	0.994	−0.006	−0.009	−0.003*	0.999	−0.001	−0.005	0.002
primiparous	1.151	0.145	−0.260	0.522	1.549	0.449	−0.011	0.917
rep. previous	1.168	0.160	−0.124	0.443	1.182	0.171	−0.175	0.531
age	0.956	−0.046	−0.092	0.000	0.947	−0.055	−0.111	−0.003*
age2	1.015	0.015	0.010	0.021*	1.010	0.010	0.003	0.016*
exit during	26.372	4.682	4.004	5.401*	14.814	3.031	2.562	3.554*
exit prior					5.515	1.805	−0.123	3.527
	180–360 days				360–540 days
intercept	0.033	−3.366	−3.706	−3.042*	0.025	−3.654	−4.119	−3.221*
male	1.091	0.090	−0.094	0.294	0.966	−0.036	−0.252	0.186
age in cohort	1.006	0.006	0.003	0.009*	0.993	−0.007	−0.011	−0.003*
primiparous	0.950	−0.053	−0.493	0.389	1.412	0.356	−0.161	0.851
rep. previous	1.171	0.164	−0.154	0.480	1.222	0.206	−0.142	0.560
age	0.963	−0.039	−0.087	0.009	1.032	0.033	−0.028	0.094
age2	1.006	0.006	−0.000	0.012	0.997	−0.004	−0.012	0.005
exit during	3.351	1.294	0.778	1.793*	0.659	−0.425	−1.101	0.233
exit prior	2.818	1.101	0.415	1.809*	0.889	−0.121	−0.944	0.622
	540–720 days				720–900 days
intercept	0.024	−3.695	−4.265	−3.201*	0.007	−4.903	−5.984	−4.037*
male	0.803	−0.224	−0.526	0.069	1.058	0.057	−0.330	0.439
age in cohort	1.001	0.001	−0.004	0.006	0.995	−0.005	−0.012	0.001
primiparous	1.368	0.322	−0.306	0.965	1.174	0.162	−0.753	1.081
rep. previous	0.808	−0.218	−0.640	0.219	1.135	0.128	−0.420	0.709
age	1.034	0.035	−0.043	0.114	1.069	0.067	−0.032	0.166
age2	0.994	−0.006	−0.017	0.005	0.995	−0.005	−0.018	0.007
exit during	2.071	0.755	−0.042	1.494	2.808	1.046	0.168	1.858*
exit prior	1.142	0.136	−0.596	0.796	2.072	0.736	0.045	1.442*

Figure 2.

Predicted probability of death across maternal ages for the 0-30 age class (solid black line). The small primiparity effect is also illustrated with the dashed line covering ages of primiparae. The oscillating grey line and rug show the distribution of maternal ages in the sample.

Coefficients for offspring age within cohorts are significant for several age classes (Table 2). However, their sign, even when significant, is not consistent. In general, being born later within a cohort decreases risk of death. How advantages arise from being born later are unclear (e.g. greater gestation length). Reproduction in the previous year, primiparity, and offspring sex are not significant predictors of mortality (Table 2). The lack of sex effect may be surprising as male infants are often considered more susceptible to death [Bhaumik et al., 2004]. Given recent theoretical attention, one might speculate absence of sex effects might be related to sex ratio variation by maternal condition where mothers in better condition are more likely to have male infants which offsets their greater frailty [Schino, 2004; Bercovitch et al., 2000]. The lack of significant primiparity effect on offspring death at Cayo Santiago has already been documented in a smaller sample [Bercovitch et al., 1998], though primate primiparae are generally described as less competent mothers and expected to lose infants at higher rates [e.g., Altmann, 1980].

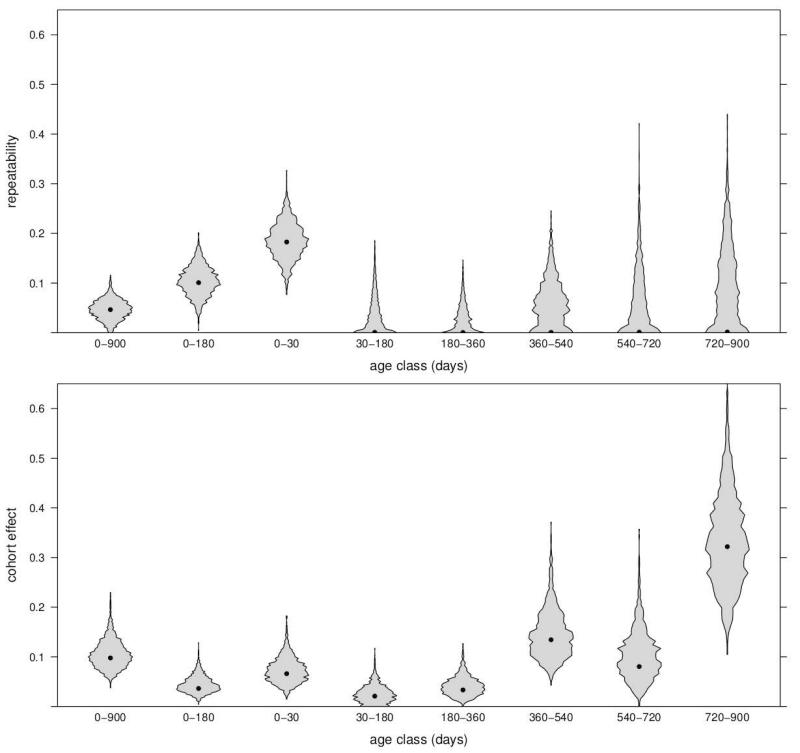
Ratios of the random effect variance components also show an initially strong effect of mothers on offspring death that quickly declines in later age classes (Table 3, Figure 3). Any interval including the first 30 days of life (0–30, 0–180, or 0–900) has a repeatability that is significantly greater than zero. This is largest when the age class is confined to 0–30 days (0.183). In all subsequent age classes, repeatabilities are essentially 0.

Table 3.

Variance component ratios and 95% credible intervals for the repeatability models in all age classes and augmented models in the three classes with repeatabilities greater than 0.

age class	repeatabilty models			augmented models
	repeatability	cohort effect	pe effect	heritability	repeatability	cohort effect
0-900	0.046: 0.008-0.084	0.098: 0.058-0.160	0.000: 0.000-0.054	0.041: 0.000-0.068	0.050: 0.020-0.090	0.099: 0.061-0.165
0-180	0.101: 0.047-0.162	0.036: 0.017-0.081	0.001: 0.000-0.124	0.000: 0.000-0.116	0.097: 0.052-0.164	0.037: 0.014-0.073
0-30	0.183: 0.116-0.260	0.066: 0.027-0.120	0.001: 0.000-0.190	0.083: 0.000-0.194	0.181: 0.115-0.265	0.065: 0.026-0.121
30-180	0.001: 0.000-0.112	0.021: 0.000-0.060
180-360	0.000: 0.000-0.084	0.033: 0.008-0.079
360-540	0.001: 0.000-0.149	0.134: 0.064-0.242
540-720	0.001: 0.000-0.197	0.080: 0.020-0.198
720-900	0.001: 0.000-0.247	0.322: 0.171-0.513

Figure 3.

Violin plots of posterior distributions for variance component ratios in the offspring age classes. Each posterior mode is indicated by the black dot corresponding to the repeatability models in Table 3.

In the augmented models, repeatabilites of offspring mortality are nearly identical to the repeatability models, but there is no statistical evidence of any familial signal. No heritability can be declared greater than 0. However, the posterior modes are a large portion of the repeatability for 0–900 and 0–30 days implying there might be some similarity among related mothers in the mortality of their offspring that would have been apparent in a larger sample with more precise pedigree information. Regardless, the interpretation of these heritabilities would be difficult. The repeatabilities could reflect maternal genetic variance for ability to prevent offspring mortality, persistent but non-genetic factors influencing maternal care, maternal contribution to the offspring genome that affects offspring mortality, their covariance, or some combination of these. Nevertheless, their rapid decline as offspring age is consistent with much of this effect being due to maternal ability to prevent mortality.

In later age classes, the lack of repeatability means mothers are no longer a reliable buffer from the environment or controller of this shared phenotype of offspring death. This should not be taken to mean mothers are no longer important in later age classes, but rather that the individual mothers become more variable in how they affect offspring as the offspring get older (i.e. increasing within mother variation). Indeed, the notable maternal presence covariate indicates that mothers, on average, are still influencing offspring mortality in these later age classes.

In contrast to the decline of the repeatability, birth cohort initially explains little variation in offspring death but rises dramatically as offspring age and may reflect seasonality of mortality risk. Cohort effects are greater than 0 in all age classes, except 30–180 (Table 3). The largest effects are in age classes 360–540 (0.135) and 720–900 (0.322, Figure 3). Redirection of maternal care away from the offspring to a newborn sibling [Devinney et al., 2001], likely exposes the yearling to annually varying conditions that mothers previously provided some buffer from.

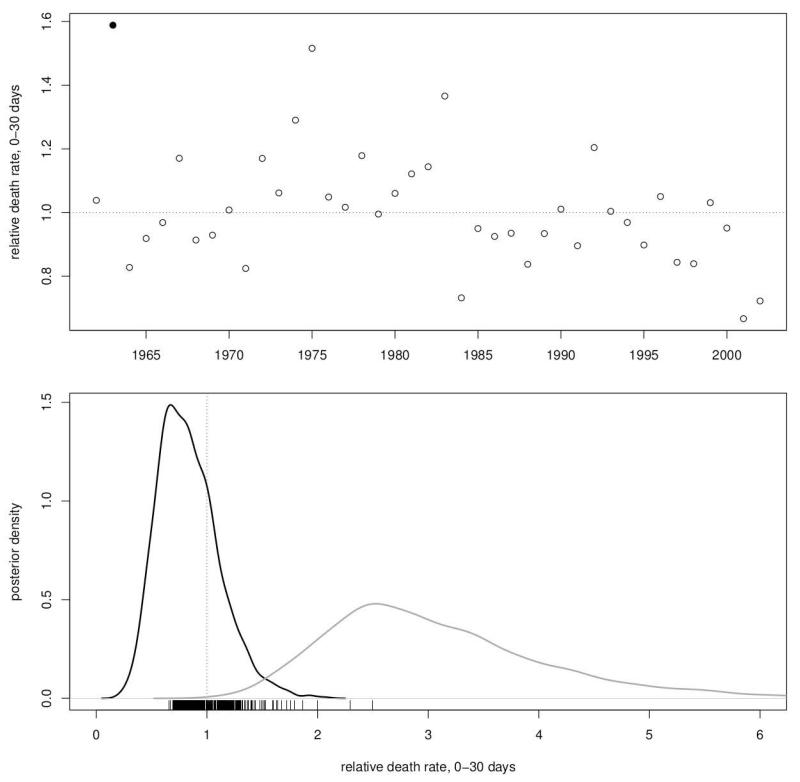
The random effect solutions provide some illustrations of the patterns summarized in the variance components ratios. Quantitative analysis of random effect solutions (a.k.a. BLUPs) in ecological settings is problematic [Hadfield et al., 2010], so I restrict discussion to a few points on the cohort effects (b) and mother identity effect (i). Among the cohort solutions for the 0–30 day age class, the highest value is for 1963, indicating it was a catastrophic year of offspring death (Figure 4). This is explained by a brutal experiment described by Sade et al. [1985, p. 36] in their Demographic Observations

The pregnant females were taken to a small building in Punta Santiago, Puerto Rico, the point of land nearest Cayo Santiago. The infants were delivered by Cesarean section and asphyxiated followed by repeated attempts at resuscitation…Most of the infants, about 18 percent of the 1963 birth crop, died as a result of the experiment.

Figure 4.

Random effect solutions for death in the 0-30 day age class scaled as death rates relative to the baseline as in Table 2 (0.03). Posterior modes of the cohort solutions (upper panel) show unusually high mortality in 1963 (filled dot). Posterior modes of solutions for individual mothers (lower panel) are given as rug along the axis and full posterior density for the extreme mothers with lowest (black) and highest mortality (grey).

More relevant to the description of maternal influence on offspring mortality are the maternal identity effects in the 0–30 day age class when repeatability is largest. The highest and lowest solutions respectively identify the mothers that were consistently the worst and best mothers for offspring mortality adjusting for all the other fixed and random effects in the model. Picking out these two mothers makes a useful contrast (Figure 4). The “worst” mother lived about 9 years and had 5 offspring, all of whom died within a few days of birth. The “best” mother lived 21 years giving birth to 14 infants, none of which died between 0 and 30 days.

CONCLUSIONS

How much do primate mothers matter for the phenotypes of their offspring like mortality? This application of generalized linear mixed model techniques generates novel results for answering this question and thinking about how primate mothers influence life histories. Mothers certainly do affect offspring mortality, but the variable maternal characteristics that either underlie the maternal age effect or the consistent differences among mothers described by the maternal variance component only have an effect on offspring survival prior to weaning, which is largely accomplished in the 180–360 age class at Cayo Santiago [Maestripieri & Hoffman, 2012]. Once in juvenile age classes, having a mother present still reduces offspring risk of death, but apparently any mother will do, at least as described by the characteristics assessed in this analysis. For yearlings and beyond, birth cohort becomes more important as mothers become less effective or less consistent buffers from the environment.

The two perspectives on maternal effects were complementary here, but they were essentially treated separately. An interesting question that blends these perspectives is whether there is heterogeneity among mothers in how they affect offspring mortality as mothers age. The regression coefficients only describe a population average trajectory of changing risk to offspring (e.g. Figure 2). The maternal variance component is about mothers being shifted above or below this average. However, it is quite possible, and evolutionary genetic models of senescence would predict, that there is variation among mothers in their rates of aging and thus whether the late life increasing risk to offspring occurs earlier or later. That is beyond what can be done with this data set, but this theoretical prediction has recently been explored with mixed support in some wild bird and mammal populations [Brommer et al., 2010; Wilson et al., 2007].

In this analysis, the maternal variance component described stable differences among mothers in how they made life safer or riskier for their infants. It does not indicate what might underlie those stable differences (e.g. behavior, hormones, morphology). But, stable differences in the sorts of maternal characteristics that might affect infants (such as maternal style, milk yield, or even body size) point to either maternal genetics or early life experiences of mothers determining these maternal effects on infant mortality [Lindström, 1999; Nickerson, 1995; Berman, 1986]. This conclusion must be tempered by the inability to separate maternal variance from offspring additive variance in this population. This severely limits interpretation of any genetic variance components and leaves the lingering question of how much of this significant repeatability of offspring mortality is due to direct effects in offspring themselves. Additional research in settings where paternity of offspring is known would help resolve this question.

A final concern with this analysis is what can be generalized to other primate or mammalian species. Cayo Santiago is a somewhat unusual population of rhesus macaques that lives at very high density, is provisioned, is closed to in- or out-migration, and has no predators. The early life strength and decline of maternal effects is a common pattern noted in reviews of mammalian maternal effects, mostly in livestock and rodents [Wilson & Réale, 2006; Cheverud, 1984]. That offspring mortality in the Cayo Santiago macaques matches this pattern is encouraging but not particularly surprising. Novel patterns might be found in primates with extensive allocare or paternal support [e.g. Aotus, Callithrix, Saguinus; Solomon & French, 1997]. Additional sources of mortality or food-stress might also be a source of divergent results, as shown in other taxa [Bethea et al., 2008; Thompson et al., 2009]. However, a recent meta-analysis of differences in variance components between favorable and unfavorable conditions in wild animal species showed that heritabilities increase in favorable conditions but there is no consistent pattern in maternal effects. This might be surprising because it would make sense that mothers matter more in unfavorable environments where there is so much more for mothers to buffer offspring from [Charmantier & Garant, 2005]. In summary, at present, there is little reason to expect dramatically different patterns elsewhere among primates though this should encourage, rather than deter, greater interest in maternal effects among primatologists.