Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Feb 25;3:1331. doi: 10.1038/srep01331

Compressed carbon nanotubes: A family of new multifunctional carbon allotropes

Meng Hu 1,4, Zhisheng Zhao 1,4,5, Fei Tian 2,4, Artem R Oganov 3, Qianqian Wang 1, Mei Xiong 1, Changzeng Fan 1, Bin Wen 1, Julong He 1, Dongli Yu 1, Hui-Tian Wang 2, Bo Xu 1,a, Yongjun Tian 1,b
PMCID: PMC3580323  PMID: 23435585

Abstract

The exploration of novel functional carbon polymorphs is an enduring topic of scientific investigations. In this paper, we present simulations demonstrating metastable carbon phases as the result of pressure induced carbon nanotube polymerization. The configuration, bonding, electronic, and mechanical characteristics of carbon polymers strongly depend on the imposed hydrostatic/non-hydrostatic pressure, as well as on the geometry of the raw carbon nanotubes including diameter, chirality, stacking manner, and wall number. Especially, transition processes under hydrostatic/non-hydrostatic pressure are investigated, revealing unexpectedly low transition barriers and demonstrating sp2→sp3 bonding changes as well as peculiar oscillations of electronic property (e.g., semiconducting→metallic→semiconducting transitions). These polymerized nanotubes show versatile and superior physical properties, such as superhardness, high tensile strength and ductility, and tunable electronic properties (semiconducting or metallic).

Carbon has the ability to adopt sp-, sp2-, and sp3-hybridized states, thus forming a wide range of allotropes including graphite, diamond, fullerenes, carbon nanotubes (CNTs), and carbynes. The creation of new multifunctional carbon allotropes has been the focus of numerous theoretical and experimental explorations because of their fundamental scientific and technological importance.

The periodic bonding motif in carbon structures can be dramatically altered under pressure, such as the well-known sp2→sp3 bonding change. By compressing different raw carbons such as graphite, fullerenes, CNTs, and vitreous carbon, diverse phases are produced including diamond, transparent superhard post-graphite phases1,2,3,4, one-, two-, and three-dimensional (3D) fullerene polymers5, fully sp3-bonded superhard amorphous carbon6, and some elusive allotropes7,8,9. However, completely clarifying the structures of these exciting carbon phases through current experimental technologies is usually unrealistic due to their limited quantity, as well as mixture of other phases. State-of-the-art theoretical tools for structure prediction are necessary and have yielded great success, such as simulated annealing10,11, genetic algorithm12,13, basin hopping14,15, metadynamics16,17, evolutionary metadynamics18,19, random sampling20,21, and particle-swarm optimization22,23. Most of these algorithms focus on the search of thermodynamically favorable structures with little consideration on the kinetics process, which is also important for metastable materials. The recently developed variable-cell nudged elastic band method18 and transition path sampling method24 enable further investigations into these kinetic processes.

By considering both thermodynamics and kinetics aspects, we proposed a novel carbon allotrope, namely Cco-C825, which can be viewed as a 3D (2,2) CNT polymer and account for the previously undetermined superhard carbon phase recovered from cold compression of CNT bundles26. Further dynamical simulations demonstrated the easy formation of Cco-C8 by compressing armchair CNT bundles. Using transition path sampling method, we found that for kinetic reasons (minimal transition barrier), room-temperature compression of graphite yields M-carbon, which was first theoretically proposed13,27 and very recently unambiguously identified experimentally28. These results inspired us to search and identify more new carbon allotropes under pressure with similar considerations. Numerous experimental studies on the high-pressure behavior of CNTs have been performed, most of which focused on the structural, electronic, and mechanical resonances of CNTs under low deformation ratio29,30. In this region, the tubes only undergo reversible polygonization, ovalization, or racetrack-shape deformations. Possible pressure-induced polymerizations of CNTs are rarely investigated except for limited cases31,32,33,34,35. Multi-walled CNTs (MWCNTs) become partially transparent under a non-hydrostatic pressure of 11 GPa and further transform into a new hard phase with complete sp3 bonding under 16 GPa35. Under higher non-hydrostatic pressures of 24 and 35 GPa, two novel superhard carbon phases with respective hardness of 62–150 GPa and 58 GPa have been synthesized by compressing single-walled CNTs (SWCNTs) with Raman spectral features indicating the polymerization of CNTs32,34. Other elusive allotropes have been obtained upon simultaneous application of temperature and pressure31,33. Although these experimental results are motivating, most of the crystal structures of these carbon phases derived from CNTs are unsolved, and the physical picture underneath the pressure-induced phase transitions of nanotubes remains unclear.

In this paper, a systematic and comprehensive study about pressure-induced CNT polymerization is presented via ab initio calculations. Significant changes in structural, electronic, and mechanical properties occur along with CNTs polymerization under pressure, yielding a variety of novel carbon allotropes strongly depending on the applied pressure and the nature of the CNTs precursor. The surprisingly low energy barrier for these transitions indicates a feasible pathway to produce new carbon allotropes with engineered properties.

Results

Polymerization under pressure

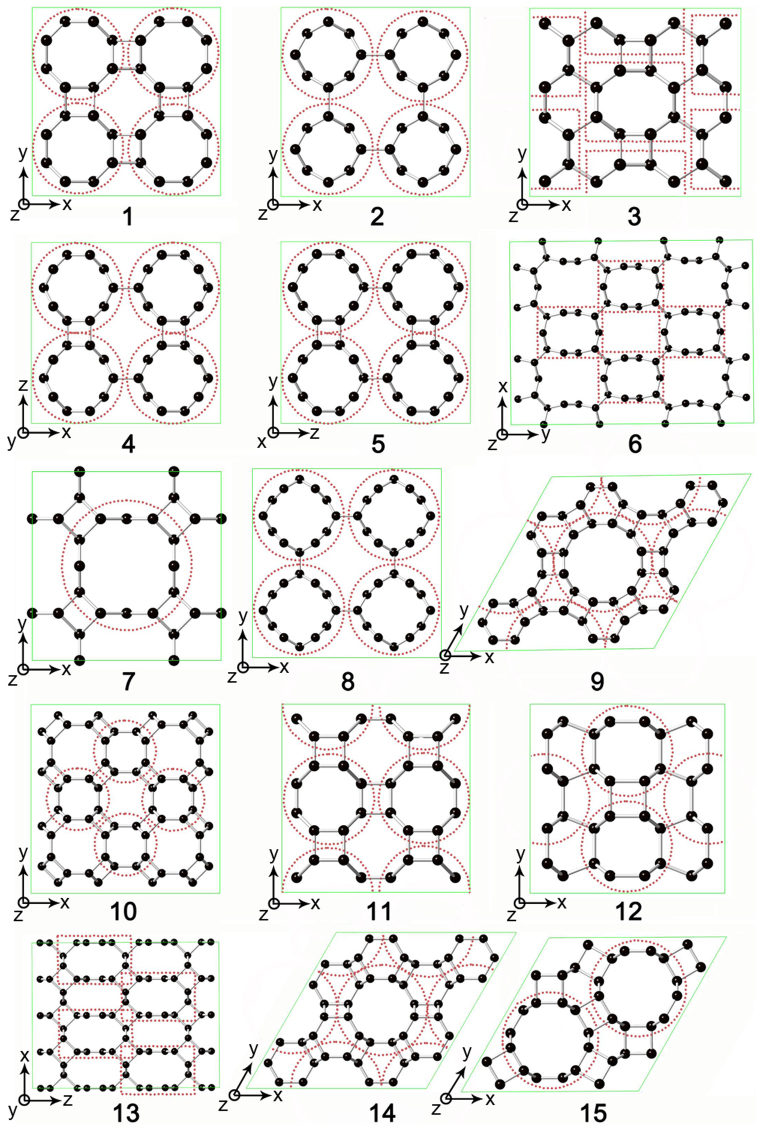
Under hydrostatic pressure, small zigzag (n,0) and armchair (n,n) SWCNTs can easily bond covalently to each other by directly shortening intertube distance from 3.4 Å to approximately 1.55 Å (Fig. 1). The compressed nanotubes manifest diverse structures related to the CNT species and initial stacking configurations. For example, 3D (4,0)-I and 3D (4,0)-III carbons can be selectively formed due to AAA and ABA stacking of (4,0) SWCNTs, respectively (Fig. S2 in Supplementary Information), whereas the difference between 3D (4,0)-I and 3D (4,0)-II carbons is due to the different orientations of CNTs inside similar tetragonal unit cells. As a consequence, a great number of metastable carbon structures can be produced by compressing small SWCNTs in our simulations. Some previously proposed structures, such as 3D (2,2)-II (Bct-C436), 3D (2,2)-III (Cco-C825), 3D (5,0)-III37, and 3D (3,3)-I38, have been identified along with more new structures. The transition pressures for small (n,0) SWCNTs are usually less than 20 GPa, whereas those for small (n,n) SWCNTs usually exceed 20 GPa. This difference can be attributed to the local flattened section in (n,n) SWCNTs, where the π bond repulsion prevents further compression (see detailed discussions below). Once this repulsion is overcome by higher pressure, the common [2+2] cycloaddition happens at intertube junctions, and four-membered rings appear in 3D (n,n) SWCNT polymer structures.

Figure 1. Top view of 3D SWCNTs polymers along the axial directions.

Figure 1

Open in a new tab

1–3: 3D (4,0)-I, -II, and -III; 4–6: 3D (5,0)-I, -II, and -III; 7–9: 3D (6,0)-I, -II, and -III; 10–12: 3D (2,2)-I, -II, and -III; 13–15: 3D (3,3)-I, -II, and -III.The corresponding x, y, and z axes of crystal structures are marked.

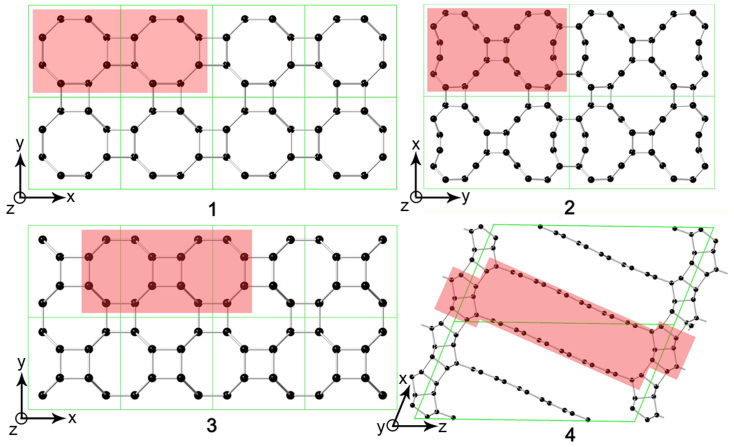
Non-hydrostatic pressure shows a much more significant effect on aligned large SWCNTs than on small SWCNTs. Under pressure, large SWCNTs have more variants and can collapse into denser polymers consisting of smaller SWCNTs with higher incompressibility. For example, (4,4), (8,0), and (12,0) SWCNTs are compressed to form 3D (2,2) (Bct-C436 and Cco-C825), 3D (4,0)-I, and 3D (6,0)-IV carbons, respectively (See Fig. 2). Further investigations on compression of larger nanotubes showed that more complicated structures can be obtained from complicated deformations of tube cross sections. For instance, aligned (10,10) SWCNTs under non-hydrostatic pressure can first transform into 3D (8,8) CNT polymer (Fig. 2), and then form a bond in the local graphite-like section of the structure under increasing pressure. The extremely complex phase behavior in compressed CNTs is fundamentally determined by the structural diversity of CNTs. It should be noted that, except for the successful assignment of Cco-C8 to a cold compressed CNTs25,26, direct comparisons between our simulated CNT polymers and other synthesized phases are hard to carry out at present. Most of experimental studies did not provide enough structural information31,32,33,34,35. In addition, the starting materials in these experiments are usually a mixture of different CNTs, making such a comparison even harder. A better control of starting SWCNT bundles, such as improved alignment and chirality/diameter purification, may make such comparisons possible in the future.

Figure 2. Top view of 3D SWCNTs polymers along the axial directions.

Figure 2

Open in a new tab

1–4: 3D (4,0)-I, (6,0)-IV, (2,2)-II, and (8,8), recovered from (8,0), (12,0), (4,4), and (10,10) SWCNTs (red regions), respectively. The corresponding x, y, and z axes of crystal structures are marked.

Structural evolution

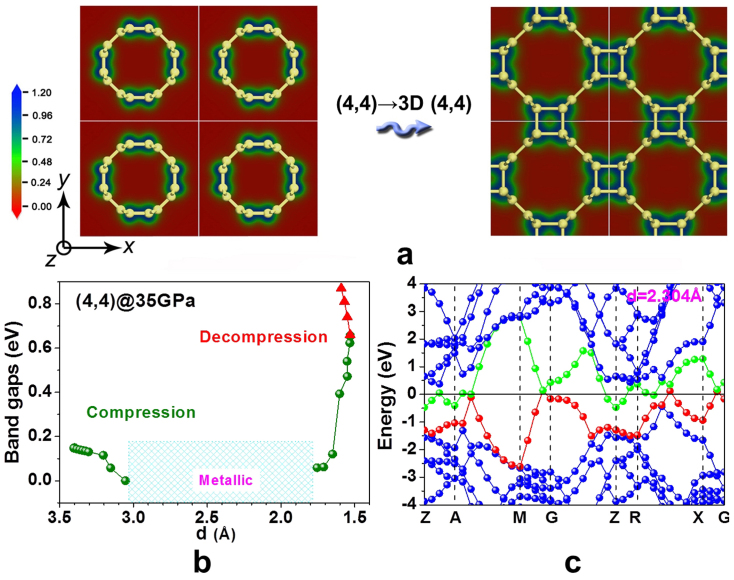
Although many experiments have suggested the structural transition of nanotubes under pressure, such as deformation, collapse, and polymerization29,30, the kinetic mechanism of transition has not been revealed up to our knowledge. To elaborate the kinetics process of phase transition, we investigated the structure evolutions of aligned (4,4) and (8,0) SWCNTs under hydrostatic and non-hydrostatic pressure, respectively (Figs. 3 and 4). For aligned (4,4) SWCNTs, adjacent nanotubes interact by weak van der Waals interactions at ambient pressure. A band gap is open at Fermi level, which is distinct from metallic isolated (n,n) SWCNTs39 but consistent with the theoretical prediction40 and experimental observation39 on (n,n) SWCNT bundles. After applying pressure, the intertube distance in aligned (4,4) SWCNTs is shortened, leading to increased intertube π–π coupling. The (4,4) SWCNTs polymerize to form 3D (4,4)38 carbon, accompanied by π→σ bonding conversion in intertube junctions under higher pressure. Such simple structural changes cause unexpectedly semiconducting→metallic→semiconducting electronic changes, as shown in Fig. 3b. When intertube distance decreases from standard 3.4 Å to 3.054 Å, enhanced intertube π–π coupling induces a downward shift of the green conduction band (Fig. 3c) near the Fermi level and closes the band gap from 0.16 eV to 0 eV (Fig. S3). Further shortening of intertube distance continuously moves the green conduction lower and the red valence band higher across the Fermi level, resulting in a conductive behavior of the compressed (4,4) tubes (Figs. 3c and S3). In this “metallic” region, the electronic total density of states (DOS) at the Fermi level is determined by the green and red bands across the Fermi level and demonstrates a non-monotonic variation. This observation is reminiscent of an earlier work about the hypothetical metallic ThSi2-structured carbon, where the metallicity was attributed to short π–π contacts41. During the final stage of compression, as soon as an intertube distance of 1.804 Å is reached, a sudden π→σ intertube bonding transition occurs companied with valence electron localization. A band gap would re-open at the Fermi level and gradually increase to 0.66 eV as the length of the σ-bond is shortened to 1.531 Å. Moreover, this 3D (4,4) carbon is quenchable with the band gap increasing from 0.66 eV to 0.87 eV after decompressing from 35 GPa to ambient pressure.

Figure 3.

Figure 3

Open in a new tab

(a): structural evolution from (4,4) SWCNT bundles to 3D (4,4) carbon under hydrostatic pressure of 35 GPa; (b): band gap evolution as a function of intertube distance d (Å), where olive spheres correspond to the compression process (@ 35 GPa) and red triangles correspond to the decompression process (@ 0 GPa); (c): electron band structure at d = 2.304 Å.

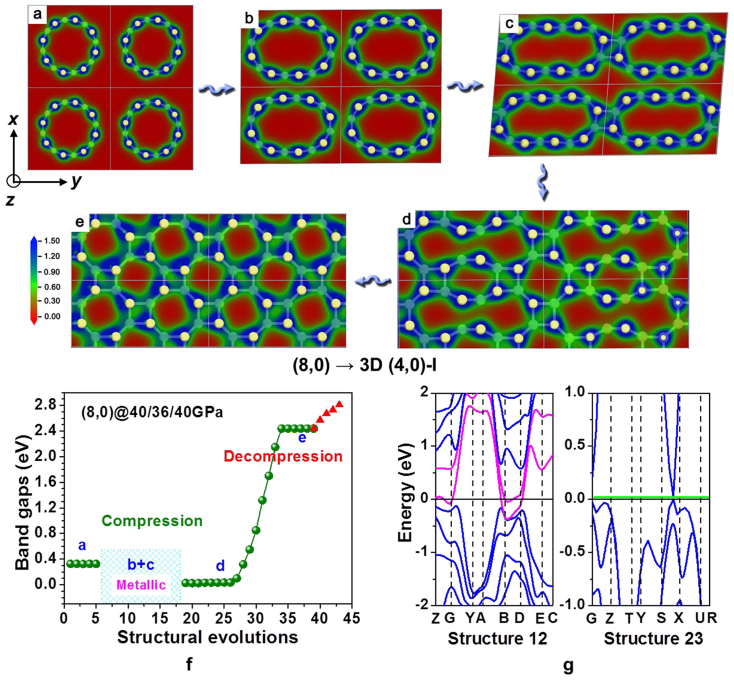
Figure 4.

Figure 4

Open in a new tab

(a–e): structural evolution from (8,0) SWCNT bundles to 3D (4,0)-I carbon under non-hydrostatic pressure of 40 GPa along x axis and z axis, and 36 GPa along y axis; (f): band gaps as a function of structural evolution in the compression process (olive spheres) and the decompression process (red triangles); (g): band structure of evolution 12 (metallic) and evolution 23 (semiconducting) in panel (f), where the magenta curves correspond to the bands crossing the Fermi level, and the green shadow emphasizes the band gap.

The structural change of aligned (8,0) SWCNTs under non-hydrostatic pressure is more complicated than that of (4,4) SWCNTs under hydrostatic pressure. Moreover, the corresponding electronic changes are more intriguing. Specifically, the aligned (8,0) SWCNTs undergo four major deformations (Fig. 4) under non-hydrostatic pressure. In the first stage, the initially circular cross-section of the nanotubes becomes oval-shaped (Fig. 4b), a phenomenon which has been previously extensively studied42,43. This deformation is reversible and induces a semiconductor→metal transition in compressed (8,0) nanotubes, consistent with previous investigation of isolated (7,0) nanotubes44. In the second stage, 1D (8,0) SWCNTs start to polymerize into 2D (8,0) nanotube polymers (hereafter named 2D (8,0) carbon) (Fig. 4c), similar to previous simulations of 2D (5,0), (7,0), and (9,0) carbon37. The 2D (8,0) carbon remains metallic because the stronger π–π coupling contributes more delocalized electrons. In the third stage, 2D (8,0) carbon transforms into 3D (8,0) carbon through further intertube bond formation (Fig. 4d). More electrons are localized in this stage, leading to a semiconductor with a very narrow band gap (ca. 0.02 eV). In the final stage, 3D (8,0) carbon is further squashed to form fully sp3-bonded denser 3D (4,0)-I carbon (Fig. 4e). As a result, the band gap rapidly increases up to 2.4 eV. This 3D (4,0)-I carbon is quenchable and the band gap increases to 2.8 eV after decompressing the pressure. This band gap oscillation is not unique, and different transition paths would lead to different electronic property changes.

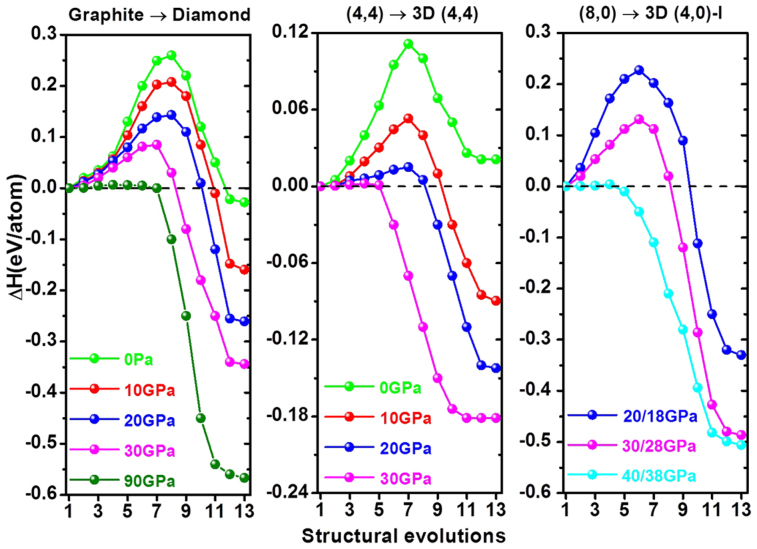
Low transition energy barrier

Although the enthalpy of CNT polymer is lower than that of its counterpart CNT, a central issue to rationalize such phase transition is pertinent to the transition barrier (Fig. 5). The result of 3R graphite→3C diamond is also presented in Fig. 5 for comparison. This transition can easily be realized by directly shortening the graphite interlayer distance and buckling the neighboring sheets. The calculated energy barriers decrease with increasing pressure. The values of 0.26 and 0.14 eV/atom at 0 and 20 GPa respectively are in good agreement with previously calculated 0.3345 and 0.1546 eV/atom, indicating the rationality of our method (See Methods section for details). The pressure-induced phase transition of (4,4) SWCNT→3D (4,4) is also simple. The calculated transition barrier for this transition is notably lower than that of graphite→diamond transition at the same pressure, implying a more feasible transition process. For (8,0) SWCNTs→3D (4,0)-I transition, the energy barrier at 20/18 GPa pressure is higher than that of graphite→diamond at 20 GPa. However, it rapidly decreases with increasing pressure and drops to 0 eV at 40/38 GPa, whereas 90 GPa is needed to drop the barrier to 0 eV for graphite→diamond.

Figure 5. Energy barrier curves from 3R graphite to cubic diamond, aligned (4,4) SWCNTs to 3D (4,4) carbon, and aligned (8,0) SWCNTs to 3D (4,0)-I carbon at hydrostatic/non-hydrostatic pressures.

Figure 5

Open in a new tab

Non-hydrostatic A/B GPa indicates the applied pressure is A GPa along x axis and z axis, and B GPa along y axis.

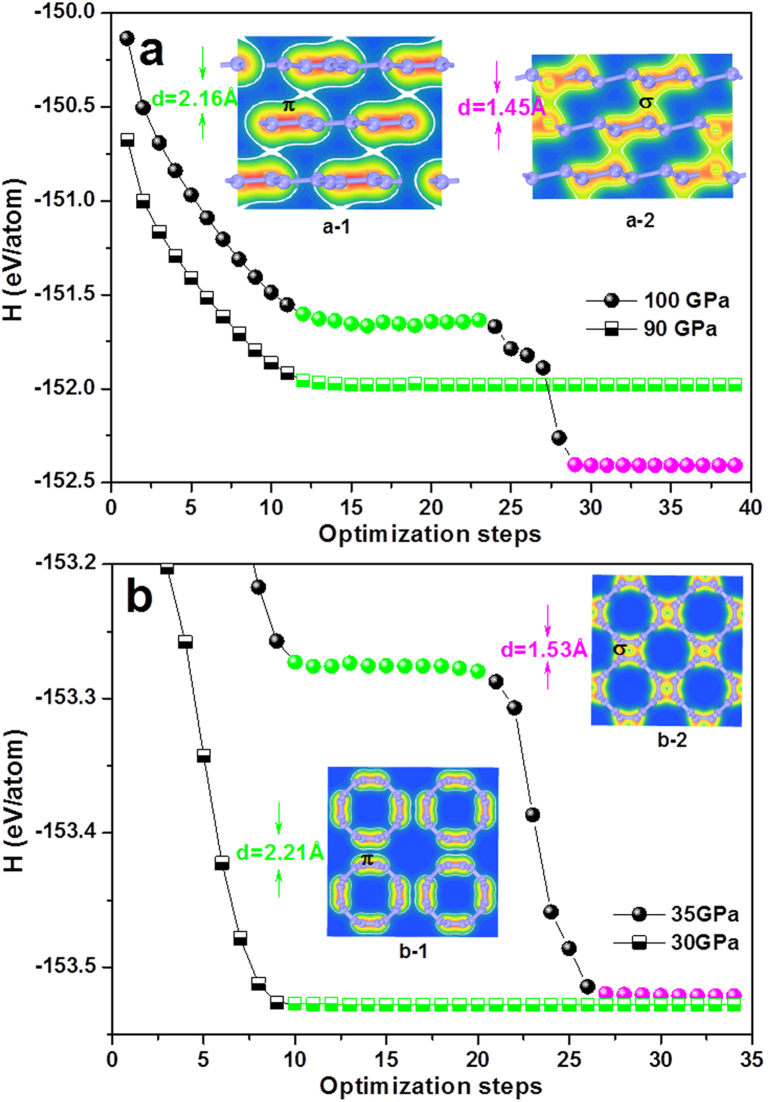
In compressed graphite or (4,4) SWCNT, the highest energy-barrier points correspond to a specific structure with interlayer or intertube spacing of ca. 2.2 Å. For instance, the relaxed equilibrium structure at 90 GPa is still graphite-like with an interlayer distance of about 2.2 Å because this much shortened distance induces strong π bond repulsion to resist external pressure (Fig. 6a). At 0 K, graphite remains to be metastable until a critical pressure of 100 GPa is applied, where π–π repulsion is conquered and π→σ bonding transition occurs accompanied by the structural change and a large enthalpy drop. By comparison, a critical pressure of as low as 35 GPa is sufficient to overcome the π–π repulsion in compressed (4,4) SWCNTs, far less than that of graphite (Fig. 6b). These results clearly indicate the easy formation of new metastable carbons through compressing small-diameter CNTs, compared with the case of graphite compression.

Figure 6. Enthalpy (H) changes as a function of optimization steps under different pressures.

Figure 6

Open in a new tab

(a) and (b): phase transitions of 3R graphite→3C diamond and (4,4) →3D (4,4) carbon, respectively. Insets (a-1) and (b-1) show the electron density profiles corresponding to the green marks in the curves, while insets (a-2) and (b-2) show the electron density profiles corresponding to the magenta spheres in the curves. A phase transition only occurs after a critical pressure being applied (100 GPa for graphite and 35 GPa for (4,4) CNT).

Electronic and mechanical properties

Band structure calculations show that 3D (4,0)-II, 3D (6,0)-II, and 3D (8,8) carbons are metallic and other carbon polymers are semiconducting with wide direct/indirect gaps from 0 eV to 3.45 eV (Table 1 and Fig. S4). CNTs process excellent mechanical properties, such as high stiffness and tensile strength, along axial direction. They are easily deformable in the radial direction which limits their application. Polymerization would greatly improve the mechanical properties in the radial direction without much loses along the axial one. The 3D CNT polymers have obviously larger Young's modulus, bulk modulus, and shear modulus compared with their 1D counterpart (Tables 1 and S5). We also estimated the hardness and tensile strength of carbon polymers based on our developed models47,48,49,50,51. The results indicate that 3D polymers composed of small CNTs are all superhard carbons, among which metallic carbons have lower hardness (Tables 1 and S2). Notably, our hardness model may not be suitable for 3D polymers composed of large CNTs with very high pores because the prevailing sp2-hybridized bonds are flexible and may not be destroyed in response to external stress. Our tensile strength model can be applied to all carbon polymers. The 3D CNT polymers have high axial tensile strength comparable to that of CNTs52, and have high radial tensile strength due to sp3-bond bucklings along the radial directions (Tables 1, S3 and S4). The Poisson's ratio53 and B/G54 values of these carbon allotropes indicate that they are more ductile (less brittle) than diamond and lonsdaleite. An assembly of these excellent physical properties would make 3D CNT polymers ultimate materials for multipurpose applications.

Table 1. The calculated energy band gap (eV), axial and radial Young's modulus Ya and Yr (TPa), Vickers hardness Hv (GPa), axial and radial tensile strength σa and σr (GPa), bulk modulus B (GPa), shear modulus G (GPa), B/G radio, and Poisson's ratio ν.

Structure gap Ya Yr Hv σa σr B G B/G ν
3D (4,0)-I 2.81 1.25 0.56 89.9 86.0 75.0 391.51 379.90 1.03 0.13
3D (4,0)-II metallic 0.91 0.37 47.9 210.0 22.2 267.52 190.54 1.40 0.21
3D (4,0)-III 3.09 1.10 0.85 91.9 89.8 97.0 398.73 416.27 0.96 0.11
3D (5,0)-I 0.29 0.86 0.21 83.2 127.1 38.3 283.13 204.84 1.38 0.21
3D (5,0)-II 0.82 0.91 0.22 84.5 127.7 39.3 284.21 220.27 1.29 0.19
3D (5,0)-III 0 1.00 0.42 83.4 147.4 49.0 264.13 200.26 1.36 0.20
3D (6,0)-I 0.69 1.03 0.73 81.07 112.2 70.5 298.63 231.11 1.29 0.19
3D (6,0)-II metallic 0.83 0.10 43.0 137.7 79.9 231.08 131.00 1.76 0.26
3D (6,0)-III 2.29 1.19 0.72 83.7 77.8 72.6 334.14 352.81 0.95 0.11
3D (6,0)-IV 0.23 0.93 0.26 80.1 34.5 60.7 212.63 257.22 0.83 0.07
3D (2,2)-I 0.23 1.05 0.80 88.1 99.2 66.5 371.07 289.22 1.28 0.19
3D (2,2)-II 3.45 1.23 0.94 93.6 96.3 112.9 415.60 434.23 0.96 0.11
3D (2,2)-III 2.97 1.22 1.10 95.2 113.0 93.4 427.68 487.06 0.88 0.09
3D (3,3)-I 1.24 1.13 0.49 90.9 130.0 76.6 343.91 283.55 1.21 0.18
3D (3,3)-II 2.01 0.94 0.73 85.5 97.9 54.7 345.58 324.28 1.07 0.14
3D (3,3)-III 2.88 1.13 0.71 85.3 99.9 69.1 356.04 345.09 1.03 0.13
Open in a new tab

Discussion

Carbon allotropes are notable due to the diversity of their structures and properties. Syntheses of these novel carbon phases depend on two important aspects of the transition process, namely the enthalpies of the initial and final states and the transition energy barrier. CNTs are a suitable choice of precursors because they possess high enthalpy with respect to graphite. On the other hand, the transition barrier can be well tuned with pressure: a lower energy barrier can be achieved under higher pressure55. We thus proposed an effective route to achieve numerous novel carbons with versatile physical properties, namely the pressure induced CNT polymerization. Specifically, the structural, electronic, and mechanical property changes of small SWCNTs, such as (4,0), (5,0), (6,0), (8,0), (12,0), (2,2), (3,3), (4,4), and (10,10) CNTs, under hydrostatic/non-hydrostatic pressure are presented. During the transition, peculiar conductance oscillations in compressed CNTs are revealed in the calculations, an effect that can be used in nanoelectromechanical systems. The estimated transition barriers of small SWCNTs under pressure are less than that of graphite, indicating an easier synthesis of polymeric CNTs. The obtained 3D polymers strongly relate to the raw CNTs with different diameters, chiralities, stacking manners, and wall numbers. These novel 3D CNT polymers show excellent mechanical properties, such as high hardness, strength, and ductility, and a wide range of electronic properties ranging from metallic to semiconducting. Similarly exciting polymorphs may also be accessible from high-pressure studies of CNTs analogs, such as boron nitride, silicon, germanium, and MoS2 nanotubes. As a final remark, we point out the possibility of achieving more exotic carbon allotropes with superior properties from compressing MWCNT bundles as well as mixture of distinct nanotubes, and related simulations are being undertaken.

Methods

Carbon nanotubes packed in periodic crystal lattices, such as hexagonal, orthorhombic, and tetragonal arrangements, with a standard intertube spacing of 3.4 Å were constructed using the Materials Studio package56. Structural relaxations and property calculations were performed based on the density functional theory (DFT) as implemented in the CASTEP code56. The Vanderbilt ultrasoft pseudopotential was used and the electron-electron exchange interaction was described by the local density approximation (LDA) exchange-correlation functional of Ceperley and Alder, as parameterized by Perdew and Zunger (CA-PZ)57,58. The plane-wave cutoff energy was 310 eV, and a k-point spacing (2π × 0.04 Å−1) was used to generate Monkhorst-Pack k-points grids for Brillouin zone sampling59. Primitive cells were used to calculate the band structures and the elastic constant, Young's modulus, bulk modulus, and shear modulus.

For the transition paths of 3R graphite→3C diamond and (4,4) →3D (4,4) under hydrostatic pressure, the intermediate structures are determined by linearly altering the lattice parameters (a, b, c, α, β, and γ) from the initial structures of 3R graphite and (4,4) to the final structures of 3C diamond and 3D (4,4), respectively. For example, ai and af are the lattice parameters of 3R graphite and 3C diamond under 30 GPa, respectively. After equally divide the difference af − ai into 50 parts, the lattice parameter of an intermediate structure can be defined as an = ai + n(af − ai)/50, where n running from 1 to 49 represents the nth intermediate phase. We then optimize the atomic positions with fixed lattice parameter at the given hydrostatic pressure (30 GPa). Similarly, for the transition path of (8,0) →3D (4,0)-I under non-hydrostatic pressure, the intermediate structures are determined by linearly altering the atomic fractional coordinates from (8,0) to 3D (4,0)-I. After that, the atomic fractional positions for each intermediate structure are fixed and the lattice is fully optimized. The corresponding enthalpies are then achieved for the optimized structures. The energy barrier can then be deduced from these enthalpies for specific applied pressure. As shown in Figure 5, thirteen typical values are selected to describe the trend of enthalpy and reveal the energy barrier in the transition process under applied pressure.

Author Contributions

B.X. and Y.J.T. designed and coordinated the overall study. M.H., Z.S.Z., F.T., Q.Q.W. and M.X. performed calculations. A.R.O., C.Z.F., B.W., J.L.H., D.L.Y., H.-T.W., B.X. and Y.J.T. analyzed all data. M.H., Z.S.Z., F.T., B.X. and Y.J.T. wrote the paper. All authors contributed to the discussion of the results.

Supplementary Material

Supplementary Information

SUPPLEMENTARY INFO

srep01331-s1.pdf (1.2MB, pdf)

Acknowledgments

This work was supported by NBRPC (Grant No. 2011CB808205), NSFC (Grants No. 51121061, No. 91022029, and No. 51272227). A.R.O. acknowledges funding from the National Science Foundation (grant EAR-1114313), and access to computing facilities at the Center for Functional Nanomaterials (Brookhaven National Laboratory), Moscow State University (Russia), and at the Joint Supercomputer Center (Russian Academy of Sciences, Moscow, Russia).

References

  1. Aust R. B. & Drickamer H. G. Carbon: A new crystalline phase. Science 140, 817–819 (1963). [DOI] [PubMed] [Google Scholar]
  2. Miller E. D., Nesting D. C. & Badding J. V. Quenchable transparent phase of carbon. Chem. Mater. 9, 18–22 (1997). [Google Scholar]
  3. Mao W. L. et al. Bonding changes in compressed superhard graphite. Science 302, 425–427 (2003). [DOI] [PubMed] [Google Scholar]
  4. Boulfelfel S. E., Oganov A. R. & Leoni S. Understanding the nature of “superhard graphite”. Sci. Rep. 2, 471 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Sundqvist B. Fullerenes under high pressures. Adv. Phys. 48, 1–134 (1999). [Google Scholar]
  6. Lin Y. et al. Amorphous diamond: A high-pressure superhard carbon allotrope. Phys. Rev. Lett. 107, 175504 (2011). [DOI] [PubMed] [Google Scholar]
  7. Hirai H. & Kondo K.-I. Modified phases of diamond formed under shock compression and rapid quenching. Science 253, 772–774 (1991). [DOI] [PubMed] [Google Scholar]
  8. Tonkov E. Y. & Ponyatovsky E. Phase transformations of elements under high pressure. Vol. 4 (CRC, 2005).
  9. El Goresy A. et al. A new natural, super-hard, transparent polymorph of carbon from the Popigai impact crater, Russia. C. R. Geoscience 335, 889–898 (2003). [Google Scholar]
  10. Kirkpatrick S., Gelatt C. D. & Vecchi M. P. Optimization by simulated annealing. Science 220, 671–680 (1983). [DOI] [PubMed] [Google Scholar]
  11. Pannetier J., Bassas-Alsina J., Rodriguez-Carvajal J. & Caignaert V. Prediction of crystal structures from crystal chemistry rules by simulated annealing. Nature 346, 343–345 (1990). [Google Scholar]
  12. Glass C. W., Oganov A. R. & Hansen N. USPEX—evolutionary crystal structure prediction. Comput. Phys. Commun. 175, 713–720 (2006). [Google Scholar]
  13. Oganov A. R. & Glass C. W. Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J. Chem. Phys. 124, 244704–244715 (2006). [DOI] [PubMed] [Google Scholar]
  14. Wales D. J. & Doye J. P. K. Global optimization by basin-hopping and the lowest energy structures of lennard-jones clusters containing up to 110 atoms. J. Phys. Chem. A 101, 5111–5116 (1997). [Google Scholar]
  15. Nayeem A., Vila J. & Scheraga H. A. A comparative study of the simulated-annealing and Monte Carlo-with-minimization approaches to the minimum-energy structures of polypeptides: [met]-enkephalin. J. Comput. Chem. 12, 594–605 (1991). [Google Scholar]
  16. Martoňák R., Laio A. & Parrinello M. Predicting crystal structures: the Parrinello-Rahman method revisited. Phys. Rev. Lett. 90, 075503 (2003). [DOI] [PubMed] [Google Scholar]
  17. Martoňák R. et al. Simulation of structural phase transitions by metadynamics. Zeitschrift für Kristallographie 220, 489–498 (2005). [Google Scholar]
  18. Zhu Q., Zeng Q. & Oganov A. R. Systematic search for low-enthalpy sp3 carbon allotropes using evolutionary metadynamics. Phys. Rev. B 85, 201407 (2012). [Google Scholar]
  19. Zhu Q., Oganov A. R. & Lyakhov A. O. Evolutionary metadynamics: a novel method to predict crystal structures. CrystEngComm 14, 3596–3601 (2012). [Google Scholar]
  20. Pickard C. & Needs R. High-pressure phases of silane. Phys. Rev. Lett. 97, 045504 (2006). [DOI] [PubMed] [Google Scholar]
  21. Pickard C. J. & Needs R. J. Highly compressed ammonia forms an ionic crystal. Nat. Mater. 7, 775–779 (2008). [DOI] [PubMed] [Google Scholar]
  22. Wang Y., Lv J., Zhu L. & Ma Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010). [Google Scholar]
  23. Wang Y., Lv J., Zhu L. & Ma Y. Calypso: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012). [Google Scholar]
  24. Dellago C., Bolhuis P. G., Csajka F. S. & Chandler D. Transition path sampling and the calculation of rate constants. J. Chem. Phys. 108, 1964 (1998). [Google Scholar]
  25. Zhao Z. et al. Novel superhard carbon: C-centered orthorhombic C8. Phys. Rev. Lett. 107, 215502 (2011). [DOI] [PubMed] [Google Scholar]
  26. Wang Z. et al. A quenchable superhard carbon phase synthesized by cold compression of carbon nanotubes. Proc. Natl. Acad. Sci. U.S.A. 101, 13699–13702 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Li Q. et al. Superhard monoclinic polymorph of carbon. Phys. Rev. Lett. 102, 175506 (2009). [DOI] [PubMed] [Google Scholar]
  28. Wang Y., Panzik J. E., Kiefer B. & Lee K. K. M. Crystal structure of graphite under room-temperature compression and decompression. Sci. Rep. 2, 520 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Venkateswaran U. et al. Probing the single-wall carbon nanotube bundle: Raman scattering under high pressure. Phys. Rev. B 59, 10928 (1999). [Google Scholar]
  30. Teredesai P. V. et al. Pressure-induced reversible transformation in single-wall carbon nanotube bundles studied by Raman spectroscopy. Chem. Phys. Lett. 319, 296–302 (2000). [Google Scholar]
  31. Khabashesku V. N. et al. Polymerization of single-wall carbon nanotubes under high pressures and high temperatures. J. Phys. Chem. B 106, 11155–11162 (2002). [Google Scholar]
  32. Popov M., Kyotani M., Nemanich R. & Koga Y. Superhard phase composed of single-wall carbon nanotubes. Phys. Rev. B 65, 033408 (2002). [Google Scholar]
  33. Kawasaki S. et al. XRD and TEM study of high pressure treated single-walled carbon nanotubes and C60-peapods. Carbon 43, 37–45 (2005). [Google Scholar]
  34. Blank V. et al. Nanostructured superhard carbon phase obtained under high pressure with shear deformation from single-wall nanotubes Hipco. Physica B: Condensed Matter 382, 58–64 (2006). [Google Scholar]
  35. Kumar R. S. et al. X-ray Raman scattering studies on C60 fullerenes and multi-walled carbon nanotubes under pressure. Diamond Relat. Mater. 16, 1250–1253 (2007). [Google Scholar]
  36. Schultz P. A., Leung K. & Stechel E. B. Small rings and amorphous tetrahedral carbon. Phys. Rev. B 59, 733–741 (1999). [Google Scholar]
  37. Yildirim T., Gülseren O., Kılıç Ç. & Ciraci S. Pressure-induced interlinking of carbon nanotubes. Phys. Rev. B 62, 12648–12651 (2000). [Google Scholar]
  38. Zhao Z. et al. Three dimensional carbon-nanotube polymers. ACS Nano 5, 7226-7234 (2011). [DOI] [PubMed] [Google Scholar]
  39. Ouyang M., Huang J. L., Cheung C. L. & Lieber C. M. Energy gaps in "metallic" single-walled carbon nanotubes. Science 292, 702–705 (2001). [DOI] [PubMed] [Google Scholar]
  40. Delaney P., Choi H. J., Ihm J., Louie S. G. & Cohen M. L. Broken symmetry and pseudogaps in ropes of carbon nanotubes. Nature 391, 466–468 (1998). [Google Scholar]
  41. Hoffmann R., Hughbanks T., Kertesz M. & Bird P. H. Hypothetical metallic allotrope of carbon. J. Am. Chem. Soc. 105, 4831–4832 (1983). [Google Scholar]
  42. Tangney P., Capaz R. B., Spataru C. D., Cohen M. L. & Louie S. G. Structural transformations of carbon nanotubes under hydrostatic pressure. Nano Lett. 5, 2268–2273 (2005). [DOI] [PubMed] [Google Scholar]
  43. Sluiter M. & Kawazoe Y. Phase diagram of single-wall carbon nanotube crystals under hydrostatic pressure. Phys. Rev. B 69, 224111 (2004). [Google Scholar]
  44. Kılıç Ç., Ciraci S., Gülseren O. & Yildirim T. Variable and reversible quantum structures on a single carbon nanotube. Phys. Rev. B 62, R16345–R16348 (2000). [Google Scholar]
  45. Fahy S., Louie S. G. & Cohen M. L. Pseudopotential total-energy study of the transition from rhombohedral graphite to diamond. Phys. Rev. B 34, 1191 (1986). [DOI] [PubMed] [Google Scholar]
  46. Zhou X.-F. et al. Ab initio study of the formation of transparent carbon under pressure. Phys. Rev. B 82, 134126 (2010). [Google Scholar]
  47. Gao F. et al. Hardness of covalent crystals. Phys. Rev. Lett. 91, 015502 (2003). [DOI] [PubMed] [Google Scholar]
  48. He J., Wu E., Wang H., Liu R. & Tian Y. Ionicities of boron-boron bonds in B12 icosahedra. Phys. Rev. Lett. 94, 015504 (2005). [DOI] [PubMed] [Google Scholar]
  49. Guo X. et al. Hardness of covalent compounds: roles of metallic component and d valence electrons. J. Appl. Phys. 104, 023503 (2008). [Google Scholar]
  50. Tian Y., Xu B. & Zhao Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 33, 93–106 (2012). [Google Scholar]
  51. Guo X. et al. Unbinding force of chemical bonds and tensile strength in strong crystals. J. Phys.: Condens. Matter 21, 485405 (2009). [DOI] [PubMed] [Google Scholar]
  52. Demczyk B. G. et al. Direct mechanical measurement of the tensile strength and elastic modulus of multiwalled carbon nanotubes. Mater. Sci. Eng. A 334, 173–178 (2002). [Google Scholar]
  53. Frantsevich I., Voronov F. & Bokuta S. Elastic constants and elastic moduli of metals and insulators handbook. Naukova Dumka, Kiev, 60–180 (1983). [Google Scholar]
  54. Pugh S. F. Xcii. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Phil. Mag. 45, 823–843 (1954). [Google Scholar]
  55. Wang J.-T., Chen C. & Kawazoe Y. Low-temperature phase transformation from graphite to sp3 orthorhombic carbon. Phys. Rev. Lett. 106, 075501 (2011). [DOI] [PubMed] [Google Scholar]
  56. Clark S. J. et al. First principles methods using CASTEP. Zeitschrift für Kristallographie 220, 567–570 (2005). [Google Scholar]
  57. Ceperley D. M. & Alder B. J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 45, 566–569 (1980). [Google Scholar]
  58. Perdew J. P. & Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 23, 5048–5079 (1981). [Google Scholar]
  59. Monkhorst H. J. & Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

SUPPLEMENTARY INFO

srep01331-s1.pdf (1.2MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES