Abstract
Triboelectric charging is common in desert sandstorms and dust devils on Earth; however, it remains poorly understood. Here we show a charging mechanism of sands with the adsorbed water on micro-porous surface in wind-blown sand based on the fact that water content is universal but usually a minor component in most particle systems. The triboelectric charging could be resulted due to the different mobility of H+/OH− between the contacting sands with a temperature difference. Computational fluid dynamics (CFD) and discrete element method (DEM) were used to demonstrate the dynamics of the sand charging. The numerically simulated charge-to-mass ratios of sands and electric field strength established in wind tunnel agreed well with the experimental data. The charging mechanism could provide an explanation for the charging process of all identical granular systems with water content, including Martian dust devils, wind-blown snow, even powder electrification in industrial processes.
The transport of dust and sand by wind can provide a major mechanism conducive to land form changes due to aeolian activity, including sandy coasts, deserts and agricultural fields. The sand movement could also play an important role in environmental problems ranging from soil erosion, nutrient loss in soil and aerosol dispersion to dust storms and desertification1. According to the statistics of the Meteorological Administration of China, from 2000 to 2009, a total of 155 dust weather occurs, of which 85 times were dust storms or strong sandstorms2. A strong electric field and electrical discharge phenomena could exist and be associated with the generation of dust storms, such as spark discharge around high-voltage wire, electronic equipment subject to interference. A magnitude of 166 kV/m electric field strength could be generated at a height of 1.7 cm in a sandstorm3, while the atmospheric electric field strength on land could be about 120 V/m.
Triboelectric charging is a type of electric charge which can be generated by contact between materials through friction. The electric field induced by triboelectric charging could change the trajectories of sands and dusts; moreover, these charges could eventually influence the electric field strength. The phenomenon is also commonly known in industry, that when industrial handling of powders, particle collisions would occur and would tend to leave smaller particles with a net negative charge and larger particles with a net positive charge and thus generating electric field by the particle collision4. However, the physical charging mechanism is still poorly understood.
Assuming stochastic distribution of electrons in different energy states on particle surfaces, electrons trapped in high-energy states on one particle surface can spontaneously transfer to the position in low-energy states on another particle surface, resulting in electron charging between two contacting particles5. Based on the theory of surface state, smaller particles would be negatively charged while larger particles would be positively charged and this phenomenon can be attributed to the asymmetric surface contact between different size particles6. Yet, this charging mechanism could not appropriately explain the charging that occurs in uniform granular system. To improve the charge transfer in collision, which would depend on the pre-existing charges7; the effective contact potential difference existing between large and small particles could attribute to the charge transfer that exist in a wind-blown sand system8.
Take a polarized particle which has a positive charge top and negative charge bottom under an external dipolar electric field, for example9, the collision between two such polarized particles in the top–bottom orientation would cause charge neutralization on contact surfaces, resulting in that the particle at a higher level would gain a net positive charge while the particle at the lower level would develop a net negative charge after separation of the particles from each other. However, as the external electric field would determine the charge distribution of particles, which means that the orientation of the induced electric field would be the same as the external electric field, therefore, this theory does not explain why smaller sands at the top of sand storms are negatively charged while larger sands at the bottom of sand storms are positively charged where the orientation of the induced electric field is opposite to the atmospheric electric field which points to the ground10.
The priori models as described above would seldom account for the impact of the collision on the dynamic energy changes of the particles leading to the charging process. In fact, the transfer of charges would be related to the slip distance between colliding particles11. It is well known that a stationary granular system cannot spontaneously generate an electrostatic field and the electrostatic field would only occur when in the moving granular system12. On the other hand, water content is universal in granular systems but usually a minor component in the air of wind-blown sand. Can water content play a major role in the charging of two contacting particles?
The previously reported experiments demonstrated that the particle charge density could be related to the relative humidity in a gas–solid fluidized bed13.
In this study, combining the ionization theory of adsorbed water with particle dynamics, a charging mechanism of sand with adsorbed water has been proposed to explain the triboelectric phenomenon in a wind-blown sand system. A CFD-DEM14 method was used for sand charging simulation by combining the charging mechanism of particles with the adsorbed water, including the interaction between the gas and the sands. The proposed charging mechanism could contribute to the understanding of the performance of electrostatic air cleaners15, air ions in ventilated rooms16 and deposition of particles in ventilation ducting in turbulent channel airflow17,18. The purpose of this paper is to present the numerical simulation of wind-blown sand in wind tunnel experiments to verify the ion dynamic transfer process in the sand system.
The adhesion interaction between solid particle surface and water vapour is controlled by dispersion forces and specific bonding forces19. Adsorption due to dispersive interactions is a purely physical phenomenon, whereas surfaces that are able to form hydrogen bond with water could exhibit a specific attraction at preferential adsorption sites. Thus, the water sorption capacity of the sand would be mainly determined by the interaction between the sand surface and the water molecules. As shown in Fig. 1(a) and (b), there are many uneven pits on sand surfaces, which would provide a large surface free energy with a high potential for water to be adsorbed at these microporous sand structures. In fact, the adsorption of water would depend on the sizes of the micropores in the sand and the water being adsorbed in a progressive way, filling the narrower micropores first in the micropore structure20. When sands are suspended in the atmosphere, the water molecules in the atmosphere would be absorbed on the potholes zone of the sand surfaces, and this would increase the weight of the sand. The amount of water adsorbed can be determined by the volume of total microporosity on the sand surface. In order to assess the capacity of sand to adsorb water, the sand samples taken from Kumtag desert were exposed in various environments with different temperature and relative humidity in experiments. Fig. 1(c) shows the capacity of the sand to adsorb water, which would increase with the relative humidity in the atmosphere; therefore, the water content and thickness of the adsorbed water on the sand surfaces would, thus increase with the relative humidity.
Figure 1.
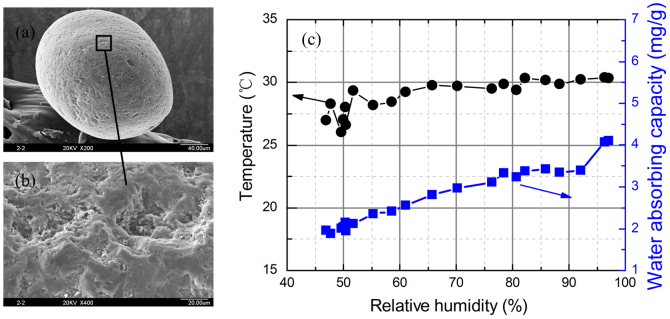
(a) The SEM image of sand surface structure, ×200.The sand surface is microporous, there are many irregular zones. (b) An enlarged image showing details on the sand surface, ×400. There are many nanoscale pores on the pit zones, which could adsorb water from atmospheric environment. (c) The water sorption capacity of the sand under different relative humidity conditions. Dots indicate the temperature of the atmosphere. The boxes represent the measured absorbent capacity of the sand.
The ion/electron comes from the film of adsorbed water on the micro-porous surfaces of the sands21. Through the contacting interface, the migration of ion/electron from the adsorbed water film of one sand to another could make the sand to become oppositely charged after separation22.
What is the driving force for the migration of ion/electron? It is well known that the initial temperature difference could drive the ions/electrons to migrate among crystals/graupels in thunderstorms to generate lightning23. But for the sand system even with the same initial temperature, the partition of the friction work between the contacting sands could cause increments in the elevation of internal energy and temperature change of the sands24. Different sand temperature increment would have a different water ionization and thus different H+/OH− concentration in the adsorbed water film. A higher temperature increase of sand would increase H+ and OH− concentrations in the adsorbed water film25. Although the migrations of H+/OH− can happen simultaneously from the high temperature sands to low temperature sands, the higher mobility of H+ than that of OH− 22 would make the high temperature sands to become negatively charged and low temperature sands to be positively charged.
In general, the wind-blown sand system is a gas-solid two-phase flow. The gas phase would provide the kinetic energy to the sand system. Together with the friction created between the contacting sands, the hysteresis deformation resulting from collision would transform the kinetic energy into internal energy of the sands. In a gas-solid two-phase flow, the temperature difference between sand and gas would enhance the heat transfer between the sand and gas. Therefore, the gas flow could affect not only the movement and collision of sands, but also the heat transfer between sand and gas, thus the dynamic charging process of the sand system.
The internal energy conversion of sands, W, may be divided into the frictional work (tangential relative slip) and the hysteresis deformation energy (normal direction) between sand i and sand j as represented by Equation (1).
Where, 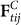 and
and 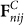 are the tangential force and normal force on the contacting interface, respectively; e is the coefficient of restitution; δt and δn are the tangential displacement and normal displacement.
are the tangential force and normal force on the contacting interface, respectively; e is the coefficient of restitution; δt and δn are the tangential displacement and normal displacement.
Assuming the internal energy conversion is equally partitioned between sand i and sand j, the temperature increment, ΔT1, of sand i can be determined by Equation (2).
Where Vi is the volume of sand i, ρ is the density of sand, c is the specific heat capacity, a1 is the conversion coefficient from mechanical energy to internal energy and in this study, a1 = 0.9 is assumed.
The heat transfer between the contacting sands is neglected owing to the short collision time. During the free movement of sand i in the gas flow after particles collision, the instantaneous temperature difference between sand i and the gas can be evaluated by Equation (3).
Where, 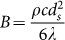 , Nu = 0.37Re0.6Pr1/3 base on the heat transfer empirical formula of the flow around a sphere26; λ is the coefficient of heat conductivity, Re is Reynolds number, and Pr is Prandtl number.
, Nu = 0.37Re0.6Pr1/3 base on the heat transfer empirical formula of the flow around a sphere26; λ is the coefficient of heat conductivity, Re is Reynolds number, and Pr is Prandtl number.
The ion/electron dynamic transfer process in the sand system with adsorbed water film is shown in Fig. 2.
Figure 2. The schematic of ion/electron dynamic transfer between two different size sands with an adsorbed water film.
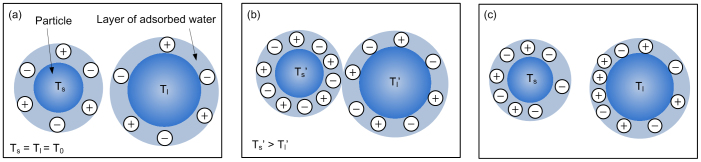
(a) The electroneutral sands would initially have the same temperature, T0. (b) The internal energy conversion by collision would cause a temperature rise of the sands while increasing the ion concentration in the adsorbed water film. The ion would migrate from the high temperature sands to low temperature particles through the contacting interface. (c) The high temperature particles would become negatively charged while the low temperature sands become positively charged due to the mobility of H+ being greater than that of OH−.
If the gas temperature is maintained constant, the ion concentration of H+ and OH− in the adsorbed water film would depend on the temperature difference between sand i and the gas. Under the mobility difference between H+ and OH−, the ion/electron flux, J, between the contacting sand i and sand j would be related to the temperature difference as shown in Equation (4).
Where, ΔTi and ΔTj are the instantaneous temperature difference between sand i/sand j and gas, respectively. The item (ΔTi − ΔTj) represents the temperature difference between two contacting sands; a2 is the electrical conductivity of the particles with the adsorbed water, and this would be influenced by the relative humidity and ambient temperature in a wind-sand system; a3 is the coefficient which describes the electrical charge flux between the sands and it is related to the ionic product of water, mobility of H+ and OH− and the amount of ion/electron on the particle surface.
The electrical conductivity a2 would increase with an increase in relative humidity27, while the coefficient a3 would vary with the relative humidity. When relative humidity is low, a slight increment of relative humidity could result in a rapid increase of ions/electrons concentrations. However when the relative humidity exceeds a threshold value, the adsorbed water film would become thicker. The rising temperature of the particles could be retarded by the cooling effect of the water vapour due to its large specific heat capacity. Therefore, the concentrations of ions/electrons on the sands surfaces would remain low.
Therefore, the opposite charges, q, of sand i and sand j would produce through the collision contact as represented by 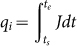 and
and 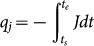 , respectively, where, ts and te are the start and end time of the sand-sand collision.
, respectively, where, ts and te are the start and end time of the sand-sand collision.
Results
From the numerical simulation results, most of the saltating sand or sand particles being suspended was charged (Fig. 3). Generally, larger size sand particles would become positively charged while smaller size sand particles would become negatively charged in the “mixture” sand system (Fig. 3(a)) which is consistent with the experimental result27.
Figure 3.
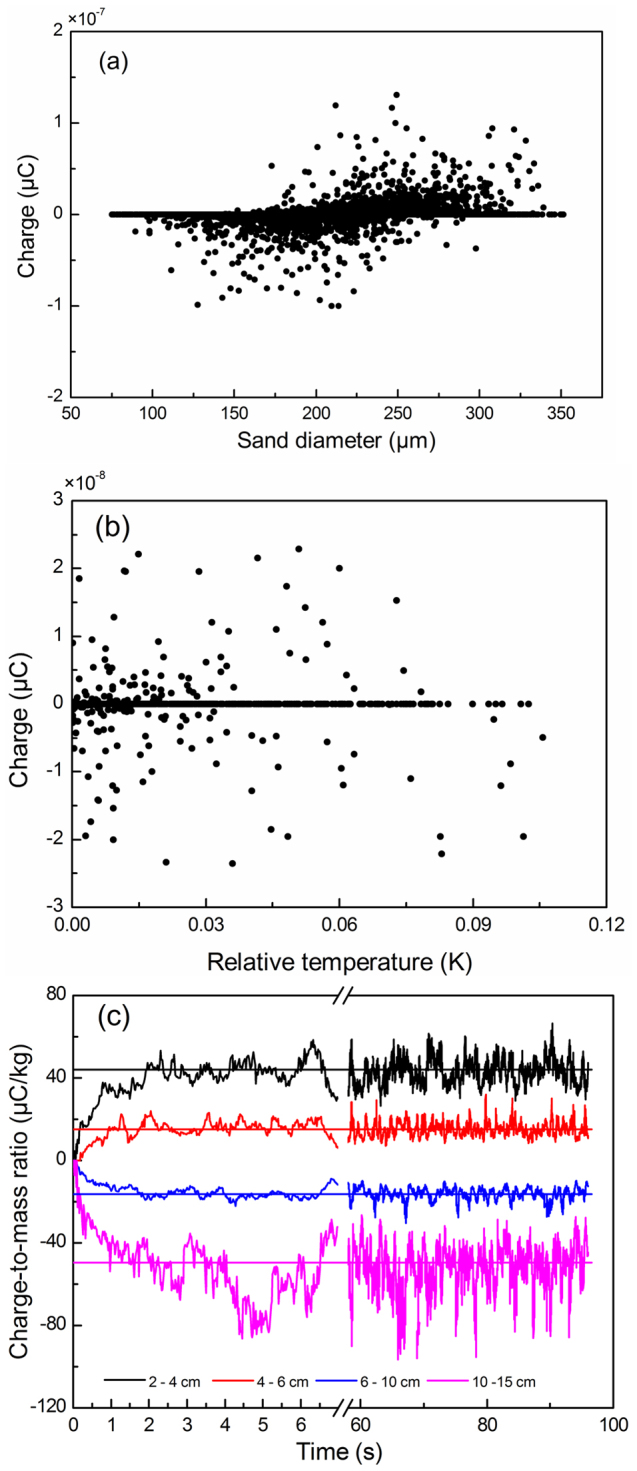
(a) The different sizes of the charged sands in a “mixture” sand system in the wind tunnel by numerical simulation, at an inlet velocity, 20 m/s.The sand diameter follows Gaussian distribution with a mean of 203 μm and a variance of 60. Almost all the sands with a diameter of more than 225 μm were positively charged while the sands with a diameter of less than 175 μm were negatively charged. (b) The charged sands and their temperature increment of the “uniform” sand system in the wind tunnel by numerical simulation, at an inlet velocity, 20 m/s; the sand diameter was 200 μm. (c) The time-varying charge-to-mass ratio of the saltating sands or sands in suspension in the “mixture” sand system at the different heights of the wind tunnel outlet by numerical simulation. The electrical conductivity of soil was between 0.005 S/m and 0.45 S/m, which increased with increasing water content41. In this study, the electrical conductivity of sand a2 = 0.01 S/m was chosen and the corresponding coefficient a3 = 0.8 was assumed.
Although the colliding particles of the same size would have the same internal energy conversion and thus the same temperature increment during each contact in the “uniform” sand system, the turbulent movement of the gas phase could induce the stochastic movement of the sand particles in a gas flow, thus resulting in different collision probability of sand particles and therefore giving different sand particle temperature increments and charges would occur (Fig. 3(b)). The charging of sand particles would depend on the collision probability rather than the diameter difference in the moving sand system, and, therefore, some different size sand particles with electric neutrality would always occur in the system as shown Fig. 3(a) and (b).
The charge-to-mass ratio of the saltating sands or sands in suspension was used in this study to illustrate the charging process in a “mixture” sand system28. The charge-to-mass ratio would increase rapidly in the initial stage of the wind-blown sand; owing to the turbulence in the gas flow and the stochastic movement of the sand particles, however, there is a fluctuation of the charge-to-mass ratio in the developed wind-blown sand system, especially at the higher level (Fig. 3(c)).
In the developed wind-blown sand flow, the average sand diameter would indicate the ensemble average of different size sand particles at a level (Fig. 4(a)). Near the surface layer of the sand bed, the charge-to-mass ratio would become positive due to the larger size sand particles with positive charges under high wind speed. However, the smaller size sand particles with negative charges would become readily suspended in the wind field, and thus the charge-to-mass ratio would convert from positive to negative at a level. The diameter of particles with zero charge-to-mass ratios would be defined as the critical diameter for the “mixture” sand system. Different experiments showed different critical sand diameter28,29, and these were related to the size distribution of the sand system, wind velocity and relative humidity. Higher wind velocity would provide more kinetic energy for the moving particle system.
Figure 4.
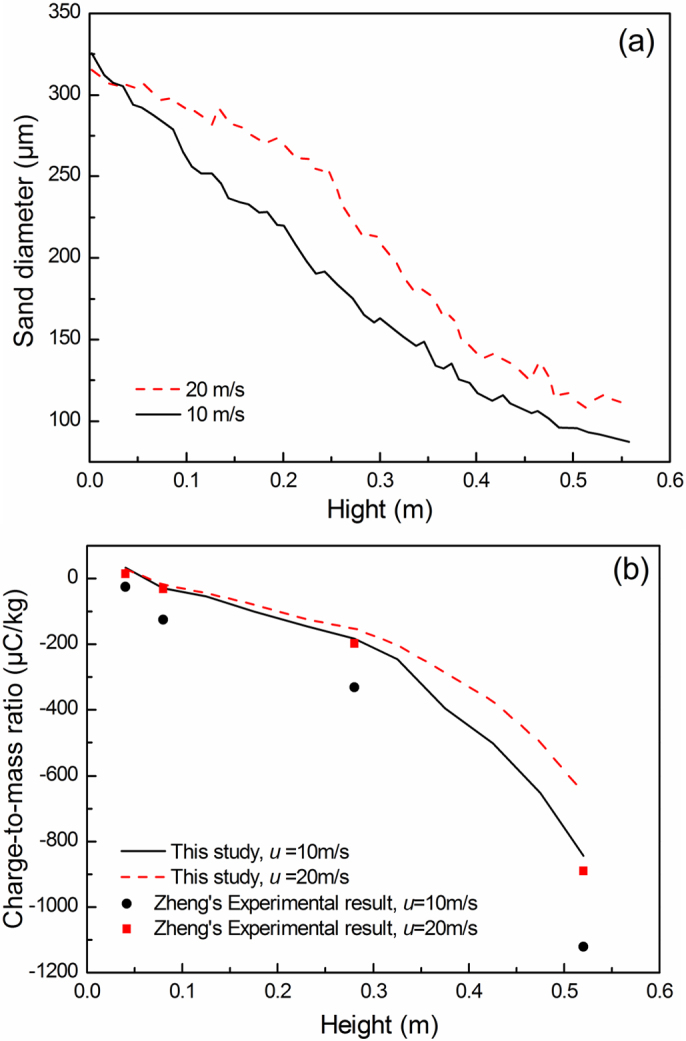
(a) The vertical distribution of the average sand diameter at the outlet of wind tunnel by numerical simulation.(b) The numerically simulated charge-to-mass ratio, in comparison with the experimental measurements at different heights28.
Two cases of the inlet velocities in the wind tunnel, 10 m/s and 20 m/s, were simulated, respectively. Fig. 4 illustrates the vertical distribution of the average sand diameter and the charge-to-mass ratio of the saltating sands or sands in suspension in the two cases. The vertical variation of the numerically simulated charge-to-mass ratio in wind tunnel agreed well with that of the experimental data28, showing the potential of the charging model of particles with adsorbed water in a moving sand system.
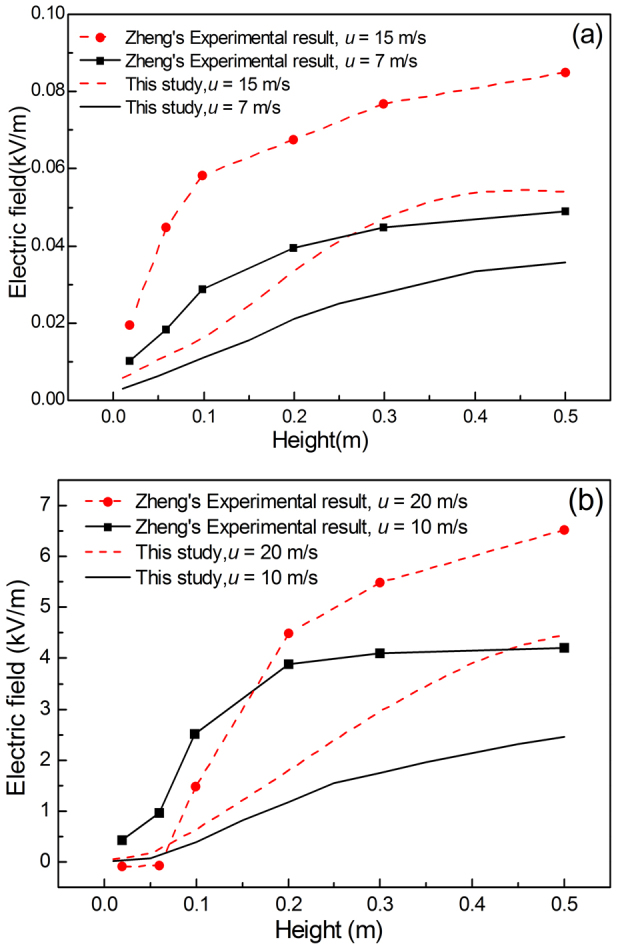
Due to the limitation of resources for the calculation, the numerically simulated flow flux of sands was far less than the actual one in wind tunnel test. Take the inlet wind velocity, u = 20 m/s for a mixture sand in the wind tunnel as an example, the numerically simulated sand flow flux was 0.06 kg/(m2s) at 0.3 m height at the outlet; however the sand flow flux measured by experiments was 1.5 kg/(m2s)30. The electric field strength shown in Fig. 5, was not directly induced by the numerically simulated charged sands; and by assuming similar collision probability of sand of unit mass, the electric field strength could be obtained through the numerically simulated electric field strength at the sand flow flux 0.06 kg/(m2s) multiplied by the ratio of the actual sand flux in wind tunnel test30 to the numerically simulated sand flux.
Figure 5. The numerically simulated electric field strength, in comparison with the experimental measurements at different heights28.
(a) uniform sands; (b) mixture sands. In wind-blown sand, the electric field at a given point P(x, y, z) due to a sand with charge qi is given by 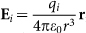 , according to Coulomb's law, where ε0 is dielectric constant and r is vector distance between the charged sand and the point P(x, y, z). Then the total electric field at the point P(x, y, z) due to all charged sands can be calculated by
, according to Coulomb's law, where ε0 is dielectric constant and r is vector distance between the charged sand and the point P(x, y, z). Then the total electric field at the point P(x, y, z) due to all charged sands can be calculated by 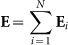 .
.
The trend in the changing electric field along the vertical direction at the wind tunnel outlet of numerically simulated electric field agreed well with that of the experimental result, as shown in Fig. 5. However, the numerical simulation result was always smaller than the experimental data. The reason for this difference may be due to the probability of the collision of the sands obtained by numerical simulation and by experiment was different. In addition, because of the influence of turbulence, the collision between grains of sands would be random.
The electric field strength is a macroscopic behaviour which is dependent on the amount of sands, while the charge-to-mass ratio is a statistical average parameter of single sand in the sand system. When the amount of sands in numerical simulation exceeds a threshold value, the charge-to-mass ratio would not increase significantly since the collision probability of the sands would remain almost the same. Thus by using periodic boundary, the charge-to-mass ratio could be calculated directly when the numerical simulation time is long enough to reach a quasi-steady wind-blown sand flow.
Discussion
The sand movement can occur not only on Earth, but also on Mars. There is evidence that water could be an important factor in shaping the Martian surface31 and water vapour supersaturation could exist in the atmosphere of Mars32. This is a hypothesis that has led to a belief that the subsurface regolith could be a substantial reservoir for Martian water33. In the light of the charging model of particles with adsorbed water in a moving granular system, strong electrostatic fields could occur in Martian dust devils34.
In the developed wind-blown sand flow, a part of sand particles could saltate or be suspended in the air flow and most of the saltating sands or sand particles being suspended would be charged. Larger size sand particles would become positively charged while smaller size sand particles would become negatively charged for the “mixture” sand system. Especially, the collision probability rather than the diameter difference in the moving particle system would determine the charging of the particles. The charging could also happen in the “uniform” sand system as well.
Water content is universal but usually a minor component in many particle systems of industrial processes or nature. The water content occurs in the form of adsorbed water on the micro-porous surface of the particles. In industrial operations, the transfer of powder materials could result in the formation of particle clouds, the gas phase would confer the kinetic energy to particles. We show that by attributing to the friction work between the contacting particles and the hysteresis deformation due to collision, the loss of kinetic energy of the particles would be portioned and transformed into internal energy of the particles, thus changing the temperature of the particles containing the adsorbed water. The triboelectric charging would be developed in the moving particle system, due to the different mobility of H+ and OH− between the contacting particles with temperature difference.
This charging model could also be used to study the electrification of a wide range of granular systems, including fluidized beds13, powder handling35, wind-blown snow36, and Martian dust devils34.
Methods
Large eddy simulation (LES)37 is a method of computational fluid dynamics (CFD), which is used to simulate the dynamic flow of gas or air. Discrete Element Method (DEM)38,39,40 is often used to simulate the particle-particle collision.
The wind-blown sand in a wind tunnel was simulated by numerical method in this study, to verify the ion dynamic transfer process in the sand system. The sand for the wind-blown sand experiments28 was sampled from a sand dune at the south-eastern edge of the Tengger desert of China. The electric charge-to-mass ratio and the electric field at some heights for different sand samples, i.e., the ‘‘uniform’’ sand and the mixture sands, were measured at the outlet of the wind tunnel. The axial inlet wind velocity from 7 m/s to 20 m/s was the velocity regime used in the wind tunnel capable of producing the wind-blown air-sand two-phase flow.
In our numerical simulation, the cyclic boundary conditions for the sands were adopted due to the limit of sand amount in simulations. The evolution of wind-blown sand in the wind tunnel was simulated and this would undergo a series of processes as follows:
Saltation of the sands in the wind field
Agitation of the sands being rebounding and splashing after the descending sand colliding with sand bed
Ionisation of the sands being charged by collision of the contacting sands
Stabilisation of wind-blown sands that flow and reaching a stable state.
At a given inlet velocity in a wind tunnel, two wind-blow sand systems, the uniform sand system and the mixture sand system, were simulated. 20,000 particles for the uniform sand system and 30,000 particles for the mixture sand system were set in the air flow, respectively. In the developed wind-blown sand 38.18% of sand particles would flow in the uniform sand system and 46.96% in the mixture sand system and these would saltate or become suspended in the air flow in our numerical simulations.
Author Contributions
Z.L. Gu: theoretical work, project planning and article writing. W. Wei: theoretical and numerical work. J.W. Su: numerical work. C.W. Yu: article writing. All authors discussed the results and commented on the manuscript.
Acknowledgments
This work was funded by the National Natural Science Foundation of China (No.10872159) and the Key-grant Project of Chinese Ministry of Education (No. 708081).
References
- Kok J. F., Parteli E. J. R., Michaels T. I. & Karam D. B. The physics of wind-blown sand and dust. Rep. Prog. Phys. 75, 106901 (2012). [DOI] [PubMed] [Google Scholar]
- China Meteorological Administration. Sand-dust Weather Almanac (2000–2009), (Meteorological Press, 2010). [Google Scholar]
- Schmidt D. S., Schmidt R. A. & Dent J. D. Electrostatic force on saltating sand. Journal of Geophysical Research-Atmospheres 103, 8997–9001 (1998). [Google Scholar]
- Inculet I. I., Peter Castle G. S. & Aartsen G. Generation of bipolar electric fields during industrial handling of powders. Chem. Eng. Sci. 61, 2249–2253 (2006). [Google Scholar]
- Lacks D. J., Duff N. & Kumar S. K. Nonequilibrium accumulation of surface species and triboelectric charging in single component particulate systems. Phys. Rev. Lett. 100 (2008). [DOI] [PubMed] [Google Scholar]
- Kok J. F. & Lacks D. J. Electrification of granular systems of identical insulators. Phys. Rev. E 79, 051304 (2009). [DOI] [PubMed] [Google Scholar]
- Desch S. J. & Cuzzi J. N. The generation of lightning in the solar nebula. Icarus 143, 87–105 (2000). [Google Scholar]
- Kok J. F. & Renno N. O. Electrostatics in wind-blown sand. Phys. Rev. Lett. 100 (2008). [DOI] [PubMed] [Google Scholar]
- Pahtz T., Herrmann H. J. & Shinbrot T. Why do particle clouds generate electric charges? Nat. Phys. 6, 364–368 (2010). [Google Scholar]
- Lacks D. J. Particle clouds frictile attraction. Nat. Phys. 6, 324–325 (2010). [Google Scholar]
- Lowell J. & Truscott W. S. Triboelectrification of identical insulators. II. Theory and further experiments. J. Phys. D. Appl. Phys. 19, 1281 (1986). [Google Scholar]
- Lacks D. J. & Sankaran R. M. Contact electrification of insulating materials. J. Phys. D. Appl. Phys. 44 (2011). [Google Scholar]
- Chen A. H., Bi H. T. & Grace J. R. Measurement of particle charge-to-mass ratios in a gas-solids fluidized bed by a collision probe. Powder Technol. 135, 181–191 (2003). [Google Scholar]
- Su J. W., Gu Z. L. & Xu X. Y. Discrete element simulation of particle flow in arbitrarily complex geometries. Chem. Eng. Sci. 66, 6069–6088 (2011). [Google Scholar]
- Tung T. C. W., Niu J. L., Burnett J. & Hung K. Determination of ozone emission from a domestic air cleaner and decay parameters using environmental chamber tests. Indoor. Built. Environ 14, 29–37 (2005). [Google Scholar]
- Fletcher L. A., Noakes C. J., Sleigh P. A., Beggs C. B. & Shepherd S. J. Air ion behavior in ventilated rooms. Indoor. Built. Environ 17, 173–182 (2008). [Google Scholar]
- Sun K., Lu L. & Jiang H. Modelling of particle deposition and rebound behaviour on ventilation ducting wall using an improved wall model. Indoor. Built. Environ 20, 300–312 (2011). [Google Scholar]
- Jiang H., Lu L. & Sun K. Computational Fluid Dynamics (CFD) Modelling of Particle Deposition in a Two-dimensional Turbulent Channel Air Flow: Study of Influence Factors. Indoor. Built. Environ 21, 264–272 (2012). [Google Scholar]
- Muster T. H., Prestidge C. A. & Hayes R. A. Water adsorption kinetics and contact angles of silica particles. Colloid Surface. A 176, 253–266 (2001). [Google Scholar]
- Alcaniz-Monge J., Linares-Solano A. & Rand B. Mechanism of adsorption of water in carbon micropores as revealed by a study of activated carbon fibers. J. Phys. Chem. B 106, 3209–3216 (2002). [Google Scholar]
- Friedman S. P. Soil properties influencing apparent electrical conductivity: a review. Comput. Electron. Agr. 46, 45–70 (2005). [Google Scholar]
- McCarty L. S. & Whitesides G. M. Electrostatic charging due to separation of ions at interfaces: Contact electrification of ionic electrets. Angew. Chem. Int. Edit. 47, 2188–2207 (2008). [DOI] [PubMed] [Google Scholar]
- Jayaratne E. R., Saunders C. P. R. & Hallett J. Laboratory studies of the charging of soft-hail during ice crystal interactions. Q. J. Roy. Meteor. Soc. 109, 609–630 (1983). [Google Scholar]
- Lu L. Y., Gu Z. L., Luo X. L. & Lei K. B. An electrostatic dynamic model for wind-blown sand systems. Acta Phys. Sin-ch. Ed 57, 6939–6945 (2008). [Google Scholar]
- Qu J. J. et al. Wind tunnel simulation experiment and investigation on the electrification of sandstorms. Sci. China Ser. D 47, 529–539 (2004). [Google Scholar]
- Eckert E. R. G. Heat and mass transfer, (McGraw-Hill, 1959). [Google Scholar]
- Awakuni Y. & Calderwo J. H. Water vapour adsorption and surface conductivity in solids. J. Phys. D. Appl. Phys. 5, 1038–1045 (1972). [Google Scholar]
- Zheng X., Huang N. & Zhou Y. Laboratory measurement of electrification of wind-blown sands and simulation of its effect on sand saltation movement. J. Geophys. Res. 108, 4322–4331 (2003). [Google Scholar]
- Greeley R. & leach R. A preliminary assessment of the effects of electrostatics on eolian processes. NASA TM 79279 236–237 (1978). [Google Scholar]
- Zhou Y. H., Guo X. & Zheng X. J. Experimental measurement of wind-sand flux and sand transport for naturally mixed sands. Phys. Rev. E 66, 021305 (2002). [DOI] [PubMed] [Google Scholar]
- Baker V. R. Water and the martian landscape. Nature 412, 228–236 (2001). [DOI] [PubMed] [Google Scholar]
- Maltagliati L. et al. Evidence of water vapor in excess of saturation in the atmosphere of Mars. Science 333, 1868–1871 (2011). [DOI] [PubMed] [Google Scholar]
- Boynton W. V. et al. Distribution of hydrogen in the near surface of Mars: Evidence for subsurface ice deposits. Science 297, 81–85 (2002). [DOI] [PubMed] [Google Scholar]
- Renno N. O. & Kok J. F. Electrical activity and dust lifting on Earth, Mars, and beyond. Space Sci. Rev. 137, 419–434 (2008). [Google Scholar]
- Matsusaka S. & Masuda H. Electrostatics of particles. Adv. Powder Technol. 14, 143–166 (2003). [Google Scholar]
- Gordon M. & Taylor P. A. The Electric Field During Blowing Snow Events. Bound-lay. Meteorol. 130, 97–115 (2009). [Google Scholar]
- Gu Z. L., Jiao J. Y., Zhang Y. W. & Su J. W. The nature of a universal subgrid eddy viscosity model in a turbulent channel flow. Europhys. Lett. 94 (2011). [Google Scholar]
- Tsuji Y., Kawaguchi T. & Tanaka T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 77, 79–87 (1993). [Google Scholar]
- Gu Z. L., Lu L. Y. & Ai L. Impact energy loss from particle surface roughness in particulate systems. Europhys. Lett. 87 (2009). [Google Scholar]
- Lu L. Y., Gu Z. L. & Lei K. B. An inter-particle contact area and time restoration for softening treatment in thermal discrete element modeling. Europhys. Lett. 87 (2009). [Google Scholar]
- McCutcheon M. C., Farahani H. J., Stednick J. D., Buchleiter G. W. & Green T. R. Effect of soil water on apparent soil electrical conductivity and texture relationships in a dryland field. Biosystems Engineering 94, 19–32 (2006). [Google Scholar]


