A New Maximum Likelihood Approach for Free Energy Profile Construction from Molecular Simulations

Abstract

A novel variational method for construction of free energy profiles from molecular simulation data is presented. The variational free energy profile (VFEP) method uses the maximum likelihood principle applied to the global free energy profile based on the entire set of simulation data (e.g from multiple biased simulations) that spans the free energy surface. The new method addresses common obstacles in two major problems usually observed in traditional methods for estimating free energy surfaces: the need for overlap in the re-weighting procedure and the problem of data representation. Test cases demonstrate that VFEP outperforms other methods in terms of the amount and sparsity of the data needed to construct the overall free energy profiles. For typical chemical reactions, only ~5 windows and ~20-35 independent data points per window are sufficient to obtain an overall qualitatively correct free energy profile with sampling errors an order of magnitude smaller than the free energy barrier. The proposed approach thus provides a feasible mechanism to quickly construct the global free energy profile and identify free energy barriers and basins in free energy simulations via a robust, variational procedure that determines an analytic representation of the free energy profile without the requirement of numerically unstable histograms or binning procedures. It can serve as a new framework for biased simulations and is suitable to be used together with other methods to tackle with the free energy estimation problem.

Introduction

Free energy simulations provide a wealth of insights into complex biomolecular problems. However, the robust calculation of free energies, and in particular free energy surfaces, remains a challenging problem for which much work has been, and continues to be, devoted.¹ One of the primary challenges involves the need to properly sample the necessary degrees of freedom from which a free energy profile can be derived. Strategies to solve this problem are manyfold, and some of the most widespread include multistage/stratified sampling,² statically^3-5 and adaptively^6-8 biased sampling, self-guided dynamics,⁹ constrained dynamics,^10,11 as well as multicanonical^12,13 and replica exchange¹⁴ algorithms. In addition, a number of simulation protocols based on nonequilibrium sampling^15-18 have also been recently proposed as well as hybrid algorithms.^19,20

One of the most widely used methods for determining free energy surfaces for chemical reactions, where often there are geometric coordinates that are known to be aligned with the overall reaction coordinate, is the “umbrella sampling”⁴ technique, which combines stratification with equilibrium, statically biased sampling. Umbrella sampling is particularly amenable to parallel execution, especially in high performance distributed environments,^21,22 as well as extension or combination with replica exchange^23,24 and alchemical simulation techniques.²⁵ There are two key difficulties in umbrella sampling methods that remain serious challenges: the problem of “data re-weighting” and of “data representation.” Data re-weighting refers to the fact that differently biased simulations can only yield accurate information about unbiased simulations after application of a corrective statistical weight. Data representation describes the problem of giving a functional form (either parametric or non-parametric, numerical or analytical) to the target expectation or statistics.

The need of overlap in data re-weighting

The data re-weighting problem has long been known in the field of molecular simulation and is, in principle, exactly solved by the free energy perturbation (FEP)/Zwanzig relation and the related expression for arbitrary mechanical observables.^4,26,27 However, naive implementation of the FEP estimator is not optimal when considering more than one sample set (see Ref 28 for a recent survey). Contemporary methods include the Bennett acceptance ratio,²⁹ weighted histogram analysis method (WHAM),³⁰ and multistate Bennett acceptance ratio (MBAR).^31,32 All of these methods are essentially equivalent in their statistical underpinning and rely on the overlap between states (windows) to perform the re-weighting, but can vary in practical applications where sampling is incomplete and, as a result, improved methods continue to be developed.^33-37 The Umbrella Integration (UI) approach of Kästner and Thiel^38-40 assumes a Gaussian model for the un-weighted probability density in each umbrella window, from which the analytic derivatives are integrated in order to recover the global probability density and hence no explicit re-weighting is necessary. In fact, UI evades the need of overlap in data re-weighting by assuming continuous first derivatives of the free energy profile between windows, even though the usage of a Gaussian model for the un-weighted probability density is not ideal in many cases.

Data representation

The data representation problem is particularly important when one is interested in studying mechanisms whereby chemical transformations occur along a minimum free energy pathway. Perhaps the simplest method of data representation is to use a histogram estimate of the probability density.^25,30,36 However, this approach is not numerically stable when data is sparse or sampling does not overlap. Alternatively, one could assume a parametric fit to the biased density in each simulation⁴¹ or apply a more robust kernel density estimator.⁴² Other methods that address the data representation problem have also been proposed. Maragakis, et al. suggested a maximum likelihood approach utilizing a Gaussian-mixture umbrella sampling (GAMUS) model for the global probability density based on the re-weighted data^43,44 in order to provide an adaptive bias in umbrella sampling simulations. Basner and Jarzynski proposed a binless estimator based upon the optimal correction to an arbitrary reference distribution.⁴⁵ Again, UI^38-40 uses Gaussian models for the un-weighted probability densities and has also recently been extended to higher order densities (i.e. skewed Gaussians).⁴⁶ The result of these assumptions is a significant reduction in the number of data points in each simulation needed to obtain a converged result. This is because parametric estimators converge much more quickly than non-parametric estimators, such as histograms, but often at the expense of increased bias. For example, the approximations/assumptions in UI require near-quadratic (or near quartic) behavior of the local free energy surface. Such behavior can be artificially imposed by using strong harmonic biasing potentials, but this often leads to low overlap between windows and the same kind of failures associated with sparsely populated histogram estimators.⁴⁷

In the present work, we introduce a new variational method for robust determination of free energy profiles (VFEP) from molecular simulation data. The method uses a maximum likelihood principle applied to the global free energy profile, and addresses common obstacles: the need for overlap in the data re-weighting and the representation problem. In the following sections, the formalism is derived, as well as formulas for estimation of statistical errors. The method is then applied to a number of numerical simulations, using two general, parametric frameworks based on Akima cubic splines and Floater-Hormann rational function interpolation. The results are compared with those derived from WHAM and MBAR (different re-weighting protocols with a histogram density estimate) as well as the UI method. For the test cases examined here, the VFEP method provides extremely robust performance relative to the other methods, particularly in the case of limited or poorly overlapping sampling and hence appears to be a promising method for robust and rapid estimation of analytic free energy profiles from molecular simulation data.

Theory

Here we briefly describe the maximum likelihood method utilized in the present work, beginning with a clarification of what is the difference between the terms “probability” and “likelihood” used in this context. In statistical modeling, probability refers to the possible outcome of data, and is usually modeled by a fixed functional form and a variable set of parameters. On the other hand, likelihood refers to how likely a given model can describe a set of observed outcome data.⁴⁸ Hence,

• Probability: p({x_n}|{θ_m}) is the probability model, defined by a fixed functional form and variable set of parameters {θ_m}, that returns the probability of observing the data set {x_n}; i.e., for a given set of model parameters {θ_m}, p({x_n}|{θ_m}) predicts the outcome for the set of data {x_n}: {θ_m} → {x_n}.

• Likelihood: $\mathcal{L}\left(\right\{{\theta }_m\}\mid \{x_n\left\}\right)$ is the likelihood that the observed data set {x_n} was generated by the probability distribution model defined by the set of parameters {θ_m}; i.e., $\mathcal{L}\left(\right\{{\theta }_m\}\mid \{x_n\left\}\right)$, for a given set of observed data {x_n}, provides an assessment of the goodness of the model parameters: {x_n} → {θ_m}.

The maximum likelihood method, or maximum likelihood estimation (MLE),^{49, 50} is the procedure of finding the optimal set of parameters that maximize the likelihood of the model probability distribution function to represent a given set of observed data.

MLE begins with the definition of the likelihood function of the sample data. The likelihood function of a set of data is the probability of obtaining that particular set of data, given the probability distribution model function defined by a chosen functional form along with a set of trial model parameters. Here we consider the probability, p(x), of observing a molecular system at a particular value of a single generalized coordinate x (the extension to multiple dimensions is straight forward). This probability is given by

$$p\left(x\right)=\frac{e^{-F\left(x\right)}}{\int e^{-F\left(x^{\prime }\right)}d{x}^{\prime }}$$ (1)

where F(x) ≡ F(x)/(k_BT) is the unitless scaled free energy profile, F(x) is the free energy profile, k_B is the Boltzmann constant and T is the absolute temperature. Consider now a parametric model for the scaled free energy profile F(x|{θ_m}) where {θ_m} is the set of parameters. The probability distribution model, p(x|{θ_m}), also contains the set of parameters, due to its relation to F(x|{θ_m}). Now considering the probability, p({x_n}|{θ_m}) of a sampled data set {x_n}, if the sampling data points are independent to each other, then:

$$p\left(\right\{x_n\}\mid \{{\theta }_m\left\}\right)=p(x_1,x_2,\dots ,x_N\mid \{{\theta }_m\left\}\right)=p(x_1\mid \{{\theta }_m\left\}\right)\cdot p(x_2\mid \{{\theta }_m\left\}\right)\cdots p(x_n\mid \{{\theta }_m\left\}\right).$$ (2)

The likelihood $\mathcal{L}$ of the trial free energy profile F{θ_m} with the given observed data set {x_n} is:

$$\mathcal{L}\left(F\right\{{\theta }_m\}\mid x_1,\dots ,x_N)=\mathcal{L}\left(\right\{{\theta }_m\}\mid x_1,\dots ,x_N)=\underset{i=1}{\overset{N}{\Pi }}p(x_i\mid \{{\theta }_m\left\}\right).$$ (3)

In the present work, instead of dealing with individual windows, we attempt to find the optimal solution of the above equation by defining a global function F(x) with a set of defined parameters {θ_m}. It is practical to use the logarithm of the likelihood function, called the log-likelihood $\widehat{\ell }$:

$$\widehat{\ell }\left(\right\{{\theta }_m\}\mid x_1,\dots ,x_N)=\frac{1}{N}\ln \mathcal{L}=\frac{1}{N}\sum _{n=1}^N\ln p(x_n\mid \{{\theta }_m\left\}\right).$$ (4)

Since the likelihood is always positive and monotonic, there is no loss of generality in formulating a variational principle based on the log-likelihood, which offers some advantages in terms of numerical stability and is conventional in the literature. Hereafter, we use the term “likelihood” generically to refer to both the likelihood or the log-likelihood, and will reference specific equations when the mathematical distinction is necessary. The MLE method estimates {θ_m} by finding the values of {θ_m} that maximize $\widehat{\ell }$:

$$\widehat{\ell }\left(\right\{{\theta }_m^{\ast }\}\mid x_1,\dots ,x_N)=\underset{\left\{{\theta }_m\right\}\in \Theta }{\text{arg max}}\widehat{\ell }\left(\right\{{\theta }_m\}\mid x_1,\dots ,x_n)=\underset{\left\{{\theta }_m\right\}\in \Theta }{\text{arg max}}\frac{1}{N}\sum _{n=1}^N\text{ln}p(x_n\mid \{{\theta }_m\left\}\right)$$ (5)

where Θ defines the space that {θ_m} can span. If a biasing potential W^α(x) is applied in the αth window in a set of umbrella sampling simulations, the probability of finding the system with a certain coordinate value x is:

$$p^{\alpha }\left(x\right)=\frac{1}{Z^{\alpha }}\exp \{-[F\left(x\right)+W^{\alpha }\left(x\right)\left]\right\},\text{where}{Z}^{\alpha }={\int }_{-\infty }^{\infty }\exp \{-[F\left(x\right)+W^{\alpha }\left(x\right)\left]\right\}dx$$ (6)

Suppose that for the simulation of the αth window, there are N^α points observed with coordinate values {$x_i^{\alpha }$}. Since they are observed points, the probability of each point is equal with value 1/N^α. The likelihood of the whole system with an overall free energy profile F(x) can be expressed as the combination of the likelihood of individual windows obtained from Eq. (4) and Eq. (6) as:

$$\begin{array}{cc}\hfill \widehat{\ell }\left(F\right)& \equiv \sum _{\alpha }^{\text{windows}}{c}^{\alpha }{\widehat{\ell }}^{\alpha }\left(\right\{{\theta }_m\}\mid \{x_n^{\alpha }\left\}\right)\hfill \\ \hfill & =-\sum _{\alpha }^{\text{windows}}{c}^{\alpha }\left\{\ln Z^{\alpha }+\frac{1}{N^{\alpha }}\sum _i^{\text{datapoints}}\left[F\right(x_i^{\alpha })+W^{\alpha }(x_i^{\alpha }\left)\right]\right\}\hfill \end{array}$$ (7)

where {c^α} are the combination weights defining the relative contribution of likelihood from different windows when combining the local likelihood into a global likelihood. When assuming all windows contribute equally, the c^α can simply be set to be equal, i.e., c^α = 1. It can also be shown that, in the exact sampling limit, the global optimal F is also the optimal F for each individual window, i.e., the choice of {c^α} does not affect the resulting optimal F(x) (see Supporting Information). In practice, for finite sampling, we observe that the overall result is largely insensitive to the choice of c^α, and for the present work, we choose c^α = 1 for all windows (also see Supporting Information). In the above equation for the global likelihood function, we have used F as the argument to emphasize that optimization of the likelihood function is with respect to the free energy profile F (by varying the {θ_m} parameters).

There remains the task of finding the F that maximizes $\widehat{\ell }\left(F\right)$. Note that in the above equation the term $W^{\alpha }\left(x_i^{\alpha }\right)$ is constant and does not need to be evaluated if the goal is to maximize the likelihood. Also, the term −lnZ^α is equivalent to the relative free energies (or free energy shifts) between windows in other re-weighting schemes. In the present VFEP approach, the “re-weighting” procedure is implicitly accomplished through the normalization against the global trial function F.

An alternate strategy is to model F(x) locally in the region of each window, F^α(x), and construct the global F(x) using the F^α(x) with the observed data density as weighting. The only variable parameters in this approach are the relative free energy shifts between every window { f^α} (the reference free energy being arbitrary) that establish the relative weights for each window. Thus, the global F(x) is defined by the parameter set { f^α} and a set of fixed local free energy profiles F^α(x). Applying the MLE procedure to F(x) with respect to the parameter { f^α} leads to the WHAM and the MBAR equations.^{31-33, 51} Note that within such a context, MBAR is also a parametric procedure where the relative free energy shifts of windows are the MLE parameters and local free energy profiles are pre-defined in data fitting procedures, whereas the proposed VFEP uses MLE parameters to construct the detailed overall free energy profiles. In summary, the WHAM and MBAR formula are equivalent to the MLE results when the global free energy profile is constructed from the local free energy profiles and the relative free energies are used as the parameters to optimize the likelihood.

In the present work, instead of dealing with individual windows, we attempt to find the optimal solution of Eq. (7) by defining a global function F(x) with a set of defined parameters {θ_m} (i.e. F(x) ≡ F(x|{θ_m})). The procedure is as follows:

1. Choose a trial function F(x) with a initial parameter set {θ_m}.

2. Evaluate the likelihood $\widehat{\ell }\left(F\right)$ of the trial function F(x) according to Eq. (7).

3. Vary the parameter set {θ_m} until the maximum of $\widehat{\ell }\left(F\right)$ is reached.

4. The trial F(x) with the maximal $\widehat{\ell }\left(F\right)$ is the desired overall free energy profile.

Two types of analytic functions were selected to model the overall free energy profile: a cubic spline function⁵² and a rational interpolation function.⁵³ Both were originally designed for interpolation usage. Nevertheless, one could treat the interpolation input data as the variable parameters; for example, a cubic spline function needs to have the {x_i, y_i} data nodes defined in order to build the desired cubic spline interpolation, where x_i is the independent variable and y_i is the corresponding observed function value. In this work, we select fixed x_i and treat y_i as the MLE parameters to be optimized, e.g. a cubic spline function defined by {x_i, y_i} will be the trial free energy function in Eq. (7) and the optimal free energy profile is reached through changing {y_i}. This is equivalent to assuming that the free energy profile varies slower than a cubic polynomial between windows or that the first and second derivatives of free energy profile are continuous between windows.

Results

A C++ program was built to test the proposed method. Two interpolation subroutines in the AlgLib (v3.5, http://www.alglib.net) package were used: The Akima spline algorithm⁵² was employed for cubic spline interpolation and the Floater-Hormann⁵³ algorithm for rational interpolation. Both the number of spline function nodes and the number of the rational interpolation poles are set to 2 times the numbers of windows minus one. There is one node located at the average data position of each window and one node located at the average position of two nodes of two adjacent windows. The results of WHAM were calculated by the program from Grossfield⁵⁴ (v2.0.4, http://membrane.urmc.rochester.edu/content/wham). The results of MBAR were calculated using the pymbar library of Shirts and Chodera³² (v2.0b, http://simtk.org/home/pymbar). The UI algorithm^38-40 was implemented as part of the VFEP program.

In order to cover a wide range of common free energy profile problems, tests were performed with a benchmark molecular dynamics simulation of a Na⁺:Cl⁻ pair in a water box, two combined quantum mechanical/molecular mechanical (QM/MM) simulations of chemical reactions, and the C-C-C-C torsion rotation of butane. These test cases represent non-bonding interactions, chemical reactions, and conformational transitions. The results for these systems are listed/described in the subsequent sections.

Na⁺:Cl⁻ pair

A Na⁺:Cl⁻ pair was put in a TIP3P water box⁵⁵ (20 Å × 20 Å × 20 Å) with the CHARMM27 force field.⁵⁶ The distance between Na⁺ and Cl⁻, defined as the relevant coordinate, was scanned from 2.4 to 7.4 Å with 21 windows separated by 0.25 Å. A biasing potential of either 5 or 100 kcal/mol/Ų was applied to each window. The NAMD package (v 2.7)⁵⁷ was used and simulations were performed under periodic boundary conditions in the NpT ensemble at 300 K and 1 atm (NAMD uses a modified Nosé-Hoover method^{58, 59} in which Langevin dynamics is used to control fluctuations in the barostat). Each window was simulated for 1 ns of equilibration and 1 ns of data collection (10,000 data points per window).

Weak biasing potential

In the first set of simulations, a biasing potential of 5 kcal/mol/Ų was applied to every umbrella sampling window, which is relatively weak, affording considerable overlap between windows. This allows fewer windows to be required to construct the overall profile than if a larger umbrella potential were used. However, in the case of weak umbrella biasing, one would expect that a quadratic approximation of the local (biased) free energy profile within any given window not to be ideal.

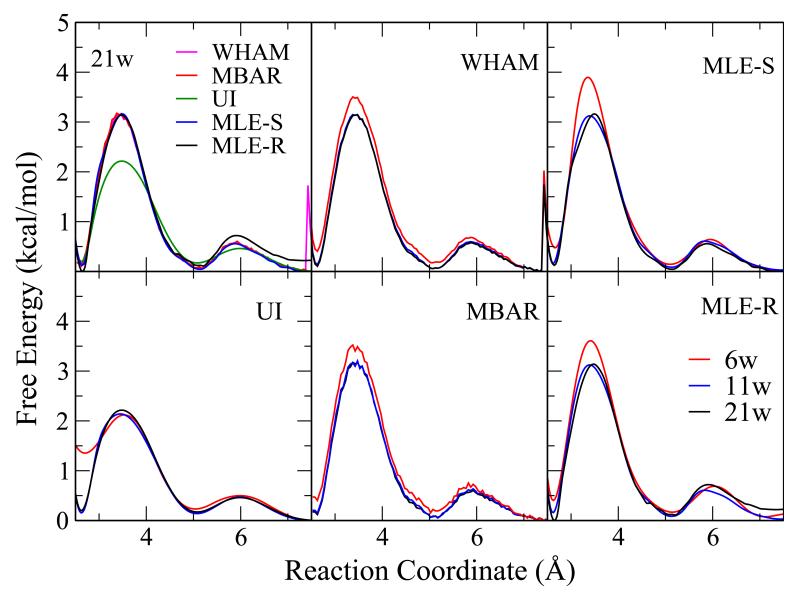
The results with the weak biasing potential of 5 kcal/mol/Ų are shown in Figure 2. The upper left panel shows the results from all methods with 21 windows. Other panels show the results from different methods with different numbers of windows (11 and 6). While all other methods converge with 21 windows (with statistic errors less than 0.05 kcal/mol, see Table 2) and give similar results with 11 or even 6 windows, UI, using a quadratic approximation, delivers a quantitatively incorrect free energy profile.

Figure 2.

The free energy profiles calculated with different methods for the Na⁺:Cl⁻ pair from a 21-window umbrella sampling simulation with a weak biasing potential of 5 kcal/mol-Ų. The upper left panel shows the results from all methods with 21 windows. Other panels show the results from individual methods with different numbers of windows: 6 (red), 11 (blue), and 21 (black) windows. While all methods converge with 21 windows and give similar results with 11 or even 6 windows, UI yields an incorrect free energy profile as expected.

Table 2.

Estimated errors for the free energy profile of the Na⁺:Cl⁻ system from VFEP andMBAR

Window (α)	x̄α	$\Delta {\widehat{\ell }}^{\alpha }(s,g)$	$\Delta {\widehat{\ell }}^{\alpha }(s,m)$	stat error (N=50)	stat error (N=100)	MBAR
1	2.629	0.022	0.060	0.018	0.018	0.043
2	2.655	0.040	0.015	0.018	0.018	0.042
3	2.686	0.125	−0.001	0.018	0.018	0.049
4	2.754	0.421	−0.034	0.018	0.018	0.070
5	3.113	0.555	−0.071	0.018	0.015	0.086
6	3.945	0.304	−0.034	0.018	0.010	0.073
7	4.275	0.160	−0.113	0.010	0.010	0.052
8	4.460	0.016	0.013	0.010	0.010	0.042
9	4.638	0.002	−0.025	0.010	0.010	0.040
10	4.797	0.002	0.007	0.009	0.009	0.040
11	4.964	0.002	0.012	0.008	0.008	0.039
12	5.127	0.003	−0.034	0.008	0.008	0.038
13	5.334	0.016	−0.008	0.009	0.008	0.039
14	5.588	0.015	−0.006	0.009	0.009	0.041
15	5.863	0.006	0.001	0.010	0.010	0.041
16	6.188	0.006	−0.012	0.010	0.011	0.038
17	6.500	0.002	−0.007	0.012	0.012	0.037
18	6.719	0.002	−0.012	0.013	0.014	0.036
19	6.955	0.000	0.010	0.015	0.015	0.035
20	7.194	0.000	−0.014	0.016	0.017	0.035
21	7.413	0.000	−0.004	0.017	0.018	0.000
RMS		0.172	0.036	0.013	0.013	0.048

The numbers here are derived from a 21-window umbrella sampling simulation on a Na⁺:Cl⁻ pair in a TIP3P water box with a biasing potential of 5 kcal/mol/Ų (see the Results section, also Figure 2). x̄^α is the average of the sampled coordinates of the αth window. $\Delta {\widehat{\ell }}^{\alpha }(s,m)$ and $\Delta {\widehat{\ell }}^{\alpha }(s,g)$ are likelihood errors defined in Eq. (8) and Eq. (9), respectively. The “stat error” is the statistical error estimated by performing bootstrap error analysis on the free energy shift term, −lnZ^α , with the same calculations performed on 50 or 100 randomly chosen data sets. The numbers reported are the standard deviations of −lnZ^α from different sets of data. MBAR errors are from the MBAR output. The last row (RMS) is the root-mean-square values of the corresponding column. All values are in units of k_BT, except for x̄^α , which is in units of Å.

Strong biasing potential

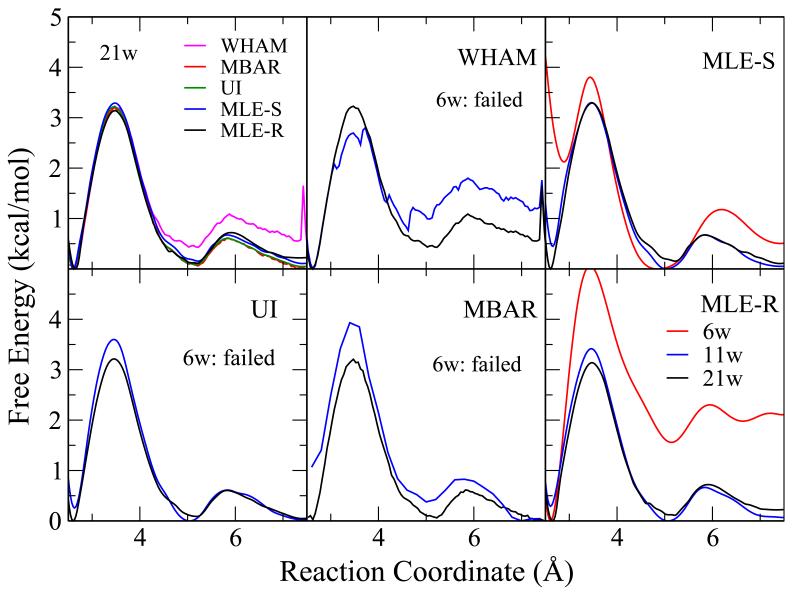
In the second set of simulations, a relatively strong biasing potential with a strength of 100 kcal/mol/Ų was applied to every window. Contrary to the weak potential set of simulations, one would expect that a quadratic approximation of the local free energy profile would perform well, but the requirement of the numbers of windows will increase since the overlap between windows will be diminished.

The results with the strong biasing potential of 100 kcal/mol/Ų are shown in Figure 3. The upper left panel again shows the results from all methods with 21 windows and other panels show the results from individual methods with different numbers of windows (11 and 6). All methods, including UI, converge with 21 windows and give similar results. With 11 windows, however, WHAM and MBAR fail to produce correct results, while with 6 windows, WHAM, UI, and MBAR all fail to converge due to the lack of sufficient overlap between windows. On the other hand, the VFEP approach, both with spline function (MLE-S) and rational interpolation function (MLE-R) gives very good results for 11 windows compared to the 21 window results, and gives qualitatively correct results with only 6 windows.

Figure 3.

The free energy profiles calculated with different methods for the Na⁺:Cl⁻ pair from a 21-window umbrella sampling simulation with a strong biasing potential of 100 kcal/mol-Ų. The upper left panel shows the results from all methods with 21 windows. Other panels show the results from individual methods with different numbers of windows: 6 (red), 11 (blue), and 21 (black) windows. All methods, including UI, converge with 21 windows and give similar results. With 11 windows, however, MBAR fails to produce correct results, while with 6 windows, WHAM, UI, and MBAR all fail to converge due to the lack of sufficient overlap between windows. On the other hand, the VFEP approach, both with spline (MLE-S) and rational interpolation (MLE-R) functions gives very good results for 11 windows compared to the 21 window results, and gives qualitatively correct results with only 6 windows.

Reduced data set

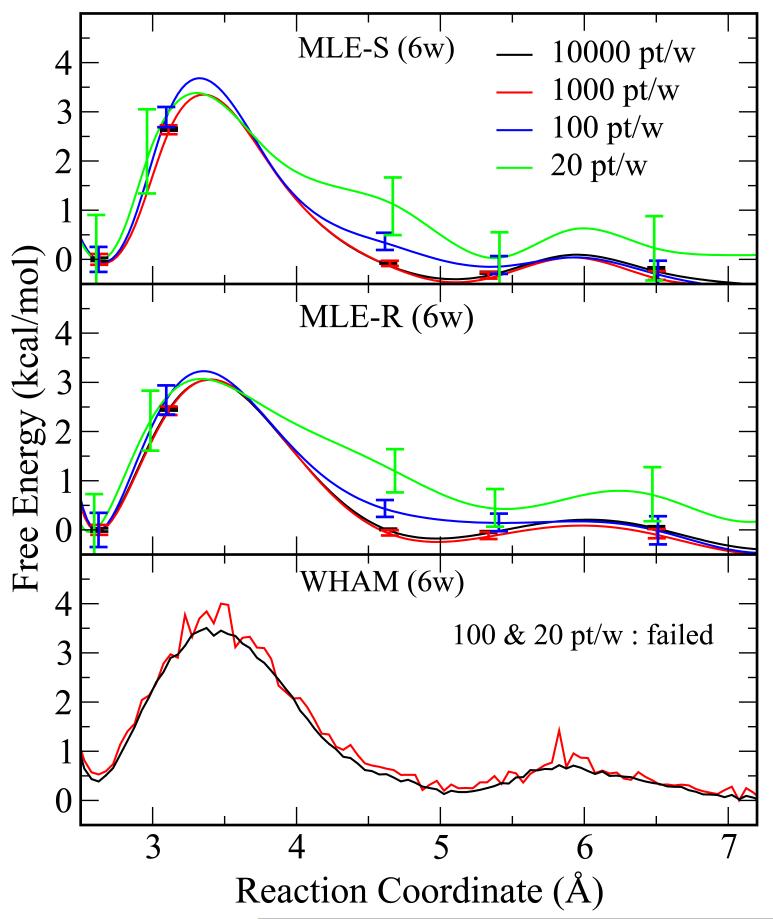
In the case of a weak biasing potential, WHAM gives good results with only 6 windows. One would expect, however, that many data points would be necessary to model individual windows well. Figure 4 shows the results with 6 windows from WHAM and the proposed VFEP methods using the weak biasing potential of 5 kcal/mol/Ų, same as the above results (Figure 2) but the data points are stripped out when performing analysis. The upper panel and middle panel show the VFEP results with spline function (MLE-S) and rational interpolation function (MLE-R), respectively, while the WHAM results are shown in the bottom panel. WHAM fails to converge with 100 data points or less per window and MBAR gives similar results, both due to insufficient data points in the histograms and hence only WHAM results are shown. VFEP still delivers qualitatively correct results with only 20 data points per window where the statistical error (by bootstrapping) is less than 1 kcal/mol (see Table 3).

Figure 4.

The free energy profiles calculated with WHAM and VFEP for the Na⁺:Cl⁻ pair from a 6-window umbrella sampling simulation with a weak biasing potential of 5 kcal/mol-Ų. The data points are reduced at different levels: 10000 pt/w (black), 1000 pt/w (red), and 100 pt/w (blue), and 20 pt/w. The error bars are bootstrap errors calculated from 100 random data sets with the same size. The upper panel and middle panel show the VFEP results with spline (MLE-S) and rational interpolation (MLE-R) functions, respectively, while the WHAM results are shown in the bottom panel. WHAM fails to converge with 100 or fewer data points per window, while VFEP still delivers qualitatively correct results with only 10 data points per window.

Table 3.

Estimated bootstrap errors (50 and 100 calculations with random data sets) of free energy shifts calculated by the VFEP method. The system is the Na⁺:Cl⁻ system with 6 windows.

		N=50		N=100
	Window	Average	S.D.	Average	S.D.
10000 pt/w	1	0.758	0.032	0.760	0.033
	2	2.139	0.026	2.141	0.026
	3	−0.153	0.017	−0.152	0.018
	4	−0.776	0.014	−0.777	0.017
	5	−0.720	0.028	−0.722	0.026
	6	−1.249	0.033	−1.250	0.032
RMS			0.026		0.026
	Window	Average	S.D.	Average	S.D.
1000 pt/w	1	0.763	0.118	0.761	0.119
	2	2.146	0.101	2.142	0.091
	3	−0.153	0.057	−0.151	0.053
	4	−0.763	0.066	−0.771	0.065
	5	−0.722	0.093	−0.721	0.089
	6	−1.270	0.111	−1.260	0.105
RMS			0.094		0.088
	Window	Average	S.D.	Average	S.D.
100 pt/w	1	0.752	0.219	0.715	0.254
	2	2.135	0.189	2.087	0.206
	3	−0.149	0.185	−0.138	0.175
	4	−0.770	0.214	−0.761	0.181
	5	−0.685	0.236	−0.664	0.246
	6	−1.283	0.299	−1.239	0.301
RMS			0.227		0.232
	Window	Average	S.D.	Average	S.D.
20 pt/w	1	0.679	0.819	0.633	0.902
	2	2.028	0.734	1.965	0.855
	3	−0.118	0.474	−0.097	0.586
	4	−0.772	0.483	−0.728	0.54
	5	−0.654	0.652	−0.647	0.653
	6	−1.162	0.775	−1.126	0.781
RMS			0.670		0.732

The numbers here are derived from a 6-window umbrella sampling simulation on a Na⁺:Cl⁻ pair in a TIP3P water box with a biasing potential of 5 kcal/mol/Ų (see the Results section, also Figure 4). The results are estimated by performing bootstrap type error analysis on the free energy shift term, −lnZ^α, with the same calculations performed on 50 or 100 randomly chosen data sets. “S.D.” is the standard deviation while “RMS” is the root-mean-square value of the corresponding column. Results from different number of data points used in a window (10000 pt/w, 1000 pt/w, 100 pt/w, and 20 pt/w) are shown. All values are in units of k_BT.

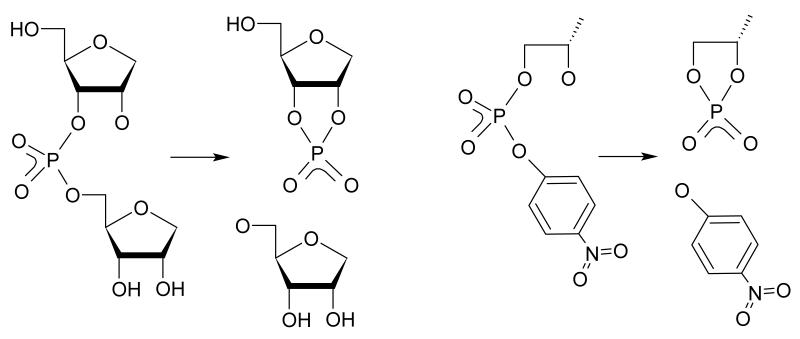
QM/MM phosphoryl transfer reactions

The phosphate 2′-O-transesterification reaction for two model compounds were simulated by QM/MM umbrella sampling using the AMBER12 simulation package⁶⁰ (Figure 1). The first model, 2-(hydroxypropyl)-4-nitrophenyl phosphate (HpPNP), contains an enhanced leaving group and is therefore expected to have a free energy profile with significantly different shape. The second is an abasic RNA dinucleotide which has been studied previously in our group. Both sets of simulations used the AM1/d-PhoT QM/MM Hamiltonian,⁶¹ which has been verified and demonstrated able to reproduce high-level DFT results within chemical accuracy in describing phosphate chemistry by our group^62-65 and others,^{66, 67} under periodic boundary conditions using QM/MM Ewald summations as implemented in AMBER12.⁶⁸ The QM region was defined as the entire solute. The reaction coordinate is defined as the difference between the nucleophile to phosphorus distance (r₁) and the phosphorus to leaving group distance (r₂). For umbrella sampling simulations a harmonic biasing potential was applied to this reaction coordinate, r₁-r₂.

Figure 1.

Reaction schemes for QM/MM phosphoryl transfer reactions of an abasic RNA dinucleotide and 2-(hydroxypropyl)-4-nitrophenyl phosphate (HpPNP), a model compound with an enhanced leaving group

HpPNP

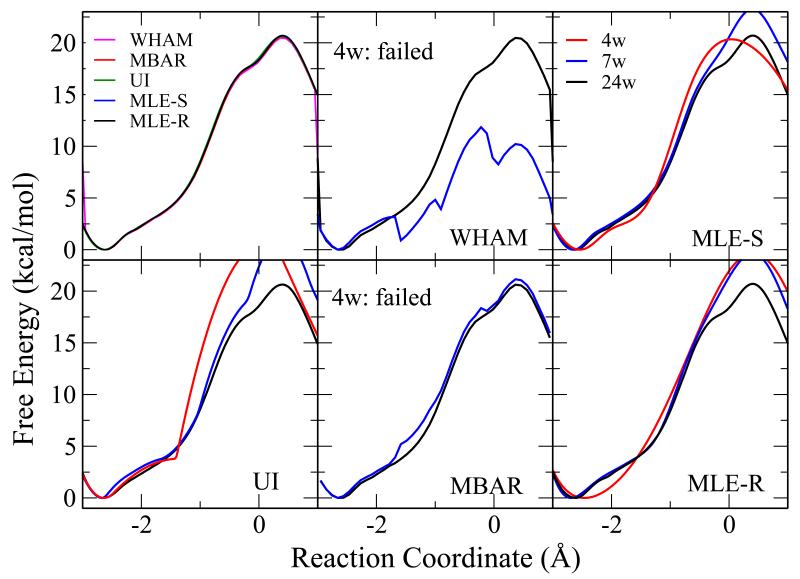
HpPNP was solvated in a box of TIP4P-Ew water⁶⁹ at 300 K using the NVT ensemble with an Andersen thermostat.⁷⁰ Twenty-five short (100 ps) umbrella sampling simulations were performed with biasing potential strength of 60 kcal/mol/Ų. The QM/MM free energy profile results for HpPNP are shown in Figure 5. Similar to Figure 2, The upper left panel shows the results from all methods with 25 windows. Other panels show the results from individual methods with different numbers of windows (15 and 5). While all methods converge with 25 windows, only the VFEP method, both with spline function (MLE-S) and rational interpolation function (MLE-R) still gives good results for 5 windows.

Figure 5.

The QM/MM free energy profile results for HpPNP. Similar to Figure 2, the upper left panel shows the results from all methods with 25 windows. Other panels show the results from individual methods with different numbers of windows: 5 (red), 15 (blue), and 25 (black) windows. For the case of 15 and 5 windows, MBAR fails due to lack of overlap between windows when 75 bins are used (no data in certain bins). While all methods converge with 25 windows, only the VFEP method, with spline (MLE-S) and rational interpolation (MLE-R) functions still gives good results for 5 windows.

Reduced data set

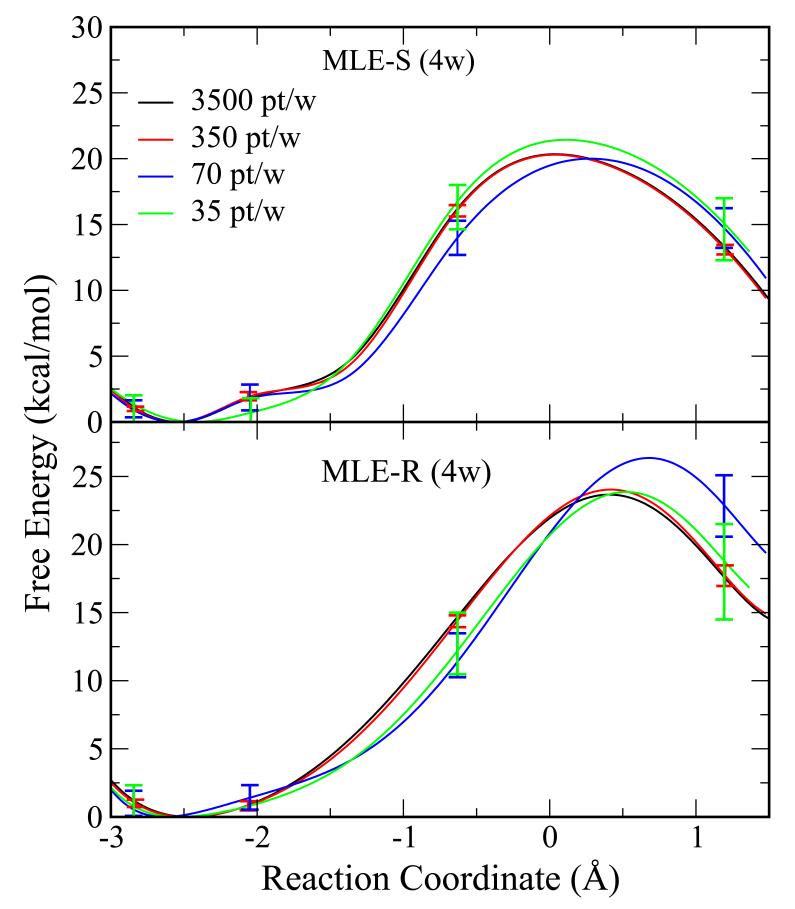
The QM/MM free energy profile results for HpPNP with reduced numbers of data points are shown in Figure 6. Similar to Figure 4. VFEP, both with spline function (MLE-S) and rational interpolation function (MLE-R), still delivers qualitatively correct results with only 20 data points per window (with 5 windows) where the bootstrapping errors are around 3 kcal/mol.

Figure 6.

The QM/MM free energy profile results for HpPNP with reduced numbers of data points (2000 pt/w (black), 400 pt/w (red), 200 pt/w (blue), and 20 pt/w). The error bars are bootstrap errors calculated from 100 random data sets with the same size. VFEP, both with spline (MLE-S) and rational interpolation (MLE-R) functions, still delivers qualitatively correct results with only 20 data points in each of 5 windows. Note that all other methods fail with only 5 windows and hence cannot be compared here.

Abasic dinucleotide

Mimicking the experimental conditions of Harris et al.⁷¹ for a UpG dinucleotide, the system was solvated in a rhombic dodecahedron of TIP3P water⁵⁵ with sodium chloride⁷² at physiological conditions (310 K) in the NVT ensemble with an Andersen thermostat.⁷⁰ Data from twenty-four long (1.75 ns each) umbrella sampling simulations were used.

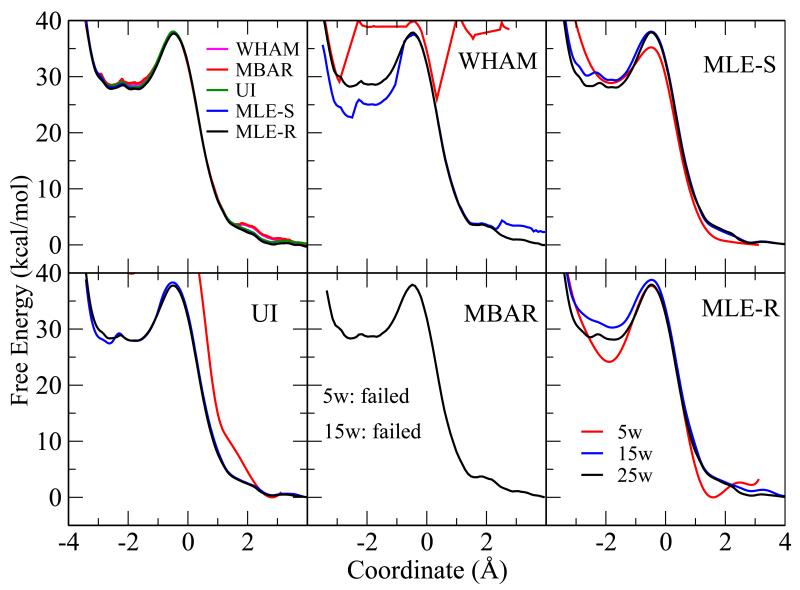
The QM/MM free energy profile results for the abasic dinucleotide are shown in Figure 7. Similar to Figure 5, the upper left panel shows the results from all methods with 24 windows. Other panels show the results from individual methods with different numbers of windows (24, 7, and 4 windows). While all methods converge with 24 windows, both WHAM and MBAR fails with 4 windows. UI and VFEP method, both with spline function (MLE-S) and rational interpolation function (MLE-R) still gives good results for 4 windows. When they succeed, all of the methods produce a free energy barrier comparable to the experimental value of 19.9 kcal/mol, as inferred from the rate constant extrapolated to “infinite” pH⁷¹ and transition state theory.

Figure 7.

The QM/MM free energy profile results for an abasic RNA dinucleotide (Figure 1). Similar to Figure 5, the upper left panel shows the results from all methods with 24 windows. Other panels show the results from individual methods with different numbers of windows: 4 (red), 7 (blue), and 24 (black) windows. While all methods converge with 24 windows, both WHAM and MBAR fail to converge with 4 windows. UI and VFEP, both with spline (MLE-S) and rational interpolation (MLE-R) functions still gives good results for 4 windows.

Reduced data set

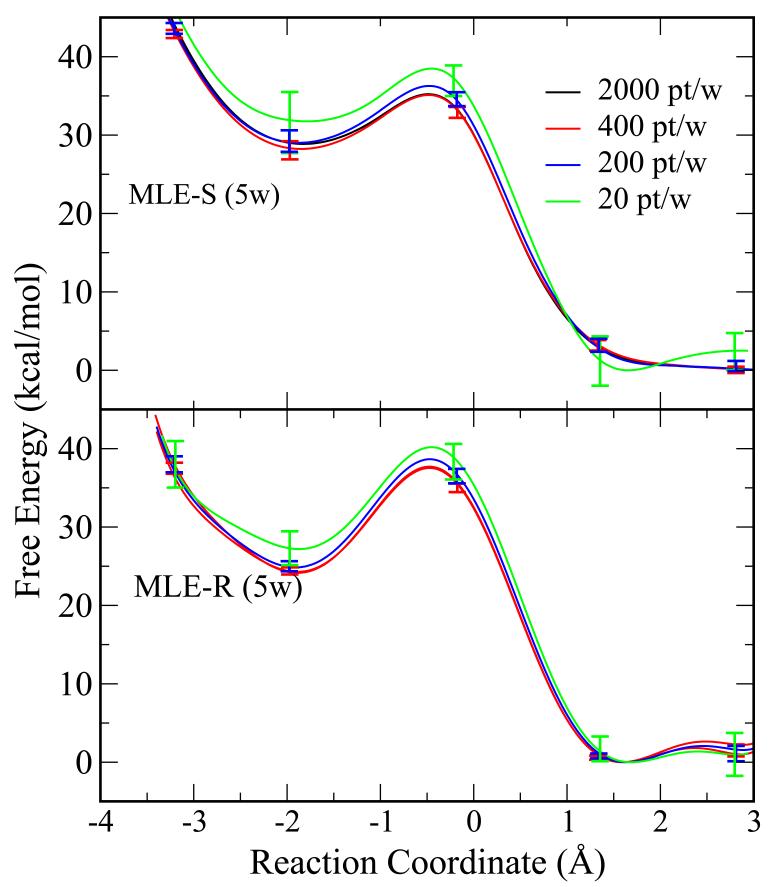
The QM/MM free energy profile results for the abasic dinucleotide with reduced numbers of data points are shown in Figure 8. VFEP, both with spline (MLE-S) and rational interpolation (MLE-R) functions, still delivers qualitatively correct results with only 35 data points in each of 4 windows. However, the quantitative inaccuracy is readily apparent in the bootstrapping errors around 3 kcal/mol.

Figure 8.

The QM/MM free energy profile results for an abasic RNA dinucleotide with reduced numbers of data points: 3500 pt/w (black), 350 pt/w (red), 70 pt/w (blue), and 35 pt/w. The error bars are bootstrap errors calculated from 100 random data sets with the same size. VFEP, both with spline (MLE-S) and rational interpolation (MLE-R) functions, still delivers qualitatively correct results with only 7 data points in each of 4 windows.

Torsion rotation of Butane

A butane molecule was modeled using the AMBER F99 force field in a generalized Born solvent at 300 K using Langevin dynamics as implemented in the AMBER12 simulation package.⁶⁰ The umbrella sampling simulations were performed by applying harmonic restraints on the C-C-C-C torsion with a force constant of 32.83 kcal/mol/rad² (0.02 kcal/mol/degree²). The equilibrium position of the torsion angle ran from −180 to 180 degrees in increments of 15 resulting in 25 windows. Each window was simulated for 0.5 ns of equilibration and 1 ns of data collection (10,000 data points per window).

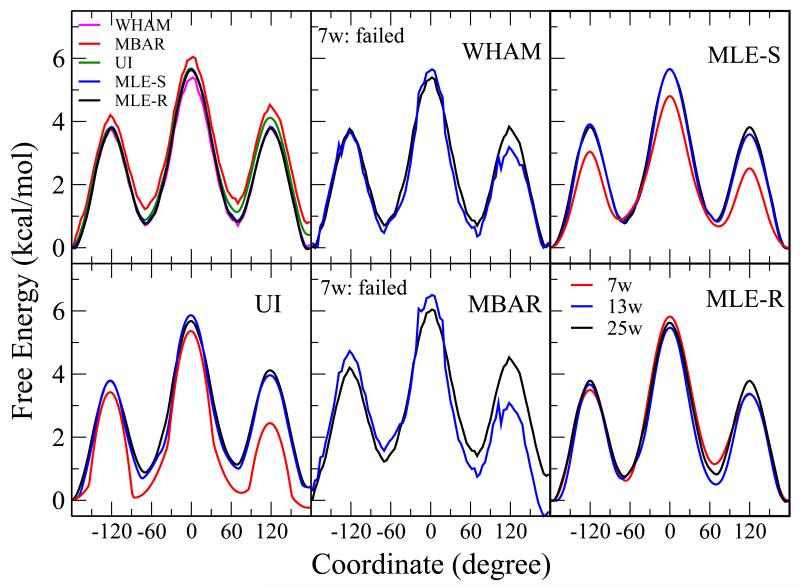
The free energy profile results for the C-C-C-C torsion of butane are shown in Figure 9. Similar to Figure 2, The upper left panel shows the results from all methods with 25 windows. Other panels show the results from individual methods with different numbers of windows (13 and 7). While all methods converge with 25 windows, only the VFEP method, both with spline (MLE-S) and rational interpolation (MLE-R) functions still gives good results for 7 windows.

Figure 9.

The free energy profile of C-C rotation of butane. Similar to Figure 5, the upper left panel shows the results from all methods with 25 windows (15-degree spacing). Other panels show the results from individual methods with different numbers of windows: 7 (red), 13 (blue), and 25 (black) windows. While all methods converge with 25 windows (MBAR and UI have some deviation due to lack of periodic constraint), both WHAM and MBAR fail to converge with 7 windows. UI and VFEP, both with spline (MLE-S) and rational interpolation (MLE-R) functions still give good results for 7 windows.

Reduced data set

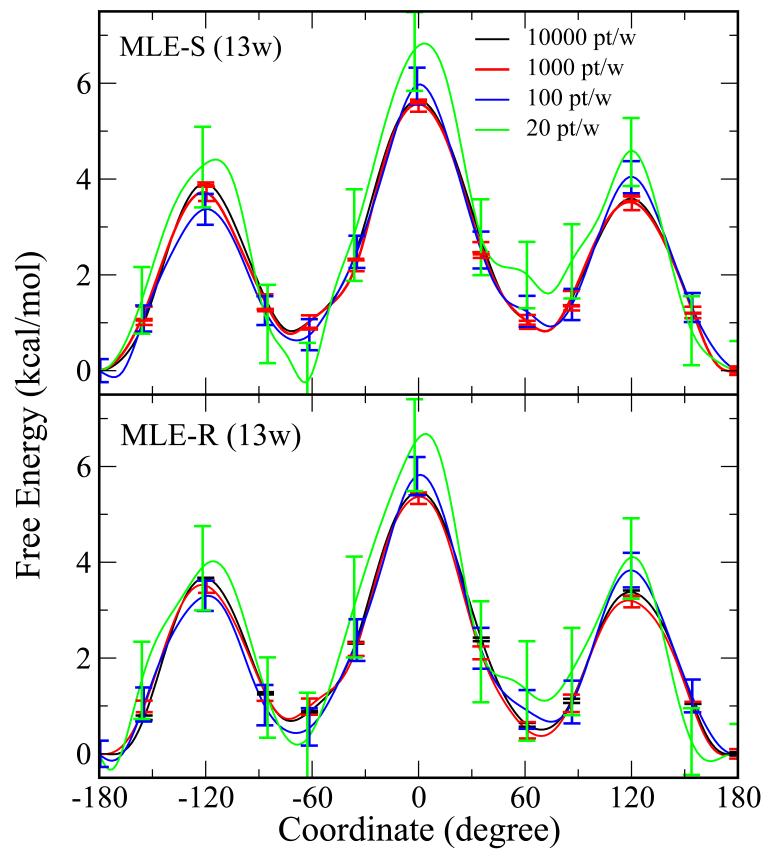
The free energy profile results for butane with reduced numbers of data points are shown in Figure 10. Similar to Figure 4. VFEP, both with spline (MLE-S) and rational interpolation (MLE-R) functions, still delivers qualitatively correct results with only 20 data points in each of 13 windows. Statistical errors from bootstrapping are around 1 kcal/mol.

Figure 10.

The free energy profile of C-C rotation of butane with reduced numbers of data points: 10000 pt/w (black), 1000 pt/w (red), 100 pt/w (blue), and 20 pt/w. The error bars are bootstrap errors calculated from 100 random data sets with the same size. VFEP, both with spline (MLE-S) and rational interpolation (MLE-R) functions, still delivers qualitatively correct results with only 20 data points in each of 13 windows.

Error Analysis

Likelihood error

The likelihood of a set of trial probability {p(x_i)} with given observed probability set {p_obs(x_i)} can be written as

$$\widehat{\ell }=\sum _i{p}_{\text{obs}}\left(x_i\right)\ln p\left(x_i\right).$$

Assuming that the trial probability is a Boltzmann distribution due to the trial effective potential F_eff and the observed data points are unbiased, then the corresponding observed likelihood function is

$$\widehat{\ell }\left(F_{\text{eff}}\right)=\sum _i\frac{1}{N}\ln \left\{\frac{1}{Z}{e}^{-F_{\text{eff}}\left(x\right)}\right\}$$

where the normalization factor Z is defined as $Z=\int e^{-F_{\text{eff}}\left(x_i\right)}dx$. For the α^th umbrella sampling simulation window, the trial effective potential is the combination of the trial free energy profile F(x) and the added biasing potential W^α(x). Hence

$$\begin{array}{cc}\hfill {\widehat{\ell }}_s^{\alpha }\left(F_{\text{eff}}\right)={\widehat{\ell }}_s^{\alpha }\left(F\right)& =-\ln Z^{\alpha }-\frac{1}{N}\sum _i\left[F\right(x_i^a)+W^{\alpha }(x_i^{\alpha }\left)\right]\hfill \\ \hfill & =-\text{ln}{Z}^{\alpha }-{\langle F\left(x\right)+W^{\alpha }\left(x\right)\rangle }_{\text{sample}}\hfill \end{array}$$

Note that the above equation is exactly the same as Eq. (7). ${\widehat{\ell }}_s^{\alpha }$ can be expressed as a functional of either F_eff or F since they only differ by a known function W^α. The subscript “s” denotes that the likelihood is calculated based on the sampling data and 〈…〉_sample indicates that the average is calculated using the observed sample probability distribution. ${\widehat{\ell }}_s^{\alpha }\left(F\right)$ is the functional to be optimized in the present work as described in the Theory section. If the trial free energy profile is the true system free energy profile and the sampling is exact and infinite, then the “ideal” likelihood is now

$$\begin{array}{cc}\hfill {\widehat{\ell }}_m^{\alpha }\left(F\right)& =-\ln Z^{\alpha }-\int e^{-\left\{F\right(x)+W^{\alpha }(x\left)\right\}}\left\{F\right(x)+W^{\alpha }(x\left)\right\}dx\hfill \\ \hfill & =-\ln Z^{\alpha }-{\langle F\left(x\right)+W^{\alpha }\left(x\right)\rangle }_{\text{model}}\hfill \end{array}$$

The subscript “m” denotes that the likelihood is calculated based on the modeled free energy profile function and 〈…〉_model indicates that the average is calculated using the modeled probability distribution. In the present work, since ${\widehat{\ell }}_s^{\alpha }\left(F\right)$ is the functional to be optimized and ${\widehat{\ell }}_m^{\alpha }\left(F\right)$ is the “ideal” target likelihood, the difference between them, denoted as $\Delta {\widehat{\ell }}^{\alpha }(s,m)$, can be viewed as the limit that the optimization process can reach, or equivalently, the lower bound error of the proposed method. That is,

$$\begin{array}{cc}\hfill \Delta {\widehat{\ell }}^{\alpha }(s,m)& \equiv {\widehat{\ell }}_s^{\alpha }\left(F\right)-{\widehat{\ell }}_m^{\alpha }\left(F\right)\hfill \\ \hfill & ={\langle F\left(x\right)+W^{\alpha }\left(x\right)\rangle }_{\text{model}}-{\langle F\left(x\right)+W^{\alpha }\left(x\right)\rangle }_{\text{sample}}.\hfill \end{array}$$ (8)

Apparently $\Delta {\widehat{\ell }}^{\alpha }(s,m)$ is just the difference in the expectation values computed with the effective potentials from the sampling data and from the optimized free energy profile.

Error due to Gaussian distribution approximation

The same concept can be applied to Gaussian distributions, as many approaches use Gaussian distributions to model the probability distribution for individual windows. The likelihood of a perfect Gaussian probability distribution is:

$${\widehat{\ell }}_g^{\alpha }=\sum _i\frac{1}{N^{\alpha }}\ln \left\{\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{(x_i^{\alpha }-{\stackrel{‒}{x}}^{\alpha })}^2}{2{\sigma }^2}}\right\}$$

where x̄^α is the average of the sample data {$x_i^{\alpha }$} and σ² is the unbiased variance defined as ${\sigma }^2={\sum }_i\frac{{(x_i^{\alpha }-{\stackrel{‒}{x}}^{\alpha })}^2}{N^{\alpha }-1}$. The likelihood can be expressed analytically as

$${\widehat{\ell }}_g\left(F\right)=-\ln \left(\sqrt{2\pi }\sigma \right)-\frac{N^{\alpha }-1}{2N^{\alpha }}.$$

The difference $\Delta {\widehat{\ell }}^{\alpha }(s,g)$, defined as

$$\begin{array}{cc}\hfill \Delta {\ell }^{\alpha }(s,g)& \equiv {\widehat{\ell }}_s^{\alpha }\left(F\right)-{\widehat{\ell }}_g^{\alpha }\hfill \\ \hfill & =-\text{ln}{Z}^{\alpha }-{\langle F\left(x\right)+W^{\alpha }\left(x\right)\rangle }_{\text{sample}}+\ln \left(\sqrt{2\pi }\sigma \right)+\frac{N^{\alpha }-1}{2N^{\alpha }},\hfill \end{array}$$ (9)

can be viewed as the likelihood of the sampling data set of the α^th window being Gaussian distributed.

Sampling error

As already mentioned in the Results section, Simple bootstrapping methods⁷³ were utilized to estimate the statistical sampling errors in the present work. The error of a target observable is estimated by calculating the standard deviation between randomly chosen data sets with the same data size.

Optimum of the trial free energy

For the entire set of umbrella sampling simulations, the likelihood is (Eq. (7)

$$\begin{array}{cc}\hfill \widehat{\ell }\left(F\right)& \equiv \sum _{\alpha }^{\text{windows}}{c}^{\alpha }{\widehat{\ell }}^{\alpha }\left(F\right)\hfill \\ \hfill & =-\sum _{\alpha }^{\text{windows}}{c}^{\alpha }\left\{\ln Z^{\alpha }+\frac{1}{N^{\alpha }}\sum _i^{\text{datapoints}}\left[F\right(x_i^{\alpha })+W^{\alpha }(x_i^{\alpha }\left)\right]\right\}\hfill \end{array}$$

The variaton of $\widehat{\ell }\left(F\right)$, $\Delta \widehat{\ell }\left(F\right)$, due to a variation of F, ΔF, can be expressed as

$$\Delta \widehat{\ell }\left(F\right)=\int \frac{\delta \widehat{\ell }\left(F\right(x\left)\right)}{\delta F\left(x\right)}\Delta F\left(x\right)dx$$ (10)

where $\frac{\delta \widehat{\ell }\left(F\right(x\left)\right)}{\delta F\left(x\right)}$ is the functional derivative of $\widehat{\ell }\left(F\right(x\left)\right)$ with respect to F(x). Explicitly taking the functional derivative on Eq. (7), we get

$$\frac{\delta \widehat{\ell }\left(F\right(x\left)\right)}{\delta F\left(x\right)}=\sum _{\alpha }^{\text{windows}}{c}^{\alpha }\left\{\frac{1}{Z^{\alpha }}{e}^{-\left\{u\right(x)+w^{\alpha }(x\left)\right\}}-\frac{1}{N^{\alpha }}\sum _i^{\text{datapoints}}\delta (x-x_i^{\alpha })\right\}$$ (11)

where $\delta (x-x_i^{\alpha })$ is the Dirac delta function. Assuming c^α = 1 for all α’s and plugging the above equations into Eq. (10), the likelihood variation becomes (Note that F can be chosen relative to an arbitrary constant, hence ΔF can simply be replaced by F):

$$\begin{array}{cc}\hfill \Delta \widehat{\ell }\left(F\right)& =\int \frac{\delta \widehat{\ell }\left(F\right)}{\delta F}\Delta Fdx\hfill \\ \hfill & =\sum _{\alpha }^{\text{windows}}\{{\langle F\left(x\right)\rangle }_{\text{model}}^{\alpha }-{\langle F\left(x\right)\rangle }_{\text{sample points}}^{\alpha }\hfill \end{array}$$ (12)

At the optimal F, $\frac{\delta \widehat{\ell }\left(F\right(x\left)\right)}{\delta F\left(x\right)}$ is zero at all x, thus ${\sum }_{\alpha }^{\text{windows}}\{{\langle F\left(x\right)\rangle }_{\text{model}}^{\alpha }-{\langle F\left(x\right)\rangle }_{\text{sample points}}^{\alpha }\}=0$ (or $\Delta \widehat{\ell }\left(F\right)=0$). Hence $\Delta \widehat{\ell }\left(F\right)=0$ can be a simple criterion of judging optimal F. The above derivation is not limited to the VFEP mehod. Any free energy profile should hold this criterion if the optimization is based on the entire system likelihood. In all simulations reported in this paper, the magnitude of $\Delta \widehat{\ell }\left(F\right)$ is 3.0 × 10⁻⁵ or less, which indicates the optimal (in terms of likelihood) F is reached in our all simulations.

Free energy shifts

While in our VFEP method there is no explicit re-weighting procedure involved, the term −lnZ^α, is the relative free energy shifts, Δ f^α, defined in MBAR or WHAM. In VFEP they are obtained implicitly through global optimization of the free energy profile, while in that MBAR and WHAM approaches they are calculated as the results of the re-weighting procedure. Calculated Δ f^α’s from VFEP, MBAR, and WHAM are listed in Table 1, for the Na:Cl system with 21 windows and with a biasing potential of 5 kcal/mol/Ų (Figure 2). The relative free energy sift $\Delta f_{\text{MLE}}^{\alpha }$ from VFEP is similar to $\Delta f_{\text{MBAR}}^{\alpha }$ from MBAR (RMS = 0.00199), which suggests that VFEP is able to implicitly re-weight windows just as MBAR. The larger differences between $\Delta f_{\text{MLE}}^{\alpha }$ and $\Delta f_{\text{WHAM}}^{\alpha }$ (RMS = 0.18273) may suggest that the number data points is still not sufficient from the WHAM approach, especially for x > 6.7. For VFEP, cubic spline functions are used for the above error analysis. Using rational interpolation functions gives virtually identical results.

Table 1.

Estimated free energy shifts of the Na⁺:Cl⁻ system from VFEP, MBAR, and WHAM.

Window (α)	x̄ α	$\Delta f_{\text{VFEP}}^{\alpha }$	$\Delta f_{\text{MBAR}}^{\alpha }$	$\Delta f_{\text{WHAM}}^{\alpha }$	$\Delta \Delta f_{\text{VFEP/MBAR}}^{\alpha }$ (×103)	$\Delta \Delta f_{\text{VFEP/WHAM}}^{\alpha }$ (×103)
1	2.629	-	-	-	-	-
2	2.655	−0.241	−0.240	−0.240	−0.840	−0.900
3	2.686	−0.021	−0.017	−0.017	−3.340	−3.350
4	2.754	0.629	0.633	0.633	−4.060	−4.030
5	3.113	1.476	1.477	1.479	−1.140	−3.010
6	3.945	1.512	1.511	1.519	0.790	−7.150
7	4.275	0.694	0.694	0.705	−0.410	−11.070
8	4.460	−0.084	−0.083	−0.071	−1.100	−13.410
9	4.638	−0.662	−0.660	−0.646	−1.520	−15.450
10	4.797	−1.048	−1.047	−1.031	−1.840	−17.370
11	4.964	−1.264	−1.262	−1.245	−2.050	−19.250
12	5.127	−1.317	−1.315	−1.297	−2.120	−20.870
13	5.334	−1.225	−1.223	−1.204	−2.040	−21.840
14	5.588	−1.056	−1.054	−1.033	−1.860	−22.610
15	5.863	−0.938	−0.937	−0.914	−1.720	−24.320
16	6.188	−0.970	−0.968	−0.943	−1.770	−26.700
17	6.500	−1.114	−1.112	−1.083	−1.930	−30.880
18	6.719	−1.285	−1.283	−1.235	−2.110	−49.640
19	6.955	−1.431	−1.429	−1.308	−2.130	−122.670
20	7.194	−1.532	−1.530	−1.206	−2.050	−325.970
21	7.413	−1.588	−1.586	−0.832	−2.500	−756.610
RMS					1.990	182.73

The numbers here are derived from the same set of simulation as in Table 2. x̄^α is the average of the sampled coordinates of the α^th window. For the VFEP approach, the $\Delta f_{\text{VFEP}}^{\alpha }$’s are calculated from −ln Z^α and the values relative to the first window are listed. $\Delta f_{\text{MBAR}}^{\alpha }$ and $\Delta f_{\text{WHAM}}^{\alpha }$ values were taken directly from the MBAR and WHAM output, respectively. The last two columns are differences (multiplied by 10³) between these three types of Δf’s. The last row (RMS) is the root-mean-square values of the corresponding column. All values are in units of k_BT, except for x̄^α, which is in units of Å.

Calculated errors

The likelihood error estimator functions mentioned above represent the lower-bound of the errors due to the usage of model functions, while the statistical sampling errors can be obtained from the bootstrapping analysis.

Table 2 lists these error estimators, $\Delta {\widehat{\ell }}^{\alpha }(s,g)$ and $\Delta {\widehat{\ell }}^{\alpha }(s,m)$, the bootstrapping errors of the free energy shifts based on 50 and 100 random data sets, as well as the errors reported from MBAR. The likelihood error estimator $\Delta {\widehat{\ell }}^{\alpha }(s,m)$ for this system is 0.0356 k_BT (RMS value) which suggests that the model functions employed here are adequate. The Gaussian likelihood error estimator $\Delta {\widehat{\ell }}^{\alpha }(s,g)$ is quite small for most of the windows. The exceptions are windows #3 to #7, which suggest that Gaussian approximation may be not ideal between x =2.5 to x =4.2. The corresponding accumulated error from this region is around 1.6 k_BT, or 1.0 kcal/mol, which qualitatively agrees with the fact that the converged UI result is off by about 1.0 kcal/mol when compared to other methods (Figure 2). The bootstrapping errors of the free energy shits are 0.013 k_BT (RMS value) for VFEP. The combined errors for VFEP (likelihood errors plus sampling errors) are roughly the same as the reported MBAR errors.

Reduce data set

Table 3 lists the bootstrapping errors for different sizes of data sets the Na:Cl system with 6 windows and with a biasing potential of 5 kcal/mol/Ų (Figure 4). The calculated average values of free energy shifts of different windows are consistent using different numbers of data points, which indicates the reliability of the calculations. The standard deviations, seen as the sampling errors, are around 0.03 kcal/mol for 10000 pt/w, 0.1 kcal/mol for 1000 pt/w, 0.2 kcal/mol for 100 pt/w, and 0.7 kcal/mol for 20 pt/w.

Discussions

Traditional methods for estimating free energy differences or free energy profiles from umbrella sampling simulations usually consist of two steps. The first step is to model the free energy profile of each window and the second step is to merge/combine the free energy profiles from individual windows into a global free energy profile. As already mentioned earlier in the Introduction section, two major types of problems are inevitably associated with these traditional methods: the reweighting (combination) problem and the data fitting problem. On the other hand, instead of dealing with individual windows, the proposed VFEP approach finds the global free energy profile that gives an optimal likelihood based on the entire set of simulation data that spans the free energy surface. In other words, VFEP looks for a global free energy profile that every data point can fit into, while traditional methods look for a global free energy profile that is the best combination of local free energy profiles of individual windows. In this section, we discuss the results presented in the last section in a broader context with regard to the re-weighting and data fitting problems and their relation with other methods.

The need of overlap in the re-weighting procedure

In traditional methods, it is necessary to have overlap information between sampling windows otherwise it is impossible to reasonably combine the free energy profiles of individual windows. Consequently, when the number of windows is not adequate and/or individual window sampling regions are too small to overlap with neighboring windows, the re-weighting problem becomes intractable. In Figure 3 a strong biasing potential leads to a small window region and UI/MBAR/WHAM all fail to converge with 6 windows. The same situation happens in the two QM/MM cases as well (shown in Figure 5 and Figure 7). Although UI evades the need of overlap in data re-weighting by assuming continuous first derivatives of free energy profile between windows, UI would fail due to numerical instability in some cases. On the other hand, the proposed VFEP approach searches for the optimal global function based on all available data, and, through the usage of cubic functions, implicitly assumes continuous first and second derivatives of free energy profile between windows; hence the lack of overlap between windows is much less severe of a problem. In all test cases, the VFEP approach gives plausible results even with very few windows, although one clearly should not expect quantitatively correct results with such sparse data. Nevertheless, the VFEP delivers a reasonable, rough estimate in these more extreme limits compared to the other methods that have been tested here.

The data fitting problem

In the traditional methods mentioned, it is desirable for the local free energy profiles of individual windows to be modeled with a stable analytic function. The quadratic approximation used in UI is often a good choice, particularly when strong biasing potentials are used, as shown in Figure 3, Figure 5, and Figure 7. However, this approach also leads to the need for a large numbers of windows, each of which is strongly localized by a harmonic biasing potential. Conversely, when weak biasing potentials are used, the quadratic approximation will begin to break down as shown in Figure 2 (the UI case). Using histograms, as in the cases of WHAM and (most commonly) MBAR will avoid this problem, but will suffer from the requirement of dense sampling in each bin in order to be numerically stable. As shown in Figure 4, WHAM will fail when the number of data points for a given window is not enough to provide sufficient sampling density. The VFEP method utilizes higher order functions to model the local free energy profiles (third order in the case of cubic spline functions) and performs very well in all test cases. Using analytic functions, VFEP also requires many fewer independent data points as shown in Figure 4, Figure 6, and Figure 8. Note that these reduced data sets are obtained by subsampling the original data and hence represent sparse independent data points. The results could be very different from those obtained using shorter simulation data sets possibly with higher correlations.

Based on the test results presented here, the proposed VFEP approach outperforms all listed methods in dealing with the above two major types of problems in estimating free energy when the overlap or the data points are not sufficient. As a result, the following potential advantages of VFEP could significantly advance the current free energy estimation techniques:

Fast estimate of rough biasing potentials

In recent years, much effort has been devoted in the field of adaptive approaches for free energy simulations.^{6, 74-77} In order to obtain optimal sampling, instead of fixed biasing potentials, the biasing potentials are modified adaptively according to knowledge obtained from the available simulation results. Nevertheless, adaptive approaches require at least some knowledge of the target free energy profile before any sensible modification of the biasing potentials can be made. Due to the two major problems of free energy estimation discussed above, the very first round of estimating the target free energy profile already requires significant computational resources. Test results here suggest that the VFEP is capable of delivering a qualitatively correct free energy profile with only ~ 5 windows and ~ 20 to 35 independent data points per windows for typical chemical reactions. With help from the VFEP approach, one may be able to establish a very quick coarse-grained picture of the free energy profile and apply an adaptive biasing potential approach to build the best biasing potentials for the next iteration of free energy estimation.

Free energy profiles in multiple dimensions

Theoretically it is possible to calculate the free energy profiles in multiple dimensions by slight modification of the WHAM, UI, and MBAR approaches.^40,43,78-80 However, in practice, it is not always feasible to do so since numerous data points are needed in order to construct a multi-dimensional free energy profile. The GAMUS approach^43,44 uses a global Gaussian fit to reduce the data points needed and can be practically used in multi-dimensional free energy profiles. However, the authors pointed out that the GAMUS approach was designed to explore free energy basins and is not necessarily appropriate to describe the location and magnitude of barriers along a minimum free energy pathway, possibly due to the limitation of the Gaussian approximation in providing sufficient resolution of the local free energy profiles. Nevertheless, the VFEP approach can easily be extended to multi-dimensional cases as Eq. (7) is not limited to the one-dimensional case. VFEP provides a way of constructing free energy profiles in multiple dimensions since it only needs a very small number of data points when only a qualitatively correct free energy profile is needed. As a result one could be able to identify free energy basins quickly and focus only on important regions instead of performing simulations in all regions. Furthermore, the VFEP approach can be used iteratively with more data points to generate the quantitatively detailed free energy profile when more data is available.

Analytic forms of biasing potentials

Another potentially significant advantage of VFEP over other methods is that the resulting free energy profiles are in analytic forms. Hence it would be straightforward to calculate the free energy derivatives with respect to the relevant coordinates. The availability of free energy derivatives will be particularly useful in the multi-dimensional case, in which the minimal free energy paths between two basins could be easily calculated. Such an approach has already been advocated in conjunction with the UI method.⁸¹ Further, these derivatives would provide biasing forces from a global biasing potential in order to smooth out the free energy landscape for improved sampling such as in metadynamics and adaptive biasing potential methods.^{5-8,74-77,82-86}

Conclusion

In the present work, we demonstrate that the two major problems in estimating free energy profiles from umbrella sampling data can be addressed through modeling the overall free energy profile based on the whole set of simulation data. The VFEP method presented here is a variational approach based on the maximum likelihood principle and is demonstrated to generally outperform other methods for a variety of test cases in terms of number of required windows and data points needed to construct the overall free energy profile. Whereas several other existing methods all converge to the correct free energy profile in the limit that there is sufficiently rich, well-distributed data, the VFEP method is shown to offer clear advantages in delivering stable, analytic free energy profiles under circumstances in which the data is more sparse, as are often encountered in practice. Test cases demonstrate that, for typical chemical reactions, only ~5 windows and ~20 to 35 data points per window are sufficient to obtain a qualitatively correct course-grained free energy profile that can be used to focus sampling in the most relevant regions of the surface, for example, in adaptive asynchronous Hamiltonian replica exchange simulations. The VFEP-modeled free energy profile behaves significant better than the quadratic function-based approaches, or methods that require significant overlap between windows. Hence, VFEP provides a potentially powerful tool in the arsenal of methods used attack the problem of free energy estimation from computer simulations of chemical reactions and processes.