Accelerating image reconstruction in three-dimensional optoacoustic tomography on graphics processing units

Abstract

Purpose: Optoacoustic tomography (OAT) is inherently a three-dimensional (3D) inverse problem. However, most studies of OAT image reconstruction still employ two-dimensional imaging models. One important reason is because 3D image reconstruction is computationally burdensome. The aim of this work is to accelerate existing image reconstruction algorithms for 3D OAT by use of parallel programming techniques.

Methods: Parallelization strategies are proposed to accelerate a filtered backprojection (FBP) algorithm and two different pairs of projection/backprojection operations that correspond to two different numerical imaging models. The algorithms are designed to fully exploit the parallel computing power of graphics processing units (GPUs). In order to evaluate the parallelization strategies for the projection/backprojection pairs, an iterative image reconstruction algorithm is implemented. Computer simulation and experimental studies are conducted to investigate the computational efficiency and numerical accuracy of the developed algorithms.

Results: The GPU implementations improve the computational efficiency by factors of 1000, 125, and 250 for the FBP algorithm and the two pairs of projection/backprojection operators, respectively. Accurate images are reconstructed by use of the FBP and iterative image reconstruction algorithms from both computer-simulated and experimental data.

Conclusions: Parallelization strategies for 3D OAT image reconstruction are proposed for the first time. These GPU-based implementations significantly reduce the computational time for 3D image reconstruction, complementing our earlier work on 3D OAT iterative image reconstruction.

INTRODUCTION

Optoacoustic tomography (OAT), also known as photoacoustic computed tomography, is an emerging imaging modality that has great potential for a wide range of biomedical imaging applications.^{1, 2, 3, 4} In OAT, a short laser pulse is employed to irradiate biological tissues. When the biological tissues absorb the optical energy, acoustic wave fields can be generated via the thermoacoustic effect. The acoustic wave fields propagate outward in three-dimensional (3D) space and are measured by use of ultrasonic transducers that are distributed outside the object. The goal of OAT is to obtain an estimate of the absorbed energy density map within the object from the measured acoustic signals. To accomplish this, an image reconstruction algorithm is required.

A variety of analytic image reconstruction algorithms have been proposed.^{5, 6, 7, 8} These algorithms generally assume an idealized transducer model and an acoustically homogeneous medium. Also, since they are based on discretization of continuous reconstruction formulae, these algorithms require the acoustic pressure to be densely sampled over a surface that encloses the object to obtain an accurate reconstruction. To overcome these limitations, iterative image reconstruction algorithms have been proposed.^{9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24} Although the optoacoustic wave intrinsically propagates in 3D space, when applying to experimental data, most studies have employed two-dimensional (2D) imaging models by making certain assumptions on the transducer responses and/or the object structures.^{10, 13, 15, 16, 19, 25} An important reason is because the computation required for 3D OAT image reconstruction is excessively burdensome. Therefore, acceleration of 3D image reconstruction will facilitate algorithm development and many applications including real-time 3D PACT.^{26, 27}

A graphics processing unit (GPU) card is a specialized device specifically designed for parallel computations.²⁸ Compute unified device architecture (CUDA) is an extension of the C/FORTRAN language that provides a convenient programming platform to exploit the parallel computational power of GPUs.²⁹ The CUDA-based parallel programming technique has been successfully applied to accelerate image reconstruction in mature imaging modalities such as x-ray computed tomography (CT)^{30, 31, 32} and magnetic resonance imaging (MRI).³³ In OAT, however, only a few works on utilization of GPUs to accelerate image reconstruction have been reported.^{20, 34} For example, the k-wave toolbox employs the NVIDIA CUDA Fast Fourier Transform library (cuFFT) to accelerate the computation of 3D FFT.³⁴ Also a GPU-based sparse matrix-vector multiplication strategy has been applied to 3D OAT image reconstruction for the case that the system matrix is sparse and can be stored in memory.²⁰ However, there remains an important need to develop efficient implementations of OAT reconstruction algorithms for general applications in which the system matrix is too large to be stored.

In this work, we propose parallelization strategies, for use with GPUs, to accelerate 3D image reconstruction in OAT. Both filtered backprojection (FBP) and iterative image reconstruction algorithms are investigated. For use with iterative image reconstruction algorithms, we focus on the parallelization of projection and backprojection operators. Specifically, we develop two pairs of projection/backprojection operators that correspond to two distinct discrete-to-discrete (D-D) imaging models employed in OAT, namely, the interpolation-based and the spherical-voxel-based D-D imaging models. Note that our implementations of the backprojection operators compute the exact adjoint of the forward operators, and therefore the projector pairs are “matched.”³⁵

The remainder of the paper is organized as follows. In Sec. 2, we briefly review OAT imaging models in their continuous and discrete forms. We propose GPU-based parallelization strategies in Sec. 3. Numerical studies and results are described in Secs. 4, 5, respectively. Finally, a brief discussion and summary of the proposed algorithms are provided in Sec. 6.

BACKGROUND

Continuous-to-continuous (C-C) imaging models and analytic image reconstruction algorithms

A C-C OAT imaging model neglects sampling effects and provides a mapping from the absorbed energy density function A(r) to the induced acoustic pressure function p(r^s, t). Here, t is the temporal coordinate, r ∈ V and r^s ∈ S denote the locations within the object support V and on the measurement surface S, respectively. A canonical OAT C-C imaging model can be expressed as^{1, 14, 36}

$$p({\mathbf{r}}^s,t)=\frac{\beta }{4\pi C_p}{\int }_{V}d\mathbf{r}A\left(\mathbf{r}\right)\frac{d}{dt}\frac{\delta \left(t-\frac{|{\mathbf{r}}^s-\mathbf{r}|}{c_0}\right)}{|{\mathbf{r}}^s-\mathbf{r}|}\equiv {\mathcal{H}}_{\mathrm{CC}}A,$$ (1)

where δ(t) is the Dirac delta function, β, c₀, and C_p denote the thermal coefficient of volume expansion, (constant) speed-of-sound, and the specific heat capacity of the medium at constant pressure, respectively. We introduce an operator notation ${\mathcal{H}}_{\mathrm{CC}}$ to denote this C-C mapping.

Alternatively, Eq. 1 can be reformulated as the well-known spherical Radon transform (SRT)^{12, 37}

$$g({\mathbf{r}}^s,t)={\int }_{V}d\mathbf{r}A\left(\mathbf{r}\right)\delta (c_{0}t-|{\mathbf{r}}^s-\mathbf{r}\left|\right),$$ (2)

where the function g(r^s, t) is related to p(r^s, t) as

$$p({\mathbf{r}}^s,t)=\frac{\beta }{4\pi C_p}\frac{\partial }{\partial t}\left(\frac{g({\mathbf{r}}^s,t)}{t}\right).$$ (3)

The SRT model provides an intuitive interpretation of each value of g(r^s, t) as a surface integral of A(r) over a sphere centered at r^s with radius tc₀.

Based on C-C imaging models, a variety of analytic image reconstruction algorithms have been developed.^{5, 6, 7, 8} For the case of a spherical measurement geometry, a FBP algorithm in its continuous form is given by⁶

$$\begin{array}{c}\hfill A\left(\mathbf{r}\right)=-\frac{C_p}{2\pi \beta c_0^2{R}^s}{\int }_{S}d{\mathbf{r}}^s{\left[\frac{2p({\mathbf{r}}^s,t)}{|\mathbf{r}-{\mathbf{r}}^s|}+\frac{1}{c_0}\frac{\partial p({\mathbf{r}}^s,t)}{\partial t}\right]}_{t=\frac{|\mathbf{r}-{\mathbf{r}}^s|}{c_0}},\end{array}$$ (4)

where R^s denotes the radius of the measurement surface S.

Discrete-to-discrete imaging models and iterative image reconstruction algorithms

When sampling effects are considered, an OAT system is properly described as a continuous-to-discrete (C-D) imaging model^{14, 22, 35, 38, 39}

$$\begin{array}{ccc}\hfill {\left[\mathbf{u}\right]}_{qK+k}& =& h^e\left(t\right){*}_t\frac{1}{S_q}{\int }_{S_q}d{\mathbf{r}}^{s}p({\mathbf{r}}^s,t){|}_{t=k{\Delta }_t},\hfill \\ & & \begin{array}{c}q=0,1,\cdots ,Q-1\hfill \\ k=0,1,\cdots ,K-1\hfill \end{array},\hfill \end{array}$$ (5)

where Q and K denote the total numbers of transducers (indexed by q) and the time samples (indexed by k) respectively. S_q is the surface area of the qth transducer, which is assumed to be a subset of S; h^e(t) denotes the acousto-electric impulse response (EIR) of each transducer that, without loss of generality, is assumed to be identical for all transducers; “*_t” denotes a linear convolution with respect to time coordinate; and Δ_t is the temporal sampling interval. The vector u represents the lexicographically ordered measured voltage signals whose (qK + k)th element is denoted by [u]_{qK + k}.

In order to apply iterative image reconstruction algorithms, a D-D imaging model is required, which necessitates the discretization of A(r). The following N-dimensional representation of the object function can be employed^{35, 38}

$$A\left(\mathbf{r}\right)\approx \sum _{n=0}^{N-1}{\left[\mathit{\alpha }\right]}_n{\psi }_n\left(\mathbf{r}\right),$$ (6)

where α is a coefficient vector whose nth element is denoted by [α]_n and ψ_n(r) is the expansion function. On substitution from Eq. 6 into Eq. 5, where p(r^s, t) is defined by Eq. 1, one obtains a D-D mapping from α to u, expressed as

$$\mathbf{u}\approx \mathbf{H}\mathit{\alpha },$$ (7)

where each element of the matrix H is defined as

$${\left[\mathbf{H}\right]}_{qK+k,n}={\left[h^e{*}_t\frac{1}{S_q}{\int }_{S_q}d{\mathbf{r}}^s{\mathcal{H}}_{\mathrm{CC}}{\psi }_n\right]}_{t=k{\Delta }_t}.$$ (8)

Here, H is the D-D imaging operator also known as system matrix or projection operator. Note that the “≈” in Eq. 7 is due to the use of the finite-dimensional representation of the object function [i.e., Eq. 6]. No additional approximations have been introduced.

Below we describe two types of D-D imaging models that have been employed in OAT:^{14, 22, 39} the interpolation-based imaging model and the spherical-voxel-based imaging model. The quantities u, H, and α (or ψ_n) in the two models will be distinguished by the subscripts (or superscripts) “int” and “sph,” respectively.

Interpolation-based D-D imaging model

The interpolation-based D-D imaging model defines the coefficient vector as samples of the object function on the nodes of a uniform Cartesian grid

$${\left[{\mathit{\alpha }}_{\mathrm{int}}\right]}_n={\int }_{V}d\mathbf{r}\delta (\mathbf{r}-{\mathbf{r}}_n)A\left(\mathbf{r}\right),n=0,1,\cdots ,N-1,$$ (9)

where r_n = (x_n, y_n, z_n)^T specifies the location of the nth node of the uniform Cartesian grid. The definition of the expansion function depends on the choice of interpolation method.¹⁹ If a trilinear interpolation method is employed, the expansion function can be expressed as⁴⁰

$${\psi }_n^{\mathrm{int}}\left(\mathbf{r}\right)=\left\{\begin{array}{cc}\hfill \left(1-\frac{|x-x_n|}{{\Delta }_s}\right)\left(1-\frac{|y-y_n|}{{\Delta }_s}\right)\left(1-\frac{|z-z_n|}{{\Delta }_s}\right),& \hfill \text{if}|x-x_n|,|y-y_n|,|z-z_n|\le {\Delta }_s\\ \hfill 0,& \hfill \text{otherwise}\end{array}\right.,$$ (10)

where Δ_s is the distance between two neighboring grid points.

In principle, the interpolation-based D-D imaging model can be constructed by substitution from Eqs. 9, 10 to Eq. 8. In practice, however, implementation of the surface integral over S_q is difficult for the choice of expansion functions in Eq. 10. Also, implementations of the temporal convolution and ${\mathcal{H}}_{\mathrm{CC}}{\psi }_n^{\mathrm{int}}$ usually require extra discretization procedures. Therefore, utilization of the interpolation-based D-D model commonly assumes the transducers to be point-like. In this case, the implementation of H_int is decomposed as a three-step operation

$${\mathbf{u}}_{\mathrm{int}}={\mathbf{H}}_{\mathrm{int}}{\mathit{\alpha }}_{\mathrm{int}}\equiv {\mathbf{H}}^e\mathbf{D}\mathbf{G}{\mathit{\alpha }}_{\mathrm{int}},$$ (11)

where G, D, and H^e are discrete approximations of the SRT [Eq. 2], the differential operator [Eq. 3], and the operator that implements a temporal convolution with EIR, respectively. We implemented G in a way^{12, 41, 42} that is similar to the “ray-driven” implementation of Radon transform in x-ray CT,⁴⁰ i.e, for each data sample, we accumulated the contributions from the voxels that resided on the spherical shell specified by the data sample. By use of Eqs. 2, 6, 9, 10, one obtains

$$\begin{array}{c}\hfill {\left[\mathbf{G}{\mathit{\alpha }}_{\mathrm{int}}\right]}_{qK+k}={\Delta }_s^2\sum _{n=0}^{N-1}{\left[{\mathit{\alpha }}_{\mathrm{int}}\right]}_n\sum _{i=0}^{N_i-1}\sum _{j=0}^{N_j-1}{\psi }_n^{\mathrm{int}}\left({\mathbf{r}}_{k,i,j}\right)\equiv {\left[\mathbf{g}\right]}_{qK+k},\end{array}$$ (12)

where ${\left[\mathbf{g}\right]}_{qK+k}\approx g({\mathbf{r}}_q^s,t){|}_{t=k{\Delta }_t}$ with ${\mathbf{r}}_q^s$ specifying the location of the qth point-like transducer, and N_i and N_j denote the numbers of divisions over the two angular coordinates of a local spherical coordinate system shown in Fig. 1b. A derivation of Eq. 12 is provided in the Appendix. The differential operator in Eq. 3 is approximated as

$$\begin{array}{c}\hfill {\left[\mathbf{D}\mathbf{g}\right]}_{qK+k}=\frac{\beta }{8\pi C_p{\Delta }_t^2}\left(\frac{{\left[\mathbf{g}\right]}_{qK+k+1}}{k+1}-\frac{{\left[\mathbf{g}\right]}_{qK+k-1}}{k-1}\right)\equiv {\left[{\mathbf{p}}_{\mathrm{int}}\right]}_{qK+k},\end{array}$$ (13)

where ${\left[{\mathbf{p}}_{\mathrm{int}}\right]}_{qK+k}\approx p({\mathbf{r}}_q^s,t){|}_{t=k{\Delta }_t}$. Finally, the continuous temporal convolution is approximated by a discrete linear convolution as⁴³

$${\left[{\mathbf{H}}^e{\mathbf{p}}_{\mathrm{int}}\right]}_{qK+k}=\sum _{\kappa =0}^{K-1}{\left[{\mathbf{h}}^e\right]}_{k-1-\kappa }{\left[{\mathbf{p}}_{\mathrm{int}}\right]}_{qK+\kappa }\equiv {\left[{\mathbf{u}}_{\mathrm{int}}\right]}_{qK+k},$$ (14)

where ${\left[{\mathbf{h}}^e\right]}_k={\Delta }_t{h}^e\left(t\right){|}_{t=k{\Delta }_t}$.

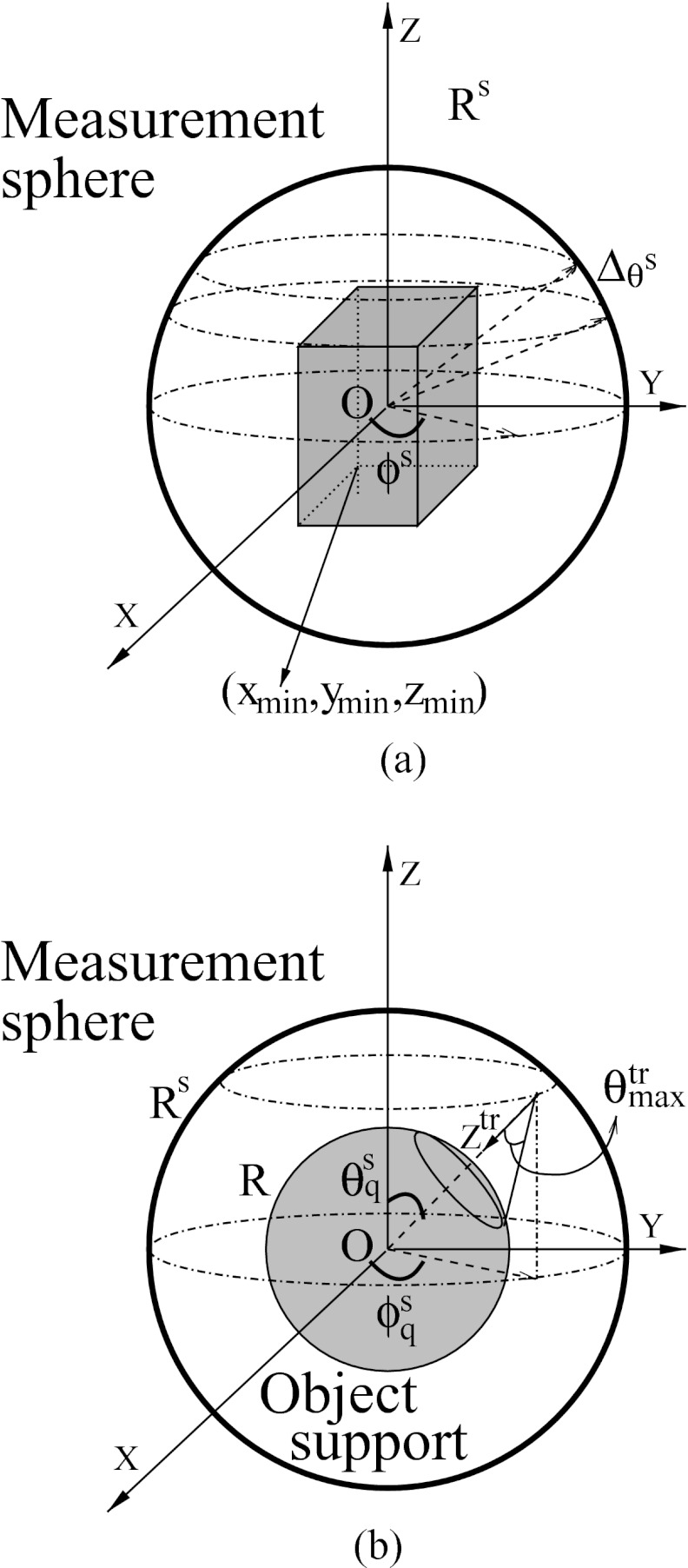
Figure 1.

(a) Schematic of the 3D OAT scanning geometry. (b) Schematic of the local coordinate system for the implementation of interpolation-based D-D imaging model.

Spherical-voxel-based D-D imaging model

The spherical-voxel-based imaging model is also widely employed in OAT.^{9, 11, 14, 22, 44} It employs the expansion functions

$${\psi }_n^{\mathrm{sph}}\left(\mathbf{r}\right)=\left\{\begin{array}{cc}\hfill 1,& \hfill \text{if}|\mathbf{r}-{\mathbf{r}}_n|\le {\Delta }_s/2\\ \hfill 0,& \hfill \text{otherwise}\end{array}\right.,$$ (15)

where r_n is defined as in Eq. 9. The nth expansion function ${\psi }_n^{\mathrm{sph}}\left(\mathbf{r}\right)$ is a uniform sphere that is inscribed by the nth cuboid of a Cartesian grid. The nth component of the coefficient vector α_sph is defined as

$${\left[{\mathit{\alpha }}_{\mathrm{sph}}\right]}_n=\frac{V_{\text{cube}}}{V_{\text{sph}}}{\int }_{V}d\mathbf{r}{\psi }_n^{\mathrm{sph}}\left(\mathbf{r}\right)A\left(\mathbf{r}\right),$$ (16)

where V_cube and V_sph are the volumes of a cubic voxel of dimension Δ_s and of a spherical voxel of radius Δ_s/2, respectively.

Unlike the interpolation-based imaging model, by use of the expansion functions defined in Eq. 15, the surface integral over S_q and ${\mathcal{H}}_{\mathrm{CC}}{\psi }_n^{\mathrm{sph}}$ in Eq. 8 can be converted to a temporal convolution and calculated analytically.^{14, 22} To avoid utilizing excessively high sampling rates to mitigate aliasing, the spherical-voxel-based imaging model can be conveniently implemented in the temporal frequency domain as²²

$$\begin{array}{ccc}& & {\left[{\tilde{\mathbf{u}}}_{\mathrm{sph}}\right]}_{qL+l}={\tilde{p}}_0\left(f\right)\sum _{n=0}^{N-1}{\left[{\mathit{\alpha }}_{\mathrm{sph}}\right]}_n\frac{1}{S_q}{\tilde{h}}_q^s({\mathbf{r}}_n,f){|}_{f=l{\Delta }_f},\hfill \\ & & \mathrm{for}l=0,1,\cdots ,L-1,\hfill \end{array}$$ (17)

where Δ_f is the frequency sampling interval, and L denotes the total number of temporal-frequency samples indexed by l. A derivation of Eq. 17 can be found in Ref. 22. The function ${\tilde{h}}_q^s({\mathbf{r}}_n,f)$ represents the temporal Fourier transform of the spatial impulse response (SIR) of the qth transducer for the source located at r_n, expressed as

$${\tilde{h}}_q({\mathbf{r}}_n,f)={\int }_{S_q}d{\mathbf{r}}^s\frac{\exp \left(-\widehat{ȷ}2\pi f\frac{|{\mathbf{r}}^s-{\mathbf{r}}_n|}{c_0}\right)}{2\pi |{\mathbf{r}}^s-{\mathbf{r}}_n|}.$$ (18)

Also, ${\tilde{p}}_0\left(f\right)$ is defined as

$$\begin{array}{c}\hfill {\tilde{p}}_0\left(f\right)=-\widehat{ȷ}\frac{\beta c_0^3}{C_{p}f}\left[\frac{{\Delta }_s}{2c_0}\cos \left(\frac{\pi f{\Delta }_s}{c_0}\right)-\frac{1}{2\pi f}\sin \left(\frac{\pi f{\Delta }_s}{c_0}\right)\right]{\tilde{h}}^e\left(f\right),\end{array}$$ (19)

where ${\tilde{h}}^e\left(f\right)$ is the EIR in temporal-frequency domain. In summary, the imaging model can be expressed in matrix form as

$${\tilde{\mathbf{u}}}_{\mathrm{sph}}={\mathbf{H}}_{\mathrm{sph}}{\mathit{\alpha }}_{\mathrm{sph}}.$$ (20)

Adjoints of the system matrices

Iterative image reconstruction algorithms employ numerical implementations of the projection operator, i.e., the system matrix H, as well as its adjoint, denoted by H†.⁴⁵ The adjoint is also referred to as the backprojection operator. Note that for most practical applications, H and H† are too large to be stored in the random access memory of currently available computers. Therefore, in practice, the actions of H and H† are almost always calculated on the fly. The same strategy was adopted in this work.

According to the definition of the adjoint operator,^{35, 43}${\mathbf{H}}_{\mathrm{int}}^{†}={\mathbf{G}}^{†}{\mathbf{D}}^{†}{\mathbf{H}}^{\mathbf{e}†}$, where

$${\left[{\mathbf{H}}^{\mathbf{e}†}{\mathbf{u}}_{\mathrm{int}}\right]}_{qK+k}=\sum _{\kappa =0}^{K-1}{\left[{\mathbf{h}}^e\right]}_{\kappa -1-k}{\left[{\mathbf{u}}_{\mathrm{int}}\right]}_{qK+\kappa }\equiv {\left[{\mathbf{p}}_{\mathrm{int}}^{\prime }\right]}_{qK+k},$$ (21)

$$\begin{array}{ccc}\hfill {\left[{\mathbf{D}}^{†}{\mathbf{p}}_{\mathrm{int}}^{\prime }\right]}_{qK+k}& =& \frac{\beta }{8\pi C_p{\Delta }_t^{2}k}({\left[{\mathbf{p}}_{\mathrm{int}}^{\prime }\right]}_{qK+k-1}-{\left[{\mathbf{p}}_{\mathrm{int}}^{\prime }\right]}_{qK+k+1})\hfill \\ & \equiv & {\left[{\mathbf{g}}^{\prime }\right]}_{qK+k},\hfill \end{array}$$ (22)

and

$$\begin{array}{ccc}\hfill {\left[{\mathbf{G}}^{†}{\mathbf{g}}^{\prime }\right]}_n& =& {\Delta }_s^2\sum _{q=0}^{Q-1}\sum _{k=0}^{K-1}{\left[{\mathbf{g}}^{\prime }\right]}_{qK+k}\sum _{i=0}^{N_i-1}\sum _{j=0}^{N_j-1}{\psi }_n^{\mathrm{int}}\left({\mathbf{r}}_{k,i,j}\right)\hfill \\ & \equiv & {\left[{\mathit{\alpha }}_{\mathrm{int}}^{\prime }\right]}_n.\hfill \end{array}$$ (23)

It can also be verified that the adjoint operator ${\mathbf{H}}_{\mathrm{sph}}^{†}$ is given by

$$\begin{array}{c}\hfill {\left[{\mathbf{H}}_{\mathrm{sph}}^{†}{\tilde{\mathbf{u}}}_{\mathrm{sph}}\right]}_n=\sum _{q=0}^{Q-1}\sum _{l=0}^{L-1}{\left[{\tilde{\mathbf{u}}}_{\mathrm{sph}}\right]}_{qL+l}{\tilde{p}}_0^{*}\left(f\right){\tilde{h}}_q^{*}({\mathbf{r}}_n,f){|}_{f=l{\Delta }_f},\end{array}$$ (24)

where the superscript “*” denotes the complex conjugate. Unlike the unmatched backprojection operators⁴⁶ that are obtained by discretization of the continuous adjoint operator, utilization of the exact adjoint operator facilitates the convergence of iterative image reconstruction algorithms.

GPU architecture and CUDA programming

The key features of GPU architecture and the basics of CUDA programming are briefly summarized in this section. We refer the readers to Refs. ^{28, 29} for additional details.

A GPU card contains multiple streaming multiprocessors. Each streaming multiprocessor is configured with multiple processor cores. For example, the Tesla C1060 possesses 30 streaming multiprocessors with 8 processor cores on each; and the Tesla C2050 possesses 14 streaming multiprocessors with 32 processor cores on each.²⁸ The processor cores in each multiprocessor execute the same instruction on different pieces of data, which is referred to as “single instruction, multiple data” (SIMD) model of parallel programming. In order to fully exploit the computing power of GPUs, one of the major challenges is to design a parallelization strategy fitting in the SIMD framework such that the largest number of processor cores can execute the computation simultaneously.²⁹

A GPU card has six types of memory that have varying capacities and different access rules and efficiencies: (1) Registers are assigned for each thread and have the fastest access. (2) Shared memory is assigned for each block and can be efficiently accessed by all threads in the block if designed appropriately. (3) Constant memory is read-only and can be accessed by all threads efficiently. (4) Texture memory is also read-only and is optimized for interpolation operations. (5) Global memory has the slowest access that takes hundred times more clock cycles than does the computation of basic arithmetic operations. (6) Local memory is assigned for each thread but has a slow access as does the global memory. Therefore, an efficient GPU-based implementation in general requires a limited number of global and local memory access.

CUDA is a platform and programming model developed by NVIDIA that includes a collection of functions and keywords to exploit the parallel computing power of GPUs.²⁹ A CUDA parallel program is composed of a host program and kernels. The host program is executed by central processing units (CPUs) and launches the kernels, which are custom-designed functions executed by GPUs. A general parallel programming strategy is to launch multiple instances of a kernel and to run the multiple instances concurrently on GPUs. In CUDA, each instance of the kernel is named as a thread and processes only a portion of the data. A hierarchy of threads is employed: Threads are grouped into blocks, and blocks are grouped into a grid. Therefore, each thread is specified by a multi-index containing a block index and a thread index within the block.

GPU-ACCELERATED RECONSTRUCTION ALGORITHMS

In this section, we propose GPU-based parallelization strategies for the FBP algorithm and the projection/backprojection operations corresponding to the interpolation-based and the spherical-voxel-based D-D imaging models.

Measurement geometry

We employed a spherical measurement geometry shown in Fig. 1a. The measurement sphere was of radius R^s centered at the origin of the Cartesian coordinate system (or the equivalent spherical coordinate system). The polar angle θ^s ∈ [0, π] was equally divided with interval ${\Delta }_{{\theta }^s}=\pi /N_r$, starting from ${\theta }_{\min }^s$. At each polar angle, a ring on the sphere that was parallel to the plane z = 0 can be specified, resulting N_r rings. On each ring, N_v ultrasonic transducers were assumed to be uniformly distributed with azimuth angle interval ${\Delta }_{{\varphi }^s}=2\pi /N_v$. Hereafter, each azimuth angle will be referred to as a tomographic view. At each view, we assumed that N_t temporal samples were acquired and the first sample corresponded to time instance t_min. For implementations in temporal-frequency domain, we assumed that N_f temporal-frequency samples were available and the first sample corresponded to f_min. The region to be reconstructed was a rectangular cuboid whose edges were parallel to the axes of the coordinate system and the left-bottom-back vertex was located at (x_min, y_min, z_min). The numbers of voxels along the three coordinates will be denoted by N_x, N_y, and N_z, respectively, totally N = N_xN_yN_z voxels. We also assumed the cuboid was contained in another sphere of radius R that was concentric with the measurement sphere shown in Fig. 1b.

Implementation of the FBP algorithm

Central processing unit-based implementations of continuous FBP formulae have been described in Refs. ^{5, 6, 7, 8}. Though the discretization methods vary, in general, three approximations have to be employed. First, the first-order derivative term ∂p(r^s, t)/∂t has to be approximated by a difference scheme up to certain order.⁴⁷ Second, the measurement sphere has to be divided into small patches, and the surface integral has to be approximated by a summation of the area of every patch weighted by the effective value of the integrand on the patch. Finally, the value of the integrand at an arbitrary time instance t = |r^s − r|/c₀ has to be approximated by certain interpolation method.

In this study, we approximated the surface integral by use of the trapezoidal rule. As described earlier, the spherical surface was divided into N_rN_v patches. For the transducer indexed by q that was located at ${\mathbf{r}}_q^s=(R^s,{\theta }_q^s,{\varphi }_q^s)$, the area of the patch was approximated by ${\left(R^s\right)}^2{\Delta }_{{\theta }^s}{\Delta }_{{\varphi }^s}\sin {\theta }_q^s$. The value at time instance $t=|{\mathbf{r}}_q^s-{\mathbf{r}}_n|/c_0$ was approximated by the linear interpolation from its two neighboring samples as

$$\begin{array}{c}\hfill p({\mathbf{r}}_q^s,t){|}_{t=\frac{|{\mathbf{r}}_q^s-{\mathbf{r}}_n|}{c_0}}\approx (k+1-\tilde{k}){\left[\mathbf{p}\right]}_{qK+k}+(\tilde{k}-k){\left[\mathbf{p}\right]}_{qK+k+1},\end{array}$$ (25)

where $\tilde{k}=\left(\right|{\mathbf{r}}_q^s-{\mathbf{r}}_n|/c_0-t_{\min })/{\Delta }_t$, and k is the integer part of $\tilde{k}$. Here, p is a vector of lexicographically ordered samples of the pressure function p(r^s, t), which is estimated from the measured voltage data vector u. Also, the first-order derivative term was approximated by

$$\frac{\partial }{\partial t}p\left({\mathbf{r}}_q^s,t\right){|}_{t=\frac{|{\mathbf{r}}_q^s-{\mathbf{r}}_n|}{c_0}}\approx \frac{1}{{\Delta }_t}({\left[\mathbf{p}\right]}_{qK+k+1}-{\left[\mathbf{p}\right]}_{qK+k}).$$ (26)

By use of these three numerical approximations, the discretized FBP formula was expressed as

$$\begin{array}{ccc}\hfill {\left[{\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}\right]}_n& =& -\frac{C_p{R}^s{\Delta }_{{\theta }^s}{\Delta }_{{\varphi }^s}}{\pi \beta c_0^3{\Delta }_t}\sum _{n_r=0}^{N_r-1}\sin {\theta }_q^s\hfill \\ & & \times \sum _{n_v=0}^{N_v-1}\{\left(1.5-\frac{k+t_{\min }/{\Delta }_t}{\tilde{k}+t_{\min }/{\Delta }_t}\right){\left[\mathbf{p}\right]}_{qK+k+1}\hfill \\ & & +\left(\frac{k+1+t_{\min }/{\Delta }_t}{\tilde{k}+t_{\min }/{\Delta }_t}-1.5\right){\left[\mathbf{p}\right]}_{qK+k}\}.\hfill \end{array}$$ (27)

Unlike the implementations of FBP formulas in x-ray cone beam CT,^{31, 32} we combined the filter and the linear interpolation. This reduced the number of visits to the global memory in the GPU implementation described below.

We implemented the FBP formula in a way that is similar to the “pixel-driven” implementation in x-ray CT,³² i.e., we assigned each thread to execute the two accumulative summations in Eq. 27 for each voxel. We bound the pressure data p to texture memory because it is cached and has a faster accessing rate. Therefore, our implementation only requires access to texture memory twice and to global memory once. The pseudocodes are provided in Algorithms 1 and 2 for the host part and the device part, respectively. Note that the pseudocodes do not intend to be always optimal because the performance of the codes could depend on the dimensions of p and ${\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}$. For example, we set the block size to be (N_z, 1, 1) because for our applications, N_z was bigger than N_x and N_y and smaller than the limit number of threads that a block can support (i.e., 1024 for the NVIDIA Tesla C2050). If the values of N_x, N_y, and N_z change, we may need to redesign the dimensions of the grid and blocks. However, the general SIMD parallelization strategy remains.

Table .

Algorithm I. Implementation of the FBP algorithm (on host).

Input:p

Output:${\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}$

1: $w=-C_p{R}^s{\Delta }_{{\theta }^s}{\Delta }_{{\varphi }^s}/\left(\pi \beta c_0^3{\Delta }_t\right)$ {Precalculate the common coefficient}

2: $\mathrm{T}\_\mathbf{p}\leftarrow \mathbf{p}$ {Bound data to texture memory}

3: K_fbp  ⟨⟨⟨ (Ny, Nx), (Nz, 1, 1) ⟩⟩⟩ (ω, $\mathrm{D}\_{\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}$)

4: ${\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}\leftarrow \mathrm{D}\_{\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}$ {Copy data from global memory to host}

Table .

Algorithm II. Implementation of kernel K_fbp   ⟨⟨⟨ (N_y, N_x), (N_z, 1, 1) ⟩⟩⟩.

Input: ω, $\mathrm{T}\_\mathbf{p}$, $\mathrm{D}\_{\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}$

Output:$\mathrm{D}\_{\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}$

1: x = (blockIdx.y)Δs + xmin; y = (blockIdx.x)Δs + ymin; z = (threadIdx.x)Δs + zmin

2: Σ = 0

3: fornr = 0 toNr − 1 do

4:   ${\theta }^s=n_r{\Delta }_{{\theta }^s}+{\theta }_{\min }^s$; zs = Rscos θs; rs = Rssin θs; w′ = wsin θs

5:   fornv = 0 toNv − 1 do

6:      ${\varphi }^s=n_v{\Delta }_{{\varphi }^s}+{\varphi }_{\min }^s$; xs = rscos ϕs; ys = rssin ϕs

7:      $\overline{t}={({(x-x^s)}^2+{(y-y^s)}^2+{(z-z^s)}^2)}^{1/2}$

8:      $t_n=(\overline{t}/c_0-t_{\min })/{\Delta }_t$; nt = floor(tn)

9:      $\Sigma +={\omega }^{\prime }\{[(n_t{\Delta }_t+t_{\min })/(t_n{\Delta }_t+t_{\min })-1.5]\mathrm{T}\_\mathbf{p}\left[n_r\right]\left[n_v\right]\left[n_t\right]+[1.5-(n_t{\Delta }_t+t_{\min })/(t_n{\Delta }_t+t_{\min })]\mathrm{T}\_\mathbf{p}\left[n_r\right]\left[n_v\right][n_t+1]\}$ {Fetch data from texture memory}

10:   endfor

11: endfor

12: $\mathrm{D}\_{\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}\left[\mathrm{blockIdx}.\mathrm{y}\right]\left[\mathrm{blockIdx}.\mathrm{x}\right]\left[\mathrm{threadIdx}.\mathrm{x}\right]=\Sigma$

Implementation of H_int and ${\mathbf{H}}_{\mathrm{int}}^{†}$

The forward projection operation H_intα_int is composed of three consecutive operations g = Gα_int, p_int = Dg, and u_int = H^ep_int that are defined in Eqs. 12, 13, 14, respectively. Both the difference operator D and the one-dimensional (1D) convolution H^e have low computational complexities while the SRT operator G is computationally burdensome. Hence, we developed the GPU-based implementation of G while leaving D and H^e to be implemented by CPUs.

The SRT in OAT shares many features with the Radon transform in x-ray CT. Thus, our GPU-based implementation is closely related to the implementations of Radon transform that have been optimized for x-ray CT.^{30, 31, 32} The surface integral was approximated according to the trapezoidal rule. First, the integral surface was divided into small patches, which is described in the Appendix. Second, each patch was assigned an effective value of the object function by trilinear interpolation. The trilinear interpolation was calculated by use of the texture memory of GPUs that is specifically designed for interpolation. Finally, GPU threads accumulated the areas of patches weighted by the effective values of the object function and wrote the final results to global memory. The pseudocodes for implementation of G are provided in Algorithms 3 and 4 for the host part and the device part, respectively. Note that we employed the “one-level”-strategy,³² i.e., each thread calculates one data sample. Higher level strategies have been proposed to improve the performance by assigning each block to calculate multiple data samples,³² which, however, caused many thread idles in OAT mainly because the amount of computation required to calculate a data sample varies largely among samples for SRT.

Table .

Algorithm III. Implementation of g = Gα_int (on host)

Input:αint

Output:g

1: $\mathrm{T}\_{\mathit{\alpha }}_{\mathrm{int}}\leftarrow {\mathit{\alpha }}_{\mathrm{int}}$ {Bound data to texture memory}

2: K_srt  ⟨⟨⟨ (Nv, Nt), (Nr, 1, 1) ⟩⟩⟩ ($\mathrm{D}\_\mathbf{g}$)

3: $\mathbf{g}\leftarrow \mathrm{D}\_\mathbf{g}$ {Copy data from global memory to host}

Table .

Algorithm IV. Implementation of kernel K_srt   ⟨⟨⟨ (N_v, N_t), (N_r, 1, 1) ⟩⟩⟩.

Input:$\mathrm{D}\_\mathbf{g}$, $\mathrm{T}\_{\mathit{\alpha }}_{\mathrm{int}}$

Output:$\mathrm{D}\_\mathbf{g}$

1: $\overline{t}=\left(\mathrm{blockIdx}.\mathrm{y}\right)c_0{\Delta }_t+c_0{t}_{\min }$; ${\theta }^s=\left(\mathrm{threadIdx}.\mathrm{x}\right){\Delta }_{{\theta }^s}+{\theta }_{\min }^s$; ${\varphi }^s=\left(\mathrm{blockIdx}.\mathrm{x}\right){\Delta }_{{\varphi }^s}+{\varphi }_{\min }^s$

2: ${\theta }_{\max }^{\prime }=\arccos (({\left(R^s\right)}^2+{\overline{t}}^2-R^2)/\left(2\overline{t}{R}^s\right))$

3: Σ = 0; ${\theta }^{\prime }={\theta }_{\max }^{\prime }$

4: while θ′ > 0 do

5:   $z^{\prime }=\overline{t}\cos {\theta }^{\prime }$; $r^{\prime }=\overline{t}\sin {\theta }^{\prime }$; ϕ′ = 0

6:   while ϕ′ < 2π do

7:      x′ = r′cos ϕ′; y′ = r′sin ϕ′

8:      x = −x′sin θ′ − (z′ − Rs)cos θ′; y = y′; z = x′cos θ′ − (z′ − Rs)sin θ′ {Convert to global coordinate system}

9:      xn = (x − xmin)/Δs; yn = (y − ymin)/Δs; zn = (z − zmin)/Δs

10:      Σ + = tex3D(xn, yn, zn) {Tri-linear interpolation}

11:      ϕ′ = ϕ′ + Δs/r′

12:   endwhile

13:   ${\theta }^{\prime }={\theta }^{\prime }-{\Delta }_s/\overline{t}$

14: endwhile

15: $\mathrm{D}\_\mathbf{g}\left[\mathrm{threadIdx}.\mathrm{x}\right]\left[\mathrm{blockIdx}.\mathrm{x}\right]\left[\mathrm{blockIdx}.\mathrm{y}\right]=\Sigma {\Delta }_s^2$

Implementation of the backprojection operator ${\mathbf{H}}_{\mathrm{int}}^{†}$ was very similar to the implementation of H_int. The operators D† and H^e_† were calculated on CPUs while G† was calculated by use of GPUs. The pseudocodes are provided in Algorithms 5 and 6. We made use of the CUDA function “atomicAdd” to add weights to global memory from each thread.

Table .

Algorithm V. Implementation of ${\mathit{\alpha }}_{\mathrm{int}}^{\prime }={\mathbf{G}}^{†}{\mathbf{g}}^{\prime }$ (on host).

Input:g′

Output:${\mathit{\alpha }}_{\mathrm{int}}^{\prime }$

1: $\mathrm{T}\_{\mathbf{g}}^{\prime }\leftarrow {\mathbf{g}}^{\prime }$ {Bound data to texture memory}

2: K_srtT  ⟨⟨⟨ (Nv, Nt), (Nr, 1, 1) ⟩⟩⟩ ($\mathrm{D}\_{\mathit{\alpha }}_{\mathrm{int}}^{\prime }$)

3: ${\mathit{\alpha }}_{\mathrm{int}}^{\prime }\leftarrow \mathrm{D}\_{\mathit{\alpha }}_{\mathrm{int}}^{\prime }$ {Copy data from global memory to host}

Table .

Algorithm VI. Implementation of kernel K_srtT   ⟨⟨⟨ (N_v, N_t), (N_r, 1, 1) ⟩⟩⟩.

Input:$\mathrm{D}\_{\mathit{\alpha }}_{\mathrm{int}}^{\prime }$, $\mathrm{T}\_{\mathbf{g}}_{\mathrm{int}}^{\prime }$

Output:$\mathrm{D}\_{\mathit{\alpha }}_{\mathrm{int}}^{\prime }$

1: $\overline{t}=\left(\mathrm{blockIdx}.\mathrm{y}\right)c_0{\Delta }_t+c_0{t}_{\min }$; ${\theta }^s=\left(\mathrm{threadIdx}.\mathrm{x}\right){\Delta }_{{\theta }^s}+{\theta }_{\min }^s$; ${\varphi }^s=\left(\mathrm{blockIdx}.\mathrm{x}\right){\Delta }_{{\varphi }^s}+{\varphi }_{\min }^s$

2: ${\theta }_{\max }^{\prime }=\arccos (({\left(R^s\right)}^2+{\overline{t}}^2-R^2)/\left(2\overline{t}{R}^s\right))$; ${\theta }^{\prime }={\theta }_{\max }^{\prime }$

3: while θ′ > 0 do

4:   $z^{\prime }=\overline{t}\cos {\theta }^{\prime }$; $r^{\prime }=\overline{t}\sin {\theta }^{\prime }$; ϕ′ = 0

5:   while ϕ′ < 2π do

6:      x′ = r′cos ϕ′; y′ = r′sin ϕ′

7:      x = −x′sin θ − (z′ − R′)cos θ; y = y′; z = x′cos θ − (z′ − R′)sin θ {Convert to global coordinate system}

8:      xn = (x − xmin)/Δs; yn = (y − ymin)/Δs; zn = (z − zmin)/Δs

9:      nx = floor(xn); ny = floor(yn); nz = floor(zn)

10:      $\mathrm{D}\_{\mathit{\alpha }}_{\mathrm{int}}^{\prime }\left[n_z\right]\left[n_y\right]\left[n_x\right]+={\Delta }_s^2(n_x+1-x_n)(n_y+1-y_n)(n_z+1-z_n)\mathrm{T}\_{\mathbf{g}}_{\mathrm{int}}^{\prime }\left[\mathrm{threadIdx}.\mathrm{x}\right]\left[\mathrm{blockIdx}.\mathrm{x}\right]\left[\mathrm{blockIdx}.\mathrm{y}\right]$ {Add weights to one of

the eight neighboring nodes by use of ‘atomicAdd'; Repeat this operation for all other seven neighboring nodes}

11:      ϕ′ = ϕ′ + Δs/r′

12:   endwhile

13:   ${\theta }^{\prime }={\theta }^{\prime }-{\Delta }_s/\overline{t}$

14: endwhile

Implementation of H_sph and ${\mathbf{H}}_{\mathrm{sph}}^{†}$

Implementation of the forward projection operation for the spherical-voxel-based imaging model is distinct from that of the interpolation-based model. The major difference is that calculation of each element of the data vector for the spherical-voxel-based imaging model requires the accumulation of the contributions from all voxels because the model is expressed in the temporal frequency domain. Because of this, the amount of computation required to calculate each data sample in the spherical-voxel-based imaging model is almost identical, simplifying the parallelization strategy.

We proposed a parallelization strategy that was inspired by one applied in advanced MRI reconstruction³³ and is summarized as follows. Discrete samples of ${\tilde{p}}_0\left(f\right)$ defined in Eq. 19 were precalculated and stored as a vector ${\tilde{\mathbf{p}}}_0$ in constant memory. Because the size of the input vector α_sph is often too large to fit in the constant memory, we divided α_sph into subvectors that matched the capacity of the constant memory. We employed a CPU loop to copy every subvector sequentially to the constant memory and call the GPU kernel function to accumulate a partial summation. The major advantage of this design is that the total number of global memory visits to calculate one data sample is reduced to the number of subvectors.

Implementation of the projection operator for the spherical-voxel-based imaging model generally involves more arithmetic operations than does the interpolation-based imaging model. Moreover, the spherical-voxel-based imaging model has been employed to compensate for the finite aperture size effect of transducers,^{14, 22} which makes the computation even more burdensome. Because of this, we further developed an implementation that employed multiple GPUs. The pseudocodes of the projection operation are provided in Algorithms 7, 8, 9. We created N_pth pthreads on CPUs by use of the “pthread.h” library. Here, we denote the threads on CPUs by “pthread” to distinguish from threads on GPUs. We divided the input vector α_sph into N_pth subvectors (denoted by α_pth's) of equal size and declared an output vector ${\tilde{\mathbf{u}}}_{\mathrm{sph}}^{\prime }$ of dimension N_pthN_rN_vN_f. By calling the pthread function “fwd_pthread,” N_sph pthreads simultaneously calculated the projection. Each pthread projected an α_pth to a partial voltage data vector ${\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }$ that filled in the larger vector ${\tilde{\mathbf{u}}}_{\mathrm{sph}}^{\prime }$. Once all pthreads finished filling their ${\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }$ into ${\tilde{\mathbf{u}}}_{\mathrm{sph}}^{\prime }$, the projection data ${\tilde{\mathbf{u}}}_{\mathrm{sph}}$ were obtained by a summation of the N_pth${\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }$'s.

Table .

Algorithm VI. Implementation of ${\tilde{\mathbf{u}}}_{\mathrm{sph}}={\mathbf{H}}_{\mathrm{sph}}{\mathit{\alpha }}_{\mathrm{sph}}$ (on host).

Input:αsph, ${\tilde{\mathbf{p}}}_0$

Output:${\tilde{\mathbf{u}}}_{\mathrm{sph}}$

1: fornpth = 0 toNpth − 1 do

2:   parm_fwdarg[npth].npth = npth

3:   parm_fwdarg[npth].${\tilde{p}}_0$ = &${\tilde{\mathbf{p}}}_0\left[0\right]$

4:   parm_fwdarg[npth].αpth=&αsph[npthNxNyNz/Npth]

5:   parm_fwdarg[npth].${\tilde{u}}_{\mathrm{pth}}^{\prime }$=$\&{\tilde{\mathbf{u}}}_{\mathrm{sph}}^{\prime }\left[n_{\mathrm{pth}}{N}_r{N}_v{N}_f\right]$ {Pass addresses

of arrays to each pthread}

6:   pthread_create(&pthreads[npth], NULL, fwd_pthread, (void *)

(parm_fwdarg+npth)) {Call function fwd_pthread}

7: endfor

8: fornpth = 0 toNpth − 1 do

9:   forn = 0 toNrNvNfdo

10:      ${\tilde{\mathbf{u}}}_{\mathrm{sph}}\left[n\right]+={\tilde{\mathbf{u}}}_{\mathrm{sph}}^{\prime }[n+n_{\mathrm{pth}}{N}_r{N}_v{N}_f]$

11:   endfor

12: endfor

Table .

Algorithm VIII. Implementation of function fwd_pthread (on host).

Input:npth, ${\tilde{\mathbf{p}}}_0$, αpth, ${\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }$

Output:${\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }$

1: ${\mathrm{C}\_\tilde{\mathbf{p}}}_0\leftarrow {\tilde{\mathbf{p}}}_0$ {Copy from host to constant memory}

2: fornx = 0 toNx/Npth − 1 do

3:   x = (nx + npthNx/Npth)Δs + xmin

4:   forny = 0 toNy − 1 do

5:      y = nyΔs + ymin

6:      $\mathrm{C}\_{\mathit{\alpha }}_{\mathrm{pth}}\leftarrow {\mathit{\alpha }}_{\mathrm{pth}}\left[n_x\right]\left[n_y\right][:]$ {Copy from host to constant

memory}

7:      K_fwdsph  ⟨⟨⟨ (Nv, Nr), (Nf, 1, 1) ⟩⟩⟩ (x, y, D_${\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }$)

8:   endfor

9: endfor

10: ${\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }\leftarrow \mathrm{D}\_{\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }$ {Copy from global memory to host}

Table .

Algorithm IX. Implementation of Kernel K_fwdsph  ⟨⟨⟨ (N_v, N_r), (N_f, 1, 1) ⟩⟩⟩.

Input:x, y, D_${\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }$, C_αpth, C_${\tilde{\mathbf{p}}}_0$

Output: D_${\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }$

1: ${\theta }^s=\left(\mathrm{blockIdx}.\mathrm{y}\right){\Delta }_{{\theta }^s}+{\theta }_{\min }^s$; ${\varphi }^s=\left(\mathrm{blockIdx}.\mathrm{x}\right){\Delta }_{{\varphi }^s}+{\varphi }_{\min }^s$; f = (threadIdx.x)Δf + fmin

2: zs = Rscos θs; xs = Rssin θscos ϕs; ys = Rssin θssin ϕs {Calculate locations of transducers}

3: Σr = 0; Σi = 0 {Initiate the partial summation including the real and imaginary parts}

4: fornz = 0 toNz − 1 do

5:   z = nzΔs + zmin

6:   d = ((x − xs)2 + (y − ys)2 + (z − zs)2)1/2

7:   ${\tilde{h}}^r=\cos (2\pi fd/c_0)/\left(2\pi d\right)$; ${\tilde{h}}^i=-\sin (2\pi fd/c_0)/\left(2\pi d\right)$ {Calculate SIR; Example here assumes point-like transducers}

8:   ${\Sigma }^r+=\mathrm{C}\_{\mathit{\alpha }}_{\mathrm{pth}}\left[n_z\right]({\tilde{h}}^r\mathrm{C}\_{\tilde{\mathbf{p}}}_0\left[\mathrm{threadIdx}.\mathrm{x}\right].r-{\tilde{h}}^i\mathrm{C}\_{\tilde{\mathbf{p}}}_0\left[\mathrm{threadIdx}.\mathrm{x}\right].i)$

9:   ${\Sigma }^i+=\mathrm{C}\_{\mathit{\alpha }}_{\mathrm{pth}}\left[n_z\right]({\tilde{h}}^r\mathrm{C}\_{\tilde{\mathbf{p}}}_0\left[\mathrm{threadIdx}.\mathrm{x}\right].i+{\tilde{h}}^i\mathrm{C}\_{\tilde{\mathbf{p}}}_0\left[\mathrm{threadIdx}.\mathrm{x}\right].r)$

10: endfor

11: $\mathrm{D}\_{\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }\left[\mathrm{blockIdx}.\mathrm{y}\right]\left[\mathrm{blockIdx}.\mathrm{x}\right]\left[\mathrm{threadIdx}.\mathrm{x}\right].r+={\Sigma }^r$

12: $\mathrm{D}\_{\tilde{\mathbf{u}}}_{\mathrm{pth}}^{\prime }\left[\mathrm{blockIdx}.\mathrm{y}\right]\left[\mathrm{blockIdx}.\mathrm{x}\right]\left[\mathrm{threadIdx}.\mathrm{x}\right].i+={\Sigma }^i$

Implementation of the backprojection operator was similar except the dividing and looping were over the vector ${\tilde{\mathbf{u}}}_{\mathrm{sph}}$ instead of α_sph. The pseudocodes for the backprojection operation are provided in Algorithms 10, 11, 12.

Table .

Algorithm X. Implementation of ${\mathit{\alpha }}_{\mathrm{sph}}^{\prime }={\mathbf{H}}_{\mathrm{sph}}^{†}\tilde{\mathbf{u}}$ (on host).

Input:$\tilde{\mathbf{u}}$, ${\tilde{\mathbf{p}}}_0$

Output:${\mathit{\alpha }}_{\mathrm{sph}}^{\prime }$

1: fornpth = 0 toNpth − 1 do

2:   parm_bwdarg[npth].npth = npth

3:   parm_bwdarg[npth].${\tilde{p}}_0$ = &${\tilde{\mathbf{p}}}_0\left[0\right]$

4:   parm_bwdarg[npth].${\tilde{u}}_{\mathrm{pth}}$=&$\tilde{\mathbf{u}}[n_{\mathrm{pth}}{N}_r{N}_v{N}_f/N_{\mathrm{pth}}]$

5:   parm_bwdarg[npth].${\alpha }_{\mathrm{pth}}^{\prime \prime }$=$\&{\mathit{\alpha }}_{\mathrm{sph}}^{\prime \prime }\left[n_{\mathrm{pth}}{N}_x{N}_y{N}_z\right]$

{Pass addresses of arrays to each pthread}

6:   pthread_create(&pthreads[npth], NULL, bwd_pthread,

(void *)(parm_bwdarg+npth)) {Call function bwd_pthread}

7: endfor

8: fornpth = 0 toNpth − 1 do

9:   forn = 0 toNxNyNzdo

10:      ${\mathit{\alpha }}_{\mathrm{sph}}^{\prime }\left[n\right]+={\mathit{\alpha }}_{\mathrm{sph}}^{\prime \prime }[n+n_{\mathrm{pth}}{N}_x{N}_y{N}_z]$

11:   endfor

12: endfor

Table .

Algorithm XI. Implementation of function bwd_pthread (on host).

Input:npth, ${\tilde{\mathbf{p}}}_0$, ${\tilde{\mathbf{u}}}_{\mathrm{pth}}$, ${\mathit{\alpha }}_{\mathrm{pth}}^{\prime \prime }$

Output:${\mathit{\alpha }}_{\mathrm{pth}}^{\prime \prime }$

1: ${\mathrm{C}\_\tilde{\mathbf{p}}}_0\leftarrow {\tilde{\mathbf{p}}}_0$ {Copy from host to constant memory}

2: fornr = 0 toNr/Npth − 1 do

3:   ${\theta }^s=(n_r+n_{\mathrm{pth}}{N}_r/N_{\mathrm{pth}}){\Delta }_{{\theta }^s}+{\theta }_{\min }^s$; zs = Rscos θs; rs = Rssin θs

4:   fornv = 0 toNv − 1 do

5:   ${\varphi }^s=n_v{\Delta }_{{\varphi }^s}+{\varphi }_{\min }^s$; xs = rscos ϕs; ys = rssin ϕs

6:   $\mathrm{C}\_{\tilde{\mathbf{u}}}_{\mathrm{pth}}\leftarrow {\tilde{\mathbf{u}}}_{\mathrm{pth}}\left[n_r\right]\left[n_v\right][:]$ {Copy from host to constant memory}

7:   K_bwdsph  ⟨⟨⟨ (Ny, Nx), (Nz, 1, 1) ⟩⟩⟩ (xs, ys, zs D_${\mathit{\alpha }}_{\mathrm{pth}}^{\prime \prime }$)

8:   endfor

9: endfor

10: ${\mathit{\alpha }}_{\mathrm{pth}}^{\prime \prime }\leftarrow \mathrm{D}\_{\mathit{\alpha }}_{\mathrm{pth}}^{\prime \prime }$ {Copy from global memory to host}

Table .

Algorithm XII. Implementation of Kernel K_bwdsph  ⟨⟨⟨ (N_y, N_x), (N_z, 1, 1) ⟩⟩⟩.

Input:xs, ys, zs, D_${\mathit{\alpha }}_{\mathrm{pth}}^{\prime \prime }$, C_${\tilde{\mathbf{u}}}_{\mathrm{pth}}$, C_${\tilde{\mathbf{p}}}_0$

Output: D_${\mathit{\alpha }}_{\mathrm{pth}}^{\prime \prime }$

1: x = (blockIdx.y)Δs + xmin; y = (blockIdx.x)Δs + ymin; z = (threadIdx.x)Δs + zmin

2: d = ((x − xs)2 + (y − ys)2 + (z − zs)2)1/2; Σ = 0 {Initiate the partial summation}

3: fornf = 0 toNf − 1 do

4:   f = nfΔf + fmin

5:   ${\tilde{h}}^r=\cos (2\pi fd/c_0)/\left(2\pi d\right)$; ${\tilde{h}}^i=-\sin (2\pi fd/c_0)/\left(2\pi d\right)$ {Calculate SIR; Example here assumes point-like transducers}

6:   $\Sigma +=\mathrm{C}\_{\tilde{\mathbf{u}}}_{\mathrm{pth}}\left[n_f\right].r({\tilde{h}}^r\mathrm{C}\_{\tilde{\mathbf{p}}}_0\left[n_f\right].r-{\tilde{h}}^i\mathrm{C}\_{\tilde{\mathbf{p}}}_0\left[n_f\right].i)+\mathrm{C}\_{\tilde{\mathbf{u}}}_{\mathrm{pth}}\left[n_f\right].i({\tilde{h}}^i\mathrm{C}\_{\tilde{\mathbf{p}}}_0\left[n_f\right].r+{\tilde{h}}^r\mathrm{C}\_{\tilde{\mathbf{p}}}_0\left[n_f\right].i)$

7: endfor

8: $\mathrm{D}\_{\mathit{\alpha }}_{\mathrm{pth}}^{\prime \prime }\left[\mathrm{blockIdx}.\mathrm{y}\right]\left[\mathrm{blockIdx}.\mathrm{x}\right]\left[\mathrm{threadIdx}.\mathrm{x}\right]+=\Sigma$

DESCRIPTIONS OF COMPUTER SIMULATION AND EXPERIMENTAL STUDIES

The computational efficiency and accuracy of the proposed GPU-based implementations of the FBP algorithm and projection/backprojection operators for use with iterative image reconstruction algorithms were quantified in computer simulation and experimental OAT imaging studies.

Computer-simulation studies

Numerical phantom

The numerical phantom consisted of nine uniform spheres that were blurred by a 3D Gaussian kernel possessing a full width at half maximum (FWHM) of 0.77 mm. The phantom was contained within a cuboid of size 29.4 × 29.4 × 61.6 mm³. A 2D image corresponding to the plane y = 0 through the phantom is shown in Fig. 2a.

Figure 2.

Slices corresponding to the plane y = 0 of (a) the phantom and the images reconstructed by use of (b) the CPU-based and (c) the GPU-based implementations of the FBP algorithm from the “128 × 90”-data.

Simulated projection data

The measurement surface was a sphere of radius R^s = 65 mm corresponding to an existing OAT imaging system.^{22, 48} As described in Sec. 3, ideal point-like transducers were uniformly distributed over 128 rings and 90 tomographic views. The 128 rings covered the full π polar angle, i.e., ${\theta }_{\min }^s=\pi /256$, while the 90 views covered the full 2π azimuth angle. The speed of sound was set at c₀ = 1.54 mm/μs. We selected the Grüneisen coefficient as $\Gamma =\beta c_0^2/C_p=2,000$ of arbitrary units (a.u.). For each transducer, we analytically calculated 1022 temporal samples of the pressure function at the sampling rate of f_sam = 20 MHz by use of Eq. 1. Because we employed a smooth object function, the pressure data were calculated by the following two steps: First, we calculated temporal samples of pressure function p_us(r^s, t) that corresponds to the nine uniform spheres by^{1, 36}

$$p_{\mathrm{us}}({\mathbf{r}}^s,t){|}_{t=k{\Delta }_t}=\sum _{i=0}^8\left\{\begin{array}{cc}\hfill A_i{\left[-\frac{\beta c_0^3}{C_p|{\mathbf{r}}^s-{\mathbf{r}}_i|}t+\frac{\beta c_0^2}{2}\right]}_{t=k{\Delta }_t},& \hfill \mathrm{if}|c_{0}k{\Delta }_t-|{\mathbf{r}}^s-{\mathbf{r}}_i||\le R_i\\ \hfill 0,& \hfill \mathrm{otherwise}\end{array},\right.$$ (28)

where r_i, R_i, and A_i denote the center location, the radius, and the absorbed energy density of the ith sphere, respectively. Subsequently, we convolved p_us(r^s, t) with a 1D Gaussian kernel with FWHM = 0.5 μs (Ref. ⁴⁹) to produce the pressure data. From the simulated pressure data, we calculated the temporal-frequency spectrum by use of FFT, from which we created an alternative data vector that contained 511 frequency components occupying (0, 5] MHz for each transducer. The simulated projection data in either the time domain or the temporal frequency domain will hereafter be referred to as “128 × 90”-data. By undersampling the “128 × 90”-data uniformly over rings and tomographic views, we created three subsets that contained varying number of transducers. These data sets will be referred to as “64 × 90”-data, “64 × 45”-data, and “32 × 45”-data, where the two numbers specify the number of rings and the number of tomographic views, respectively.

Reconstruction algorithms

The GPU accelerated FBP algorithm was employed to reconstruct the object function sampled on a 3D Cartesian grid with spacing Δ_s = 0.14 mm. The dimension of the reconstructed images ${\widehat{\mathit{\alpha }}}_{\mathrm{fbp}}$ was 210 × 210 × 440.

We employed an iterative image reconstruction algorithm that sought to minimize a penalized least-squares (PLS) objective.^{45, 50} Two versions of the reconstruction algorithm were developed that utilized the interpolation-based imaging model and the spherical-voxel-based imaging model, respectively. The two versions sought to solve the optimization problems by use of the linear conjugate gradient (CG) method^{51, 52}

$${\widehat{\mathit{\alpha }}}_{\mathrm{int}}=\arg \underset{{\mathit{\alpha }}_{\mathrm{int}}}{\min }{\Vert \mathbf{u}-{\mathbf{H}}_{\mathrm{int}}{\mathit{\alpha }}_{\mathrm{int}}\Vert }^2+\mu R\left({\mathit{\alpha }}_{\mathrm{int}}\right)$$ (29)

and

$${\widehat{\mathit{\alpha }}}_{\mathrm{sph}}=\arg \underset{{\mathit{\alpha }}_{\mathrm{sph}}}{\min }{\Vert \tilde{\mathbf{u}}-{\mathbf{H}}_{\mathrm{sph}}{\mathit{\alpha }}_{\mathrm{sph}}\Vert }^2+\mu R\left({\mathit{\alpha }}_{\mathrm{sph}}\right),$$ (30)

respectively, where R(α) is a regularizing penalty term whose impact is controlled by the regularization parameter μ. The penalty term was employed only when processing the experimental data as described in Sec. 4B. The reconstruction algorithms required computation of one projection and one backprojection operation at each iteration. Hereafter, the two reconstruction algorithms will be referred to as PLS-Int and PLS-Sph algorithms, respectively. We set Δ_s = 0.14 mm. Therefore, both the dimensions of ${\widehat{\mathit{\alpha }}}_{\mathrm{int}}$ and ${\widehat{\mathit{\alpha }}}_{\mathrm{sph}}$ were 210 × 210 × 440.

Performance assessment

We compared the computational times of 3D image reconstruction corresponding to the GPU- and CPU-based implementations. The CPU-based implementations of the PLS-Int and PLS-Sph algorithms take several days to complete a single iteration even for the “32 × 45”-data. Therefore, we only recorded the computational time for the CPU-based implementations to complete a single iteration when the data vector contained a single transducer. We assumed that the computational times were linearly proportional to the number of transducers in the data sets because the CPU-based implementations are sequential.

The GPU-based implementations employed the single-precision floating-point format rather than the conventional double-precision utilized by CPU-based implementations. In order to quantify how the single-precision floating-point format would degrade the image accuracy, we calculated the root-mean-square-error (RMSE) between the reconstructed image and the phantom defined by

$$\mathrm{RMSE}=\sqrt{\frac{1}{N}{(\widehat{\mathit{\alpha }}-\mathit{\alpha })}^{\mathrm{T}}(\widehat{\mathit{\alpha }}-\mathit{\alpha })},$$ (31)

where α and $\widehat{\mathit{\alpha }}$ are the samples of the phantom and the coefficients of the reconstructed images, respectively.

Hardware specifications

All implementations were tested on the platform consisted of dual quad-core Intel(R) Xeon (R) CPUs with a clock speed 2.40 GHz. The GPU-based implementations of the FBP and the PLS-Int algorithms were tested on a single Tesla C2050 GPU, while the PLS-Sph algorithm was tested on 8 Tesla C1060 GPUs.

Experimental studies

The FBP, PLS-Int, and PLS-Sph algorithms were investigated by use of an existing data set corresponding to a live mouse.^{22, 48} The scanning geometry and dimensions were the same as those employed in the computer-simulation studies except that only 64 rings were uniformly distributed over the polar angle ranging from 14° to 83°. The transducers were of size 2 × 2 mm². The raw data were acquired at 180 tomographic views, which are referred to as “full data.” We undersampled the “full data” uniformly over the tomographic views, constructing a subset containing 45 tomographic views. The subset will be referred to as “quarter data.”

Unlike in the idealized computer-simulation studies, the transducer response has to be compensated for when processing the experimental data. When implementing the FBP algorithm, the EIR was compensated for by a direct Fourier deconvolution, expressed in temporal frequency domain as³

$$\tilde{p}({\mathbf{r}}^s,f)=\frac{\tilde{u}({\mathbf{r}}^s,f)}{{\tilde{h}}^e\left(f\right)}\tilde{W}\left(f\right),$$ (32)

where $\tilde{W}\left(f\right)$ is a window function for noise suppression. In this study, we adopted the Hann window function defined as

$$\tilde{W}\left(f\right)=\frac{1}{2}\left[1-\cos \left(\pi \frac{f_c-f}{f_c}\right)\right],$$ (33)

where the cutoff frequency was chosen as f_c = 5 MHz. When applying iterative image reconstruction algorithms, the transducer effects were implicitly compensated for during iteration by employing imaging models that incorporates the transducer characteristics.^{14, 22} We incorporated the EIR into the interpolation-based imaging model while incorporating both the EIR and the SIR into the spherical-voxel-based imaging model.

For both PLS-Int and PLS-Sph algorithms, we employed a quadratic smoothness penalty to mitigate measurement noise⁵⁰

$$\begin{array}{ccc}\hfill R\left(\mathit{\alpha }\right)& =& \sum _{n=0}^{N-1}{({\left[\mathit{\alpha }\right]}_n-{\left[\mathit{\alpha }\right]}_{n_x})}^2+{({\left[\mathit{\alpha }\right]}_n-{\left[\mathit{\alpha }\right]}_{n_y})}^2\hfill \\ & & +{({\left[\mathit{\alpha }\right]}_n-{\left[\mathit{\alpha }\right]}_{n_z})}^2,\hfill \end{array}$$ (34)

where n_x, n_y, and n_z were the indices of the neighboring voxels before the nth voxel along the three Cartesian axes, respectively.

RESULTS

Computational efficiency

As shown in Table 1, the GPU-based implementations took less than 0.1%, 0.8%, and 0.4% of the computational times required by corresponding CPU-based implementations for the FBP, the PLS-Int, and the PLS-Sph algorithms, respectively. The relative computational times for the GPU-based implementations are nearly linearly proportional to the amount of data. Note that the “64 × 90”-data and the “quarter data” are of the same size. However, the computational times of the “quarter data” are more than 1.8 times those of the “64 × 90”-data. This is because the calculation of the SIR increases the computational complexity of the reconstruction algorithm.

Table 1.

Computational times of the 3D image reconstructions by use of the CPU- and GPU-based implementations.

Data sets	FBP [s]		PLS-Int [min/iteration]		PLS-Sph [min/iteration]
	CPU	GPU	CPU	GPU	CPU	GPU
“32 × 45”	6189	6	2448	20	7961	22
“64 × 45”	12 975	12	4896	35	15 923	43
“64 × 90”	26 190	23	9792	68	31 845	86
“128 × 90”	53 441	46	…	…	…	…
“Quarter data”	12 975	12	4896	35	19 776	78
“Full data”	53 441	46	19 968	137	79 177	313

Computational accuracy

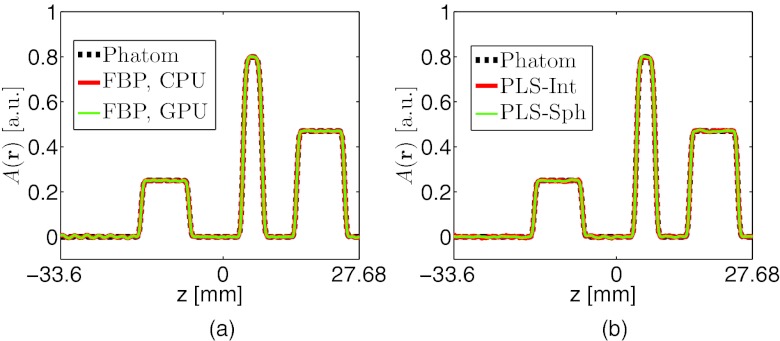
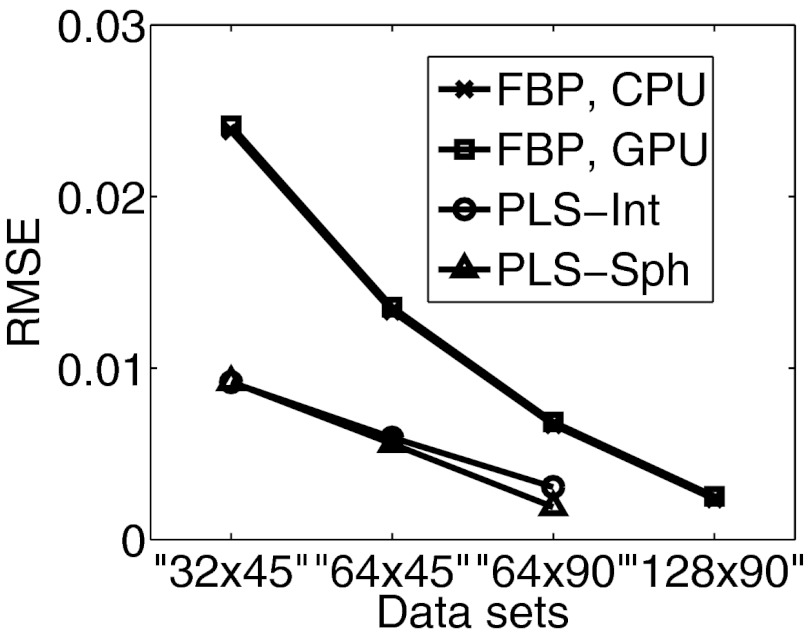
Images reconstructed by use of the CPU- and GPU-based implementations of the FBP algorithm are almost identical. From the “128 × 90”-data, in which case, transducers were densely distributed over the measurement surface, both implementations reconstructed accurate images, as shown in Figs. 2b, 2c. The profiles along the three arrows in Fig. 2 are plotted in Fig. 5a, suggesting a nearly exact reconstruction. As expected, when the amount of measurement data are reduced, the reconstructed images contain more artifacts as shown in Fig. 3. However, the images reconstructed by use of GPU- and CPU-based implementations remain indistinguishable. The plots of the RMSE versus the amount of measurement data employed in Fig. 6 overlap, also suggesting the single-precision floating-point format employed by the GPU-based implementation has little impact on the computational accuracy.

Figure 5.

Profiles along the line (x, y) = (−6.58, 0) mm of the images reconstructed by use of (a) the CPU- and GPU-based implementations of the FBP algorithm from the “128 × 90”-data, and (b) the GPU-based implementations of the PLS-Int and the PLS-Sph algorithms from the “64 × 90”-data.

Figure 3.

Slices corresponding to the plane y = 0 of the images reconstructed by use of the FBP algorithm with (a) the CPU-based implementation from the “64 × 90”-data, (b) the CPU-based implementation from the “64 × 45”-data, (c) the CPU-based implementation from the “32 × 45”-data, (d) the GPU-based implementation from the “64 × 90”-data, (e) the GPU-based implementation from the “64 × 45”-data, and (f) the GPU-based implementation from the “32 × 45”-data.

Figure 6.

Plots of the RMSE against the amount of data by use of the FBP, the PLS-Int and the PLS-Sph algorithms.

The GPU-based implementations of the PLS-Int and PLS-Sph algorithms both reconstructed accurate images as displayed in Fig. 4. As expected, the images reconstructed by use of both iterative algorithms contain fewer artifacts than those reconstructed by use of the FBP algorithm from the same amount of data. Unlike the images reconstructed by use of the FBP algorithm from the “64 × 90”-data [Figs. 3a or 3d], the images reconstructed by use of both iterative algorithms [Figs. 4a, 4d] appear to be identical to the numerical phantom. The profiles along the two arrows in Figs. 4a, 4d are plotted in Fig. 5b, further confirming the computational accuracy of iterative image reconstruction algorithms. The plots of the RMSE versus the amount of measurement data employed in Fig. 6 suggest the iterative image reconstruction algorithms in general outperform the FBP algorithm from the same amount of data.

Figure 4.

Slices corresponding to the plane y = 0 of the images reconstructed by use of the GPU-based implementations of (a) the PLS-Int algorithm from the “64 × 90”-data, (b) the PLS-Int algorithm from the “64 × 45”-data, (c) the PLS-Int algorithm from the “32 × 45”-data, (d) the PLS-Sph algorithm from the “64 × 90”-data, (e) the PLS-Sph algorithm from the “64 × 45”-data, and (f) the PLS-Sph algorithm from the “32 × 45”-data.

Experimental results

The maximum intensity projection (MIP) of the 3D mouse images reconstructed by use of the GPU-based implementations reveal the mouse body vasculature as shown in Fig. 7. Images reconstructed by use of both the PLS-Int and the PLS-Sph algorithms appear to have cleaner background than the images reconstructed by use of the FBP algorithm from the same amount of data. All images reconstructed by iterative algorithms were obtained by 20-iterations starting with uniform zeros as the initial guess. The PLS-Int algorithm took approximately a half day and 2 days to process the “quarter data” and the “full data,” respectively. The PLS-Sph algorithm took approximately 1 day and 4 days to process the “quarter data” and the “full data,” respectively. Alternatively, if the CPU-based implementations were utilized, the PLS-Int algorithm would take an estimated 68 days and 277 days to process the “quarter data” and the “full data,” respectively. The PLS-Sph algorithm would take an estimated 275 days and 1100 days to process the “quarter data” and the “full data,” respectively.

Figure 7.

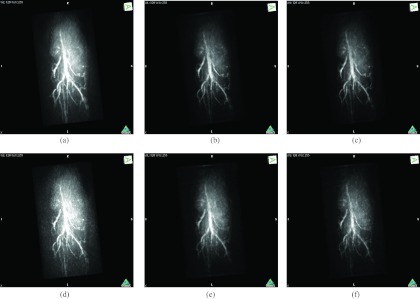
MIP renderings of the 3D images of the mouse body reconstructed by use of the GPU-based implementations of (a) the FBP algorithm from the “full data,” (b) the PLS-Int algorithm from the “full data” with μ = 1.0 × 10⁴, (c) the PLS-Sph algorithm from the “full data” with μ = 1.0 × 10⁴, (d) the FBP algorithm from the “quarter data,” (e) the PLS-Int algorithm from the “quarter data” with μ = 1.0 × 10³, and (f) the PLS-Sph algorithm from the “quarter data” with μ = 1.0 × 10³. The grayscale window is [0,12.0].

DISCUSSION AND CONCLUSION

In this study, we developed and investigated GPU-based implementations of the FBP algorithm and two pairs of projection/backprojection operators for 3D OAT. Our implementation of the FBP algorithm improved the computational efficiency over 1000 times compared to the CPU-based implementation. This work complements our earlier studies that demonstrated the feasibility of 3D iterative image reconstruction in practice.^{21, 22}

Our current implementations of the iterative image reconstruction algorithms still require several days to process the densely sampled data set, which, however, can be further improved. First, the amount of measurement data required for accurate image reconstruction can be further reduced by developing advanced image reconstruction methods.^{13, 15, 22, 53} Second, the number of iterations required can be reduced by developing fast-converging optimization algorithms.^{22, 54, 55}

The proposed parallelization strategies by use of GPUs are of general interest. The implementation of the FBP algorithm⁶ can be adapted to other analytic image reconstruction algorithms, including those described in Refs. ^{5, 7, 56, 57, 58}. We demonstrated the feasibility of PLS algorithm that utilized the proposed GPU-based implementations of the projection/backprojection operators. By use of these implementations, many advanced image reconstruction algorithms may also be feasible in practice.²² Though we described our parallelization strategies for the projection/backprojection operators that utilized two discrete-to-discrete imaging models, these strategies can also be applied to other D-D imaging models.^{9, 11, 20, 59} Therefore, the proposed algorithms will facilitate the further investigation and application of advanced image reconstruction algorithms in 3D OAT.

APPENDIX: DISCRETIZATION OF SRT

Derivation of Eq. 12

The integrated data function g(r^s, t) in Eq. 2, evaluated at the qth transducer and the kth time instance, can be expressed as

$$g\left({\mathbf{r}}_q^s,t\right){|}_{t=k{\Delta }_t}={\int }_{|{\mathbf{r}}_q^s-\mathbf{r}|=k{c}_0{\Delta }_t}d\mathbf{r}A\left(\mathbf{r}\right),$$ (A1)

where ${\mathbf{r}}_q^s$ denotes the location of the qth point-like transducer. We defined a local coordinate system, distinguished by a superscript “tr,” centered at the qth transducer with the z^tr-axis pointing to the origin of the global coordinate system as shown in Fig. 1b. Assuming the object function A(r) is compactly supported in a sphere of radius R, the integral surface is symmetric about the z^tr-axis. Thus, the orientations of the x^tr- and y^tr-axes can be arbitrary within the z^tr = 0 plane. Representing the right-hand side of Eq. A1 in the local spherical coordinate system, one obtains

$$\begin{array}{ccc}\hfill g\left({\mathbf{r}}_q^s,t\right){|}_{t=k{\Delta }_t}& =& {\left(k{c}_0{\Delta }_t\right)}^2{\int }_0^{{\theta }_{\max }^{\mathrm{tr}}}d{\theta }^{\mathrm{tr}}\sin {\theta }^{\mathrm{tr}}\hfill \\ & & \times {\int }_0^{2\pi }d{\varphi }^{\mathrm{tr}}A(k{c}_0{\Delta }_t,{\theta }^{\mathrm{tr}},{\varphi }^{\mathrm{tr}}),\hfill \end{array}$$ (A2)

where ${\theta }_{\max }^{\mathrm{tr}}$ is half of the apex angle of the cone that corresponds to the intersectional spherical cap as shown in Fig. 1b. The polar angle θ^tr and the azimuth angle ϕ^tr were discretized with intervals ${\Delta }_{{\theta }^{\mathrm{tr}}}$ and ${\Delta }_{{\varphi }^{\mathrm{tr}}}$ that satisfied

$$k{c}_0{\Delta }_t{\Delta }_{{\theta }^{\mathrm{tr}}}=k{c}_0{\Delta }_t\sin {\theta }^{\mathrm{tr}}{\Delta }_{{\varphi }^{\mathrm{tr}}}={\Delta }_s.$$ (A3)

Therefore, Eq. A2 can be approximated by

$$g\left({\mathbf{r}}_q^s,t\right){|}_{t=k{\Delta }_t}\approx {\Delta }_s^2\sum _{i=0}^{N_i-1}\sum _{j=0}^{N_j-1}A\left(k{c}_0{\Delta }_t,{\theta }_i^{\mathrm{tr}},{\varphi }_j^{\mathrm{tr}}\right),$$ (A4)

where $N_i=\lfloor {\theta }_{\max }^{\mathrm{tr}}/{\Delta }_{{\theta }^{\mathrm{tr}}}\rfloor$, $N_j=\lfloor 2\pi /{\Delta }_{{\varphi }^{\mathrm{tr}}}\rfloor$, ${\theta }_i^{\mathrm{tr}}=i{\Delta }_{{\theta }^{\mathrm{tr}}}$, and ${\varphi }_j^{\mathrm{tr}}=j{\Delta }_{{\varphi }^{\mathrm{tr}}}$. We denoted by r_{k, i, j} the location in the global coordinate system corresponding to the location vector $(k{c}_0{\Delta }_t,{\theta }_i^{\mathrm{tr}},{\varphi }_j^{\mathrm{tr}})$ in the local coordinate system in Eq. A4. On substitution from the finite-dimensional representation Eq. 6 into Eq. A4 with α and ψ_n(r) defined by Eqs. 9, 10, respectively, we obtained

$$\begin{array}{ccc}\hfill g\left({\mathbf{r}}_q^s,t\right){|}_{t=k{\Delta }_t}& \approx & {\Delta }_s^2\sum _{n=0}^{N-1}{\left[{\mathit{\alpha }}_{\mathrm{int}}\right]}_n\sum _{i=0}^{N_i-1}\sum _{j=0}^{N_j-1}{\psi }_n^{\mathrm{int}}\left({\mathbf{r}}_{k,i,j}\right)\hfill \\ & \equiv & {\left[\mathbf{g}\right]}_{qK+k}.\hfill \end{array}$$ (A5)