AN APPROACH FOR CALCULATING A CONFIDENCE INTERVAL FROM A SINGLE AQUATIC SAMPLE FOR MONITORING HYDROPHOBIC ORGANIC CONTAMINANTS

Abstract

The use of passive sampling devices (PSDs) for monitoring hydrophobic organic contaminants in aquatic environments can entail logistical constraints that often limit a comprehensive statistical sampling plan, thus resulting in a restricted number of samples. The present study demonstrates an approach for using the results of a pilot study designed to estimate sampling variability, which in turn can be used as variance estimates for confidence intervals for future n = 1 PSD samples of the same aquatic system. Sets of three to five PSDs were deployed in the Portland Harbor Superfund site for three sampling periods over the course of two years. The PSD filters were extracted and, as a composite sample, analyzed for 33 polycyclic aromatic hydrocarbon compounds. The between-sample and within-sample variances were calculated to characterize sources of variability in the environment and sampling methodology. A method for calculating a statistically reliable and defensible confidence interval for the mean of a single aquatic passive sampler observation (i.e., n = 1) using an estimate of sample variance derived from a pilot study is presented. Coverage probabilities are explored over a range of variance values using a Monte Carlo simulation.

INTRODUCTION

Passive sampling devices (PSDs) have been widely used for environmental monitoring since their invention more than 30 years ago [1]. They sequester and accumulate freely dissolved contaminants from the environment, providing a time-weighted average of their concentration. The semipermeable membrane device is one of the most commonly employed PSDs for monitoring hydrophobic organic contaminants in aquatic environments [2]. More recently, variations of semipermeable membrane devices that do not contain triolein, sometimes called lipid-free tubing (LFT), have been verified and applied [3–6]. Standardized field-deployment hardware was designed and patented by Environmental Sampling Technologies. Although other configurations exist, the most widely utilized hardware consists of a stainless steel cage that holds five sampler carriers. These cages are placed in the water column or other environmental media.

A reoccurring issue with the application of semipermeable membrane devices and LFT passive sampling is a small sample size due to a limited ability to achieve extensive, true sampling replication in the field. Though some researchers have addressed the issue of reduced sample size by extracting and chemically analyzing each of the five sampling membranes from a cage individually [2], it is more common for the five samplers to be chemically analyzed as a composite. The practice of a composite analysis not only significantly improves the analytical detection limits [2,6,7] but also acknowledges that the cage, and not the individual sampling membrane, is the sampling unit. However, a number of factors limit the ability of researchers to obtain replicate samples, including practical considerations such as the cost of equipment, the weight of the gear, and the space required for an adequate rigging system.

In the collection of aquatic contaminants using PSDs, the greatest amount of variation, more so than analytical measurement, will likely be due to sampling (deployment and collection), sample preparation (extraction and concentration), and the environment (location of site, season, and year) [8]. Specifically, extracting multiple sampling membranes that were deployed together in a single cage and analyzing them individually in order to achieve a higher sample size and measure of variability compromises chemical detection limits and can be accurately characterized as pseudoreplication, wherein the analytical variance from multiple filters or multiple aliquots from a single sampling device is used as the measure of the sampling error. Analytical variance (i.e., the variability due to multiple chemical analyses of the membranes from the same cage or multiple aliquots) will always underestimate the variance due to sampling.

To the authors’ knowledge, a review of replication issues in passive sampling has not been published; however, a number of studies show apparently limited replication [2,5–7,9,10], which the authors have had to address in other elements of their study design or analysis. In some cases, small sample sizes necessitate grouping samples into more broadly defined populations for the purposes of statistical analysis. For example, all samples obtained from sites within a Superfund area can be grouped and compared with all sites located outside of the area when site-specific comparisons are complicated by small sample sizes [6]. However, broadly grouping samples can obscure important, unique characteristics present at specific sites in highly heterogeneous areas, such as the Portland Harbor Superfund site.

We therefore present a method for calculating a statistically reliable and defensible confidence interval (CI) for the mean using a single aquatic PSD observation (i.e., n = 1) and an estimated pooled variance from a feasible pilot study of restricted spatial and temporal scope. We explored the reproducibility of measurements within and between PSDs using readily available statistical methodology. We performed a Monte Carlo simulation to assess the performance of the CI. Lastly, we present the results of one “single sampler study” as an application of our approach.

MATERIALS AND METHODS

Sample collection

All samples were obtained using PSDs, which were deployed on the lower Willamette River in Portland, Oregon, USA. The Willamette River flows north through part of Oregon’s central valley to its confluence with the Columbia River. The lower Willamette River has been the site of heavy industrial use. In 2000, a section of the river, between river miles 3.5 and 9.2, was designated as a Superfund Megasite due to contamination with metals, polycyclic aromatic hydrocarbons (PAHs), polychlorinated biphenyls, dioxins, and organochlorine pesticides [11]. For over a decade, PSDs have been employed to monitor organic contaminants in the Willamette River.

All lipid-free tubing PSDs used in the present study were constructed from polyethylene tubing using methods detailed elsewhere [6]. Briefly, additive-free, 2.7-cm-wide, low-density polyethylene membrane from Brentwood Plastic was cleaned with hexanes, cut into 100-cm strips, fortified with deuterated fluorene-D10 p,p′-DDE-D8and benzo[b]fluoranthene-D10 as PRCs, and heat-sealed at both ends. Five 1-m PSDs were deployed in each stainless steel deployment cage. The PSDs used in 2009 and 2010 were constructed from the same raw material and met identical quality and analytical background standards.

Chemicals

Thirty-three PAH analytes were included in analyses: naphthalene, 1-methylnaphthalene, 2-methylnaphthalene, 1,2-dimethylnaphthalene, 1,6-dimethylnaphthalene, acenaphthylene, acenaphthene, fluorene, dibenzothiophene, phenanthrene, 1-methylphenanthrene, 2-methylphenanthrene, 3,6-dimethylphenanthrene, anthracene, 2-methylanthracene, 9-methylanthracene, 2,3-dimethylanthracene, 9,10-dimethylanthracene, fluoranthene, pyrene, 1-methylpyrene, retene, benz[a]anthracene, chrysene, 6-methylchrysene, benzo[b]fluoranthene, benzo[k]fluoranthene, benzo[e]pyrene, benzo[a]pyrene, indeno[1,2,3-c,d]pyrene, dibenz[a,h]anthracene, benzo[g,h,i]perylene, and dibenzo[a,l]pyrene. Deuterated PAHs, naphthalene-D8, acenaphthylene-D8, phenanthrene-D10, fluoranthene-D10, pyrene-D10, benzo[a]pyrene-D12, and benzo[g,h,i]perylene-D12 were used as surrogate recovery standards; and perylene-D12 was the internal standard. Solvents used for precleaning, cleanup, and extraction were Optima grade or better (Fisher Scientific).

Sample preparation and analysis

Following the deployment period, PSDs were retrieved from the field, transported to the laboratory, and cleaned with hydrochloric acid and isopropanol to remove superficial fouling and water. Samplers were extracted by dialysis in n-hexane, 40 ml per PSD for 4 h; the dialysate was decanted, then dialysis was repeated for 2 h and the dialysates were combined. All samples were quantitatively concentrated to a final volume of 1 ml.

Extracts from PSDs were analyzed using the Agilent 5975B gas chromatograph-mass spectrometer, with a DB-5MS column (30 m × 0.25 mm × 0.25 um) in electron impact mode (70 eV) using selective ion monitoring. The gas chromatograph parameters were injection port–maintained at 300°C, 1.0 ml min⁻¹ helium flow, 70°C initial temperature, 1-min hold, 10°C min⁻¹ ramp to 300°C, 4-min hold, 10°C min⁻¹ ramp to 310°C, 4-min hold. The mass spectrometer temperatures were 150, 230, and 280°C for the quadrupole, source, and transfer line, respectively. Sample concentrations were determined by the relative response of the deuterated internal standard to the target analyte in a nine-point calibration curve with a correlation coefficient greater than 0.98.

Surrogate standards were added to each PSD sample prior to dialysis and quantified during instrumental analysis. This allows for accurate determination of analyte losses during sample preparation and concentration. Mean surrogate standard recoveries varied between 46 and 108% for naphthalene-D8 and benzo[g,h,i]perylene-D12, respectively. Lower and more variable recoveries were observed for relatively volatile two- to three-ring PAHs, due to losses during sample preparation. Target analytes were recovery-corrected based on the measured recovery of the surrogate with the most similar structure according to ring number.

Quality control accounted for over 30% of the samples and included laboratory preparation blanks, field and trip blanks for each deployment/retrieval, laboratory cleanup blanks, and reagent blanks. All target compounds were below the detection limit in all blank quality-control samples. Instrument calibration verification standards were analyzed at the beginning and end of every run of no more than 10 samples; acceptable accuracy was ±15%.

RESULTS AND DISCUSSION

The present study was conducted concurrently with ongoing site characterization studies on the lower Willamette River, including Portland Harbor. It was designed specifically to respond to issues of reproducibility and variability associated with sampling with PSDs at the Portland Harbor Superfund site. Future study plans for Portland Harbor contemplated site-specific hypotheses that were not evaluated in prior work, which focused on broader spatial and temporal trends [5,6,12]. The study presented here was proposed to help preemptively define study-design and analysis options for future work as well as examine options for incorporating data from earlier studies with limited replication into current and future site assessments (such as evaluating the success of remediation).

A CI for a single observation and an estimated variance from pilot data are presented as a solution to the problem when only one aquatic sample is obtained at each deployment site and time in a future study. The reproducibility of measurements observed in the pilot study is discussed. In circumstances where a chemical was identified in some samples but not others, the missing data were coded as “NaN”; that is, nondetects were not substituted with a constant such as one-half detection limit. Statistical algorithms were implemented in MATLAB R2011a (version 7.12.0.635; Mathworks).

Reproducibility of measurements

Recall that in the collection of aquatic contaminants using PSDs, analytical measurement often results in far less variability than that observed due to sampling (deployment and collection), sample preparation (extraction and concentration), and the environment at large [8]. As such, a feasible pilot study of restricted spatial and temporal scope was conducted in which samplers were deployed for 30-d periods in summer and fall of 2009 and 2010 (Supplemental Data, Table S1). Two sampling events that involved multiple cages deployed at the same site were carried out in 2009. During both of these events, five cages were deployed at the same location on the Willamette River within the Portland Harbor Superfund site. The five cages were attached to separate flotation systems at the same depth in the water column with no more than 30 m separating the most distant cages and no less than 5 m between each cage. Two of the cages from the first deployment were not used for chemical analysis due to losses in the field. Each cage contained five LFT samplers that were extracted and analyzed as a single composite sample. In 2010, three sampling cages were deployed during three different time periods at two different locations within the Superfund site. Each of these cages contained five LFT samplers, which were extracted and analyzed independently.

Although 33 PAH analytes were included in the chemical analyses, only 26 resulted in quantifiable amounts in 2009 and 2010 (Supplemental Data, Table S2). In order to assess within-and between-sampling device reproducibility, the 26 chemicals with a complete variance profile were used. The data were transformed to the log₁₀ scale to stabilize the variance across the dynamic range of the observed PAH values.

We first explored the homogeneity of variance within and between sampling cages. Levene’s test, which is robust against nonnormality, was employed to determine if there was statistical evidence of heterogeneous variance [13]. In contrast, other widely available tests, such as Bartlett’s test, will fail under nonnormality. The normality assumption is of practical concern since sample sizes are often small. In a comprehensive simulation study, Lim and Loh [14] found that Levene’s test is by far the most robust for assessing variance homogeneity, even for small sample sizes. The 2009 PAH data were used to determine if there was evidence of heterogeneous variance between cages. The 2010 PAH data were used to determine if there was evidence of heterogeneous variance between LFT samplers within a cage. Levene’s test results are summarized in Supplemental Data, Table S2, for within-cage variance and Supplemental Data, Table S3, for between-cage variance. Two PAHs (benzo[a]pyrene and naphthalene) resulted in a significant Levene’s test for within-cage variance (p = 0.048 and 0.014, respectively; Supplemental Data, Table S2), and two PAHs (benzo[g,h,i]perylene and indeno[1,2,3-c,d]pyrene) resulted in a significant Levene’s test for between-cage variance (p = 0.049 and 0.042, respectively; Supplemental Data, Table S3). The number of significant tests was within the range of what we would expect by chance alone. That is, we would expect to see two out of 26 significant results, assuming there is a 5% chance of declaring statistical significance for a single PAH when, in fact, there is no evidence to reject the null hypothesis of equal variances. We therefore conclude there is no strong statistical evidence of unequal variances, within or between cages, across the pool of PAH analytes. Consequently, the same conclusion would have been derived if we had used the Bonferroni and Benjamini-Hochberg false discovery rate adjustments (data not shown). As such, we pooled individual sample variances to obtain pooled estimates of within- and between-sampling cage variances.

The pooled variance, in which the individual sample variances are weighted by their degrees of freedom, is a single estimate which can be used to judge performance between and within sampling devices [15]. That is, we can compare a weighted average of the between-sampling device variance to the weighted average of the within-sampling device variance to determine if the sampling variability due to LFT within a cage is larger than the sampling variability due to cage.

For each sampler deployed in 2010 (m = 3), the variation among the five PSDs within each sampling device was calculated. The pooled within-sampling device variance was calculated as

$$S_{\mathit{Within}(\mathit{pooled})}^2=\frac{{\displaystyle \sum _{j=1}^m}\left(n_j-1\right)S{(W)}_j^2}{{\displaystyle \sum _{j=1}^m}{n}_j-m}\text{for}j=1\dots m$$ (1)

for which S(W)² is the variance between n LFT samplers for sampling cage j.

For each season in 2009 (k = 2), the variation between sampling devices was calculated. Then, combining the two independent estimates of between-sampling device variance, the between-device pooled variance was calculated as

$$S_{\mathit{Between}(\mathit{pooled})}^2=\frac{{\displaystyle \sum _{i=1}^k}\left(n_i-1\right)S{(B)}_i^2}{{\displaystyle \sum _{i=1}^k}{n}_i-k}\text{for}i=1,2$$ (2)

for which S(B)² is the variance between n cages for sampling event i.

The variance results are summarized in Supplemental Data, Tables S2 and S3. Across the 26 PAHs, 19 resulted in a pooled within-sampling cage variance less than the pooled between-sampling cage variance. Conversely, seven PAHs resulted in $S_{\mathit{Between}(\mathit{pooled})}^2<S_{\mathit{Within}(\mathit{pooled})}^2$, which exceeds the number we would expect to see by chance alone if we assume a 5% false-positive error rate. The seven PAHs that showed $S_{\mathit{Between}(\mathit{pooled})}^2<S_{\mathit{Within}(\mathit{pooled})}^2$ are low–molecular weight, two-to three-ring PAHs (three naphthalene compounds, acenaphthene, dibenzothiophene, fluorine, and phenanthrene), which are semivolatile and show significantly more variable recoveries than less volatile, higher–molecular weight PAHs in controlled laboratory studies. The variability in the recovery of these compounds was assessed during the development of the extraction method and is primarily associated with losses during laboratory processing and the solvent concentration phase of the preparation of the samples. Nevertheless, a pooled estimate of variance is a statistically reasonable and reliable method of estimating the population sample variance.

Confidence interval for the mean using a single sample

Our approach to calculating a CI for the log₁₀ mean from a single sample is an extension of that of Rocke and Lorenzato [16], who showed exact and approximate CIs for single analytical measurements. Whereas Rocke and Lorenzato [16] used a two-component multiplicative model to capture analytical measurement error, we suggest a single-component model to capture sampling error. That is, a CI for the log₁₀ mean of a single sample is an approximate 95% CI for μ using a z value of 1.96 [15] and the $S_{\mathit{Between}(\mathit{pooled})}^2$ as an estimate variance. These CIs are robust for comparisons of PAH values across time and sites since the pilot study design included two sites, seasons, and years. Specifically, assuming log₁₀(x) is approximately normally distributed with mean μ and variance σ²—that is, log₁₀(x)~ N(μ,σ²)—the approximate CI is of the form

$$\left(\left({log}_{10}(x)-1.96\sqrt{S_{\mathit{Between}(\mathit{pooled})}^2}\right),\left({log}_{10}(x)+1.96\sqrt{S_{\mathit{Between}(\mathit{pooled})}^2}\right)\right)$$ (3)

Conversely, the approximate CI for the mean is of the form

$$\left({10}^{\left({log}_{10}(x)-1.96\sqrt{S_{\mathit{Between}(\mathit{pooled})}^2}\right)},{10}^{\left({log}_{10}(x)+1.96\sqrt{S_{\mathit{Between}(\mathit{pooled})}^2}\right)}\right)$$ (4)

Although the approximate interval is symmetric on the log₁₀ scale, it will be asymmetric on the original measurement scale.

Simulation study

A simulation study was performed to explore the coverage probabilities of the proposed CI. This small simulation study is included to illustrate the performance of the CI over a range of possible $S_{\mathit{Between}(\mathit{pooled})}^2$ variance estimates. Data sets were generated that correspond to the conditions that are likely to be observed in aquatic samples obtained with PSDs for monitoring hydrophobic organic contaminants. The value of a single observation was held constant, and the variance estimate, $S_{\mathit{Between}(\mathit{pooled})}^2$, was varied from the smallest observed in the pilot study (0.0019) to a maximum of 0.19. Each simulation condition was replicated 10,000 times. The observed coverage probabilities were calculated as the proportion of time the constructed CI contains the parameter (i.e., single observation x). The CI achieved nominal coverage over the varied levels of $S_{\mathit{Between}(\mathit{pooled})}^2$. The coverage probabilities ranged from 95.18% ( $S_{\mathit{Between}(\mathit{pooled})}^2=0.0019$) to 94.65% ( $S_{\mathit{Between}(\mathit{pooled})}^2=0.1900$).

An example of application

A single-sampler study on the lower Willamette River was performed to assess the statistical methodology on real data. A single sampler was deployed at three different sites during one sampling event in fall of 2009 and events in the summer and fall of 2010. Samples were obtained from the same three sites at all three times. The three sampling sites were located on the lower Willamette River: two within and one upstream of the Portland Harbor Superfund site. The two sites within the Superfund were approximately three miles apart, and the third site was approximately six miles upstream from the nearest Superfund sampling location. Data for the 26 analytes, for which variance estimates were available, were transformed so that log₁₀(x) ~ N(μ, σ²).

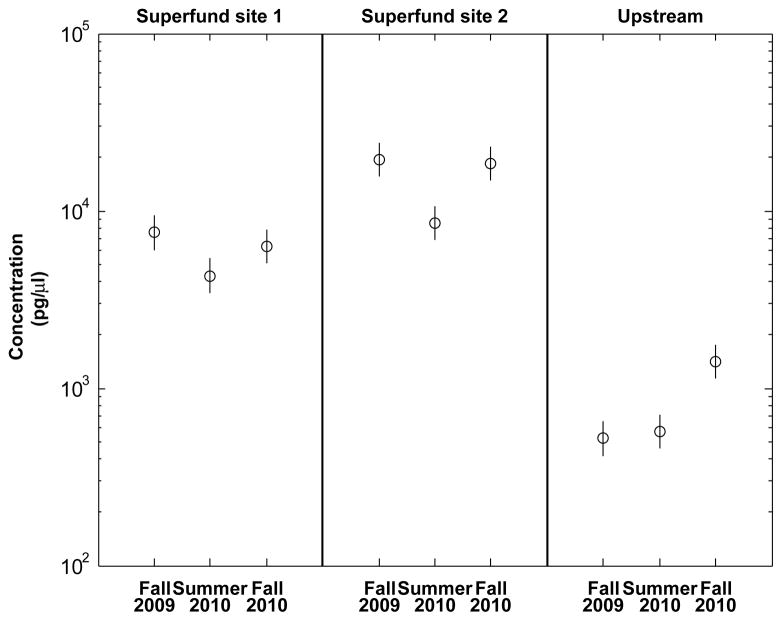
The observed values and 95% CI for the log₁₀ mean using Equation 3 are summarized in Supplemental Data, Table S4. Confidence intervals are inferential error bars and, thus, allow the user to make a judgment as to whether samples are significantly different. Confidence intervals using a variance estimate from a pilot study can be interpreted in a similar fashion as those based on replicate observations from a current sampling event. When comparing across two CIs, statistically significant differences between the two groups cannot be concluded if the mean of one interval is within the CI of the other [17]. For example, consider the single measurements for pyrene. Figure 1 shows the single observation and a 95% CI for the mean concentration (pg/μl) calculated using Equation 4 for each site× time. The observed concentration of pyrene at the sites located within the Superfund area in fall 2009 and fall 2010 are within the other’s CI, while the mean for summer 2010 does not overlap. At the upstream site, the observed concentration of pyrene for fall 2009 and summer 2010 are within the other’s CI and the fall 2010 mean value does not overlap the CI for the other two times. Therefore, it is concluded that the mean concentration of pyrene significantly decreases in the summer in the Superfund areas, although the upstream site showed a significant increase in pyrene concentration in fall 2010.

Fig. 1.

The 95% confidence intervals for pyrene concentration based on single-observation sampling events at the Portland Harbor Superfund during fall 2009 to fall 2010. Confidence interval half-widths were calculated as $1.96\ast \sqrt{S_{\mathit{Between}(\mathit{pooled})}^2}$, where $S_{\mathit{Between}(\mathit{pooled})}^2$ for pyrene is based on the pilot study. The confidence interval for log₁₀(x) was calculated using Equation 3 and backtransformed to the original scale using Equation 4. When comparing across two confidence intervals, statistically significant differences between the two groups cannot be concluded if the mean of one interval is within the confidence interval of the other.

Implications of using variance from a pilot study for future studies

Pilot studies are used across a large array of fields including manufacturing, medical studies, consumer research, questionnaire development, and environmental sampling, all with a common goal to prepare for a larger and more costly study [18–20]. Generally included in the goal of the pilot study is to obtain a variance estimate of the outcome(s) of interest. Often, the estimate of variance is used to refine the necessary sample size in a larger follow-up study. For subsequent studies of the Portland Harbor Superfund, because routine multiple-cage sampling is not financially or logistically feasible, we elected to directly use the estimated variance to calculate a CI rather than perform sample size calculations for future sampling events. Some inherent risks are associated with this method. Of practical importance is that if the variance is underestimated, the subsequent CIs will be very tight about the single observation and a comparison across CIs will likely result in false significant differences; conversely, if the variance is overestimated, the subsequent CI will have a large spread about the single observation and will likely result in a conclusion of no evidence of a statistically significant difference between two deployment sites/times. Nonetheless, we believe our method is an improvement upon approaches that use analytical variance (multiple filters or multiple aliquots) for significance calculations. Analytical variance will always underestimate the amount of true variance in the environmental system being sampled and thereby result in an overestimate of significant differences between sites and times.

CONCLUSIONS

We have shown that a feasible pilot study of restricted spatial and temporal scope can provide a modest estimate of sampling variance within an aquatic system and, subsequently, that a finite 100(1-α)% CI for the mean can be calculated for single-sample studies over time and/or sites. Moreover, the approach we have presented is applicable for any aquatic system for which PSDs are to be deployed. The obvious drawback of the single-observation intervals is that we learn nothing about the variance of the distribution of the current sample. Future efforts should focus on extending the basic one-component variance model to include multiple sources of variation and account for possible heterogeneity between sampling variance, using a more statistically robust sampling design. Nevertheless, the single-sample CI we have presented is useful to the area of environmental assessment, specifically for long-term monitoring of Superfund sites after remediation, when obtaining any number of replicate samples is neither logistically nor financially feasible.